Автоматика и телемеханика, № 8, 2023

Управление в технических системах

В.М. ГЛУМОВ, д-р техн. наук (vglum@ipu.ru),

А.С. ЕРМИЛОВ канд. техн. наук (44eas@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

УПРАВЛЕНИЕ УГЛОВЫМ ДВИЖЕНИЕМ БОЛЬШОЙ

КОСМИЧЕСКОЙ КОНСТРУКЦИИ С УПРУГИМИ ЭЛЕМЕНТАМИ¹

Решается задача угловой ориентации и стабилизации космической кон-

струкции при ее сборке на орбите. Рассматривается вариант конструкции,

в состав которой входят упругие элементы, устанавливаемые в процессе

сборки. Упругие элементы конструкции не имеют датчиков для получе-

ния информации о параметрах их деформаций. Предлагаются алгоритмы

управления, обеспечивающие устойчивость углового движения конструк-

ции. Для получения необходимой информации используется нелинейный

расширенный фильтр Калмана. Разработан алгоритм совместного оце-

нивания координат углового движения рассматриваемой механической

системы и координат тонов упругих колебаний, а также алгоритм иден-

тификации их ненаблюдаемых параметров. Приведены результаты ма-

тематического моделирования варианта механической системы космиче-

ской конструкции, которые подтверждают работоспособность и эффек-

тивность разработанных алгоритмов оценки координат и параметров.

Ключевые слова: математическая модель, алгоритм управления, космиче-

ская конструкция, гироскопический привод, демпфирование колебаний,

оценивание координат.

DOI: 10.31857/S0005231023080081, EDN: HCPDXK

1. Введение

Современные космические аппараты (КА) представляют собой динамиче-

ские объекты управления, механические структуры которых содержат упру-

гие элементы. В [1] отмечается, что по мере увеличения размеров и услож-

нения механической структуры таких аппаратов растет влияние упругих

свойств конструкции на динамику режима ориентации. Кроме того, суще-

ствует тенденция к усложнению самой конструкции современных КА, напри-

мер использование протяженных упругих элементов. Возмущение в динами-

ку КА привносит и трансформация элементов изменяемость конструкции в

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (грант № 20-08-00073).

122

процессе эксплуатации КА [2]. С развитием космических технологий появи-

лись крупногабаритные космические конструкции, получившие наименова-

ние «большие космические конструкции» (БКК), которые могут создаваться

в космосе различными способами. БКК — многомерная многочастотная ме-

ханическая система с изменяющимися параметрами [3, 4].Одними из первых

БКК рассматривались крупногабаритные зонтичные рефлекторы, создание

конструкций которых предполагалось с помощью сборки в космосе [5]. Раз-

витие космической робототехники позволяет решать задачи сборки БКК с

использованием различных роботизированных устройств [6]. В [7] отмеча-

ется, что развитие космической робототехники характеризуется наличием

двух тенденций. С одной стороны, предполагается совершенствование эле-

ментов перспективной космической инфраструктуры типа крупногабаритных

многомодульных КК, например орбитальных станций, у которых неотъемле-

мой составляющей являются средства робототехники. С другой стороны, все

больше обращается внимание на робототехническое сервисное обслуживание,

трактуемое в широком смысле и подразумевающее также роботизированные

монтажные операции применительно к весьма широкому классу объектов [8].

Из робототехнических средств предполагается активное использование кос-

мических манипуляционных роботов [9], в том числе свободно летающих ро-

ботов [10].

В настоящей работе рассматривается собираемая в космосе БКК зонтич-

ного типа, которая представляет собой динамический объект управления с

переменными параметрами, с большим и дискретно изменяющимся во вре-

мени числом степеней свободы. Как механическая система, такая БКК может

рассматриваться в виде последовательности формируемых в процессе сбор-

ки промежуточных механических структур. Конструкция содержит упругие

элементы, устанавливаемые в процессе сборки с помощью космического ма-

нипулятора или свободно летающего космического манипуляционного робота.

Рассматривается вариант БКК, у которой упругие элементы не имеют датчи-

ков информации о координатах и параметрах колебаний. Одними из основ-

ных задач управления БКК являются управление ориентацией и стабилиза-

ция осей корпуса конструкции. Решение этой задачи традиционно получается

на основе релейных или дискретных алгоритмов [11]. Разрывный характер

управляющих воздействий на корпус и ударные воздействия при установке

новых элементов конструкции являются причинами возникновения упругих

колебаний БКК. При управлении угловым движением БКК возникает про-

тиворечие между основной целью управления упругим динамическим объ-

ектом как жестким телом и необходимостью демпфирования возникающих

упругих колебаний. Отсутствие сил атмосферного сопротивления приводит

к накоплению энергии упругих колебаний в процессе управления «жестким»

движением БКК. Превышение критической амплитуды упругих колебаний и

близость их частот к частотам управления «жестким» движением приводят

к неустойчивости системы [12]. Отсутствие точного определения переменных

параметров математической модели (ММ) в наземных условиях приводит

123

к необходимости решать задачу устойчивого и точного управления угловым

движением на всех этапах сборки БКК с использованием методов робастного

или адаптивного управления динамическими объектами [13].

В [14] предлагается алгоритм управления ориентацией БКК при наличии

низких частот упругих колебаний, существенно влияющих на качество пе-

реходных процессов вследствие близости собственных частот конструкции к

частоте управления ее «жестким» движением. В [15] решается задача обеспе-

чения робастной устойчивости упругих колебаний КА с нелинейной системой

управления ориентацией, использующей двигатели-маховики. Решение осно-

вано на целенаправленном изменении границ областей устойчивости в про-

странстве параметров объекта и регулятора с целью максимизации числа

робастно устойчивых упругих компонент конструкции КА. Следует отме-

тить, что алгоритмы, обеспечивающие робастное управление, эффективны

для окончательно собранной комической конструкции (КК). Предлагаемый

в [14, 15] подход ограничен необходимостью получения текущей информации

о состоянии системы и параметрах ее ММ. Алгоритмы адаптивного управле-

ния позволяют обеспечить устойчивость и гашение колебаний в достаточно

широком диапазоне значений собственных частот упругих колебаний БКК

при минимальном значении конструкционного демпфирования. В [16] были

определены три типа стратегии адаптивного управления КК на последова-

тельности этапов ее изменения при сборке в космосе. Первый тип: управ-

ление с использованием анализа и прогноза состояния упругих колебаний

БКК. Второй тип: управление с оценкой фазы доминирующей колебатель-

ной составляющей в спектре частот упругих колебаний в момент переклю-

чения управления. Третий тип: управление на основе нечеткой логики [17].

В [18] предлагается алгоритм адаптивного управления с эталонной моделью

угловым движением собираемой БКК. Его функционирование не зависит от

интенсивности и спектрального состава входных воздействий и не требует

оценивания упругих колебаний БКК. Однако алгоритм обеспечивает высо-

кую точность управления при больших энергетических затратах. В настоя-

щее время уделяется внимание реализации первого типа стратегии адаптив-

ного управления БКК, при котором используются методы идентификации и

оценивания состояния механической системы конструкции. В [11] предложе-

но активное демпфирование упругих колебаний конструкции Международ-

ной космической станции двигателями ориентации с использованием алгорит-

мов идентификации. Для получения необходимой информации для управле-

ния угловым движением космической конструкции с упругой механической

системой целесообразно использовать алгоритмы оценивания на основе тео-

рии фильтрации Калмана-Бьюси [19]. В [20] решена задача оценивания коор-

динат упругих колебаний КК с использованием нелинейного расширенного

фильтра Калмана. В настоящей работе (в развитие [20]) разработан алгоритм

совместного оценивания координат углового движения механической систе-

мы и неизмеряемых координат тонов упругих колебаний, а также алгоритм

идентификации их ненаблюдаемых параметров. Решается задача формиро-

124

вания алгоритмов управления угловой стабилизацией КК на этапах сбор-

ки. Предполагается, что на каждом этапе сборки происходит подсоединение

элемента конструкции, вызывающее упругие колебания, которые необходимо

демпфировать в течение заданного промежутка времени с использованием

силовых гироскопических исполнительных органов системы угловой стаби-

лизации БКК.

2. Математическая модель углового движения БКК

Структуру механической системы БКК зонтичного типа будем рассмат-

ривать в виде совокупности твердых тел, одно из которых является несу-

щим. Остальные (носимые) тела являются строительными элементами, при-

соединяемыми в том или ином порядке к несущему телу при использовании

спиральной схемы сборки каркаса «зонтичного» типа. Такая механическая

система содержит нежесткие элементы и характеризуется дискретно изме-

няющимся числом степеней свободы [21]. В точках присоединения элементов

конструкции учитываются вращательная степень свободы в рассматривае-

мой плоскости движения и упругая связь, ограничивающая возможные сме-

щения элементов областью малых отклонений относительно состояния рав-

новесия [22]. При использовании в качестве исполнительного органа соби-

раемой БКК гироскопического силового привода, содержащего три одинако-

вых гиродина (ГД), установленных по схеме трехлучевой звезды, возникают

взаимосвязи каналов гиростабилизации, которые обусловлены инерционны-

ми и гироскопическими влияниями [23]. Упрощенная ММ пространственного

углового движения механической системы рассматриваемого типа БКК, по-

лученная из полной ММ, подробно представлена в [23]. Для решения задачи

аналитического синтеза структуры алгоритмов управления ГД модель дви-

жения БКК с гиросиловым приводом, пренебрегая перекрестными влияния-

ми движений ГД, можно упростить до трех однотипных каналов управления

и гиростабилизации БКК вида

∑

I_x χ +

I_i,x q_i,x - Hβ + aI_β

β_s + F(χ˙) = M_x,

i=1

(1)

a_i,x χ + q_i,x + b_i,x

˙q_i,x + c_i,xq_i,x = 0, i = 1,n_x,

I_β

β+k_dβ˙+Hχ+aI

β_s = M_u(u_x),

где χ = (ψ, ϕ, ϑ)^T — вектор углов ориентации корпуса, β = (β_ψ, β_ϕ, β_ϑ)^T —

вектор углов прецессии рамок ГД, q = (q_k)^T — составной вектор коорди-

нат, характеризующих упругие колебания элементов конструкции по каж-

дому из трех каналов углов ориентации так, что q_k = (q_i,k)^T, i = 1, n_x,

где n_x — число учитываемых в канале χ_k упругих координат, (k = 1, 3);

β_s = [(β_ϕ + β_ϑ),(β_ψ + β_ϑ),(β_ϕ + β_ψ)]^T; a = cos(π/4 = 0,707 (для установки ГД

типа “звезда”), I_β — моменты инерции рамок ГД; H = diag(h₁, h₂, h₃) — диа-

125

гональная матрица кинетических моментов ГД; k_d — коэффициент демпфи-

рования по оси подвеса ГД; a_i,x, b_i,x, c_i,x — параметры уравнений колебаний

∑

упругих элементов; I_x

I_x +

I_i,x, где

I_x — диагональная матрица осевых

i=1

моментов инерции корпуса

I_i,x — матрица инерционного влияния i-го упру-

гого элемента на динамику конструкции; F (χ˙) — вектор нелинейных функ-

ций, содержащих произведения χ_iχ_j, i, j = 1, 3, i = j; M_x — вектор возму-

щающих моментов внешних сил, действующих на корпус; M_u(u_x) — вектор

управляющих моментов, прикладываемых относительно осей рамок ГД; u_x —

вектор управляющих напряжений, компоненты которого подаются на входы

соответствующих моментных приводов ГД.

В режиме угловой ориентации и стабилизации БКК на этапе сборки зна-

чения скоростей χ˙_k достаточно малые, что позволяет пренебречь в F (χ˙) про-

изведениями χ_iχ_j , i, j = 1, 3, i = j. При аналитическом исследовании гироси-

лового управления с тремя одинаковыми ГД целесообразно пренебречь меж-

канальными перекрестными связями и считать в (1) aI_β

β_s = 0 [22]. Тогда

система (1) имеет вид

∑

I_x χ +

I_i,xq_i,x - Hβ = M_x,

i=1

(2)

a_i,x χ + q_i,x + b_i,x

˙q_i,x + c_i,xq_i,x = 0, i = 1,n_x,

I_β

β+k_dβ˙+Hχ+aI

β_s = M_u(u_x).

ММ (2) является основой для декомпозиции ее на три подсистемы, которые

соответствуют изолированным каналам гиростабилизации [22].

3. Алгоритмы управления угловым движением БКК

Синтез алгоритмов управления динамическими объектами с ММ вида (1)

или (2) традиционно проводится последовательно двумя шагами [22]. На пер-

вом шаге определяются тип и параметры алгоритмов, формирующих величи-

ны компонент вектора u_x(t), до начала сборки без учета упругих колебаний

(q = 0). Такие алгоритмы называются базовыми, при синтезе которых ММ

(2) преобразуется к виду

I_x χ - Hβ = M_x,

(3)

I_β

β+k_dβ˙+Hχ+aI

β_s = M_u(u_x).

На втором шаге синтеза для стабилизации и гашения упругих колебаний

предлагается дополнительно к базовому алгоритму сформировать алгоритм

управления, в котором используется информация об упругих колебаниях эле-

ментов и их параметрах.

126

В качестве базовых алгоритмов управления гиродинами в режиме стаби-

лизации БКК на этапе сборки целесообразно применение ПД-алгоритмов в

каждом k-м канале в виде

u_x,k(t) = p1,kχ_k(t) + p2,kχ˙_k(t), k = 1,3,

где p1,k, p2,k — коэффициенты, которые выбираются с учетом параметров

уравнений (3) и без учета упругости конструкции из условий обеспечения

устойчивости и требуемого качества управления.

Управляющие моменты, прикладываемые относительно осей прецессии

ГД, формируются в виде [22]

(4)

M_u,k(u_x,k) = p0,k(p1,kχ_k(t) + p2,kχ˙_k

(t)), k = 1, 3,

где коэффициенты p0,k определяются конкретными конструкционными ха-

рактеристиками корпуса и устанавливаются в зависимости от моментов инер-

ции I_x на этапе сборки. Следует отметить, что ММ (3) с алгоритмами (4)

описывают линейную динамическую систему с постоянными параметрами

на этапе сборки, для которой из анализа ее характеристических уравнений в

каждом k-м канале определяется условие устойчивости по вектору угловых

скоростей χ˙ в виде [22]

(5)

k_d(h_k + p0,kp2,k) > I_βp0,kp1,k

k = 1,3.

На основе тех же характеристических уравнений решается задача опре-

деления значений коэффициентов p1,k, p2,k алгоритмов (4), которые обеспе-

чивают требуемое время регулирования t_r,k ≈ 3/η^∗k, k = 1, 3 по координатам

вектора χ. Здесь η^∗k — заданные значения степеней устойчивости характери-

стических уравнений [22].

Исследования динамики БКК зонтичного типа показали, что при увели-

чении числа упругих элементов в спектре частот появляются пониженные

частоты упругих колебаний. Следует отметить, что гиросиловая система с

базовым алгоритмом (4) обеспечивает необходимое демпфирование высоко-

частотных упругих колебаний. Однако при этом в указанной низкочастот-

ной области процессы демпфирования упругих колебаний средствами базо-

вого управления (4) при условии (5) оказываются излишне затянутыми [22].

Подобная динамика процессов ориентации и стабилизации углового положе-

ния БКК является неудовлетворительной. Кроме этого, увеличение времени

демпфирования упругих колебаний создает известные трудности при исполь-

зовании свободно летающего космического манипуляционного робота в про-

цессе сборки БКК [24]. Указанные недостатки требуют усложнения исходно-

го базового алгоритма управления (4). Возможный путь коррекции базового

алгоритма состоит в организации подсистемы дополнительной гиросиловой

стабилизации низкочастотных упругих колебаний БКК, использующей оцен-

ки q_i,x,ˆ˙qi,x соответствующих упругих координат. Дополнительная подсистема

127

подключается после окончания маневра переориентации и установки элемен-

та конструкции на этапе сборки. Для ускорения гашения колебаний подси-

стема формирует на входах ГД дополнительные воздействия вида

∑

(6)

M_d,k(u_q,k) =

p1,k,iq_k,i +

p2,k,iqk,i,

k = 1,3,

i=1

где

qk,

q_k

— векторы оценок упругих координат и их производных,

p1,k,i, p2,k,i — постоянные на этапе сборки коэффициенты.

При выборе значений коэффициентов в (6) необходимо учитывать значе-

ния оценок параметров в уравнениях упругих колебаний ММ (2). Оценки зна-

чений парциальных частот ω_i,x =

√c_i,x из низкочастотного спектра упругих

колебаний позволяют выбрать коэффициенты p1,k,i, p2,k,i, которые обеспечи-

вают устойчивость и минимальное время гашения упругой компоненты [22].

При использования оценок χ,ˆχ с учетом (6) управляющие моменты форми-

руются в виде

[

(

)

∑

(7)

M_u,k(u_x,k) = p0,k p1,k

χ_k - I-1

I_i,k q_i,k

i=1(

)]

∑

+p2,k

χ_k - I-1

I_i,k

q_i,k

k = 1,3.

i=1

Коэффициенты усиления в (7) при оценках q_i,k,

˙q_i,k зависят от значе-

ни

I_i,k, которые могут быть меньше значений I_x на порядок и более. Для

ускоренной активной компенсации влияния упругих колебаний на угловую

ориентацию БКК целесообразно в (7) ввести перенастраиваемые коэффици-

енты p1,k,i, p2,k,i. Тогда алгоритмы (7) принимают вид

[ (

)

∑

(8) M_u,k(u_x,k) = p0,k p1,k

χ_k -

p1,k,iq_i,k

i=1

(

)]

∑

+p2,k

χ_k -

p2,k,iqi,k

k = 1,3,

i=1

где p1,k,i ≫ p1,kI-1x

I_i,

p2,k,i ≫ p2,kI-1x

I_i.

Если упругие элементы не имеют датчиков информации, то необходимо

решать задачу получения оценок q и параметров упругих колебаний на каж-

дом этапе сборки БКК после его окончания. Для решения данной задачи

используется модифицированный вариант предложенного в [20] алгоритма

оценивания на основе фильтра Калмана.

128

4. Синтез алгоритма совместного оценивания координат

упругих колебаний и их параметров

Синтез алгоритма совместного оценивания координат углового движения

и координат колебаний (тонов) упругих элементов конструкции проведем на

примере изолированного канала χ₂ = ϕ, который получается из ММ (2) в

виде

∑

I_ϕ

ϕ+

I_iq_i - h₂β˙ = M_ϕ,

i=1

(9)

a_i

ϕ+q_i +bi˙qi + ciqi = 0, i = 1,nx,

I_β

β + k_dβ˙ + h₂ϕ˙ = M_u(u_ϕ),

где M_u(u_ϕ) = p_ϕu_ϕ, p_ϕ = (p1,ϕ, p2,ϕ) — вектор коэффициентов, u_ϕ = (ϕ,ϕ˙)^T.

При синтезе алгоритма оценивания полагаем M_ϕ = 0. Тогда система (9)

преобразуется к виду [20]:

¯ϕ - I-1ϕh₂β˙ = 0,

⎛

⎞

(

)

∑

1-I-1

a_i

I_i

a_j

I_j⎠ (b_i

˙q_i + c_iq_i) +

qi +^⎝1 - Iϕ1

i=1

i=1,j=i

(10)

∑

+a_i

I_j(b_j

˙q_j + c_jq_j) + a_ih₂β˙ = 0,

i=1,j=i

(

)

∑

I_β

β+k_dβ˙+h₂

ϕ-I-1

I_i

q_j

=p_ϕu_ϕ.

i=1

и угол ϕ определяется выражением

∑

(11)

ϕ=

ϕ-I-1ϕ

I_iq_i,

i=1

где

ϕ — угол поворота корпуса, вызванный вращением БКК как жесткого

объекта.

Представление координаты ϕ в виде (11) позволяет применять алгорит-

мы фильтрации для совместного оценивания координат углового движения

рассматриваемой механической системы БКК с ГД, неизмеряемых коорди-

нат q_i тонов упругих колебаний, а также идентификации параметров упру-

гих колебаний в реальном времени. Следует отметить, что в отличие от [20]

система (10) нелинейная, так как содержит неизвестные параметры. Для по-

лучения оценок используется нелинейный расширенный фильтр Калмана.

При синтезе алгоритма оценивания представим уравнения ММ (10) и (11) в

форме Коши

(12)

x(t) = f(x(t)) + du_ϕ

+ Cw(t),

129

где x ∈ R5n+4 — вектор состояния, x = (

ϕ,¯ϕ,β,β,q_i,

˙q_i,a_i,b_i,c_i)^T, i = 1,n,

b ∈ R5n+4 с ненулевым элементом d₄ = 1, f(x) — нелинейная вектор-функ-

ция, определяемая из (10) и (11),

f₁ = x₂, f₂ = I-1ϕh₂x2n+4, f2i+1 = x2i+2, f2n+3 = x2n+4,

[

(

)]

∑

f2n+4 = I-1

d₄u_ϕ - k_dx2n+4 - h₂ x₂ - I-1

I_ix2i+2

i=1

⎡

f2i+2 = (·)-1 ⎣x2n+4+ih₂x2n+4 - (·)_j(x3n+4+ix2i+2 + x4n+4+ix2i+1) -

⎤

∑

-x2n+4+i

I_j(x3n+4+jx2j+2 + x4n+4+jx2j+1)^⎦ ,

j=1,j=i

∑

где (·) = 1 - I-1ϕ

a_i

I_i, (·)_j = 1 - I-1

a_j

I_j, j = 1,n, j = i,

j=1,j=i

i=1

f2n+4+i = f3n+4+i = f4n+4+i = 0; w ∈ R4n+2 — вектор шумов,

C = diag(C0 ···Ci ···) — блочно-диагональная матрица шумов объекта,

содержащая блоки C₀ ∈ R4×2, C_i ∈ R5×4. Элементы матрицы C₀ нулевые,

кроме c₂₁ = c₄₂ = 1, в матрицах C_i также нулевые элементы, кроме c21,i =

=c32,i =c43,i =c64,i =1 .

Предполагается, что в (10) неизвестные параметры упругих колебаний

приняты постоянными на этапе сборки. При необходимости в вектор состоя-

ния χ можно включить любые параметры, что приводит к громоздкости ма-

тематических выражений.

Если на борту БКК измеряются только координаты ϕ и ϕ˙, то уравнение

измерений имеет вид

(13)

z(t) = Gx(t) + v(t),

∑

где вектор измерений z ∈ R² имеет координаты z₁ = x₁ - I-1ϕ

I_ix4+i + v₁,

i=1

∑

z₂ = x₂ - I-1ϕ

I_ix4+n+i + v₂; v — вектор шумов измерителей.

i=1

Структура матрицы измерений G ∈ R2×(5n+4) имеет вид [20]

G = [C₁G2 ···Gi+2],

где C₁, G₂, Gi+2 — присоединенные матрицы, i = 1, n; G₁ — квадратная еди-

ничная матрица, G₂ — квадратная нулевая матрица; матрица Gi+2 ∈ R2×5

состоит из следующих ненулевых элементов: g11,i = g22,i = -I-1ϕ

I_ϕ.

Предполагается, что начальные значения x(t₀), w, v независимы между со-

бой, w и v — гауссовские белые шумы с нулевыми математическими ожида-

ниями и корреляционными функциями:

M〈w(t)w^T(τ)〉 = Q_w(t)δ(t - τ), M〈v(t)v^T(τ)〉 = Q_v(t)δ(t - τ).

130

Здесь δ — дельта-функция Дирака, диагональные матрицы интенсивности

шумов Q_w(t) и Q_v(t) непрерывны и положительно определены для t ≥ t₀. То-

гда задача синтеза алгоритма оценивания координат x(t) по измерениям z(t)

сводится к частному случаю непрерывного нелинейного расширенного филь-

тра Калмана [20] с постоянными матрицами C и G:

^x(t) = f(x) + du(t) + P (t)G^TQ-1v[z(t) - Gx(t)],

(14)

(t) = D(x)P (t) + P (t)D-1(x) - P (t)G^TQ-1vGP (t) + CQ_w(t)C^T,

где x(t) — вектор оценок координат вектора x(t), P (t) — ковариационная

матрица, D(x) = ∂f(x)/∂x — матрица Якоби.

5. Математическое моделирование

Исследование возможностей алгоритма управления (8) для активной ком-

пенсации упругих колебаний при угловой ориентации БКК по координа-

те ϕ проведено с помощью математического моделирования с использова-

нием в (8) оценок, получаемых на основе алгоритма (14). Предполагалось,

что количество тонов и величины их параметров известны и одинаковы как

в ММ (9), так и в алгоритме оценивания (14), кроме тех параметров, кото-

рые считаются в (14) неизвестными. Для сокращения времени моделирования

в (9) исследовались только два тона, т.е. n = 2, а для формирования момента

управления использовались оценки

ϕ,ϕиqi,˙qi БКК. В качестве неизвестных

были выбраны постоянные параметры c₁ и c₂, а их оценки ĉ₁ и ĉ₂ использо-

валась в (14).

Сигнал управления формируется на основе (8) в виде

∑

(15)

u_φ = p₁

ϕ-

p1,iq1,i + p₂ϕ-

p2,iq2,i,

i=1

где коэффициенты p1,i, p2,i имеют тот же порядок, что и p1 и p2 соответ-

ственно.

При моделировании динамики угловой ориентации с целью получения из-

мерений в качестве ММ использовался вариант системы (9) с алгоритмом (15)

в виде [20]

(16)

y=Ay

du_ϕ,

где y ∈ R⁸ — вектор состояния, y = (ϕ,¯ϕ,β,β,q1,q2,q1,q2)T

d ∈ R⁸ — вектор

с одним ненулевым элементо

d₄ = 1.

На основе (16) формировался вектор измеряемых координат z = (ϕ^∗,ϕ˙^∗)^T

с помощью выражения z =Gy + v, где матрица

G∈ R2×8 имеет ненуле-

вые элементы g1,1 = g2,2 = 1, g1,5 = g2,7 = -I-1ϕ

I₁,

g2,6 = g2,8 = -I-1ϕ

I₂, v =

= (v₁, v₂)^T — вектор шумов измерений.

131

В (14) использовалась ММ (12) с вектором x ∈ R¹⁰, в который включе-

ны идентифицируемые неизвестные параметры c₁ и c₂, x = (ϕ,¯ϕ,β,β,qi,qi,

c₁,c₂)^T, i = 1,2, d ∈ R10 — вектор с одним ненулевым элементом d4 = 1.

C ∈ R10×6 — матрица шумов с ненулевыми элементами c2,1 = c4,2 = c6,3 =

= c8,4 = c9,5 = c10,6 = 1. Модель измерений для алгоритма (14) формируется

в виде z = Gx, где матрица G ∈ R2×10 отличается от матрицы ^G наличием де-

вятого и десятого нулевых столбцов. Матрицы Q_w ∈ R6×6 и Q_v ∈ R2×2 в (14)

приняты постоянными.

Начальные значения при t₀ = 0 координат и параметров, а также векто-

ров y, x и элементов диагональной ковариационной матрицы P (0) приняты

следующими [20]:

y₁(0) = 0,017; y₂(0) = 0,016 c-1; y₃(0) = 0,18 · 10-3;

y₄(0) = 0,7 · 10-4 c-1; y₅(0) = 0,017; y₆(0) = 0,19 · 10-4 c-1;

y₇(0) = 0,37 · 10-2; y₈(0) = 0,13 · 10-4 c-1;

a₁ = 1,2; a₂ = 2,32; b₁ = 0,24 c-1; b₂ = 0,12 c-1;

c₁ = (0,34)² c-2; c₂ = (0,47)² c-2;

I_ϕ = 69200 Нмc²;

I₁ = 1270 Нмc²;

I₂ = 2500 Нмc²;

I_β = 1,1 Нмc²; k_d = 2,5 Нмc; h = 240 Нмc;

p1,1 = 3,9 · 10-6; p2,2 = 3,8 · 10-6 c-2; p3,3 = 0,49 · 10-2;

p4,4 = 6,1 · 10-4 c-2; p5,5 = 4,7 · 10-4; p6,6 = 0,54 · 10-2 c-2;

p7,7 = 0,11 · 10-4; p8,8 = 0,11 · 10-6 c-2;

p9,9 = 1,1 · 10-3 c-4; p10,10 = 1,8 · 10-3 c-4.

Использовались начальные значения оценок:

x₁(0) = ϕ^∗,

x₂(0) =ϕ˙^∗,

x_j(0) = 0 ∀j = 3,8;

если учесть, что параметры c₁ и c₂ могут быть только положительными, то

x₉(0) = 0,002 c-2; x₁₀(0) = 0,005 c-2.

Для моделирования дискретных аналогов непрерывных белых шумов объ-

екта и измерителей принимались следующие среднеквадратические откло-

нения:

σw,1 = 1,5 · 10-5 c-2; σw,2 = 2 · 10-5 c-2; σw,3 = 2,2 · 10-6 c-2;

σw,4 = 1,8 · 10-6 c-2; σw,5 = 4,8 · 10-2 c-1; σw,6 = 3,6 · 10-2 c-1;

σv,1 = 2,6 · 10-4; σv,2 = 1,34 · 10-5 c-1.

Матрицы интенсивности белых шумов Q_w и Q_v приняты диагональными

вследствие отсутствия корреляции между шумами объекта и шумами в кана-

лах измерений. Элементы этих матриц вычисляются с помощью выражений

q_w,kk = 2σ2w,kτ, k = 1,6 и q_w,jj = 2σ2v,jτ, j = 1,2,

132

c¹

1,0

c¹

10¹

0,6

±2

±2₂

0,2

0,6

1,0

t, c

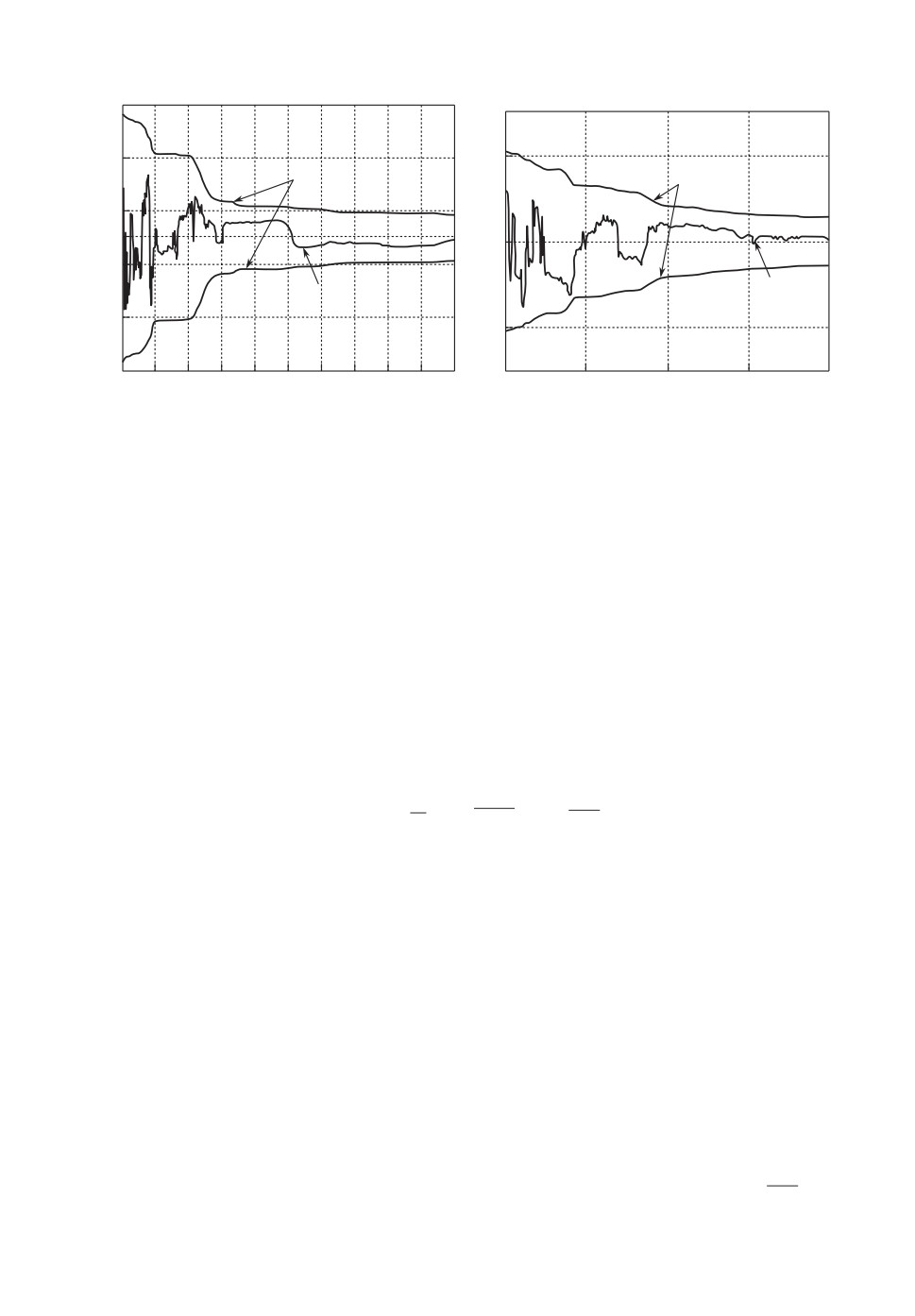
Рис. 1. Ошибки идентификации парциальных частот.

где τ — время корреляции, τ ≤ Δt, Δt — шаг интегрирования. При этом

приняты следующие значения:

qw,11 = 2,3 · 10-12 c-3; qw,22 = 0,49 · 10-14 c-3; qw,33 = 4,8 · 10-14 c-3;

qw,44 = 3,2 · 10-14 c-3; qw,55 = 2,3 · 10-6 c-3; qw,66 = 1,3 · 10-6 c-3;

qv,11 = 4,7 · 10-12 c; qv,22 = 2,9 · 10-13 c-1.

При статистическом моделировании дискретизация уравнений (14) про-

водилась с использованием метода Рунге-Кутты четвертого порядка с Δt,

который выбирался в диапазоне от 0,002 до 0,005 с.

На рис. 1 представлены графики ошибок идентификации неизмеряемых

парциальных частот Δω_i(t) =

√c_i -^√ĉ_i(t), i = 1,2 с удвоенными средне-

квадратическими отклонениями, рассчитанными как соответствующие диа-

гональные элементы матрицы P (t): σw,1 = p-49,9, σw,2 = p-410,10. Из результатов

статистического моделирования следует, что время сходимости оценок пара-

метров c₁ до 2% от максимальной величины начального значения составляет

в среднем от 3 до 6 с. При этом время сходимости оценок координат

до 2% от их максимальных величин составляет в среднем 20-25 с.

С целью проверки возможности применения алгоритма (15) для активной

компенсации влияния колебаний упругих частей БКК на его угловую дина-

мику проведено математическое моделирование в режиме угловой стабилиза-

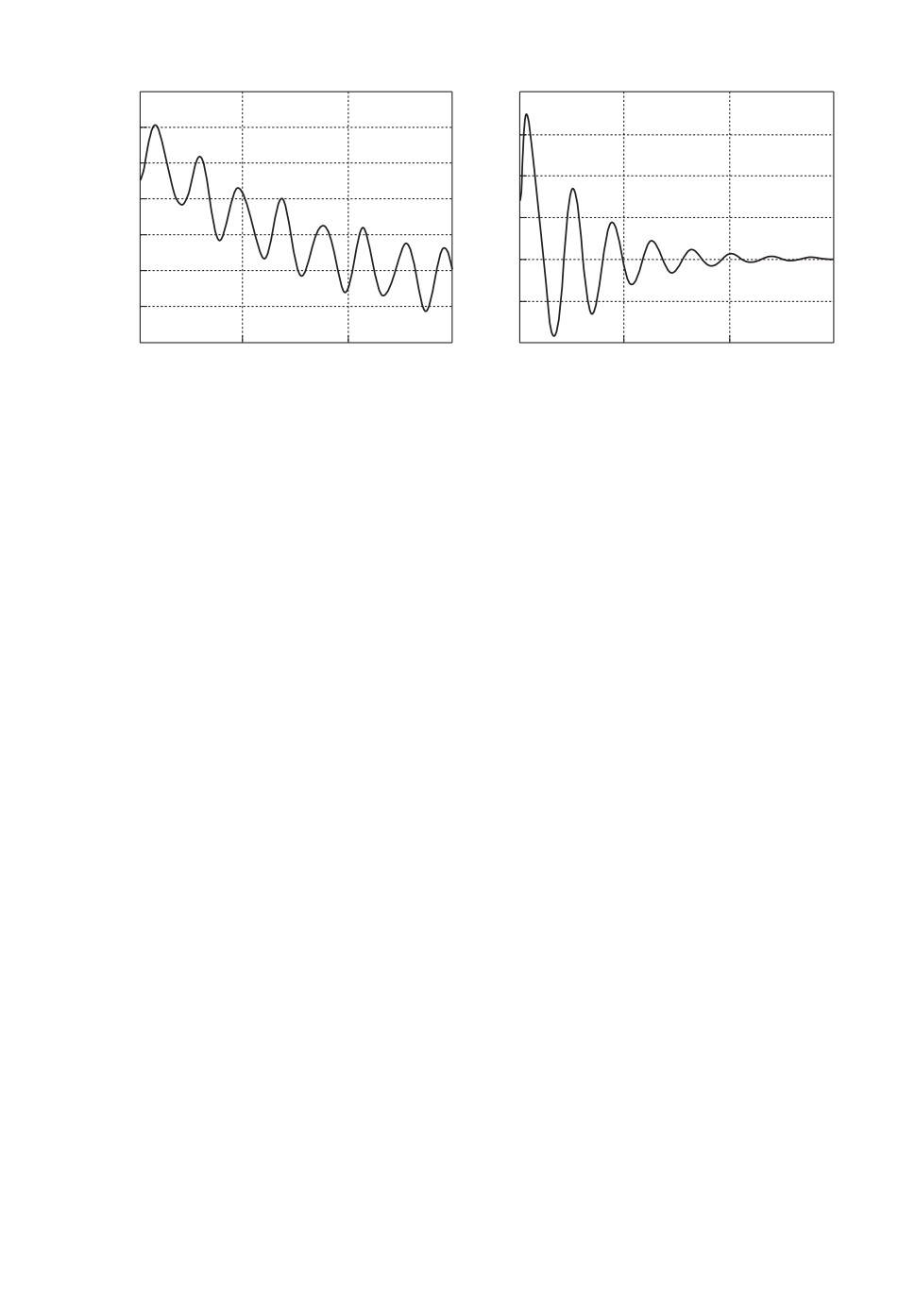
ции. Результаты сравнительного моделирования углового движения БКК по

координате ϕ с алгоритмом управления (7) и алгоритмом (15) представлены

на рис. 2.

На рис. 2,а представлены графики реальных значений ϕ (11), получен-

ных при использовании алгоритма (7) с p1,i = 0,017, p2,i = 0,01, i = 1, 2, на

рис. 2,б — при использовании алгоритма (15), в котором p1,i = 3,6, p2,i = 2,3.

133

, рад

k, рад

0,025

0,03

0,020

0,02

0,015

0,01

0,010

0,005

0,01

0,005

0,02

100

t, c

100

t, c

Рис. 2. Процессы стабилизации угла поворота конструкции.

В первом случае затухание упругих колебаний до 2% от максимального зна-

чения начального значения амплитуды происходит за ∼ 6000 с, во втором

случае при активной компенсации влияния упругих колебаний — за ∼ 80 с.

При моделировании процесса стабилизации угла поворота до 150 с (см.

рис. 2,б ) ошибки идентификации парциальных частот колебались в диапа-

зоне от 0,7 до 1,6% от истинных значений параметров ω_i.

6. Заключение

При управлении угловым движением собираемой на орбите БКК, содержа-

щей упругие элементы, возникает проблема демпфирования колебаний при

отсутствии информации о новых механических параметрах собираемой кон-

струкции и начальных характеристиках, возникающих на каждом этапе сбор-

ки новых упругих компонент. Это требует обеспечения не только своевре-

менной смены стратегии оценивания и соответственно управления при пе-

реходе конструкции из одного класса механических систем в другой, но и

применения принципов адаптивного управления на интервале развития кон-

струкции внутри каждого этапа сборки выше первого. При необходимости на

этапе сборки должна решаться задача оптимизации коэффициентов в алго-

ритме (8) при координатах тонов упругих колебаний с точки зрения быстро-

действия.

Синтезированный алгоритм совместного оценивания координат углового

движения БКК, тонов упругих колебаний конструкции и их параметров поз-

воляет только по показаниям измерителей углового движения БКК в отсут-

ствие какой-либо объективной информации об упругих колебаниях получать

с высокой точностью оценки их неизмеряемых координат и параметров в ре-

альном времени.

Следует отметить, что при построении расширенного фильтра Калмана

для оценки координат движения и их параметров такой сложной механиче-

134

ской системы, как рассматриваемая в работе БКК зонтичного типа, требуется

использование полной ММ значительно более высокого порядка, в которой

учитывается взаимное влияние колебательных компонент. Такую задачу це-

лесообразно решать при разработке системы для конкретного варианта со-

бираемой конструкции с использованием соответствующего объема вычисли-

тельных средств. В данной работе рассматривается принципиальная возмож-

ность использования предлагаемого подхода для решения задачи оценивания

таких сложных динамических объектов.

Использование синтезированных алгоритмов (8) и (14) при сборке БКК

имеет ряд достоинств. Так, при установке первого упругого элемента раз-

мерность вектора состояния в алгоритме оценивания увеличивается на пять

неизмеряемых координат: две координаты тона упругих колебаний и три па-

раметра колебаний. Так как эти параметры длительное время остаются по-

стоянными, то после их идентификации они становятся известными и даль-

нейшая идентификация их нецелесообразна, тогда эти три параметра мож-

но исключить из вектора состояния. После установки следующего упругого

элемента указанное выше изменение размерности повторяется и вектор со-

стояния увеличивается на пять координат. После процедуры идентификации

следующих постоянных параметров вектор состояния также уменьшается на

следующие три координаты и т.д. Таким образом, вектор состояния после

идентификации параметров колебаний всех упругих элементов БКК увели-

чивается только на 2n координат, где n — количество установленных на БКК

упругих элементов.

Результаты статистического математического моделирования доказывают

возможность активной компенсации влияния колебаний упругих частей кон-

струкции БКК на динамику угловой ориентации и стабилизации самого БКК

с помощью управления вида (15). При моделировании алгоритма идентифи-

кации параметров a, b, c проверялись три варианта оценивания, в которых

выбирался один из трех параметров, а остальные два считались известными.

СПИСОК ЛИТЕРАТУРЫ

1. Акуленко Л.Д., Крылов С.С., Марков Ю.Г., Тун Тун Вин, Филиппова А.С. Ди-

намика космического аппарата с упругими и диссипативными элементами в

режиме ориентации // Изв. РАН. Теория и системы управления. 2014. № 5.

C. 106-115.

2. Геча В.Я., Гриневич Д.В., Чирков В.П., Канунникова Е.А. Влияние упругих

трансформируемых элементов конструкции на точность стабилизации космиче-

ского аппарата // Справочник. Инженерный журнал. 2013. № 5. С. 3-6.

3. Nurre G.S., Ryan R.S., Scofield H.N., Sims J.L. Dynamics and control of large space

structures // J. of Guidance, Control, Dynam. 1984. V. 7. No. 5. P. 514-526.

4. Рутковский В.Ю., Суханов В.М. Большие космические конструкции: модели,

методы исследования и принципы управления. Ч. 1 // АиТ. 1996. № 7. С. 52-65.

Rutkovsky V.Yu., Sukhanov V.M. Large Space Structure: Models, Methods of Study

and Control // Autom. Remote Control. 1996. V. 57. No. 7. Part 1. P. 953-963.

135

Mikulas M.M., Collins T.J., Hedgepeth J.M. Preliminary design considerations for

10-40 meter-diameter precision truss reflectors // J. Spacecraft Rockets. 1991. V. 28.

No. 4. P. 439-447.

Boning P., Dubowsky S. Coordinated control of space robot teams for the on-orbit

construction of large flexible space structures // Advanced Robotics. 2010. V. 24.

No. 3. P. 303-323.

Белоножко П.П. Космическая робототехника для монтажа и сервиса. Потен-

циальные задачи, концепции перспективных систем // Воздушно-космическая

сфера. 2018. № 4. С. 84-97.

Flores-Abad A., Ma O., Pham K., Ulrich S. A review of space robotics technologies

for on-orbit serving // Progr. Aerospace Scie. 2014. No. 68. P. 1-26.

Papadopoulos E., Aghili F., Ma O., Lampariello R. Manipulation and capture in

space: A survey // Front. Robot. AI. 2021. No. 8. P. 1-36.

10.

Ishijima Yo., Tzeranis D., Dubowsky S. The on-orbit maneuvering of large space

flexible structures by free-flying robots // Pros. of the 8 Int. Symp. on Artificial

Intelligence, Robotics and Automation in Space (SAIRAS-2005), Munich, 5-8 Sept.,

2005, Noordwijk: ESTEC. 2005. P. 419-426. (ESA SP ISSN 1609-042X. No. 603).

11.

Тимаков С.Н., Жирнов А.В. Алгоритм активного демпфирования упругих ко-

лебаний конструкции Международной космической станции // Вестник МГТУ

им. Н.Э. Баумана. Сер. «Приборостроение». 2014. № 3. С. 37-53.

12.

Крутова И.Н., Суханов В.М. Особенности динамики управления деформируе-

мым космическим аппаратом в процессе его преобразования в большую косми-

ческую конструкцию // АиТ. 2008. № 5. С. 41-56.

Krutova I.N., Sukhanov V.M. Dynamic features of flexible spacecraft control in

process of its transformation into a large space structure // Autom. Remote Control.

2008. V. 69. No. 5. P. 774-787.

13.

Теория управления (дополнительные главы): Учебное пособие / под ред.

Д.А. Новикова. М.: ЛЕНАНД, 2019.

14.

Крутова И.Н., Суханов В.М. Синтез модифицированного PD-алгоритма управ-

ления угловым движением большой космической конструкции // АиТ. 2009. № 1.

С. 39-50.

Krutova I.N., Sukhanov V.M. Design of modified PD algorithm to control angular

motion of large space structure // Autom. Remote Control. 2009. V. 70. No. 1.

P. 33-42.

15.

Крутова И.Н., Суханов В.М. Синтез дискретной системы управления дефор-

мируемым космическим аппаратом, обеспечивающей робастную устойчивость

упругих колебаний // АиТ. 2009. № 7. С. 25-36.

Krutova I.N., Sukhanov V.M. Design of discrete control system of flexible spacecraft

maintaining robust stability of elastic oscillations // Autom. Remote Control. 2009.

V. 70. No. 7. P. 1109-1119.

16.

Rutkovsky V.Yu., Sukhanov V.M., Zemlyakov S.D., Glumov V.M. Models

and methods of control of large space structures with discretely changing

construction // Proceedings of International Conference on Nonlinear Problems in

Aviation and Aerospace (ICNPAA-2008). Cambridge Scientific publishers. Ed. by

S. Sivasundaram. 2009. Plenary paper, chapter 12. P. 115-142.

17.

Глумов В.М., Крутова И.Н., Суханов В.М. Адаптивная система управления на

основе нечеткой логики для большой космической конструкции в процессе ее

сборки на орбите // АиТ. 2004. № 10. С. 109-127.

136

Glumov V.M., Krutova I.N., Sukhanov V.M. Fuzzy Logic-based Adaptive Control

System for In-orbit Assembly of Large Space Structures // Autom. Remote Control.

2004. V. 65. No. 10. P. 1618-1634.

18.

Rutkovsky V.Yu., Glumov V.M., Sukhanov V.M. New Adaptive Algorithm of

Flexible Spacecraft Control // Complex Systems. Relationships between Control,

Communications and Computing. Dordrecht, The Netherlands: Springer Interna-

tional Publishing. 2016. P. 313-326.

19.

Kalman R.E., Bucy R. New Results in Linear Filtering and Prediction Theory //

Trans. ASME. J. Basic Eng. 1961. V. 83D. P. 95-108.

20.

Ермилов А.С., Ермилова Т.В. Оценивание ненаблюдаемых координат упругих

колебаний больших космических конструкций с гиросиловым приводом // АиТ.

2013. № 9. С. 143-156.

Ermilov A.S., Ermilova T.V. Estimating Nonmeasurable Coordinates of Elastic

Oscillations for Large Space Constructions with a Gyroforse Engine // Autom.

Remote Control. 2013. V. 74. No. 9. P. 1545-1556.

21.

Глумов В.М., Крутова И.Н., Суханов В.М. Метод построения математической

модели дискретно развивающейся большой космической конструкции // АиТ.

2003. № 10. С. 15-33.

Glumov V.M., Krutova I.N., Sukhanov V.M. A Method of Constructing the

Mathematical Model of a Discretely Developing Large Space Structure // Autom.

Remote Control. 2003. V. 64. No. 10. P. 1527-1543.

22.

Глумов В.М., Крутова И.Н., Суханов В.М. Особенности гиросиловой стабили-

зации собираемой на орбите большой космической конструкции // Проблемы

управления. 2016. № 1. С. 82-89.

Glumov V.M., Krutova I.N., Sukhanov V.M. Some Features of Powered Gyrostabi-

lization of a Large Space Structure Assembled in Orbit // Autom. Remote Control.

2017. V. 78. No. 12. P. 1345-1355.

23.

Динамика и управление космическими объектами / под ред. В.М. Матросова,

М.Ф. Решетнева, Новосибирск: Наука. Сиб. отд-ние РАН, 1992.

24.

Glumov V.M. Adaptive Control of Free-Flying Space Manipulation Robot in the

Working Area when Assembling a Large Space Structure in Orbit // Proceedings

of the 12th International Conference “Management of Large Space System Develop-

ment” (MLSD) M: IEEE. 2019. P. 1-4.

https//ieeeexplore.ieee.org/document/8911089

Статья представлена к публикации членом редколлегии А.И. Матасовым.

Поступила в редакцию 12.10.2022

После доработки 06.02.2023

Принята к публикации 30.03.2023

137