Автоматика и телемеханика, № 8, 2023

Оптимизация, системный анализ

и исследование операций

В.А. КОСТЕНКО, канд. техн. наук (kostmsu@gmail.com),

И.А. ФЕДОРЕНКО (iliasfedorenko@mail.ru)

(Московский государственный университет им. М.В. Ломоносова),

Ц. ГАО, канд. физ.-мат. наук (gaojiexing@huawei.com)

(Московский исследовательский центр компании Хуавэй),

Ч.М. СУН, PhD (sunchumin@huawei.com),

Ц. СУН, PhD (j.sun@huawei.com)

(Гонконгский исследовательский центр компании Хуавэй)

АЛГОРИТМ ИМИТАЦИИ ОТЖИГА ДЛЯ ПОСТРОЕНИЯ СПИСОЧНЫХ

РАСПИСАНИЙ С ОГРАНИЧЕНИЕМ НА КОЛИЧЕСТВО

МЕЖПРОЦЕССОРНЫХ ПЕРЕДАЧ ДАННЫХ

Предложен алгоритм имитации отжига для построения многопроцес-

сорных списочных расписаний минимальной длительности с дополни-

тельным ограничением на количество передач между процессорами. Дан-

ное ограничение характерно для вычислительных систем с жесткими

ограничениями на ресурсы межпроцессорной сети передачи данных. В це-

лом задача минимизации длительности расписания возникает при разра-

ботке систем обработки данных в реальном масштабе времени, таких как

бортовые и телекоммуникационные системы. Также задача актуальна для

периферийных вычислений (edge computing). Экспериментальное иссле-

дование свойств алгоритма показало его высокую точность, стабильность

и масштабируемость.

Ключевые слова: комбинаторная оптимизация, списочные расписания,

алгоритм имитации отжига.

DOI: 10.31857/S0005231023080093, EDN: HDDNWC

1. Введение

Алгоритмы построения расписаний можно разделить на два больших

класса.

Класс 1. Алгоритмы начинают процесс построения расписания с пусто-

го расписания, не содержащего работ, а затем на каждом шаге добавляют

работы в расписание. К алгоритмам этого класса относятся жадные алгорит-

мы [1, 2], алгоритмы, сочетающие жадные стратегии, и ограниченный пере-

бор [3], алгоритмы, основанные на методе ветвей и границ [4, 5].

138

Класс 2. Алгоритмы работают с полным расписанием (содержащим все ра-

боты). На каждом шаге такие алгоритмы изменяют расписание, пытаясь его

улучшить. К этому классу относятся алгоритмы имитации отжига [6, 7], гене-

тические и эволюционные алгоритмы [8-11], муравьиные алгоритмы [12-14],

алгоритмы случайного поиска [15].

Рассматриваемая в работе задача построения списочных расписаний от-

личается от классической [2, 16] наличием дополнительного ограничения на

корректность расписаний. Задается ограничение на максимально возможное

число передач данных между процессорами. Наличие дополнительного огра-

ничения может приводить к тому, что алгоритмы первого класса заходят в

тупик: есть еще не размещенные в расписание работы, при этом ни одна из

них не может быть размещена без нарушения дополнительного ограничения

на корректность расписания. Для алгоритмов второго класса дополнительное

ограничение может приводить к невозможности перехода между двумя кор-

ректными расписаниями при помощи переноса работ между процессорами

по одной: такой перенос может увеличить число межпроцессорных передач,

приводя к нарушению ограничения.

Ограничение на максимально возможное число передач данных между

процессорами позволяет только за счет планирования вычислений умень-

шить нагрузку на сеть обмена данными. При этом граф потока данных не

изменяется. Изменение графа потока данных означает разработку нового ал-

горитма решения прикладной задачи. Данная задача актуальна для систем с

жесткими ограничениями на доступные ресурсы, такие как вычислительная

мощность, объем оперативной памяти, пропускная способность сети. К та-

ким системам относятся, в частности, встроенные и бортовые управляющие

системы, системы цифровой обработки сигналов. Также задача актуальна

для периферийных вычислений (edge computing), для выполнения которых

нет возможности использовать высокопроизводительные вычислители.

В работе математически сформулирована постановка задачи построения

списочных расписаний с дополнительным ограничением на количество пере-

дач данных между процессорами, рассмотрены подходы к решению близких

задач, предложен алгоритм имитации отжига для этой задачи и приведе-

ны результаты экспериментального исследования точности и вычислитель-

ной сложности алгоритма.

2. Задача построения списочных расписаний

с дополнительным ограничением

Общая задача построения списочных расписаний заключается в распреде-

лении фиксированного множества работ на процессоры и задания порядка их

выполнения таким образом, чтобы оптимизировать желаемую меру эффек-

тивности расписания и выполнить заданные ограничения, которые обеспе-

чивают корректность полученного решения. Прежде чем конкретизировать

постановку задачи построения расписаний, определим модели исходных дан-

ных и самого расписания.

139

Модель прикладной программы. При определении модели прикладной про-

граммы предполагается, что работы, подлежащие планированию, и паралле-

лизм, допускаемый при выполнении программы, заданы (выявлены) предва-

рительно. Модель программы задается графом потока данных. Это ориен-

тированный ациклический граф G с N вершинами и M ребрами. Каждой

вершине графа соответствует работа из набора работ P = {p_i}Ni=1. Каждому

ребру графа соответствует однонаправленная передача данных между рабо-

тами. Директивные сроки для работ не определены.

Модель вычислительной системы. Вычислительная система HW пред-

ставляет собой S одинаковых по функциональным возможностям и произ-

водительности процессоров: SP = {sp_i}Si=1, каждый из которых может од-

новременно выполнять одну работу. Времена выполнения работ p_j на лю-

бом из процессоров определяются вектором времен выполнения: C = {c_j },

j = 1,...,N. Работы непрерываемы, каждая работа должна быть целиком

выполнена на одном процессоре.

Связь между процессорами sp_i и sp_j задается согласно матрице связно-

сти процессоров D = {d_ij }, i = 1, . . . , S, j = 1, . . . , S, причем d_ij = 0 при i = j.

Значение d_ij задает задержку на передачу данных от sp_i к sp_j, т.е. если рабо-

ты p_k и p_l находятся на процессорах sp_i и sp_j соответственно и в графе потока

данных присутствует ребро (p_k, p_l), то завершение p_k и старт p_l должны быть

разделены по времени не менее чем на d_ij .

Размеры данных и конфликты доступа к среде передачи данных не рас-

сматриваются. На процессоре возможно выполнение работы, даже если с это-

го процессора передаются и/или на этот процессор принимаются данные.

Модель расписания. Расписание HP выполнения прикладной программы

определено для заданного набора работ и набора процессоров, если заданы:

1) привязка работ к процессорам; 2) порядок выполнения работ на каждом

процессоре.

Будем рассматривать расписание в списочной форме. Списочная форма

расписания HP представляет собой ориентированный граф G_HP , вершины

которого соответствуют работам. В состав G_HP входят:

— для каждого процессора — простая цепь из привязанных к этому про-

цессору работ, задающая порядок выполнения работ на этом процессоре;

— для каждой межпроцессорной передачи данных — секущее ребро между

цепью процессора-отправителя и цепью процессора-получателя, соединяю-

щее две работы, участвующие в передаче данных.

Отметим, что в G_HP отсутствуют ребра, соответствующие передачам дан-

ных между работами, выполняющимися на одном процессоре и не являющи-

мися соседними в цепи этого процессора.

Расписание HP корректно, если выполнены следующие ограничения.

1) Каждая работа назначена на процессор.

2) Любую работу обслуживает лишь один процессор, без прерывания.

140

3) Процессор в каждый момент времени выполняет не более одной работы.

4) Частичный порядок, заданный графом потока данных G, сохранен в

HP: G ⊂ G^∗HP, где G^∗HP - транзитивное замыкание отношения G_HP.

5) Расписание HP должно быть беступиковым (необходимо для построе-

ния временной диаграммы расписания). Достаточным условием беступиково-

сти при неограниченном размере буферов обмена данными является отсут-

ствие контуров в графе G_HP .

6) Ограничение на долю межпроцессорных передач данных: CR ≤ CR_U ;

CR = MpM , где Mp - количество передач данных между работами, находящи-

мися на разных процессорах; CR_U - исходно заданное число.

Ограничения 1-5 являются основными. Они обеспечивают корректность

расписания и однозначность построения временной диаграммы по списочной

форме расписания. Ограничение 6 является дополнительным. В дальнейшем

будем обозначать HP ∈ HP∗1-5 или HP ∈ HP∗1-6, если расписание HP удовле-

творяет ограничениям 1-5 или 1-6 соответственно. Нижний индекс в HP∗1-5

и HP∗1-6 указывает ограничения, налагаемые на расписание.

Временная диаграмма выполнения программы. Временная диаграмма

определена для расписания и модели вычислительной системы, если каждая

работа назначена на процессор (из расписания), определены времена начала

и завершения каждой работы. Время начала работы определяется как мини-

мальное возможное с учетом передачи данных от работ-предшественников и

порядка выполнения работ на процессорах.

Задачу построения расписаний будем рассматривать в следующем вари-

анте постановки.

Дано: G - модель прикладной программы, HW - модель вычислительной

системы, CR_U - ограничение на число межпроцессорных передач.

Требуется: построить расписание HP выполнения программы.

Минимизируемый критерий: длительность расписания, т.е. время завер-

шения последней работы в расписании. Времена старта и завершения работ

определяются по временной диаграмме расписания.

Ограничение корректности: HP ∈ HP∗1-6.

3. Алгоритмы решения близких задач

При выборе классов алгоритмов для решения поставленной задачи учиты-

вается масштабируемость алгоритмов, так как в настоящей работе графы по-

тока данных для оценки качества результатов алгоритма содержат несколько

тысяч (до 10 000) работ.

Рассматриваемая задача построения списочных расписаний представляет

собой один из вариантов задачи построения многопроцессорных расписаний

и является NP-трудной [17]. В связи с этим вряд ли возможно разработать

полиномиальный алгоритм, находящий точное решение поставленной зада-

141

чи. Существующие решения, основанные на таких методах, как метод ветвей

и границ и динамическое программирование, имеют плохую масштабируе-

мость. Например, алгоритм на основе метода ветвей и границ, предложенный

в [18], был применен к наборам данных с числом процессоров до 16 и гра-

фами, содержащими до 100 вершин, и продемонстрировал экспоненциальный

рост времени работы.

Попытки применения методов целочисленного линейного программирова-

ния к задаче построения многопроцессорного расписания [19] привели к алго-

ритму, время выполнения которого на примере, содержащем 8 процессоров и

граф с 30 вершинами, составляло несколько часов. При увеличении размера

входных данных время выполнения существенно увеличивалось. В [20] ука-

зано, что такие алгоритмы могут быть использованы для входных данных,

содержащих до 50 вершин в графе потока данных.

Для задачи построения многопроцессорного расписания было предложено

множество жадных алгоритмов, многие из которых основаны на последова-

тельной схеме планирования [10, 21, 22]. В такой схеме работы линейно упо-

рядочиваются в соответствии с некоторым критерием, с учетом частичного

порядка, заданного графом потока данных. В полученном порядке работы

выбираются для назначения на процессоры. Алгоритм, сочетающий жадные

стратегии и ограниченный перебор, предложен в [3]. Качество работы жад-

ной стратегии сильно зависит от класса исходных данных. Однако жадные

алгоритмы можно использовать для генерации начального приближения для

алгоритмов, перечисленных ниже.

Для решения задачи построения многопроцессорного расписания также

предлагались генетические и эволюционные алгоритмы [23]. Основная про-

блема алгоритмов этого класса в их ограниченной масштабируемости. На-

пример, в [24] наиболее быстрый алгоритм обрабатывал задачу с 1000 работ

порядка 1,5 ч на процессоре с частотой 2 ГГц. Одна из причин такого большо-

го времени выполнения заключается в том, что генетические и эволюционные

алгоритмы работают с популяциями, содержащими десятки и даже сотни ре-

шений.

В отличие от генетических и эволюционных алгоритмов алгоритм имита-

ции отжига работает с единственным решением. В [6] предложен алгоритм

имитации отжига для задачи построения многопроцессорного списочного рас-

писания без задержек на передачу данных. Этот алгоритм хорошо масшта-

бируем и может быть адаптирован к рассматриваемой задаче посредством

учета времени передачи данных при вычислении длительности расписания.

Для решения рассматриваемой задачи в качестве основы был выбран именно

этот алгоритм.

Муравьиные алгоритмы также используются для построения многопро-

цессорных расписаний. В [25] эксперименты были ограничены наборами дан-

ных с 11 процессорами и 120 вершинами. Авторы работы [25] делают вывод:

чтобы гарантировать сходимость муравьиного алгоритма, необходимо точно

142

настроить его многочисленные параметры, что серьезно усложняет примене-

ние его к задаче с разными размерами графов.

По результатам обзора не было найдено работ, в которых описаны алго-

ритмы, поддерживающие ограничение по числу межпроцессорных передач.

Поэтому выбранный алгоритм нуждается в доработке в части процедуры вы-

бора начального приближения и операций, применяемых к расписанию.

4. Алгоритм имитации отжига

Введем следующие обозначения и понятия:

T₀

—T =

- схема изменения температуры, где T₀ - начальная

log(1 + (i + 1))

температура, i - номер текущей итерации (схема Больцмана);

— F(HP) - функция оценки качества расписания HP;

— HP_best - лучшее найденное корректное расписание, причем HP_best ∈

∈HP∗1-6;

— критерий останова — выполнение заданного числа итераций без изме-

нения лучшего корректного решения.

Алгоритм имитации отжига построен по следующей схеме:

1) Инициализация. Задать начальное корректное расписание HP₀ ∈

∈ HP∗1-6 и считать его текущим: HP = HP₀. Вычислить длительность полу-

ченного расписания HP . Сохранить начальное расписание как лучшее най-

денное на данный момент: HP_best = HP .

2) Применить операцию преобразования расписания к HP и получить но-

вое расписание HP^′. Вычислить длительность расписания HP^′. Если дли-

тельность расписания HP^′ является меньшей, чем у ранее сохраненного

HP_best, и HP^′ ∈ HP∗1-6, то сохранить его как лучшее найденное: HP_best =

=HP^′.

3) Найти изменение функции оценки качества расписания ΔF = F (HP^′)-

-F(HP):

(i) Если ΔF ≤ 0 (т.е. нашлось расписание лучшее, чем текущее), то новое

расписание становится текущим: HP = HP^′.

(ii) Если ΔF > 0, то с вероятностью e^-

T принять новое расписание в

качестве текущего.

4) Повторить заданное число раз шаги 2 и 3 без изменения текущей тем-

пературы.

5) Если критерий останова выполнен, то завершить работу алгоритма.

6) Изменить текущее значение температуры T в соответствии с выбранной

схемой и перейти к шагу 2.

Инициализация. Обычно начальное расписание строится с помощью раз-

личных жадных схем. Однако с их помощью тяжело построить расписание,

которое бы удовлетворяло ограничению на количество межпроцессорных пе-

143

редач, поскольку после построения частичного расписания со сбалансиро-

ванным распределением работ по процессорам жадный алгоритм заходит в

тупик и не может добавить в расписание новые работы без нарушения этого

ограничения.

Поэтому первоначально был использован простой вариант построения на-

чального расписания, гарантирующий выполнение этого ограничения, — на-

значение всех работ на один процессор. Таким образом, CR = 0, так как меж-

процессорные передачи отсутствуют. Порядок работ на процессоре определя-

ется топологической сортировкой графа G. То есть между работами установ-

лен такой порядок, чтобы любое ребро графа G, соответствующее передаче

данных, вело от работы с меньшим номером к работе с большим номером.

Построенное этим способом начальное приближение по результатам экспери-

ментов не приводило к решению, близкому к оптимуму, при числе процессо-

ров S ≥ 10. Вместо этого происходило сбалансированное распределение работ

на меньшее число процессоров, после чего алгоритм имитации отжига не мог

улучшить данное решение.

Для решения проблемы сбалансированного распределения работ по про-

цессорам при построении начального расписания было использовано про-

граммное средство METIS [26], включающее в себя реализацию алгоритма

разбиения графов на заданное число подграфов, минимизирующего число ре-

бер между полученными подграфами. Если подать на вход алгоритму граф

потока данных G, выбрать число разбиений, равное числу процессоров, и

сопоставить каждый полученный подграф процессору, то получится распре-

деление работ по процессорам с минимизацией числа межпроцессорных пе-

редач.

Различия в размерах (количестве вершин) подграфов управляются пара-

метром ufactor [27], ограничивающим отношение максимального размера под-

графа к его среднему размеру. Увеличивая этот параметр, всегда возможно

достичь необходимого отношения числа ребер между подграфами к общему

числу ребер, т.е. удовлетворить заданному ограничению на количество меж-

процессорных передач за счет меньшей сбалансированности распределения

работ по процессорам.

После построения начального распределения работ по процессорам при

помощи METIS порядок выполнения работ на процессорах определяется по

следующей схеме. Для каждой работы по алгоритму ALAP [28] определяется

наиболее позднее время ее завершения. Это время может быть вычислено,

поскольку для работ определено их распределение по процессорам, а значит,

известны и задержки на передачу данных между работами. Работы упоря-

дочиваются по возрастанию наиболее позднего времени завершения. В соот-

ветствии с полученным порядком происходит выбор работ для включения в

расписание. Если для очередной работы обнаружено, что она может быть по-

ставлена раньше какой-то из уже включенных в расписание работ на том же

процессоре без нарушения условий HP∗1-6, она будет помещена перед этой

144

работой, в противном случае работа ставится в конец расписания на процес-

соре.

Операции преобразования расписания. Для представления расписания ис-

пользуется ярусная форма наибольшей высоты [6] с указанием привязки ра-

бот к процессорам. Эта форма в ходе выполнения алгоритма переводится во

временную диаграмму для расчета времени работы программы с заданным

расписанием (асимптотическая сложность перевода такого представления во

временную диаграмму — O(M)). Ярусная форма наибольшей высоты харак-

теризуется тем, что на каждом ярусе находится ровно одна работа и для лю-

бой работы p_i все работы-предшественники расположены на более высоких

ярусах, чем p_i.

Для изменения расписания использовалась функционально полная систе-

ма операций преобразования расписаний {O₁, O₂}, описанная в [29]. При

представлении расписания в ярусной форме максимальной высоты операции

выглядят следующим образом:

1) O₁(p_i, sp_m → sp_k) — операция изменения привязки работы. Переносит

работу p_i с процессора sp_m на процессор sp_k на тот же ярус;

2) O₂(p_i, sp_m, c) — операция изменения порядка работ на процессоре. Пере-

мещает работу p_i на ярус c, смещая остальные работы в сторону изначальной

позиции работы p_i на процессоре.

Сложность операции O₁ равна O(1), а операции O₂ — O(N).

Функция оценки качества расписания. Состоит из двух слагаемых: первое

отвечает за длительность полученного расписания, второе — за превышение

ограничения CR:

T ime(HP )

F (HP ) = K

+ (1 - K)CR_above,

∑

C_i + N max

D_ij

i,j=1...S

где T ime(HP ) - длительность полученного расписания, CR_above = CR-CR_U ,

если CR > CR_U , иначе CR_above = 0.

Знаменатель дроби в первом слагаемом отвечает за нормировку длитель-

ности расписания. Это выражение является верхней оценкой длительности

расписания.

В [29] сформулирована и доказана следующая

Теорема 1. Если HP₁ ∈ HP∗1-5 и HP₂ ∈ HP∗1-5 - произвольные кор-

ректные варианты расписания, то существует конечная цепочка операций

{O_i}Ki=1, O_i ∈ {O₁, O₂}, переводящая расписание HP₁ в HP₂, такая что все

K промежуточных расписаний являются корректными (HP_t ∈ HP∗1-5) и

K ≤ 4N, где N - количество работ.

Введенные выше операции изменения расписания могут преобразовывать

его так, что получившееся расписание уже не будет удовлетворять ограни-

чению на количество межпроцессорных передач (HP∗1-6). Возможность рас-

145

сматривать расписания с невыполненным ограничением необходима, так как

в общем случае множество решений не является связным относительно опе-

раций, не нарушающих ограничение CR ≤ CR_U . Добавление штрафа за его

нарушение предотвращает слишком большое отклонение алгоритма от мно-

жества корректных решений. Из всего вышесказанного для данного алгорит-

ма справедливо следующее

Утверждение 1. Используемая в алгоритме система операций пре-

образования расписаний позволяет перейти от произвольного начального

приближения HP₁ ∈ HP∗1-6 к оптимальному расписанию HP₂ ∈ HP∗1-6 за

K ≤ 4N шагов применения операций, причем для каждого из промежуточ-

ных расписаний HP_t верно, что HP_t ∈ HP∗1-5.

5. Экспериментальное исследование свойств алгоритма

Для исследования использовались различные наборы входных данных с

известным оптимумом, удовлетворяющие дополнительному ограничению с

CR_U = 0,4. Число процессоров S варьировалось от 2 до 64; число работ N —

от 10 до 1000 с шагом 100 и от 1000 до 10 000 с шагом 1000; плотность графа,

выражающаяся в отношении числа ребер к числу вершин (M/N) в графе G,

для всех наборов входных данных примерно равнялась 5; времена выполне-

ния работ варьировались от 1 до 10; время передачи данных между процес-

сорами — от 1 до 3, в зависимости от пары процессоров. В качестве критерия

останова алгоритма было установлено 10 000 итераций без изменения лучшего

корректного решения. Наборы с отношением N/S < 10 не рассматривались.

Набор входных данных, для которого известен оптимум (т.е. длитель-

ность оптимального расписания), формируется по следующей схеме. Пред-

полагается, что каждый процессор непрерывно (без простоев) занят от мо-

мента 0 до заданного момента L, который и будет длительностью оптималь-

ного расписания. Для каждого процессора интервал его занятости [0; L] раз-

деляется на части случайной длительности, выбираемой между заданны-

ми минимальной и максимальной длительностью (в рассматриваемом слу-

чае между 1 и 10). Эти части являются работами, размещенными на дан-

ный процессор, и для каждой из них по построению определено время стар-

та. Затем случайным образом добавляются передачи данных между работа-

ми (т.е. пары <работа-отправитель, работа-получатель>) так, чтобы время

старта работы-получателя было не меньше, чем время завершения работы-

отправителя плюс длительность передачи данных между конкретной парой

процессоров; при добавлении передач данных контролируется выполнение

условия CR ≤ CR_U . Затем по расписанию восстанавливается граф потока

данных; для этого имеются все необходимые данные: длительность работ,

наличие и длительность передач данных между работами. Значение L выби-

рается так, чтобы с учетом минимальной и максимальной допустимой дли-

тельности работ было возможно деление совокупности интервалов занятости

всех процессоров на суммарное количество частей, равное требуемому коли-

146

1,25

1,20

1,15

1,10

1,05

1,00

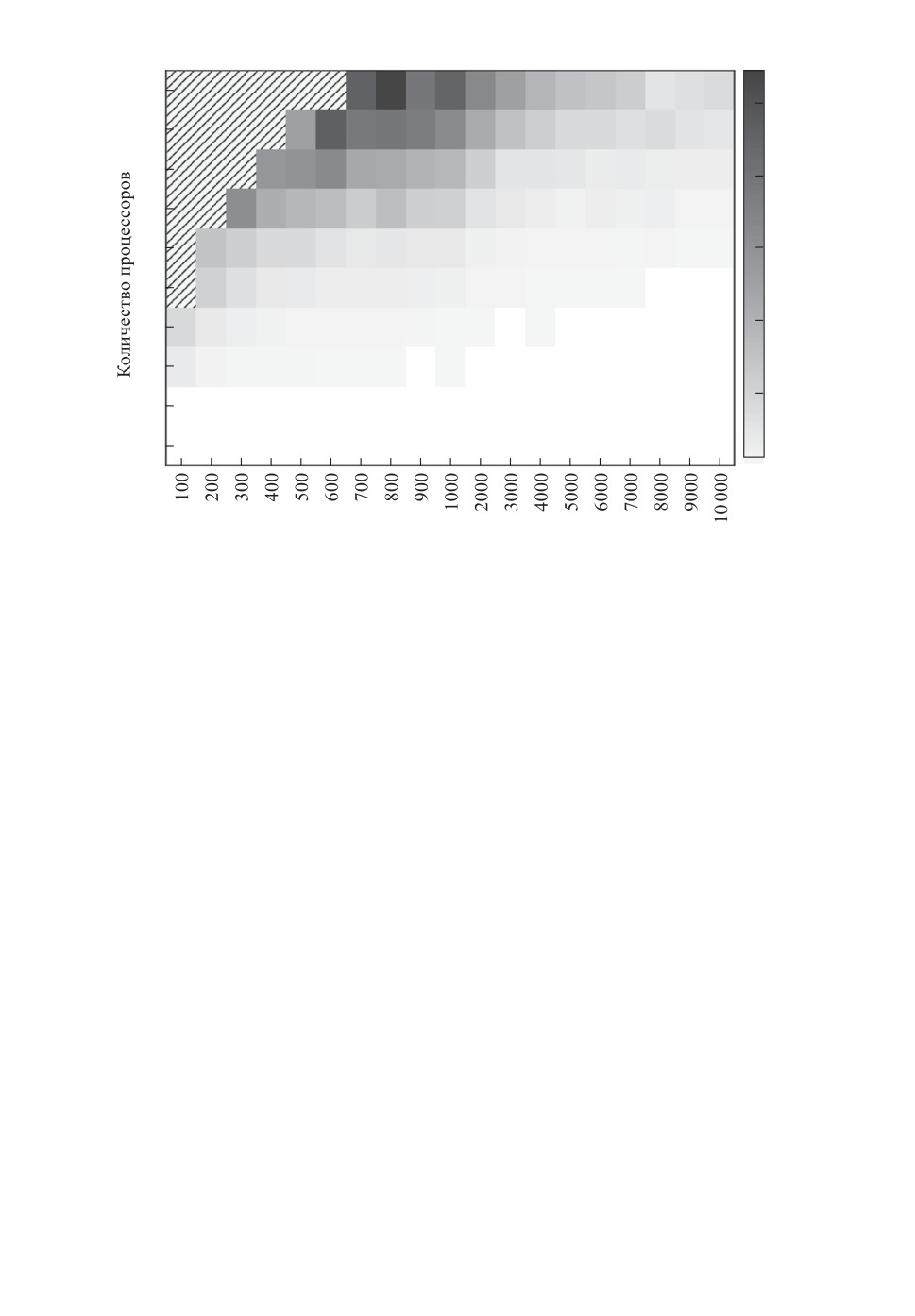
Количество работ

Рис. 1. Тепловая карта отношения длительности полученного расписания

к длительности оптимального расписания.

честву работ. Передачи данных между работами добавляются до достижения

требуемой плотности графа потока данных.

Утверждение 2. Расписание, по которому согласно описанной схеме

«восстанавливается» граф потока данных, является оптимальным, пото-

му что оно не содержит простоев и для каждого процессора интервал за-

нятости один и тот же: [0; L].

Поскольку для каждого использованного в экспериментах набора вход-

ных данных известна длительность оптимального расписания, для оценки

качества алгоритма было выбрано отношение длительности полученного им

расписания к длительности оптимального расписания. Это отношение всегда

больше 1 и чем оно ниже, тем лучше результат работы алгоритма. На рис. 1

изображена тепловая карта, отображающая это отношение. По горизонталь-

ной оси располагается число работ, по вертикальной оси — число процессоров.

Отношение отображается градациями серого, соответствующая шкала изоб-

ражена справа от графика. Алгоритм запускался на каждом наборе входных

данных 5 раз. Результат усреднялся.

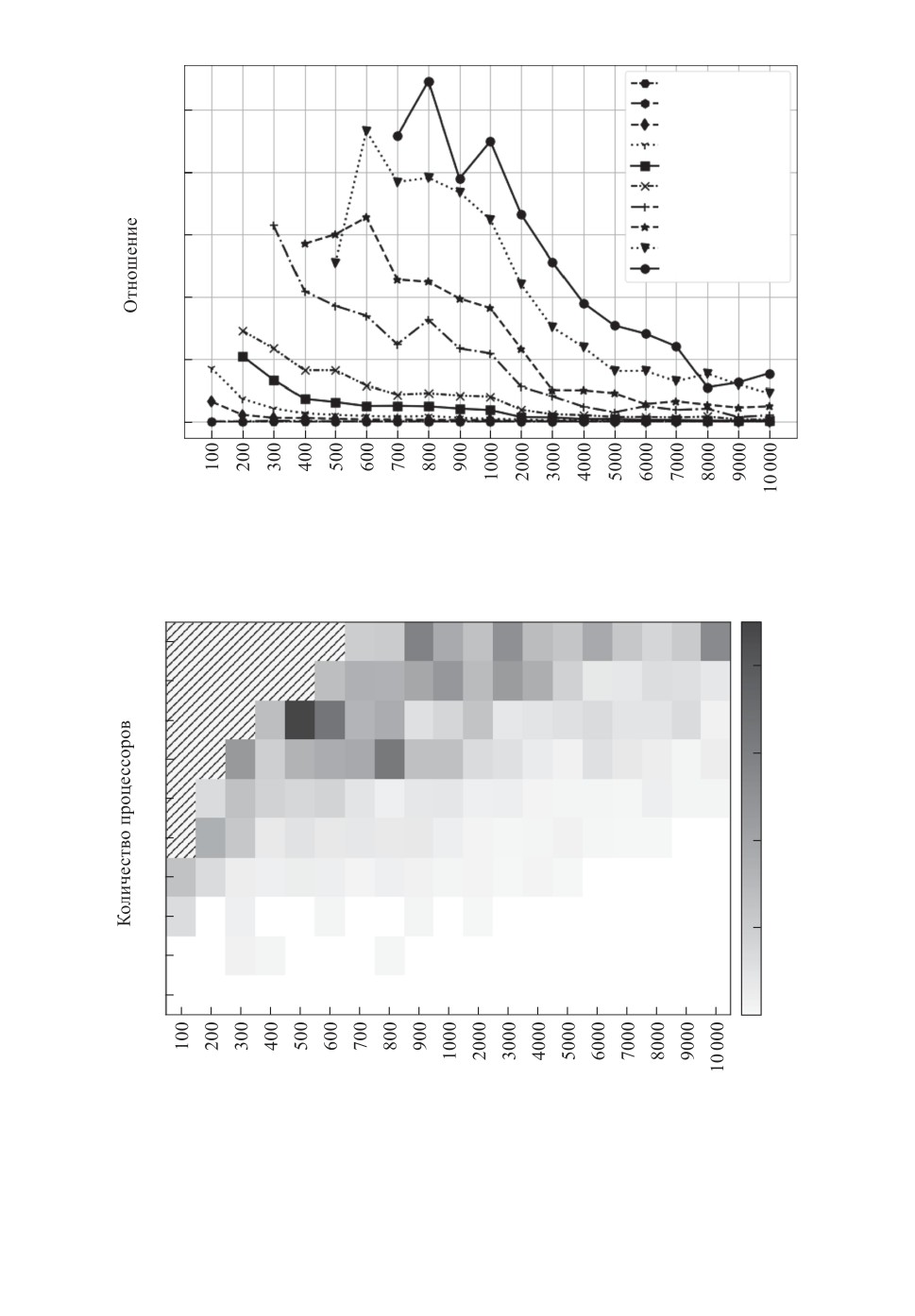
На рис. 2 показана та же информация в виде графиков. Каждой линии

соответствуют наборы входных данных для фиксированного числа процес-

соров. По горизонтальной оси указано число работ, по вертикальной оси —

отношение длительности полученного расписания к длительности оптималь-

ного расписания.

147

По результатам экспериментального исследования предлагаемого алгорит-

ма отношение длительности построенного расписания к оптимуму почти все-

гда меньше 1,1, однако на отдельных наборах данных превышает это зна-

чение. Такое высокое отношение наблюдается на наборах данных с низким

числом работ и высоким числом процессоров. Это можно объяснить тем,

что при такой конфигурации среднее число работ на процессоре невелико и

при переносе одиночной работы между процессорами длительность расписа-

ния сильно возрастает; вследствие этого измененное расписание с высокой

вероятностью не принимается, что приводит к малому количеству перено-

сов работ между процессорами, особенно при сниженной температуре. При

увеличении числа работ на наборах данных с большим числом процессоров

качество полученного решения улучшается.

Поскольку предлагаемый алгоритм является рандомизированным, необ-

ходимо исследовать его стабильность. На тепловой карте (рис. 3) показано

среднеквадратическое отклонение отношения длительности полученного рас-

писания к длительности оптимального расписания.

По тепловой карте на рис. 3 можно сделать вывод о высокой стабильности

алгоритма. Для большинства наборов входных данных среднеквадратическое

отклонение не поднимается выше 0,02. Более высокие (выше 0,03) значения

отклонения на большом числе процессоров и малом числе задач возникают

по тем же причинам, что и относительно невысокое качество решения в этой

же ситуации.

Эксперименты выполнялись на компьютере с процессором Intel Core i5-

8250U, 1,6 ГГц. Ни на одном наборе данных время выполнения алгоритма не

превышало 6 мин. Следует отметить, что алгоритм демонстрирует приемле-

мое время выполнения и высокую точность в том числе на наборах входных

данных, существенно превосходящих по масштабу те наборы, на которых про-

водилось исследование в статьях, рассмотренных в обзоре.

6. Заключение

Разработан алгоритм имитации отжига для построения многопроцессор-

ных списочных расписаний минимальной длительности с дополнительным

ограничением на количество передач между процессорами. Проблема выбора

начального распределения работ по процессорам, удовлетворяющего допол-

нительному ограничению и являющегося сбалансированным (что существен-

но для длительности расписания), решена с использованием алгоритма из

библиотеки METIS.

Проведенное экспериментальное исследование показало высокую точность

и стабильность разработанного алгоритма, в особенности на наборах данных

с достаточно большим (от 3000 до 10 000) количеством работ. Важным пре-

имуществом алгоритма по сравнению с алгоритмами, рассмотренными в об-

зоре, является его высокая масштабируемость.

149

Разработанный алгоритм может применяться для построения расписаний

в многопроцессорных вычислительных системах с ограниченными ресурса-

ми межпроцессорной сети, например в бортовых и телекоммуникационных

системах.

СПИСОК ЛИТЕРАТУРЫ

Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. М.:

МЦНМО, 2000.

Теория расписаний и вычислительные машины / Под ред. Э.Г. Коффмана. М.:

Наука, 1984.

Костенко В.А. Алгоритмы комбинаторной оптимизации, сочетающие жадные

стратегии и ограниченный перебор // Известия РАН. Теория и системы управ-

ления. 2017. № 2. C. 48-56.

Kostenko V.A. Combinatorial Optimization Algorithms Combining Greedy Strate-

gies with a Limited Search Procedure // J. Comput. Syst. Sci. Int. 2017. V. 56. No. 2.

P. 218-226. https://doi.org/10.1134/S1064230717020137

Lawler E.L., Wood D.E. Branch-and-Bound Methods: A Survey // Oper. Res. 1966.

V. 14. No. 4. P. 699-719. https://doi.org/10.1287/opre.14.4.699

Fujita S. A Branch-and-Bound Algorithm for Solving the Multiprocessor Scheduling

Problem with Improved Lower Bounding Techniques // IEEE Transact. Comput.

2011. https://doi.org/10.1016/j.procs.2016.07.216

Калашников А.В., Костенко В.А. Параллельный алгоритм имитации отжига

для построения многопроцессорных расписаний // Известия РАН. Теория и си-

стемы управления. 2008. № 3. С. 133-142.

Kalashnikov A.V., Kostenko V.A. A Parallel Algorithm of Simulated Annealing for

Multiprocessor Scheduling // J. Comput. Syst. Sci. Int. 2008. V. 47. No 3. P. 455-463.

https://doi.org/10.1134/S1064230708030155

Зорин Д.А., Костенко В.А. Алгоритм имитации отжига для решения задач по-

строения многопроцессорных расписаний // АиТ. 2014. № 10. С. 97-110.

Zorin D.A., Kostenko V.A. Simulated annealing algorithm in problems of multipro-

cessor scheduling // Autom. Remote Control. 2014. V. 75. No. 10. P. 1790-1801.

https://doi.org/10.1134/S0005117914100063

Holland J.N. Adaptation in Natural and Artificial Systems / Ann Arbor, Michigan:

Univ. of Michigan Press, 1975.

Скобцов Ю.А. Основы эволюционных вычислений. Донецк: ДонНТУ, 2008.

10.

Akbari M., Rashidi H. An Efficient Algorithm for Compile-Time task scheduling

problem on heterogeneous computing systems // Int. J. Academ. Res. 2015. V. 7.

No. 1. P. 192-202. https://doi.org/10.7813/2075-4124.2015/7-1/A.45

11.

Rzadca K., Seredynski F. Heterogeneous Multiprocessor Scheduling with Differential

Evolution // IEEE Congress on Evolutionary Computation, 2005. V. 3. P. 2840-2847.

https://doi.org/10.1109/CEC.2005.1555051

12.

Dorigo M. Optimization, Learning and Natural Algorithms // Ph.D. Thesis.

Dipartimentodi Elettronica. Milano: Politechnico Di Milano, 1992.

13.

Штовба С.Д. Муравьиные алгоритмы: теория и применение // Программиро-

вание. 2005. № 4. С. 1-15.

150

Shtovba S.D. Ant Algorithms: Theory and Applications // Program. Comput.

Software. 2005. V. 31. No. 4. P. 167-178. https://doi.org/10.1007/s11086-005-0029-1

14.

Myszkowski P.B., Skowronski M.E., Olech L.P. et al. Hybrid ant colony optimization

in solving multi-skill resource-constrained project scheduling problem // Soft

Comput. 2015. V. 19. No. 12. P. 3599-3619.

https://doi.org/10.1007/s00500-014-1455-x

15.

Растригин Л.А. Статистические методы поиска. М.: Наука, 1968.

16.

Шахбазян К.В., Тушкина Т.А. Обзор методов составления расписаний для мно-

гопроцессорных систем // Зап. научн. сем. ЛОМИ. 1975. Т. 54. C. 229-258.

17.

Garey M.R., Johnson D.S. Computers and Intractability: A Guide to the Theory of

NP-Completeness. W.H. Freeman & Co., 1979.

18.

Rahman M. Branch and Bound Algorithm for Multiprocessor Scheduling // M.S.

Thesis, Dept. Comput. Eng., Dalarna Univ., Sweden, 2009.

19.

Venugopalan S., Sinnen O. Optimal Linear Programming Solutions for Multipro-

cessor Scheduling with Communication Delays // Proc. ICA3PP 2012: Algorithms

and Architectures for Parallel Processing, 2012. P. 129-138.

https://doi.org/10.1016/j.jpdc.2016.03.003

20.

Mallach S. Improved Mixed-Integer Programming Models for the Multiprocessor

Scheduling Problem with Communication Delays // J. Combinat. Optim. 2018.

V. 36. P. 871-895. https://doi.org/10.1007/s10878-017-0199-9

21.

Hwang R., Gen M., Katayama H. A Comparison of Multiprocessor Task Scheduling

Algorithms with Communication Costs // Comput. Oper. Res. 2008. V. 35. P. 976-

993. https://doi.org/10.1016/j.cor.2006.05.013

22.

Красовский Д.В. Алгоритмы решения задачи составления оптимального распи-

сания без прерываний // Дисс

канд. физ.-мат. наук, 05.13.18 Москва, 2007,

109 с.

23.

da Silva E.C., Gabriel P.H.R. Genetic Algorithms and Multiprocessor Task Schedu-

ling: A Systematic Literature Review // Proc. ENIAC 2019. P. 250-261.

https://doi.org/10.5753/eniac.2019.9288

24.

Sheikh H.F., Ahmad I., Fan D. An Evolutionary Technique for Performance-Energy-

Temperature Optimized Scheduling of Parallel Tasks on Multi-Core Processors //

IEEE Trans. Parallel Distributed Syst., 2016. V. 27. No. 3. P. 668-681.

https://doi.org/10.1109/TPDS.2015.2421352

25.

Lo S.-T., Chen R.-M., Huang Y.-M., Wu C.-L. Multiprocessor System Scheduling

with Precedence and Resource Constraints Using an Enhanced Ant Colony System //

Expert Syst. Appl. 2008. V. 34. No. 3. P. 2071-2081.

https://doi.org/10.1016/j.eswa.2007.02.022

26.

METIS — Serial Graph Partitioning and Fill-reducing Matrix Ordering: [Электрон-

ный ресурс]. URL: http://glaros.dtc.umn.edu/gkhome/metis/metis/overview (Дата

обращения: 21.11.2022).

27.

METIS. A Software Package for Partitioning Unstructured Graphs, Partitioning

Meshes, and Computing Fill-Reducing Orderings of Sparse Matrices Version 5.1.0:

[Электронный ресурс].

URL: http://glaros.dtc.umn.edu/gkhome/fetch/sw/metis/manual.pdf (Дата обра-

щения: 21.11.2022).

151