Автоматика и телемеханика, № 8, 2023
Оптимизация, системный анализ
и исследование операций
© 2023 г. И.Н. СИНИЦЫН, д-р техн. наук (sinitsin@dol.ru),
Ю.П. ТИТОВ, канд. техн. наук (kalengul@mail.ru)
(Московский авиационный институт
(национальный исследовательский университет);
Федеральный исследовательский центр
“Информатика и управление” РАН, Москва)
УПРАВЛЕНИЕ НАБОРАМИ ЗНАЧЕНИЙ ПАРАМЕТРОВ СИСТЕМЫ
МЕТОДОМ МУРАВЬИНЫХ КОЛОНИЙ
Рассматриваются модификация и применение метода муравьиных ко-
лоний для задачи направленного перебора значений параметров системы
при выполнении расчетных многократных вычислений. Взаимодействие
с пользователем позволяет останавливать процесс полного перебора на-
боров значений параметров, а применение модификации метода мура-
вьиных колоний позволит рассмотреть рациональные наборы на ранних
итерациях. Если пользователь не завершает работу алгоритма, то пред-
ложенные модификации позволяют перебрать все решения методом му-
равьиных колоний. Для модификации метода муравьиных колоний пред-
ложены новая вероятностная формула и различные алгоритмы метода
муравьиных колоний, позволяющие для каждого агента находить новый
набор значений параметров. Оптимальным алгоритмом, по результатам
исследований, является применение повторного бесконечного цикличе-
ского поиска нового решения. Данная модификация позволяет рассмот-
реть все решения и при этом найти все оптимальные решения среди пер-
вых 5% рассмотренных решений.
Ключевые слова: метод муравьиных колоний, параметрический граф, из-
менение порядка следования, вычислительный кластер, оптимизация ги-
перпараметров.
DOI: 10.31857/S000523102308010X, EDN: HDNFSR
1. Введение
В настоящее время в связи с развитием вычислительных кластеров множе-
ство расчетных и оптимизационных задач переносится с человека-эксперта на
вычислительные машины. Для таких систем возникают задачи нахождения
рациональных значений параметров для решения расчетной задачи, назы-
ваемые оптимизацией гиперпараметров [1]. Среди алгоритмов оптимизации
153
гиперпараметров выделяют Байесовский оптимизатор, позволяющий на ос-
нове гипотез и апостериорной информации находить закономерности влия-
ния значений отдельных параметров (и различных комбинаций) на критерии
эффективности [2]. Для многокритериальных и многоэкстремальных задач
часто необходимо рассмотрение всех наборов значений параметров, обычно
методом полного перебора. В работе рассматривается возможность примене-
ния метода муравьиных колоний для решения задачи направленного перебо-
ра наборов гиперпараметров перед отправкой на вычислительную систему. За
счет взаимодействия с пользователем возможна остановка работы метода до
рассмотрения всех наборов значений параметров при нахождении удовлетво-
ряющего пользователя набора. Направленный перебор методом муравьиных
колоний позволит рассмотреть рациональные наборы значений параметров
как можно раньше, но в случае неудовлетворенности пользователя результа-
тами перебрать все наборы значений.
Метод муравьиных колоний первоначально разрабатывался для реше-
ния задачи коммивояжера [3, 4]. Современные исследования позволяют при-
менять метод муравьиных колоний для поиска непрерывной оптимизации.
Поиск методами CACO (ContinuousAntColonyOptimization — непрерывная
оптимизация колонией муравьев) [5], ACOR (Ant Colony Optimization for
continuous domain) [6] и CIAC (ContinuousInteractingAntColony — непрерыв-
но взаимодействующая колония муравьев) [7, 8] не предполагает использо-
вания графа и активно исследовался, в том числе и российскими исследо-
вателями [9, 10]. Исследования описывают возможность применения метода
муравьиных колоний для решения задач на графах: задачи о назначении
с нечетким временем выполнения [11, 12], задачи нахождения оптимальных
маршрутов для группы коммивояжеров [13, 14], задачи поддержки процессов
поставок запасных частей [15]. В мировом сообществе активно исследуются
параметрические задачи, связанные с поиском оптимального набора парамет-
ров, классификации, выявления зависимостей и т.д. [16-19]. Для подобных
задач происходит создание специальной структуры графа. Представленные
методы и модификации метода муравьиных колоний предназначены для по-
иска приближенных, рациональных решений. Обычно все агенты (муравьи)
должны сойтись к одному решению. Поиск новых решений осуществляется
путем мультистарта [9].
Для направленного перебора значений параметров необходимо не сойтись
к одному решению (набору значений параметров), а последовательно рас-
сматривать новые решения до остановки работы метода пользователем или
рассмотрения всех возможных решений. В работе предложены модифика-
ции алгоритма для рассмотрения всех решений, а не сходимости к одному.
Предложенный подход позволяет решать задачи с векторным критерием оп-
тимальности и многомодальными целевыми функциями без повторного за-
пуска алгоритма. При этом сохраняется свойство алгоритмов оптимизации:
наискорейшее нахождение оптимальных решений.
154
2. Модели и методы
В основе метода муравьиных колоний лежит вероятностный поиск дуги в
графе в соответствии с формулой
β
ταij · μ
ij,t
(1)
Pij,k(t) =
).
∑ (
ταiz · μβ
iz,t
z∈Ji,k
С помощью (1) определяется вероятность перехода агента из текущей верши-
ны i в вершины из множества Ji,k на итерации t. По результатам вычислений
определяется вероятность перехода в вершину j для k-го агента. В (1) учи-
тывается информация о длине дуги ταij (удаленность) и некотором весе μβij,t
(феромоне). Значение ταij является фиксированным и не зависит от номера
итерации t. Количество весов μβij,t изменяется между итерациями, обновляя
состояние графа, внешнюю среду для движения агентов.
Для определения значений параметров системы (решения) предлагается
представить наборы значений в виде параметрического графа. Каждое кон-
кретное значение одного параметра представляет вершину графа. Все зна-
чения одного параметра объединяются в слои. Из каждой вершины одного
слоя имеется дуга в каждую вершину следующего слоя. Слои вершин распо-
ложены в определенном порядке, что позволяет уменьшить количество дуг в
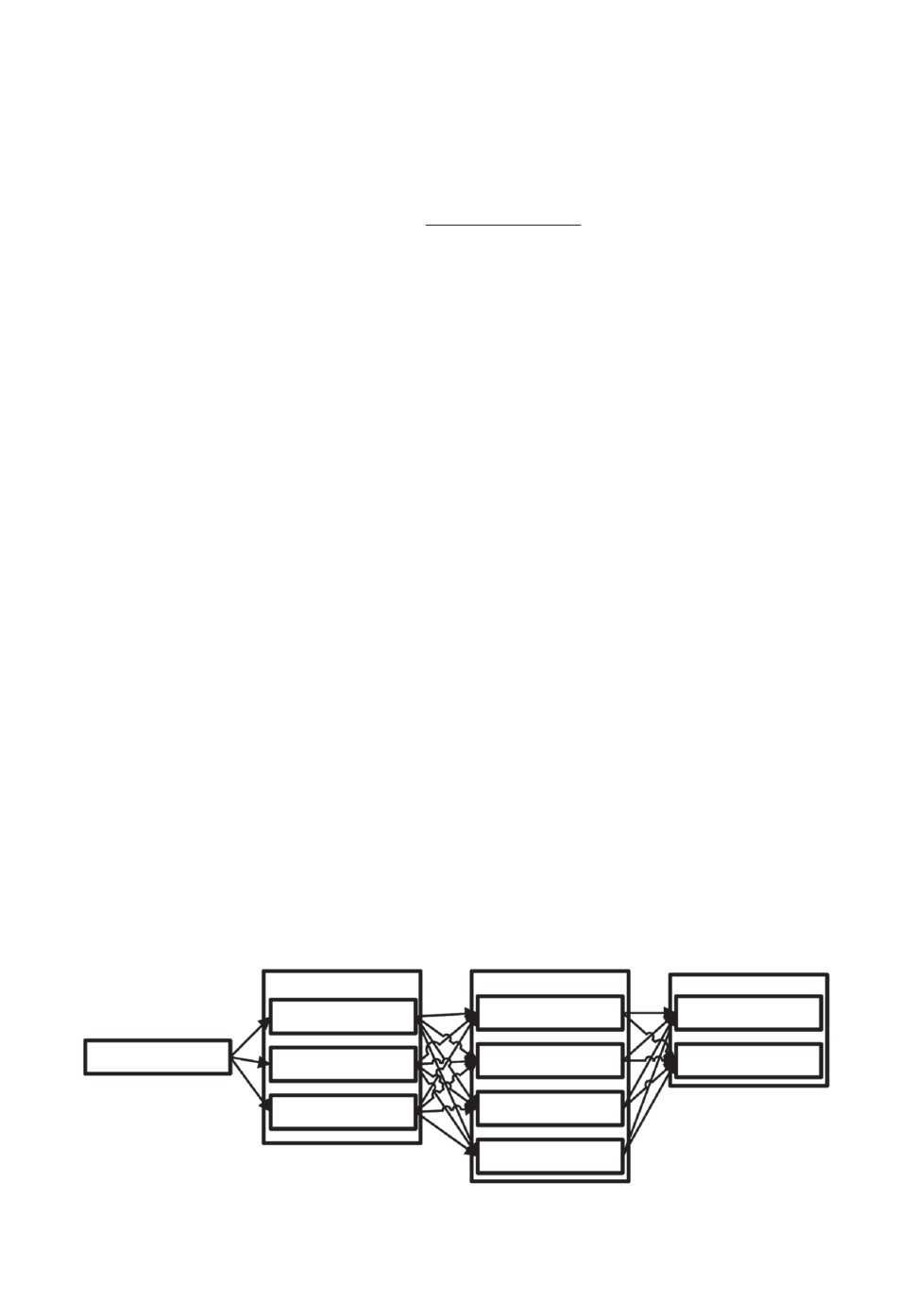
графе. Пример параметрического графа приведен на рис. 1. Подобные графы
встречались в [13, 15, 18-21].
Веса (феромон) в подобном графе заносятся не на дуги, а на вершины.
В результате дуги являются фиктивными, и подобный параметрический граф
может быть представлен в виде множества слоев (параметров) и множества
вершин (значений параметра) [22].
Для параметрического графа в вероятностной формуле (1) значение ταij
может быть задано только на основе априорной информации от эксперта, но
в общем виде данный параметр не может быть определен. При использова-
нии в вероятностной формуле одного сомножителя увеличивается стагнация
Слой 1. Параметр 1
Слой 2. Параметр 2
Слой 3. Параметр 3
Значение 1
Значение 1
Значение 1
Начальная вершина
Значение 2
Значение 2
Значение 2
Значение 3
Значение 3
Значение 4
Рис. 1. Схема структуры параметрического графа.
155
процесса поиска решения. При этом алгоритм сходится к первому хорошему
решению и не продолжает поиск оптимального.
Для решения проблемы стагнации можно производить «сброс» парамет-
рического графа, перевод состояния вершин графа в начальное состояние или
модифицировать вероятностную формулу
(
)β
(
)γ
1
kol(t)ij,t
k1 · μαnormij,t + k2 ·kol(
+ k3 ·
t)ij,t
M axKolj,t
(2)
Pij,k(t) =
(
).
(
)β
(
)γ
∑
kol(t)iz,t
1
k1 · μαnormiz,t + k2 ·
+ k3 ·
kol(t)iz,t
M axKolz,t
z∈Ji,k
Формула (2) представляет собой линейную свертку (а не мультипликатив-
ную, как в (1)) трех слагаемых и весовых коэффициентов. Первое слагаемое
μαnormij,t определяется количеством весов у i-й вершины j-го параметра (слоя
параметрического графа) на итерации t. Для применения данного параметра
во взвешенной сумме необходимо использовать нормализованное значение.
1
Второе слагаемое (
)β определяется количеством посещений агентами
kol(t)ij,t
i -й вершины j -го параметра за время работы алгоритма. Данное слагаемое
увеличивает вероятность посетить вершину, которая редко присутствует в
решениях и позволяет избегать стагнации на ранних итерациях метода мура-
вьиных колоний. В третьем слагаемом (kol(t)ij,t )γ учитывается максималь-MaxKol
j,t
ное количество возможных посещений вершины — значения MaxKolj,t для
параметра j на итерации t. Так как в параметрическом графе на каждом
слое необходимо выбрать одну вершину (одно значение параметра), то мож-
но вычислить общее количество решений, наборов значений параметров. Об-
щее количество решений может быть вычислено как произведение количества
вершин в каждом слое. Максимальное количество решений, в которых может
содержаться конкретная вершина параметрического графа, вычисляется как
отношение общего количества решений и количества вершин в данном слое,
т.е. для каждой вершины слоя j значение MaxKolj,t будет одинаковым. Тре-
тье слагаемое на поздних итерациях позволяет увеличить вероятность выбора
вершины, для которой рассмотрено большинство вариантов решений. Если
для вершины рассмотрены все возможные решения, то из вероятностного по-
иска данную вершину можно исключить. Аддитивная свертка позволяет ком-
пенсировать значения слагаемых. Вершины с большим количеством весов и
частыми посещениями (часто рассматриваемые вершины) могут быть ком-
пенсированы вершинами с небольшим количеством посещений (редкие вер-
шины) или вершинами, для которых рассмотрены практически все решения.
Другой особенностью модификации алгоритма является необходимость
взаимодействия с внешней вычислительной системой. Для таких модифи-
каций необходимо хранить состояние системы, вычисленное для конкретного
решения. Если метод муравьиных колоний повторно находит решение, то дан-
ное решение повторно не отправляется на вычислитель, а значение целевой
функции берется из Хэш-таблицы [15, 21].
156
StartACO(): для АСО
Задание параметров метода
муравьиных колоний
Все ли
Да
Пока
Да
итерации завершены?
не пройдены все
StartACO():
не нулевые агенты
Нет
Нет
Создание N агентов СreateAnt():
Конец
Для каждой вершины из
пути агента увеличить:
1) Количетво весов на
Пока все
величину весов у агента
Да
агенты не определили
2) Количество посещений
уникальный набор
вершины на 1
параметров
Нет
Итератор
Ant.AntArr[NomAnt].way=next(wayPg)
Переход к следующему агенту
Все слои
Да
пройдены агентом?
while i<len(Array Node)
Испарение весов с
параметрического графа:
Нет
DecreasePar(Value: float):
Выбрать вершину из соседнего слоя
Нормализация весов
Если количество посещений
в вершинах
вершины меньше количества
параметрического графа
возможных решений, то
увеличиваем сумму в
знаменателе на новые слагаемые
Переход на следующую
в соответствии с вероятностной
итерацию алгоритма
формулой sum = sum +
ProbabilityNode(FrrayNode[i)])
Добавляем значение суммы
в массив probability
Генерируем число и вычисляем
номер следующей вершины
while rnd>probability[i]/sum:
Вычисление хэш-функции
Вычисление значений критериев
полученного набора значений
для определенного набора
до PathStr(path: array of int)
параметров по рузельтатам
работы имитационной модели
Взять значение целевой функции
из Хэш-таблицы и определить
Значение
Нет
количество весов агента
Занесение значения хэш-функции
Хэш-функции есть
в хэш-таблицу
в Хэш-таблице?
addPath(path: array of int; OF: float)
Установить количество весов
для агента = 0
Да
Установить количество весов
агента из значений целевой
В зависимости от
Выполнить повторный
функции
выбранного алгоритма
циклический поиск
Итератор
Ant.AntArr[NomAnt].way=next(wayPg)
Выполнить поиск нового
решения путем обхода дерева
Переход к следующему агенту
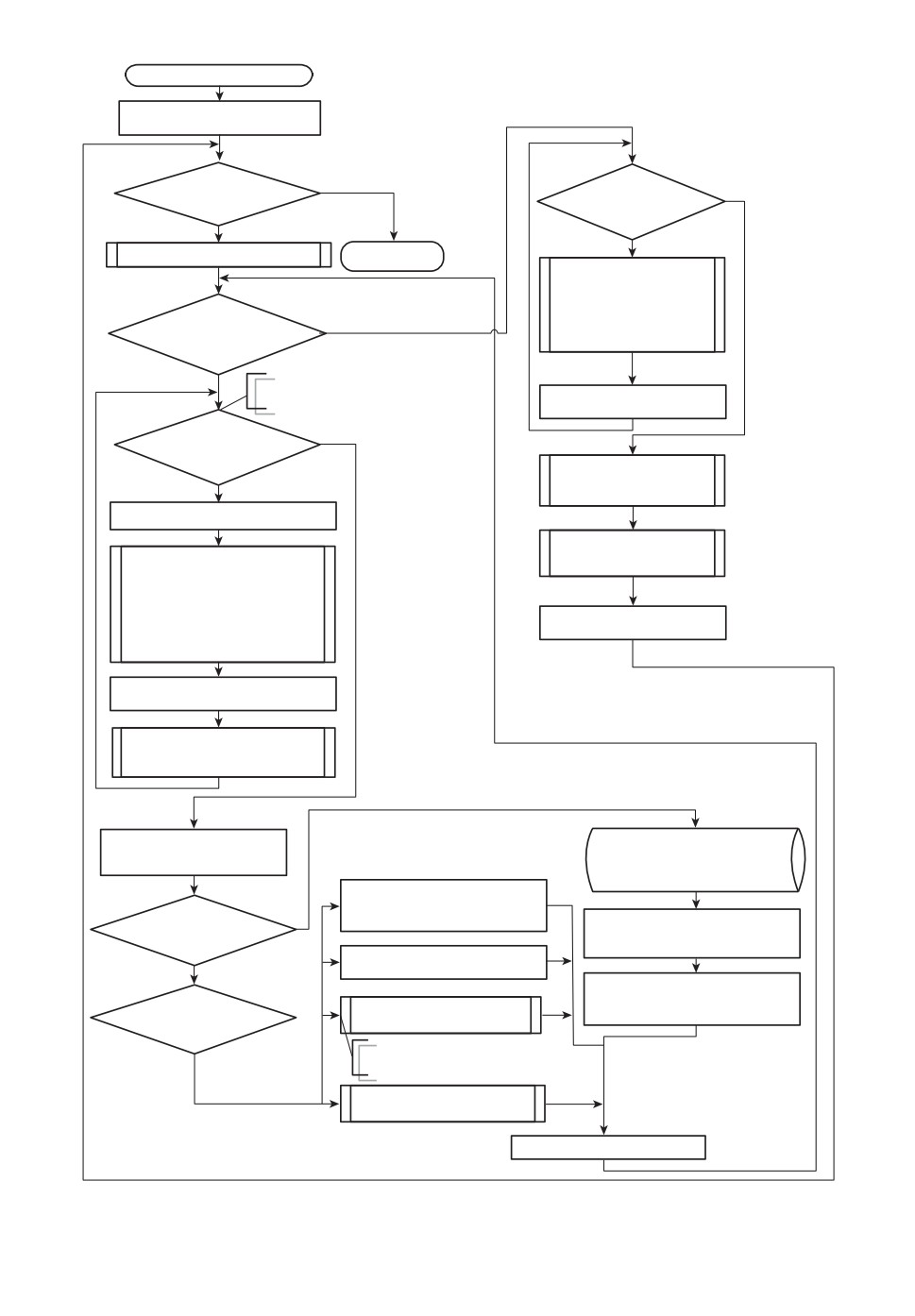
Рис. 2. Схема алгоритма модифицированного метода муравьиных колоний.
157
Для рассматриваемого алгоритма важен поиск нового решения на каждой
итерации и поэтому, если решение уже имеется в Хэш-таблице, возможны
различные действия:
1. Используя значения целевой функции из Хэш-таблицы, занести веса,
как в оригинальном алгоритме.
2. Игнорировать агента. Агент не заносит веса на параметрический граф.
3. Повторный поиск нового, еще не рассмотренного на вычислителе, реше-
ния методом муравьиных колоний с ограничением на количество ите-
раций. Если за установленное количество итераций не найдено новое
решение, то агент игнорируется.
4. Повторный поиск нового, еще не рассмотренного на вычислителе, реше-
ния методом муравьиных колоний неограниченным количеством итера-
ций. Ограничение в пункте № 3 может решить проблему стагнации.
5. Повторный поиск нового решения другим алгоритмом. Рассматрива-
лась возможность обхода параметрического графа как дерева.
Схема алгоритма предлагаемой модификации метода муравьиных колоний
приведена на рис. 2.
3. Эксперимент
Задачами направленного перебора значений параметров являются:
— перебор всех, без исключения, наборов значений параметров;
— наискорейшее получение оптимального набора значений параметра.
Можно заметить, что обе задачи противоречат друг другу, так как среди
всех наборов значений параметров всегда будет наилучший. Но так как си-
стема взаимодействует с вычислителем и пользователем в режиме реального
времени, то имеется возможность остановки программы пользователем, ес-
ли найдено удовлетворяющее его решение. Также следует отметить возмож-
ность использования векторного критерия, переводящего задачу в область
поддержки принятия решений и многокритериальной оптимизации [20].
Эффективность модификаций метода муравьиных колоний определяется
двумя основными оценками:
— возможность алгоритма рассмотреть все решения. Определяется значе-
нием критерия: «оценка вероятности найти новое решение агентом». Данная
оценка вычисляется путем отношения количества найденных решений за вре-
мя работы алгоритма на общее количество рассмотренных решений;
— скорость нахождения оптимального решения. Определяется значением
критерия: «оценка математического ожидания номера итерации, на котором
данное решение было найдено».
Проведение экспериментов осуществлялось на программном обеспечении
ACO Cluster, написанном на языке Python. В качестве тестовых данных рас-
сматривалось большинство из бенчмарков, взятых из [22, 23], и тестовые гра-
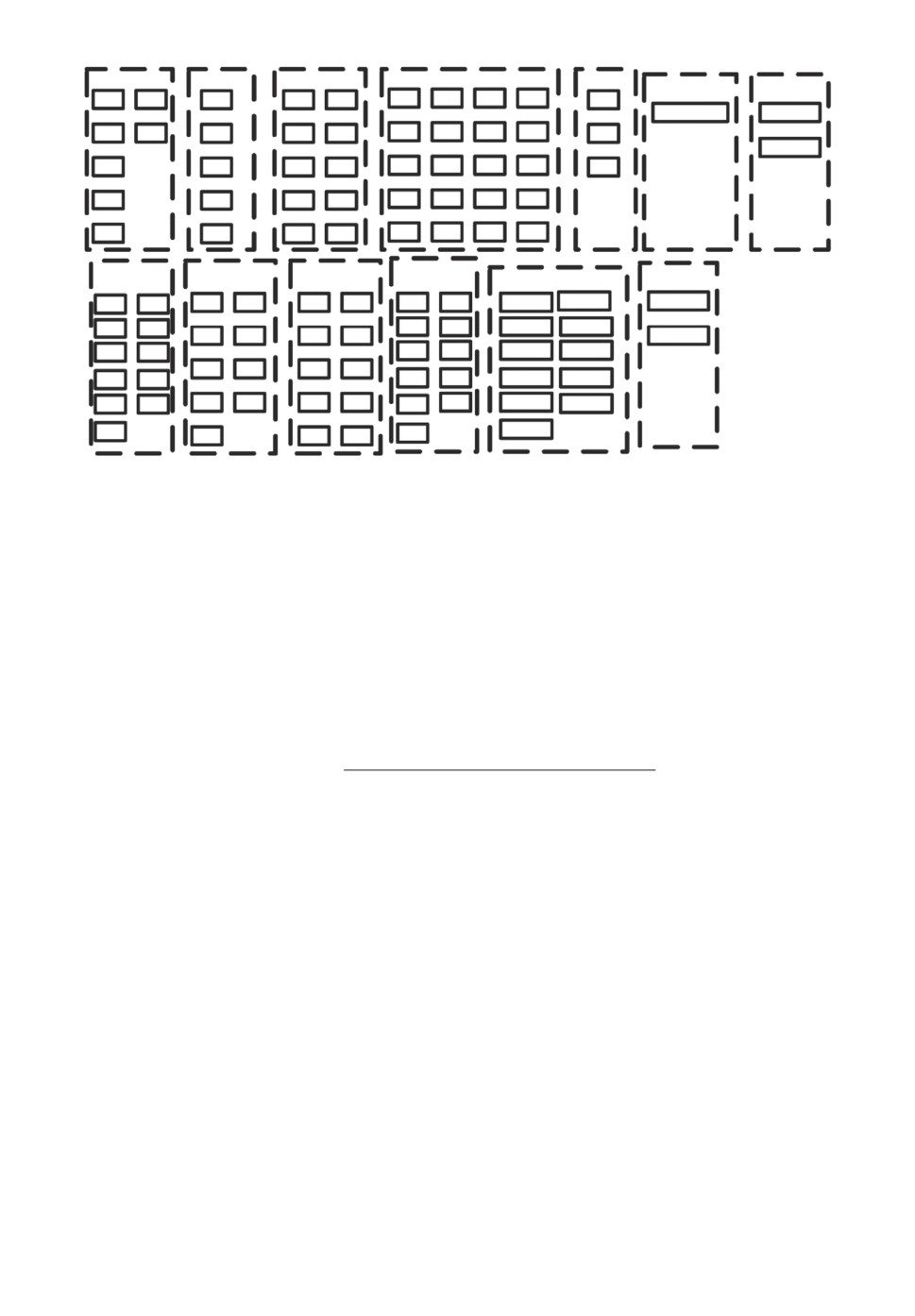
фы большой размерности [21]. Структура графа большой размерности при-
ведена на рис. 3. Представленный граф большой размерности содержит бо-
158
Прибор 1
Прибор 2
Прибор 3
Прибор 4
Прибор 5
Нагрузка
Нагрузка
1
6
1
1
6
1
6
11
16
1
Отсутствует
Паретто
2
7
2
2
7
2
7
12
17
2
Свертка
3
3
3
8
3
8
13
18
3
4
4
4
9
4
9
14
19
5
5
5
10
5
10
15
20
Размер
Размер
Размер
Размер
Давление
Размер детали 5
детали 1
детали 2
детали 3
детали 4
5,24
5,30
15,3
16,3
1
6
0,01
0,30
10*10^4
40*10^4
Сильное
5,25
5,31
0,05
0,35
15*10^4
45*10^4
15,5
16,5
2
7
Слабое
5,26
5,32
0,10
0,40
20*10^4
50*10^4
15,7
16,7
3
8
5,27
5,33
0,15
0,45
25*10^4
55*10^4
5,28
5,34
15,9
16,9
4
9
0,20
0,50
30*10^4
60*10^4
5,29
35*10^4
16,1
5
10
0,25
Рис. 3. Схема параметрического графа большой размерности.
лее 109 решений по 13 параметрам, заданных в дискретных и качественных
шкалах. При 25 агентах на одной итерации и 20 000 итерациях максимально
может быть рассмотрено только 0,05% решений от общего числа.
Для анализа работы алгоритма при поиске последних (еще не рассмот-
ренных) решений в результатах приведены исследования функции «Carrom
table function»:
(
)2
cos(x1) cos(x2)e|100-(x1+x2)0,5|
(3)
f (x) = -
30
Параметрический граф для функции (3) содержит два слоя, для парамет-
ров x1 и x2. В каждом слое параметрического графа имеется по 201 вер-
шине, определяющих конкретные значения параметра в диапазоне [-10, 10]
с точностью 0,1. Для рассмотрения всех решений 25 агентами необходимо
1936 итераций метода муравьиных колоний при условии, что каждый агент
найдет новое решение.
4. Результат
В работе проведено исследование следующих модификаций алгоритма му-
равьиных колоний:
— ACOCC (ACO Cluster Classic) — Классический метод муравьиных ко-
лоний. В (2) коэффициенты k2 и k3 равны 0. В данном случае формула
аддитивной свертки 2 становится мультипликативной сверткой формулы (1)
с параметром ταij = 1. Если найдено уже рассмотренное алгоритмом решение,
то значение целевой функции определяется из Хэш-таблицы.
159
Таблица 1. Оценка математического ожидания времени (в сек.) поиска решения
одним агентом
Кол-во
ACOCC ACOCN ACOCNI ACOCCy3 ACOCCyI
ACOCT
итер.
2500 1,404 · 10-4 1,547 · 10-4 1,562 · 10-4 1,627 · 10-4 1,619 · 10-4
1,887 · 10-4
5000 1,381 · 10-4 1,517 · 10-4 1,560 · 10-4 1,648 · 10-4 1,636 · 10-4
2,745 · 10-4
7500 1,388 · 10-4 1,505 · 10-4 1,567 · 10-4 1,665 · 10-4 1,647 · 10-4
4,158 · 10-4
10000 1,391 · 10-4 1,501 · 10-4 1,578 · 10-4 1,690 · 10-4 1,654 · 10-4
5,645 · 10-4
12500 1,370 · 10-4 1,547 · 10-4 1,562 · 10-4 1,706 · 10-4 1,657 · 10-4
6,980 · 10-4
15000 1,364 · 10-4 1,526 · 10-4 1,569 · 10-4 1,700 · 10-4 1,650 · 10-4
8,593 · 10-4
17500 1,328 · 10-4 1,472 · 10-4 1,585 · 10-4 1,695 · 10-4 1,655 · 10-4
9,776 · 10-4
20000 1,325 · 10-4 1,469 · 10-4 1,582 · 10-4 1,741 · 10-4 1,688 · 10-4 10,549 · 10-4
Таблица 2. Оценка вероятности найти новое решение одним агентом на итерации
метода муравьиных колоний
Кол-во итер. ACOCC ACOCN ACOCNI ACOCCy3 ACOCCyI ACOCT
2500
0,248
0,618
0,966
1,000
1,000
1,000
5000
0,122
0,381
0,951
1,000
1,000
1,000
7500
0,082
0,282
0,942
1,000
1,000
1,000
10000
0,063
0,223
0,935
1,000
1,000
1,000
12500
0,049
0,184
0,929
1,000
1,000
1,000
15000
0,041
0,158
0,925
1,000
1,000
1,000
17500
0,035
0,136
0,921
1,000
1,000
1,000
20000
0,030
0,125
0,918
1,000
1,000
1,000
— ACOCN (ACO Cluster New) — Аналогичный классическому методу му-
равьиных колоний, но в (2) коэффициенты k2 и k3 равны 1. Вероятность
перехода определяется аддитивной сверткой.
— ACOCNI (ACO Cluster New Ignor) — В (2) коэффициенты k2 и k3 равны
1. Если найдено решение, уже записанное в Хэш-таблицу, то данный агент
игнорируется, не заносит веса на вершины параметрического графа.
— ACOCCy3 (ACO Cluster Cycle3) — В (2) коэффициенты k2 и k3 рав-
ны 1. Если найдено решение, уже записанное в Хэш-таблицу, то производит-
ся повторный поиск решения методом муравьиных колоний. Поиск нового
решения производится циклически. Установлено ограничение на количество
итераций повторного поиска, равное 3. Если за установленное количество
итераций не найдено новое решение, то агент игнорируется.
— ACOCCyI (ACO Cluster Cycle Infinity) — В (2) коэффициенты k2 и k3
равны 1. Если найдено решение, уже записанное в Хэш-таблицу, то произво-
дится повторный поиск решения методом муравьиных колоний. Поиск нового
решения производится циклически без ограничения на количество итераций.
— ACOCT (ACO Cluster Tree) — В (2) коэффициенты k2 и k3 равны 1.
Если найдено решение, уже записанное в Хэш-таблицу, то производится по-
160
Таблица 3. Оценка вероятности найти новое решение одним агентом на итерации
метода муравьиных колоний
Кол-во итер. ACOCC ACOCN ACOCNI ACOCCy3 ACOCCyI ACOCT
2500
0,03
0,31
0,21
0,27
0,24
0,13
5000
0,03
0,49
0,26
0,26
0,33
0,25
7500
0,03
0,50
0,35
0,30
0,32
0,24
10000
0,02
0,60
0,22
0,32
0,31
0,33
12500
0,03
0,78
0,32
0,37
0,42
0,27
15000
0,02
0,71
0,31
0,44
0,37
0,31
17500
0,03
0,74
0,28
0,39
0,44
0,26
20000
0,03
0,72
0,41
0,46
0,43
0,39
Таблица 4. Оценка математического ожидания номера решения (в %), на котором
были найдены оптимальные значения параметров
Кол-во
ACOCC ACOCN ACOCNI ACOCCy3 ACOCCyI ACOCT
итер.
2500 0,801·10-6 2,956·10-6 3,404·10-6
2,970 · 10-6
3,299 · 10-6
2,863 · 10-6
5000 1,122·10-6 3,191·10-6 4,501·10-6
4,415 · 10-6
5,648 · 10-6
5,030 · 10-6
7500 1,014·10-6 3,378·10-6 5,701·10-6
6,137 · 10-6
5,830 · 10-6
6,838 · 10-6
10000 1,142·10-6 3,667·10-6 5,693·10-6
5,337 · 10-6
5,910 · 10-6
7,704 · 10-6
12500 0,829·10-6 3,770·10-6 6,779·10-6
6,320 · 10-6
8,108 · 10-6
5,269 · 10-6
15000 0,740·10-6 3,741·10-6 8,240·10-6 10,174·10-6
8,794 · 10-6
7,834 · 10-6
17500 1,393·10-6 3,845·10-6 8,175·10-6
9,221 · 10-6 11,678 · 10-6
15,820·10-6
20000 1,119·10-6 3,936·10-6 9,864·10-6 11,344·10-6 10,513·10-6
23,592·10-6
вторный поиск нового решения другим алгоритмом. Рассматривается обход
параметрического графа как дерева.
Оценки результатов работы модификаций для параметрического графа
большой размерности приведены в табл. 1-4. При применении алгоритма
ACOCN количество решений, необходимых для поиска наилучшего набора
значения параметров, минимально, и слабо возрастает с увеличением ко-
личества итераций (3-й столбец табл. 4). Быстрее находит решение только
алгоритм ACOCC, но вероятность найти оптимальное решение алгоритмом
ACOCC менее 0,1 (2-й столбец табл. 3). Алгоритм ACOCC стагнирует на бли-
жайшем рациональном решении. Алгоритмы, использующие повторный по-
иск для нулевых агентов (ACOCCy3, ACOCCyI и ACOCT), для каждого аген-
та находят новое решение (столбцы 5-7 табл. 2). Для 25 агентов за 2 · 104 ите-
раций представленными алгоритмами будет рассмотрено 5 · 105 наборов зна-
чений параметров. Время, затраченное на поиск агентом решения, для боль-
шинства алгоритмов не зависит от количества итераций алгоритма (табл. 1).
В результате возможно прогнозировать необходимое количество итераций
для поиска всех решений. Исключением является алгоритм ACOCT, который
при увеличении количества итераций требует больше времени на поиск пути
одним агентом. По возрастанию времени поиска агентом решения можно про-
161
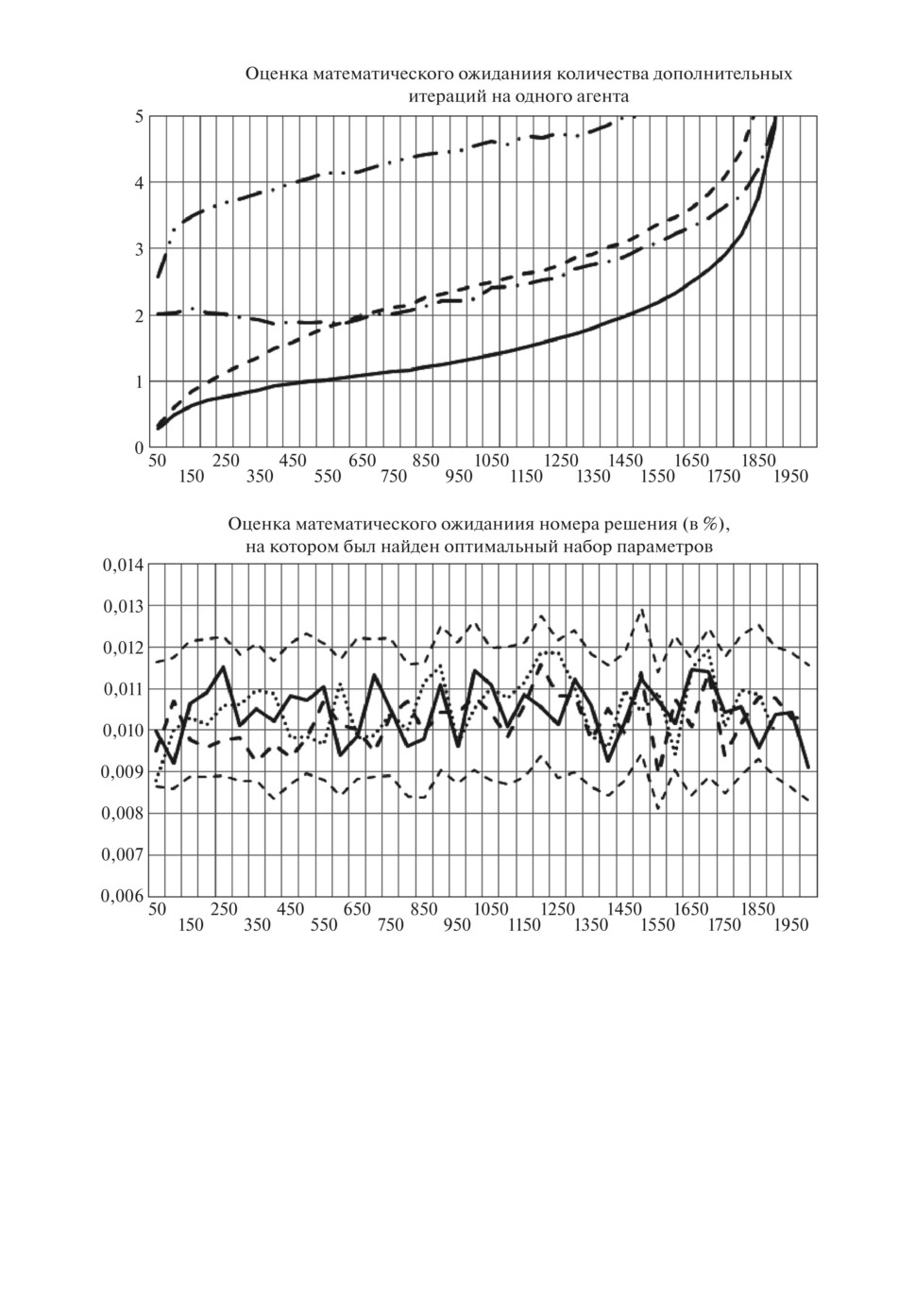
Рис. 4. Зависимость эффективности работы алгоритма от количества итераций ме-
тода муравьиных колоний для параметрического графа «Carrom table function».
ранжировать алгоритмы ACOCC, ACOCN, ACOCNI, ACOCCy3 и ACOCCyI.
Время поиска агентом решения в алгоритмах ACOCCy3 и ACOCCyI близкое,
так как количество дополнительных итераций чаще всего меньше ограниче-
ния в 3 итерации.
Следует отметить, что циклический поиск фактически увеличивает коли-
чество итераций, так как работает по правилам метода муравьиных колоний.
Если среди десяти агентов на итерации один не нашел нового решения и ему
162
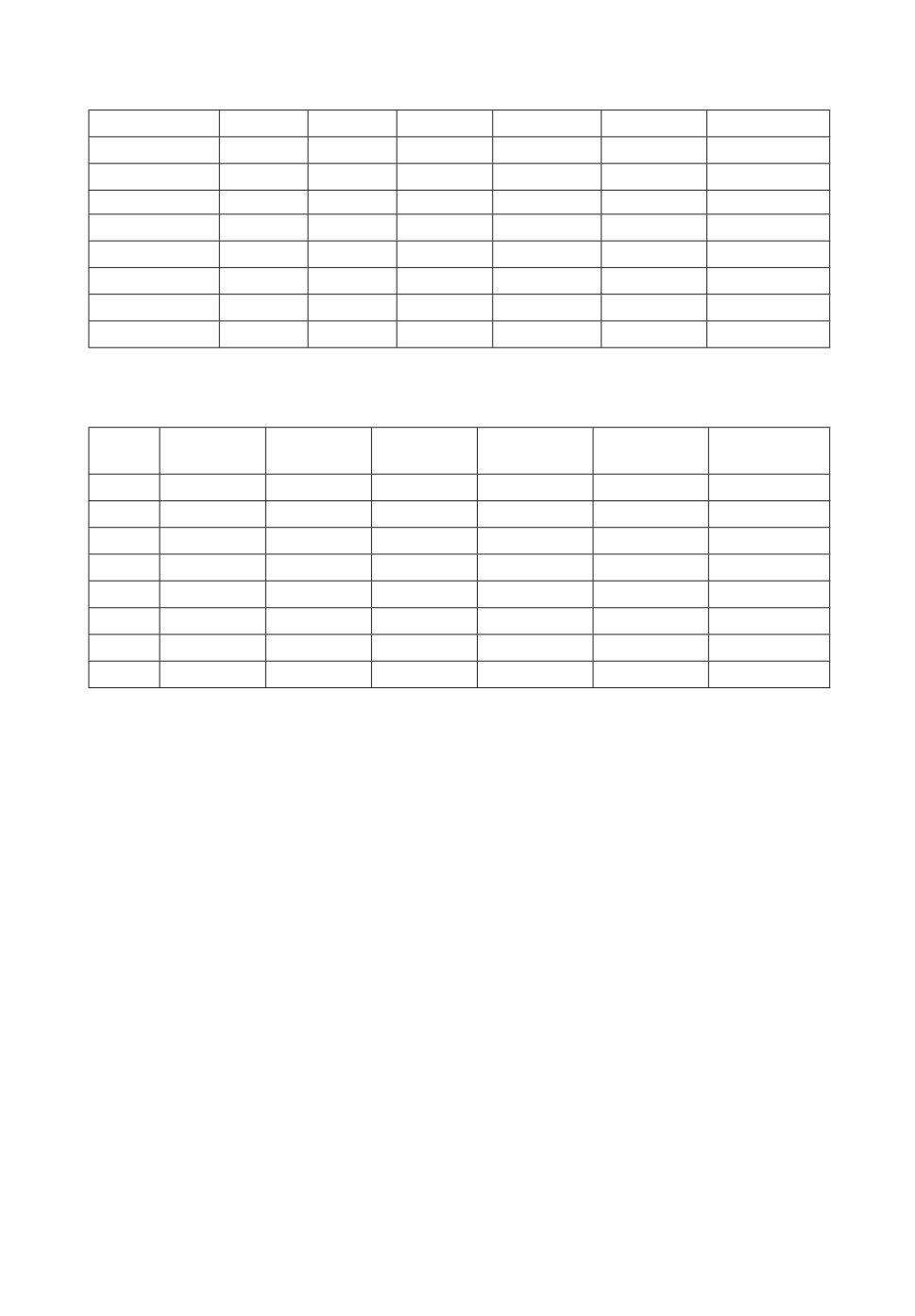
Таблица 5. Оценка математического ожидания количества дополнительных
итераций модификации ACOCCyI
№ итер.
1900
1910
1920
1930
1940
1950
k2=0; k3=0;
8,379
8,712
9,582
10,487
23,004
25,153
k2=0; k3=0; ignor;
8,399
9,028
9,880
10,719
19,658
18,996
k2=0; k3=1;
5,035
5,248
5,735
6,536
13,408
12,861
k2=0; k3=1; ignor;
5,054
5,291
5,711
6,558
10,658
10,299
k2=1; k3=0;
7,049
7,780
8,990
11,493
44,962
42,247
k2=1; k3=0; ignor;
7,113
7,744
8,698
10,263
13,658
13,533
k2=1; k3=1;
4,864
5,312
5,990
7,383
19,585
19,828
k2=1; k3=1; ignor;
4,874
5,314
5,977
7,268
11,172
11,292
потребовалось десять дополнительных итераций, то фактически было вы-
полнено двадцать итераций. В отличие от двадцати итераций оригинального
алгоритма для данных итераций не происходит обновления весов на парамет-
рическом графе и возможен контроль необходимого количества итераций.
Так как модификации ACOCCy3 и ACOCCyI показали хорошую сходи-
мость к оптимальному решению и каждый агент в данном алгоритме на-
ходит новое решение (табл. 2), то исследуем возможность нахождения всех
решений в параметрическом графе. Для исследования воспользуемся гра-
фом малой размерности (40 401 решение) с целевой функцией (3) «Carrom
table function». Результаты применения модификации ACOCCyI приведены
на рис. 4. В отличие от ACOCCyI модификацией ACOCNI за 2000 итераций
рассмотрено только 35% решений. При исследовании модификации ACOCCyI
изменялись значения коэффициентов k2 и k3 в (2).
Длинные штрихпунктирные линии с точками на рис. 4 определяют мо-
дификацию, у которой k2 = 0 (при k3 = 0 — двойная точка, при k3 = 1 —
одна точка). При k2 = 0 оптимальное решение с вероятностью 1 определя-
ется только после 1000 итераций (более 60% рассмотренных решений). Бо-
лее эффективными являются модификации, в которых k2 = 1 (при k3 = 0 —
штриховая линия, при k3 = 1 — сплошная линия). При любом количестве
итераций оптимальное решение находится после рассмотрения от 0,009%
(40401 · 0,009 = 363) решений до 0,012% (484 решений) — доверительный ин-
тервал с доверительной вероятностью 0,99 (нижний график рис. 4). Для на-
хождения 0,99% оптимального решения требуется в 2 раза меньше рассмот-
ренных решений, наборов значений параметров. Для модификации ACOCNI
(линия из точек) требуется аналогичное количество рассмотренных решений
для нахождения оптимального.
На верхнем графике рис. 4 отображено количество требуемых дополни-
тельных итераций на одного агента. В среднем агенту требуется менее 5 до-
полнительных итераций при рассмотрении большинства возможных реше-
ний. В результате устанавливать ограничение, как в модификации ACOCCy3,
неэффективно. Минимальное количество дополнительных итераций, необхо-
163
Carrom table function
2000
0
5
1500
10
1000
15
20
500
25
10
5
10
5
0
0
5
5
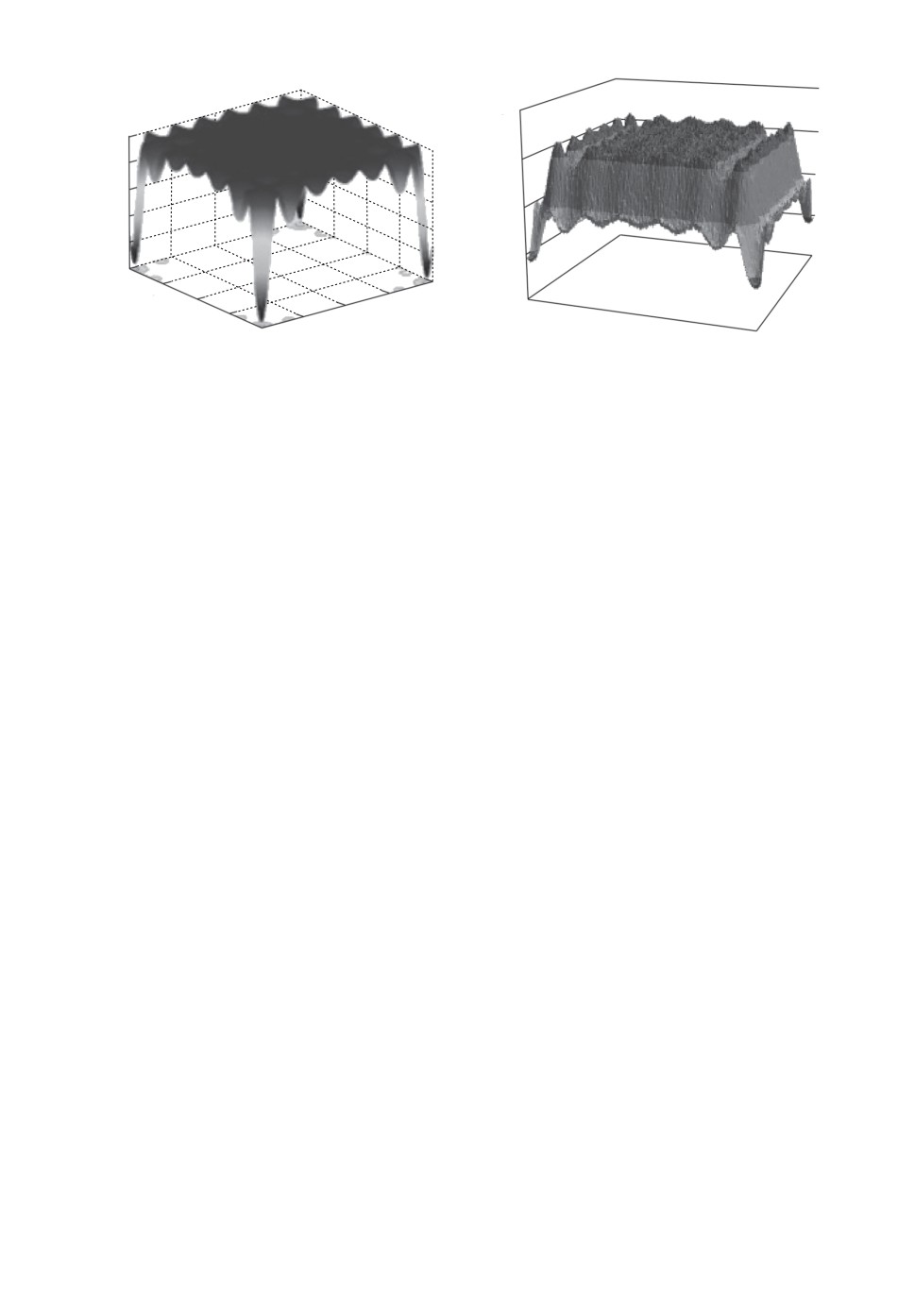
10
Рис. 5. График функции и оценки номера решения для «Carrom table function».
димых для поиска нового, еще не рассмотренного, набора значений парамет-
ров, гарантирует минимальные задержки по времени работы алгоритма.
Неэффективное поведение модификации происходит на последних
36-ти итерациях, на которых необходимо найти последние 900 оставшихся
не рассмотренными решений (табл. 5). Четные строки таблицы с пометкой
ignor — это результаты работы модификации ACOCCyI с условием игнори-
рования вершин, для которых рассмотрены все решения. Модификация не
рассматривает вершины, у которых kol(t)ij,t = MaxKolj,t в вероятностной
формуле (2).
Результаты, представленные в табл. 5, доказывают эффективность при-
менения третьего слагаемого суммы в формуле (2). При k3 = 1 количество
необходимых дополнительных итераций существенно меньше, чем при k3 = 0.
Меньшее количество дополнительный итераций соответствует меньшему вре-
мени поиска оставшихся не рассмотренными наборов значений параметров.
Высокую эффективность показывает игнорирование вершин, для которых
рассмотрены все возможные решения (строки с надписью ignor).
Оба тестовых параметрических графа имеют несколько оптимальных
(равных по значению целевой функции) значений параметров. На рис. 5 при-
ведены график функции «Carrom table function» и график оценки номера
решения, на котором рассматривались конкретные значения параметров x1
и x2 при 3000 прогонах модификации ACOCCyI метода муравьиных коло-
ний. При множестве прогонов алгоритм находит все 4 оптимума на самых
ранних итерациях. График оценки номера итерации визуально повторяет
график функции, т.е. оптимальные и рациональные решения, предложенные
модификацией метода муравьиных колоний, статистически определяются на
начальных операциях.
5. Заключение
В работе рассматривалась задача направленного перебора наборов значе-
ний параметров. Для решения задачи используется параметрический граф, в
164
котором набор параметров представлен в виде множества вершин, объединен-
ных в группы — слои. В данном графе отсутствуют дуги, и необходимо опре-
делиться с порядком следования слоев, что может приводить к расхождению
в эффективности предложенных модификаций. Но достоинством данного ви-
да параметрического графа является простота его создания для пользовате-
ля. Для метода муравьиных колоний рассматривалась задача перебора всех
значений параметров системы. Оптимизационные свойства метода позволят
рассмотреть оптимальный набор значений параметров как можно раньше.
Предложены модификации, позволяющие упростить и контролировать поиск
новых наборов значений параметров методом муравьиных колоний. Предпо-
лагается использование интерфейса для взаимодействия с пользователем с
целью обеспечения возможности остановки работы метода при нахождении
удовлетворяющего пользователя набора значений параметров системы. Если
такой набор не найден, то метод муравьиных колоний рассмотрит все ком-
бинации дискретных значений параметров. Данный подход также позволит
решать многоэкстремальные и многокритериальные задачи.
Рассмотренный метод муравьиных колоний является достаточно мощным
инструментом решения поставленной задачи, благодаря вероятностной фор-
муле выбора следующей вершины. Предложена простая модификация веро-
ятностной формулы, позволяющая существенно улучшить показатели эф-
фективности работы алгоритма. Данная модификация определяет вероят-
ность выбора следующей вершины как аддитивную свертку трех компонен-
тов: весов в вершине, количества посещений вершины агентами и количества
оставшихся решений, содержащих данную вершину.
В работе предложены модификации, позволяющие выбирать различные
алгоритмы поведения при получении агентом уже рассмотренного решения.
Проверка найденного решения осуществляется с помощью Хэш-таблицы. По-
вторный циклический поиск показал хорошую сходимость к оптимальному
решению и наилучшую работу при поиске последних наборов значений пара-
метров на различных параметрических графах. На графе большой размерно-
сти повторный циклический поиск показывает результаты хуже, чем работа
оригинального алгоритма с новой вероятностной формулой.
Рассмотрение всех возможных комбинаций значений параметров систе-
мы является специфической задачей, так как перебрать все варианты можно
полным перебором и в результате найти оптимальное решение. Большинство
алгоритмов перебора вариантов системы нацелены на поиск рационального
решения путем сходимости к нему, и “плохие” решения подобные алгоритмы
не рассматривают. Несмотря на вероятностную сходимость метода муравьи-
ных колоний к одному решению, в работе доказана возможность алгоритмом
рассмотреть все решения, даже все неоптимальные, при любом распределе-
нии вероятностной формулы. Для многомодальных функций можно отка-
заться от процедуры мультистарта, вносящей дополнительную стохастику в
работу алгоритма.
165
К недостаткам метода муравьиных колоний относят наличие большого ко-
личества свободных параметров [9]. Параметры, относящиеся к “классическо-
му” методу муравьиных колоний (количество агентов на итерации, коэффи-
циент испарения весов и коэффициент добавления), подробно рассмотрены
в [21]. При исследовании асинхронного поведения метода муравьиных коло-
ний при взаимодействии с асинхронным вычислительным кластером пред-
полагается устанавливать количество агентов равным количеству потоков,
осуществляющих вычисления на кластере. Отсутствие сходимости алгорит-
ма к одному решению не требует установки граничных условий и параметров
мультистарта. Но наличие коэффициентов в новой вероятностной формуле
требует дополнительных исследований. Исследованы различные дискретные
значения весовых и степенных коэффициентов в формуле (2). Оптимальны-
ми являются значения, равные 1. При этом следует отметить, что ситуация,
когда весовые коэффициенты принимают вещественные значения и в сумме
дают 1, требует дальнейших исследований. Также дальнейших исследований
требует динамическое изменение значений коэффициентов, так как коэффи-
циент k1 эффективен на ранних итерациях для быстрого поиска оптимально-
го набора значений параметров, а коэффициент k3 — для поиска оставшихся
решений на последних итерациях.
Дальнейшее развитие предполагается в следующих направлениях.
1. Предложенный альтернативный алгоритм поиска нового решения путем
обхода дерева показал низкую эффективность и требует доработки.
2. Не рассматривалась ценность отдельных слоев-параметров параметри-
ческого графа. Данное исследование позволит выделить наиболее и наи-
менее значимые параметры технической системы.
3. Вероятностная формула выбора агентом следующей вершины является
очень мощным инструментом, и возможна ее модификация с учетом
ценности отдельных слоев.
4. Необходимо дальнейшее исследование структуры параметрического
графа, разделение слоя на подслои, перестановки слоев и способов фор-
мирования графа.
5. Применение предложенного метода для решения задач с векторным
критерием. Исследования модификаций для быстрого рассмотрения на
кластере всех решений из множества Парето.
6. При работе метода муравьиных колоний совместно с асинхронным
вычислителем. Предполагается получение значений целевой функции
асинхронно по отношению к работе метода муравьиных колоний. Для
такой модификации предлагается каждого агента просчитывать в сво-
ем потоке, и в результате рассмотреть асинхронную работу метода му-
равьиных колоний. Добавление и испарение весов с параметрического
графа может осуществляться в виде отдельных потоков.
166
СПИСОК ЛИТЕРАТУРЫ
1.
Feurer M., Hutter F., Vanschoren J. Hyperparameter Optimization // The Springer
Series on Challenges in Machine Learning. Springer, Cham. 2019.
2.
Koehrsen W. A conceptual explanation of bayesian hyperparameter optimization
for machine learning. 2018. (Открытый доступ 18.01.2023:
based-hyperparameter-optimization-for-machine-learning-b8172278050f)
3.
Colorni A., Dorigo M., Maniezzo V. Distributed Optimization by Ant Colonies //
Proc. First Eur. Conf. on Artific. Life, Paris, France, Elsevier Publishing. 1992.
Р. 134-142.
4.
Dorigo M., Stützle T. Ant Colony Optimization // MIT Press. 2004. P. 321.
5.
Socha K., Dorigo M. Ant colony optimization for continuous domains // Eur. J.
Oper. Res., 2008, V. 185. Issue 3. pp. 1155-1173.
6.
Mohamad M., Tokhi M., Omar O.M. Continuous Ant Colony Optimization for
Active Vibration Control of Flexible Beam Structures // IEEE International Conf.
on Mechatronics (ICM). Apr., 2011. P. 803-808.
7.
Карпенко А.П., Чернобривченко К.А. Эффективность оптимизации методом
непрерывно взаимодействующей колонии муравьев (CIAC) // Наука и образо-
вание: научное издание МГТУ им. Н.Э. Баумана. 2011. № 2.
8.
Карпенко А.П., Чернобривченко К.А. Мультимемеевая модификация гибридно-
го муравьиного алгоритма непрерывной оптимизации HCIAC. // Наука и обра-
зование: научное издание МГТУ им. Н.Э. Баумана. 2012. № 9.
9.
Карпенко А.П. Современные алгоритмы поисковой оптимизации. Алгоритмы,
вдохновленные природой // М.: Изд-во МГТУ им. Баумана. 2-е изд. 2017. 446 с.
10.
Саймон Д. Алгоритмы эволюционной оптимизации : практическое руководство.
М.: ДМК Пресс. 2020. 1002 с.
11.
Sudakov V.A., Titov Y.P. Modified Method of Ant Colonies Application in Search
for Rational Assignment of Employees to Tasks // Proceedings of 4th Computational
Methods in Systems and Software 2020. Vol. 2, Vsetin: Springer Nature, 2020. P. 342-
348. DOI 10.1007/978-3-030-63319-6_30
12.
Хахулин Г.Ф., Титов Ю.П. Система поддержки решений поставок запасных
частей летательных аппаратов военного назначения // Изв. Самарского научн.
центра РАН. 2014. Т. 16. № 1-5. С. 1619-1623.
13.
Синицын И.Н., Титов Ю.П. Развитие стохастических алгоритмов муравьиной
организации // Бионика - 60 лет. Итоги и перспективы. Сборник статей Первой
Междунар. науч.-практ. конф. Под редакцией А.П. Карпенко. 17-19 декабря
2021 г., г. Москва. Под ред. 2022. C. 210-220.
14.
Титов Ю.П. Модификации метода муравьиных колоний для решения задач раз-
работки авиационных маршрутов // АиТ. 2015. № 3. С. 108-124.
Titov Y.P. Modifications of the ant colony method for aviation routing // Autom.
Remote Control. 2015. V. 76. no 3. P. 458-471.
167
15.
Судаков В.А., Батьковский А.М., Титов Ю.П. Алгоритмы ускорения работы
модификации метода муравьиных колоний для поиска рационального назначе-
ния сотрудников на задачи с нечетким временем выполнения // Современные
информационные технологии и ИТ-образование. 2020. Т. 16. № 2. С. 338-350.
16.
Parpinelli R., Lopes H., Freitas A. Data mining with an ant colony optimization
algorithm // IEEE Trans. Evol. Comput. 2002. V. 6. No. 4 P. 321-332.
17.
Junior I.C. Data mining with ant colony algorithms // ICIC. LNCS. 2013. V. 7996.
P. 30-38.
18.
Martens D., De Backer M., Haesen R., Vanthienen J. Classification with ant colony
optimization // IEEE Trans. Evol. Comput. 2007. V. 11. No. 5. P. 651-665.
19.
Pasia J.M., Hartl R.F., Doerner K.F. Solving a Bi-objective Flowshop Scheduling
Problem by Pareto-Ant Colony Optimization // ANTS 2006. P. 294-305.
20.
Титов Ю.П. Опыт моделирования планирования поставок с применением мо-
дификаций метода муравьиных колоний в системах высокой доступности //
Системы высокой доступности. 2018. Т. 14. № 1. С. 27-42.
21.
Синицын И.Н., Титов Ю.П. Оптимизация порядка следования гиперпарамет-
ров вычислительного кластера методом муравьиных колоний // Системы высо-
кой доступности. 2022. Т. 18. № 3. С. 23-37.
22.
Mishra Sudhanshu K. Some New Test Functions for Global Optimization and
Performance of Repulsive Particle Swarm Method // University Library of Munich,
23.
Layeb Abdesslem. New hard benchmark functions for global optimization. 2022.
Статья представлена к публикации членом редколлегии О.П. Кузнецовым.
Поступила в редакцию 23.01.2023
После доработки 21.03.2023
Принята к публикации 09.06.2023
168