БИОФИЗИКА, 2019, том 64, № 6, с. 1169-1192

БИОФИЗИКА CЛОЖНЫX CИCТЕМ

УДК 57.055

ДИНАМИКА ПОПУЛЯЦИЙ:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ И РЕАЛЬНОСТЬ

Н.И. Нуриева*, В.М. Терешко*^, ****

*Институт теоретической и экспериментальной биофизики РАН,

142290, Пущино Московской области, ул. Институтская, 3

**Биологический факультет Белорусского государственного университета,

220030, Минск, просп. Независимости, 4, Белоруссия

***Институт математических проблем биологии РАН - филиал Института прикладной математики

им. М.В. Келдыша РАН, 142290, Пущино Московской области, ул. Профессора Виткевича, 1

****Объединенный институт проблем информатики НАН Беларуси,

220012, Минск, ул. Сурганова, 6, Белоруссия

E-mail: alexander_medvinsky@yahoo.com

Поступила в редакцию 05.09.2019 г.

После доработки 05.09.2019 г.

Принята к публикации 06.09.2019 г.

Присущий математическому моделированию редукционистский подход к анализу природных явле-

ний неизбежно ставит вопрос о соответствии результатов моделирования реальным процессам.

Статья посвящена анализу проблем, возникающих при сопоставлении результатов математическо-

го моделирования популяционных процессов и данных, полученных в ходе мониторинга природ-

ных экосистем. Эти проблемы обусловливаются тем, что далеко не всегда вид зависимостей между

переменными, описывающими динамику популяционных процессов, равно как и выбор числен-

ных значений параметров математических моделей, удается обосновать, опираясь на результаты

мониторинга конкретной экосистемы. В статье предлагается подход, позволяющий в ходе матема-

тического моделирования учитывать воздействие всего комплекса биотических и абиотических

факторов на динамику популяций. Такой подход базируется на принятии во внимание данных мо-

ниторинга экосистем и прямом включении этих данных в математические модели популяционной

динамики. Реализация этого подхода позволяет, в частности, оценивать степень влияния отдельных

факторов среды обитания как на вариации популяционного обилия, регистрируемые в ходе мони-

торинга, так и на такие характеристики популяционных процессов, которые непосредственно не

измеряются в ходе мониторинга, но являются результатом математического моделирования.

Ключевые слова: популяционная динамика, математическое моделирование, анализ временных рядов.

DOI: 10.1134/S0006302919060176

Популяция как динамический объект. Пред-

ние и гибель), а наряду с ними - экологические

ставление о популяции как о динамическом объ-

процессы (миграции, межпопуляционные тро-

екте является теоретической идеализацией. В

фические взаимодействия, изменения условий

рамках этой идеализации обычно отвлекаются от

обитания). Сложная мозаика факторов, обуслов-

индивидуальных особенностей отдельных особей

ливающих колебания популяционного обилия,

(организмов), формирующих популяцию, подоб-

во многих случаях нерегулярные, существенно

но тому, как часто пренебрегают свойствами от-

затрудняет попытки выделить основные движу-

дельных молекул при исследовании динамики

щие факторы, ответственные за наблюдаемые в

жидкостей или газов. Подобно газу и жидкости,

природе колебания плотности популяций.

популяция может характеризоваться плотностью

Для того чтобы обойти это затруднение, при-

(популяционным обилием), т.е. числом особей

бегают к редукции. Такая редукция, в частности,

или массой на единицу площади или объема.

реализуется в механистических моделях, в рамках

Плотность природных популяций подвержена

которых динамика популяций описывается как

изменениям как в пространстве, так и во време-

результат суммирования независимых процессов

ни. В основе таких изменений лежат биологиче-

(например, размножения и смертности). При

ские процессы (рост организмов, их размноже-

этом в предположении, что модельная популяция

1169

1170

МЕДВИНСКИЙ и др.

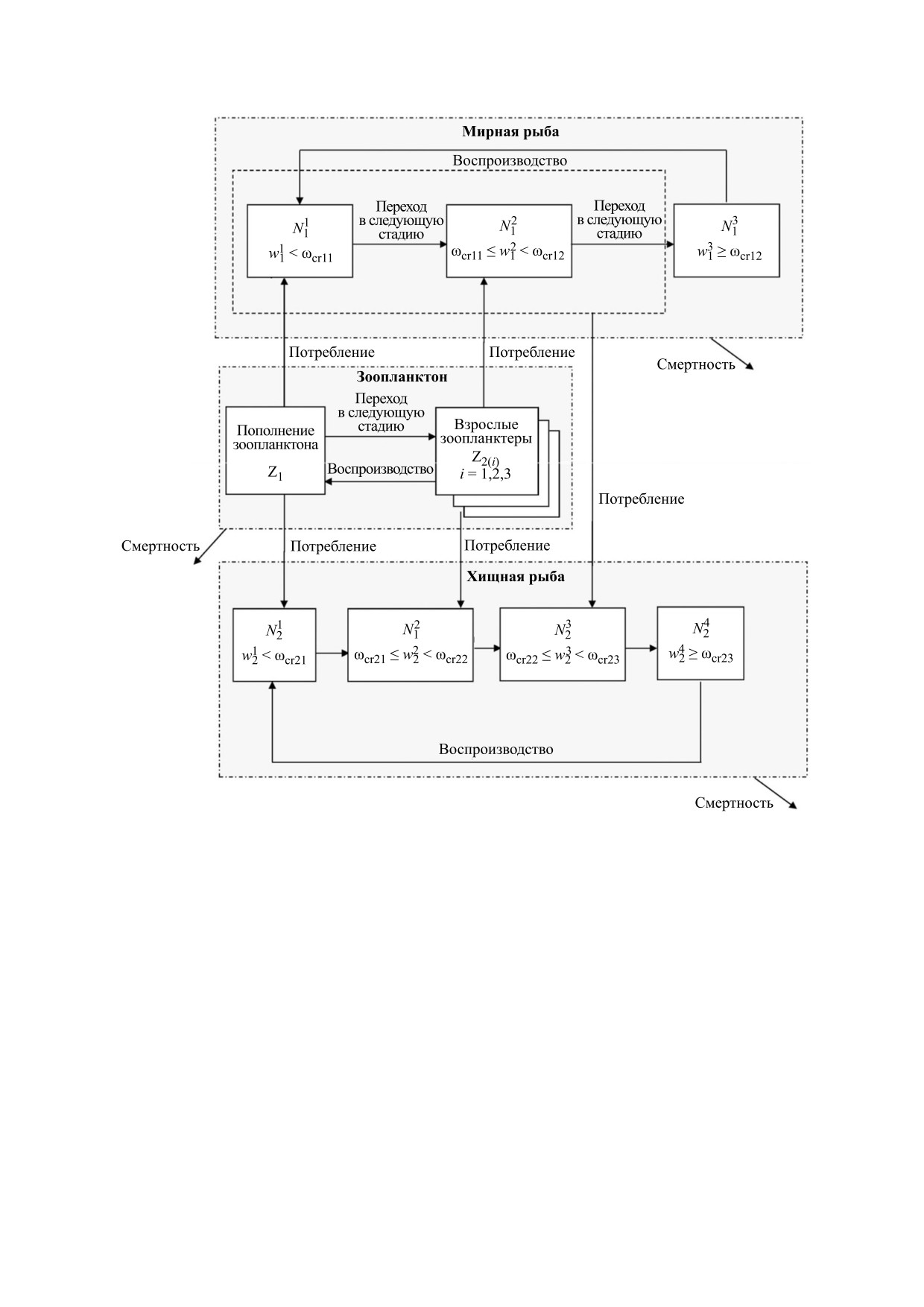
Рис. 1. Схема жизненных циклов и трофических отношений гидробионтов: Nik — численность мирной (i = 1) и хищной

(i = 2) рыбы на k-й стадии жизненного цикла; ω_ik — средняя масса мирной (i = 1) и хищной (i = 2) рыбы на k-й стадии

жизненного цикла; ωcrij — пороговое значение массы при переходе из одной стадии жизненного цикла в другую; п.с.с. —

переход в следующую стадию [5].

распределена равномерно в области ее обитания

ционной динамики часто принимается во внима-

и не подвергается внешним воздействиям ни со

ние внутренняя структура популяций (например,

стороны других популяций, ни в результате влия-

их возрастной состав) [3]. В качестве примера на

ния абиотических факторов, изменение во време-

рис. 1 показана блок-схема математической мо-

ни численности такой популяции определяется

дели, описывающей трофические взаимодей-

алгебраической суммой скорости размножения и

ствия между популяциями гидробионтов - рыбы

скорости гибели организмов, входящих в ее со-

и зоопланктона - с учетом внутренней структуры

став.

этих популяций [4,5]. Из рис. 1 видно, что попу-

ляция взрослых зоопланктеров состоит из трех

В реальности - и это учитывается во многих

возрастных групп Z2(i), i = 1, 2, 3. Схематически

математических моделях - популяции включены

в сложную систему трофических взаимодействий

динамика популяции зоопланктона определяется

[1,2]. Кроме того, в ходе моделирования популя-

следующими двумя соотношениями:

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1171

Пополнение зоопланктона =

могут оказывать влияние на динамику зоопланк-

= размножение - смертность -

тона и рыбы, а именно: многовидовой состав

- потребление зоопланктона мирной рыбой -

рыбного сообщества, трофические взаимодей-

потребление зоопланктона хищной рыбой;

ствия и зоопланктона, и рыбы с фитопланкто-

ном, колебания температуры и пр. Подобная ре-

Численность зоопланктона

дукция, т. е. сведение сложного к простому, ши-

в данной возрастной группе = переход

роко используется при математическом

из предыдущей возрастной группы -

моделировании популяционной динамики в по-

- смертность - потребление зоопланктона

пытке выявить базисные механизмы наблюдае-

мирной рыбой - потребление зоопланктона

мых эффектов. В случае модели, представленной

хищной рыбой.

на рис. 1, такой редукционистский подход позво-

В рамках представленной на рис. 1 модели по-

лил идентифицировать факторы (скорость по-

пуляция мирной рыбы N₁ состоит из трех групп

полнения популяции зоопланктона, величина

особей, которые различаются по массе. Кроме

пороговой массы, которая определяет переход

процессов воспроизводства представленная мо-

рыбы к хищничеству, а также предельная дли-

дель описывает динамику численности и измене-

тельность жизни хищной рыбы), которые могут

ние средней массы в каждой из этих групп. Пере-

определять наблюдаемые в природе долгоперио-

ход из одной группы в другую происходит при до-

дические (с периодом, составляющим десятки

стижении порогового значения массы.

лет) колебания численности рыбных популяций

Схематически уравнение динамики численно-

[4,5].

стей N₁₁ и N₁₂ (рыб, не достигших половой зрело-

Необходимо отметить, что представленная вы-

сти) имеет вид:

ше математическая модель, равно как и многие

Численность(t + 1) = численность(t) -

другие модели, используемые в математической

- смертность(t) - (потребление хищной

экологии (см., например, работу [7]), не позволя-

рыбой)(t) - (численность рыб,

ют сделать однозначный вывод о применимости

перешедших в следующую группу)(t) +

результатов математического моделирования к

+ (пополнение из предыдущей группы)(t).

конкретной экосистеме. Поскольку любая мате-

матическая модель неизбежно является продук-

Пополнением первой стадийной группы явля-

том редукционистского подхода к изучению при-

ется молодь, выжившая в процессе созревания

роды, возникает проблема уточнения того уровня

икры, второй - молодь из первой стадии, достиг-

редукционизма, который был бы достаточен для

шая порогового значения массы тела.

выявления причинных взаимосвязей между ком-

Молодь хищной рыбы (группы N₂₁ и N₂₂) , до

понентами сложно организованной экосистемы с

достижения рыбой пороговой массы, питается

целью идентификации их вклада в динамику при-

зоопланктоном, так же как и мирная рыба

родных популяций и в предсказуемость этой ди-

(рис. 1). Переход к хищничеству обусловлен уве-

намики [8].

личением потребности в энергии с ростом по-

движности и массы тела [6]. Для хищной рыбы на

Факторы, определяющие характер и предсказу-

стадиях, которые характеризуются потреблением

емость динамики популяций. Численность многих

зоопланктона (группы N₂₁ и N₂₂), описание дина-

популяций характеризуется значительной вариа-

мики численности схоже с описанием динамики

бельностью во времени значений амплитуды и

численности молоди мирной рыбы (группы N₁₁ и

периода колебаний [1,9-12]. Такая нерегуляр-

N₁₂). Существенным отличием является то, что

ность в некоторых случаях «навязывается» попу-

убыль популяции хищной рыбы происходит

ляционной динамике стохастичностью условий

только за счет естественной смертности. После

обитания популяций. Случайные экзогенные

перехода на хищничество (стадия N₂₃) пищевым

возмущения во взаимодействии с нелинейными

ресурсом хищной рыбы является молодь мирной

эндогенными факторами, такими как трофиче-

рыбы (группы N₁₁ и N₁₂; рис.1). Особи, достигшие

ские взаимодействия между популяциями, могут

половозрелого возраста (стадия N₁₃ мирной рыбы

порождать хаотические колебания популяцион-

и стадия N₂₄ хищника; рис. 1), прекращают по-

ного обилия [7].

требление и влияют на динамику численности

В теоретических концепциях хаос рассматри-

популяций только путем воспроизводства (по-

вается как режим, внутренне присущий нелиней-

дробное описание и обоснование модели см. в ра-

ной динамической системе или, иными словами,

боте [4]).

проявляющийся в отсутствие каких бы то ни бы-

Несмотря на сложность взаимосвязей между

ло внешних воздействий. Под хаосом при этом

популяциями зоопланктона и рыбы, представ-

подразумевается нерегулярный колебательный

ленных на рис. 1, математическая модель, описы-

процесс в нелинейных системах, характеризую-

вающая динамику этих популяций, все еще не

щийся зависимостью от начальных условий, а

учитывает огромное число факторов, которые

именно - экспоненциальной неустойчивостью.

БИОФИЗИКА том 64

№ 6

2019

1172

МЕДВИНСКИЙ и др.

Мерой хаотичности может служить доминантный

лученных в ходе мониторинга. К таким данным

показатель Ляпунова (Λ): поведение динамиче-

относятся: изменение обилия (численности, био-

ской системы является хаотическим, если Λ > 0

массы) отдельных популяций и функциональных

(см., например, [13]). Хаотичность обусловливает

сообществ организмов, вариации ресурсов, необ-

ограниченную предсказуемость колебательного

ходимых организмам для поддержания их жизне-

процесса. Его предсказуемость оказывается огра-

способности, колебания условий обитания попу-

ниченной горизонтом предсказуемости (T_pr) [14],

ляций (например, температуры) и пр. Часто такие

т. е. длительностью временного интервала, в те-

данные представляются в виде временных рядов,

чение которого малое различие в начальных усло-

наглядно демонстрирующих динамику измеряе-

виях (вызванное небольшим возмущением мо-

мых характеристик конкретной экосистемы [3].

дельной фазовой траектории или погрешностью

Необходимо отметить, что данные, регистри-

измерений в случае реального эксперимента) воз-

руемые в ходе мониторинга экосистем (см., на-

растает настолько, что корреляция между про-

пример, работы [19,20]), являют собой результат

гнозом и наблюдением уменьшается практически

трофических взаимосвязей, а также внешних воз-

до нуля. Горизонт предсказуемости (T_pr) умень-

действий на исследуемые экосистемы (эти дан-

шается при увеличении хаотичности поведения

ные отражают, кроме того, и эффект наблюдате-

динамической системы [15]:

ля, т. е. те неточности, которые неизменно при-

сутствуют в процессе измерений). Иными

(1)

словами, временные ряды, полученные в ходе мо-

Tpr ≈ Λ-1.

ниторинга, характеризуют экосистему как целое.

В отличие от многих модельных систем при-

Мониторинг экосистем может рассматриваться

родные экологические системы и их компоненты

как проявление холистического подхода к их ис-

(в частности, популяции) не могут рассматри-

следованию, и такой подход делает актуальным

ваться как объекты, изолированные от внешних

математический анализ временных рядов. Одной

воздействий. Взаимное влияние экзогенных и эн-

из содержательных целей такого анализа является

догенных факторов на динамику популяций спо-

численная оценка предсказуемости популяцион-

собно приводить к неожиданным результатам.

ной динамики.

Так, например, периодические (сезонные) изме-

нения температуры, будучи наложенными на эн-

догенные периодические колебания численности

АНАЛИЗ ВРЕМЕННЫХ РЯДОВ

популяции, могут порождать хаотические коле-

Реконструкция популяционной динамики. По-

бания [16]. В неоднородной среде обитания, т. е.

пуляции, связанные трофическими взаимодей-

при наличии нескольких граничащих между со-

ствиями и объединенные сходными экзогенными

бой биотопов, ограниченно предсказуемый хаос,

влияниями, образуют динамическую систему. Ее

характеризующий динамику планктона в одном

образом является аттрактор - замкнутое множе-

из биотопов, может проникать в соседний биотоп

ство A, для которого существует окрестность N та-

в результате обмена биомассой планктона между

кая, что (см., например, работу [21])

этими биотопами [17,18]. Математическое моде-

лирование такой динамической инвазии проде-

limt→∞ f ^t(N) = A,

(2)

монстрировало, что в результате может возник-

где f - отображение. Различные динамические

нуть ситуация, когда динамика популяции стано-

процессы (например, колебания во времени чис-

вится еще менее предсказуемой, чем в случае

ленности отдельных популяций), принадлежа од-

возникновения динамического хаоса. Падение

ному и тому же аттрактору, взаимосвязаны. В ре-

предсказуемости в этом конкретном случае обу-

зультате, в системе «хищник - жертва», к приме-

словливается конкуренцией двух сосуществую-

ру, информация об изменениях численности

щих аттракторов - хаотического аттрактора и

популяции хищника позволяет в принципе су-

предельного цикла - с фрактальной структурой

дить о свойствах динамики популяции жертвы.

бассейнов притяжения к каждому из этих аттрак-

В качестве примера, следуя работе [22], рас-

торов. При такой структуре бассейнов притяже-

смотрим в E-мерном фазовом пространстве тра-

ния даже слабый экзогенный шум индуцирует

ектории, притягивающиеся к d-мерному (d ≤ E)

практически непредсказуемые обратимые пере-

аттрактору A. Для точки m(t), лежащей на одной

ходы между конкурирующими аттракторами [17].

из таких траекторий (t - время), выполняется

Сопоставление результатов математического

следующее условие:

моделирования с результатами мониторинга при-

m(t + 1) = f(m(t)).

родных экосистем является необходимым шагом

в процессе исследования механизмов, обусловли-

При Е = 3 точка m(t) может быть представлена

вающих наблюдаемые режимы функционирова-

следующим образом: m(t) = [X(t), Y(t), Z(t)]. Пусть

ния популяций. С этой целью первостепенной за-

X - наблюдаемый динамический процесс, один

дачей является проведение анализа данных, по-

из тех, которые задают отображение f в E-мерном

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1173

фазовом пространстве, а соответствующий вре-

Реконструкция динамических процессов была

менной ряд длины L: {X} = {X(1), ..., X(L)}. Задавая

использована, в частности, для анализа данных

E-мерное пространство вложения, можно полу-

вылова сардины и хамсы в Тихом океане. Пред-

чить множество A_X точек x(t) с координатами X(t),

полагалось при этом, что данные вылова отража-

X(t - τ), …, X(t - (E - 1)τ); здесь лаг τ > 0. В общем

ют реальные колебания численности популяций

случае точки x(t) на множестве A_X однозначным

рыбы. Временные ряды, построенные по этим

данным, характеризуются двумя очевидными

образом связаны с точками m(t) на множестве A

свойствами: во-первых, нерегулярностью коле-

[23].

баний, а во-вторых - тем, что периоды макси-

Если два процесса - X и Y - связаны между со-

мальной численности сардины приходятся на па-

бой причинным образом (например, в рамках си-

дение численности хамсы. На основании этого

стемы «хищник - жертва»), то, поскольку они

обстоятельства были высказаны предположения

имеют общий аттрактор A, появляется возмож-

о том, что (1) сардина и хамса могут являться кон-

ность провести реконструкцию (Y^∧(t)|A_X) времен-

курентами [24] или (2) сардина и хамса хотя и сов-

местно, но по-разному реагируют на изменения

ного ряда Y(t), используя для этого временной ряд

X(t), и затем сравнить результат такой рекон-

каких-то экзогенных факторов, характеризую-

струкции с исходным временным рядом Y(t).

щих общую для сардины и хамсы среду обитания

Иными словами, характер динамики популяции

[25]. С помощью метода реконструкции времен-

жертвы может быть восстановлен на основе име-

ных рядов было продемонстрировано [22], что

колебания обилия популяций хамсы и сардины

ющейся информации (временного ряда) для по-

пуляции хищника (или наоборот). Алгоритм та-

слабо коррелируют с соответствующими рекон-

кой реконструкции состоит в следующем [22].

струируемыми временными рядами, а значит, не

могут описываться в рамках представления о еди-

Рассматриваются два временных ряда: {X} =

ном для этих колебаний аттракторе. Ответствен-

= X(1), ..., X(L)} и {Y} = {Y(1), ..., Y(L)}. Для вре-

ными за наблюдаемый характер динамики рыб-

менного ряда {X} находятся векторы x(t) с коор-

ных популяций оказались экзогенные факторы (в

динатами X(t), X(t - τ), …, X(t - (E - 1)τ), которые

первую очередь - колебания температуры).

формируют множество A_X. Затем находятся такие

Предсказуемость популяционной динамики. Для

моменты времени t₁, … tE+1 , которые соответ-

количественной оценки предсказуемости нерегу-

ствуют векторам, отличающимся от каждого из

лярных колебаний часто используется алгоритм,

векторов x(t) на величину меньше пороговой,

предложенный в работе [26]. Этот алгоритм дела-

определяя таким образом ближайших соседей

ет возможным сравнение участков временных ря-

векторов x(t). Эти ближайшие соседи использу-

дов, которые соответствуют наблюдаемым коле-

ются для идентификации предполагаемых бли-

баниям, с прогнозом. Для временного ряда N_t, где

жайших соседей Y(t_i), i = 1, …, E+1, которые и ис-

t ∈ [0,T], этот алгоритм подразумевает следующие

пользуются для реконструкции:

этапы:

(1) построение вектора

| A

=∑wY t ),

где

, N

,…, N

T/2

(

T/2

−1

T/2

−2

T/2

d-1

)

(

)

(

)

(

) (

)

где d - размерность пространства вложения [27];

∑u

(2) поиск на интервале [0,T/2] вектора

, P

…,P

⎧

d x(t),x(t )]⎫

(

−1

−2

−

(

−1

)

i =1,2,⋯, m

exp

−

⎨

⎬

⎩

d x(t),x(t

)]⎭

такого, что

≪

;

а d [x(t), x(t_j)] суть эвклидово расстояние между

(3) предсказание значения на один шаг вперед

соответствующими векторами. Аналогично про-

во времени:

водится реконструкция временного ряда X(t), для

этого используется временной ряд Y(t). Если про-

;

(

/2)

∑

цессы X и Y взаимосвязаны, то при увеличении

длины ряда L реконструкция Ŷ(t)|A_X будет при-

(4) построение вектора N'(T/2+1) в соответствии

ближаться к Y(t), а реконструкция (t)|A_Y - к X(t);

с пунктом (1), используя предсказанное значение

N'(T/2+1) в качестве уже известного;

в результате реконструируемые и наблюдаемые

временные ряды оказываются хорошо коррели-

(5)

следующая итерация на интервале

рованными [22]. Тем самым может быть провере-

[0,T/2+1], и так далее вплоть до достижения

на взаимосвязанность процессов X и Y.

предсказания в точке T;

БИОФИЗИКА том 64

№ 6

2019

1174

МЕДВИНСКИЙ и др.

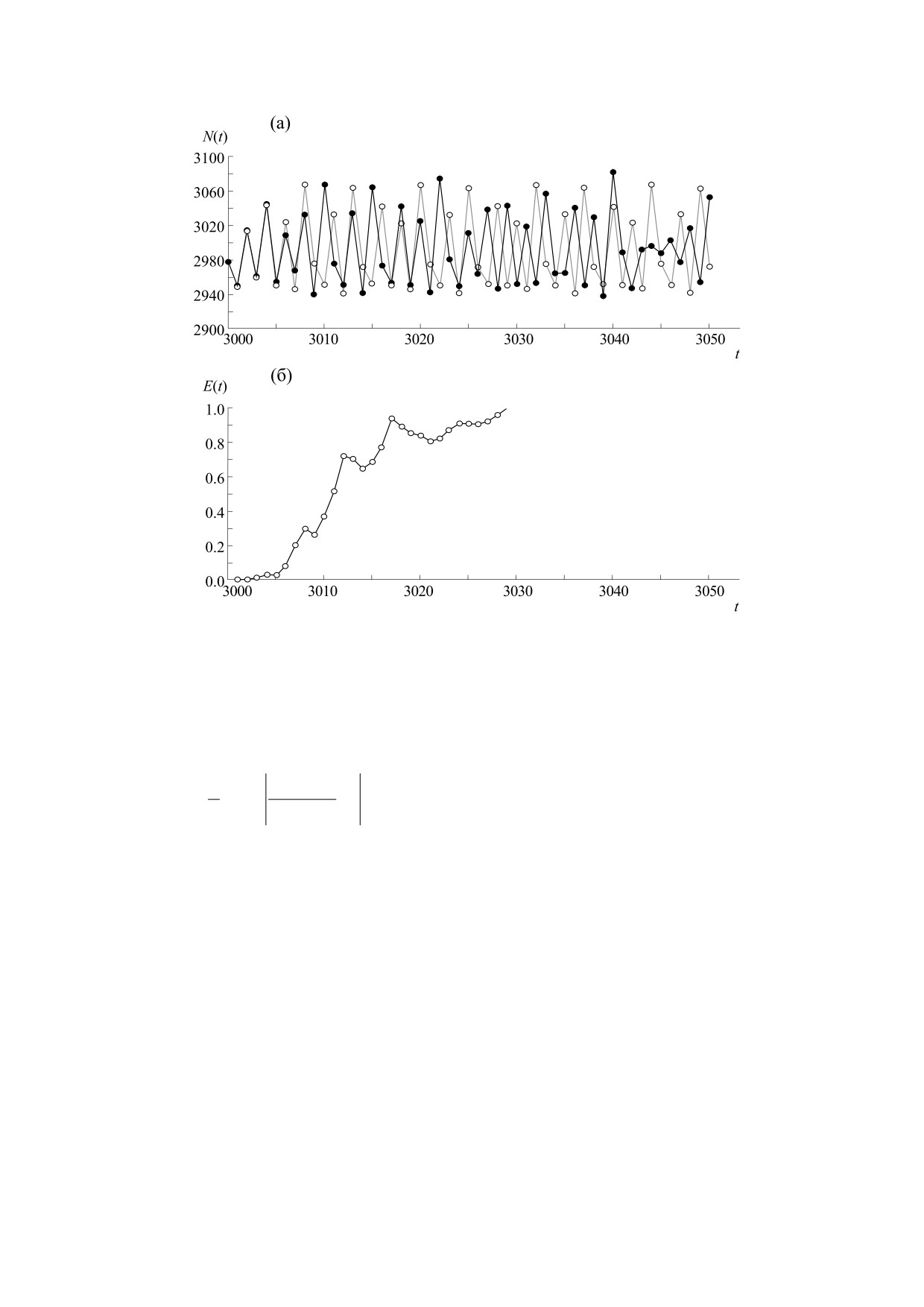
Рис. 2. (а) - Участок хаотического временного ряда N(t). Предсказанные значения отмечены светлыми кружками, а

реальные - темными ромбами. (б) - Ошибка предсказания E(t), вычисленная по формуле (3). Вертикальная пунктирная

линия обозначает момент начала предсказания. В данном случае оценка величины T_pr проведена, исходя из значения

EL = 0,1, что соответствует горизонту предсказуемости, равному четырем временным шагам [28].

(6) расчет ошибки предсказания на n-й итера-

приведенного выше алгоритма к «реальным» по-

ции [28]:

пуляционным процессам в связи с тем, что длина

соответствующих временных рядов, полученных

T/2+n

−

в ходе полевых наблюдений, часто недостаточна

t -1

(

)

−1

∑ t

;

(3)

для релевантной оценки горизонта предсказуе-

t=T /2+

−

t−1

мости этих процессов.

(7) оценка горизонта предсказуемости (T_pr).

Примечательно, что горизонт предсказуемо-

Для количественной оценки T_pr устанавливается

сти может зависеть от временного масштаба. В

предельное значение ошибки предсказания

работе [29] было продемонстрировано, что ин-

E_L << 1.

тервалы времени, характеризующиеся хаотично-

стью колебаний популяционного обилия, спо-

Из выражения (3) видно, что чем ближе пред-

собны периодически воспроизводиться. В ре-

сказанное значение N' к реальной величине N,

зультате в то время как на сравнительно

тем меньше ошибка предсказания. Численное

небольших временных интервалах динамика по-

значение горизонта предсказуемости T_pr при

пуляции является хаотической и, следовательно,

этом возрастает, т.е. динамика становится более

ее предсказуемость ограничена величиной T_pr, на

предсказуемой при уменьшении численного зна-

больших временных масштабах, характерных для

чения Е(n). Пример предсказания хаотического

воспроизводства хаоса, такая динамика проявля-

временного ряда с использованием приведенного

ет регулярность, свойственную периодическим

выше алгоритма показан на рис. 2. Отметим, что

процессам.

точность предсказания существенно зависит от

числа зарегистрированных осцилляций, предва-

Предсказуемость хаотической динамики, вви-

ряющих процесс предсказания. Это обстоятель-

ду соотношения (1), может быть связана с вели-

ство существенно ограничивает применимость

чиной доминантного показателя Ляпунова

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1175

(Λ > 0): чем сильнее хаос, т.е. чем больше поло-

⎛

⎞

жительное значение доминантного показателя

S(τ)

+τ)

−

X(i

+τ)||

∑

⎜

∑X(t *

⎟

Ляпунова, тем хуже предсказуемость, т.е. тем

⎝k t*)

i∈U

⎠

меньше T_pr. Однако следует принимать во внима-

где М = t - (E - 1)τ, возрастает линейно до тех

ние, что взаимозависимость Λ и T_pr, задаваемая

пор, пока норма разности между векторами

соотношением (1), в некоторых случаях наруша-

X(t* + τ) и X(i + τ) остается меньше размера хао-

ется. К таким случаям относятся:

тического аттрактора. Наклон линейного участка

S(τ) позволяет (при удачном выборе параметров Е

(а) - сосуществование и конкуренция не-

и ε; подробности см. в работе [31]) оценить вели-

скольких аттракторов. Если бассейны притяже-

чину доминантного показателя Ляпунова Λ.

ния к каждому из конкурирующих аттракторов

имеют сложную структуру, уже небольшой внеш-

Поскольку природные экосистемы, а значит, и

ний шум способен заставить систему постоянно

динамика заселяющих их популяций, открыты

дрейфовать, перемещаясь из бассейна в бассейн.

для воздействия внешних факторов (прежде

Динамика при этом становится практически не-

всего - температуры), то численное значение Λ,

предсказуемой, невзирая на динамические свой-

полученное при анализе колебаний популяцион-

ства - хаотичность или регулярность - каждого

ного обилия, характеризует не только собствен-

из конкурирующих аттракторов [17,30];

ные свойства таких колебаний, но и их чувстви-

тельность к изменениям внешних факторов. При

(б) - хорошо предсказуемый хаос, для которо-

этом положительная величина Λ может соответ-

го (в отсутствие внешних воздействий) доми-

ствовать не столько собственной хаотичности по-

нантный показатель Ляпунова Λ является конеч-

пуляционной динамики, сколько ее неустойчи-

ной и положительной величиной, в то время как

вости по отношению к внешним воздействиям.

Tpr→ ∞. Хорошо предсказуемый хаос реализуется

Хаос в подобных случаях является наведенным

тогда, когда вариации максимальных и мини-

[9].

мальных значений хаотических колебаний суще-

Необходимо указать на то, что точность оцен-

ственно меньше разницы между этими макси-

ки горизонта предсказуемости T_pr и точность вы-

мальными и минимальными значениями [28].

числения доминантного показателя Ляпунова Λ

Отметим, что для временных рядов, получен-

существенно зависят от длины временного ряда.

ных не в результате математического моделиро-

В частности, для коротких временных рядов

вания, а в ходе полевых наблюдений, величина

обычно не удается воспроизводить линейный

Tpr зависит от множества эндогенных и экзоген-

участок функции S(τ), и это препятствует числен-

ных факторов, таких как трофические взаимо-

ной оценке величины Λ.

действия между популяциями, колебания темпе-

В то время как длина временных рядов, гене-

ратуры и пр. Это означает, что величина горизон-

рируемых в ходе математического моделирова-

та предсказуемости колебаний численности

ния, в основном определяется самими исследова-

конкретной популяции отражает не только лишь

телями в зависимости от решаемых ими задач и от

характер самой этой динамики, но является отра-

инструментов, находящихся в их распоряжении,

жением динамических свойств исследуемой эко-

длина временных рядов, характеризующих коле-

системы во всей их полноте. Поэтому численное

бания численности природных популяций, суще-

значение горизонта предсказуемости может рас-

ственно определяется периодичностью и дли-

сматриваться как холистическая величина.

тельностью полевых наблюдений, а они не в пол-

Методы численной оценки хаотичности и пред-

ной мере зависят от самого исследователя. Для

сказуемости динамики популяций. В соответствии

анализа сравнительно коротких временных рядов

с выражением (1) численные значения горизонта

был предложен метод [9], в рамках которого полу-

предсказуемости T_pr хаотического процесса и до-

ченный в ходе наблюдений временной ряд ис-

минантного показателя Ляпунова Λ взаимосвяза-

пользуется для реконструкции динамики за пре-

ны. Однако оценка положительного значения Λ

делы того короткого интервала, в течение которо-

на основании анализа временного ряда может

го проводились наблюдения. С этой целью

быть проведена и независимо от оценки горизон-

исследуемый динамический процесс u(t) пред-

та предсказуемости [31]. Для этого, как и выше,

ставляется в виде функции F(u(t - 1), u(t - 2), …,

временному ряду {X} = {X(1), ..., X(L)} ставится в

u(t - p), ε(t)), где t - время, ε - экзогенная пере-

соответствие вектор X(t) = [X(t), X(t - τ), …, X(t -

менная, описывающая воздействия (например,

(E - 1)τ] в Е-мерном пространстве вложения. За-

вариации температуры), не связанные непосред-

тем для некоторого значения t = t* находятся k(t*)

ственно с внутрисистемными взаимодействиями,

векторов X(i), попадающих в малую эвклидову ε-

а p - временной лаг, за пределами которого угаса-

окрестность (U(t*)) вектора X(t*), после чего

ет функциональная связь динамики с величиной

определяется среднее изменение нормы ||X(t*) -

u(t). Далее строится временной ряд u*(t), такой

‒ X(i)|| за время τ. Функция

что u*(t) = u*(t - 1)exp[f(t) +ε(t)]. При этом пред-

БИОФИЗИКА том 64

№ 6

2019

1176

МЕДВИНСКИЙ и др.

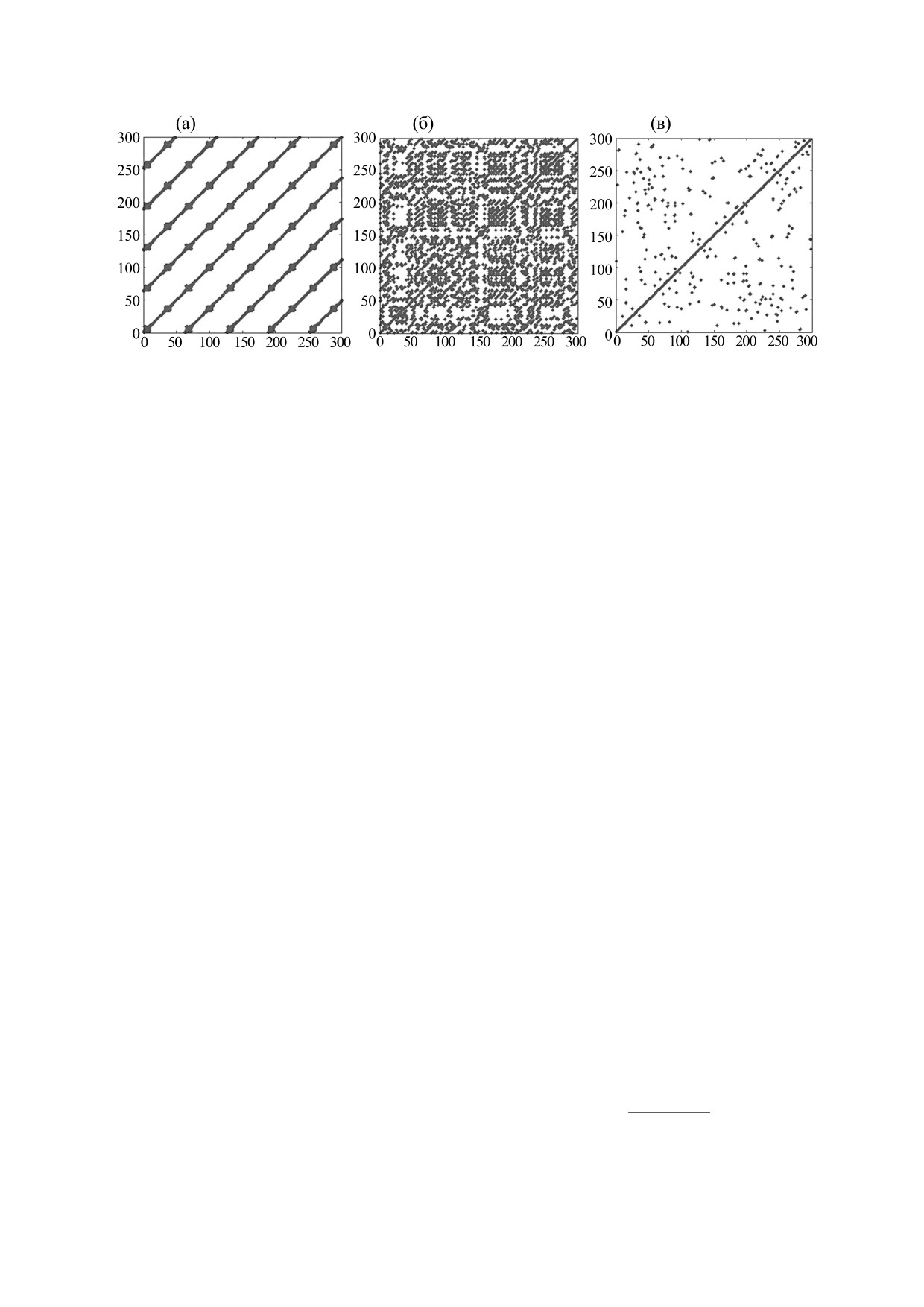
Рис. 3. Рекуррентные диаграммы, соответствующие периодическому процессу (а), хаосу (б) и случайному процессу (в) [10].

полагается, что функция f(t), описывающая эндо-

||...|| - эвклидова норма. Матрица (4) используется

генные процессы, задается полиномом a₀ + a₁X +

для визуализации рекуррентности в виде рекур-

рентных диаграмм. Рекуррентные диаграммы мо-

a₂Y + a₃X² + a₄Y² + a₅XY, где a_j (j = 1, 2, 3, 4, 5) -

гут быть представлены в виде набора точек в си-

константы, X = u(t - 1)ϑ1, а Y = u(t - 2)ϑ2. Подбор

стеме координат (i, j); черные точки при этом со-

численных значений параметров a_j и ϑ_i (i = 1,2)

ответствуют значениям Rij = 1, а белые

производится таким образом, чтобы функция

значениям R_ij = 0. Такие рекуррентные диаграм-

u*(t) максимально приближала функцию u(t). Те-

мы симметричны относительно линии Rii = 1. На

перь временной ряд u*(t), достаточно хорошо вос-

рис. 3 показаны рекуррентные диаграммы, соот-

производящий реальный динамический процесс,

ветствующие разным динамическим режимам:

может быть продлен за пределы промежутка, в те-

периодическим колебаниям, хаотической дина-

чение которого проводились наблюдения. С по-

мике и случайному процессу.

мощью такой реконструкции снимаются те огра-

ничения на определение численного значения

Из рис. 3 видно, что периодические колебания

доминантного показателя Ляпунова, которые на-

на рекуррентной диаграмме предстают в образе

кладываются длиной временных рядов.

периодических диагональных линий; хаотиче-

Метод реконструкции был использован для

ской динамике соответствуют апериодические

оценки численных значений Λ в приложении к

структуры, а случайному процессу - случайное

реальным временным рядам, базирующимся на

распределение точек. В случае хаотической дина-

данных наблюдений над колебаниями обилия по-

мики сравнительно короткие диагональные от-

пуляций различных животных [9]. Для большин-

резки длиной l, параллельные диагональной ли-

ства таких временных рядов величина Λ оказыва-

нии R_ii= 1, порождаются рекуррентностью фазо-

лась отрицательной, но и положительные ее зна-

вой траектории [34] , так что в течение l моментов

чения были близки к нулю, т.е. мало отличались

времени сегмент этой фазовой траектории оказы-

от величины, разделяющей хаос и регулярную ди-

вается практически параллельным другому, близ-

намику. Этот факт явился одним из аргументов в

ко расположенному к нему сегменту. Длина таких

пользу гипотезы о «жизни на краю хаоса» [32,33].

диагональных отрезков удовлетворяет следующе-

Еще один подход к анализу временных рядов,

му тождеству [35]:

численный рекуррентный анализ, базируется на

l-1

том, что динамическая система может возвра-

(

1−

)(

1−

)

= 1,

i−1

j−1

i+1

j+1

∏

i+k j+k

щаться к своему начальному состоянию [34]. По-

k=0

вторяемость (рекуррентность) состояний дина-

где Ri-1, j-1 = 0, если R1, j = 1 или Ri,1 = 1 и Ri+k, j+k = 0,

мической системы может быть представлена в ви-

де рекуррентной матрицы

если RN,j = 1 или Ri,N = 1 [4]. Горизонт предсказуемо-

сти в этом случае - это усредненная длина диагональ-

R_ij(ε) = H(ε - ||X(i) - X(j)||, i, j = 1, …, N,

(4)

ных отрезков:

где X(k), k = i, j, - вектор, описывающий состоя-

ние исследуемой системы, N - число точек вре-

lP l)

менного ряда, ε - малый параметр (феноменоло-

∑

l=l

min

(5)

гические критерии выбора численного значения ε

P l)

представлены в [35]), H - функция Хевисайда,

⁼∑

l=l

min

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1177

где P(l) - это гистограмма распределения диаго-

колебательных процессов; фаза φ здесь является

нальных отрезков длиной l:

линейной функцией времени [37]:

l -1

⎛

−

⎞

P l)

1−

;

(

i−1

j−1

)(

i+1

j+1

)

i+k j+k

≠ j

ϕ(j)

2π

≤

∑

∏

⎜

⎟

n+1

−

⎝

n+1

⎠

где lmin - пороговое значение длины диагональ-

Здесь jk (k = n, n+1) - это моменты времени (k -

ного отрезка, позволяющее исключить из рас-

их последовательные номера), которые соответству-

смотрения те короткие отрезки, которые соответ-

ют одинаковым фазам (например - локальным мак-

ствуют временным интервалам, в течение ко-

симумам временного ряда). Для строго синхронизо-

торых автокорреляция, заметная вначале,

ванных временных рядов PLI = 1, а при полном от-

приближается к нулю.

сутствии синхронизации PLI = 0. Разумеется, для

большинства случаев, соответствующих реальной

Отметим, что численный рекуррентный ана-

динамике, численные значения PLI лежат в проме-

лиз хорошо адаптирован к оценкам предсказуе-

жутке между 0 и 1. Для проверки статистической

мости сравнительно коротких временных рядов,

значимости численных оценок степени фазовой

типичных для результатов многих полевых на-

синхронизации между временными рядами исполь-

блюдений. Это связано с отсутствием необходи-

зуется метод суррогатных данных [31].

мости восстанавливать линейный участок функ-

ции S(τ), которая возникает в описанном выше

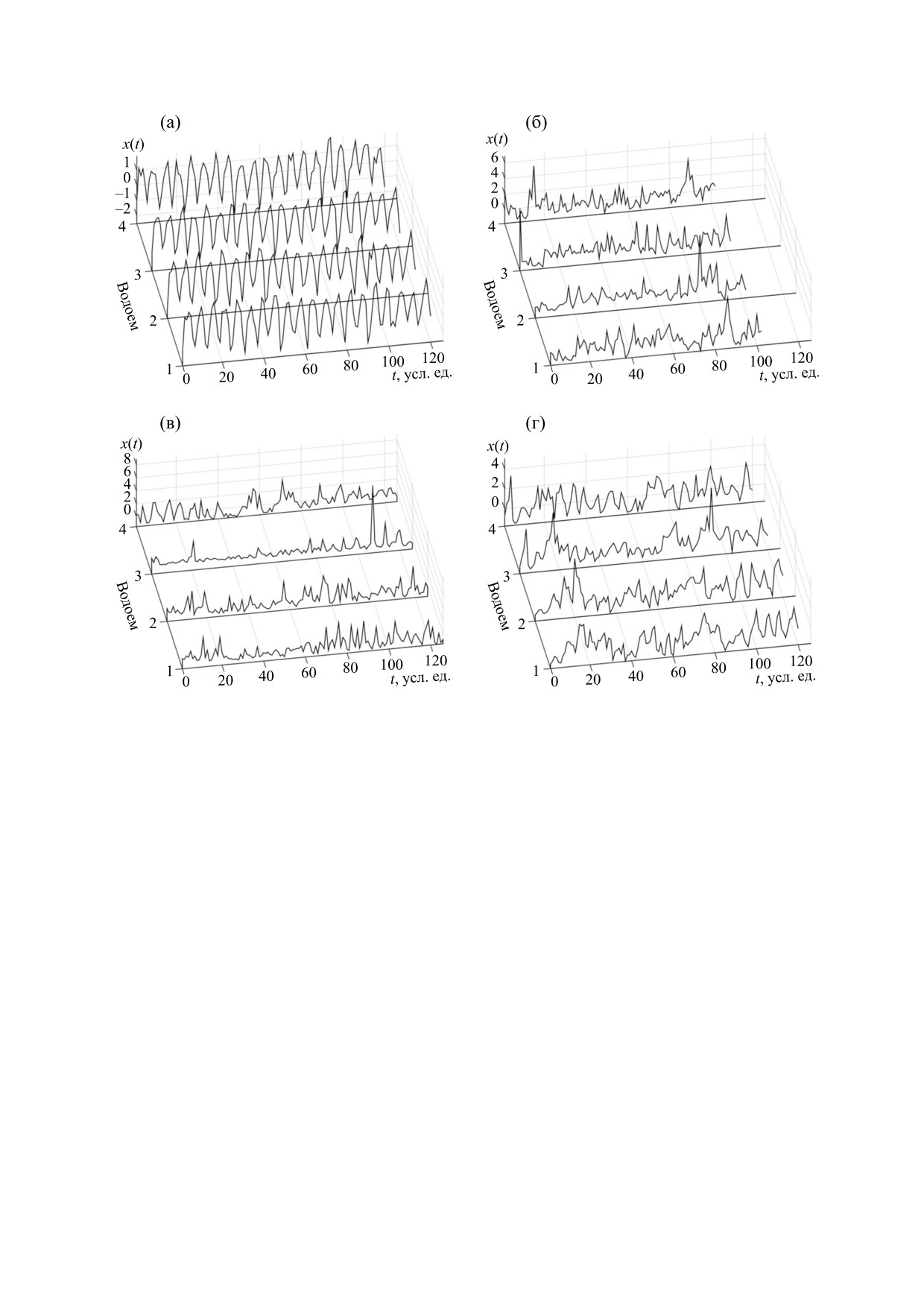
На рис. 4 представлены временные ряды, ха-

методе оценки горизонта предсказуемости,

рактеризующие динамику планктонных популя-

предусматривающим предварительное восста-

ций и колебания температуры воды в каждом из

новление такого участка и определение числен-

озер Нарочанской группы.

ного значения доминантного показателя Ляпуно-

В качестве примера численной оценки син-

ва с последующим использованием зависимости

хронизации эндогенных воздействий и планк-

(1) между показателем Ляпунова и горизонтом

тонной динамики рассмотрим влияние колеба-

предсказуемости. С помощью численного рекур-

ний температуры на динамику фитопланктона. С

рентного анализа удалось, в частности, провести

этой целью представим результаты вычисления

оценку горизонта предсказуемости сравнительно

индекса захвата фазы, PLI, определяя тем самым

коротких временных рядов, полученных в резуль-

степень фазовой синхронизации динамики фито-

тате мониторинга экосистемы Нарочанских озер

планктона и температуры. Рис. 5 демонстрирует

[11]. Численные значения горизонта предсказуе-

численные значения PLI, а также распределения

мости колебаний обилия фитопланктона в каж-

величины PLI для соответствующих суррогатных

дом из водоемов, входящих в систему Нарочан-

данных, полученных с помощью случайного пе-

ских озер, составили 2,4 месяца для малого плеса

ремешивания исходных данных, характеризую-

оз. Нарочь, 2,3 месяца для большого плеса оз. На-

щих динамику температуры и популяций фито-

рочь и 2,5 месяца для оз. Мястро и оз. Баторино

планктона.

[11]. Детальное описание методов анализа вре-

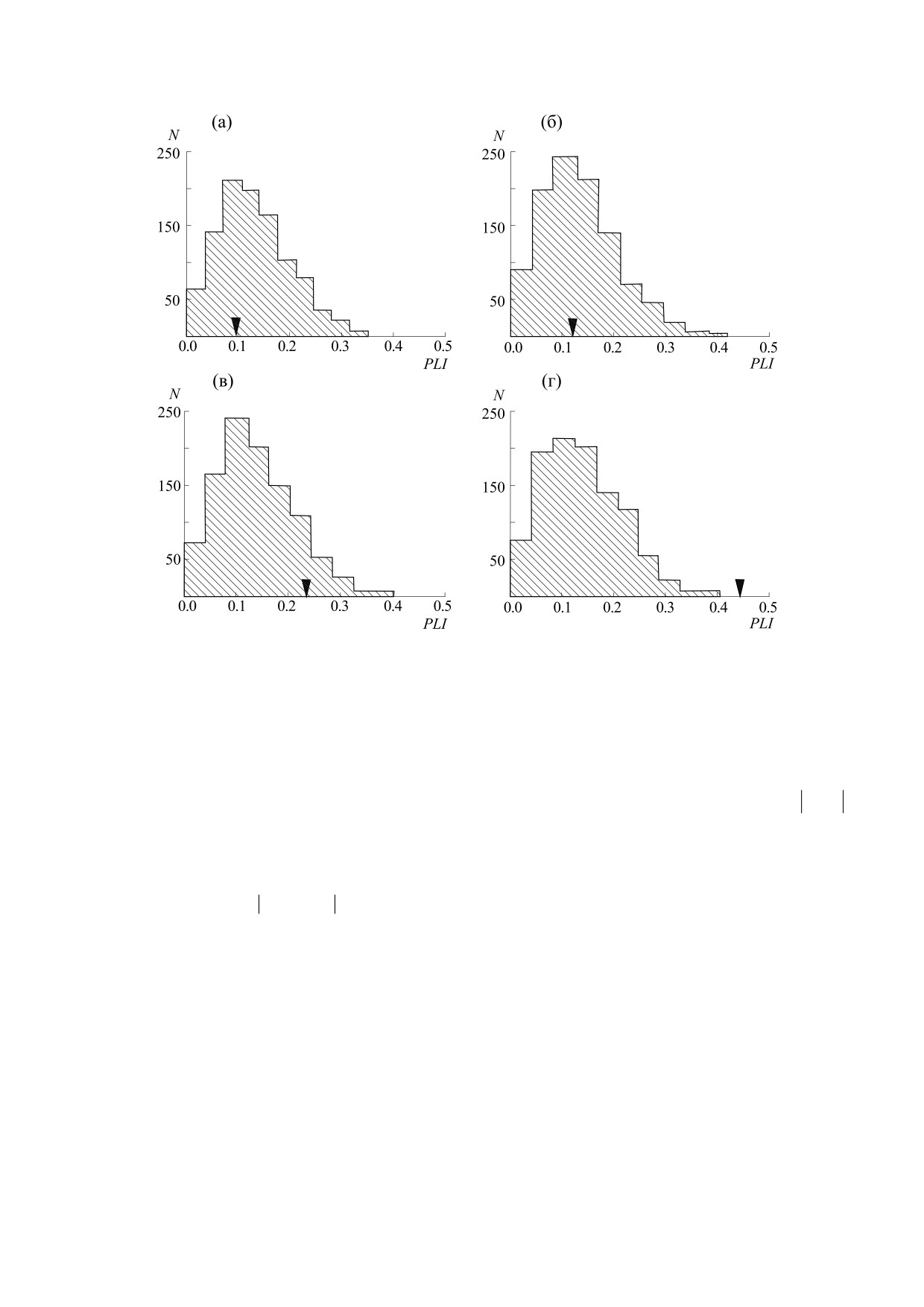
Видно, что значения PLI для оз. Нарочь

менных рядов представлено в работах [26] и [31].

(рис. 5а,б) и оз Мястро (рис. 5в) лежат внутри рас-

Методы численной оценки взаимосвязей попу-

пределений численных значений PLI, получен-

ляционных колебаний и их сопряженности с экзо-

ных для соответствующих суррогатных данных.

генными факторами. Необходимо отметить, что

Это означает, что динамика фитопланктона в

анализ временных рядов позволяет не только

этих водоемах не синхронизуется с колебаниями

оценивать степень хаотичности популяционной

температуры. Однако такая синхронизация имеет

динамики, но и выявлять степень влияния внеш-

место в оз. Баторино (рис. 5г). Отметим, что от-

них факторов, например колебаний температуры,

сутствие синхронизации не обязательно предпо-

на регистрируемые в ходе мониторинга природ-

лагает отсутствие влияния температуры на дина-

ных экосистем вариации популяционного оби-

мику популяции. В данном случае это просто

лия. Один из подходов к выявлению таких факто-

означает, что воздействие температуры на дина-

ров заключается в вычислении индекса захвата

мику фитопланктона не является определяющим

фазы (Phase Locking Index, PLI), величина кото-

(помимо температуры на динамику фитопланк-

рого может характеризовать степень фазовой

тона могут влиять колебания концентрации био-

синхронизации двух колебательных процессов

генов и трофические взаимодействия между по-

[36]:

пуляциями озерной экосистемы).

В отличие от фитопланктона колебания оби-

-1

-iΔϕ(j)

лия бактериопланктона продемонстрировали

PLI

(6)

∑

фазовую синхронизацию с вариациями темпера-

N j=

туры во всех озерах Нарочанской группы. Ока-

где N - число измерений (длина дискретного вре-

залось, что выявленная таким образом неодно-

менного ряда), Δφ - разница фаз исследуемых

значность влияния температуры на планктонную

БИОФИЗИКА том 64

№ 6

2019

1178

МЕДВИНСКИЙ и др.

Рис. 4. Динамика планктонных популяций и динамика температуры в каждом из водоемов Нарочанской группы озер: (а) -

температура, (б) - зоопланктон, (в) - фитопланктон, (г) - бактериопланктон (1 - Малый плес оз. Нарочь, 2 - Большой

плес оз. Нарочь, 3 - оз. Мястро, 4 - оз. Баторино); один шаг во времени (t) на представленных графиках соответствует

одному месяцу реального времени. Исходные данные, на основании которых построены показанные здесь временные

ряды, представляют собой результаты мониторинга колебаний во времени температуры (°С), а также вариаций обилия

планктона: зоопланктнона (г/м³) - с 1994 по 2013 гг., фитопланктона (г/м³) - с 1993 по 2013 гг. и бактериопланктона

(10⁶ кл./мл) - с 1995 по 2013 гг. [11,38,44]. Исходные данные приведены к нулевому среднему и единичной дисперсии.

динамику может объясняться не столько прямым

методов анализа для сопоставления результатов,

воздействием колебаний температуры на дина-

полученных этими методами. Такое сопоставле-

мику планктонных популяций, сколько наличи-

ние может быть полезно для оценки относитель-

ем или отсутствием взаимосвязанности колеба-

ной роли различных экзогенных факторов в фор-

ний обилия фитопланктона и динамики бакте-

мировании наблюдаемых колебаний популяци-

риопланктона (см. работу

[38]).

Такая

онного обилия. Ниже с этой целью будет

взаимосвязанность, в свою очередь, существенно

проведено сравнение результатов метода, пред-

определяется воздействиями со стороны других

полагающего оценку степени фазовой синхрони-

трофических уровней - обилия зоопланктона

зации временных рядов, характеризующих коле-

[39-41] и концентрации биогенов в воде [42,43].

бания планктонного обилия и температуры в На-

Необходимо отметить, что точность и адекват-

рочанских озерах

[38], с методом, в рамках

ность результатов математического анализа вре-

которого фазовая синхронизация экологических

менных рядов, являющихся итогом мониторинга

процессов непосредственно не учитывается. При

природных экосистем, в значительной мере зави-

этом необходимо принимать во внимание огра-

сят от объема и качества данных, полученных в

ниченность объема данных, полученных в ходе

ходе полевых наблюдений. Возникает необходи-

мониторинга экосистемы Нарочанских озер. В

мость использования отличающихся друг от друга

результате оказывается практически невозмож-

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1179

Рис. 5. Численные значения PLI (показаны стрелками), характеризующие фазовую синхронизацию динамики

фитопланктона и вариаций температуры, а также распределения значений PLI для 1000 наборов суррогатных данных: (а) -

Малый плес оз. Нарочь (PLI = 0,11), (б) - Большой плес оз. Нарочь (PLI = 0,13), (в) - оз. Мястро (PLI = 0,23), (г) -

оз. Баторино (PLI = 0,44) [38].

ным использовать статистические подходы и

f_xx(ω) является нормированным спектром авто-

усреднение по ансамблю наборов данных для

корреляционной функции для временного ряда x,

оценки сопряженности исследуемых колебаний.

или нормированным спектром мощности

( )

Для анализа взаимного влияния двух процес-

сов - x(t) и y(t) - мы воспользуемся величиной

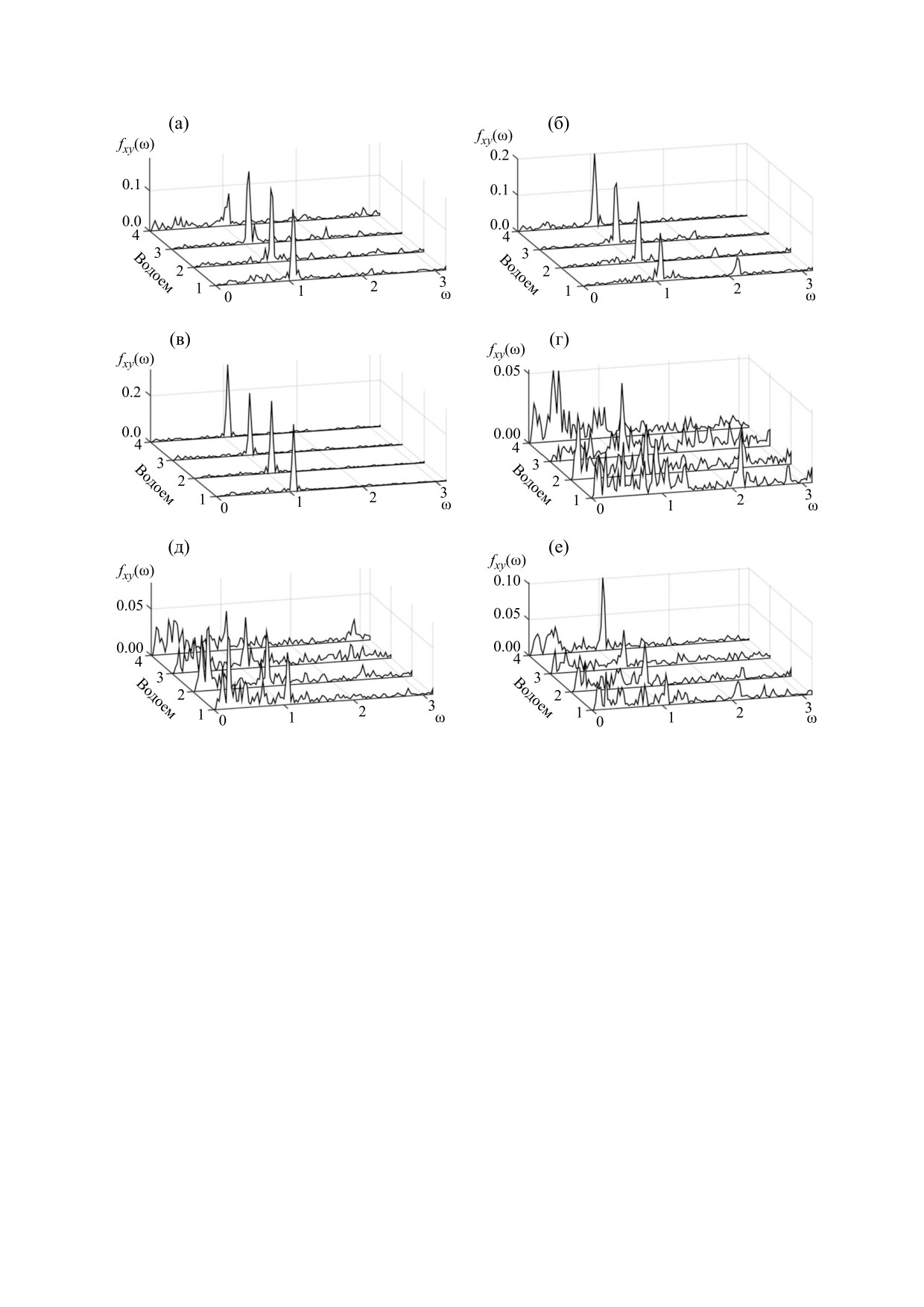
На рис. 6 представлены спектры f_xy(ω), харак-

нормированного спектра взаимных корреляций

двух сигналов, который определяется следующей

теризующие взаимные корреляции колебаний

формулой:

обилия бактериопланктона, фитопланктона, зоо-

планктона и вариаций температуры в каждом из

(ω)

x ω)y(ω)

(7)

водоемов Нарочанской группы (см. рис. 4). Вид-

В формуле (7) x и

- фурье-образы функций

но, прежде всего, что корреляции колебаний тем-

x и y, нормировочная константа λ выбирается из

пературы с колебаниями обилия планктонных

условия:

популяций характеризуются ярко выраженными

max

пиками. Эти пики отражают сезонные колебания

(

)

dω =1,

температуры [44]. Сезонность гораздо менее вы-

min

ражена во взаимных корреляциях колебаний

планктонного обилия, что отражает наличие до-

где ω_min и ω_max - границы спектра (7). Границы

полнительных факторов, влияющих на эти кор-

спектров заданы, коль скоро задан временной

реляции (например, трофические взаимодей-

шаг и число отсчетов временных рядов (в соот-

ветствии с теоремой Уиттакера-Найквиста-Ко-

ствия и связанные с ними колебания концентра-

тельникова-Шеннона). В диагональном случае

ций биогенов).

БИОФИЗИКА том 64

№ 6

2019

1180

МЕДВИНСКИЙ и др.

Рис. 6. Спектры взаимных корреляций колебаний временных рядов, представленных на рис. 5: (а) - температура -

зоопланктон, (б) - температура - фитопланктон, (в) - температура - батериопланктон, (г) - зоопланктон -

фитопланктон, (д) - зоопланктон - бактериопланктон, (е) - фитопланктон - бактериопланктон (1 - Малый плес оз.

Нарочь, 2 - Большой плес оз. Нарочь, 3 - оз. Мястро, 4 - оз. Баторино) [44].

Для количественной оценки информативно-

[45], такой метод хорошо известен. Он получил

сти спектров нами используется энтропия Шен-

название спектральной энтропии и широко при-

нона

меняется в различных приложениях, таких как:

распознавание речи, энцефалография, механика,

исследования климата (см., например, работы

S n)

(

)

[46-49]). В табл. 1 представлены численные зна-

чения кросс-корреляционной энтропии Шенно-

на для каждого из водоемов системы Нарочан-

которая численно характеризует распределение

ских озер.

по частотам спектров взаимных корреляций; в

данном случае n = 126 (это - длина дискретных

Из табл. 1 видно, что кросс-корреляционная

временных рядов, представленных на рис. 4, а

энтропия спектров взаимных корреляций, харак-

также число точек на осях абсцисс каждого из

теризующихся непрерывной структурой, выше,

спектров взаимных корреляций, представленных

чем кросс-корреляционная энтропия спектров,

на рис. 6). В диагональном случае, когда спектр

которые имеют прерывную структуру (ср. с

является спектром мощности или, что то же са-

рис. 6). Среди последних наименьшие значения

мое, косинус-фурье-преобразованием симмет-

энтропии характеризуют спектры взаимных кор-

ричной и четной автокорреляционной функции

реляций температуры и бактериопланктона

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1181

Таблица 1. Кросс-корреляционная энтропия Шеннона спектров взаимных корреляций [44]

Корреляция

Нарочь 1

Нарочь 2

Мястро

Баторино

Температура - зоопланктон

3,757

3,816

3,719

4,372

Температура - фитопланктон

4,002

3,793

3,774

3,730

Температура - бактериопланктон

3,252

3,134

3,505

3,149

Зоопланктон - фитопланктон

4,361

4,459

4,565

4,362

Зоопланктон - бактериопланктон

4,106

4,178

4,433

4,393

Фитопланктон - бактериопланктон

4,291

4,310

4,533

4,140

Пpимечание. Нарочь 1 - Малый плес оз. Нарочь, Нарочь 2 - Большой плес оз Нарочь. Отметим, что значения энтропии

спектров взаимных корреляций заметно меньше величин энтропии случайного сигнала длиной n, для которого на всех

частотах (с учетом нормировки) спектр f = 1/n. Для такого случайного сигнала энтропия Шеннона S = ln n, так что при

n = 126 S = 4,836.

(табл. 1). Интересно, что при этом динамика бак-

ляции экологических процессов, требует (наряду

териопланктона оказывается статистически зна-

с проведением долговременных наблюдений за

чимо синхронизованной (по фазе) с вариациями

состоянием экосистем) развития адекватных ма-

температуры во всех водоемах системы Нарочан-

тематических моделей. При этом необходимо

ских озер [38]. Однако такая сопряженность ве-

принимать во внимание неизбежность редукции

личин кросс-корреляционной энтропии Шенно-

исследуемых процессов до уровня, позволяющего

на с численными значениями PLI, характеризую-

формулировать математические модели таким

щими уровень фазовой синхронизации динамики

образом, чтобы результаты их анализа (например,

гидробионтов и вариаций температуры, не в пол-

в пространстве параметров) были достаточно

ной мере распространяется на связь вариаций

прозрачны и открывали возможность интерпре-

температуры с колебаниями обилия фитопланк-

тации этих результатов. При этом, естественно,

тона. Из табл. 1 видно, что кросс-корреляцион-

возникает вопрос о соответствии результатов ана-

ная энтропия Шеннона спектров взаимных кор-

лиза редуцированной модельной системы про-

реляций температуры и фитопланктона выше

цессам, протекающим в реальных экосистемах.

соответствующих величин для связи «температу-

ра - бактериопланктон» во всех водоемах, вклю-

чая оз. Баторино. Однако именно в этом озере,

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

которое отличается от других водоемов Нарочан-

И РЕАЛЬНОСТЬ

ской группа озер степенью эвтрофирования [50],

вариации температуры и колебания биомассы

Пролегомены. Математическая модель - это

фитопланктона статистически значимо синхро-

инструмент, который необходим для того, чтобы

формализовать и подвергнуть анализу гипотезу о

низованы по фазе (см. рис. 5). Таким образом,

сравнительно высокие значения энтропии в этом

механизмах изучаемого исследователем явления.

случае, тем не менее, сочетаются с фазовой син-

И гипотеза, и математическая модель, будучи

хронизацией колебаний. Это сочетание, по-ви-

продуктами человеческого сознания, отсекают те

свойства реальности, которые представляются (в

димому, обусловливается разной чувствительно-

рамках данного исследования) менее существен-

стью кросс-корреляционной энтропии и фазовой

синхронизации вариаций температуры с динами-

ными. Конечно, любая математическая модель

развивается на основе ранее накопленных дан-

кой фитопланктона к процессам, влияющим на

ных, полученных в ходе ранее проведенных экс-

трофический статус водоема. В общем случае фа-

периментов и наблюдений. Однако планирова-

зовая синхронизация и кросс-корреляционная

ние этих экспериментов и наблюдений уже само

энтропия Шеннона могут, по-видимому, рас-

по себе предполагает избирательность и тем са-

сматриваться как независимые и дополняющие

мым - редукцию картины мира. В результате все

друг друга характеристики степени сопряженно-

теоретические конструкты и представляющие их

сти колебательных процессов (в том числе - про-

переменные, параметры, операторы математиче-

цессов, протекающих в экосистемах).

ских моделей являются результатом подобной ре-

Содержательное изучение механизмов, лежа-

дукции. В качестве примера рассмотрим динами-

щих в основе синхронизации и взаимной корре-

ку модельной системы «фитофаг - энтомофаг».

БИОФИЗИКА том 64

№ 6

2019

1182

МЕДВИНСКИЙ и др.

Портрет содержит 21 область. Эти области харак-

теризуются разными фазовыми портретами, при

этом некоторые из фазовых портретов оказыва-

ются топологически тождественными, так что в

результате параметрический портрет обладает

определенной симметрией [56]. Фазовые портре-

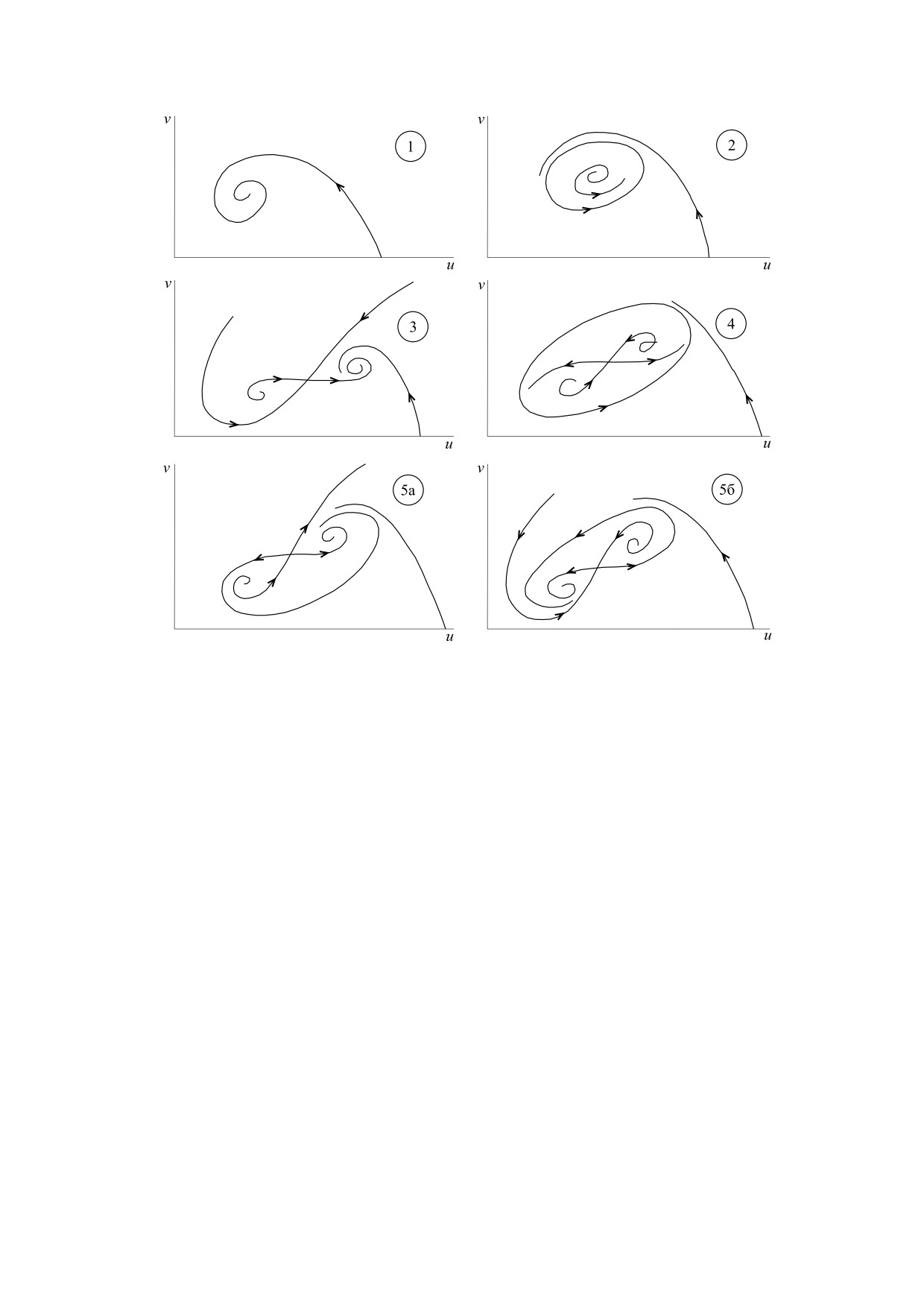
ты показаны на рис. 8 и 9. В частности, рис. 8 де-

монстрирует стереотипы модельной динамики,

т. е. те динамические режимы, которым могут

быть поставлены в соответствие данные, полу-

ченные в ходе наблюдений, касающихся числен-

ности различных видов лесных насекомых [54]:

устойчивое равновесие (рис. 8, 1), автоколебания

(рис. 8, 2), вспышки массовых размножений

(прочие фазовые портреты, представленные на

рис. 8).

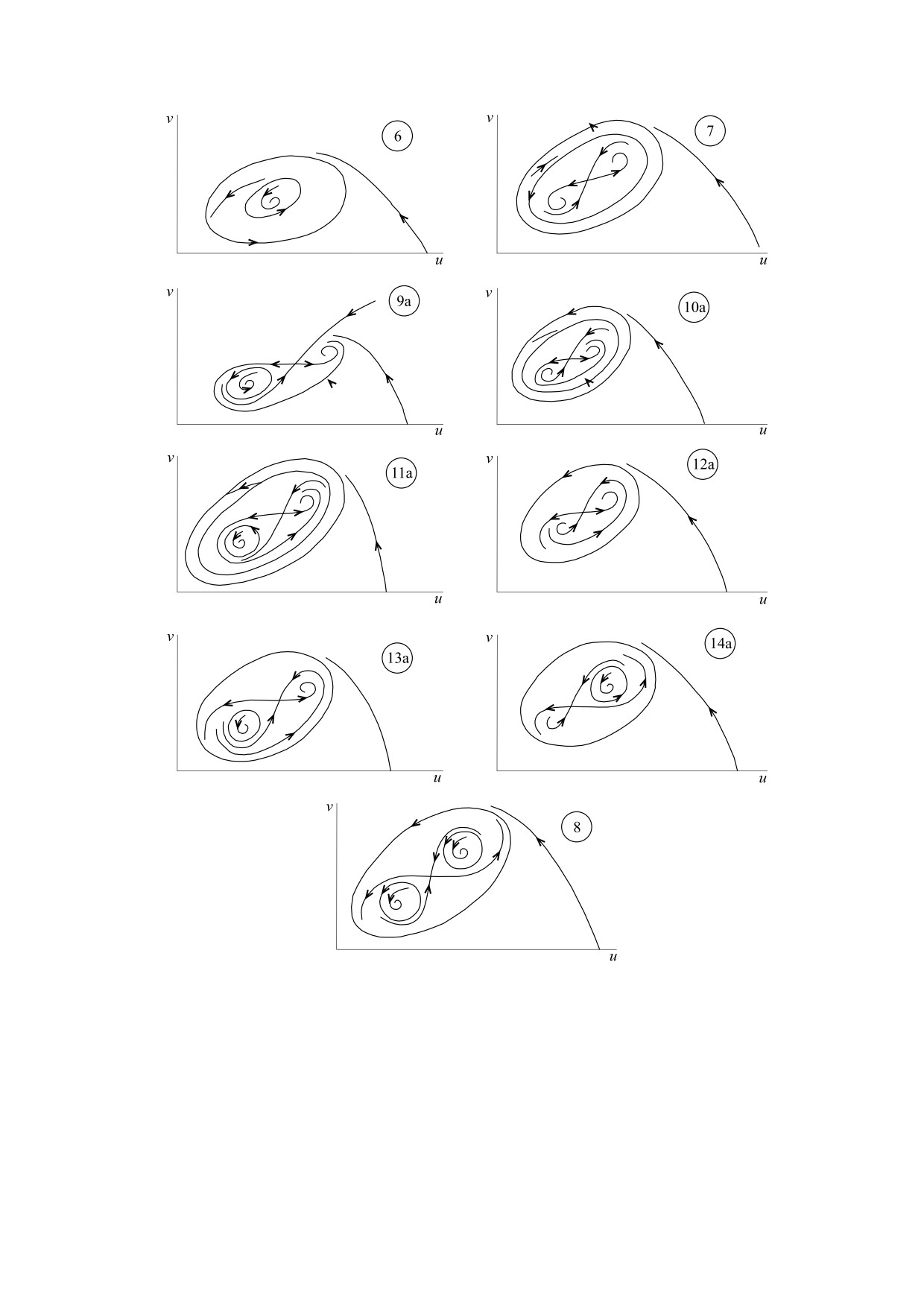
На рис. 9 показаны фазовые портреты, кото-

рые характеризуются зависимостью типа дина-

мики от начальных условий. Такую зависимость

часто рассматривают как проявление динамиче-

ского хаоса [21]. Однако в модели (8), представ-

ленной лишь двумя дифференциальными урав-

нениями, возникновение хаоса невозможно [57].

В данном случае зависимость от начальных усло-

вий отражает конкуренцию между сосуществую-

щими нехаотическими притягивающими множе-

ствами (аттракторами). Примечательно, что бо-

гатство динамических режимов, представленное

Рис. 7. Параметрический портрет модели (8) [55].

на рис. 8 и 9, описывается простой моделью (8).

Вместе с тем такое богатство является прямым

Цель этой математической модели - выявление

вызовом при попытке сопоставить модельный

существенных особенностей функционирования

динамический режим динамике насекомых в

популяций насекомых. Модели динамики насе-

конкретной лесной экосистеме.

комых, а именно лесных насекомых, развивались

Очевидная трудность связана, например, с

многими авторами [51-54]. Приведенные ниже

возможной зависимостью (как на рис. 9) характе-

результаты представлены в работе [55]. В этой ра-

ра динамики природных, а не модельных популя-

боте предложена нелинейная пятипараметриче-

ций от начальных условий. Если такая зависи-

ская модель динамики системы «фитофаг - энто-

мость действительно имеет место в реальности, то

мофаг», учитывающая миграцию насекомых:

предсказуемость изменения численности насеко-

мых существенно ограничивается вероятностью

du = u(u − l)(1−

−

α,

переключений между различными типами дина-

(8)

мики, обусловленной сосуществованием конку-

=-γv(m-u

βv)

рирующих аттракторов. Но, кроме того, иденти-

фикация конкретного динамического режима с

Здесь u и v - суть плотности популяций фито-

использованием модели (8) требует сопоставле-

фага и энтомофага соответственно; α, β, γ, l, m -

ния численных значений модельных параметров

параметры модели, их биологический смысл та-

результатам полевых измерений. При этом воз-

ков: l < 1 - отношение нижней критической плот-

никает вопрос: возможно ли в полевых условиях

ности популяции фитофага к плотности, обу-

реализовать достаточно точные измерения чис-

словленной ресурсами этой популяции в отсут-

ленных значений отношения нижней критиче-

ствие энтомофага; mγ

- мальтузианский

ской плотности популяции фитофага к плотно-

параметр, причем γ - это коэффициент перера-

сти, обусловленной ресурсами этой популяции в

ботки биомассы фитофагов в биомассу энтомо-

отсутствие энтомофага (параметр l модели (8)),

фагов; α - скорость миграционного потока насе-

или мальтузианского параметра mγ, или парамет-

комых; β - параметр, характеризующий конку-

ра β, характеризующего конкуренцию между эн-

ренцию между энтомофагами.

томофагами? Такое сопоставление модельных

Параметрический портрет модели (8) в виде

параметров и реальности представляется нам ма-

среза на плоскость (m, β) представлен на рис. 7.

ловероятным.

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1183

Рис. 8. Стереотипы динамики модели (8), нумерация которых соответствует областям параметрического пространства

(рис. 7) [55].

В тех случаях, когда выбор численных значе-

Понятно, что использование математических

ний модельных параметров все же базируется на

моделей с целью исследования механизмов, кото-

результатах полевых измерений (как это имеет

рые обусловливают характер и предсказуемость

место в математической модели водного сообще-

динамики популяций, вовлеченных в сложную

ства, представленной схемой на рис. 1), часто

сеть трофических взаимодействий (подобную

оказывается, что эти измерения проводились при

той, что показана на рис. 10) и к тому же подвер-

разных условиях и на разных объектах (в частно-

женных воздействию экзогенных факторов,

сти, в разных водоемах). Таким образом, в таких

практически невозможно без привлечения суще-

случаях результаты моделирования сопоставля-

ственной редукции исходной природной структу-

ются не с конкретной экосистемой, а скорее - с

ры взаимодействий между популяциями, а

некоторой обобщенной ситуацией.

также - между популяциями и факторами внеш-

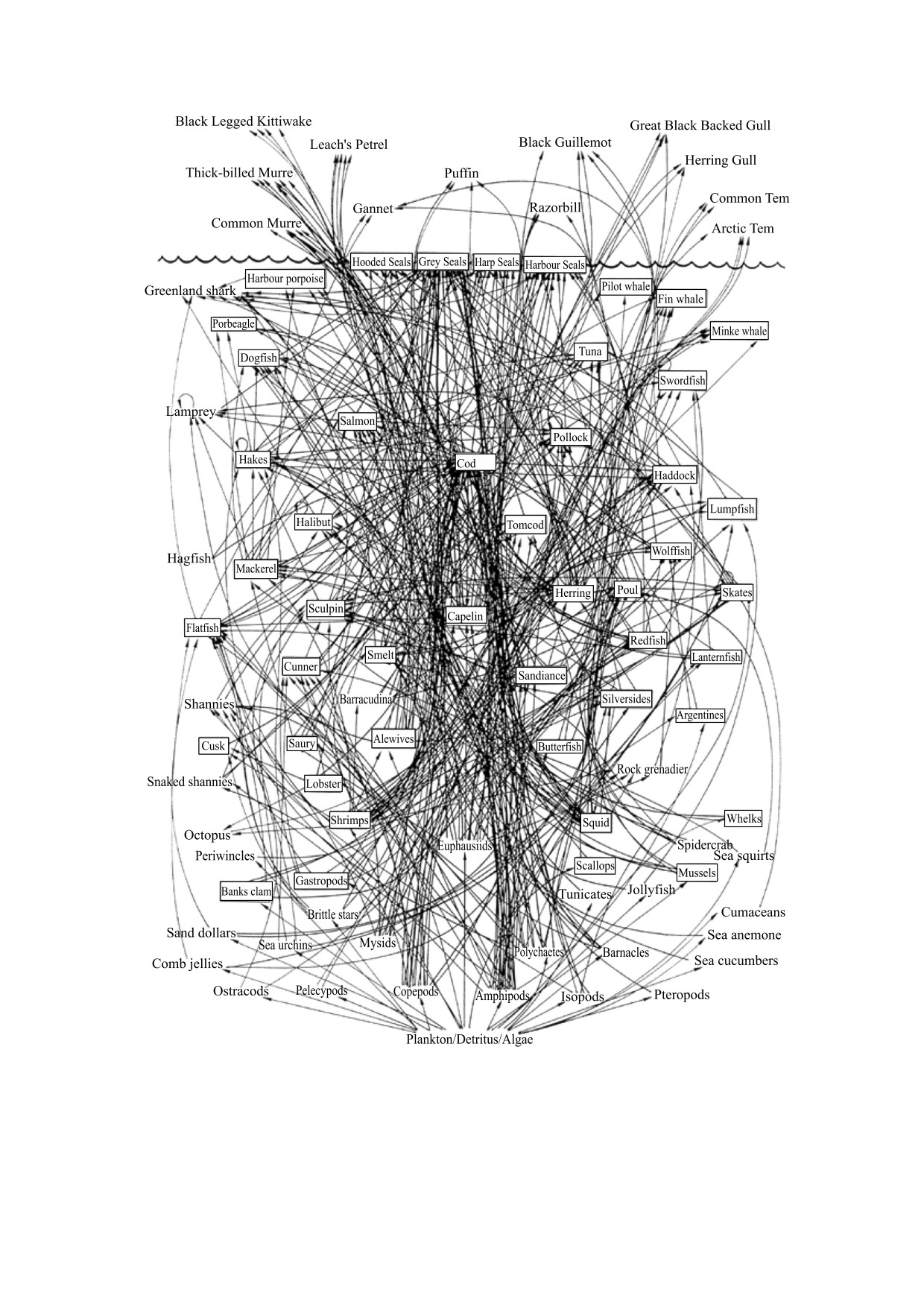
Отметим, что в реальности сеть трофических

ней среды. Острота проблемы, связанной с необ-

взаимодействий между популяциями гораздо бо-

ходимостью совмещения редукционистского

лее сложна, чем те схемы, которые обычно рас-

подхода с полнотой описания популяционной

сматриваются в рамках математического модели-

динамики, при этом очевидна.

рования. Чтобы убедиться в этом, достаточно

Математическое описание динамики популяций:

сравнить рис. 1, на котором представлена схема

отношений между модельными гидробионтами, с

выбор функций, описывающих популяционные про-

рис. 10, демонстрирующим схему взаимодей-

цессы. Многие математические модели динами-

ствий (упрощенную!) между популяциями, оби-

ческих взаимодействий между популяциями фак-

тающими в прибрежной зоне Атлантического

тически являются частными случаями модели

океана.

Гаузе-Колмогорова [58,59]:

БИОФИЗИКА том 64

№ 6

2019

1186

МЕДВИНСКИЙ и др.

Таблица 2. Примеры вида трофической функции f(N,P) [9, 60]

Корреляция

Вид зависимости

Постоянная функция

Линейная функция

Гиперболическая функция

aN/(1 + ahN)

Экспоненциальная (функция Ивлева)

R(1 - exp(-N/a)

То же, но g(N) → g(N/P)

R(1 - exp(-bN/P)

Сигмоидная функция № 1

cN²/(d² + N²)

Сигмоидная функция № 2

kN²/(1 + gN + khN²)

θ-сигмоидная функция

cN^θ/(d^θ + N^θ)

Механистическая интерференция функция

aN/(1 + awP)

Линейная интерференция

cN/P

Функция Хассела-Варли (Hassell-Varley)

cN/P^m

Функция Хассела-Варли-Xоллинга (Hassell-Varley-Holling)

c(N/P^m)/(1 + aw(N/P^m))

Функция Бeддингтона-ДеАнжелиса (Beddington-DeAngelis)

aN/(1 + awP + ahN)

Функция Ардити-Гинзбурга (Arditi- Ginzburg)

min (aN/P, R)

Функция Ардити-Гинбурга-Контуа (Arditi-Ginzburg-Contois)

a(N/P)/(1 + ah(N/P))

Функция Базыкина-Кроули (Bazykin-Crowley)

(aN/(1 + ahN))(1/(1 + βP))

Функция Трана (Trân) № 1

(N/P)(1 - (1 - ετ)P/τ)

Функция Трана (Trân) № 2

(N/P)(1 - exp(εP))

Функция Тютюнова № 1

(aN)/((P/P₀) + exp(-P/P₀) + ahN

Функция Тютюнова № 2

(aN)/((P/P₀) + (1/(1 + P/P₀)) + ahN

e - коэффициент, описывающий преобразование

rg (N)N = rN

1−

(10)

потребляемых хищниками жертв в численность

(

)

популяции хищников. Выбор численных значе-

или в виде функции Гомперца

ний параметров модели (9), а также функций g(N)

и f(N,P) определяется динамическими свойства-

rg (N)N = rNln

(11)

(

)

ми моделируемых популяционных процессов -

воспроизводство популяции жертв и потребление

В уравнениях (10) и (11) r и K - константы.

жертв хищниками соответственно. Отметим, что

Здесь необходимо отметить, что результаты

в некоторых математических моделях, в которых

математического моделирования популяцион-

не принимается во внимание конкуренция хищ-

ной динамики очень чувствительны, во-первых,

ников за ресурс (взаимная интерференция хищ-

к численным значениям модельных параметров

ников), f(N,P) → f(N), а в ряде других, где взаимная

и, что не менее важно, к выбору вида функций,

интерференция учитывается, f(N,P) ≡ f(N/P). Не-

описывающих популяционные процессы. По

которое представление о том многообразии вида

этой причине такой выбор (наряду с параметри-

трофической функции f(N,P), которое было пред-

зацией) существенно определяет адекватность

математических моделей динамики популяций,

ложено исследователями популяционной дина-

т. е. их соответствие реальности [61].

мики, дает табл. 2.

Математическое описание динамики популяций:

Слагаемое rg(N)N в первом уравнении модели

гибридные модели. Данные, накопленные в ходе

(9), которое описывает воспроизводство популя-

мониторинга процессов, протекающих в экоси-

ции жертв, чаще всего представляется (см. работу

стемах, представляют собой тот материал, на ко-

[7]) или в виде логистической зависимости

тором базируется математическое моделирова-

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1187

ние, а именно: выбор размерности той или иной

Таблица 3. Средние значения 〈Z〉 и 〈P〉 в г/м³

модели, выбор функций, выбор параметров, а

Нарочь 1

Нарочь 2

Мястро

Баторино

также - численных значений этих параметров.

Такой выбор является проявлением редукцио-

низма, неизбежно сопутствующего математиче-

〈Z〉

0,9811

1,0569

1,4286

2,3605

скому моделированию. В то же время результаты

полевых измерений, к примеру, временные ряды,

〈P〉

0,5372

0,5816

2,6513

9,1592

демонстрирующие динамику конкретных попу-

ляций, являются продуктом взаимодействия

Пpимечание. Нарочь 1 - Малый плес оз. Нарочь, Нарочь 2 -

Большой плес оз. Нарочь.

множества биотических и абиотических процес-

сов, влияющих на динамику данной популяции.

Отметим, что в результате такой временной ряд

функция уже ранее использовалась при модели-

отражает свойства исследуемой системы как це-

ровании динамики фитопланктона [63].

лого (при этом он также несет в себе отпечаток

Неизвестная функция G может быть найдена в

процесса измерений, проводимых в ходе монито-

виде временного ряда непосредственно из урав-

ринга; таким образом проявляется «эффект на-

нения (12) с учетом задания трофической функ-

блюдателя»). Взаимодействия между популяция-

ции, которая в данном случае определяется урав-

ми, а также взаимосвязь между популяциями и

нением (13), при условии, что известны времен-

факторами окружающей среды позволяют, в

ные ряды P(t) и Z(t). После введения новых

частности (при наличии достаточного объема

переменных

данных), проводить реконструкцию колебаний

популяционного обилия и судить как о характере

P t)

Z t)

(t)

таких колебаний, так и о факторах, которые могут

обусловливать наблюдаемые эффекты (см. раздел

где 〈P〉 и 〈Z〉 - средние значения биомасс фито-

«Реконструкция популяционной динамики»).

планктона и зоопланктона соответственно, урав-

Гибридные математические модели (см. ни-

нение, описывающее динамику пополнения по-

же), учитывающие результаты мониторинга при-

пуляции фитопланктона, с учетом уравнения (13)

родных экосистем, представляют собой другой

принимает следующий вид:

подход к исследованию популяционной динами-

P t)

ки. А именно, такой подход предполагает непо-

⎛

−

⎞

средственное включение данных мониторинга в

=ΔP

A⎜1

−

⎟Z

(14)

⎜

⎟

математическую модель. В качестве примера рас-

⎝

⎠

смотрим простейшую трофическую цепочку: фи-

где

топланктон (популяция жертвы), P - зоопланк-

тон (популяция-потребитель), Z. Такая цепочка

G t)

(t)

,ΔP

(t)

(

)

−

(t)

может описываться разностным уравнением:

P(t + 1) - P(t) = G(c,P(t)) - f(m,P(t))Z(t).

(12)

В уравнении (12) t - время, G - функция, опи-

сывающая пополнение популяции фитопланкто-

Средние значения 〈P〉 и 〈Z〉 приведены в табл. 3

на (она может принимать как положительные,

Из табл. 3 видно, что численные значения как

так и отрицательные значения), f - трофическая

〈Z〉, так и 〈P〉 монотонно возрастают в цепочке

функция. Функция G зависит как от обилия попу-

«оз. Нарочь → оз. Мястро → оз. Баторино», что

ляции фитопланктона P, так и от большого числа

особенно заметно для среднего значения биомас-

параметров, влияющих на воспроизводство

сы фитопланктона. Такой рост отражает установ-

планктона; эти параметры задаются вектором c,

ленный в ходе мониторинга экосистемы Наро-

размерность которого велика и заранее не опре-

чанских озер факт - увеличение продуктивности

делена. Трофическая функция f в уравнении (12)

водоемов в указанной выше цепочке [64].

предполагается зависимой от P, а также от пара-

В уравнении (14) используются временные ря-

метров, число которых обычно не превышает 3

ды P(t) и Z(t). Эти временные ряды представляют

(см. табл. 2). В качестве примера трофической

колебания во времени обилия фитопланктона и

функции мы в данном случае выбираем функцию

зоопланктона в каждом из Нарочанских озер за

Ивлева [62], а именно:

период с 1993 по 2017 гг. (примеры таких времен-

P t)

ных рядов, но на более узком временном интерва-

⎛

⎞

ле, с 1993 по 2013 гг., представлены на рис. 4). За-

(m,

P t))

A⎜1−

⎟

(13)

⎜

⎟

висимость G(t) непосредственно не измеряется в

⎝

⎠

ходе мониторинга. Тем не менее эта зависимость,

В уравнении (13) m = (A, b). Выбор функции

которая в виде временного ряда, аппроксимиру-

Ивлева обусловлен тем обстоятельством, что эта

ющего зависимость G(t), отражает динамику по-

БИОФИЗИКА том 64

№ 6

2019

1188

МЕДВИНСКИЙ и др.

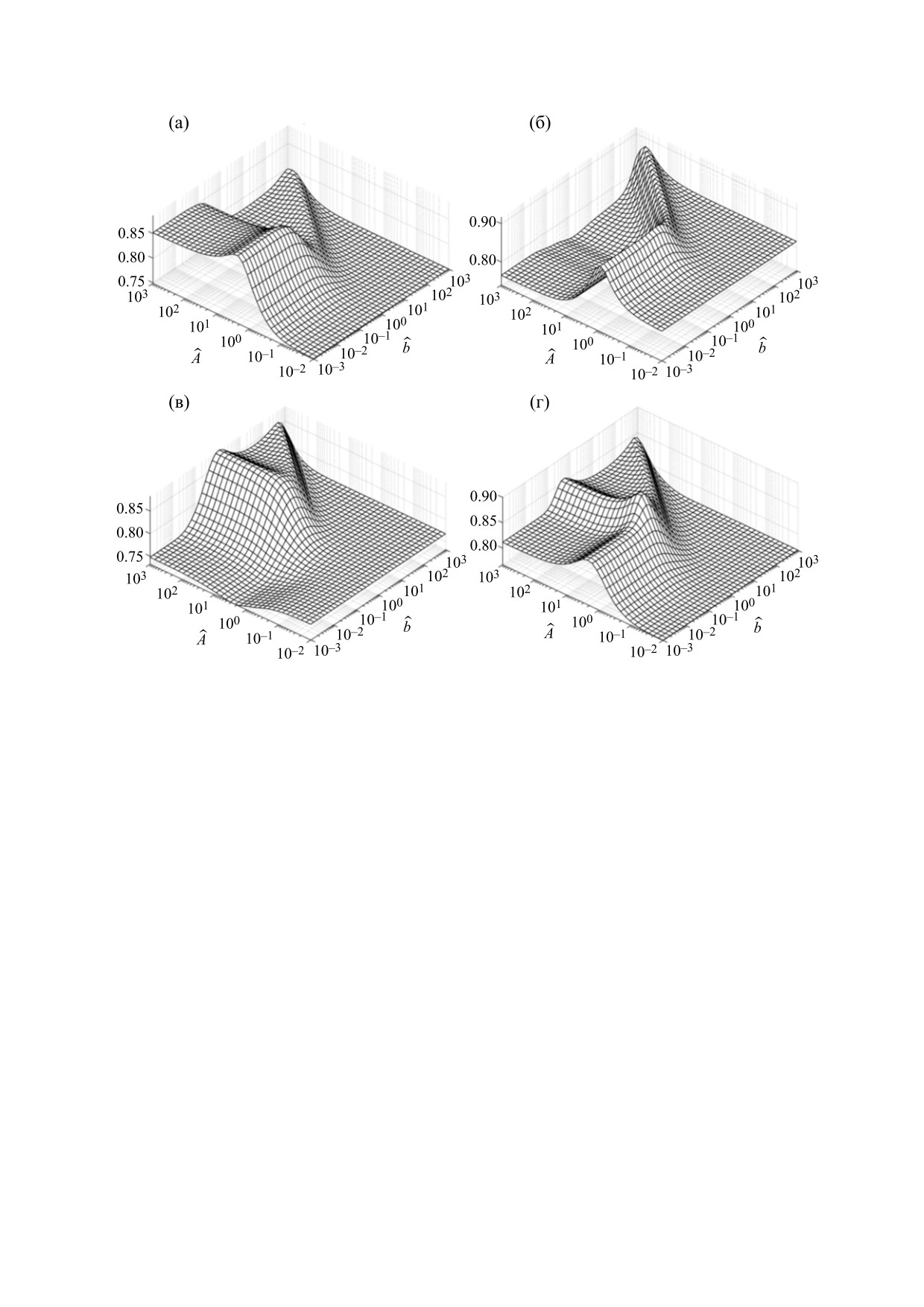
Рис. 11. Зависимости кросс-корреляционной энтропии от коэффициентов A

и b

при учете корреляции между G(t) и

температурой: (а) - Малый плес оз. Нарочь, (б) - Большой плес оз. Нарочь, (в) - оз. Мястро, (г) - оз. Баторино.

полнения популяции фитопланктона, может

Сравнение графиков зависимостей кросс-кор-

быть выявлена с помощью уравнения (14).

реляционной энтропии от коэффициентов Â и

Скорость пополнения популяций фитопланк-

уравнения (14) показывает, что численные зна-

тона зависит как от численности этих популяций,

чения этих коэффициентов для минимальных ве-

так и от экзогенных факторов, таких, например,

личин энтропии при учете корреляции между G(t)

как температура и концентрация биогенов в воде

и температурой, могут отличаться от соответству-

водоемов. В частности, представляет интерес

ющих значений коэффициентов для корреляции

корреляция между функцией G(t) и отношением

между G(t) и N(t)/P(t) (см. рис. 11 и 12).

концентрации растворенного в воде азота к кон-

центрации растворенного в воде фосфора (N/P)

Выбор минимальных значений кросс-корре-

[64]. Многолетний мониторинг экосистемы На-

ляционной энтропии определяется несколькими

рочанских озер позволяет соотнести характери-

обстоятельствами. Во-первых, необходимо при-

стики временных рядов, характеризующих вариа-

нять во внимание тот факт, что отношение N/P,

тивность факторов, которые могут влиять на ди-

отражающее процессы лимитирования роста фи-

намику популяций, с зависимостью G(t). С этой

топланктона при недостаточно высокой концен-

целью оказываются полезными численные оцен-

трации растворенных в воде биогенов азота [65]

ки кросс-корреляционной энтропии (подробнее

и/или фосфора [66], в значительной мере влияет

об использовании кросс-корреляционной энтро-

на скорость пополнения популяций фитопланк-

пии для анализа временных рядов см. раздел «Ме-

тона. Во-вторых, оказывается, что при выборе

тоды численной оценки взаимосвязей популяци-

минимальных значений кросс-корреляционной

онных колебаний и их сопряженности с экзоген-

энтропии, характеризующих сопряженность вре-

ными факторами»).

менных рядов G(t) и N(t)/P(t), численные значе-

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1189

Рис. 12. Зависимости кросс-корреляционной энтропии от коэффициентов A

и b

при учете корреляции между G(t) и

N(t)/P(t): (а) - Малый плес оз. Нарочь, (б) - Большой плес оз. Нарочь, (в) - оз. Мястро, (г) - оз. Баторино.

ния кросс-корреляционной энтропии, характе-

ЗАКЛЮЧЕНИЕ

ризующие сопряженность колебаний G(t) и тем-

Присущий математическому моделированию

пературы, хотя и несколько возрастают, но при

редукционистский подход к анализу природных

этом остаются меньшими, чем соответствующие

явлений неизбежно ставит вопрос о соответствии

значения для корреляций между G(t) и N(t)/P(t).

результатов моделирования реальным процессам.

Это свидетельствует о существенной роли темпе-

Важность такого вопроса становится вполне оче-

ратуры в поддержании роста фитопланктона. На-

видной в тех случаях, когда исследуются системы,

конец, в третьих, именно при выборе тех мини-

характеризующиеся сложной организацией про-

мальных значений кросс-корреляционной эн-

цессов, поддерживающих функционирование

тропии, которые соответствуют корреляциям

подобных систем (в качестве примера см. рис. 10).

между G(t) и N(t)/P(t), величины энтропии для

В поисках ответа на этот вопрос необходимо при-

каждого из водоемов Нарочанской группы озер,

нимать во внимание то обстоятельство, что ре-

соответствуют росту продуктивности водоемов в

альность обычно предстает перед исследователем

цепочке оз. Нарочь → оз. Мястро → оз. Баторино.

в виде экспериментальных результатов и/или

А именно, наименьшие значения энтропии име-

данных, полученных в ходе наблюдений. При

ют место для оз. Баторино, которое характеризу-

этом планирование и постановка экспериментов,

ется наибольшей продукцией планктона (табл. 3).

равно как и организация наблюдений неизбежно

Численные значения кросс-корреляционной эн-

предполагают некоторую заведомую редукцию

тропии приведены в табл. 4.

реальности.

БИОФИЗИКА том 64

№ 6

2019

1190

МЕДВИНСКИЙ и др.

Таблица 4. Кросс-корреляционная энтропия Шенно-

которые непосредственно не регистрируются в

на (нормированная на энтропию случайного сигнала)

ходе мониторинга. Например, в модели (12) такой

спектров взаимных корреляций между G(t) и экзоген-

характеристикой является скорость пополнения

ными факторами в водоемах Нарочанской группы

популяции фитопланктона. Поскольку времен-

озер

ные ряды, включаемые в гибридную модель, яв-

ляются результатом не только тех трофических

Факторы

Нарочь 1

Нарочь 2

Мястро

Баторино

взаимодействий, которые прямо описываются

моделью, но также множества биотических и

Температура

0,79

0,75

0,74

0,82

абиотических факторов, воздействующих на кон-

кретную исследуемую экосистему, использова-

N/P

0,91

0,89

0,80

ние гибридных моделей позволяет до некоторой

Пpимечание. Нарочь 1 - Малый плес оз. Нарочь, Нарочь 2 -

степени снять противоречие между редукциониз-

Большой плес оз. Нарочь.

мом, неизбежно сопутствующим математическо-

му моделированию, и холизмом как взглядом на

природу, не сводящим целое к сумме частей.

В этом смысле исследование популяционных

Принятие во внимание дополнительной инфор-

процессов не является исключением. Изучение

мации (например, учет временных рядов, харак-

механизмов, лежащих в основе таких процессов,

теризующих колебания концентрации биогенов,

требует сочетания математического моделирова-

как в разделе «Математическое описание дина-

ния, лабораторных экспериментов и мониторин-

мики популяций: гибридные модели») позволяет

га природных экосистем. В тех случаях, когда

соотнести эту информацию с результатами мате-

речь идет об изучении конкретной экосистемы,

матического моделирования. Такое соотнесение

далеко не всегда выбор численных значений па-

в случае модели (12) проявляется в виде корреля-

раметров математической модели, а также функ-

ции спектров колебаний факторов окружающей

циональных зависимостей между переменными,

среды - температуры и отношения концентраций

описывающих динамику популяционных про-

растворенных в воде биогенов азота и фосфора -

цессов в конкретной экосистеме, удается обосно-

с полученными в результате моделирования

вать, опираясь исключительно на результаты по-

спектрами колебаний пополнения популяций

левых наблюдений. Это может быть связано как с

фитопланктона. В модели

(12) трофическая

недостаточным объемом данных, полученных в

функция f(m,P(t) задана в виде функции

ходе мониторинга исследуемой экосистемы, так

Ивлева (13). В общем случае выбор трофической

и с неоднозначностью, характерной для выделе-

функции (см., например, табл. 2), равно как и вы-

ния из целостной системы процессов и функцио-

бор области изменения численных значений

нальных зависимостей, включаемых в математи-

(пусть и сравнительно небольшого числа) пара-

ческую модель [61,67].

метров трофической функции, определяется са-

В качестве альтернативы математическому мо-

мим исследователем и в оптимальном случае дол-

делированию с целью исследования характера

жен базироваться на результатах мониторинга ис-

колебаний и предсказания популяционного оби-

следуемой экосистемы. Представленная выше

лия динамики были предложены подходы рекон-

модель (12) описывает простую двухзвенную тро-

струкции динамики популяций с использовани-

фическую цепь типа «ресурс - потребитель».

ем временных рядов, которые были получены в

Усложнение гибридной модели может быть реа-

ходе экспериментов или полевых наблюдений

лизовано при условии, что имеется достаточно

[68]. В ряде случаев эти подходы, использующие

полная информация о трофических взаимодей-

методы нелинейной динамики [21,26,27,31] (см.

ствиях и о факторах, влияющих на динамику со-

также раздел «Анализ временных рядов» в насто-

обществ исследуемой экосистемы.

ящей статье), продемонстрировали свою эффек-

тивность. В частности, методы реконструкции

Как реконструкция популяционной динами-

динамики популяций показали, что не межвидо-

ки, так и непосредственное включение в матема-

вая конкуренция, а фактор окружающей среды,

тическую модель данных полевых наблюдений

температура, ответственен за вариации во време-

предполагает тесное сотрудничество теоретиков

ни численности тихоокеанских популяций хамсы

и исследователей, проводящих мониторинг эко-

и сардины [22] (подробнее см. раздел «Рекон-

систем. Такое сотрудничество предполагает, в

струкция популяционной динамики»).

частности, совместное участие соответствующих

В свою очередь, непосредственное включение

исследовательских групп и/или координацию их

в математическую модель временных рядов, по-

деятельности в ходе организации и проведении

лученных в результате мониторинга природных

как полевых, так и математических исследований

экосистем (гибридное моделирование популяци-

с целью выявления и изучения факторов, суще-

онной динамики), позволяет выявлять характер

ственно влияющих на предсказуемость и харак-

колебаний таких популяционных характеристик,

тер динамики природных популяций.

БИОФИЗИКА том 64

№ 6

2019

ДИНАМИКА ПОПУЛЯЦИЙ

1191

ФИНАНСИРОВАНИЕ РАБОТЫ

22.

G. Sugihara, et al., Science 338, 496 (2012).

23.

F. Takens, Dynamical Systems and Turbulence 898,

Авторы благодарны Российскому фонду фун-

366 (1981).

даментальных исследований за финансовую под-

24.

G. I. Murphy and J. D. Isaacs, California Cooperative

держку проводимой ими работы (грант РФФИ 17-

Oceanic Fisheries Investigations 7, 1 (1964).

07-00048) и Белорусскому республиканскому

25.

R. Lasker and A. Mac Call, In Proc. Joint Oceanograph-

фонду фундаментальных исследований за под-

ic Assembly 1982. General Symposia (1983), p. 110.

держку исследований на Нарочанских озерах.

26.

D. Kaplan and L. Glass, Understanding Nonlinear Dy-

namics (Springer, New York, 1995).

КОНФЛИКТ ИНТЕРЕСОВ

27.

E. Ott, Chaos in Dynamical Systems (Cambridge Uni-

versity, Cambridge, 2002).

Авторы заявляют об отсутствии конфликта

интересов.

28.

A. B. Medvinsky and A. V. Rusakov, Chaos, Solitons

and Fractals 44, 390 (2011).

29.

A. B. Medvinsky, A. V. Rusakov, and N. I. Nurieva,

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

Ecol. Complexity 14, 108 (2013).

Настоящая работа не содержит описания ка-

30.

А. С. Братусь, А. С. Новожилов и А. П. Платонов,

Динамические системы и модели биологии (Физмат-

ких-либо исследований с использованием людей

лит, Москва, 2010).

и животных в качестве объектов.

31.

H. Kantz and T. Schreiber, Nonlinear Time Series Anal-

ysis (Cambridge University, Cambridge, 1997).

СПИСОК ЛИТЕРАТУРЫ

32.

S. Kauffman, The Origins of Order: Self-Organization

and Selection in Evolution (Oxford Univrsity, Ox-

1. I. Valiela, Marine Ecological Processes (New York:

ford,1993).

Springer, 1995).

33.

R. V. Solé and J. Bascompte, Self-Organization in Com-

2. Г. Ю. Ризниченко и А. Б. Рубин, Биофизическая ди-

plex Ecosystems (Princeton University, Princeton,

намика продукционных процессов (Институт ком-

2006).

пьютерных исследований, Москва-Ижевск,

2004).

34.

H. Poincaré, Acta Mathematica 13, 1 (1890).

3. В. Д. Фёдоров и Т. Г. Гильманов, Экология (Изд-во

35.

N. Marwan, et al., Phys. Reports 438, 237 (2007).

МГУ, М., 1980).

36.

Y. Kuramoto, Chemical Oscillations, Waves, and Turbu-

4. A. B. Medvinsky, et al., Rus. J. Num. Analysis Math.

lence (Springer, Berlin, 1984).

Model. 30, 55 (2015).

37.

A. Pikovsky, M. Rosenblum, and J. Kutrth, Synchroni-

5. А. В. Русаков и др., Компьютерные исследования и

zation. A Universal Concept in Nonlinear Sciences (Cam-

моделирование 8, 229 (2016).

bridge University, Cambridge, 2001).

6. G. G. Mittelbach, et al., in Size-structured Populations,

38.

A. B. Medvinsky, et al., Ecol. Complexity 32, 90 (2017).

Ed. by B. Ebenman and L. Persson (Springer, Berlin,

39.

R. D. Gulati, Hydrobiologia 200-201, 99 (1990).

Heidelberg, 1988), p. 219.

40.

R. Perissinotto, Marine Ecol. Progr. Series 79, 243

7. M. Kot, Elements of Mathematical Ecology (Cambridge

(1992).

University, Cambridge, 2001).

41.

T. B. Gurung, M. Nakanishi, and J. Urabe, Limnol.

8. O. J. Schmitz, Resolving Ecosystem Complexity (Prince-

Oceanography 45, 1689 (2000).

ton University, Princeton, Oxford, 2010).

42.

J. Le, J. D. Wehr, and L. Campbell, Appl. Environ. Mi-

9. P. Turchin, Complex Population Dynamics. A Theoreti-

crobiol. 60, 2086 (1994).

cal/Empirical Synthesis (Princeton University, Prince-

43.

K Vrede, et al., Limnol. Oceanography 44, 1616 (1999).

ton, Oxford, 2003).

44. Д. А. Тихонов и А. Б. Медвинский, Биофизика 64

10. А. Е. Бобырев и др., Биофизика 57, 140 (2012).

(4), 747 (2019).

11. A. B. Medvinsky, et al., Ecol. Complexity 23, 61 (2015).

45.

C. V. Heer, Statistical Mechanics, Kinetic Theory, and

12. E. Benincà, et al., Proc. Natl. Acad. Sci. USA 112,

Stochastic Processes (Acad. Press, New York, London,

6389 (2015).

1972).

13. А. Ю. Лоскутов, Успехи физ. наук 180 1305 (2010).

46.

J.-L. Shen, J. Hung, and L.-S. Lee, In Int. Conf. on

14. J. Lighthill, Proc. Roy. Soc. Lond. A 407, 35 (1986).

Spoken Language Processing (1998), Paper 0232.

15. G. Boffetta, et al., Phys. Reports 356, 367 (2002).

47.

X. Li, et al., In Bio-Inspired Computational Intelligence

16. Kot M et al., Bul. Math. Biol. 54, 619 (1992).

and Applications, Ed. by M. Fei, G. W. Irwin, and S. Ma

17. А. Б. Медвинский и др., Успехи физ. наук 172, 31

(Springer, Berlin, Heidelberg), p. 36.

(2002).

48.

W. Yi, et al., J. NeuroEngineer. Rehabilitation 10, 106

18. A. B. Medvinsky, et al., Biol. Invasions 7, 877 (2005).

(2013).

19. H. W. Ducklow, S. C. Doney, and D. K. Steinberg, An-

49.

V. Sharma and A. Parey, Proc. Engineer. 144, 253

nu. Rev. Marine Sci. 1, 279 (2009).

(2016).

20. M. Ushio, et al., Nature 554, 360 (2018).

50.

B. V. Adamovich, et al., Ecol. Indicators 97, 120 (2019).

21. N. Boccara, Modeling Complex Systems (Springer, New

51.

V. A. Kostitzin, La Biologie Mathematique (A. Colin,

York, 2004).

Paris, 1937).

БИОФИЗИКА том 64

№ 6

2019

1192

МЕДВИНСКИЙ и др.

52. Ю. М. Свирежев и Д. О. Логофет, Устойчивость

60. Ю. В. Тютюнов и Л. И. Титова, Журн. общ. биоло-

биологических сообществ (Наука, Москва, 1978).

гии 79, 428 (2018).

53. A. A. Berryman, N. C. Stenseth, and A. S. Isaev, Oeco-

61. M. W. Adamson and A. Y. Morozov, Proc. Roy. Soc.

logia 71, 174 (1987).

Lond. A 469, 20120500 (2013).

62. В. С. Ивлев, Экспериментальная экология питания

54.

А. С. Исаев и др., Популяционная динамика лесных

рыб (Пищепромиздат, Москва, 1955).

насекомых (Наука, Москва, 2001).

63. W. C. Gentleman and A. B. Neuheimer, J. Plankton

55.

А. Д. Базыкин и др., Докл. РАН 333, 673 (1993).

Res. 30, 1215 (2008).

56.

А. Д. Базыкин, Нелинейная динамика взаимодей-

64. Б. В. Адамович и др., Водные ресурсы 43, 535

ствующих популяций (Институт компьютерных ис-

(2016).

следований, Москва-Ижевск, 2001).

65. D. W. Schindler, Limnol. Oceanigraphy 51, 356 (2006).

57.

В. С. Анищенко, Знакомство с нелинейной динами-

66. R. G. Wetzel, Limnology. Lake and River Ecosystems

кой (URSS, Москва, 2008).

(Acad. Press, San Diego, 2001).

58.

G. F. Gause, The Struggle for Existence (Williams and

67. S. N. Wood and M. B. Thomas, Proc. Roy. Soc. Lond.

Wilkins, Baltimore, 1934).

B 266, 565 (1999).

59.

А. Н. Колмогоров, Проблемы кибернетики 25, 100

68. C. T. Perretti, S. B. Munch, and G. Sugihara, Proc.

(1972).

Natl. Acad. Sci. USA 110, 5253 (2013).

Population Dynamics: Mathematical Modeling and Reality

A.B. Medvinsky*, B.V. Adamovich**, A.V. Rusakov*, D.A. Tikhonov*^, ***,

N.I. Nurieva*, and V.M. Tereshko*^, ****

*Institute of Theoretical and Experimental Biophysics, Russian Academy of Sciences,

Institutskaya 3, Pushchino, Moscow Region, 142290 Russia

** Faculty of Biology, Belorusian State University, prosp. Nezavisimosti 4, Minsk, 220030 Belarus

*** Institute of Mathematical Problems of Biology - Branch of Keldysh Institute of Applied Mathematics,

ul. Professora Vitkevicha 1, Pushchino, Moscow Region, 142290 Russia

****United Institute of Informatics Problems, ul. Surganova 6, Minsk, 220012 Belarus

Model reduction technique applied in mathematical modeling for the analysis of natural phenomena inevi-

tably raises the question about whether simulation results reflect real processes. The paper presents the anal-

ysis of problems associated with a comparison of the results obtained with mathematical modeling of popu-

lation processes and data collected while monitoring natural ecosystems. These problems arise because it is

often not possible even based on monitoring data from a particular ecosystem to substantiate the type of de-

pendencies between variables that determine population dynamics, as well as to justify the choice of numer-

ical values assigned to the parameters of mathematical models. In this paper, we propose an approach to take

into account the impact of the whole complex of biotic and abiotic factors on population dynamics in math-

ematical modeling. Consideration and application of ecosystem monitoring data in mathematical models of

population dynamics is the core of .this approach. This approach would make it possible, in particular, to as-

sess the degree of influence of individual environmental factors both on variations in population abundance

recorded during monitoring and on those characteristics of population processes that are not directly mea-

sured during monitoring, but are the result of mathematical modeling.

Keywords: population dynamics, mathematical modeling, time series analysis

БИОФИЗИКА том 64

№ 6

2019