БИОФИЗИКА, 2020, том 65, № 5, с. 967-977

БИОФИЗИКА СЛОЖНЫХ СИСТЕМ

УДК 577.3

ДИНАМИКА СИСТЕМЫ «ХИЩНИК-ЖЕРТВА»

СО СТАДНЫМ ПОВЕДЕНИЕМ В ОБОИХ СЛУЧАЯХ

И СИЛЬНЫМ ЭФФЕКТОМ ОЛЛИ У ЖЕРТВЫ

*Отдел математики Национального технологического института Пудучерри, Караикал-609609, Индия

**Средняя школа Чандрахати Дилипа Кумара (Х.С.), Чандрахати, Западная Бенгалия, 712504, Индия

***Отдел математики Индийского института инженерных наук и технологий, Шибпур, Хора-711103, Индия

E-mail: biswassoumen84@gmail.com

Поступила в редакцию 11.03.2020 г.

После доработки 11.03.2020 г.

Принята к публикации 08.05.2020 г.

Работа посвящена динамике хищника и жертвы, когда и жертва, и хищник демонстрируют стадное

поведение. Положительность, ограниченность, некоторые критерии вымирания, устойчивость воз-

можных точек равновесия обсуждаются в инновационном подходе, в связи с некоторым глобаль-

ным поведением. Для пояснения аналитических дискуссий представлены результаты численного

моделирования. Биологические последствия аналитических и численных результатов с целью под-

держания экологического баланса в природе обсуждаются отдельно. Представлены возможности

будущих исследований по этой теме.

Ключевые слова: хищник-жертва, стадное поведение, эффект Олли, вымирание, устойчивость.

DOI: 10.31857/S0006302920050142

Моделирование двумерных динамических си-

была подробно обсуждена в работе [15]. Здесь мы

стем является широко обсуждаемой концепцией

будем использовать функцию роста и соответ-

в различных сферах экологии в наше время. Все

ствующее уравнение роста, использованное авто-

исследования популяционных моделей прошлого

рами в работах [16-19]. Уравнение роста описы-

столетия исходили в основном из модели Лотки-

вается выражением

Вольтерра [1-4], тогда как были предложены и

некоторые другие возможные динамики, кроме

=αM

1−

(1.1)

(

)

классического предположения о квадратичных

взаимодействиях. Прежде всего, мы можем на-

где M(T) обозначает плотность населения в мо-

звать систему Холлинга-Танера [5-7], зависи-

мент времени T, α - собственная скорость роста

мую от соотношения численностей RD-модель

на душу населения, а K - несущая способность

[8, 9], и функциональные реакции Холлинга

окружающей среды. Можно отметить, что темп

типа II и типа III [1, 2, 10]. Последние, однако,

роста на душу населения является уменьшаю-

требуют большего изучения и обсуждения [11-

щейся функцией размера населения и достигает

13], чтобы быть обоснованными должным обра-

нуля в насыщенной фазе, когда население дости-

зом. Более того, квадратичные взаимодействия,

гает размера K. Из-за ограниченности ресурсов,

основанные на законе действующих масс, ис-

таких как еда, пространство и основные пита-

пользуются даже сегодня в более сложной модели

тельные вещества, каждая популяция растет к на-

пищевой цепи [14].

сыщенной фазе и не может расти дальше. Любая

В нашей настоящей статье мы рассматриваем

популяция, достигшая размера выше K, получит

систему двух популяций по-другому, используя в

отрицательный темп роста. Исследователи обна-

некоторых случаях подходящие допущения для

ружили много доказательств в реальных жизнен-

обсуждения различного динамического поведе-

ных ситуациях, когда у роста населения наблюда-

ния. Важнейшими компонентами любой модели

ется обратная тенденция при низкой плотности

являются выбор функции роста жертвы и функ-

населения [20-25], явление положительной зави-

циональный ответ хищника. Концепция группо-

симости плотности прироста населения при низ-

вой защиты с подходящими предположениями о

кой плотности известно как эффект Олли [23-

форме и типе функциональных реакций жертвы

26]. Эффект Олли обуславливают проблема адап-

967

968

БИСВАС и др.

тации к окружающей среде, снижение оборони-

где M(T) обозначает плотность добычи в момент

тельной бдительности, трудности в поиске парт-

времени T, β - эффективность поиска хищником

нера, снижение защиты от хищников и многие

жертвы, а T_h - среднее время обработки хищни-

другие причины [20-23]. Вот почему эффект Ол-

ком каждой жертвы.

ли можно разделить на два разных типа в зависи-

Теперь попробуем осветить концепцию стад-

мости от скорости снижения темпов роста на ду-

ного поведения. Словарное значение понятия

шу населения при низкой плотности населения:

стада - это большая группа животных, особенно

сильный эффект Олли [27-30] (или критическая

копытных, которые живут вместе как домашний

диспенсация [31-33]) и слабый эффект Олли [26,

скот. Несколько причин побуждают вид демон-

34] (или некритическая диспенсация [31-34]).

стрировать стадное поведение. Например, стадо

Моделирование эффекта Олли обычно представ-

может защитить жертв от хищников. С другой

ляется уравнением роста следующего вида

стороны, для хищников стая может быть более

эффективной стратегией, чтобы уничтожить ста-

M M



=αM

1−

−1,

(1.2)

до добычи. Таким образом, здесь возникает необ-

(

)



K



ходимость поиска подходящей формы функцио-

нального ответа для описания этого социального

где M(T) - плотность населения в момент време-

поведения. Понятие о том, что квадратный ко-

ни T, K - несущая способность среды, α - соб-

рень из переменной, задающей плотность попу-

ственная скорость роста на душу населения, и

ляции хищника, может быть использован в функ-

0 < K₀ << K. Условия, при которых значение K₀

ции, описывающей показатель встречаемости в

является положительным и размер популяции

двумерной системе, было введено в работе [51].

ниже порогового уровня K₀, показывают, что тем-

Точно так же две трети силы хищника в показате-

пы прироста населения уменьшаются и исчезают

ле встречаемости лучше описывают такое группо-

[27, 35-37]. Здесь был использован сильный эф-

вое поведение хищников в трехмерных системах.

фект Олли, хотя описание слабого эффекта Олли

Эту концепцию можно найти в работе [52]. Но в

также доступно [29, 38]. Показав аддитивный эф-

работах [53] и [54] была предложена другая кон-

фект Олли, упомянем другую форму функции ро-

цепция в этой области. Прежде чем продолжить,

ста, которую можно найти в работах [39, 40]. Так-

мы должны описать основные идеи этих работ.

же можно найти сравнение между логистической

Пусть М - плотность населения, которое со-

функцией роста (1.1) и функцией, представляю-

бирается в стада. Предположим, что стадо зани-

щей эффект Олли уравнением (1.2), в работе [16].

мает область H. Количество особей, находящихся

в самых удаленных местах в стаде, пропорцио-

Теперь обратимся к функции, которая описы-

нально длине периметра участка, где находится

вает количество добычи, потребляемой хищни-

стадо. Таким образом, его длина пропорциональ-

ком на единицу времени для заданных популяций

жертв и хищников, и называется функциональ-

на H. Следовательно,

будет подсчитывать

ной реакцией или тропной функцией. Исследо-

индивидуумов на краю участка, тогда как М рас-

ватели разработали множество подходящих

пределяется по двумерной области. Следователь-

функциональных реакций, в зависимости от по-

но, при моделировании атаки хищника на эту по-

ведения популяций, реагирования скорости хищ-

пуляцию функциональная реакция должна быть

ничества на изменение плотности жертв у раз-

выражена в виде квадратного корня из популяции

личных популяций жертв. Как мы упоминали ра-

добычи. Эта идея была впервые представлена в

нее, семейство функциональных ответов

работе [53]. В работе [54] был введен новый функ-

Холлинга наиболее разработано, что подтвержда-

циональный отклик, в котором показатель плот-

ют работы [41-47]. Но в динамике хищников

ности жертв в выражении (1.3) заменяется его

очень популярной стала функциональная реак-

квадратным корнем. Было также принято пред-

ция Холлинга II типа [48-50]. Этот тип функцио-

положение, что среднее время обработки T_h рав-

нальной реакции включает в себя тот факт, что

но нулю в его расчетной части. Для настоящей

одна особь может питаться только до тех пор, по-

статьи мы хотели бы использовать эти наблюде-

ка желудок не заполнится, и поэтому функцию

ния для построения нашего нынешнего функци-

насыщения лучше описать как прием пищи. Эта

онального отклика. Эта модель может быть более

концепция похожа на закон убывающей отдачи,

подходящей для крупных хищников по отноше-

заимствованный из исследования операций, то

нию к их добыче. Подобные рассуждения приве-

есть гиперболу, поднимающуюся до асимптоти-

ли в работе [52] к созданию модели планктона, в

ческого значения. Другими словами, функцио-

которой токсичный фитопланктон высвобождает

нальный ответ будет иметь вид

яд через поверхность трехмерного пятна. В реаль-

ной жизни мы можем легко найти некоторые ви-

βM

ды хищников, которые сравнительно существен-

G(M)

(1.3)

1+T

βM

но сильнее, чем виды их жертв, и поэтому среднее

БИОФИЗИКА том 65

№ 5

2020

ДИНАМИКА СИСТЕМЫ «ХИЩНИК-ЖЕРТВА»

969

время обработки хищником для каждой добычи

следующий набор нелинейных дифференциаль-

может быть проигнорировано. Более того, аргу-

ных уравнений

мент авторов работы [53] мотивирует нас модели-

ровать функцию реакции жертвы, которая де-

M M



=αM

1−

−1

−β

M N

монстрирует стадное поведение, в терминах квад-

(

)





K K



(2.1)

ратного корня из показателя популяции добычи.

Итак, не говоря уже о функциональном ответе,

= -δN

+ βγ

M N

использованном авторами работ [16, 54-56], мы

рассматриваем хищнический функциональный

с начальными условиями

ответ как

M(0) > 0, N(0) > 0,

(M) = β M,

(1.4)

где α - собственная скорость роста на душу насе-

где β и M такие же, как в выражении (1.3). Приме-

ления, K - пропускная способность жертвы, K₀ с

чательно, что жизнь в стадах может быть полез-

ной, если население восприимчиво к эффекту

0 < K₀ << K - порог Олли популяции добычи в от-

Олли. Исследователи предположили, что группо-

сутствие хищника, δ - смертность хищника в от-

вое поведение может уменьшить риски исчезно-

сутствие добычи. Из-за стадного поведения здесь

вения, вызванные эффектом Олли. В присут-

мы использовали модифицированный функцио-

ствии хищника такое поведение играет ключевую

нальный отклик (1.4) для представления взаимо-

роль в отношении бдительности и риска хищни-

действия между добычей и хищником. Следова-

чества [24]. В большинстве работ, связанных с

тельно, β и γ представляют эффективность поис-

этой концепцией, предполагается, что добыча

ка хищника и степень конверсии биомассы

имеет логистический рост. Заинтересованные чи-

соответственно. Попробуем объяснить логику

татели могут обратиться к работе [55] и приведен-

наших предположений. Предположения о стад-

ным в ней ссылкам. Но авторы работ [16, 17] рас-

ном поведении и эффекте Олли уже рассматрива-

смотривали свои модели со стадным поведением

лись в работах многих авторов [16, 17]. Но предпо-

жертв и стадным поведением и жертв, и хищни-

ложение о том, что среднее время обработки хищ-

ков соответственно, причем обе модели имели

ника для каждой жертвы равно нулю, лучше всего

сильный эффект Олли. Анализируя эти работы,

объяснить подходящим примером. Хищники, ко-

здесь мы пытаемся построить и исследовать но-

торые сравнительно сильнее, чем их жертвы, не

вую модель с некоторыми подходящими допуще-

тратят время, чтобы справиться со своей добы-

ниями.

чей. В практической жизни мы видим, что мелкие

рыбы проглатываются более крупными. На са-

Следующий раздел содержит краткое обсужде-

мом деле в нашей вселенной очень много хищни-

ние предположений и параметров. Раздел 3 дан-

ков, для которых мы можем без всяких сомнений

ной работы объясняет положительность и огра-

пренебречь термином «среднее время обработки

ниченность системы. Некоторые критерии вы-

каждой добычи». Очевидно, что все используе-

мирания как для жертвы, так и для хищника

мые здесь параметры положительны.

описаны в разделе 4, а в разделе 5 можно найти

возможные точки равновесия и анализ их устой-

чивости. В разделе 6 представлен анализ бифур-

Если мы перемасштабируем

каций. Численная проверка наших аналитиче-

ских результатов дана в разделе 7. Наконец, в раз-

для уменьшения количества парамет-

деле 8 представлены заключительные замечания

^=αK

ров в выражении (2.1), то после некоторых упро-

для наших аналитических и численных наблю-

щений получим систему:

дений.

dm=m(1−m)(m−r)−a m n

2. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

(2.2)

Здесь мы рассмотрим некоторые подходящие

dn =−dn+b m n

предположения для построения нашей модели.

Позже мы должны дать некоторую логику этого.

βK

δK

βγK

Пусть M(T) и N(T) - плотность жертвы и хищни-

где

αK

ка соответственно. Мы считаем, что обе популя-

ции живут в стадах, предполагаем также мульти-

3. ПОЛОЖИТЕЛЬНОСТЬ

пликативный эффект Олли в росте популяции

И ОГРАНИЧЕННОСТЬ

добычи. Теперь самое важное предположение о

том, что среднее время обработки хищника для

Для обеспечения положительности системы (2.2)

каждой жертвы равно нулю, побуждает нас ввести

необходимо рассмотреть следующую теорему.

БИОФИЗИКА том 65

№ 5

2020

970

БИСВАС и др.

Теорема

3.1. Решения системы уравнений

Также можно получить

(2.2), область которых есть

R+

, положительны

(m(0)

−

r)m(1 −

m),

всегда.

Доказательство: Доказательство этой теоремы

где m(0) - r > 0.

простое и поэтому незначительно для нашего на-

Это означает, что

limsup

mt)

≤

1, что противо-

стоящего исследования.

t→∞

Для ограниченности системы (2.2) можно рас-

речит нашему предположению. Следовательно,

смотреть следующую теорему.

оно верно.

Соответственно, из вышеописанных двух слу-

Теорема 3.2. Начиная с

R+

, все решения систе-

чаев мы имеем

limsup

mt)

≤

мы уравнений (2.2) равномерно ограничены.

t→∞

Доказательство. Если будет иметься какое-ли-

Теперь пусть U = bm + an. Тогда для больших t

бо решение {m(t), n(t)} системы уравнений (2.2),

имеем

то у нас должно быть два возможных случая.

Случай 1: Если m(0) ≤ 1, мы будем утверждать,

dU = bm(1−

m)(m-r)

−

adn,

что m(t) ≤ 1 для всех t ≥ 0. Если предположить, что

наше утверждение не соответствует действитель-

dU = bm

{

(1+

m-r −m

}

−

adn,

ности, то можно найти два положительных дей-

ствительных числа t₁ и t₂ такие, что m(t₁) = 1 и

dU ≤ b(1

r)m-adn

m(t) > 1 для всех t ∈ (t₁, t₂). Теперь для всех t ∈ (t₁, t₂)

из системы уравнений (2.2) имеем

dU ≤ b(1

)

−λ





mt)

m(0)exp

f m(s),n(s))ds,



где l = min{(1 + r), d}.





Следовательно, имеем



a nt)

где

f m(t),n(t))

(1−

mt))(mt)

−



dU +λU ≤ b(1



mt)

Это означает, что

Применяя теорию дифференциальных нера-

венств, мы легко получаем







mt)=

m(0) exp

f m(s),n(s))ds

xp

f m(s),

ns))ds





2b(1

)

U m(0),n(0))





≤

U m

≤

 

e^λ





и для t → ∞

mt)

m(t

)exp



f m(s),n(s))ds







2b(1+

)

≤

U m n

≤

для всех t ∈ (t₁, t₂).

Следовательно, все решения системы уравне-

Поэтому для всех t ∈ (t₁, t₂) имеем f(m(t), n(t)) < 0

ний (2.2) входят в область

как r < 1, следовательно, m(t) < m(t₁) = 1, что про-

тиворечит нашему предположению что m(t) > 1

2b(1

B = m,n):0

≤

U m n

≤

+ε

для всех t ∈ (t₁, t₂). Следовательно, наше предпо-

{

}

ложение верно.

для любого

> 0.

Случай 2: Пусть m(0) > 1, мы утверждаем, что

Таким образом, теорема доказана.

. Допустим, что наше утверждение

limsup

mt)

≤

t→∞

не соответствует действительности. Тогда m(t) > 1

4. СЦЕНАРИИ ВЫМИРАНИЯ

для всех t > 0. Таким образом, f(m(t), n(t)) < 0, при-

чем

Любая модель, подобная нашей, может пред-

ставить некоторые условия для исчезновения



a nt)

хищников и жертв. Итак, в этом разделе мы по-

f m(t),n(t))

(1−

mt))(mt)

−





mt)

пытаемся найти некоторые критерии относи-

тельно вымирания с помощью логического ана-

Поэтому из первого уравнения системы урав-

лиза. Сначала попытаемся установить два усло-

нений (2.2) мы получаем

вия, при которых популяция жертв может





исчезнуть, а условие, обеспечивающее исчезно-

mt)

m(0)exp

f m(s),n(s))

 <

(0).

вение популяции хищников, будет в конце этого







раздела.

БИОФИЗИКА том 65

№ 5

2020

ДИНАМИКА СИСТЕМЫ «ХИЩНИК-ЖЕРТВА»

971

Пусть

limsup

mt)

lim inf

nt). Таким

Доказательство: Пусть

lim

mt)

=μ>

0, тогда

t→∞

из определенияmдля любого ε, удовлетворяюще-

образом, мы можем использовать

, что сле-

m≤

го условию

, существует t_ε > 0 такое,

0<ε<r -m

дует из доказательства теоремы 3.2.

что

mt) <m+ε

для любого t > t_ε. Далее, для t > t_ε

Теорема 4.1. Если

m≤

1, то

lim

mt)

t→∞

первое уравнение системы уравнений (2.2) дает:







a m s)

ns)

mt)

m(0)exp



(1−

m s))(m s)

−

ds





m s)











mt)

m(0)exp



+ε-

)

ds

(





mt)

m(0)exp

{

−(

r - m

-ε)

}

→

0,если

→∞,

что является противоречием, и, следовательно,

Доказательство: Поскольку

m≤

1, для любого

наша теорема доказана.

ε, удовлетворяющего условию 0 < ε < 1, существу-

Здесь наша попытка может создать условия,

ет t_ε > 0 такое, что m(t) < 1 + ε для любого t > t_ε.

при которых хищник может играть жизненно

Также для любого ε′, удовлетворяющего условию

важную роль, чтобы «вымыть» популяцию жертв

из системы.

<ε<

−

существует t_ε′

> 0 такое, что

Теорема 4.2. Если

(1−

, то

lim

mt)

nt)

>n-ε

для t > t_ε′. Теперь для t > max{τ_ε, t_ε′}

t→∞

из второго уравнения системы уравнений (2.2)

Доказательство: Если возможно, пусть

имеем:

lim

mt)

=ς>

0. Поскольку

m≤1, для любого

t→∞

(

−d n+b m

)

0 < ε < 1 - r существует t_ε > 0 такое, что m(t) < 1 + ε

для любого t > t_ε. Определение nвключает в себя,

(

−d n+ b

1+ε

)

что для любого ε′, удовлетворяющего условию





<ε′

−

r)2, существует tε′ > 0 такое, что

<-d n n

−







nt) >n-ε для t > tε′. Теперь для t > max{ tε, tε′} пер-



2

<-d n n

−ε-

вое уравнение системы уравнений (2.2) предпола-







гает, что

Следовательно,

limn(t)

0, и теорема доказана.

t→∞

dm< m(1

+ε-

−

a m n

5. ТОЧКИ РАВНОВЕСИЯ

am n

m(1

+ε-

−

, если

1+ε

И ИХ УСТОЙЧИВОСТЬ

1+ε

Здесь будут обсуждаться возможные равновес-



a n

− ε

m2(1−

)

−



ные решения и их устойчивость относительно си-





стемы (2.2). На рис. 1 показаны изоклины с нуле-

2 2₍₁

вым ростом для этой системы. Для точек равнове-

dm<−am n

−ε-

)

{

}

сия и условий их существования мы должны

следовать нижеуказанным леммам и теореме.

Это в свою очередь означает, что

lim

mt)

Лемма 5.1. Нулевое равновесие E₁(0,0) систе-

t→∞

т.е. данное противоречие доказывает теорему.

мы уравнений (2.2) существует всегда, и два сво-

бодных (аксиальных) равновесия E₂(0,0) и E₃(r,0)

Следующая теорема касается вымирания хищ-

также существуют безоговорочно.

ников.

Заметим, что теорема 3.1 обеспечивает поло-

жительность решения нашей системы уравнений

Теорема 4.3. Если

, то

limn(t)

t→∞

(2.2). Опять же, для существования внутреннего

БИОФИЗИКА том 65

№ 5

2020

972

БИСВАС и др.

(1+

−

4(r

)

, и дискриминант

4ab

квадратного уравнения равняется

(1-

−

(после упрощения). Мы также видим, что

0, когда

< r

1. Следовательно,

4ab

−

≥

гарантирует, что хотя бы одно из

значений y должно быть положительным. Следо-

вательно, согласно лемме 5.2, внутреннее равно-

весие существует. Теорема доказана.

Теперь пришло время обсудить стабильность

всех возможных точек равновесия. Линеаризация

системы уравнений (2.2) вокруг E₁(0,0), E₂(0,0) и

E₃(r,0) невозможна, поэтому локальная устойчи-

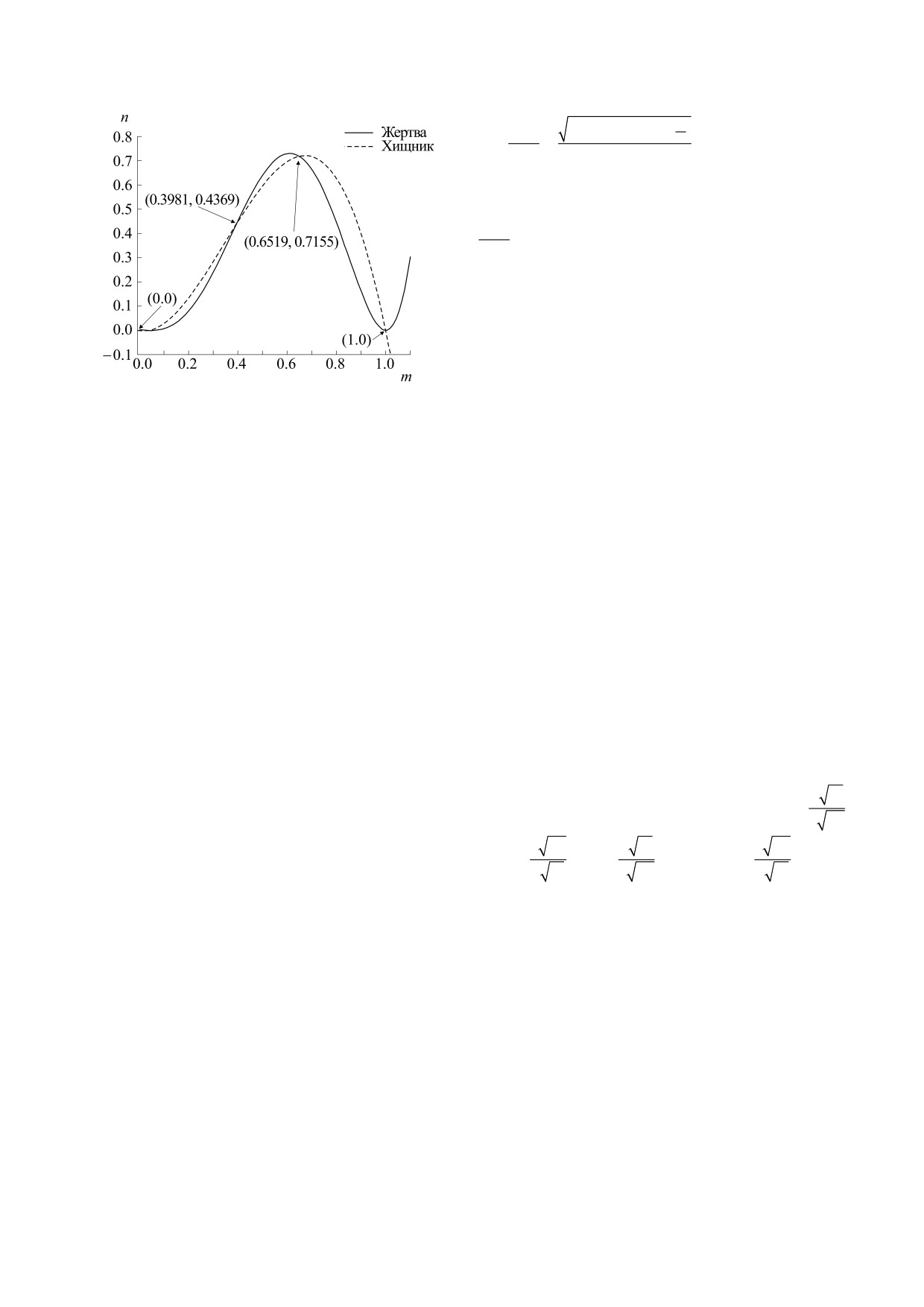
Рис. 1. Изоклины с нулевым ростом для системы (2.2)

в случае r = 0.05, a = 0.2, b = 0.22 и d = 0.21.

вость не может быть изучена. Но E₁(0,0) глобаль-

но устойчиво, если выполнено хотя бы одно из

равновесия системы, мы можем получить усло-

двух условий:

вие, изложенное в следующей лемме.

1) Теоремы 4.1 и 4.3 выполняются одновре-

Лемма 5.2. Внутреннее равновесие E^*(m^*,n^*)

менно.

существует, если и только если уравнение

2) Теоремы 4.2 и 4.3 выполняются одновре-

менно.

−

(1+

r)y + r

В нашем настоящем исследовании мы не за-

трагиваем изложение этих результатов.

имеет положительный корень.

Для наиболее важной точки равновесия

Таким образом, мы имеем следующую теоре-

му, гарантирующую существование внутреннего

E^*(m^*,n^*) мы имеем матрицу Якоби следующего

равновесия.

вида:

Теорема 5.1. Необходимое и достаточное усло-

вие существования внутреннего равновесия





J(E

)

4ab

= 



E^*(m^*,n^*) - это

−

≥

a



Доказательство: Допустим, что внутреннее рав-

a n

где

(1−

)

(

−

r)(1 −

)

−

новесие существует. Тогда, согласно лемме 5.2,

2 m

уравнение

a m

b n

b m

=-d

−

(1+

r)y + r

имеет положительный вещественный корень.

Следовательно, дискриминант уравнения должен

Характеристическое уравнение для J(E^*):

быть больше или равен нулю. Далее, дискрими-

нант квадратного

уравнения равняется

γ² + Aγ + B = 0,

4ab

где A = -trJ(E^*) = - a₁₁ - a₂₂ и B = det J(E^*) =

(1-

−

(после упрощения). Поэтому

= a₁₁a₂₂ - a₁₂a₂₁.

4ab

(1-

−

≥

Теперь, применяя концепцию правила знаков

Декарта, оба корня характеристического уравне-

4ab

С другой стороны, пусть

−

≥

0. Рас-

ния для J(E^*) будут отрицательными тогда и толь-

ко тогда, когда A > 0 и B > 0. Следовательно, если

смотрим уравнение

−

r)y + r

0, из

внутреннее равновесие существует, то следующая

которого

можно

получить,

что

теорема обеспечивает устойчивость E^*.

БИОФИЗИКА том 65

№ 5

2020

ДИНАМИКА СИСТЕМЫ «ХИЩНИК-ЖЕРТВА»

973

Теорема 5.2. Необходимыми и достаточными

Теорема 5.3. Если E^*(m^*,n^*) локально асимптоти-

условиями локально асимптотической устойчи-

чески устойчиво с d > b + r + 2, то E^* привлекает все

вости E^* являются A > 0 и B > 0.

решения системы уравнений (2.2), лежащие в Γ.

Далее попробуем найти некоторое глобальное

поведение равновесия E^*.

Доказательство: Пусть

P m

n = dm

Пусть Γ = {(m,n) ∈ R²: 0 < m < 1, n > 0}. Ясно,

что E^*(m^*,n^*) ∈ Γ, поэтому имеем следующую тео-

Q m

n = dn, тогда для всех (m,n) ∈ Γ получим

рему:

∂P

∂Q

a n

b m

m(1−

(m-r)(1 −

2m)

−

∂m

∂n

∂P

∂Q

≤

2rm- r −d + b m

∂m ∂n

∂P

∂Q

≤

r - d + b

0, если

d > b + r

m ∂n

∂

Следовательно, согласно критерию Бендиксо-

7. ЧИСЛЕННЫЙ АНАЛИЗ

на, предельный цикл отсутствует, таким образом,

В этом разделе мы предоставляем компьютер-

наша теорема следует из теоремы Пуанкаре-Бен-

ное моделирование некоторых решений системы

диксона.

уравнений (2.2) с использованием программного

обеспечения MATLAB. Этим численным анали-

зом можно проверить достоверность наших ана-

6. БИФУРКАЦИЯ ХОПФА

литических наблюдений.

В этом разделе используем теорему бифурка-

Для начала возьмем следующие параметры си-

ции Хопфа [50, 57, 58], чтобы предусмотреть не-

стемы уравнений (2.2): r = 0.05, a = 0.2, b = 0.22,

которые условия возникновения простой бифур-

d = 0.21 и начальные условия (m(0), n(0)) = (0.04,

кации Хопфа вблизи внутреннего равновесия

0.01). Легко проверить, что в этом случае

E^*(m^*,n^*) системы уравнений (2.2).

0.04 = m(0) < r = 0.05. Следовательно, согласно

теореме 4.1, популяция жертв вымрет. Однако вы-

Теорема 6.1. Если равновесие E^*(m^*,n^*) суще-

мирание жертв автоматически влечет за собой ис-

ствует, то бифуркация Хопфа происходит при

чезновение популяций хищников. Этот факт

проиллюстрирован на рис. 2. Таким образом, на-

−

(1−

)

, если r^*

{

}

ша теорема 4.1 верифицирована.

1−

Теперь, если мы рассмотрим параметры точно

положительно при m^* ≠ 1/2 и ab > d².

те же, как на рис.

2, то обнаружим, что

Доказательство: Мы видим, что

i) [trJ(E^*)]r=r* = 0;

ab −d

ii) [det J(E

)]

при ab > d²;

r=r

iii) При r = r* получаем характеристическое

уравнение γ² + det J(E^*) = 0, имеющее чисто мни-

мые корни;

d



iv)

(trJ(E

))

−1

≠

при

≠

dr



r=r

Отсюда вытекает наша теорема, поскольку

все условия теоремы Хопфа о бифуркации вы-

полнены.

До сих пор обсуждалась только аналитическая

сторона нашей модели. Следующий раздел будет

посвящен численной проверке наших аналитиче-

Рис. 2. Поведение системы (2.2) при r = 0.05, a = 0.2,

ских результатов.

b = 0.22, d = 0.21 и (m(0), n(0)) = (0.04, 0.01).

БИОФИЗИКА том 65

№ 5

2020

974

БИСВАС и др.

касающейся устойчивости точки равновесия, а

рис. 3 делает эту картину достаточно ясной.

Теперь выберем параметры r = 0.05, a = 0.2,

b = 0.22, d = 2.3 и начальные условия (m(0),

n(0)) = (0.22, 0.09). Тогда можно найти, что

2.3 = d > b + r + 2 = 2.27, и согласно теореме 5.3

внутреннее равновесие притягивает все решения

системы уравнений (2.2), лежащие в области

Γ = {(m,n) ∈ R²: 0 < m < 1, n > 0}. Это доказывает

неизбежность теоремы 5.3 (см. рис. 4).

Далее демонстрируем поведение популяций с

течением времени. Принимая начальные условия

(m(0), n(0)) = (0.6, 0.8) и выбирая параметры

r = 0.05, a = 0.2, b = 0.22, d = 0.21, мы можем ви-

деть, что обе популяции сходятся к своему состо-

янию равновесия за конечное время. Графически

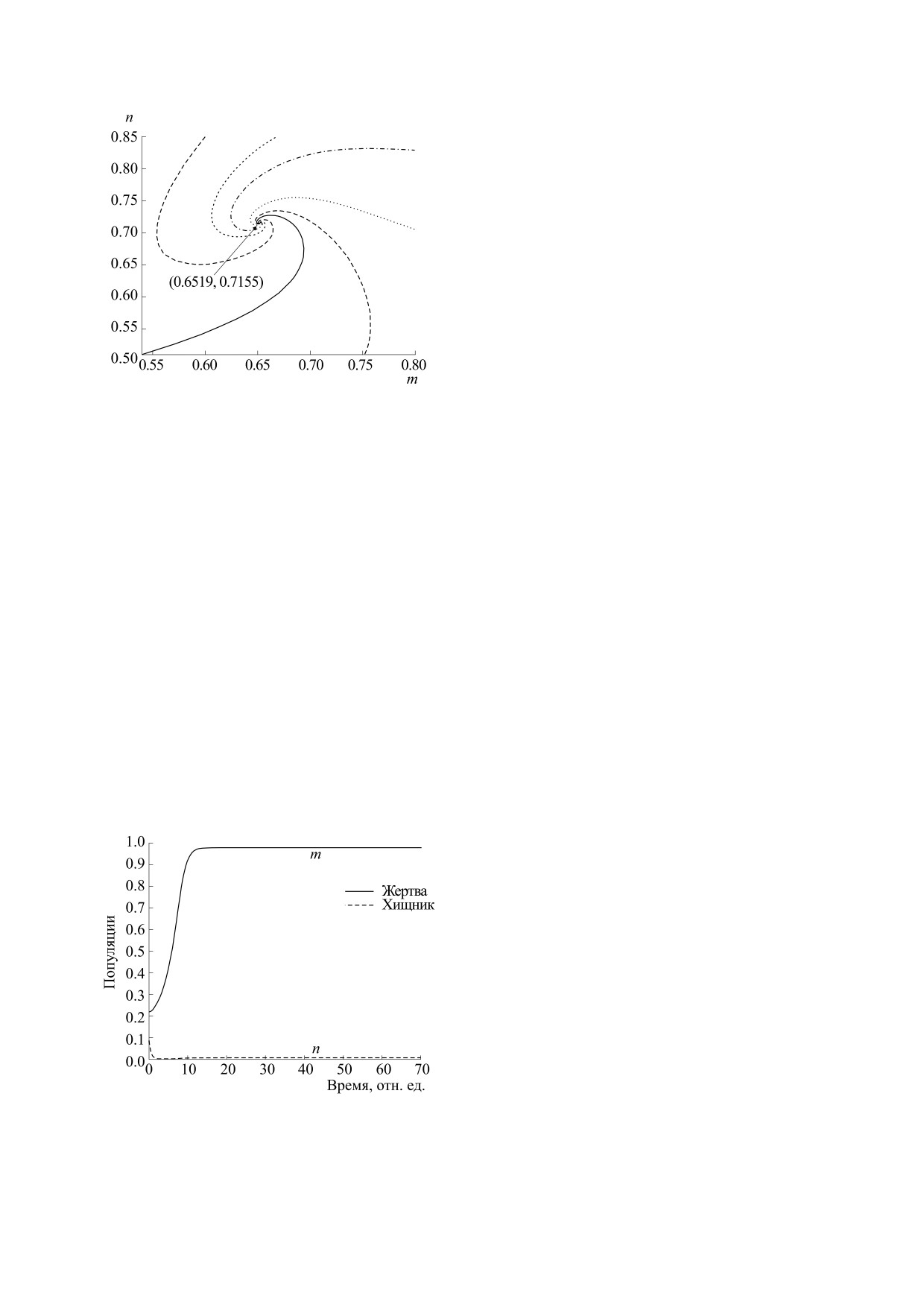
Рис. 3. Фазовый портрет системы (2.2), показываю-

такое поведение представлено на рис. 5. Такое

щий сходимость траекторий к точке Е*(0.6519,

графическое представление поможет нам прове-

0.7155) при r = 0.05, a = 0.2, b = 0.22, d = 0.21 и различ-

рить, что точка стабильного равновесия является

ных начальных условиях.

целью популяции.

Наконец, если мы примем начальные условия

4ab

(m(0), n(0)) = (0.66, 0.7) и параметры те же, что были

(1-

−

0.06440476

≥

и по теореме 5.1

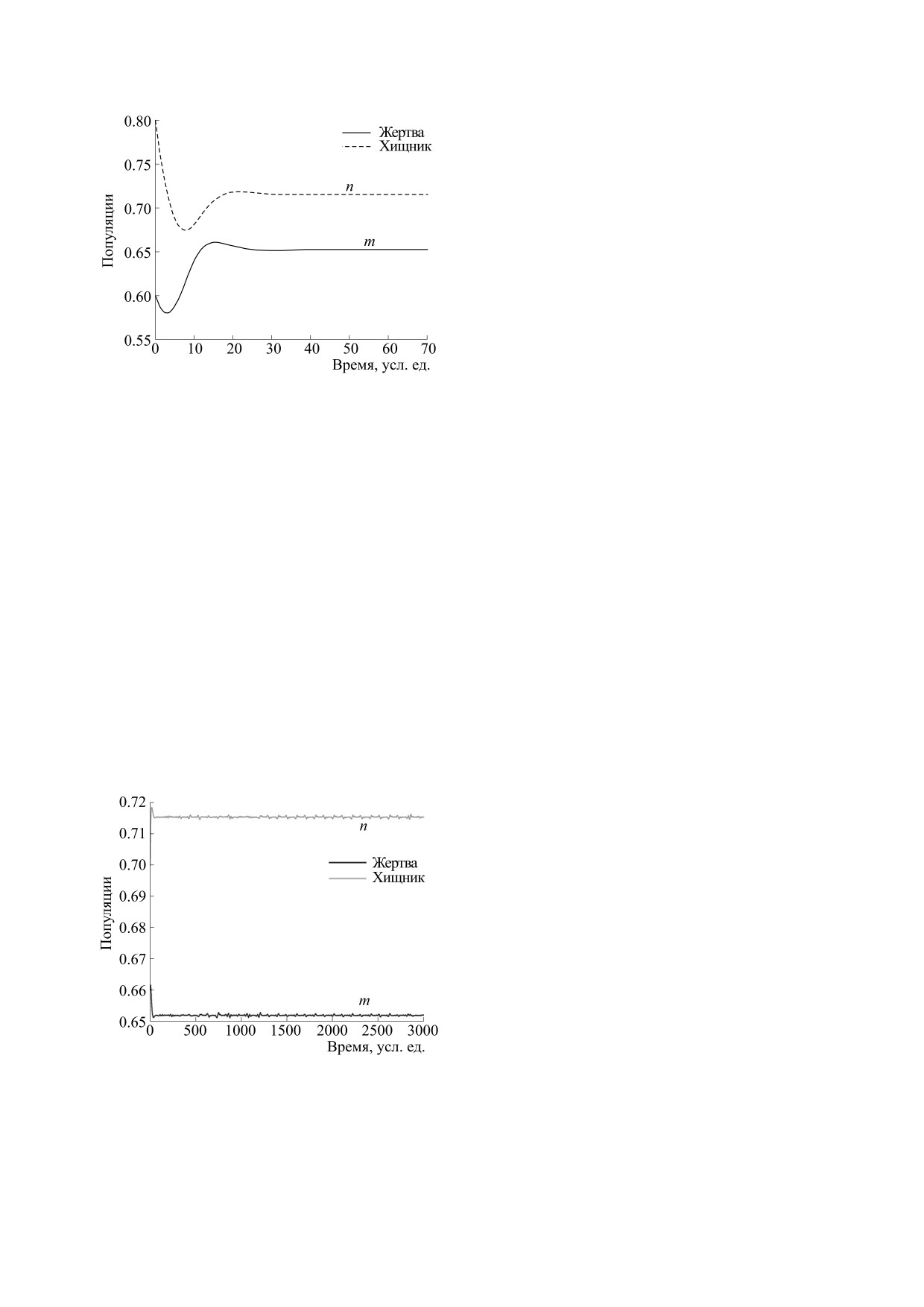
использованы на рис. 5, то можно обнаружить коле-

внутреннее равновесие существует. Следователь-

бательное поведение нашей системы (2.2), которое

показано на рис. 6. Видим, что обе популяции де-

но, можно найти две точки равновесия: E*(0.3981,

монстрируют осцилляции в ограниченном диапазо-

0.4369) и E*(0.6519, 0.7155). Используя выражения

не. Интересно, что этот график подтверждает ста-

из раздела 5, вычисляем значения A и B для обеих

бильность точки внутреннего равновесия, показы-

точек равновесия. Находим, что A = -0.1008014 < 0

вая, что виды и хищников, и жертвы сходятся к

и B = -0.01060852 < 0 для E*(0.3981, 0.4369);

своему устойчивому равновесию.

A = 0.16569803

> 0 и B = 0.01737317

> 0 для

E*(0.6519, 0.7155). Следовательно, по теореме 5.2,

E*(0.6519, 0.7155) - устойчивая точка, а E*(0.3981,

8. ВЫВОДЫ

0.4369) - неустойчивая. Соответствующий фазо-

Представленное исследование направлено на

вый портрет для точки E*(0.6519, 0.7155) дан на

дальнейшее развитие моделей типа «хищник-

рис. 3 для различных вариантов начального усло-

жертва» с квадратичными функциональными от-

вия. Все эти наблюдения подтверждают справедли-

кликами и сильным эффектом Олли. Многие

вость теоремы 5.1 о существовании и теоремы 5.2,

работы, касающиеся этой концепции, были про-

цитированы в данной статье. Исследователи при-

менили в своих работах собственные инноваци-

онные идеи. Как развитие предыдущих исследо-

ваний, здесь мы рассмотрели модель «хищник-

жертва» с квадратичным функциональным от-

кликом и сильным эффектом Олли на жертву, что

актуально в реальной жизни, где предполагается,

что среднее время обработки хищника для каж-

дой жертвы равно нулю. Это предположение бы-

ло впервые введено П.А. Браза [54] для упроще-

ния его рабочих уравнений. Но наша нынешняя

модель отличается от работы [54], так как там не

учитывался эффект Олли. Также нами было при-

нято во внимание стадное поведение для обеих

популяций. Мы использовали некоторое подхо-

дящее масштабирование для уменьшения коли-

чества параметров нашей модели. Были даны тео-

ремы для положительности и ограниченности ре-

Рис. 4. Фазовый портрет системы (2.2) при r = 0.05,

шений наших рабочих уравнений, а также

a = 0.2, b = 0.22, d = 2.3 и (m(0), n(0)) = (0.22, 0.09).

теоремы, обеспечивающие биологическое пове-

БИОФИЗИКА том 65

№ 5

2020

ДИНАМИКА СИСТЕМЫ «ХИЩНИК-ЖЕРТВА»

975

уравнений (2.2) обсуждались отдельно. В связи с

этим мы сформулировали соответствующие лем-

мы и теоремы. Также были получены некоторые

условия глобального поведения для внутреннего

равновесия. Наконец, численное моделирование

с графическим представлением было представле-

но, чтобы подтвердить нашу аналитическую дис-

куссию. Таким образом, благодаря этой модели

наши усилия помогают развитию работ в этой об-

ласти.

Методы и результаты нашего настоящего ис-

следования могут быть полезны для формирова-

ния эталона в моделях типа «хищник-жертва».

Анализ устойчивости всегда помогает поддержи-

вать экологический баланс в природе. Следова-

тельно, теоремы 5.2 и 5.3 могут сыграть ключевую

Рис. 5. Фазовый портрет системы (2.2) при

роль в равновесии в экологии, что является важ-

r = 0.05, a = 0.2, b = 0.22, d = 0.21 и (m(0),

ной целью для исследователей во всем мире. Та-

n(0)) = (0.6, 0.8). Видно, что обе популяции

ким образом, данная статья может легко вступить

сходятся к своему состоянию равновесия.

в новую эру будущих работ с эффектом Олли у

хищника, стохастическими моделями, моделью

задержки и так далее. В то же время мы должны

дение системы. В разделе 4 также приведены не-

признать, что существует необходимость даль-

которые критерии исчезновения для жертвы и

нейшего изучения в этой области. Цитируемые

хищника. Удивительно, что нам удалось найти

работы [59-64] могут помочь сформировать но-

некоторые условия, касающиеся глобальной ста-

вые модели реакции-диффузии. Можно, следуя

бильности тривиального равновесия для нашей

работе [65], перейти к новой концепции сравни-

нынешней системы. Агрессивность хищника ха-

тельного исследования моделей, зависящих от

рактеризуется высоким значением a, а сильный

соотношения хищника и жертвы. Таким образом,

эффект Олли лучше всего объяснить, принимая

более сложные модели могут быть проанализиро-

r ≈ 1. Итак, мы видим, что теорема 4.2 может вы-

ваны и объяснены с надлежащей разработкой и

полняться автоматически, если хищник агресси-

объяснением.

вен или эффект Олли очень силен. Более того,

хищник может вымереть, если максимальная вы-

КОНФЛИКТ ИНТЕРЕСОВ

года хищника не сможет преодолеть его исчезно-

вение из-за смертности. Существование и устой-

Авторы заявляют об отсутствии конфликта

чивость всех возможных решений для системы

интересов.

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

Настоящая работа не содержит описания ка-

ких-либо исследований с использованием людей

и животных в качестве объектов.

СПИСОК ЛИТЕРАТУРЫ

1. H. Malchow, S. Petrovskii, and E. Venturino, Spatio-

temporal patterns in Ecology and Epidemiology (CRC,

Boca Raton, 2008).

2. J. D. Murray, Mathematical Biology (Springer-Verlag,

New York, 1989).

3. V. Volterra and U. D'Ancona, in Materials of VII Congr.

int. acqui. et de pêche (Paris, 1931), pp. 1-14.

4. A. J. Lotka, Elements of Mathematical Biology (Dover,

New York, 1956).

Рис. 6. Колебательное поведение системы

5. C. S. Holling, Memories Entomol, Soc. Can. 45, 3

(2.2) при значениях параметров r = 0.05,

(1965).

a = 0.2, b = 0.22, d = 0.21 и (m(0), n(0)) =

6. J. T. Tanner, Ecology 56, 855 (1975).

= (0.66, 0.7).

7. P. A. Braza, SIAM J. Appl. Math. 63 (3), 889 (2003).

БИОФИЗИКА том 65

№ 5

2020

976

БИСВАС и др.

8. S. B. Hsu, T. W. Hwang, and Y. Kuang, J. Math. Biol.

and R. Dilao (E-papers Servios Editoriais Ltda., 2007),

42, 490 (2001).

pp. 219-232.

9. S. B. Hsu, T. W. Hwang, and Y. Kuang, Math. Biosci.

38. E. Gonźalez-Olivares, and A. Rojas-Palma, Bull.

181, 55 (2003).

Math. Biol. 73, 1378 (2011).

10. P. H. Leslie and J. C. Gower, Biometrika 47, 219

39. P. Aguirre, E. Gonźalez-Olivares, and E. Sáez, Nonlin-

(1960).

ear Anal. RWA 10, 1401 (2009).

11. H. R. Akcakaya, Ecol. Monogr. 62, 119 (1992).

40. P. Agiurre, E.Gonźalez-Olivares, and E. Sáez, SIAM J.

12. P. A. Abrams, Ecology 75 (6), 1842 (2003).

Appl. Math. 69, 1244 (2009).

13. P. A. Abrams and L. R. Ginzburg, Trends. Ecol. Evol.

15, 337 (2000).

41. C. S. Holling, Can. Entomol. 91, 385 (1959).

14. T. Matsuoka and H. Seno, Math. Model. Nat. Phen-

42. A. Hastings and T. Powell, Ecology 72, 896 (1991).

om. 3 (4), 131 (2008).

43. S. Gakkhar and A. Shing, J. Math. Anal. Appl. 385, 423

15. H. I. Freedman and G. Wolkowitz, Bull. Math. Biol.

(2012).

48, 493 (1986).

44. T. V. Ton and A. Yagi, Communications on Stochastic

16. A. Maiti, P. Sen, D. Manna, and G. P. Samanta, Non-

Analysis 2, 371 (2011).

linear Dynamics and Systems Theory 16 (1), 86 (2016).

45. D. Xiao, W. Li, and M. Han, J. Math. Anal. Appl. 324,

17. A. Maiti, R. Paul, and S. Alam, J. Stat. Math. Engineer.

14 (2006).

2 (1), 1 (2016).

18. A. Maiti, R. Paul, and S. Alam, Int. J. Res. Engineer.

46. B. Mukhopadhyay and R. Bhattacharyya, Nonlinear

Technol. 5 (9), 233 (2016).

Analysis: Modelling and Control 16 (1), 77 (2011).

19. A. Maiti, R. Paul, and S. Alam, Int. J. Res. Publ. Engi-

47. C. S. Holling, Can. Entomol. 91, 293 (1959).

neer. Technol. 2 (9), 22 (2016).

48. A. Maiti and G. P. Samanta, J. Math. Ed. Sci. Tech. 36,

20. L. Berec, E. Angulo, and F. Courchamp, Trends Ecol.

65 (2005).

Evol. 22, 185 (2006).

49. S. Ruan and D. Xiao, SIAM J. Appl. Math. 61, 1445

21. T. H. Clutton-Brock, D. Gaynor, G. M. Mcllrath,

(2001).

et al., J. Anim. Ecol. 68, 672 (1999).

22. F. Courchamp, T. Clutton-Brock, and B. Grenfell,

50. J. D. Murray, Mathematical Biology (Springer-Verlag,

Trends Ecol. Evol. 14, 405 (1999).

New York, 1993).

23. F.Courchamp, L. Berec, and J. Gascoigne, Allee Effects

51. C. Cosner, D. L. DeAngelis, J. S. Ault, and D. E. Ol-

in Ecology and Conservation (Oxford University Press,

son, Theor. Pop. Biol. 56, 65 (1999).

Oxford, 2008).

52. J. Chattopadhyay, S. Chatterjee, and E. Venturino, J.

24. M. S. Mooring, T. A. Fitzpatrick, T. T. Nishihira, and

Theor. Biol. 253, 289 (2008).

D. D. Reisig, J. Wildlife Management 68, 519 (2004).

53. V. Ajraldi, M. Pittavino, and E. Venturino, Nonlinear

25. D. J. Rinella, M. S. Wipfli, C. A. Stricker, et al., Canad.

Anal. RWA 12, 2319 (2011).

J. Fish. Aquat. Sci. 69, 73 (2012).

54. A. P. Braza, Nonlinear Anal. RWA 13, 1837 (2012).

26. P. A. Stephens, W. J. Sutherland, and R. P. Freckleton,

Oikos 87, 185 (1999).

55. S. P. Bera, A. Maiti, and G. P. Samanta, World J. Mo-

27. M. Kot, Elements of Mathematical Biology (Cambridge

del. Simulation 11, 3 (2015).

University Press, Cambridge, 2001).

56. S. P. Bera, A. Maiti, and G. P. Samanta, Nonlinear

28. G. A. K. van Voorn, L. Hemerik, M. P. Boer, and

Analysis: Modelling and Control 21 (3), 345 (2016).

B. W. Kooi, Math. Biosci. 209, 451 (2007).

57. D. K. Arrowsmith and C. M. Place, Dynamical Systems:

29. M. H. Wang and M. Kot, Math. Biosci. 171, 83 (2001).

Differential Equations, Maps, and Chaotic Behaviour

30. J. Wang, J. Shi, and J. Wei, J. Math. Biol. 62, 291

(Chapman & Hall, London, 1992).

(2011).

58. B. D. Hassard, N. D. Kazarinoff, and Y. H. Wan, The-

31. C. W. Clark, Mathematical Bioeconomic: The Optimal

ory and Application of Hopf-bifurcation (Cambridge

Mmanagement of Renewable Resources (Wiley, New

University Press, Cambridge, 1981).

York, 1990).

59. M. R. Garvie, Bul. Math. Biol. 69 (3), 931 (2007).

32. C. W. Clark, The Worldwide Crisis in Fisheries: Econom-

ic Models and Human Behavior (Cambridge University

60. L. N. Guin and P. K. Mandal, Appl. Math. Model. 38

Press, Cambridge, 2007).

(17-18), 4417 (2014).

33. M. Liermann and R. Hilborn, Fish Fish. 2, 33 (2001).

61. L. N. Guin and P. K. Mandal, Int. J. Biomathematics 7

34. G. Wang, X. G Liang, and F. Z Wang, Ecol. Model.

(5), 1450047 (2014).

124, 183 (1999).

62. L. N. Guin, Appl. Math. Comput. 226, 320 (2014).

35. A. D. Bazykin, F. S. Berezovskaya, A. S. Isaev, and

63. L. N. Guin, M. Haque, and P. K. Mandal, Appl. Math.

R. G. Khlebopros, J. Theor. Biol. 186, 267 (1997).

Model. 36 (5), 1825 (2012).

36. E. D. Conway and J. A. Smoller, SIAM J. Appl. Math.

64. L. N. Guin, S. Chakravarty, and P. K. Mandal, Nonlin-

46, 630 (1986).

ear Analysis: Modelling and Control 20 (4), 509 (2015).

37. J. D. Flores, J. Mena-Lorca, B. Gonźalez-Yaňez and

E. Gonźalez-Olivares, in Proc. Int. Symp. on Mathe-

65. L. N. Guin and H. Baek, Math. Comput. Simulation

matical and Computational Biology, ed. by R. Mondaini

146, 100 (2018).

БИОФИЗИКА том 65

№ 5

2020