БИОФИЗИКА, 2020, том 65, № 6, с. 1184-1195

БИОФИЗИКА СЛОЖНЫХ СИСТЕМ

УДК 574.4 + 519.6, 519.6

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ ТУНДРОВОЙ

БИОЛОГИЧЕСКОЙ ПОПУЛЯЦИИ ЛЕММИНГОВ

, В.О. Поляновский**

Д.А. Саранча*

*Вычислительный центр им. А.А. Дородницына Федерального исследовательского центра «Информатика

и управление» РАН, 119333, Москва, ул. Вавилова, 44/2

E-mail: gkk@ccas.ru

**Институт молекулярной биологии им. В.А. Энгельгардта РАН, 119991, Москва, ул. Вавилова, 32

E-mail: polyanovskyvo@yandex.ru

Поступила в редакцию 26.02.2020 г.

После доработки 13.07.2020 г.

Принята к публикации 14.07.2020 г.

Рассмотрена автономная модель биологической популяции леммингов феноменологического ти-

па, полученная в рамках комплексных исследований тундровых сообществ. В модели динамика по-

пуляции описывается через разностное уравнение, связывающее численность популяции в двух со-

седних годах и зависящее от трех параметров биолого-экологического генезиса. Совокупность со-

четаний значений параметров, входящих в рассматриваемое уравнение, определяет класс

одномерных унимодальных отображений динамической системы, в котором были аналитически и

численно исследованы бифуркационные свойства, асимптотика и устойчивость траекторий. В на-

стоящей статье основное внимание уделяется проблеме идентификации модели. Калибровку моде-

ли предлагается осуществлять методом множеств идентификации, основанном на аппроксимации

и визуализации маломерных проекций многомерного графика функции ошибок, заданного на про-

странстве трех экологических и двух популяционных параметров. Приведен пример идентифика-

ции на данных по тундровой популяции леммингов полуострова Таймыр. Показано, что в этом слу-

чае два биолого-экологические параметра допускают устойчивую локализацию.

Ключевые слова: биологическая популяция, дискретное отображение, динамика численности, циклич-

ность, устойчивость, метод множеств идентификации.

DOI: 10.31857/S0006302920060196

КОМПЛЕКСНЫЙ ПОДХОД

динамического типа, в основе которой лежит

К ИССЛЕДОВАНИЮ ТУНДРОВЫХ

макроскопическая характеристика размера попу-

СООБЩЕСТВ

ляции в единичном биотопе и в которой детали-

Математическое моделирование популяций и

зированное описание поведения особей, их пита-

сообществ - один из ведущих разделов биофизи-

ния и размножения, а также поведения их врагов

ки сложных систем. Начиная с работ А. Лотки и

заменены немногочисленными макроскопиче-

В. Вольтерра [1, 2], для математической экологии

скими параметрами окружающей среды. Опишем

классической считается задача описания дина-

кратко, из какого микроскопического описания

мики численности животных [3-8].

была получена эта модель и каковы ее основные

В классической физике для построения моде-

свойства.

лей вещества используются два подхода - термо-

Успех или неудача моделирования во многом

динамический и подход с позиций статистиче-

определяются наличием у выбранного объекта

ской физики. Первый подход - феноменологиче-

«тестирующего эффекта». При моделировании

ский, он основан на обобщении опытных фактов,

тундровых популяций и сообществ таким тести-

в основе которого лежит макроскопическая ха-

рующим эффектом обладает динамика численно-

рактеристика температуры, не применимая к от-

дельным элементам структуры вещества. Второй

сти леммингов (лемминги - своего рода «эколо-

подход основан на вероятностном агрегировании

гическая дрозофила»): отмечены регулярные пи-

детального описании элементов вещества с боль-

ки численности животных, в среднем раз в три-

шим числом степеней свободы. Мы рассмотрим

четыре года [9-13], на полуострове Таймыр - раз

феноменологическую модель популяции термо-

в три года [9, 13].

1184

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ

1185

Наличие тестирующего эффекта позволяет ис-

пользовать при моделировании принцип мини-

мальности - использование минимально воз-

можной математической структуры, - который

уравновешивается принципами соответствия

(экологичности) - привлечением предположе-

ний, не противоречащим доступным экологиче-

ским данным, и системности - учетом многооб-

разия связей внутри и вне изучаемого объекта.

Исходя из тестирующего эффекта, осуществляет-

ся выбор методов его математического описания,

под которые подбирается информация об объек-

те, дополненная экспертными оценками.

В настоящей работе рассматривается автоном-

ная модель биологической популяции, получен-

ная в рамках комплексных исследований тундро-

вых сообществ, которые включали в себя всю по-

следовательность операций: сбор, отбор, анализ и

Рис. 1. Функция последования, связывающая отно-

переработку исходной (биологической) инфор-

сительную численность леммингов за два соседних

мации с формированием набора взаимосвязан-

года.

ных моделей разной степени детализации на их

основе, гипотез о ведущих механизмах исследуе-

с ним взаимодействии. В случае недостаточности

мого явления, согласованных с экспертами [14].

данных использовали экспертные оценки с при-

В основе первого этапа разработки рассматри-

влечением данных по близкородственным видам

ваемой модели тундровой биологической попу-

[9, 15].

ляции лежала апробированная математическая

модель трофических взаимодействий (обобще-

Если в случае моделирования тундрового со-

ние взаимодействия типа «хищник-жертва»).

общества важнейшим аспектом моделирования

являлся поиск необходимой для модели биологи-

При этом определяющими факторами явля-

ческой информации, то при моделировании по-

лись: первое - долговременное существование

пуляции леммингов полностью использовали

объекта, математически выражаемое в сохранении

данные В.А. Орлова [9] по процессам размноже-

траекторий в положительном квадранте; второе -

наличие релаксационных колебаний по типу «кра-

ния, дополненные информацией по смертности,

оцененной по близко родственным видам. Дан-

ха», что и позволяет впоследствии использовать

ные, дополненные соответствующими эксперт-

одномерные разностные уравнения; третье - на-

ными оценками, были полностью использованы

личие определенного порядка чередования пиков.

при моделировании. Но это относилось только к

Биофизический анализ структуры пастбищ-

сезону размножения. Для описания периода пе-

ной (наземной) части тундрового биоценоза поз-

резимовки данных о популяционных параметрах

волил на втором этапе разработки феноменоло-

и характеристиках не было. Единственное, чем

гической модели автономно рассматривать сооб-

мы располагали - это величины численности

щество «растительность - лемминги - песцы»

(плотности) популяций в конце и в начале перио-

(более детально биофизический анализ описан в

да вегетации (бесснежного периода). В связи с

работах [14, 15]).

этим фундаментальное значение для понимания

На третьем этапе разработки стремление

процессов и способов их формализованного опи-

приблизиться к большему пониманию механиз-

сания имели значения «сезонной функции последо-

мов формирования динамики численности тунд-

вания». Эта функция описывает зависимость по-

ровых животных привело к формированию моде-

пуляции в следующем году от ее численности в

ли популяции леммингов [9, 15] с учетом возраст-

текущем. Пример функции последования, лежа-

ной структуры. Она использована для изучения

щей в основе рассматриваемой в статье модели,

поведения популяций двух видов леммингов За-

приведен на рис. 1. Видовые различия заключены

падного Таймыра: сибирского и копытного.

в кривой, описывающей «сезон перезимовки»,

Если при моделировании тундрового сообще-

посредством которой реализуются релаксацион-

ства рассматривали некую обобщенную ситуа-

ные колебания по «типу краха». Описания пере-

цию, то в случае моделирования популяции лем-

зимовки являются определяющими при описа-

мингов осуществлялась

«привязка модели» к

нии релаксационных колебаний. Для сезона раз-

конкретному участку тундры, в районе поселка

множения важна только их

«интегральная

Тарея Западного Таймыра. Модель настраивалась

характеристика» - скорость прироста численно-

под конкретные данные В.А. Орлова [9], в тесном

сти за этот период в благоприятный год (когда от-

БИОФИЗИКА том 65

№ 6

2020

1186

КАМЕНЕВ и др.

сутствует плотностное лимитирование). В связи с

изучения различных регионов тундры, для анали-

этим «летние» популяционные параметры (кото-

за кардинальных изменений ее свойств, в частно-

рые только доступны для большинства биологи-

сти вследствие антропогенных воздействий (из-

ческих исследований) играют менее важную роль

менений климата и т.д.), необходимо разработать

по сравнению с выживаемостью в период перези-

методы идентификации параметров модели под

мовки. Эти рассуждения позволяют разделить

конкретный биотоп и временной период, а для

экологические показатели по степени их влияния

более детального анализа использовать полную

на суммарную динамику.

имитационную модель [17]. Настоящая статья по-

священа методу калибровки модели.

На заключительном этапе разработки феноме-

нологической модели анализ результатов вычис-

лительных экспериментов с обеими взаимодо-

ОБЪЕКТ ИССЛЕДОВАНИЯ. АВТОНОМНАЯ

полняющими моделями привел к обоснованию

ТРЕХПАРАМЕТРИЧЕСКАЯ МОДЕЛЬ

упрощенной модели в виде одномерного разност-

ТУНДРОВОЙ БИОЛОГИЧЕСКОЙ

ного уравнения (функции последования), связы-

ПОПУЛЯЦИИ

вающего численности леммингов в двух соседних

Предложенная в работах [14, 15] модель дина-

годах.

мики тундровой популяции основана на следую-

Отметим, что особая роль функций последова-

щих упрощенных предположениях, хорошо вы-

ния в исследовании колебаний численности по-

полняющихся для популяции леммингов в усло-

пуляций тундровых животных привела к поиску

виях полуострова Таймыр.

более тесной связи функций последования и ис-

1. Влияние численности хищников (песцов) на

ходной модели тундрового сообщества «расти-

популяцию (леммингов) пренебрежимо мало.

тельность - лемминги - песцы» [14, 15].

2. В условиях достаточной обеспеченности

Применение комплексного подхода при моде-

кормом, т.е. растительностью, популяция (лем-

лировании тундровых популяций и сообществ

мингов) растет монотонно и линейно. Рост огра-

[14, 15] позволило сформулировать количествен-

ничивается запасом растительности. Когда запа-

ные гипотезы о ведущих (главных, определяю-

сы корма снижаются до такого уровня, что не мо-

щих) механизмах формирования колебаний чис-

гут

обеспечить

существующий уровень

ленности тундровых животных. Как указано вы-

численности, происходит рост смертности и сни-

ше, ведущим фактором, определяющим эти

жение численности.

колебания, является динамика численности по-

3. Существует некий «оптимальный биотоп»

пуляции леммингов. Эта динамика в свою оче-

для данной популяции, т.е. такое сочетание

редь определяется тремя биолого-экологически-

внешних условий (наличие корма, климатиче-

ми показателями: 1) скоростью прироста биомас-

ские условия и т.д.), при котором некоторый уро-

сы в благоприятный год;

2) максимальной

вень численности остается постоянным. Это

численностью; 3) выживаемостью в наиболее не-

означает, что смертность и рождаемость (точнее,

благоприятных условиях. Первый показатель ха-

доля выжившего потомства) равны. Понятие «оп-

рактеризует баланс между процессами рождаемо-

тимальный биотоп» было введено в работах [14,

сти и смертности в отсутствие «давления среды»;

15] и подразумевает область пространства обита-

второй - характеризует экосистему в целом и от-

ния с оптимальными условиями проживания.

ражает коэволюцию леммингов и кормовой базы;

третий характеризует адаптационные свойства

Таким образом, при недостатке корма сниже-

леммингов в экстремальных условиях и во мно-

ние численности происходит до достижения раз-

гом определяется локальными характеристика-

мера популяции оптимального биотопа.

ми, в частности рельефом местности в местах пе-

Получаем три состояния популяции, каждому

резимовки. Полученные выводы хорошо согласу-

из которых соответствует своя область в отобра-

ются с одной из распространенных гипотез о том,

жении функции последования (рис. 1).

что формирует колебания численности популя-

Первой области соответствует восходящая

ций не какой-то отдельно взятый фактор, а неко-

прямая с угловым коэффициентом P, равным

торая их комбинация [9-13].

скорости роста, третья область представляет со-

Полученные количественные соотношения,

бой горизонтальную прямую, находящуюся на

связывающие обобщенные показатели с характе-

расстоянии d от оси абсцисс. Вторую область

ристиками динамики численности, могут быть

определяет нисходящая прямая с угловым коэф-

использованы в процедурах оценки параметров

фициентом r, исходя из следующего соображе-

реальных популяций, таких как плодовитость,

ния: «В предположении слабого влияния вариа-

смертность и т.д. Разностные уравнения могут

ций в описании этой зоны на динамику числен-

служить простым инструментарием для прогноза

ности популяции опишем переходную зону

возможной численности леммингов и песцов. В

отрезком прямой, соединяющим первый и тре-

то же время для адаптации такого подхода для

тий фрагменты» ([14], с. 106).

БИОФИЗИКА том 65

№ 6

2020

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ

1187

Представим разностное уравнение, связываю-

Y(t) в двух соседних годах, как Y(t + 1) = F(Y(t),

щее нормированную на максимально возмож-

λ)), λ = (P, r, d), где

ную, т.е. относительную численность популяции



≤



, λ )

1

−

r(Y

−

P),

P <Y

≤

(1−



−

r < Y

≤



Здесь P - прирост биомассы леммингов в бла-

впервые появляются циклы периодов 4 и 6, нахо-

гоприятный год; коэффициент r характеризует

дятся все четные циклы.

изменение биомассы леммингов в условиях не-

Треугольное отображение со ступенькой ана-

хватки кормов в весенний период; величина d -

литически изучалось в работах [17, 18]. C помо-

нормированная биомасса леммингов в оптималь-

щью специально разработанной технологии «ли-

ном биотопе, λ - вектор трех биолого-экологиче-

ний возврата» проводилось «бифуркационное ис-

ских параметров, характеризующих основные

следование»

- определение циклов, которые

факторы влияния окружающей среды.

возникают по мере опускания ступеньки. Одной

Функция F постоянна при Y ∈ [1/P + (1 - d)/r,

из целей этих исследований была проверка усло-

1] и равна d, поэтому величину d будем в дальней-

вий выполнения теоремы Шарковского [20], точ-

шем называть ступенькой. Мы будем рассматри-

нее, его утверждения о порядке наличия циклов

вать область параметров λ, где P, r > 1 и 0 < d < 1.

различных периодов. Для треугольного отобра-

Нас, как правило, будет интересовать случай

жения со ступенькой было получено некоторое

1/P + (1 - d)/r ≤ 1, при невыполнения этого усло-

подтверждение порядков Шарковского и сфор-

вия будут рассматриваться только решения с

мулирован ряд утверждений (гипотез) о порядке

F(Y(t), λ) ≤ 1. Отображение (1) имеет единствен-

следования циклов при изменении бифуркаци-

ную нетривиальную стационарную точку A со

онного параметра d. Эти утверждения проверя-

свойством A = F(A, λ). Нетрудно видеть, что при

лись с помощью вычислительных экспериментов

d ≤ 1/P + (1 - d)/r справедливо A = (P + r)/[(1 +

и, частично, с помощью аналитических выкладок

+ r)P], а при d > 1/P+ (1 - d)/r выполняется A = d.

[17, 18].

Свойства трехпараметрической динамической

СВОЙСТВА АВТОНОМНОЙ МОДЕЛИ

модели с отображением (1) впервые численно ис-

При аналитическом и численном исследова-

следовались в работе [18]. Были выделены три ти-

нии приведенной автономной модели тундрового

па областей в пространстве параметров: зоны ста-

сообщества основной интерес представляли

бильности, переходные и аномальные зоны. Бы-

прежде всего периодические режимы численно-

ло показано, что:

сти популяции (циклы) и их устойчивость при из-

1) при монотонном изменении каждого из па-

менении параметров.

раметров последовательно появляются зоны ста-

Аналитически свойства рассматриваемой мо-

бильности (периодических траекторий или цик-

дели тундровой популяции были исследованы

лов), которые отделены переходными зонами со

для различных частных случаев отображения (1):

сложными режимами;

при P = 2, r = 2, d = 0 (треугольное отображение

2) внутри зон стабильности период траекторий

без ступеньки); P = 2, r = 2 (треугольное отображе-

постоянный, при переходе от одной зоны ста-

ние со ступенькой) - однопараметрическое отоб-

бильности к другой период изменяется в порядке

ражение.

натурального ряда, кратно (в частности, бифур-

Для треугольного отображения без ступеньки

кация удвоения периода), а также и в более слож-

в работах [19, 17, 20] получены явные формулы

ном порядке изменения периода;

для циклов заданного периода, рассчитано их

3) в каждой из переходных зон при небольшом

число, получены соотношения для размеров (ши-

изменении параметров период траекторий значи-

рины) соседних областей, в которых реализуются

тельно изменяется (упорядоченный хаос, аналог

циклы с удвоенным периодом. Показано, что ес-

стохастического поведения);

ли при процедуре последовательного увеличения

4) существуют периодические траектории с пе-

периода циклов возник цикл некоторого периода

риодом, большим любого наперед заданного на-

n, то непосредственно за ним возникают циклы с

турального числа, соответствующие так называе-

периодом n ⋅ 2^m (m = 1, 2, 3…) и внутри последова-

мым аномальным зонам, в которых траектория,

тельности таких циклов нет циклов других пери-

будучи ограниченной, никогда не опускается на

одов. Также показано, что в этом случае между

ступеньку - аналог «катастрофы голубого неба»

интервалами области параметров, при которых

(«Blue sky catastrophe» [21]).

БИОФИЗИКА том 65

№ 6

2020

1188

КАМЕНЕВ и др.

В работах [17, 22, 23] были исследованы асимп-

Таким образом, для решения задачи идентифика-

тотические свойства траекторий системы, для зон

ции экологические параметры должны быть допол-

стабильности были построены аттракторы траек-

нены популяционными параметрами L_max и Y₀.

торий, исследована их деформация при малом из-

Если задано значение расширенного вектора

менении параметров, построены бифуркацион-

параметров μ = (P, d, r, L_max, Y₀), то, рассчитав по

ные диаграммы для произвольных контуров в

модели ряд L(t, μ), можно сравнить его с рядом

пространстве параметров. В частности, в работах

[22, 23] был приведен пример построения бифур-

данных L^E(t). Чтобы численно измерить близость

кационной диаграммы вдоль контура в простран-

расчетного ряда с рядом данных, определим

стве параметров, заходящего в аномальную зону,

ошибку идентификации на участке времени от T₁

что позволяет рассмотреть случай динамики по-

до T₂, используя показатель среднеквадратичного

пуляции с учетом временного параметрического

нормированного отклонения:

дрейфа параметров моделируемого отображения

1/2

в рамках данного класса в критических климати-



(L t,μ) −

L t))





ческих условиях. В частности, было показано, что



t=T

,...,T



E(μ)





наличие медленных биосферных ритмов, вклю-

−T

+1)

max





чающих временные периоды с экстремальными





для моделируемого сообщества условиями про-

Функция E(μ), определенная на пространстве

живания (хаотическая динамика и области «ката-

расширенных параметров (в данном случае пяти-

строфы голубого неба»), при сохранении «опти-

мерном), представляет собой свертку погодовых

мального биотопа» не приводит к вырождению

ошибок идентификации - отклонений предска-

популяции, а экстремальные режимы существо-

заний модели от наблюдений - и называется

вания сменяются вполне упорядоченным поведе-

функцией ошибки идентификации. Могут быть ис-

нием со структурами в виде популяционных цик-

пользованы и другие виды свертки погодовых

лов малого периода.

ошибок, например, максимальная ошибка за рас-

сматриваемый период.

Задача идентификации модели традиционно

МЕТОД ИССЛЕДОВАНИЯ.

формулируется как поиск значения расширенно-

ИДЕНТИФИКАЦИЯ АВТОНОМНОЙ

го вектора параметров μ, доставляющего мини-

МОДЕЛИ ТУНДРОВОЙ ПОПУЛЯЦИИ

НА ДАННЫХ ТЕРРИТОРИАЛЬНОГО

мум функции ошибок E на некотором множестве

ПРОИСХОЖДЕНИЯ

допустимых значений вектора параметров M:

E(μ) → min {μ ∈ M}.

Задача идентификации рассматриваемой мо-

дели тундровой популяции на данных территори-

При решении этой задачи в рассматриваемом

ального происхождения заключается в определе-

случае возникают следующие проблемы:

нии вектора биолого-экологических параметров

1) рассматриваемая модель нелинейна, опти-

λ = (P, r, d) по данным наблюдений за динамикой

мизируемая функция ошибки не является непре-

численностью популяции леммингов на рассмат-

рывной;

риваемой территории. Предполагается, что рас-

2) данные рядов являются результатами годо-

сматриваемая территория содержит в себе един-

вого агрегирования территориально распреде-

ственный оптимальный биотоп популяции. В

ленных полевых наблюдений в сложных условиях

этом случае, однако, биолого-экологические па-

(см. первый раздел работы) и, как правило, име-

раметры отображения (1) должны быть дополне-

ют низкое качество, особенно при малых числен-

ны параметрами, характеризующими данную

ностях популяции, нередки лакуны (пропуски

конкретную популяцию - максимально-возмож-

данных) за отдельные годы;

ной численностью популяции и ее значением на

момент начала наблюдений.

3) исследуемый биотоп может занимать значи-

тельную территорию с существенно варьирую-

Обозначим через L^E(t), t = 0, 1, …, T временной

щимися климатическими параметрами окружаю-

ряд наблюдаемых значений численности популя-

щей среды.

ции. Отображение (1) определяет динамику относи-

Указанные особенности задачи идентифика-

тельной численности Y(t). Пусть задано начальное

ции приводят к тому, что сочетания параметров,

состояние относительной численности популяции в

обеспечивающие глобальный минимум функции

момент t = 0: Y(0) = Y₀. Для заданного значения век-

ошибки, должны быть дополнительно исследова-

тора параметров λ рассмотрим траекторию системы

ны на единственность и глобальную устойчи-

(1), полученную при Y(0) = Y₀: Y(1), …, Y(T). Обо-

вость, и только в случае устойчивости оптимума

значим через L(t) абсолютную численность популя-

для некоторого параметра оптимальное значение

ции: L(t) = L_maxY(t), где L_max - максимально воз-

этого параметра может быть принято в качестве

можная численность популяции в данном биотопе.

решения задачи идентификации. Для решения

БИОФИЗИКА том 65

№ 6

2020

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ

1189

Рис. 2. Оцифрованные данные наблюдений для популяции леммингов полуострова Таймыр.

задач идентификации в условиях неопределенно-

(2001 г.). Таким образом, первые пять лет наблю-

сти [24, 25] и плохих данных [26, 27] разработан

дений оставим для «настройки» системы на регу-

метод множеств идентификации [28-30], состоя-

лярный режим, ошибки идентификации по ним

щий в аппроксимации методами [31, 32] проек-

не включаются в функцию ошибок.

ций и срезов многомерного графика функции

Рассмотрим на некотором множестве пара-

ошибок с помощью метрических сетей К. Шен-

метров M проекцию графика функции ошибок

нона [33] и визуализации их с помощью диалого-

E(μ) = E(P, d, r, L_max, Y₀) в пространство (P, E), т.е.

вых карт решений [34]. В настоящей работе мы не

множество

будем подробно рассматривать эту методологию,

ограничившись результатами ее применения для

Z^PE(M) = {(P, E): (P, d, r, L_max, Y₀) ∈ M,

рассматриваемой задачи.

E = E(P, d, r, L_max, Y₀)}.

ИДЕНТИФИКАЦИЯ МОДЕЛИ ДЛЯ

Аналогично определим множества Z^dE(M),

ПОПУЛЯЦИИ ЛЕММИНГОВ ТАЙМЫРА

ZrE(M), ZLmaxE(M) и ZY0E(M). Такие множества в

подходе [28-30] называются множествами иден-

Рассмотрим данные работ [13, 23] по популя-

тификации, они аппроксимируются покрытиями

ции леммингов полуострова Таймыр (Lemmus Di-

crostonyx) за 1960-2001 гг. Это пример данных до-

К. Шеннона (коллекциями шаров или кубов ма-

лого размера) и анализируются визуально.

статочно высокого качества. Оцифрованный ва-

риант данных представлен на рис. 2 (оригинал см.

Выберем наиболее широкий стартовый диапа-

в работах [13, 35]).

зон возможных значений вектора параметров μ:

Из рисунка видно, что колебания численности

M_∞ = {(P, d, r, L_max, Y₀): 1 < P < 10, 0 < d < 1,

популяции в рассматриваемом биотопе прибли-

1 < r < 10, 0 < L_max < 44, 0 < Y₀ < 1}.

зительно соответствуют циклу периода три (мак-

симумы численности достигаются раз в три года),

Таким образом, согласно определению, в мно-

однако в силу различной амплитуды этих макси-

жестве Z^PE(M_∞) каждому значению параметра P,

мумов нельзя исключить и вариант более сложно-

1 < P < 10, соответствует множество точек с раз-

го цикла с периодом, кратным трем. Следует так-

личными значениями функции ошибок E(P, d, r,

же отметить, что характер колебаний численно-

L_max, Y₀) при варьировании всех прочих парамет-

сти после 1992 г. существенно отличается. По

ров d, r, L_max, Y₀: 0 < d < 1, 1 < r < 10, 0 < L_max < 44,

известным историческим причинам эти данные

могут быть существенно худшего качества. По

0 < Y₀ < 1. Множество Z^PE(M_∞) изображено на

причинам, указанным в первом разделе, наблю-

рис. 3 справа. Из рисунка видно, что при 1 < P < 10

дения в окрестности минимума популяции также

существуют такие комбинации значений осталь-

ненадежны.

ных параметров ((P, d, r, L_max, Y₀) ∈ M_∞), что

Рассмотрим задачу идентификации модели на

ошибка идентификации E превышает 7 (700%). В

данных популяции леммингов Таймыра. Выбе-

то же время имеются решения со значениями

рем t = 0 для 1960 г., T₁ = 5 (1965 г.), T₂ = 41

ошибки менее

0.3

(30%). Часть множества

БИОФИЗИКА том 65

№ 6

2020

1190

КАМЕНЕВ и др.

Рис. 3. Множество идентификации, т.е. проекция графика функции ошибок E(μ) = E(P, d, r, L_max, Y₀), заданного на

множестве параметров M_∞, в пространство (P, E) (справа) и ее часть с малой ошибкой идентификации (слева).

ZPE(M_∞), удовлетворяющая условию Е ≤ 0.3,

Множество Z^PE(M_0.3) изображено на рис. 4

изображена на рис. 3 слева. Из рисунка видно, что

справа. Из рисунка видно, что возможна дальней-

шая локализация параметра P: 2.3 < P < 3.

глобальный минимум функции ошибки иденти-

фикации находится в диапазоне 1.5 < P < 5. Для

В итоге можно получить следующую локализа-

ускорения расчетов на основе визуализации мно-

цию параметров, при которых ошибка идентифи-

кации не превышает 0.173:

жеств Z^dE(M_∞), Z^rE(M_∞), ZLmaxE(M_∞) и ZY0E(M_∞)

локализуем множество параметров, при которых

M_0.173 = {(P, d, r, L_max, Y₀): 2.4 < P < 3,

ошибка идентификации не превышает 0.3:

0.04 < d < 0.11, 3 < r < 10, 4 < L_max < 6,

0 < Y₀ < 0.63}.

M_0.3 = {(P, d, r, L_max, Y₀): 1.5 < P < 5,

0.01 < d < 0.4, 1 < r < 10, 2 < L_max < 12,

Множество Z^PE(M_0.173) изображено на рис. 4

0 < Y₀ < 1}.

слева. Глобальный минимум функции ошибок,

Рис. 4. Множество идентификации, т.е. проекция графика функции ошибок E(μ) = E(P, d, r, L_max, Y₀), заданного на

множествах параметров M_0.3 (справа) и M_0.173 (слева), в пространство (P, E).

БИОФИЗИКА том 65

№ 6

2020

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ

1191

Рис. 5. Данные наблюдений L^E(t) (круглые маркеры) и ряд модели L(t, μ*) (квадратные маркеры), откалиброванной

сочетанием параметров μ* с минимальной ошибкой.

находящийся в множестве M_0.173, равен E* =

r** = 3.82, L_max** = 4.40, Y₀** = 0.203. Соответ-

= 0.16632 (16.6%) и соответствует сочетанию па-

ствующая ему траектория изображена на рис. 6

раметров μ*: P*

=2.77, d* = 0.0595, r* = 9.93,

(пунктиром представлены данные наблюдений).

L_max* = 5.75, Y₀* = 0.0009 (здесь и далее приводят-

Заметим, что, несмотря на очень близкое к гло-

бальному минимуму E* = 0.16632 значение функ-

ся округленные значения параметров μ). Соот-

ции ошибок E** = 0.1686, полученное решение

ветствующая ему траектория на оптимизируемом

существенно отличается от него по всем парамет-

периоде от T₁ до Т₂ изображена на рис. 5 (пункти-

рам, кроме P (P* = 2.77, P** = 2.49), и представля-

ром представлены данные наблюдений). Заме-

ет собой трехлетний, а не шестилетний цикл.

тим, что полученное решение представляет собой

шестилетний цикл с промежуточным максиму-

Дальнейшая локализация глобального мини-

мом через три года.

мума невозможна по причине недостаточной точ-

ности наблюдений. Кроме того, при малом уров-

От глобального минимума по величине функ-

не ошибки (менее 0.17) имеет место замещение

ции ошибок незначительно (на 1.37%) отличается

параметров P и d, как это видно из рис. 7.

субоптимальное решение задачи идентификации

с E** = 0.1686 (16.9%), которое соответствует со-

На нем изображено множество M^Pd(0.169) пар

четанию параметров μ**: P** = 2.49, d** = 0.103, параметров (P, d), для которых в множестве M су-

Рис. 6. Данные наблюдений L^E(t) (круглые маркеры) и ряд модели L(t, μ**) (квадратные маркеры), откалиброванной

сочетанием параметров μ** с cубминимальной ошибкой.

БИОФИЗИКА том 65

№ 6

2020

1192

КАМЕНЕВ и др.

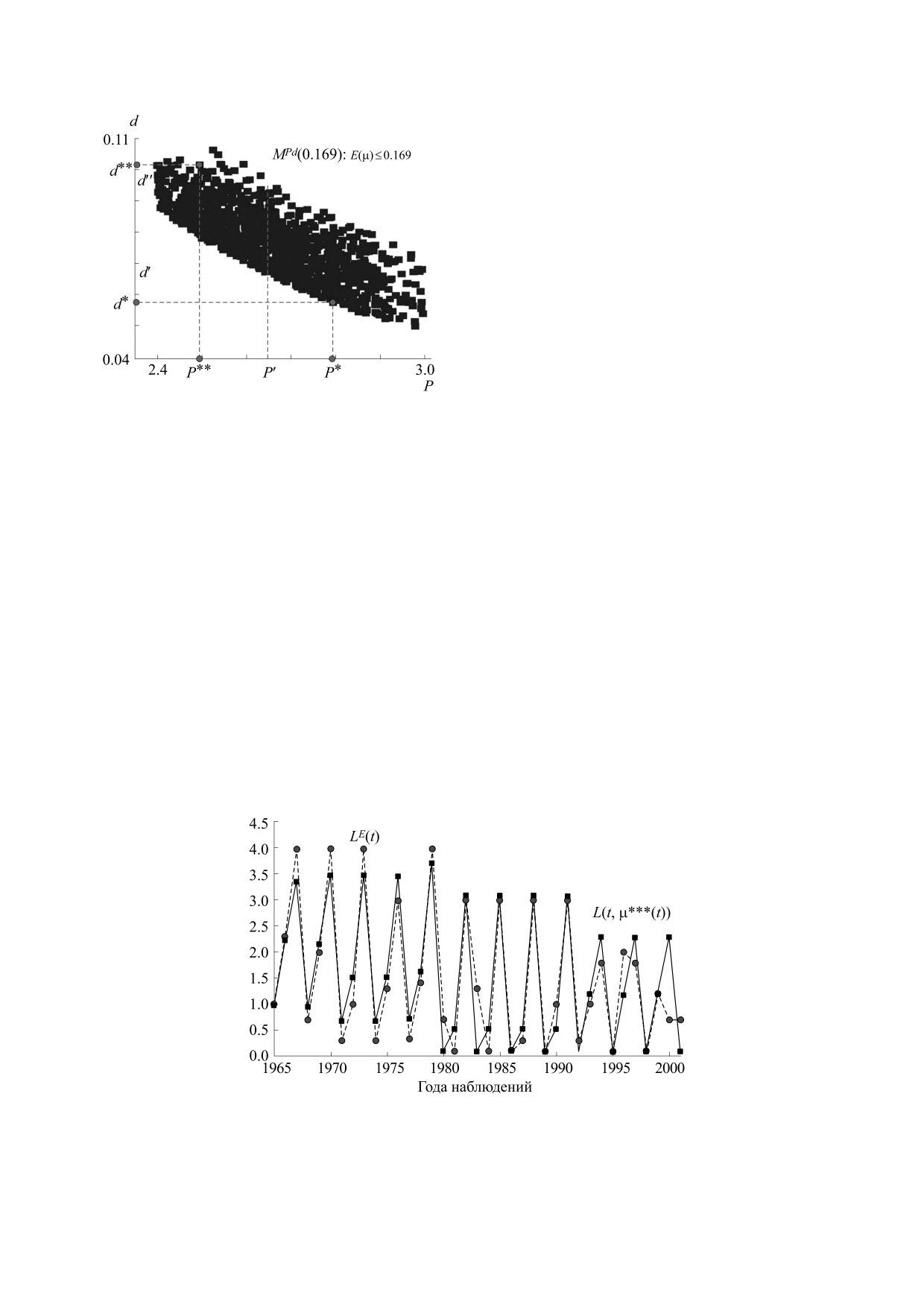
В приведенном на рис. 7 множестве M^Pd(0.169)

отличие по уровню ошибки от глобального мини-

мума не превышает 0.002 (0.2%), при этом пара-

метр P варьируется от 2.4 до 3.0, а параметр d - от

0.05 до 0.11. Между калибровочными параметрами

P и d в этом случае имеется некоторая обратная

связь - каждому значению P соответствует неболь-

шой, смещающийся диапазон значений d (напри-

мер, на рис. 7 для P' - между d' и d''). Этот диапазон

смещается вниз с увеличением значения P. В таком

случае для дальнейшей локализации этих парамет-

ров требуется внешняя экспертная оценка одного

из этих параметров. В рассматриваемом случае это

может быть следующее соображение. Как правило,

данные наблюдений на минимуме численности

популяции (вблизи ступеньки d) существенно за-

нижены (зверьков отловить достаточно сложно).

Рис.

7. Множество субоптимальных параметров

Поэтому среди различных решений задачи иден-

M^Pd(0.169), т.е. проекция графика функции ошибок

тификации предпочтительно выбирать решения с

) в пространство (P, d) с

E(μ) = E(P, d, r, L_max, Y₀

большим значением d (вариант μ** предпочесть

ошибкой E(μ) ≤ 0.169.

варианту μ*).

Итак, проведенный анализ позволяет в каче-

ществуют значения вектора параметров μ с ошиб-

стве решения задачи идентификации модели по-

кой идентификации E(μ) не более 0.169 (в то вре-

пуляции леммингов полуострова Таймыр при-

нять значения параметров P** = 2.49, d** = 0.103,

мя как минимум ошибки составляет 0.16632), где

r** = 3.82, с интервальной оценкой P = 2.5 ± 0.5,

d = 0.08 ± 0.03, при этом локализация параметра r

M^Pd(E) = {(P, d): (P, d, r, L_max, Y₀) ∈ M,

является неустойчивой.

E(P, d, r, L_max, Y₀) ≤ E}.

ИДЕНТИФИКАЦИЯ МОДЕЛИ

Такие множества в подходе [28-30] называют-

ДЛЯ ПОПУЛЯЦИИ ЛЕММИНГОВ ТАЙМЫРА

ся множествами субоптимальных параметров. Яс-

ПРИ ИЗМЕНЯЮЩЕМСЯ

но, что при построении множества M^Pd(0.169)

ВО ВРЕМЕНИ БИОТОПЕ

можно вместо зондирования всей области воз-

Мы подробно рассмотрели процесс калибров-

можных значений параметров M_∞ ограничиться

ки модели на данных по конкретному территори-

множеством M_0.173, построенном на предыдущих

альному биотопу для одного периода времени, на

этапах.

котором параметры окружающей среды были вы-

Рис. 8. Данные наблюдений L^E(t) (круглые маркеры) и ряд модели L(t, μ***(t)) (квадратные маркеры), откалиброван-

ной сочетанием параметров μ***(t) с минимальной ошибкой.

БИОФИЗИКА том 65

№ 6

2020

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ

1193

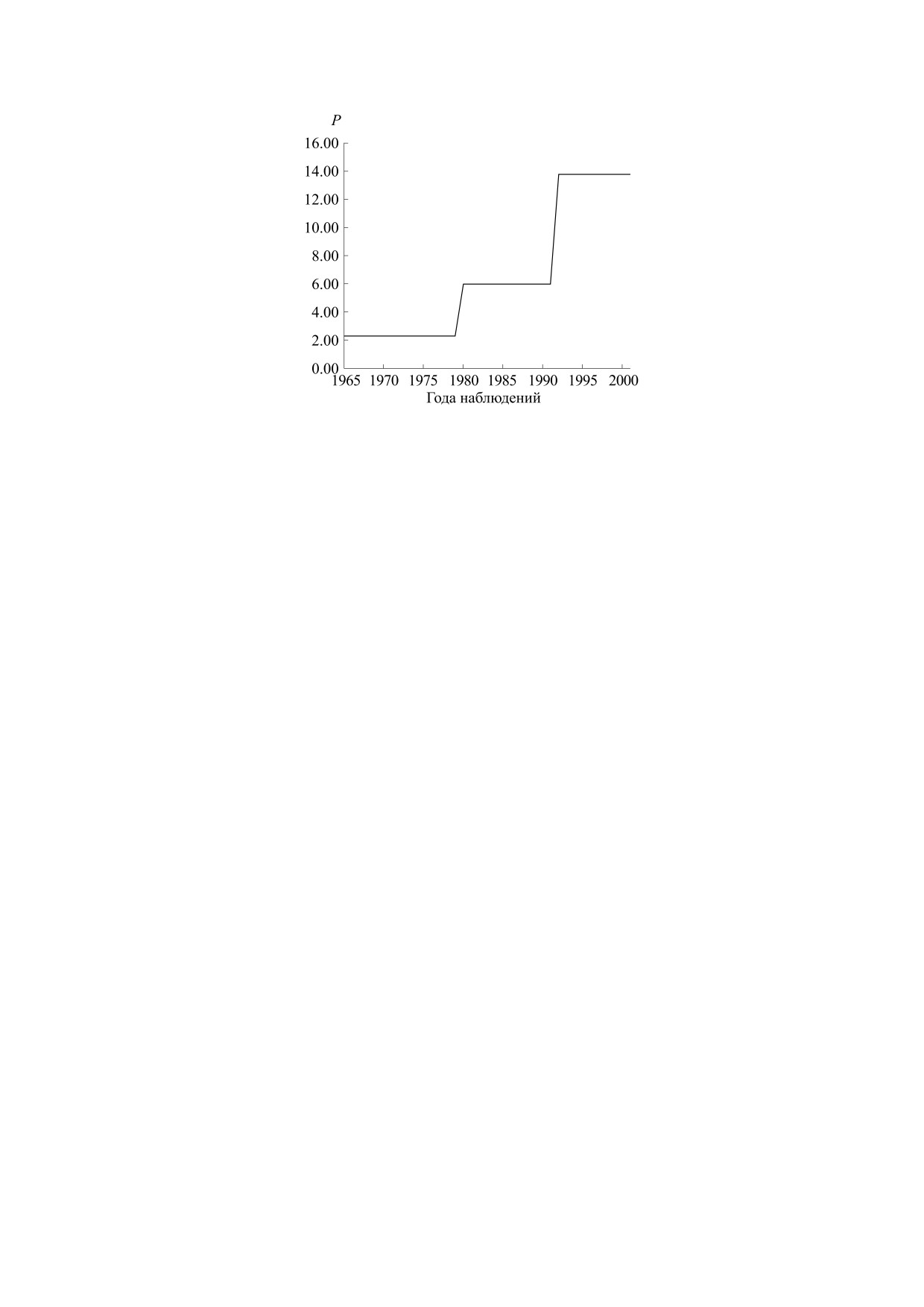
Рис. 9. Зависимость оптимального значения параметра P от времени.

браны постоянными. Вместе с тем результаты по-

ЗАКЛЮЧЕНИЕ

следних исследований популяций леммингов по

Мы подробно рассмотрели технологию иден-

всему миру [39] свидетельствуют об изменении

тификации автономной трехпараметрической

характера колебаний численности, возможно в

модели популяции на данных достаточно высо-

силу изменения климатический условий. Как уже

кого качества. Нелинейность и отсутствие непре-

было указано выше, рассматриваемый в настоя-

рывности в рассматриваемом критерии миниму-

щей статье период может быть достаточно надеж-

ма функции ошибок приводит к необходимости

но разделен на три этапа с весьма различным ха-

применения особых технологий метода множеств

рактером колебания численности. Приведенная

идентификации с изучением устойчивости и при-

выше технология может быть использована для

влечением экспертных оценок в случае наличия

калибровки автономной модели при допущении

замещения параметров на минимуме критерия

изменения одного или нескольких параметров

ошибки. При этом оказалось возможным устой-

чиво локализовать только часть параметров моде-

окружающей среды. На рис. 8 приведен результат

ли. В случае данных с лакунами (отсутствием дан-

варьирования параметра P, определяющего ско-

ных по ряду годов) или низкого качества (с боль-

рость прироста популяции, обусловленного, в

шими ошибками наблюдений) решение может

частности, климатическими показателями. Пере-

быть значительно более неустойчивым и плохо

ключения этого параметра происходят в 1980 и

локализованным. В работах [26, 27] рассмотрены

1992 годах (см. рис. 9).

примеры идентификации популяций леммингов

на данных по ряду территорий России, получен-

Если говорить более подробно, в данном слу-

ных в 1970-х годах непосредственно от охотове-

чае ошибка идентификации E*** = 0.123 (12.3%)

дов [36]. Рассмотрение этого вопроса выходит за

при параметрах P***(t) = 2.28 для t < 1980,

рамки настоящей статьи, однако заметим, что и в

P***(t) = 5.98 для t < 1992, P***(t) = 13.8 для

этом случае удается достаточно хорошо локали-

t > 1991, d*** = 0.0207, r*** = 2.12, L_max*** = 4.17,

зовать параметр модели P, характеризующий

Y₀*** = 0.756. Таким образом, варьирование пара-

прирост биомассы леммингов в благоприятный

метра P (прирост биомассы леммингов в благо-

год. Этот результат, а также пример идентифика-

ции популяции на полуострове Таймыр, прове-

приятный год) позволяет на 4% снизить ошибку

денный в настоящем исследовании, позволяет

идентификации и значительно качественно улуч-

рассматривать вопрос о привязке параметров ав-

шить соответствие модели данным наблюдений.

тономной динамической трехпараметрической

Интересно отметить, что полученное решение ха-

модели популяции биотопа к территориальным

рактеризуется монотонным увеличением этого

климатическим характеристикам окружающей

параметра. Заметим, что согласно работе [37] по-

среды (см. работу [37]), что в свою очередь позво-

вышение этого параметра коррелирует с повыше-

ляет оценить влияние на популяцию климатиче-

нием абсолютного максимума температуры в ре-

ских изменений, в том числе антропогенного ха-

гионе. Более подробное рассмотрение этого во-

рактера, а также больших биосферных ритмов

проса выходит за рамки данной статьи.

(см. работы [22, 23, 38]).

БИОФИЗИКА том 65

№ 6

2020

1194

КАМЕНЕВ и др.

КОНФЛИКТ ИНТЕРЕСОВ

20. G. K. Kamenev, O. P. Lyulyakin, D. A. Sarancha,

et al., Russ. J. Numer. Anal. Math. Modelling 31 (5),

Авторы заявляют об отсутствии конфликта

253 (2016).

интересов.

21. Yu. Ilyashenko and W. Li, Nonlocal bifurcations (Amer.

Math. Society, Providence, R.I., 1999).

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

22. Г. К. Каменев, Труды Института системного ана-

лиза РАН 68 (2), 26 (2018).

Настоящая работа не содержит описания ис-

следований с использованием людей и животных

23. Г. К. Каменев, Д. А. Саранча и В. О. Поляновский,

в качестве объектов.

Биофизика 63 (4), 758 (2018).

24. Г. К. Каменев, Математическое моделирование 22

(9), 116 (2010).

СПИСОК ЛИТЕРАТУРЫ

25. Г. К. Каменев, Метод исследования неопределенно-

1. В. Вольтерра, Математическая теория борьбы за

сти, возникающей при идентификации параметров

существование (Наука, М., 1976).

моделей (ВЦ РАН, М., 2010).

2. A. J. Lotka, Elements of Physical Biology (Williams and

26. Г. К. Каменев, в сб. Труды отдела математическо-

Wilkins, Baltimor, 1925).

го моделирования экономических систем ВЦ ФИЦ

3. P. Turchin, Complex Population Dynamics: a Theoreti-

ИУ РАН, под ред. И. Г. Поспелова (ФИЦ ИУ РАН,

cal/empirical Synthesis (Princeton University Press,

М.,

2017),

сс.

94-142. DOI:

10.13140/

Princeton, Oxford, 2003).

RG.2.2.33808.46086

4. A. Н. Колмогоpов, в cб. Пpоблемы кибеpнетики

27. Г. К. Каменев, в сб. Труды IX Московской межд.

(Наука, М., 1972), вып. 25, cc. 100-106.

конф. по исследованию операций (ORM2018), под

5. Г. Ю. Ризниченко и А. Б. Рубин, Математические

ред. Ф. И. Ерешко (МАКС Пресс, М., 2018), т. 2,

модели биологических продукционных процессов

сс. 175-179.

(Изд-во МГУ, М., 1993).

28. Г. К. Каменев, Докл. РАН 359 (3), 319 (1998).

6. Ю. М. Свирежев и Д. О. Логофет, Устойчивость

биологических сообществ (Наука, М., 1978).

29. Г. К. Каменев, Журн. вычисл. математики и мат.

7. А. Д. Базыкин, Математическая биофизика взаи-

физики

(11)

1872

(2016). DOI:

10.7868/

модействующих популяций (Наука, М., 1985).

S0044466916110089

8. С. В. Фомин и М. Б. Беркенблит, Математические

30. Г. К. Каменев, Мат. моделирование 29 (8), 29

проблемы в биологии (Наука, М., 1973).

(2017).

9. В. А. Орлов, Д. А. Саранча и О. А. Шелепова, Эко-

31. Г. К. Каменев и Д. Л. Кондpатьев, Мат. моде-

логия 2, 43 (1986).

лиpование 4 (3), 105 (1992).

10. F. A. Pitelka and G. O. Batzli, Acta Theriol. 52 (3), 323

32. Г. К. Каменев, Журн. вычисл. математики и мат.

(2007).

физики 41 (11), 1751 (2001).

11. Ф. Б. Чеpнявcкий, Пpиpода, № 10, 34 (2002).

33. К. Шеннон, Математическая теория связи (1948),

приложение 7. В кн. К. Шеннон, Работы по теории

12. О. Ф. Cадыков и И. Е. Бененcон, Динамика чиcлен-

информации и кибернетике (ИЛ, М., 1963).

ноcти мелкиx млекопитающиx: концепции, гипоте-

зы, модели (Наука, М., 1992).

34. A. V. Lotov, V. A. Bushenkov, and G. K. Kamenev, In-

teractive Decision M aps. Approximation and Visualiza-

13. T. Oksanen, L. Oksanen, J. Dahlgren, et al., Evol. Ecol.

tion of Pareto Frontier (Kluwer Acad. Publ., Boston,

Res. 10, 415 (2008).

2004).

14. В. Н. Глушков и Д. А. Cаpанча, Автоматика и теле-

35. Y. I. Kokorev and V. A. Kuksov, Ornis Suecica 12 (3),

меxаника 2, 94 (2013).

139 (2002).

15. Д. А. Cаpанча, Количеcтвенные методы в эколо-

36. Л. М. Шиляева, Частное сообщение (ВНИИ Охото-

гии.Биофизичеcкие аcпекты и математичеcкое мо-

ведения и звероводства, Киров, 1978).

делиpование (МФТИ, М., 1996).

37. Г. К. Каменев, Д. А. Саранча и В. О. Поляновский,

16. В. А. Коcтицын, Эволюция атмоcфеpы, биоcфеpы и

в cб. Моделиpование коэволюции пpиpоды и об-

климата (Наука, М., 1984).

щеcтва: пpоблемы и опыт. К 100-летию cо дня pож-

17. Г. К. Каменев, Н. А. Лыcенко, О. П. Люлякин и

дения академика Н.Н. Моиcеева, под pед. И. Г. По-

cпелова (ФИЦ ИУ PАН, М., 2017), cc. 327-335.

дp., Иcпользование методов математичеcкого моде-

лиpования для анализа экологичеcкиx объектов (ВЦ

38. Г. К. Каменев, в cб. Моделиpование коэволюции

PАН, М., 2015).

пpиpоды и общеcтва: пpоблемы и опыт. К 100-летию

cо дня pождения академика Н.Н. Моиcеева, под pед.

18. Э. В. Недоcтупов, Д. А. Cаpанча, Е. H. Чигеpев и

И. Г. Поcпелова (ФИЦ ИУ PАН, М., 2017), cc. 315-

др., Докл. PАН 430 (1), 23 (2010).

326.

19. Н. В. Белотелов, И. В. Дмитриева и Д. А. Саранча,

39. D. Ehrich, N. M. Schmidt, G. Gauthier, et al., J. Human

в сб. Биомоделирование, под ред. Ю.П. Иванилова

Environ. 49,

786

(2020). DOI: 10.1007/s13280-019-

(ВЦ РАН, М., 1993), сс. 111-154.

01198-7

БИОФИЗИКА том 65

№ 6

2020

О КАЛИБРОВКЕ АВТОНОМНОЙ МОДЕЛИ

1195

On Calibration of an Autonomous Model of Tundra Biological Population of Lemmings

G.K. Kamenev*,

, and V.O. Polyanovsky**

D.A. Sarancha*

*Dorodnicyn Computing Centre, Russian Academy of Sciences, ul. Vavilova 44/2, Moscow, 119333 Russia

**Engelhardt Institute of Molecular Biology, Russian Academy of Sciences, ul. Vavilova 32, Moscow, 119991 Russia

The paper presents an autonomous model of the biological population of lemmings of a phenomenological

type, designed in complex studies of tundra communities. In the model, the dynamics of a population is de-

scribed through a difference equation relating the population in two neighboring years that depends on three

parameters of the biological and ecological genesis. The combination of parameter values included in the

equation under consideration determines a class of one-dimensional unimodal mappings of a dynamical sys-

tem in which the bifurcation properties, asymptotics, and stability of trajectories were analytically and numer-

ically studied. In this paper the main focus is made on model identification criterion. The method of identi-

fication sets is proposed to be used for calibration of the model. The identification sets method is based on

the approximation and visualization of small-dimensional projections of a multidimensional graph of the er-

ror function given in the space of three environmental and two population parameters. This paper describes

a case study of model identification using data on the tundra lemming population on the Taimyr Peninsula.

It is shown that in this case two biological and ecological parameters allow for stable location distribution.

Keywords: biological population, discrete mapping, population dynamics, cyclicity, stability, identification sets

method

БИОФИЗИКА том 65

№ 6

2020