БИОФИЗИКА, 2021, том 66, № 3, с. 546-554
БИОФИЗИКА СЛОЖНЫХ СИСТЕМ
УДК 519.63
ИДЕАЛЬНОЕ СВОБОДНОЕ РАСПРЕДЕЛЕНИЕ В МОДЕЛИ
«ХИЩНИК-ЖЕРТВА» ПРИ МНОГОФАКТОРНОМ ТАКСИСЕ
© 2021 г. П.А. Зеленчук, В.Г. Цибулин
Южный федеpальный унивеpcитет, 344006, Pоcтов-на-Дону, ул. Большая Cадовая, 105/42
E-mail: zelenchukpavel@mail.ru, vgcibulin@sfedu.ru
Поступила в редакцию 10.07.2020 г.
После доработки 10.07.2020 г.
Принята к публикации 31.07.2020 г.
Анализируется концепция идеального свободного распределения для системы «хищник-жертва»
на неоднородном кольцевом ареале. Уравнения диффузия-реакции-адвекции моделируют много-
факторный таксис с учетом различных законов роста жертвы. Установлены соотношения на пара-
метры, при которых реализуется идеальное свободное распределение. Изучены трансформации ре-
шений при отклонениях параметров от условий, обеспечивающих идеальное свободное распреде-
ление, а также возникновение автоколебательных режимов.
Ключевые слова: популяционная динамика, идеальное свободное распределение, таксис, модель «хищ-
ник-жертва».
DOI: 10.31857/S0006302921030145
Параллельно развивались исследования, рас-
Концепция идеального свободного распреде-
сматривающее ИСР в системах двух или несколь-
ления (ИСР), введeнная в работе [1], изначально
ких конкурирующих за единый ресурс видов, ди-
рассматривала один вид, особи которого имеют
намика которых описывается уравнениями типа
полное представление о среде обитания и могут
диффузия-реакция-адвекция [9,10,11]. При этом
свободно перемещаться в любую еe точку. Это
под ИСР подразумевается размещение особей,
была чисто поведенческая концепция, не учиты-
пропорциональное количеству доступного ресур-
вающая динамики популяции. Позднее она была
са. В работе [12] было показано, что ИСР для та-
распространена на среду с двумя конкурирующи-
кого рода моделей обычно является необходи-
ми видами с учeтом изменения численности по-
мым и часто достаточным условием эволюцион-
пуляций [2], а затем и на случай нескольких ви-
но устойчивой стратегии.
дов, находящихся во взаимодействии «хищник-
жертва» [3,4].
К настоящему времени авторам неизвестны
При исследовании локальных («точечных»)
работы, в которых бы рассматривалась ИСР в мо-
моделей «хищник-жертва» с ИСР рядом авторов
делях «хищник-жертва», описываемых уравне-
использовались различные предположения отно-
ниями реакция-диффузия-адвекция. Между тем
сительно миграции видов между двумя участками
именно это направление представляет значитель-
ный интерес для пространственно неоднородных
ареала
[5,6]. Сами модели базировались на
классических уравнениях Лотки-Вольтерры,
систем и задач с неравномерным распределением
модифицированных функциональным откликом
ресурса [13,14]. Важным является не только во-
Холлинга II рода для хищника или же логистиче-
прос о том, даeт ли ИСР конкурентные преиму-
ским законом роста для жертвы.
щества по сравнению с другими стратегиями, но
и анализ устойчивости сообщества «хищник-
В некоторых работах для системы «хищник-
жертва» с ИСР при возмущениях параметров си-
жертва» концепция ИСР связывалась с идеями
стемы.
теории игр и адаптивной динамики [7] и характе-
ризовалась как эволюционно устойчивая страте-
При исследовании динамики системы «хищ-
гия. В работе [8] было исследовано влияние неод-
ник-жертва» обычно исходят из большей актив-
нородности ресурсов в модели клеточного авто-
ности хищника. Так, для уравнений типа диффу-
мата 30 × 30 на динамику локальной системы
зия-реакция коэффициент диффузии хищника
«хищник-жертва» при ИСР.
зачастую на порядок превосходит соответствую-
щий коэффициент жертвы [15], а для уравнений
Сокращениe: ИСР - идеальное свободное распределение.
типа диффузия-реакция-адвекция направленной
546
ИДЕАЛЬНОЕ СВОБОДНОЕ РАСПРЕДЕЛЕНИЕ
547
миграцией (таксисом) обладает хищник [16,17].
линомиальной функцией, позволяющей полу-
Для многих реальных биологических систем та-
чить как стационарное, так и автоколебательное
кое описание вполне оправдано, тем не менее,
решение для системы. Анализируются условия,
интересны случаи, когда жертва также обладает
при которых получаются решения, отвечающие
адвекцией и диффузией, скорости которых соиз-
ИСР, их устойчивость и трансформации при ма-
меримы или равны соответствующим скоростям
лых отклонениях параметров.
хищника [18].
В работе рассматривается система «хищник-
жертва» на кольцевом ареале с учетом неоднород-
ДИНАМИКА СИСТЕМЫ «ХИЩНИК-
ного распределения ресурса жертвы и многофак-
ЖЕРТВА» НА НЕОДНОРОДНОМ АРЕАЛЕ
торного таксиса. На основе уравнений диф-
фузии-реакции-адвекции строится модель, в
Рассматривается следующая система уравне-
которой рост популяции жертвы описывается по- ний диффузии-адвекции-реакции:
∂
u =−q′ +
u
[
η
f u)
−μ
v
]
,
q
=-k
u′+uαQ′ -
uβQ′
,
1
1
n
1
1
1
1
1
1
2
∂t
(1)
∂v
⎡
u⎤
=-q′ +
v
−η
+μ
,
q
=-k
v′ + vβ
Q′
,
2
⎢
2
2
⎥
2
2
2
3
∂t
⎣
p⎦
где u и v - плотности популяций жертвы и хищ-
функций будет определять характер простран-
ника соответственно, p - ресурс жертвы, q1, q2 -
ственного распределения видов.
миграционные потоки, а штрих означает произ-
Система (1) дополняется условиями перио-
водную по x.
дичности:
Рост популяции жертвы при отсутствии хищ-
u
(0,
t
)
=
u
(a
,
t
)
,
v
(0,
t
)
=
v
(a
,
t
)
ника определяется полиномиальной функцией
(3)
q
(0,
t)
=
q
(
a,
t
)
,
i
=
1,2
fn(u):
i
i
и начальными условиями
n
⎛
u⎞
f u)
=
u
1−
,
n
=
0, 1, 2 ...
(2)
n
⎜
⎟
u
(x,0)
=u x)
,
v
(
x,0
)
=
v
(
x
)
(4)
⎝
p⎠
0
0
В выражении (2) при n = 0 будем иметь логи-
Функция ресурса p(x), определяющая неоднород-
стический, а при n = 1 гиперболический законы
ность жизненных условий, является положитель-
роста. Влияние хищника описывается слагаемым
ной функцией и определяется выражением
μ1uv из классической модели Лотки-Вольтерра.
p(x) = eμ(x), где μ(x) - вспомогательная функция,
удовлетворяющая условию μ(0) = μ(a).
В отсутствие жертвы хищник вымирает с экс-
поненциальной скоростью, описываемой членом
(-η2v). Рост хищника задаeтся функцией μ2uv/p,
ЛОКАЛЬНАЯ МОДЕЛЬ
которая позволяет учитывать скорость размноже-
Стационарные решения (1) при отсутствии
ния хищника в зависимости от численности
пространственных потоков (q1 = q2 = 0) находятся
жертвы и еe ресурса. Если соотношение u/p мало,
из системы:
скорость размножения хищника также мала, если
же u/p → 1, скорость хищника становится макси-
u
[
η
f u)
−μ
v
]
=
0,
1
n
1
мальной.
⎡
u
⎤
(5)
В состав миграционного потока жертвы q1 вхо-
v
−η
2
+μ
2
=
0.
⎢
⎥
⎣
p
⎦
дит диффузионное слагаемое (-k1u'), отвечающее
за естественное стремление особей вида «распро-
При положительных коэффициентах имеются
страниться» и занять весь ареал, и два адвектив-
тривиальное равновесие (0, 0), равновесие без
ных слагаемых, первое из которых (uα1Q1') харак-
хищника (p, 0) и решение с обоими видами:
теризует таксис жертвы направленный на ресурс,
η
p
η
f
(u)
2
1
n
а второе (-uβ1Q2') - таксис жертвы, направлен-
u
=
,
v
n
=
(6)
μ
2
μ
1
ный от хищника. Миграционный поток хищника
q2 содержит диффузионное слагаемое (-k2v') и
Решение (6) устойчиво (в линейном прибли-
таксис, направленный на жертву (vβ2Q3').
жении [19]) при выполнении следующих условий:
Функции Qj (j = 1, 2, 3) характеризуют страте-
n
+
1
η
<μ
<
η
(7)
2
2
(
)
2
гии направленной миграции. Именно выбор этих
n
БИОФИЗИКА том 66
№ 3
2021
548
ЗЕЛЕНЧУК, ЦИБУЛИН
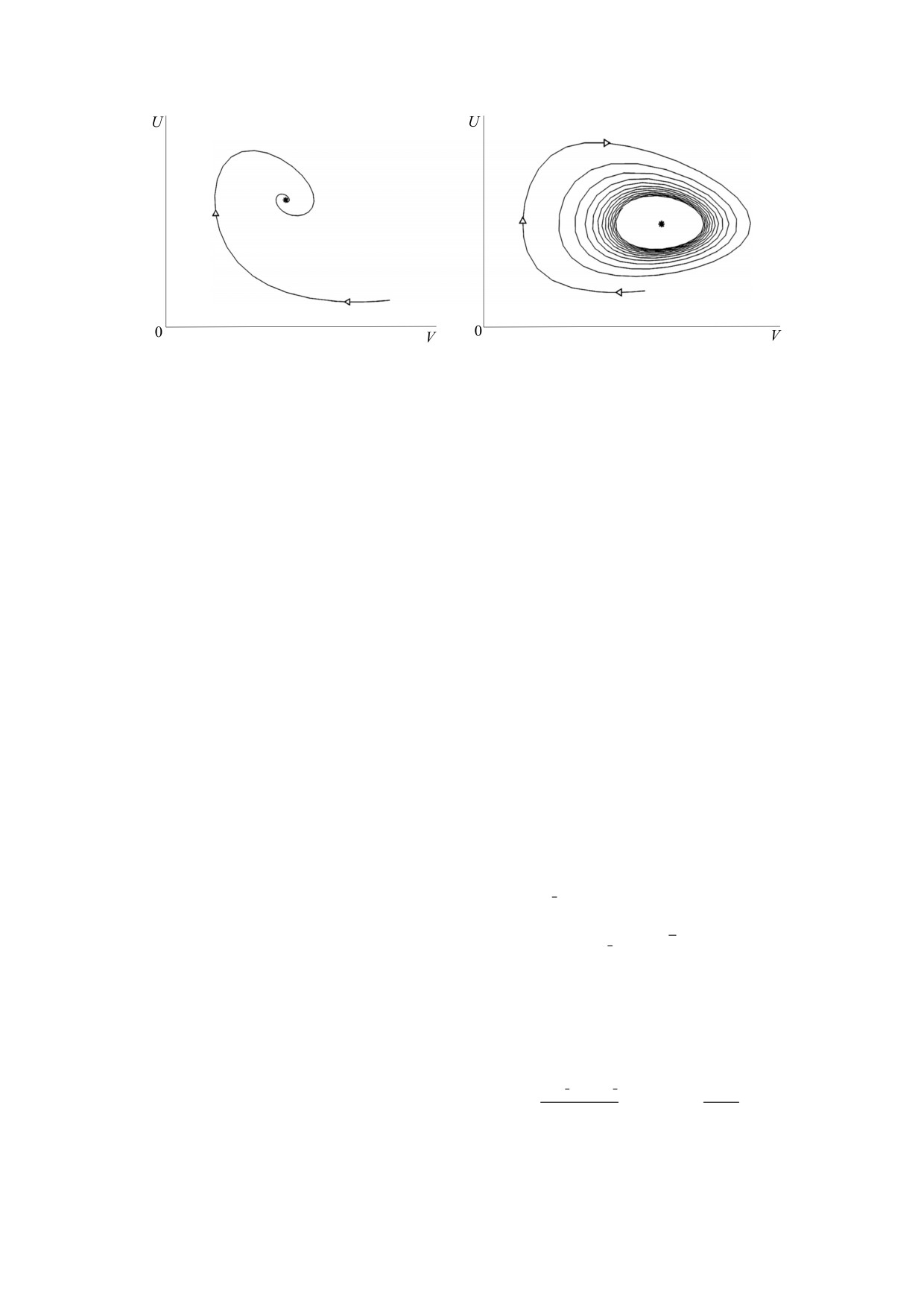
Рис. 1. Фазовые портреты системы (1) без потоков: (а) - устойчивое равновесие, n = 0, η2 < μ2; (б) - неустойчивый
фокус и установление к предельному циклу, n = 1, μ2 > 2η
2.
Для n = 0 правая часть неравенства (7) теряет
Таким образом, получаются условия на коэф-
свой смысл и поэтому для этого случая условие
фициенты системы, при которых имеется стаци-
устойчивости примет вид η2 < μ2. При n = 0 реше-
онарное решение (6):
ние (6) представляет собой «фокус» (рис. 1а),
β
2
устойчивый при выполнении неравенства η2 < μ2
k
=α
−
nβ
, k
=
(11)
1
1
1
2
n
и теряющий устойчивость при его нарушении.
Если n ≠ 0, решение (6) также устойчиво при вы-
В случае, когда n = 0, производная v' = 0 и усло-
полнении неравенства (7). В случае μ2 > 2η2 воз-
вие (10) будет выполнено, если:
никает устойчивый предельный цикл (см.
k
=α
,
β
=
0.
(12)
1
1
2
рис. 1б).
Далее рассмотрим систему (1) на одномерном
При n = 0 ограничений на возрастание коэф-
кольцевом интервале Ω = [0, a] для случая гипер-
фициента μ2 нет и колебаний нет. Для n = 1 ин-
болического закона роста жертвы (n = 1), инте-
тервал устойчивости (7) максимален, выход из
ресного с точки зрения существования стацио-
этого интервала при возрастании μ2 сопровожда-
нарных решений и периодических колебаний.
ется появлением колебаний. С ростом n интервал
Кольцевой ареал довольно распространeнное яв-
устойчивости сокращается.
ление в природе, например узкая береговая линия
озера или уровень постоянной высоты вокруг го-
ры [15].
УЧЕТ МИГРАЦИОННЫХ ПОТОКОВ
Для численного анализа задачи (1)-(4) с учe-
Покажем, что при наличии в системе (1) ми-
том (8), (11) используем интегро-интерполяцион-
грационных потоков распределение видов хищ-
ный метод смещeнных сеток аналогично [18].
ника и жертвы будет пропорционально ресурсу
Плотности популяций хищника и жертвы опре-
p(x) при логарифмическом виде функций Qj:
деляются в узлах основной сетки
u(
k
x t),
v(x
k
,t),
Q
= lnp,
Q
= lnv,
Q
= lnu
(8)
а миграционные потоки в узлах вспомогательной
1
2
3
сетки
q
,
i
=
1,2 :
Для сохранения полной системой (1) стацио-
1
i,k+
2
нарного решения (6) необходимо выполнение
условий:
1
x
k
=
kh,
x
1
=
k
+
h,
k
=
0,…,n,
(13)
k+
(
)
2
2
′
′
k
1
u′
−
uα
1
(ln
p)
+
uβ
1
(ln
v)
=
0,
(9)
′
k
2
v′ - vβ
2
(ln
u)
=
0.
где h = a/ns шаг равномерной дискретизации про-
странственного интервала.
Подставляя выражения (6) в выражения (8), с
Так, разностный аналог для популяции жерт-
учeтом уравнения (2) получим:
вы запишется в виде:
η
2
p′(
k
1
−α
1
+
nβ
1
)
=
0,
q
−
q
1
1
μ2
1,k+
1,k−
∂u
k
2
2
⎛
⎛1
−
u
k
⎞
⎞
(10)
=-
+u
η
u
−μ
v
,
(14)
n
k
⎜
1,k k
⎜
⎟
1,k k
⎟
η
⎛η
⎞ ⎛
η
⎞
n
∂t
h
⎝
⎝
p
⎠
⎠
1
2
2
k
1
−
p
p
′
[
nk
−β
]
=
0.
⎜
⎟ ⎜
⎟
2
2
μ
1
⎝
μ
2
⎠
⎝
μ
2
⎠
а уравнение для потока будет иметь вид:
БИОФИЗИКА том 66
№ 3
2021
ИДЕАЛЬНОЕ СВОБОДНОЕ РАСПРЕДЕЛЕНИЕ
549
⎛u
k
−
u
k−1
⎞
q
1
=-k
1
⎜
⎟
+
(u
k−1
+
u
k
)[α
1,k−1
Lp
k
−β
1,k
Lv
k
],
1,k−
⎝
h
⎠
2
(15)
(p
k
−
p
k-1
)
/
h
Lp
k
=
p
k
+
p
k
−1
Аналогичным образом выводятся выражения
Рис. 3 иллюстрирует характер установления
для плотности популяции хищника. В результате
к ИСР при отклонении начальных
*
*
получается система обыкновенных дифференци-
условий:
0
u x)
= 1.2u x)
0
,
0
v x)
= 0.7v
0
(x),
где
альных уравнений относительно uk, vk, которая
отвечают решению (6). Приведены
u x)
(
)
0
0
,
v
x
интегрируется методом Рунге-Кутты четвeртого
графики изменения по времени численностей
порядка в среде MATLAB.
популяций в средней точке интервала. В обоих
случаях происходит выход на стационарное
распределение, соответствующее ИСР.
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ
Далее были проведены численные экспери-
Численные расчeты динамики системы (1) при
менты по изучению трансформации ИСР-реше-
различных значениях параметров подтвердили
ний при малых (ε = 0.05) отклонениях миграци-
реализацию ИСР-решений (6) при выполнении
онных параметров
k
,
α
,
β
,
k
,
β
от соотношений,
1
1
1
2
2
(8) и (11).
обеспечивающих ИСР.
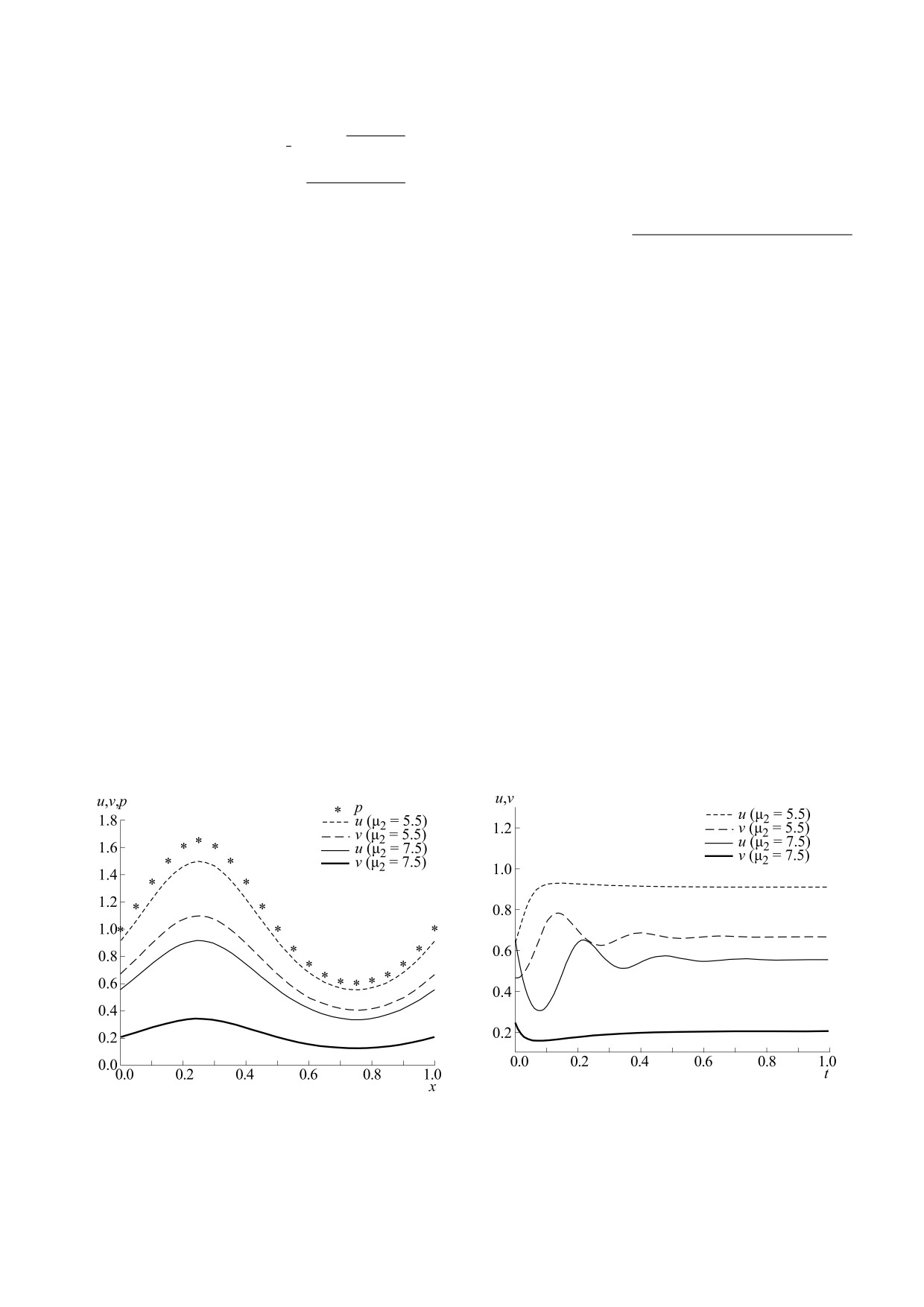
На рис. 2 приведены стационарные ИСР-рас-
На рис. 4 представлены результаты вычисле-
пределения популяций жертвы и хищника, полу-
ченные для двух значений параметра μ2. Значения
ний при отклонении коэффициента миграции
*
остальных коэффициентов были фиксированы:
жертвы
k
=k
+ε,
остальные параметры равны:
1
1
μ1 = 2, k1 = 0.1, α1 = 0.2, β1 = 0.1, η1 = 5, η2 = 5, k2 =
μ
= 4, μ
= 6.5, η
= 5,η
= 5, α
= 0.2, β
= 0.1,
k2 =
1
2
1
2
1
1
0.2, β2 = 0.2. Функция ресурса задавалась выраже-
= 0.2, β2 = 0.2. На верхнем левом графике показа-
нием:
но финальное распределение жертвы, хищника
и ресурса вдоль ареала. На правом верхнем гра-
sin 2πx
p(x)
=
exp
(16)
фике - относительное отклонение распределе-
(
)
2
ний от решения ИСР. На нижних графиках даны
Из рис. 2 видно, что жертва и хищник, распре-
графики изменения по времени численностей
делились по ареалу пропорционально ресурсу,
популяций в средней точке ареала. Видно, что
изменение параметра μ2 сказывалось только на
устанавливающиеся распределения близки к ре-
соотношении численностей популяций.
шению ИСР, но имеются незначительные откло-
Рис. 2. Идеальное свободное распределение жертвы и
Рис. 3. Установление к идеальному свободному рас-
хищника по ареалу для двух значений параметра μ2.
пределению для двух значений параметра μ2.
БИОФИЗИКА том 66
№ 3
2021
550
ЗЕЛЕНЧУК, ЦИБУЛИН
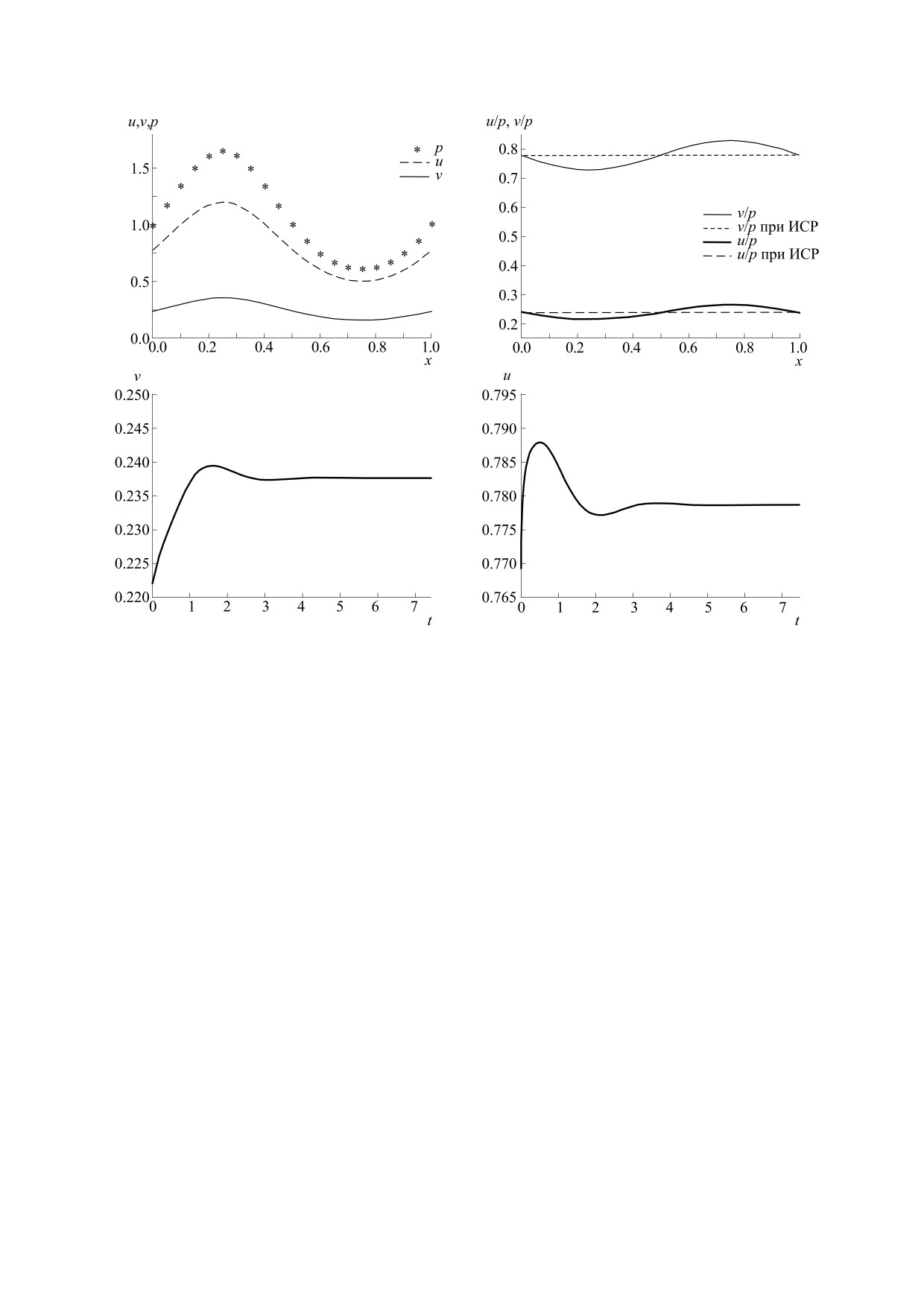
Рис. 4. Графики зависимостей плотностей популяций жертвы u и хищника v от координаты (вверху) и времени (внизу)
при k1 = 0.15.
нения в численности популяций и характере рас-
метров. При этом будем возмущать начальные
пределения.
значения плотностей популяций.
Подобные трансформации происходят при из-
На рис. 6 представлены пространственно-вре-
менении других миграционных параметров. При
менные распределения популяций жертвы и
этом реализуются устойчивые стационарные ре-
*
хищника при
α
1
=α
1
−ε
и следующих значениях
шения, близкие к ИСР, но с перераспределением
параметров: μ1 = 4, μ2 = 10.5, η1 = η2 = 5, k2 = 0.1,
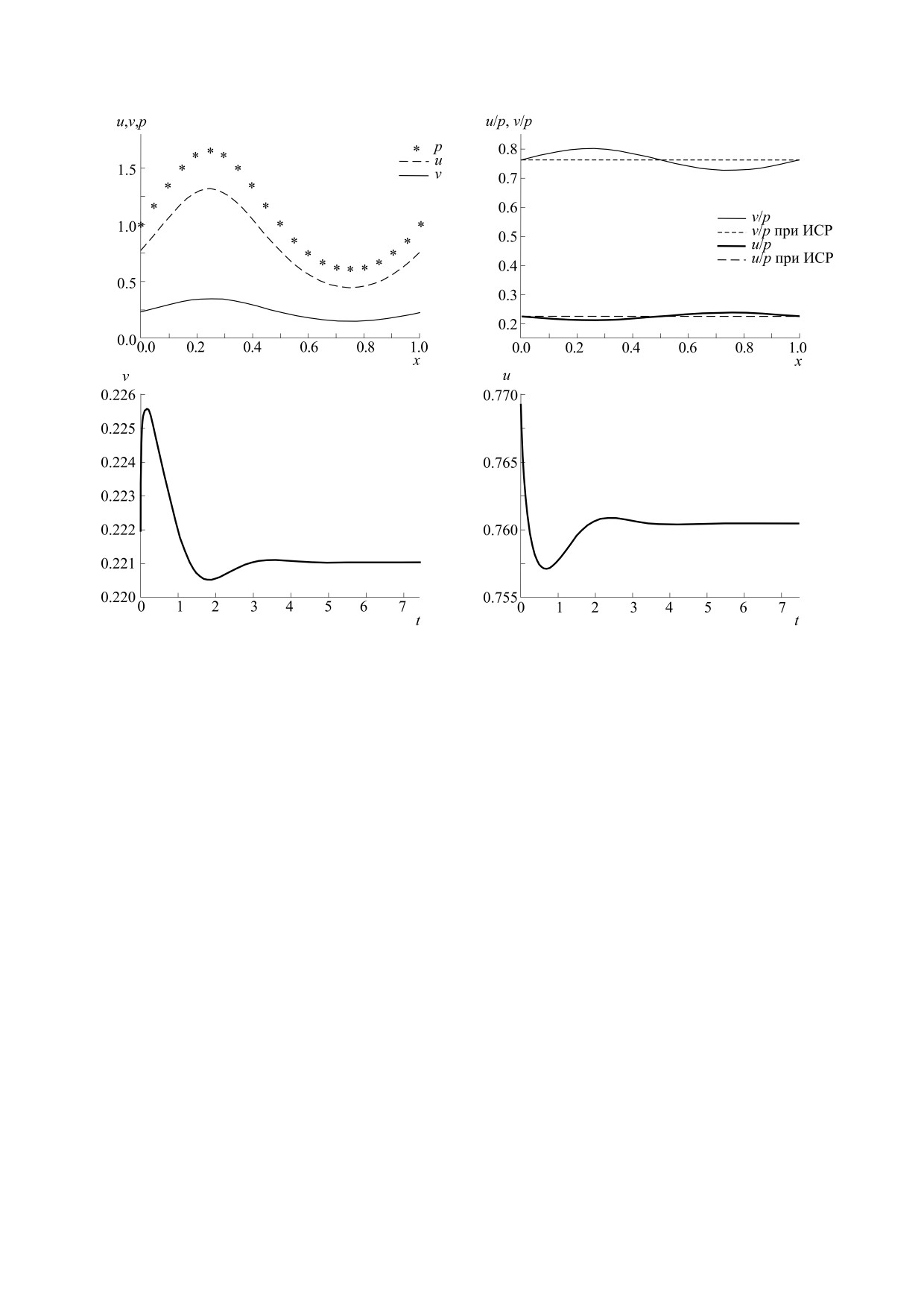
видов вдоль ареала. Так, например, на рис. 5
β1 = 0.1, k2 = β2 = 0.2. Соответствующие двумер-
представлены результаты вычислений при откло-
ные графики представлены на рис. 7. Из графи-
нении коэффициента таксиса хищника
*
ков видно, что получающийся колебательный ре-
β
=β
−ε
при тех же значениях остальных пара-
2
2
жим напоминает решение, отвечающее ИСР.
метров. Видно, что выросла популяция жертвы
(хищник снизил свою поисковую активность), а
Однако картина существенно изменяется, ес-
популяция хищника уменьшилась. Распределе-
ли коэффициенту таксиса жертвы, направленно-
ние изменилось и стало разнонаправленным для
го на ресурс, дать отклонение в противополож-
хищника и жертвы.
*
ную сторону
α
=α
+ε
На рис. 8 представлены
1
1
Теперь рассмотрим вопрос о решениях с ИСР
трeхмерные графики поведения популяций для
при параметрах, отвечающих автоколебательно-
этого случая (α1 = 0.25) и тех же значений осталь-
му режиму для локальной системы. Выберем зна-
ных параметров. Колебания численностей попу-
чение параметра μ2, нарушающее неравенство (7)
ляций со временем затухают, и система выходит
для случая n = 1, и проведeм исследования с теми
на стационарный режим, сохраняя при этом
же малыми отклонениями миграционных пара-
ИСР.
БИОФИЗИКА том 66
№ 3
2021
ИДЕАЛЬНОЕ СВОБОДНОЕ РАСПРЕДЕЛЕНИЕ
551
Рис. 5. Графики зависимостей плотностей популяций жертвы u и хищника v от координаты (вверху) и времени (внизу)
при β2 = 0.15.
Аналогичным образом, были проведены ис-
ние, соответствующее ИСР. Представлены чис-
следования остальных миграционных парамет-
ленные результаты, демонстрирующие устойчи-
ров, показавшие, что отклонение в одну сторону
вость найденных решений и их трансформацию
не нарушает колебательного режима, а в
при нарушении соотношений между параметра-
другую - приводят к установлению стационар-
ми. Исследованы условия, при которых появля-
ного режима.
ются колебательные решения. Показано, что из-
менение миграционных параметров (нарушение
ИСР) может стабилизировать колебательные
ЗАКЛЮЧЕНИЕ
режимы пространственно распределeнной сис-
На основе дифференциальных уравнений в
темы.
частных производных параболического типа рас-
смотрена пространственно-временная эволю-
Для нелинейных уравнений математической
ция системы «хищник-жертва». Задача характе-
физики отыскание явных аналитических реше-
ризуется неоднородным распределением ресурса
ний является достаточно редким событием. Ста-
жертвы и многофакторным таксисом обоих ви-
ционарные распределения, отвечающие концеп-
дов. Локальный рост популяции жертвы опреде-
ции ИСР и существующие при найденных соот-
ляется полиномиальной функцией, позволяю-
ношениях на параметры, позволяют далее
щей рассмотреть логистический и гиперболиче-
организовать исследование динамики системы
ский законы, а изменение популяции хищника
при нарушениях этих соотношений. Для анализа
зависит от отношения численности жертвы к еe
многовидовых систем это может быть полезно в
ресурсу.
сочетании с подходом на основе теории косим-
Для задачи на кольцевом ареале найдены усло-
метрии [20,21]. В таких задачах также устанавли-
вия на параметры системы, при которых имеется
ваются соотношения на параметры, при которых
ненулевое стационарное аналитическое реше-
появляются непрерывные семейства стационар-
БИОФИЗИКА том 66
№ 3
2021
552
ЗЕЛЕНЧУК, ЦИБУЛИН
Рис. 6. Пространственно-временные распределения u и v, α1 = 0.15.
Рис. 7. Графики зависимостей плотностей популяций жертвы u и хищника v от координаты (вверху) и времени (внизу)
при α1 = 0.15.
БИОФИЗИКА том 66
№ 3
2021
ИДЕАЛЬНОЕ СВОБОДНОЕ РАСПРЕДЕЛЕНИЕ
553
Рис. 8. Пространственно-временные распределения u и v, α1 = 0.25.
ных решений. Эта идеальная ситуация является
11. R. S. Cantrell, C. Cosner, S. Martinez, and N. Torres,
далее отправной для анализа вероятных сценари-
J. Diff. Equations 265, 3464 (2018).
ев на основе аппарата селективной функции.
12. R. S. Cantrell, C. Cosner, D. L. Deangelis, and V. Pad-
Исследование проводилось пpи финансовой
ron, J. Biol. Dynam. 1 (3), 249 (2007).
поддержке Российского фонда фундаментальных
13. Дж. Д. Мюррей, Математическая биология. Т. II.
исследований (грант № 18-01-00453).
Пространственные модели и их приложения в биоме-
дицине (НИЦ «Регулярная и хаотическая динами-
ка», М.-Ижевск, 2011).
СПИСОК ЛИТЕРАТУРЫ
14. Г. Ю. Ризниченко and А. Б. Рубин, Математиче-
1. S. D. Fretwell and H. L. Lucas, Acta Biotheoretica 19,
ские методы в биологии и экологии. Биофизическая
16 (1970).
динамика продуктивных процессов в 2 ч. (Изд-во
2. C. M. Lessells, Animal Behav. No. 49, 487 (1995).
Юрайт, М., 2019), ч. 2.
3. S. Schwinning and M. L. Rosenzweig, OIKOS, No. 59,
15. А. Д. Базыкин, Математическая биофизика взаи-
85 (1990).
модействующих популяций (Наука, М., 1985).
4. C. Bernstein, A. Kacelnik, and R. Krebs, Tree 7 (2), 50
16. R. Arditi, Yu. Tyutyunov, Α. Morgulis, et al., Theor.
(1992).
Popul Biol., No. 59, 207 (2001).
5. P. Auger, C. Bernstein, and J. C. Poggiale, Am. Natu-
17. Ю. В. Тютюнов, Н. Ю. Сапухина, А. Б. Моргулис и
ralist 153 (3), 267 (1999).
В.Н. Говорухин, Журн. общ. биологии 62 (3), 253
6. R. Cressman and V. Křivan, Am. Naturalist 168 (3),
(2001).
384 (2006).
18. А. В. Будянский и В. Г. Цибулин, Биофизика 64
7. R. Cressman, G. Garay, and V. Křivan, Am. Naturalist
(2), 343 (2019).
164 (4), 473 (2004).
19. Н. Н. Баутин и Е. А. Леонтович, Методы и приeмы
8. A. V. Bell, R. B. Rader, S. L. Peck, and A. Sih, Theor.
качественного исследования динамических систем
Popul. Biol., No. 76, 52 (2009).
на плоскости (Наука, М., 1990).
9. R. S. Cantrell, C. Cosner, and Y. Lou, Math. Biosci.
20. А. В. Епифанов и В. Г. Цибулин, Биофизика 61 (4),
Engineer. 7 (1), 17 (2010).
823 (2016).
10. I. Averill, Y. Lou, and D. Munther, J. Biol. Dynam. 6
21. A. V. Budyansky, K. Frischmuth, and V. Tsybulin, Dis-
(2), 117 (2012).
crete Contin. Dynam. Syst. 24 (2), 547 (2019).
БИОФИЗИКА том 66
№ 3
2021
554
ЗЕЛЕНЧУК, ЦИБУЛИН
Ideal Free Distribution in the Predator-Prey Model with Multifactor Taxis
P.A. Zelenchuk and V.G. Tsybulin
Southern Federal University, ul. Bolshaya Sadovaya 105/42, Rostov-on-Don, 344006 Russia
The concept of ideal free distribution is analyzed for the predator-prey system on an inhomogeneous ring
range. The diffusion-reaction-advection equations model multifactorial taxis taking into account various laws
of prey growth. Relations are established for the parameters at which the ideal free distribution is realized. We
studied the transformation of solutions with deviations of the parameters from the conditions under which
ideal free distribution can be seen and autooscillating systems occur.
Keywords: population dynamics, ideal free distribution, taxis, predator-prey model
БИОФИЗИКА том 66
№ 3
2021