БИОФИЗИКА, 2022, том 67, № 1, с. 150-159
БИОФИЗИКА СЛОЖНЫХ СИСТЕМ
УДК 517.958.531.3-324
НЕИНВАЗИВНЫЙ ПОДХОД В ГИДРОДИНАМИКЕ СПИННОМОЗГОВОЙ
ЖИДКОСТИ В СПИНАЛЬНОЙ ПОЛОСТИ
© 2022 г. А.Г. Зверев, Ю.Н. Токарев
Институт проблем безопасного развития атомной энергетики РАН, 115191, Москва, Большая Тульская ул., 52
E-mail: ytokarev@ya.ru
Поступила в редакцию 21.09.2021 г.
После доработки 21.09.2021 г.
Принята к публикации 18.11.2021 г.
Предложена модель движения спинномозговой жидкости в спинальной полости позвоночника,
позволяющая рассчитать профили скоростей и расходы ликвора в зависимости от размеров полости
и пульса пациента. Полученные аналитическими методами зависимости позволяют делать количе-
ственные оценки движения ликвора в спинальной полости позвоночника и более обоснованно ста-
вить диагнозы при его патологии.
Ключевые слова: спинномозговая жидкость, ликвор, профиль скорости, число Уомерсли.
DOI: 10.31857/S0006302922010161
В живых биологических системах некоторые
связь этих систем, но к единой терминологии это
процессы являются периодическими, характери-
так и не привело.
зующимися частотой и амплитудой. К таким про-
В данной работе проводится моделирование
цессам относятся сердечные сокращения, дыха-
движения ликвора в позвоночнике, точнее в спи-
ние, движение спинномозговой жидкости. Их ча-
нальной полости (подпаутинном пространстве).
стоты находятся в диапазоне от 0.0-1.2 Гц в покое
Спинальная полость представляет собой нерав-
до 3.5 Гц при нагрузках [1, 2].
номерную кольцевую (коаксиальную) трубку, ко-
До XIX века пока аппаратура по измерению ча-
торая в шейном и поясничном отделе имеет утол-
стот еще не была создана, главным инструментом
щение в виде раструба, а в грудном - обычную
для их определения являлась пальпация. С ее по-
кольцевую трубку. Длина полости ~ 0.5 м, от
мощью при определенной тренировке измерялся
большого затылочного отверстия до точки L2. На-
пульс, дыхательный ритм, а в некоторых случаях
ружная стенка (паутинная оболочка), плотно
и колебания спинномозговой жидкости [1-3].
примыкает к твердой мозговой оболочке. Внут-
Систематическое исследование ритмов началось
ренняя стенка, мягкая оболочка спинного мозга,
с конца XIX века, с появлением электрокардио-
крепится к твердой мозговой оболочке зубчаты-
графа, а позднее, в 50 годы XX века - капнографа
ми связками через паутинную оболочку. Схема-
и реоэнцефалографа, 80 годы XX века - транскра-
тично геометрия спинальной полости приведена
ниальной допплерографии, ультразвуковых ис-
на рис. 2 [8].
следований, магнитно-резонансной томографии.
Одной из главных особенностей ликвора явля-
Проводились также инвазивные исследования
ется его дренажная функция, т.е. отведение про-
[3-6]. Технический прогресс позволил сократить
дуктов жизнедеятельности из спинного мозга и
затрачиваемое время на постановку диагноза по
спинномозговых нервов, и компенсаторная (ста-
глубоким патологиям и более адекватно описы-
билизация внутричерепного давления), которая
вать сам диагноз (рис. 1) [7]. Появилась возмож-
влияет на всасывание части ликвора в спинно-
ность управлять этими параметрами в спорте [8,
мозговые нервы [11], обеспечивая их работоспо-
9]. Параллельно изучался состав ликвора и его
собность.
пульсации при изменении давления [9, 10].
Конструкция шейных и поясничных каналов
Исторически сложилось так, что сердечно-со-
имеет расширение типа валторны. Ликвор, по-
судистая, дыхательная и ликворная системы изу-
ступающий из черепа, имеет начальную среднюю
чались по отдельности и для их описания приме-
скорость порядка 0.01 м/с, которая возрастает по-
нялись не связанные между собой системы тер-
чти в три раза при входе в грудной канал и допол-
минов. Дальнейшее изучение выявило взаимную
нительно возрастает в центре вследствие уменьше-
150
НЕИНВАЗИВНЫЙ ПОДХОД В ГИДРОДИНАМИКЕ
151
Рис. 1. Синхронизованные спектральные реоэнцефалограммы, транскраниальные допплерограммы, электрокардиограм-
мы и дыхание.
ния проходного сечения. В грудном канале ско-
це, поэтому к уравнению (1) присоединим гра-
рость возрастает примерно в полтора раза. В
ничные условия:
поясничном канале вследствие его расширения
u
=
0,
скорость падает в полтора раза. Из опытных данных
r=r1
(2)
следует, что расход ликвора на уровне большого за-
u
=
0
r=r2
тылочного отверстия составляет ~(1-3)×10-6 м3/с,
Приведем уравнение (1) к безразмерному ви-
средняя скорость по поперечному сечению - 0.01-
ду. Для этого введем безразмерные координаты и
0.07 м/с [8, 10].
время:
r′ = r/r2, z′ = z/r2, τ = t/tP
(3)
МОДЕЛИРОВАНИЕ ДВИЖЕНИЯ ЛИКВОРА
В выражении (3) tP - период пульсаций
Примем, что ликвор является ньютоновской
давления. Градиент давления в рассматривае-
жидкостью, имеющей плотность ρ = 966÷1007 кг/м3
мой задаче является периодической функци-
и динамическую вязкость μ = 0,0007÷0,001 Н/м2,
ей; поскольку величина p/ρ имеет размер-
движущейся по бесконечной кольцевой трубке с по-
ность квадрата скорости, представим его в
стоянным поперечным сечением. В этом случае
виде
уравнения Навье-Стокса сводятся к единственно-
му уравнению для осевой скорости, которое в ци-
линдрических координатах записывается в следую-
щем виде:
∂u
1
∂
∂u
1∂p
=ν
r
−
,
(1)
(
)
∂t
r
∂r
∂r
ρ∂z
где u - скорость вдоль оси, t - время, v - кинема-
тическая вязкость, r - текущий радиус, r1 < r < r2,
p - давление, ρ - плотность, z - продольная коор-
дината.
Конвективный член в уравнении (1) опущен,
так как поперечное сечение постоянно. Скорость
ликвора принимает нулевые значения на грани-
Рис. 2. Геометрия кольцевого канала.
БИОФИЗИКА том 67
№ 1
2022
152
ЗВЕРЕВ, ТОКАРЕВ
2
r
(r
-
r
)
r
1∂p
t
u
p
t
2
2
1
2
α
β=
=
=
;
−
=
AP
=
P
(4)
ρ∂z
t
r
t
νt
P
νt
P
(r
2
−
r
1
)
1−ξ
P
2
P
(r
2
−
r
1
)
r
2
(1 −ξ
)
Функция P(τ) в уравнении (4) будет периоди-
α =
=
;
(11)
νt
νt
ческой, изменяясь в пределах (-1, 1) на отрезке
P
P
2
(0, 1), например, можно положить P(τ) = sin(2πτ).
uν
uu
ν
u
P
U
=
=
;
u
=
U
Величина uP характеризует амплитуду колебаний
2
2
r
u
u
u
2
P
P
ν
градиента давления:
Параметр α в выражении (11) с точностью до
2
u
множителя
2π
является числом Уомерсли. Гра-
p
A
=
,
u
=
Ar
(5)
ничные условия (2) примут вид
2
p
r
2
U
r=ξ
=
0,
Из имеющихся исходных данных можно со-
(12)
U
=
0.
ставить еще одну величину, имеющую размер-
r
=1
ность скорости и равную
В выражениях (11) и (12) введено обозначение
ν
r
1
ξ=
(13)
u
ν
=
(6)
r
r2
2
Таким образом, уравнение (10) с периодиче-
Обезразмерить скорость можно с использова-
скими функциями U и P с граничными условиями
нием как uP (5), так и uv (6). В рассматриваемом
(13) рассматриваем на отрезке [ξ, 1] в промежутке
случае нас интересует влияние частотных и гео-
времени [0, 1].
метрических факторов, поэтому положим
Решение уравнения (10). Применим метод Фу-
рье для разделения переменных [12]. Найдем не-
u
u′ =
(7)
обходимые для дальнейшего собственные функ-
u
P
ции оператора вязкости
Опуская штрихи у всех переменных, кроме u,
1
∂
∂
u
n
2
−
r
=λ
un n
(14)
приводим уравнение (1) в результате замен (3) и
r∂r
∂r
(7) к следующему виду:
Общим решением уравнения (14) будет функ-
ция
2
r
2
∂u′
1
∂
∂ ′ r
2
u
P
=
r
+
P t)
(8)
un = bnJ0(rλn) + cnY0(rλn).
(15)
(
)
ν
t
P
∂t
r
∂r
∂
r
ν
В уравнении (15) bn и cn - произвольные кон-
Уравнение (8) показывает целесообразность
станты, J0(x) и Y0(x) - цилиндрические функции.
еще одной замены:
Граничные условия (12) с учетом уравнения (15)
приводят к алгебраической системе
u
′ν
U
=
(9)
ru
b
n
J
0
(
ξλ
n
)
+
c
n
Y
0
(ξλ
n
)
=
0,
2
P
(16)
b
J
(
λ
)
+
c
Y
(
λ
)
=
0.
n
0
n
n
0
n
В результате замены (9) уравнение (8) приво-
дится к виду
Для того, чтобы однородная система уравнений
имела нетривиальное реше-
с неизвестными bn и cn
2
∂U
1
∂
∂
U
β
=
r
+
P t)
(10)
(
)
ние, ее детерминант должен равняться нулю. Это
∂t
r∂r
∂r
условие дает характеристическое уравнение, из ко-
В уравнении (10) обозначено:
торого можно найти собственные значения λn:
J
0
(
ξ
λ
n
)
Y
0
(ξλ
n
)
X
(λ
n
,ξ)
=
=
J
0
(ξλ
n
)Y
0
(λ
n
)
−
J
0
(
λ
n
)Y
0
(
ξ
λ
n
)
=
0.
(17)
J
(
λ
)
Y
(λ
)
0
n
0
n
Ниже везде при вычислении числовых значе-
Корни уравнения (17) легко находятся с помо-
ний будем полагать r2 = 0.01. График характери-
щью метода Ньютона, который в рассматривае-
стической функции X(λ,ξ) представлен на рис. 3.
мом случае выражается итерационной формулой
БИОФИЗИКА том 67
№ 1
2022
НЕИНВАЗИВНЫЙ ПОДХОД В ГИДРОДИНАМИКЕ
153
Рис. 3. График характеристической функции при r1 =
Рис. 4. Собственные функции вязкостного оператора.
= 0.0075 м.
k+1
k
1
d
X
(λ,ξ)
λ
n
=λ
n
−
,
k
=
0, 1, 2, 3
(18)
X
(λ
,ξ)
dλ
k
n
λ=λ
n
Приведем несколько первых собственных зна-
1
2
2
чений для ξ = 0.7:
u
=
ru
(r)
dr =
n
n
ξ
(25)
λ1 = 12.5533, λ2 = 25.1261, λ3 = 37.6947,
2
1
2
λ4 = 50.2622, λ5 = 62.8292.
(19)
=
- ξ
[
Y
0
(λ
n
)J
1
(λ
n
ξ)
−
J
0
(λ
n
)Y
1
(λ
n
ξ)]2
2
π2λ
2
n
В нулях характеристической функции из урав-
На рис. 4 представлены несколько первых
нений (16) имеем
нормированных собственных функций для r1 =
0.0075 м.
c
J
(ξλ
)
J
(λ
)
n
0
n
0
n
−
=
=
(20)
По определению ортонормированных функ-
b
n
Y
0
(ξλ
n
)
Y
0
(λ
n
)
ций, справедливо равенство
Из выражения (20) следует, что коэффициен-
1
ты bn и cn можно выбрать по формуле
U
n
=
(
U
n
,U
n
)
=
n
rU r)2
d
r
=
1.
(26)
ξ
b
n
=Y
0
(λ
n
),
c
n
= -J
0
(
λ
n
)
(21)
После нахождения ортонормированных соб-
С учетом выражений (21) формула (15) запи-
ственных функций (24) дальнейший ход решения
шется в виде
совпадает со стандартной процедурой этого мето-
да (см. работу [12]). Представим решение в виде
n
u r)
=Y
0
(λ
n
)J
0
(rλ
n
)
−J
0
(
λ
n
)
Y
0
(rλ
n
)
(22)
разложения в ряд Фурье по системе ортонорми-
рованных собственных функций с коэффициен-
Сравнивая уравнения (22) и (17), видим, что
тами, зависящими от числа Фурье:
после нахождения собственных чисел λn соб-
∞
ственные функции можно выразить через харак-
U
(
r
,
τ)
=
d
n
(τ)U r)
n
(27)
теристическую функцию
n=1
un(r) = X(λn,r).
(23)
Подставляя выражение (27) в уравнение (10) и
учитывая соотношение (14), получим
Определим ортонормированные собственные
∞
функции в соответствии с выражением
2
∂
d
2
n
β
+λ
d
U
(r)
=
P
(τ
)
(28)
n n
n
n=1
∂
τ
u
n
(
r
U
(r)
=
).
(24)
n
Умножая уравнение (28) на rUn(r) и интегрируя
u
n
на отрезке (0,1), получаем
Используя уравнение (22), вычислим норму
1
2
∂d
n
2
собственной функции
u
, входящей в выраже-
β
+λ
d = p
P
(τ)
,
p
=
(1,
U
)
=
rU r.
(29)
n
n n
n
n
n
n
ние (24):
∂τ
ξ
БИОФИЗИКА том 67
№ 1
2022
154
ЗВЕРЕВ, ТОКАРЕВ
Вычисления приводят к следующей формуле:
2{2
+ πλ
n
ξ
[
J
0
(λ
n
)Y
1
(λ
n
ξ)
−Y
0
(λ
n
)J
1
(λ
n
ξ)]}
p
n
=
(30)
2
2
2
2
2
λ
n
4
−π
λ
n
ξ
{
[
J
0
(λ
n
)Y
0
(λ
n
ξ)
−
Y
0
(λ
n
)J
0
(λ
n
ξ)]
+
[
J
0
(
λ
n
)
Y
1
(
λ
n
ξ)
−
Y
0
(λ
n
)J
1
(λ
n
ξ)]
}
При получении уравнения (29) было исполь-
давлении P(τ), являются число ξ, однозначно
зовано соотношение
(26). Общим решением
определяющее множество значений λn, и число
уравнения (29) будет функция
Уомерсли α.
2
2
λ
n
λ
n
Как было сказано выше,
τ
τ
-
τ
p
n
β
β
d
(τ)
=
e
P(
)
τ τ+ g
e
(31)
P(τ) = sin(2πτ).
(35)
n
2
n
0
β
Тогда выражение (34) для Dn(τ) примет вид
Неизвестную константу gn в уравнении (31)
2
sin
(
2
πτ - ψ
)
найдем из условия периодичности решения по
n
β
D
(τ)
=
;
ψ
=
arctg
2
(36)
n
n
π
времени:
4
λ
n
λ
n
2
+
4
π
d
(0)
=d
(τ
)
(32)
n
n
0
β
Подставляя в условие (32) выражение (31), по-
Величина ψn в выражении (36) является сдви-
лучим
гом по фазе n-й гармоники скорости ликвора по
2
λ
отношению к фазе давления. Из выражения (36)
1
n x
p
n
β
видно, что этот сдвиг монотонно убывает и мак-
g
=
e
P x)dx
(33)
n
2
λ
n
0
симален для n = 1. Формула для безразмерной
2
β
скорости принимает вид
α
e
−
1
∞
∞
1
U
(r,τ
)
=
d
(τ)U r)
=
p
D
(τ)U
(r)
(37)
n
n
2
n
n
n
Подставляя выражение (33) в уравнение (31),
n=1
β
n=
1
получим окончательное выражение для dn(τ):
Размерная скорость, зависящая от размерных
2
времени и радиуса, определится с учетом уравне-
p
(1
−ξ)
n
d
n
(τ)
=
D
n
(τ)
=
p
n
D
n
(τ);
ния (11) соотношением
2
2
β
α
2
(34)
2
λ
u
n
τ
P
r
t
2
1
2
u(
r
,
t
)
=
U
,
(38)
λ
β
λ
n
τ
e
P
τ
d
τ
−
n
τ
u
r
t
τ
(
)
ν
2
p
β
0
β
D
n
(τ)
=
e
P
(τ)
d
τ+
2
e
0
λ
n
Вычислим, используя соотношение (38), рас-
β
ход ликвора и размерную среднюю скорость, пе-
e
−1
реходя к безразмерному радиусу r → r2r′ в соответ-
Из формул (27), (30) и (34) следует, что пара-
ствии с уравнением (3), подставляя формулу (37)
метрами, влияющими на скорость при заданном
и применяя уравнение (29):
2
r
r
2
2
2
1
u
2
u
P
r
P
Q
=
2
π
rudr
=2
π
r
U
,
τ
dr
=
2πr
rU
(
r
,
τ
)dr
=
2
u
r
u
1
r
r
1
ν
2
ν
ξ
1
∞
∞
1
2
2
2
2
u
P
1
r
2
u
P
1
=
2π
r
r
p
D
(τ)U r)
dr
=
2π
p
D
(τ)
rU r)
dr
=
2
2
n
n
n
2
n
n
n
u
ν
β
ξ
n
=1
u
ν
β
n=1
ξ
(39)
2
2
∞
r
u
1
2
2
P
=
2
π
D
(τ)
p
,
2
n
n
u
β
ν
n
=1
2
∞
2
2
u
P
1
1
−ξ
2
u =Q
π
(
r
2
−
r
1
)
=
2
D
n
(
τ
)
p
n
2
uν
α
1
+ξ
n
=1
БИОФИЗИКА том 67
№ 1
2022
НЕИНВАЗИВНЫЙ ПОДХОД В ГИДРОДИНАМИКЕ
155
Полученные формулы (39) дают решение ис-
Для коэффициента p1 в формуле (30) в случае,
ходной задачи, но являются сложными для ис-
когда значение ξ близко к единице, справедлива
пользования. Их упрощение возможно в случае,
следующая формула:
когда значение ξ близко к единице, то есть когда
3
кольцевой канал по форме приближается к плос-
p
=
1−ξ
(42)
1
2
кому каналу. В этом случае, раскладывая характе-
Используя формулу (40) для D1(τ) и значение
ристическое уравнение (17) в ряд Тейлора в точке
сдвига по фазе из формулы (36), получаем следу-
ξ = 1 и оставляя только первые три члена, нахо-
ющее выражение:
дим, что первое собственное значение можно
приблизить формулой
2
α
π
2
D
(τ)
≈
sin
2πτ -
arctg
α
(43)
1
(
(
))
2
4
3
2 9
+
4π
α
λ
=
6 .
(40)
1
Формула (36) показывает, что функции Dn(τ)
1-ξ
быстро убывают с ростом n, поэтому для получе-
При ξ → 1 первая собственная функция долж-
ния приближенных оценок ограничимся первым
членом ряда в формуле (37):
на быть квадратичной, обращаться в нуль на
стенках и удовлетворять условию (26). Эти усло-
3 10
2
sin(2πτ - ψ
n
вия приводят к выражению
U
(r,τ)
≈
α
)(r
−ξ)(1−
r)
(44)
4
2
4
9
+
π
α
Беря первые члены рядов (39) и используя
30
U r)
=
(r -ξ)(1 −r)
(41)
1
5
формулы (42) и (43), вычислим приближенные
(1-ξ)
2
значения средней скорости и расхода:
2
2
π
2
3u
(1 −ξ)
1
P
= A
sin
2πτ -
arctg
α
;
A
=
;
(
(
))
2
4
3
4
1+ξ
uν
9
+
4π
α
(45)
2
2
2
2
2
r
u
(1
−ξ)3
π
3
2
P
Q
=
A
sin
2πτ -
arctg
α
;
A
=π
(
r
−
r
)
A
= π
Q
(
(
))
Q
2
1
u
3
4
4
uν
9
+4π2α
где
A
и
A
- амплитуды расхода и средней ско-
и по формуле (45) вычисляем A . После этого ве-
Q
u
Q
рости соответственно. Ликвор движется по кана-
личина
A
в любом сечении со своим значением
u
лу с меняющимся внутренним радиусом r1 или,
ξ определяется из соотношения
по другому, параметром ξ, но величина
A
в лю-
Q
2
2
A
= A
π(1
−ξ
)
r
(46)
бом сечении при этом остается постоянной, по-
Q
2
скольку ликвор является несжимаемой жидко-
Сделаем числовые оценки и построим графи-
стью. Поэтому способ определения амплитуды
ки изменения ключевых величин. Амплитуду гра-
средней скорости
A
в любом сечении заключа-
u
диента давления, присутствующую в уравнении
ется в следующем. Берем относительно протя-
(4), опираясь на работу [13] приближенно поло-
женный участок канала с известным градиентом
жим равной 0.025 мм рт.ст./см. Это позволяет вы-
давления, определяем up, используя формулу (5),
числить
∂
p
1
2
A
=
1max
=
(0.025* 133.3224 *
100)
=
0.333м/c
,
u
=
Ar
=
0.0577м/c.
p
2
ρ
∂
z
1000
Период пульсаций давления tP = 1 с для вели-
ко от внутреннего радиуса и времени. Формулы
(45) дадут значения амплитуд средней скорости и
чины пульса 60 уд./мин. Везде ниже полагаем v =
расхода.
10-6 м2/с, r2 = 0.01 м. В этих условиях число Уо-
Рассмотрим характер изменения скорости
(r
2
−
r
1
)
r
2
(1 −ξ
)
ликвора в зависимости от радиуса и времени при
мерсли
α =
=
=
10
(1 −ξ)
Под-
нескольких значениях внутреннего радиуса r1, от
νt
P
νt
P
ставляя это в формулы (30), (36) и (37), получаем
которого зависит величина α, оставляя r2 посто-
формулы для скорости ликвора, зависящей толь-
янным. Покажем также график изменения сред-
БИОФИЗИКА том 67
№ 1
2022
156
ЗВЕРЕВ, ТОКАРЕВ
Рис. 7. Профили скорости для нескольких моментов
Рис. 5. Зависимость скорости ликвора в различных
времени при r1 = 0.0075 м.
точках канала от времени при r1 = 0.0075 м.
нормированный градиент давления uPP(t), опре-
ней скорости во времени. Чтобы наглядно проде-
монстрировать отставание фазы скорости ликво-
деляемый формулами (5) и (35).
ра от фазы градиента давления, покажем также на
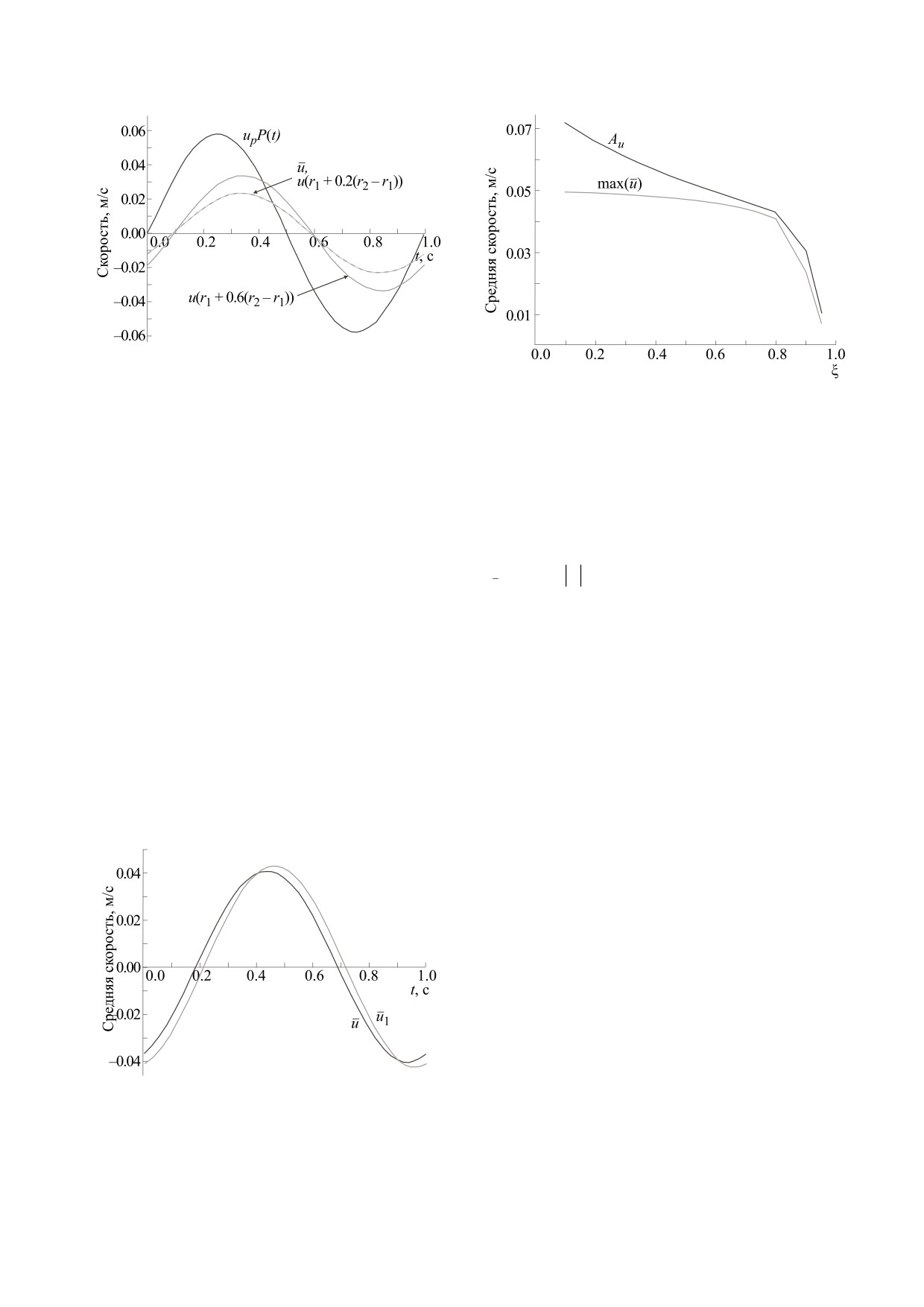
Рис. 5 показывает, что скорости в значительно
графике соизмеримый со скоростью ликвора отстоящих друг от друга точках канала довольно
близки и близки к средней скорости. Величина
uPP(t) носит тот же характер, хотя имеет место
значительное отставание по фазе. На рис. 6 пред-
ставлены профили скорости для нескольких мо-
ментов времени, которые вблизи стенок канала и
в его центре могут быть направлены в разные сто-
роны.
Из рис. 7 видно, что при приближении внут-
реннего радиуса к значению r1 = 0.0080 м форма
профилей скорости приближается к параболиче-
ской.
На рис. 8 представлены профили скорости при
дальнейшем увеличении внутреннего радиуса,
соответствующем r1 = 0.0090 м.
Видим, что профили скорости принимают
форму, близкую к профилю Пуазейля, для любых
моментов времени. Посмотрим на изменение
скорости во времени для различных точек сече-
Рис. 6. Профили скорости для нескольких моментов
Рис. 8. Профили скорости для нескольких моментов
времени при r1 = 0.0060 м (а) и r1 = 0.0075 м (б).
времени при r1 = 0.0090 м.
БИОФИЗИКА том 67
№ 1
2022
НЕИНВАЗИВНЫЙ ПОДХОД В ГИДРОДИНАМИКЕ
157
Рис. 9. Зависимость скорости ликвора в различных точ-
ках канала от времени при r1 = 0.0090 м.
Рис. 11. Сравнение амплитуд средних скоростей, вы-
численных по точной и приближенной формулам в диа-
ния. График изменения скорости ликвора в двух
пазоне 0.1 ≤ ξ ≤ 0.95.
точках в зависимости от времени, а также средняя
скорость
u
и величина uPP(t) для r1 = 0.0090 м
На рис. 11 представлены графики величин
A
,
представлены на рис. 9.
представляющих собой амплитуду приближен-
Рис. 9 показывает, что в любой момент време-
ной средней скорости (45) и максимальные зна-
ни скорости по всему сечению канала имеют
чения
средней
скорости
за
период
один знак, то есть всегда направлены в одну сто-
рону для всех точек сечения канала. Кроме того,
A
=
{
max(u
),0
≤τ ≤1
}
, где
u
- точное значе-
u
величины скоростей стали существенно меньше
ние средней скорости, определяемой по
величины uPP(t) и заметно уменьшилось отстава-
формуле (39).
ние по фазе по сравнению с рис. 5. Объясняется
это возрастанием сил вязкости по сравнению с
Вычисления делали в точках r1 = 0.0012, 0.0016,
силами инерции.
0.0075, 0.0080, 0.0090 и 0.0095 м, затем проводили
На рис. 10 представлено сравнение средней
линейную интерполяцию. Видно, что прибли-
скорости, вычисленной по точной формуле (39) и
женная формула (45) дает неплохое совпадение с
по приближенной формуле (45) для r1 = 0.0075 м
точной формулой (39) для 0.6 ≤ ξ ≤ 0.8. Интерес-
на протяжении периода. Видим, что имеет место
но, что вплоть до значения ξ ≈ 0.75 амплитуда
хорошее совпадение как по фазе, так и по моду-
средней скорости, вычисленная как амплитуда
лю. Интересно также сравнить амплитуды сред-
точного решения, даваемого формулой (39), на
них скоростей, вычисленных по точной и при-
промежутке времени, равном периоду, меняется
ближенной формулам.
слабо. И лишь при значениях ξ > 0.8 начинается
крутое падение. Данное сравнение имеет своей
целью оценку точности приближенного реше-
ния, но не имеет отношения к реальному движе-
нию ликвора в спинальной полости, где при ме-
няющихся по длине соотношениях внутреннего и
внешнего радиусов сохраняется постоянство рас-
хода.
Чтобы получить значения амплитуды скоро-
сти во всех сечениях позвоночника, сначала нуж-
но по приведенным формулам вычислить ампли-
туду скорости на относительно протяженном
участке позвоночника с известными перепадом
давлений и радиусами, определяющими значение
ξ0, и затем для остальных участков позвоночника
воспользоваться соотношением, вытекающем из
Рис. 10. Сравнение за период средних скоростей, вы-
численных по точной и приближенной формулам при
постоянства расхода в любом сечении позвоноч-
r1 = 0.0075 м.
ника
БИОФИЗИКА том 67
№ 1
2022
158
ЗВЕРЕВ, ТОКАРЕВ
Гидродинамические параметры и числа Уомерсли расчетной модели
r1, м
α
A
,
м/с
u
A
u
,
м/с
0.0012
8.8
0.0191
0.0200
0.0016
8.4
0.0194
0.0201
0.0025
7.5
0.0201
0.0210
0.0050
5.0
0.0251
0.0260
0.0075
2.5
0.0431
0.0450
0.0080
2.0
0.0524
0.0550
0.0090
1.0
0.0990
0.1030
0.0095
0.5
0.1930
0.2020
2
и 7. В этом случае вычисления необходимо про-
1−ξ
0
A
u
(ξ)
=
A
u
(ξ
0
)
(47)
водить по точной формуле (39). На самых широ-
2
1-ξ
ких участках большого затылочного отверстия и
L2 течение имеет также сложный профиль. При
В таблице представлены числовые значения
амплитуд средней скорости, определенные по
этом в некоторые моменты времени в разных точ-
ках сечения скорости ликвора противоположны,
точной и приближенной формулам для значения
что на практике означает его большее перемеши-
ξ ≈ 0.75, а также для вычисленного выше значения
вание. Несмотря на сложные профили скорости
A = 0.333 м/с2, отражающего перепад давлений на
при определенных параметрах, средняя скорость
участке определенной длины и пересчитанных
ликвора не превышает 0.1 м/c, и оценка числа
затем для остальных значений r1 по формуле (47).
Рейнольдса показывает, что течение остается ла-
минарным.
ВЫВОДЫ
КОНФЛИКТ ИНТЕРЕСОВ
Значения скоростей, приведенные в нашей
таблице, имеют хорошее совпадение с величина-
Авторы заявляют об отсутствии конфликта
ми, представленными в работе [8]. Это позволяет
интересов.
на основе предложенной модели, а также экспе-
риментального определения расхода и попереч-
ного сечения с помощью магнитно-резонансной
СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ
томографии фазового контраста, вычислить ско-
Настоящая работа не содержит описания ис-
рость потока в любом позвоночно-двигательном
следований с использованием людей и животных
сегменте. Экспериментальное изучение показы-
в качестве объектов.
вает, что в случае патологий канал спинальной
полости всегда сужается. Использование полу-
ченных в работе соотношений позволяет опреде-
СПИСОК ЛИТЕРАТУРЫ
лить влияние этого факта на гидродинамику
ликвора.
1. И. А. Егорова, Краниальная остеопатия (СПбМА-
ПО, СПб, 2006).
Для грудного отдела примерными параметра-
2. М. Керн, Мудрость тела («Сударыня», СПб,
ми являются следующие: α ≤ 7.5, r2 ~ 0.0075 м, r1 ~
2006).
0.0012 м. При этих параметрах скорости ликвора
3. M. Czosnyka, Z. Czosnyka, Sh. Momjian, and
можно вычислить по приближенным формулам
J. D. Pickard, Physiol. Meas. 25 (5), R51 (2004).
(45). Профиль скорости в момент достижения
4. N. Alperin, M. Mazda, T. Lichtor, and S. H. Lee,
максимального расхода ликвора напоминает про-
Curr. Med. Imaging Rev. 2 (1), 117 (2006). DOI:
филь Пуазейля (стационарное течение в кольце-
10.2174/157340506775541622
вом канале). Для шейного и поясничного отде-
5. Ю. Е. Москаленко, Г. Б. Вайнштейн, Н. А. Рябчи-
лов, где инерция движения ликвора играет боль-
кова и др., Региональное кровообращение и мик-
шую роль, что соответствует значениям α > 7.5,
роциркуляция 9 (3), 43 (2010).
r2 ~ 0.0090 м, r1 ~ 0.0050 м, профиль скорости ста-
6. L. M. Levy and G. Di Chiro, Neuroradiology 32, 399
новится более сложным, как показано на рис. 6
(1990).
БИОФИЗИКА том 67
№ 1
2022
НЕИНВАЗИВНЫЙ ПОДХОД В ГИДРОДИНАМИКЕ
159
7. Остеопатия: учебник для медицинских вузов, под
10. Г. П. Бургман и Т. Н. Лобкова, Исследование спи-
ред. Т. И. Кравченко (СпецЛит, СПб, 2014), т. 1,
номозговой жидкости («Медицина», М., 1968).
сс. 334-335.
11. В. И. Решетилов, Вопросы нейрохирургии, № 6,
8. F. Loth, M. A. Yardimci, and N. Alperin, J. Biomech.
45 (1982).
Eng. 123 (1), 71 (2001). DOI: 10.1115/1.1336144
12. В. С. Владимиров и В. В. Жаринов, Уравнения
9. Ю. Е. Москаленко, Г. Б. Вайнштейн, П. Хальвор-
математической физики (Физматлит, М., 2004).
сон и др., Региональное кровообращение и мик-
13. N. J. Alperin, S. H. Lee, F. Loth, et al., Radiology 217
роциркуляция 9 (2), 18 (2010).
(3), 877 (2000).
Noninvasive Approach in the Hydrodynamics of the Cerebrospinal Fluid
in the Spinal Cavity Spine
A.G. Zverev and U.N. Tokarev
Nuclear Safety Institute, Russian Academy of Sciences, Bolshaya Tulskaya ul. 52, Moscow, 115191, Russia
A convenient method for the analytical calculation of the flow speed and mass flow rate of the cerebrospinal
fluid in model of the spinal cavity, depending on the patients pulse is suggested. Velocity values and velocity
profiles are provided, which allows using them for real spine calculation. These estimates allow a more infor-
mative description of the diagnosis of spinal pathology.
Keywords: cerebrospinal fluid, liquor, velocity profile, Womersley number
БИОФИЗИКА том 67
№ 1
2022