БИОФИЗИКА, 2022, том 67, № 1, с. 174-182

БИОФИЗИКА СЛОЖНЫХ СИСТЕМ

УДК 577.3

МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИЙ НА НЕОДНОРОДНОМ

АРЕАЛЕ: ИНВАЗИЯ И МУЛЬТИСТАБИЛЬНОСТЬ

*Донской государственный технический университет, 344000, Ростов-на-Дону, пл. Гагарина, 1

**Южный федеральный университет, 344006 г. Ростов-на-Дону, ул. Большая Садовая, 105/42

E-mail: a_v_budyansky@mail.ru

Поступила в редакцию 29.04.2021 г.

После доработки 08.10.2021 г.

Принята к публикации 12.10.2021 г.

Моделируется взаимодействие двух популяций на основе эволюционных уравнений, учитывающих

диффузию, таксис и логистический рост. Рассмотрены сценарии конкуренции в условиях биологи-

ческой инвазии с учетом неоднородности ареала. Для прогнозирования инвазии предложен подход,

основанный на анализе структуры пространства параметров с учетом косимметрии модели. В этом

случае возникает мультистабильность - семейство устойчивых стационарных распределений ви-

дов. Популяционные сценарии при нарушении косимметрии изучены при помощи вычислитель-

ного эксперимента. Для параметров диффузии и роста, удовлетворяющих условиям косимметрии,

определена структура разбиения плоскости параметров таксиса на шесть зон, соответствующих воз-

можным сценариям (выживание отдельных видов и их сосуществование). При изменении одного

из параметров роста структура разбиения плоскости сохраняется, но деформируются границы зон.

В случае значительного отклонения параметра роста от условия косимметрии возможно возникно-

вение дополнительных зон сосуществования видов.

Ключевые слова: популяционная динамика, инвазия, уравнения диффузии-таксиса-реакции, косиммет-

рия, метод прямых.

DOI: 10.31857/S0006302922010197

Проблема инвазии биологических видов имеет

мерные вопросы об определении областей пара-

важное социально-экономическое значение.

метров, для которых могут реализовываться

Виды-вселенцы могут существенно влиять на

различные популяционные сценарии, и каче-

экологическое равновесие, конкурируя с абори-

ственном анализе процессов, приводящих к сов-

генными видами и вытесняя их [1-4]. Для изуче-

местному существованию и исчезновению видов.

ния угроз нежелательных инвазий и управления

процессами инвазии необходима разработка ин-

В данной работе рассматривается система не-

струментов прогнозирования динамики экоси-

линейных уравнений, описывающая динамику

стем [5, 6]. Натурные эксперименты в этом случае

двух популяций, конкурирующих за неоднородно

затруднительны, а порой и опасны, что делает ак-

распределенный ресурс. Одна популяция - або-

туальным разработку и исследование моделей по-

риген или резидент, занимающий экологическую

пуляционной динамики. При этом важны как ис-

нишу, а другая - инвайдер или вселенец. Модель

следования, ориентированные на описание кон-

учитывает диффузионное распространение ви-

кретных экосистем, так и построение и анализ

дов, направленную миграцию вследствие неодно-

моделей, в которых учитываются ключевые про-

родности ресурса (емкости среды) и локальный

цессы популяционной динамики.

рост логистического типа. Особое внимание уде-

Актуальным является исследование задач, в

ляется исследованию мультистабильности - воз-

которых существенны эффекты диффузии, так-

можности реализации различных сценариев ди-

сиса (направленной миграции) и конкуренции за

ресурсы [7-9]. Используемые при этом системы

намики популяций, в том числе в виде непрерыв-

уравнений, как правило, нелинейны и содержат

ного семейства стационарных распределений

много параметров. При этом возникают законо-

сосуществующих видов [10-12].

174

МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИЙ

175

МАТЕМАТИЧЕСКАЯ

длины a: Ω = [0,a]. Уравнения баланса плотно-

И ВЫЧИСЛИТЕЛЬНАЯ МОДЕЛИ

стей популяций u(x,t) и v(x,t) записываем анало-

Рассматривается пространственно-временное

гично работам [11, 12], используя миграционные

взаимодействие двух видов на одномерном ареале потоки q_i и локальное взаимодействие:

∂u

∂q

∂u

∂p

u + v

+η

=-k

+α

1−

(1)

∂t

∂x

∂v

∂q

∂v

∂p

+η

=-k

+α

(2)

∂t

∂x

Миграционные потоки q₁ и q₂ учитывают диф-

u(x,0) = u⁰(x), v(x,0) = v⁰(x).

(4)

фузионное распространение и направленную ми-

Для численного решения задачи (1)-(4) при-

грацию - таксис, который определяется неравно-

меняется метод прямых с дискретизацией на ос-

мерностью распределения емкости среды p(x).

нове смещенных сеток аналогично описанному в

Относительные плотности, емкость среды

работе [12]. По переменной x вводится равномер-

(carrying capacity) в современной литературе на-

ная сетка: +1, h = a/n. Плотности распределения

зывают также ресурсом [2].

популяций в узле x_r далее обозначаются через u_r и

В формулах (1) и (2) k₁ и k₂ являются диффузи-

v_r. Для вычисления потоков q_i применяется сме-

онными коэффициентами, а α₁ и α₂ - коэффици-

щенная сетка: xr+1/2 = -h/2 + rh, r = 1, 2, …, n.

ентами направленной миграции. Изменение

плотности популяций определяется логистиче-

По пространственным переменным вводится

ским законом с параметрами роста η₁ и η₂. Далее

разностный оператор первого порядка на двухто-

чечном шаблоне и оператор вычисления сред-

под аборигеном понимается популяция u(x,t), а

него:

популяция v(x,t) является инвайдером.

На границе ареала Ω = [0,a] ставятся условия

−ω

+ω

r+1

(

dω)

(δω)

отсутствия потоков:

r+12

q₁(0,t) = q₁(a,t) = q₂(0,t) = q₂(a,t) = 0.

(3)

В результате аппроксимации уравнений (1)-

Система уравнений (1)-(3) дополняется на-

(2) на основе интегро-интерполяционного мето-

чальными распределениями плотностей популя-

да [13] получается следующая система обыкно-

ций:

венных дифференциальных уравнений:

∂u

[

−dq

+η

]

(5)

∂t

∂v

[

−dq

+η

]

0,,

(6)

∂t

−1

r +

1/2





dxdy

0,r

1−

= 



(7)



p(x)



r -

1/2



Потоки qi,r-1/2 (r = 1, …, n) вычисляются по

u_r = u⁰(x_r), v_r = v⁰(x_r).

(10)

следующим формулам:

(q₁)r-1/2 = [-k₁du + α₁dpδu]r-1/2, (q₂)r-1/2 =

КОСИММЕТРИЯ

= [-k₂du + α₂dpδu]r-1/2.

(8)

И МУЛЬТИСТАБИЛЬНОСТЬ

Принцип Гаузе [14] утверждает, что невозмож-

Дискретные аналоги краевых условий записы-

но устойчивое сосуществование двух популяций,

ваются с применением законтурных узлов:

если рост ограничен одним жизненно важным ре-

qi,-1/2 = qi,1/2; qi,n+1/2 = qi,n-1/2, i = 1, 2.

(9)

сурсом. Однако в работе [11] было показано, что

при определенных соотношениях на параметры

Из уравнения (4) получаются начальные усло-

системы (1)-(4) наблюдается сильная неедин-

вия для выражений (5)-(9):

ственность решений сосуществующих видов.

БИОФИЗИКА том 67

№ 1

2022

176

БУДЯНСКИЙ, ЦИБУЛИН

При этом сама модель относится к классу косим-

будет являться косимметрией системы (1)-(4)

метричных динамических систем [15], для кото-

при выполнении следующих соотношений на па-

рых возможно возникновение непрерывных се-

раметры:

мейств стационарных состояний. Для уравнения



= γ

(11)

косимметрия

представляет собой

нетривиальный оператор, который ортогонален F

В этом случае задача имеет континуальное се-

в каждой точке фазового пространства [16]. В ра-

мейство устойчивых стационарных решений, ко-

боте [11] было доказано, что вектор-функция

торое может быть параметризовано следующим

образом:

L = M(γv,-u)^T, M = exp(-a₂p/k₂)

u = (1- θ)w,

=θw,

θ∈

[0,1],

(12)

где w - решение краевой задачи

′



w

w′-α

wp′

+η

1−

w′-α

wp′

(13)

[

]





0,a



p

Данный факт устанавливается подстановкой

S(Y)= -(Q(Y, ε), L(Y)), где L - косимметрия век-

выражений (12) в исходную систему уравнений

торного поля F, а Q(Y, ε) - возмущение системы,

(1)-(3) с учетом соотношений (11) и (13). При

причем Q(Y, ε) = 0. Селективное уравнение на се-

этом у каждого члена косимметричного семей-

мействе Y(θ) ∈ [0,1] дается равенством S(Y(θ)) = 0

ства, характеризуемого индивидуальным соотно-

и автоматически выполняется при ε = 0.

шением плотностей видов на ареале, существует

Гипотеза. Для системы (1)-(4) существуют не

своя область начальных данных, из которых дан-

удовлетворяющие условиям косимметрии

(11)

ное решение реализуется.

наборы параметров, при которых наблюдается

Выполнение всех условий (11) является доста-

мультистабильность.

точно редким явлением при моделировании ре-

Для анализа данного предположения приме-

альных процессов. Это означает идеальную ситу-

няется вычислительный эксперимент и подход на

ацию сосуществования видов при любых их ком-

основе [15]. Используются два параметра возму-

бинациях. Анализ условий, при которых

щения: коэффициенты роста и миграции популя-

происходит распад семейства, позволяет лучше

ции v, нарушающие условия (11):

понять динамику системы. Для этого применяет-

ся подход, основанный на теории косимметрич-

= γη

+ε,

= γα

+δ

(14)

ного дефекта и понятии селективной функции

[15]. Для дифференциального уравнения Y =

Звездочками обозначены параметры с учетом

= F(Y) + Q(Y,ε) в гильбертовом пространстве H

возмущений. Тогда косимметричный дефект да-

косимметричный дефект определяется формулой

ется формулой



∂q



∂q







∂v

∂p

-

+ηuf

Mγv

−

+η

uf Mudx,

+α







∂x





∂x



∂x

В результате интегрирования по частям и учета краевых условий дефект D записывается в виде:

(k

u′

−α γ(up′

M′v+Mv′)

+ηuMvγf

v′

−α

vp′

M′u+Mu

′)

−η

Muvf

dx

(15)





(

)(



С учетом условий на коэффициенты (11) имеем



α

p′u





δvp′

−

u′ -ε

uvf

M dx

(16)

















После подстановки параметризованного семейства решений (12) получается селективная функция,

зависящая от параметров ε и δ:

БИОФИЗИКА том 67

№ 1

2022

МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИЙ

177



α

p′w







S(θ)

=θ(1−θ)

M δwp′

−

w′ -εw

1−

(17)

















p

Нулями селективной функции являются θ = 0

с одним параметром ε. Тогда при ε = 0 также по-

и θ = 1, отвечающие выживанию одной из попу-

лучается S(θ) = 0. Формально обращение в ноль

ляций. Если параметры ε и δ связаны соотноше-

функции (17) соответствует трансформации в но-

нием δ = με, то получается селективная функция

вое семейство решений, по крайней мере, при

dε

dδ

δ=0

(18)

α





w

p′

−

ww′p′dx,I

−

dx,











k





p

В вычислительных экспериментах было уста-

лой, соответствующей случаю ареала с одной бла-

новлено, что имеются наборы значений ε и δ

гоприятной зоной:

,η

при которых реализуются распределения

(

)



πx

сосуществующих популяций.

p x)

3 sin

0.1.





Начальное распределение популяции u (абориге-

РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНОГО

на) отвечает полному заполнению экологической

ЭКСПЕРИМЕНТА

ниши при отсутствии направленной миграции

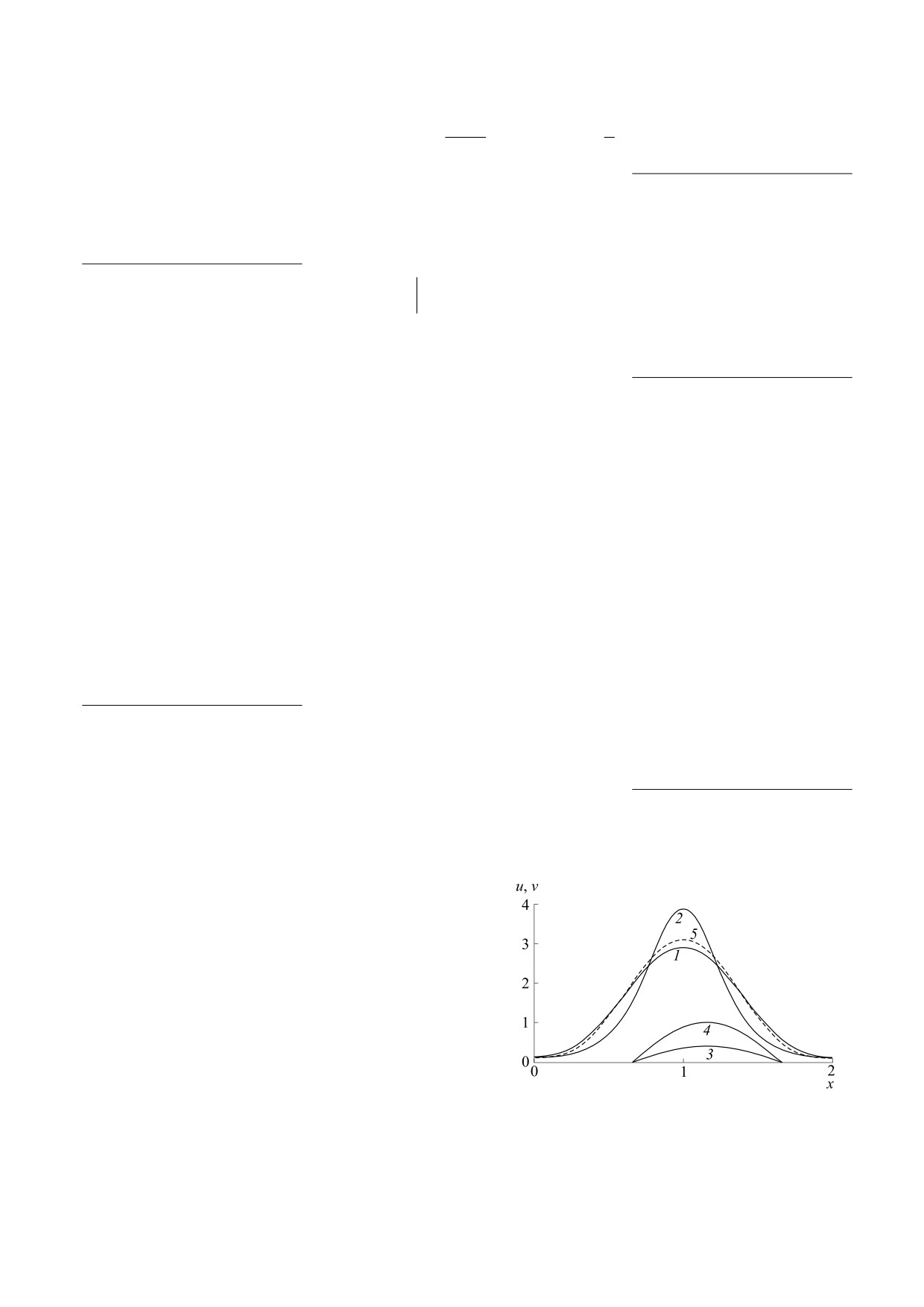
(α₁ = 0) и при ее наличии (α₁ = 0.06), см рис. 1. В

Далее представлены результаты расчетов ди-

намики популяций на ареале Ω = [0, 2], (a = 2).

работе [17] было показано, что миграция, вызван-

Вычисления проводили для различных значений

ная неравномерностью ресурса, влияет на запол-

параметров миграции α₁ и α₂, коэффициента ро-

няемость ареала, и установлено существование

оптимального значения миграционного парамет-

ста η₂ и при следующих фиксированных парамет-

ра, при котором наблюдается наибольшая плот-

рах: коэффициентов диффузии k₁ = 0.03, k₂ = 0.04

ность на ареале. Начальные распределения попу-

и роста η₁ = 3. Таким образом в соотношении (11)

ляции v (инвайдера) были локализованы и отли-

γ = k₁/k₂ = 3/4, а функция ресурса дается форму-

чались концентрацией вторжения:



2π



2π

0.6sin

∈Ω

sin

∈Ω

v x)

)

(19)





∈Ω

[

0.66;1,66

]

;



∈Ω

Стоит отметить, что для любых комбинаций

практически нулевые собственные значения.

начальных распределений u и v выполняется не-

Остальные собственные значения находятся в ле-

равенство

pdx

≤

Это приводит к



конкурентной борьбе видов на начальном этапе

динамического процесса.

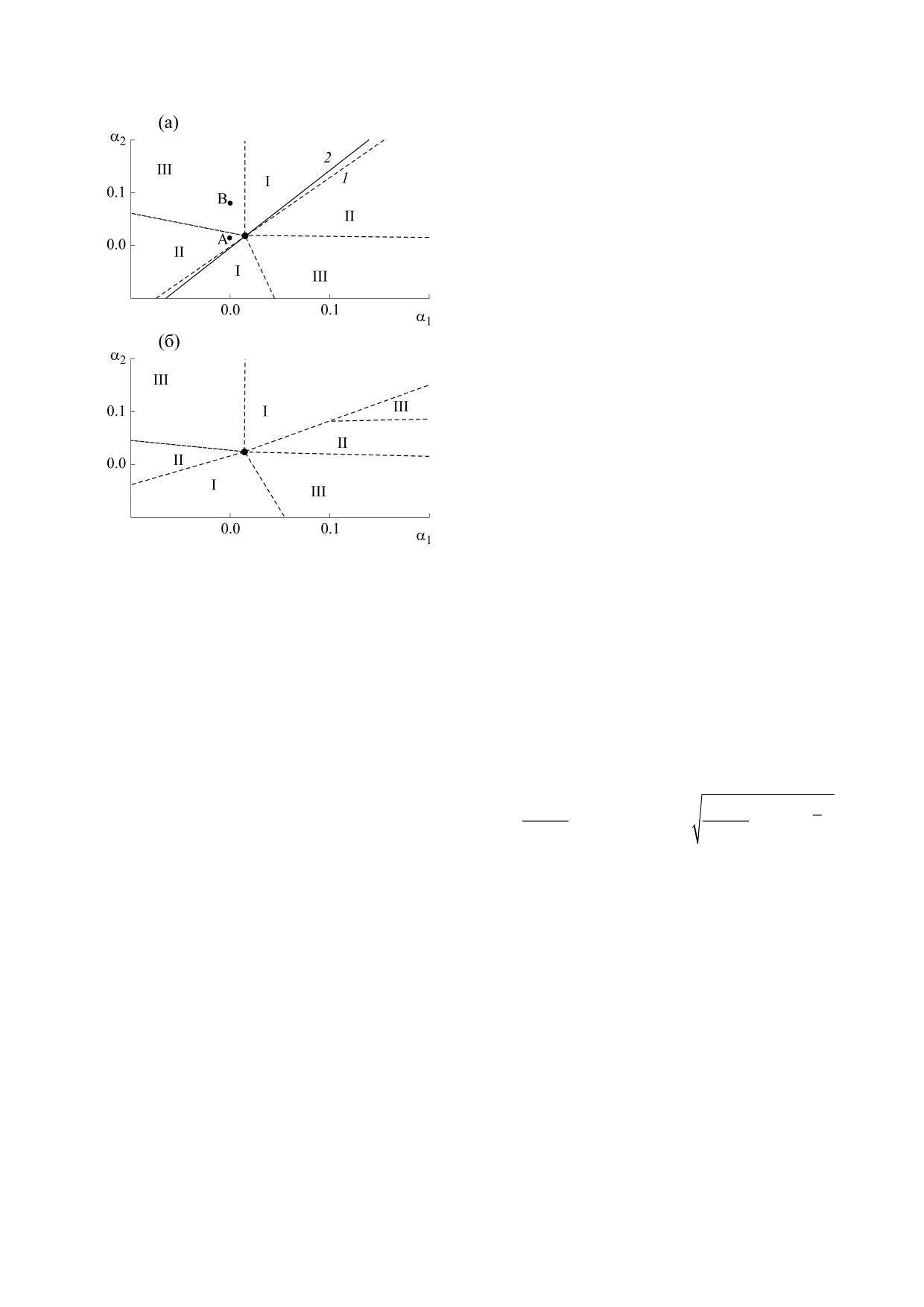
На рис. 2 представлены карты параметров α₁ и

α₂ c зонами, соответствующими сосуществова-

нию видов (III) и выживанию одной из популя-

ций (I и II). На рис. 2a пунктиром даны границы

зон по результатам расчетов при η₂ = 4, причем

прямая 1 (α₂ = γα₁) отвечает существованию ко-

симметричного семейства равновесий (12), чле-

нами которого являются стационарные распреде-

ления каждого вида и их различные комбинации.

В случае косимметрии наблюдается сосущество-

Рис. 1. Начальные распределения u при α₁ = 0 (кривая 1)

вание видов, а в спектре устойчивости для фи-

и α₁ = 0.06 (кривая 2); начальные распределения v (кри-

нальных стационарных распределений имеются

вые 3 и 4); функция ресурса (кривая 5).

БИОФИЗИКА том 67

№ 1

2022

178

БУДЯНСКИЙ, ЦИБУЛИН

Вычисления показали, что увеличение η₂ по

сравнению с тем значением, которое удовлетво-

ряет соотношениям (11), дает расширение обла-

стей II за счет областей I. Это означает предостав-

ление инвайдеру больших возможностей в конку-

рентной борьбе с аборигеном. Стоит отметить,

что прямые 1 и 2 на рис. 2a пересекаются в точке

, в которой соприкасаются области, соот-

(

)

,α

ветствующие различным сценариям распределе-

ния популяций.

На рис. 2б дана карта миграционных парамет-

ров, отвечающая случаю η₂ = 1. Видно, что доста-

точно большое отклонение η₂ от значения η₂ = 4,

соответствующего условию (11), приводит к де-

формации структуры областей для разных режи-

мов выживания популяций. При этом между зо-

нами I и II появляется область сосуществования

видов (зона III).

Различные сценарии инвазии демонстрирует

рис. 3. Расчеты проведены для наборов парамет-

ров, отвечающих точкам A и B на рис. 2а, у абори-

гена отсутствовала направленная на ресурс ми-

грация (α₁ = 0). Динамика вытеснения аборигена

дана на рис. 3a, а рис. 3б иллюстрирует сценарий

сосуществования видов. При малом значении ко-

Рис. 2. Карта миграционных параметров α₁ и α₂

эффициента миграции инвайдера (α₂ = 0.02) на-

областями, отвечающими сосуществованию видов

блюдается вытеснение аборигена, а при его уве-

(III) и выживанию популяции u (I) или v (II) при η₂ =

личении (α₂ = 0.08) происходит разделение ареа-

4.0 и 4.5 (а); при η₂ = 1.0 (б).

ла: вселенец концентрируется в благоприятной

зоне, вытесняя аборигена на границы ареала.

вой полуплоскости, что означает устойчивость в

На рис. 4 представлены траектории установле-

трансверсальном к семейству направлению.

ния к устойчивым стационарным состояниям

На рис. 2a также приведены результаты вычис-

(точки A, B, C₁, C₂, D₁, D₂) из различных началь-

лений при коэффициенте роста η₂ = 4.5, не удо-

ных распределений, отмеченных на рис. 1. Кри-

влетворяющем соотношениям (11). В этом случае

вые даны на плоскости среднеквадратичных от-

наблюдается смещение линии, отвечающей су-

клонений распределений σu и σv:

ществованию семейства стационарных распреде-

n+1

лений (прямая 2). В спектре устойчивости данных

σu

−

решений имеются практически нулевые соб-



r=0

ственные значения (σ ≈ 10^-6). Данный факт де-

монстрирует справедливость гипотезы, сформу-

Рис. 4 демонстрирует возможные стратегии

лированной в разделе «Косимметрия и мульти-

инвайдера в зависимости от величины миграци-

стабильность».

онного параметра аборигена α₁. При α₁ = 0 и

α₂ = 0, η₂ = 4 выполняется косимметричное соот-

Формула (18) дает хорошую оценку для опре-

деления параметров возмущения ε и δ (см. фор-

ношение на параметры системы (11). В этом слу-

мулу (14)). Например, при заданных k₁ = 0.03,

чае из различных начальных распределений (точ-

ки S₁, S₂) реализуются стационарные решения,

η₁ = 3, γ = 3/4 и α₁ = 0.06 было найдено численное

отвечающие сосуществованию популяций (точки

решение задачи (13), по квадратурным формулам

C₁, C₂). Данные решения входят в непрерывное

вычислены интегралы (18) и получено I_* ≈ 90.7.

семейство стационарных состояний (прямая 1 на

При вычислительных экспериментах с

рис. 4). Расчеты показывают, что в случае отсут-

системой (1)-(4) при α₁ = 0.06 была получена

ствия направленной миграции у аборигена ин-

мультистабильность для

= 4.5

= 0.08536.

вайдер может использовать стратегию, основан-

Таким образом, параметры возмущения оказа-

ную на выборе подходящего коэффициента так-

лись равны ε = 0.5 и δ = 0.00536, а их отношение

сиса α₂. При этом возможно как вытеснение

составило δ/ε ≈ 93.5, что близко к I_*.

аборигена (точка A на рис. 4), так и выход на ре-

БИОФИЗИКА том 67

№ 1

2022

МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИЙ

179

Рис. 3. Установление стационарных распределений α₂= 0.02 (а) и α₂ = 0.08 (б); α₁ = 0, η₂ = 4.0.

шение, отвечающее сосуществованию видов

(18), но нарушающим условия (11). Для обоих на-

(точка B на рис. 4). Отметим, что начальное рас-

боров параметров из различных начальных состо-

пределение влияет на траекторию установления к

яний получаются устойчивые распределения по-

финальному состоянию.

Косимметричное семейство стационарных

распределений сосуществующих популяций воз-

никает также при α₁, α₂ ≠ 0. Прямая 2 на рис. 4 от-

вечает семейству стационарных состояний при

выполнении условий (11) для следующих значе-

ний параметров: α₁ = 0.06, α₂ = 0.08, η₂ = 4. В этом

случае из-за ненулевого таксиса (α₁ = 0.06) про-

исходит перераспределение плотности аборигена

(см. рис. 1), что приводит к смещению начальных

данных (точки Q₁, Q₂). В результате установления

равновесий получаются распределения сосуще-

ствующих популяций аборигена и инвайдера.

Как при отсутствии таксиса, так и при его учете

плотность распределения инвайдера зависит от

плотности в начальный момент времени.

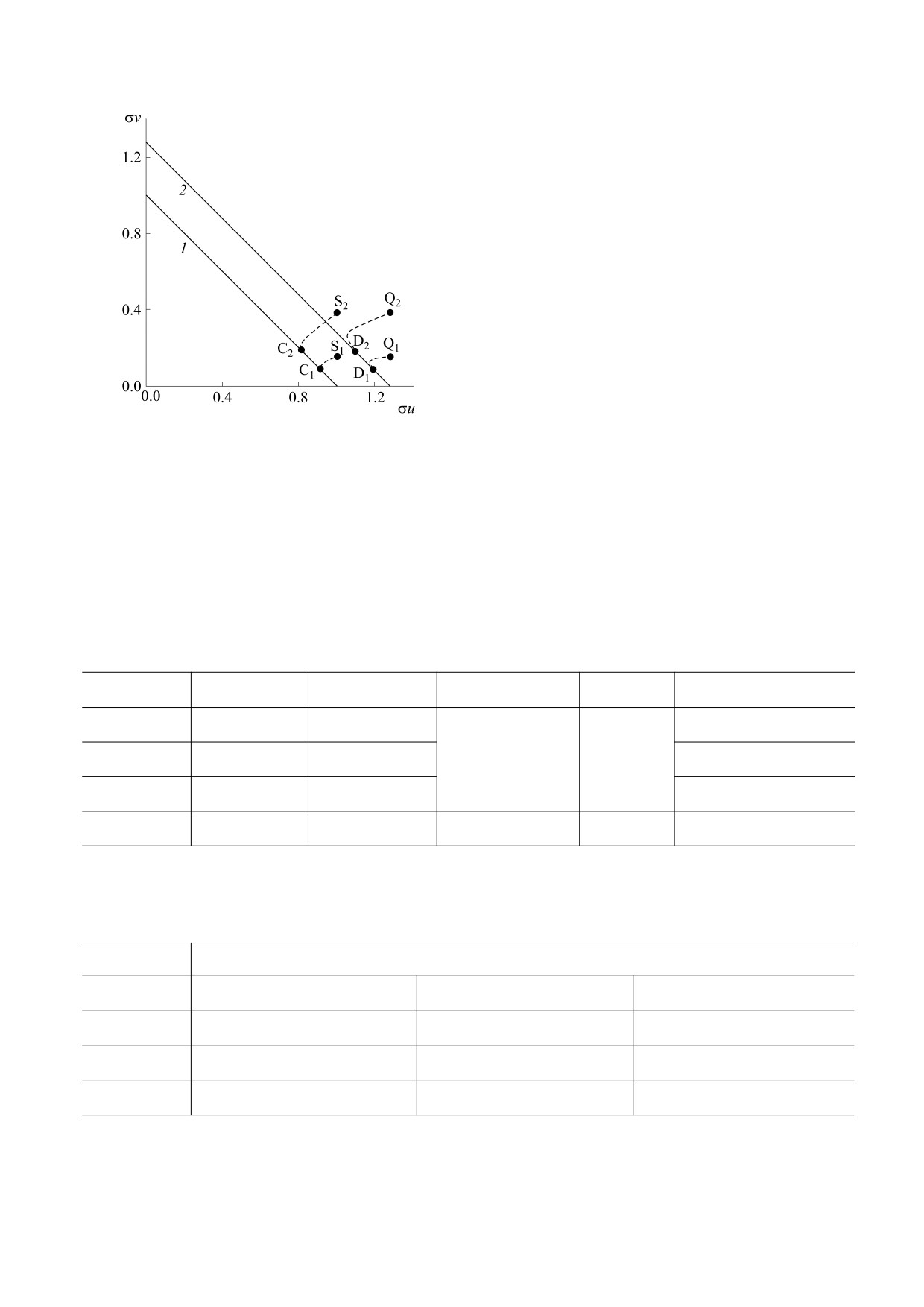
На рис. 5 демонстрируется динамика популя-

ций из различных начальных данных (см. табл. 1

и рис. 1) для двух наборов параметров: α₁ = 0,

Рис. 4. Установление равновесий (A, B, C_j, D_j) из

α₂ = 0.0029, η₂ = 3.5 и α₁ = 0.06, α₂ = 0.0746,

начальных распределений (S_j, Q_j) при различных α₁ и

η₂ = 3.5. Данные значения параметров были по-

α₂ (см. табл. 1 и рис. 1); прямые 1 и 2 отвечают

лучены в ходе вычислительного эксперимента и

соответственно семействам равновесий при α₁ = α₂ =

близки к величинам, отвечающим соотношениям

= 0 и α₁ = 0.06, α₂ = 0.08; η₂ = 4.0.

БИОФИЗИКА том 67

№ 1

2022

180

БУДЯНСКИЙ, ЦИБУЛИН

этих решений говорит о мультистабильности -

сосуществовании видов и успешности инвазии. В

табл. 2 приведены наиболее близкие к мнимой

оси элементы спектра устойчивости этих финаль-

ных состояний.

На рис. 6 дана эволюция во времени профилей

распределения популяций, соответствующая тра-

ектории Q₂D₂ на рис. 5. Видно, что в начале уста-

новления равновесия происходит резкий спад

плотности популяции аборигена за счет появле-

ния инвайдера, а затем плавный выход на стацио-

нарное решение.

ЗАКЛЮЧЕНИЕ

Взаимодействие двух популяций рассматрива-

лось на основе системы нелинейных параболиче-

ских уравнений, учитывающих диффузию,

) из начальных

Рис. 5. Установление равновесий Cj (D_j

таксис (направленную миграцию) и логистиче-

= 0.0029 и

распределений S_j (Q_j) при α₁ = 0, α₂

ский рост. Построены карты миграционных па-

= 0.0746; прямые 1 и 2 соответствуют

α₁ = 0.06, α₂

раметров, описывающие различные сценарии

= 3.5.

семействам равновесий (см. рис. 4); η₂

конкурентной борьбы в условиях биологической

инвазии. С использованием аппарата теории ко-

симметрии и численно-аналитического исследо-

пуляций, схожие с теми, что отображены на

вания показано, что по сравнению с работами [11,

рис. 4. Наличие практически нулевых собствен-

12] формирование непрерывного семейства сосу-

ных значений (σ ≈ 10^-6) в спектре устойчивости ществующих популяций (мультистабильность)

Таблица 1. Миграционные параметры и эволюция от начальных распределений (точки S_j, Q_j на рис. 4) к

финальным (точки A, B, C_j, D_j)

α₁

α₂

t = 0

u⁰

v⁰

Установление

0.00

S₁(S₂)

C₁(C₂)

0.00

0.02

S₁(S₂)

3(4)

0.00

0.08

S₁(S₂)

0.06

0.08

Q₁(Q₂)

3(4)

D₁(D₂)

Примечание. Номера u⁰ и v⁰ соответствуют кривым на рис. 1.

Таблица 2. Главные элементы спектра устойчивости стационарных распределений

C₁

-2.2∙10^-6

-0.07

-0.92

C₂

-1.6∙10^-7

-0.08

-0.39

D₁

-0.1∙10^-6

-0.05

-0.09

D₂

-0.2∙10^-6

-0.08

-0.18

Примечание. α₁ = 0.06, α₂ = 0.0746, η₂ = 3.5.

БИОФИЗИКА том 67

№ 1

2022

МОДЕЛИРОВАНИЕ ДИНАМИКИ ПОПУЛЯЦИЙ

181

Рис. 6. Пространственно-временная эволюция плотностей популяций, соответствующая траектории Q₂D₂ на рис. 5.

возможно для большего набора параметрических

Ю. Ю. Дгебуадзе, В. Г. Петросян и Л. А. Хляп, Са-

зависимостей. Описанный в работе метод позво-

мые опасные инвазионные виды России (ТОП-100)

ляет указывать комбинации параметров, при

(Т-во научных изданий КМК, М., 2018).

которых возможна успешная инвазия. Данный

N. Shigesada and K. Kawasaki, Biological invasions:

подход может быть использован для изучения

theory and practice (Oxford University Press, Oxford,

явления мультистабильности в нелинейных мно-

1997).

гопараметрических задачах математической био-

логии [18]. Полученные результаты позволят усо-

А. В. Никитина, А. И. Сухинов, Г. А. Угольниц-

вершенствовать методы анализа инвазии и ее по-

кий и др., Математич. моделирование 28 (7), 96

следствий.

(2016).

R. S. Cantrell, C. Cosner, and K.-Y. Lam, J. Differen-

tial Equations 263, 4565 (2017).

ФИНАНCИPОВАНИЕ РАБОТЫ

Y. Cai and S.A.H. Geritz, J. Math. Biol. 81, 907

Работа выполнена при финансовой поддержке

(2020).

Правительства Российской Федерации (соглаше-

ние № 075-15-2019-1928).

R. Cantrell, C. Cosner, M. Lewis, and Y. Lou, J.

Math. Biol. 80, 3 (2020).

10.

Е. С. Ковалева, В. Г. Цибулин и К. Фришмут, Ма-

КОНФЛИКТ ИНТЕРЕСОВ

тематич. моделирование 20 (2), 85 (2008).

Авторы заявляют об отсутствии конфликта

11.

А. В. Будянский и В. Г. Цибулин, Биофизика 60

интересов.

(4), 758 (2015).

12.

A. V. Budyansky, K. Frischmuth, and V. G. Tsybulin,

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

Discrete & Continuous Dynamical Systems B 24 (2),

547 (2019).

Настоящая работа не содержит описания иссле-

дований с использованием людей и животных в

13.

А. А. Самарский, Введение в теорию разностных

схем (Наука, М., 1989).

качестве объектов.

14.

Г. Ф. Гаузе, Борьба за существование (М.-Ижевcк,

2002).

СПИСОК ЛИТЕРАТУРЫ

15.

В. И. Юдович, Докл. РАН 398 (1), 57 (2004).

1. Дж. Мюррей, Математическая биология. Про-

16.

В. И. Юдович, Математич. заметки 49 (5), 142

странственные модели и их приложения в биомеди-

(1991).

цине, Т. 2 (Ин-т компьютерных исслед., М.-

Ижевск, 2011).

17.

А. В. Будянский и В. Г. Цибулин, Биофизика 64

2. Е. Я. Фрисман, М. П. Кулаков, О. Л. Ревуцкая и

(2), 343 (2019).

др., Компьютерные исследования и моделирова-

18.

Г. Ю. Ризниченко и А. Б. Рубин, Математические

ние 11 (1), 119 (2019).

методы в биологии и экологии. Биофизическая дина-

3. C. Cosner, Discrete and continuous dynamical sys-

мика продуктивных процессов, часть 2 (Изд-во

tems 34 (5), 1701 (2014).

Юрайт, М., 2019).

БИОФИЗИКА том 67

№ 1

2022

182

БУДЯНСКИЙ, ЦИБУЛИН

Modeling the Dynamics of Populations in Heterogeneous Environment:

Invasion and Multistability

A.V. Budyansky* and V. G. Tsybulin**

*Don State Technical University, pl. Gagarina 1, Rostov-on-Don, 344000 Russia

**Southern Federal University, ul. Bol’shaya Sadovaya 105/42, Rostov-on-Don, 344006 Russia

We created the model of interactions between two populations based on evolutionary equations which took

into account the diffusion, taxis, and logistic growth. Scenarios of competing populations in a biological in-

vasion context were considered in view of environmental heterogeneity. We propose an approach, which is

based on the analysis of the spatial structure parameters in a cosymmetic model, to predicting the invasion.

In this case, the multistability, that is, a family of stable stationary distributions of species, arises. We under-

took a computational experiment to study population scenarios in response to a violation of the cosymmetry

property. When the parameters of diffusion and growth satisfied the cosymmetry conditions, we determined

six zones on the plane of taxis parameters corresponding to different scenarios (survival of individual species

and species coexistence). When one of the growth parameters changes, the structure of the plane partition is

kept, but zone boundaries are deformed. In case of significant deviations of the growth parameter from the

cosymmetry condition, additional zones of coexistence of species may arise.

Keywords: population dynamics, invasion, diffusion-taxis-reaction equations, cosymmetry, method of lines

БИОФИЗИКА том 67

№ 1

2022