БИОФИЗИКА, 2022, том 67, № 2, с. 229-233

МОЛЕКУЛЯРНАЯ БИОФИЗИКА

УДК 577.2.01:(57.052.2+577.322.23+577.322.54)

НОВАЯ ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТА ХИЛЛА

*Воронежский государственный университет, 394018, Воронеж, Университетская пл., 1

**Институт молекулярной биологии им. В.А. Энгельгардта РАН, 119991, Москва, ул. Вавилова, 32

E-mail: lavrinenko_ia@bio.vsu.ru

Поступила в редакцию 27.12.2021 г.

После доработки 04.02.2022 г.

Принята к публикации 07.02.2022 г.

Предложена модификация уравнения Хилла, описывающего процесс кооперативного связывания

макромолекулой лиганда. Вводимый нами в это уравнение параметр «относительный коэффициент

кооперативности» позволяет обеспечить сопряжение коэффициента Хилла с числом взаимодей-

ствующих субъединиц в олигомере. Это позволяет прояснить физический смысл данного коэффи-

циента и объясняет природу его нецелочисленных значений. Нормирование относительного коэф-

фициента кооперативности даeт дополнительную возможность сопоставлять такие коэффициенты

для олигомеров с различным числом протомеров. Предлагаемый относительный коэффициент ко-

оперативности может быть полезным при решении широкого круга задач, связанных с описанием

согласованного взаимодействия элементов на всех уровнях пространственной организации белков,

нуклеиновых кислот, их комплексов, а также такого взаимодействия для рецепторов и их медиа-

торов.

Ключевые слова: кооперативное связывание лигандов, изотерма адсорбции, кривая диссоциации оксиге-

моглобина, уравнение Хилла, коэффициент Хилла, относительный коэффициент кооперативности

DOI: 10.31857/S000630292202003X

Обратимое связывание кислорода гемоглоби-

Однако высокие значения коэффициентов до-

ном является необходимым условием функцио-

стоверности аппроксимации (r²) не являются са-

нирования кислородтранспортной системы кро-

модостаточными и определяющими при подборе

ви [1, 2]. Зависимость степени оксигенации гем-

моделей оксигенации. Это объясняется тем, что

белка от парциального давления этого газа гра-

высокие значения r² также можно достичь и по-

фически представляется в виде кривой диссоциа-

средством интерполирующих полиномов высших

ции оксигемоглобина [3, 4]. Построенные по

порядков, например Лагранжа, Ньютона, Фурье,

ограниченному дискретному набору экспери-

Чебышёва и др., которые в данном случае не име-

ментальных данных кривые диссоциации оксиге-

ют физического смысла [17-19].

моглобина могут быть в дальнейшем аппрокси-

Поэтому, несмотря на приближенное описа-

мированы рядом математических функций [5].

ние кислородсвязывающих свойств гемоглобина,

Это необходимо, прежде всего, для нахождения

уравнение Хилла не утратило своей актуальности

величин полунасыщения гемоглобина кислоро-

в силу минимума необходимых априорных зна-

дом (p₅₀) [6, 7], зарядного напряжения (p₉₅) [8], а

ний процесса оксигенации [20] (оно широко при-

также значений параметров, характеризующих

меняется и для описания других кооперативных

уровень оксигенации в артериальной (SaO₂) [9,

процессов). Главным параметром в уравнении

10] или венозной (SvO₂) крови [11, 12].

Хилла является одноименный коэффициент (h), с

Разработанные к настоящему времени мате-

помощью которого можно охарактеризовать сте-

матические модели оксигенации позволяют свя-

пень кооперативности процесса оксигенации.

зывать коэффициенты уравнений с некоторыми

Однако несоответствие числа взаимодействую-

параметрами кислородсвязывающих свойств

щих субъединиц тетрамера (n) нецелочисленному

гембелка [13-15]. Для наиболее известных моде-

значению h затрудняет понимание физического

лей связывания кислорода гемоглобином, по-

смысла этого коэффициента [21-23].

строенных на степенных и экспоненциальных за-

В настоящей работе предпринята попытка

висимостях, нами ранее была проведена оценка

снять это кажущееся противоречие путем введе-

аппроксимирующей способности [16].

ния в уравнение сопрягающего коэффициента,

229

230

ЛАВРИНЕНКО и др.

проясняющего физический смысл этого уравне-

Можно представить пул молекул гемоглобина

ния. Заметим, что переосмысление интерпрета-

в виде набора димерных и тетрамерных форм с

ции коэффициента Хилла может оказаться важ-

различной весовой долей, аналогично ассоциа-

ным при описании взаимодействия «лиганд-ре-

там гембелка. Однако в эритроцитах данный бе-

цептор»

[24], а также других кооперативных

лок находится главным образом в виде тетрамера

систем.

(99.3-99.4%), что следует из расчетов по данным

референтных значений концентрации гемогло-

бина в клетке (4300-5500 мкмоль/л) [29] и кон-

МЕТОДЫ ИССЛЕДОВАНИЙ

станты диссоциации (K_4,2 = 0.2 мкмоль/л) при

В качестве объекта исследования была исполь-

нормальном атмосферном давлении, pH и темпе-

зована модель Хилла и набор экспериментальных

ратуре 7.0 и 37°C соответственно [30]. Из этого

данных, полученных в работе [25]. Оптимизация

следует, что коэффициент Хилла, равный 2.52 (и

параметров модели проведена методом наимень-

вычисленный нами по известным данным [25])

ших квадратов [26]. Необходимые вычисления

должен соответствовать доле тетраметров 25.9%.

выполнены с помощью пакета программ MS

Это возможно при концентрации белка

Excel.

0.1 мкмоль/л и явно противоречит приведенным

выше значениям.

Тем не менее уравнение Хилла получило ши-

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

рокое распространение, так как наряду с просто-

Предложенное Г. Гюфнером в 1890 г. уравне-

той вычисления и хорошей аппроксимирующей

ние оксигенации, выведенное из закона действу-

способностью [31] позволяет непосредственно

ющих масс, не могло описать S-образность кри-

находить величину p₅₀, а одноименный коэффи-

вой диссоциации оксигемоглобина [27]. Поэтому

циент этого уравнения (в аналогичных публика-

А. Хилл в 1910 г. предложил рассматривать про-

циях обозначаемый как n_H [32, 33], h [34, 35] или

цесс оксигенации как взаимодействие лиганда с

некоторыми другими символами и их сочетания-

макромолекулярным ассоциатом белка, т.е. как

ми [36, 37]) дает некоторую оценку кооператив-

химическую реакцию n-го порядка [13]:

ности составляющих его субъединиц.

(Hb)

⇌

(HbO

)

(1)

Для того чтобы снять противоречие между

способностью уравнения Хилла при минимуме

(2)

параметров хорошо аппроксимировать экспери-

ментальные данные и несоответствием показате-

ля степени этого уравнения целочисленному зна-

где Hb - дезоксигемоглобин, O₂ - кислород,

чению [38], мы предлагаем представить коэффи-

HbO₂ - оксигемоглобин, y - степень насыщения

циент Хилла h, как произведение числа

гемоглобина кислородом, p - парциальное давле-

взаимодействующих структурных элементов n (в

ние кислорода, p₅₀ - давление кислорода при

частности, субъединиц гембелка) на коэффици-

y = 0.5 (50% насыщение лигандом) и n - степень

ент пропорциональности a, отождествляемый со

агрегации гемоглобина (порядок реакции по ли-

степенью кооперативного взаимодействия этих

ганду, совпадающий со стехиометрическим ко-

элементов:

эффициентом этой реакции при выполнении за-

кона действующих масс).

(3)

Так как при анализе данных показатель степе-

ни n обычно принимал нецелочисленные значе-

ния, то физический смысл данного уравнения

Однако при отсутствии кооперативности, ко-

оказался неясным. Чтобы объяснить нецелочис-

торая характеризуется коэффициентом Хилла h

ленные значения своего параметра, Хилл предло-

равным единице, коэффициент пропорциональ-

жил рассматривать n как некоторое усреднение

ности a будет принимать различные значения, за-

по множеству молекулярных ассоциатов гембел-

висящие от числа субъединиц n, что затрудняет

ка с различной степенью их агрегации [13, 28].

интерпретацию последнего.

Однако в 1925 г. Г. Эдером было показано, что

Мы предлагаем произведение an в уравнении

молекула гемоглобина представляет собой тетра-

Хилла привести к следующему виду:

мер [14]. Хотя это не противоречило представле-

h = an = θ(n)(n - 1) + 1,

(4)

ниям о существовании молекулярных ассоциа-

тов, но и не объясняло, почему коэффициент это-

где θ(n) - вводимый нами «относительный коэф-

го уравнения приобретает значения меньше

фициент кооперативности» белка, состоящего из

четырех единиц. Такое несоответствие снова

n субъединиц. Тогда θ(n) = 0 указывает на отсут-

привело к противоречиям в физической трактов-

ствие кооперативности, и коэффициент Хилла

ке модели Хилла [21-23].

будет равен единице при любых n.

БИОФИЗИКА том 67

№ 2

2022

НОВАЯ ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТА ХИЛЛА

231

r2 = 99.94%, что демонстрирует приведенную мо-

дель статистически значимой.

При помощи этого уравнения по приведен-

ным данным для тетрамера гемоглобина мы вы-

числили значения величин p₅₀ и θ(4), которые со-

ставили 28.8 мм рт. ст. и 0.507 соответственно. Та-

ким образом, этот коэффициент может быть

использован для описания степени взаимодей-

ствия между субъединицами в составе олигомера.

Он показывает, насколько «необходимо» взаимо-

действовать протомерам для текущего «выполне-

ния» макромолекулой своей функциональной за-

дачи, исходя из максимальной возможности,

определяемой числом ее субъединиц.

Важным применением θ(n), на наш взгляд,

также может быть сопоставление степени коопе-

ративности, например, для димерных и тетрамер-

ных форм гемоглобина, учитывающее количе-

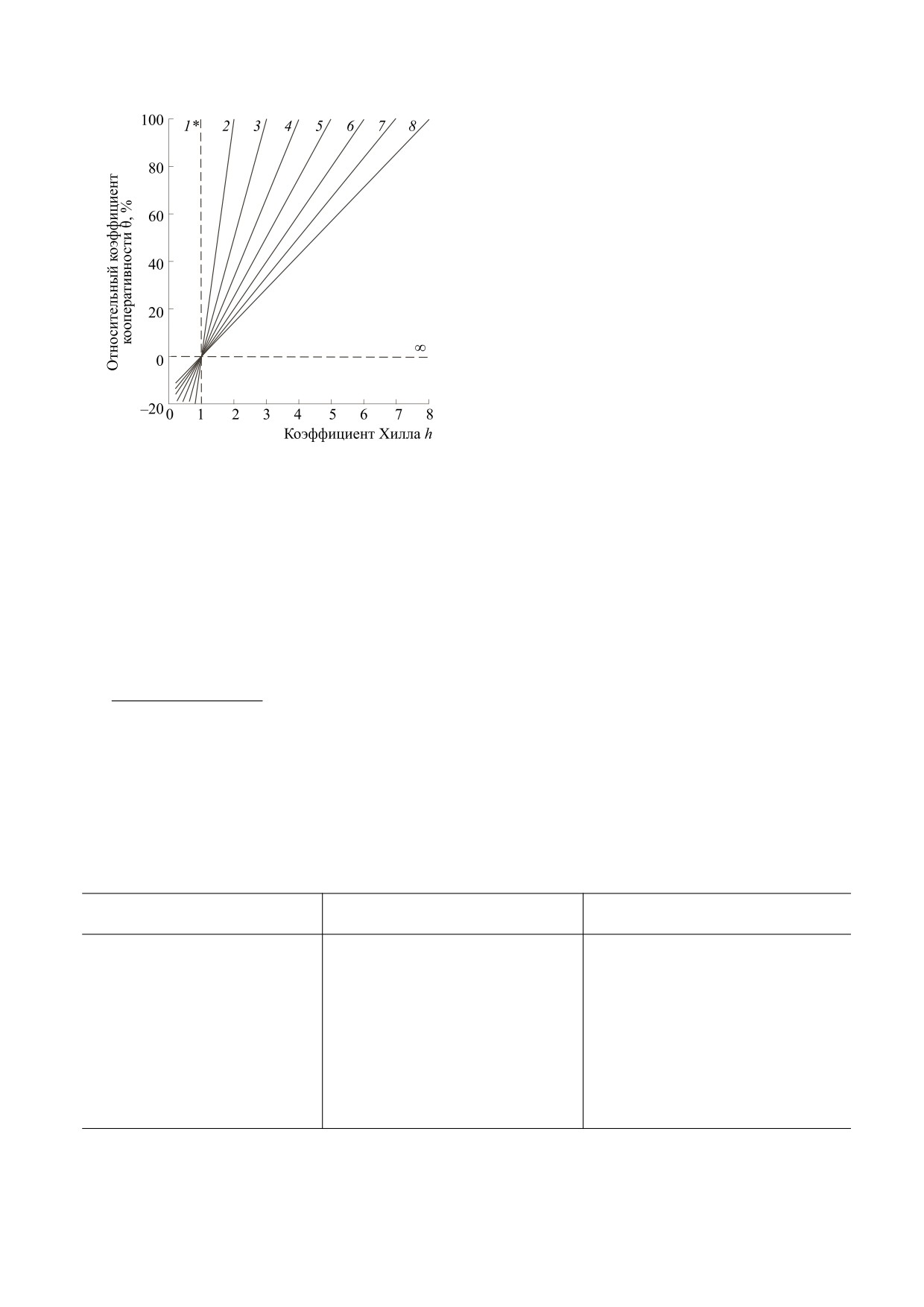
Зависимость относительного коэффициента коопе-

ство взаимодействующих субъединиц. Если дис-

ративности от коэффициента Хилла для макромоле-

социация тетрамера гембелка на его димеры

кулы, состоящей из n субъединиц. Для молекулы ге-

приведет к ожидаемому уменьшению коэффици-

моглобина актуальными являются значения n = 2 и 4.

ента Хилла, то по нормированному значению θ(n)

Обозначения: номера линейных моделей соответ-

степень кооперативности может остаться преж-

ствуют количеству субъединиц в составе макромоле-

ней. В общем виде нормированное значение θ(n)

кулы. Примечание: для n = 1 - значение θ(n) не опре-

можно получить путем приведения к димерной,

делено, для n → ∞ и при h = const получаем θ(n) → 0.

тетрамерной или любой другой форме белка ис-

ходя из зависимостей, представленных на рисун-

В конечном варианте в нашей записи уравне-

ке. Также следует отметить граничные условия.

ние Хилла (при p > 0) будет выглядеть следующим

Для молекулы, состоящей из одной субъединицы

образом:

(n = 1), значение θ(n) не определено (пунктирная

линия 1*), так как в этом случае кооперативность

θ(n)

n−1

−1

θ(n)(n−1)+1

(

)

отсутствует как физическое явление. Для θ(n) = 0

⎛

⎞

⎛

⎞

⎜1

⎟

(5)

коэффициент Хилла всегда будет равен единице

θ(n)(n−1)+1

⎜

⎟

⎝

⎠

⎝

⎠

при любых n > 1 (см. рисунок).

Для проверки адекватности данной математи-

Для тех случаев, когда раствор гемоглобина яв-

ческой модели экспериментальным данным [25]

ляется смесью димерных и тетрамерных форм

использовали критерий Фишера. Результаты ана-

белка с усредненной величиной n, значение θ(n)

лиза однофакторной регрессии показали следую-

можно получить исходя из вычисленного значе-

щее: F_расч (103905.36) >> F_табл (3.99, α = 0.05), при

ния n приведенного диапазона (таблица).

Доля тетрамерных форм оксигемоглобина (χ) и среднее арифметическое число субъединиц (n

^_) в составе

макромолекулы в зависимости от концентрации белка (C)

C, моль/л

χ, %

10^-9

0.50

2.010

10^-8

4.55

2.091

10^-7

26.79

2.536

10^-6

64.17

3.283

10^-5

86.82

3.736

10^-4

95.63

3.913

10^-3

98.60

3.972

10^-2

99.55

3.991

Примечание. Значения приведены для температуры 37°C, pH 7.0 и нормального атмосферного давления.

БИОФИЗИКА том 67

№ 2

2022

232

ЛАВРИНЕНКО и др.

Еще одним важным применением вводимой

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

нами в рассмотрение величины θ(n) может быть

Настоящая статья не содержит каких-либо ис-

анализ степени кооперативных взаимодействий

следований с участием людей или животных в ка-

гибридов валентности, в частности, гетеротетра-

честве объектов исследований.

меров гемоглобина, как комбинации α-, β- и дру-

гих типов субъединиц с различной степенью

СПИСОК ЛИТЕРАТУРЫ

окисления гемового железа (2⁺/3⁺).

R. F. Schmidt and G. Thews, Human Physiology

(Springer-Verlag, Berlin - Heidelberg - New York,

ЗАКЛЮЧЕНИЕ

2013).

W. F. Boron and E. L. Boulpaep, Medical Physiology

Предложена модификация уравнения Хилла,

(Elsevier Health Sciences, Philadelphia, 2017).

описывающего процесс кооперативного связыва-

R. N. Sladen, Int. Anesthesiol. Clin. 19 (3), 39 (1981).

ния лиганда макромолекулой на примере оксиге-

DOI: 10.1097/00004311-198119030-00006

нации гемоглобина. Мы ввели в рассмотрение

параметр θ(n) - относительный коэффициент ко-

E. Antonini, Crit. Care Med. 7 (360), 367 (1979).

оперативности, который позволяет обеспечить

S. M. Gadrey, C. E. Lau, R. Clay, et al., Physiol.

сопряжение вычисляемого коэффициента Хилла

Meas. 40 (11), 115008 (2019). DOI: 10.1088/1361-

с числом взаимодействующих субъединиц в оли-

6579/ab5154

гомере n и устраняет проблему физического

Z. Chu, Y. Wang, G. You, et al., Artif. Cells Nanomed.

смысла этого коэффициента - объясняет приро-

Biotechnol.

(1),

867

(2020).

DOI:

ду его нецелочисленных значений. Нормировка

относительного коэффициента кооперативности

10.1080/21691401.2020.1770272

дает дополнительную возможность сопоставлять

R. M. Winslow, Artif. Cells Blood Substit. Immobil.

эти коэффициенты для олигомеров с разными

Biotechnol.

(1),

(2005). DOI: 10.1081/bio-

значениями n.

200046634

Таким образом, θ(n) может быть полезным при

N. Willis, M. C. Clapham, and W. W. Mapleson, Br. J.

решении широкого круга задач, связанных с ко-

Anaesth

(9),

1160

(1987). DOI:

10.1093/

оперативными взаимодействиями [39-41]. Раз-

bja/59.9.1160

витый нами подход может быть применен для

J.-A. Collins, A. Rudenski, J. Gibson, et al., Breathe

описания изотерм адсорбции (кривых связыва-

11 (3), 194 (2015). DOI: 10.1183/20734735.001415

ния) лигандов разного рода с макромолекулами

10.

M. A. Danish, Cureus 13 (2), e13240 (2021). DOI:

[42-45], в частности, взаимодействия рецепторов

10.7759/cureus.13240

и их медиаторов [46, 47].

11.

J. Melius, Am. J. Crit. Care 3 (5), 353 (1994).

12.

J.-L. Teboul, O. Hamzaoui, and X. Monnet, Crit.

БЛАГОДАРНОСТИ

Care 15 (6), 1005 (2011). DOI: 10.1186/cc10491

13.

A. V. Hill, J. Physiol. 40, i (1910).

Авторы считают своим приятным долгом вы-

14.

G. S. Adair, A. V. Bock, and H. Field Jr., J. Biol.

разить благодарность А. Бучельникову и А. Засе-

Chem. 63, 529 (1925).

дателеву за плодотворные дискуссии и полезные

замечания, а также рецензентам за критический

15.

S. R. Bernard, Bull. Math. Biophys. 22, 391 (1960).

анализ рукописи и ценные замечания.

DOI: 10.1007/BF02476722

16.

И. А. Лавриненко, Г. А. Вашанов, В. Ю. Сулин

и др., Биофизика

(6)

1065

(2021). DOI:

ФИНАНСИРОВАНИЕ РАБОТЫ

10.31857/S000630292106003X

17.

H. Bateman and A. Erdelyi, Higher Transcendental

Работа выполнена при частичной финансовой

Functions (McGraw-Hill, New York, 1953), Vol. 2.

поддержке Программы фундаментальных науч-

ных исследований в Российской Федерации на

18.

J. P. Boyd, Chebyshev and Fourier spectral methods

долгосрочный период (2021-2030 годы) (тема

(Dover Publications, New York, 2001).

121052600299-1).

19.

E. Meijering, Proc. IEEE 90 (3), 319 (2002). DOI:

10.1109/5.993400

20.

S. A. Frank, Biol. Direct 8 (1), 1 (2013). DOI:

КОНФЛИКТ ИНТЕРЕСОВ

10.1186/1745-6150-8-31

Авторы заявляют об отсутствии конфликта

21.

M. L. Coval, J. Biol. Chem. 245 (23), 6335 (1970).

интересов.

DOI: 10.1016/S0021-9258(18)62614-6

БИОФИЗИКА том 67

№ 2

2022

НОВАЯ ИНТЕРПРЕТАЦИЯ КОЭФФИЦИЕНТА ХИЛЛА

233

22.

J.-H. S. Hofmeyr and H. Cornish-Bowden, Bioinfor-

35.

C. F. S. Bonafe, D. F. L. Neto, E. A. Martínez, et al.,

matics 13 (4), 377 (1997). DOI: 10.1093/bioinformat-

Chem. Papers

(9),

2861

(2020). DOI:

ics/13.4.377

10.1007/s11696-020-01125-1

36.

S. Srinivasan, F. H. Waghu, S. Idicula-Thomas, et al.,

23.

S. Goutelle, M. Maurin, F. Rougier, et al., Fund. Clin.

Biochim. Biophys. Acta - Biomembranes 1862 (4),

Pharmacol. 22 (6), 633 (2008). DOI: 10.1111/j.1472-

183242 (2020). DOI: 10.1016/j.bbamem. 2020.183242

8206.2008.00633.x

37.

A. Horovitz and T. Mondal, J. Phys. Chem. B 125 (1),

24.

J. N. Weiss, FASEB J. 11 (11), 835 (1997).

70 (2021). DOI: 10.1021/acs.jpcb.0c09351

25.

R. M. Winslow, M. Swenberg, R. L. Berger, et al., J.

38.

M. Żebrowska, M. Weippert, and M. Petelczyc, Front.

Biol Chem 252, 2331 (1977). DOI: 10.1016/S0021-

Physiol.

(945),

(2021).

DOI:

10.3389/

9258(17)40559-X

fphys.2021.695569

26.

F. M. Dekking, C. Kraaikamp, H. P. Lopuhaä, et al.,

39.

L. Acerenza and E. Mizraji, Biochim. Biophys. Acta

A Modern Introduction to Probability and Statistics: Un-

1339

(1),

155

(1997). DOI:

10.1016/s0167-

derstanding Why and How (Springer-Verlag, London,

4838(96)00228-2

2005). DOI: 10.1007/1-84628-168-7

40.

A. Horovitz, Proc. Roy. Soc. Lond. B: Biol. Sci. 229

(1256), 315 (1986). DOI: 10.1098/rspb.1986.0088

27.

G. Hüfner, Arch. Physiol. 31, 28 (1890).

41.

T. R. Chay and C. Ho, Proc/ Natl/ Acad/ Sci/ USA 70

28.

J. T. Edsall, J. Hist. Biol. 5 (2), 205 (1972). DOI:

(12), 3914 (1973). DOI: 10.1073/pnas.70.12.3914

10.1007/BF00346659

42.

I. M. Klotz, J. Biol. Chem. 279 (1), 1 (2004). DOI:

29.

A. H. B. Wu, Tietz clinical guide to laboratory tests (El-

10.1074/jbc.X300006200

sevier Science, St. Louis, MO, 2006).

43.

H. A. Saroff, Biochemistry 30 (42), 10085 (1991).

30.

N. Griffon, V. Baudin, W. Dieryck, et al., Protein Sci

DOI: 10.1021/bi00106a004

7 (3), 673 (1998). DOI: 10.1002/pro.5560070316

44.

Ю. Д. Нечипуренко, Анализ связывания биологиче-

ски активных соединений с нуклеиновыми кислота-

31.

N. Kaihnsa, Y. Ren, M. Safey El Din, et al., J. Math.

ми (Ин-т комп. исслед. (ИКИ), М. - Ижевск,

Biol. 81 (4-5), 1169 (2020). DOI: 10.1007/s00285-

2015).

020-01540-8

45.

D. Leipply and D. E. Draper, Biochemistry 49 (9),

32.

H. Abeliovich, Biophys. J. 89 (1), 76 (2005). DOI:

1843 (2010). DOI: 10.1021/bi902036j

10.1529/biophysj.105.060194

46.

A. F. Kolodziej, T. Tan, and D. E. Koshland, Jr., Bio-

33.

O. Rapp and O. Yifrach, PLoS One 12 (8), e0182871

chemistry

(47),

14782

(1996). DOI: 10.1021/

(2017). DOI: 10.1371/journal.pone.0182871

bi961481v

34.

H. Dahl, S. Taudorf, D. M. Bailey, et al., Exp. Physiol.

47.

A. Whitty, Nat. Chem. Biol. 4 (8), 435 (2008). DOI:

105 (7), 1063 (2020). DOI: 10.1113/EP088615

10.1038/nchembio0808-435

New Interpretation of the Hill Coefficient

I.A. Lavrinenko*, G.A. Vashanov*, and Yu.D. Nechipurenko**

*Voronezh State University, Universitetskaya pl. 1, Voronezh, 394018 Russia

**Engelhardt Institute of Molecular Biology, Russian Academy of Sciences, ul. Vavilova str. 32, Moscow, 119991 Russia

A modification of Hill's equation describing the process of cooperative binding of a ligand by a macromole-

cule is proposed. The parameter “relative coefficient of cooperativity” introduced by us into this equation al-

lows us to ensure the conjugation of the Hill coefficient with the number of interacting subunits in the oligo-

mer. This makes it possible to clarify the physical meaning of this coefficient and explains the nature of its

non-integer values. Normalization of the relative coefficient of cooperativity gives an additional opportunity

to compare such coefficients for oligomers with different numbers of protomers. The proposed relative coef-

ficient of cooperativity can be useful in solving a wide range of problems related to the description of the co-

ordinated interaction of elements at all levels of the spatial organization of proteins, nucleic acids, their com-

plexes, as well as such interaction for receptors and their mediators.

Keywords: cooperative binding of ligands, adsorption isotherm, dissociation curve of oxyhemoglobin, Hill’s equa-

tion, Hill’s coefficient, relative coefficient of cooperativity

БИОФИЗИКА том 67

№ 2

2022