БИОФИЗИКА, 2022, том 67, № 2, с. 289-300

БИОФИЗИКА КЛЕТКИ

УДК 51-76

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФЕРЕНТНОЙ РЕГУЛЯЦИИ

МЫШЕЧНОГО СОКРАЩЕНИЯ

*Санкт-Петербургский политехнический университет Петра Великого,

195251, Санкт-Петербург, ул. Политехническая, 29

E-mail: skrebenkovea@gmail.com

**Институт физиологии им. И.П. Павлова РАН, 199034, Санкт-Петербург, наб. Макарова, 6

E-mail: olvlasova@yandex.ru

Поступила в редакцию 10.12.2021 г.

После доработки 17.01.2022 г.

Принята к публикации 18.01.2022 г.

Рассматривается реализация гипотезы популяционного кодирования в простой нейромеханиче-

ской модели, в которой входом является активность кодирующих направление движения нейронов.

Входная активность преобразуется популяцией модельных интернейронов «интегрировать-и-сра-

ботать», затем трансформируется в уровень активации мышцы, которая, в свою очередь, действует

на простую механическую модель с одним суставом. Механическое движение моделируется на фик-

сированном промежутке времени, конечное положение является выходом модели. Модель позво-

ляет оценить необходимое преобразование входной активности для достижения кодируемого на-

правления движения. Для множества начальных угловых положений механической системы опре-

делены зависимости популяционной активности интернейронов от кодируемого направления,

оценена сложность реализации этих зависимостей синаптическими соединениями кодирующих

нейронов с гомогенной популяцией интернейронов. Для единственного начального углового поло-

жения механической системы подобраны параметры, позволяющие провести преобразование вход-

ной активности в соответствующее движение.

Ключевые слова: моторные нейроны, биомеханика, моторный контроль, нейромеханическое моделиро-

вание.

DOI: 10.31857/S0006302922020120

Управление произвольными движениями в

Было неоднократно показано, что активность

живых системах - сложный, иерархически орга-

нейронов первичной моторной коры кодирует

низованный процесс. Различные нейрофизиоло-

направления движения кисти [6-8].

гические механизмы отвечают за комплексную

Интерпретация результатов этих исследова-

интеграцию сенсорной и приобретенной из опы-

та информации при планировании и реализации

ний подразумевает, что у каждого такого нейрона

целенаправленного движения. Исследование

есть определенная настройка на направление

этих механизмов представляет как фундамен-

движения. Активность отдельного нейрона (ча-

тальный, так и практический интерес. Изучение

стота возникновения потенциалов действия) зо-

кодирования и преобразования двигательной ин-

ны двигательной коры, ответственной за кисть,

формации вносит вклад в понимание общих

тем выше, чем ближе направление движения (в

принципов функционирования нервной системы

декартовой системе окружающей среды) кисти к

[1]. Более прикладные исследования, связанные с

направлению, которое этот нейрон «предпочита-

мозг-компьютерными интерфейсами, нейропро-

ет» (preferred direction [6]). Если направление дви-

тезированием и технологиями нейрореабилита-

жения очень близко к «предпочитаемому» на-

ции, также нуждаются в более ясном понимании

правлению нейрона, проявляется максимальная

данных механизмов [2, 3].

активность. Кроме корреляции с направлением

Многочисленные исследования установили

движения более поздние исследования показали

связь между активностью нейронов первичной

отображение других кинематических перемен-

моторной коры и некоторыми механическими

ных, таких как линейные и угловые скорости и

параметрами сопутствующего движения [4-6].

ускорения, в активности нейронов [3, 7, 8].

289

290

СКРЕБЕНКОВ, ВЛАСОВА

Методология этих работ подразумевает поиск

жение. Модель состоит из популяции нейронов,

корреляций между активностью нейронов, коди-

моделируемых уравнениями «интегрировать-и-

рующих механические параметры, и непосред-

сработать», модели динамики мышечной актива-

ственно движением. Вследствие этого неясными

ции и простой биомеханической модели. Целью

остаются промежуточные этапы преобразования

данной работы является разработка составной

кодируемой информации, а именно, как высоко-

нейромеханической модели для исследования

уровневые параметры движения, закодирован-

механизмов трансформации активности мотор-

ные в активности нейронов, трансформируются в

ных нейронов, определение условий и ограниче-

активность спинальных мотонейронов и впо-

ний такой модели. В данной работе рассматрива-

следствии в активацию мышц. При помощи мате-

ется простое движение при заданном направле-

матических моделей [9-12], объединяющих био-

нии, в расчет не принимаются переходные

механическую составляющую и нейронную акти-

процессы, планирование движения цепочки ак-

вацию, было показано, что корреляции такого

тиваций для сложных движений.

типа могут быть просто следствием устройства

скелетно-мышечного аппарата. Также необходи-

мо отметить, что, несмотря на высокую значи-

МАТЕРИАЛЫ И МЕТОДЫ

мость этих результатов, они не позволяют понять,

Модель кодирующих нейронов. Согласно экс-

как кодирующие нейроны взаимодействуют, как

периментальным данным [19], каждый нейрон

формируется кодируемое направление.

генерирует потенциал действия тем чаще, чем

В работе, посвященной проблеме согласова-

ближе кодируемое направление к предпочитае-

ния кодирования различных параметров движе-

мому этим нейроном направлению. Иными сло-

ния [13], был проведен обстоятельный анализ ко-

вами, каждый нейрон как бы «настроен на свое

дирующих способностей нейронов моторной ко-

направление», выражаемое углом в двумерной

ры, в частности, исследовались нейроны,

системе координат. Совокупная активность ней-

активность которых коррелировала с общим на-

ронов с различными «предпочитаемыми направ-

правлением свободного движения, нейроны, ко-

лениями» образует таким образом популяцион-

дирующие конечное положение в пространстве

ный вектор, который определяет общее направ-

таких движений и конечную суставную конфигу-

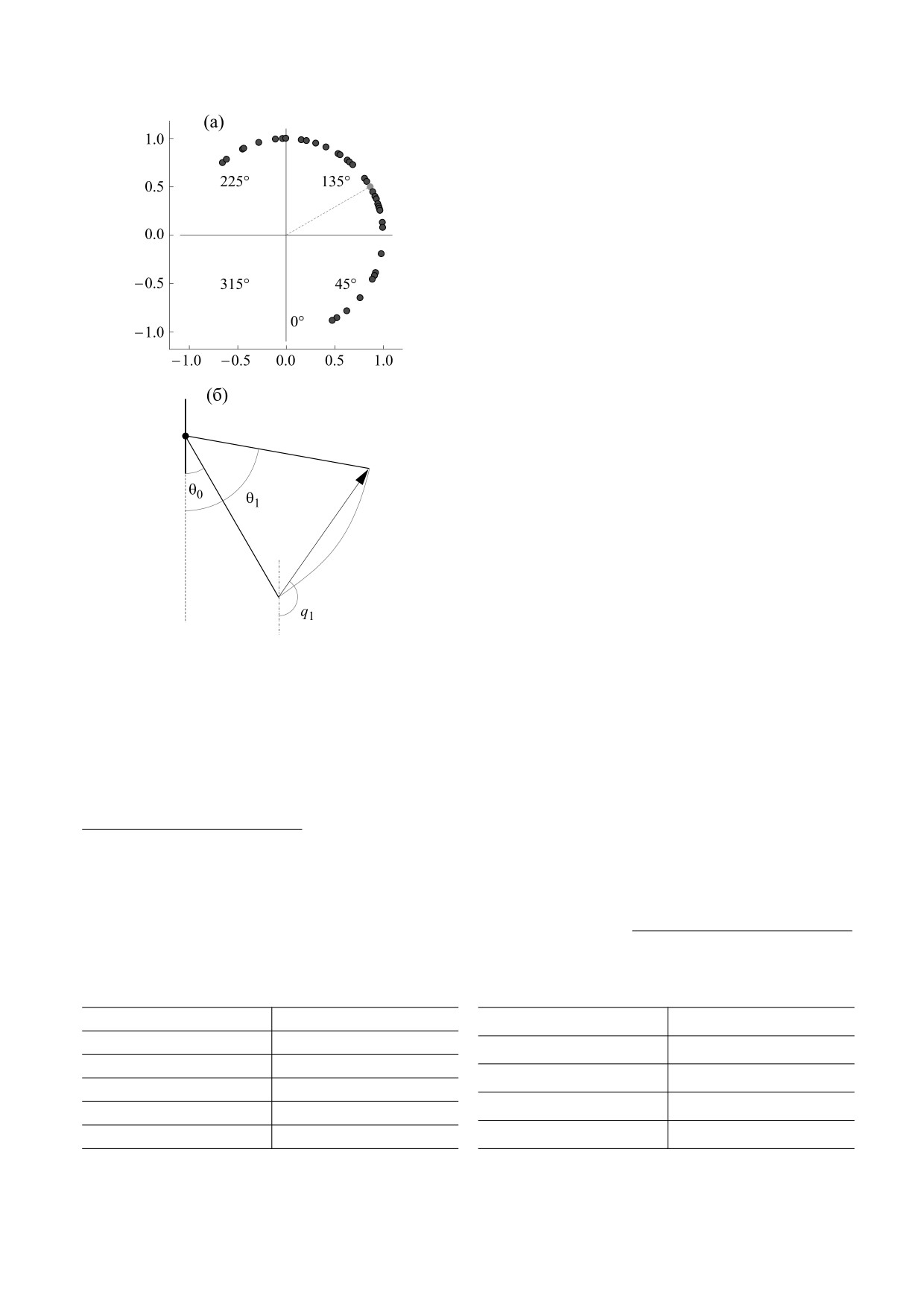
ление верхней конечности (рис. 1а). Каждый

рацию. Представленные результаты говорят о на-

кодирующий нейрон моделируется генератором

личии различных по своей настройке нейронов,

спайков постоянной частоты. Частота генерации

которые вносят вклад в общую активность.

спайков кодирующих нейронов рассчитывается

по формуле:

Хотя подобные исследования, несомненно,

проливают свет на функциональную роль нейро-

cos(q

–

нов моторной коры, вместе с тем остается невы-

ясненным вопрос о дальнейшем преобразовании

активности на более низких уровнях моторной

где ν_i - частота спайков i-го кодирующего нейро-

инфраструктуры. Мы предполагаем, что можно

на; a_i и b_i- коэффициенты i-го кодирующего ней-

применить математическое моделирование для

рона; q - кодируемое направление (рис. 1б); q_0i -

анализа преобразования сигнала при передаче

информации в нейромеханических системах.

предпочитаемое направление нейрона.

Объединение моделирования процессов на раз-

В моделировании было использовано N = 400

личных уровнях возникновения движения позво-

кодирующих нейронов. Предпочитаемые на-

лит сопоставить нейронную активность каждого

правления генерировались случайно, согласно

уровня и механическое движение.

нормальному распределению со средним q_mean и

Насколько известно нам, описанные в литера-

стандартным отклонением q_std (табл. 1).

туре работы, объединяющие моделирование ней-

Коэффициенты a и b также генерировались

ронов и механической системы, посвящены в ос-

случайно по нормальному закону со значениями

новном вопросам устройства центральных гене-

среднего и отклонения, взятыми произвольно, на

раторов паттерна либо интеграции афферентных

основании значений из работы [19]. Случайно

сигналов от рецепторов. Входная активность если

выбирались значения b и I - модуляции нейрона.

и рассматривается в таких работах, имеет чисто

Значения для a рассчитывалось по формуле:

регуляторный характер, не рассматривается ак-

a = I·b. Значения среднего и отклонения приведе-

тивность нейронов, кодирующих какие-либо

ны в табл. 1.

признаки движения [14-18].

Нами разработана простая нейромеханиче-

Популяция интернейронов. Потенциалы дей-

ская модель, входом которой является активность

ствия, генерируемые «кодирующими нейрона-

кодирующих направление движения нейронов, а

ми», являются входным сигналом для импульс-

выходом - соответствующее механическое дви-

ной нейронной сети, состоящей из N_int нейро-

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФЕРЕНТНОЙ РЕГУЛЯЦИИ

291

интегратора описывается уравнением:

du/dt = - (u -E_l)/τ_m,

где u - потенциал мембраны нейрона; E_l - потен-

циал утечки; τ_m - временная константа.

Значения параметров уравнения представле-

ны в табл. 2.

Кодирующие нейроны случайным образом и с

высокой вероятностью (p_ci = 0.8) соединены си-

напсами с популяцией интернейронов. Потенци-

ал действия пресинаптического, i-го кодирующе-

го нейрона вызывает изменение мембранного по-

тенциала u_j постсинаптического интернейрона на

величину w_ci. Интернейроны связаны между со-

бой синаптически с вероятностью p_ii = 0.8, изме-

нение потенциала на постсинаптическом нейро-

не происходит на величину w_ii (табл. 2).

Динамика мышечной активации. Популяцион-

ная активность интернейронов в свою очередь

является входом для модели динамики активации

мышцы. Моделирование активации основано на

подходе, использованном в работе [20], с внесе-

нием модификаций, связанных с использовани-

ем входа от популяции нейронов. Уровень акти-

вации мышцы зависит от концентрации ионов

Ca²⁺, связанных с сократительными филамента-

ми, а скорость изменения этой концентрации

пропорциональна свободному Ca²⁺ саркоплазмы

и концентрации доступных для связывания фи-

ламентов. Скорость изменения концентрации

Рис. 1. (а) - Пример распределения «предпочитаемых

направлений» кодирующих нейронов, показаны на-

свободного Ca²⁺ в свою очередь зависит от нали-

правления отдельных нейронов, выраженные углом;

чия действия стимула, который возникает в ре-

отмечено значение θ_mean = 120°; (б) - принцип рабо-

зультате потенциала действия, полученного от

ты кодирующих нейронов. Показан вектор движе-

популяции интернейронов. Вывод уравнений на

ния; q₁ - кодируемое направление, выраженное через

угол для этого движения.

базе первоначальных предпосылок представлен в

оригинальной работе [20]. Система уравнений,

связывающая потенциалы действия и уровень ак-

нов-интеграторов с утечкой. Состояние нейрона-

тивации мышцы выглядит следующим образом:

⎧

dCa

(

−

)(

−

)

(

C -Ca−Ca

)

(

C -S −Ca−Ca

)

⎪

⎨

dCa

⎪

= -

−

(

)(

)

⎩

Таблица 1. Параметры активности кодирующих ней-

Таблица 2. Параметры «интегрировать-и-сработать»

ронов

нейронов

q_mean

140°

N_int

100

q_std

50°

E_l

-70 мВ

b_mean

20 Гц

τ_m

5 мс

b_std

7.5 Гц

w_ci

1.6 мВ

I_mean

0.9

I_std

0.45

w_ii

0.05 мВ

БИОФИЗИКА том 67

№ 2

2022

292

СКРЕБЕНКОВ, ВЛАСОВА

где Ca - безразмерная концентрация свободного

Таблица 3. Параметры уравнений мышечной акти-

кальция; Ca_f - безразмерная концентрация каль-

вации

ция, связанного с сократительными филамента-

ми; k₃- константа скорости связывания свободно-

го кальция с сократительными филаментами; k₄ -

k₁₀

50 Гц

константа скорости высвобождения кальция, свя-

k₂₀

10 Гц

занного с сократительными филаментами.

k₃

100 Гц

Максимальное значение Ca_f = 1 соответствует

k₄

35 Гц

максимальной активации мышцы. Присутствие

стимула для высвобождения Ca²⁺ из саркоплаз-

τ_s

5 мс

матического ретикулума описывается линейным

дифференциальными уравнением:

го падения; r - расстояние до центра тяжести сег-

dstim

stim_,

мента; i - момент инерции сегмента; T - сово-

купный момент внешних сил.

где stim - уровень стимуляции; τ_s - временная

Для имитации физиологического диапазона

константа угасания стимуляции.

движений при расчете совокупного момента бы-

Потенциал действия синаптически соединен-

ли учтены силы трения. Момент силы трения

ного интернейрона вызывает изменение пере-

действует на сегмент в диапазоне θ < 15° и равен

менной stim на величину Δstim. Скорости измене-

T_fric = dθ·200. Совокупный момент является сум-

ния концентрации Ca²⁺ в присутствии и в отсут-

ствие стимула выражаются системами уравнений:

мой T = T_mus + T_fric. Длина мышечно-сухожиль-

ной единицы и плечо действия силы сокращения

⎧k

stim

0.01

на сегмент рассчитываются по формулам:

=⎨

иначе

⎩

⎧k

stim

0.01⎫

−

cosθ,

lmt

=⎨

⎬

иначе

⎩

⎭

sin θ

o i

где k10 - константа скорости высвобождения

lmt

кальция из саркоплазматического ретикулума;

k₂₀ - константа скорости связывания свободного

где p_o - расстояние от шарнира до точки крепле-

кальция.

ния мышцы к оси; p_i - расстояние от шарнира до

Параметры, использованные для моделирова-

точки крепления мышцы к сегменту.

ния динамики мышечной активации, представ-

лены в табл. 3.

Механическая модель. Завершающий компо-

нент модели - ее механическая часть. Механиче-

ская модель позволяет получить результат выше-

описанного моделирования нейронов в виде дви-

жения, генерируемого простой механической

системой. Входным для этого этапа является пе-

ременная Ca_f, отражающая уровень активации

мышцы. Моделируемая механическая система

образуется сегментом с равномерно распределен-

ной массой, проксимальный конец которой со-

единен при помощи шарнира с неподвижной

осью. На сегмент действует сила тяжести и сила

мышцы, которая генерирует усилие в зависимо-

сти от уровня активации (рис. 2).

Для моделирования динамики движения сег-

мента было использовано уравнение:

T -mgr

sin θ

Рис. 2. Схема механической модели, состоящей из

где θ - собственный угол; T - момент внешних

вращающегося сегмента, на который действует сила,

сил; m - масса сегмента; g - ускорение свободно-

генерируемая мышцей, и сила тяжести.

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФЕРЕНТНОЙ РЕГУЛЯЦИИ

293

Таблица 4. Параметры уравнений механической си-

Таблица 5. Параметры уравнений мышечного сокра-

стемы

щения

2.4 кг

9.8 м/с²

F_m0

575 Н

0.15 м

l_t0

0.01 м

m · l²/3

l_m0

0.1 м

p_i

0.1 м

V_mmax

10 м/с

p_o

0.02 м

0.45

Использованные значения параметров урав-

l_lmt = l_t + l_mcosα,

нения механического движения представлены в

F_m = F_ce + F_pe

табл. 4.

Для моделирования динамики мышечного со-

F_t = F_se = F_mcosα,

кращения используется классическая трехкомпо-

нентная модель Хилла. Мышца состоит из трех

где l_lmt - длина мышечно-сухожильной единицы;

элементов: последовательного пассивного, пред-

l_t - длина сухожилия, последовательного пассив-

ставляющего сухожилие, параллельного пассив-

ного элемента; l_m - длина мышцы (без сухожи-

ного, представляющего соединительно-тканные

лия); α - угол перистости; F_m - сила, генерируе-

оболочки, и сократительного, представляющего

мая мышцей, сократительным и параллельным

мышечные волокна (рис. 3). Используется допу-

пассивным элементами; F_t - сила, действующая

щение, что механическое напряжение в последо-

вательных элементах одинаково, а при объедине-

на сухожилие, последовательный пассивный эле-

нии параллельных суммируется в общее.

мент.

При этом допущении длины элементов моде-

Сила, возникающая в активном элементе (па-

ли и силы, действующие на элементы модели,

раллельном пассивном и сократительном), зави-

описываются следующими уравнениями:

сит от длины мышцы и скорости сокращения:

(

ce ce

)

[

)

(

)

(pe m

)]

где f_l - нормированная зависимость силы сокра-

Значения параметров уравнений мышечного

щения от длины мышечного волокна; f_v - норми-

сокращения представлены в табл. 5.

рованная зависимость силы сокращения от ско-

рости изменения длины мышечного волокна.

Эта зависимость позволяет выразить скорость

сокращения мышцы через обратную функцию

для f_v(v) [21]:

—

−Ca

⋅

lce

(0.25

0.75)⋅V

max

где b - константа уравнения Хилла [22].

F_m может быть найдена при помощи F_se, кото-

рая зависит от длины сухожилия l_lmt. Зависимость

силы сокращения от длины сократительного эле-

мента моделируется гауссианой с центром в точке

Рис. 3. Трехкомпонентная модель Хилла: SE - последо-

оптимальной длины:

вательный пассивный элемент, представляет сухожи-

лие мышцы; PE - параллельный пассивный элемент,

exp(−

−

/γ

l,ce

(

)

представляет соединительную ткань брюшка мышцы;

CE - сократительный элемент, представляет миоциты,

где γ - коэффициент формы [21].

активно генерирующие усилие.

БИОФИЗИКА том 67

№ 2

2022

294

СКРЕБЕНКОВ, ВЛАСОВА

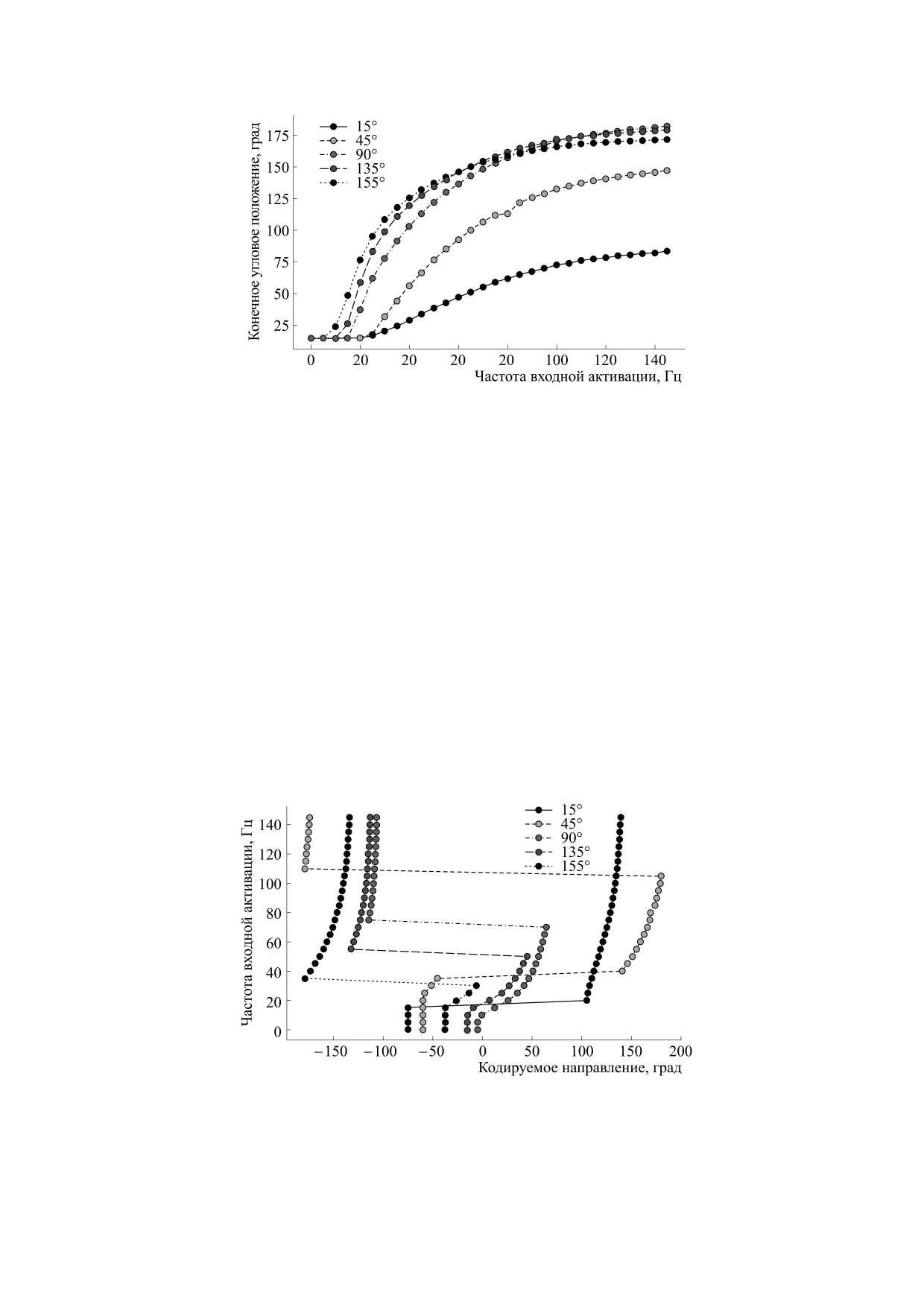
Рис. 4. Пример моделирования механического действия при начальном угловом положении в 90°: (а) - угловое положение;

(б) - динамика активации мышцы, показаны разные частоты активации модели кальциевой динамики.

Численное моделирование компонентов мо-

РЕЗУЛЬТАТЫ

дели до механической проводили на промежутке

Анализ зависимости механического движения от

времени в 800 мс, для моделирования механиче-

частоты активации кальциевой динамики. Для со-

ского движения использовали первые 500 мс ре-

поставления уровней активации кальциевой ди-

зультатов, предполагая, что кодируется направле-

намики и результирующих угловых положений

ние движения, которое достигается за это время.

сустава модели было проведено моделирование

Численное моделирование проводили при по-

механического движения при различных началь-

мощи языка программирования Python 3.8 и до-

ных углах и различных уровнях активации мыш-

полнительных библиотек. Моделирование по-

цы. Механическое действие и кальциевая дина-

тенциалов действия кодирующих нейронов,

мика для единственного начального положения

активности популяции «интегрировать-и-срабо-

показаны на рис. 4. На вход модели кальциевой

тать» нейронов и динамики кальция выполняли

динамики через одиночный синапс подавали по-

при помощи библиотеки Brian 2 [23]. Для реали-

тенциалы действия постоянной частоты, исполь-

зации механической части модели использовали

зуя значение параметра Δstim = 1. Диапазон ча-

библиотеку SciPy [24], а для модели мышечного

стот потенциалов действия, подававшихся на

сокращения была взята версия M. Дуарте и Р. Ва-

вход, [0, 150] Гц с шагом 5 Гц, расчеты проведены

танабе [25].

для набора начальных положений θ₀ = {15°, 45°,

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФЕРЕНТНОЙ РЕГУЛЯЦИИ

295

Рис. 5. Результаты действия различных частот на динамику мышечной активации, наборы точек соответствуют различным

начальным угловым положениям системы.

90°, 135°, 155°}. Результат механического дей-

вых положениях θ₀ = {90°, 135°, 155°} довольно

ствия системы, выраженный конечным соб-

близки между собой, и значительно отличаются

ственным углом для разных начальных положе-

от них и между собой кривые для θ₀= 15° и

ний, представлен на рис. 5.

θ₀ = 45°. Эти же данные используются для сопо-

ставления направления движения, то есть на-

Кривые, представляющие результаты такого

правления от начального к результирующему уг-

анализа, показывают нелинейное соотношение

ловому положению, и уровня активации мышцы,

между частотой воздействия на модель кальцие-

который необходим для реализации такого на-

вой динамики и конечным угловым положением

правления движения (рис. 6).

механической системы. Также следует отметить,

что значительно отличается поведение механиче-

Разбиение кривых на пары соответствует раз-

ской системы в соответствии с равным шагом на-

делению движения на сгибание и разгибание, для

чальных угловых положений, так кривые, отра-

разных стартовых позиций присутствует пробле-

жающие поведение системы при начальных угло-

ма значимых различий в кривых. Также следует

Рис. 6. Результаты действия различных частот на динамику мышечной активации; выраженная через кодируемое направ-

ление зависимость необходимой частоты активации модели кальциевой динамики и механической модели от кодируемого

направления.

БИОФИЗИКА том 67

№ 2

2022

296

СКРЕБЕНКОВ, ВЛАСОВА

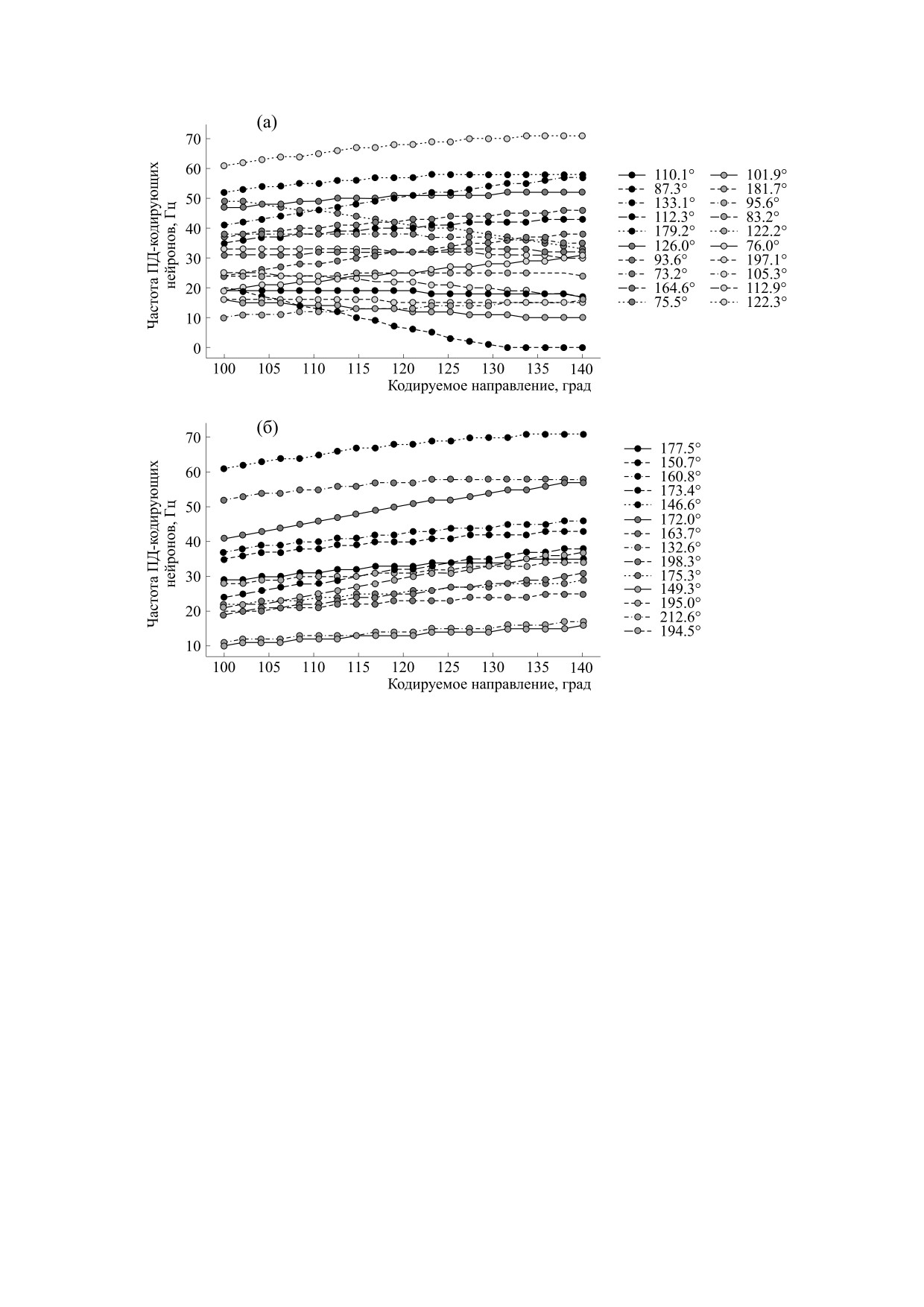
Рис. 7. Пример зависимости активности кодирующих нейронов от кодируемого направления, показаны направления, ак-

туальные для сгибательного движения при начальном угловом положении 15°: (а) - случайная подвыборка кодирующих

нейронов; (б) - нейроны, обеспечивающие увеличение частоты при увеличении угла направления кодируемого движения.

отметить, что значительное изменение частоты

Зависимость активности кодирующих нейро-

воздействия на динамику мышечной активации

нов от кодируемого направления показывает

соответствует небольшим изменениям кодируе-

(рис. 7а), что только часть нейронов способна

мого направления. Так, например, для точек, со-

обеспечить необходимый диапазон частот

ответствующих начальному углу в θ₀ = 15°, диапа-

(рис. 7б), чтобы удовлетворить соотношению

зон достигаемых направлений составляет при-

диапазона активности низкого уровня к диапазо-

мерно от 100° до 140°, при этом частота активации

ну кодируемых направлений. Увеличение часто-

меняется от 20 до 150 Гц. Это означает, что вариа-

ты следования спайков при увеличении угла на-

тивность направления на нижних уровнях модели

правления обеспечивается только для кодирую-

должна обеспечиваться вкладом активности

«второстепенных» кодирующих нейронов в боль-

щих нейронов, отвечающих за большие, чем

шей степени, нежели нейронов с наибольшим

кодируемые углы направления. Из-за случайного

модулем активности.

выбора предпочитаемого направления наблюда-

ется картина, при которой кодирующие нейроны

Способность кодирующих нейронов предо-

разделяются на три группы: увеличивающие ак-

ставить необходимую активность можно оценить

из соотношения их активности от кодируемого

тивность при кодировании больших углов сгиба-

направления (рис. 6).

ния, уменьшающие и относительно нейтральные.

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФЕРЕНТНОЙ РЕГУЛЯЦИИ

297

Рис. 10. Результаты механического моделирования

под действием активности кодирующих нейронов:

кружки

- кодируемые (потребное) направление,

сплошная линия - среднее значение результатов мо-

делировании, пунктирные линии - стандартное от-

клонение.

при увеличении угла направления показано на

рис. 8.

Результаты моделирования кодирования движе-

ния. По результатам анализа диапазона частот по-

тенциалов действия кодирующих нейронов и со-

отношения уровня активации мышцы и кодируе-

мого направления была скомпонована модель,

Рис. 8. Средняя частота активации кодирующих нейро-

состоящая из кодирующих нейронов, интерней-

нов в зависимости от кодируемого направления: (а) -

ронов и нейромеханической части. Параметры

для всех кодирующих нейронов; (б) - для нейронов,

обеспечивающих увеличение частоты при увеличении

подбирали таким образом, чтобы обеспечить

угла направления.

более слабую и пологую зависимость популяци-

онной активности интернейронов от пресинап-

тического уровня активности. Синаптически со-

Сравнение диапазонов общей активности ко-

единены с интернейронами были только кодиру-

дирующих нейронов и активности нейронов, ко-

ющие нейроны, обеспечивающие увеличение

торые обеспечивают увеличение частоты спайков

частоты спайков при увеличении угла направле-

ния. Ниже представлены результаты попытки

при помощи одной гомогенной популяции ин-

тернейронов обеспечить управление простой

биомеханической системой. Результаты серии

расчетов, в каждом из которых с одинаковой ве-

роятностью случайно генерировались синаптиче-

ские связи между кодирующими нейронами и

интернейронами, а также связи внутри популя-

ции интернейронов, представлены на рис. 9 (для

популяционной частоты интернейронов) и

рис. 10 (для механического действия).

При кодировании близких к начальному поло-

жению направлений, то есть при невысокой

необходимой активации мышцы, наблюдается

нестабильность популяционной активности ин-

Рис. 9. Активность интернейронов: среднее и стандарт-

тернейронов во времени, что впоследствии выли-

ное отклонение для 100 решений прямого прохода

по кодируемым углам для начального углового положе-

вается в нестабильную активацию и механиче-

ния 15°.

ский выход для таких углов.

БИОФИЗИКА том 67

№ 2

2022

298

СКРЕБЕНКОВ, ВЛАСОВА

Рис. 11. Результаты моделирования при кодировании угла направления от 100° до 140° с шагом 2°: (а) - активность

интернейронов; (б) - кальциевая динамика.

ОБСУЖДЕНИЕ

механической системы модель способна реализо-

вывать закодированноe направление движения.

К настоящему времени осуществлен значи-

Полученные данные можно интерпретировать

тельный прогресс в понимании механизмов мо-

так, что преобразование моторной команды стро-

торного контроля, в частотности, установлены

ится на разделении кодирующих нейронов на

многие механические параметры, которые коди-

подвыборки, характерные для начальных поло-

руются нервной системой. Однако не так хорошо

жений, и на нелинейном отклике интернейро-

исследованы механизмы преобразования актив-

нов, который позволяет получить необходимую

ности кодирующих нейронов в уровень актива-

мышечную активацию. Разделение кодирующих

ции мышц, которые, действуя непосредственно

на скелетную систему, реализуют закодирован-

нейронов на подвыборки осуществляется паттер-

ное движение.

ном синаптических связей с промежуточными

нейронами, а отклик популяции интернейронов

В данной работе для решения этой проблемы

зависит от их параметров [26]. Эти выводы не со-

была использована математическая модель ней-

гласуются с абстрактной моделью в работе [27], в

ромеханической системы. Такой подход позво-

которой предполагался общий пул интернейро-

лил обратиться к промежуточным элементам си-

нов для преобразования направления движения в

стемы трансформации управляющей активности,

уровень активации мышцы. Однако подобный

в частности, разработанная модель позволила со-

способ обработки информации, заключающийся

поставить активность кодирующих нейронов с

в разделении сигнала на несколько афферентов,

активностью популяции промежуточных нейро-

нов и соответствующим механическим действием

каждый из которых несет линейно закодирован-

(рис. 5 и 6). Эти результаты позволили осуще-

ную информацию, был выявлен в работах, посвя-

ствить подбор синаптических связей между коди-

щенных преобразованию первичных сенсорных

рующими и промежуточными нейронами таким

сигналов [28-30], в частности, автор работы [28]

образом, что для одного начального положения

отмечал, что в простых случаях нервная система

БИОФИЗИКА том 67

№ 2

2022

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭФФЕРЕНТНОЙ РЕГУЛЯЦИИ

299

ведет себя как линейный оператор. Также в этих

A. Tankus, Y. Yeshurun, T. Flash, and I. Fried, J. Neu-

работах показано, что кодируемый параметр пе-

rosurg. 110 (6), 1304 (2009).

редается только на некотором диапазоне актив-

C. S. R. Li, C. Padoa-Schioppa, and E. Bizzi, Neuron

ности, который характеризуется стабильностью

30 (2), 593 (2001).

нервной активности. Такое ограничение наблю-

R. N. Holdefer and L. E. Miller, Exp. Brain Res. 146

дается в нашей модели (рис. 11), что было показа-

(2), 233 (2002).

но благодаря применению модели кальциевой

B. Amirikian and A. P. Georgopoulos, Neurosci. Res.

динамики в нейромышечном синапсе.

36 (1), 73 (2000).

Развитие этой работы может быть направлено

A. P. Georgopoulos, FASEB J. 2 (13), 2849 (1988).

в сторону приложения реализованного подхода к

механической системе с большим количеством

A. P. Georgopoulos, A. B. Schwartz, and R. E. Ket-

степеней свободы. Также, возможно, интерес

tner, Science 233 (4771), 1416 (1986).

представляет сравнительный анализ для различ-

T. Flash and T. J. Sejnowski, Encycl. Neurosci. 11 (6),

ных начальных положений.

9 (2009).

10.

T. Takei, F. Crevecoeur, T. M. Herter, et al., J. Neuro-

ВЫВОДЫ

sci. 38 (36), 7787 (2018).

11.

S. H. Scott, Nat. Neurosci. 3 (4), 307 (2000).

1. В рамках данной работы впервые удалось ре-

ализовать математическую модель, объединяю-

12.

E. Todorov, Nat. Neurosci. 3 (4), 391 (2000).

щую моделирование нейронов, кодирующих па-

13.

T. N. Aflalo and M. S. A. Graziano, Proc. Natl. Acad.

раметры движения и механической системы под

Sci. USA 103 (8), 2909 (2006).

их управлением.

14.

N. A. Shevtsova, A. E. Talpalar, S. N. Markin, et al.,

2. Результаты исследования модели in silico

J. Physiol. 593 (11), 2403 (2015).

позволяют сделать вывод о том, что преобразова-

ние активности кодирующих нейронов происхо-

15.

S. N. Markin, A. N. Klishko, N. A. Shevtsova, et al.,

дит за счет передачи сигнала от подвыборки ко-

Physiol. Behav. 176 (1), 139 (2017).

дирующих нейронов и биофизических свойств

16.

T. McMillen, T. Williams, and P. Holmes, PLoS

интернейронов. Изоляция такой подвыборки

Comput. Biol. 4 (8), (2008).

осуществляется набором синаптических связей

17.

K. R. S. Holzbaur, W. M. Murray, and S. L. Delp,

между кодирующими и промежуточными нейро-

нами. Характер зависимости частоты активации

Ann. Biomed. Eng. 33 (6), 829 (2005).

интернейронов от входного сигнала позволяет

18.

I. A. Rybak, K. Stecina, N. A. Shevtsova, and

осуществить необходимое для уровня активации

D. A. McCrea, J. Physiol. 577 (2), 641 (2006).

мышцы нелинейное преобразование.

19.

A. P. Georgopoulos, J. F. Kalaska, R. Caminiti, and

J. T. Massey, J. Neurosci. 2 (11), 1527 (1982).

ФИНАНСИРОВАНИЕ РАБОТЫ

20.

T. L. Williams, G. Bowtell, and N. A. Curtin, J. Exp.

Работа выполнена при финансовой поддержке

Biol. 201 (6), 869 (1998).

Российского фонда фундаментальных исследова-

21.

D. G. Thelen, J. Biomech Eng. 125 (1), 70 (2003).

ний (проект № 20-31-90044).

22.

J. M. Winters, Ann. Biomed. Eng. 23 (4), 359 (1995).

23.

M. Stimberg, R. Brette, and D. F. Goodman, Elife 8,

КОНФЛИКТ ИНТЕРЕСОВ

e47314 (2019).

Авторы заявляют об отсутствии конфликта

24.

P. Virtanen, R. Gommers, and T. E. Oliphant, Nat.

интересов.

Methods 17, 261 (2020).

25.

M. Duarte and R. N. Watanabe, GitHub Repos. Pub-

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

lished online (2018).

Настоящая работа не содержит описания ка-

26.

N. Brunel, J. Comput. Neurosci. 8 (3), 183 (2000).

ких-либо исследований с использованием людей

27.

A. Georgopoulos, Brain Res. Cogn. Brain Res. 3 (2),

и животных в качестве объектов.

151 (1996).

28.

V. Mountcastle, W. Talbot, I. Darian-Smith, Science

СПИСОК ЛИТЕРАТУРЫ

155 (3762), 596 (1967).

1. G. B. Stanley, Nat. Neurosci. 16 (3), 259 (2013).

29.

E. R. Perl, D. G. Whitlock, and J. R. Gentry, J. Neu-

rophysiol. 25, 337 (1962).

2. G. Panuccio, M. Semprini, L. Natale, et al., Brain

Neurosci. Adv. 2, 1 (2018).

30.

C. C. Hunt, J. Physiol. 155, 175 (1961).

БИОФИЗИКА том 67

№ 2

2022