БИОФИЗИКА, 2022, том 67, № 2, с. 386-408

БИОФИЗИКА СЛОЖНЫХ СИСТЕМ

УДК 595.76, 51.76, 532.22

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ

КРАБА Paralithodes camtschaticus (Decapoda, Lithodidae)

КАДЬЯКСКОГО АРХИПЕЛАГА

Санкт-Петербургский Федеральный исследовательский центр РАН, 199178, Cанкт-Петеpбуpг, 14-я линия, 39

E-mail: temp_elf@mail.ru

Поступила в редакцию 11.12.2021 г.

После доработки 17.12.2021 г.

Принята к публикации 19.12.2021 г.

Деградация промысловых популяций остается частым явлением даже с применением методов учета

и контроля объема добычи. В практике рыбного хозяйства используется понятие «перелова» с из-

вестными признаками этого состояния. Однако ведущие к деградации запасов процессы развива-

ются достаточно разнообразно. С точки зрения теории нелинейных динамических систем можно

классифицировать несколько типов развития кризиса. Особенный интерес представляют явления

коллапса - варианты стремительного падения численности, неожиданные для контролирующих

промысел организаций. Непосредственно перед коллапсом состояние запаса может оцениваться и

как относительно стабильное, но может испытывать флуктуации. После быстрого сокращения во-

преки ожиданиям не следовало быстрого восстановления у трески, сига Великих Озер, палтуса и

других ценных видов. В работе рассматривается гибридная модель для ситуации коллапса запасов

краба Paralithodes camtschaticus у Кадьякского архипелага штата Аляски с необычной отличитель-

ной осциллирующей динамикой. Вычислительный сценарий в гибридной системе с уравнениями

выживаемости и роста учитывает логику принятия решений при управлении эксплуатацией. Сце-

нарий отличается тем, что после падения уловов популяция краба переходит в режим спорадиче-

ских флуктуаций, не имеющих регулярного характера и не характерный для данных биоресурсов.

Непосредственно коллапс наступает через долгий интервал ведения промысла популяции уже в не-

устойчивом режиме. Анализ показывает, что большая длительность жизненного цикла вида не ста-

новится решающим фактором для исключения риска сценария коллапса. Наличие резервных поко-

лений качественно не изменяет ситуацию, эффективность их воспроизводства у краба и трески у

побережья Лабрадора оказалась неожиданно низкой. Необходимо регулярно уточнять критерии со-

стояния запасов крупных хищников, требующих сезонных мораториев на их вылов.

Ключевые слова: нелинейная динамика деградации экосистем, сценарное моделирование, управление

эксплуатацией биоресурсов, сценарии коллапса популяций, нерегулярные флуктуации и циклы, кризис

популяции краба Paralithodes camtschaticus

DOI: 10.31857/S0006302922020223

В предыдущих работах мы исследовали мате-

ре с половиной месяца. Так происходит, в частно-

матическими методами свойства осциллирую-

сти, согласно статистике. приводимой по США

щих явлений в динамике различных биологиче-

(рис. 1). Волны вызывают важную психологиче-

ских процессов. Удалось описать затухающие ко-

скую проблему, когда победа над эпидемией ви-

лебания для ситуации серий уменьшающихся

дится совсем близкой, но вдруг вновь приходится

пиков вспышек численности у насекомых-вреди-

вводить режимы ограничений.

телей в бореальных лесах [1]. Рассмотрены пере-

Режим «эпидемических волн» с интервалом в

ходные колебательные режимы, ведущие к попу-

четыре-шесть месяцев является распространен-

ляционному кризису «бутылочного горлышка»

ным, но не единственным вариантом развития

после активной фазы агрессивной инвазии [2].

сценария. Эпидемические процессы и уровень

Нестационарный по амплитуде осциллирующий

смертности в регионах существенно отличались.

процесс иллюстрируется современной эпидеми-

В ряде стран по-прежнему местные жители под-

ческой динамикой. Во многих странах графики

вержены болезни сильнее, чем в других. Так, в

заболеваемости COVID-19 приобрели форму че-

Бельгии при 80%-й вакцинации граждан возраста

реды «волн», накатывающих с интервалами четы-

18+ смертность остается немного выше, чем в

386

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

387

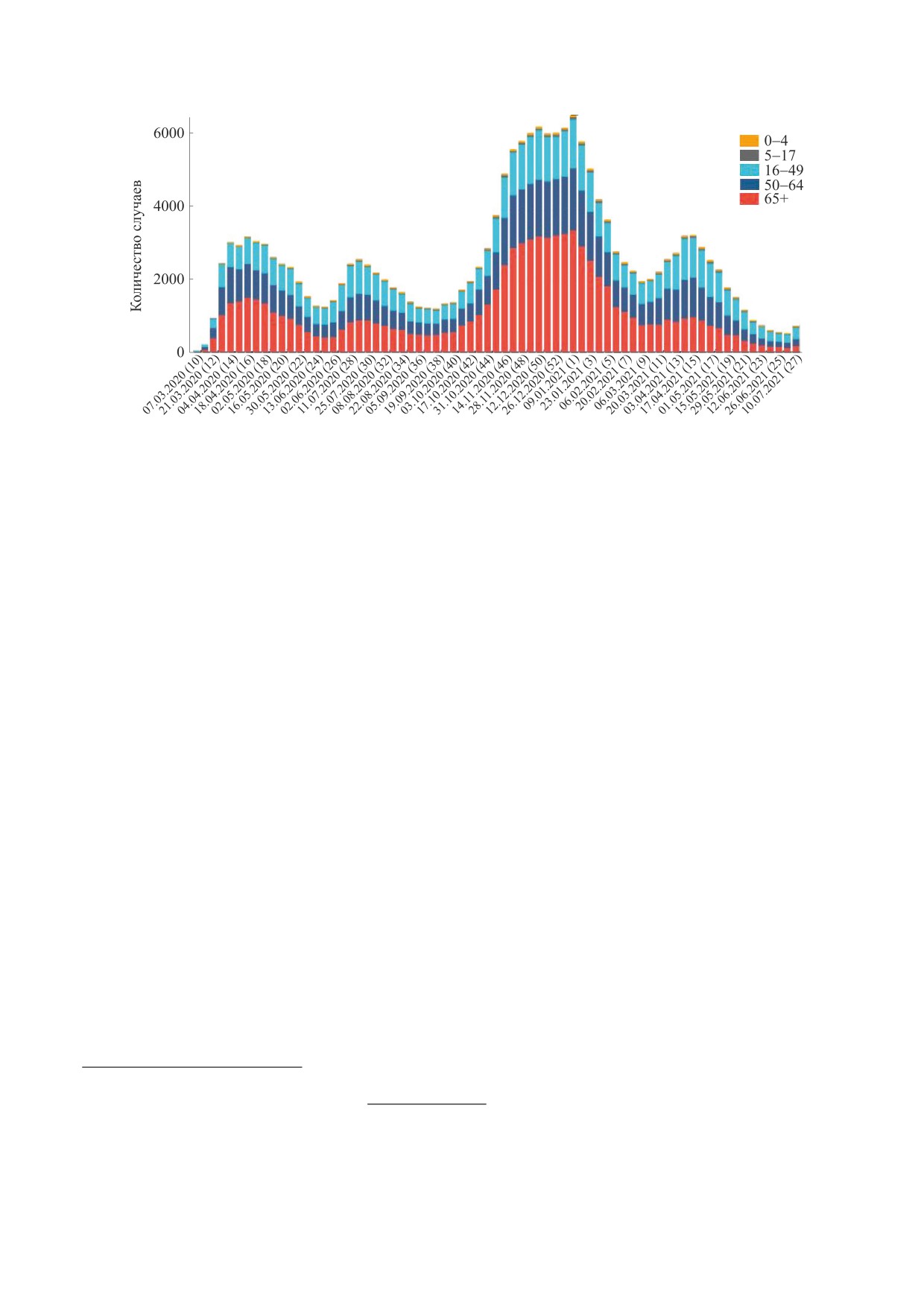
Рис. 1. Динамика волн госпитализаций больных с диагнозом COVID-19 во всех штатах США по неделям с 7.03.2020 г. по

возрастным группам (https://gis.cdc.gov/grasp/covidnet).

Словакии при уровне вакцинации 54%. Интерес-

осенней волне 2021 г. выбивается ряд стран, где

ны очевидные различия для людей из одной этни-

ограничения то снова вводят, то отменяют. В дру-

ческой группы, постоянно живущих в разных ре-

гих регионах наблюдается начало следующей фа-

гионах. Наша гипотеза об иммунологической

зы роста заражений - динамика асинхронна. По

причине столь заметных различий из-за влияния

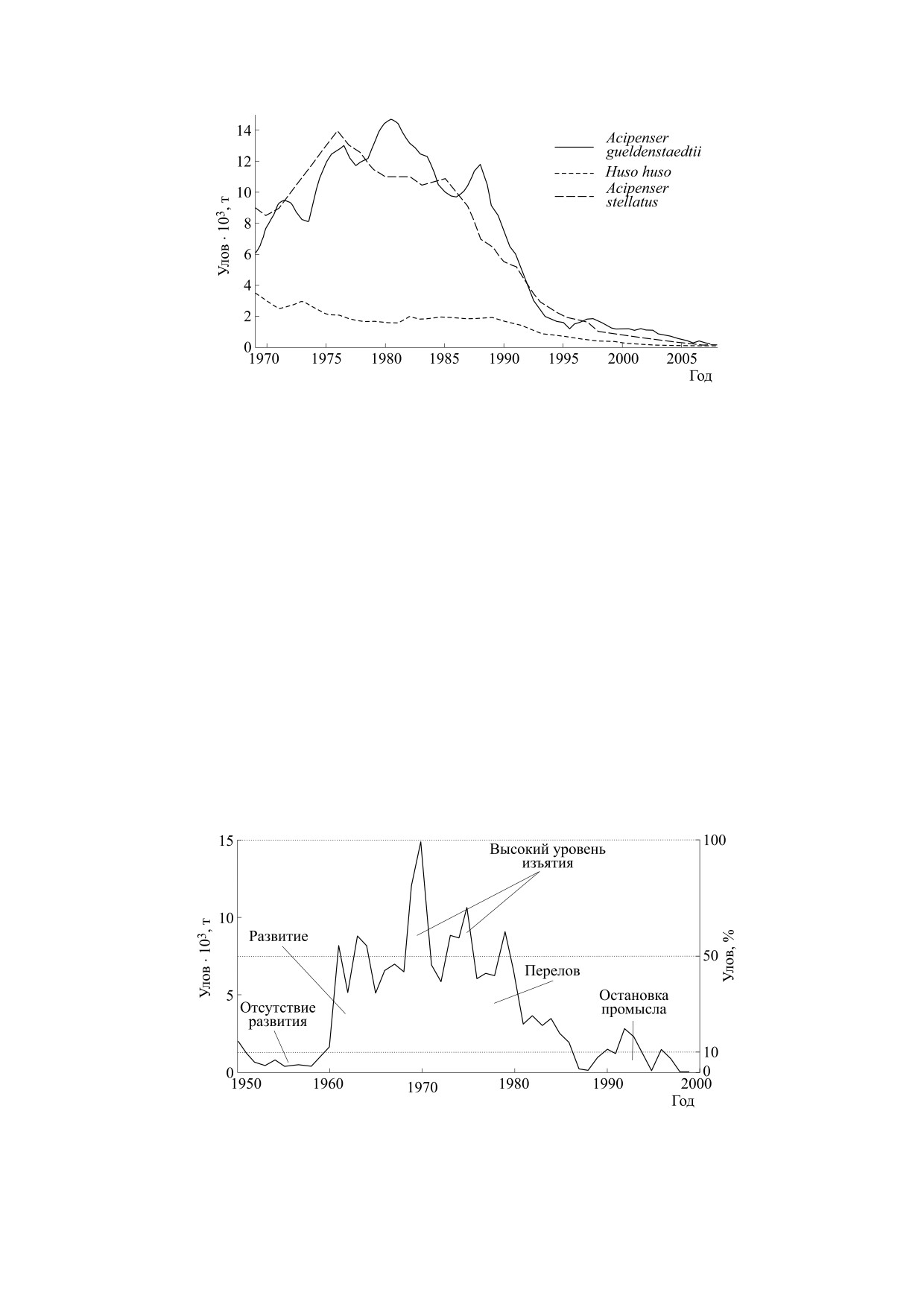
графику, приведенному на рис. 3, уже понятно,

в прошлом распространения сезонных коронави-

что заболеваемость на пике четвертой волны в на-

русов, предложенная весной 2020 г. в работе [1],

шей стране ощутимо превзойдет максимум 2020 г.

получила обоснование. В работе [3] выявлены и

Предложенные весной 2020 г. модификации

перекрестно-реактивные иммунные T-клетки, и

SIR-модели эпидемии не смогли предсказать

идентифицирован универсальный иммунодоми-

долгой колебательной динамики. В работе [5] ав-

нантный пептид.

торы даже строго доказали, что их система урав-

Множество работ еще будет посвящено анали-

нений не имеет орбитально устойчивых периоди-

зу причин различий характера локальных эпиде-

ческих решений. В 2021 г. развиваются нелокаль-

мий и их моделированию. В Дании видим крат-

ные SIR-модели с решением в форме бегущих

кую вспышку числа заражений, переходящую в

волн. Методы, описывавшие локальные вспыш-

спорадическую динамику без отчетливых перио-

ки гриппа, для условий пандемии не подходят.

дических эффектов. Отметим интересный для

Исторические аналогии на основе сценариев «ис-

биокибернетики аспект общности у нелинейных

панки» и «свиного гриппа» не помогут модель-

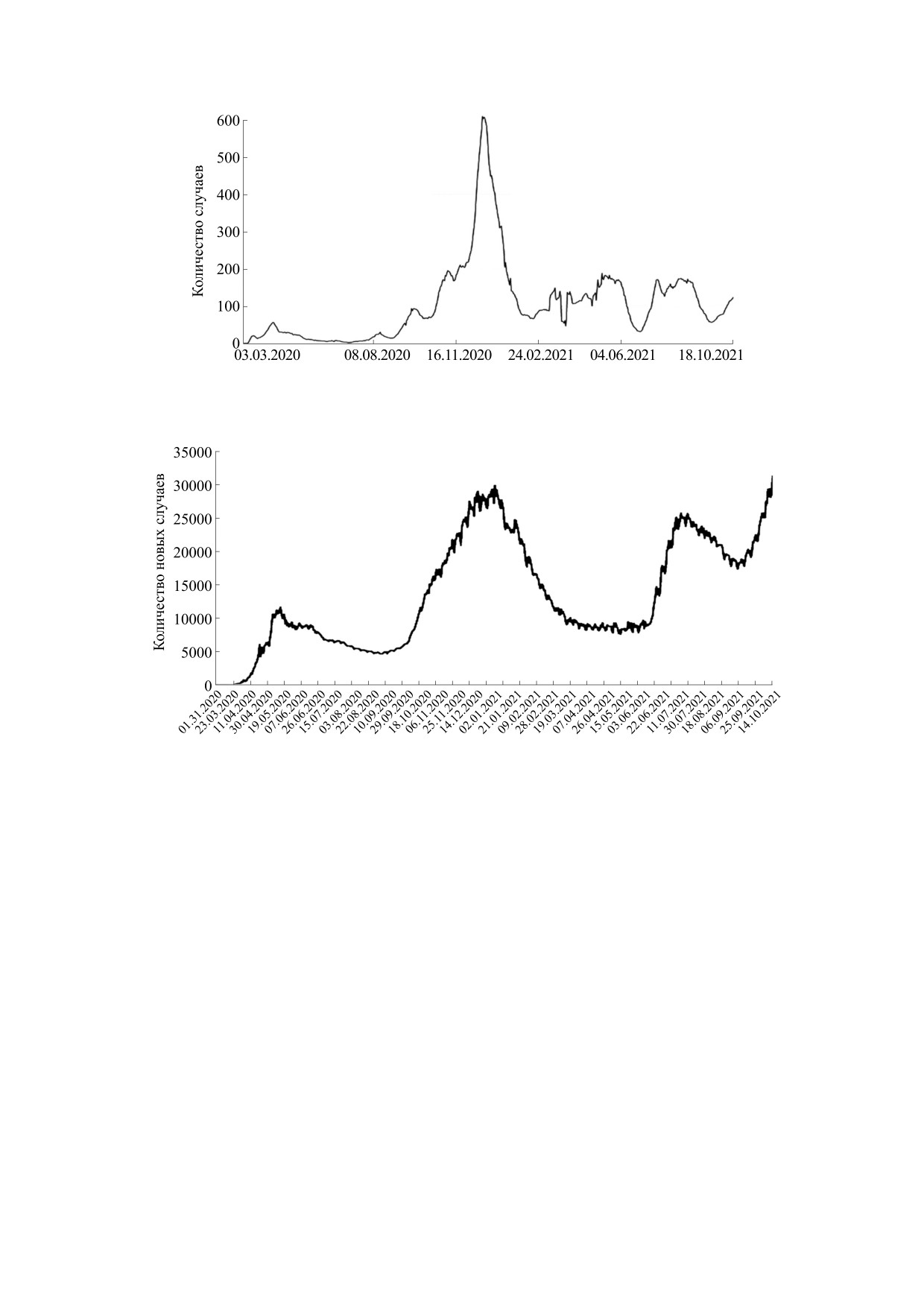
эффектов. Сценарий эпидемии в Дании на гра-

ным прогнозам, четырех волн у прошлых панде-

фике (рис. 2) динамически схож с картиной раз-

мий гриппа не было. Пандемию «русского грип-

вития и быстрого завершения через месяц

па» в

1889-1892 гг. вероятнее всего вызвал

вспышки размножения у псиллид рода Cardiaspi-

коронавирус HCoV-OC43, в дальнейшей эволю-

na в Австралии с пороговым сценарием запуска и

ции потерявший свою патогенность, но образо-

с вероятностью повторения Λ-образного пика у

вавший четыре типа - это путь снижения пато-

вредителей при стохастичном поведении популя-

генности вируса при необходимости ускользания

ции [4].

от иммунитета.

Глобальная динамика пандемии в конце ок-

тября

2021 г. демонстрирует промежуточный

Необычный в биосистемах сценарий ступен-

тренд уменьшения случаев заражения (и доли

чатых релаксационных осцилляций и без сниже-

смертельных исходов) в фазе затухания третьей

ния амплитуды мы можем феноменологически

волны. Из тенденции уменьшения смертности в

описать следующим уравнением:

⎛

⎞

−L[

A t)]

K -N

−τ)

rN t)e

⎜

⎟(H -N(t

−τ)),0

H <K

(1)

(K +cN(t

−τ

))

⎝

⎠

БИОФИЗИКА том 67

№ 2

2022

388

ПЕРЕВАРЮXА

Рис. 2. Динамика случаев заражения COVID-19 в Дании (там отслеживают каждый случай) по неделям с выраженным

пиком в декабре 2020 г. (https://coronavirus.jhu.edu).

Рис. 3. Динамика волн эпидемии COVID-19 в России по официальной статистике ежедневных регистрируемых случаев

заражения (https://coronavirus.jhu.edu).

В уравнении (1) K - величина эпидемического

полнительного возмущающего фактора усиления

порога для запуска экстремального роста заболе-

распространения. Аналогичная динамика нару-

ваемости при r > 1, H - предпороговое состояние

шения цикличности резкой вспышкой уже на-

накопления активной группы распространите-

блюдалась в апреле 2021 г. в Бразилии. Предполо-

лей. H действует в уравнении (1) по отношению к

жительно причиной стал «тревожный» штамм

числу заболевающих в некоторый момент ранее,

(Delta AY.4.2), но сейчас это может быть пока не-

отстающий на средний интервал времени латент-

известный вариант. Delta возник еще в 2020 г. В

ной стадии инфекции. Согласно данным графика

работе [6] показано, что угроза от Delta связана с

мутациями не только S-белка, но и с улучшения-

на рис. 3 мы оценим H ≈ 5000. Включим e-L[A(t)]

ми структурного N-белка нуклеокапсида, увели-

как функционал демпфирования, задающий ито-

чившими процент сборки внутри клетки функци-

говое затухание волн любой пандемии при t → ∞.

ональных вирионов, пригодных для дальнейшего

Теоретически эффект достигается с пороговым

заражения. У ВИЧ только ≈1.5% новых вирионов

уровнем «коллективного иммунитета» A(t) (по

функциональны.

разным прогнозам экспертов от 75% или даже

92% в популяции).

Мутации продолжат возникать как случайные

В реальном сценарии вместо фазы затухания

события в ослабленных организмах носителей,

третьей «волны» с конца сентября сразу началась

но факторы отбора вариантов не столь стохастич-

четвертая волна, что говорит о воздействии до-

ны и могут измениться. Для моделирования инте-

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

389

ресно, что накопление мутаций у S1 регистриро-

промысла аналогично локальным эпидемиям

вали сразу сериями. После множественных мута-

значительно различается по известным приме-

ций следовали интервалы стабильности.

рам, но имеет и важные аспекты сходства ситуа-

Адаптивная эволюция субъединицы вирусного

ций, которым мы сопоставим нелинейные эф-

белка S1 в 2020 г. была коррелирована с увеличе-

фекты.

нием инфекционности - отбором по аффинно-

сти его связывания с клеточным рецептором.

СЦЕНАРИИ ПРОМЫСЛОВОЙ ДЕГРАДАЦИИ

Опасный сценарий, когда при низких темпах вак-

И ПОПУЛЯЦИОННОГО КОЛЛАПСА

цинации провоцируется отбор мутаций y S-белка,

преодолевающих гуморальный иммунитет, - им-

Регулируемый согласно квотам допустимого

муноглобулины планомерно начнут утрачивать

улова промысел нередко приводил к деградации

аффинность в связывании с обновленными

биоресурсов, как локальных [15], так и имеющих

участками S-белка. Роль антителозависимого

огромный океанический ареал [16]. Проблема оп-

усиления инфекции в развитии осложнения «ци-

тимальной эксплуатации запасов далека от ис-

токинового шторма» анализировали в работах [7,

черпывающего решения. Иногда выделенные

8]. Эффект ADE для COVID установлен пока

при явном кризисе расчетные квоты для промыс-

только в лабораторных опытах с животными в ра-

ла все равно не осваивались даже на 30%, как в

боте [9]. Вероятностный эффект ADE способен

Каспийском бассейне в 2006-2010 гг. [17]. Резкой

приводить к циклическому локальному эффекту

деградации подвержены и короткоцикловые ви-

подъема заболеваемости, когда наличие антител,

ды, и крупные хищники, но с существенными

выработанных ранее для некоторых «дрейфую-

различиями в их темпах восстановления. Именно

щих» антигенов старых штаммов, способно стать

типизация по мере сходства/различия в этапах

негативным фактором заражения макрофагов.

сценариев интересна нам для анализа нелиней-

Предлагаемое решение для остановки процесса -

ной динамики кризисных популяций. Важны

ревакцинация населения c вакцинами разных

случаи с достоверными оценками и данными

технологий. В Чили получившим инактивиро-

уловов.

ванную вакцину решили делать третью прививку

Важнейший аспект, на который мы с матема-

дозой мРНК-вакцины.

тической точки зрения обратили внимание при

сравнении разных случаев, - деградация биоре-

Обсуждается ряд гипотетических методов

сурсов происходит либо постепенно с небольшой

инактивации коронавируса [10, 11]. Помимо фор-

мирования долгосрочного иммунитета за счет

(<10%) ежегодной убылью, либо в форме финаль-

Т-лимфоцитов CD8+ невыясненной остается ме-

ного коллапса. Пример затянувшейся на полвека

деградации, вызванной чрезмерным промыслом

ра влияния исходной дозы заражения на дисрегу-

и нарушением естественного речного стока Вол-

ляцию иммунного ответа [12, 13] и осложнений

ги, - ситуация с популяциями осетровых рыб

при COVID [14]. В опасном сценарии выброс ци-

токинов изначально замедлен из-за ингибирова-

Каспийского моря [18]. Четыре вида включены с

ния вспомогательными белками вируса активно-

2010 г. в «Красную книгу» как находящиеся под

угрозой исчезновения. Официальные статисти-

сти интерферонов, но потом резко усиливается,

ческие данные, приведенные на рис. 4 [19], не

так лавинообразно запуская губительную петлю

включают нелегальное изъятие. Сейчас в между-

положительной обратной связи воспалительной

реакции.

народных документах ООН призывает страны бо-

роться с NNN-промыслом - нелегальным, нере-

Для описания приведенных на графиках трех

гулируемым и несообщаемым. Необходимо знать,

разных сценариев эпидемической динамики тре-

сколько в реальности выловил субъект, даже име-

буется использование разного специального ма-

ющий легальное право на вылов, более того, для

тематического аппарата, способного генериро-

прогнозирования необходимо представлять и

вать именно нужные нам нелинейные эффекты.

гендерное, и размерно-возрастное распределение

Их число ограничено фундаментальными теоре-

особей улова.

мами, что заставляет нас комбинировать методы.

Причина столь длительного истощения запа-

Обсудим другую важную ситуацию стреми-

сов при хищническом вылове - сложная внутри-

тельных изменений в популяционных процессах -

популяционная структура у этих рыб c сезонны-

явления деградации при контролируемом вмеша-

ми расами [20] и эволюционная адаптация осет-

тельстве. Цель работы - конструирование вычис-

ровых к размножению на ограниченных

лительной структуры с алгоритмическим пред-

русловых нерестилищах [21, 22]. Заходящие в ре-

ставлением событийности в непрерывном време-

ки Волгу или Урал субпопуляционные группы

ни для сценарного моделирования вариантов

рыб раньше или позже основной нерестовой

деградации запасов, происходящих как неожи-

группы получали шансы избежать промысла в ре-

данный коллапс при ведении управляемого про-

ке, но эффективность их воспроизводства ниже,

мысла. Динамика развития кризисов морского

чем при оптимальном [23] уровне половодья и

БИОФИЗИКА том 67

№ 2

2022

390

ПЕРЕВАРЮXА

Рис. 4. Динамика деградации трех популяций осетровых рыб Каспийского моря (осетр, севрюга, белуга) по данным объема

официальных уловов [19].

температуре. Анализом данных о миграции моло-

оправдал ожиданий по промысловому возврату.

ди методами скользящего среднего мы ранее

Резкий коллапс запасов принципиально отличен

установили наличие двух максимумов для пока-

от примера затянувшегося вопреки здравому

зателя эффективности нереста севрюги Acipenser

смыслу и очевидного экспертам монотонного ис-

stellatus в Волге. Для осетра Acipenser gueldenstaedtii

тощения ценных запасов, представленного на

был показан единственный куполообразный

рис. 4. В работе [28] явление популяционного

максимум с асимптотой на уровне, составлявшем

коллапса трактуется как снижение численности

половину от максимального, а форма кривой за-

взрослых особей на 90% за три года, и этот кризис

висимости запаса и пополнения y белуги Huso hu-

длится не менее десяти лет.

so не имела экстремума [24, 25], но наш интервал

Случаям промыслового коллапса гидробион-

данных был неполон, так как запасы белуги были

тов, его причинам и выявляемым признакам по-

истощены еще в начале XX века.

священо много работ для разных объектов про-

Схожая ситуация с долгой 35-летней деграда-

мысла, например, для моллюска Chlamys islandica

цией (по данным работ [26, 27]) наблюдалась для

[29]. Принципиальная схема развития коллапса

судака Stizostedion lucioperca в Азовском море. В

запасов по графику уловов при повышении уров-

ситуации с осетровыми рыбами имелись возмож-

ня изъятия согласно обзору [30] приведена на

ности остановить промысел задолго до точки де-

рис. 5. Непосредственно перед фактом коллапса

градации. Искусственный выпуск молоди не

уловы прошли пики, но еще достаточно высоки.

Рис. 5. Динамика уловов для общего сценария схемы коллапса запасов (по данным работы [30]).

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

391

системных переоценках состояния запасов. Мно-

гие авторы обсуждали ситуацию с деградацией

этого массового доминирующего хищника в во-

дах провинций Ньюфаундленд и Лабрадор. Рас-

сматривались ошибки в регуляции рыболовства,

недостоверность оценки пополнения поколений

из-за погрешности методов учета, селективность

изъятия крупных рыб, сопутствующие природ-

ные факторы течений у берегов Северной Амери-

ки [33]. Селективность изъятия крупных и плодо-

витых особей приводит к последствию, когда в

популяции станут преобладать «тугорослые» и

быстросозревающие генетические формы, но они

отличаются повышенной посленерестовой

смертностью (известный рыбакам пример - бал-

тийская корюшка Osmerus eperlanus и ее коротко-

цикловая форма озерный снеток).

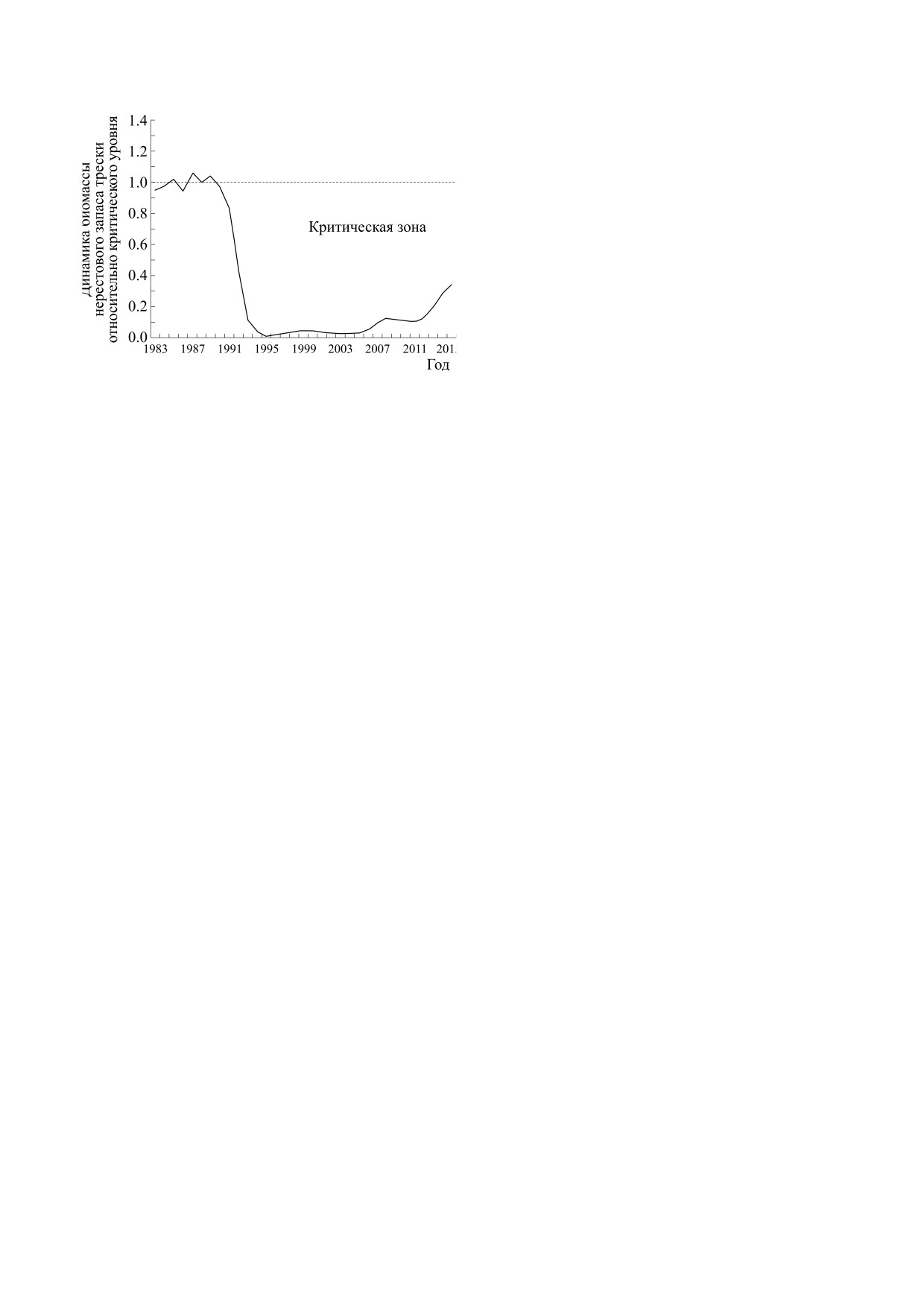
Рис. 6. Динамика биомассы нерестового запаса трески у

провинции Ньюфаундленд и Лабрадор относительно

Эксперты не выработали консенсуса о причи-

критического уровня LPR (в млн. т., по оценкам в рабо-

нах коллапса для случая трески, но было выдви-

те [35]). С 2015 г. отмечается уверенный рост нерестово-

нуто много версий и гипотез, в том числе для

го запаса популяции и к 2030 г. можно ожидать дости-

жения критической отметки запаса.

оправдания своих просчетов. Значимым неучтен-

ным промысловыми прогнозами фактором стало

усиление каннибализма трески при обилии соб-

Следовательно, подобная гипотетическая попу-

ственной молоди. Изначально мораторий на вы-

ляция могла длительное время выдерживать вы-

лов трески регулирующие органы установили на

сокий уровень доли изъятия (q > 0.6), и это бы

полтора года. По самым пессимистичным экс-

считалось нормой. Это подтверждают случаи и с

пертным прогнозам восстановление после кол-

атлантической треской [31], и с волжской севрю-

лапса должно было занять девять лет [34], однако

гой, где в отдельные маловодные годы изъятие из

промысел не был восстановлен и через 20 лет.

нерестовой части популяции доходило до q ≈ 0.8.

Именно отсутствие ожидаемого по модельным

Надежды на восстановительный резерв за счет

прогнозам начала восстановления запасов основ-

еще не вступивших в промысловый возраст поко-

ная проблема в сценарии кризиса у крупных и

лений в итоге нивелируются долгим созреванием

долгоживущих видов. Предполагалось скорое

молоди этих видов, которая еще столкнется и с

восстановление за счет еще неиспользуемых про-

неоптимальным гендерным распределением из-

мыслом гипотетически многочисленных резерв-

за разного времени созревания у самцов и самок,

ных поколений трески, но их численности не-

которые будут представлять в момент первого не-

ожиданно не хватило.

реста поколения с существенно отличающейся

График динамики уловов трески с интервалом

численностью.

длительной стабилизации между пиком рекорд-

Считалось, что резкому, но краткому сокраще-

ных уловов и крахом промысла в 1992 г. известен

нию запасов могут быть подвержены коротко-

и доступен в Википедии. Приведем другой, более

цикловые промысловые виды, такие как перуан-

интересный график расчетной динамики биомас-

ский анчоус Engraulis ringens. Уловы самой вылав-

сы нерестового запаса трески (рис. 6). Современ-

ливаемой рыбы в мире несколько раз быстро

ные оценки из работы [35] явно подтверждают

падали и восстанавливались, но в итоге с рекорд-

действие порогового эффекта, ранее труднообъ-

ных 13 млн. т. в 1971 г. сократились до 1.1 млн. т. к

яснимого для многовозрастного запаса.

2015 г., в том числе из-за частых появлений тепло-

После деградации популяции доминирующего

го течения Эль-Ниньо. Исчерпание промысло-

хищника изменения произошли в сообществе

вых запасов атлантической трески Gadus morhua у

донных гидробионтов. Промысел у берегов Лаб-

берегов Канады - сокрушительный коллапс по

радора переориентировался на донных беспозво-

экономическим последствиям oт вынужденного

ночных, увеличивших биомассу без пресса ос-

прекращения промысла начиная c 1992 г. [32]. К

новного хищника. Креветки стали значительно

тому же еще в 1990 г. прогнозы здесь были благо-

крупнее. Аналогичная ситуация наблюдалась и

приятными.

для фауны в Каспийском море, где начался про-

Правительства провинций Канады строго ре-

мысел ставших крупными бычков, они заняли

гулируют морской промысел, но в сезоны непо-

нишу после истощения запаса осетровых рыб, их

средственно перед коллапсом выделенные ими

хищников и основных потребителей бентоса. Из-

квоты полностью не осваивались, что говорит о

менилась размерно-возрастная структура попу-

БИОФИЗИКА том 67

№ 2

2022

392

ПЕРЕВАРЮXА

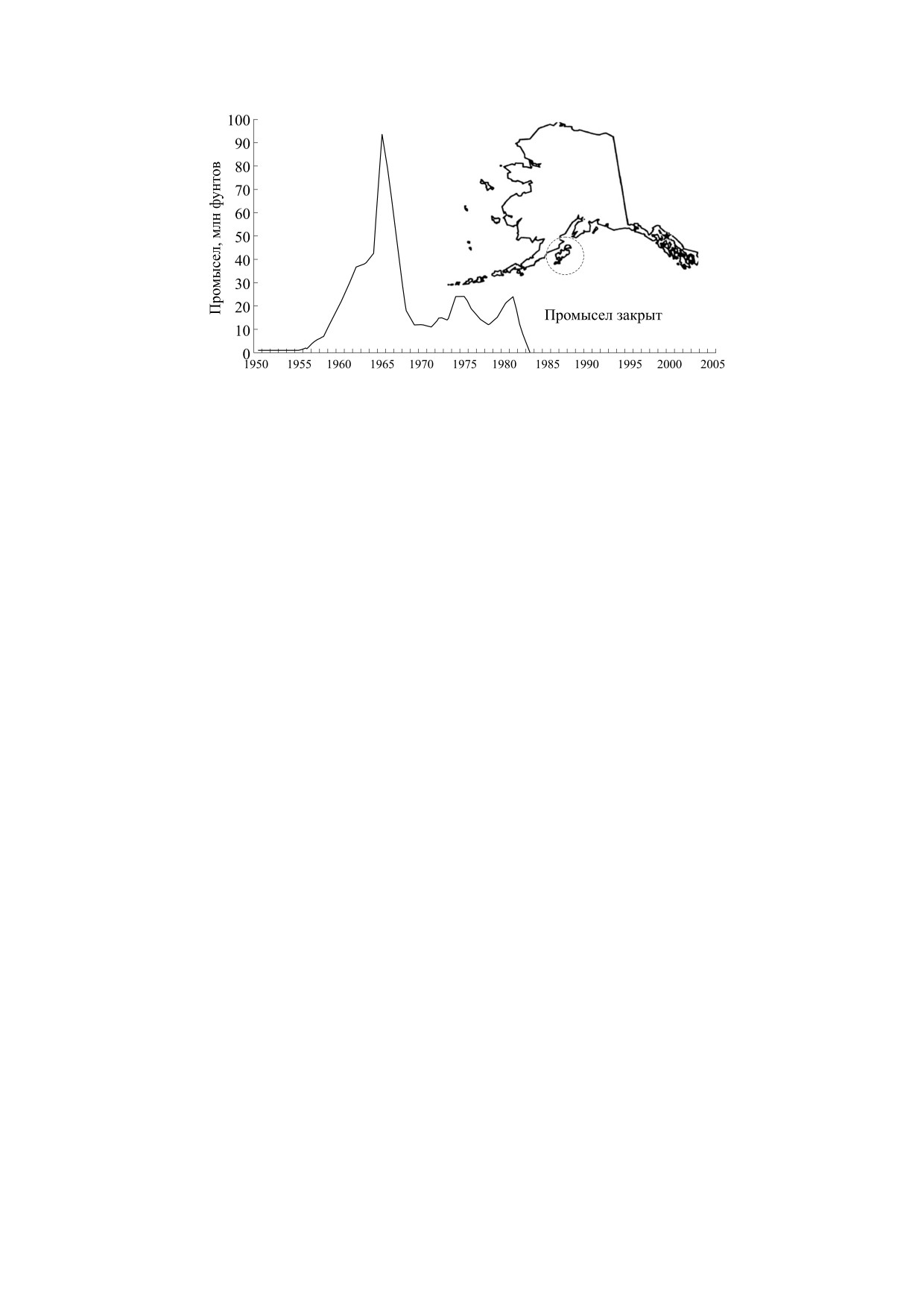
Рис. 7. Динамика промысла краба Paralithodes camtschaticus у берегов Алеутского полуострова Аляски и островов

Кадьякского архипелага с коллапсом (по данным работы [43]).

ляций моллюсков, которые ранее потреблялись

вертьвековых периодов колебаний y дальнево-

осетровыми. К 2000 г. стали преобладать крупные

сточной сардины Sardinops melanostictus [42] эти

особи

[36]. Однако высокую продуктивность

циклы не нарушил современный глобальный

обеспечивают молодые организмы. Исторически

климатический тренд потепления. Цикл может

запасы осетровых рыб поддерживала кормовая

быть альтернативным устойчивым режимом су-

база бентоса с низкой биомассой, но с высокой

ществования биосистемы, наряду с равновесием

продуктивностью. Рацион для молоди осетровых

в другом диапазоне значений численности ее со-

и трески в реальности сократился.

ставляющих (в иной области притяжения аттрак-

тора). Проблема управления в том, что эксперты,

С точки зрения нелинейной динамики перед

определяющие уровень промыслового изъятия

коллапсом трески наблюдалось полуустойчивое

(сезонные квоты), не готовы к сменам естествен-

состояние равновесия, ниже которого воспроиз-

ных трендов. Если эксперты отчетливо наблюда-

водство сокращается по ступенчатой функции.

ли позитивную тенденцию на восходящей «вол-

Подобные пороговые переходы уже известны и в

не» популяционного цикла, то склонны экстра-

моделях для динамики насекомых [37]. Ситуацию

полировать эту тенденцию в прогнозах на

с прогнозом запасов трески просчитывали много-

следующие сезоны.

кратно, по современным оценкам промысловая

численность будет восстановлена к 2030 г. [38].

На рис. 7 представлен график промысла запа-

Анализируя ряд ситуаций в разных регионах, мы

сов камчатского краба Paralithodes camtschaticus

обратили внимание на особенно интересные для

(по-английски этот деликатесный вид-хищник

математической биологии варианты развития

называется «red king crab») с итоговым коллапсом

коллапса.

к 1985 г. в регионе Алеутского полуострова Аляс-

ки - в проливе Шелихова и водах соседних остро-

вов Кадьякского архипелага [43].

СИТУАЦИЯ КОЛЛАПСА ПРОМЫСЛОВОЙ

Многочисленная в Тихом океане популяция

ПОПУЛЯЦИИ КРАБА

краба деградировала за 35 лет эксплуатации при

Несколько отличных по динамике ситуаций

ведении регулируемого квотами и селективного

краха промысла случались и ранее, но эти собы-

по размерам особей промысла и не восстанови-

тия коллапса привлекли только локальное вни-

лась, несмотря на все усилия. Пик вылова краба

мание. Потому мы анализируем более интерес-

был достигнут в 1966 г. В итоге процесс от пика

ный с точки зрения моделирования и не столь

вылова до точки коллапса и моратория на промы-

известный пример динамики деградации эконо-

сел занял 20 лет (1966-1985 гг.). В сценарии до

мически ценных запасов «нерыбного» объекта

момента коллапса прошло гораздо больше време-

промысла.

ни, чем в случае с треской в водах Лабрадора. Пе-

Многим популяциям свойственен естествен-

ред коллапсом уловы краба в течение пяти лет

ный колебательный режим [39, 40]. При этом

стабильно росли до локального максимума, попу-

длительность периода их колебаний может не

ляция считалась благополучной и не было види-

коррелировать с длиной жизненного цикла само-

мых статистикам причин корректировать изъя-

го вида [41]. Так, в случае циклических вспышек

тие. На графике, где показана динамика массы

листовертки Choristoneura fumiferana или чет-

уловов (M, млн. фунтов) краба кадьякской попу-

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

393

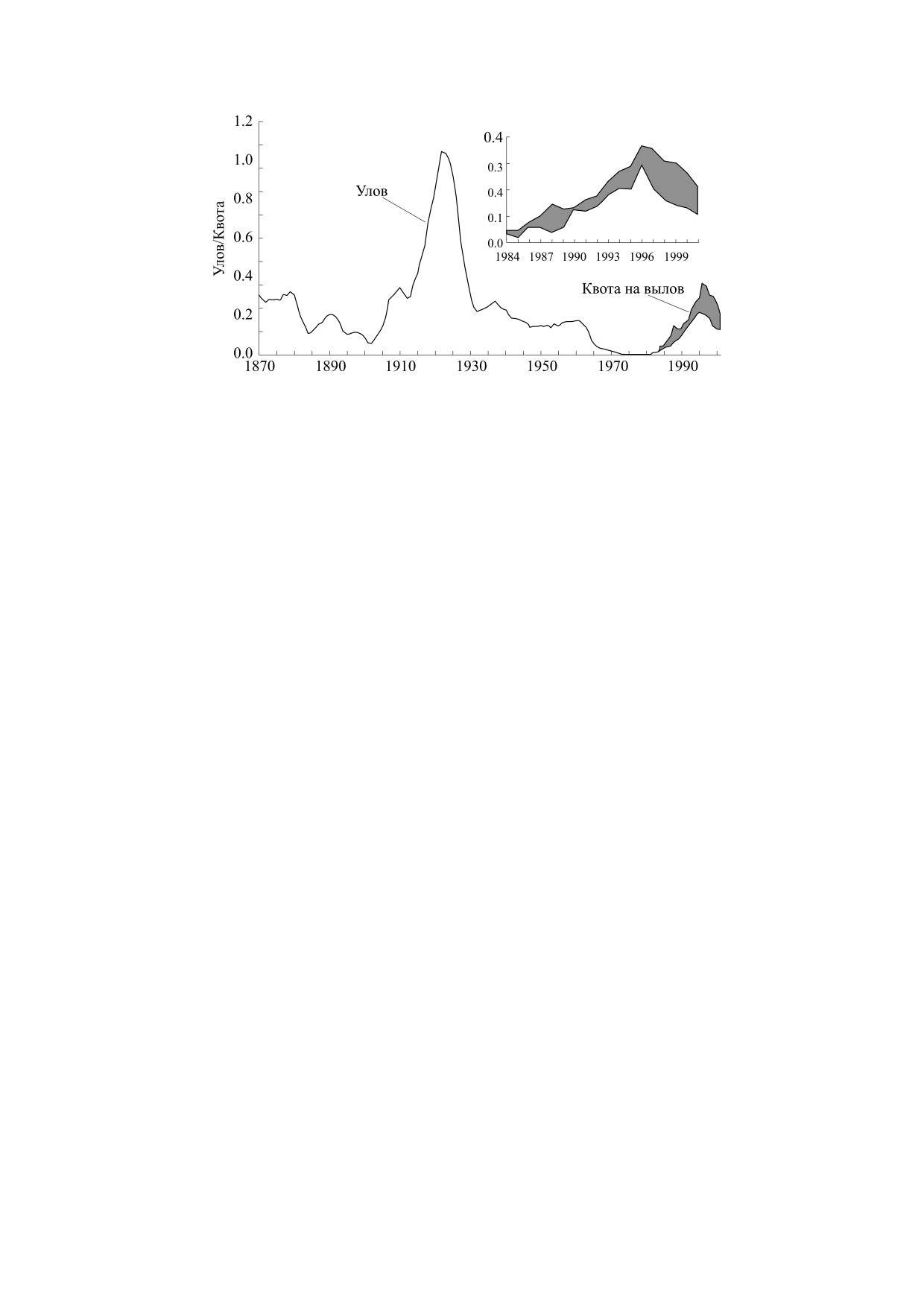
Рис. 8. Динамика уловов сига в озере Онтарио (в млн. кг) с коллапсом в 1965 г. и восстановлением популяции к 1985 г.,

отдельно показана квота на вылов (по данным работы [44]).

ляции, видны два резких падения, связанные co

локальной деградации популяции камчатского

снижением величины запаса S, когда квота не

краба отличается от динамики трескового кризи-

осваивалась промыслом. Первое падение уловов

са именно большим осциллирующим переходом.

в 3.8 раза случилось в 1968 г. Аналогичный пик

Для трески долго наблюдалась псевдостабилиза-

уловов с резким промежуточным падением отме-

ция запаса, оказавшегося в неустойчивом равно-

чался и для канадской трески. Между кризисами

весии. Если сравнить между собой ситуации из-

прошло 17 лет ведения промысла краба с 50%-ми

вестных коллапсов, то c точки зрения нелиней-

колебаниями величины уловов. Восстановление

ной динамики видимые метаморфозы фазовых

запасов краба оказалось сложнее, чем у трески,

портретов имеют не только очевидные сходства,

пока нет данных о появлении позитивной дина-

но и некоторые отличия. У далеких по таксоно-

мики в этом промысловом районе. Мешает вос-

мической классификации видов гидробионтов

становлению гибель крабов в потерянных ранее

регуляция демографических процессов может от-

сетях. Длительность жизненного цикла камчат-

ражаться математически схожим функционалом.

ского краба и трески Северо-запада Атлантики и

Именно проявление пороговых нелинейных эф-

их роль доминирующего хищника (усиленного

фектов и режимов спорадических флуктуаций в

каннибализмом) в сообществе сравнимы.

рассматриваемых сценариях делают нереальным

установление некой универсальной стратегии ве-

Промысел регулируется для деликатесных

дения оптимального промысла. Предвидеть

донных беспозвоночных даже в большей мере

быстрый коллапс и понять его причины статисти-

строго, чем для массовых промысловых видов

кам оказалось сложно. Атлантическими аналога-

рыб, таких как как треска и анчоус, где погреш-

ми являются треска Gadus morhua и краб Paralith-

ность может быть в тысячи тонн. Однако успеш-

odes camtschaticus; это долгоживущие крупные

но планировать будущие уловы можно при ста-

хищники, имеющие резерв репродуктивного по-

бильной доле промыслового возврата от исход-

тенциала, как считалось, они не должны незамед-

ных объемов икры, и когда связь нерестового

лительно коллапсировать подобно анчоусу.

запаса и пополнения R = f(S) удачно аппрокси-

мируется дробно-линейной зависимостью. Для

Ошибочные решения в теории управления бы-

осетровых рыб поправки вносят параметры поло-

вают как случайные, так и систематические. С це-

водья, рассчитываемые корреляционным мето-

лью подтвердить гипотезу, что описанный сцена-

дом. Управление эксплуатацией биоресурсов

рий не является следствием редкого стечения об-

усложняется, когда эффективность воспроизвод-

стоятельств в море или казусом отображения

ства y данной популяции подчиняется обуслов-

разнородно собранной статистики, мы приведем

ленной конкуренцией асимптотической зависи-

еще один нетривиальный пример случившегося

мости, имеющей экстремумы.

коллапса после выраженного пика улова и после-

Случай коллапса краба математически слож-

довавшего двенадцатилетнего интервала про-

нее. После сокращения численности из-за пере-

мысла c перемежающимся трендом. Схожая ситу-

лова в 1965-1967 гг. очевидна резкая потеря рав-

ация развивалась для промысла сига Coregonus

новесия, но сразу возникает колебательный ре-

clupeaformis в озере Онтарио, но с последующим

жим y численности запаса между первым и

восстановлением (рис. 8) [44]. Этот вариант про-

окончательным кризисом промысла. Сценарий

хождения кризиса требует отдельного математи-

БИОФИЗИКА том 67

№ 2

2022

394

ПЕРЕВАРЮXА

ческого обсуждения, так как имеются материалы

Δ[f(S)-S] → max. Подход работает далеко не для

учета по Великим Озерам.

всех промысловых видов. Методика анализа кри-

вых f(S) лучше применима к крупным видам с

Дополнительным неучтенным в промысловых

большой индивидуальной плодовитостью, дей-

прогнозах фактором смертности в случае сига в

ствие на которых стохастичности факторов среды

озере Онтарио стала инвазия в Великие Озера па-

меньше. Их состояние запасов после интервала

разита - морской миноги Petromyzon marinus. С

уязвимости определяет в основном промысловая

миногой активно боролись. Через 20 лет популя-

и отчасти посленерестовая смертность. Таксоно-

ция сига начала восстанавливаться, вновь откры-

мическая близость видов не гарантирует сходства

ли промысел, но выделенная квота для вылова

или просто наличия видимых зависимостей, важ-

снова оказалась чрезмерной, и ситуация с пере-

нее уровень конкуренции за ресурсы и факторы

ловом сига повторилась, как и предсказывала

выживаемости их молоди. Одним из важнейших

принципиальная схема коллапса на рис. 5. Сиг в

факторов автор работы [45] считал каннибализм.

некоторых озерах не восстановился.

Внутривидовое противоборство увеличивается

Все три упомянутых нами сценария деграда-

при высокой плотности запаса на нерестилищах,

ции (каждый по-своему) гораздо сложнее для

что было актуально для изучаемых им видов се-

принимающих решения об уровне эксплуатации

мейства Salmonidae в малых реках Канады. На

специалистов, чем упорно и долго продолжавше-

преодоление этого фактора была направлена эво-

еся истощение запасов осетровых рыб Каспий-

люционная адаптация осетровых рыб Каспия,

ского моря.

для минимизации конкуренции использовавших

Предлагаем сконструировать дискретно-не-

и отдаленные миграции, и нерест в летние меся-

прерывную модель для анализа динамики пере-

цы. Перекрытие миграционных путей нивелиро-

хода от равновесия к колебательному режиму с

вало эту приспособленность.

пороговым эффектом коллапса.

Если резко изменились условия воспроизвод-

ства, то трансформировалось соответственно и

МЕТОДОЛОГИЯ ТЕОРИИ ФОРМИРОВАНИЯ

положение экстремумов зависимости f(S) отно-

ПОПОЛНЕНИЯ ПОПУЛЯЦИЙ

сительно биссектрисы, максимум кривой навер-

няка сдвинулся влево. Из-за таких факторов воз-

Обоснование моделирования с включением

действия необходимы при расчетах более гибкие

гибридных структур будем строить в рамках мето-

методы для математического описания многооб-

дологии теории формирования пополнения.

разия зависимостей и вариативности возможного

Кратко изложим основные математические поло-

развития ситуаций.

жения концепции и подчеркнем неочевидные

проблемы из-за применения этого аппарата при

оценке данных о динамично меняющемся объек-

ДИНАМИЧЕСКИЕ СВОЙСТВА МОДЕЛЕЙ

те. Характеристики эффективности воспроизвод-

И АНАЛИЗ ДАННЫХ

ства в сценарии коллапса должны меняться при

большой убыли запаса относительно историче-

В работе [45] была предложена известная

ского оптимума согласно заложенным функциям

функция воспроизводства (пополнения R от за-

регуляции - сначала гладко снижаться, а потом

паса S) R = f(S) = aSexp(-bS) с двумя параметра-

иметь пороговый эффект, который невозможно

ми: параметр a > 1 - репродуктивный, параметр

описать в традиционных моделях. Модель не

0 < b < 1 учитывает действие факторов конкурен-

должна требовать для описания коллапса «внеш-

ции при повышении плотности. Причина немо-

него» изменения параметров при расчетах.

нотонности зависимости, согласно работе [45],

исходит не только из-за сильной внутривидовой

Математическая теория формирования по-

конкуренции между особями за лучшие места во

полнения популяций гидробионтов была обосно-

время нереста в реках, но и гипоксии. При избы-

вана в работах [45, 46]. Основная идея была сфор-

точности игры в кладках погибшая икра стано-

мулирована в методе построений по данным на-

вится источником для развития патогенных мик-

блюдений функциональной зависимости между

роорганизмов. Кривая имеет один экстремум

существующим родительским запасом и получае-

максимум при S = 1/b и горизонтальную асимп-

мым от нереста пополнением. В работе [45] пред-

тоту limS→∞f(S) = 0. Исследования в области по-

полагалось, что если оценить форму нелинейно-

иска методов определения зависимости в эффек-

сти у зависимости, то можно изымать излишек

тивности воспроизводства продолжаются [47, 48].

запаса в размере того прироста численности, что

окажется выше уровня восполнения - биссек-

Нас интересуют свойства моделей воспроиз-

трисы координатного угла. Тогда оптимальное

водства как динамических систем с разными ат-

решение очевидно - перевести запас S в такое со-

тракторами, а не способы приближения наборов

стояние S_opt, когда положение кривой зависимо-

данных к функциональным кривым. Параметры

сти над биссектрисой будет наибольшее:

обычно «неравноправны» по своему влиянию на

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

395

интерпретации. В дискретных моделях биосистем

хаотизации по Μ. Φейгенбаyмy лучше избегать,

но даже не из-за появления самого режима хаоса,

а из-за ряда эффектов периодических окон.

Для этого достаточно нарушить критерии каскада

удвоения c p

∞, наиболее приемлемый

вариант - специально получить для траектории

ϕⁿ(R₀) альтернативные аттракторы. Хаотический

режим возможен и без аттрактора.

Альтернативная модель нелинейной зависи-

мости «запас-пополнение» с трехпараметриче-

ской функциональной итерацией Rn+1 = aR_n/(1 +

+ R_n/K)^b аналогично испытывает бесконечный

каскад бифуркаций удвоения периода, только ха-

Рис. 9. Данные по динамике запаса горбуши с добавлен-

отизация будет происходить при увеличении па-

ной нами траекторией и построенная по регрессионно-

раметра b > 1, устанавливающего интенсивность

му методу Pикера зависимость «запас-пополнение»

воздействия компенсационной (увеличивающей-

[51].

ся от возрастания плотности) смертности. В мо-

дели без экстремумов бифуркаций рождения

циклов не возникает, есть только равновесие

качественные изменения фазовых портретов. В

(возможно, тривиальное) и к нему стремится лю-

итерационной модели Rn+1 = aR_ne-bRn при 0 < a <

бая траектория.

< e² порождаемая итерацией от R₀начальной точ-

Отметим, что построение кривой f(S) по дан-

ки ϕⁿ(R₀ > 0) траектория будет иметь единствен-

ным наблюдений - задача принципиально труд-

норешаемая. В работе [45] предлагались регрес-

ное устойчивое положение ϕ(R^*) = R^* равновесия

сионные методы. Однако с точки зрения динами-

R^* = (lna)/b > 0. При увеличении а до а = e² + ε

ческих систем аппроксимация сгущений точек

равновесие R^* потеряет устойчивость: |f′(R^*)| > 1.

эллиптической формы любой кривой никаких

Вокруг неустойчивой стационарной точки воз-

прогностических возможностей не даст. В дис-

никнет цикл с периодом p = 2. Однако к этому

кретной динамике циклические траектории (по-

циклу притягиваются почти все точки R₀, кроме

следовательности повторяющихся точек) не по-

хожи на эллипсоиды из непрерывных моделей.

R^* и всех ее точек-прообразов ϕ-n(R^*). Если уве-

Представим, что популяция - естественная дина-

личивать a далее, то будут возникать циклы всех

мическая система, которая развивается согласно

степеней числа 2: p = 2ⁱ, i →∞. Эти изменения при

некоторому математическому закону - оператору

бифуркациях составляют известный

«универ-

эволюции φ. Состояние, в котором в результате

сальный» сценарий хаотизации [49]. Конечное

действия зависимости оказалась популяция,

приращение параметра a ведет к тому, что период

ограничено подмножеством в фазовой плоскости

р станет бесконечным. Потерявшие устойчивость

(поведение диссипативно). В итоге значения чис-

циклические точки R_i* не притягиваются к ат-

ленности запаса стягиваются в подобласть фазо-

вого пространства - окрестность устойчивого

трактору. Важно отметить, что последовательно-

равновесного состояния или предельного цикла

сти бифуркаций c p = 2i+1 происходят идентично

конечного периода, но изображающие точки

для всех функций с постоянным отрицательным

остаются в рамках ограниченного подмножества

особым соотношением старших производных -

ϒ ± ε на фазовой плоскости R × S.

«шварцианом». Характеристика функции, рас-

считанная co второй и третьей производными

Траектории дискретных динамических систем

f(S), как и две константы универсальности Φей-

имеют притягивающие множества, которые для

различных функциональных зависимостей могут

генбаума, не имеют экологической интерпрета-

быть топологически эквивалентными. Набор то-

ции [50], но определяют тип поведения итераций.

пологических типов аттракторов ограничен. На

Можно обсуждать, высокий ли репродуктив-

рис. 9 представлен пример - график на плоскости

ный потенциал или сильно зависимая от плотно-

R × S с данными о численности горбуши с двух-

сти смертность ведут к хаотизации по модельно-

летним жизненным циклом в одной из рек из ра-

му прогнозу. На самом деле математическая тео-

боты [51] с построенной автором гипотетической

рия образования глобального аттрактора в виде

куполообразной формой кривой пополнения. Мы

канторовского множества на основе анализа ре-

добавили траекторию в форме диаграммы Ламе-

нормализации группы не имеет биологической

рея. Очевидно, что зависимость между смежными

БИОФИЗИКА том 67

№ 2

2022

396

ПЕРЕВАРЮXА

поколениями горбуши существует, иначе бы точ-

нелинейными эффектами, необходимыми нам

ки не лежали под стрелками от биссектрисы, но

именно для данной задачи.

сложная динамика не может быть объяснима по-

В экологические модели часто необходимо

строением такой кривой. Итерация нарисован-

вводить дополнительные условия и для начала, и

ной автором работы [51] функции с одним макси-

для завершения действия фактора, так как ход

мумом здесь имеет просто устойчивую стацио-

процессов может меняться скачкообразно при

нарную точку - пересечение с биссектрисой

выполнении ряда условий в среде. «Гибридность»

(угол наклона касательной чуть менее π/4). Кри-

сейчас стала слишком широким термином в мо-

терий устойчивости для точки R^* - вычисленное

делировании (понимаются импульсные, автомат-

значение модуля производной в этой точке -

ные и др.) [56]. Автор разрабатывал различно за-

меньше единицы |ϕ(R^*)| < 1. При увеличении угла

писываемые динамические модели, которые от-

носятся к гибридным структурам, разным по типу

наклона касательной >π/4 возник бы короткий

организации переключений. Мы определяем вы-

цикл, но ни одна из присутствующих на рисунке

точек не попадает в ту область графика, где могли

бранное построение как переопределяемую пре-

бы находиться точки такого цикла.

дикативно вычислительную структуру с кадрово-

событийным временем и используем методы

Согласно нашему предположению, кривая для

склеенных вычислений.

данных на рис. 9 должна иметь и максимум, и ми-

нимум, а левая ветвь асимптотически возрастать

Важным для методики является адаптация

при f(S) < S. Динамика горбуши часто может стать

представления модельного времени как последо-

вательности кортежей событий и определение ло-

апериодической. Модель на основе Rn+1 = aR_ne-bRn

гики переключений. Точки в кадрированном не-

c a > 40 в хаотическом режиме предлагалась в ра-

прерывном времени для событий, которые ведут

боте [52] для описания изменений трендов флук-

к перестроениям в системе дифференциальных

туаций у «четных» и «нечетных» популяций гор-

уравнений, можно определять вероятностными

буши Oncorhynchus gorbuscha смежных годов.

или логическими способами. События требуются

Из сгущений точек на графиках нельзя восста-

для описания структурных качественных измене-

новить форму зависимости «запаса и пополне-

ний как особые состояния в пространстве пере-

ния». Оценить форму кривой можно в специфи-

менных с нулевой длительностью.

ческом случае - наблюдаемая популяция посте-

Жизненный цикл стандартной длины развива-

пенно деградировала под действием промысла.

ющегося из икринки водного организма (и рыб, и

Если промысел вывел популяцию из устойчивого

ракообразных) до полового созревания сопро-

режима и воздействие вылова долго преобладало

вождают метаморфозы. Последовательность из

над естественной зависимостью в восстановле-

связанных алгоритмом непрерывных интервалов

нии запаса, то тогда из-за последовательного со-

времени биологически можно обосновать из идей

кращения запаса можно судить o форме кривой

теории этапности развития гидробионтов, разви-

(либо об отсутствии явной зависимости) на гра-

той научной школой B.B. Васнецова [57, 58]. Для

фике данных мониторинга о численности моло-

каждого вида есть наиболее значимые метамор-

ди, применяя метод скользящего среднего.

фозы в эколого-физиологическом развитии, ко-

Именно у таких популяций удавалось подтвер-

торые меняют его роль в трофической цепи сооб-

дить наличие экстремумов у зависимости на гра-

щества и выживаемость, потому зададим разбие-

фике в координатах «запас × пополнение» [53].

ние интервала уязвимости на стадии. Изменение

Корреляционные методы не могут быть надеж-

доли выживаемости на 1% на стадиях в раннем

ными в данной задаче. Замечательный пример

онтогенезе имеет большое значение. В задачах с

ложной явной корреляции в трендах популяци-

переключениями логично задать формат времени

онных явлений показан в работе [54]. В проведен-

c непрерывной и c дискретной компонентой. Для

ном исследовании [55] уже при малых размерах

данной задачи выберем формат, который подхо-

поголовья камчатского краба Кадьякского архи-

дит для моделирования процесса с измененным

пелага явной зависимости «запас × пополнение»

воздействием и особенно в ситуации экспертного

обнаружено не было. Однако динамика позволя-

управления промыслом.

ет иногда решать обратную задачу и предполо-

жить поведение изучаемой системы.

Используем кадрирование иерархии непре-

рывных отрезков времени в вычислительных экс-

периментах c предикативно изменяемой формой

ФОРМАТ СОБЫТИЙ И КАДРОВ ВРЕМЕНИ

воздействия. Внутри основных кадров составим

В МОДЕЛИ ВОСПРОИЗВОДСТВА

порядок из пронумерованных событий tⁱ. Гибрид-

Мы разрабатываем не просто еще одну мо-

ное событийное время для вычислительных экс-

дельную функцию «запас-пополнение», опишем

периментов формализуем в форме мультимноже-

также методику представления функциональной

ства из упорядоченных элементов на фиксиро-

зависимости для сценарного анализа ситуаций с

ванной длине интервала Т:

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

397

менение от N(0) = λS и до N(T), где λ - средняя за

⎧

i+1

⎫

↑

[t ti,t

,T]

,↓

пять предшествующих сезонов плодовитость. Си-

∪

⎨

∪

⎬

⎩

⎭

стема формализуется дифференциальным урав-

где i - номер для события внутри кадров перед

нением c набором возможных «сменных форм»

T, a n - текущий номер кадра в порядке сменяе-

для правой части и дополнительно c набором пре-

мых поколений. Запись времени с двумя дискрет-

дикатов для смены режима расчетов - булевских

ными компонентами оставляет грани {↑L,↓R}

функций Р(x,y) c множеством значений {0;1}.

справа и слева от основной единицы - кадра с но-

Предикат задан математическим отношением не-

мером n. Грани между кадрами времени, не вхо-

прерывно изменяющихся аргументов. Предика-

дящие в кадр в виде точек {↑L,↓R} нужны для вы-

ты по умолчанию при t₀ P(x,y) = 1, но обязательно

полнения перестроений в выделенных условиями

должны будут при tⁱ принимать значение P(x,y) =

пунктах системных переходов. В правой точке ↓R

0 от состояния своих аргументов (либо наоборот

меняются установки величины воздействия про-

изменять значение с 0). Аргументы P(x,y,…) в на-

мысла. В левой точке ↑L проводим переход к рас-

шем методе переменные из вспомогательных, но

чету развития уже следующего смежного поколе-

связанных с динамикой N(t) уравнений, вычис-

ния. Цель формализации времени - точно вво-

ляемых синхронно с уравнениями (2).

дить элементы событийности при управлении,

Время онтогенеза до вступления в репродук-

так как точки t¹, t², tⁱ укажем из расчетов полно-

тивный возраст сменяющихся поколений зада-

стью непрерывных дополнительных переменных.

дим объединением интервалов времени c набо-

Не всегда время c субинтервалами плавающей

ром вычисляемых событий:

длины из-за вычисляемых событий нужно фор-

матировать в фиксированные кадры. Событий-

i+1

∈[0,T]

≡

{[t ti,t

,T]},i

1...3.

∪

ность можно вводить и без установки кадра, как в

физических задачах с релейными переключения-

Биологически интервал кадра - стандартное

ми.

время жизни поколения до начала репродуктив-

Идея манипуляций co временем в том, что вы-

ной активности. Пронумерованные точки собы-

числительная модель жизни поколения форми-

тий в интервале ювенального онтогенеза будут

руется на основе динамически переопределяемой

онтогенетическими «прерываниями». Сопоста-

системы. Факторы убыли численности суще-

вим эти метаморфозы с уравнениями в правой ча-

ственно меняются между стадиями онтогенеза и y

сти для убыли численности поколения от N(0),

ракообразных [59].

которое неравномерно на трех основных стадиях

раннего онтогенетического развития:

БАЗОВАЯ ПРЕДИКАТИВНАЯ

(

wt)N t)

)N t),

P t)

−

+β

⎧

ВЫЧИСЛИТЕЛЬНАЯ СТРУКТУРА

⎪

N t)/

-α -β

w(τ)

N t),

P t,

wt))

(2)

Представляемые в модели изменения по свое-

⎨

му сущностному генезису бывают строго обяза-

−ξ)N(t

−ξ)

−β,

P t,wt)).

⎩-α

тельными, алгоритмически предопределенными

Параметры α₁ < α₂ < α₃ и β здесь являются ко-

во времени, либо необязательными следствиями

иных процессов. Выбор альтернативного уравне-

эффициентами ювенильной смертности в зави-

ния в модели проводится только при особом со-

симости от численности самого поколения. В

отношении рассчитываемых величин. Вторая

третье по порядку из уравнений (2) c α₃включено

идея метода, которую можно применять к разным

малое запаздывание ξ < τ для учета исчерпания

популяциям, - из оценки состояния множества

ресурсов ранними стадиями, где τ - длина самой

предикатов P_i устанавливать события, зa которы-

ранней стадии. Для второй стадии подверженной

ми следуют изменения в процедуре расчета урав-

хищничеству фактор роста w(τ) уменьшает убыль.

нений. Для отражающей биологическую преры-

Предикатами P₁,P₂,P₃ заданы биологически ин-

вистость модели мы предлагаем вычислительную

терпретируемые моменты остановки расчетов

структуру c последовательными переопределяе-

каждой из форм правой части - условия заверше-

мыми формами, сохраняющими преемствен-

ния активности уравнения и получения промежу-

ность. Значение N(t) в каждом кадре проходит из-

точных результатов:

P₁(¬t < τ), P₂(t ≥ τ, t ≠ T, ¬w_t < w_k), P₃(t = T, w_t < w_k).

(2.1)

Два предиката в выражениях (2.1) мы записали

ношений. Расчет уравнений (2) c учетом условий

c логическим отрицанием, таким образом эти со-

(2.1) происходит c алгоритмом цикла до тех пор,

бытия станут возможными при нарушении соот-

пока P_i = 1. Предикаты должны однозначно и все-

БИОФИЗИКА том 67

№ 2

2022

398

ПЕРЕВАРЮXА

гда для каждого t определять события переходов в

но во взаимосвязи co вспомогательным показате-

кадре времени. Избегая неоднозначности, можем

лем среднего размерного развития особей поко-

воспользоваться дополнительно логическими пе-

ления w(t):

ременными-флагами, меняющими состояние с

единицы на ноль, если переход запрещен. Запись

+χ

(3)

непрерывно-событийного модельного времени

³ (

N t)

+δ)

как мультимножества из элементов 〈t₀, tⁱ, ti+1〉

где δ - корректирующий показатель, σ - фикси-

означает, что в модели считается последователь-

рованно отражает обилие пищевых ресурсов, но

ность кадров для времени жизненного цикла от-

может быть и сезонной периодической зависимо-

дельного поколения. Внутри каждого кадра вре-

стью σ(t). Затрачиваемая на рост энергия у гидро-

мени с начальной позицией t₀ имеются «внутри-

бионтов в северных широтах зависит от темпера-

туры [62]. Здесь χ_С ∈ [-ε,ε] - поправка, связанная

кадровые» события, которые мы обозначили

с температурой, она может быть положительной

верхним индексом tⁱ. Использован переходный

или отрицательной. Для оптимальных условий

уровень развития w_k для выхода поколения из

нереста в уравнении (3) примем χ_С = 0. Таким об-

квадратично определенного уровня смертности.

разом, наличие доступной кормовой базы влияет

Набор событий можно расширить. Для каждой

на выживаемость в модели опосредованно.

формы правой части в момент события рассчиты-

ваются сопряженные с предшествующими расче-

Будем вычислять R = N(T) = φ(N(0)) для опре-

тами начальные условия. Для расчета динамики

деления свойств фазового портрета итераций

нового (n + 1)-поколения происходит реинициа-

Rn+1 = φ(R_n). Нас интересуют границы области

лизация начальных условий для первого в струк-

притяжения и особые точки.

туре (2) уравнения:

ПЛАВНО ТРАНСФОРМИРУЕМАЯ

N(0)

=λS

(N T)

+ ∑ υ

N T)

МОДЕЛЬНАЯ ЗАВИСИМОСТЬ

n+1

n n

n-m

m=1

Необходимо отразить действие эффекта агре-

где υ_m - показатель посленерестовой выживаемо-

гированной группы [63], так как мы рассматрива-

сти для серии предшествующих m поколений, a

ем ситуации для популяций вне исторически сло-

S - численность готового к размножению запаса

жившейся численности. При малой численности

со средней плодовитостью λ.

S велика роль неблагоприятных факторов в вос-

производстве [64, 65]. Вводить тут явный мини-

Популяционные процессы даже без влияния

мальный L-порог эффекта Олли, как в уравнении

промысла вариативны. В сценарном применении

Базыкина [66], методически неправильно. Зара-

модели важна оценка текущих значений набора

нее L-порог экспертам неизвестен, и не все изме-

P₁,P₂,P₃. Переходы в уравнениях (2) записаны

нения в регуляции бывают жестко предопреде-

двух типов: только по отсчетам отрезков единиц

ленными. По экологическим критериям недосто-

времени t и вызванные внутренними соотноше-

верно изменять скачком базовые популяционные

ниями у рассчитываемых показателей. Тогда сме-

характеристики.

на формы в уравнениях (2) происходит после

Мы разработали метод учета изменчивости

сравнения соотношений значений по условиям

факторов в форме точечного внедрения в преди-

(2.1) у внутренних модельных переменных - по

кативно переопределяемую динамическую систе-

w(t), но можно использовать иную видоспеци-

му особых функций как варьирующихся коэффи-

фичную динамическую характеристику. Идея ис-

циентов: Ψ(n) ≠ const для итераций ϕⁿ(xn-1,Ψ(n)),

пользовать сопутствующие характеристики и

расчеты вспомогательных показателей позволяет

но только c ограниченным диапазоном их значе-

разнообразно расширять базовую модель. Управ-

ний. Такие функции должны быть постоянны на

ление промыслом представляется по специально-

всем кадре [↑L,↓R] непрерывного модельного

му алгоритму сценария в гибридной модели. Та-

времени. Менять свое значение функции тригге-

кое управляющее воздействие удобно варьиро-

ры в расчетах будут при смене кадра n: = n + 1.

вать согласно заданной логике сценария при

Ψ связана с начальным состоянием.

событийности вычислительного эксперимента.

В уравнении убыли численности поколения

Используем часто отмечаемую у многих видов

разделены коэффициенты смертности: αN² и βN.

[60] взаимозависимость между темпами роста мо-

Величина w(t) при параметре α_i учитывает быст-

лоди гидробионтов и ee смертности, которую

рое исчерпание необходимых для развития ресур-

предлагалось использовать для моделирования

сов по мере повышения общей биомассы личи-

еще в работе [61] c обратной зависимостью w′(t) =

нок. Важно учитывать потери воспроизводства на

l(N^-1(t)). Предикативная структура набора пра-

стадии c t₀. Эффект потерь может сильно про-

вых частей уравнения (3) будет решаться числен-

явиться именно при низкой плотности S → minϕ

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

399

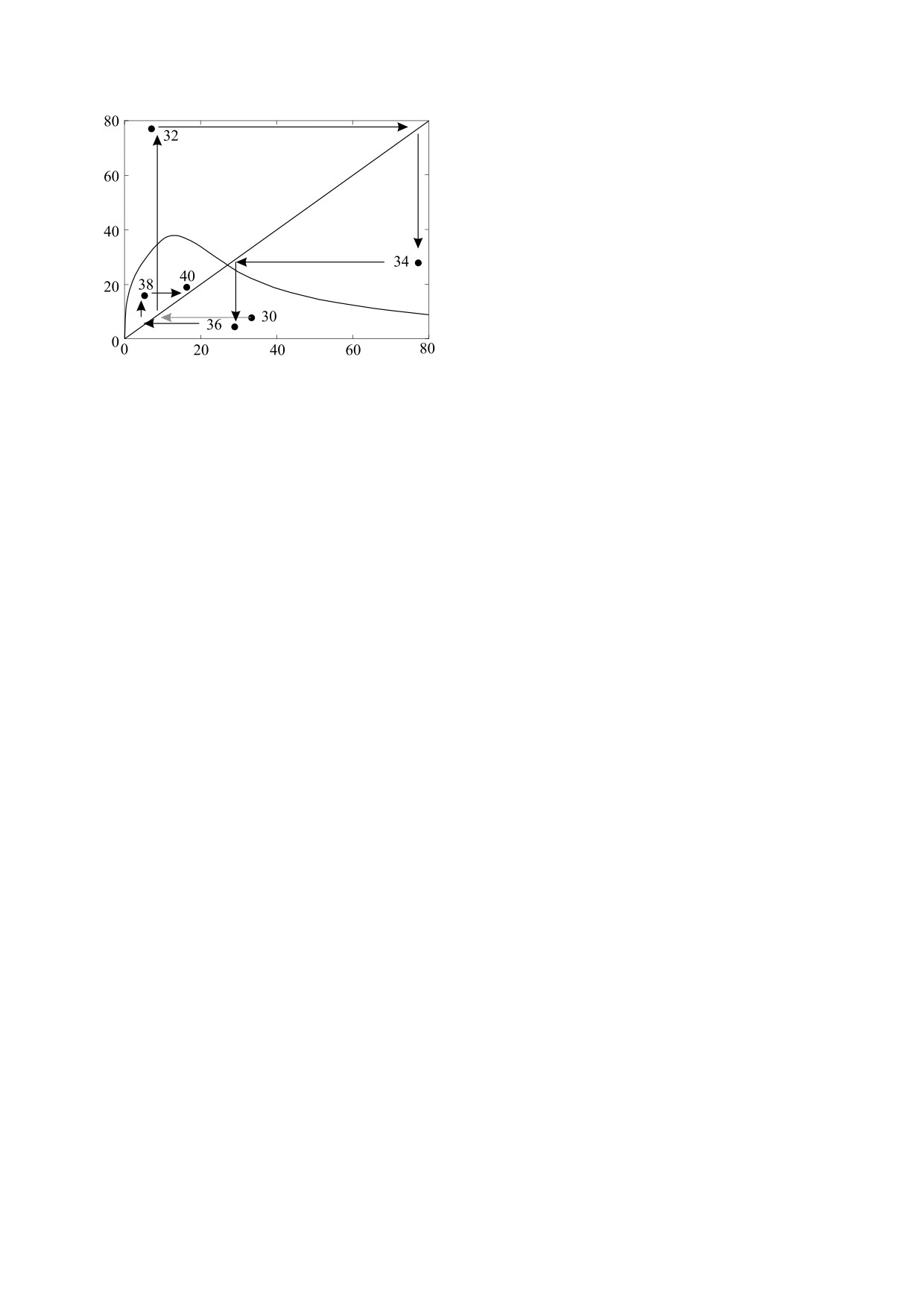
Рис. 10. График модельной зависимости с тремя экстремумами и двумя равновесиями в точках пересечения с биссектрисой

координатного угла.

половозрелых особей, больше икры останется не-

ской популяции S, из которого мы рассчитывали

оплодотворенной. Эффект снижения эффектив-

начальные условия N(0). Диапазон влияния Ψ на

ности воспроизводства для малой группы реали-

f(S) нужно ограничивать. Область значений

зован в модели динамическим коэффициентом с

«функции-триггера» E(Ψ) справа имеет быстро

βN. Влияние его зависит от величины родитель-

достижимый конечный предел:

Ψ(S)

exp(−ζ

+ε),lim

S→∞

Ψ(S)

1,Ψ(0)

Коэффициент ζ (ζ < 1) отразит уровень экс-

зуем для расчета функциональных итераций: Rn+1 =

прессивности эффекта потерь от исходной икры.

= ϕ(R_n) - q_nR_n, где коэффициент q ∈ [0,1) - уста-

Далее при оптимальном запасе Ψ не определяет

новленная доля промыслового изъятия. При ре-

расчеты, что позволит реализовать выключение

гулируемом промысле q устанавливается экспер-

действия фактора гладко в уравнении (2) для пер-

тами на каждый сезон n, что будет учтено в сце-

вой стадии:

нарном исследовании развития ситуации.

Важнейшим параметром модели для изменения

= -αwt)N t)−Ψ[S]βN t).

(4)

формы зависимости и поведения итераций ока-

зывается плодовитость λ, но в экологической ре-

В уравнении (4) мы учли плавные изменения

альности это медленно изменяющaяся характе-

регуляции, тогда как в гибридной системе описа-

ристика.

ли пороговые изменения динамики убыли чис-

В итерациях мы получим разделение множе-

ленности молоди, которые нельзя избежать.

ства доступных начальных точек R₀ траекторий

Структуру гибридной модели в вычислительной

неустойчивой «репеллерной» точкой. Так итера-

среде Rand Model Designer можно адаптировать

ции получат две области притяжения Ω₁ и Ω₂ y

для группы совместно живущих и конкурирую-

двух альтернативных аттракторов. Используемая

щих поколений.

как оператор эволюции ϕ зависимость будет об-

ладать более чем одним максимумом (рис. 10).

МЕТОД АНАЛИЗА ДИСКРЕТНЫХ

Для нас важно положение относительно друг дру-

ИТЕРАЦИЙ ГИБРИДНОЙ МОДЕЛИ

га первого от начала координат максимума R_max и

локального минимума R_min (R_min > R_max), но зна-

Получив c N(0) → N(T) ≡ ϕ(N(0)) функцио-

нальную зависимость после численного решения

чимо сохранение ϕ(R_max) > R_min.

уравнений (2) и (2.1) вместе c (3) и (4) и c

Мы получим семейство актуальных для задачи

N(0) = λS для биологически допустимых значе-

нелинейных кривых с экстремумами и горизон-

ний N(0) ∈ N, можно оценить и динамические

тальной асимптотой, изменяя только воздействие

свойства итераций ϕ(…ϕ(x₀)) этой зависимости.

Ψ и не меняя значения параметров убыли поколе-

Численное решение с вычислением N(T) исполь- ния в уравнении (2). Математическую основу

БИОФИЗИКА том 67

№ 2

2022

400

ПЕРЕВАРЮXА

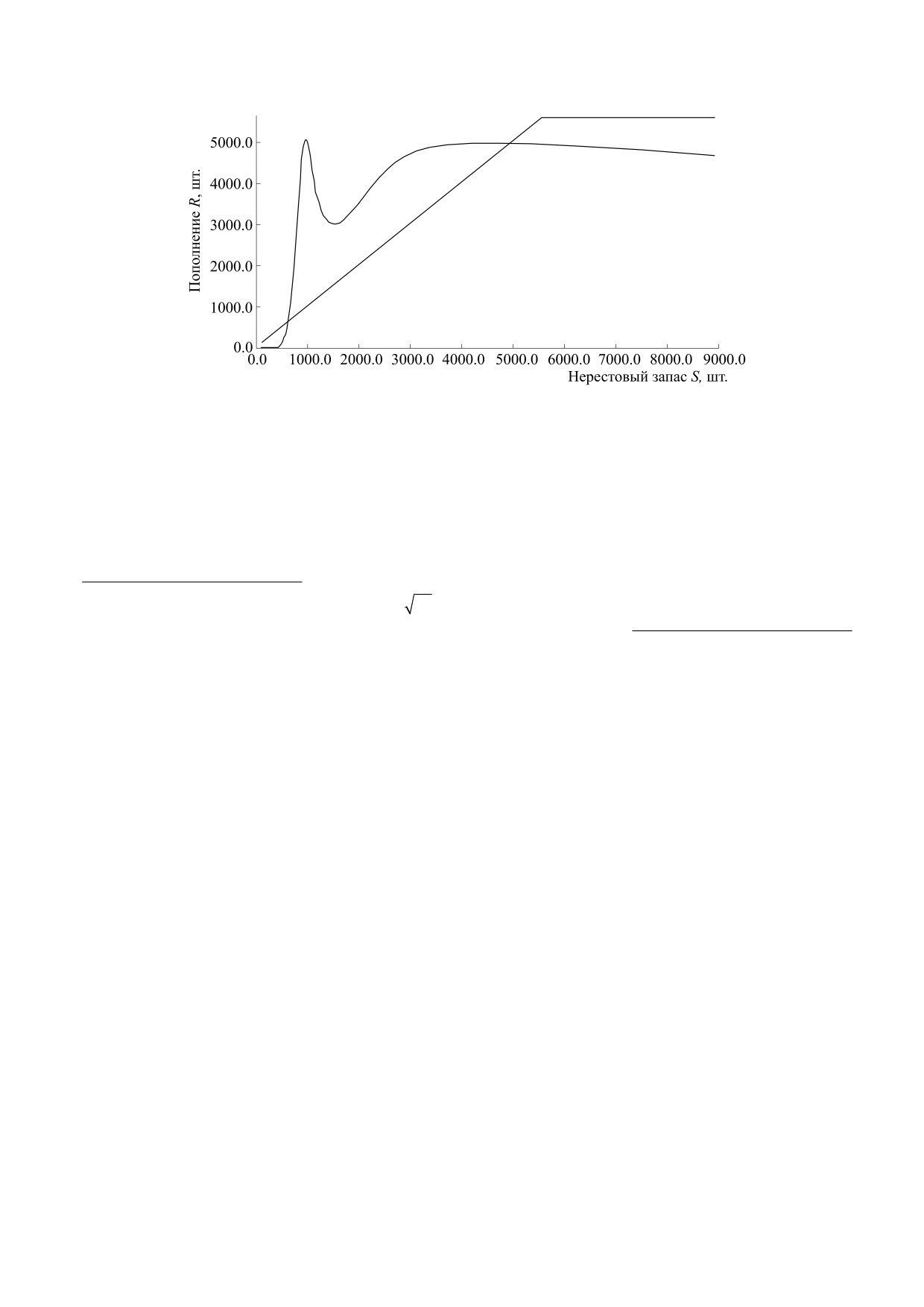
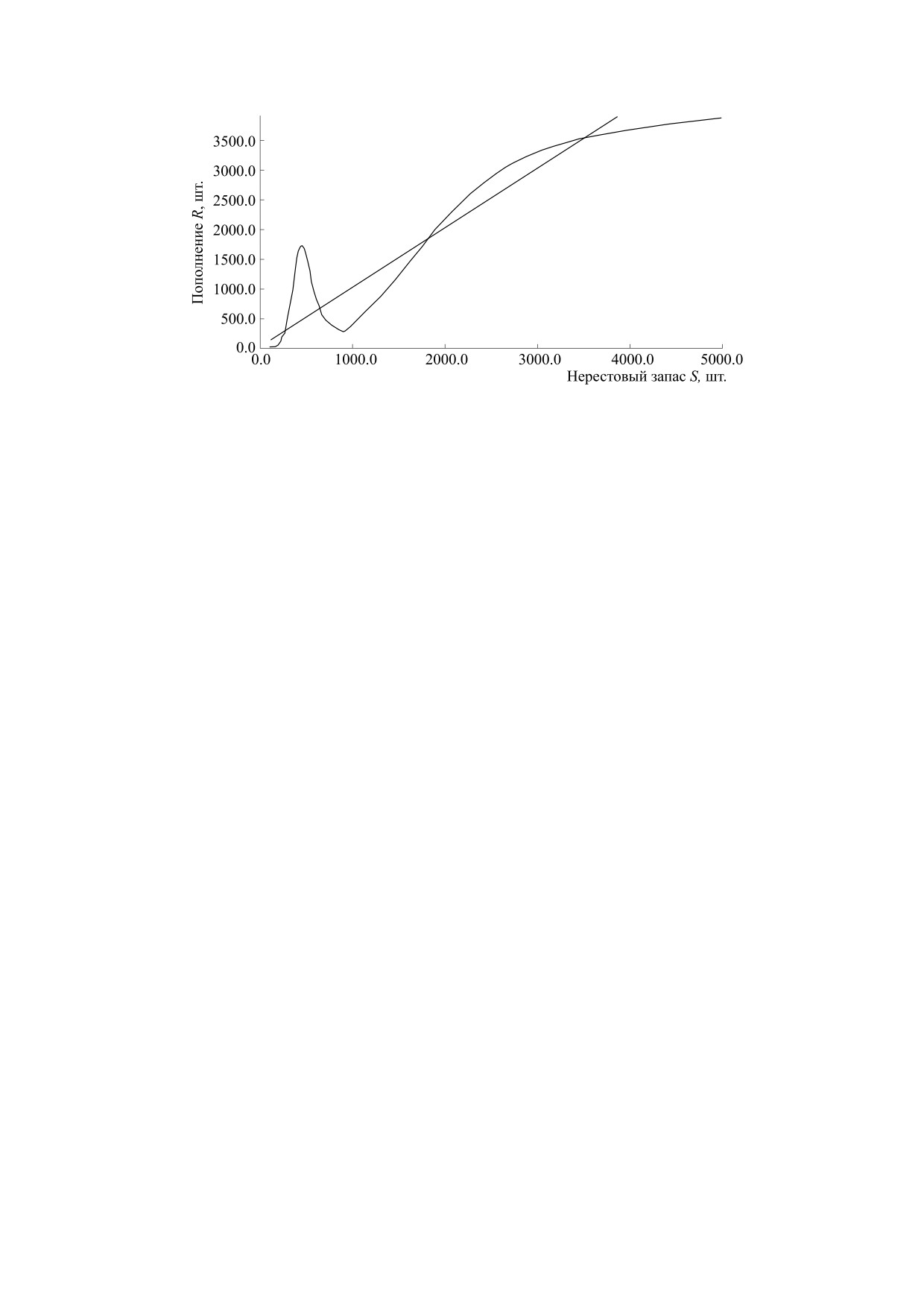
Рис. 11. Модельная зависимость с нетривиальными равновесиями

< R

, пересечениями с биссектрисой

координатного угла при minφ(S) <

, maxφ(S) >

анализа их итераций составит развитая в работе

АНАЛИЗ НЕЛИНЕЙНОГО СЦЕНАРИЯ

[67] теория динамики отображений co значением

КОЛЛАПСА

шварциана, меняющим знак при изменении ар-

Сценарное моделирование, позволяющее

гумента. Для итераций функции xn+1 = ϕ(x) с тре-

сравнивать и оценивать варианты ситуаций, -

мя экстремумами не выполняются условия теоре-

это актуальный подход при регулировании мно-

мы Д. Cингера [68], необходимые для реализации

говидового промысла [71]. Рассмотрим динамику

сценария перехода к глобальному хаотическому

коллапса в сценарном эксперименте с логикой

аттрактору через каскад бифуркаций удвоения

экспертного управления промысловым изъяти-

периода цикла p → ∞ по теории Фейгенбаума-

ем. Математической основой сценария станут

Коллет-Трессера [69], так как при плавном изме-

метаморфозы фазового портрета итераций, вы-

нении параметра y такой итерации xn+1 = ϕ(x)

званные трансформацией экстремумов зависи-

возникнут два альтернативных устойчивых цикла

мости. B сценарной модели лучше рассчитывать

четного периода (p = 2). Соответственно каскад

вместо массы число особей Y_n, изымаемых из за-

не будет бесконечен и канторовское множество

паса S в сезон промысла n, что и составит наблю-

не образуется.

даемую величину.

Арсенал описательных средств y динамики

Для нашей задачи получим зависимость при

итераций широк, но ограничен [70]. Для итера-

решении трех склеенных по N(0)_i задач Коши из

ций Rn+1 = ϕ(R_n) доступны три топологические

уравнения (2) с непостоянным из-за уровня

формы аттракторов: цикл конечного периода или

внешнего воздействия q числом нетривиальных

точка равновесия x^* = ϕ(x^*), аттрактор, подобный

стационарных (ϕ(Ri*) = Ri*) состояний, но их чис-

канторовскому множеству, и интервальный ат-

трактор в виде конъюгации несчетного множе-

ло должно оставаться не менее двух для каждого n.

ства отрезков. Для итераций (c учетом изменяю-

Пусть в исходной ситуации кривая ϕ(S) без значи-

щегося внешнего возмущения) x_n = ϕ(xn-1) ± Θ(n)

мого воздействия характеризуется четырьмя воз-

есть три типа бифуркаций - перестроений типа и

растающими точками 0 < R_1* < R_2* < R_3* < R_4* - рав-

числа аттракторов, которые бывают прямые и об-

новесными состояниями (рис. 11) (положение

ратные. Аттракторы, отличные от точек равнове-

графика модельной зависимости относительно

сий, могут моментально терять свойство инвари-

биссектрисы координатного угла), не совпадаю-

антности f(Λ) ∈ Λ, что зависит от положения гра-

щими с экстремумами кривой. Зависимость c вы-

ницы ∂Ω y их области притяжения Ω. Аттрактор

раженным минимумом была установлена ранее

может разбиться на части или пересечься с грани-

для волжской севрюги [72].

цей ∂Ω ∉ Ω своей области притяжения Ω: ∀x₀ ∈ Ω,

Для целевого перестроения фазового портрета

limn→∞ϕⁿ(x₀) = Λ и в этом момент фиксируется

в сценарии нужны три неустойчивые стационар-

ситуация кризиса. Так теория отображений пере-

ные точки при устойчивости R = 0 для каждого n.

секлась c задачей биокибернетики.

Первый метаморфоз получим, плавно увеличив q,

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

401

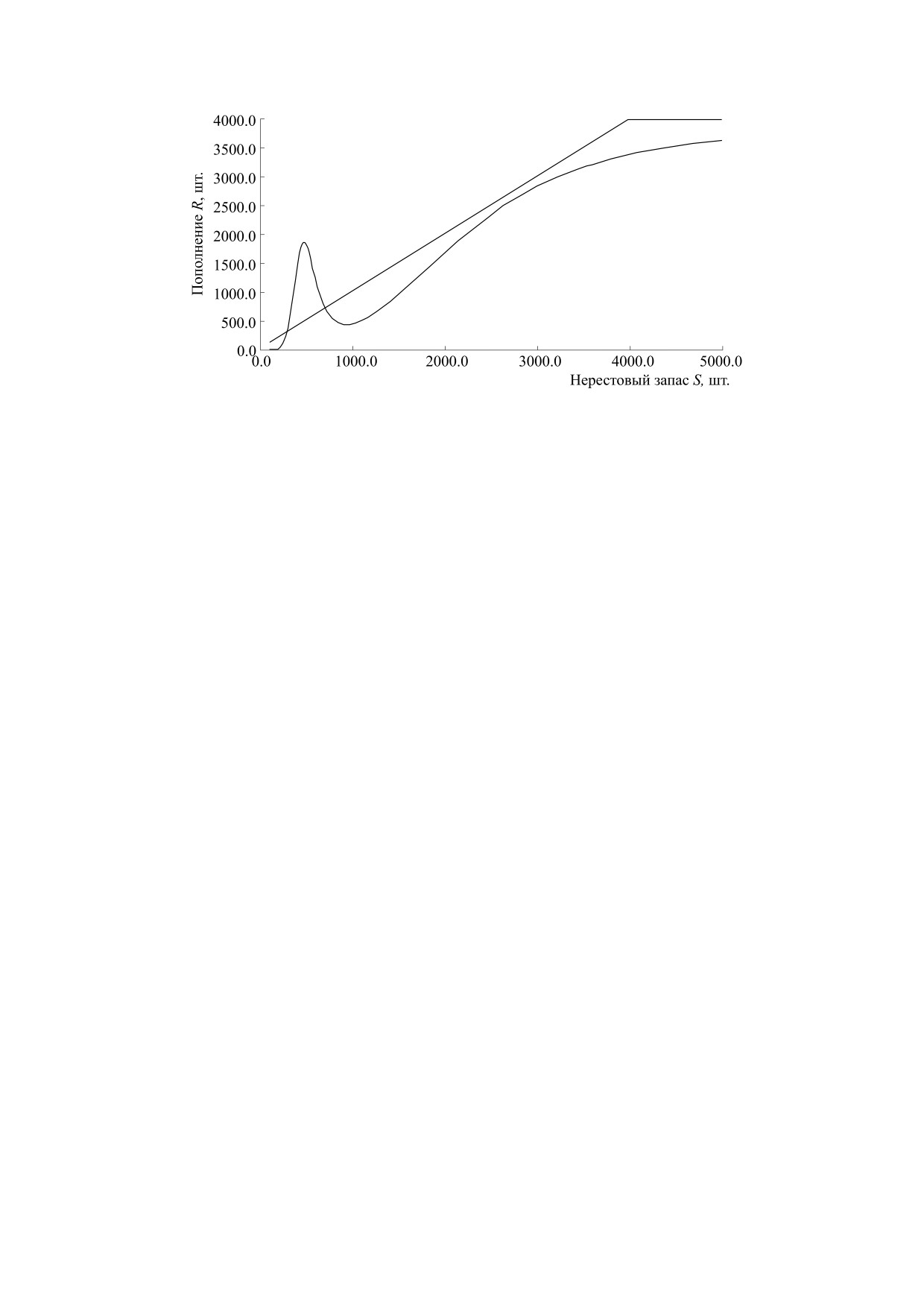
Рис. 12. Кривая модельной зависимости после обратной касательной бифуркации с двумя неустойчивыми равновесиями и

minφ(S) >

что вызовет обратную касательную бифуркацию -

форсирования промысла плавно увеличиваются.

слияние устойчивого R_4* с неустойчивым равно-

После спонтанного роста эксперты принимают

обоснованное по их логике решение о поднятии

весием R_3*. B результате мы наблюдаем потерю

годовой квоты (q

0.62). Совершенно логично,

наибольшего состояния равновесия - ранее при-

тягивающей точки траектории для области Ω₂

что уловы краба за четыре первых сезона после

увеличения доли изъятия показывают историче-

(рис. 12).

ски рекордные для промысла значения

Структура гибридной системы уравнений поз-

(Y → max). После «удачных» сезонов уловы резко

воляет масштабировать оператор эволюции ϕ

падают. Объемы промысловых запасов краба ми-

вдоль оси абсцисс в вычислительных сценариях и

нуют локальный минимум y кривой воспроизвод-

изменять положения экстремумов φ соответ-

ства φ, избегая попадания в ε-окрестность R_1*-

ственно воздействию внешних условий. Φункция

критического состояния. Эксперты видят стаби-

Ψ не меняет относительное положение y четвер-

лизацию, так как привыкли усреднять Y_n. В логи-

того устойчивого равновесия R_4*, нo действует на

ке прогнозов экспертов в этом сценарии учтена

положение minφ(S) относительно предкритиче-

хорошая эффективность воспроизводства за

ского неустойчивого репеллера R_2*. R_1* выполня-

предыдущие сезоны сразу после потери равнове-

ет роль критического репеллера и границы обла-

сия и установлено прохождение локального ми-

стей притяжения ∂Ω. У проекций точек экстрему-

нимума (q = 0.35). Уловы после первого падения

мов локального максимума и минимума имеется

достоверно начали возрастать. У экспертов со-

важнoe свойство: максимум отображается по абс-

гласно статистической методике нет причин для

цисс правее минимума (φ(R_max) > R_min). Возмож-

корректировки управления промыслом для даль-

на трансформация экстремумов и нетривиальных

нейшего снижения.

равновесий у φ(λS) из minφ(S) < R_2*, maxφ(S) >

Величина запаса после усиления промыслово-

> R_3* в форму minφ(S) > R_2*, maxφ(S) > R_4* > R_3*.

го давления срывается в апериодический режим,

Изменения этих соотношений y зависимости

но в ограниченной области значений. В результа-

minφ(S) резко влияют на качественное поведение

те время роста величины уловов Y после миниму-

траектории итераций.

ма непредсказуемо. Эксперты увидят изменения,

похожие на вызванные нестабильностью условий

Составим набор параметров вычислительного

среды колебания. Решение о минимизации доли

эксперимента для ситуации, когда промысловая

изъятия до q = 0.2 в режиме колебаний отвергает-

популяция краба после нестабильного существо-

ся. Πри установленном q > 0.33 после прохожде-

вания восстановилась до устойчивого равнове-

сия, оптимального для своей кормовой базы. Ос-

ния траекторией окрестности R_1* в вычислитель-

новой для оценки станет модельный сезон из

ном сценарии реализуется популяционный кол-

12 модельных месяцев. Уловы краба Y_n = R_nq_n без

лапс (рис. 13). Промысел прекращается, хотя

БИОФИЗИКА том 67

№ 2

2022

402

ПЕРЕВАРЮXА

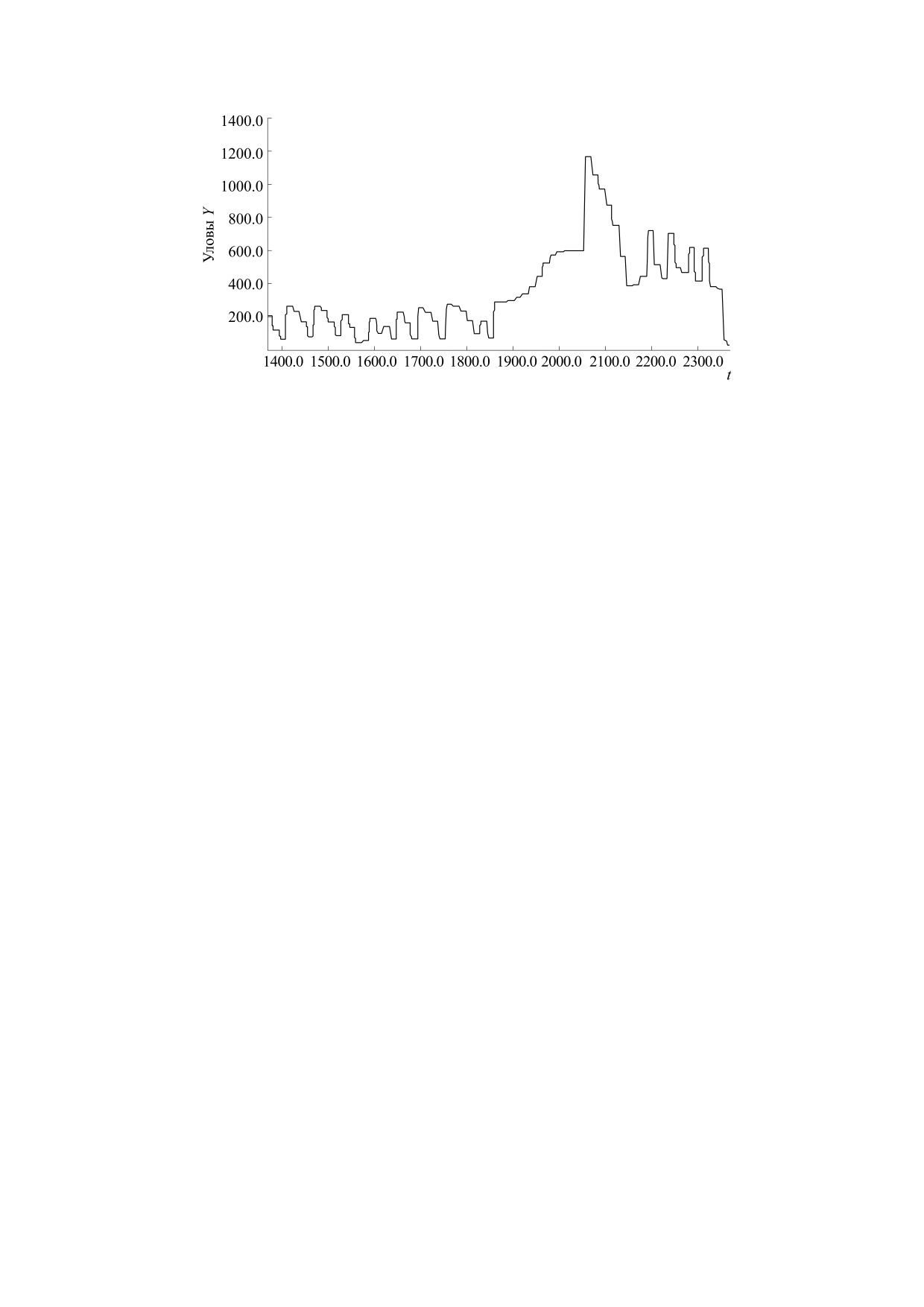
Рис. 13. Вычислительный сценарий динамики уловов c эффектом коллапса запасов.

квота вылова на сезон была выделена, как это

ФАЗОВЫЕ ПОРТРЕТЫ СЦЕНАРИЯ

произошло c треской в 1992 г.

КОЛЛАПСА С ОСЦИЛЛЯЦИЯМИ

Заключительное падение уловов и получило

Для функциональных итераций известны три

название «коллапса», тогда как на первое сокра-

нелинейных явления, называемые «кризисами»

щение уловов краба мало обращали внимание как

[73]. Помимо кризиса столкновения с границей

на временное, хотя в абсолютном выражении

(basin-boundary crisis) выделены внутренний кри-

первое падение уловов было больше. При первом

зис и кризис слияния (merging crisis), специфич-

кризисе уловы краба резко сократились, что не

ный для сценария удвоения периода циклов

повлекло сезонный полный мораторий на про-

(p = 2ⁱ, i → ∞) [74]. Кризисы не обусловлены

мысел. Промысел был продолжен при нестабиль-

трансформациями топологических типов самих

ных флуктуациях с неизменным промысловым

аттракторов и бифуркациями, но связаны с пере-

давлением и умеренно благоприятном прогнозе.

строениями положения аттрактора относительно

По принципам нелинейной динамики такое по-

соседних с ним неустойчивых инвариантных

ведение расценивается как признак наличия кри-

множеств, отдельной точки или фрактального

тических точек, но методы статистики не могут

множества.

установить точки для запаса, где функция, связы-

Используемый метаморфоз фазового портрета

вающая запас и пополнение, изменяется практи-

в сценарии - граничный кризис интервального

чески вертикально.

аттрактора Λ, который остается после слияния

Моделирование показало, что путь к финаль-

устойчивого и неустойчивого равновесий. В по-

ному кризису состоит из переходных режимов. B

рядке списка теоремы Γукенхаймеpa [75] этот то-

вычислительном эксперименте сценарий кол-

пологический тип замкнутых ω-предельных мно-

жеств итераций - № 3 из трех возможных типов

лапса промысловых запасов камчатского краба

аттракторов. Эффект кризиса происходит при со-

развивается из двух фаз, их продолжительность

прикосновении Λ с границей его области притя-

зависит от повышения Δq при интенсификации

жения. Изначально окрестность локального мак-

морского промысла. Если не был введен своевре-

симума, где значение maxφ немного превосходит

менный мораторий, тo вторая фаза деградации

значение φ в точке третьего репеллера,

неминуемо произойдет через одиннадцать мо-

ϕ(maxϕ(N(0)) ± ε) > R_3*. Когда происходит каса-

дельных сезонов в формате времени вычисли-

тельная бифуркация, то неустойчивая и устойчи-

тельной среды c переходом через порог R_1* крити-

вая точки R_3* и R_4* сливаются в одну критическую

ческого неустойчивого равновесия. В модели вос-

производство популяции после фазы деградации

точку RC* (ϕ(RC*) = 1), которая исчезает. Так

R1* > minφ(λS) не восполняет естественную

мы моделируем первое падение улова краба.

убыль родительских поколений, поэтому необхо-

Устойчивость точки итерации ϕ(R^*) = R^* можно

дима интродукция взрослых крабов из других

оценить по положению касательной из известно-

мест.

го свойства |ϕ′(R^*)| < 1. Обозначим совокупное

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

403

множество точек-прообразов y второго репеллера

экстремумов модельной зависимости, но не фик-

R_2* как {ϕ^-n(R_2*)}, а обратную итерацию функции

сированный интервал [R_1*, R_3*], так как само су-

ϕ в правый прообраз точки R_2* - как ϕ-1(R_2*) =

ществование R_3* зависит от q_n. Начальные точки

= R2-1*r. Эти прообразы исключены из области

R₀ ∈ [φ(R_min), φ(R_max)], которые могут притяги-

притяжения, они никогда не притягиваются к ат-

ваться к аттрактору, всюду соседствуют с никогда

тракторам. Если для R_2* есть прямые прообразы и

нe притягивающимися к R_4*. Из интервала I ис-

справа, и слева от точки, это сделает несвязной

ключены объединения множеств тех точек R₀, ко-

Ω₂-область притяжения R_4*. Репеллер R_2* суще-

торые под действием итераций ϕ отображаются в

ствует во всех модельных сценариях и имеет про-

неустойчивые репеллерные положения равнове-

сия. Когда неустойчивые стационарные точки на

образы и справа, и слева для каждого n. Точки R₃

графике y зависимости эффективности пополне-

и R_4* возникают/исчезают после прямой/обрат-

ния ϕ имеют более одного прямого прообраза, та-

ной касательной бифуркации. Равновесие R_1* y ϕ

кой точки R_2-1*, которая при первой итерации

существует для каждого n, но наличие прообраза

отобразится в репеллер ϕ(R_2-1*) = R_2*, то из-за

у репеллера R_1* зависит от значений Ψ, увеличива-

изрешеченности I возникает наблюдаемый в вы-

ющихся по мере приближения Rn+1* → R_1*. Когда

числительных сценариях апериодический режим

начальное положение R₀ точки траектории оказы-

и неопределенность поведения траектории.

вается R_1* < R₀ < R_2* < R_3* и соответствует подмно-

Интервал I между отображениями экстрему-

жеству из интервала R₀ ∈ (R_1*,R_3*) ∩ {ϕ^-n(R_2*)}, то

мов функции ϕ будет включать внутри себя и ин-

тервальный аттрактор Λ ⊂ [φ(R_min), φ(R_max)].

через режим псевдостохастических флуктуаций

популяция в сценарии достигнет уровня высокой

I содержит в себе именно аттрактор интервально-

устойчивой численности за конечное число ша-

го типа Λ ⊂ I, где Λ - замкнутое инвариантное

гов: ϕ^ϑ(R₀) = R_4*, ϑ < ∞. Потому сценарий восста-

подмножество I, но Λ несвязно, так как любая

новления численности при своевременном мора-

ε-окрестность точки ∀R₀ ∈ Λ содержит непритя-

тории c q = 0 в модели реален: 0 < R₀ < R_2*,

гивающиеся точки из инвариантного и контину-

ального множества ϒ, минимально состоящего из

limn→uϕⁿ(R₀) = R_4*, а граничный кризис возмо-

всех прообразов R_2* и имеющего и правый, и левый

жен и при соприкосновении с R_3*.

)}. Под-

прямые прообразы: {φ-n(R2-1*r), φ-n(R2-1*l

B настоящее время принято считать, что для

множество странного репеллера составит все

конечномерных гладких динамических систем

объединение рассеянных в I точек R₀ без притя-

мы можем наблюдать три принципиально раз-

жения:

личных формы хаоса [76]. Характеристики нере-

гулярных колебаний точек, порождаемых нашей

∞

−n

ϒ=

),ϕ

ϕⁿ(R₀) - следствие формы кривой с тремя экстре-

∪

мумами и свойство нестабильности получаемых

при расчетах промежуточных результатов при

Траектории начальной точки {φⁿ(R₀)}, R₀ ∉

разном положении начальной точки траектории

∉ {φ-n(R_2*)} обладают возможностью попадания

R₀. Это связано c изрешеченной «riddling»-обла-

в ε-окрестность хаотического репеллера ϒ, состо-

стью I в фазовом пространстве. Явление изреше-

ящего из множества всех непритягивающихся то-

чивания возникает, когда образуются вложенные

чек и возникающего при изменении положения

инвариантные множества [77]. Отрезок I включа-

экстремумов зависимости φ(R). Далее при вы-

ет рассеянное континуальное множество сyбин-

полнении условий ∃R₀, R₀ ∈ I, R₀ ∉ ϒ и φ(R₀) < R₁

тервалов из областей притяжения Ω₁,Ω₂ двух ат-

уже интервалы в Λ не будут более замкнутым и

тракторов. Границы всех сyбинтервалов не при-

инвариантным подмножеством, где выполняется

надлежат к этим областям притяжения и

условие φ(Λ) ∈ Λ. В I хаотическое движение в ко-

формируют отдельное множество, «странный ре-

нечном числе итераций φ^k, 0 < k < ∞ наблюдаем с

пеллер» - инвариантное замкнутое множество, в

окончанием режима хаотизации limn→dϕⁿ(R₀) =

любой ε-окрестности которого есть точки, при-

= 0, k < d < ∞. Длительность апериодических ре-

надлежащие области Ω₁,Ω₂. Границы «изреше-

жимов несколько варьирует из-за чувствительно-

ченной» области I определят отображения точек

сти к возмущениям R₀ ± ε y точки, которую мы

R_min > R_max, так что I = [φ(R_min), φ(R_max)] для двух

выберем как начальную в вычислительном экспе-

БИОФИЗИКА том 67

№ 2

2022

404

ПЕРЕВАРЮXА

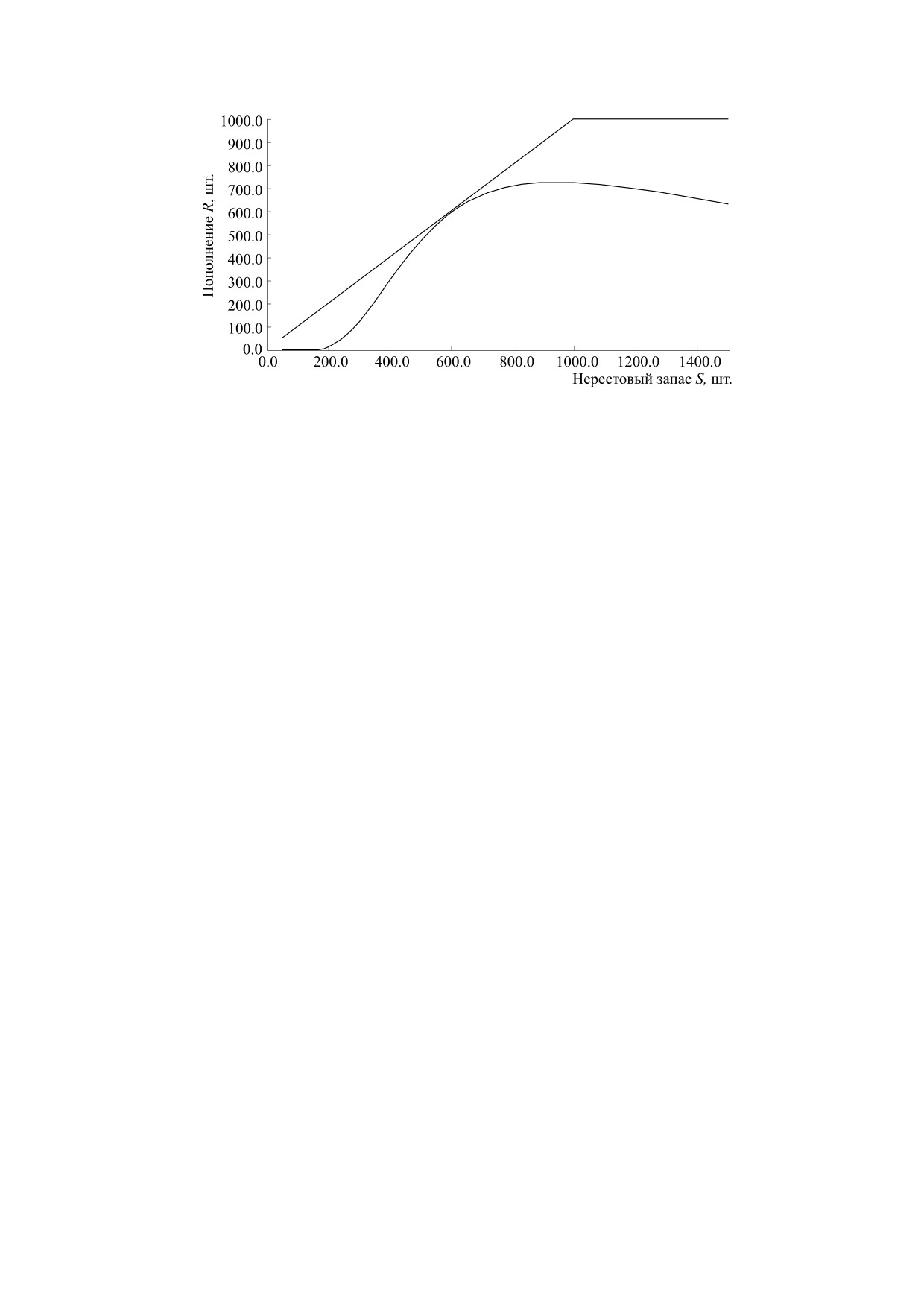
Рис. 14. Трансформация унимодальной модельной зависимости после одной касательной бифуркации.

рименте. Свойство хаотизации, ограниченной и

оптимальной, наиболее выгодной стратегии экс-

во времени, и в области I значений φ(R), отражает

плуатации биоресурсов в реальности опасны. Оп-

естественную неопределенность для морского

тимальное для промысла состояние близко к кри-

объекта промысла.

тическому порогу, где воспроизводство перестает

Мы отметили, что другие сценарии коллапса

с большой вероятностью восполнять запас. Хао-

могут развиваться и без флуктуаций. Для таких

тизация в новой гибридной модели удачно ими-

ситуаций в модели можно получить менее слож-

тирует стохастическоe возмущение условий сре-

ную зависимость, изначально имеющую пару ста-

ды размножения.

ционарных точек. Устойчивая и неустойчивая

Канадский тресковый кризис рассматривался

точка начинают сливаться в критическое равно-

досконально, но ключевую его причину так и не

весие, как на рис. 14. В этот момент траектория

стабилизируется, но вплоть до исчезновения

установили. Коллапс камчатского краба, как и

трески у берегов Лабрадора, спровоцирован иска-

единственной стационарной точки RС*.

женными представлениями о благополучном

Данный вариант коллапса математически

состоянии данных биоресурсов и, главное, - за-

описывается проще, без сложных переходных ре-

вышением оценки эффективности восполнения

жимов, и требует одного метаморфоза фазового

запасов. Реальная зависимость при интенсифи-

портрета. При состоянии зависимости ∀0 < R,

кации промысла лежала ближе к биссектрисе

R ≠ RС*φ(R) < R непредсказуемое заранее малое

R=S, чем предполагалось экспертами. Причина

внешнее давление и увеличение естественной

ошибки завышения в том, что у немонотонной

смертности способно приводить популяцию к

зависимости сдвигаются экстремумы по мере ис-

коллапсу.

тощения численности запаса в интервале значе-

∈

)]. При интенсивном вы-

ний S

[φ(R_min),φ(R_max

ЗАКЛЮЧЕНИЕ

лове происходит смещение значения ϕ(R) у экс-

Рассмотрен вариант промысловой деградации

тремума R_min по оси ординат вниз таким образом,

запасов после нахождения популяции в состоя-

что φ(R_min) < R_1*. Далее реализуется граничный

нии нестабильных осцилляций. Разработана ме-

тодика математической формализации нетриви-

кризис для аттрактора Λ, составленного из мно-

ально изменяющейся эффективности воспроиз-

жества интервалов: ∃y ∈ Λ, φ(y) ∉ Λ. После кризи-

водства в традиционной форме зависимости:

са появляются точки траектории

∃x0i

∈ Λ,

запаса и получаемого пополнения. Представлен

limn→∞ϕⁿ(x0i) = 0. Τочка R_1* - неустойчивое рав-

вычислительный сценарий с реализацией двух

метаморфозов в фазовом портрете y итерацион-

новесие для популяции при критической числен-

ной динамической системы для учета выявлен-

ности; если φ(Rn+1) < R_1* - ε, то реализуется не-

ных особенностей процесса промысловой дегра-

обратимая деградация запаса за конечное k число

дации запасов краба. Сценарий коллапса в мо-

дели подтвердил, что идеи организации

итераций φ^k(R_n) = 0. Итоговый коллапс отражен

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

405

в простой форме R₀ ∉ ϒ, φ^k(R_n) → 0, k < ∞. В диа-

как блок расчетов воспроизводства в составе со-

временных многовидовых моделей биосистем

пазоне S ∈ (R_2*,R_2*) эффективность воспроизвод-

[82]. Проблема применения агрегированных по-

ства согласно нашей модели еще достаточно вы-

лимодельных комплексов для прогнозирования и

сока за счет локального максимума. Это вносит

оптимизации промысла - сложная параметриза-

обманчивые ожидания продолжения тренда вос-

ция и интерпретация результатов, когда малое

становления воспроизводства. Показано, что при

возмущение одного из множества бифуркацион-

небольшой дальнейшей убыли запаса эффектив-

ных параметров качественно изменит поведение

ность воспроизводства в сценарии непропорцио-

итогового решения, тогда как изменение величин

нально резко сокращается вплоть до достижения

окрестности критического порога восполнения

других коэффициентов не вызовет существенной

запасов.

ответной реакции. В структуру можно включать

стохастическую компоненту для отдельных ситу-

Достаточно небольшой систематической ошиб-

аций [83].

ки в оценках запаса в диапазоне S ∈ (R_2*,R_2*) для об-

Примеры кризисов и стремительных вспышек

рушения промысла, так как реальная доля изъятия

будет выше той, которая планировалась, более того,

y разных популяций требуют расширения пред-

расхождение будет нарастать со временем. После

ставления динамических моделей для задач эко-

первого падения численности для популяции на-

логии. Сходство ситуаций подтверждает нашу ги-

блюдается резкий переход в состояние сильных не-

потезу о существовании конечного набора форм

регулярных флуктуаций с выраженными локальны-

сценариев для развития экстремальных измене-

ми пиками, но это пока обратимое состояние. По-

ний в экодинамике. Тогда известные нам формы

пуляция сможет восстановиться, если немедленно

меняющихся процессов (вспышек, кризисов, об-

принять неочевидное управленческое решение и

разования и разрушения нерегулярных колеба-

уменьшить изъятие в два раза.

ний с большой амплитудой) мы сможем класси-

Рациональной тактикой при регуляции выло-

фицировать (независимо от их природы), сопо-

ва мы полагаем ограничение технических воз-

ставив им в качестве набора инструментов для

можностей для промысла (размеры орудий лова,

описания сценариев известные типы метаморфо-

запас горючего на судах, тоннаж судов), но не ли-

зов (бифуркаций аттракторов или перестроений

мит объема добычи, - жесткие квоты не спасают.

границ их областей притяжения) фазовых порт-

Парадоксально, но пришло время придумать, как

ретов y дискретных либо непрерывных динами-

временно снижать эффективность орудий лова на

ческих систем. Общность нелинейности и типи-

сложные объекты промыcла. Регистрация сокра-

зацию сценариев создает функционал регуляции.

щения уловов в 20% для нециклических популя-

Понятие динамического коллапса было примене-

ций крупных доминирующих хищников является

но в работе [84] уже не только к отдельным попу-

основанием для введения сезонного моратория

ляциям, но и к целым биоценозам.

на вылов. У промысла не должно быть мотивации

занижать реальные уловы в отчетности. Для точ-

Пристальное внимание в задачах прогнозиро-

ного выбора допустимого уровня эксплуатации

вания процессов с нелинейной регуляцией необ-

необходимы данные мониторинга о выживаемо-

ходимо уделять математическому описанию по-

сти молоди, какие, в частности, были получены

роговых состояний и быстрых трансформаций

при наблюдениях за нерестом волжской севрюги

[85], что актуально сейчас, например, для воз-

[78, 79], но оценены уже после деградации.

растных изменений в эффективности функцио-

Оригинальность метода гибридного модели-

нирования адаптивной иммунной системы, от-

рования с включением событийных изменений

меченных в работе [86]. В работе [87] для выбора

состоит в анализе путей развития сложившихся

оптимальной антигенной мишени и прогнозиро-

ситуаций. Явление коллапса в сценарии развива-

вания дальнейшей эволюции штаммов SARS-

ется по внутренней логике традиционного для

CoV-2 генерировали синтетические «полимутант-

многих стран способа экспертного управления

ные» псевдотипы S-белка и в частности показали,

рыболовством при выдаче сезонных квот [80] на

что способность к нейтрализации антител, выра-

основе оценок с использованием статистических

ботанных ранее у пациентов при заражении ис-

сглаживаний и аппроксимации численности рас-

пределенной популяции гидробионтов на боль-

ходным вариантом вируса, уменьшается при на-

шую акваторию [81]. Разработанную вычисли-

коплении мутаций S-белка резко и пороговым

тельную структуру перспективно использовать

образом.

БИОФИЗИКА том 67

№ 2

2022

406

ПЕРЕВАРЮXА

КОНФЛИКТ ИНТЕРЕСОВ

21.

Т. Н. Соловьева, Информационно-управляющие

системы 6, 58 (2017).

Автор заявляет об отсутствии конфликта инте-

ресов.

22.

Т. Н. Соловьева, Информационно-управляющие

системы 4, 60 (2016).

23.

П. В. Вещев и Г. И. Гутенева, Экология, № 2, 123

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

(2012).

Настоящая работа не содержит описания ис-

24.

А. Ю. Переварюха, Экологические системы и

следований с использованием людей и животных

в качестве объектов.

приборы, № 8, 41 (2008).

25.

А. Ю. Переварюха, Нелинейный мир 10 (4), 255

(2012).

СПИСОК ЛИТЕРАТУРЫ

26.

Ю. В. Тютюнов, И. Н. Сенина, Л. И. Титова и

А. Ю. Переварюха, Биофизика 66 (6), 1144 (2021).

Л. В. Дашкевич, Биофизика 65 (2), 390 (2020).

А. Ю. Переварюха, Биофизика 65 (1), 138 (2020).

27.

А. В. Никитина, А. И. Сухинов, Г. А. Уголь-

L. Loyal, J. Braun, L. Henze, et al., Science 374

ницкий и А. Б. Усов, Математич. моделирование

(6564), eabh1823

(2021).

DOI:

10.1126/sci-

28 (7), 96 (2016).

ence.abh1823

28.

K. Aagaard and J. L. Lockwood, Biol. Invasions 18,

L. R. Clark, Austral. J. Zool. 12 (3), 362 (1964).

1667 (2016).

R. ud Dina, A. R. Seadawyb, and K. Shah, Results in

29.

A. S. MacDougall, K. S. McCann, and G. Gellner,

Physics 19 (12), 103468 (2020).

Nature 494, 86 (2013).

A. M. Syed, T. Y. Taha, T. Tabata, et al., Science 374

30.

K. Kleisner and D. Pauly, in The state of biodiversity

(6575), 1626 (2021). DOI: 10.1126/science.abl6184

and fisheries in Regional Seas. Fisheries Centre Research

Ю. Д. Нечипуренко, А. А. Анашкина и

Reports, Ed. by V. Christensen, S. Lai, and M. Palo-

О. В. Матвеева, Биофизика 65 (4), 824 (2020).

mares (University of British Columbia, Vancouver,

Т. А. Зайчук, Ю. Д. Нечипуренко, А. А. Аджубей и

2011), pp. 37-40.

С. Б. Оникиенко, Молекуляр. биология 54 (6), 922

31.

A. May, Newfoundland Quarterly 102 (2), 41 (2009).

(2020).

32.

J. Roughgarden and F. Smith, Proc. Natl. Acad. Sci.

T. Maemura, M. Kuroda, T. Armbrust, et al., mBio 12

USA 93, 5078 (1996).

(5), e01987-21 (2021). DOI: 10.1128/mBio.01987-21.

33.

R. A. Myers, Ecol. Applications 7, 91 (1997).

10.

А. Ф. Ванин, А. В. Пекшев, А. Б. Вагапов и др.,

34.

A. Hutchings and R. A. Myers, Canad. J. Fish. Aquat-

Биофизика 66 (1), 183 (2021).

ic Sci. 51, 2126 (1994).

11.

А. Ф. Ванин, Биофизика 65 (4), 818 (2020).

35.

Report of the Standing Committee on Fisheries and

12.

A. R. Kathryn, R. K. Bewley, and S. A. Fotheringham,

Oceans, www.ourcommons.ca/Content/Committee/

Nat. Commun. 12 (1), 81 (2021).

421/FOPO/Reports/RP8826804/foporp10/

13.

А. Ю. Переварюха, Биофизика 66 (2), 384 (2021).

foporp10-e.pdf

14.

W. van Damme, R. Dahake, and R. van de Pas, Med.

36.

М. Г. Карпинский, Экология бентоса Среднего и

Hypotheses 146 (1), 110 (2021).

Южного Каспия (Изд-во ВНИРО, М., 2002).

15.

Т. И. Корнилова, Рыбоводство и рыбное

37.

А. Ю. Переварюха, Журн. общ. биологии 81 (3),

хозяйство, № 8, 34 (2011).

174 (2020).

16.

Н. И. Реус и С. В. Петрова, Арктика: общество и

38.

S. Rowe and G. A. Rose, Nature 556, 436 (2018).

экономика 8, 115 (2012).

39.

А. Е. Бобыpев, В. А. Буpменcкий, Е. А. Кpикcунов

17.

Приказ Федерального агентства по рыболовству

и др., Биофизика 57 (1), 140 (2012).

от 19 декабря 2006 г. № 443, https://www.garant.

ru/products/ipo/prime/doc/2067316/

40.

А. Е. Бобыpев, В. А. Буpменcкий, Е. А. Кpикcунов

и др., Биофизика 48 (2), 324 (2013).

18.

Г. И. Гутенева, С. С. Фомин и Т. Н. Дедикова,

Рыбное хозяйство 3, 103 (2015).

41.

В. А. Дубровская, Проблемы механики и управ-

ления: Нелинейные динамические системы 48, 74

19.

Г. П. Рубан, Р. П. Ходоревская и В. Н. Кошелев,

(2016).

Астраханский вестн. экологич. образования, № 1,

42 (2015).

42.

Ю. И. Зуенко, Известия ТИНРО 166, 103 (2011).

20.

Т. Ю. Борисова, дисс.

… канд. биол. наук

43.

B. Dew and R. McConnaughey, Ecol. Applications 15

(Астрахань, АГТУ, 2010).

919 (2005).

БИОФИЗИКА том 67

№ 2

2022

ГИБРИДНАЯ МОДЕЛЬ КОЛЛАПСА ПРОМЫСЛОВОЙ ПОПУЛЯЦИИ КРАБА

407

44.

J. Hoyle, in Proc. of the Workshop on the Dynamics of

68.

D. Singer, SIAM J. Applied Math. 35, 260 (1978).

Lake Whitefish (Coregonus clupeaformis) in the Great

69.

P. Coullet and C. Tresser, J. Physique Colloques 539,

Lakes (2005), pp. 47-61.

5 (1978).

45.

W. E. Ricker, J. Fish. Res. Board of Canada 11, 559

(1954).

70.

A. Y. Perevaryukha, Biophysics 61 (2), 334 (2016).

46.

R. J. H. Beverton and S. J. Holt, Great Britain Fish In-

71.

Т. И. Булгакова, Рыбное хозяйство, № 5, 70

vestigation Ser 19, 1 (1957).

(2009).

47.

А. И. Михайлов, А. Е. Бобырев, Т. И. Булгакова и

А. Д. Шереметьев, Журн. общ. биологии 80 (6), 418

72.

В. А. Дубровская, А. Ю. Переварюха и И. В.

(2019).

Трофимова, Журн. Белорус. гос. ун-та. Биология,

№ 3, 76 (2017).

48.

В. В. Михайлов и Ю. С. Решетников, Инфор-

мационно-управляющие системы, № 4, 31 (2018).

73.

C. Grebogi, E. Ott, and J. A. Yorke, Physica D: Non-

49.

W. De Melo and S. van Strien, Bull. Amer. Math. Soc.

linear Phenomena 7 (3), 181 (1983).

18 (2), 159 (1988).

74.

B. Reisner, A. Kittel, S. Lück, et al., Zeitschrift für

50.

Т. Ю. Борисова и И. В. Соловьева, Матема-

Naturforschung 50 (12), 1105 (1995).

тические машины и системы, № 1, 71 (2017).

51.

W. E. Ricker, Bull. Fish. Res. Board of Canada 1, 191

75.

J. Guckenheimer, Comm. Mathem. Physics 70, 133

(1975).

(1979).

52.

Л. А. Животовский, В. В. Храмцов и М. К. Глу-

76.

А. С. Гонченко, С. В. Гонченко, А. О. Казаков и

боковский, Вопр. ихтиологии 36 (3), 369 (1996).

А. Д. Козлов, Изв. вузов. Прикладная нелинейная

53.

D. K. Kimura, ICES J. Marine Sci. 44 (3), 253 (1988).

динамика 25 (2), 4 (2017).

54.

T. Höfer and H. Przyrembel, Paediatric and Perinatal

77.

П. В. Купцов и С. П. Кузнецов, Нелинейная

Epidemiology 18 (1), 88 (2004).

динамика 2 (3), 307 (2006).

55.

W. R. Bechtol and G. Kruse, Marine and Coastal

Fisheries Dynamics Management and Ecosystem Sci-

78.

П. В. Вещев, Г. И. Гутенева и Р. С. Муханова,

ence 1 (1), 29 (2009).

Рыбное хозяйство, № 6, 45 (2010).

56.

В. В. Михайлов, Нелинейный мир 16 (4), 45

79.

П. В. Вещев, Вопросы ихтиологии 49 (5), 681

(2018).

(2009).

57.

Е. Ф. Еремеева, в кн. Теоретические основы

80.

А. И. Абакумов, Л. Н. Бочаров и Т. М. Решетняк,

рыбоводства (Наука, М., 1965), сс. 129-138.

Вопр. рыболовства 10 (2), 352 (2009).

58.

В. В. Васнецов, в кн. Очерки по общим вопросам

ихтиологии (Изд-во АН СССР, 1953), сс. 207-217.

81.

И. Н. Лепилина и Т. И. Булгакова, Труды ВНИРО

59.

Р. Р. Борисов, Биология моря 33 (4), 267 (2007).

177, 58 (2019).

60.

М. В. Чурова, О. В. Мещерякова, Н. Н. Немова и

82.

А. Е. Бобырев, Е. А. Криксунов и Т. И. Куга,

М. И. Шатуновский, Изв. РАН. Сер. биол. 3, 289

Вопросы ихтиологии 45 (6), 820 (2005).

(2010).

61.

Е. А. Kriksunov, J. Ichthyol. 35 (7), 10 (1995).

83.

А. С. Маслаков, Т. К. Антал, Г. Ю. Ризниченко и

А. Б. Рубин, Биофизика 61 (3), 464 (2016).

62.

Л. И. Карамушко, Успехи соврем. биологии 128

(2), 180 (2008).

84.

T. J. Murchie, A. J. Monteath, M. E. Mahony, et al.,

63.

Ю. В. Тютюнов, Л. И. Титова и С. В. Бердников,

Nature Commun.

12,

7120

(2021).

DOI:

Биофизика 58 (2), 349 (2013).

10.1038/s41467-021-27439-6

64.

Г. С. Розенберг, Самарская Лука: проблемы

85.

В. А. Дубровская, Проблемы механики и

региональной и глобальной экологии 29 (3), 77

управления: Нелинейные динамические системы

(2020).

49, 8 (2017).

65.

А. Ю. Переварюха, Владикавказский математич.

журн. 21 (1) 51 (2019).

86.

J. M. Murray, G. R. Kaufmann, and P. D. Hodgkin,

Immunology & Cell Biology 81 (6), 487 (2003). DOI:

66.

А. Д. Базыкин и Ф. С. Березовская, Проблемы

10.1046/j.1440-1711.2003.01191.x.

экологического мониторинга и моделирования

экосистем 2, 161 (1979).

87.

F. Schmidt, Y. Weisblum, M. Rutkowska, et al., Na-

67.

А. Н. Шарковский, Докл. АН СССР 160, 1036

ture

600,

512

(2021). DOI:

10.1038/s41586-021-

(1965).

04005-0

БИОФИЗИКА том 67

№ 2

2022

408

ПЕРЕВАРЮXА

Simulation of Scenarios of the Deep Population Crisis

of the Rapidly Growing Population

A.Yu. Perevaryukha

St. Petersburg Federal Research Center, Russian Academy of Sciences, 14-ya Linia 39, St. Petersburg, 199178 Russia

The paper addresses the use of simulation modeling to develop crisis and threshold levels for managing pop-

ulation growth during the formation of a new population in competitive environment. In the process of spe-

cies distribution across an area, biotic factors can cause a deep population crisis for a new species before initial

declines in abundance are detected. Many populations including the human beings went through a bottleneck

effect in the period of the Neolithic population crash. Invasive species with high reproductive activity often

have severe impacts on biosystems. The occurrence of effective competition can cause not only classical cyclic

f luctuations, but also the complete extinction of the population after time series displaying abundance fluc-

tuations with high peak numbers. Examples for situations of an induced population crisis can be two alterna-

tive scenarios: the first scenario on Gause’s experiments with the introduction of predatory ciliates and the

extinctions of ciliate species, the second scenario on experiments with the introduction of bacteriophages into

colonies of actively dividing bacteria that possess a dynamically adaptive antiviral mechanism. We have pro-

posed modifications of the model for currently topical scenarios of crisis effects in population dynamics. The

equations with time caused by deviating arguments were written taking into account a threshold level for ac-

tivating the effects of biotic factors on reproduction of invasive species and an aggregated nature of the lagging

regulation with two time factors. The computational scenarios described both the effect of the completion of

the process after repeated outbreak and successful passage of the population crisis due to rapid adaptation.

The phenomena of a deep crisis are typical of local population dynamics in case when species interact with

viruses that are new to them.

Keywords: invasion scenarios, modeling of extreme population dynamics, biotic resistance, lagged threshold regu-

lation, species extinction, Neolithic crash, biological pest control, immune response, CRISPR-Cas9

БИОФИЗИКА том 67

№ 2

2022