БИОФИЗИКА, 2023, том 68, № 1, с. 41-56

БИОФИЗИКА КЛЕТКИ

УДК 577.352.3; 577.352.4;576.314;576.32/.36

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

В ЦИТОПЛАЗМАТИЧЕСКИХ МЕМБРАНАХ

*Новосибирский государственный архитектурно-строительный университет (Сибстрин),

Ленинградская ул., 113, Новосибирск, 630008, Россия

**Институт теплофизики им. С.С. Кутателадзе СО РАН, просп. Лаврентьева, 1, Новосибирск, 630090, Россия

***Новосибирский государственный университет, ул. Пирогова, 1, Новосибирск, 630090, Россия

^#E-mail: pavel.mokrushnikov@bk.ru

Поступила в редакцию 20.01.2022 г.

После доработки 10.11.2022 г.

Принята к публикации 16.11.2022 г.

Представлена аналитическая модель латеральной диффузии липидов в неоднородных нативных

цитоплазматических мембранах. Методом Фурье-преобразования решено уравнение диффузии для

функции распределения липидов по координатам в периодически-неоднородной мембране, в

которой коэффициент диффузии описывается гармонической функцией от координат. Показано,

что в мембране существует адвекция-диффузия. Модель объясняет наблюдавшиеся ранее

экспериментально различные виды диффузии липидов появлением в мембране в результате

структурных переходов периодически расположенных неподвижных белок-липидных доменов,

связанных со спектрин-актин-анкириновой сетью. Если эти домены одинаковые, то в

экспериментах можно наблюдать супер- и субдиффузию, когда среднеквадратичное смещение

липидов нелинейно зависит от времени, а их среднее смещение равно нулю. Дрейфовый снос при

адвекции меньше хаотического броуновского перемещения липидов, адвекция в эксперименте не

наблюдается. В случае, когда не все мембранные белки, связанные со спектрин-актин-

анкириновой сетью, одинаково меняют свою конформацию при взаимодействии с лигандами, в

мембране возникают две периодические подрешетки неоднородностей из неподвижных белок-

липидных доменов вокруг мембранных белков, связанных с цитоскелетом и вложенных одна в

другую. В этом случае в экспериментах может наблюдаться хмелевая диффузия, когда периоды

нелинейной диффузии молекул сменяются периодами адвекции-диффузии, при которой среднее

смещение молекул не равно нулю. Адвекция носит локальный характер и возникает около

отдельных белок-липидных доменов. В работе аналитически получены критерии, при которых в

периодически-неоднородной мембране экспериментально наблюдается хмелевая диффузия.

Ключевые слова: диффузия липидов, структурные переходы в биомембранах, адвекция в неоднородных

слоях.

DOI: 10.31857/S0006302923010052, EDN: NZMXGY

Диффузия липидов в цитоплазматических

ской задачи о поступательном движении включе-

мембранах является важным механизмом при эн-

ния в мембране, окруженной вязкой жидкостью.

доцитозе и экзоцитозе, связывании лигандов с

Эта модель не описывает адекватно все экспери-

плазматическими рецепторами, выбрасывании

ментальные данные, поскольку она не учитывает

нейротрансмиттеров в синаптическую щель [1, 2].

существование в мембране областей с разной

В этих процессах к месту связывания лиганда с

плотностью или вязкостью [4]. В качестве приме-

мембраной должны диффундировать за несколь-

ра можно рассмотреть взаимодействие мембран

ко миллисекунд определенные липиды и белки

эритроцитов с андрогенами и гормонами стресса

для образования из них рафтов. Это возможно,

(в дальнейшем просто гормоны). Эти гормоны

если после присоединения лиганда к мембране

связываются с адренорецепторами в плазматиче-

около места присоединения в цитоплазматиче-

ских мембранах, которые, в свою очередь,

ской мембране возникает адвекция-диффузия

взаимодействуют с подмембранной спектрин-ак-

этих определенных липидов.

тин-анкириновой цитоплазматической сетью.

Первой моделью диффузии крупных молекул

Конформация адренорецепторов менялась, ме-

или группы молекул в мембране была модель

нялась и конформация белков спектрин-актин-

Саффмана-Дельбрюка [3], которая представляет

анкириновой сети, между активными группами

собой приближенное решение гидродинамиче-

этих белков усиливались связи, возникали новые.

МОКРУШНИКОВ, РУДЯК

Усиливались также связи между этими белками и

движной квазипериодической сети белок-ли-

окружающими их липидами. Белки сильнее при-

пидных доменов [5]. Она не является строго пе-

тягивали окружающие их липиды. Вследствие

риодической,

поскольку

подмембранная

этого вокруг белков, с которыми связались гор-

спектрин-актин-анкириновая сеть, к которой

моны, образовывались белок-липидные домены,

сеть этих доменов крепится, является квазипери-

в которых липиды перешли из жидкой неупоря-

одической.

доченной фазы в жидкую упорядоченную фазу

Чем больше изменяется конформация этих

Ld → Lo или даже в гель-фазу Ld → Lβ. Изменение

мембранных белков, например, при взаимодей-

структуры липидного бислоя около белков при-

ствии с некоторыми лигандами, тем сильнее их

водили к значительному увеличению микровяз-

связи с окружающими их липидами, тем больше

кости липидного бислоя в белок-липидных до-

по размеру эти домены. Внутри доменов диффу-

менах (до 40%) [5]. Между этими доменами, в

зия липидов затруднена, между доменами образу-

области липид-липидных взаимодействий, обра-

ются легкопроницаемые липидные области [5].

зуются мезополосы разрыхления, в которых ли-

Из физических соображений понятно, что липи-

пиды находятся в жидкой неупорядоченной фазе

ды будут стремиться передвигаться вдоль этих

Ld, микровязкость в этих мезополосах ниже (ко-

легкопроницаемых областей, будет возникать не-

эффициент диффузии липидов выше), чем в об-

линейная диффузия липидов в цитоплазматиче-

ласти белок-липидных взаимодействий. Возни-

ских мембранах. Эта нелинейная диффузия была

кает неподвижная квазипериодическая сеть бе-

ранее экспериментально обнаружена [6-10].

лок-липидных доменов, которая через узловые и

Экспериментально диффузия липидов в мем-

анкириновые комплексы связана с цитоскеле-

бране изучалась различными методами, напри-

том. Но деформации липидного бислоя из-за уве-

мер, флуоресцентной корреляционной спектро-

личения плотности липидов в белок-липидных

скопией, методом истощения стимулированного

доменах не происходят свободно, этому мешают

излучения [6-10]. В этих работах строились тра-

нити спектрин-актин-анкириновой сети. В мем-

ектории частиц при их перемещении вдоль мем-

бране возникают механические напряжения рас-

браны и измерялись зависимости среднеквадра-

тяжения-сжатия. Кроме этого, изменение кон-

тичного смещения частиц и среднего смещения

формации адренорецепторов передается цитос-

от времени. По этим результатам, используя эйн-

келету, нити спектрина сжимаются, создавая в

штейновский закон диффузии [11], вычислялась

мембране продольные и поперечные усилия.

зависимость коэффициента диффузии липидов

Мембрана теряет устойчивость, покрывается

от времени. В результате были выделены следую-

складками. Эти выводы следуют из следующих

щие виды диффузии липидов: замедленная

экспериментальных результатов. Методами

(slowed lipid diffusion), ограниченная (confined dif-

атомно-силовой микроскопии установлено, что

fusion), простая броуновская (simple-Brownian),

при взаимодействии с гормонами мембрана эрит-

направленная диффузия (directed) и хмелевая

роцита теряет устойчивость и покрывается пери-

(hop diffusion) [6, 7].

одически расположенными складками с длиной

волны 100, 200 или 300 нм и так далее, т.е. с пери-

Экспериментаторы следующим образом опи-

одом, кратным 100 нм [5]. Это можно объяснить

сывают эти различные виды диффузий. На на-

возникновением в мембране периодического по-

чальном участке зависимости среднеквадратич-

ля механических сжатий-растяжений, создавае-

ного смещения от времени по формуле Эйнштей-

мого белок-липидными доменами. То, что имен-

на определяется коэффициент диффузии. При

но белки являются инициаторами образования

замедленной диффузии кажущийся коэффици-

белок-липидных доменов, следует из измерения

ент диффузии меньше среднего значения коэф-

микровязкости мембран флуоресцентным мето-

фициента диффузии по мембране. При ограни-

дом. При взаимодействии гормонов с мембраной

ченной диффузии частицы во время броуновско-

го движения не выходили за пределы некоторого

именно в области белок-липидных взаимодей-

очень малого компартмента. При направленной

ствий сильнее увеличивается микровязкость, в

диффузии среднеквадратичное смещение части-

области липид-липидных взаимодействий она

цы нелинейно зависело от времени. При хмеле-

возрастает слабее. Результаты ИК-спектроско-

вой диффузии наблюдалось чередование адвек-

пии также подтверждают этот вывод, в мембране

ции-диффузии (латерального потока частиц с

наблюдается увеличение интенсивности связей

наложенным на нее хаотическим броуновским

внутри белков, белок-липидных и липид-липид-

движением) с ограниченной диффузией [6, 7].

ных связей. Кратность длины волны складок 100

При этих разных видах диффузии среднее смеще-

нм, равной размеру ячейки спектрин-актин-ан-

ние частицы равно нулю, а зависимость средне-

кириновой сети, крепящейся к мембране со сто-

квадратичного смещения частицы R² пропор-

роны цитоплазмы, говорит о том, что именно

мембранные белки, соединенные с цитоскеле-

ционально времени наблюдения t^α. Степени α > 1

том, являются инициаторами образования непо-

соответствует супердиффузия, α = 1 - простая

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

броуновская диффузия и α < 1 - субдиффузия.

влияние неоднородности распределения плотно-

При хмелевой диффузии наблюдалось чередова-

сти флюида вблизи стенки в нанометровом кана-

ние адвекции-диффузии (латерального потока

ле на диффузию молекул флюида. Показано, что

частиц с наложенным на неё хаотическим бро-

это может приводить к их аномальной диффузии.

уновским движением) с ограниченной диффузи-

Неизотропность самодиффузии молекул флюида

ей [6,7]. Траектория движения отдельного липида

достаточно естественна и ранее уже устанавлива-

похожа плеть хмеля, когда участок траектории

лась методом молекулярной динамики [19], в бо-

при ограниченной диффузии похож на шишечку,

лее сложной среде типа пористой возможна и

а участок траектории при адвекции похож веточ-

аномальная диффузия [20].

ку. В цитоплазматических мембранах экспери-

Подводя итог этому краткому обзору, необхо-

ментально обнаружены все эти виды диффузии

димо отметить, что до сих пор не ясно, при каких

липидов [6, 7].

условиях в мембране наблюдается хмелевая диф-

Экспериментально установлено, что на вид

фузия. Целью данной работы является изучение

диффузии влияют мембранные белки, связанные

диффузии липидов в неоднородной нативной

со спектрин-актин-анкириновой сетью, высти-

плазматической мембране. Рассматривались две

лающим изнутри мембрану. Частичная деполи-

модели периодически неоднородной мембраны,

меризация актинового мембранного скелета по-

в которых коэффициент диффузии описывается

сле обработки латрункулином-A приводила к

гармонической функцией от координат. В первой

тому, что почти все (90%) траектории фосфоли-

модели все мембранные белки, связанные с ци-

пидов, наблюдаемые в мембранах, были класси-

тоскелетом, одинаково меняют свою конформа-

фицированы как простой броуновский режим

цию и одинаково притягивают к себе окружаю-

[12]. Это можно объяснить тем, что при деполи-

щие их липиды. Образующиеся при этом белок-

меризации белков связи между активными груп-

липидные домены образуют одну периодическую

пами белков и окружающих их липидов ослабева-

неподвижную решетку неоднородностей в мем-

ли, белки переставали притягивать к себе окружа-

бране. Во второй модели не все мембранные бел-

ющие их липиды и белок-липидные домены в

ки одинаково меняют свою конформацию, по-

мембране не образовывались. Мембрана стано-

разному притягивают к себе окружающие их ли-

вилась однородной средой, в которой и наблюда-

пиды, так что в мембране образуется две подре-

лась броуновская диффузия. В исследовании [13]

шетки неоднородностей, вложенных одна в дру-

использовали флуоресцентную микроскопию

гую. Аналитически получены критерии, при ко-

полного внутреннего отражения в сочетании с от-

торых в периодически-неоднородной мембране

слеживанием нескольких отдельных молекул со

наблюдается хмелевая диффузия. Модель строит-

сверхвысоким разрешением, чтобы создать карты

ся в парадигме классической работы Эйнштейна

локальной вязкости мембраны с высоким разре-

[11] (см. также работу [21]).

шением. Перед этим образцы промывали в не-

скольких буферах, так что с них были смыты все

ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ЛИПИДОВ

лиганды, взаимодействующие с мембранными

В КОНФИГУРАЦИОННОМ ПРОСТРАНСТВЕ

белками и меняющие их конформацию. В резуль-

тате белок-липидные домены в мембране не воз-

Жидкостно-мозаичная модель природной

никали, не было обнаружено областей с разным

биологической мембраны описывает наличие в

коэффициентом диффузии, везде была простая

ней липидов и мембранных белков и взаимное

броуновская диффузия.

влияние их конформаций друг на друга [22-24].

Установлено, что мембранные белки и липиды

Для объяснения экспериментальных результа-

образуют белок-липидные домены. Некоторые из

тов ранее изучалась зависимость латеральной

них могут перемещаться по мембране и носят на-

диффузии от геометрии мембраны и размера

звания «рафтов» [25]. Есть домены, образующие-

диффундирующей частицы методом Монте-Кар-

ло в работе [14]. В частности, здесь было показано

ся вокруг мембранных белков, связанных со

влияние на величину коэффициента диффузии

спектрин-актин-анкириновой сетью, объединен-

аспектного отношения частицы. В одной из мо-

ной с цитоскелетом [5]. Они не перемещаются в

делей исследовалась диффузия частиц в плоском

мембране. Мембранные белки, связанные со

неоднородном слое, состоящем из периодически

спектрин-актин-анкириновой сетью, располага-

чередующихся слабопроницаемых и легкопрони-

ются в вершинах равносторонних треугольников

цаемых участков (модель «гребенки»), методом

со стороной 100 нм, образуя гексагональную сеть

Монте-Карло [15]. Была установлена возмож-

[26]. При изменении своей конформации они

ность существования хмелевой диффузии. Для

усиливают имеющиеся и создают новые связи с

этой же модели в работах [16, 17] выполнено мо-

окружающими их липидами, притягивают силь-

делирование адвекции в пористой среде аналити-

нее их к себе, создавая вокруг себя белок-липид-

чески. Решение получено в интегральном виде.

ные домены с повышенной плотностью липидов

Наконец, стоит упомянуть недавнюю работу [18],

[5, 27, 28]. В этих доменах коэффицент диффузии

где методом молекулярной динамики изучено

липидов меньше, чем в области между доменами.

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

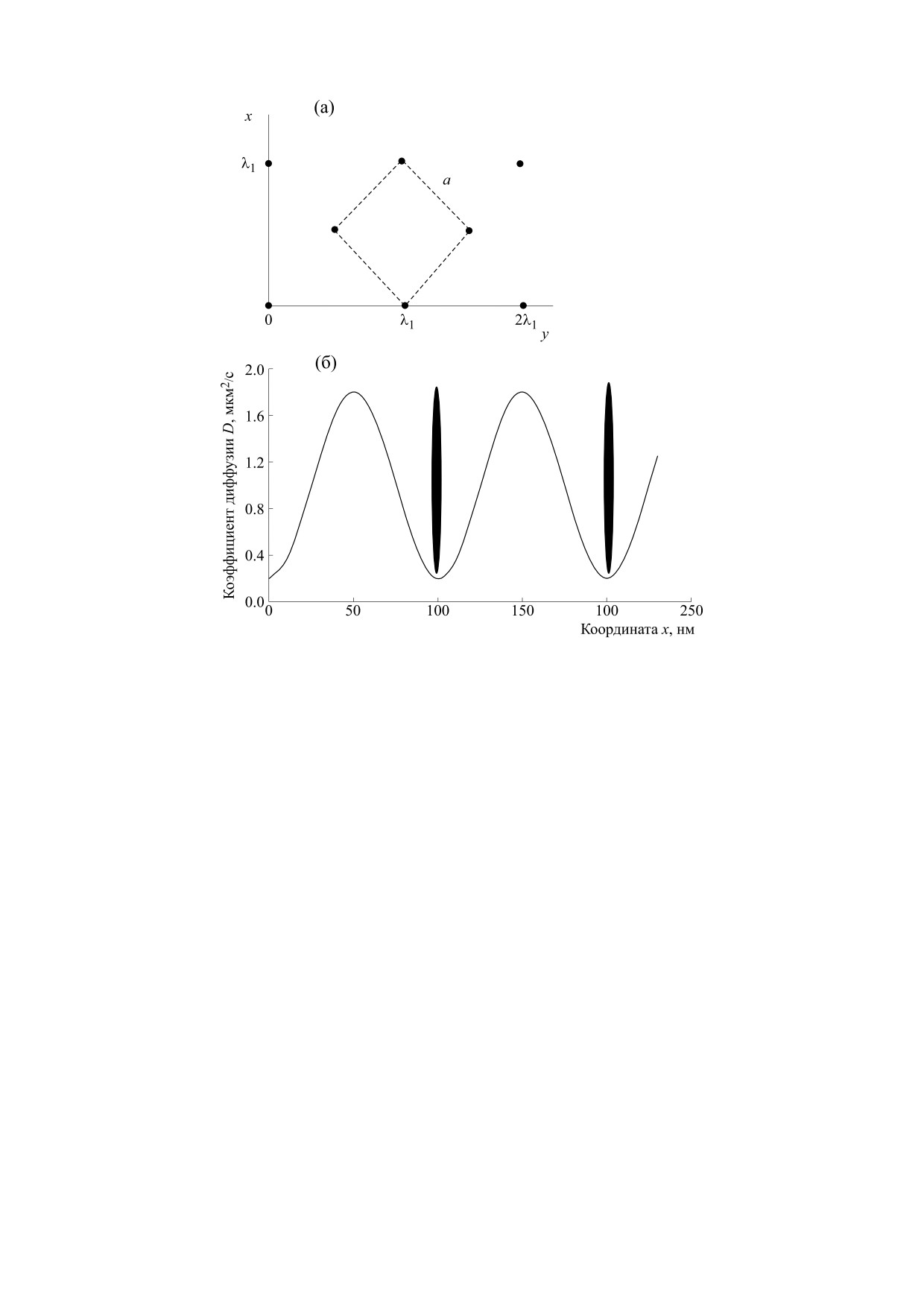
Рис. 1. (a) - Расположение мембранных белков, связанных с цитоскелетом; (б) - зависимость коэффициента

диффузии D из (1) от координаты х при y = 0. Первый коэффициент диффузии D₀ = 10^-12 м²/с, второй коэффициент

диффузии D₁ = 0.8 D₀.

Таким образом, при взаимодействии с некото-

осей ОХ и ОY равными, соответственно, c и d. В

рыми лигандами мембрана разбивается на

случае, если бы мембрана представляла собой од-

квазипериодически расположенные неподвиж-

нородную в пространстве и времени плоскость,

ные белок-липидные домены с увеличенной

подвижность липидов определялась бы лишь ко-

плотностью липидов около мембранных белков,

эффициентом динамической вязкости среды η и

связанных с цитоскелетом, между этими домена-

эффективным гидродинамическим радиусом ли-

ми липидный бислой разрыхлен [5, 27, 28]. Мем-

пида R. Диффузия липидов имела бы броунов-

брана представляет из себя неоднородную среду,

ский характер. Соответствующий коэффициент

в которой слабо- и легкопроницаемые участки

диффузии тогда был бы равен D₀ = k_B T/(4πηR),

чередуются в шахматном порядке. Для простоты

где k_B - постоянная Больцмана.

в представленной ниже модели предполагается,

что белки, связанные со спектрин-актин-анки-

In vitro показано, что коэффициент диффузии

риновой сетью, располагаются в вершинах равно-

липидов в цитоплазматической мембране меня-

бедренных прямоугольных треугольников с катета-

ется в диапазоне от 10^-13 до 10^-11 м²/с [6, 7]. В

ми а = 71 нм и гипотенузой 100 нм.

данной работе принимается D₀ = 10^-12 м²/с. Бе-

В декартовой системе координат направим оси

лок-липидные домены, связанные с цитоскеле-

ОХ и ОY вдоль плоскости мембраны, считая ее

том, будут снижать или повышать коэффициент

бесконечной. Расположение мембранных бел-

диффузии в зависимости от координаты рассмат-

ков, связанных с цитоскелетом, в рассматривае-

риваемой точки мембраны. При связывании с не-

мой модели представлено на рис. 1a. Будем счи-

которыми лигандами в мембране появляются пе-

тать, что давление и температура Т постоянны.

риодически расположенные, неподвижные бе-

Изучим зависимость диффузии от времени моле-

лок-липидные

домены с повышенной

кулы липида с начальными координатами вдоль

плотностью липидов, разделенных липидными

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

мезополосами, где плотность липидов понижена

ность окружающих их липидов увеличивается.

[5, 27, 28]. Предположим сначала, что образова-

Коэффициент диффузии липидов D около этих

лись белок-липидные домены с одинаковой

белков (в области белок-липидных взаимодей-

плотностью липидов вокруг каждого белка, тогда

ствий) наименьший. На границах доменов, в об-

коэффициент латеральной диффузии липидов в

ласти липид-липидных взаимодействий, коэф-

мембране D(x,y) можно интерполировать в виде:

фициент D наибольший. Такое изменение коэф-

D = D₀ - D₁cos(k₀x)cos(k₀y),

(1)

фициента диффузии можно интерполировать

гармонической функцией от координат (1). Экс-

где D₀ и D₁ - первый и второй коэффициенты

периментально in vitro установлено, что макси-

диффузии. Первый коэффициент диффузии D₀

мальное значение коэффициента D в одной мем-

есть формула Стокса-Эйнштейна для однород-

бране может превышать минимальное значение в

ной среды, она соответствует броуновской

20 раз [6, 7], т.е. значение второго коэффициента

диффузии в однородной мембране, в которой

в формуле (1) может достигать значения D₁ =

нетбелок-липидных доменов. Волновое число

0.9D₀. На рис. 1б D₁ = 0.8D₀.

k₀ = 2π/λ₁, где λ₁ = 100 нм. На рис. 1б показана за-

висимость коэффициента диффузии D, описыва-

Рассмотрим диффузию на бесконечной плос-

емой уравнением (1), от координаты х при y = 0.

кости N_p частиц. Введем функцию распределения

Первый коэффициент диффузии D₀ = 10^-12 м²/с,

частиц по координатам

Ψ(x, y,t)dxdy = dn(x, y,t),

второй - D₁ = 0.8D₀, λ₁ = 100 нм. Овалами обозна-

где dn(x,y,t) - число частиц в области, ограничен-

чены неподвижные мембранные белки, связан-

ной отрезками [x,x+dx] и [y,y+dy], в момент вре-

ные со спектрин-актин-анкириновой сетью. При

мени t. Вследствие диффузионного характера

у = 0 нм они имеют по х координату 0, 100, 200 нм

движения липидов в мембране, функция распре-

и т.д. При изменении своей конформации они

деления должна удовлетворять уравнению диф-

сильнее притягивают к себе липиды, упорядочен-

фузии:

∂Ψ

∂ 

∂Ψ(x,y,t)

∂



∂Ψ(x,y,t)

= D(x,y)

+ D(x,y)

(2)



∂t

∂x

∂x



∂y

∂y



Получим решение этого уравнения с помощью преобразования Фурье. Подставляя выражение (1)

в уравнение (2), находим:

∂Ψ(x,y,t)

(sin(k

(x - y))+sin(k

(x+y)))

∂t

∂x

∂

Ψ(x,y,t)

∂

Ψ(x,y,t)

−

(cos(k

(x - y))+ sin(k

(x+y)))

{

}





∂x

∂y





∂Ψ(

x,y,t

)

(-sin(

k (x - y))+sin(k (x+y

)))

∂y

Применим обратное преобразование Фурье к этому уравнению:

∞ ∞

∂Ψ(x,y,t)

exp

(

−ik

x-ik

)

dxdy =



∂t

-∞

∞ ∞

∂

Ψ(x, y,t)

(sin(

(x - y))+

sin

(x+y)))



{

∂x

-∞

∂

Ψ(x,y,t)

∂

Ψ(x,y,t)





+ D

−

(cos(k

(

x - y))+cos

(x+y)))









∂

∂y





∂Ψ(x,y,t)



(−sin(k

(x - y))

+sin

(

x+y)))

exp

(

–ik

x-ik

)

dxdy,

∂



где i - мнимая единица. Заменив гармониче-

лера, для компонент Фурье-образов вместо

ские функции экспонентами по формуле Эй-

уравнения (2) получим:

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

∂Ψ

^*(

,k ,t

)

–k

)

x y

(

–k ,k

+k ,t

)

–

∂t

)

–k

)

–

(

–k

)

(

–k ,k

–k ,t

)

–

)

–

(

+k ,k

+k ,t

)

–D

(

)

(

)

{

(

–k

)

(

)

}

(

–k ,k

+k ,t

)

(

)

(

-k

)

(

+k ,k

–k

)

(3)

{

}

(

–k

)

(

-k

)

(

–k

)

{

}

{

(

)

(

)

}

(

+k ,k

+k ,t

)

−

(

)

(

–k

)

−

(

–k ,k

+k ,t

)

(

+k ,k

–k ,t

)

(

–k

)

Dk1

(

)

(

–k ,k

–k ,t

)

–

(

+k ,k

+k ,t

)

∞ ∞

Для дальнейшего решения докажем, что

где

(

x y

,k ,t

)

(

x,y,t

)exp

(

-ik

x-ik

)

dxdy.



-∞

(

+k ,k

+k ,t

)

exp(–i

(

k x+k y

))Ψ

(

)

(4)

x y

Действительно, пусть k₀ = const, тогда

∞ ∞

(

+k ,k

+k ,t

)

exp

(

x+ik

)



(2π)

∞

-∞

∞ ∞

(

+k ,k

)

exp

(i[(

)

(

)

y - k x-k y

])



(2π

)

-∞

∞

(

)

(

)

∞ ∞

′

exp

′

x+ik

′

y - ik x − ik y

′



(

x y

)

(

)

(2π

)

-∞

∞

∞ ∞

exp

(

−

[

k x+k y

])

(

x y

,k ,t

)

exp

(

x+ik

)



(2π

)

-∞

Здесь сделана замена переменных в интеграле:

k′

′=k

. Аналогично можно

доказать, что

(

-k ,k

-k

)

=exp i(

k x+k y

))

(

)

(5)

x y

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

Используя преобразования (4) и (5), урав-

∂Ψ

(

,k ,t

)

x y

нение диффузии для компонент Фурье-обра-

(

,kx y

)

(

x y

,k ,t

)

(6)

∂t

зов (3) можно записать в следующем виде:

где

(

)

{

−

(

)

}

exp

(ik

(x - y))

x y

{

(

−

)

}

exp(−

(x - y))+

{

−

(

−

)

}

exp(ik

(x+y

))+

+ 1{(k +k )k +(k +k )k

-ik (x + y

D (k2+k

}

(

))

)

exp

Решением уравнения (6) является

Если в начальный момент времени все диф-

фундирующие броуновские частицы находились

(

,k ,t

)

=Ψ

(

)

exp F(

k ,,k t

в точке с координатами (c,d), то Ψ(x,y,0)dydx =

x y

N_pδ(c,d), где N_p - число диффундирующих ча-

где

стиц, δ(x,y) - дельта-функция:

∞ ∞

(

,k ,0

)

(x, y,

exp

(

−ik

x-ik

)

dxdy

x y



-∞

∞ ∞

(

x y

,k ,

)

δ(

c,d

)

exp

(

−ik

x-ik

)

dxdy = N

exp

(

−ik

c- ik

)



-∞

Тогда для функции распределения получается следующее выражение:

∞ ∞

(x,y,t

)

exp

{F(

,kx y

)

t+ik

(

x - c

)+ik

(y − d

)}



(

2π

)

-∞ -∞

или, вычисляя последний интеграл,



−

x - c

−

y - c



[

(

)]

[

(

)]

(

x,y,t

)

exp



−



(7)

4π





где

Q =

¹(

cos(

(

x - y))+

cos(

(x+y)))

{

}

u =

(sin

(

(x − y

))+ sin

(

x+y)))

u =

(−

sin

(

x - y

))+

sin

(

x+y)))

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

Рис. 2. Зависимость коэффициента диффузии D из (8) от координаты х при y = 0.

Здесь u₁ и u₂ есть компоненты двухмерного

ских мембран [21, 22]. Те адренорецепторы, с ко-

вектора u скорости адвекции липидов (дрейфо-

торыми гормоны не связались, свою конформа-

вой скорости) вдоль осей OX и OY соответствен-

цию не поменяли, поэтому слабее притягивают

но. Формула (7) описывает адвекцию-диффузию

окружающие их липиды. Плотность окружающих

в плоском слое [16, 17].

их липидов ниже, чем вокруг адренорецепторов, с

Возможны ситуации, когда не все мембранные

которыми гормоны связались и которые сильно

белки, связанные со спектрин-актин-анкирино-

поменяли свою конформацию.

вой сетью, одинаково меняют свою конформа-

Таким образом, около некоторых адреноре-

цию при взаимодействии с лигандами. Некото-

цепторов липиды находятся в более упорядочен-

рые меняют свою конформацию очень сильно,

ном состоянии, чем липиды около других мем-

усиливая связи с окружающими их липидами или

бранных белков, тоже связанных со спектрин-

образуя дополнительные связи, так что липиды

актин-анкириновой сетью, но конформация ко-

около таких белков находятся в более

торых изменилась слабо. В мембране возникает

упорядоченном состоянии, чем липиды около

других белков, чья конформация поменялась не

две подрешетки неоднородностей липидов,

так сильно [21, 22]. Например, если концентра-

встроенных одна в другую: одна с увеличенной

ция молекул адреналина или норадреналина ма-

упорядоченностью липидов, в другой решетке

ла, то при их инкубации с эритроцитами они

упорядоченность липидов тоже увеличилась, но

связываются специфически не со всеми своими

слабее. Коэффициент диффузии в этом случае

адренорецепторами на поверхности плазматиче-

будет иметь вид



D= D -

cos

(8)

где



- первый, второй и третий коэффи-

коэффициент диффузии



D ,

0.1

0.8

циенты диффузии соответственно. Если рассмат-

λ₁ = 100 нм, λ₂ = 400 нм. Oвалами обозначены

ривать мембранные белки, имеющие координату

мембранные белки, связанные со спектрин-ак-

у = 0, то вдоль оси ОХ λ₁ = 100 нм - расстояние

тин-анкириновой сетью, конформация которых

между ближайшими мембранными белками, ко-

очень сильно изменилась. Они имеют вдоль оси

торые слабо изменили свое конформационное

OX координату 0, 400, 800 нм и т.д. Коэффициент

состояние, λ₂ - расстояние вдоль оси ОХ между

диффузии D около них наименьший.

ближайшими мембранными белками, которые

сильно изменили свое конформационное состоя-

Можно найти решение уравнения диффузии

ние, k₀ = 2π/λ₁, k₂ = 2π/λ₂. На рис. 2 показана за-

(2) для коэффициента диффузии вида (8). Прове-

висимость коэффициента диффузии D из выра-

дя выкладки, аналогичные приведенным выше,

жения (8) от координаты х при y = 0. Первый ко-

получим для функции распределения следующее

эффициент диффузии D₀ = 10^-12 м²/с, второй

выражение:

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ



ut-

(x-c

+ u

(y-c



[

)]

[

)]

Ψ(x, y,t)=

exp-

,

(9)

4πG





где

G =

D -

(cos(

k (x - y))+cos(

k (x + y)))

–

(cos(

k (x - y))+cos(

k (x + y)))

{

}

= 1k

(sin(

k (x - y))+sin(

k (x + y)))+ 2k

(sin(k

(x - y))+sin(

k (x + y))),



= 1k

(–sin

(x - y))+sin

(x + y)))+ 2k

(–

sin

(x - y))+sin(k

(x + y)))

Здесь

₁

₂

и есть компоненты двухмерного

ды дрейфуют к локальному центру притяжения,

вектора u скорости адвекции липидов (дрейфо-

где вязкость мембраны наименьшая, а коэффи-

вой скорости) вдоль осей OX и OY соответственно

циент диффузии наибольший.

[16, 17]. Формула (7) является частным случаем

Используя функции распределения (7) или (9),

выражения (9), когда третий коэффициент диф-

фузии из выражения (8) равен нулю. Адвекция в

можно найти среднее смещение частицы вдоль

обоих моделях носит локальный характер, липи-

осей OX и OY:

∞ ∞

-1

x-c

(x-c)Ψ(x, y,t)

dxdy,

y-d

(

y-d)Ψ(x, y,t)

dxdy.

(10)



-∞

Среднеквадратичное смещение частицы составит

∞ ∞

-1

R2 t)

{

(

x-c)

+(y-d

)

² Ψ(

x, y,t)dxdy.

(11)



-∞

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

∂Ψ(x,t)

= 0.

(12)

Функции (7) и (9) характерны для двумерной

∂x

адвекции-диффузии [16, 17], которая в экспери-

Уравнение

(12) является трансцендентным

ментах может наблюдаться как хмелевая диффу-

уравнением относительно квадрата координаты

зия [6, 7]. Но дрейфовый снос X = ut в рассматри-

максимума функции распределения (9)

(t),

max

ваемых моделях не всегда больше дисперсии

имеющей бесконечное число решений. Это озна-

t. Когда дрейфовый снос меньше дисперсии,

чает, что функция

(t)

через определенные

max

адвекции липидов не видно на фоне их хаотиче-

промежутки времени меняет свой знак. Но отри-

ского теплового движения, траектория липидов в

цательным квадрат координаты максимума

мембране соответствует нелинейной диффузии.

функции распределения быть не может. Это

Получим аналитически условие, когда дрейфо-

означает, что в промежуток времени, когда

(t)

max

вый снос при адвекции липидов больше диспер-

меньше нуля согласно решению уравнения (12),

сии

, т.е. когда хмелевая диффузия будет

адвекции не существует, а существует только

X≥

диффузия. Далее наступает промежуток времени,

видна в экспериментах. Для этого рассмотрим

когда существует одновременно адвекция и диф-

эволюцию во времени центрального максимума

фузия. Затем опять наступает промежуток только

функции распределения (9), который в началь-

диффузионного движения липидов и так далее.

ный момент времени находится в точке (c, d). Для

простоты анализа исследуем движение вдоль од-

Для оценки промежутка времени, когда

(t)

x ≥0

max

ной оси OX, начальную точку берем (0, 0):

и существует дрейфовый снос, гармонические

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

функции в уравнении (12) разложим в ряд Тейло-

+bx

(13)

max

{

(

max

)

max

}

max

лучим алгебраическое уравнение:

где

AC2 - B2C

- BCt + C; b = - ABCt2+

2B2+ AC

t; c = 2AB2t2 +2A.

{

}

(

)

В свою очередь,

A=D -



новых чисел двух подрешеток q = k₂/k₀. Тогда

Решая уравнение (13), можно найти зависи-

уравнение (14) превратится в

мость квадрата координаты максимума функции

распределения

(9)

(t)

от времени. Когда

max

(β

+β

> 4(1−

−

)

(15)

функция a(t) равна нулю,

(t)

меняет знак.

+β

max

Один из корней уравнения a(t) = 0 всегда отрица-

При известных коэффициентах неоднородно-

телен, другой - положителен. Отсюда следует,

стей β₂ и β₃ из неравенства (15) можно получить

что в начальный промежуток времени от нуля

критическое значение отношения волновых чи-

−

сел двух подрешеток q, при котором начинает на-

до

существует только диффу-

блюдаться хмелевая диффузия в мембране.

B2 - AC

зия, а далее - диффузия и адвекция. Если в урав-

Вычисление среднего смещения липидов и

нении (12) оставить в разложении большие степе-

среднеквадратичного смещения частицы под-

ни xmax, чем в уравнении (13), получится алгеб-

тверждает критерии (14) и (15), полученные из

раическое уравнение более высокого порядка,

аналитического исследования уравнений (7) и

чем уравнение (13). Соответственно, получится

(9). Среднее смещение частицы по формуле (10) и

не два, а больше моментов времени, когда

среднеквадратичное смещение (11) для разных

max

меняет свой знак, можно рассчитать временные

начальных координат частицы (c, d) вычисляли с

интервалы большего числа диффузионных и ад-

помощью программы Mathcad. Для диффузии в

векционных режимов перемещения липидов.

однорешеточной модели, описываемой функци-

Можно сделать оценку, когда в режиме одновре-

ей распределения (7), результаты расчетов пока-

менной адвекции и диффузии дрейфовый снос

заны на рис. 3, где приведена эволюция R² при

вдоль одной координаты будет больше диспер-

разных начальных координатах частицы. Здесь

сии, т.е. когда в эксперименте будет наблюдаться

D₀ = 10^-12 м²/с, D₁ = 0.8D₀, зависимость коэффи-

адвекция. Время, когда наблюдается максималь-

циента диффузии от координаты х показана на

ный дрейфовый снос, возьмем равным

рис. 1б. На рис. 3а представлено среднеквадра-

t_max = 1/2B. Время tmax немного больше времени

тичное смещение R²на малом времени наблю-

t₀ и лежит в промежутке, где существует адвекция:

дения (от 0 до 700 мкс). Кривая 1 соответствует

 kt

смещению частицы, имеющей начальные коор-

0 max

+  kt

2 max

(

D - -

)

max

(14)

динаты с = 3 нм, d = 50 нм (область липид-липид-

Делая оценку (14) для модели с одной ре-

ных взаимодействий, коэффициент диффузии в

шеткой неоднородности, описываемой уравне-

этой точке D = 1.786D₀). Кривая 2 соответствует

нием (1), введем коэффициент неоднородности

смещению частицы, имеющей начальные коор-

решетки β = D₁/D₀. Решая уравнение (14), най-

динаты с = 3 нм, d = 5 нм (область белок-липид-

дем, учитывая, что

что дрейфовый снос

ных взаимодействий, коэффициент диффузии в



будет больше дисперсии при β > 0.8. При мень-

этой точке D = 0.253D₀). Для сравнения дано сме-

ших значениях коэффициента неоднородности

щение при простой диффузии с коэффициентом

решетки β адвекция не будет видна на фоне хао-

D₀ = 10^-12 м²/с (пунктирная прямая 3). На рис. 3б

тического теплового движения липида. Делая

представлено среднеквадратичное смещение на

оценку (14) для модели с двумя подрешетками не-

больших временах наблюдения (от 0 до 5000 мкс),

однородностей, описываемой уравнением (8),

обозначения те же, что и на рис. 3а. Кривые 1 и 2

введем второй коэффициент неоднородности ре-

на этом графике слились вместе при времени на-

шетки



третий коэффициент неодно-

блюдения большем 1500 мкс. Для сравнения здесь

родности решетки



и отношение вол-

снова приведена эволюция при простой броунов-

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

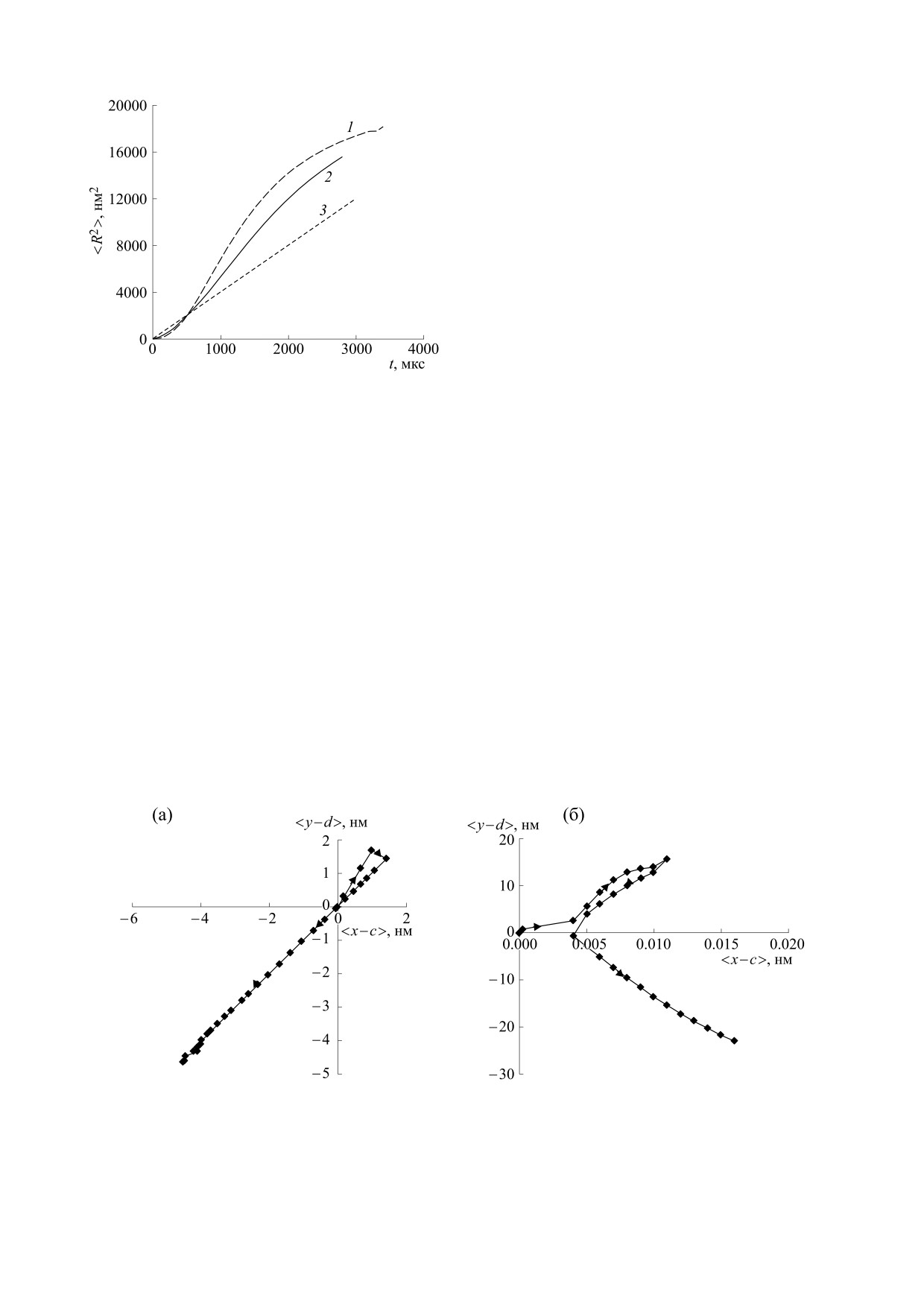
Рис. 3. Эволюция среднеквадратичного смещения частицы от времени при ее различных начальных координатах:

(a) - на малых временах, (б) - на больших временах. Кривая 1 соответствует смещению частицы, имеющей начальные

координаты с = 3 нм, d = 50 нм; кривая 2 соответствует смещению частицы, имеющей начальные координаты с = 3 нм,

d = 5 нм; прямая 3 соответствует смещению при простой диффузии с коэффициентом D₀ = 10^-12 м²/с.

вая 3 на рис. 3а). Такой режим в работах [6, 7]

ской диффузии с D₀ = 10^-12 м²/с (пунктирная

трактуется как направленная диффузия, но не

прямая).

хмелевая. В промежутке времени от 0 до 300 мкс

Анализ рис. 3 показывает, что среднеквадра-

среднеквадратичное смещение выше у частицы,

тичное смещение нелинейно зависит от времени,

стартовавшей из области белок-липидных взаи-

диффузия частиц в неоднородной мембране не

модействий около мембранного белка. В проме-

является простой броуновской, ее среднеквадра-

жуток времени от 300 до 1000 мкс квадратичное

тичное смещение нелинейно растет со временем.

смещение выше у частицы, стартовавшей из об-

Но хмелевая диффузия при этом не наблюдается.

ласти липид-липидных взаимодействий, находя-

Согласно критерию (14) для этого коэффициент

щейся между белок-липидными мембранами

неоднородности решетки β должен быть больше

(рис. 3а).

0.8, а в рассматриваемом примере β = 0.8, такой

неоднородности недостаточно для возникнове-

На больших временах (больше 1500 мкс), как

ния хмелевой диффузии. Частица, стартовавшая

уже отмечалось, кривые 1 и 2 на рис. 3б сливают-

из точки с координатами с = 3 нм, d = 5 нм (об-

ся. Это означает, что липиды в результате столк-

ласть белок-липидных взаимодействий), в про-

новений с другими молекулами мембраны и об-

межуток времени от 0 до 300 мкс движется в ре-

мене с ними энергией забывают о своем началь-

жиме субдиффузии (кривая 2 на рис. 3а), когда

ном положении и движутся в одинаковом

D ~ t^α, где α < 1. Она перемещается внутри белок-

режиме. Время релаксации для исследуемой диф-

липидного домена, связанного с цитоскелетом.

фузии липидов, когда характеристики движения

Затем частица покидает свой компартмент (свой

выравниваются равно 1.5 мс. Средние смещения

белок-липидный домен) и движется в режиме су-

частиц x - c, y - d вдоль осей x и y на рассмат-

риваемом промежутке времени от 0 до 5000 мкс

пердиффузии (кривая 2 на рис. 3а), когда D ~ t^α,

равны нулю, направленного перемещения (ад-

где α > 1. У частицы, стартовавшей из точки с ко-

векции) липидов вдоль слоя не наблюдается. Та-

ординатами с = 3 нм, d = 50 нм (область липид-

ким образом, если при структурном изменении

липидных взаимодействий) на начальной стадии

(t < 300 мкс), среднеквадратичное смещение

мембраны в ней появлялись неподвижные белок-

липидные домены, связанные с цитоскелетом,

меньше среднеквадратичного смещения при про-

стой броуновской диффузии (кривая 3 на рис. 3а).

причем плотность липидов около неподвижных

Ее движение, следуя терминологии, принятой в

мембранных белков, связанных с цитоскелетом,

работах [6, 7], можно назвать режимом замедлен-

была одинаковой, то для липидов мембраны реа-

ной диффузии. При t > 300 мкс диффузия части-

лизовывался режим ограниченной диффузии,

цы трансформируется в супердиффузию

или замедленной диффузии, или направленной

(кривая 1 на рис. 3а), здесь ее среднеквадратич-

диффузии. Хмелевая диффузия при этом не на-

ное смещение больше среднеквадратичного сме-

блюдается. Для этого коэффициент неоднород-

щения при простой броуновской диффузии (кри-

ности мембраны должен быть больше 0.8, что в

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

начальных координатах. Здесь D₀ = 10^-12 м²/с,

= 0.1D₀,

D₂ = 0.8D₀, λ₁ = 100 нм, λ₂ = 400 нм,

второй коэффициент неоднородности β₂ = 0.1,

третий коэффициент неоднородности β₃ = 0.8,

отношение волновых чисел двух подрешеток

q = 0.25. Если подставить эти значения в крите-

рий (15), то он выполнится. Это означает, что в

системе будет наблюдаться хмелевая диффузия

(адвекция). Кривая 1 на рис. 4 соответствует сме-

щению частицы, имеющей начальные координа-

ты с = 5 нм, d = 3 нм (область белок-липидных

взаимодействий, коэффициент диффузии в этой

точке D = 0.11D₀). Кривая 2 соответствует квадра-

тичному смещению частицы, имеющей началь-

ные координаты с = 3 нм, d = 50 нм (область ли-

пид-липидных взаимодействий, коэффициент

Рис. 4. Эволюция среднеквадратичного смещения ча-

стицы для двух разных ее начальных координат. Кри-

диффузии в этой точке D = 0.533D₀). Для сравне-

вая 1 соответствует смещению частицы, имеющей на-

ния приведена прямая 3, соответствующая про-

чальные координаты с = 5 нм, d = 3 нм; кривая 2 со-

стой броуновской диффузии с коэффициентом

ответствует квадратичному смещению частицы,

D₀ = 10^-12 м²/с, второй и третий коэффициенты

имеющей начальные координаты с = 3 нм, d = 50 нм;

прямая 3 соответствует простой броуновской диффу-

диффузии равны нулю.

зии с коэффициентом D₀ = 10^-12 м²/с.

Кривые 1 и 2 на рис. 4 соответствуют хмелевой

диффузии липидов в плазматической мембране.

экспериментах встречается очень редко. Режим

Это подтверждают и средние смещения частиц от

определяется начальным положением липида.

времени, приведенные на рис. 5. На рис. 5а даны

средние смещения от времени в плоскости OXY

Если в результате структурных изменений

частиц, стартовавших соответственно из началь-

мембраны образуются две вложенные одна в дру-

ной точки с координатами с = 5 нм, d = 3 нм (об-

гую подрешетки неоднородностей, то коэффици-

ласть белок-липидных взаимодействий), что со-

ент диффузии описывается формулой (8). Каче-

ответствует кривой 1 на рис. 4 и с = 3 нм, d = 50 нм

ственно диффузия такая же, как и для однореше-

(область липид-липидных взаимодействий), что

точной модели. Но в этой модели в эксперименте

соответствует кривой 2 на рис. 4. Промежуток

может наблюдаться хмелевая диффузия. Резуль-

времени наблюдения на рис. 5а и 5б от 0 до

таты расчетов диффузии для этого случая показа-

3100 мкс. Старт движения частиц на рис. 5 нахо-

ны на рис. 4, где представлена эволюция средне-

дится в точках с координатами (0; 0). На рис. 5

квадратичного смещение частицы при разных ее

каждый квадрат соответствует среднему смеще-

Рис. 5. Среднее смещение в плоскости xy от времени частиц c начальными координатами: (а) - с = 5 нм, d = 3 нм

(область белок-липидных взаимодействий); (б) - с = 3 нм, d = 50 нм (область липид-липидных взаимодействий).

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

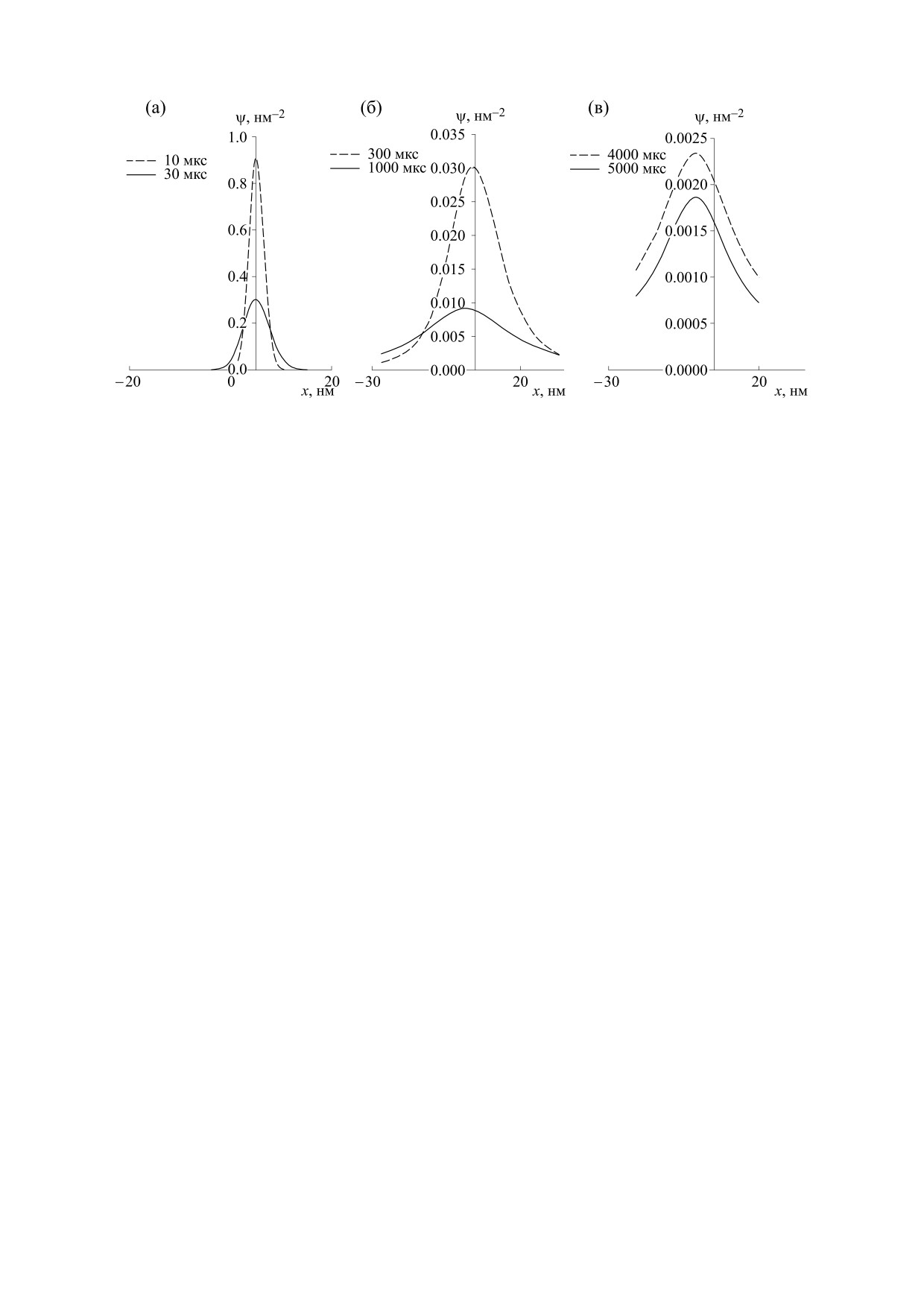
Рис. 6. Сечение функции распределения липида вдоль оси х при постоянной координате y = 3 нм, стартовавшего из

области белок-липидного взаимодействия с начальными координатами с = 5 нм, d = 3 нм в разные моменты времени.

нию частицы через каждые 100 мкс. Квадраты со-

пидного взаимодействия. Последнее хорошо ил-

единены линией, которая соответствует усред-

люстрируется сопоставлением эволюции частиц

ненной по времени траектории движения части-

1 и 2, приведенных, соответственно на рис. 5а

цы вдоль мембраны. Стрелками показаны

и 5б.

направления движения частицы.

Различия характеров диффузии липидов, стар-

Характер диффузии частиц в обоих случаях ка-

товавших из разных областей мембраны можно

чественно подобен и меняется с течением време-

увидеть и с помощью функций распределения.

ни. На начальной стадии эволюции имеет место

На рис. 6 изображены последовательно в разные

супердиффузия. Однако кривые 1 и 2 в промежут-

моменты времени сечение функции распределе-

ке времени от 0 до 50 мкс имеют наклон меньше,

ния липида вдоль оси х при постоянной коорди-

чем у прямой, описывающий эволюцию при про-

нате y = 3 нм, стартовавшего из области белок-ли-

стой диффузии (рис. 4). Это значит, что в этом

пидного взаимодействия с начальными коорди-

промежутке диффузия частицы затруднена и ее

натами с

5 нм, d

3 нм. Функции

эффективный коэффициент диффузии ниже, что

распределения соответствует кривой 1 на рис. 5.

согласно работам [6, 7] можно трактовать как ре-

По оси абсцисс отложена координата х, по оси

ординат - функция распределения. Функция

жим замедленной диффузии. На этом промежут-

ке времени среднее смещение частицы вдоль осей

распределения Ψ имеет размерность нм^-2, N_p = 1.

OX и OY равно нулю (рис. 5а). Далее, начиная с

Ось ординат пересекает ось абцисс при х = 5 нм.

времени 850 мкс характер диффузии обеих частиц

На рис. 6а отложены функции распределения при

меняется, причем наклон кривых среднеквадра-

10 и 30 мкс после начала наблюдения, на рис. 6б -

тичного смещения оказывается выше, чем у пря-

спустя 300 и 1000 мкс, на рис. 6в - спустя 4000 и

мой 3 для простой диффузии (рис. 4). На этом

5000 мкс. Рис. 6а показывает, что функции рас-

промежутке времени осуществляется адвекция-

пределения имеют гауссовский характер, макси-

диффузия, среднее смещение частицы при этом

мумы распределения находятся при х = 5 нм. За-

не равно нулю (см. рис. 5). Время начала режима

тем после времени t₀ из решения уравнения (13)

адвекции совпадает с оценкой t₀ из решения урав-

(см. рис. 6б) происходит латеральное ненулевое

нения (13). Происходит перенос частицы к ло-

среднее смещение частицы (адвекция), кривые

кальному центру притяжения. В промежутке вре-

распределения стали несимметричны и их макси-

мени t > 2900 мкс частица движется в режиме суб-

мумы смещаются. На рис. 5а это соответствует

диффузии (ограниченной диффузии согласно

участку с ненулевым средним смещением. При

работам [6, 7]). Изменение начальных координат

300 мкс максимум находится в точке х = 5 нм, при

частиц лишь количественно влияет на характер

1000 мкс - х = 2 нм. Отсюда можно оценить сред-

эволюции частиц 1 и 2. Среднее смещение липи-

нюю скорость адвекции частиц мембраны в этот

да, стартовавшего из области липид-липидного

период времени, она оказывается равной около

взаимодействия, в три раза больше, чем смеще-

3 нм/мс. При 4000 и 5000 мкс максимумы функ-

ние липида, стартовавшего из области белок-ли-

ции распределения оставались на одном месте, а

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

функции распределения - симметричны. Это

не, считается, что они одинаковые. Таким обра-

означит, что адвекция прекратилась и снова на-

зом, не рассматриваются эффекты перекрестной

ступил период диффузии.

диффузии. Сама модель бесконечного монослоя,

в котором происходит диффузия, тоже не совсем

При появлении в мембране двух подрешеток

точно отражает строение замкнутой мембраны.

неоднородностей, вставленных одна в другую, на

Далее, в нашей модели рассматривается переме-

участке мембраны размером около λ₂ на λ₂ появ-

щение липидов на участке мембраны размером

ляется центр притяжения для липидов. В этом

примерно 50×50 нм², что примерно в сто раз

центре липидный бислой разрыхлен, коэффици-

меньше размера мембраны эритроцита. При та-

ент диффузии наибольший. Появляется адвекция

ком приближении рассматривать диффузию ли-

липидов, но это локальные потоки, направлен-

пидов в мембране эритроцита как диффузию в

ные к этому центру притяжения. Суммарного по-

плоском бесконечном монослое вполне допусти-

тока вдоль всей мембраны не возникает. Если в

мо. С другой стороны, если рассматривать диф-

этом центре притяжения находится какой-ни-

фузию липидов при больших временах, то необ-

будь лиганд, к нему устремляются липиды и бел-

ходимо будет учитывать конечность мембраны и

ки, необходимые для образования вокруг него бе-

ее замкнутость.

лок-липидного домена (рафта), который необхо-

дим этому лиганду, например, для эндоцитоза. В

Ранее установлено, что структурные измене-

этом центре притяжения вокруг лиганда и проис-

ния в плазматических мембранах изменяют

ходит самосборка рафта. После отсоединения ли-

функции мембран и клеток [32-48]. Несмотря на

ганда от мембраны адвекция молекул к этому ли-

указанные ограничения предлагаемой модели,

ганду прекращается.

она качественно описывает один из механизмов

влияния структурных переходов в биомембранах

Возможно, при создании двух подрешеток не-

на их функции. В однородной мембране реализу-

однородностей в мембране появляются нанока-

ется простая броуновская диффузия частиц,

налы, заполненные молекулами воды, попадая в

среднее смещение подвижных молекул мембра-

которые липиды начинают направленно переме-

ны равно нулю. При взаимодействии с лигандами

щаться вдоль мембраны. Наноканалы могут по-

мембрана испытывает структурный переход, из-

являться в мезополосах разрыхления, между бе-

за этого латеральная диффузия липидов ста-

лок-липидными доменами [5]. Характер движе-

новится облегченной, может возникнуть адвек-

ния липидов в этих наноканалах может

ция - локальный поток липидов к центру притя-

отличаться от характера движения в мембране.

жения. Это облегчает образование подвижных

Похожее явление наблюдается при движении на-

белок-липидных доменов рафтов, с помощью ко-

ночастиц в наноканалах [29-31]. Связано это с

торых происходит эндоцитоз лигандов.

тем, что уравнения переноса в стесненных усло-

виях содержат не только тензор напряжений и

вектор теплового потока, но и межфазные силы,

ВЫВОДЫ

ответственные за передачу количества движения

и тепла из-за взаимодействия с поверхностями

В данной работе аналитическими методами

стенок наноканалов [29-31]. Было обнаружено,

исследована модель нелинейной диффузии липи-

что вязкость жидкости в наноканале сильно зави-

дов в цитоплазматической мембране, которая

сит от потенциала взаимодействия между жидко-

возникает после появления в ней сети неподвиж-

стью и молекулами стенки канала. В частности,

ных периодически расположенных белок-липид-

увеличение глубины потенциальной ямы этого

ных доменов, связанных с цитоскелетом. Коэф-

взаимодействия приводит к увеличению вязкости

фициент диффузии липидов в этих доменах ни-

жидкости. В то же время, если глубина потенци-

же, чем в промежутках между доменами, так что в

альной ямы мала, вязкость жидкости в нанокана-

мембране он приблизительно описывается пери-

ле может быть даже ниже, чем ее вязкость в не-

одической от координат функцией. Аналитиче-

ограниченной системе. Таким образом, вязкость

ски показано, что для этой модели существует ре-

жидкости в наноканале и, следовательно, сопро-

жим адвекции-диффузии. Было рассмотрено два

тивление потоку в канале зависит от материала

случая. Если мембранные белки, связанные с ци-

стенок наноканала.

тоскелетом, меняют свою конформацию одина-

Если говорить об адекватности модели, в пред-

ково, в мембране возникает неоднородная струк-

ложенной модели рассматривается латеральная

тура из одинаковых неподвижных белок-липид-

диффузия липидов в одном липидном монослое.

ных доменов, образованных вокруг этих

Их перескоки из одного монослоя в другой (пере-

мембранных белков. Аналитически показано че-

ходы типа «флип-флоп») не учитываются. Между

редование режимов нелинейной диффузии и сов-

тем в реальных процессах они происходят, осо-

местной адвекции-диффузии. Показано, что от

бенно при искривлении мембраны. Кроме того,

нуля до некоторого времени t₀ наблюдается нели-

не учитывается разный состав липидов в мембра-

нейная диффузия, далее наступает период адвек-

БИОФИЗИКА том 68

№ 1

2023

МОДЕЛЬ ДИФФУЗИИ ЛИПИДОВ

ции-диффузии, далее опять период нелинейной

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

диффузии и т.д. В эксперименте это не всегда на-

Настоящая работа не содержит описания ис-

блюдается в виде хмелевой диффузии. Когда

следований с использованием людей и животных

дрейфовый снос при адвекции меньше диспер-

в качестве объектов.

сии, адвекции липидов не видно на фоне их хао-

тического теплового движения, траектория липи-

дов в мембране соответствует нелинейной диф-

СПИСОК ЛИТЕРАТУРЫ

фузии. Аналитически получены критерии, при

K. Suzuki, K. Ritchie, E. Kajikawa, et al., Biophys. J.,

выполнении которых в эксперименте можно на-

88 (5), 3659 (2005).

блюдать адвекцию липидов. Аналитически пока-

R. G. Parton and M. A. del Pozo, Nat. Rev. Mol. Cell

зано, что адвекция липидов в случае одной ре-

Biol., 14 (2), 98 (2013).

шетки неоднородностей не наблюдается, по-

P.G. Saffman, M. Delbrück, Proc. Natl. Acad. Sci.

скольку

коэффициент

неоднородности

USA, 72, 3111 (1975).

мембраны β должен быть очень высоким (β > 0.8),

E. P. Petrov and P. Schwille, Biophys. J., 94 (5), 45

что редко выполняется в эксперименте. При

(2008).

меньших значениях коэффициента неоднород-

П. В. Мокрушников, Л. Е. Панин, В. Е. Панин

ности решетки β адвекция не будет видна на фоне

и др., Структурные переходы в мембранах эритро-

хаотического теплового движения липида.

цитов (экспериментальные и теоретические моде-

ли) (НГАСУ, Новосибирск, 2019).

Во втором случае, когда мембранные белки,

T. Fujiwara, K. Ritchie, H. Murakoshi, et al., J. Cell

связанные со спектрин-актин-анкириновой се-

Biol., 157 (6), 1071 (2002).

тью по-разному меняют свою конформацию, они

T. K. Fujiwara, K. Iwasawa, Z. Kalay, et al., Mol. Biol.

по разному притягивают к себе окружающие их

Cell, 27 (7), 1101 (2016).

липиды. Образующиеся при этом белок-липид-

P. F. Lenne, L. Wawrezinieck, F. Conchonaud, et al.,

ные домены будут разными, плотность липидно-

EMBO J., 25 (14), 3245 (2006).

го бислоя можно представить как наложение одну

A. Honigmann, S. Sadeghi, J. Keller, et al., Elife, 3,

на другую двух или более подрешеток неоднород-

e01671 (2014).

ной плотности липидов. Показано, что характер

10.

M. Renner, Y. Domanov, F. Sandrin, et al., PLoS One,

диффузии липидов при этом качественно остает-

6 (9), e25731 (2011).

ся прежним, как и для модели с одной решеткой

11.

A. Einstein, Annal. Der Physik, 322(8), 549 (1905).

неоднородности. Но в этом случае уже может на-

12.

K. Ayscough, Methods Enzymol., 298,18 (1998).

блюдаться хмелевая диффузия, при которой не-

13.

G. I. Mashanov, T. A. Nenasheva, A. Mashanova,

линейная диффузия сменяется периодами адвек-

et al., Faraday Discuss., 232, 358 (2021).

ции-диффузии. Адвекция носит локальный ха-

14.

M. N. Costa, K. Radhakrishnan, and J. S. Edwards, J.

рактер, сосредоточена около белок-липидных

Biotechnol., 151 (3), 261 (2011).

доменов, в которых увеличение плотности липи-

15.

Y. A. Domanov, S. Aimon, G. E. S. Toombes, et al.

дов наибольшее. Среднее смещение частиц при

Proc. Natl. Acad. Sci. USA, 108 (31), 12605 (2011).

адвекции выше у молекул, стартовавших из обла-

16.

O. A. Dvoretskaya and P. S. Kondratenko, J. Exp. The-

сти липид-липидных взаимодействий. Аналити-

or. Physics, 116, 698 (2013).

чески получен критерий, при соблюдении кото-

17.

P. S. Kondratenko and A. L. Matveev, J. Exp. Theor.

рого в эксперименте может наблюдаться хмеле-

Physics, 157 (4), 703 (2020).

вая диффузия. Эта модель хорошо на

18.

G. J. Wang and N. G. Hadjiconstantinou, Langmure,

качественном уровне объясняет эксперименталь-

34 (23), 6976 (2018).

ные результаты измерения перемещения липидов

19.

V. Andryushchenko and V. Rudyak, Defect and Diffu-

в цитоплазматической мембране.

sion Forum 312-315, 417 (2011).

20. V. A. Andryushchenko and V. Ya. Rudyak, Reports of

the Academy of Sciences of the Higher School of the

ФИНАНСИРОВАНИЕ РАБОТЫ

Russian Federation, 2 (15), 6 (2010).

21. В. Я. Рудяк, Статистическая аэрогидромеханика

Работа выполнена при финансовой поддержке

гомогенных и гетерогенных сред. Т. 2. Гидромеханика

Министерства науки и высшего образования РФ

(НГАСУ. Новосибирск, 2005).

(Соглашение No. 075-15-2021-575) и Российского

22. S. J. Singer and G. L. Nicolson, Science, 175, 720

фонда фундаментальных исследований (грант

(1972).

No. 20-01-00041).

23. G. L. Nicolson, Biochim. Biophys. Acta, 457 (1), 57

(1976).

24. P. V. Mokrushnikov, in Lipid Bilayers: Properties, Be-

КОНФЛИКТ ИНТЕРЕСОВ

havior and Interactions, Ed. by M. Ashrafuzzaman (No-

va Science Publishers, NY, 2019), pp. 43-91.

Авторы заявляют об отсутствии конфликта

25. J. Morel, S. Claverol, S. Mongrand, et al, Mol. Cell

интересов.

Proteomics, 5 (8), 1396 (2006).

БИОФИЗИКА том 68

№ 1

2023

МОКРУШНИКОВ, РУДЯК

26. S.-C. Liu, L. H. Derick, J. Palek, Journal of cell biology

38. P. V. Mokrushnikov, J. Physics: Conf. Ser. The Conf.

104, 527 (1987).

Proc. STS35 (Kutateladze Institute of Thermophysics,

Sib. Branch of the RAS), 012161 (2019).

27. L. E. Panin, P. V. Mokrushnikov, V. G. Kunitsyn, and

B. N. Zaitsev, J. Phys. Chem. B, 114, 9462 (2010).

39. P. V. Mokrushnikov, E. V. Lezhnev, and V. Ya. Rudyak,

AIP Conf. Proc., 2351, 040054 (2021).

28. L. E. Panin, P. V. Mokrushnikov, V. G. Kunitsyn, and

40. P. V. Mokrushnikov, V. Ya. Rudyak, and E. V. Lezhnev,

B. N. Zaitsev, J. Phys. Chem. B, 115, 14969 (2011).

Nanosystems: Physics, Chemistry, Mathematics, 12

29. V. Yа. Rudyak and A. A. Belkin, Doklady Physics, 59,

(1), 22 (2021).

604 (2014).

41. L. E. Panin and P. V. Mokrushnikov, Biophysics, 59

30. V. Yа. Rudyak and A. A. Belkin, Nanosystems: Physics,

(1), 127 (2014).

Chemistry, Mathematics 6 (3), 366 (2015).

42. P. V. Mokrushnikov, L. E. Panin, and B. N. Zaitsev,

31. V. Yа. Rudyak and A. A. Belkin, Nanosystems: Physics,

Gen. Physiol. Biophys., 34 (3), 311 (2015).

Chemistry, Mathematics 9 (3), 349 (2018).

43. P. V. Mokrushnikov, Biophysics, 62 (2), 256 (2017).

32. Л. Е. Панин и П. В. Мокрушников, Вестн. Новоси-

44. Л. Е. Панин, П. В. Мокрушников, Р. А. Князев

бирского гос. пед. ун-та, 5 (15), 101 (2013).

и др., Атеросклероз, 6, 12 (2012).

33. P. V. Mokrushnikov, A. N. Dudarev, T. A. Tkachenko,

45. В. Г. Куницын, П. В. Мокрушников и Л. Е. Панин,

et al., Biochemistry (Moscow). Suppl. Ser. A: Mem-

Бюл. Сибирского отделения РАМН, 5 (127), 28

brane and Cell Biology, 11 (1), 48 (2017).

(2007).

46. П. В. Мокрушников, Бюл. Сибирского отделения

34. L. E. Panin, P. V. Mokrushnikov, V. G. Kunitsyn, et al.,

РАМН, 1 (147), 38 (2010).

Phys. Mesomechanics, 14 (3-4), 167 (2011).

47. О. Н. Потеряева, Г. С. Русских, П. В. Мокрушни-

35. P. V. Mokrushnikov, L. E. Panin, N. S. Doronin, et al.,

кови др. Вестн. Уральской мед. акад. науки, 48 (2),

Biophysics, 56 (6), 1074 (2011).

149 (2014).

36. P. V. Mokrushnikov, Biophysics, 65 (1), 65 (2020).

48. П. В. Мокрушников, Л. П. Осипова, Т. В. Гольцова

37. A. I. Kozelskaya, A. V. Panin, I. A. Khlusov, et al, Tox-

и А. А. Розуменко, Якутский мед. журн. 54 (2), 15

icol. in Vitro, 37, 34 (2016).

(2016).

Model of Lipid Diffusion in Cytoplasmic Membranes

P.V. Mokrushnikov* and V.Ya. Rudyak*^,**^, ***

*Novosibirsk State University of Architecture and Civil Engineering (SIBSTRIN),

Leningradskaya ul. 113, Novosibirsk, 630008 Russia

**Kutateladze Institute of Thermophysics, Siberian Branch of the Russian Academy of Sciences,

ul. Akademika Lavrent'eva 1, Novosibirsk, 630090 Russia

***Novosibirsk State University, ul. Pirogova 1, Novosibirsk, 630090 Russia

An analytical model of lateral lipid diffusion in heterogeneous native cytoplasmic membranes is presented.

The Fourier transform method was used to solve the diffusion equation for the coordinate distribution func-

tion of lipids in a periodically inhomogeneous membrane, in which the diffusion coefficient is described by

a harmonic function of the coordinates. It is shown that advection and diffusion are present in membrane.

The model explains different types of lipid diffusion in membrane observed previously in experiments as a re-

sult of structural transitions of periodically located fixed protein-lipid domains associated with the spectrin-

actin-ankyrin network. If these domains are the same, then super- and subdiffusion can be seen in experi-

ments, when the mean square displacement of lipids depends non-linearly on time, and their average dis-

placement is zero. Drift during advection was less than the chaotic Brownian displacement of lipids, advec-

tion was not observed in the experiment. When not all membrane proteins associated with the spectrin-actin-

ankyrin network undergo conformational change in the same way upon ligand binding, two periodic sublat-

tices of inhomogeneities arise in the membrane from fixed protein-lipid domains around membrane proteins

associated with the cytoskeleton and nested in one another. In this case, hop diffusion can be found in exper-

iments, when periods of nonlinear diffusion of molecules are replaced by periods of advection-diffusion, in

which the average displacement of molecules is not zero. Advection is local in nature and occurs near indi-

vidual protein-lipid domains. In the presented work, criteria are analytically obtained under which hop dif-

fusion is experimentally observed in a periodically inhomogeneous membrane.

Keywords: lipid diffusion, structural transitions in biomembranes, advection in heterogeneous layers

БИОФИЗИКА том 68

№ 1

2023