БИОФИЗИКА, 2023, том 68, № 5, с. 837-849

МОЛЕКУЛЯРНАЯ БИОФИЗИКА

УДК 577.322

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

В РАСТВОРАХ БИОМОЛЕКУЛ: ВОЗМОЖНОСТИ ПОДХОДА,

ОСНОВАННОГО НА 3D-РАСПРЕДЕЛЕНИИ АТОМНОЙ

ПЛОТНОСТИ РАСТВОРИТЕЛЯ

*Институт химии растворов им. Г. А. Крестова РАН, ул. Академическая, 1, Иваново, 153045, Россия

**Ивановский государственный университет, Россия, 153025, Иваново, ул. Ермака, 39

***Институт теоретической и экспериментальной биофизики РАН,

Институтская ул., 3, Пущино Московской области, 142290, Россия

^#E-mail: genchuev@rambler.ru

Поступила в редакцию 03.07.2023 г.

После доработки 18.07.2023 г.

Принята к публикации 19.07.2023 г.

Биомолекулярная сольватация играет одну из ключевых ролей в живой природе. От особенностей

протекания данного процесса зависит биологическая активность молекул и выполнение ими своих

целевых функций. Однако исследование гидратации биомолекул является нетривиальной задачей

как для экспериментальных методов, так и для компьютерного моделирования. В работе

демонстрируются возможности неэмпирического подхода 3D-SDFT/3D-RISM, основанного на

3D-распределении атомной плотности растворителя, для исследования особенностей гидратации

биомолекул на примере ряда аминокислот - Gly-ZW, L-Ala-ZW, L-Val-ZW, L-Pro-ZW, двух

модельных белков - BPTI (ингибитора трипсина бычьей поджелудочной железы) и PTP1B

(белковой тирозинфосфатазы

1B), а также комплексов белка PTP1B с ингибиторами.

Представленные результаты показывают, что подход позволяет в деталях и одновременно целостно

описывать структуру гидратной оболочки биомолекул.

Ключевые слова: биомолекулы, гидратация, структура гидратной оболочки, методы теории

жидкостей.

DOI: 10.31857/S0006302923050010, EDN: PFYCDD

ния молекул воды в биологической среде. Опре-

В живом организме биомолекулы вовлечены в

деление параметров данного процесса с помощью

большое количество межмолекулярных взаимо-

действий - с водой (гидратация), между собой

экспериментальных методов во многих случаях

(ассоциация, самоагрегация), с присутствующи-

представляет значительную проблему, как техни-

ми в среде ионами (ассоциация) или с лигандами

ческую (исследования требуют больших времен-

(комплексообразование). Среди них одну из клю-

ных затрат, а интерпретация получаемых данных

чевых ролей играют взаимодействия с водой, от

затруднена необходимостью разделения различ-

специфики проявления которых существенным

ных эффектов, определяющихся множеством

образом зависит биологическая активность моле-

взаимодействий), так и финансовую (стоимость

кул. В то же время изучение гидратации биомоле-

многих соединений, реактивов довольно высо-

кул, особенно биомакромолекул, на атомном и

ка). Поэтому для подобных исследований ис-

атомно-молекулярном уровнях является нетри-

пользуются различные подходы численного мо-

виальной задачей из-за динамического поведе-

делирования, начиная от квантово-химических

расчетов и заканчивая расчетами методом моле-

Сокращения: MOZ - молекулярная модель Орнштейна- кулярной динамики. Современные вычислитель-

Цернике, RISM - модель взаимодействующих силовых

центров, SDFT - теория классического функционала

ные методы дают широкие возможности для изу-

атомной плотности, 3D-RISM - трехмерная модель взаи-

чения физико-химических свойств растворов

модействующих силовых центров, ПФР - пространствен- биомолекул, позволяя сузить эксперименталь-

ные функции распределения, ПГЧ - полное гидратное

ный поиск. Будучи комплементарными к экспе-

число, BPTI - ингибитор трипсина бычьей поджелудоч-

риментальным подходам, вычислительные мето-

ной железы, PTP1B - белковая тирозинфосфатаза 1B.

837

838

КРУЧИНИН и др.

ды позволяют, в том числе, исследовать особен-

вать точное распределение растворителя, подоб-

ности сольватации биомолекул в растворах и

но методам молекулярной динамики с учетом яв-

определить молекулярные детали структуры их

ного растворителя, но при этом сохранять

сольватной (гидратной) оболочки, оценить тер-

относительно низкие вычислительные затраты

модинамические и структурные параметры соль-

как в случае методов с моделями неявного раство-

ватированных (гидратированных) комплексов и

рителя.

пр. Наиболее активно подобные исследования

Методы теории жидкостей основаны на аппа-

ведутся методами молекулярной динамики. Од-

рате функций распределения, поскольку они рас-

нако использование этих методов для исследова-

сматривают жидкость как статистическое распре-

ния сольватированных биомолекул ограничено

деление частиц (атомов, молекул или ионов). В

значительными затратами вычислительных ре-

этом смысле теория классического функционала

сурсов (объема оперативной памяти и процессор-

атомной плотности (SDFT) [21-25], которая опе-

ного времени), что, в том числе, связано с необхо-

рирует с атомной плотностью растворителя как

димостью учитывать влияние растворителя на со-

коллективной переменной, может рассматри-

стояние биомолекулы. Так, при использовании в

ваться как обобщенная теория для методов, бази-

расчетах моделей явного растворителя эти мето-

рующихся на распределении атомной плотности,

ды оказываются чрезвычайно дорогостоящими в

например, для RISM-подхода. В таком контексте

вычислительном отношении, а сами расчеты (да-

RISM, как и общий подход SDFT, исследует

же на суперкомпьютерах) занимают недели или

атомную плотность ρ_i(r) (жирным шрифтом здесь

месяцы при выполнении одной задачи [1-3]. От-

и далее указывается вектор), определяя распреде-

метим, что для воды на сегодняшний день пред-

ление i-ых атомов молекул растворителя (s) во-

ложено более 40 таких моделей [4, 5], однако все

круг растворенного вещества:

они имеют те или иные расхождения с экспери-

ментальными свойствами воды. Наиболее точны-

ми с точки зрения воспроизведения эксперимен-

(r)

δ(r

)

(1)



тальных структурных характеристик считаются

модели SPC/E (Simple Point Charge Extended

где N - общее число молекул растворителя, x_si -

model) [6] и TIP3P (Transferable Intermolecular Po-

их мгновенные положения.

tential with 3 Points) [7], которые очень популярны

в моделировании биомолекул [8], включая белки.

С другой стороны, трехмерную модель взаимо-

Существуют более быстрые, но менее точные

действующих силовых центров (3D-RISM) [26,

методы моделирования, в которых растворитель

27] можно рассматривать как приближение моде-

рассматривается как неявный континуум (моде-

ли MOZ или как 3D-версию SDFT [28], которая

ли неявного растворителя), такие как обобщен-

учитывает детали уже молекулярной структуры

ный метод Борна [9, 10] и метод Пуассона-

компонентов раствора. Само по себе использова-

Больцмана [11]. Вместе с тем, если растворитель

ние модели MOZ для расчетов биомолекулярной

представляется как сплошная диэлектрическая

сольватации очень затратно, поскольку модель

среда, то учет эффектов растворителя, связанных

MOZ требует вычисления шестимерных интегра-

с его молекулярной структурой, становится не-

лов. Поэтому такие вычисления не просто очень

возможным. Как результат, такой метод не может

сложны, но и плохо поддаются анализу и интер-

предсказать расположение молекул растворителя

претации. Как результат, вычислительные ресур-

вокруг растворенного вещества. Однако про-

сы, требуемые для MOZ-расчетов, сопоставимы с

странственное распределение молекул раствори-

теми, что требуются для молекулярной динами-

теля имеет решающее значение для понимания

ки.

того, какую роль сольватация играет в протека-

3D-RISM подход, оперирующий с 3D-распре-

нии различных физико-химических процессов.

делением частиц в статистическом ансамбле, по-

Существует альтернативный вариант выше-

стулирует, что молекулярная жидкость может

описанным методам с явным и неявным модели-

рассматриваться как

«эффективный» раствор

рованием растворителей - это статистико-меха-

атомов, но при этом учитывает меж- и внутримо-

нические подходы теории жидкостей, в частно-

лекулярные взаимодействия только через вос-

сти, подходы теории классического функционала

приимчивость однородной системы (т.е. через

плотности

[12-14] или теории интегральных

атом-атомные структурные факторы невозму-

уравнений, такие как молекулярная модель Орн-

щенной молекулярной жидкости). Благодаря

штейна-Цернике (MOZ) [15-17] и модель взаи-

этому теоретическому упрощению, метод 3D-

модействующих силовых центров (RISM) [18-

RISM стал чрезвычайно популярным и активно

20]. В этих подходах обычно используется ато-

используется для расчета свойств систем с раз-

марная модель явного растворителя без явного

личными сольватированными биомолекулами,

моделирования его движения в растворе. Это поз-

включая белки и их комплексы с лигандами (см.,

воляет методам теории жидкостей прогнозиро-

например, работы [29-50]).

БИОФИЗИКА том 68

№ 5

2023

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

839

Методы, основанные на 3D-распределении

ности частиц (например, атомов молекул раство-

атомной плотности, дают возможность исследо-

рителя) ρ_i(r) и эффективного парного потенциала

вать параметры сольватации молекул с учетом

межчастичных взаимодействий J_i(r), и дальней-

вкладов каждого из компонентов в энергетиче-

ших его оценках. Плотности и эффективный по-

ские и структурные изменения, происходящие в

тенциал должны быть получены соответствую-

растворах, установить взаимосвязь этих измене-

щей минимизацией функционала. Опуская все

ний с типом межчастичных взаимодействий, что

технические детали, которые можно найти в ра-

является принципиальным для понимания на

ботах [24, 25, 51], мы приводим здесь только

молекулярном и атомно-молекулярном уровне

окончательные соотношения для плотностей и

различных эффектов, проявляемых в биологиче-

эффективного потенциала. В векторной форме

ских системах. Отметим, что вышеназванные ме-

они могут быть записаны как

тоды, кроме определения параметров структуры

гидратной оболочки, дают также возможность

-βJ

ρ(r)

=ρ

+ξ([J],r

)]

e r)

оценить свободную энергию сольватации, кон-



(2)

J r)

=υ

(r)

+φ(r)

формационную стабильность молекул, энергию и



места связывания лигандов с белками.

Смысл соотношений (2) довольно прост. Пер-

В данной работе мы продемонстрируем только

вое уравнение характеризует плотность неодно-

один аспект применения таких методов, а имен-

родной молекулярной жидкости, находящейся

но, их применение для описания структуры гид-

под действием эффективного потенциала J(r), а

ратной оболочки ряда биомолекул по результатам

второе определяет сам эффективный потенциал,

собственных исследований.

включающий в себя потенциал межмолекулярно-

го взаимодействия «биомолекула-растворитель»

υ(r) и потенциал межмолекулярного взаимодей-

МЕТОДЫ, ОСНОВАННЫЕ

ствия «растворитель-растворитель» ϕ(r). Первое

НА 3D-РАСПРЕДЕЛЕНИИ АТОМНОЙ

из соотношений (2) содержит член ξ([J], r), назы-

ПЛОТНОСТИ РАСТВОРИТЕЛЯ

ваемый функционалом корреляционной поло-

Задача описания структурных особенностей

сти, который описывает внутримолекулярные

гидратации биомолекулы в методе 3D-SDFT сво-

корреляции растворителя. Из-за наличия послед-

дится к оценке профилей плотности атомов мо-

них корреляционная полость определяет откло-

лекул воды ρ_i(r) (i = O, H), находящейся под дей-

нение распределения атомной плотности раство-

ствием внешнего потенциала взаимодействия

рителя от Больцмановского распределения. Все

«биомолекула-растворитель» υ(r). Как было по-

разнообразие моделей SDFT заключается в выра-

казано нами ранее [24, 25, 51], строгая классиче-

жениях для функционала корреляционной поло-

ская формулировка SDFT должна быть основана

сти и межмолекулярного потенциала ϕ(r). В об-

на построении производящего функционала, за-

щем случае последний можно представить в виде

висящего от двух связанных переменных - плот-

функционала плотности:

−1

-1

−βφ(r)

(

(r r′)

−

(r r′)

)

Δρ(r′)

dr b ρ(

r)),

(3)



где S_m(r) и S(r) - структурные факторы одной мо-

(s)

s-1

TrD







лекулы растворителя (воды) и однородной жид-

ξ([J],r

)

(4)



-1

кости (воды) соответственно, b(ρ(r)) - мостико-

вый (бридж-) функционал, учитывающий вкла-

где М - общее количество атомов молекулы рас-

ды, выходящие за пределы линейного отклика.

творителя. Отметим, что внутримолекулярная

Для последнего можно использовать различные

корреляционная функция 2-го порядка D⁽²⁾(r) за-

приближения, а его зависимость от расстояния

висит только от длин связей l_ij, 3-го порядка - от

можно извлечь из результатов молекулярного мо-

длин связей и углов между связями, 4-го - от

делирования (см., например, работы [52, 53]).

длин связей, углов между связями и двугранных

углов и т.д.

Функционал корреляционной полости может

быть представлен как кластерное разложение че-

В методе 3D-RISM, как и в упрощенной вер-

сии SDFT, предполагается, что функционал кор-

рез функцию Майера, f(r) = e-βJ(r) - 1, и внутри-

реляционной полости зависит только от длин

молекулярные корреляционные функции s-го

связей и может быть выражен следующим обра-

порядка, D^(s):

зом [25]:

БИОФИЗИКА том 68

№ 5

2023

840

КРУЧИНИН и др.

RISM

−1

ξ(r)

≈ξ

(r)

≡

exp

1−

−

r′)

Δρ(r′)dr′

−1.

(5)

(

)





Если ввести новую переменную - прямую

αγ - внутримолекулярное расстояние между ато-

корреляционную функцию c(r):

мами α и γ молекулы растворителя, h_αγ(r) - меж-

молекулярная атом-атомная полная корреляци-

c(r) ≡ ∫S^-1(|r - r'|)Δρ(r')dr',

(6)

онная функция растворителя, ρ_α - плотность рас-

то 3D-RISM-уравнения могут быть записаны в

творителя. Из-за пренебрежения угловыми

форме:

зависимостями во внутримолекулярных корреля-

Δρ(r)

ционных функциях вычислительные затраты ме-

−βυ(r)+

-c(r)+b(r)

тода 3D-RISM на два порядка меньше, чем расче-

ρ(r)

(7a)

ты SDFT по формулам (2)-(4).

(r)

Δρ

В общем виде замыкание для уравнения (8) мо-

Δρ(r)

 S

−

r′)c(r′)

dr′,

h(r)

(7б)

жет быть записано [21] как:

Второе уравнение (7б) в этой системе является

g_γ(r) = exp[-βU_γ(r) + h_γ(r) - c_γ(r) + b_γ(r)],

(10)

интегральным уравнением Орнштейна-Церни-

где U_γ(r) - потенциал взаимодействия атома γ мо-

ке, которое связывает прямую корреляционную

функцию с(r) с полной корреляционной функци-

лекулы растворителя и молекулы растворенного

ей h(r). Так как обе эти функции неизвестны, то

вещества, β = 1/k_BT, k_B - постоянная Больцмана,

используют еще одно уравнение, чтобы замкнуть

Т - абсолютная температура.

систему. Таким замыкающим уравнением для

На сегодняшний день предложены несколько

(7б) является (7a).

видов замыканий, которые отличаются друг от

Метод 3D-RISM оперирует с пространствен-

друга математической формулировкой бридж-

ными (3D-) функциями распределения (ПФР)

функционала (или бридж-функции) b_γ(r). Среди

g_γ(r) взаимодействующих атомов молекул раство-

них замыкание Коваленко-Хираты считается од-

рителя γ вокруг молекулы растворенного вещества,

ним из лучших с точки зрения как численной ста-

находящейся в положении r. ПФР g_γ(r) ≡ g_γ(r,Ω)

бильности, так и разумной точности [55, 56] по-

представляет собой трехмерную функцию рас-

лучаемого решения, и наиболее часто использу-

пределения плотности атомов растворителя в ло-

ется в

3D-RISM-расчетах биомолекулярной

кальной системе координат, связанной с молеку-

сольватации. Оно имеет вид:

лой растворенного вещества. Для ее получения

exp

(

(r)) −1,

(r)

≤

молекулу растворенного вещества фиксируют в

(r)

=

начале локальной (сферической) системы коор-

(r),

)

(11)



динат и характеризуют локальные плотности ато-

(r)

= -β

(r)

мов, вычисляя как радиальные r, так и угловые

(Ω = (θ, φ)) координаты вектора r.

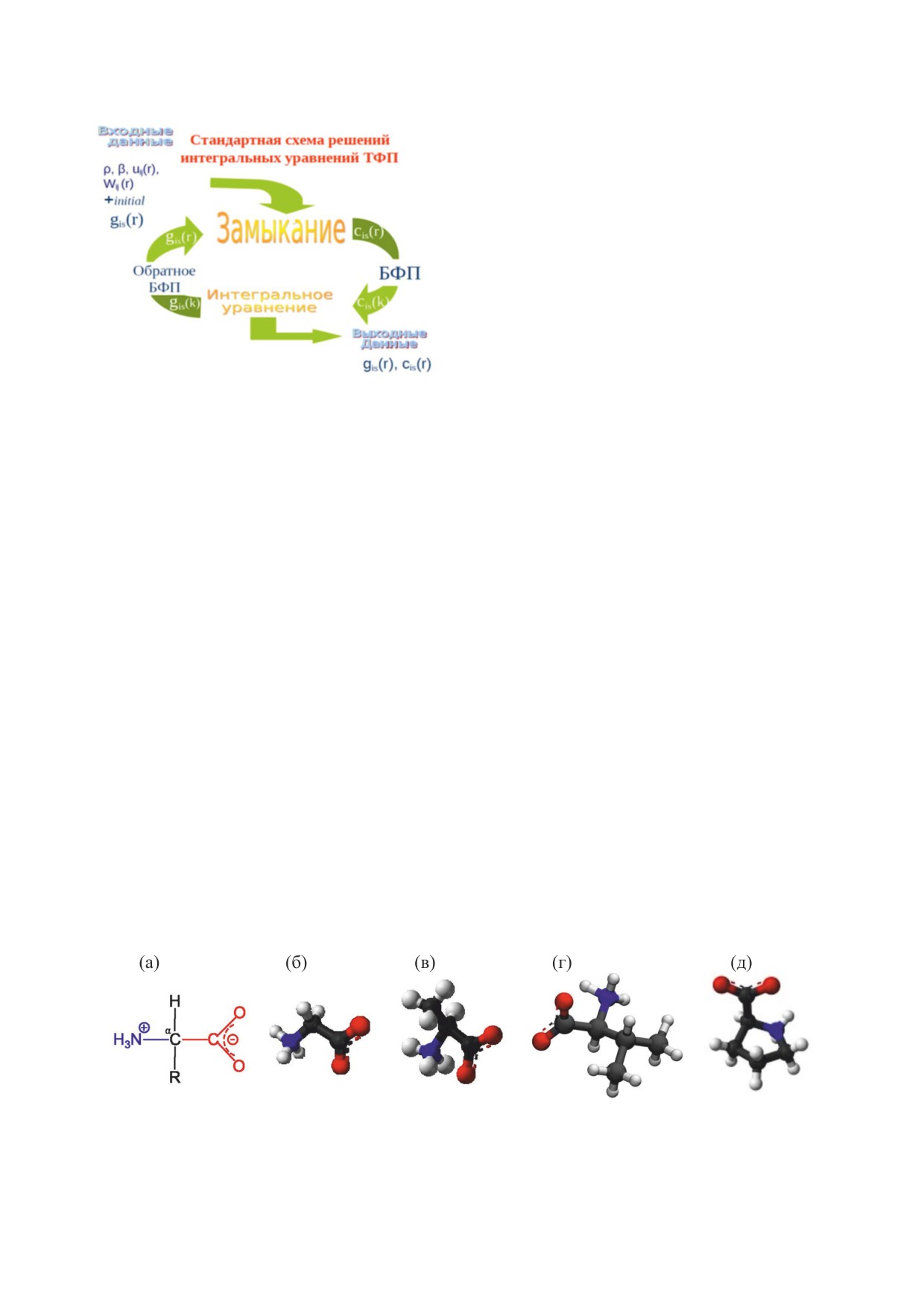
Исходя из вышеизложенного, в численной

Конкретизируя схему получения структурных

схеме решения интегральных уравнений метода-

параметров гидратации биомолекул, 3D-RISM

ми 3D-SDFT/3D-RISM, основанными на 3D-

уравнение в форме Орнштейна-Цернике для

распределении атомной плотности растворителя,

корреляций

«растворенное вещество-раствори-

входными данными являются межмолекулярный

тель» может быть переформулировано следующим

потенциал взаимодействия «биомолекула-рас-

образом [54]:

творитель» U_γ(r); восприимчивость чистого рас-

творителя χ_αγ(r), напрямую связанная с его внут-

(8)

hγ(r) = ∑α∫dr' cα(r - r')χαγ(r'),

римолекулярными корреляционными функция-

где h_γ(r) и c_γ(r) - полная и прямая атомно-молеку-

ми, ω_αγ(r); мостиковая функция (или

лярные корреляционные функции атомов γ моле-

функционал) b(r) и параметры, определяющие

кулы растворителя (воды в интересующем нас

термодинамическое состояние растворителя (T и

случае). При этом ПФР определяется как g_γ(r) =

ρ) (рис. 1). В наших расчетах мы использовали

= h_γ(r) + 1. Атом-атомная восприимчивость чи-

модель воды SPC/E. Результатом численного ре-

шения 3D-интегральных уравнений являются

стого растворителя χ_αγ(r) - существенный пара-

ПФР g_γ(r), при помощи которых выполняется

метр для 3D-RISM уравнения, она имеет вид:

анализ сольватационных эффектов в растворах

(9)

χαγ(r) = ωαγ(r) + ρα^hαγ(r),

биомолекул. Кроме межмолекулярных расстоя-

ний, из 3D-функции может быть рассчитано пол-

где

( )

=Δ

(

r - l

)

/(4πl

- внутримолеку-

αγ

)

ное гидратное число (ПГЧ) биомолекулы путем ин-

лярная корреляционная функция растворителя,

тегрирования ПФР «биомолекула-атом кислорода

БИОФИЗИКА том 68

№ 5

2023

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

841

дут продемонcтрированы результаты примене-

ния метода 3D-SDFT/3D-RISM к описанию осо-

бенностей структуры гидратной оболочки четы-

рех протеиногенных аминокислот с разными

радикалами (R) - глицина (Gly-ZW), L-аланина

(L-Ala-ZW), L-валина (L-Val-ZW) и L-пролина

(L-Pro-ZW) [34-38, 57, 58].

Методы, основанные на 3D-распределении

атомной плотности, при помощи ПФР позволя-

ют определить локализацию растворителя вблизи

функциональных групп биомолекул. На рис. 3 в

качестве примера приведены ПФР атомов кисло-

рода и водорода молекул воды вокруг L-Val-ZW.

Из рис. 3 видно, что молекулы воды ориентирова-

ны атомами водорода к отрицательно заря-

женной карбоксильной группе, а атомами кисло-

рода - к положительной заряженной аминогруп-

Рис. 1. Стандартная численная схема решений инте-

гральных уравнений теории классического функцио-

пе аминокислоты. Соответствующие характе-

нала атомной плотности для молекулярной жидкости

ристические расстояния между молекулами рас-

(ТФП - теория функционала плотности, БФП - быст-

рое Фурье-преобразование).

творителя и L-Val-ZW составляют в случае груп-

пы -СОО^- 0.29 нм (r_O(W)-СОО) и 0.16 нм (r_Н(W)-

СОО), в случае группы -NH₃₊ 0.29 нм (r_O(W)-

молекулы воды (O_w)» по объему первой гидратной

NH₃) и 0.18 нм (r_Н(W)-NH₃), в случае метильных

оболочки:

групп 0.30-0.35 нм (r_O(W)-СН₃). По результатам

=ρ

(r)dV

(12)

расчетов ПГЧ данной аминокислоты составляет



Ow Ow

26 молекул воды. При этом в ближнем окружении

групп -СОО^- и -NH₃₊ находится по 5 молекул

воды, в ближнем окружении гидрофобной груп-

ОСОБЕННОСТИ ГИДРАТАЦИИ

пы -CH₃, ближайшей к аминогруппе - 9 молекул

АМИНОКИСЛОТ

воды, в ближнем окружении гидрофобной груп-

Аминокислоты - важнейшие органические со-

пы -CH₃, удаленной от аминогруппы - 7 моле-

единения, в числе прочих обеспечивающие суще-

кул воды. В то же время локализация растворите-

ствование и функционирование живых систем. В

ля отсутствует вблизи гидрофобных фрагментов

живом организме они могут находиться в свобод-

-СН аминокислоты.

ном состоянии и как отдельные структурные ком-

На основе ПФР можно также определить ко-

поненты белков и пептидов. Их молекулы содер-

личество водородных связей, образующихся меж-

жат карбоксильную группу и аминогруппу, кото-

ду L-Val-ZW и растворителем. Так, по получен-

рые играют существенную роль в управлении

ным данным, из 5 молекул воды, находящихся в

гидрофильностью и, таким образом, взаимодей-

первой гидратной оболочке группы

-СОО^-,

ствием биомолекулы с водой и растворенными

4 молекулы формируют Н-связи с группой, а из

гидрофильными и/или заряженными соединени-

5 молекул воды, находящихся в ближнем окруже-

ями. В водных растворах при физиологическом

рН аминокислоты существуют преимущественно

нии группы -NH₃₊, - только 2 молекулы Н-свя-

в цвиттер-ионной (ZW) форме (рис. 2а). Ниже бу-

заны с ней. Как показали результаты исследова-

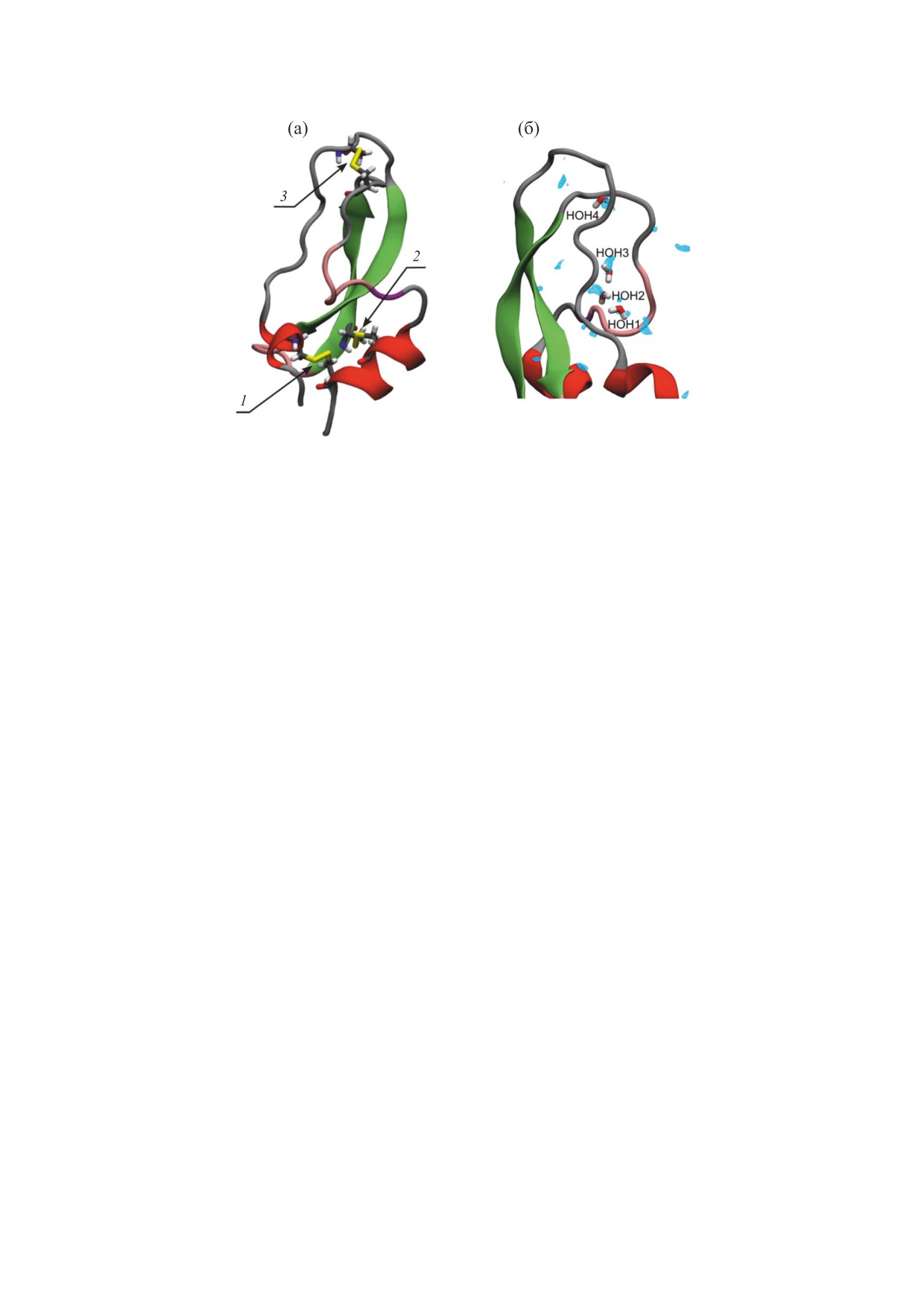
Рис. 2. Структурная формула аминокислоты в цвиттер-ионной (ZW) форме (а). Пространственные конфигурации Gly-

ZW (б), L-Ala-ZW (в), L-Val-ZW (г) и L-Pro-ZW (д).

БИОФИЗИКА том 68

№ 5

2023

842

КРУЧИНИН и др.

Рис. 3. ПФР атомов кислорода (синий цвет) и водорода (белый цвет) молекул воды вокруг L-Val-ZW. (а) -

Изоповерхности (I) ПФР вблизи карбоксильной группы соответствуют

; (б) - изоповерхности (I)

ПФР вблизи карбоксильной группы соответствуют

; (в) - изоповерхности (II)

ПФР вблизи аминогруппы и гидрофобной части соответствуют

ний, возможность образования Н-связей между

Pro-ZW (табл. 1) показывает, что карбоксильная

метильными группами и молекулами воды суще-

группа более гидрофильна и образует большее ко-

ствует, но вероятность такого Н-связывания

личество Н-связей с молекулами воды, чем ами-

очень низка.

ногруппа. При этом число молекул воды вблизи

аминогруппы (иминогруппы в случае пролина) и

В табл. 1 приведена обобщенная информации

число образуемых ею Н-связей практически оди-

о структуре гидратной оболочки исследованных

наковы для всех аминокислот, а аналогичные па-

аминокислот, согласно которой, все биомолеку-

лы хорошо гидратированы, что следует из их

раметры карбоксильной группы отличаются

ПГЧ, а также количества молекул воды в ближ-

(табл. 1). Данная структурная особенность связа-

нем окружении их функциональных групп. Сле-

на со стерическими ограничениями по отноше-

дует отметить, что ПГЧ увеличивается в ряду Gly-

нию к карбоксильной группе, которые появляют-

ZW → L-Ala-ZW → L-Val-ZW, т.е. по мере усложне-

ся из-за конкретной локализации радикала в

ния строения, а именно, радикала молекулы ами-

L-Ala-ZW, L-Val-ZW и L-Pro-ZW в сравнении с

нокислоты (табл. 1, рис. 2). Однако ПГЧ L-Pro-

Gly-ZW, где радикал отсутствует (рис. 2). Отме-

ZW оказывается меньше, чем у L-Val-ZW

тим также, что количество растворителя в ближ-

(табл. 1), что связано с компактным простран-

нем окружении группы -СОО^- пролина суще-

ственным расположением пирролидинового

кольца, и соответственно, меньшим объемом, ко-

ственно выше по сравнению с таковым у других

торый занимает гидратная оболочка пролина.

аминокислот, что обусловлено особенностями

Сравнительный анализ структурных параметров

его структуры - карбоксильная группа L-Pro-ZW

гидратации Gly-ZW, L-Ala-ZW, L-Val-ZW и L-

значительно удалена от его пирролидинового

Таблица 1. Структурные параметры гидратации Gly-ZW, L-Ala-ZW, L-Val-ZW и L-Pro-ZW

Гидратное

Функциональная

число (ГЧ) и

Gly-ZW

L-Ala-ZW

L-Val-ZW

L-Pro-ZW

группа

число Н-связей

ГЧ

Карбоксильная

группа

Н-связи

ГЧ

Амино(имино)

группа

Н-связи

Гидрофобная

13 (пирролиди-

ГЧ

6 (группа -CH₂)

11 (группа -CH₃)

16 (группы -CH₃)

часть

новое кольцо)

Аминокислота

Полное ГЧ

БИОФИЗИКА том 68

№ 5

2023

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

843

Рис. 4. (a) - Визуализация 3D-конформации белка BPTI в кристаллической форме II (PDB id: 5PTI). Дисульфидные

связи обозначены 1 (Cys5-Cys55), 2 (Cys30-Cys51), 3 (Cys14-Cys38). (б) - Расположение внутренних молекул воды

(HOH1, HOH 2, HOH 3 и HOH 4) в структуре BPTI, полученное из 3D-SDFT/3D-RISM расчета (показаны голубым

цветом) и найденное в эксперименте (показаны в виде молекул) [59].

кольца и, таким образом, доступна для взаимо-

леньких и простых глобулярных белков с молеку-

действия с молекулами воды.

лярной массой 6.62 кДа (рис. 4a). Его аминокис-

лотная последовательность, состоящая из 58 ами-

Как видно из представленных результатов,

подход, основанный на 3D-распределении атом-

нокислотных остатков, стабилизирована тремя

ной плотности растворителя, позволяет в деталях

дисульфидными связями (рис. 4a) [60], что обес-

печивает формирование компактной и очень ста-

и одновременно целостно описывать структуру

гидратной оболочки аминокислот.

бильной третичной структуры, которая даже в

водном растворе близка к кристаллической [61].

ОСОБЕННОСТИ ГИДРАТАЦИИ БЕЛКОВ

Помимо дисульфидных связей, дополнитель-

ную стабилизацию структуры BPTI обеспечивают

Хорошо известно, что гидратация белков в

четыре молекулы воды, «заглубленные» внутри

растворах играет одну из определяющих ролей в

белка («внутренние» молекулы воды) [62]. Эти

протекании множества жизненно важных про-

сильно и специфически связанные (Н-связями)

цессов. Взаимодействия белков c водой имеют

молекулы воды являются неотъемлемым элемен-

решающее значение для их структуры, динамики,

том нативной структуры белка не только в

фолдинга, функционирования, а также могут

его кристаллической форме, но и в водном рас-

оказывать существенное влияние на стабилиза-

творе [61, 64]. Как видно из рис. 4б, результаты

цию их комплексов с лигандами. Метод 3D-SD-

3D-SDFT/3D-RISM-расчетов [49] хорошо согла-

FT/3D-RISM, как было неоднократно показано

суются с рентгенокристаллографическими дан-

(см., напр., [30, 32, 42, 46, 47]), довольно точно

ными [59] - «внутренние» молекулы воды нахо-

воспроизводит 3D-молекулярную картину гидра-

дятся в положениях, близких к эксперименталь-

тации белка с уровнем детализации, как правило,

ным, а именно, внутри белка вблизи остатков

не доступным эксперименту. Ниже будут проде-

Glu7, Tyr10, Pro13, Arg39 и Lys41. Положения бы-

монстрированы результаты его применения к

ли определены из ПФР

(r)

(рис. 5). При

описанию особенностей структуры гидратной

BPTI-O_W

оболочки белков на примере ингибитора трипси-

этом молекула воды W4 пространственно изоли-

на бычьей поджелудочной железы (BPTI) и бел-

рована в небольшой полости BPTI, а остальные

ковой тирозинфосфатазы 1B (PTP1B), а также

молекулы W1, W2 и W3 образуют Н-связанный

комплексов PTP1B с ингибиторами [49, 50].

кластер в большой щели (рис. 4б). Как показал

анализ ПФР

BPTI-H

(r)

(рис. 5б), все «внутрен-

ние» молекулы воды образуют водородные связи

БЕЛКОВЫЙ ИНГИБИТОР ТРИПСИНА

с соответствующими остатками белка: W4 с остат-

Ингибитор трипсина бычьей поджелудочной

ками Cys38, Cys14, Thr11, а W1, W2 и W3 с остатка-

железы (PDB id: 5PTI [59]) - один из самых ма- ми Pro8, Tyr10, Asn43, Lys41 и Asn44 [49].

БИОФИЗИКА том 68

№ 5

2023

844

КРУЧИНИН и др.

Рис. 5. Изоповерхности ПФР атомов растворителя вокруг BPTI: (a) - изоповерхность ПФР атомов кислорода

(голубой) молекул воды при

; (б) - изоповерхности ПФР атомов кислорода (голубой) при

и атомов водорода (оранжевый) молекул воды при

На рис. 5 приведены пространственные функ-

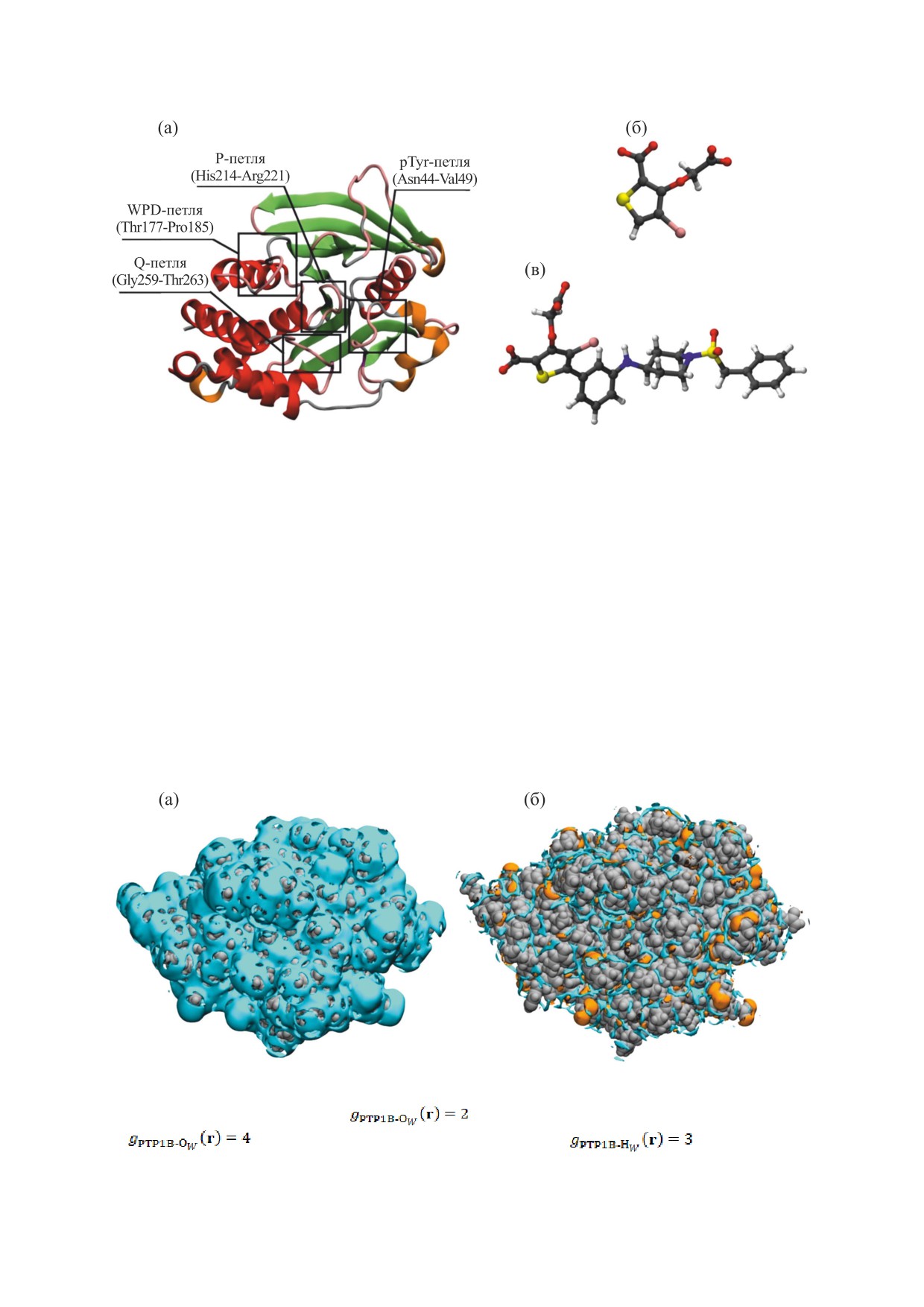
БЕЛКОВАЯ ТИРОЗИНФОСФАТАЗА 1B

ции распределения атомов кислорода и водорода

И ЕЕ КОМПЛЕКСЫ С ИНГИБИТОРАМИ

молекул воды вокруг и внутри BPTI, которые

Белковая тирозинфосфатаза

1B (PDB ID:

позволяют описать структуру гидратной оболоч-

2HNP) - внутриклеточный фермент, который яв-

ки белка. Практически полностью окружающая

ляется одним из членов-основателей семейства

белок изоповерхность при

(r)=

BPTI-O

белковых тирозинфосфатаз и поэтому часто ис-

(рис. 5а) характеризует протяженный гидратный

пользуется как модельная система для изучения

слой толщиной 0.39 нм и свидетельствует о том,

свойств этого семейства. Его аминокислотная по-

что BPTI хорошо гидратирован. Подтверждением

следовательность состоит из 435 аминокислот-

служит также рассчитанное по формуле (12) пол-

ных остатков. Однако только первые 298 остатков

ное гидратное число, которое составляет

соответствуют домену активного центра, состоя-

332.6 молекул воды [49]. Изоповерхности атомов

щего из сайта связывания и каталитического сай-

кислорода и водорода молекул воды при

та. Этот домен, имеющий 8 α-спиралей и 12 β-це-

пей, практически одинаков для всех других нере-

BPTI-O

(r)=

BPTI-H

(r)=

соответственно

цепторных белковых тирозинфосфатаз (рис. 6а).

(рис. 5б) характеризуют распределение раствори-

Он содержит 6 петель, из которых только 4 явля-

теля, локализованное вблизи гидрофильных

ются структурно важными областями для связы-

участков поверхности BPTI. При этом, как следу-

вания ингибитора

[64]: pTyr-петля (остатки

ет из полученных данных (рис. 5б), изоповерхно-

Asn44-Val49), WPD-петля (остатки Thr177-

сти ПФР атомов водорода преимущественно на-

Pro185), Р-петля (остатки His214-Arg221) и Q-пет-

ходятся около групп, которые могут выступать

ля (остатки Gly259-Thr263) (рис. 6а). Следует от-

акцепторами Н-связей (карбоксильные и гидрок-

метить, что WPD-петля имеет две различные кон-

сильные группы), а изоповерхности ПФР атомов

формации: открытую в несвязанном состоянии и

кислорода - вблизи групп, способных быть доно-

закрытую, активную в комплексе «белок-инги-

рами Н-связей (аминогруппы, гидроксильные

битор» [65, 66].

группы и т.д.). Таким образом, изоповерхности

Рассмотрим сначала особенности гидратации

на рис. 5б демонстрируют распределение молекул

белка PTP1B с открытой конформацией WPD-

воды первой гидратной оболочки, образующих

петли (PDB id:

2HNP, молекулярная масса

Н-связи с полярными участками BPTI, и позво-

~37 кДа [67]). Полученные результаты показыва-

ляют определить их расположение, включая рас-

ют [50], что подобно BPTI, белок PTP1B хорошо

положение «внутренних» молекул воды, о чем

гидратирован, о чем свидетельствует полное гид-

было сказано выше.

ратное число, равное 1071.9, и протяженный гид-

БИОФИЗИКА том 68

№ 5

2023

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

845

Рис. 6. Визуализация 3D-структуры белка PTP1B (PDB id: 2HNP [67]) (а) и пространственные структуры ингибиторов

в комплексах 2HB1 (б) и 2QBP (в).

ратный слой толщиной 0.39 нм (изоповерхность

тельное количество комплексов с ингибиторами,

при

(r)=

на рис. 7а). Как следует из

структуры которых задепонированы в онлайн-

PTP1B-O

банке данных трехмерных структур белков (PDB-

анализа распределения растворителя, локализо-

банке). Для исследования нами были выбраны

ванного вблизи гидрофильных участков PTP1B

два комплекса с ингибиторами компактного

(рис. 7б), белок способен к Н-связыванию с мо-

(PDB id: 2HB1 [68]) и разветвленного (PDB id:

лекулами воды при помощи функциональных

2QBP [69]) строения (рис. 6 б,в). Отметим, что

групп, которые могут действовать как доноры

структура PTP1B в комплексе с лигандом, как

(амино-, гидроксильные группы и др.,

правило, имеет закрытую конформацию WPD-

(r)=

4) на рис.

7б) или акцепторы

PTP1B-O

петли.

(карбоксильные, гидроксильные группы, фраг-

Как известно, ингибиторы нацелены на сайт

менты -SO2-,

(r)=

на рис. 7б) Н-связи.

PTP1B-H

связывания, и, таким образом, ингибитор как ли-

Как потенциальная мишень для лекарствен-

ганд изменяет структуру гидратной оболочки

ных препаратов, PTP1B имеет довольно значи- лишь локально - вблизи того места, где он присо-

Рис. 7. Изоповерхности ПФР атомов растворителя вокруг PTP1B в апо-состоянии: (а) - изоповерхности ПФР атомов

кислорода (голубой) молекул воды при

; (б) -изоповерхности ПФР атомов кислорода (голубой)

при

и атомов водорода (оранжевый) молекул воды при

БИОФИЗИКА том 68

№ 5

2023

846

КРУЧИНИН и др.

Рис. 8. Изоповерхности ПФР атомов кислорода молекул воды вокруг ингибиторов в области активного сайта

связывания в комплексах 2HB1 (a) и 2QBP (б). Изоповерхности ПФР обозначены красным цветом в случае

свободного ингибитора (g_Ow(r) = 4), синим цветом - в случае связанного ингибитора (g_Ow(r) = 10).

единяется к белку. Поэтому особенности гидра-

нием ингибитором части молекул воды из обла-

тации комплексов далее рассматриваются имен-

сти активного центра, что неоднократно отмеча-

но в этой области гидратной оболочки.

лось в литературе [70, 71]. В качестве примера на

рис. 9 показано распределение атомов кислорода

Первое, что можно определить при помощи

молекул воды внутри и вблизи области активного

метода 3D-SDFT/3D-RISM, - это изменения в

центра для белка в комплексе с лигандом (2QBP).

структуре гидратной оболочки ингибитора при

его переходе из несвязанного состояния в связан-

Кристаллографические структуры комплексов

ное. На рис. 8 представлены изоповерхности

2HB1 и 2QBP содержат соответственно 171 и 117

ПФР растворителя вокруг лигандов в несвязан-

молекул воды, часть которых локализована внут-

ном (свободном) состоянии и связанном состоя-

ри домена активного центра. Эти локализован-

нии, т.е. в комплексе с PTP1B в области сайта

ные молекулы воды прочно связаны с комплек-

связывания. Как видно из рисунка, при форми-

сом и способствуют стабильности его структуры.

ровании комплекса области с наиболее вероят-

При помощи ПФР, рассчитанных методом 3D-

ным расположением атомов кислорода воды во-

SDFT/3D-RISM, с использованием программы

круг ингибиторов существенно уменьшаются,

что свидетельствует об их значительной дегидра-

тации при связывании с PTP1B [50]. Подтвержде-

нием этому служат также изменения в гидратных

числах лигандов. По результатам расчетов, в ре-

зультате связывания количество молекул воды

вблизи ингибиторов значительно снижается: в

случае комплекса 2HB1 - с 32.4 (свободный ин-

гибитор) до 5.5 (связанный ингибитор), в случае

комплекса 2QBP - с 71.3 (свободный ингибитор)

до 23.6 (связанный ингибитор) [50].

Другие результаты, полученные методом 3D-

SDFT/3D-RISM, позволяют охарактеризовать

состояние сайта связывания белка. Для этого

сравнивались данные для белка с удаленным из

структуры лигандом («нелигандный» белок) с

данными для белка в комплексе с лигандом. В

первом случае гидратное число составило 48.4 для

2HB1 и 130.3 для 2QBP [50], что свидетельствует о

том, что домен активного центра «нелигандного»

белка хорошо гидратирован. При связывании

белка с ингибитором домен частично дегидрати-

руется: его гидратное число уменьшается на ~10%

и становится равным 43.7 в случае комплекса

Рис. 9. Распределение атомов кислорода молекул

2HB1 и на ~19% до 105.4 - в случае комплекса

воды внутри и вблизи области активного центра

2QBP [50]. Данный процесс обусловлен вытесне-

белка в случае комплекса 2QBP.

БИОФИЗИКА том 68

№ 5

2023

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

847

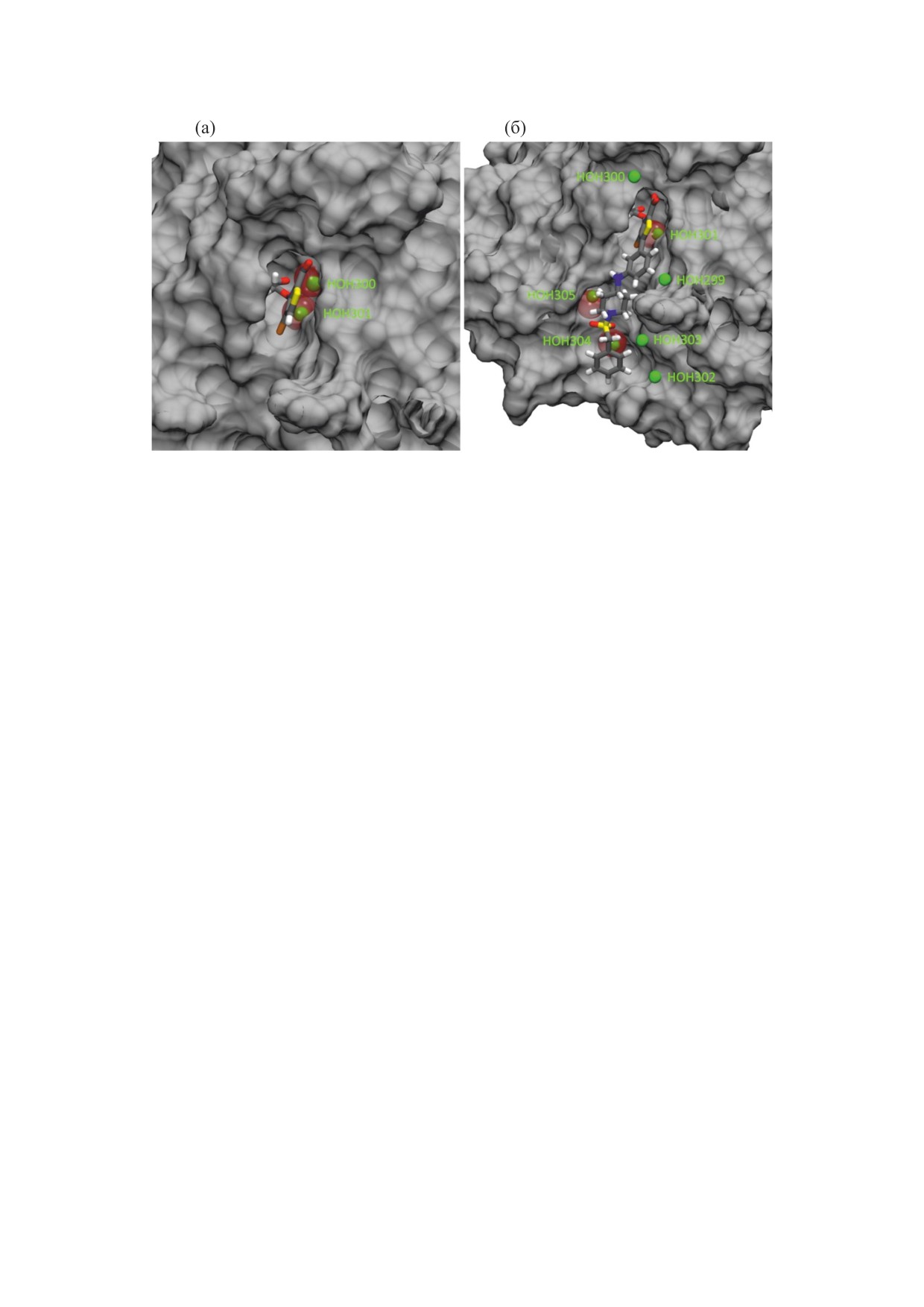
Рис. 10. Расположение атомов кислорода молекул воды внутри области активного центра по данным PDB банка

(красные полупрозрачные сферы) и данным 3D-RISM (зеленые сферы) для комплексов 2HB1 (a) и 2QBP (б).

metatwist [72] были определены наиболее вероят-

Вместе с тем, в силу динамического поведения

ные положения молекул воды в области активно-

молекул воды в биологической среде, во многих

го центра (рис. 10, показаны только атомы кисло-

случаях экспериментальное определение пара-

рода молекул воды). Как видно из рис. 10, внутри

метров гидратации биомолекул представляет зна-

домена активного центра присутствуют две моле-

чительные трудности. В данной работе мы проде-

кулы растворителя в случае комплекса 2HB1

монстрировали возможности неэмпирического

(рис. 10a) и семь молекул растворителя в случае

подхода, основанного на

3D-распределении

комплекса 2QBP (рис. 10б). При этом расположе-

ние двух молекул (комплекс 2HB1) и трех моле-

атомной плотности растворителя, для исследова-

кул (комплекс 2QBP) воды, наиболее прочно свя-

ния особенностей гидратации биомолекул на

занных с комплексом, совпадает с соответствую-

примере ряда аминокислот (Gly-ZW, L-Ala-ZW,

щими экспериментальными данными из PDB

L-Val-ZW, L-Pro-ZW), белков (BPTI, PTP1B) и

банка [68, 69]. О наличии таких прочно связан-

комплексов белка PTP1B с ингибиторами. Пред-

ных молекул воды также сообщается в работах

ставленные результаты показали, что метод 3D-

[73, 74], где исследовались комплексы PTP1B с

SDFT/3D-RISM позволяет успешно в деталях и

другими ингибиторами.

одновременно целостно описывать структуру

Основываясь на представленных результатах,

гидратной оболочки биомолекул. В частности,

можно констатировать, что подход, основанный

подход дает возможность пространственного

на 3D-распределении атомной плотности раство-

рителя, позволяет в деталях описывать структур-

представления их ближнего окружения с опреде-

ные особенности гидратации белков и белковых

лением локализации растворителя вблизи их по-

комплексов.

лярных и неполярных участков, а также количе-

ственной оценки их гидратации с помощью гид-

ратных чисел и количества Н-связей, как для

ЗАКЛЮЧЕНИЕ

биомолекулы целиком, так и для ее функцио-

Биомолекулярная сольватация играет одну из

нальных групп. Кроме того, в случае биомакро-

определяющих ролей в протекании множества

молекул метод позволяет найти расположение

жизненно важных процессов. Знание ее особен-

«внутренних» молекул воды, которые обеспечи-

ностей на молекулярном и атомно-молекулярном

вают стабилизацию структуры белков и белковых

уровнях необходимо для установления влияния

комплексов, а также описать особенности гидра-

данного процесса на выполнение биомолекулами

своих целевых функций, и, как результат, для по-

тации в области активного сайта связывания бел-

нимания молекулярных механизмов их действия.

ков с ингибиторами.

БИОФИЗИКА том 68

№ 5

2023

848

КРУЧИНИН и др.

ФИНАНСИРОВАНИЕ РАБОТЫ

22. Y. Liu, J. Fu, and J. Wu, J. Phys. Chem. Lett., 4 (21),

3687 (2013);

Работа была выполнена при поддержке гранта

23. Y. Liu, S. Zhao, and J. Wu, J. Chem. Theory Comput.,

РНФ № 22-23-00184 (https://rscf.ru/project/22-23-

9 (4), 1896 (2013).

00184/).

24. M. Valiev and G. N. Chuev, J. Stat. Mech. Theory

Exp., 2018 (9), 093201 (2018).

КОНФЛИКТ ИНТЕРЕСОВ

25. G. N. Chuev, M. V. Fedotova, and M. Valiev, J. Chem.

Phys., 152 (4), 041101 (2020).

Авторы заявляют об отсутствии конфликта

интересов.

26. Q. H. Du, D. Beglov, and B. Roux, J. Phys. Chem. B,

104 (4) 796 (2000);

27. A. Kovalenko and F. Hirata, J. Chem. Phys., 110 (20),

СОБЛЮДЕНИЕ ЭТИЧЕСКИХ СТАНДАРТОВ

10095 (1999).

Статья не содержит описания исследований,

28. Y. Liu, S. Zhao, and J. Wu, J. Chem. Theory Comput.,

выполненных кем-либо из авторов, с участием

9 (4), 1896 (2013).

людей или использованием животных в качестве

29. T. Imai, A. Kovalenko, and F. Hirata, Chem. Phys.

объектов.

Lett., 395 (1-3), 1 (2004).

30. N. Yoshida, S. Phongphanphanee, and F. Hirata, J.

Phys. Chem. B, 111 (17), 4588 (2007).

СПИСОК ЛИТЕРАТУРЫ

31. J. S. Perkyns, G. C. Lynch, J. J. Howard, et al., J.

G. J. Rocklin, D. L. Mobley, K. A. Dill, et al., J. Chem.

Chem. Phys. 132 (6), 064106 (2010).;

Phys., 139 (18), 184103 (2013).

32. D.J. Sindhikara and F. Hirata, J. Phys. Chem. B, 117

J. W. Kaus, L. T. Pierce, R. C. Walker, et al., J. Chem.

(22), 6718 (2013).

Theory Comput., 9 (9), 4131 (2013).

33. S. Gusarov, B. S. Pujari, and A. Kovalenko, J. Comput.

P. Mikulskis, S. Genheden, and U. Ryde, J. Chem. Inf.

Chem., 33 (17), 1478 (2012).

Model., 54 (10), 2794 (2014).

34. M. V. Fedotova and S. E. Kruchinin, Biophys. Chem.,

B. Guillot, J. Mol. Liq., 101 (1-3), 219 (2002).

190-191, 25 (2014).

J. F. Ouyang and R. P. Bettens, Chimia (Aarau), 69 (3),

35. O. A. Dmitrieva and M. V. Fedotova, New J. Chem., 39

104 (2015).

(11), 8594 (2015).

H. J. C. Berendsen, J. R. Grigera, and T. P. Straatsma,

36. A. Eiberweiser, A. Nazet, M. V. Fedotova, et al., J.

J. Phys. Chem., 91 (24), 6269 (1987).

Phys. Chem. B, 119 (49), 15203 (2015).

W. L. Jorgensen, J. Chandrasekhar, J. D. Madura,

37. M. V. Fedotova and O.A. Dmitrieva, Amino Acids, 48

et al., J. Chem. Phys., 79 (2), 926 (1983).

(7), 1685 (2016).

A. V. Onufriev and S. Izadi, Wiley Interdisc. Rev.:

38. O. A. Dmitrieva, M. V. Fedotova, and R. Buchner,

Comput. Mol. Sci., 8 (2), e1347 (2017).

Phys. Chem. Chem. Phys., 19 (31), 20474 (2017).

W. C. Still, A. Tempczyk, R. C. Hawley, et al., J. Am.

39. M. V. Fedotova, S. E. Kruchinin, and G. N. Chuev,

Chem. Soc., 112 (16), 6127 (1990).

New J. Chem., 41 (3), 1219 (2017).

10.

B. N. Dominy and C. L. Brook, J. Phys. Chem B, 103

40. M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 244,

(18), 3765 (1999).

489 (2017).

11.

B. Honig and A. Nicholls, Science, 268 (5214), 1144

41. S. Güssregen, H. Matter, G. Hessler, et al., J. Chem.

(1995).

Inf. Model., 57 (7), 1652 (2017).

12.

J. Wu, AIChE J., 52 (3), 1169 (2006).

42. N. Yoshida, J. Chem. Inf. Model., 57 (11), 2646 (2017).

13.

J. Wu and Z. Li, Annu. Rev. Phys. Chem., 58 (1), 85

43. M. V. Fedotova, J. Mol. Liq., 292, 111339 (2019).

(2007).

44. M. V. Fedotova, S. E. Kruchinin, and G. N. Chuev, J.

14.

S. Zhao, R. Ramirez, R. Vuilleumier, et al., J. Chem.

Mol. Liq., 304, 112757 (2020).

Phys., 134 (19), 194102 (2011).

45. S. Friesen, M. V. Fedotova, S. E. Kruchinin, et al.,

15.

L. Blum, J. Chem. Phys., 57, 1862 (1972).

Phys Chem Chem Phys 23 (2), 1590 (2021).

16.

M. Ikeguchi and J. Doi, J. Chem. Phys., 103 (12), 5011

46. M. Sugita, I. Onishi, M. Irisa, et al., Molecules, 26 (2),

(1995).

271 (2021).

17.

R. Ishizuka and N. Yoshida, J. Chem. Phys., 139 (8),

47. D. Roy and A. Kovalenko, Int. J. Mol. Sci., 22 (10),

084119 (2013).

5061 (2021).

18.

D. Chandler and H. C.Andersen, J. Chem. Phys., 57

48. N. Kumawat, A. Tucs, S. Bera, et al., Molecules, 27

(5), 1930 (1972).

(3), 799 (2022).

19.

F. Hirata, P. J. Rossky and B. M. Pettitt, J. Chem.

49. S. E. Kruchinin, E. E. Kislinskaya, G. N. Chuev, et al.,

Phys., 78 (6), 4133 (1983).

Int. J. Mol. Sci., 23 (23), 14785 (2022).

20. J. Perkyns and B. M. Pettitt, J. Chem. Phys., 97 (10),

50. S. E. Kruchinin, G. N. Chuev, and M. V. Fedotova, J.

7656 (1992).

Mol. Liq., 384, 122281 (2023).

21. D. Chandler, J. D. Mccoy, and S. J. Singer, J. Chem.

51. G. N. Chuev, M. V. Fedotova, and M. Valiev, J. Stat.

Phys., 85 (10), 5971 (1986).

Mech., 2021, 033205 (2021).

БИОФИЗИКА том 68

№ 5

2023

In silico ИССЛЕДОВАНИЕ СОЛЬВАТАЦИОННЫХ ЭФФЕКТОВ

849

52. B. Kezic and A. Perera, J. Chem. Phys., 135 (24),

64. D. S. Cui, J. M. Lipchock, D. Brookner, et al., J. Am.

234104 (2011).

Chem. Soc., 141 (32), 12634 (2019).

53. G. N. Chuev, I. Vyalov, and N. Georgi, J. Comput.

65. L. Tabernero, A. R. Aricescu, E. Y. Jones, et al., FEBS

Chem., 35 (13), 1010 (2014).

J., 275 (5), 867 (2008).

54. A. Kovalenko, In Molecular Theory of Solvation, Ed. By

66. A. J. Barr, E. Ugochukwu, W. H. Lee, et al., Cell, 136

F. Hirata (Kluwer Acad. Publ.: Dordrecht, The Neth-

(2), 352 (2009).

erlands, 2003), pp.169-275.

67. D. Barford, A. J. Flint, and N. K. Tonks, Science, 263

55. A. Kovalenko and F. Hirata, J. Chem. Phys., 112 (23),

(5152), 1397 (1994).

10391 (2000).

68. Z.-K. Wan, J. Lee, W. Xu, et al., Bioorg. Med. Chem.

56. A. Kovalenko, Pure Appl. Chem., 85 (1), 159 (2013).

Lett., 16 (18), 4941 (2006).

57. M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 169,

69. D. P. Wilson, Z.-K. Wan, W.-X. Xu, et al., J. Med.

1 (2012).

Chem., 50 (19), 4681 (2007).

58. M. V. Fedotova and O. A Dmitrieva, Amino acids, 47

70. J. L. Thomaston, N. F. Polizzi, A. Konstantinidi, et al.,

(6), 1015 (2015).

J. Am. Chem. Soc., 140 (45), 15219 (2018).

59. A. Wlodawer, J. Walter, R. Huber, et al., J. Mol. Biol.,

71. B. Z. Zsidó and C. Hetényi, Curr. Opin. Struct. Biol.,

180 (2), 301 (1984).

67, 1 (2021).

60. B. Kassell and M. Laskowski Sr, Biochem. Biophys.

Res. Commun., 20 (4), 463 (1965).

72. D. A. Giambasu, D. M. Case, and G. M. York, J. Am.

Chem. Soc., 141 (6), 2435 (2019).

61. K. D. Berndt, P. Güntert, L. P. Orbons, et al., J. Mol.

Biol., 227 (3), 757 (1992).

73. A. K. Pedersen, G. H. Peters, K. B. Møller, et al., Acta

62. V. P. Denisov, J. Peters, H. D. Hörlein, et al., Biochem-

Crystallogr. D - Biol. Crystallogr., 60 (Pt 9), 1527

istry, 43 (38), 12020 (2004).

(2004).

63. G. Otting, K. Wüthrich, J. Am. Chem. Soc., 111 (5),

74. A. Özcan, E. O. Olmez, and B. Alakent, Prot. Struct.

1871 (1989).

Funct. Bioinf., 81 (5), 788 (2013).

In silico Study of Solvation Effects in Solutions of Biomolecules: Possibilities

of an Approach Based on the 3D-Distribution of Solvent Atomic Density

S.E. Kruchinin*, M.V. Fedotova*, E.E. Kislinskaya**, and G.N. Chuev***

*G.A. Krestov Institute of Solution Chemistry, Russian Academy of Sciences, Akademicheskaya ul. 1, Ivanovo, 153045 Russia

**Ivanovo State University, ul. Ermaka 39, Ivanovo, 153025 Russia

***Institute of Theoretical and Experimental Biophysics, Russian Academy of Sciences,

Institutskaya ul. 3, Pushchino, Moscow Region, 142290 Russia

Biomolecular solvation plays one of the key roles in nature. The biological activity of molecules and the per-

formance of their target functions depend on the features of this process. However, the study of the biomol-

ecule hydration is a non-trivial task for both experimental methods and computer simulations. The paper

demonstrates the possibilities of the non-empirical 3D-SDFT/3D-RISM approach based on the 3D-distri-

bution of the solvent atomic density to study the features of biomolecule hydration using the example of a

number of amino acids such as Gly-ZW, L-Ala-ZW, L-Val-ZW, L -Pro-ZW, two model proteins such as BP-

TI (bovine pancreatic trypsin inhibitor) and PTP1B (protein tyrosine phosphatase 1B), as well as complexes

of the PTP1B protein with inhibitors. The presented results show that the approach allows one to describe in

detail and at the same time a holistic description of the hydration shell structure of biomolecules.

Keywords: biomolecules, hydration, hydration shell structure, methods of the theory of liquids

БИОФИЗИКА том 68

№ 5

2023