БИОХИМИЯ, 2022, том 87, вып. 12, с. 1998 - 2011

УДК 591.526:612.6:577.24

ИСТОРИЧЕСКИЕ ТРЕНДЫ ВИДОВОЙ ПРОДОЛЖИТЕЛЬНОСТИ

ЖИЗНИ ЧЕЛОВЕКА И АКТУАРНОЙ СКОРОСТИ СТАРЕНИЯ*

¹Academic Research Centers, NORC at the University of Chicago,

60637 Chicago, IL, USA; e-mail: lagavril@yahoo.com

²Институт демографических исследований, ФНИСЦ РАН, 109028 Москва, Россия

Поступила в редакцию 02.11.2022

После доработки 16.11.2022

Принята к публикации 16.11.2022

В работе был проведён анализ компенсационного эффекта смертности (КЭС) с использованием

данных о повозрастной смертности из Human Mortality Database (HMD). Были получены оценки

видовой продолжительности жизни человека, которые оказались близки к оценкам, опубликован-

ным ранее. Три модели (Гомперца-Мейкема, Гомперца-Мейкема с центрированным возрастом

и Гомперца) дали схожие оценки видовой продолжительности жизни. Эти оценки продемонстриро-

вали некоторое увеличение со временем. Попытки измерить скорость старения с помощью углово-

го коэффициента регрессии в модели Гомперца привели к выводу, что актуарная скорость старения

оставалась стабильной в течение большей части XX века, но недавно продемонстрировала рост

в большинстве (74%) изученных популяций. Это недавнее явление, скорее всего, вызвано более бы-

стрым историческим снижением смертности в более молодых возрастах по сравнению со старшими

возрастными группами, что делает возрастной градиент смертности более крутым с течением време-

ни. Нет никаких биомедицинских оснований полагать, что скорость старения человека увеличилась

в последнее время. Из этого следует, что актуарная скорость старения, вероятно, не является хоро-

шим показателем истинной скорости старения (скорости потери функции). Поэтому необходимо

разработать более точные методы оценки скорости старения.

КЛЮЧЕВЫЕ СЛОВА: старение, смертность, модель Гомперца-Мейкема, видовая продолжительность

жизни, скорость старения.

DOI: 10.31857/S0320972522120168, EDN: NIFSPX

ВВЕДЕНИЕ

угловой коэффициент характеризует скорость

увеличения смертности с возрастом.

Для того чтобы понять фундаментальные

Однако предыдущие предварительные ис-

основы биологии старения и разработать ре-

следования показали, что угловой коэффи-

альные антивозрастные вмешательства, важно

циент наклона не является идеальной мерой

сначала выяснить, какова наилучшая оцен-

скорости старения как по практическим, так

ка скорости старения человека, а также фак-

и по теоретическим причинам. Например, ис-

торы, её определяющие. Скорость старения

пользование углового коэффициента наклона

часто оценивают как угловой коэффициент

в качестве меры скорости старения приводит к

регрессии в модели Гомперца (в полулогариф-

контринтуитивному выводу, что женщины ста-

мических координатах), описывающей экспо-

реют быстрее мужчин, несмотря на более низ-

ненциальное увеличение смертности с возрас-

кий уровень смертности и более высокую про-

том (также известный как наклон Гомперца

должительность жизни («парадокс мужской и

или Gompertz slope). Этот подход интуитивно

женской скорости старения») [1]. Кроме того,

привлекателен, поскольку гипотетические не-

надежностная теория старения показывает,

стареющие популяции имеют угловой коэф-

что угловой коэффициент наклона опреде-

фициент наклона, равный нулю, и поскольку ляется не только скоростью потери функции

Принятые сокращения: КЭС - компенсационный эффект смертности; HMD - Human Mortality Database.

* Комментарий к статье будет опубликован в журнале «Биохимия», выпуск 1 2023 г.

** Адресат для корреспонденции.

1998

ВИДОВАЯ ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ ЧЕЛОВЕКА

1999

с возрастом («истинная скорость старения»),

характеристик продолжительности жизни.

но и начальным уровнем резервирования (на-

Действительно, параметры корреляции Стреле-

чальная резервная ёмкость) [1, 2]. Скорость

ра-Милдвана, связывающие величины R₀ и α,

старения на основе параметра наклона Гом-

будут видоспецифическими инвариантами

перца часто называют актуарной скоростью

вследствие самого принципа, используемо-

старения, чтобы отличить её от истинной ско-

го для их расчёта. Гаврилов и Гаврилова под-

рости старения, связанной с потерей функ-

вергли сомнению подход Стрелера-Милдвана

ции [3]. Таким образом, существует необходи-

и показали, что изменения параметра Мейке-

мость в разработке более точных и адекватных

ма (A) от 0 до 0,01 в год достаточно для полу-

оценок скорости старения.

чения ложной корреляции Стрелера-Милдва-

Цель данной статьи - изучить изменения

на [1]. Сравнение этой ложной корреляции с

актуарной скорости старения за последнее

корреляцией, опубликованной Стрелером и

время в человеческих популяциях. Значения

Милдваном (1960), показало очень хорошее

актуарной скорости старения различны в раз-

совпадение между этими двумя корреляциями.

ных популяциях и устроены таким образом,

Попытки использовать корреляцию Стрелера

что более низкая начальная смертность ком-

и Милдвана при построении математических

пенсируется её более быстрым ростом с воз-

моделей старения могут привести к абсурдным

растом. Это означает, что высокая смертность

результатам. Действительно, из данных, при-

в неблагополучных популяциях (в пределах

ведённых в статье Стрелера и Милдвана (1960),

данного вида) компенсируется низкой акту-

следует, что угловой коэффициент наклона

арной скоростью старения (более длительным

линейной регрессии lnR₀ по α составляет все-

периодом удвоения смертности). В результате

го 68,5 лет. Однако, согласно «Общей теории

такой компенсации относительные различия в

смертности и старения» Стрелера и Милдвана

уровнях смертности имеют тенденцию умень-

(1960), эта величина должна соответствовать

шаться с возрастом в пределах данного биоло-

возрасту, в котором так называемая жизне-

гического вида [1]. В данном исследовании мы

способность, «способность индивидуального

более подробно анализируем компенсацион-

организма оставаться живым» (стр. 15), стано-

ный эффект смертности (КЭС), уделяя особое

вится равной нулю. На нелепость этих резуль-

внимание количественным показателям этого

татов, полученных из корреляции Стрелера и

явления, таким как видовая продолжитель-

Милдвана, указывалось неоднократно [5, 6].

ность жизни [1].

Компенсационный эффект смертности. Поз-

Корреляция Стрелера-Милдвана. В 1960 г.

же Гаврилов и Гаврилова попытались усовер-

американские исследователи Бернард Л. Стре-

шенствовать подход, применённый Стрелером

лер и Альберт С. Милдван опубликовали ста-

и Милдваном, и учесть параметр Мейкема (A).

тью под названием «Общая теория смертно-

В ходе этого исследования был обнаружен так

сти и старения» в ведущем научном журнале

называемый компенсационный эффект смерт-

Science [4]. В этой статье они описали обрат-

ности [1]. Оказалось, что в пределах данного

ную зависимость между параметрами закона

биологического вида значения смертности,

Гомперца:

зависящей от возраста (слагаемое Гомперца

в уравнении Гомперца-Мейкема), коррели-

μ_x = A + R₀ exp(αx),

(1)

руют таким образом, что при экстраполяции

сходятся в одной точке. КЭС означает схож-

где μ_x - интенсивность смертности в возрас-

дение кривых смертности, когда более высо-

те x, а A, R₀ и α - параметры.

кие значения параметра наклона (в функции

Стрелер и Милдван, пренебрегая парамет-

Гомперца) компенсируются более низкими

ром Мейкема (A) уравнения (1), обнаружили,

значениями параметра пересечения R₀ в раз-

что в тех странах, где значения предэкспонен-

личных популяциях данного биологического

циального множителя (обозначаемого как R₀)

вида [1, 7]. КЭС может быть количественно

были высокими, значения экспоненциального

оценен с помощью обратной линейной зави-

индекса (α) уменьшались. Впоследствии это

симости параметров Гомперца в уравнении

наблюдение стало известно как корреляция

Гомперца-Мейкема:

Стрелера-Милдвана, и оно приобрело статус

фундаментального закона, описывающего вы-

lnR₀ = lnM - Bα.

(2)

живаемость организмов.

Легко заметить, что это явление, если оно

Координата, соответствующая возрасту, в

действительно существует, имеет большое зна-

котором пересекаются все траектории смерт-

чение для определения видоспецифических

ности (B), была названа видовой продолжи-

БИОХИМИЯ том 87 вып. 12 2022

2000

ГАВРИЛОВ, ГАВРИЛОВА

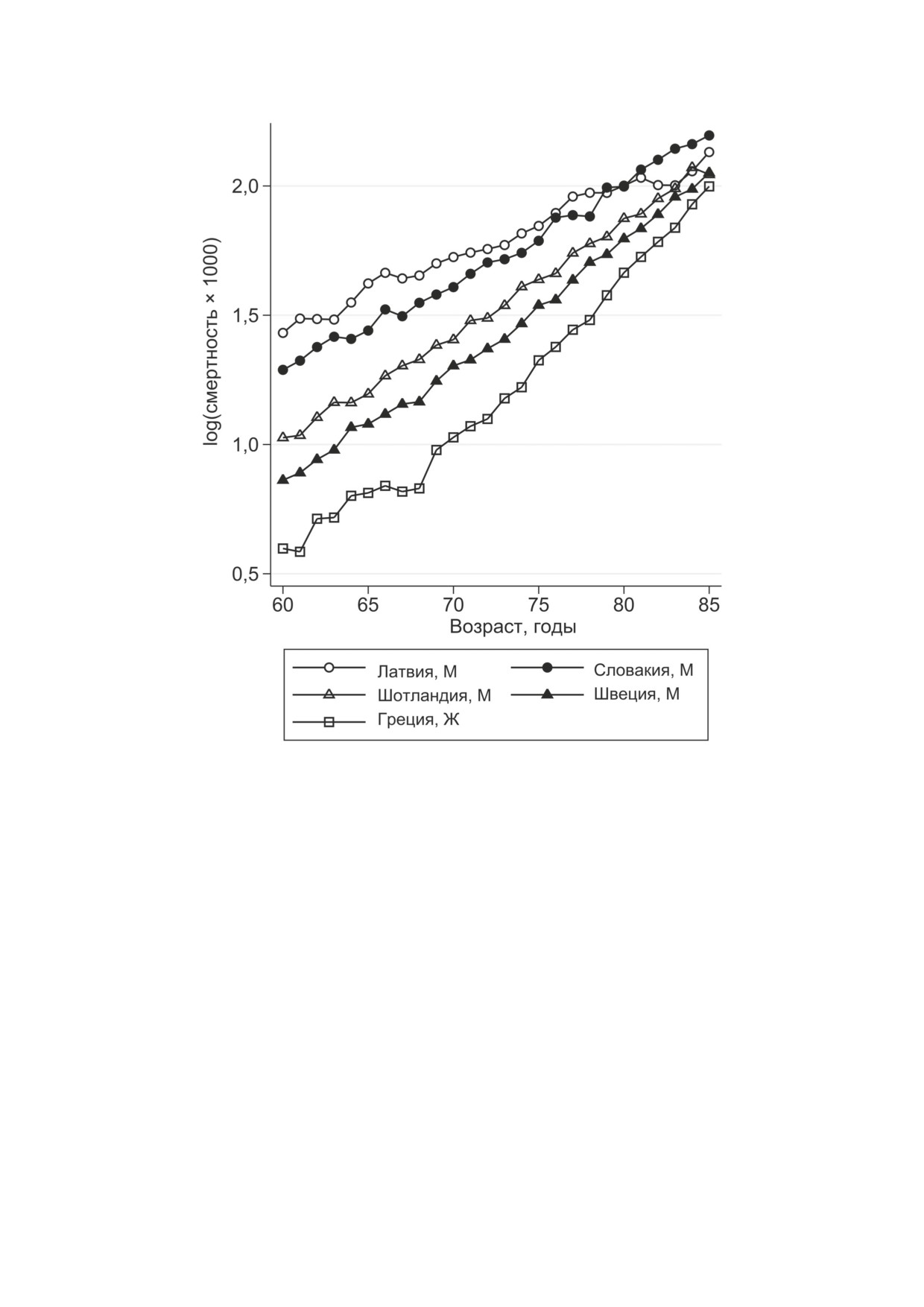
Рис. 1. Сближение траекторий смертности в пожилом возрасте для пяти европейских популяций в 2010 г., иллюстрирую-

щее компенсационный эффект смертности для мужчин (M) и женщин (Ж)

тельностью жизни [1]. Установлено, что для

ками параметра Гомперца [3, 12]. Этот подход

человека её значение равно 95 ± 2 годам [1].

уже подвергался критике со стороны некото-

Следует отметить, что компенсационный эф-

рых исследователей [13]. В двух публикациях

фект смертности можно наблюдать при про-

представлены графики обратной корреляции

стом визуальном сравнении траекторий смерт-

между параметрами Гомперца с использовани-

ности без расчёта параметров Гомперца (см.

ем данных из базы Human Mortality Database

рис. 1). Кроме того, КЭС можно наблюдать

(HMD) [14, 15], но не делается никаких попы-

не только у человека, но и у некоторых других

ток оценить количественные показатели КЭС.

биологических видов [1, 7].

Одна из задач данного исследования - про-

Обобщая эти ранние исследования по дан-

вести широкомасштабное эмпирическое изуче-

ной теме, необходимо отметить, что они были

ние корреляции между параметрами Гомперца

проведены давно, и с тех пор было выполнено

с учётом параметра Мейкема (также извест-

не так много новых эмпирических исследова-

ного как фоновая смертность [1, 16]) и прове-

ний КЭС или корреляции Стрелера-Милд-

рить компенсационный эффект смертности,

вана. Большинство исследований по данной

используя современные данные. Особое вни-

теме посвящены теоретическим разработкам

мание было уделено количественным показа-

теории старения Стрелера-Милдвана [8-11].

телям КЭС и исторической эволюции видовой

В нескольких эмпирических исследованиях на

продолжительности жизни. Также рассмотре-

эту тему не учитывался параметр Мейкема, что

ны возможные факторы, которые могут вы-

приводило к ложной корреляции между оцен-

звать ложную зависимость между параметрами

БИОХИМИЯ том 87 вып. 12 2022

ВИДОВАЯ ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ ЧЕЛОВЕКА

2001

Гомперца [7]. Bongaarts показал, что в совре-

коллинеарности [21, 22]. Этот подход умень-

менных популяциях фоновая смертность (па-

шает коллинеарность, но не устраняет её пол-

раметр Мейкема) действительно не зависит

ностью [22]. Было показано, что подгонка по

от возраста, и её значения близки к нулю [16].

методу наименьших квадратов часто приводит

По этой причине мы предполагаем, что в случае

к проблеме оптимизации, которая чрезвычай-

современных популяций учёт параметра Мей-

но чувствительна к выборочным ошибкам [23].

кема не так важен, как это было в прошлом.

Наилучшая подгонка для параметров Гомпер-

ца в этом случае оказывается реализованной

формой корреляции Стрелера-Милдвана [23].

МАТЕРИАЛЫ И МЕТОДЫ

Свойство регрессионной модели заключается

в том, что она всегда проходит через средние

Одной из целей данного исследования

значения x и y. В результате статистическая

было проверить компенсационный эффект

вариация минимальна при центрированных

смертности, обнаруженный в более ранних

значениях x. Таким образом, чтобы уменьшить

работах [1, 17], используя современные дан-

проблему ложной корреляции между пара-

ные. Для обеспечения преемственности ре-

метрами Гомперца, мы оцениваем параметры

зультатов компенсационный эффект смертно-

уравнения Гомперца-Мейкема, используя

сти проверялся с использованием поперечных

возраст, центрированный на 60 лет (примерно

или текущих данных о смертности, как это

середина возрастного интервала для оценки

было сделано в предыдущих исследованиях на

параметров).

ту же тему [1, 4, 14, 17]. Поперечные данные о

Наконец, модель №3 - это модель Гомпер-

смертности позволяют исследователям ана-

ца, использованная Стрелером и Милдваном

лизировать информацию за более длительные

(1960) [4]. Эта модель используется для демон-

исторические периоды и широко используют-

страции величины смещения, вызванного иг-

ся демографами в исследованиях параметри-

норированием параметра Мейкема. Мы пред-

ческих моделей смертности, включая модель

полагаем, что оценки параметров для этой

Гомперца [16, 18-20].

модели будут схожи с оценками для моделей с

Методы. На первом этапе анализа были

параметром Мейкема, учитывая почти нуле-

рассчитаны параметры R₀ и α модели Гомпер-

вую фоновую смертность в современных попу-

ца-Мейкема (уравнение 1). Параметры мо-

ляциях [16, 18].

дели Гомперца-Мейкема оценивали методом

Для каждой модели была оценена линей-

нелинейной регрессии в возрастном интервале

ная регрессия между параметрами Гомперца

30-80 лет (процедура nlin в пакете Stata, вер-

(lnR₀ и α) в форме, представленной в уравне-

сия 14), как это было предложено ранее [18].

нии 2. Таким образом, была оценена видовая

Пороговое значение 30 лет было выбрано для

продолжительность жизни (параметр накло-

того, чтобы избежать избытка внешних смер-

на, B) и свободный член (lnM).

тей в более молодом возрасте. Некоторые ис-

При исследовании недавних исторических

следователи используют логистическую мо-

изменений актуарной скорости старения па-

дель с параметром Мейкема для изучения

раметры модели Гомперца-Мейкема оценива-

исторических изменений смертности, чтобы

лись для каждой популяции (страны) методом

учесть замедление смертности после 85-летне-

нелинейной регрессии в возрастном интер-

го возраста [16, 18]. В нашем исследовании мы

вале 60-85 лет. Оценки смертности, получен-

анализируем смертность в возрасте до 85 лет,

ные для однолетних возрастных интервалов,

поэтому применение моделей Гомперца или

демонстрируют значительный статистический

Гомперца-Мейкема вместо логистической яв-

разброс и более стабильны в старших возрас-

ляется обоснованным.

тах (см. рис. 1). Поэтому возрастной интервал

Параметры оценивались для следующих

60-85 лет был выбран для получения более ста-

трёх моделей:

бильных оценок параметров Гомперца-Мейке-

1. Традиционная модель Гомперца-Мей-

ма и избежания колебаний смертности в более

кема.

молодых возрастах, характерных для совре-

2. Модель Гомперца-Мейкема с центри-

менных популяций с низкой смертностью. Для

рованным возрастом (x - 60).

изучения исторических изменений актуарной

3. Модель Гомперца, использованная

скорости старения параметры оценивались для

Стрелером-Милдваном.

традиционной модели Гомперца-Мейкема.

Модель №2 основана на традиционных

Данные. В качестве источника данных о

статистических подходах использования цен-

смертности для данного исследования исполь-

трированных переменных для уменьшения

зовалась база данных HMD (www.mortality.org).

БИОХИМИЯ том 87 вып. 12 2022

2002

ГАВРИЛОВ, ГАВРИЛОВА

Эта база данных содержит данные о смертно-

Оценки видовой продолжительности жизни,

сти для 45 стран с достаточно хорошим каче-

основанные на модели Гомперца, дают более

ством демографической статистики. В целом,

высокие значения: 89,4 ± 0,6 года. Эти значения

мы использовали повозрастные коэффициен-

находятся ближе к оценкам, опубликованным

ты смертности для 3662 популяций, доступ-

ранее [1].

ных в HMD, охватывающие периоды с 1900

В модели с центрированной переменной

по 2014 г. Изучение исторических изменений

возраста наблюдается значительное снижение

актуарной скорости старения было сосредо-

значений коэффициента корреляции между

точено на последних тенденциях после 2000 г.

оценками параметров Гомперца (см. табли-

В базе данных имеются показатели смертности

цу 1). Сила связи между параметрами Гом-

мужчин и женщин для возрастов от 0 до 110 лет

перца может быть выражена путём возведения

и старше. Данные о повозрастной смертно-

коэффициента корреляции в квадрат и умно-

сти доступны с шагом в один год по возрасту

жения на 100. После центрирования возраста

и времени, обозначаемые как M_x, где x означа-

процент объясняемой дисперсии снизился с

ет один год возраста. Смерти в возрасте 110 лет

86,5% (r = -0,93) до 32,5% (r = -0,57) при учё-

и старше объединены вместе.

те статистической корреляции между оценка-

ми параметров. Таким образом, 54% вариации

может быть объяснено статистической лож-

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

ной корреляцией между параметрами Гомпер-

ца. Тем не менее корреляция между оценками

Компенсационный эффект смертности. В таб-

параметров Гомперца не исчезает полностью

лице 1 приведены количественные характе-

после процедуры центрирования, и видовые

ристики КЭС, полученные с использованием

оценки продолжительности жизни остаются

данных HMD. Оценки видовой продолжитель-

такими же, как и в случае модели Гомперца-

ности жизни на основе традиционной модели

Мейкема (см. таблицу 1).

Гомперца-Мейкема и данных HMD (83,4 ± 0,6)

Как и ожидалось, модель Гомперца даёт

оказались ниже, по сравнению с ранее опу-

оценки видовой продолжительности жизни,

бликованными оценками (95 ± 2 года) [1].

близкие к оценкам, полученным с помощью

Таблица 1. Характеристики компенсационного эффекта смертности, основанные на трёх моделях

Коэффициенты регрессии*

Коэффициент

Число

Популяция

корреляции

популяций

lnM ± σ

B ± σ, годы

между lnR0 и α

Стандартная модель Гомперца-Мейкема

Мужчины

-1,76 ± 0,03

84,62 ± 0,37

-0,9665

3662

Женщины

-1,50 ± 0,06

89,01 ± 0,50

-0,9473

3662

Оба пола

-2,04 ± 0,06

83,44 ± 0,56

-0,9264

3662

Модель Гомперца-Мейкема с возрастом, центрированным на 60 лет

Мужчины

-1,76 ± 0,03

24,62 ± 0,37

-0,7383

3662

Женщины

-1,50 ± 0,06

29,01 ± 0,50

-0,6941

3662

Оба пола

-2,04 ± 0,06

23,44 ± 0,56

-0,5685

3662

Модель Гомперца

Мужчины

-1,31 ± 0,04

89,80 ± 0,45

-0,9571

3662

Женщины

-1,18 ± 0,06

92,60 ± 0,56

-0,9400

3662

Оба пола

-1,49 ± 0,06

89,42 ± 0,63

-0,9209

3662

Примечание. * Расчёты параметров регрессии проводились в интервале 30-80 лет.

БИОХИМИЯ том 87 вып. 12 2022

ВИДОВАЯ ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ ЧЕЛОВЕКА

2003

модели Гомперца-Мейкема, когда использу-

следованных моделей. Единственное различие

ются современные данные с низкой фоновой

наблюдалось для модели Гомперца-Мейкема и

смертностью (см. таблицу 1).

модели Гомперца в 1925 г. Фоновая смертность

Оценки R₀ и α (особенно α), полученные

(слагаемое Мейкема) в 1925 г. была относитель-

в пределах одной страны в разные момен-

но высокой для всех стран, поэтому её игно-

ты времени, часто очень стабильны в исто-

рирование в случае модели Гомперца должно

рии [1, 18, 24]. В результате обратная корреля-

было привести к появлению ложной корре-

ция между lnR₀ и α сильно зависит от точности

ляции Стрелера-Милдвана. Действительно,

оценки параметра Гомперца для каждого от-

видовая продолжительность жизни, получен-

дельного года времени. По этой причине мы

ная с помощью модели Гомперца (64 ± 7 лет),

провели дополнительный анализ данных (см.

была ниже по сравнению с оценкой, получен-

таблицу 2) и оценили параметры обратной за-

ной с помощью модели Гомперца-Мейкема

висимости между параметрами Гомперца для

(73 ± 7 лет). Оценка видовой продолжитель-

следующих отдельных календарных лет: 1925,

ности жизни для модели Гомперца близка к

1955, 1985 и 2010. Таким образом, были проана-

оценке, полученной Стрелером и Милдваном

лизированы изменения в оценках параметров

(68,5 лет) [4]. Оценки видовой продолжитель-

обратной зависимости, происходящие во вре-

ности жизни, полученные для более позднего

мени. Этот анализ показал увеличение оценок

периода времени (2010 г.), близки к оценкам,

видовой продолжительности жизни с течением

опубликованным ранее

[1]. Оценки видо-

времени: с 73 ± 7 лет в 1925 г. до 90 ± 3 лет в

вой продолжительности жизни могут зави-

2010 г. (модель Гомперца-Мейкема). Аналогич-

сеть не только от исторического периода, но и

ные результаты были получены и для других ис-

от возрастного интервала оценки параметров.

Таблица 2. Характеристики компенсационного эффекта смертности, основанные на трёх моделях, в зависимости от

календарного периода

Коэффициенты регрессии*

Коэффициент

Год

корреляции

Число популяций

lnM ± σ

B ± σ, годы

между lnR0 и α

Модель Гомперца-Мейкема

1925

-2,73 ± 0,72

73,08 ± 7,22

-0,9222

1955

-2,09 ± 0,25

81,02 ± 2,47

-0,9867

1985

-2,30 ± 0,28

81,31 ± 2,82

-0,9751

2010

-1,87 ± 0,26

90,40 ± 2,53

-0,9840

Модель Гомперца-Мейкема с возрастом, центрированным на 60 лет

1925

-2,73 ± 0,72

13,08 ± 7,22

-0,3927

1955

-2,09 ± 0,25

21,02 ± 2,47

-0,8446

1985

-2,30 ± 0,28

21,31 ± 2,82

-0,7553

2010

-1,87 ± 0,26

30,40 ± 2,53

-0,8802

Модель Гомперца

1925

-3,46 ± 0,63

64,15 ± 6,97

-0,9082

1955

-2,10 ± 0,27

80,89 ± 2,78

-0,9833

1985

-2,02 ± 0,34

84,22 ± 3,51

-0,9647

2010

-1,84 ± 0,27

91,37 ± 2,73

-0,9818

Примечание. * Расчёты параметров регрессии проводились в интервале 30-80 лет (оба пола вместе).

БИОХИМИЯ том 87 вып. 12 2022

16*

2004

ГАВРИЛОВ, ГАВРИЛОВА

Таблица 3. Характеристики компенсационного эффекта смертности, основанные на стандартной модели Гомперца-

Мейкема*

Коэффициенты регрессии

Коэффициент

Популяция

корреляции

Число популяций

lnM ± σ

B ± σ, годы

между lnR0 и α

Интервал для расчёта параметров: 30-80 лет

Мужчины

-1,76 ± 0,03

84,62 ± 0,37

-0,9665

3662

Женщины

-1,50 ± 0,06

89,01 ± 0,50

-0,9473

3662

Интервал для расчёта параметров: 60-85 лет

Мужчины

-1,06 ± 0,02

92,13 ± 0,21

-0,9909

3601

Женщины

-0,62 ± 0,06

97,17 ± 0,17

-0,9944

3601

Примечание. * Расчёты параметров регрессии проводились в интервале 30-80 лет (верхняя панель) и 60-85 лет (ниж-

няя панель).

Показатели смертности в более молодом воз-

тим, что оценки видовой продолжительности

расте подвержены значительным колебани-

жизни с использованием вновь рассчитанных

ям и искажениям экспоненциального роста

параметров модели Гомперца-Мейкема бли-

смертности. Оценки смертности в возрастном

же к значению видовой продолжительности

интервале 60-85 лет выглядят более гладкими

жизни, полученному ранее (95 ± 3 года) [1].

и лучше следуют стандартному экспоненци-

Эти результаты ещё раз подтверждают суще-

альному росту с возрастом, чем в более моло-

ствование компенсационного эффекта смерт-

дом возрасте, когда смертность крайне низка.

ности и стабильность его количественных

В таблице 3 представлены оценки видовой про-

характеристик.

должительности жизни при оценке параметров

Наличие исторических данных по акту-

Гомперца-Мейкема с использованием различ-

арной скорости старения дало возможность

ных возрастных интервалов. Можно заметить,

изучить тенденции актуарной скорости старе-

что оценка параметров в возрастном интервале

ния в разных странах. Наши предыдущие ис-

60-85 лет даёт более высокие значения видо-

следования показали, что значения актуарной

вой продолжительности жизни.

скорости старения относительно стабильны во

В целом, мы можем заключить, что оценки

времени, по крайней мере, до 1960-х гг. [1, 24].

видовой продолжительности жизни, основан-

Исследования Bongaarts подтвердили этот пер-

ные на современных данных, демонстрируют

воначальный вывод [16, 18]. При использова-

хорошее соответствие с более ранней публи-

нии более длинных временных рядов стало

кацией [1]. Это означает, что количественные

ясно, что значения актуарной скорости ста-

показатели КЭС для человека достаточно ста-

рения имеют более сложные траектории по-

бильны. В современных популяциях фоновая

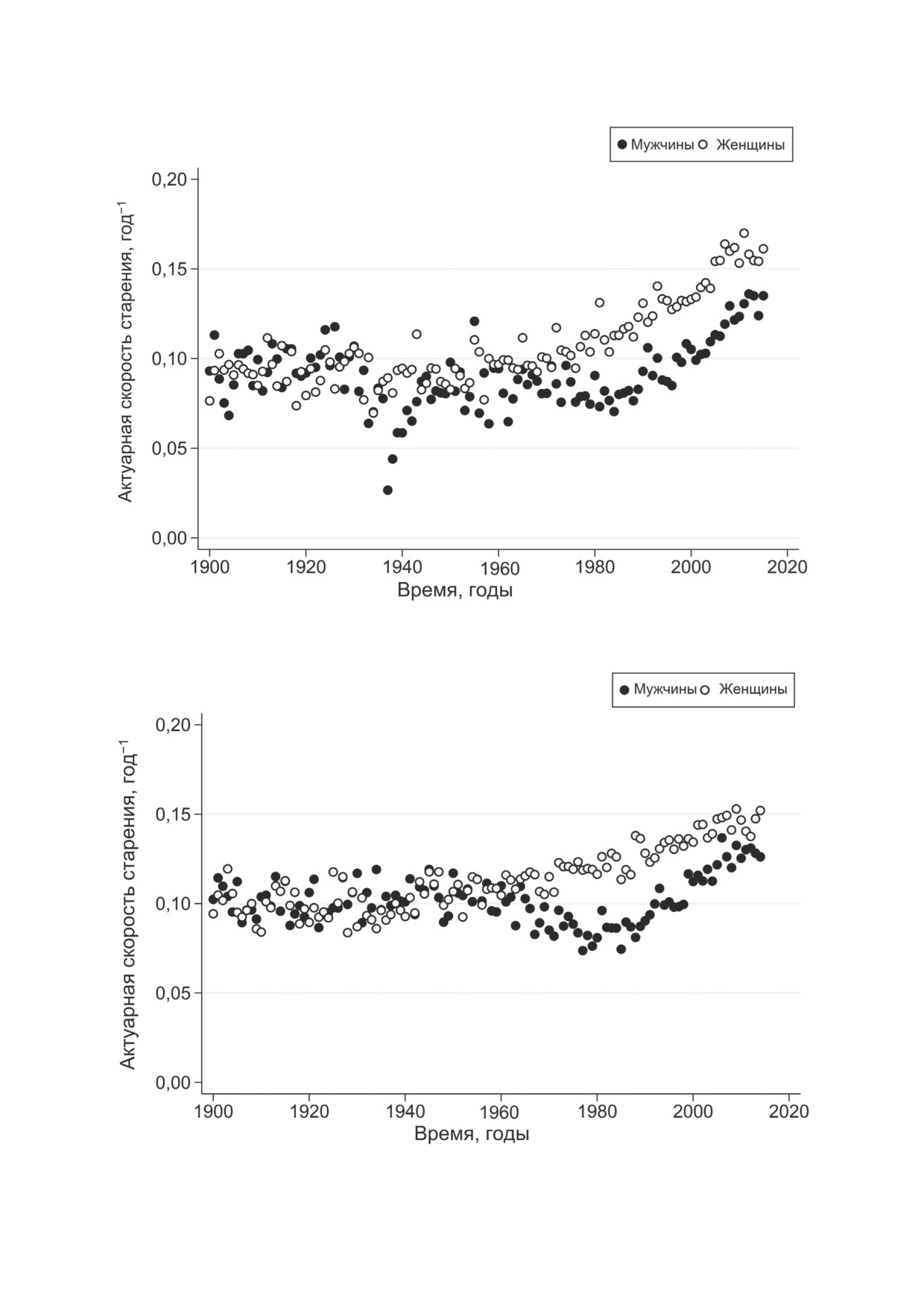
сле 1960-х гг. На рис. 2 и 3 показаны истори-

смертность очень низка [1, 16, 18], поэтому для

ческие тренды актуарной скорости старения в

количественной оценки КЭС можно использо-

Финляндии и Норвегии. Эти результаты под-

вать модель Гомперца без параметра Мейкема.

тверждают стабильность значений актуарной

Исторические изменения актуарной ско-

скорости старения до 1970-х гг., в то время как

рости старения. Мы проанализировали по-

после этого времени значения актуарной ско-

возрастные коэффициенты смертности за

рости старения начали расти в соответствии с

1900-2014 гг., используя поперечные данные.

более сложными траекториями.

При работе с данными стало ясно, что оценки

Принимая во внимание эти сложные вре-

смертности в возрасте до 60 лет имеют очень

менные траектории актуарной скорости старе-

большой разброс и не являются стабильны-

ния, мы проанализировали самые последние её

ми. По этой причине параметры модели Гом-

тенденции после 2000 г. Для каждой страны была

перца-Мейкема оценивались в возрастном

оценена линейная регрессия актуарной скоро-

интервале 60-85 лет. С помощью этих оценок

сти старения (параметра наклона Гомперца)

мы пересчитали параметры компенсационно-

как функции времени, чтобы оценить общую

го эффекта смертности (см. таблицу 3). Отме-

тенденцию для актуарной скорости старения.

БИОХИМИЯ том 87 вып. 12 2022

2006

ГАВРИЛОВ, ГАВРИЛОВА

Таблица 4. Исторические изменения значений актуарной скорости старения* после 2000 г.

Мужчины

Женщины

Число

Страна

Коэффициент

популяций

наклона линейной

p-значение

наклона линейной

p-значение

регрессии, ×10³

Австралия

1,5114

0,001

1,2951

<0,001

Австрия

2,7407

<0,001

1,9276

<0,001

Бельгия

1,8230

<0,001

1,4875

0,001

Болгария

2,4305

0,054

1,8606

0,010

Беларусь

0,3843

0,386

1,2828

0,001

Канада

1,0965

0,026

-0,0790

0,769

Швейцария

2,1124

<0,001

0,8233

0,026

Чешская Республика

2,1886

<0,001

2,3290

<0,001

Чили

2,7909

0,220

3,4081

0,002

Восточная Германия

1,8330

0,017

2,4485

<0,001

Германия

2,1047

<0,001

2,4264

<0,001

Западная Германия

2,1980

<0,001

2,4446

<0,001

Дания

2,6976

<0,001

1,2245

<0,001

Испания

1,6905

<0,001

1,4617

<0,001

Эстония

0,8753

0,296

0,5735

0,225

Финляндия

2,4491

<0,001

1,7940

0,001

Франция,

2,2854

<0,001

1,5790

0,001

гражданское население

Франция,

2,2854

<0,001

1,5790

0,001

всё население

Англия и Уэльс,

2,0366

<0,001

1,8550

<0,001

гражданское население

Англия и Уэльс,

2,0366

<0,001

1,8550

<0,001

всё население

Северная Ирландия

1,1501

0,136

2,1498

0,002

Великобритания

1,9767

<0,001

1,7956

<0,001

Шотландия

1,9311

<0,001

1,5401

0,001

Греция

2,1401

0,005

3,2622

<0,001

Венгрия

1,7999

0,004

1,9305

<0,001

Ирландия

2,4650

<0,001

2,4127

<0,001

БИОХИМИЯ том 87 вып. 12 2022

ВИДОВАЯ ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ ЧЕЛОВЕКА

2007

Таблица 4 (продолжение)

Мужчины

Женщины

Число

Страна

Коэффициент

популяций

наклона линейной

p-значение

наклона линейной

p-значение

регрессии, ×10³

Исландия

2,3997

0,130

3,8444

0,075

Израиль

2,2684

<0,001

1,4485

0,003

Италия

3,2138

<0,001

2,2241

<0,001

Япония

1,5498

<0,001

1,0220

<0,001

Литва

2,3446

0,001

2,2812

<0,001

Люксембург

-0,3850

0,731

1,8877

0,183

Латвия

-1,3286

0,194

0,6781

0,242

Нидерланды

1,7530

<0,001

0,9418

0,006

Норвегия

1,2504

0,003

0,5473

0,108

Новая Зеландия,

2,0541

0,063

-0,0909

0,937

не маори

Новая Зеландия

1,5989

0,005

0,7302

0,185

Польша

1,4253

<0,001

2,3798

<0,001

Португалия

2,9999

<0,001

3,5276

<0,001

Россия

-0,6028

0,019

1,3931

<0,001

Словакия

1,7801

0,003

2,5763

<0,001

Словения

2,7497

0,020

2,1366

0,011

Швеция

1,2518

<0,001

0,4516

0,146

Тайвань

-0,8695

0,015

0,3212

0,114

Украина

-0,8367

0,003

0,4007

0,091

США

0,2857

0,026

-0,1836

0,214

Примечание. Коэффициенты наклона линейной регрессии зависимостей актурной скорости старения от времени.

* Расчёты оценок параметров модели Гомперца-Мейкема осуществлялись в возрастном интервале 60-85 лет. Ста-

тистически значимые изменения отмечены жирным шрифтом.

В таблице 4 представлены угловые коэффици-

ная скорость старения не показала статистиче-

енты наклона линейной регрессии и соответ-

ски значимых изменений. Таким образом, 74%

ствующие p-значения. Отметим, что в боль-

исследованных популяций показали увеличе-

шинстве стран актуарная скорость старения

ние актуарной скорости старения после 2000 г.

увеличилась со временем. Актуарная скорость

Можно сделать вывод, что на поперечных

старения увеличилась в 34 случаях для муж-

данных актуарная скорость старения за послед-

чин, в 34 случаях для женщин, и в 30 случаях

нее время увеличилась. Возможным объясне-

она увеличилась для обоих полов. В 9 случаях

нием тенденции увеличения актуарной скоро-

для мужчин и 12 случаях для женщин актуар-

сти старения в поперечных данных может быть

БИОХИМИЯ том 87 вып. 12 2022

2008

ГАВРИЛОВ, ГАВРИЛОВА

неодинаковая скорость исторического сни-

источника возможных артефактов, вызываю-

жения смертности среди старших и младших

щих ложную корреляцию Стрелера-Милдвана:

возрастных групп взрослого населения. Было

статистическую корреляцию между параметра-

установлено, что смертность столетних людей

ми Гомперца [23] и игнорирование параметра

не снижается с течением времени, по крайней

Мейкема [1]. Он предположил, что обобщён-

мере, в течение последних 20-30 лет. Впервые

ный закон Гомперца-Мейкема имеет чёткую

это явление было замечено Drefahl для лиц

биологическую интерпретацию своих параме-

столетнего возраста в Швеции [25]. Позже это

тров, несмотря на существующие проблемы

явление было обнаружено для США [26] и че-

(которые могут быть устранены) [7].

тырёх европейских стран [27]. В то же время

Также было установлено, что фоновая

смертность в более молодых возрастах продол-

смертность в современных популяциях очень

жает снижаться [28]. В этом случае возрастные

низкая [1, 16] и, следовательно, не оказывает

траектории смертности неизбежно становятся

заметного влияния на оценки видовой продол-

более крутыми. До этого времени наблюдался

жительности жизни (см. таблицу 1 и 2).

параллельный сдвиг смертности вниз (в полу-

В данном исследовании также были изуче-

логарифмических координатах), а актуарная

ны последние тенденции актуарной скорости

скорость старения оставалась стабильной [29].

старения. Было установлено, что на протя-

Основываясь на этом явлении, Bongaarts пред-

жении большей части XX века актуарная ско-

ложил свой метод прогнозирования смертно-

рость старения демонстрировала удивитель-

сти (метод сдвига смертности) [18].

ную стабильность, когда снижение смертности

было вызвано преимущественно уменьшени-

ем параметра Мейкема (фоновой смертно-

ДИСКУССИЯ И ЗАКЛЮЧЕНИЕ

сти) [1, 16, 18]. Это наблюдение подтверждается

данными по Финляндии и Норвегии, представ-

Исследование количественных показате-

ленными на рис. 2 и 3. Однако в последние 20-

лей компенсационного эффекта смертности с

30 лет значения актуарной скорости старения

использованием современных данных подтвер-

начали увеличиваться во многих странах. Здесь

дило, что обратная корреляция между ln(R₀) и

необходимо упомянуть работу Tai и Noymer,

параметром наклона Гомперца (α) уравнения

которые провели крупномасштабное исследо-

Гомперца-Мейкема действительно существу-

вание актуарной скорости старения для всех

ет и является высоко статистически значимой

популяций, доступных в HMD, в историческом

при сравнении различных популяций челове-

аспекте, начиная с XIX века [14]. Авторы изме-

ка. Оценки видовой продолжительности жиз-

ряли актуарную скорость старения, используя

ни (параметр B) для современных популяций

модели Гомперца и Гомперца-Мейкема, хотя

близки к оценкам, полученным в более ран-

очевидно, что несмещённые исторические

ней публикации [1]. Также было обнаружено,

тренды актуарной скорости старения могут

что оценки видовой продолжительности жиз-

быть получены только с помощью последней

ни являются более низкими в исторически бо-

модели. Тем не менее авторы поместили в свою

лее ранние периоды даже после учёта фоновой

аннотацию следующий вводящий в заблужде-

смертности. С течением времени эти оценки

ние вывод: «С течением времени в человече-

увеличиваются.

ских популяциях параметр наклона Гомперца

Использование центрированных значений

увеличивался, что указывает на всё более кру-

возраста для учёта коллинеарности приводит к

той рост смертности с увеличением возраста».

снижению оценок коэффициентов корреляции

Однако их собственные результаты, основан-

между параметрами Гомперца, но не изменя-

ные на модели Гомперца-Мейкема, ясно по-

ет оценок видовой продолжительности жизни.

казывают, что показатели актуарной скорости

Недавно было заявлено, что корреляция Стре-

старения стабильны в течение очень долгого

лера-Милдвана может быть вызвана статисти-

времени, а затем (примерно в 1990-х гг.) испы-

ческим артефактом из-за ложной корреляции

тывают рост (рис. 6 и 7 в работе Tai et al. [14]).

между оценками параметров Гомперца [23].

Стабильность актуарной скорости старения

Уменьшение коллинеарности с использовани-

была более выражена для мужчин [14].

ем центрированных оценок возраста показы-

Tai и Noymer представили свои данные для

вает, что ложная корреляция между оценками

смеси многих популяций, доступных в HMD,

параметров Гомперца может быть ответственна

поэтому из их работы невозможно сделать вы-

за 54% объясняемой вариации, но не устраняет

вод о том, является ли недавнее увеличение

полностью корреляцию между оценками пара-

актуарной скорости старения общим явлени-

метров Гомперца. Голубев [7] рассмотрел два

ем, или оно наблюдается лишь в небольшом

БИОХИМИЯ том 87 вып. 12 2022

ВИДОВАЯ ПРОДОЛЖИТЕЛЬНОСТЬ ЖИЗНИ ЧЕЛОВЕКА

2009

количестве популяций. В нашем исследовании

делает траектории смертности более крутыми

мы проанализировали исторические тренды

и, таким образом, будет способствовать ком-

актуарной скорости старения для каждой по-

прессии смертности и заболеваемости, когда

пуляции (страны) отдельно. Оказалось, что

больные и немощные организмы будут быстро

действительно большинство популяций (74%)

умирать. Компрессию смертности можно срав-

демонстрирует увеличение актуарной скоро-

нить с медленным феноптозом, когда старый

сти старения после 2000 г. При этом в 23% по-

организм быстро погибает по собственному

пуляций показатели актуарной скорости ста-

механизму острого феноптоза для устранения

рения остаются стабильными.

особей, которые не могут быть вовлечены в

Наблюдаемый рост актуарной скорости

естественный отбор [30]. Недавний рост акту-

старения показывает, что попытки измерить

арной скорости старения показывает, что акту-

скорость старения с помощью параметра на-

арная скорость старения не является хорошей

клона Гомперца представляются проблематич-

мерой скорости биологического старения, поэ-

ными. Недавнее увеличение актуарной скоро-

тому необходимо разработать более совершен-

сти старения контринтуитивны, поскольку нет

ные показатели скорости старения.

никаких биомедицинских оснований пола-

гать, что темпы старения человека в последнее

Вклад авторов. Л.Г. разрабатывал план ис-

время ускорились. На самом деле, противопо-

следований, анализировал полученные резуль-

ложная гипотеза кажется более правдоподоб-

таты, редактировал рукопись. Н.Г. проводила

ной, учитывая снижение уровня повозрастной

статистический анализ данных и подготавли-

смертности и увеличение продолжительности

вала рукопись.

жизни.

Финансирование. Работа частично поддер-

Изучая этот парадокс увеличения актуар-

жана грантом Национального института здо-

ной скорости старения, мы обнаружили, что

ровья (NIH R21AG054849).

он, скорее всего, вызван более быстрым исто-

Благодарности. Авторы благодарят аноним-

рическим снижением смертности в младших

ных рецензентов статьи за конструктивные за-

возрастных группах взрослого населения по

мечания.

сравнению со старшими, что делает возрастной

Конфликт интересов. Авторы заявляют об

градиент смертности более крутым с течени-

отсутствии конфликта интересов в финансовой

ем времени. Это явление ставит под сомнение

или иной сфере.

существующий метод прогнозирования смерт-

Соблюдение этических норм. Данная статья

ности, основанный на стабильности актуарной

не содержит описания каких-либо исследова-

скорости старения во времени [16, 18]. Недав-

ний с использованием людей и животных в ка-

нее увеличение актуарной скорости старения

честве объектов изучения.

СПИСОК ЛИТЕРАТУРЫ

1. Gavrilov, L. A., and Gavrilova, N. S. (1991) The

7. Golubev, A. (2019) A 2D analysis of correlations

Biology of Life Span: A Quantitative Approach,

between the parameters of the Gompertz-Makeham

Harwood Academic Publisher, New York.

model (or law?) of relationships between aging,

2. Gavrilov, L. A., and Gavrilova, N. S. (2006) Reliability

mortality, and longevity, Biogerontology, 20, 799-821,

Theory of Aging and Longevity, in Handbook of the

doi: 10.1007/s10522-019-09828-z.

Biology of Aging (Masoro, E. J., and Austad, S. N. eds)

8. Burger, O., and Missov, T. I. (2016) Evolutionary

6 Edn., Academic Press, San Diego, pp. 3-42.

theory of ageing and the problem of correlated

3. Hawkes, K., Smith, K. R., and Blevins, J. K. (2012)

Gompertz parameters, J. Theor. Biol., 408, 34-41,

Human actuarial aging increases faster when back-

doi: 10.1016/j.jtbi.2016.08.002.

ground death rates are lower: a consequence of dif-

9. Li, T., and Anderson, J. J. (2015) The Strehler-

ferential heterogeneity? Evolution,

66,

103-114,

Mildvan correlation from the perspective of a two-

doi: 10.1111/j.1558-5646.2011.01414.x.

process vitality model, Popul. Stud.,

69,

91-104,

4. Strehler, B. L., and Mildvan, A. S. (1960) General

doi: 10.1080/00324728.2014.992358.

theory of mortality and aging, Science, 132, 14-21,

10. Yashin, A. I., Ukraintseva, S. V., Boiko, S. I., and

doi: 10.1126/science.132.3418.14.

Arbeev, K. G. (2002) Individual aging and mortality

5. Гаврилов Л.А. (1984). Существует ли предел про-

rate: how are they related? Soc. Biol., 49, 206-217,

должительности жизни? Биофизика, 29, 908-909.

doi: 10.1080/19485565.2002.9989059.

6. Le Bras, H. (1976) Mortality laws and limited age,

11. Li, T., Yang, Y. C., and Anderson, J. J.

(2013)

Population, 31, 655-692, doi: 10.2307/1530761.

Mortality increase in late-middle and early-old age:

БИОХИМИЯ том 87 вып. 12 2022

2010

ГАВРИЛОВ, ГАВРИЛОВА

heterogeneity in death processes as a new explanation,

human populations, Demography, 36, 475-495, doi:

Demography,

50,

1563-1591, doi:

10.1007/s13524-

10.2307/2648085.

013-0222-4.

21.

Velilla, S. (2018) A note on collinearity diagnostics

12.

Yashin, A. I., Begun, A. S., Boiko, S. I., Ukraintse-

and centering, Am. Stat., 72, 140-146, doi: 10.1080/

va, S. V., and Oeppen, J. (2002) New age patterns

00031305.2016.1264312.

of survival improvement in Sweden: do they

22.

Wood, F. S. (1984) Comment: effect of centering on

characterize changes in individual aging? Mech.

collinearity and interpretation of the constant, Am.

Ageing Dev.,

123,

637-647, doi:

10.1016/s0047-

Stat., 38, 88-90, doi: 10.2307/2683240.

6374(01)00410-9.

23.

Tarkhov, A. E., Menshikov, L. I., and Fedichev, P. O.

13.

Golubev, A.

(2004)

Does Makeham make

(2017) Strehler-Mildvan correlation is a degenerate

sense? Biogerontology,

159-167, doi:

10.1023/

manifold of Gompertz fit, J. Theor. Biol., 416, 180-

B:BGEN.0000031153.63563.58.

189, doi: 10.1016/j.jtbi.2017.01.017.

14.

Tai, T. H., and Noymer, A.

(2018) Models for

24.

Gavrilov, L. A., Gavrilova, N. S., and Nosov, V. N.

estimating empirical Gompertz mortality: with an

(1983) Human life span stopped increasing: why?

application to evolution of the Gompertzian slope,

Gerontology, 29, 176-180, doi: 10.1159/000213111.

Popul. Ecol.,

60,

171-184, doi:

10.1007/s10144-

25.

Drefahl, S., Lundstrom, H., Modig, K., and Ahlbom,

018-0609-6.

A. (2012) The era of centenarians: mortality of the

15.

Yashin, A. I., Begun, A. S., Boiko, S. I., Ukraintse-

oldest old in Sweden, J. Intern. Med., 272, 100-102,

va, S. V., and Oeppen, J. (2001) The new trends in

doi: 10.1111/j.1365-2796.2012.02518.x.

survival improvement require a revision of traditional

26.

Gavrilov, L. A., Gavrilova, N. S., and Krut’ko, V. N.

gerontological concepts, Exp. Gerontol., 37, 157-167,

(2017) The future of human longevity, Gerontology, 63,

doi: 10.1016/s0531-5565(01)00154-1.

524-526, doi: 10.1159/000477965.

16.

Bongaarts, J.

(2009) Trends in senescent life

27.

Robine, J. M., and Cubaynes, S. (2017) Worldwide

expectancy, Popul. Stud., 63, 203-213, doi: 10.1080/

demography of centenarians, Mech. Ageing Dev., 165,

00324720903165456.

59-67, doi: 10.1016/j.mad.2017.1003.1004.

17.

Гаврилов Л.А., Гаврилова Н.С., Ягужинский Л.С.

28.

Tuljapurkar, S., Li, N., and Boe, C.

(2000) A

(1978) Основные закономерности старения и ги-

universal pattern of mortality decline in the G7

бели животных с точки зрения теории надежно-

countries, Nature,

405,

789-792, doi:

10.1038/

сти, Ж. общей биологии, 39, 734-742.

35015561.

18.

Bongaarts, J.

(2005) Long-range trends in adult

29.

Гаврилов Л.А., Гаврилова Н.С. (2020) Что мы мо-

mortality: Models and projection methods, Demo-

жем узнать о старении и COVID-19, изучая смерт-

graphy, 42, 23-49, doi: 10.1353/dem.2005.0003.

ность? Биохимия,

85,

1766-1772, doi:

10.31857/

19.

Missov, T. I., Lenart, A., Nemeth, L., Canudas-

S0320972520120039.

Romo, V., and Vaupel, J. (2015) The Gompertz

30.

Skulachev, V. P., Shilovsky, G. A., Putyatina, T. S.,

force of mortality in terms of the modal age at

Popov, N. A., Markov, A. V., Skulachev, M. V., and

death, Demogr. Res., 32, 1031-1047, doi: 10.4054/

Sadovnichii, V. A. (2020) Perspectives of Homo sapiens

DemRes.2015.32.36.

lifespan extension: focus on external or internal

20.

Wilmoth, J. R., and Horiuchi, S. (1999) Rectan-

resources? Aging,

12,

5566-5584, doi:

10.18632/

gularization revisited: variability of age at death within

aging.102981.

TRENDS IN HUMAN SPECIES-SPECIFIC LIFESPAN

AND ACTUARIAL AGING RATE*

Leonid A. Gavrilov^1,2** and Nataliya S. Gavrilova^1,2

¹Academic Research Centers, NORC at the University of Chicago,

60637 Chicago, IL, USA; e-mail: lagavril@yahoo.com

²Institute for Demographic Research, Federal Center of Theoretical and Applied Sociology,

Russian Academy of Sciences, 109028 Moscow, Russia

The compensation effect of mortality (CEM) was tested and species-specific lifespan was estimated

using data on one-year age-specific death rates from the Human Mortality Database (HMD). CEM was

confirmed using this source of the data and human species-specific lifespan estimates were obtained, which

were similar to the estimates published before. Three models (Gompertz-Makeham, Gompertz-Makeham

with mean-centered age, and Gompertz) produced similar estimates of the species-specific lifespan. These

estimates demonstrated some increase over time. Attempts to measure aging rates through the Gompertz

БИОХИМИЯ том 87 вып. 12 2022