Акустические методы

УДК 620.179.162:534.87

ПРИМЕНЕНИЕ ПРОЦЕДУРЫ «ВЫБЕЛИВАНИЯ» ЭХОСИГНАЛОВ

ДЛЯ УМЕНЬШЕНИЯ УРОВНЯ СТРУКТУРНОГО ШУМА ПРИ ПРОВЕДЕНИИ

УЛЬТРАЗВУКОВОГО КОНТРОЛЯ

¹ООО «Научно-производственный центр «ЭХО+», Россия 123458 Москва,

ул. Твардовского, 8, Технопарк «Строгино»

²Московский Энергетический Институт (Национальный исследовательский университет), Россия 111250

Москва, Красноказарменная ул., 14

^*E-mail: bazulin@echoplus.ru

Поступила в редакцию 18.04.2019; после доработки 30.05.02019

Принята к публикации 10.06.2019

При ультразвуковом контроле промышленных объектов часто приходится иметь дело с металлами, обладающими

повышенным уровнем структурного шума, который формируется множеством импульсов перерассеянных на структур-

ных неоднородностях материала. На фоне структурного шума выделение полезного сигнала представляет собой нетри-

виальную задачу. Дело в том, что спектры и пространственное распределение импульсов структурного шума и эхосиг-

нала от отражателя близки друг к другу и обычные способы уменьшения уровня помех неприменимы. Поэтому для

уменьшения уровня структурного шума разработаны специальные методы. Один из них метод выбеливания (декорреля-

ции) эхосигналов, разработанный для радиолокации, и заключающийся в превращении коррелированных импульсов

структурного шума в белый шум, который хорошо подавляется обычными когерентными методами восстановления

изображения отражателей, типа C-SAFT. В численных экспериментах эхосигналы со структурным шумом рассчитыва-

лись с помощью метода конечных разностей во временной области (КРВО) при формировании областей по правилу

построения диаграмм Вороного. Как альтернативный вариант, структурный шум рассчитывался с учетом многократного

перерассеяния зондирующего импульса на точечных отражателях. Показано, что эффект уменьшения структурного

шума возможен в случае, когда корреляционная матрица структурного шума известна с точностью не менее чем ≈10 %.

В модельных экспериментах метод выбеливания удалось успешно применить для устранения реверберационных помех.

Ключевые слова: антенная решетка, двойное сканирование, Full Matrix Capture (FMC), выбеливание, декорреляция,

C-SAFT, Total Focusing Method (TFM).

DOI: 10.1134/S0130308219110010

1. ВВЕДЕНИЕ

Ультразвуковой неразрушающий контроль (УЗК) в настоящее время является широко

используемым методом благодаря его высокой чувствительности к основным типам отражате-

лей (таким как трещины и непровары) и к широкому спектру контролируемых материалов

(металлы, пластмассы, композитные материалы и т.д.). Наличие серийно выпускаемых прибо-

ров и методик проведения контроля делают УЗК достаточно дешевым. Основными недостатка-

ми УЗК являются высокие требования к состоянию поверхности объекта контроля (ОК), труд-

ность оценки реального размера отражателя, а также сложность контроля крупнозернистых

металлов, которые выделяют в отдельный класс — материалы со структурным шумом [1].

В отличие от шума приемной усилительной аппаратуры, который условно можно считать

белым, в структурных материалах отношение сигнал/шум не увеличивается при увеличении

энергии зондирующего сигнала, так как помимо увеличения амплитуды импульсов, рассеянных

отражателями, так же увеличивается и амплитуда импульсов, рассеянных на структуре. Ни

согласованная фильтрация, ни применение сложных зондирующих сигналов из-за подобия

спектров эхосигнала и структурной помехи не повышают отношение сигнал/шум. Когерентная

обработка эхосигналов, полученных при сканировании преобразователем, также недостаточно

эффективна, так как пространственно-временное распределение эхосигналов, рассеянных отра-

жателями и структурой материала, достаточно близки. В современной аппаратуре для УЗК шум

приемных усилителей удалось значительно ослабить, и проблема уменьшения уровня струк-

турного шума стала весьма актуальной.

Использование в УЗК для регистрации эхосигналов сканирующих пьезоэлектрических преоб-

разователей и антенных решеток (АР) является, на сегодняшний день, перспективным направле-

нием, так как позволяет анализировать не одномерные эхосигналы, а двумерные изображения

отражателей, что позволяет на качественно более высоком уровне решать задачи по выявлению

отражателей, их классификации и определения размеров. Ультразвуковые АР могут работать или

Е.Г. Базулин, Д.А. Коновалов

в составе ФАР-дефектоскопов или в составе ЦФА-дефектоскопов. Аббревиатура ФАР расшифро-

вывается как фазированная антенная решетка [2], а ЦФА — как цифровая фокусировка антенной

[3]. Сравнение возможностей ЦФА-дефектоскопов и ФАР-дефектоскопов, проведенное в статье

[4], позволило сделать вывод, что ЦФА-дефектоскопы предоставляет исследователю больше воз-

можностей для применения разных методов обработки эхосигналов в сравнении с ФАР-

дефектоскопом. ЦФА-дефектоскоп измеряет эхосигналы в режиме двойного сканирования (в

зарубежной литературе Full Matrix Capture (FMC)), когда первый элемент АР излучает импульс,

а все остальные элементы находятся в режиме приема, после чего процедура повторяется для

всех остальных элементов АР. Измеренный набор эхосигналов для каждого элемента называется

выстрелом. Эхосигналы всех выстрелов называются залпом. Изображение отражателей по изме-

ренным эхосигналам восстанавливается методом Combined Synthetic Aperture Focusing Technique

(C-SAFT). Таким образом, метод ЦФА предполагает регистрацию эхосигналов в режиме двойно-

го сканирования и восстановление изображения отражателей методом C-SAFT. Далее изображе-

ния, восстановленные методом ЦФА, будут называться ЦФА-изображениями.

В статье для уменьшения уровня структурного шума изображения отражателей предлагается

использовать метод выбеливания (декорреляции) эхосигналов структурного шума [5—7].

Восстановление ЦФА-изображения отражателей по выбеленным эхосигналам должно повысить

отношение сигнал/структурный шум [7].

2. МЕТОДЫ УМЕНЬШЕНИЯ СТРУКТУРНОГО ШУМА ПРИ ПРОВЕДЕНИИ

УЛЬТРАЗВУКОВОГО КОНТРОЛЯ

Структурный шум возникает при контроле материала, в котором зондирующий сигнал, помимо

отражения от дефекта, многократно перерассеивается на неоднородностях структуры материала,

например, на границах зерен кристаллитов. Именно эти перерассеянные импульсы интерфериру-

ют между собой (спекловый шум) и формируют структурный шум, который из-за характерного

вида на А-скане образно называют «травой».

2.1. Использование коротких импульсов

Одним из самых простых методов борьбы со структурным шумом является использование

коротких зондирующих импульсов [8]. Уменьшение уровня структурного шума объясняется тем,

что когерентное сложение коротких импульсов уменьшает вероятность возникновения интерфе-

ренционных импульсов большой амплитуды. Уменьшение длительности импульса τ за счет аппа-

ратных решений имеет свои ограничения, связанные в первую очередь с демпфированием пьезоэ-

лементов [9]. Применяя к измеренным эхосигналам методы достижения сверхразрешения, можно

в несколько раз уменьшить длительности импульсов τ, что приведет к повышению отношения

сигнал/структурный шум.

2.2. Метод расщепления спектра

Суть метода заключается в разбиении спектра эхосигнала s(t) на несколько поддиапазонов, то

есть вместо одного короткого импульса рассматривается несколько более длинных импульсов s_i(t).

После частотной фильтрации, присвоения каждому импульсу s_i(t) своего весового коэффициента w_i

и суммирования формируется новый эхосигнал. Однако, как упоминалось выше, спектр импульсов

структурного шума подобен спектру зондирующего сигнала и по этой причине сложно ожидать

заметного уменьшения уровня структурного шума [10]. Широкого самостоятельного применения

метод расщепления спектра не получил. Тем не менее он используется в качестве структурной части

более сложных алгоритмов для обработки сигналов [11,12]. В [13] для повышения отношения сиг-

нал/шум метод расщепления спектра было предложено объединить с методом экстраполяции спек-

тров эхосигналов за счет построения их AR-модели. В [14] показана эффективность такого подхода

для уменьшения уровня структурного шума при контроле композитного шва.

2.3. Восстановление отражателей корреляционным методом

Пространственно-временная обработка эхосигналов позволяет уменьшить уровень шума изо-

бражения отражателей. Решение прямой задачи, то есть расчет рассеянного поля p по известному

коэффициенту перерассеяния ε, в линейном случае можно записать в виде

Дефектоскопия

№ 11

2019

Применение процедуры «выбеливания» эхосигналов ...

p = Gε + n,

(1)

где матрица G описывает распространение поля от источника в области S_t до точечного отражате-

ля с координатами (x_i, z_i) и до приемника в области приема S_r, n — шум измерений. Так как задача

(1) неустойчива, то ее решение нельзя свести к простому расчету G^-1. Один из вариантов нахожде-

ния приближенного решения (1) заключается в применении метода наименьших квадратов

argmin

(

)

где χ

−p

(2)

позволяющее найти такую оценку

, которая порождает рассеянное поле минимально отличаю-

щееся от измеренного p. Для задачи (2) существует приближенное решение, которое представляет

собой формулу корреляции

≈G

(3)

Восстановление изображения отражателей корреляционным методом или методом C-SAFT,

эффективно повышает отношение сигнал/белый шум, но уровень структурного шума снижается

менее эффективно. Если приемные преобразователи разнести на расстояние большее, чем радиус

корреляции структурного шума контролируемого материала, то структурный шум можно рассма-

тривать как белый [15] и применение формулы (3) эффективно уменьшит его уровень. Так как

радиус корреляции может оказаться больше половины длины волны, то линейные методы обработ-

ки не позволят получить изображения с низким уровнем «боковых лепестков».

2.4. Восстановление изображения отражателей методом МЭ

Как упоминалось в разделе 2.1, уменьшение длины импульса, в том числе за счет математиче-

ской обработки, приводит к уменьшению уровня структурного шума [14]. Для решения некоррект-

ных задач А.Н. Тихоновым был разработан метод регуляризации [16], основанный на переходе от

задачи в форме (1) к задаче оптимизации, которая устойчива к малым изменениям p

argmin (χ

(ε)+ αΩ

(ε)),

(4)

i,x

×N

i,z

ε∈R

где Ω(ε) — стабилизирующий функционал, который учитывает некую априорную информацию о

решении и таким образом уменьшает область поиска решений, Ni,x × Ni,z — число точек в восста-

навливаемом изображении вдоль оси x и z. Метод МЭ сводится к решению оптимизационной

задачи (4), где в качестве стабилизирующего функционала используется энтропия

H(ε)

∑

= -Ω(

ε).

(5)

i =1

Метод МЭ имеет ряд преимуществ перед корреляционным методом и методом C-SAFT:

1) для получения высококачественно изображения можно использовать менее 10 % эхосигна-

лов, что повышает скорость их регистрации;

2) можно нарушить теорему Котельникова и пользоваться прореженными антенными решетка-

ми для получения изображения с малым уровнем «боковых лепестков», что очень важно при реги-

страции эхосигналов с шагом больше, чем радиус корреляции структурного шума [15];

3) восстановленные изображения отражателей имеют пониженный уровень структурного

шума из-за повышения продольной и фронтальной разрешающих способностей изображения.

К недостаткам метода МЭ можно отнести повышенные требования к объему оперативной

памяти компьютера, так нужно хранить три большие матрицы (G, G^T и Гессиан целевой функции)

для поиска минимума функции (4) методами второго порядка.

2.5. Методы уменьшения уровня коррелированных помех в радиолокации и сотовой связи

Немало методов ультразвукового контроля основаны на достижениях радиолокации, бурное

развитие которой проходило во второй половине XX в. Развитие методов борьбы со структурным

шумом в радиолокации также не было обойдено вниманием. К помеховым сигналам радиолокаци-

онной станции (РЛС) относятся собственные шумы приемных устройств и внешние естественные

и искусственные помехи. Внешнюю естественную помеху могут сформировать пассивные переиз-

Дефектоскопия

№ 11

2019

Е.Г. Базулин, Д.А. Коновалов

лучающие отражатели и неоднородности среды распространения радиоимпульса. Искусственные

помехи создаются противником для маскировки полезного сигнала от цели. Внешние помехи, как

правило, коррелированы с полезным сигналом. Задача заключатеся в том, чтобы учитывать в алго-

ритмах обнаружения цели радиолокационную обстановку, которая может меняться как постепен-

но, например, движение облаков, так и быстро, например, в случае постановки активных помех

[17].

Один из методов пространственной отстройки от коррелированных помех для ФАР-систем,

заключается в том, на основе известного или определенного направления на источник шумового

сигнала, сформировать диаграмму (ДН) направленности АР таким образом, чтобы обеспечивать ее

максимум в направлении источника полезного сигнала и, в идеальном случае, создавать «нули»

ДН в направлении на источники помех. Пересчет формы ДН должен происходить при изменении

положения источников полезного сигнала и помех [18]. Подобный подход (технология «умных

антенн») применяется в сотовой связи для уменьшения уровня межканальных помех [18,19].

2.6. Вычитание шаблона структурных помех

Примитивный вариант уменьшения уровня структурных помех заключается в измерении p^s в

точно таком же объекте, что и объект контроля, и вычитания p^s из измеренных эхосигналов

p_sub = p - p^s.

(6)

Однако такой подход не реализуем в практике УЗК, поэтому были разработаны методы,

использующие не явный вид структурного шума p^s, а его корреляционные свойства.

3. МЕТОД ВЫБЕЛИВАНИЯ (ДЕКОРРЕЛЯЦИИ) СТРУКТУРНОГО ШУМА

Алгоритм выбеливания эхосигналов структурного шума основан на методе максимального

правдоподобия (ММП) [20].

3.1. Функция правдоподобия

Функцией правдоподобия называется совместная плотность вероятности многомерного векто-

ра случайных величин

(

, x

,,

)

∈

L x)

= p(x

, x

,x

Особое место занимает нормальное (Гауссово) многомерное распределение, которое записывается

в виде

−1

(x−µ)

(x)

(x−µ)

p(x)

µ∈

(7)

N/2

1/2

(2π)

| Σ(x)|

где Σ(x) — ковариационная матрица (неотрицательно определенная симметричная) многомерного

вектора случайных величин x; μ — математическое ожидание случайной величины x. В задачах

УЗК под вектором x подразумеваются измеренные эхосигналы, длина N которого может достигать

значения 10⁶ и более отсчетов, а под μ — искомое решение, которое доставляет максимум функции

L(x).

Если случайные величины независимы и имеют одинаковую дисперсию σ, то функцию прав-

доподобия можно записать через произведение вероятностей

x−µ

^- 2σ2

L(x)

p(x

)

(8)

∏

N/2

i=1

(2π)

Из формулы (8) видно, что максимум функции правдоподобия достигается при

x-µ

→ min.

То есть для случая независимых случайных величин x максимум правдоподобия сводится к мето-

ду наименьших квадратов (2), что гарантирует максимальное отношение сигнал/шум. Если x = p,

а µ = Gε , то ММП выбирает такую оценку рассеянного поля Gε , которая с максимальной вероят-

ностью близка к измеренным эхосигналам p.

Дефектоскопия

№ 11

2019

Применение процедуры «выбеливания» эхосигналов ...

3.2. Алгоритм выбеливания структурного шума

В [5], на основе принципа ММП, был предложен метод многоканальной пространственно-вре-

менной обработки радиолокационных сигналов для достижения минимального уровня структур-

ного шума при формировании изображения отражателей. Суть метода заключается в переходе в

такую систему координат, в которой случайные зависимые величины x становятся независимыми

(декоррелируются или выбеливаются) и ковариационная матрица Σ(x) в формуле (7) становится

диагональной. Это позволяет вместо формулы (7) воспользоваться формулой (8). Изображение

отражателей, восстановленное корреляционным методом (3) или методом C-SAFT по выбеленным

эхосигналам, будет иметь оптимальное отношение сигнал/шум.

Обозначим через матрицу p_trm эхосигналы выстрела номер trm. Матрица

{

, ,

}

состоит из эхосигналов (столбцов) p_trm,rcv, измеренных в объекте кон-

trm

trm,1

trm,2

trm,N

троля, где rcv = 1, 2,… N_e , а N_e — число элементов в антенной решетке. Обозначим через ε^c(r)

функцию, описывающую структуру контролируемого материала. Черезp^strm обозначим матрицу

эхосигналов структурного шума, измеренную на той же аппаратуре на свидетеле-образце, струк-

тура которого описывается функцией ε^c(r). Корреляционная матрица R эхосигналов выстрелаp^strm

имеет блочную структуру и определяется следующим образом:

1,1

1,2



1 Ne



2,1

2,2

2,N

(

R ε r))

где

= corr(p

m,n

trm,m trm,n









4,2

Под операцией

corr(p

)

подразумевается нахождение функции корреляции между

trm,m trm,n

двумя эхосигналами

одного выстрела trm. Так как эхосигналы структурного

trm,

шума нестационарные из-за уменьшения амплитуды импульсов от времени, то корреляцион-

ную функцию нужно рассчитывать для разных временных точек t₁ и t₂. Для стационарного

сигнала функция корреляции зависит только от расстояния между двумя временными точками

∆t = t₁ - t₂. Опыт работы с алгоритмом выбеливания не показал его критичной зависимости от

способа расчета функции корреляции — в предположении стационарного или нестационарно-

го вида структурного шума на временных апертурах в десятки микросекунд. Для упрощения

записи будем полагать R = R(ε^s(r)). Обратную матрицу R^-1, которая удовлетворяет условию

RR^-1 = E, где E — единичная матрица, запишем в виде блочной матрицы

−1

−

−1



1,1

1,2

1,N

−1

−

−1



−1

2,1

2,2

2,N







−1

−

-1



−1

Значок «крышечка» указывает на то, что произведение

R R

не обязано должно быть

trm,k trm,k

равно E. Рассчитав матрицу R^-1, выбеленные эхосигналы

p для выстрела trm можно получить

по формуле

N_e

-1

(9)

trm,rcv

=∑

n,rcv

trm,n

n=1

где

— эхосигналы, измеренные в объекте контроля. Матрица

ptrm

состоит из выбеленных

trm,

,rcv

{

,p

}

эхосигналов

trm

trm,1

trm,2

trm,N

. После процедуры выбеливания по формуле (9) декорре-

лированные эхосигналы всех выстрелов

{

p ,p

,p

} можно использовать для восстановле-

ния изображения отражателей корреляционным методом или методом C-SAFT.

Дефектоскопия

№ 11

2019

Е.Г. Базулин, Д.А. Коновалов

3.3. Регуляризация при обращении корреляционной матрицы

Корреляционная матрица R плохо обусловлена и обычные методы обращения матриц не дают

приемлемого результата. Для регуляризированной оценки обратной матрицы R^-1 можно восполь-

зоваться так называемым диагональным нагружением (diagonal loading) [21], который заменяет

матрицу R на матрицу R_α

R_α = R + αE,

(10)

где α — это регуляризирующий коэффициент, который можно положить равным дисперсии диа-

гональных элементов матрицы R. Данный прием позволяет повысить устойчивость решения зада-

чи обращения корреляционной матрицы R, заменив ее на матрицу R_α.

3.4. Определение корреляционной матрицы структурного шума

Эффективность работы алгоритма выбеливания (9) зависит от того, насколько точно корреля-

ционная функция R(ε^s(r)) образца структурного шума, рассчитанная по эхосигналам p^s, совпадает

с корреляционной функцией R(ε^c(r)) структурного шума объекта контроля. Задача определения

корреляционной матрицы шума нетривиальна и трудоемка. В радиолокации она решается за счет

создания отдельного канала сбора и анализа данных РЛС, чтобы постоянно оценивать и прогнози-

ровать вид корреляционной матрицы R для меняющейся помеховой обстановке [17]. Для УЗК

такой подход затруднителен, так как одновременно измеряются эхосигналы от отражателя и струк-

туры материала.

3.4.1. Одинаковый средний размер кристаллитов

Для УЗК идеальным являлся бы вариант, когда эталонный образец для измерения структурно-

го шума p^s изготовлен по той же технологии, что и объект контроля, и его структура характеризу-

ется только средним размером зерна

= ε

(r)

. В этом случае для расчета обратной корреляци-

онной матрицы R^-1 на эталонном образце измеряются эхосигналы структурного шума p^s. Если

средний размер материала контролируемого объекта зерна

= ε

(r)

совпадает с эталонным δ^s,

то можно было бы ожидать эффективного выбеливания эхосигналов p по формуле (9). Однако, как

показало численное моделирование, если корреляционные матрицы R(ε^c(r)) и R(ε^s(r)) структурно-

го шума двух образцов для случая δ^c= δ^s отличаются более чем на 20 %, то процедура выбеливания

(9) не эффективна.

3.4.2. Смещение структуры материала как целого

Пусть структура ε^s(r) объекта контроля слабо меняется вдоль сварного соединения объекта

контроля, например, смещается на небольшую величину ∆r, так что

ε r)

≈ε

(r + ∆r). Если кор-

реляционная матрица R(ε^s(r)), рассчитанная по эхосигналам без отражателей, будет отличаться от

корреляционной матрицей R(ε^c(r)) меньше чем на 10 %, то можно ожидать эффективной работы

процедуры выбеливания (9).

4. ПРИМЕНЕНИЕ МЕТОДА ВЫБЕЛИВАНИЯ В ЧИСЛЕННЫХ ЭКСПЕРИМЕНТАХ

Эффективность метода выбеливания проверялась на эхосигналах со структурным шумом, рас-

считанным методом конечных разностей во временной области (КРВО) [22]. Такой подход позво-

ляет моделировать рассеяние упругой волны на анизотропных кристаллитах, сформированных по

принципу построения диаграмм Вороного. Однако такие расчеты требуют много времени и поэто-

му, как альтернатива, структурный шум эмулировался эхосигналами, рассеянными на точечных

отражателях, с помощью разложения в ряд Борна [23] для заданного количества перерассеяний.

4.1. Выбеливание по точно известному структурному шуму

На рис. 1а показано распределение упругой константы C₁₁ объекта, состоящего из областей

анизотропного материала кубической симметрии, сформированных по принципу построения диа-

грамм Вороного со средним размером зерна δ^s = 0,25 мм [22]. Функция, описывающая структуру

Дефектоскопия

№ 11

2019

Применение процедуры «выбеливания» эхосигналов ...

-20

1800

1600

Антенная решетка

1400

-10

1200

1000

-5

800

600

400

200

-20

-15

-10

-5

x, мм

250

-2

200

Структурный

шум и «ревер-

150

берация»

100

«Негативное» изобра-

Блик дна

жение тени отверстия

-10

-5

-10 -8 -6 -4 -2

8 10

x, мм

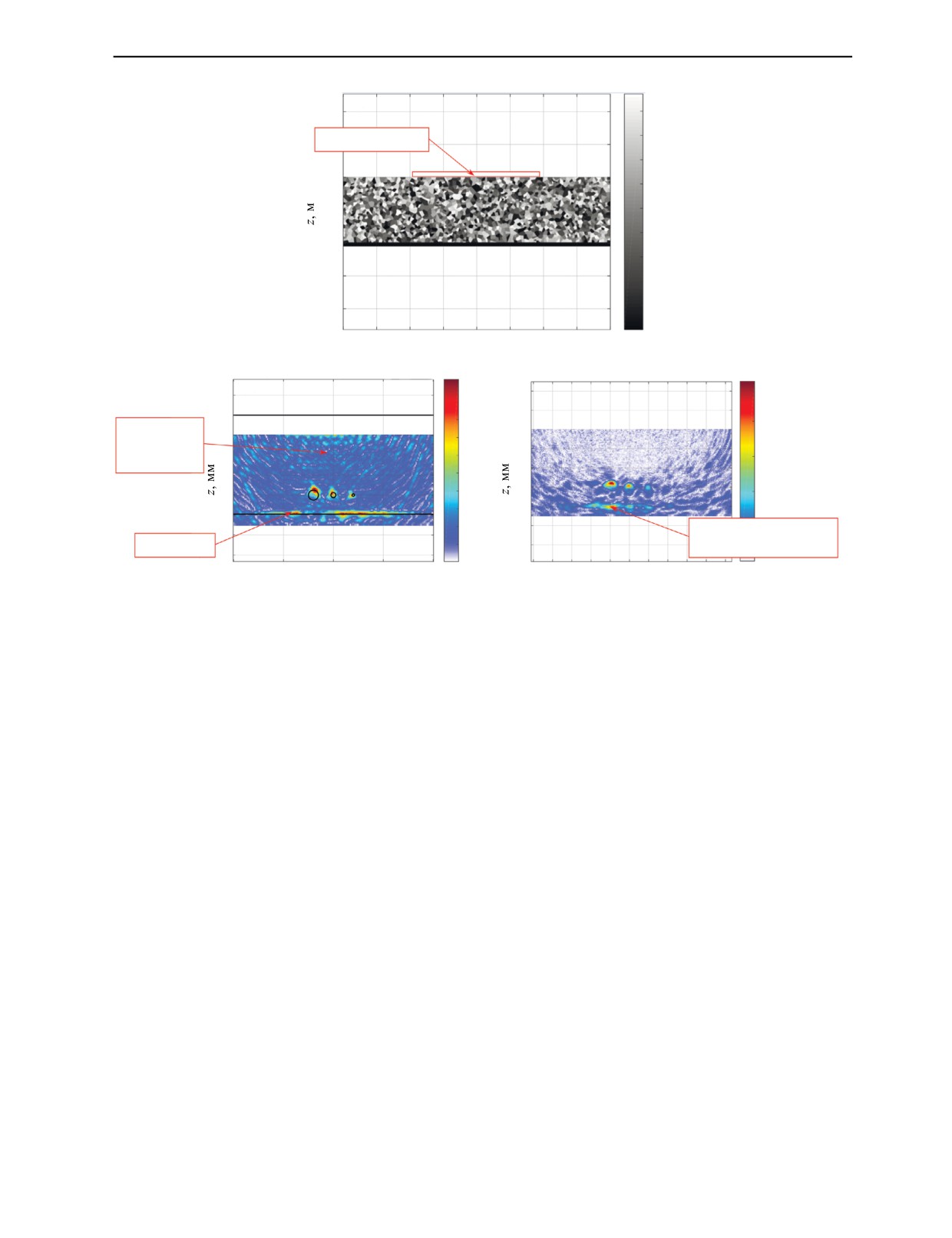
Рис. 1. Распределение упругой константы C₁₁ образца с областями, сформированными по принципу построения диа-

грамм Вороного (а), ЦФА-изображения, восстановленные по исходным эхосигналам (б), и после выбеливания (в).

ε r)

{

C r),

C r),C

(r)

}

, представляет собой распределение трех упругих констант для случая

кубической симметрии. Плотность образца полагалась постоянной. Поворот кристаллографиче-

ской оси θ в каждой области выбирался случайным образом. Для «регистрации» эхосигналов

использовалась АР (5 МГц, 32 элемента, размер пьезоэлемента 0,5 мм, зазор между пьезоэлемен-

тами 0,1 мм), установленная на поверхность образца. На рис. 1а АР схематически показана прямо-

угольником красного цвета. Образец без отверстий использовался для расчета матрицы корреля-

ции R(ε^s(r)) структурного шума p^s. Для расчета эхосигналов p в этом же образце были «просвер-

лены» три отверстия диаметрами 0,5, 1,0 и 3,0 мм на глубине 8 мм, которые на рис. 1б показаны

окружностями черного цвета. Таким образом образцы имели одну и ту же структуру кристаллитов,

то есть ε^s(r) = ε^с(r), за исключением областей с отверстиями.

На рис. 1б представлено ЦФА-изображение отражателей, восстановленное по исходным эхо-

сигналам p. Все три блика от границ отверстий и блик дна образца уверенно обнаруживаются, с

превышением их амплитуды уровня шума на 6 дБ. Отметим, что на малых глубинах (кроме струк-

турного шума) присутствует и «реверберационный» шум, сформированный Релеевской волной и

головной волной, распространяющихся вдоль поверхности образца, на которую установлена АР.

ЦФА-изображение, полученное по выбеленным эхосигналам (рис. 1в), имеет малый уровень

структурного и «реверберационного» шума и искомые отражатели хорошо видны. Так как в эхо-

сигналах p^s, используемых для расчета корреляционной матрицы, присутствовали отраженные от

дна импульсы, то они также считались шумом, и поэтому после выбеливания блик дна исчез, но

стала видна тень от отверстий.

Приведенные изображения позволяют сделать вывод, что алгоритм выбеливания работоспосо-

бен и запрограммирован правильно. Но случай ε^s(r) = ε^с(r) тривиальный, так как, вычитая эхосиг-

налы структурного шума из эхосигналов с отражателями по формуле (6), можно получить практи-

чески такой же результат, как на рис. 1в, используя незначительные вычислительные ресурсы.

Попытка выбеливания эхосигналов, рассчитанных методом КРВО для разных реализаций струк-

Дефектоскопия

№ 11

2019

Е.Г. Базулин, Д.А. Коновалов

туры со одинаковым средним размером δ^c= δ^s, не увенчалась успехом, так как функции корреляции

двух вариантов структурного шума отличались более чем на 20 %.

4.2. Выбеливание по другой реализации структурного шума

Более быстрый, чем расчет методом КРВО, способ моделирования структурного шума p^s

заключается в расчете эхосигналов при многократном рассеянии импульсов на точечных отра-

жателях, имитирующих структуру материала. Точечные отражатели с коэффициентом отраже-

ния -0,5 располагались в узлах сетки с шагом 2 мм, после чего случайным образом смещались

по обеим осям в диапазоне [-δ^s/2, δ^s/2]. В данном случае ε^s(r) — это список координат точечных

отражателей, их амплитуд и средний размер «зерна» δ^s = 2 мм. Образцом структурного шума

считались эхосигналы, рассчитанные с учетом трехкратного перерассеяния (три члена ряда

Борна), для АР (5 МГц, 16 точечных элементов с шагом 0,6 мм). Расчет эхосигналов p проходил

с учетом трехкратного перерассеяния для нового варианта размещения точечных отражателей

структуры ε^с(r) на сетке с шагом δ^c = 2 мм с добавлением трех точечных отражателей с коэффи-

циентом отражения -1,0 (см. раздел 3.4.1). На рис. 2 месторасположение трех отражателей, под-

лежащих обнаружению, указаны выносками с номерами отражателей.

350

3,5

300

250

2,5

200

150

1,5

100

Ложные

блики

Ложные блики

0,5

остались

-10 -8 -6 -4

-2

-10 -8

-6 -4

-2

x, мм

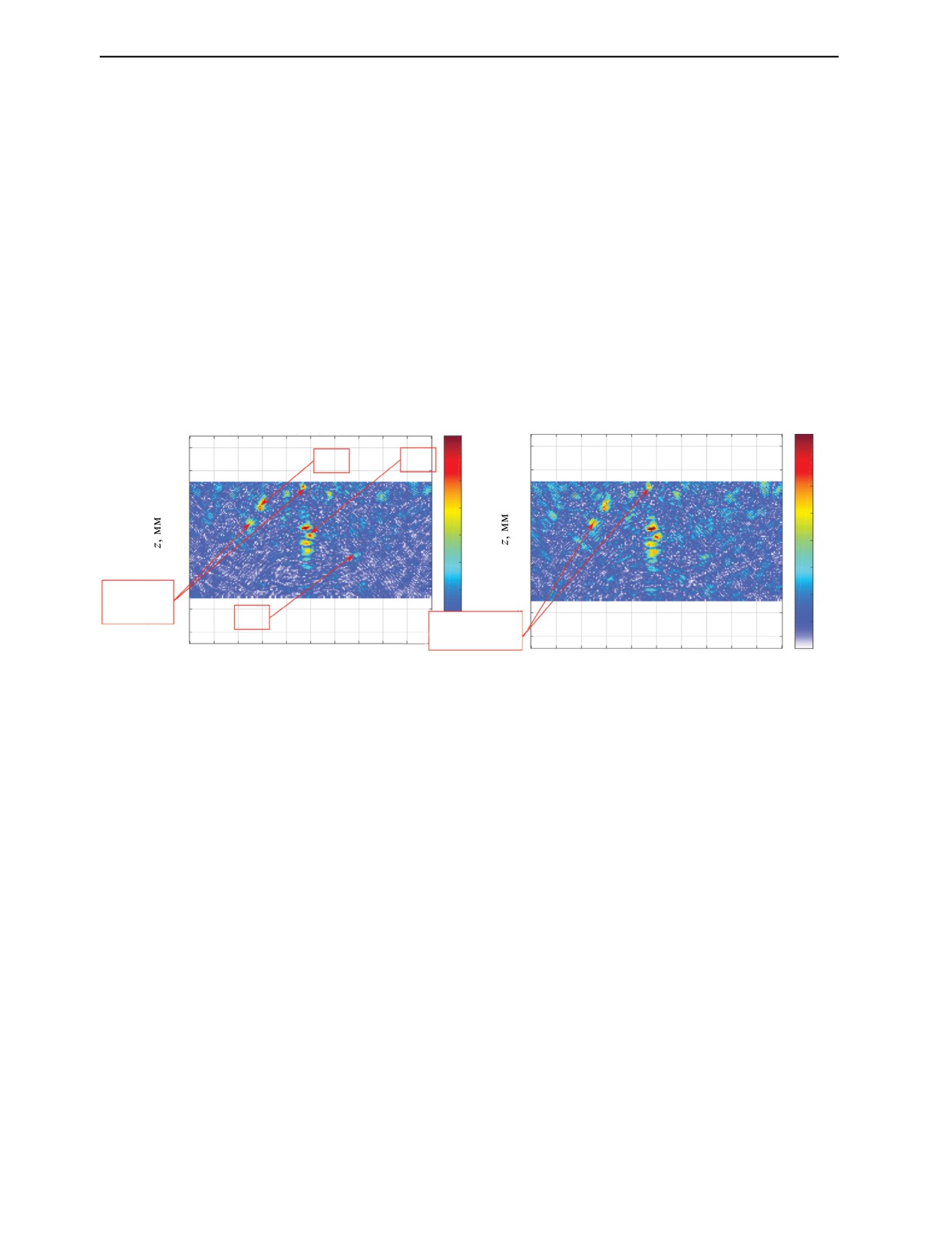
Рис. 2. ЦФА-изображения эхосигналов, восстановленные по исходным эхосигналам (а), после выбеливания (б).

На рис. 2а показано ЦФА-изображение, восстановленное по исходным эхосигналам со струк-

турным шумом, по которому из-за большого количества ложных бликов невозможно обнаружить

три отражателя с коэффициентами отражения -1,0. На рис. 2б показано ЦФА-изображение, вос-

становленное по выбеленным эхосигналам. После выбеливания блики структурного шума практи-

чески не уменьшились, и обнаружить три искомых отражателя не удается. Попытка уменьшить

шум с использованием формулы (6) не увенчалась успехом.

Неэффективное выбеливание связано с тем, что корреляционные функции R(ε^s(r)) и R(ε^с(r))

отличаются друг от друга больше, чем на 20 %, хотя структурный шум генерировался с одина-

ковыми статистическими характеристикам δ^s = δ^с = 2 мм. На рис. 3а приведены графики корре-

ляционных функций эхосигналов для двух реализаций структурного шума ε^s(r) и ε^с(r). На

рис. 3б показаны две пространственные корреляционные функции эхосигналов восьмого

выстрела по отношению к эхосигналу первого элемента АР для двух реализаций шума. Видно,

что корреляционные функции как во времени, так и в пространстве отличаются друг от друга

более, чем на 20 %, что и привело к неэффективной работе процедуры выбеливания.

4.3. Расчет и выбеливание одного варианта структурного шума со смещением

В практике ультразвукового контроля встречаются случаи, когда структурные неоднородно-

сти сварного соединения плавно меняются на протяжении некоторого участка сварного соедине-

ния объекта контроля (см. раздел 3.4.2). Для имитации такого случая точечные отражатели с

коэффициентом отражения -0,5 располагались со случайным смещением в узлах сетки с шагом

2,0 мм. Образцом структурного шума ε^s(r) считались эхосигналы p^s, рассчитанные с учетом трех-

Дефектоскопия

№ 11

2019

Применение процедуры «выбеливания» эхосигналов ...

1,0

0,9

0,8

0,7

Сильное различие

0,6

корреляционных

0,5

функций

0,4

0,3

0,2

0,1

-5 -4 -3

-2

-1

t, мкс

x, мм

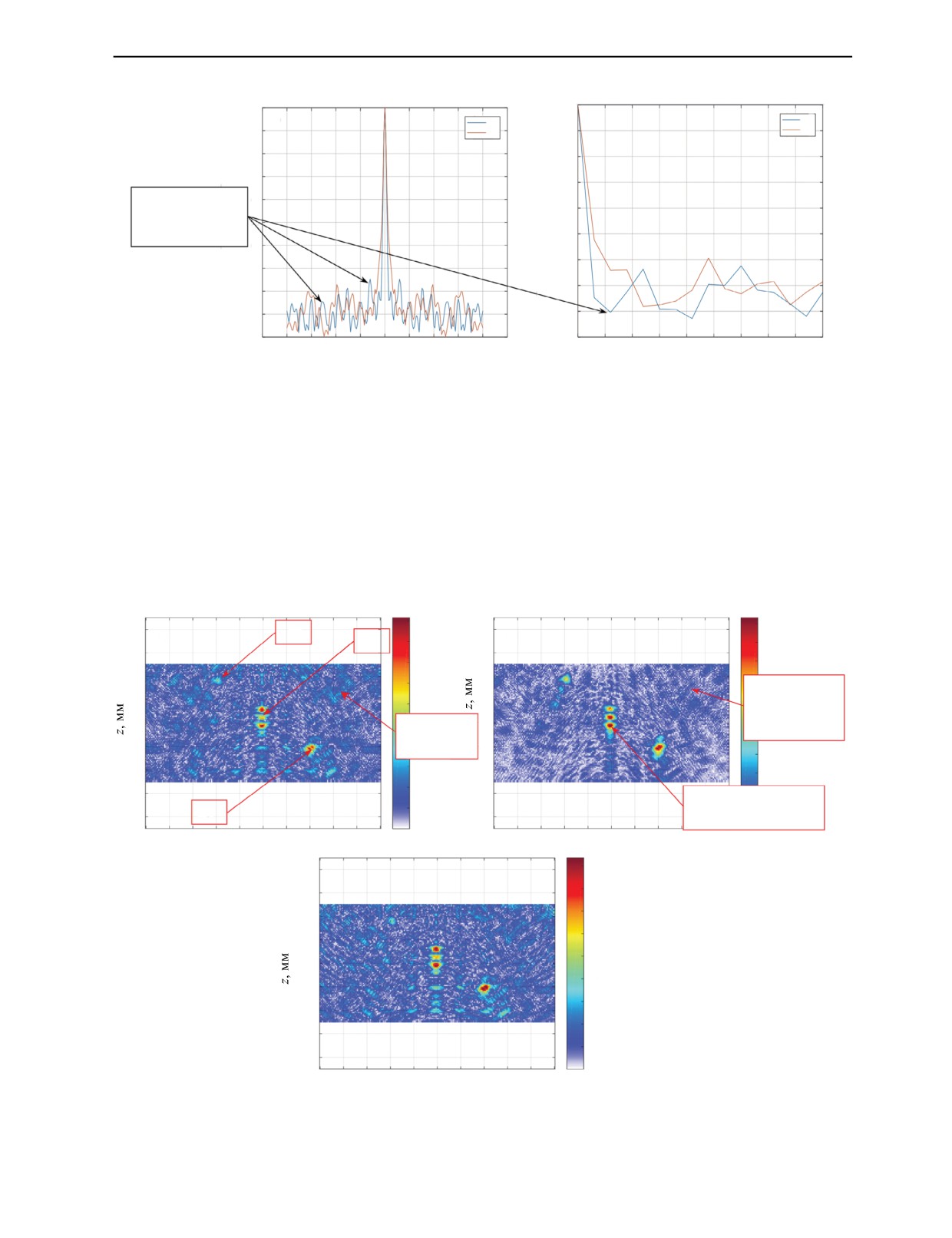
Рис. 3. Две временные корреляционные функции эхосигналов двух реализаций структурного шума (а), две простран-

ственные корреляционные функции эхосигналов восьмого выстрела (б).

кратного перерассеяния, для АР с параметрами как в предыдущем разделе. Для расчета эхосигна-

лов p созданный ранее вариант размещения точечных отражателей смещался как целое на 0,1 мм

(9 % от длины волны) по оси z, к ним добавлялись три точечных отражателя с коэффициентом

отражения -1,0, то есть ε^с(r) = ε^s(r + ∆r), где ∆r = (0, -0,1) мм, и проводился расчет эхосигналов

с учетом трехкратного перерассеяния.

На рис. 4 представлены ЦФА-изображения, восстановленные по исходным эхосигналам (а),

по выбеленным эхосигналам (б) и после вычитания эхосигналов образца структурного шума (в).

500

450

400

350

Структурный

300

шум

уменьшился

Структурный

шум

150

100

Некоторые ложные

блики остались

-10 -8 -6 -4

-2

-10 -8 -6 -4

-2

x, мм

450

400

350

300

250

200

150

100

-10 -8 -6 -4 -2

x, мм

Рис. 4. ЦФА-изображения эхосигналов, восстановленные по исходным эхосигналам (а), после выбеливания (б) и после

вычитания образца структурного шума (в).

Дефектоскопия

№ 11

2019

Е.Г. Базулин, Д.А. Коновалов

В отличии от изображения на рис. 2б, процедура выбеливания (рис. 4б) привела к уменьшению

амплитуды многих бликов структурного шума (в среднем примерно на 3 дБ), что позволило уве-

рено обнаружить три отражателя. Понятно, что в эхосигналах p^s в образце структурного шума

ε^s(r) отсутствуют импульсы, связанные с перерассеянием на структуре, и трех искомых точеч-

ных отражателях. Кроме того, алгоритм ЦФА не учитывает эффект многократного перерассея-

ния. По этим двум причинам не удалось получить идеальный результат в виде трех бликов в

местах расположения отражателей с коэффициентом отражения -1,0. Вычитание эхосигналов

структурного шума по формуле (6) не позволило уменьшить уровень структурного шума

(рис. 4в).

1,0

0,9

0,8

0,7

Функции корреляции

0,6

отличаются на ≈10 %

0,5

0,4

0,3

0,2

0,1

0,2

0,1

-5 -4 -3

-2

-1

t, мкс

x, мм

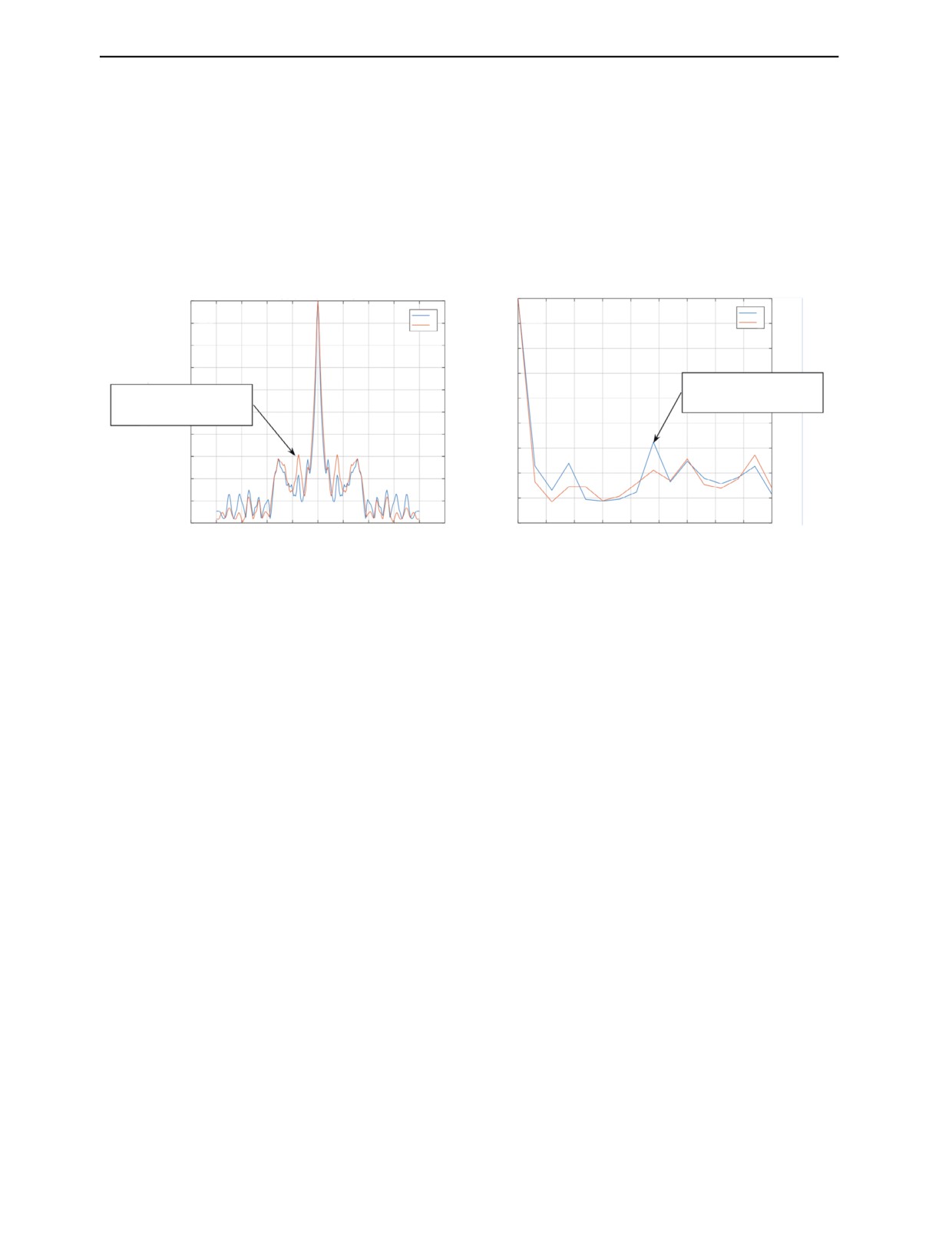
Рис. 5. Две временные корреляционные функции эхосигналов двух реализаций структурного шума (а), две простран-

ственные корреляционные функции эхосигналов восьмого выстрела (б).

На рис. 5, как и на рис. 3, приведены корреляционные функции эхосигналов (а) и эхосигна-

лов восьмого выстрела (б) для двух рассмотренных вариантов структурного шума ε^s(r) и ε^с(r) =

= ε^s(r + ∆r). Видно, что отличие между корреляционными функциями приблизительно 10 %.

Таким образом, можно утверждать, что при максимальном различии функций корреляций около

10 % работа метода выбеливания достаточно эффективна.

5. ВЫБЕЛИВАНИЕ РЕВЕРБЕРАЦИОННОГО ШУМА

Реверберационный шум возникает из-за того, что зондирующий сигнал, проходя границу

«призма-объект контроля», частично отражается обратно в призму и после многократных отра-

жений регистрируется элементами АР. Импульсы реверберационного шума обычно довольно

статичны и один из стандартных методов борьбы с ним заключается в простом вычитании

шаблона реверберационного шума из измеренных эхосигналов. Однако такой метод становится

неэффективным для случая, когда реверберационный шум меняется при сканировании антенной

решеткой, например, из-за изменения качества акустического контакта.

При проведении модельного эксперимента использовался ЦФА-дефектоскоп «АВГУР АРТ»,

разработанный и изготавливаемый «Научно-производственным центром неразрушающего кон-

троля «ЭХО+» [24]. Для регистрации эхосигналов использовалась АР (5 МГц, 32 элемента, раз-

мер пьезоэлемента 0,9×10 мм, зазор между пьезоэлементами 0,1 мм), установленная на рексоли-

товую призму с углом наклона 35 град. На рис. 6а представлены ЦФА-изображения границы

отверстия бокового сверления диаметром 2,0 мм с центром на глубине 12,0 мм в стальном

образце толщиной 18,0 мм, восстановленные на поперечной волне по исходным эхосигналам. На

изображениях, восстановленных по выбеленным эхосигналам, уровень реверберационного

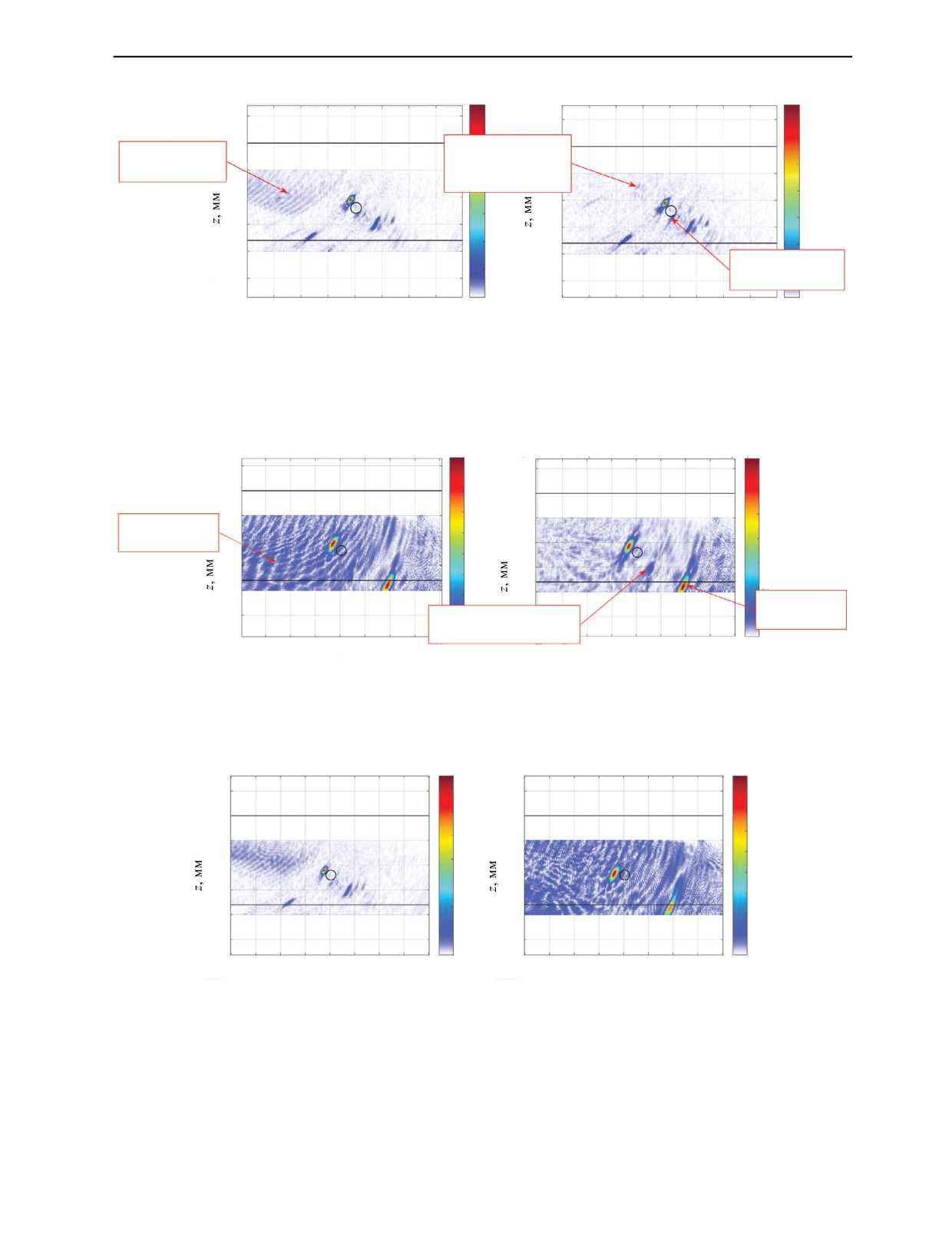
шума уменьшился примерно на 12 дБ (рис. 6б).

На рис. 7а показано ЦФА-изображение, восстановленное на продольной волне по исходным

эхосигналам, а на рис. 7б — по выбеленным эхосигналам. На изображениях, восстановленных по

выбеленным эхосигналам, уровень реверберационного шума также уменьшился примерно на 12 дБ.

Дефектоскопия

№ 11

2019

Применение процедуры «выбеливания» эхосигналов ...

1,4

–5

-5

1,2

Блик при

Реверберацион-

трансформации

ный шум

типа волны

на отверстии

0,8

1,5

0,6

0,4

Блик релеевской

0,5

волны обегания

–15 -10 -5

-20 -15 -10 -5

x, мм

Рис. 6. ЦФА-изображения, восстановленные на поперечной волне по исходным эхосигналам (а) и по выбеленным (б).

–5

0,35

-5

0,3

0,25

Реверберацион-

0,2

ный шум

0,15

0,1

Блик

Блик при

поперечной

трансформации типа

волны

волны на отверстии

-15 -10 -5

-10 -5

15 20

x, мм

Рис. 7. ЦФА-изображения, восстановленные на продольной волне по исходным эхосигналам (а) и по выбеленным (б).

–5

3,5

-5

2,5

1,5

0,5

-20 -15 -10 -5

x, мм

Рис. 8. ЦФА-изображения, восстановленные на поперечной волне (а) и на продольной волне (б) по эхосигналам, после

вычитания шаблона реверберационного шума.

На рис. 8 показаны ЦФА-изображения, восстановленные по эхосигналам, после вычитания из

них шаблона реверберационного шума. На рис. 8а показано изображение, восстановленное на

поперечной волне, а на рис. 8б — на продольной. Видно, что они практически не отличаются от

исходных изображений, представленных на рис. 6а и 7а.

Дефектоскопия

№ 11

2019

Е.Г. Базулин, Д.А. Коновалов

Таким образом, метод выбеливания позволил уменьшить уровень слабо меняющегося

реверберационного шума. Это стало возможным благодаря тому, что корреляционные функ-

ции реверберационного шума для разных положений АР отличаются друг от друга меньше,

чем на 10 %.

6. ВЫВОДЫ

Таким образом, по результатам исследований, изложенных в данной статье, можно сделать

следующие выводы:

1. Основная проблема эффективного применения процедуры выбеливания по формуле (9) —

знание корреляционной матрицы R: использование функции корреляции одной реализации

структурного шума ε^s(r) для выбеливания эхосигналов для другой реализации ε^c(r) с одинаковы-

ми средними размерами зерна δ^c = δ^s не привело к уменьшению структурного шума, так как кор-

реляция функций R(ε^s(r)) и R(ε^c(r)) двух реализаций структурного шума отличались друг от друга

более, чем на 20 %.

В случае различия функций корреляции двух реализаций структурного шума менее, чем на

10 %, метод выбеливания в численном эксперименте позволил увеличить отношение сигнал/шум

примерно на 3 дБ.

2. Возможно, что для сварных соединений, в которых их структура меняется плавно вдоль

соединения, процедура выбеливания окажется достаточно эффективной.

3. Процедуру выбеливания эхосигналов можно применять для уменьшения слабо меняющего-

ся реверберационного шума.

СПИСОК ЛИТЕРАТУРЫ

1. Качанов В.К., Карташев В.Г., Соколов И.В., Воронкова Л.В., Шалимова Е.В. Структурный шум в

ультразвуковой дефектоскопии. М.: Издательский дом МЭИ, 2016. 180 с.

2. Advances in Phased Array Ultrasonic Technology Applications. Publisher: Waltham, MA: Olympus

NDT, 2007. URL: http://www.olympus-ims.com/en/books/ (дата обращения: 04.12.2018).

3. Воронков В.А., Воронков И.В., Козлов В.Н., Самокрутов А.А., Шевалдыкин В.Г. О применимости

технологии антенных решеток в решении задач ультразвукового контроля опасных производственных

объектов // В мире неразрушающего контроля. 2011. № 1 (51). С. 64—70.

4. Базулин Е.Г. Сравнение систем для ультразвукового неразрушающего контроля, использующих

антенные решетки или фазированные антенные решетки // Дефектоскопия. 2013. № 7. С. 51—75.

5. Кремер И.Я. Пространственно-временная обработка сигналов. М.: Радио и связь, 1984. 224 с.

6. Фалькович С.Е. Оценка параметров сигнала. М.: Советское радио, 1970. 336 с.

7. Карташев В.Г., Качанов В.К., Шалимова Е.В. Основные положения теории пространственно-

временной обработки сигналов применительно к задачам ультразвуковой дефектоскопии изделий из

сложноструктурых материалов // Дефектоскопия. 2010. № 4. С. 19—29.

8. Ермолов И.Н. К вопросу о выборе оптимальных параметров эхо-метода ультразвуковой дефекто-

скопии // Дефектоскопия. 1965. № 6. С. 51—61.

9. Ермолов И.Н. Теория и практика ультразвукового контроля. М.: Машиностроение, 1981. 240 с.

10. Качанов В.К., Карташев В.Г., Соколов И.В., Туркин М.В. Проблемы выделения УЗ сигналов из

структурного шума при контроле изделий из сложноструктурных материалов // Дефектоскопия. 2007.

№ 9. С. 71—86.

11. Сайт про методы НК. URL: http://www.ntcexpert.ru/85-acenter/953-metody (дата последнего обра-

щения 04.12.2018).

12. Split-spectrum amplitude-decorrelation angiography with optical coherence tomography Yali Jia1, Ou

Tan, 2012 Optical Society of America.

13. Базулин Е.Г. Повышение отношения сигнал/шум при совместном использовании методов экс-

траполяции и расщепления спектра // Дефектоскопия. 2006. № 1. С. 68—78.

14. Базулин Е.Г., Вопилкин А.Х., Тихонов Д.С. Повышение достоверности ультразвукового контроля.

Часть 2. Повышение отношения сигнал/шум // Контроль. Диагностика. 2015. № 9. C. 10—27.

15. Козлов В.Н., Самокрутов А.А., Яковлев А.В., Шевалдыкин В.Г., Ковалев А.В. Акустическая В- и

С- томография крупноструктурных материалов импульсным эхо-методом // Приборы и системы управ-

ления. 1989. № 7. С. 21—23.

16. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1986. 288 с.

17. Тяпкин В.Н., Фомин А.Н. Основы построения радиолокационных станций радиотехнических

войск. Красноярск: СФУ, 2011. 536 с.

18. Бердышев В.П., Гарин Е.Н., Фомин А.Н. и др. Радиолокационные системы / Учебник. Под общ.

ред. В.П. Бердышева. Красноярск: Сибирский федеральный университет, 2011. 400 с.

19. Баданис К.А., Иоанидес П.И. Введение в смарт антенны. М.: Техносфера, 2012. 200 с.

Дефектоскопия

№ 11

2019