УДК 620.179.14
ИЗМЕРЕНИЕ МАГНИТНОЙ ПРОНИЦАЕМОСТИ МОНОЛИТНЫХ
КОЛЬЦЕВЫХ МЕР В ПЕРЕМЕННОМ МАГНИТНОМ ПОЛЕ
© 2019 г. В.А. Сясько1,*, С.С. Голубев2, Я.Г. Смородинский3, 4, П.В. Соломенчук5,
Е.Б. Брюховецкая5
1Горный университет, Россия 199106 Санкт-Петербург, Васильевский остров, 21 линия, 2
2Росстандарт, Россия 109074 Москва, Китайгородский пр., 7, стр. 1
3Институт физики металлов имени М.Н. Михеева УрО РАН, Россия
620108 Екатеринбург, ул. С. Ковалевской, 18
4Уральский федеральный университет имени первого Президента России Б.Н. Ельцина, Россия 620002
Екатеринбург, ул. Мира, 19
5ФГУП ВНИИМ им. Д.И. Менделеева, Россия 190005 Санкт-Петербург, Московский пр-т, 19
*E-mail: 9334343@gmail.com
Поступила в редакцию 10.06.2019; после доработки 25.07.2019
Принята к публикации 16.08.2019
Описывается методика измерения относительной магнитной проницаемости монолитных электропроводящих коль-
цевых образцов в переменном магнитном поле частотой от 50 Гц до 5 МГц, с применением тороидальных обмоток,
намотанных на них. Обозначены причины существенного влияния удельной электрической проводимости образцов на
результаты измерения. В предложенной методике применяется поправочный коэффициент, зависящий от величины
удельной электрической проводимости образца и определяемый по двумерной градуировочной таблице, полученной
при конечно-элементном моделировании данной задачи измерения, с учетом отклонения геометрических размеров изме-
ряемого образца от размеров образца конечно-элементной модели.
Ключевые слова: магнитная проницаемость стали в переменном магнитном поле, кольцевые образцы с тороидаль-
ной обмоткой, конечно-элементное моделирование.
DOI: 10.1134/S0130308219110058
Измерение магнитной проницаемости μ ферромагнитных металлов и сплавов необходимо для
расчета параметров любых электрических машин, использующих магнитопроводы или ферромаг-
нитные сердечники. Помимо этого, параметры ферромагнитных металлов и сплавов необходимо
контролировать во всех задачах неразрушающего контроля (НК), где возникает взаимодействие
магнитного поля и объекта контроля, в частности, при измерении толщины покрытий, наносимых
на ферромагнитные металлы, магнитными и вихретоковыми методами [1].
Существует несколько методов измерения μ в постоянном магнитном поле [2—4] и в перемен-
ных магнитных полях [5, 6]. Существует оборудование, позволяющее проводить измерение маг-
нитных характеристик магнитомягких материалов в низкочастотном синусоидальном [7], линейно
нарастающем [8] и импульсном [9] переменном магнитном поле. Также известны методы измере-
ния магнитных параметров ферромагнитных неэлектропроводящих материалов (ферритов и т.п.)
[10, 11]. Методы измерения μ в переменном магнитном поле необходимы в первую очередь для НК
листовых металлов и шихтованных ферромагнитных сердечников, применяемых в электрических
машинах и аппаратах. Особенностью всех перечисленных методов является ограниченность их
применения (при относительно низких частотах магнитного поля или для шихтованных сердечни-
ков, составленных из относительно тонких листов металла). При необходимости измерения μ
металлов, которые изготавливаются не в виде тонких пластин, а в виде монолитных прутков и
относительно толстых листов, необходимо изготавливать из контролируемого металла шихтован-
ные образцы, составленные из тонких кольцевых образцов, что очень трудоемко и увеличивает
погрешность измерения μ.
В качестве основы для предлагаемой методики измерения μ металлов взят мостовой метод,
предназначенный для измерения магнитных параметров ферритов, описанный в [10, п. 2.1]. Этот
метод применим для измерения магнитных параметров неэлектропроводящих материалов при
частоте магнитного поля от 10 кГц до 1 МГц и предполагает проведение измерения магнитных
параметров кольцевых образцов, на которые наматывается тороидальная обмотка, подключаемая
к источнику переменного тока.
Для рассматриваемого случая вносимая индуктивность L′ тороидальной обмотки будет равна
L′ = Lx - LXX,
(1)
46
В.А. Сясько, С.С. Голубев, Я.Г. Смородинский и др.
где Lx — измеренное значение индуктивности тороидальной обмотки, намотанной на измеряемый
образец из ферромагнитного металла, LXX — измеренное значение индуктивности тороидальной
обмотки, намотанной на образец той же формы и размеров, но изготовленный из неферромагнит-
ного неэлектропроводящего материала. При этом в соответствии с [10] L′ связана с μ (действи-
тельной составляющей относительной магнитной проницаемости материала кольцевого образца)
соотношением
7
L′⋅D
⋅10
г
µ=
+1,
(2)
2
4⋅S⋅W
где W — число витков обмотки, намотанной на кольцевой образец; Dг — гармонический диаметр
измеряемого образца, равный
D -D
н
в
D
=
,
(3)
г
D
н
ln
D
в
где Dн — наружный диаметр кольцевого образца; Dв — внутренний диаметр кольцевого образца
высотой h, а S — площадь его сечения.
D -D
н
в
S
=
⋅
h
(4)
2
Кольцевая форма измеряемого образца предпочтительна, т.к. при его намагничивании с при-
менением равномерной тороидальной обмотки практически не возникают поля рассеяния, искажа-
ющие результаты измерения. Точность измерений может быть близка к теоретическому пределу.
Как известно, значение μ зависит от частоты магнитного поля, в связи с чем необходимо учиты-
вать ее изменение в интересующем нас диапазоне частот применительно к рассматриваемой задаче
измерений.
Основным недостатком рассматриваемого метода является то, что если материал кольцевого
образца имеет существенную удельную электрическую проводимость, то в нем образуются вих-
ревые токи, искажающие результаты измерений. В случае измерения ферромагнитных металлов,
например, стали, пренебречь влиянием вихревых токов в инженерных расчетах можно только при
частоте магнитного поля не более 10 Гц [6]. При больших частотах магнитного поля необходимо
учитывать влияние вихревых токов на результаты измерений.
Как было указано выше, под воздействием вихревых токов происходит вытеснение первичного
магнитного поля, тем самым происходит уменьшение эффективной площади сечения образца, в
котором накапливается магнитное поле.
Для анализа влияния вихревых токов на результаты измерений в среде моделирования Ansoft
Maxwell была построена конечно-элементная модель (КЭ модель) кольцевого образца с намотан-
ной на него тороидальной обмоткой (рис. 1).
Рис. 1. Конечно-элементная модель кольцевого образца с намотанной на него тороидальной обмоткой.
Дефектоскопия
№ 11
2019
Измерение магнитной проницаемости монолитных кольцевых мер...
47
Размеры кольцевого образца заданы переменными значениями для определения степени их
влияния на результаты измерения, тороидальная обмотка задана замкнутой с заданным током воз-
буждения в сечении одного из витков. Для повышения точности вычислений по всей поверхности
кольцевого образца задана поверхностная сетка конечных элементов с уменьшенным размером
ячейки. Генерация сетки с загрублением внутри кольцевого образца и пошаговое учащение сетки
производится штатными алгоритмами, количество адаптивных шагов задано одинаковым для всех
решений - 7 шагов. Выходными параметрами модели является индуктивность и активное сопро-
тивление обмотки.
В модели производился расчет индуктивности и активного сопротивления обмотки, намотан-
ной на кольцевой образец. Анализ результатов моделирования показал, что влияние вихревых
токов на результаты измерения µ имеет множество составляющих (источников), причем на часто-
тах порядка нескольких мегагерц превалирующими составляющими становятся такие, как толщи-
на изоляции провода и плотность укладки обмотки на поверхность образца (зазор между проводом
и поверхностью образца). Очевидно, что учесть эти технологические параметры в аналитическом
расчете сложно и нерационально.
Для решения данной задачи была разработана методика измерений и построена градуировоч-
ная характеристика с использованием КЭ модели, учитывающая влияние вихревых токов.
В соответствии с предлагаемой методикой, вычисление μ′ (действительной составляющей
относительной магнитной проницаемости с учетом влияния вихревых токов) производится по
формуле:
7
L′⋅D
⋅10
г
µ′=
+1
⋅k,
(5)
2
4⋅S⋅W
где k — коэффициент, учитывающий влияние вихревых токов, зависящий от μ, σ, f, а также от гео-
метрических размеров кольцевого образца и технологических параметров тороидальной обмотки.
Для ограничения числа возможных решений, фиксированными принимаются геометрические
размеры кольцевого образца (Dн = 20 мм, Dв = 6 мм, h = 8,5) и технологические параметры торои-
дальной обмотки, соответствующие требованиям, изложенным в [10]. Неоднородность намагни-
чивания кольцевого образца оказывает влияние на результат измерений и учитывается в вычисля-
емом коэффициенте k как одна из его неотъемлемых составляющих. Для указанных условий
выполнен расчет КЭ модели с массивом параметров μКЭ, σКЭ, f в интересующих диапазонах каж-
дого из параметров:
μКЭ от 1 до 10000 с шагом по 10 отсчетов на декаду (41 отсчет на заданный диапазон, распре-
деленные приближенно линейно на логарифмической шкале);
σКЭ от 1 до 10 МСм/м с шагом по 10 отсчетов на декаду (11 отсчетов на заданный диапазон,
распределенные приближенно линейно на логарифмической шкале);
f принимает значения 50, 500 Гц, 5, 50, 500 кГц, 5 МГц.
Полученный массив данных, разделенный на группы по частотам f магнитного поля, исполь-
зуется в математическом модуле (на основе Excel) двумерной градуировки, где производятся
вычисления и построение градуировочной характеристики по описанному ниже алгоритму.
По (2) вычисляется значение μ для каждого решения КЭ модели, после чего вычисляется
поправочный коэффициент k как
µ
КЭ
k
=
,
(6)
µ
где μКЭ — задаваемое в КЭ модели значение относительной магнитной проницаемости материала
кольцевого образца.
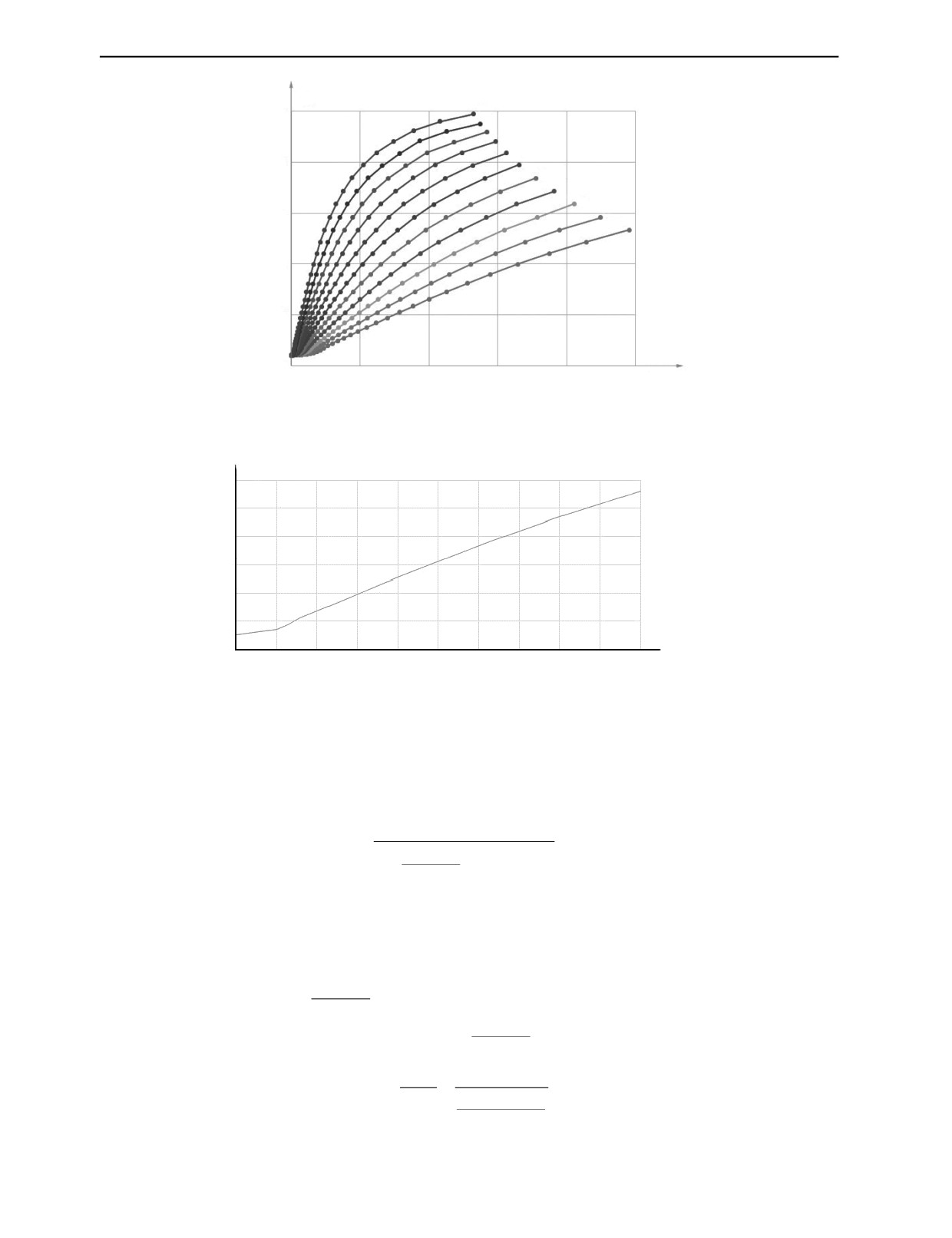
Далее строится группа функций k(L′) для каждого значения σКЭ (рис. 2). Для каждой функции
k(L′) строится градуировочная характеристика, основанная на методе кусочно-линейной интерпо-
ляции.
По результатам физических измерений значений Lx и LXX по (1) вычисляется значение L′.
Используя полученное значение L′ и набор градуировочных характеристик k(L′) вычисляется груп-
па значений k для каждого значения σКЭ. Строится функция k(σКЭ) для полученного массива дан-
ных (рис. 3).
Для каждой функции k(σКЭ) строится градуировочная характеристика второго уровня, основан-
ная на методе кусочно-линейной интерполяции.
Используя измеренное значение σ кольцевого образца, определяется значение k для измеряемо-
го кольцевого образца.
Дефектоскопия
№ 11
2019
48
В.А. Сясько, С.С. Голубев, Я.Г. Смородинский и др.
25
1
23 4
20
56
7
8
9
15
10
11
10
5
L′, Гн
0
0
0,0005
0,001
0,0015
0,002
0,0025
Рис. 2. Группа функций k(L′) для каждого значения σКЭ, МСм/м:
1 — 10; 2 — 7,943; 3 — 6,31; 4 —5,012; 5 — 3,981; 6 —3,162; 7 —2,512; 8 — 1,995; 9 — 1,585; 10 — 1,259; 11 — 1.
k, у.е.
12
10
8
6
4
2
σКЭ, МСм/м
00
1
2
3
4
5
6
7
8
9
10
Рис. 3. Функция k(σКЭ).
КЭ модель построена с учетом номинальных геометрических размеров кольцевого образца.
Для учета отклонений геометрических размеров реального кольцевого образца от номинальных
значений в (5) необходимо добавить поправочные коэффициенты:
7
L′⋅D ⋅a⋅10
г
µ′′=
+1⋅k,
(7)
н
D -D
в
2
4⋅
⋅b⋅h⋅c⋅W
2
где μ′′ — значение действительной составляющей относительной магнитной проницаемости с
учетом влияния вихревых токов и допусков на геометрические размеры кольцевых образцов; a, b,
c — коэффициенты, учитывающие отношение геометрических размеров реального кольцевого
образца к геометрическим размерам образца в КЭ модели и характеризующие соотношение раз-
D -D
н
меров, соответственно Dг,
в и h, вычисляемые по формулам (8) — (10):
2
D -D
н
в
D
н
ln
D
D
г
в
a
=
=
,
(8)
D
нКЭ
D -D
вКЭ
гКЭ
D
нКЭ
ln
D
вКЭ
Дефектоскопия
№ 11
2019
Измерение магнитной проницаемости монолитных кольцевых мер...
49
D -D
н
в
2
b
=
,
(9)
D -D
нКЭ
вКЭ
2
h
c
=
,
(10)
hКЭ
где DгКЭ, DнКЭ, DвКЭ, hКЭ — геометрические размеры кольцевого образца в КЭ модели.
Использование коэффициентов k, a, b и c вместо значения μ при работе по градуировочными
характеристиках обусловлено тем фактором, что размеры физически изготовленных образцов
имеют допуски и при проведении серии измерений потребовалось бы проведение серии вычисле-
ний аналогичных КЭ моделей, что занимает существенное количество времени (сотни часов
машинного времени для каждого размера кольцевого образца). Очевидно, что изменение размера
образца, в пределах технологического допуска на его изготовление, окажет соответствующее вли-
яние на результат измерений по формуле (2), однако значение поправочного коэффициента изме-
нится ничтожно мало. По этой причине для всех кольцевых образцов с номинальными значениями
геометрических размеров, в пределах технологических допусков, используется одна и та же КЭ
модель, один и тот же коэффициент k, но различные коэффициенты a, b и c.
Непосредственное измерение значения σ кольцевого образца невозможно. По этой причине
для проведения измерений по описываемой методике (помимо кольцевого образца из измеряемого
материала) из той же заготовки изготавливается образец для измерения σ. Измерение производит-
ся по методу ван дер Пау [13], а форма образца и условия измерений должны соответствовать
требованиям, описанным в [1, 14, 15].
При проведении измерений μ по описываемой методике следует учитывать тот факт, что μ
нелинейно зависит от индукции магнитного поля в образце. Результаты данного исследования
предназначены для их использования в неразрушающем контроле металлопродукции вихретоко-
выми и магнитными методами с использованием очень слабых магнитных полей. В таких услови-
ях можно утверждать, что значение μ соответствует значению μнач (соответствующего напряжен-
ности внешнего магнитного поля Н → 0) для наиболее часто применяемых в промышленности
сталей и является постоянной величиной. В связи с этим, в КЭ модели сделано допущение о том,
что значение μ является постоянным.
В рассматриваемой методике спорным является тот факт, что ключевым звеном, определяю-
щим точность измерений, является не допускаемая погрешность используемых средств измере-
ний, а допускаемые отклонения результатов измерений, полученных в КЭ модели, от действитель-
ных значений. В настоящее время не существует аттестованных методик оценки метрологических
характеристик КЭ моделей. Опыт применения КЭ моделирования показывает, что при должном
подходе к построению КЭ модели и при использовании для расчета ЭВМ с достаточными ресур-
сами (в первую очередь объемом оперативной памяти) допускаемые отклонения результатов изме-
рений, проведенных с использование КЭ модели, могут укладываться в интервал 0,1 %, что под-
тверждается при проведении измерений с применением реальных измерительных приборов.
Для экспериментального исследования описываемой методики были изготовлены кольцевые
образцы из сталей, часто используемых в промышленности: Ст. 20, Р6М5, 40Х, а также из преци-
зионного сплава 81НМА (после термообработки), обладающего высокой магнитной проницаемо-
стью в магнитных полях с малой индукцией. На кольцевые образцы проводом литцендратом марки
ЛЭШО были намотаны тороидальные обмотки с количеством витков 40, а концы провода сплете-
ны на длину 100 мм.
Для измерения удельной электрической проводимости указанных металлов были изготовлены
соответствующие образцы и контактная оснастка [1]. Внешний вид кольцевого образца без обмот-
ки, образца с намотанной на него тороидальной обмоткой, а также образца для измерения удель-
ной электрической проводимости приведены на рис. 4.
Удельную электрическую проводимость измеряли по методу ван дер Пау с применением ла-
бораторного источника тока, мультиметра Gwinstek GDM-8245 (в режиме измерения силы тока)
и нановольтметра Keysight 34420A, а индуктивность тороидальных обмоток — с применением
анализатора иммитанса Wine Kerr WK65120P на частотах 50 и 500 Гц, 5, 50 и 500 кГц, а также
5 МГц (соответствующих частотам, используемым в КЭ модели). Сила тока возбуждения составляла
10 мА. Результаты измерений приведены в табл. 1.
Дефектоскопия
№ 11
2019
50
В.А. Сясько, С.С. Голубев, Я.Г. Смородинский и др.
Рис. 4. Внешний вид образцов для измерения удельной электрической проводимости, кольцевых образцов без обмотки
и с намотанными на них тороидальными обмотками.
Таблица
1
Измеренное значение μ′′ — действительной составляющей относительной магнитной проницаемости с учетом
влияния вихревых токов и допусков на геометрические размеры кольцевых образцов
Материал кольцевого образца
Р6М5
40Х
Ст. 20
81НМА
σ, МСм/м
2,38
4,27
5,11
1,22
50 Гц
60,47
50,82
116,5
15865
500 Гц
54,86
45,79
106,8
11264
5 кГц
49,92
41,21
87,43
4388
50 кГц
36,80
27,58
47,68
1077
500 кГц
15,89
10,68
15,65
207
5 МГц
1,995
1,48
1,617
16
Результатом данной работы является методика и технология измерения относительной маг-
нитной проницаемости ферромагнитных электропроводящих материалов (сталей) с примене-
нием монолитных кольцевых образцов при частоте магнитного поля от 50 Гц до 5 МГц. Дан-
ная методика и оборудование применяются в составе опытного образца распределенного эта-
лонного комплекса свойств металлических покрытий, разрабатываемого в рамках государ-
ственного контракта на выполнение опытно-конструкторской работы в области обеспечения
единства измерений для обеспечения нужд Федерального агентства по техническому регули-
рованию и метрологии, для определения электрических и магнитных свойств оснований мер
свойств покрытия.
Работа выполнена в рамках государственного задания Минобрнауки России (тема «Диагности-
ка», № АААА-А18-118020690196-3).
СПИСОК ЛИТЕРАТУРЫ
1. Syas'ko V.A. , Golubev S.S., Smorodinskii Ya. G. Measurement of Electromagnetic Parameters of Metal-
[Сясько В.А., Голубев С.С., Смородинский Я. Г. и др. Измерение электромагнитных параметров мер
толщины металлических покрытий // Дефектоскопия. 2018. № 10. С. 25—36.]
2. ГОСТ 8.377—80 ГСОЕИ Материалы магнитомягкие. Методика выполнения измерений при опре-
делении статических магнитных характеристик. М.: Изд-во стандартов, 1980. 26 с. Введен с 01.07.1981.
3. ГОСТ 12119.1—98 Сталь электротехническая. Методы определения магнитных и электрических
свойств. Методы измерения магнитной индукции и коэрцитивной силы в аппарате Эпштейна и на коль-
цевых образцах в постоянном магнитном поле. М.: Стандартинформ, 2003. 9 с. Введен с 01.07.1999.
4. ГОСТ 12119.2—98 Сталь электротехническая. Методы определения магнитных и электрических
свойств. Метод измерения магнитной индукции в пермеаметре. М.: Стандартинформ, 2003. 7 с. Введен
с 01.07.1999.
Дефектоскопия
№ 11
2019
Измерение магнитной проницаемости монолитных кольцевых мер...
51
5. ГОСТ 12119.6—98 Сталь электротехническая. Методы определения магнитных и электрических
свойств. Метод измерения относительной магнитной проницаемости и удельных магнитных потерь
мостом переменного тока. М.: Стандартинформ, 2003. 8 с. Введен с 01.07.1999.
6. ГОСТ 18334—73 Материалы магнитомягкие. Методы испытаний в диапазоне частот 50 Гц —
10 кГц. Не действует с 01.01.1979.
7. Матюк В.Ф., Осипов А.А. Установка УИМХ для измерения магнитных характеристик магнито-
мягких материалов и изделий // Дефектоскопия. 2007. № 3. С. 12—25.
8. Мельгуй М.А., Осипов А.А. Установка для измерения динамических и квазистатических магнит-
ных характеристик // Дефектоскопия. 1991. № 3. C. 34—39.
9. Дидик Ю. И., Корзунин Г. С., Дидик М.Ю. Установка для измерения магнитных свойств магнито-
мягких материалов в импульсном режиме намагничивания // Дефектоскопия. 2001. № 7. С. 13—24.
10. ГОСТ 12635—67 Материалы магнитомягкие высокочастотные. Методы испытаний в диапазоне
частот от 10 кГц до 1 МГц. М.: Изд-во стандартов, 1967. 40 с. Введен с 01.01.1969.
11. ГОСТ 12636—67 Материалы магнитомягкие высокочастотные. Методы испытаний в диапазоне
частот от 1 до 200 МГц. М.: Изд-во стандартов, 1967. 25 с. Введен с 01.01.1969.
12. ГОСТ 12637—67 Материалы магнитомягкие высокочастотные. Методы испытаний в диапазоне
частот от 200 до 2000 МГц. М.: Изд-во стандартов, 1967. 26 с. Введен с 01.01.1969.
13. van der PAUW L.J. A method of measuring specific resistivity and Hall Effect of discs of arbitrary
shape // Philips Research Reports, 1958. V. 13. No. 1—9.
14. Thompson A.M. and Lampard D.G.. A new theorem in electrostatics and its application to calculable
standards of capacitance // Natue. 1956. V. 177. P. 888.
15. Соломенчук П.В., Смирнова Н.И. Измерение удельной электрической проводимости цветных
металлов, приборы и средства метрологического обеспечения // В мире НК. 2017. № 3. С. 54—57.
Дефектоскопия
№ 11
2019