Радиационные методы
УДК 620.179.15
ОСОБЕННОСТИ РАСПОЗНАВАНИЯ МАТЕРИАЛОВ
МУЛЬТИЭНЕРГЕТИЧЕСКИМ РЕНТГЕНОВСКИМ МЕТОДОМ
© 2019 г. С.П. Осипов1,*, Е.Ю. Усачев2, С.В. Чахлов1,**, С.А. Щетинкин2, О.С. Осипов3
1Национальный исследовательский Томский политехнический университет, Россия 634028 Томск,
пр-т Ленина, 30
2МИРЭА — Российский технологический университет, Россия 119454 Москва, пр-т Вернадского, 78
3Сольвейг Мультимедиа, Россия 634055 Томск, пр-т Развития, 3
E-mail: *osip1809@rambler.ru; **chakhlov@tpu.ru
Поступила в редакцию 21.12.2018; после доработки 21.01.2019;
принята к публикации 01.02.2019
Рассмотрены особенности распознавания материалов объектов контроля и их структурных фрагментов методом
мультиэнергий. Показан подход к комплексному использованию метода линий уровней и метода мультиэнергий, пред-
назначенный для повышения точности оценки эффективного атомного номера. Приведен алгоритм формирования и
обработки информации в методе мультиэнергий, позволяющий измерить эффективный атомный номер и массовую
толщину фрагментов объекта контроля с высокой точностью. Методом имитационного моделирования продемонстри-
рована эффективность применения анализируемого способа распознавания материалов.
Ключевые слова: досмотровый контроль, рентгеновское излучение, мультиэнергетическая цифровая радиография,
метод дуальных энергий, распознавание материалов.
DOI:10.1134/S0130308219040079
ВВЕДЕНИЕ
Повышение уровня безопасности перевозок всеми видами транспорта продолжает оставать-
ся важнейшей проблемой, стоящей перед современным обществом. Пресечение перевозки запре-
щенных или незадекларированных товаров является одной из наиболее важных целей, стоящих
перед рентгеновскими досмотровыми системами с функциями распознавания материалов объек-
тов контроля (ОК) и их структурных фрагментов. Основным параметром распознавания материала
является его эффективный атомный номер. Для его оценки широко используется метод дуальных
энергий (МДЭ) [1—4]. Этот метод базируется на различии зависимостей массовых коэффициентов
ослабления (МКО) гамма-излучения с веществом для основных видов взаимодействия от эффек-
тивного атомного номера. Для низких энергий рентгеновского излучения превалирующими эффек-
тами взаимодействия излучения с веществом являются фотоэффект, эффект Комптона, для высо-
ких энергий — эффекты Комптона и рождения пар.
Можно выделить два способа классификации реализаций МДЭ. Первый связан с оценивае-
мыми параметрами ОК и с соответствующими алгоритмами обработки первичной информации.
Второй определяется технической реализацией метода.
Рассмотрим первый способ классификации реализаций МДЭ. Измеренные параметры ослабле-
ния для двух различных эффективных энергий поглощенного рентгеновского излучения являются
основой для оценки двух параметров МДЭ или двух параметров объекта контроля [5—7]. Параме-
тры МДЭ определяются в реализациях метода, в которых МКО ослабления излучения представ-
ляется в виде суммы МКО для двух превалирующих эффектов взаимодействия гамма-излучения с
веществом. Для этих реализаций один из параметров МДЭ пропорционален произведению толщи-
ны ОК в сантиметрах H на плотность его материала ρ в г/см2. Произведение ρH называют массовой
толщиной. Второй параметр МДЭ пропорционален произведению массовой толщины ОК — ρH
на функцию F от эффективного атомного номера материала ОК — Z. В системах досмотрового
контроля с функцией распознавания материалов параметры МДЭ являются промежуточными, они
служат для оценки Z. В другой группе реализаций МДЭ не осуществляется разделение эффек-
тов взаимодействия излучения с веществом, анализируется зависимость параметров ослабления
рентгеновского излучения непосредственно от параметров ОК ρH и Z.
Второй способ классификации позволяет разделить совокупность реализаций МДЭ на две груп-
пы. К первой группе относятся реализации, в которых исходные радиографические изображения
МДЭ для максимальных энергий рентгеновского излучения E1 и E2 формируются одним многока-
нальным радиометрическим детектором [6, 8]. Формирование изображений может осуществлять-
ся сканированием ОК щелевым пучком рентгеновского излучения методом «вперед—назад» или
44
С.П. Осипов, Е.Ю. Усачев, С.В. Чахлов и др.
с чередованием импульсов излучения с энергиями E1 и E2. Во второй группе оба изображения МДЭ
формируются за одно сканирование [8—10] с использованием детекторов с нежесткой энергети-
ческой дискриминацией, так как излучение регистрируется линейкой сэндвич-детекторов. Такие
детекторы состоят из двух радиационно-чувствительных объемов (РЧО) с регистрацией светового
излучения фотоприемниками. При этом РЧО расположены последовательно по направлению рас-
пространения излучения. Первый РЧО поглощает преимущественно низкоэнергетическую состав-
ляющую рентгеновского излучения, а второй — преимущественно высокоэнергетическую состав-
ляющую. Для повышения средней энергии фотонов, попадающих на фронтальную поверхность
второго РЧО, поток фильтруется.
Досмотровые системы с функцией распознавания материалов помимо производительности
характеризуются систематической погрешностью оценки эффективного атомному номеру DZ и
диапазонами изменения: массовой толщины ОК — (ρH)min ≤ ρH ≤ (ρH)max; эффективного атомного
номера — Zmin ≤ Z ≤ Zmax.
Качество распознавания материалов методом дуальных энергий существенным образом за-
висит от пар максимальных энергий рентгеновского излучения EL и EH. Объекты досмотрового
контроля имеют неопределенную структуру. Фрагменты ОК могут значительно отличаться по мас-
совой толщине ρH и эффективному атомному номеру Z. Подобрать в этом случае пару энергий E1
и E2, для которой одинаково качественно распознаются фрагменты с малой и большой массовой
толщиной и фрагменты с малым и большим значением эффективного атомного номера, является
сложной задачей. Следует также отметить, что негладкий характер зависимости МКО гамма-излу-
чения от Z при одновременной оценке массовой толщины ρH и эффективного атомного номера не
позволяет оценить Z с необходимой для практических приложений точностью. Способ определе-
ния Z методом линий уровней [1, 4, 6], основанный на измерении отношения коэффициентов осла-
бления для низких и высоких энергий рентгеновского излучения, компенсирует указанный фактор,
но не позволяет осуществить точную оценку Z на всей области изменения пары (ρH, Z).
Повышение эффективности методов распознавания материалов достигается с помощью различных
реализаций метода мультиэнергий (ММЭ) [11—16]. Формирование дополнительных радиографиче-
ских изображений происходит аналогично методу дуальных энергий. В литературе не в полной мере
рассмотрены особенности распознавания материалов ОК и его фрагментов методом мультиэнергий.
1. ОСНОВЫ РАСПОЗНАВАНИЯ МАТЕРИАЛОВ МЕТОДОМ МУЛЬТИЭНЕРГИЙ
Массовый коэффициент ослабления гамма-излучения m зависит от энергии фотонов E и эффек-
тивного атомного номера ослабляющего материала Z. Способы распознавания материалов методом
мультиэнергий и методом дуальных энергий основаны на существенном различии функций m(Z)
для разных диапазонов изменения энергий фотонов E. Для анализа зависимостей m(E, Z) с целью
выбора энергий фотонов используются базы данных по ослаблению гамма-излучения [17, 18], в
которых приведены МКО m или сечения взаимодействия s гамма-излучения с веществом.
Связь сечения взаимодействия гамма-излучения с веществом se (барн/электрон) с МКО m опи-
сывается выражением [17, 19]
s
(E,Z)ZN
e
A
m(E,Z)
=
=a(Z)s
e
(E,Z)N
A
,
(1)
M(Z)
здесь M(Z) — атомная масса элемента с атомным номером Z; NA — число Авогадро.
Для каждого химического элемента существует свой характерный уровень энергии гамма-излу-
чения, для которого вклад эффекта рентгеновской флуоресценции в общее сечение взаимодействия
гамма-излучения является значимым [20]. До этого уровня функция se(Z) имеет несколько локаль-
ных максимумов, что исключает возможность однозначной оценки Z. При превышении указанного
уровня функция se(Z) является монотонно возрастающей и может использоваться для однознач-
ной оценки Z.
Дискретная функция a(Z) = Z/M(Z) для Z∈{1; 2; 3; ... ; 91} далека от константы [17]. Для иллю-
страции на рис. 1 приведен график функции a(Z) [17].
Функцию a(Z) невозможно аппроксимировать непрерывной гладкой монотонной функцией,
что является ограничением для оценки эффективного атомного номера с высокой точностью мето-
дом мультиэнергий.
Классическая реализация ММЭ основана на просвечивании ОК пучками рентгеновского из-
лучения с различными значениями Emax∈ E = {E1, E2, …, El} и формировании первичных радио-
Дефектоскопия
№ 4
2019
Особенности распознавания материалов мультиэнергетическим рентгеновским методом
45
Рис. 1. Функция α(Z).
α(Z)
0,55
графических изображений ОК в цифровой
радиографии или проекций в компьютерной
томографии [13, 21—23]. Первичные радио-
0,45
графические изображения I1, I2, …, Il после
калибровок и преобразований трансформи-
руются в конечные изображения Y1, Y2, …,
Yl, представляющие собой матрицы одного
размера, элементы которых равны толщи-
0,35
нам ОК в длинах свободного пробега (д.с.п.)
2
12
22
32
42
52
62
72
82
92
Z
для соответствующих максимальных энер-
гий рентгеновского излучения.
1.1. Уравнения связи конечных изображений в ММЭ с параметрами ОК
Рассмотрим объект с массовой толщиной ρH из материала с эффективным атомным номером Z.
В этом случае для максимальной энергии Emax искомое уравнение, описывающее связь толщины ОК
в д.с.п. Y с параметрами объекта ρH и Z, имеет вид
Emax
g(E,E
)E
(E)ε(E)exp(-m(E,Z)rH)dE
∫
max
ab
0
Y(E
)
=-ln
,
(2)
max
E
max
g(E,E
)E
(E)ε(E)dE
∫
max
ab
0
здесь g(E, Emax) — распределение числа фотонов источника излучения по энергии; Eab(E) — энер-
гия, оставленная в детекторе зарегистрированным фотоном; ε(E) — эффективность регистрации
радиометрического детектора.
Система уравнений вида (2) для всех значений Emax∈E представляет собой совокупность урав-
нений связи конечных изображений в ММЭ с параметрами ОК.
1.2. Алгоритмы обработки информации в ММЭ
Реализации ММЭ отличаются по способу получения исходной информации и алгоритмами ее
обработки. Ниже рассмотрим две основных реализации.
Первая реализация является расширением реализации МДЭ Альвареса и Маковски [24—27].
Алгоритм обработки информации в этой реализации состоит из двух этапов. На первом этапе опре-
деляются вспомогательные параметры ММЭ, а на втором этапе — эффективный атомный номер
материала ОК Z и массовая толщина ОК ρH.
Во второй реализации непосредственно определяются два параметра ОК — Z и ρH. Поэтому
эту реализацию ММЭ можно назвать двухпараметрической.
1.2.1. Реализация Альвареса метода мультиэнергий
В реализации Альвареса ММЭ используется то, что взаимодействие гамма-фотонов с веще-
ством определяется несколькими эффектами [27, 28], например: рентгеновской флуоресценции;
фотоэлектрического поглощения; когерентного и некогерентного рассеяния; рождения пар. Каж-
дый из указанных эффектов значим для определенного диапазона энергий фотонов, зависящего от
атомного номера ослабляющего вещества.
В рассматриваемой реализации массовый коэффициент ослабления m для фотонов с энергией
E представляется в виде суммы
m(E,Z)
=a
(Z)
f
(E) +a
(Z)
f
(
E +...+a
(Z)
f
(E),
(3)
1
1
2
2
q
q
где q — количество значащих эффектов; fj(E), j = 1, q — функции от энергии, характеризующие
эффекты взаимодействия фотонов с веществом; aj(Z), j = 1, q — коэффициенты, зависящие от Z и
не зависящие от энергии фотонов.
Дефектоскопия
№ 4
2019
46
С.П. Осипов, Е.Ю. Усачев, С.В. Чахлов и др.
Отметим, что учет рентгеновской флуоресценции отличается сложностью, поэтому его в пред-
ставлении (3) учитывают при анализе ММЭ в области небольших уровней максимальных энергий
рентгеновского излучения.
После подстановки (3) в (2) получим уравнение связи параметров ММЭ Aj = aj(Z)ρH, j = 1…q
с толщиной ОК в д.с.п. Y для максимальной энергии Emax
E
max
q
f
(E,E
)E
(E)ε(E)exp(-
A
f
(E))dE
∫
max
ab
∑
j
j
0
j=1
Y(E
)
=-ln
(4)
max
E
max
f
(E,E
)E
(E)ε(E)dE
∫
max
ab
0
Сопоставим A1 с фотоэффектом, A2 — с когерентным рассеянием, A3 — с эффектом Комптона и
A4 — с эффектом рождения пар. Их связь с Z и ρH описывается выражениями:
A1 = a(Z)ZbρH, A2 = a(Z)ZρH, A3 = a(Z)ρH, A4 = a(Z)ZρH,
(5)
где a(Z) = Z/M(Z). Теоретическое значение параметра β для фотоэффекта равно 4, в литературе наи-
более часто используют β = 2,94 [29].
Параметры МДЭ с точностью до множителя a(Z) = Z/M(Z) совпадают с первой, третьей и чет-
вертой формулами из (5). Когерентное рассеяние в МДЭ выступает фактором, который приводит к
смещению оценки Z.
Из анализа выражений (5) следует, что для оценки эффективного атомного номера Z достаточно
определения одной из пар параметров ММЭ — A1, A3 или A3, A4. Для оцененной величины Z массо-
вая толщина ρH находится из формул (5).
В досмотровом контроле применяются источники рентгеновского излучения из трех диапазонов
[30—33]: малых максимальных энергий — от 50 до 300 кэВ; средних энергий — от 300 кэВ до 1 МэВ;
высоких энергий — от 1 до 10 МэВ. Использовать источники излучения из диапазона малых энер-
гий и высоких энергий для одного и того же ОК не представляется возможным из-за многократного
различия коэффициентов ослабления. Из анализа данных по ослаблению гамма-излучения можно
сделать вывод, что для диапазонов малых и средних максимальных энергий одновременно можно
оценить параметры A1, A2, A3, а для диапазона высоких энергий — A3, A4. Для диапазонов малых и
средних максимальных энергий значение l = 3, а для диапазона высоких энергий — l = 2.
Рассмотрим диапазоны малых и средних энергий рентгеновского излучения.
Практическая реализация процедуры оценки параметров ММЭ основывается на просвечива-
нии тестового объекта рентгеновским излучением с максимальными энергиями Emax из множества
E и формировании калибровочных функций Gi(A1, A2, A3) = Y(Ei), i = 1…3. Тестовый объект состоит
из фрагментов с различными характеристиками (ρH, Z), которые в соответствии с формулами (5)
определяют различные наборы параметров ММЭ (A1, A2, A3).
Система уравнений для оценки параметров ММЭ — Aj, j = 1…3 имеет вид
G
(A
,
A
, A
)
=Y
1
1
2
3
1
G
(A
,
A
, A
)
=Y
(6)
2
1
2
3
2
G
(
A
,
A
,
A
)
=Y
3
1
2
3
3
С формальной точки зрения система нелинейных параметрических уравнений (6) имеет един-
ственное решение [24, 27], если выполняется следующее условие:
∂G
(
A
, A
, A
)
∂G
(
A
, A
, A
)
∂G
(
A
, A
, A
)
1
1
2
3
1
1
2
3
1
1
2
3
∂A
∂
A
∂
A
1
2
3
∂G
(
A
, A
, A
)
∂G
(
A
, A
, A
)
∂G
(
A
, A
,
A
)
2
1
2
3
2
1
2
3
2
1
2
3
≠
0
(7)
∂
A
∂
A
∂
A
1
2
3
∂G
(
A
,
A
,
A
)
∂G
(
A
,
A
,
A
)
∂G
(
A
,
A
,
A
)
3
1
2
3
3
1
2
3
3
1
2
3
∂A
1
∂A
2
∂A
3
Система (6) при соблюдении условия (7) может быть решена [34] методами Ньютона, секущих
или наименьших квадратов.
Дефектоскопия
№ 4
2019
Особенности распознавания материалов мультиэнергетическим рентгеновским методом
47
1.2.2. Двухпараметрическая реализация метода мультиэнергий
Теоретической базой двухпараметрической реализации ММЭ является выражение (2) [29].
Практическое воплощение этой реализации основывается на предварительном формировании ка-
либровочных функций F1(ρH, Z) и F2(ρH, Z) для двух максимальных энергий рентгеновского из-
лучения E1, E2. Искомые оценки параметров ОК ρH и Z являются решением системы уравнений
F
(rH
,
Z
)
=Y
1
1
(8)
(rH
,
Z
)
=Y
F2
2
Условие существования и единственности решения системы (8) аналогично (7).
Тестовые образцы для формирования функций F1(ρH, Z), F2(ρH, Z) состоят из набора фрагмен-
тов, отличающихся по массовой толщине и атомному номеру материала.
Известно, что функции F1(ρH, Z) и F2(ρH, Z) не являются гладкими относительно Z, что связано
с характером описанной выше функции a(Z). Для уменьшения влияния функции a(Z) на качество
распознавания в досмотровых комплексах в качестве параметра распознавания Q используют от-
ношение толщин ОК в длинах свободного пробега [29, 35]
Q = Y1/Y2.
(9)
Из анализа выражения (9) с учетом (1) следует, что для источников моноэнергетического гам-
ма-излучения параметр распознавания Q не зависит от функции a(Z). На рис. 2 представлены гра-
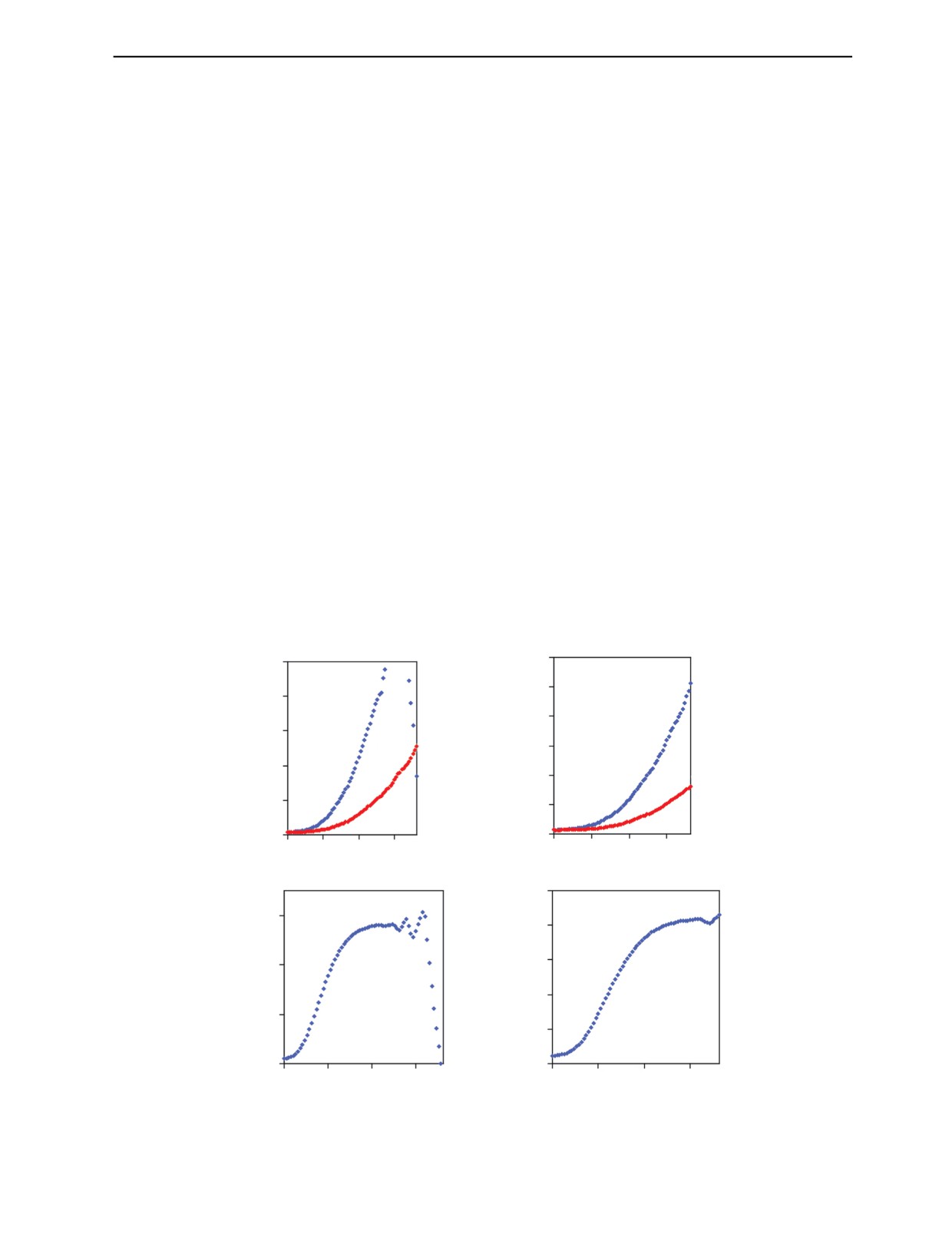
фики функций m(Z) и Q(Z) для различных пар энергий E1 и E2.
Из анализа данных, приведенных на рис. 2, можно сделать два основных вывода: подтверждается
негладкий характер функций m(Z) для различных энергий гамма-излучения; для любых пар энергий
гамма-излучения E1 и E2 существует интервал изменения Z — (Zmin, Zmax), для которого функция Q(Z)
гладкая и монотонно возрастающая. Этот интервал можно назвать интервалом монотонности. Из
второго вывода следует существование на описанном интервале обратной функции Q-1 (Z). С увели-
чением энергий E1 и E2 наблюдается существенное увеличение Zmax и меньшее увеличение Zmin.
Из вышесказанного следует вывод о необходимости использования ММЭ для точной оценки
эффективного атомного номера из широкого диапазона его изменения.
m, г/см2
10,0
m, г/см2
6,0
60 кэВ
5,0
100 кэВ
8,0
4,0
6,0
100 кэВ
3,0
4,0
2,0
150 кэВ
2,0
1,0
0,0
0,0
1
20
39
58 Z
1
20
39
58 Z
Q
Q
3,5
4,0
3,0
3,0
2,5
2,0
2,0
1,5
1,0
1,0
1
20
39
58 Z
1
20
39
58 Z
E
= 60 кэВ, E2 = 100 кэВ
E1 = 100 кэВ, E2 = 150 кэВ
1
Рис. 2. Функции m(Z), Q(Z) для гамма-излучения.
Дефектоскопия
№ 4
2019
48
С.П. Осипов, Е.Ю. Усачев, С.В. Чахлов и др.
Q
Q
2,0
2,5
3
3
1,8
2
2,0
2
1,6
1
1
1,4
1,5
1,2
1,0
1,0
1
20
39
58 Z
1
20
39
58 Z
E1 = 100 кэВ, E2 = 150 кэВ
E1 = 160 кэВ, E2 = 250 кэВ
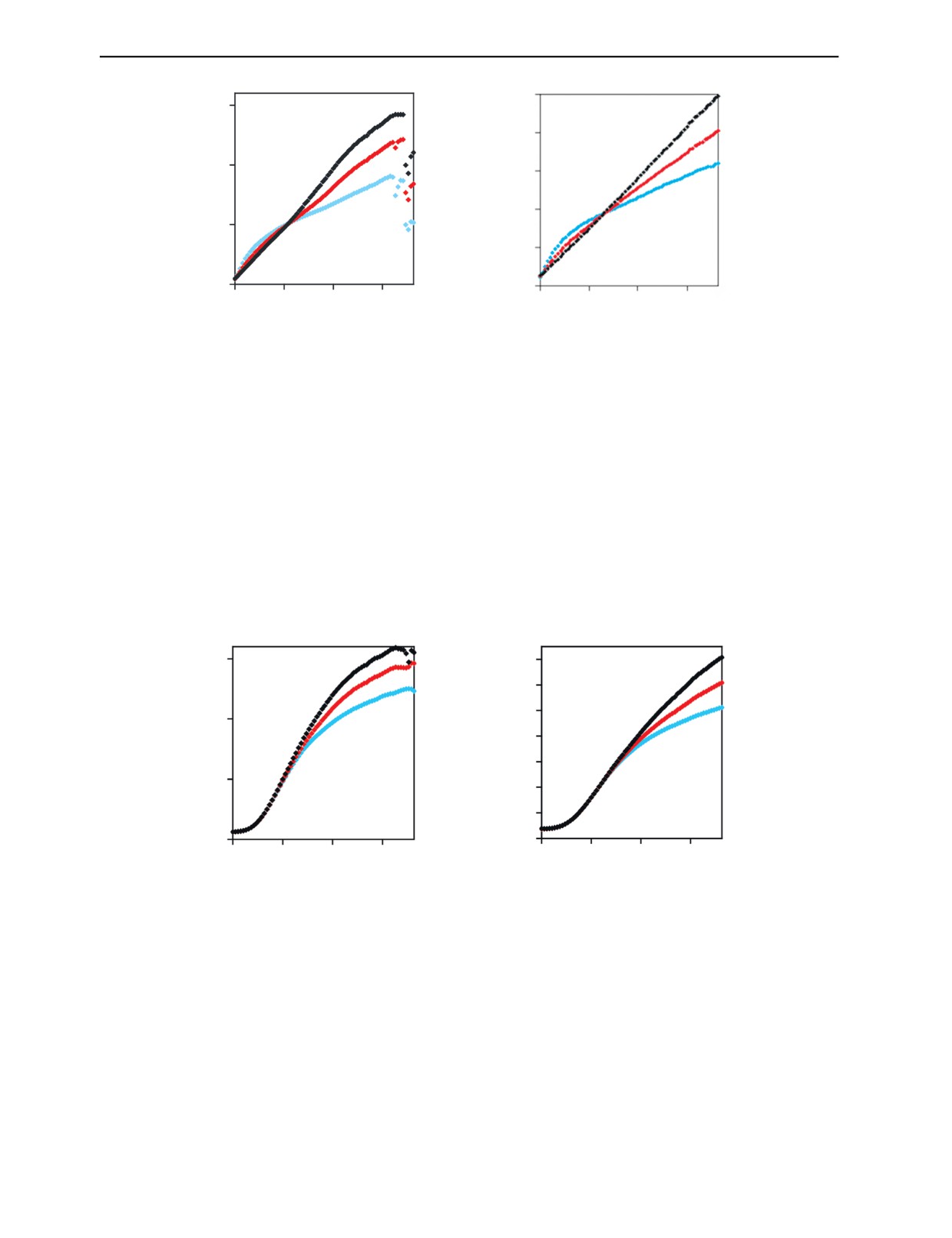
Рис. 3. Функции Q(Z):
1 — ρH = 2 г/см2; 2 — ρH = 5 г/см2; 3 — ρH = 10 г/см2.
С целью проверки обоснованности выводов и следствий из них для источников рентгенов-
ского излучения были рассчитаны функции Q(Z) для различных уровней массовой толщины ОК
ρH. На рис. 3 приведены графики функций Q(Z) для различных пар максимальных энергий E1 и
E2. Для корректного сравнения с гамма-излучением максимальные энергии подбирались из усло-
вия близости эффективных энергий.
Вид функций Q(Z) для рентгеновского излучения схож с аналогичными функциями для гамма-
излучения. Из анализа данных, представленных на рис. 3, можно сделать вывод о существенности
зависимости параметра распознавания Q от ρH при фиксированном значении Z. Отмеченная за-
висимость является убывающей до уровня Z ≈ 26-29 и возрастающей свыше этого уровня. Этот
фактор не позволяет оценивать Z с высокой точностью. В [36] отмечена эффективность примене-
ния предварительной фильтрации для повышения точности оценки Z для высокоэнергетического
рентгеновского излучения. На рис. 4 приведены графики Q(Z) для максимальных энергий E1 и E2
для толщин предварительных фильтров из меди hf = 5 мм.
Q
Q
2,5
2,5
3
3
2
2
1
2,0
2,0
1
1,5
1,5
1,0
1,0
1
20
39
58 Z
1
20
39
58 Z
E1 = 100 кэВ, E2 = 150 кэВ
E1 = 160 кэВ, E2 = 250 кэВ
Рис. 4. Функции Q(Z) с предварительной фильтрацией медной пластиной hf = 5 мм:
1 — ρH = 2 г/см2; 2 — ρH = 5 г/см2; 3 — ρH = 10 г/см2.
Сравнение графиков Q(Z) для различных значений массовых толщин ОК подтверждает эф-
фективность применения предварительной фильтрации рентгеновского излучения и для рас-
сматриваемого диапазона максимальных энергий. Причем существует диапазон изменения Z,
для которого функции Q(Z) практически не зависят от массовой толщины ρH. Например, для
пары максимальных энергий E1 = 100 кэВ, E2 = 150 кэВ указанный диапазон Z — от 1 до 28, а
для E1 = 150 кэВ, E2 = 250 кэВ — от 1 до 35.
На практике параметрами, характеризующим ослабление объектом контроля применительно к
распознаванию материалов, является пара (Q, Y1). Это означает, что необходимо исследовать функ-
ции Q(Z) для различных уровней Y1. Максимальный уровень Y1 — Ymax определяется разрядностью
АЦП и величиной цифрового сигнала Dmin за максимальной толщиной ОК из материала с эффек-
тивным атомным номером Z
Дефектоскопия
№ 4
2019
Особенности распознавания материалов мультиэнергетическим рентгеновским методом
49
k
2
-1
Y
=
ln
(10)
max
.
D
min
Например, для разрядности АЦП k = 16 и Dmin = 100 значение Ymax близко к 6,5.
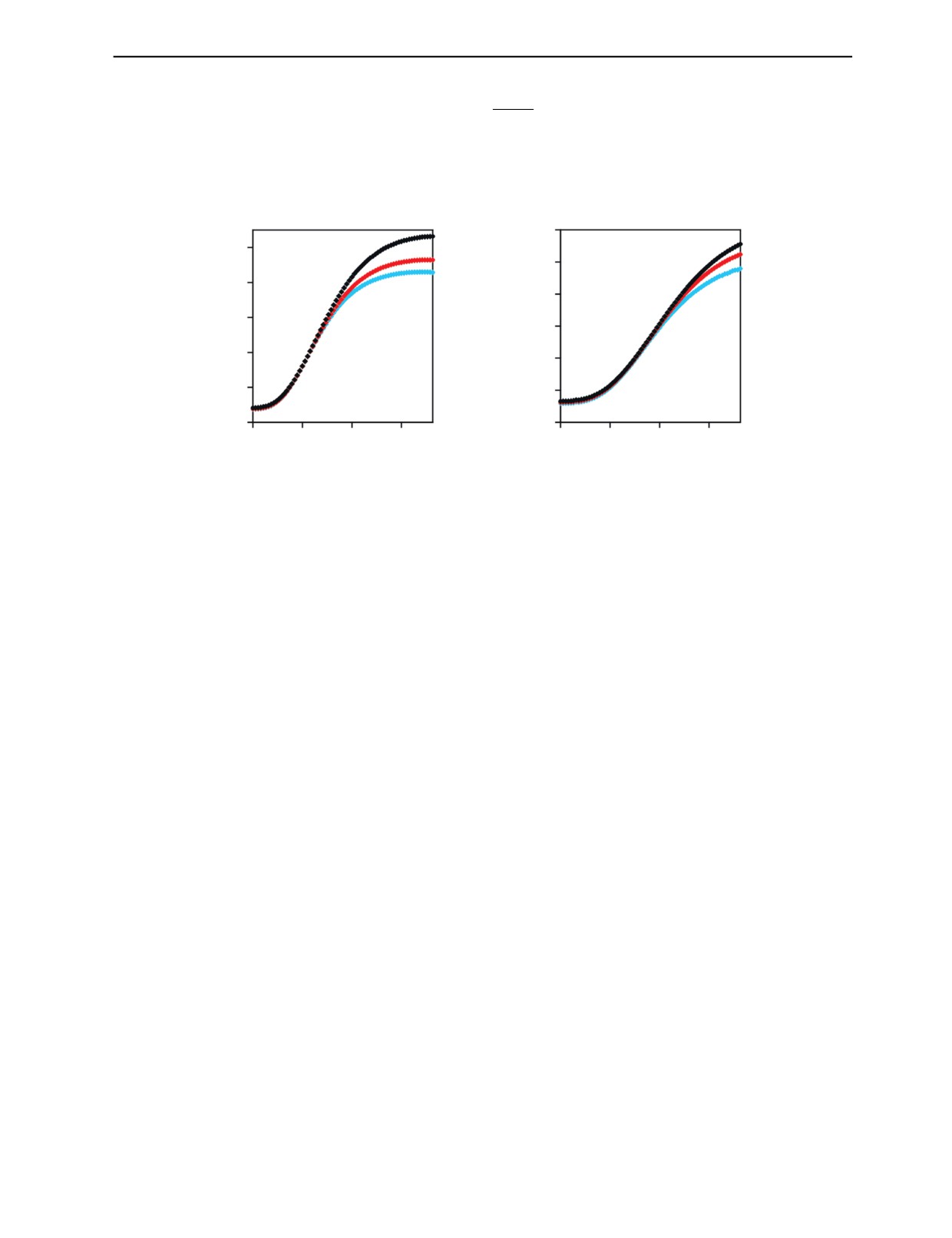
Для иллюстрации на рис. 5 приведены графики функций Q(Z) для различных пар максималь-
ных энергий E1, E2, толщин медных фильтров hf и уровней Y1 от 0,5 до 6,5 д.с.п.
Q
Q
2,2
2,0
3
3
2
2,0
2
1,8
1
1,8
1
1,6
1,6
1,4
1,4
1,2
1,2
1,0
1,0
1
20
39
58 Z
1
20
39
58 Z
E1 = 150 кэВ, E2 = 250 кэВ, hf = 5 мм
E1 = 250 кэВ, E2 = 450 кэВ, hf = 20 мм
Рис. 5. Функции Q(Z) с предварительной фильтрацией медной пластиной:
1 — Y1 = 1,5 д.с.п.; 2 — Y1 = 3 д.с.п.; 3 — Y1 = 6,5 д.с.п.
Из анализа рис. 5 можно сделать вывод о возможности точной оценки эффективного атомного
номера по параметру распознавания для диапазона Z от 5 (бор) до 37 (рубидий) и массовых толщин
ОК в д.с.п. от 1,5 до 6,5. Следует отметить, что увеличение максимальных энергий с одновремен-
ным увеличением толщины предварительных фильтров приводит к повышению точности измере-
ния Z в области высоких значений и увеличению верхней границы диапазона изменения надежно
распознаваемого эффективного атомного номера до 50 (олово).
Любая из рассматриваемых в пунктах 1.2.1 и 1.2.2 реализаций ММЭ позволяет оценить два
основных параметра ОК — Z и ρH.
Сравнительный анализ двух рассматриваемых реализаций ММЭ показывает, что они могут
быть использованы в досмотровом контроле для распознавания. Ниже рассмотрим особенности
реализации ММЭ (8), так как она отличается меньшей сложностью в практическом использовании
по сравнению с реализацией (6).
Использование более двух максимальных энергий в двухпараметрической реализации ММЭ
связано с необходимостью одновременного точного измерения Z в диапазонах от 5 до 26 и от 26
до 40 и выше. Так для первого диапазона изменения Z эффективно использование пар максималь-
ных энергий до 150 кэВ, а для второго диапазона — свыше 200 кэВ. Известно, что увеличение
количества уровней энергий в ММЭ снижает уровень шумов в изображениях параметров ММЭ
применительно к КТ [21].
2. О ВЫБОРЕ КОЛИЧЕСТВА УРОВНЕЙ МАКСИМАЛЬНЫХ ЭНЕРГИЙ
В ДВУХПАРАМЕТРИЧЕСКОЙ РЕАЛИЗАЦИИ ММЭ
Специфической особенностью объектов досмотрового контроля является неопределенность их
внутренней структуры. Неопределенность внутренней структуры ОК заключается в количестве и
разнообразии фрагментов объекта по размерам, массовой толщине, эффективному атомному но-
меру. В настоящее время предпринимаются меры для внедрения технологий, снижающих указан-
ную неопределенность, при автомобильных перевозках товаров и перевозках контейнеров на всех
видах транспорта. К багажу и ручной клади такие технологии неприменимы в силу уникальности
каждого багажа и ручной клади.
Из сформулированного в конце предыдущего раздела замечания следует, что основным вопро-
сом метода мультиэнергий, является выбор необходимых уровней максимальных энергий рентге-
новского излучения и их количества.
Выше показано, что исследуемая реализация ММЭ позволяет оценить всего два параметра ОК
и его структурных фрагментов — Z и ρH. Это означает достаточность двух максимальных энергий
Дефектоскопия
№ 4
2019
50
С.П. Осипов, Е.Ю. Усачев, С.В. Чахлов и др.
рентгеновского излучения для определения отмеченных параметров ОК, но для частичных диапазо-
нов их изменения. Сложность ситуации заключается в том, что максимальные энергии в парах долж-
ны обеспечивать заданные точности оценки Z и ρH для всего диапазона изменения этих параметров.
Выбор количества уровней максимальных энергий определяется диапазонами изменения ρH —
(ρH)min, (ρH)max и эффективного атомного номера материала Z — Zmin, Zmax.
Из сказанного выше и анализа рис. 3—5 следует вывод о достаточной точности измерения Z
при возможном его изменении от 5 до 60 для количества уровней максимальных энергий в ММЭ,
равного трем (E1 < E2 < E3). Пара максимальных энергий (E1, E2) предназначена для оценки эффек-
тивного атомного номера Z от 5 до 35, а пара максимальных энергий (E2, E3) — от 35 до 60. Из-
лишнее уменьшение уровня E1 приведет к увеличению статистической и систематической состав-
ляющих погрешности оценки Z, что связано с уменьшением проникающей способности излучения
и конечной разрядностью АЦП.
Отметим, что разрешающая способность по эффективному атомному номеру DZ (см. рис. 5)
зависит не только от соответствующей пары энергий, но и от толщины ОК в единицах д.с.п. для
меньшей максимальной энергии рентгеновского излучения. Этот факт существенен для материа-
лов ОК с большим значением эффективного атомного номера.
В методе распознавания материалов ОК классическим способом линий уровней анализируются
значения Q с соотнесением материала по этому параметру к одному из широких классов материалов.
Этот факт не в полной мере удовлетворяет потребителей систем досмотрового контроля. Помимо Q и
Z представляет интерес также значения массовых толщин ОК — ρH, что позволяет оценить массу ОК
и его структурных фрагментов и повысить вероятность обнаружения ОК, запрещенных к перевозке.
Подбор уровней максимальных энергий в ММЭ может быть осуществлен расчетным либо экс-
периментальным путем. Расчеты базируются на выражениях (2), (9), а эксперименты — на по-
строении калибровочных зависимостей (8) с последующей оценкой параметра распознавания (9).
В обоих случаях на начальном этапе процесса выбора должны быть заданы границы изменения
массовой толщины и эффективного атомного номера.
Ниже обсудим алгоритм формирования и обработки информации в ММЭ, предназначенный
для одновременной оценки ρH и Z.
3. АЛГОРИТМ ФОРМИРОВАНИЯ И ОБРАБОТКИ ИНФОРМАЦИИ В ММЭ
Алгоритм формирования и обработки информации в ММЭ состоит из нескольких взаимосвя-
занных последовательных этапов.
3.1. Предварительные расчеты
На этапе предварительных расчетов производится ориентировочный выбор количества и уров-
ней максимальных энергий рентгеновского излучения, формируются рекомендации по структуре
тестовых образцов.
Исходными данными для расчетов являются: максимальная толщина объекта контроля — Hmax;
диапазон изменения эффективного атомного номера — Zmin, Zmax; разрядность АЦП — k; мини-
мальное значение цифрового сигнала за ОК — Dmin; плотность материала с эффективным атомным
номером Zmin — rmin.
Максимальная толщина фрагментов тестового объекта (ТО) в д.с.п Ymax находится по формуле (10).
Уровни толщин фрагментов ТО в д.с.п. Yl, l = 1 … L определяются выражением
Yl = Ymin + (Ymax - Ymin) l/L.
(11)
Уровни эффективных атомных номеров материалов ТО Z1, Z2, …, ZJ выбираются из условия
перекрытия диапазона Zmin, Zmax, а их количество — из условия обеспечения требуемого разреше-
ния по эффективному атомному номеру — DZ.
Толщины фрагментов (rH)lj , l = 1 ...L, j = 1 … J в г/см2 находятся из уравнения
Emax
g(E,E
max
)E
ab
(E)ε(E)exp(-m(E,Z
j
)(rH
lj
) )dE
∫
0
Y
=-ln
(12)
l
Emax
g(
E,E
)E
(E)ε(E)dE
∫
max
ab
0
Дефектоскопия
№ 4
2019
Особенности распознавания материалов мультиэнергетическим рентгеновским методом
51
Отметим, что существует различие подходов для адаптированной, относительно уровней макси-
мальных энергий, и неадаптированной систем ММЭ. Здесь под адаптацией понимается подстройка
коэффициентов преобразования и разрядности АЦП под конкретный уровень максимальной энергии.
Очевидно, что адаптация приводит к увеличению материальных затрат. Ниже будем рассматривать
неадаптированные системы ММЭ. Для таких систем естественно считать, что наиболее неоптималь-
ными условиями являются условия формирования радиографических изображений для Emax = E1.
3.2. Этап калибровок
На начальном этапе формирования информации в ММЭ ТО сканируется пучками рентгенов-
ского излучения со всеми необходимыми уровнями максимальных энергий. Тестовый объект со-
стоит из дискретного набора фрагментов, которые характеризуются парами (ρH, Z)∈ PH = [(ρH)min,
(ρH)max]×[Zmin, Zmax]. Результатом сканирования является совокупность дискретных наборов тол-
щин фрагментов в единицах д.с.п. Y1(ρH, Z), Y2(ρH, Z), …, Yn(ρH, Z).
Указанная совокупность трансформируется (преобразование (9)) в совокупность параметров
распознавания Qi = Yi(ρH, Z)/Yn(ρH, Z). Для описания зависимостей Qi(Yi) для всех уровней Yi и Zj
применяется двухмерная полиномиальная регрессия FQ(Y, Z), используемая для оценки эффектив-
ного атомного номера.
Дополнительно на основе совокупности Y1(ρH, Z), Y2(ρH, Z), …, Yn(ρH, Z) строятся калибровоч-
ные функции F1(ρH, Z), F2(ρH, Z), …, Fn(ρH, Z). Здесь n, n ≥ 1 — количество уровней максимальных
энергий. По отношению к распознаванию, сводящемуся к оценке эффективного атомного номера
Z, эти функции применительно к методу линий уровней играют вспомогательную роль, но являют-
ся основными при последующей оценке ρH.
Функции FQ(Y, Z) и F1(ρH, Z), F2(ρH, Z), …, Fn(ρH, Z) могут быть использованы для анализа
точности оценки массовой толщины ρH и эффективного атомного номера Z.
3.3. Оценка Z и ρH методом мультиэнергий
На вход этапа оценки Z поступают значения Y1 1, Y1 2, …, Y1 n-1 и Q1, Q2, …, Qn-1.
1. Для i=1 … n-1 проверим условие Y1 i ∉ [ Ymin, Ymax]. Если выполняется для одного или не-
скольких значений i, то для этих значений i оценка Z является неопределенной.
2. Если для одного или нескольких значений i из указанного выше диапазона выполняется ус-
ловие Y1 i ∈ [Ymin, Ymax], то для таких i проверяется условие принадлежности значения Qi интервалу
монотонности [Qi-, Qi+]. Этому интервалу соответствует интервал [Zi-, Zi+]. Если Qi < Qi-, то оценка
эффективного атомного номера Zi = Zi-, если Qi > Qi+, то оценка эффективного атомного номера
Zi = Zi+. Оценка эффективного атомного номера для Qi ∈ [Qi-, Qi+] находится обращением функции
FQ для уровня Y1 i, то есть Zi = F-1Q(Y1 i, Qi). Для нескольких оценок эффективного атомного номера,
входящих в интервалы [Zi-, Zi+], в качестве результирующей оценки Z берется среднее значение
оценок. Если оценки эффективного атомного номера принадлежат множеству Z- ={Zi-, i = 1…n-1},
то Z = min(Z-), если Zi ∈ Z+={Zi+, i = 1…n-1}, то Z = max(Z+).
3. Оценка массовой толщины ρH осуществляется обращением функций F1(ρH, Z), F2(ρH, Z), …,
Fn(ρH, Z) для соответствующего значения Z: (ρH)i = F-1i(Yi, Z). В качестве итоговой оценки массовой
толщины выбирается среднее значение полученных оценок. Точность оценки ρH выше для тех пар
максимальных энергий, для которых произведена оценка эффективного атомного номера материа-
ла методом обращения функции FQ.
Ожидается высокая точность оценки эффективного атомного номера в ММЭ при надлежащем
выборе уровней Emax, что обусловлено гладкостью функции Q(Z) и наличием у нее интервалов
монотонного возрастания для толщин фрагментов, отличных от нуля.
Достичь высокой точности оценки массовых толщин ОК и их фрагментов для материалов, которые
существенно отличаются по эффективному атомному номеру практически невозможно. Отмеченный
вывод связан с физической невозможностью устранения влияния функции a(Z) на точность оценки ρH.
Ниже рассмотрим пример имитационного моделирования формирования и обработки инфор-
мации в исследуемом методе мультиэнергий.
4. ПРИМЕР ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ ФОРМИРОВАНИЯ И ОБРАБОТКИ
ИНФОРМАЦИИ В ММЭ
В качестве ТО выберем объект, фрагменты которого представляют собой параллелепипеды раз-
мером a×a×H, где толщина H является переменной величиной. Материал фрагментов характеризу-
Дефектоскопия
№ 4
2019
52
С.П. Осипов, Е.Ю. Усачев, С.В. Чахлов и др.
ется плотностью r и эффективным атомным номером Z. Эффективный атомный номер варьирова-
ли в диапазоне от Zmin = 4 до Zmax = 64 с шагом DZ = 3. Массовую толщину фрагментов ТО изменяли
в диапазоне от (ρH)min = 0,2 до (ρH)max = 9,2 с шагом D(ρH) = 0,5 г/см2.
С целью обеспечения высокой точности оценки эффективного атомного номера Z в диапазо-
не его изменения от 5 до 63 были выбраны следующие уровни максимальных энергий: E1 = 100;
E2 = 150; E3 = 250 кэВ.
Калибровочные функции FQ(Y, Z) и F1(ρH, Z), F2(ρH, Z), F3(ρH, Z) строились на основе ана-
лиза рассчитанных таблиц толщин фрагментов ОК в д.с.п. для соответствующих уровней макси-
мальных энергий.
В качестве примера ОК был выбран объект, аналогичный ТО. Эффективный атомный номер
материалов фрагментов ОК изменяли от 5 до 63 с шагом DZ = 1. Массовую толщину фрагментов
ОК варьировали от 0,2 до 9 с шагом 0,2 г/см2.
С целью оценки предельных возможностей рассматриваемого метода распознавания расчеты
проводились для разрядности АЦП k = ∞.
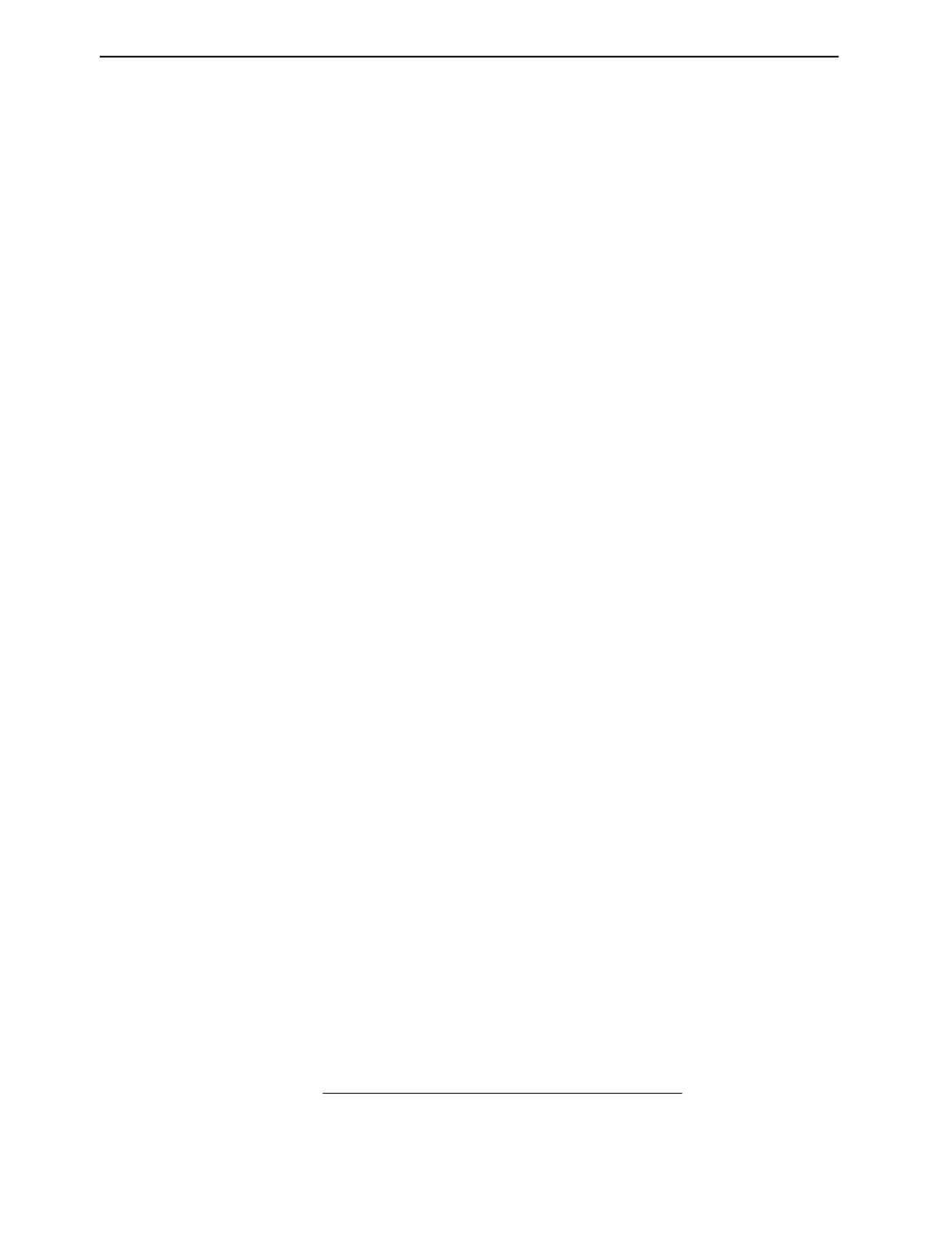
На рис. 6 для исследуемого ОК приведена визуализация оценок эффективного атомного номера
Zm(Z, rH) и массовой толщины (rH)m(Z, rH) методом ММЭ в исследуемом диапазоне изменения
атомных номеров и толщин. На рис. 6a черным цветом отмечены фрагменты, абсолютная погреш-
ность оценки эффективного атомного номера которых превышает уровень 0,5. На рис. 6б выделе-
ны фрагменты, для которых относительная погрешность оценки (rH)m превосходит 10 %.
а
Z = 5
Z = 63
0,2 г/см2
9 г/см2
0,2 г/см2
9 г/см2
ρH
ρH
E1 = 100 кэВ, E3 = 250 кэВ
б
E2 = 150 кэВ, E3 = 250 кэВ
Z = 5
Z = 63
0,2 г/см2
9 г/см2
0,2 г/см2
9 г/см2
ρH
ρH
Рис. 6. Визуализация оценок эффективного атомного номера Zm(Z, ρH ) — a и массовой толщины (ρH)m(Z, ρH) —
б методом ММЭ (k = ∞).
Анализ результатов, приведенных на рис. 6, позволяет сделать вывод о достаточно высокой точ-
ности оценки эффективного атомного номера материалов фрагментов ОК и массовой толщины, не-
смотря на намеренно грубую градацию фрагментов ТО по Z и rH. Для улучшения точности оценки Z
и rH фрагментов ОК можно рекомендовать использование на стадии калибровки ТО с фрагментами
с более детальной градацией по эффективному атомному номеру и массовой толщине. Расширение
диапазона и количества максимальных энергий приведет к увеличению диапазона массовых толщин
фрагментов ОК в сторону меньших и больших значений с надежным распознаванием материалов.
Дефектоскопия
№ 4
2019
Особенности распознавания материалов мультиэнергетическим рентгеновским методом
53
а
Z = 5
Z = 63
0,2 г/см2
9 г/см2
0,2 г/см2
9 г/см2
ρH
ρH
E1 = 100 кэВ, E3 = 250 кэВ
б
E2 = 150 кэВ, E3 = 250 кэВ
Z = 5
Z = 63
0,2 г/см2
9 г/см2
0,2 г/см2
9 г/см2
ρH
ρH
Рис. 7. Визуализация оценок эффективного атомного номера Zm(Z, ρH) — a и массовой толщины (ρH)m(Z, ρH) —
б методом ММЭ (k = 16).
а
Z = 5
Z = 63
0,2 г/см2
9 г/см2
0,2 г/см2
9 г/см2
ρH
ρH
E1 = 100 кэВ, E3 = 250 кэВ
б
E2 = 150 кэВ, E3 = 250 кэВ
Z = 5
Z = 63
0,2 г/см2
9 г/см2
0,2 г/см2
9 г/см2
ρH
ρH
Рис. 8. Визуализация оценок эффективного атомного номера Zm(Z, ρH) — a и массовой толщины (ρH)m(Z,ρH) — б
методом ММЭ (k = 24).
Дефектоскопия
№ 4
2019
54
С.П. Осипов, Е.Ю. Усачев, С.В. Чахлов и др.
В настоящее время в досмотровом контроле наибольшее применение получили АЦП с разряд-
ностью k = 16, но намечается увеличение разрядности до k = 24. На рис. 7, 8 приведена визуализа-
ция анализируемых оценок для разрядности АЦП k = 16 и k = 24. Сравнение данных, приведенных
на рис. 6—8, подтверждает значимое влияние разрядности АЦП на точность оценок эффективного
атомного номера и массовой толщины методом мультиэнергий.
ВЫВОДЫ И РЕЗУЛЬТАТЫ
Рассмотрены особенности распознавания материалов объектов контроля и их структурных
фрагментов методом мультиэнергий. Показан подход к комплексному использованию метода
линий уровней и метода мультиэнергий, предназначенный для повышения точности оценки эф-
фективного атомного номера. Приведен алгоритм формирования и обработки информации в ме-
тоде мультиэнергий, позволяющий измерить эффективный атомный номер и массовую толщину
фрагментов объекта контроля с высокой точностью. Методом имитационного моделирования
продемонстрирована эффективность применения анализируемого способа распознавания мате-
риалов.
Исследование проводилось в Томском политехническом университете в рамках гранта Про-
граммы повышения конкурентоспособности Томского политехнического университета.
СПИСОК ЛИТЕРАТУРЫ
1. Duvillier J., Dierick M., Dhaene J., Van Loo D., Masschaele B., Geurts R., Hoorebeke L.V., Boone M.N.
Inline multi-material identification via dual energy radiographic measurements // NDT & E International. 2018.
V. 94. P. 120—125.
2. Karoly S. Technologies to counter aviation security threats // AIP Conference Proceedings. AIP
Publishing. 2017. V. 1898. No. 1. No article 050002.
3. Chen G., Bennett G., Perticone D. Dual-energy X-ray radiography for automatic high-Z material
detection // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials
and Atoms. 2007. V. 261. No. 1—2. P. 356—359.
4. Осипов С.П., Удод В.А., Ван Я. Распознавание материалов методом дуальных энергий при радиа-
ционном контроле объектов // Дефектоскопия. 2017. № 8. С. 33—56.
5. Клименов В.А., Осипов С.П., Темник А.К. Идентификация вещества объекта контроля методом
дуальных энергий // Дефектоскопия. 2013. № 11. С. 40—50.
6. Runkle R.C., White T.A., Miller E.A., Caggiano J.A., Collins B.A. Photon and neutron interrogation
techniques for chemical explosives detection in air cargo: A critical review // Nuclear Instruments and Methods
in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 2009.
V. 603. No. 3. P. 510—528.
7. Paziresh M., Kingston A.M., Latham S.J., Fullagar W.K., Myers G.M. Tomography of atomic number
and density of materials using dual-energy imaging and the Alvarez and Macovski attenuation model // Journal
of Applied Physics. 2016. V. 119. No. 21. P. 214901-1—214901-11.
8. Rebuffel V., Dinten J.M. Dual-energy X-ray imaging: benefits and limits // Insight-non-destructive testing
and condition monitoring. 2007. V. 49. No. 10. P. 589—594.
9. Brooks R.A., Di Chiro G. Split-detector computed tomography: A preliminary report // Radiology. 1978.
V. 126. P. 255—257.
10. Barnes G.T., Sones R.A., Tesic M.M., Morgan D.R., Sanders J.N. Detector for dual-energy digital
radiography // Radiology. 1985. V. 156. No. 2. P. 537—540.
11. McCollough C.H., Leng S., Yu L., Fletcher, J.G. Dual-and multi-energy CT: principles, technical
approaches, and clinical applications // Radiology. 2015. V. 276. No. 3. P. 637—653.
12. Ишханов Б.С., Курилик А.С., Руденко Д.С., Стопани К.А., Шведунов В.И. Многопучковый метод
сканирования объектов // Изв. РАН. Сер. физическая. 2008. Т. 72. № 6. С. 908—911.
13. Politte D.G., Lu J., O’Sullivan J.A., Johnson E., Bosch C. Multi-energy penalized maximum-
likelihood reconstruction for x-ray security imaging / Anomaly Detection and Imaging with X-Rays (ADIX) II.
— International Society for Optics and Photonics, 2017. V. 10187. No. article 101870D.
14. Ермаков А.Н., Ишханов Б.С., Курилик А.С., Шведунов В.И. Измерение атомного номера неиз-
вестных объектов на ускорителе электронов с перестраиваемой энергией // Изв. РАН. Сер. физическая.
2012. Т. 76. № 11. С. 1337—1337.
15. Paulus C., Moulin V., Perion D., Radisson P., Verger L. Multi-energy x-ray detectors to improve air-
cargo security / Anomaly Detection and Imaging with X-Rays (ADIX) II. — International Society for Optics
and Photonics, 2017. V. 10187. No. article 101870I.
16. Белышев С.С., Ишханов Б.С., Курилик А.С., Стопани К.А. Измерения атомного номера и коли-
чества вещества объектов с помощью радиоактивных источников // Изв. РАН. Сер. физическая. 2013.
Т. 77. № 7. С. 1008—1008.
Дефектоскопия
№ 4
2019
Особенности распознавания материалов мультиэнергетическим рентгеновским методом
55
17. X-ray mass attenuation coefficients. NIST Standard Reference Database 126. URL: https://www.nist.
18. Storm E., Israel H.I. Photon cross sections from 0.001 to 100 MeV for elements 1 through 100. Los
Alamos Scientific Lab., N. Mex., 1967. № LA-3753. 257 p.
19. Singh K., Singh H., Sharma V., Nathuram R., Khanna A., Kumar R., Bhatti S.S., Sahota H.S. Gamma-
ray attenuation coefficients in bismuth borate glasses // Nuclear Instruments and Methods in Physics Research
Section B: Beam Interactions with Materials and Atoms. 2002. V. 194. No. 1. P. 1—6.
20. Janssens K. X-ray fluorescence analysis / Handbook of Spectroscopy, 2003. WILEY-VCH Verlag
GmbH & Co. KGaA, Weinheim. P. 363—420.
21. Li Z., Leng, S., Yu L., Manduca A., McCollough C.H. An effective noise reduction method for multi-
energy CT images that exploit spatio-spectral features // Medical physics. 2017. V. 44. No 5. P. 1610—1623.
22. Maitrejean S., Perion D., Sundermann D. Multi-energy method: a new approach for measuring x-ray
transmission as a function of energy with a Bremsstrahlung source and its application for heavy element
identification / Hard X-Ray and Gamma-Ray Detector Physics and Applications. International Society for
Optics and Photonics, 1998. V. 3446. P. 114—134.
23. Naydenov S.V., Ryzhikov V.D., Smith C.F. Multi-energy approach in radiography and introscopy //
Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and
Associated Equipment. 2005. V. 537. No. 1—2. P. 462—466.
24. Lehmann L.A., Alvarez R.E. Energy-selective radiography a review / Digital Radiography. Springer,
Boston, MA, 1986. P. 145—188.
25. Baek C.H., Kim D. X-ray beam design for multi-energy imaging with charge-integrating detector:
A simulation study // Nuclear Instruments and Methods in Physics Research Section A: Accelerators,
Spectrometers, Detectors and Associated Equipment. 2015. V. 799. P. 132—136.
26. Kim D., Lee S., Jeon P.H. Experimental results of use of triple-energy X-ray beam with K-edge filter in
multi-energy imaging // Journal of Instrumentation. 2016. V. 11. No. 4. No. article P04009.
27. Alvarez R.E. Invertibility of the dual energy X-ray data transform // Medical Physics. 2018. https://doi.
28. Martz H.E., Glenn S.M., Smith J.A., Divin C.J., Azevedo S.G. Poly-versus mono-energetic dual-
spectrum non-intrusive inspection of cargo containers // IEEE Transactions on Nuclear Science. 2017. V. 64.
No. 7. P. 1709—1718.
29. Gorshkov V. The effective atomic number and the mass attenuation coefficient of a multicomponent
object for the continuous spectrum of the radiation // Nondestructive Testing and Evaluation. 2017. V. 32.
No. 1. P. 79—89.
30. Iovea M., Neagu M., Duliu O.G., Mateiasi G. High accuracy x-ray dual-energy experiments and non-
rotational tomography algorithm for explosives detection technique in luggage control. Presented at the Int.
Symp. Digital Industrial Radiology and Computed Tomography, Lyon, France, 2007. 8 p.
31. Mery D., Mondragon G., Riffo V., Zuccar I. Detection of regular objects in baggage using multiple
X-ray views // Insight-Non-Destructive Testing and Condition Monitoring. 2013. V. 55. No. 1. P. 16—20.
32. Shikhaliev P.M. Megavoltage cargo radiography with dual energy material decomposition // Nuclear
Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated
Equipment. 2018. V. 882. P. 158—168.
33. Chen G., Bennett G., Perticone D. Dual-energy X-ray radiography for automatic high-Z material
detection // Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials
and Atoms. 2007. V. 261. No. 1—2. P. 356—359.
34. Rheinboldt W.C. Methods for solving systems of nonlinear equations. V. 70. 2nd edn. SIAM,
Philadelphia, 1998.
35. Ogorodnikov S., Petrunin V. Processing of interlaced images in 4-10 MeV dual energy customs system
for material recognition // Physical Review Special Topics-Accelerators and Beams. 2002. V. 5. No. 10.
No. article 104701.
36. Osipov S.P., Chakhlov S.V., Osipov O.S., Li S., Sun X., Zheng J., Hu X., Zhang G. Physical and technical
restrictions of materials recognition by the dual high energy X-ray imaging // International Journal of Applied
Engineering Research. 2017. V. 12. No. 23. P. 13127—13136.
Дефектоскопия
№ 4
2019