УДК 620.179.16
ДИСПЕРСИОННОЕ УРАВНЕНИЕ ДЛЯ ПРОДОЛЬНОЙ ВОЛНЫ В СЛОИСТОЙ
СРЕДЕ С НЕОДНОРОДНЫМИ ГРАНИЧНЫМИ УСЛОВИЯМИ ПРИ
РАЗЛИЧНЫХ НАПРАВЛЕНИЯХ РАСПРОСТРАНЕНИЯ
© 2020 г. К.Е. Аббакумов1,*, А.В. Вагин1,**
1Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова
(Ленина), Россия 197376 Санкт-Петербург, ул. Профессора Попова, 5
E-mail: *keabbakumov@etu.ru; **av.vagin@bk.ru
Поступила в редакцию 24.09.2019; после доработки 21.10.2019
Принята к публикации 01.11.2019
Исследовано распространение продольной волны в слоистой среде с неоднородными граничными условиями при
двух вариантах геометрии распространения волны относительно слоев структуры: параллельно и перпендикулярно
слоям. Выведены дисперсионные уравнения для продольной волны для рассматриваемых случаев распространения.
Решены относительно волнового числа найденные дисперсионные уравнения для нахождения зависимостей эффектив-
ных скоростей продольной волны от относительной толщины слоя и параметров материалов. Полученные зависимости
используются в задачах нахождения физико-механических характеристик среды на основе акустических измерений.
Ключевые слова: продольная волна, дисперсионное уравнение, слоистая среда, неоднородные граничные условия.
DOI: 10.31857/S0130308220010030
ВВЕДЕНИЕ
Распространению продольных волн в слоистом микронеоднородном полупространстве уделя-
ется большое внимание. Результаты анализа распространения продольных волн в микронеодно-
родной слоистой среде используются для задач определения и контроля основных физико-механи-
ческих характеристик материала, что является важной задачей неразрушающего контроля качества
материалов, изделий и конструкций, а также структуроскопии.
При четкой аналитической связи между параметрами волны и свойствами материала контро-
лируемое свойство может быть определено с высокой степенью достоверности. Так, модуль Юнга,
модуль сдвига, коэффициент Пуассона однозначно определяются по измеренным значениям ско-
ростей распространения продольной и поперечной волн.
В [1] приведено исследование распространения продольных волн в мелкослоистой среде с
однородными граничными условиями на границах слоев при распространении параллельно слоям
структуры, результатом которого является вывод дисперсионного уравнения для продольной
волны. Стоит отметить, что ранее в [2, 3] решение дисперсионного уравнения относительно вол-
нового числа и построение зависимости скорости продольной волны от относительной толщины
слоя материала и параметров сред приводили к некоторым ошибкам, которые заключались в том,
что при увеличении относительной толщины слоя зависимость начинала спадать, что не подчиня-
ется физическому смыслу при распространении волны в однородной среде.
Аналогично рассмотренному выше случаю, в [4, 5] рассматривается распространение продоль-
ной волны в слоистой неоднородной среде, где получены зависимости продольной волны, распро-
страняющейся в структуре «сталь—сталь» с шероховатостью между прилегающими средами.
Полученные результаты также разнятся с представлениями о распространении волн в неоднород-
ных средах, так как полученные зависимости не отражают правильных значений скоростей рас-
пространения в поперечной плоскости исследуемой структуры.
Распространение плоских волн в слоистом композитном материале с начальными напряжениями
периодической структуры рассматривается в [6, 7], где все результаты получены для полного контак-
та слоев, однако не приводится решение дисперсионного уравнения волны относительно волнового
числа, что, в свою очередь, не дает четкой аналитической связи между параметрами распространя-
ющейся волны (скорость) и свойствами контролируемого материала. Аналогичные исследования для
случая полного проскальзывания слоев представлены в статье [8]. Поскольку в этих работах полу-
чены результаты для двух крайних случаев контакта между слоями, то представляет интерес их
сравнение для оценки распространения волн при других видах степеней жесткости [9, 10].
Стоит отметить, что данное сравнение применительно к распространению волн в слоистом
композите отсутствует в классической теории (без начальных напряжений) [11]. В [12] рассмотре-
Дисперсионное уравнение для продольной волны в слоистой среде...
23
но распространение волн в среде с периодически расположенными твердыми слоями при полном
контакте. Результаты этих исследований также приведены в монографии [3].
Разнообразие конструкционных материалов, используемых в современном производстве чрез-
вычайно велико, и имеет устойчивую тенденцию к нарастанию. Расширение номенклатуры
используемых материалов опирается на появление новых технологий, что, в свою очередь, сопро-
вождается и появлением новых видов неоднородностей, для обнаружения которых необходимо
создавать новые или совершенствовать уже имеющиеся средства контроля. Разработка таких
средств контроля должна опираться на физические предпосылки, связанные с особенностями вол-
новых процессов в неоднородных материалах.
Особый вид неоднородных сред представляют слоистые структуры, хорошо моделирующие
свойства не только сред геологического происхождения, но и композиционных материалов, а
также материалов, используемых в аддитивных технологиях. Для определения требуемых параме-
тров в таких средах с помощью ультразвуковых средств контроля необходимо проводить пред-
измерительные изыскания, предпринимаемые с целью получения максимального количества
информации о структуре исследуемой среды.
Целью статьи является вывод дисперсионного уравнения для продольной волны, распространя-
ющейся параллельно и перпендикулярно слоям слоистой структуры с неоднородными граничными
условиями. То есть необходимо рассмотреть два случая геометрии распространения продольной
волны: распространение в неоднородной среде параллельно и перпендикулярно слоям. Однородная
среда описывается граничными условиями, учитывающими полную передачу составляющих упру-
гих смещений и упругих напряжений. В качестве неоднородной среды рассматриваем микронеодно-
родную структуру, описываемую граничными условиями, учитывающими неполную передачу
составляющих упругих смещений при сохранении передачи упругих напряжений [13].
Под микронеоднородными слоистыми средами понимается слоистая структура, составленная
из неоднородной слоистой среды и включений, расстояние между которыми и их размеры много
меньше длины волны, распространяющейся в этой среде [14]. Среда, состоящая из чередующихся
слоев двух однородных и изотропных веществ, называется слоистой. Если слоистая среда рассма-
тривается в среднем, то есть когда слои структуры достаточно тонкие, причем условие тонкости
слоев означает, что их толщины малы по сравнению с длинами волн сжатия и сдвига в материалах
этих сред, то она рассматривается уже как однородная, но анизотропная, при этом такая среда
называется мелкослоистой [1, 3].
Микронеоднородные слоистые среды, изготовление которых не имеет каких-либо технологи-
ческих трудностей, а свойства могут быть очень разнообразны (анизотропия скоростей распро-
странения и поглощений как для волн сжатия, так и для волн сдвига), представляют несомненный
практический интерес в акустике, авиации и космической технике, сейсмологии, акустооптике.
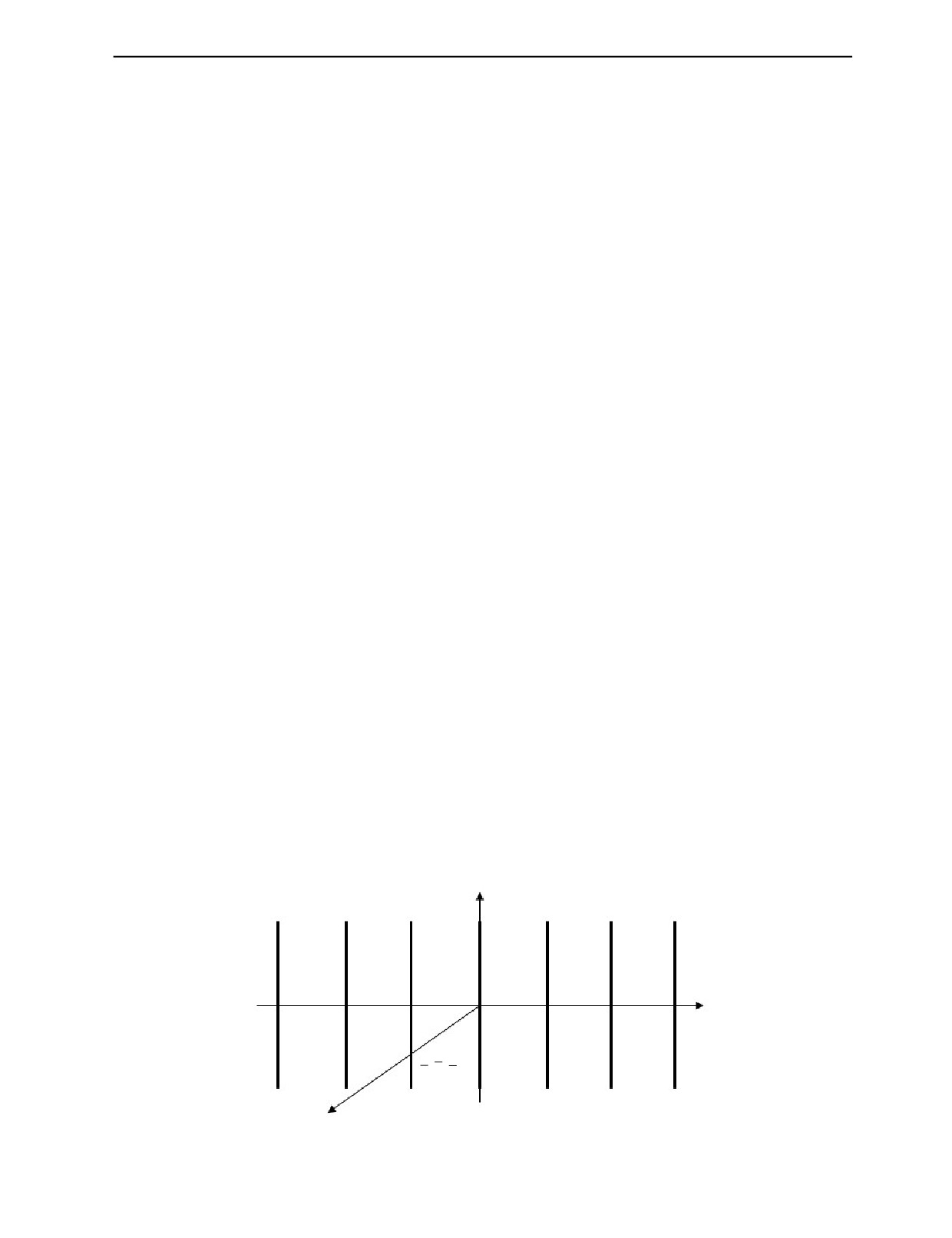
Описание распространения волн в слоистых средах. Рассмотрим модель слоистого полу-
пространства с чередующимися слоями толщиной a и b, параметрами ρ, λ, μ — для первой среды
и ρ, λ, µ — для второй среды (рис. 1). В качестве первой среды рассматриваем сталь, в качестве
второй — графит. Общая толщина слоя принимается равной 1 мм, а частота ультразвука при моде-
лировании процессов определения скорости волны на основе акустических измерений — 1 МГц.
На рис. 1 ρ — плотность среды, λ, μ — параметры Лямэ. Аналогичные параметры для второй
среды обозначаем с чертой сверху.
z
2-й слой
1-й слой
a
x
b
0
ρ, λ, µ
ρ, λ, μ
y
Рис. 1. Модель слоистой структуры.
Дефектоскопия
№ 1
2020
24
К.Е. Аббакумов, А.В. Вагин
Слоистая среда, представленная на рис. 1, в отношении своих упругих свойств является кри-
сталлом гексагональной симметрии, то есть для описания ее полного упругого поведения необхо-
димо и достаточно задать пять упругих постоянных. Однако среда с микротрещинами может быть
описана с помощью эффективных динамических модулей упругости, расчет которых является
непростой задачей и достигается на основе методов статистической механики [15] и метода само-
согласованного поля [16].
Волновое уравнение для продольной волны, распространяющейся в слоистой структуре, имеет
следующий вид:
2
∂
ξ
l
ρ
−
(
λ+2µ
)
∆ξ
=
0,
2
l
∂t
где ξl — вектор продольного смещения, ∆ξl = graddiv(ξl).
Общее решение для волнового уравнения для продольной волны запишем через частное реше-
ние, которое разделено на косинусную (симметричную) и синусоидальную (несимметричную)
части относительно середины слоев [3].
Для слоя материала 1 имеем следующие выражения для продольных смещений в направлении
оси x и z:
−ikx
P′ z)
−ikx
Q′ z)
−ikx
−ikx
ξ
=
P z)e
,
ξ
=
e
,
ξ
=-
e
,
ξ
=Q z)e
,
(1)
lx
lz
tx
tz
ik
ik
где ξlx, ξlz — продольные и ξlx, ξlz — поперечные смещения в направлении x и z соответственно,
k — волновое число. Причем:
a
a
2
2
2
P
(
z
)
=
Acosα
z
−
+
Bsin
α
z
−
,
α
=
k
−k
,
l
2
2
(2)
a
a
2
2
2
Q
(
z
)
=
Ccosβ
z
−
+
Dsin
β
z
−
,
β
=
k
−k
,
t
2
2
где A, B, C, D — пока неопределенные постоянные; kl, kt — волновые числа продольной и попереч-
ной волн соответственно.
Выражения для компонент тензора механических напряжений для первого слоя:
2
2
2
2
k
−β
λ
k
+2µα
ikx
l
ikx
−
−
σ
=
2µ
P′ z)+
Q z)
e
,
σ
=
0,
σ
=
P z)+2µQ′ z)
e
xz
yz
zz
(3)
2ik
ik
Аналогичные параметры во второй среде для уравнений (1) — (3) обозначаются с чертой
сверху.
Для описания поведения упругих смещений и механических напряжений на границах
между слоями введем неоднородные граничные условия, описывающие неполную передачу
компонент упругих смещений при сохранении передачи механических напряжений для каждо-
го слоя структуры:
σ
(0)
xz
ξ
(0)
=ξ
(0)−
,
σ
(0)
=σ
(0),
x
x
xz
xz
KGT
(4)
σ
zz
(0)
ξ
(0)
=ξ
(0)−
,
σ
(0)
=σ
(0),
z
z
zz
zz
KGN
где KGT, KGN — тангенциальный и нормальный коэффициенты жесткости.
Нормальный коэффициент жесткости определяет передачу нормальных составляющих упру-
гих смещений, а тангенциальный — передачу касательных составляющих. Коэффициенты жест-
кости зависят от коэффициента перфорации, характеризующего степень сплошности между при-
легающими средами структуры «сталь—графит», а также от величины шероховатости.
Разрывы в передаче упругих смещений на плоской границе двух упругих полупространств воз-
никают за счет совокупности взаимодействия выступов и впадин микрорельефа. Выступы и впа-
дины микрорельефа можно смоделировать введением величины шероховатости в коэффициенты
жесткости. Тогда смоделированная шероховатость будет определяться средним расстоянием
между соседними неоднородностями на контактирующих поверхностях [17].
Дефектоскопия
№ 1
2020
Дисперсионное уравнение для продольной волны в слоистой среде...
25
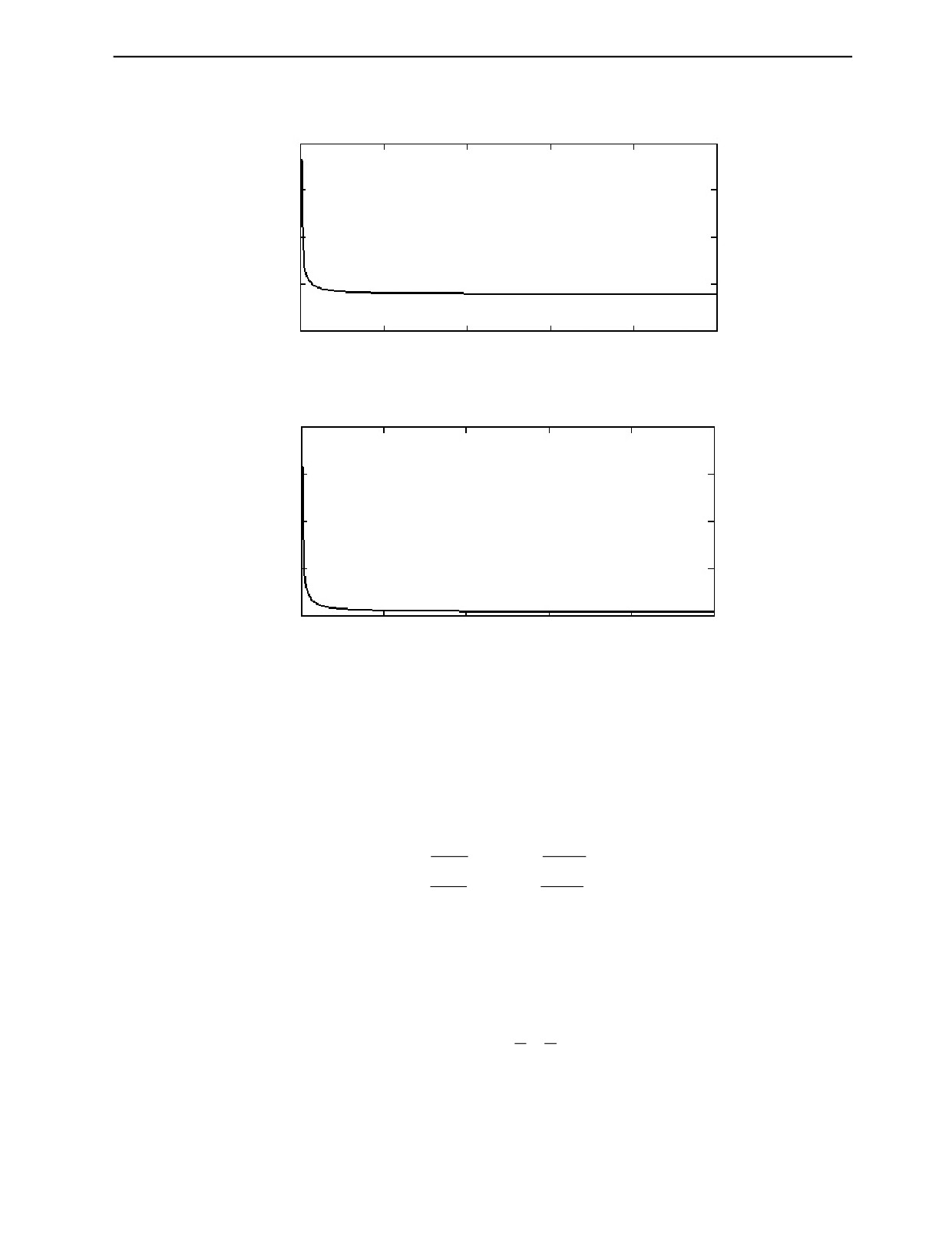
Построим графические зависимости нормального (рис. 2) и тангенциального (рис. 3) коэффи-
циентов жесткости от величины шероховатости Rz.
KGN
6,40∙1016
5,70∙1014
5,00∙1012
4,30∙1010
0
1∙10-5
2∙10-5
3∙10-5
4∙10-5
Rz, м
Рис. 2. Зависимость нормального коэффициента жесткости от величины шероховатости.
KGT
1,35∙1014
1,30∙1012
1,25∙1010
1,20∙108
0
1∙10-5
2∙10-5
3∙10-5
4∙10-5
Rz, м
Рис. 3. Зависимость тангенциального коэффициента жесткости от величины шероховатости.
В данной работе при дальнейших расчетах величина шероховатости принималась равной
Rz = 40 мкм, а среднее расстояние между соседними неоднородностями на контактирующих
поверхностях равным 0,1 мкм.
Как видно из графических зависимостей на рис. 2 и 3, при Rz = 40 мкм оба коэффициента жест-
кости имеют минимальные значение, что говорит о нарушенной сплошности между средами,
которая обуславливается наличием выступов и впадин на поверхности рассматриваемых сред.
Введем в рассмотрение также граничные условия периодичности, которые описывают непре-
рывное поведение упругих смещений и механических напряжений на границе слоев:
ξ
(a)
=ξ
(b),
σ
(a)
=σ
(b),
x
x
xz
xz
(5)
ξ
(a)
=ξ
(b),
σ
(a)
=σ
(b),
z
z
zz
zz
то есть указанные величины в первом слое при z = a должны равняться тем же величинам во вто-
ром слое при z = b. Подставляя компоненты для упругих смещений (1) и механических напряже-
ний (3) в неоднородные граничные условия (4), получаем 8 уравнений для постоянных
A,
B,
C
,
D,
A,
B,
C
,
D,
которые распадаются на продольную и поперечную волны [18].
Распространение продольной волны параллельно слоям. Пусть в направлении оси z рас-
пространяется продольная волна. Для продольной волны коэффициенты В и С в первой и во вто-
рой среде равны 0. Тогда с учетом условия B = C = B = C = 0 продольные смещения в (1) будут
четны относительно средины слоев, благодаря чему в слоистой структуре будет иметь место толь-
ко сжатие. Тогда подставляя соответствующие четные компоненты упругих смещений и механиче-
ских напряжений в неоднородные граничные условия, получаем четыре уравнения для продоль-
ной волны [1]:
Дефектоскопия
№ 1
2020
26
К.Е. Аббакумов, А.В. Вагин
b
2
b
2
2ikµαsin
α
µ
k
−β
sin
β
(
)
a
a
b
2
2
b
Aikcos
α
-
Dβcos
β
=
Aikcos
α
+
+
D
-βcos
β
,
2
2
2
KGT
KGT
2
2
2
b
b
λk
l
+2µα
cos
α
2ikµβcos
β
(
)
a
a
2
b
b
2
Aαsin
α
-
Diksin
β
=
A
-αsin
α
-
Diksin
β
-
,
2
2
KGN
2
2
KGN
a
2
2
a
b
2
2
b
A2
µαiksinα
+
D
µ
(
k
−β
)
sinβ
=-A2µαiksinα
+
Dµ
(
k
−β
)
sinβ
,
2
2
2
2
2
2
a
a
2
2
b
b
A
(
λk
l
+
2µα
)
cos
α
+
D
2µβik
cosβ
=
A
(
λk
l
+2µα
)
cos
α
+
D2µβ
ikcosβ
2
2
2
2
Составим из этих четырех уравнений детерминант и приравняем его к нулю. Очевидно, что систе-
ма четырех уравнений является однородной и совместной, то есть всегда имеет решение:
b
2
2
b
2
µα
iksinα
µ
k
−β
sinβ
(
)
a
a
b
2
2
b
ikcos
α
-β
cosβ
ikcosα
+
-βcosβ
2
2
2
KGT
KGT
2
2
2
b
b
(
λk
l
+2µα
)
cosα
2
µβikcosβ
a
a
2
b
b
2
αsin
α
-
ik
sinβ
-αsin
α
ik
sinβ
-
=
0.
2
2
KGN
2
2
KGN
a
2
2
a
b
2
2
b
2µαiksin
α
µ
(
k
−β
)
sinβ
-
2µα
ik
sin
α
µ
(
k
−β
)
sinβ
2
2
2
2
2
2
a
a
2
2
b
b
(
λk
+2µα
)
cos
α
2µβ
ikcos
β
λk
l
+
2
µα
cos
α
2
µβikcosβ
l
(
)
2
2
2
2
Решая данный определитель разложением по первой строке с учетом граничных условий пери-
одичности (5), получим дисперсионное уравнение, определяющее значение скорости продольной
волны cl = ω/k (ω — частота):
2
βb
αb
2
k
l
ctg
k
ctg
2
2
2
ω
ρ
β
a
2
2
2
4
(
µ-µ
)
XX
1
−
+ω
ρ
-
4
(
µ-µ
)
X
⋅ tg
1−
+ω
ρ×
2
KGN
k
2
KGT
(6)
α
b
αb
2
ρk
ctg
ρk
lctg
2
4
ω
ρ
2
βb ω
ρρ
βb
β
a
2
×
+
4
(
µ-µ
)
+
X
⋅
tg
−
Y
tg
+
Y
tg
1
−
=
0,
2
2
k
KGT
2
2
2
2
KGN
k
k
l
где введены следующие обозначения:
βa
α
a
β
b
α
b
2
2
X =k
tg
+ αβtg
,
X =k
tg
+ αβtg
,
2
2
2
2
β
a
α
b
βb
α
a
2
2
Y =k
tg
− αβtg
,
Y =k
tg
− αβ
tg
2
2
2
2
Дефектоскопия
№ 1
2020
Дисперсионное уравнение для продольной волны в слоистой среде...
27
Дисперсионное уравнение (6) определяет волновое число продольной волны при любых значе-
ниях толщин слоев рассматриваемой структуры «сталь—графит». Если в данном уравнении коэф-
фициенты жесткости KGT, KGN→∞, что соответствует сплошному контакту на границе между
средами, то получим дисперсионное уравнение для однородной среды, что соответствует резуль-
татам, полученным в [1].
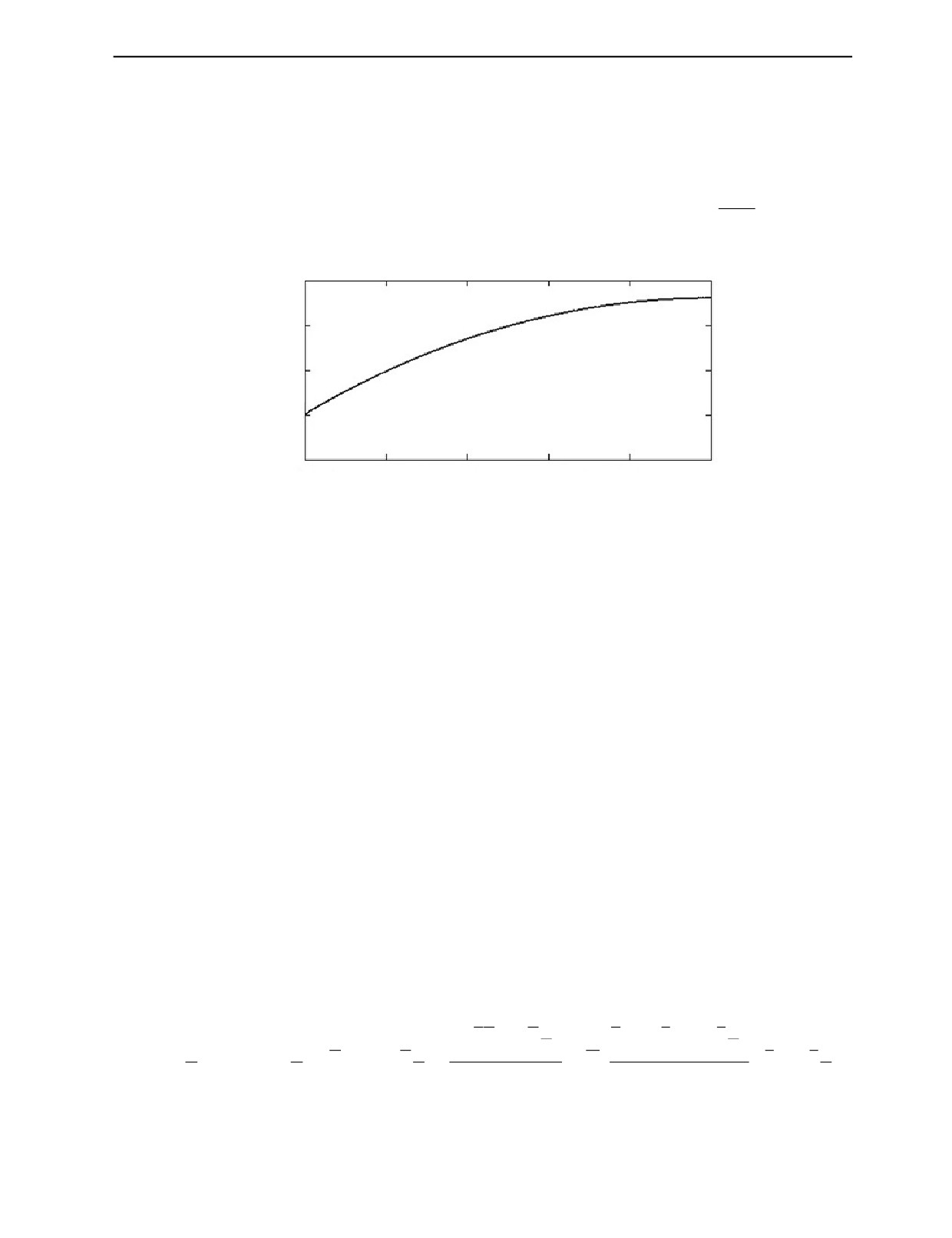
Решим дисперсионное уравнение (6) относительно волнового числа и построим графическую
a+b
зависимость скорости продольной волны cl от относительной толщины слоя
n
=
при распро-
a
странении волны параллельно слоям (рис.4).
cl, м/с
5900
5000
4100
3200
0
0,2
0,4
0,6
0,8
n
Рис. 4. Зависимость скорости продольной волны от относительной толщины слоя при распространении параллельно
слоям.
Ранее, в [2, 3], вид данной графической зависимости приводил к некоторым ошибкам, которые
заключались в том, что при увеличении относительной толщины слоя зависимость начинала убы-
вать, то есть скорость продольной волны в структуре «сталь—графит» начинала стремиться к
значению скорости в графите, что противоречит физическому смыслу при прохождении волны из
более плотной среды (сталь) в более мягкую (графит). Полученная зависимость используется в
задачах определения физико-механических характеристик (модуль упругости, коэффициент
Пуассона, модуль Юнга) материалов на основе акустических измерений.
Распространение продольной волны перпендикулярно слоям. Пусть в направлении оси x
распространяется продольная волна. Как уже было сказано, для такой волны коэффициенты В и С
в первой и во второй средах равны 0. При распространении продольной волны перпендикулярно
⊥
слоям, отличной от нуля будет только компонента упругого смещения
(
z e ikx
P
ξ
=
[19]. Для
lz
случая поперечной волны, в которой смещение параллельно слоям, отличной от нуля будет компо-
⊥
−ikx
нента упругого смещения
ξ
=Q z)e
При такой геометрии распространения волн, их распро-
tz
странение можно рассматривать независимо друг от друга [20].
Как известно из [21], если матрица-функция A(t) периодична, то есть A(t) ≡ A(t + T ), то любая
ее фундаментальная матрица Φ(t) имеет вид
Φ t)
=Ψ t eBt
, где B — постоянная, а Ψ(t) — непре-
рывно дифференцируемая функция. Данное утверждение описывает теорему Флоке.
Тогда, согласно теореме Флоке, в выражениях, описывающих распространение волн перпенди-
кулярно слоистой структуре (1), величины P(z) и Q(z) должны быть периодическими функциями с
периодом структуры h = a + b. Неоднородные граничные условия и условия периодичности долж-
⊥
ны выполняться для амплитуд
ξ
σ в попереч-
lx
ной волне.
Подставляя соответствующие компоненты для случая перпендикулярного распространения
продольной волны в неоднородные граничные условия (4), получаем уравнения для коэффициен-
тов A и D в первой и во второй средах:
b
2
b
2
2ikµαsin
α
µ
k
−β
sin
β
(
)
a
a
b
2
2
b
Aikcos
α
-
Dβcos
β
=
Aikcos
α
+
+
D
-βcos
β
,
2
2
2
KGT
KGT
2
Дефектоскопия
№ 1
2020
28
К.Е. Аббакумов, А.В. Вагин
2
2
a
1
λk
l
+2µα
a
b
a
b
Acos
α
1+
-
Dsin
β
=
Acos
α
-
D
sin
β
+2µβcos
β
,
2
KGN
ik
2
2
2
2
a
2
2
a
b
2
2
b
A4
ikµαsinα
-
D
(
k
−β
)
sinβ
=
A4ikµαsinα
-
D
(
k
−β
)
sinβ
,
2
2
2
2
2
2
a
a
2
2
b
b
A
(
λk
+
2µα
)
cos
α
+
D2µβikcos
β
=
A
λk
l
+2µα
cos
α
+
D2µβikcos
β
l
(
)
2
2
2
2
Из полученных уравнений для коэффициентов A и D для первой и второй сред составим
детерминант и приравняем его к нулю:
b
2
2
b
2µαiksinα
µ
k
−β
sinβ
(
)
a
a
b
2
2
b
ikcos
α
-βcosβ
ikcos
α
+
-βcosβ
2
2
2
KGT
KGT
2
2
2
a
1
λk
l
+2µα
a
b
a
b
cosα
1+
-sinβ
cosα
-sinβ
+2µβcosβ
2
KGN
ik
2
2
2
2
=
0.
a
2
2
a
b
2
2
b
4ikµαsin
α
-
(
k
−β
)
sin
β
4ik
µαsinα
-
(
k
−β
)
sinβ
2
2
2
2
2
2
a
a
2
2
b
b
(
λ
k
l
+2µα
)
cosα
2
µβikcosβ
(
λ
k
l
+
2µα
)
cosα
2µβ
ikcosβ
2
2
2
2
Решая данный определитель разложением по первой строке с учетом граничных условий пери-
одичности (5), получим дисперсионное уравнение (7) для продольной волны, распространяющей-
ся перпендикулярно слоям структуры «сталь—графит»:
2
λ+2µ
k
(
λ+2µ
)
k
1−χ
(
)
l
l
1
cos
k
a
cos
k
b
+1
+
sin
k
a
sin
k
b
-1-
cos
k
a+b
0,
(7)
(
l
)
(
l
)
(
l
)
(
l
)
(
)
=
KGT
2
χ
KGN
1
(
λ+2µ
)
k
l
χ
=
где
1
(
λ+
2µ
)
k
l
Если в данном дисперсионном уравнении (7) устремить коэффициенты жесткости к бесконеч-
ности, KGT , KGN → ∞, что будет соответствовать распространению волны в однородной среде,
которая описывается классическими неразрывными граничными условиями, то получим диспер-
сионное уравнение для волны в однородной среде, что согласуется с результатами, представлен-
ными в [3].
⊥
⊥
Дисперсионное уравнение (7) определяет волновое число для продольной волны
k
l
=ω/c
l
,
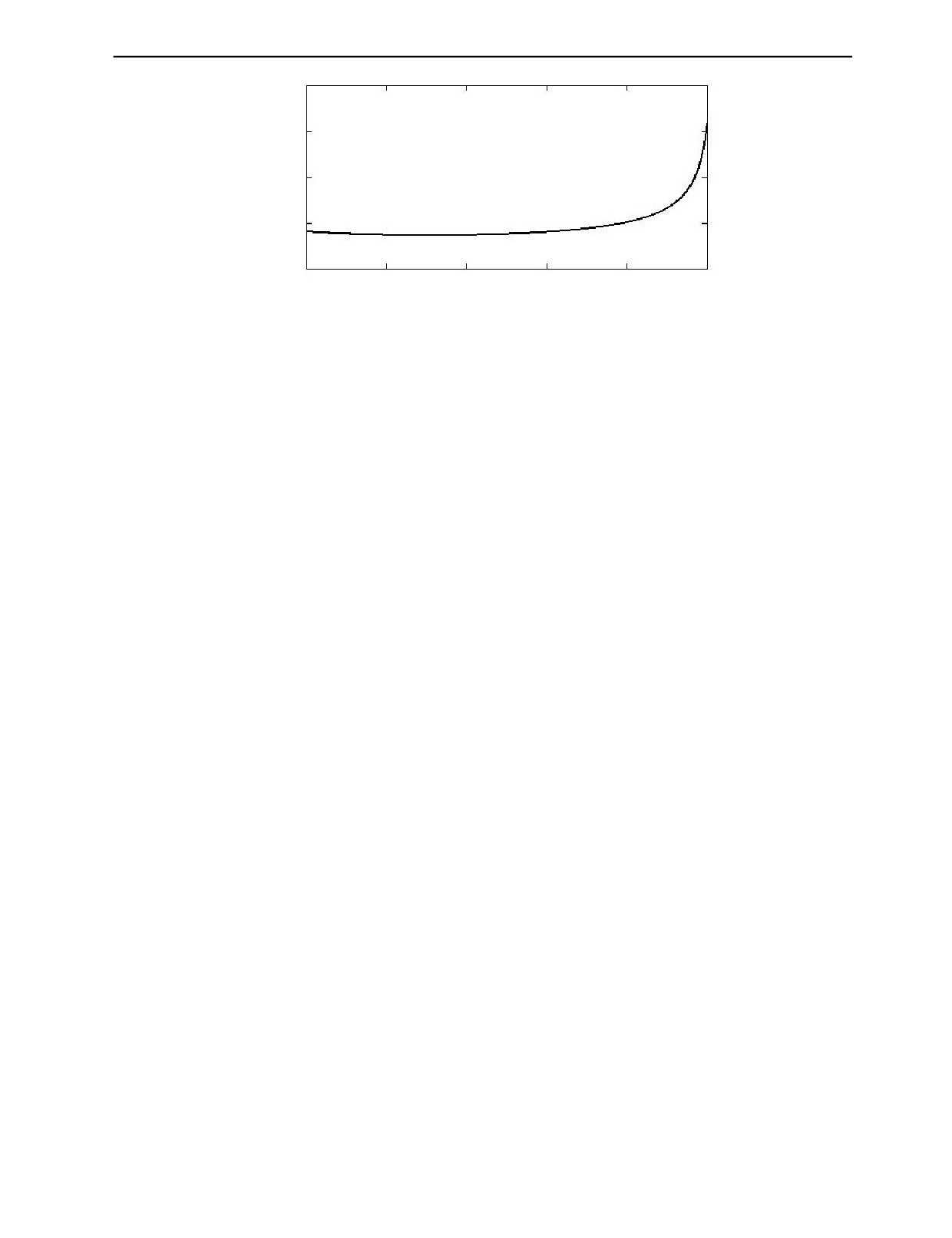
распространяющейся перпендикулярно слоям структуры. Решая данное уравнение относительно
c⊥ от
относительной толщины слоя n (рис. 5).
Как видно из данной графической зависимости, значение скорости продольной волны в случае
распространения перпендикулярно слоям при увеличении относительной толщины слоя начинает
возрастать, что согласуется с экспериментальными данными, приведенными в [18, 22]. В случае
однородной среды вид данной графической зависимости сохраняется, однако значение скорости
продольной волны несколько выше, чем в неоднородной среде, что связано с наличием переотра-
жений волн между слоями и рассеянием на структурных неоднородностях среды [23].
Имея полученные зависимости скорости продольной волны от относительной толщины слоя
материала образца контроля, можно перейти к задаче о нахождении скорости поверхностной
волны. Однако для рассмотрения этого случая необходимо знать скорости поперечных волн, вер-
тикальной и горизонтальной поляризации. Контроль физико-механических характеристик матери-
ала с помощью поверхностной волны имеет очень важное значение, так как в этом случае с доста-
точной точностью можно получить интересующие характеристики [24]. Это обусловлено тем, что
Дефектоскопия
№ 1
2020
Дисперсионное уравнение для продольной волны в слоистой среде...
29
cl⊥, м/с
5000
4000
3000
2000
0
0,2
0,4
0,6
0,8
n
Рис. 5. Зависимость скорости продольной волны от относительной толщины слоя при распространении перпендикулярно
слоям.
вся энергия поверхностной волны локализуется в приповерхностном слое образца контроля тол-
щиной порядка двух длин волн, что дает существенную зависимость параметров поверхностной
волны от свойств слоя, в котором она распространяется.
ВЫВОДЫ
1. Показано влияние на абсолютные значения фазовых скоростей продольных волн таких пара-
метров микротрещин, как величина шероховатости, взаимодействующих в приближении «линей-
ного скольжения» краев трещин и других неоднородностей среды.
2. Решена задача о нахождении скорости продольной волны при двух вариантах распростране-
ния (параллельно и перпендикулярно слоям) в неоднородной среде с объемной трещиноватостью
путем решения относительно волнового числа дисперсионного уравнения.
3. Полученные зависимости используются применительно к задачам нахождения основных
физико-механических характеристик материала на основе акустических измерений, а также в
качестве основного материала для проведения предизмерительных изысканий с целью получения
максимального объема информации без применения средств ультразвукового контроля.
СПИСОК ЛИТЕРАТУРЫ
1. Аббакумов К.Е., Вагин А.В. Волновые процессы в мелкослоистой среде // Изв. СПбГЭТУ
«ЛЭТИ». 2018. № 8. С. 87—91.
2. Рытов С.М. Акустические свойства мелкослоистой среды // Акустический журн. 1956. Т. 2. № 1.
С. 71—83.
3. Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973. 340 с.
4. Jose M. Carcione anisotropic Q and velocity dispersion of finely layered media // Geophysical
Prospecting. 1992. V. 40. P. 761—783.
5. Luk’yashko O.A., Saraikin V.A. Transient one-dimensional wave processes in a layered medium //
Journal of Mining Science. 2007. V. 43. P. 145—158.
6. Гузь А.Н. Упругие волны в телах с начальными напряжениями. Киев: Наукова думка, 1986. 536 с.
7. Brun M., Guenneau S., Movchan A.B., Bigoni D. Dynamics of structural interfaces: Filtering and
focussing effects for elastic waves // J. Mech. Physics Solids. 2010. V. 58. P. 1212—1224.
8. Panasyuk O.N. Propagation of Quasishear Waves in Prestressed Materials with Unbonded Layers // Int.
Appl. Mech. 2011. V. 47. P. 276—282.
9. Кристенсен Р. Введение в механику композитов. М.: Мир, 1982. 336 с.
10. Guz A.N., Rushitsky J.J. Short Introduction to Mechanics of Nano-composites. Rosemead: Scien. and
Academic Publishers, 2013. 280 p.
11. Панасюк О.Н. Анализ влияния граничных условий на распространение волн в слоистых компо-
зитных материалах // Прикладная механика. 2014. № 4. С. 52—58.
12. Akbarov S.D., Guliev M.S., Kepceler T. Propagation of axisymmetric waves in an initially twisted
circular compound bimaterial cylinder with a soft inner and a stiff outer constituents // Mech. Comp. Mater.
2011. V. 46. P. 627—638.
13. Khlybov A. A. Studying the Effect of Microscopic Medium Inhomogeneity on the Propagation of
Surface Waves // Russian Journal of Nondestructive Testing. 2018. V. 54. No. 6. P. 385—393. [Хлыбов А.А.
Исследование влияния микронеоднородности среды на распространение поверхностных волн // Дефек-
тоскопия. 2018. № 6. С. 3—10.]
Дефектоскопия
№ 1
2020
30
К.Е. Аббакумов, А.В. Вагин
14. Петрашень Г.И. Распространение волн в анизотропных упругих средах. Л.: Наука, 1980. 280 с.
15. Чабан И.А. Расчет эффективных параметров микронеоднородных сред методом самосогласо-
ванного поля // Акустический журн. 1965. № 1. С. 102—109.
16. Чабан И.А. Метод самосогласованного поля в применении к расчету эффективных параметров
микронеоднородных сред // Акустический журн. 1964. № 3. С. 351—358.
17. Аббакумов К.Е., Кириков А.В., Львов Р.Н. Преломление упругих волн на плоской границе раз-
дела с нарушенной адгезией твердых сред // Изв. СПбГЭТУ «ЛЭТИ». 2003. № 1. С. 10—17.
18. Evel’son R.L. A fine-layered medium of finite-thickness in an electromagnetic field // Journal of
communications technology and electronics. 2015. V. 60. I. 6. P. 552—559.
19. Вавакин А.С., Салганик Р.Л. Эффективные упругие характеристики тел с изолированными тре-
щинами, полостями и жесткими неоднородностями // Механика твердого тела. 1978. № 2. С. 95—107.
20. Шермергор Т.Д. Теория упругости микронеоднородных сред. М.: Наука, 1977. 400 с.
21. Floquet M.G. Sur les equations differentielles lineaires a coefficients periodiques // Annales
scientifiques de I’Ecole Normale Superieure. 1983. V. 12. P. 47—88.
22. Купрадзе В.Д., Соболев С.Л. Упругие волны на границах двух сред // Тр. Сейсмического ин-та
АН СССР. 1930. № 10. С. 58—67.
23. Викторов И.А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике.
М.: Наука, 1996. 196 с.
24. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 287 с.
Дефектоскопия
№ 1
2020