УДК 620.179.16
ИСПОЛЬЗОВАНИЕ МЕТОДА АКУСТОУПРУГОСТИ ДЛЯ КОНТРОЛЯ УПРУГИХ
МЕХАНИЧЕСКИХ НАПРЯЖЕНИЙ В МАТЕРИАЛЕ КОЛЕЦ ПОДШИПНИКОВ
© 2020 г. А.О. Рыжова1,*, С.А. Бехер1,**, А.А. Попков1,***
1Сибирский государственный университет путей сообщения, Россия 630049
Новосибирск, ул. Дуси Ковальчук, 191
E-mail: *annalodo@yandex.ru, **beher@stu.ru, ***zabagy@gmail.com
Поступила в редакцию 04.08.2020; после доработки 23.09.2020
Принята к публикации 29.09.2020
Разработаны и изготовлены настроечные образцы натяга колец подшипников на шейку оси колесной пары вагона и
выполнена аттестация гидравлического стенда для нагружения колец подшипников, имитирующего их прессовую
посадку на ось. Создана и решена математическая модель способа контроля механических напряжений кольца подшип-
ника акустоупругим методом при хордовом прозвучивании, учитывающая изменение угла между направлением распро-
странения волны и осью главных механических напряжений. Экспериментально при нагружении кольца подшипника
определен коэффициент акустоупругости продольной волны в стали ШХ15. Проведены измерения натяга колец под-
шипников на настроечных образцах натяга методом акустоупругости.
Ключевые слова: акустоупругость, ультразвуковой контроль, хордовое прозвучивание, внутренние кольца подшип-
ников, прессовая посадка, неразрушающий контроль, механические напряжения.
DOI: 10.31857/S0130308220110032
ВВЕДЕНИЕ
Надежность неподвижных разъемных соединений колец буксовых подшипников, напрессо-
ванных на шейки осей колесных пар, напрямую влияет на количество отказов железнодорожных
транспортных средств в эксплуатации. Внутренние кольца удерживаются на осях колесных пар
силами трения, которые линейно зависят от упругих механических напряжений в материале колец.
Технология ремонта вагонов предусматривает контроль разности диаметров (натяга) шеек осей
и колец подшипников до прессовой посадки. Допустимое значение натяга в действующей техни-
ческой документации (РД ВНИИЖТ 27.05.01—2017) находится в диапазоне от 45 до 110 мкм и
соответствует упругим механическим напряжениям в материале колец от 70 до 170 МПа. Много-
кратный демонтаж и повторный монтаж внутренних колец являются причиной образования зади-
ров на шейках осей, появление которых приводит к браковке и списанию осей в металлолом. Для
увеличения среднего срока службы осей колесных пар при плановых видах ремонта внутренние
кольца подшипников, удовлетворяющие требованиям нормативной и технической документации,
допускается не снимать.
В процессе эксплуатации колесных пар с буксовыми узлами прочность посадки колец подшип-
ников снижается, что может быть вызвано нарушениями как технологии ремонта, так и условий
эксплуатации. Нагрев буксовых узлов вызывает тепловое расширение колец, следствием которого
является проворот и сошлифовывание части шейки оси. Недостаточная защита буксовых узлов от
воздействия атмосферы приводит к фреттинг-коррозии. Этот тип повреждения является причиной
интенсивного износа сопрягаемых поверхностей и последующего уменьшения натяга.
Для контроля упругих механических напряжений в материале колец при плановых видах ре-
монта перспективно использовать акустические методы, основанные на явлении акустоупругости.
К преимуществам акустических методов относится возможность контроля не только поверхност-
ных, но и внутренних напряжений. Контроль с использованием акустоупругости является инте-
гральным, что позволяет определять не локальные, а средние значения упругих напряжений на
пути распространения волны [10].
Акустические методы контроля напряжений основаны на зависимости скорости распростра-
нения упругой волны от упругих деформаций (напряжений) материала объекта контроля. В на-
стоящее время метод акустоупругости подробно исследован [1—3, 5, 11—15], разработаны спо-
собы измерения скоростей распространения [6—9], основанные на автоциркуляции и корреляции
регистрируемых сигналов. Достигаемая при этом точность измерения скоростей распространения
с пределом допускаемой относительной погрешности, равным 10-5 [8], обеспечивает абсолютную
погрешность измерения напряжений не более 1 МПа.
Использование метода акустоупругости для контроля упругих механических напряжений...
29
Несмотря на наличие развитой теории акустоупругости, отдельные вопросы, необходимые для
решения задачи контроля упругих напряжений в кольцах подшипников, проработаны недостаточ-
но. Учитывая аксиальную симметрию прессового соединения, необходимо, например, решение ме-
тодических вопросов контроля объектов, при прозвучивании которых угол между волновым векто-
ром и осью главных механических напряжений изменяется на всем пути распространения волны.
Целью исследования является создание способов экспериментального определения механиче-
ских напряжений с использованием явления акустоупругости в кольцах подшипников, напрессо-
ванных на шейки осей колесных пар с натягом.
ОПИСАНИЕ ЭКПЕРИМЕНТА
Исследование акустоупругих характеристик материала колец подшипников проводились на
специализированном стенде и образцах натяга. Гидравлический стенд воспроизводит упругое на-
пряженно-деформированное состояние кольца подшипника (рис. 1а), создавая на внутренней по-
верхности гидравлическое давление P. С помощью тензометрического комплекса «Динамика-3»
[17] выполнена тарировка манометра стенда для определения зависимости механических дефор-
маций (напряжений) от давления в гидравлической системе стенда. Тензодатчик проволочный типа
ПКС-7 [16] наклеивался на внешнюю поверхность кольца подшипника и ориентировался вдоль
окружности для измерения растягивающих деформаций. Рассчитанные при этом значения напря-
жений σ линейно зависят от давления в гидравлической системе стенда в диапазоне от 5 до 28 МПа
с коэффициентом корреляции более 0,99:
σ = α · P - β,
(1)
где α = (2,42 ± 0,03), β = (10,2 ± 0,5) МПа — коэффициенты линейной регрессии, полученные мето-
дом наименьших квадратов; P — давление в гидравлической системе, МПа.
а
б
Кольцо
Манометр
Акустическая задержка
подшипника
Излучающий
Принимающий
преобразователь
преобразователь
Напряжение, σ
Манометр
Давление, P
P
Кольцо
подшипника
Гидроцилиндр
Ультразвуковой
Осциллограф
дефектоскоп
Рис. 1. Схема прозвучивания кольца подшипника продольными волнами (б) при механических испытаниях в нагружаю-
щем устройстве (а).
Образцы натяга изготавливались из бывших в эксплуатации и новых колец подшипников ро-
ликовых цилиндрических типа 36-42726E2М по ГОСТ 18572—2014, напрессованных на валы, из-
готовленные из стали марки 45 по ГОСТ 1050—88 с шероховатостью поверхности Ra < 1,25 мкм.
Валы и кольца с погрешностью размеров не более 5 мкм подбирались по диаметрам таким обра-
зом, чтобы значения натягов образцов равномерно распределялись в диапазоне от 40 до 120 мкм.
Дефектоскопия
№ 11
2020
30
А.О. Рыжова, С.А. Бехер, А.А. Попков
Акустические импульсы в излучающем пьезоэлектрическом преобразователе (ПЭП) возбужда-
лись дефектоскопом УД2-102 (зарегистрирован в государственном реестре средств измерений под
№ 18007-06). Электрические сигналы с принимающего ПЭП регистрировались цифровым запоми-
нающим осциллографом TBS-2104 (номер в государственном реестре средств измерений № 66636-
17). Прибор обеспечивает регистрацию сигналов с частотой дискретизации до 1 нс и сохранение
оцифрованных сигналов длительностью до 20 мс.
Кольца подшипников «прозвучивались» продольными волнами по раздельной схеме (рис. 1б).
Регистрируемые сигналы сохранялись в цифровой форме с частотой дискретизации 1 ГГц и обра-
батывались с использованием разработанного алгоритма в программной среде Mathcad.
Ультразвуковые волны вводились в кольцо подшипника по хорде с использованием акустиче-
ской задержки, изготовленной из стали марки 20 по ГОСТ 1050—88 (рис. 2). Поверхность, прилега-
ющая к кольцу, повторяла форму внешней поверхности кольца. Акустическая задержка устанавли-
валась на предварительно смазанную трансформаторным маслом поверхность кольца подшипника
и притиралась для обеспечения минимальной толщины слоя контактной жидкости. К акустической
задержке соосно приклеены излучающий и принимающий прямые преобразователи П111-2,5-К12
с резонансной частотой 2,5 МГц. Принимающим ПЭП регистрировались все типы ультразвуковых
волн: продольные, поперечные и поверхностные, как прошедшие через кольцо, так и прошедшие
через акустическую задержку. В данной работе анализировался только первый сигнал на интервале
времени от 19 до 22 мкс относительно зондирующего импульса (рис. 3), связанный с продольной
волной, прошедшей по кратчайшему пути от источника до приемника. При снятии акустической
задержки с кольца сигнал исчезает.
105,0±0,1
А(2:1)
А
Пропил
1,00±0,02
Излучающий
Принимающий
Акустическая задержка
преобразователь
преобразователь
83,7±0,1
Рис. 2. Акустическая задержка с излучающим и принимающим ПЭП для хордового прозвучивания кольца подшипника
продольной волной.
0,1
Эхосигналы
Зондирующий
импульс
0
-0,1
0
10
20
30
40
Время, мкс
Рис. 3. Вид сигнала на принимающем преобразователе при хордовом прозвучивании кольца подшипника продольными
волнами.
Скорости распространения ультразвуковых волн составили: в кольце — 5,92 мм/мкс, в аку-
стической задержке — 5,86 мм/мкс, в оси (валу) — 5,91 мм/мкс. Разница скоростей в кольце под-
шипника и акустической задержке не превышает 1 %, отклонение направления распространения
волны в направлении акустической оси в результате двухкратного преломления при переходе через
границы «акустическая задержка — кольцо подшипника» и «кольцо подшипника — акустическая
Дефектоскопия
№ 11
2020
Использование метода акустоупругости для контроля упругих механических напряжений...
31
задержка» не превышает 2°. Это угловое отклонение приводит к смещению луча на приемнике на
2,0—2,5 мм и компенсируется изменением высоты приемного преобразователя относительно из-
лучающего.
С момента времени 22 мкс сигнал носит случайный характер, вызванный наложением волн раз-
личных типов, переотраженных в акустической задержке и в кольце подшипника. Информативный
сигнал и шумы удалось разделить на временной оси только благодаря пропилам глубиной 13 мм в
акустической задержке и сошлифовыванию средней части цилиндрической поверхности акустиче-
ской задержки до диаметра 160 мм (см. рис. 2).
ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ
Изменение скорости распространения ультразвуковой волны при нагружении кольца измеря-
лось косвенным методом по задержке сигнала относительно опорного, полученного на полностью
разгруженном кольце подшипника (рис. 4а). Наибольшее значение задержки времени распростра-
нения волны составило 9,5 нс, что существенно меньше периода колебаний T = 400 нс. Прямой
метод измерения по сдвигу сигнала на заданном уровне (пороговый метод) не обеспечивает не-
обходимую точность измерений малых по сравнению с периодом колебания временных интерва-
лов, так как даже незначительные вариации амплитуды сигнала при растяжении кольца вызывают
существенные изменения времени (более 5 нс). Для повышения точности измерений времени за-
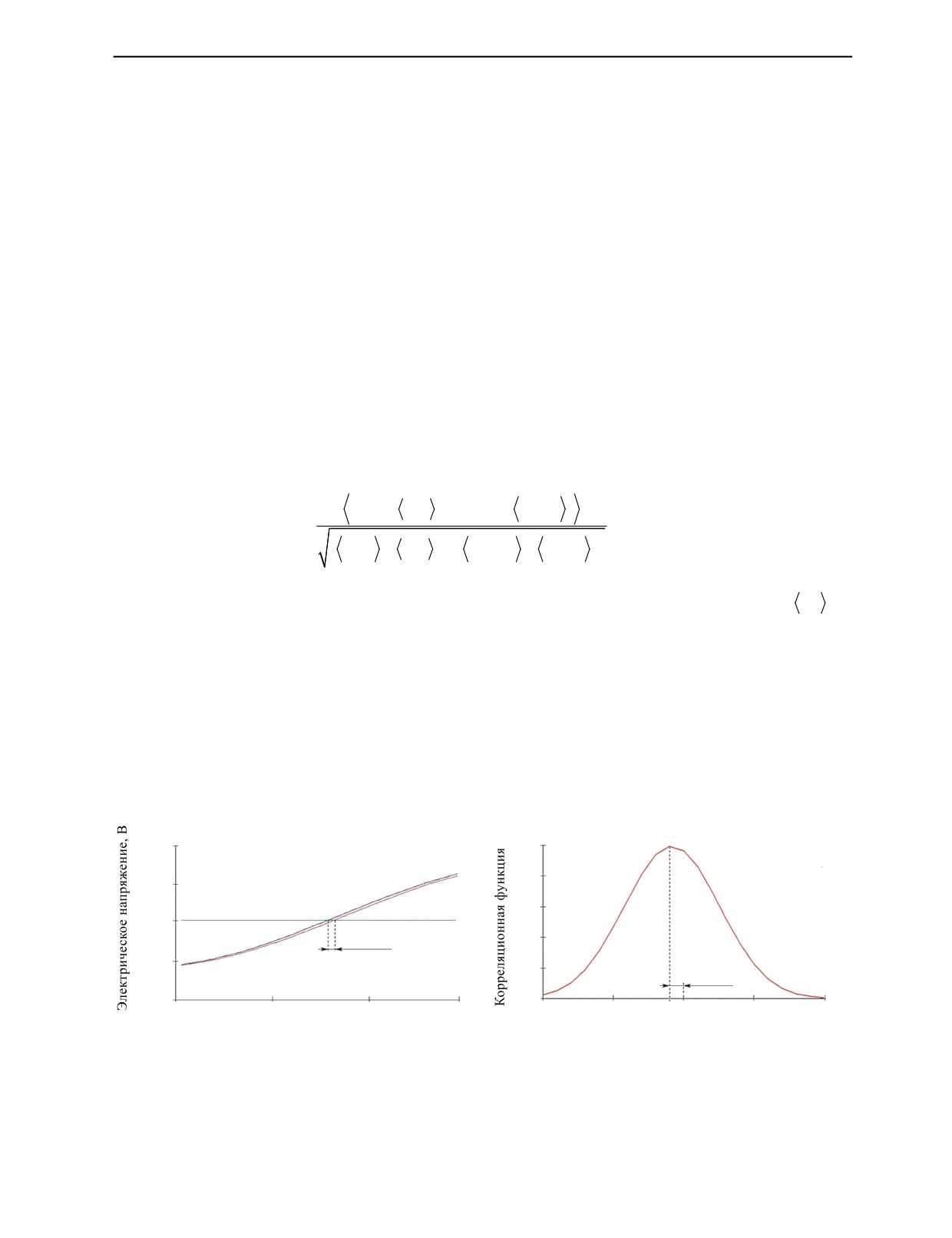
держки в программной среде Mathcad реализован корреляционный метод, основанный на опреде-
лении максимума дискретной корреляционной функции Afj двух сигналов U1i и U2i на интервале
от t1 до t2:
U1
−
U1
U2
−
U2
(
i
i
)⋅(
i+ j
i+ j
)
Af
=
,
j
(2)
2
2
2
2
U1
−
U1
U2
−
U2
(
i
i
)⋅(
i+ j
i+ j
)
где Afj — значения корреляционной функции в j-ый момент времени; U1i и U2i — значения элек-
трического напряжения опорного и регистрируемого сигналов в i-ый момент времени, мВ;
—
оператор усреднения на интервале от t1 до t2.
График корреляционной функции сигнала, зарегистрированного при нагружении кольца
подшипника до уровня относительных деформаций 100·10-6, с опорным сигналом приведен на
рис. 4б. Для наглядности отложенная по вертикальной оси корреляционная функция возведена
в 50-ю степень. Максимум корреляционной функции соответствует смещению сигналов на 2 нс.
Использование алгоритма, основанного на анализе коэффициента корреляции сигналов относи-
тельно опорного, позволяет оценивать временной сдвиг между ними с неопределенностью не более
± 1 нс. Полученное значение сдвига является интегральным параметром сигнала, который рассчи-
тывается усреднением на интервале t2 - t1 = 3 мкс, что соответствует (5—6) периодам колебаний.
а
б
0,10
1,0
Опорный сигнал
на ненагруженном
0,8
0,05
кольце
Сигнал при
0,6
нагружении
0
кольца
0,4
Задержка
времени
-0,05
Задержка
0,2
времени
-0,10
0
20,5
20,55
20,60
20,65
-20
-10
0
10
20
Время, мкс
Время, нс
Рис. 4. Способы определения времени задержки сигналов: пороговый (а) и по максимуму корреляционной функции (б).
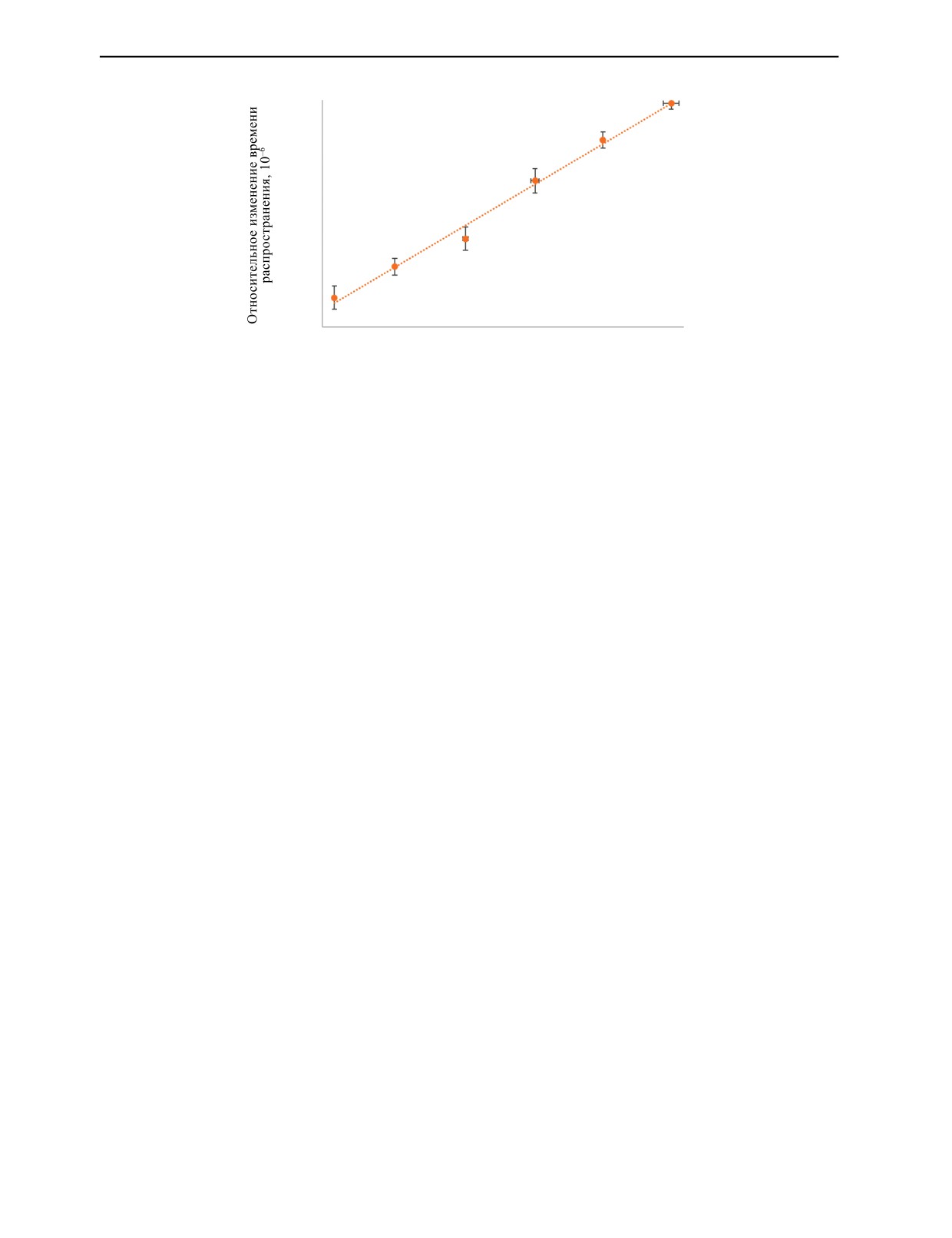
Задержка времени акустического импульса продольной волны относительно опорного сигнала
линейно зависит от механических напряжений в кольце подшипника с коэффициентом корреляции
более 0,99 (рис. 5). Экспериментальные данные получены как при нагружении, так и при разгрузке
Дефектоскопия
№ 11
2020
32
А.О. Рыжова, С.А. Бехер, А.А. Попков
600
500
400
300
200
100
0
0
10
20
30
40
50
60
Напряжение, МПа
Рис. 5. Зависимость относительного изменения времени распространения продольной волны при хордовом прозвучива-
нии кольца подшипника от механических напряжений.
кольца. Методом наименьших квадратов установлены параметры линейной функции, аппроксими-
рующей экспериментальную зависимость:
δt = d × σ + c,
(3)
где δt — относительное изменение времени распространения, 10-6; σ — механическое напряже-
ние, МПа; d = 9,77 ТПа-1 — коэффициент пропорциональности и с = 45,74× 10-6 — коэффициент
смещения.
Коэффициент пропорциональности d является коэффициентом акустоупругости по времени
распространения, который при постоянной базе прозвучивания, очевидно, равен с обратным зна-
ком коэффициенту акустоупругости по скорости распространения волны:
d = 9,77 ТПа-1.
(4)
Среднее квадратическое отклонение коэффициента d составляет 0,68ТПа-1 (7 %). Справочные
значения коэффициента акустоупругости по времени при постоянной базе прозвучивания для раз-
ных сталей варьируются в диапазоне от 2,70 до 28,79 ТПа-1 [4]. Коэффициент d, определяемый
выражением (4), равен коэффициенту акустоупругости только в рамках модели, в которой допу-
стимо пренебречь изменениями угла между направлением распространения волны и осью главных
механических напряжений.
АНАЛИЗ РЕЗУЛЬТАТОВ
Математический аппарат для количественного описания явления акустоупругости основан на
использовании тензорного исчисления [4]. В случае одноосного напряженно-деформированного
состояния изотропного материала с единственной ненулевой компонентой тензора механических
напряжений σ3, 3≠ 0, акустические характеристики материала описываются тензором акустоупругих
коэффициентов βi, j, где i, j — индексы координатных осей (1, 2, 3) направления распространения
волны и направления колебаний соответственно. Тензор βi,j имеет девять компонент, измеряемых в
ТПа-1, из которых независимыми являются только пять: β3,3, β1,1, β1,3, β3,1, β1,2.
Относительное изменение скорости распространения, вызванное действием упругих меха-
нических напряжений, описывается тензором δvi,j. Первый индекс i определяет направление рас-
пространения волны, второй индекс j — поляризацию волны. Очевидно, что δv1,1, δv2,2, δv3,3 —
относительные изменения скоростей продольных волн, распространяющихся вдоль осей x, y, z
соответственно.
В случае одноосного напряженного состояния изотропного материала с единственной нену-
левой компонентой тензора механических напряжений σ3,3 относительные изменения скоростей
распространения продольных волн описываются выражением:
Дефектоскопия
№ 11
2020
Использование метода акустоупругости для контроля упругих механических напряжений...
33
δvi, j = βi, j × σ3,3.
(5)
В случае сложного напряженного состояния, отличного от одноосного растяжения—сжатия,
тензор δvi, j относительного изменения скоростей распространения связан с тензором напряжений
σi, j в произвольном базисе координатных осей выражением:
δvi, j = γi, j, m,n × σm,n,
(6)
где γi,j, m,n — тензор акустоупругости для произвольного тензора напряжений σm, n; m, n — индексы
координатных осей в произвольном базисе. Связь тензора γi, j, m,n с тензором βi, j приведена в [4].
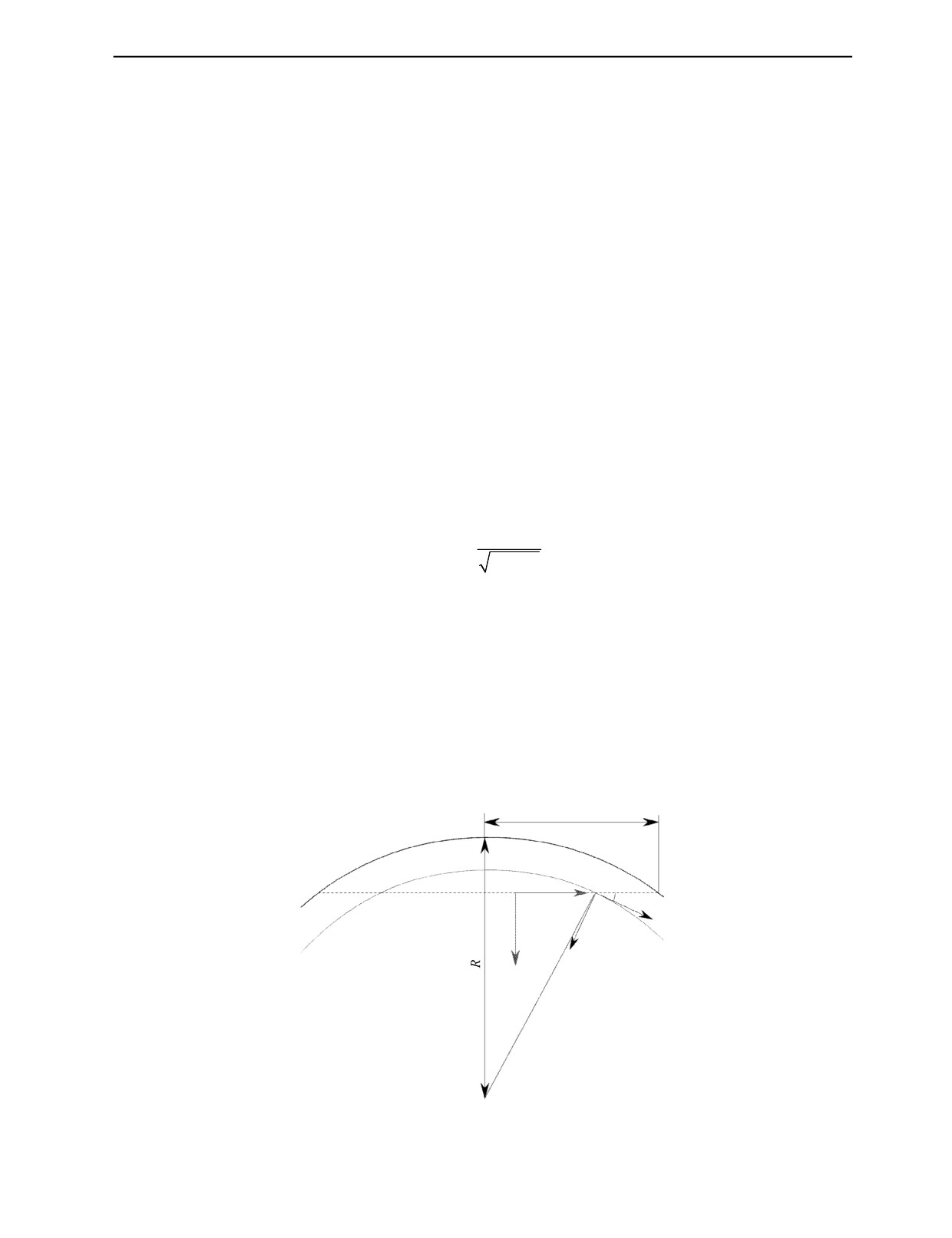
Использование выражения (6) для решения практических задач затрудняет физическую интер-
претацию результатов в случае наклонного распространения волн относительно главных осей на-
пряжений, когда базисы скоростей и механических напряжений не совпадают. В этом случае вы-
ражение (6) представимо в виде, в котором тензор механических напряжения задан в собственном
базисе и преобразуется к базису скоростей (рис. 6):
δv
=γ
⋅
A
⋅
A
⋅σ
,
(7)
i,
j
i j,m′,n′
m′,m n′,n
m,n
где
A
и
A
— матрицы перехода от базиса x, y, z к базису, привязанному к направлению рас-
m′,m
n′,n
пространения волны x', y', z'.
Расчет изменения времени распространения, учитывающий неколлинеарность направлений
распространения волны и действия механических напряжений, проводился с использованием тен-
зорной модели (рис. 6). В каждой точке луча волны угол φ между базисами главных напряжений
z, y и волны z', y' определяется выражением:
z′
tg(ϕ)
=
(8)
2
2
R
-l
Тензор перехода от базиса напряжений к базису скоростей выражается через угол между хор-
дой и касательной к окружности φ (рис. 6) и в матричной форме имеет вид:
1
0
0
A=
0
cos(ϕ)
sin(ϕ)
(9)
0
− ϕ) cos(ϕ)
Для одноосного напряженно-деформированного состояния только одна компонента тензора на-
пряжений отлична от нуля σ3,3= σ0 (в соответствии с рис. 6):
l
Наружная
поверхность
кольца
z'
φ
Направление
Базис
распространения
волны
z
Базис
волны
главных
напряжений
y
σ
3,3
y'
Рис. 6. Схема ориентации базиса волны z', y' и базиса главных напряжений z, y при распространения продольной волны
в кольце подшипника.
Дефектоскопия
№ 11
2020
34
А.О. Рыжова, С.А. Бехер, А.А. Попков
0
0
0
0
0
0
(10)
σ=
0
0
σ
0
Подстановка (9) и (10) в (7) дает выражение для относительного изменения скорости волны в
виде функции угла φ для продольных и поперечных волн с поляризацией по оси y' волн:
2
2
δv
3,3
=σ
0
⋅
(
β
2,2
⋅(sin(ϕ))
+β
3,3
⋅(cos(ϕ))
)
,
(11)
2
2
δv
=σ
⋅
β
⋅(sin(ϕ))
+β
⋅(cos(ϕ))
(12)
3,2
0
(
1,3
3,1
)
Выражения (11) и (12) после замены тригонометрических функций их выражениями через рас-
стояния и координаты из (8) позволяют установить зависимости скоростей распространения волн
от координаты zʹ:
2
2
2
z′
R - l)
δv
=σ
⋅β
⋅
+β
⋅
,
(13)
3,3
0
2,2
2
2
2
3,3
2
2
2
R - l)
+
z′
R - l)
+
z
′
2
2
2
z′
R - l)
δv
=σ
⋅β
⋅
+β
⋅
(14)
3,2
0
1,3
2
2
2
3,1
2
2
2
R - l)
+
z′
R - l)
+
z
′
После алгебраических преобразований уравнения (13) и (14) принимают вид:
2
2
2
β
⋅ z′
+β
⋅
R - l)
2,2
3,3
(
)
δv
=σ
⋅
,
(15)
3,3
0
2
2
2
R - l)
+
z′
2
2
2
β
⋅ z′
+β
⋅
R - l)
1,3
3,1
(
)
δv
=σ
⋅
(16)
3,2
0
2
2
2
R - l)
+
z′
В общем виде в условиях малости δv << 1 выражение для скорости продольной и поперечной
ультразвуковых волн можно представить в виде функции переменной zʹ:
v(zʹ) = C × (1 + δv(zʹ)).
(17)
Дифференциальное уравнение движения волны по хорде:
dz′
=
v z′).
(18)
dt
Выражение (18) с учетом (17) интегрируется методом разделения переменных:
l
dz′
t+∆t
=
dt
(19)
∫
0
∫
0
C⋅(1+δv(
z′))
С учетом малости δv << 1 (19) приводится к определенным интегралам:
l
l
t+∆t
dz′-∫ δv(z
′)
dz′=C
⋅
dt
(20)
∫
0
0
∫
0
После интегрирования и преобразований уравнение (20) принимает вид:
1
l
δ
t
=-
⋅
δv(z′)
dz
′
(21)
∫
0
l
Дефектоскопия
№ 11
2020
Использование метода акустоупругости для контроля упругих механических напряжений...
35
Для продольной волны подстановка (15) в (21) и преобразования позволяют определить отно-
сительное изменение скорости:
2
2
1
l
z′
l
R - l)2
δt
= -σ
⋅
⋅β
⋅
⋅ dz′+β
⋅
⋅ dz′
(22)
l
0
2,2
∫
2
2
2
3,3
∫
2
2
2
0
0
l
R
−l
+
z′
R
−l
+
z′
Второй интеграл в выражении (22) является табличным, первый интеграл может быть пред-
ставлен в виде суммы табличных интегралов, которые после интегрирования приводят выражение
(22) для относительного времени задержки продольной акустической волны к виду:
2
1
δt
= -σ
⋅
β
+
(
β
−β
⋅
(
R
/ l
)
−1⋅arctg
(23)
l
0
(
2,2
3,3
2,2
))
2
(
R
/ l
)
−1
По аналогии с (23) относительное изменение времени задержки поперечной волны:
2
1
δt
= -σ
⋅
β
+
(
β
−β
⋅
(
R
/ l
)
−1⋅arctg
(24)
t
0
(
1,3
3,1
1,3
))
2
(
R
/ l
)
−1
В схеме прозвучивания, представленной на рис. 2, аргумент выражений (23) и (24) равен:
(25)
(
R/l
)2
−1 =1,6.
В рассматриваемой модели хордового прозвучивания кольца подшипника относительные вре-
мена задержки акустических волн, вызванные упругими растягивающими напряжениями, прини-
мают вид:
δt
l
= -σ
0
⋅
(
0,89
⋅β
3,3
+0,11⋅β
2,2
)
(26)
δt
= -σ
⋅
0,89
⋅β
+0,11⋅β
(27)
t
0
(
3,1
1,3
)
Для большинства сталей выполняется соотношение между акустоупругими коэффициентами
β
2,2
0,1
≈
и, следовательно, второе слагаемое в выражении (26) не превышает 1,2 % первого сла-
β
3,3
гаемого. Используя результат аппроксимации (4) для коэффициента пропорциональности относи-
тельного времени задержки и упругих механических напряжений и формулу (26) для времени за-
держки при хордовом прозвучивании, значение коэффициента акустоупругости материала колец
подшипников в изделии составит:
d
β
=-
=-
11,0
ТПа-1 (±8 %).
(28)
3,3
0,89
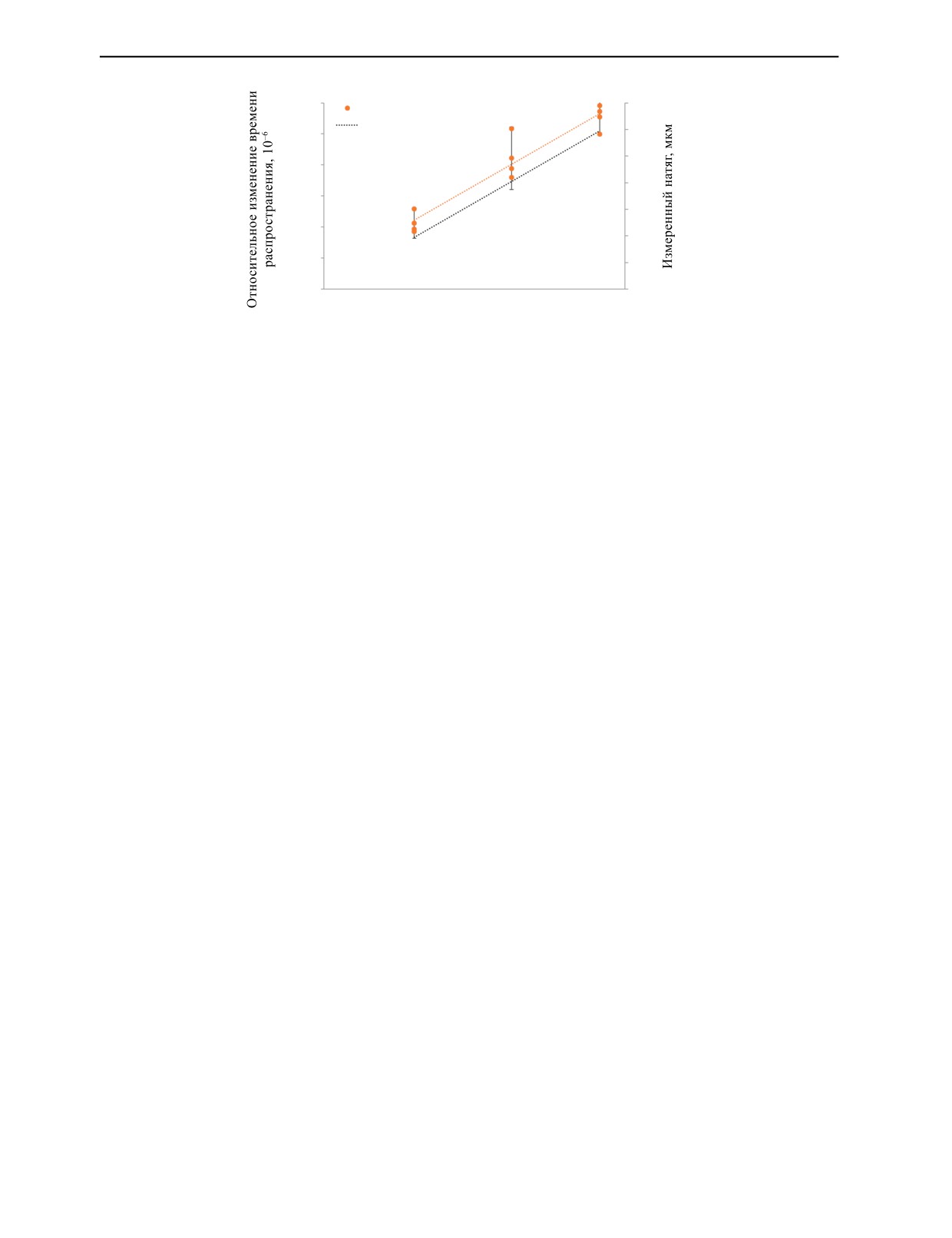
Используя полученные значения акустоупругого коэффициента (4), (28) для продольной
волны, проведены испытания образцов натяга колец подшипников (рис. 7). На каждом из трех
образцов натяга 40, 80 и 120 мкм выполнены измерения в четырех точках, расположенных че-
рез 90°. Средние квадратические отклонения относительного измерения времени распростра-
нения в каждой точке составили от 200·10-6 до 500·10-6. Такие высокие, более 40 % среднего
значения, случайные разбросы результатов наблюдений связаны со слабой повторяемостью
параметров акустического контакта при повторных установках преобразователя на объект кон-
троля. При изменении слоя контактной жидкости на 1 мкм абсолютное время распространения
изменяется на 0,7 нс, а относительное изменение времени распространения волны на 40·10-6.
Таким образом соответствующие вариации толщины контактного слоя жидкости находятся в
диапазоне от 5 до 10 мкм и отражают точность изготовления акустической задержки и коль-
ца подшипника. Рассчитанный по времени задержки в образцах акустический коэффициент
β3,3 = -15,6 ± 4,8 ТПа -1 и с учетом погрешности соответствует экспериментальным результатам
на нагружающем устройстве.
Дефектоскопия
№ 11
2020
36
А.О. Рыжова, С.А. Бехер, А.А. Попков
3000
140
— 1
— 2
120
2500
100
2000
80
1500
60
1000
40
500
20
0
0
0
20
40
60
80
100
120
Натяг настроечного образца, мкм
Рис. 7. Зависимость относительного изменения времени распространения продольной волны (1) и измеренных значений
натяга (2) от натягов настроечных образцов.
ВЫВОДЫ
Разработаны и изготовлены образцы прессовых соединений со значениями натяга в диапазоне
от 38 до 119 мкм с погрешностью не более ± 7 мкм. С использованием тензометрической системы
аттестовано нагружающее устройство для испытания колец подшипников, обеспечивающее на-
пряженно-деформированное состояние с упругими деформациями до 550·10-6, эквивалентными
состоянию колец в прессовом соединении с натягом от 0 до 70 мкм.
Разработана и изготовлена акустическая задержка для хордового прозвучивания продольными
волнами колец подшипников, напрессованных на шейку оси, с базой прозвучивания в материале
кольца, равной 84 мм. Экспериментально определен коэффициент пропорциональности относи-
тельного изменения времени распространения продольной волны и механических напряжений d
= 9,77 ТПа-1. Для модели хордового прозвучивания кольца подшипника при растяжении кольца
аналитически получены зависимости, связывающие акустоупругие коэффициенты продольной
β3,3 и поперечной β3,1 волн с коэффициентом пропорциональности d. Коэффициент акустоупру-
гости для стали ШХ15 в готовом изделии (кольце подшипника) с учетом поправок составил
β3,3 = -11,0 ТПа-1 (±8 %).
При акустическом контроле образцов натяга показано, что невоспроизводимость акустического
контакта при повторной установке преобразователя на объект контроля с вариациями контактного
слоя (5—10) мкм вносит основной вклад в погрешность измерений акустоупругих коэффициен-
тов — 30 %. Кроме того, разброс значений может быть обусловлен неравномерностью посадки по
окружности кольца подшипника из-за конусности и овальности сопрягаемых поверхностей. По-
грешность определения натягов в образцах методом акустоупругости c усреднением в трех точках
составила от 20 до 40 %.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта
№ 19-38-90016.
СПИСОК ЛИТЕРАТУРЫ
1. Gushcha O.I., Lebedev V.K. The effect of stresses on the velocity of propagation for ultrasonic waves in
metals // Soviet Applied Mechanics. 1972. V. 2. P. 52—53.
2. Landau L.D., Lifshitz E.M. Course of theoretical physics // Butterworth-Heinemann. 1986. V. 7 (3rd ed.).
3. Muravyev V.V., Muravyeva O.V., Strizhak V.A., Pryakhin A.V., Balobanov E.N., Vvolkova L.V. Evaluation
of residual stresses in rims of wagon wheels using the electromagnetic-acoustic method // Russian journal of
nondestructive testing. 2011. V. 47. No. 8. P. 512—521.
4. Анисимов В.А., Каторгин Б.И., Куценко А.Н., Малахов В.П., Рудаков А.С., Чванов В.К. Неразруша-
ющий контроль. Справочник в 8 т. Т. 4. Кн. 1. Акустическая тензометрия / Под общ. ред. В.В. Клюева.
М.: Машиностроение, 2006. 226 с.
5. Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. М.: Изд-во ино-
странной литературы, 1959. 457 с.
6. Бобренко В.М., Куценко А.Н., Шереметиков А.С. Общий вид уравнений акустоупругости для
главных напряжений // Дефектоскопия. 1982. № 6. С. 23—27.
Дефектоскопия
№ 11
2020
Использование метода акустоупругости для контроля упругих механических напряжений...
37
7. Гузь А. Н., Махорт Ф. Г., Гуща О. И. Определение напряжений в твердых телах ультразвуковым
методом / Неразрушающий контроль материалов и элементов конструкций. Киев: Наукова думка, 1981.
С. 115—146.
8. Гузь А.Н., Махорт Ф.Г., Гуща О.М. Введение в акустоупругость. Киев: Наукова думка, 1977. 152 с.
9. Гузь А.Н., Махорт Ф.Г. Физические основы ультразвукового неразрушающего метода определе-
ния напряжений в твердых телах // Прикладная механика. 2000. Т. 36. № 9. С. 3—34.
10. Муравьев В.В., Волкова Л.В., Лапченко М.А. Ультразвуковой контроль остаточных напряжений в
бандажах локомотивных колес при производстве // Дефектоскопия. 2015. № 5. С. 3—16.
11. Муравьев В.В., Волкова Л.В. Оценка величины натяга бандажей локомотивных колес методом
акустоупругости // Дефектоскопия. 2013. № 9. С. 40—46.
12. Муравьев В.В., Муравьев Т.В. Расчет процесса передачи акустического сигнала через трибосо-
пряжение внутреннего кольца подшипника и оси колесной пары // Дефектоскопия. 2007. № 2. С. 16—26.
13. Муравьев В.В., Муравьева О.В., Леньков С.В. Оценка остаточных напряжений цельнокатаных и
бандажированных колес с использованием эффекта акустоупругости // В мире неразрушающего кон-
троля. 2018. Т. 21. № 1. С. 25—29.
14. Новожилов В.В. Основы нелинейной теории упругости. М.: Гостехиздат, 1948. 212 с.
15. Новожилов В.В. Теория упругости. Ленинград: Судпромгиз, 1958. 370 с.
16. Степанова Л.Н., Лебедев Е.Ю., Кабанов С.И., Канифадин К.В., Бехер С.А., Никитенко М.С.
Исследование характеристик проволочных и полупроводниковых тензодатчиков, используемых для из-
мерения ударных процессов // Датчики и системы. 2013. № 1. С. 28—33.
17. Степанова Л.Н., Кабанов С.И., Бехер С.А. Микропроцессорные многоканальные тензометриче-
ские системы для динамических испытаний конструкций // Датчики и системы. 2011. № 8. С. 29—34.
Дефектоскопия
№ 11
2020