Электромагнитные методы
УДК 620.179.14
СПОСОБ ОБРАБОТКИ РЕЗУЛЬТАТОВ МАГНИТНОЙ ДЕФЕКТОСКОПИИ
ДЛЯ ДОСТОВЕРНОГО ОБНАРУЖЕНИЯ ОПАСНЫХ ДЕФЕКТОВ
СПЛОШНОСТИ В РЕАЛЬНОМ ВРЕМЕНИ
© 2020 г. А.Н. Печенков1,*
1Институт физики металлов имени М.Н. Михеева УрО РАН, Россия 620108 Екатеринбург,
ул. С. Ковалевской, 18
*E-mail: Pechenkov@imp.uran.ru
Поступила в редакцию 01.10.2020; после доработки 09.10.2020
Принята к публикации 16.10.2020
Обратные задачи магнитостатики для дефектов сплошности могут быть сформулированы различными способами.
Можно ставить задачу определения дефектов с высокой точностью и разрешением или ограничить задачу обнаружени-
ем нескольких заданных видов дефектов («опасных» дефектов) с той или иной степенью вероятности. При этом дру-
гие реальные дефекты будут либо пропущены программой («мелкие» дефекты), либо «заменены» дефектами из числа
заданных дефектов. Проблема минимизации функционала невязки экспериментальных и расчетных данных является
основной проблемой для решения любых обратных задач. Как в реальном времени, так и в режиме off-line. В работе рас-
смотрен подход к расчетам упрощенной обратной задачи в реальном времени, без накопления баз экспериментальных
данных.
Ключевые слова: обратная задача магнитостатики, методы распознавания образов, интегральное уравнение магнито-
статики, расчет магнитного поля, дефекты «сплошности», проблема минимизации, метод перебора.
DOI: 10.31857/S0130308220120064
ВВЕДЕНИЕ
Расчеты магнитных полей дефектов традиционно являются одной из актуальных задач в со-
временной магнитной дефектоскопии в связи с поиском постановки и методов решения обратных
задач определения параметров дефектов, которые можно было бы реализовать в компьютерных
программах дефектоскопов [1—3, 8—11].
В настоящее время компьютеры дефектоскопов используются только для визуализации резуль-
татов измерений магнитных и электрических полей. Однако было бы желательно использовать их
также для приближенного оценивания размеров и положения дефектов.
Современные компьютеры, которые доступны для комплектования дефектоскопов, не обла-
дают достаточной вычислительной мощностью для решения обратных задач в реальном мас-
штабе времени, с высоким разрешением [4]. Поэтому остается только возможность сформулиро-
вать более простую обратную задачу как задачу распознавания образов на заданном множестве
моделей дефектов. Эти модели дефектов либо накапливаются в виде картин магнитного поля в
некоторой базе данных экспериментальным или расчетным способом, либо используются как
математические модели для расчетов в реальном времени, без накопления баз данных. Расчеты
без накопления результатов в базе данных не требуют новых баз данных при смене характери-
стик контролируемого изделия. Основное достоинство накопления баз данных заключается в
том, что это можно делать экспериментально, в заданных условиях измерений, без привлечения
модельных расчетов.
Результаты решения обратной задачи имеют, конечно, приближенный и вероятностный харак-
тер при любом способе решения. Источников ошибок много. Например:
базы данных измеренных или рассчитанных полей дефектов очень не полны, т.к. не охватыва-
ют большинства возможных форм и положений дефектов;
вид и параметры математических моделей отличаются от характеристик реального материала
образца, вида дефекта и способа измерения;
случайные шумы и систематические погрешности измерений делают бессмысленными вычис-
ления с большой точностью;
математическая обработка не обеспечивает достижения глобальных минимумов, т.к. миними-
зируемый функционал существенно нелинейный и процедуры минимизации заканчиваются в од-
ном из локальных минимумов.
Поэтому нет необходимости в точных расчетах (измерениях) для баз данных или для расчетов
без накопления баз данных.
Способ обработки результатов магнитной дефектоскопии для достоверного...
59
В данной работе рассматривается вариант упрощенной обратной задачи с использованием не-
которых моделей дефектов для расчетов в реальном времени без накопления баз данных.
«Опасный» дефект задается в виде одной ячейки прямоугольной расчетной сетки. Размеры та-
кого дефекта и, соответственно, размеры ячеек сетки задаются по требованию заказчика. Этот де-
фект может иметь различные размеры вдоль осей координат. Например, он может быть «вытянут»
вдоль любой из осей. Все ячейки сетки одинаковы, т.е. «опасный» дефект определяет вид сетки.
В компьютерной программе предусмотрены модели «опасных» дефектов, вытянутых вдоль каж-
дой из осей координат. Если реальный дефект расположен иначе, то он будет зафиксирован (с той
или иной степенью вероятности) как некоторый дефект из числа заданных «опасных» дефектов.
Дополнительно можно задать набор дефектов других форм и положений на заданной сетке.
РАСЧЕТНЫЕ ФОРМУЛЫ И АЛГОРИТМЫ
В данной работе рассматриваются измерения на линейном участке петли гистерезиса, т.е. в не
очень сильных внешних полях. Как отмечено выше, результаты расчетов обязательно будут очень
приближенными. При использовании в реальном времени сеточных (непараметрических) мето-
дов расчетная сетка должна содержать небольшое число ячеек. В связи с этим возникает вопрос
об очень приближенном решении интегрального уравнения магнитостатики для учета влияния
ячеек сетки друг на друга. Например, можно было бы ограничиться применением приближения
насыщения, когда намагниченность всех «недефектных» ячеек сетки задана и одинакова [5], что
существенно уменьшает время вычислений. Тем не менее в нашем расчетном алгоритме было
оставлено приближенное решение уравнения для напряженности магнитного поля внутри сетки
при каждом изменении магнитной восприимчивости ячеек сетки в процессе решения обратной
задачи [1,7]:
4π
H(r
p
)
=∇div
M r)⋅νdr;
r
p
∈G
(1)
∫
G
Под напряженностью поля рассеяния понимается разность напряженности результирующего
магнитного поля и напряженности приложенного внешнего поля.
Это решение, в свою очередь, определяет распределение намагниченности внутри изделия.
После чего производится расчет напряженности магнитного поля рассеяния вне расчетной сетки:
∗
4π
H
(r
)
=∇div
M r)
⋅ν
dr;
r
∉G,
p
∫
p
(2)
G
где H* — напряженность магнитного поля рассеяния вне области G; H — напряженность маг-
нитного поля рассеяния внутри области G; H0 — напряженность внешнего магнитного поля;
M = χ(H + H0) — намагниченность образца; χ — магнитная восприимчивость образца;
ν =1/mod(rp - r) — функция Грина для свободного пространства; rp — точка расчета магнитного
поля; r — точка внутри области G; ∇ — оператор градиента; G — область образца, содержащая
расчетную сетку.
Магнитная восприимчивость задается одной скалярной величиной, т.е. изделие считается изо-
тропным и однородным, петля гистерезиса не учитывается.
Отметим, что одним из достоинств метода интегральных уравнений является то, что расчетная
сетка требуется только в области изделия G. Расчет поля в произвольных точках вне изделия по
уравнению (2) не требует дополнительной сетки между образцом и точками расчета.
Прямоугольная форма «однородно намагниченных» ячеек сетки хороша тем, что магнитное
поле, созданное каждой такой ячейкой в любой точке пространства, можно выразить простыми
аналитическими формулами [6, 7]:
a b;c
(z- z
)(y− y
)
1
p
p
H
(r
)
=
-M
arctg
+
M
lnR
+(z- z
)
+
M
lnR
+(y- y
)
;
(3)
x
p
x
y
p
z
p
4π
(x- x
)R
p
−a;−b;−c
a b;c
(z- z
)(x− x
)
1
p
p
H
(r
)
=
M
lnR
+(
z- z
)
-
M
arctg
+
M
lnR
+(x- x
)
;
(4)
y
p
x
p
y
z
p
4π
(y- y
)R
p
−a;−b;−c
a b;c
(x- x
)(y− y
)
1
p
p
H
(r
)
=
M
lnR
+(y- y
)
+
M
lnR
+(x- x
)
-
M
arctg
(5)
z
p
x
p
y
p
z
4π
(z- z
)R
p
-a;−b;−c
Дефектоскопия
№ 12
2020
60
А.Н. Печенков
Справа от квадратных скобок стоят пределы интегрирования, т.е. x изменяется от - a до a, y
изменяется от - b до b, z изменяется от - c до c. Эти пределы соответствуют координатам вершин
данной ячейки сетки. Внутри каждой ячейки магнитная восприимчивость, намагниченность, маг-
нитное поле считаются постоянными величинами. Отметим также, что в интегральном уравнении
(1) не выделено в явном виде «собственное» поле в центре каждой ячейки ( -М / 3), как это обычно
делается. Это объясняется тем, что поля вне и внутри каждой ячейки рассчитываются по единым
формулам (3)—(5). При этом указанное значение поля в центре каждой кубической ячейки полу-
чается автоматически.
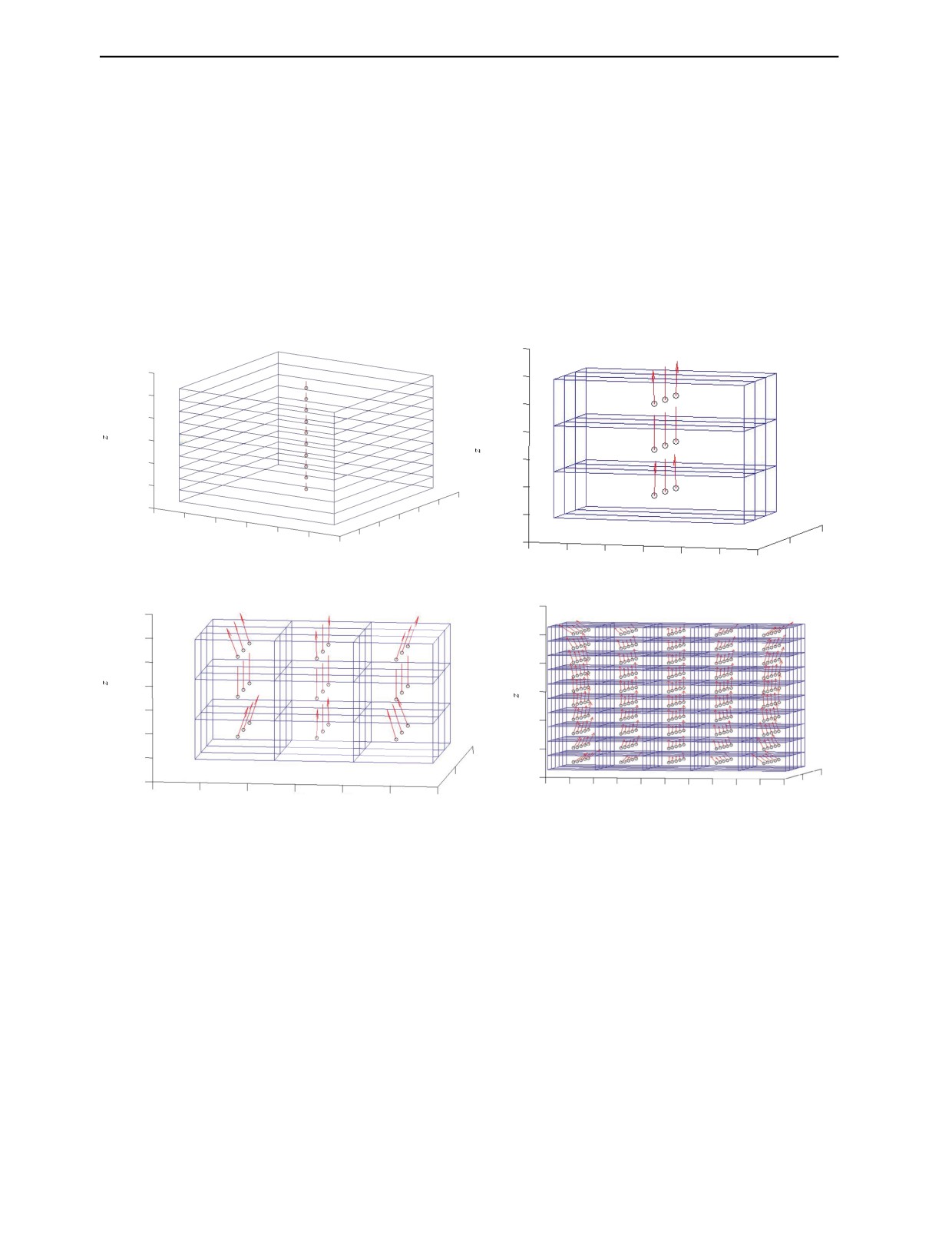
Примеры решения уравнения (1) на прямоугольных сетках с числами ячеек: 1×1×10 = 10,
1×3×3 = 9, 3×3×3 = 27 и 5×5×10 = 250 показаны ниже. Внешнее намагничивающее поле Hz0 направ-
лено вдоль оси Z. В центре каждой ячейке показан рассчитанный вектор однородной намагничен-
ности М этой ячейки. Число ячеек влияет на время работы и выбор алгоритма (см. ниже).
0,014
0,012
0,012
0,01
0,01
0,008
0,008
0,006
0,004
0,006
0,002
0,004
0,08
0
0,07
0,002
0,02
0,06
0,03
0,05
0,04
0,05
0,06
0,04
y
0,1
0,07
0,03
0
0,08
0,05
x
0,02
0,03
y
0,04
0,05
0,06
0,07
0,08
x
12
0,014
10
0,012
0,01
8
0,008
6
0,006
4
0,004
2
0,002
0,1
y
0
10
0
0,05
5
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
5
5,5
y
0,01
0,02
0,03
0,04
0,05
0,06
x
x
Рис. 1. Расчетные сетки без дефектов.
Внешнее намагничивающее поле Hz0 коллинеарно оси Z. На рисунке хорошо виден симметрич-
ный «поток» векторов намагниченности вдоль оси Z. В данном случае — это вид, перпендикулярно
оси X. Точно такой же вид мы получим, если смотреть перпендикулярно оси Y. Такой вид «потока»
намагниченности обусловлен, как и должно быть, несимметричным влиянием на поверхностные
ячейки со стороны других ячеек сетки. Достаточно однородная намагниченность получается толь-
ко вблизи оси симметрии сетки. Отметим также, что если реальный образец совпадает с расчетной
сеткой, то показанный «поток» векторов намагниченности реален. Если же данная сетка наложена
только на часть образца, то показанные краевые эффекты сетки являются фиктивными.
Вне расчетной сетки рассчитывается поле рассеяния H*, используя уравнение (2).
«Дефект сплошности» соответствует нулевой магнитной восприимчивости некоторых ячеек
сетки, т.е. когда в них нет материала изделия. Решение обратной задачи заключается в поиске этих
ячеек. В процессе поиска магнитная восприимчивость каждой ячейки становится неизвестной
переменной величиной. Количество ячеек сетки определяет число этих неизвестных, по которым
Дефектоскопия
№ 12
2020
Способ обработки результатов магнитной дефектоскопии для достоверного...
61
проводятся процедуры минимизации. При каждом зафиксированном наборе значений магнитной
восприимчивости ячеек вычисляется поле H* и сравнивается с экспериментально измеренным
полем H.
Минимизируемый по некоторой норме функционал можно записать в виде:
*
F =
h
z
−h
z
(6)
Здесь взята одна компонента вектора поля, так как измеряется обычно тоже одна компонента.
Для расчета берутся относительные разности рассчитанных и измеренных полей:
*
*
H
−
H
H
−
H
z
z1
*
z
z1
h
=
;
h
=
,
(7)
z
z
*
H
H
z1
z1
где Hz и Hz* — рассчитанное и измеренное поле на сетке и образце с дефектом; Hz1 и Hz1* — рас-
считанное и измеренное поле на сетке и образце без дефектов.
Вид функций (7) выбран таким потому, что сетка расчетной области вблизи датчиков не охва-
тывает всего намагничиваемого изделия целиком. Поэтому поле модели не может сопоставляться
с измеренным полем без таких преобразований. В результате минимизации функционала (6) полу-
чается некоторый набор значений магнитных восприимчивостей ячеек заданной сетки, который и
должен показать какие ячейки «дефектные», а какие — нет.
Существует два класса алгоритмов минимизации. В первом классе магнитные восприимчиво-
сти ячеек считаются непрерывными величинами. Во втором классе они считаются дискретными
переменными.
Наиболее хорошо разработаны и обычно применяются алгоритмы первого класса. К сожале-
нию, любой из этих алгоритмов всегда дает множество «локальных» минимумов функционала
F, зависящих от исходного значения магнитных восприимчивостей ячеек. Эти минимумы могут
быть очень малы, т.е. расчетное поле очень близко к измеренному полю, но полученный на-
бор значений магнитных восприимчивостей будет вообще не похож на реальный набор. Чтобы
найти этот реальный набор, нужно найти minimum minimorum функционала F, или, иначе го-
воря, «глобальный минимум» этого функционала. Процедуры поиска глобального минимума в
пространстве большого числа переменных приводят к неприемлемым требованиям к времени
вычислений, мощности компьютеров, параллельности вычислений. Кроме того, они не гаранти-
руют достижения глобального минимума, т.к. содержат вероятностные процедуры. Таким обра-
зом, вычислительные эксперименты показывают, что алгоритмы непрерывной минимизации не
подходят для решения обратной задачи в реальном времени.
Алгоритмы минимизации второго класса предполагают, что в процессе минимизации магнит-
ная восприимчивость каждой ячейки сетки может принимать только два значения: (χ, 0). Величина
χ одинакова для всех ячеек. Это ограничение на область изменения переменных минимизации пра-
вильно отражает физическую модель изделия.
Очевидно, что глобальный минимум функционала будет найден после полного перебора всех
возможных сочетаний «дефектных» ячеек на данной сетке. Число таких сочетаний, как известно,
равно:
N
N
!
K
=
∑
,
(8)
n=1
n
!(N-n)!
где N — полное число ячеек сетки; n — число «дефектных» ячеек.
Легко убедиться, что число K очень быстро растет с ростом числа N. Например, если сетка
содержит всего N = 10 ячеек, то число возможных вариантов «дефектов» уже будет K = 1024,
т.е., если бы мы накапливали, например, полную базу данных для полей такого изделия с воз-
можными дефектами указанного вида, то потребовалось бы запомнить 1024 картинки поля.
Следовательно, на сетках с большим числом ячеек этот подход кажется неприменимым. Для
таких сеток единственной возможностью вычислений в реальном масштабе времени является
ограничение набора допустимых дефектов (вида и положения дефекта на сетке). В частности,
можно ограничиться поиском дефектов, состоящих из очень небольшого числа ячеек. Например,
из одной или двух ячеек. В этом случае полное число возможных сочетаний «дефектных» ячеек
на данной сетке будет не очень большим:
Дефектоскопия
№ 12
2020
62
А.Н. Печенков
L
N!
K
= ∑
,
(9)
n=1
n!(N-n)!
где L — максимальное число ячеек в дефекте.
Такой подход к решению обратной задачи может быть обоснован введением понятия «опасно-
го» дефекта, имеющего размер одной ячейки сетки, т.е. сетка строится на основе размера заданно-
го опасного дефекта. Таким образом, при решении обратной задачи все дефекты, много меньшие
ячейки сетки, с большой вероятностью не будут определяться программой. Дефекты с размерами
больше размеров ячейки будут «аппроксимированы» некоторой «дефектной» ячейкой. Из несколь-
ких раздельных опасных дефектов будут определены только один (если L = 1) или два (если L = 2).
Следует отметить, что размер «опасного» дефекта должен быть согласован с физическими раз-
мерами области изделия, на которую «накладывается» расчетная сетка. Чем меньше эта область,
тем меньше и размер «опасного» дефекта.
РЕЗУЛЬТАТЫ РАСЧЕТОВ
Для моделирования решения обратной задачи в реальном времени был использован отмечен-
ный выше алгоритм поиска «опасного» дефекта в виде одной ячейки «крупной» сетки, содержа-
щей всего 1×3×3 = 9 ячеек. Для моделирования измеренного поля использовалась более «мелкая»
сетка, содержащая 5×5×10 = 250 ячеек. На этой сетке можно было задавать и мелкие, и более круп-
ные дефекты. Центры ячеек с дефектами отмечены звездочками.
На рис. 2 показан случай двух «мелких» дефектов в ячейках, центры которых можно указать в
координатах номера ячейки вдоль осей координат: (2,4,1) и (4,4,5). Алгоритм не нашел «опасного»
дефекта в какой-либо ячейке «крупной» сетки, т.е. дефект в любой ячейке этой сетки дает поле рас-
сеяния, больше отличающееся от поля модели дефектов, чем поле сетки без дефектов.
0,012
0,035
0,01
0,03
0,008
0,025
0,006
0,02
0,015
0,004
0,01
0,002
0,08
0,04
0,06
0,005
0,04
0
0,02
y
0,005
0,02
0,01
0,015
0,02
0,025
0
0,005 0,01 0,015 0,02 0,025 0,03 0,035 0,04 0,045 0,05 0,05 0,055
y
x
x
Рис. 2. Алгоритм не обнаружил «опасного» дефекта.
На рис. 3 показаны модели двух «крупных» дефектов, каждый из которых состоит из ряда ячеек
«мелкой» сетки и занимает значительную ее часть. В обоих случаях алгоритм за несколько секунд
указал на наличие «опасного» дефекта в центральной нижней ячейке «крупной» сетки.
Приведенные примеры показывают способность предложенного алгоритма распознавать опас-
ные дефекты в реальном времени.
ВЫВОДЫ
1. Разработан алгоритм для работы в реальном времени на современных магнитостатиче-
ских дефектоскопах. Алгоритм может быть отнесен к алгоритмам распознавания образов, но
без накопления баз данных полей дефектов. Накопление баз данных полей дефектов путем ре-
альных измерений привлекательно простотой и универсальностью. Предложенный алгоритм
можно рекомендовать в тех случаях, когда затруднительно накопление больших эксперимен-
тальных баз полей дефектов или их обновление при смене условий измерений и материала
изделий.
Дефектоскопия
№ 12
2020
Способ обработки результатов магнитной дефектоскопии для достоверного...
63
Рис. 3. Алгоритм указывает на наличие «опасного» дефекта
в центральной нижней ячейке «крупной» сетки для обоих
показанных моделей дефектов на «мелкой» сетке.
2. Работа в реальном времени обеспечивается упрощением постановки обратной задачи: поля
рассеяния реальных дефектов сравниваются с рассчитанным полем заданных моделей «опасных»
дефектов.
3. Расчетная сетка для расчета полей дефектов определяется предполагаемым размером и по-
ложением «опасного» дефекта вдоль осей координат. Время расчетов составляет несколько секунд.
Возможно дополнение алгоритма другими формами «опасных» дефектов, при условии малого вре-
мени расчетов. В перспективе данный алгоритм может быть реализован и на параллельных вычис-
лительных устройствах.
4. Можно использовать одну или несколько компонент поля рассеяния.
5. Метод дискретной минимизации путем перебора вариантов позволяет:
обеспечить заданную магнитную восприимчивость всех ячеек сетки, что стабилизирует рас-
четы и соответствует физической модели;
настроить алгоритм на поиск одной или нескольких ячеек сетки с «опасными» дефектами.
Наиболее простой и быстрый вариант — поиск положения одного «опасного» дефекта на заданной
сетке, что достаточно для целей практического предупреждения опасных дефектов
Работа выполнена в рамках государственного задания ФАНО России (тема «Диагностика»,
№ АААА-А18-118020690196-3).
СПИСОК ЛИТЕРАТУРЫ
1. Дякин В.В. Математические основы классической магнитостатики. Екатеринбург: РИО УрО РАН,
2016. 403 с.
2. Dyakin V.V., Umergalina O.V., Raevskii V.Ya. The field of a finite defect in a 3D semispace // Russ. J.
Nondestr. Test. 2005. V. 41. No. 8. P. 502—513.
3. Dyakin V.V., Raevskii V.Ya., Kudryashova O.V. The field of a finite defect in a plate // Russ. J. Nondestr.
Test. 2009. V. 45. No. 3. P. 199—209.
4. Pechenkov A.N., Scherbinin V.E. Influence of calculation accuracy on the time and results of solving
the inverse problem of magnetostatic nondestructive testing. Need of parallel computations // Diagnostics,
Resource and Mechanics of materials and structures. 2015. № 5. P. 22 (9 pp.).
Дефектоскопия
№ 12
2020
64
А.Н. Печенков
5. Dyakin V.V., Kudryashova O.V., Raevskii V.Ya. Inverse Problem of Magnetostatics in Saturation Fields //
Rus. J. Nondestr. Test. 2019. V. 55. No. 10. P. 746—755.
6. Pechenkov A.N., Shcherbinin V.E. In Nekotorye pryamye i obratnye zadachi tekhnicheskoi
magnitostatiki(Some Direct and Inverse Problems in Technical Magnetostatics). Yekaterinburg: Ural Branch,
Russ. Acad. Sci., 2004 (in Russian).
7. Pechenkov A.N., Scherbinin V.E., Shleenkov S.A., Bulychev O.A. Computational Relationships for the
Development of Software for Calculating Magnetostatic Fields from Flaws in Arbitrarily Shaped Ferromagnetic
Products // Russian Journal of Nondestructive Testing. 2017. V. 53. No. 11. P. 755—764.
8. Jiang Feng, Liu Shulin. Evaluation of cracks with different hidden depths and shapes using surface
magnetic field measurements based on semi-analytical modeling // J. Phys. D: Appl. Phys. 2018. V. 51.
P. 125002 (10 p.).
9. Wautischer Gregor, Bruckner Florian, Abert Claas, Suess Dieter, Koeck Helmut, Eizaguirre Sanchez
Mikel. Solving the inverse magnetostatic problem using fictitious magnetic charges // AIP Advances. 2018.
V. 8. P. 056005.
10. Ravan Maryam, Khalaj Amineh Reza, Koziel Slawomir, Nikolova Natalia K., Reilly James P. Sizing of
3-D Arbitrary Defects Using Magnetic Flux Leakage Measurements // IEEE Trans. Magn. 2010. V. 46. No. 4.
P. 1024—1033.
11. Calvetti D., Morigi S., Reichel L., Sgallari F. Tikhonov regularization and the L-curve for large discrete
ill-posed problems // J. Comput. Appl. Math. 2000. V. 123. P. 423—446.
Дефектоскопия
№ 12
2020