УДК 620.179.16
ОПРЕДЕЛЕНИЕ СКОРОСТИ ОСНОВНЫХ ТИПОВ АКУСТИЧЕСКИХ ВОЛН
В МЕТАЛЛАХ ПРИСТАВНЫМ ДАТЧИКОМ
© 2020 г. С.Э. Бабкин1,*
1ФГБУН «УдмФИЦ УрО РАН», Россия 426000 Ижевск, ул. Кирова, 132
E-mail: babkin.s.e@mail.ru
Поступила в редакцию 03.02.2020; после доработки 02.03.2020
Принята к публикации 03.03.2020
Предложен метод использования приставного датчика поверхностных волн на основе электромагнитно-акустиче-
ских меандровых преобразователей для определения скоростей поверхностных, продольных и поперечных волн в ме-
таллах. Метод применим на образцах с плоскопараллельными границами при одностороннем доступе к изделию. Все
три скорости определяются за одну установку датчика на поверхность образца. Решены проблемы точного измерения
пути распространения и временного отсчета принятых импульсов. Показано на примерах, что точность определения
скоростей звука может быть не хуже 0,5 %.
Ключевые слова: поверхностные волны Рэлея, поперечные и продольные волны, электромагнитно-акустический
преобразователь, скорость звука, точность измерений.
DOI: 10.31857/S0130308220040041
ВВЕДЕНИЕ
Ультразвуковые методы — одни из самых распространенных методов неразрушающего кон-
троля металлов. Одним из важных информационных параметров ультразвуковых методов является
скорость звука. Скорость звука используется, с одной стороны, для целей дефектоскопии, когда
изменяется при прохождении в дефектном образце [1, 2], и, с другой стороны, для решения задач
структуроскопии, таких как определение упругих модулей, параметров напряженно-деформиро-
ванного состояния и анизотропии различных свойств материала [3—5].
Скорость звука в металле можно определять с высокой точностью при использовании резо-
нансных методов, но при одностороннем доступе к изделию точное определение скорости звука
имеет ряд трудностей [1, 6].
Основным методом генерации и приема ультразвука в металлах является метод, использующий
пьезоэлементы [7]. Однако проблема контакта является для него постоянным мешающим факто-
ром. Метод электромагнитно-акустической (ЭМА) генерации и приема ультразвуковых колебаний
в металлах благодаря бесконтактности имеет некоторые преимущества перед традиционным мето-
дом пьезоэлементов, оперирует теми же методическими приемами ультразвукового контроля, но и
привносит свою новизну [8, 9].
Как и в других твердых телах, в металлах имеются три основных типа звуковых волн — про-
дольные, поперечные и поверхностные (волны Рэлея). Они распространяются с разными скоростя-
ми. Как для пьезоэлементов, так и для методов ЭМА-преобразования эти скорости определяются
в разных экспериментах, использующих разные преобразователи-датчики. В данной работе пред-
лагается определять скорости всех трех основных волн одним приставным датчиком на основе
ЭМА-метода за одну установку на поверхность образца с точностью не хуже 0,5 %.
1. ИЗМЕРЕНИЕ СКОРОСТИ ВОЛН РЭЛЕЯ
Традиционный метод измерения поверхностных волн Рэлея заключается в следующем. На
поверхность образца устанавливаются два преобразователя — один генерирует поверхностную
волну, другой — ее принимает (рис. 1) [1, 10]. В случае ЭМА-преобразования преобразователя-
ми являются одинаковые решетки, выполненные из провода или напыленные в виде меандра, с
системой подмагничивания, в случае пьезоэлементов преобразователи могут выполняться, на-
пример, в виде гребенки [7]. Расстояние между центрами преобразователей обозначим за d. Если
считать, что волна распространяется от центра одного преобразователя до центра другого, то
скорость волны Рэлея определяется формулой СR = d/tR, где tR — время распространения волны
Рэлея.
Определение скорости основных типов акустических волн в металлах...
33
а
U
б
Дефектоскоп
tR
Г
У
H
LC-корр.
LC-корр.
0
t
A?
B
Рис.1. Датчик волн Рэлея на поверхности образца (а) и его осциллограмма (б).
Из этой формулы понятны две проблемы точного определения скорости: определение расстоя-
ния d и определение времени tR, соответствующее указанному расстоянию.
Определить расстояние d можно штангенциркулем (между геометрическими серединами
преобразователей или от начала генерирующего преобразователя до начала приемного). Точ-
ность измерения +0,05 мм, что при обычной величине базы 50 мм дает относительную погреш-
ность +0,1 %. Реально будет хуже из-за ручной установки штангенциркуля. Также погрешности
изготовления и намотки датчика (датчик может быть многовитковым) приводят к тому, что ре-
альный «центр тяжести» датчика может не совпадать с геометрическим. Практика показывает,
что, таким образом, погрешность измерения может составлять 0,5 мм. Это дает относительную
погрешность около 1 %, что уже слишком много.
Вторая проблема — это корректное определение временного интервала tR, соответствующее
распространению волны между центрами преобразователей. Генерирующий преобразователь
формирует на поверхности образца колоколообразный импульс смещений поверхностной вол-
ны, который распространяется в обе стороны от преобразователя. Импульс, движущийся в сто-
рону приемного преобразователя, наводит в нем колоколообразный приемный сигнал. Верши-
ну этого импульса можно взять за конец отсчета временного интервала распространения волны
между центрами преобразователей (на рис. 1б на всех осциллограммах приведены огибающие
детектированных импульсов). А вот где брать точку начала отсчета временного интервала, со-
ответствующего расстоянию d (т. А), неясно. Погрешности, вызванные неточным определением
начала и конца временного интервала, можно значительно сократить, если измерять временной
интервал между импульсами отраженных волн по следующим методикам.
Предлагается измерять скорость рэлеевской волны на образце в форме прямоугольного парал-
лелепипеда. При этом толщина образца не важна, главное, чтобы она была больше 3λR (λR — длина
волны Рэлея, соответствующая периоду меандра). Для реальных датчиков λR составляет ≈ 1 мм
(для датчиков 2 МГц) и 2 мм (для датчиков 1 МГц). Это дает толщину образца более 6 мм, что
вполне реально.
Тогда скорость рэлеевской волны можно измерять в двух режимах.
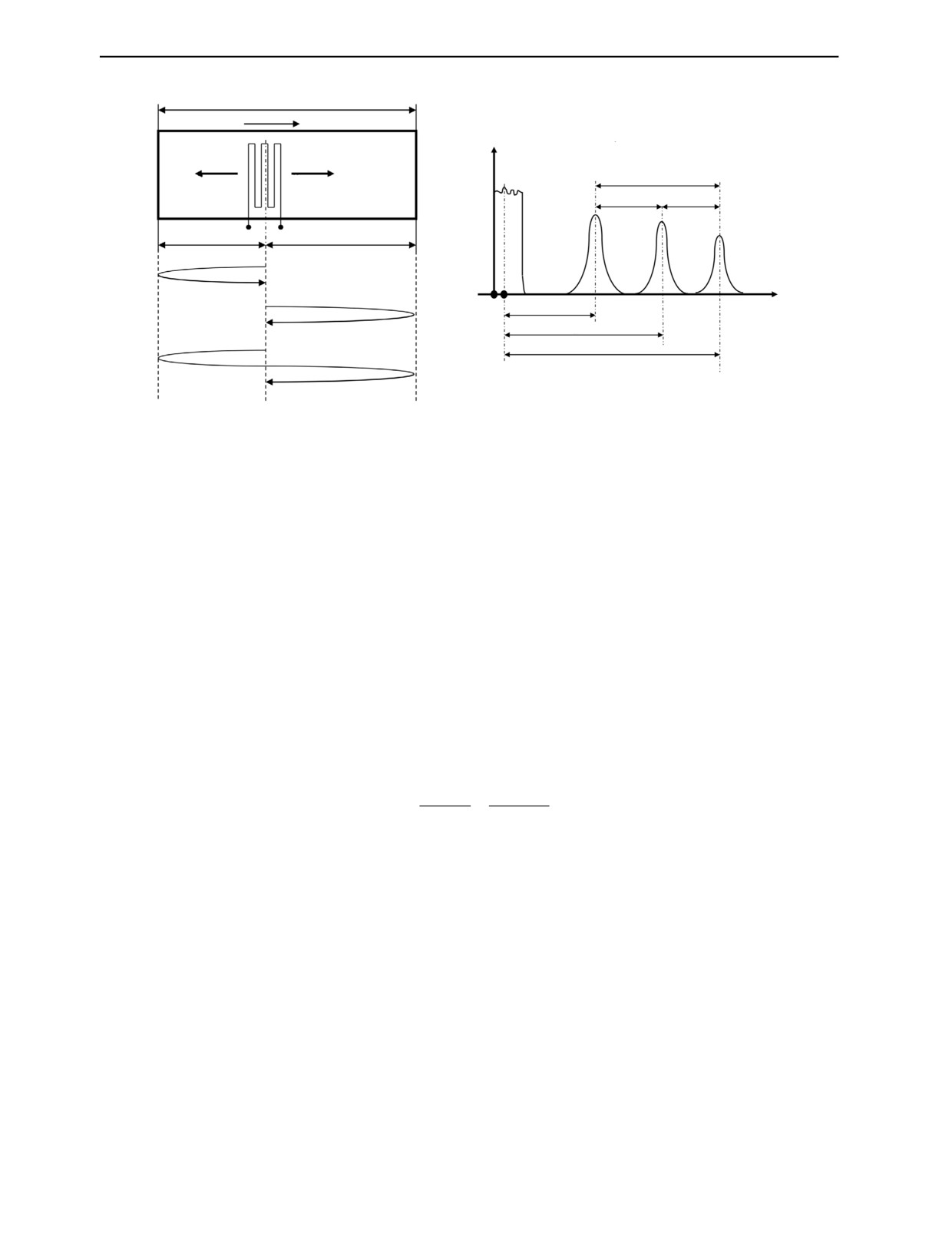
1. Измерение одним преобразователем в совмещенном режиме (рис. 2). B этом случае дат-
чик-преобразователь устанавливается на поверхность образца параллельно краю (этого добива-
ются по максимуму принятого сигнала). Волна генерируется датчиком в обе стороны, отражается
от краев и принимается тем же датчиком. Осциллограмма показана на рис. 2б: 0 — зондирующий
импульс, 1 — импульс от ближнего края, 2 — импульс от дальнего края, 3 — импульс двойного
отражения.
Если при полной длине образца L обозначить за x расстояние от левой грани образца до центра
датчика, то путь каждого импульса:
S1 = 2x = СRt1,
S2 = 2L - 2x = СRt2,
S3 = 2L = СRt3,
где t1, t2, t3 — время, отсчитываемое от «центра тяжести» зондирующего импульса по осцилло-
грамме измерения (т. А).
Дефектоскопия
№ 4
2020
34
С.Э. Бабкин
а
б
L
H
U
R-волна
R-волна
t31
t21
t32
0
x
L-x
1
2
3
S1
0
A?
t
t1
S2
t2
t3
S3
Рис. 2. Меандровый ЭМА-преобразователь в совмещенном режиме (а) и его осциллограмма (б).
Из этих уравнений получаем:
∆S21 = S2 - S1 = 2L - 4x = СRt21;
(1)
∆S31 = S3 - S1 = 2L - 2x = СRt31;
(2)
∆S32 = S3 - S2 = 2x = СRt32,
(3)
где t21, t31, t32 — соответствующие временные интервалы (см. рис. 2б).
Отсюда получаем простые соотношения:
t1 = t32, t2 = t31, t21 + t32 = t31.
(4)
Из этих формул методом обратного отсчета легко можно определить точку А — центр тяжести
зондирующего импульса.
Сложив (2) и (3), с учетом (4) получаем простые формулы для определения скорости рэлеев-
ской волны:
2L
2L
CR
=
=
(5)
t
31
+t
32
t
21
+2t
32
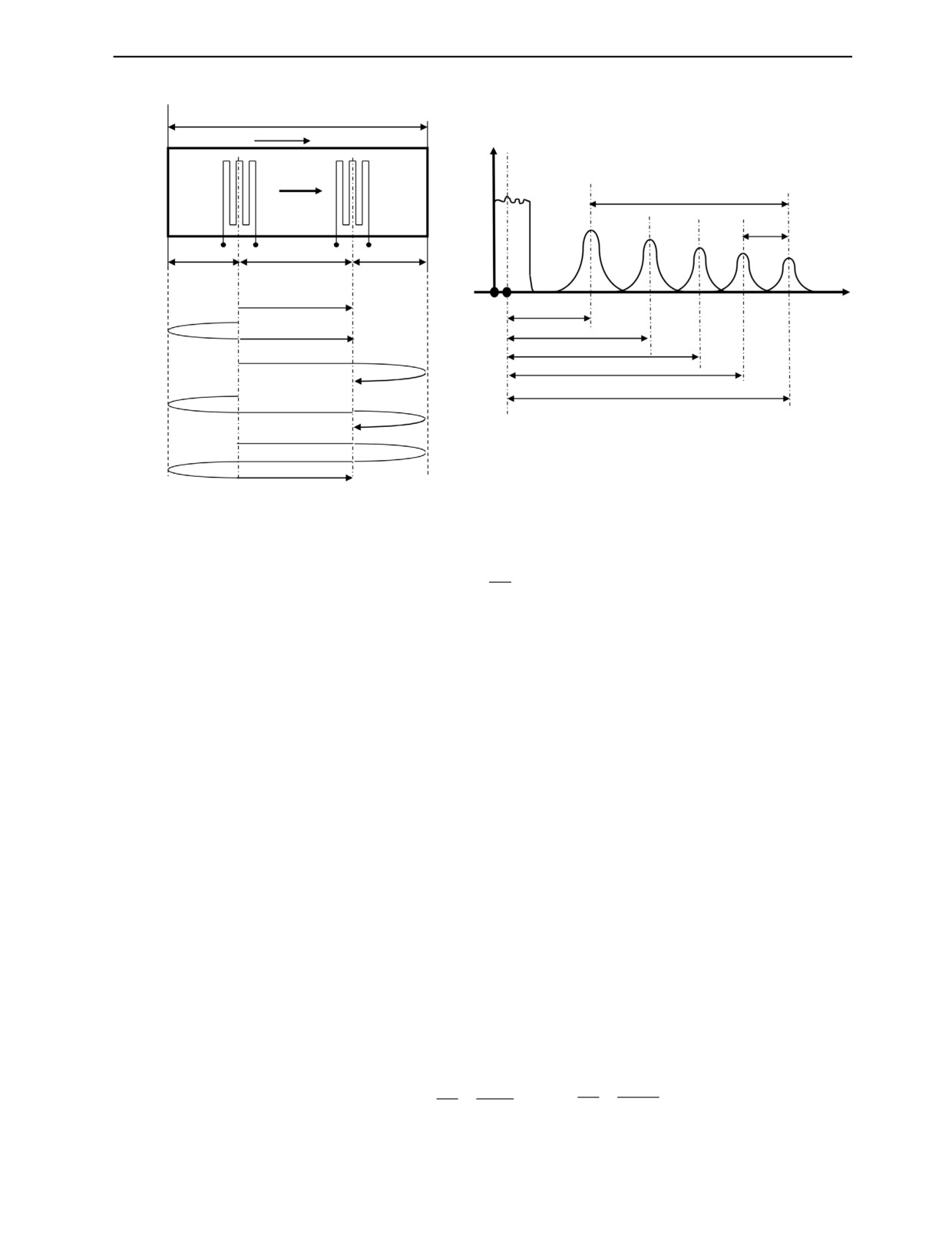
2. Измерение двумя преобразователями в раздельном режиме. Меандровые преобразовате-
ли устанавливаются параллельно друг другу и краям образца (по максимуму сигнала). Пусть рас-
стояние генераторного (левого) преобразователя до левой грани — х, а расстояние между центрами
преобразователей — d, тогда остальные расстояния понятны из рисунка (рис. 3). Также из рисунка
понятны пути прохождения первых пяти характерных принятых импульсов, показанных на осцил-
лограмме (рис. 3б):
S
1
=
d =c
tR 1
,
S
=
d
+2
x = c
t
,
2
R 2
S
=
2L−2x-d = c
t
,
3
R 3
S
=
2L-d =c
t
,
4
R 4
S
5
=
2L+d =c
tR 5
Проведем простые математические преобразования, аналогичные (1)—(4), и получим простую
формулу для определения скорости:
Дефектоскопия
№ 4
2020
Определение скорости основных типов акустических волн в металлах...
35
а
L
б
H
U
Г
R-волна
П
t51
t54
1
x
d
L- d -x
2
3
4
5
0
A?
t
S1
t1
S2
t2
t3
S3
t4
t5
S4
S5
Рис. 3. Меандровые ЭМА-преобразователи в раздельном режиме (а) и их осциллограмма (б).
2L
CR
=
(6)
t
51
Отметим, что формулы (5), (6) не зависят от расположения «центра тяжести» зондирующего
импульса, а точность измерений зависит от точности измерения длины образца и временных рас-
стояний между принятыми импульсами.
Заметим, что при известной скорости СR, можно получить формулу для определения d такого
датчика:
C t
d =
R 54 .
2
2. ИЗМЕРЕНИЕ СКОРОСТИ ОБЪЕМНЫХ ВОЛН
С помощью приставного датчика, состоящего из двух меандровых ЭМА-преобразователей, ра-
ботающих в раздельном режиме, можно измерить не только скорость поверхностной волны Рэлея,
но и скорости объемных волн — продольной и поперечной. Это возможно в образце с плоскопа-
раллельными границами.
Для этого ЭМА-преобразователи и намагничивающая система фиксируются в единую кон-
струкция (см. рис. 1). При генерации волны Рэлея частота заполнения токового импульса должна
соответствовать частоте поверхностной волны fГ = fR = СR/λR. Этого добиваются с помощью под-
строечных элементов. При такой частоте будет синхронизация волновых колебаний вдоль поверх-
ности, что обеспечит эффективную генерацию и прием импульсов поверхностной волны [11]. Каж-
дый токовый элемент генерирующей решетки генерирует вокруг себя, помимо поверхностной, еще
две объемные цилиндрические волны — продольную волну (со скоростью Сl) и поперечную волну
(Сt), идущие вглубь образца [12]. Однако при частоте fR ни по какому направлению синхронизация
этих волн невозможна. Это поясняет рис. 4. Чтобы в некотором направлении АВ была синхрониза-
ция колебаний, должно выполнятся условие (например, для поперечной волны):
2π
2π
f
2π
2π
f
t
R
kR =
kt cos α, kt =
=
,
kR =
=
,
λ
C
t
λ
C
R
где kR, kt — модули волнового вектора поверхностной и поперечной волны.
Дефектоскопия
№ 4
2020
36
С.Э. Бабкин
A
kR(fR)
α
kl(fR)
kt (fR)
kt (ft)
kl(fl)
B
Рис. 4. Расположение волновых векторов поверхностной, поперечной и продольной волн в образце.
Из рисунка понятно, что при частоте fR это невозможно, так как СR < Сt.
При увеличении частоты генерации мы увеличиваем вектор k, при некоторой частоте ft по на-
правлению АВ будет выполняться условие синхронизации для поперечной волны, и эта волна будет
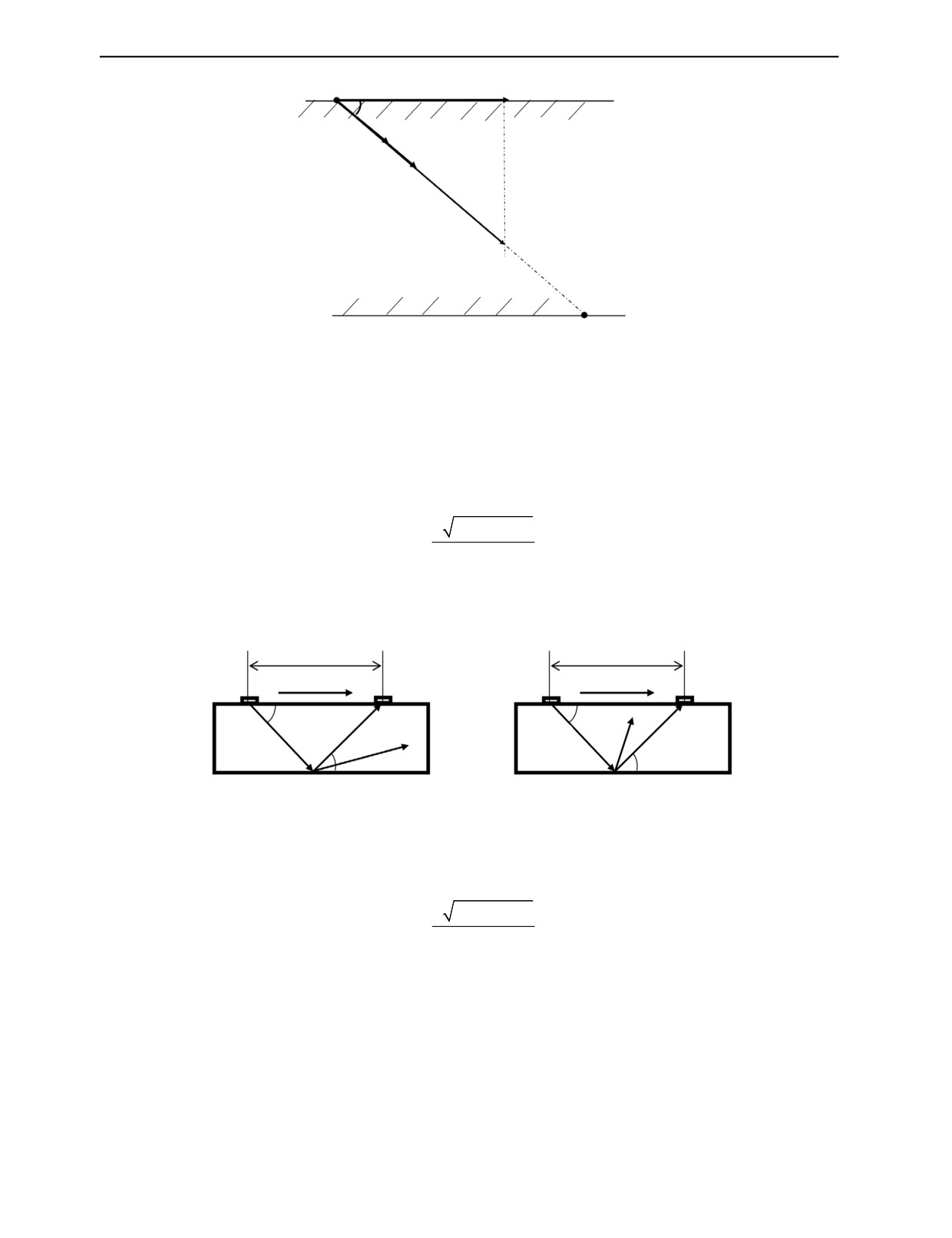
эффективно распространяться в этом направлении. Если точка В — середина проекции отрезка АС
на нижнюю грань (рис. 5а), то при плоскопараллельных границах образца эта волна отразится от
нижней грани в точке В и попадет в точку С (приемная меандровая ЭМА-катушка). В этом случае
при известных толщине образца Н и расстоянии d легко вычислить скорость поперечной волны [12]:
2
2
2
H
+d
/4
C
=
,
t
t
t
где tt — время прохождения поперечной волны от центра генерирующего преобразователя до цен-
тра приемного.
а
б
d
d
A
CR(fR)
C
CR(fR)
A
C
α
α
Ct(fl)
Ct(ft)
h
Cl(ft)
h
Cl(fl
)
Cl(fl)
C(ft)
B
t
α
B α
Рис. 5. Распространение волн внутрь образца: поперечная волна (а), продольная волна (б).
При дальнейшем увеличении частоты мы увеличиваем волновой вектор продольной волны и
при некоторой частоте fl получаем условие ее синхронизации в направлении АВ: kR = kl(fl) cos α
(рис. 5б).
Для этого случая
2
2
2
H
+d
/4
C
=
,
l
t
l
где tl — время прохождения продольной волны.
На рис. 5а показано, что при отражении поперечной волны от нижней грани образца в точке В
формируются две волны: продольная и поперечная, но первая волна уходит в сторону, не создавая
помехи при приеме второй волны. Рис. 5б поясняет, что при отражении в точке В продольной
волны, когда также возникают две волны, поперечная волна идет мимо приемника (С), не мешая
продольной.
При известной толщине образца и расстоянии d датчика основную трудность метода состав-
ляют идентификация принятого осциллографом дефектоскопа сигнала и измерение времени его
распространения. На рис. 6 показан общий случай экрана осциллографа для всех трех волн, но
реально эти импульсы появляются на экране по очереди при перестройке частоты.
Дефектоскопия
№ 4
2020
Определение скорости основных типов акустических волн в металлах...
37
U
t
t
tR
∆t
tl
t
A
Рис. 6. Импульсы трех волн на одной осциллограмме.
В [12] показано, как можно просто рассчитать случай совпадения импульсов R-волны и t-волны.
Это неблагоприятный случай, при котором при перестройке частоты с fR до ft принятый импульс
R-волны будет уменьшаться, и на этом же месте “вырастет” импульс t-волны. Желательно, чтобы
между ними был временной промежуток ∆t, так легче наблюдать, идентифицировать и измерять
два импульса. Идентификация волн подробно описана в [12]. При перестройке частоты на про-
дольную волну неблагоприятный случай совмещения импульсов получить гораздо труднее из-за
высокой скорости этой волны (2СR ≈ Сl ).
Рассчитаем благоприятное соотношение между d преобразователя и толщиной образца, при
котором удобно наблюдать и измерять принятые импульсы. Обозначим временной интервал между
вершинами принятых импульсов рэлеевской и поперечной волн за ∆t (рис. 6), тогда время распро-
странения поперечной волны:
2
2
2
H
+d
/4
t
=
,
t
C
t
где Ct — скорость волны, Н — толщина образца.
Условие различимости импульсов tt = tR + ∆t:
2
2
2
H
+d
/
4
=
d
/ C
+∆t
R
Ct
Отсюда легко переходим к квадратному уравнению относительно d:
d2(A2 - 1) + 2ABd + B2 - 4H2 = 0 ,
где A = Ct/CR , B = Ct ∆t — параметры эксперимента.
d, мм
200
180
160
140
120
100
80
60
40
20
0
-200
10
20
30
40
50 H, мм
Рис. 7. График зависимости оптимальной базы датчика от толщины образца.
Дефектоскопия
№ 4
2020
38
С.Э. Бабкин
Подставляя в это уравнение ориентировочные значения скоростей материала из справочни-
ков, а также принимая значение ∆t = 2 μS (для надежности измерений, хотя возможно значение
1 μS), получаем численное уравнение, которое удобно решать с помощью программы MATHCAD.
Результатом расчетов является график зависимости d = f (H), по которой для конкретной тол-
щины материала можно определить примерное расстояние между преобразователями, либо при
фиксированном d датчика определить желательную толщину образца.
На рис. 7 представлены рассчитанные таким образом кривые для стального листового проката
(Ct = 3300 м/с, CR = 3000 м/с). Так для толщины проката 15 мм оптимальной является база 40 мм.
Аналогичные графики легко получить для любого материала с известным ориентировочно зна-
чением скоростей звука.
3. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Для примера определим скорость звуковых волн для двух материалов: армко-железа и нике-
ля. Был изготовлен приставной датчик с двумя раздельными ЭМА-преобразователями в виде ме-
андровых решеток и П-образной системой подмагничивания (см. рис. 1). Расстояние между цен-
трами преобразователей было выставлено на уровне 40 мм, более точно измерялось по методике
раздела 1 и составило 39,32 мм. Шаг меандровых решеток λм = 2 мм задавал длину волны Рэлея.
В качестве образцов были взяты пластина армко-железа толщиной Н = 15 мм и пластина никеля
толщиной Н = 12 мм, продольные размеры значительно больше размеров датчика. Инженерный
расчет [7] показывает, что в неблагоприятную зону совмещения импульсов рэлеевской и попереч-
ной волн оба образца не попадают. Таким образом, мы можем за одну установку датчика на поверх-
ность образца определить все три основные скорости.
Подстраивая частоту для каждого типа волны, получаем сигнал в приемном преобразователе,
настраиваем его на максимум. По приведенной методике определяем положение точки А (начало
правильного отсчета временных интервалов) на временной шкале. Время ОА оказалось равным
0,71 мкс для обоих образцов. Это объясняется примерно одинаковыми размерами образцов и оди-
наковым индуктивным влиянием их на колебательный контур меандровых ЭМА-катушек. Более
массивные образцы сильнее изменили бы индуктивность контуров и форму токового сигнала. С
помощью цифрового осциллографа DSO 2100 измеряем времена распространения каждой волны
tR, tt, tl и производим расчет (данные заносим в табл. 1).
Таблица
1
Параметр
Армко-железо
Никель
d = SR = SAC
39,32 мм
39,32 мм
St =Sl = SABC
49,44 мм
46,06 мм
H
15,01 мм
12,03 мм
cos ά
0,8
0,86
fR
≈ 1,5 МГц
≈ 1,33 МГц
ft
≈ 2,0 МГц
≈ 1,7 МГц
fl
≈ 3,6 МГц
≈ 2,8 МГц
tR
12,91 мкс
14,41 мкс
tt
15,14 мкс
15,31 мкс
tl
7,82 мкс
8,99 мкс
СR
3046 м/с
2729 м/с
Сt
3266 м/с
3008 м/с
Сl
6322 м/с
5178 м/с
По точности измерений:
1. Подстройка частоты осуществляется до достижения максимума сигнала. Она приведена при-
близительно, более точно ее можно определить с помощью фурье-анализа принятого сигнала.
В принципе, частоту волны можно подсчитать, исходя из равенства проекций волновых векто-
ров на поверхность образца:
Дефектоскопия
№ 4
2020
Определение скорости основных типов акустических волн в металлах...
39
C
t,l
f
t,l
=
f
R
,
C
cosα
R
эта же формула позволяет при точном определении частоты волн определять соотношение скоро-
стей волн СR/ Сt, СR/ Сl, Сl / Сt даже без сложного измерения временных интервалов.
2. Точность измерения метрических величин d, H составляет +0,01 мм, что дает вклад в общую
погрешность порядка 0,1 %. В принципе точность измерения этих величин можно увеличить.
3. Основную погрешность при измерения скорости дает измерение временных интерва-
лов. Сюда входит погрешность цифрового осциллографа, которая в этом диапазоне составляет
+0,25 %, то есть при измерении временного интервала около 10 мкс абсолютная погрешность
составляет величину около +0,025 мкс. Отметим, что при современной аппаратуре вполне ре-
ально достигнуть точности +0,01мкс и выше.
Полная погрешность измерения скорости звука в нашем случае составит +0,5 % (в абсолют-
ных величинах +10 м/с).
ЗАКЛЮЧЕНИЕ
Таким образом, разработана методика определения скорости поверхностных волн Рэлея с
помощью меандровых ЭМА-преобразователей. Получены простые формулы для определения
скорости.
Методика позволила определить точки отсчета временных интервалов при распространении
продольных, поперечных и поверхностных волн. Благодаря этому удалось за одну установку ЭМА-
датчика на поверхность образца генерировать, принять и определить скорости всех трех волн с
точностью + 0,5 %. Методика подходит для образцов с плоскопараллельными границами и может
найти применение для решения задач структуроскопии (контроль по скорости) как ферромагнит-
ных образцов (например, конструкционных сталей), так и проводящих неферромагнитных метал-
лов (алюминий, медь).
СПИСОК ЛИТЕРАТУРЫ
1. Неразрушающий контроль и диагностика / Справочник под. ред. В.В. Клюева. М.: Машиностро-
ение, 2003. 656 с.
2. Муравьева О.В., Муравьев В.В. Методические особенности использования SH- волн и волн Лэмба
при оценке анизотропии свойств листового проката // Дефектоскопия. 2016. № 7. С. 3—11.
3. Maxfield B., Kuramoto A., Hulbert I. Оценка конструкции ЭМА-преобразователей для избранных
применений // Mater. Eval. 1987. V. 45. № 10. P. 1163—1183.
4. Муравьев В.В., Муравьева О.В., Волкова Л.В. Влияние анизотропии механических свойств тонко-
листного стального проката на информационные параметры волн Лэмба // Сталь. 2016. № 10. С. 75—79.
5. Murav'ev V.V., Gushchina L.V. et al. Evaluating Damage Accumulated in Car Wheelset Axle Journals
by the Ultrasonic Method Using Rayleigh and Head Waves // Russian Journal of Nondestructive testing. 2019.
V. 55. No. 10. P. 713—722. [Муравьев В.В., Гущина Л.В., Казанцев С.А. Оценка накопленной поврежден-
ности шеек осей колесных пар вагонов ультразвуковым методом с использованием релеевских и голов-
ных волн // Дефектоскопия. 2019. № 10. С. 14—23.]
6. Кондратьев А.И., Римлянд В.И., Драчев К.А. Применение резонансного метода для изучения аку-
стических свойств тонких образцов // Дефектоскопия. 2015. № 12. С. 3—10.
7. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 288 с.
8. Комаров В.А. Квазистационарное электромагнитно-акустическое преобразование в металлах.
Свердловск: УНЦ АН СССР, 1986. 235 с.
9. Thompson R.B. Model for the Electromagnetic Generation and Detection of Rayleigh and Lamb Waves
// IEEE Trans. Sonics and Ultras. 1973. V. 20. № 4. P. 340—346.
10. Ильясов Р.С., Бабкин С.Э., Комаров В.А. О механизмах ЭМА-преобразования волн Рэлея в фер-
ромагнетиках при низких частотах // Дефектоскопия. 1988. № 10. С. 77—82.
11. Бабкин С.Э., Ильясов Р.С., Комаров В.И., Рубцов В.И. Устройство для бесконтактного возбужде-
ния и приема волн Рэлея в ферромагнетиках // Дефектоскопия. 1989. № 6. С. 93—94.
12. Бабкин С.Э. Определение коэффициента Пуассона ферромагнитных изделий ЭМА-способом //
Дефектоскопия. 2015. № 5. С. 51—55.
Дефектоскопия
№ 4
2020