УДК 620.179.17
РЕКОНСТРУКЦИЯ АМПЛИТУДЫ ИЗЛУЧЕНИЯ ДЕФЕКТА ПО СИГНАЛАМ
АКУСТИЧЕСКОЙ ЭМИССИИ В УСЛОВИЯХ ПЛОСКОГО НАПРЯЖЕННОГО
СОСТОЯНИЯ
© 2020 г. В.Н. Беркович1,*, С.И. Буйло2,**
1Донской казачий государственный институт пищевых технологий и бизнеса (ДКГТПТиБ), филиал
Московского государственного университета технологий и управления им. К.Г. Разумовского (Первый
казачий университет), Россия 344007 Ростов-на-Дону, ул. Семашко, 55
2Институт математики, механики и компьютерных наук им. И.И. Воровича Южного федерального
университета (ЮФУ), Россия 344090 Ростов-на-Дону, ул. Мильчакова, 8А
E-mail: *vberkovich@mail.ru; **sibuilo@yandex.ru
Поступила в редакцию 30.12.2019; после доработки 27.02.2020
Принята к публикации 03.03.2020
Рассмотрена задача об установившихся колебаниях, порождаемых дефектом в упругом материале, находящемся
на стадии предразрушения в условиях плоского напряженного состояния. Исследован процесс излучения акустиче-
ской эмиссии (АЭ) от дефекта, выходящего на свободную границу упругого тела. Поставлена задача восстановления
амплитуд излучения дефекта по сигналам АЭ на свободной границе тела. Обратная задача восстановления исследо-
вана и решена на основе вариационного подхода. Приведены данные численного расчета параметров излучения для
алюминия.
Ключевые слова: акустическая эмиссия, граничное интегральное уравнение, интегральное преобразование, мате-
матическая модель, неразрушающий контроль, обратная задача, предразрушающее состояние, плоское напряженное
состояние, смешанная краевая задача, тензор Грина.
DOI: 10.31857/S0130308220040053
Как известно, метод акустической эмиссии (АЭ) обеспечивает уже вполне удовлетворительную
достоверность при оценке стадий предразрушения исследуемого материала [1—5]. Тем не менее
проблема повышения достоверности результатов АЭ диагностики всегда находилась в поле зре-
ния специалистов. Одним из аналитических подходов к решению указанной проблемы является
использование математического моделирования волнового процесса при появлении сигналов АЭ
для получения дополнительной информации о взаимосвязи параметров АЭ с параметрами дефек-
та. Данный подход был реализован нами в работе [6] в рамках классической постановки краевой
задачи динамической теории упругости, но лишь для случая антиплоской деформации, которая,
к сожалению, неизбежно приводит к наличию трансляционной симметрии, что не является ха-
рактерным для случаев возникновения АЭ излучения, имеющего достаточно локальный характер.
Моделирование АЭ от дефекта в условиях плоского напряженного состояния представляется, на
наш взгляд, более адекватным отражением изучаемого процесса.
Цель работы — разработка метода повышения достоверности восстановления амплитуд излу-
чения растущего дефекта в условиях плоского напряженного состояния на основе построения фи-
зико-математической модели взаимосвязи между параметрами акустического излучения дефекта
внутри упругого тела и откликом свободной поверхности этого тела.
Сформулированная проблема связана с решением обратных задач динамической теории упру-
гости [7]. В настоящей работе развивается подход, который позволяет осуществить восстановление
амплитуд излучения дефекта по сигналам АЭ, основанный на использовании метода граничных
интегральных уравнений.
Для целей разработки математической модели и анализа рассматриваемой проблемы могут
быть использованы соотношения плоской деформации теории упругости c параметрами λ*,ν*, ко-
торые, как известно [8], переходят в соответствующие соотношения плоского напряженного состо-
*
*
ν
2λ
µ
яния при замене коэффициента Пуассона ν* на дробь
ν=
и параметра Лямэ λ* на
λ=
*
1+ν
1+2µ
Описанные рассуждения порождают постановку следующей задачи.
1. Рассматривается математическая модель акустической эмиссии (АЭ) от линейного дефекта,
выходящего под произвольным углом на границу упругого тела, находящегося в условиях плоско-
го напряженного состояния. Поскольку в условиях нагружения тела сигналы АЭ излучает лишь
последнее образовавшееся звено дефекта, ближайшее к свободной границе и, в конечном итоге,
Реконструкция амплитуды излучения дефекта по сигналам акустической эмиссии...
41
выходящее на эту границу, будем рассматривать процесс распространения АЭ лишь от одного из-
лучающего дефекта.
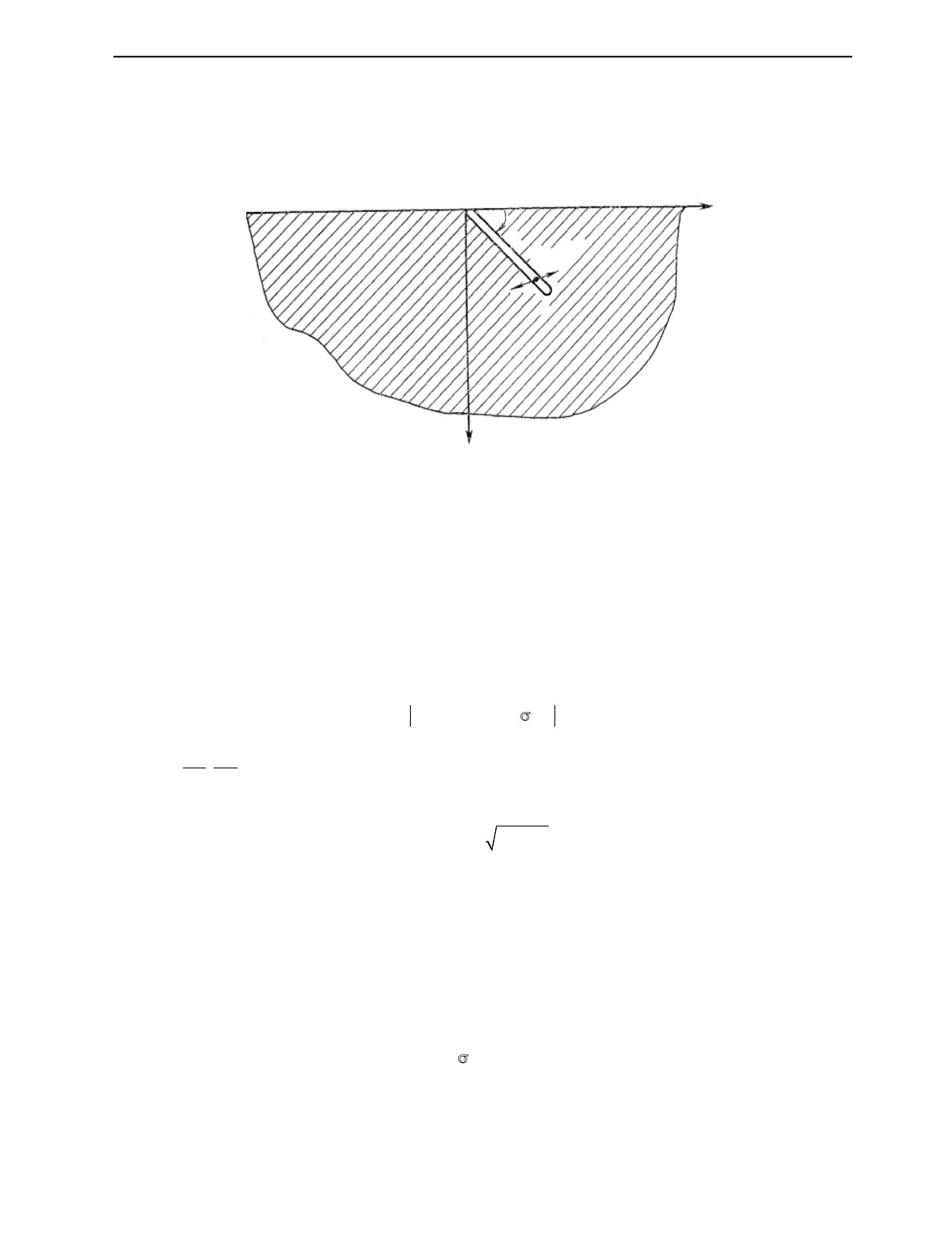
В рассматриваемой задаче тело моделируется упругой полуплоскостью, а линейный дефект —
разрезом J конечной длины l, выходящим на границу Г под углом α (рис.1).
x
Г
α
t
u0e-iωt
J
y
Рис. 1. Линейный дефект J, выходящий на свободную границу полупространства.
Предполагается, что берега разреза J± являются источниками плоских гармонических колеба-
±
ω
t
ний с векторами смещений
u
(x,
y e−i
,(x,
y
)
∈
J±
0
В предположении установившихся колебаний изучается взаимосвязь между распределениями
амплитуды вектора смещений v(x, y,t) на свободной границе Г и на границе дефекта J. При оты-
ω
t
скании вектора смещений точек полупространства в виде
v(x,y,t)
=
u(x,
y e-i
указанная поста-
новка приводит к следующей смешанной краевой задаче для динамических уравнений плоской
теории упругости [9] относительно комплексных амплитуд
u=
{
u
(x, y), u
(x, y)
}
:
1
2
2
2
µ∇
u(x, y) + (λ +µ)∇(∇⋅u) + Dω
u = 0,
(1)
u
=u
(x,
y
),
σ u)
=0,
J±
0
Г
∂
∂
где
,
∇=
— набла-оператор Гамильтона; λ,μ — параметры Лямэ; D — плотность матери-
∂x ∂ y
ала; l — длина дефекта;
u
— амплитуда вектора смещений берегов дефекта; σ(u) — амплитуда
0
вектора напряжений. Источники установившихся колебаний на границах разреза J± предполагают-
2
2
ся когерентными и равноинтенсивными. При
r= x
+y
→ ∞ смещения и напряжения исчезают
и, кроме того, удовлетворяют условиям излучения Зоммерфельда [10].
Замечание 1. Появление импульсов АЭ от дефекта связано с высвобождением упругой энергии
в зоне подрастания дефекта и генерирует, вообще говоря, нестационарный волновой процесс в
упругом теле, возбуждающий колебания обеих границ дефекта, амплитуды которых неизвестны и
подлежат определению. Поэтому размещение когерентных источников установившихся колебаний
равной интенсивности на берегах дефекта будет приближенно описывать данный процесс и явля-
ется, в некотором смысле, одним из промежуточных этапов математического моделировании этого
процесса. Освобождение от указанных ограничений возможно на следующих этапах моделирова-
ния процесса АЭ при дальнейшем развитии данного подхода.
Для представления смещений, удовлетворяющих (1), воспользуемся формулой Бетти [10]:
1
n
u(x,
y)
=
G(x,
y ξ,η)
⋅σ
(
ξ,η
)
−u ξη
⋅T G
(x,
y ξ,η)
dl
,
{
}
n
∫
(2)
2π
C
где С — граница плоской области; n — внешняя нормаль к границе С; (x, y) —точка наблюдения;
Ĝ
— тензор Грина для смещений; Tn — дифференциальный оператор напряжений. В рассматри-
ваемом случае тензор
Ĝ удовлетворяет условию
Дефектоскопия
№ 4
2020
42
В.Н. Беркович, С.И. Буйло
n
T G
=
0
(3)
y=0
и представляется в следующем виде:
Ĝ(x, y |ξ, )
η =G
(kR )
+G
(kR+)
+G
(x, y |ξ,
η);
(4)
0
0
1
±
2
2
2
2
−1
R
=
(x
−ξ)
+(y
±η)
,
K
=
Dω
µ
В выражении (4) тензора Грина
Ĝ использован фундаментальный тензор колебаний
G
=
{
g
(0)
}
, построенный в [11], тензор
G
=
{
g
(1)
}
характеризует волноводное действие гра-
0
ij
1
ij
ницы, связан с появлением поверхностных волн Релея и, как будет показано ниже, позволяет
удовлетворить условию (3).
2. Получим вспомогательные соотношения для фундаментального тензора колебаний
0
Ĝ . Его
Ê— единичный тензор):
представление в инвариантной форме Лурье [12] имеет следующий вид (
1
(1)
1
(1)
(1)
G
(x, y |ξ,η)
=
H
(kR)E
−
H
∇∇ γkR)−H
(kR);
(5)
0
0
2
0
0
µ
Dω
0,
i≠ j
2
1-2
ν
E
=
{
δ
ij
}
,
δ
ij
=
,
γ
=
a
p
/
a
s
=
(i,
j
=1,2);
1,
i= j
2(1−ν)
2
2
2
2
−1
R= (x
-ξ)
+(y
−η)
,
k
=
Dω
µ
В соотношении (5) ∇∇ — тензор в форме диадного произведения вектор-операторов ∇ Га-
(1)
мильтона;
0
H
(kR) — функция Ханкеля нулевого порядка; ω —круговая частота; k — волно-
вое число поперечных волн; ap, as — скорости продольных и поперечных волн соответственно;
μ — модуль сдвига; ν —коэффициент Пуассона; R — расстояние между точками «наблюдения»
(x, y) и «источника» (ξ, η). Для целей дальнейшего исследования представим функция Ханкеля в
выражении (5) с помощью функции Макдональда K0(κR) [13]:
(1)
2
2
2
H
0
(kR)
=
K
0
(κR),
R
= ρ
+
r
− ρrcos(
ψ-ϕ),
κ=-ik,
iπ
где ψ, φ — углы между положительным направлением оси абсцисс и полярными радиусами (ρ, r)
точки «источника» и точки «наблюдения» соответственно. Тогда фундаментальный тензор колеба-
ний примет вид:
2
1
µG
(x, y |ξ,η)
=
K0(κR)E
+
[
K
∇∇ γκR)−K
(κR)
]
0
2
0
0
}
i
π
κ
Для получения матричного представления этого тензора в полярной системе координат
(ρ,ψ) необходимо в предыдущую формулу внести выражение оператора Гамильтона
∂
1
∂
∇=
e
+
e
в полярной системе координат и выполнить действия:
ρ
ψ
∂ρ
ρ ∂ψ
2
2
∂
1
∂
∂
1
∂
∂
2
∂
∂
1
∂
∇∇ =
e
+
e
e
+
e
=
e
e
+
e
e
∇
−
+
(
e
e
+
e
e
)
ρ
ψ
ρ
ψ
ρ ρ
2
ψ ψ
2
ρ ψ
ψ ρ
∂ρ
ρ ∂ψ
∂ρ
ρ ∂ψ
∂ρ
∂ρ
∂ρρ ∂ψ
При получении равенства были использованы методики преобразования тензоров в их диадном
представлении [12], а также соотношения, получаемые непосредственно:
∂e
∂e
∂e
∂e
ρ
ψ
ρ
ψ
=
=
0,
=
e
ψ
,
=-e
ρ
,
(6)
∂ρ
∂ρ
∂ψ
∂ψ
Дефектоскопия
№ 4
2020
Реконструкция амплитуды излучения дефекта по сигналам акустической эмиссии...
43
2
2
1
∂
∂
1
∂
1
1
∇
=
ρ
+
,
∇e
=
e
e
,
∇e
=-
e
e
2
2
ρ
ψ ψ
ρ
ψ ρ
ρ ∂ρ
∂ρ ρ
∂ψ
ρ
ρ
Учитывая формулы дифференцирования для функций Макдональда [14]:
m
d
m
−ν-m
z-νK
(z)=
(−1)
z
K
(z),
ν+m
ν+m
zdz
придем к соотношениям:
∂
ρ-rcos(ψ-ϕ)
K
0
(κ
R)
= -κK
1
(κR)
= -κK
1
(κR)cosθ;
∂ρ
R
2
∂
1
K
(κR)
= κ
2[
K
(κR)cosθ+
K
(κ
R
)
]
;
(7)
2
0
2
0
∂ρ
2
2
∂
iπδ
(ρ- δ
r
ψ-ϕ)
1
2
∇
−
K
(
κR)
=-
- κ
2[
K
(κ
R
)cos2θ-
K
(κR)
]
;
2
0
2
0
∂ρ
2
ρ
2
∂
1
∂
1
2
K
(κR)
= κ
K
(κR) sin 2θ,
κ=-ik,
0
2
∂ρ ρ ∂ψ
2
где δ(r) — дельта-функция Дирака; θ — угол между полярным радиусом ρ источника и расстоянием
R между точкой (ρ, ψ) локализации источника источником и точкой наблюдения (r,φ). Используя
соотношения (6), (7), получаем:
1
2
2
2
2
2
2
∇∇
[
K
(γκR) −
K
(κR)
]
=
e
e
γ
κ
K
(γκ
R)-æ
K
(κR)cos2θ+γ
κ
K
(γκR) −κ
K
(κR)
−
0
0
ρ ρ
{
2
2
0
0
}
2
1
2
2
2
2
2
2
−
e
e
γ
κ
K
(γκR
)
−κ
K
(
κ
R)cos2θ-γ
κ
K
(γκR) −κ
K
(
κ
R
)
+
ψ ψ
{
2
2
0
0
}
2
1
2
2
2
+
(
e
e
+e
e
)
γ
κ
K
(γκR
) −κ
K
(
κR)sin 2θ
ρ ψ
ψ ρ
2
2
2
Тогда матричное представление тензора
∇∇
[
K
(γκR) - K
(κR)
] в полярной системе координат
0
0
принимает вид:
1
cos2θ
sin 2θ
1
1
0
2
2
2
2
2
2
γ
κ
K
(
γκR)
−κ
K
(
κR)
+
γ
κ
K
(
γκ
R)−κ
K
(κR)
2
2
0
0
2
sin 2θ
-cos2
θ
2
0
1
На основе полученных выражений приходим к следующему матричному представлению G
фундаментального тензора колебаний
Ĝ в полярной системе координат:
Г
(r,
ϕ ρ
ψ
)
=G
(r,
ϕ ρ
ψ)+G
(r,
ϕ ρ
ψ
);
0
γ
1
0
cos2
θ
sin 2θ
1
µ
G
(r,
ϕ ρ
ψ
)
=
K
(κR)
−K
(κR
)
;
(8)
0
0
2
iπ
0
1
sin 2
θ
-
cos2θ
1
0
cos2
θ
sin 2θ
1
2
µG
(r,
ϕ ρ
ψ)
=
γ
K
(γκR)
+K
(γκ
R
)
;
γ
0
2
i
π
0
1
sin 2
θ
-cos2θ
2
2
2
1-2ν
R
= ρ
+
r
−2
ρ
rcos(
ψ-ϕ) ,
κ=-
ik
,
γ
=
2(1−ν)
Дефектоскопия
№ 4
2020
44
В.Н. Беркович, С.И. Буйло
Для получения интегрального представления фундаментальной матрицы колебаний
G0(r,φ | ρ,ψ) (8) следует воспользоваться формулой Крама [14], из которой вытекают соотношения:
∞
1
K
(κR)
=
K
(κρ)K
(κr)ch(π-|ψ-ϕ|)τdτ;
(9)
0
∫
−iτ
-iτ
π
−∞
∞
cos2θ
ReK
(κρ)ch(π- |ψ-ϕ |)τ
1
2−iτ
K
2
(κR)
=
K
−iτ
(κr)dτ
∫
sin 2θ π
ImK
(κρ)sh(π- |ψ-ϕ |)τ
−∞
2−iτ
При использовании матричного представления фундаментального тензора колебаний будем
применять обозначения:
(1)
(2)
(1)
(1)
(1)
g
g
u
u
u
=
e
u
+e
u
ρρ
ρψ
ρ
ρ
ρ ρ
ψ ψ
G
(r,
ϕ ρ
ψ)
=
=
,
,
(10)
0
(1)
(2)
(2)
(2)
(2)
g
g
u
u
u
=
e
u
+e
u
ψρ
ψψ
ψ
ψ
ρ ρ
ψ ψ
(2)
(1)
где для соответствующих компонент
u
=
g
=
g
=
u
имеют место указанные равенства в
ρ
ρψ
ψρ
ψ
силу симметрии фундаментального тензора колебаний. При этом каждая компонента матричного
представления тензора колебаний содержит два слагаемых в соответствии с (4).
Окончательные матричные представления тензоров (4) с помощью (9) могут быть представле-
ны в следующем виде:
1
0
cos2θ
sin 2
θ
1
µG
(r,
ϕ ρ
ψ)
=
K
(κR)
−K
(
κR)
;
0
0
2
iπ
0
1
sin 2θ
-cos2θ
0,
i≠ j
2
1-2ν
E
=
{
δ
ij
}
,
δ
ij
=
,
γ
=
(i,
j
=
1,2);
1,
i= j
2(1−ν)
G
(x,
y ξ,η)
=
{
g
(1)
}
,
i,
j=1,2;
(11)
1
ij
2
1
−
(
y+η)
σ
2
2
−(
y
+η)
σ
1
−
yσ
1
−ησ
2
−
yσ
2
−ησ
1
z
σ
2
−iz|x−ξ|
g
(1)
=
−σ
σ
e
−α
e
+se
+e
e
dz;
11
2
1
2
}
k
µ
∫{
R z)
L
1
2
−(
y+η
)σ
2
−(
y+η
)σ
1
iz
−iα|x
−ξ
|
g
12
(1)
=
−α
σ
1
σ
2
e
+
e
}
e
dz
+
2
∫{
R z)
k
µ
L
1
2
-
y
σ
−ησ
−
yσ
−ησ
−iz|x−ξ|
1
2
2
1
iz
+
s
α
e
+σ
σ
e
e
dz;
2
1
2
}
∫{
R z)
k
µ
L
2
1
2
2
2
g
21
(1)
=-g
12
(1) ,
s=z
− k
,
R z)
=s
−z
σ
1
σ
2
,
2
2
2
2
2
2
σ
= z
−γ
K
,
σ
= z
−K
1
2
Ĝ позволяет удовлетворить условию (3). При получении компо-
Выбор компонент тензора
1
Ĝ в формулах (11
нент тензора
1
) были использованы методы интегральных преобразований, а
(1)
2
2
также представление функции Ханкеля
H
0
(k x
+y
) в форме интеграла Фурье по переменной
x [14], ν — коэффициент Пуассона. В соответствии с принципом предельного поглощения [11], кон-
тур интегрирования L выходит из - ∞, обходит сверху отрицательный корень уравнения Релея R(z) =
= 0 и точки ветвления z = - K, z = - γK, пересекает в нуле вещественную ось и, обходя снизу по-
ложительный корень уравнения Релея и точки ветвления z = K, z = γK, уходит в + ∞. Дальнейшие
преобразования компонент gij осуществляются с использованием известной в теории аналитических
функций техники преобразования контурных интегралов и не приводятся ввиду их громоздкости.
3. Получим граничные интегральные соотношения между смещениями и напряжениями на де-
фекте J, моделирующем излучающее и выходящее на свободную границу Г дефекта J. Выбирая
Дефектоскопия
№ 4
2020
Реконструкция амплитуды излучения дефекта по сигналам акустической эмиссии...
45
в (1.2) C = Г∪J, учитывая граничные условия (3), (4) и условия убывания на бесконечности, при-
ходим к соотношению (T — оператор напряжений Лурье [12]):
1
n
u(x,
y)
=
∫
{
G(x,
y
|ξ,η) ⋅σ
(
ξ,η
)
[
- u ξ,η)
]
⋅ T G(x,
y
|ξ,η)
}
dl
n
;
(12)
J
J
2π
J+
+
-
+
-
2[σ]
=σ
−σ
, 2[u]
=u
−u
J
J
При наличии когерентности и равной интенсивности излучения источников на правом J+ и J-
левом берегах разреза скачок смещений [u]J обращается в 0. Тогда, устремляя в (12) точку наблюде-
ния (х, у) на свободную границу Г, получаем следующее выражение вектора смещений свободной
границы Г (τ — локальная координата вдоль разреза):
l
πu(x,0)
=
∫
[
2G
0
(KR)
1
+G x,0|ξ,η)
]
⋅ p(τ)dτ;
(13)
0
2
2
R= x
+t
−2xτcosα ,
| x|>l;
1
−
2p(τ)
=µ
[
σ τcos
α τsinα)
]
,
p=
{p}
i
,
u=
{
u
i
}
,
i
=1,2.
J
Соотношения (13) являются соотношениями связи смещений свободной поверхности и скачка
вектора напряжений p(τ) и смещений на разрезе J.
Получим интегральное уравнение относительно скачка вектора напряжений p(t). Для этого в
соотношении (12) устремим точку наблюдения (х, у) на правый берег разреза J+. В результате при-
ходим к граничному интегральному уравнению (ГИУ):
1
1
Kq
=
∫ k
(r,ρ)⋅p(ρ)dρ =f(r),
0 ≤ r ≤1;
(14)
π
0
−
+
k(r,ρ)
=
G
0
(KR
1
) + G
0
(KR
2
) + G
1
(x,
η ξ,η);
−
+
2
2
R
=
|
r
−ρ
|,
R
=
r
+ρ
−2
rρcos2α;
1
2
−1
±
f(r)
=l
u
(τcos
α,
τ
sinα
),
τ=
lr
0
Элементы матриц G0, G1 определяются компонентами тензоров
G
,
G
с помощью соотноше-
0
1
ний (10), (11). Полученное интегральное представление тензора
Ĝ , позволяет представить опера-
тора K левой части ГИУ (2.3), в виде K = K0 + K1, где оператор K0 порождается составляющими
G0 ядра ГИУ и является однозначно обратимым оператором, а оператор K1, порождаемый состав-
ляющей G1 ядра ГИУ, — вполне непрерывным. Указанные результаты предварительно доказыва-
ются для случая κ > 0, а затем используются принципы аналитического продолжения в область
комплексной плоскости κ, содержащую точку κ = -ik. Свойства операторов K0, K1 в пространствах
±
12
дробной гладкости [15] Соболева—Слободецкого
W
2
(0,1)
детально рассмотрены в [16, 17]. Это
позволяет свести ГИУ (14) к эквивалентной системе ГИУ II рода с вполне непрерывным операто-
ром и сделать известные выводы о разрешимости, построить решение методом [16] и восстановить
(1)
волновое поле в пространствах Соболева
W
(Ω) .
2
4. Для реализации сформулированного подхода воспользуемся вариационным принципом
Гамильтона-Остроградского [18] и введем функционал действия H(u):
t
2
t
2
H
(v)
=∫a
(v)dt -∫b
(v)dt
,
v v r,θ,t),
∀t
>t
>
0,
(15)
2
1
t
1
t
1
где W(v) — упругий потенциал относительно вектора смещений v, D — плотность материала сре-
ды. Известно, что из условия стационарности δH(v) = 0 функционала Гамильтона-Остроградского
(15), вытекают все соотношения, определяющие начально-краевую задачу для системы уравнений
теории упругости.
Для случая установившихся колебаний v(x, y,t) = u(x, y)exp(-iωt) в силу произвольности мо-
ментов времени t2 > t1 условие стационарности функционала H(v) приводит к условию минимума
функционала
Дефектоскопия
№ 4
2020
46
В.Н. Беркович, С.И. Буйло
1
2
2
Ψ(g)
=
a
(g)
+
ω
D
g
d
Ω>
0,
∫∫
(16)
2
Ω
где вектор g — действительная либо мнимая части комплексного вектора амплитуды u = u1 + iu2.
Для построения приближенного представления комплексных амплитуд смещений среды от излуча-
ющего дефекта J будем отыскивать эти амплитуды, приближая их линейными комбинациями вида:
N
u(x,
y)
≈
Au x,
y)
=
u
(x,
y
);
∑
n n
N
n=1
(17)
1
u
=
G
(x,
y
|
ξ
,η
)⋅
e
,
e
=
,
(ξ
,η
)∉ Ω,
n
n
n
1
1
n
n
0
где коэффициенты An подлежат определению. Система квадратично суммируемых вектор-функций
{un(x, y)}, n = 1,2, … обладает свойством полноты [10] в любой конечной подобласти Ω*, если по-
следовательность точек (ξn, ηn) имеет точку сгущения при n→∞. Это означает, что приближение
линейными комбинациями (17) можно осуществить с любой степенью точности, и, в частности,
в смысле Ψ(u - uN) < ε, где ε > 0 сколь угодно мало, когда N достаточно велико. Условие δΨ(u) = 0
есть условие минимума функционала Ψ(u), который достигается на точном решении задачи [18].
Неизвестные коэффициенты An отыскиваются из условий минимума функционала Ψ(u - uN),
используя полноту системы функций {un(x, y)}, n = 1,2, …, которые удовлетворяют граничному
условию
σ(
u
n
)
=
0 .
Γ
∂Ψ(u−u
N
)
Приравнивая нулю производные
=
0,
n
=
1,2,...,N
и преобразуя левые части по-
∂An
лученных уравнений с помощью формул Грина, а также учитывая, что выбранные вектор-функции
un(x, y) удовлетворяют уравнению (1), граничным условиям (2) и условиям на бесконечности кра-
евой задачи (1), приходим к следующей системе линейных алгебраических уравнений для неиз-
вестных An:
N
∑
A
u
⋅σ
(
u
)
dl
−
f
⋅
σ
(
u
)
dl
=
0,
m
=1,2,...,N
n
∫
m
k
∫
m
(18)
k=1
J
J
В соотношениях (18) σ(um) — вектор напряжений, вычисленный на N векторах полной системы
{um}. Однозначная разрешимость уравнений (17) вытекает из однозначной разрешимости системы
ГИУ (14). Подставляя найденные
=A f |l,
)
j
j
A
α
как линейные функционалы от амплитуды f сиг-
налов АЭ, излучаемых дефектом, в выражение смещений (13) свободной поверхности Г, получим
интегральное соотношение связи неизвестных амплитуд смещений f, распределенных на дефекте J
*
с амплитудами смещений
u
=
f
, полученными на основе измерений на свободной поверхности.
Г
Для восстановления амплитуд f излучения дефекта на основе результатов измерений f*(xm,0),
m = 1,2, …, M достаточно представить интеграл
(
)
⋅
dl
σ
u
в виде конечной суммы с помощью
n
∫f
J
квадратурной формулы, а затем применить известные процедуры метода наименьших квадратов
для оценки параметров вектора амплитуд смещений свободной поверхности y = 0:
2
P N
*
A
(f
,f
,
f
,...,f
ω,l,α
)
u
(
x
,0)
−
f
(x
,0)
→
min.
(19)
∑
∑
n
1
2
3
P
n k
k
k
=1
n
=1
В выражении (19)
f
1
=
{
f
11
,
f
12
}
,
f
2
=
{
f
21
,
f
22
}
,
f
3
=
{
f
31
,
f
32
}
,...,
f
P
=
{
f
P1
,
f
P2
} — неизвестные зна-
чения компонент вектора амплитуд f в P узлах квадратурной формулы для контура J+. Восстанов-
ленные амплитуды позволяют восстановить также и вектор амплитуды скачков напряжений p(ρ) на
дефекте J с помощью ГИУ (14) .
5. Для получения численных результатов введем эллиптические координаты (ξ, η), связанные с
контуром дефекта J по формулам ( n — внешняя нормаль к J):
t = lchξcosη, n = lshξsinη,
-π≤η≤π
π
π
Тогда весь контур J-дефекта t = lcosη будет представлен соотношениями
ξ=
0,
−
≤η≤
, и
2
2
ГИУ преобразуется к виду:
Дефектоскопия
№ 4
2020
Реконструкция амплитуды излучения дефекта по сигналам акустической эмиссии...
47
π
2
1
π
(cosη, cos
′
η ⋅p(cosη′) sinη′dη=f(cosη),
0
≤η≤
(20)
∫k
π
2
0
Предполагая, что функция f(cosη) разлагается в ряд Фурье, а, следовательно, и в ряд по функ-
циям Матье
(
,
)
m
ce
η′
q
[19], ограничимся рассмотрением случая
π
f(cosη)
=f
cos(klcosη),
f =
{f },i
0
≤η≤
,
i
=1,2.
2
Пользуясь тем, что выбранная система функций Матье обладает полнотой, будем отыскивать
решение (20) в форме ряда по функциям Матье:
∞
∞
1
p(cosη′)
=
x
ce
(
η′,q)
+
x
ce
(η′,q);
(21)
∑
2n
2n
∑
2n+1
2n+1
sinη′
n
=0
n
=0
2
2
K
l
π
x
m
=
{
x
i
(m)
}
,
p
=
{p}
i
,
q
=
,
0
≤η′
≤
(i
=1,2;
m
=1,2,...).
4
2
В выражении (21) векторы xm = xm(q, γ) подлежат определению. При этом скачок вектора напря-
жений p(cos ηʹ) в концевой точке разреза содержит характерную для контактных задач теории упру-
гости степенную особенность, определяемую в используемых координатах множителем sin ηʹ ,
как показано в работе [20]. В этой работе в функциях Матье построено точное решение смешанной
задачи об антиплоских колебаниях полосового штампа на границе упругого полупространства, где
возникает ГИУ, аналогичное рассматриваемому.
Подставим решение в форме (21) в уравнение (20), умножим обе части на cem(η, q) и произве-
π
дем интегрирование по отрезку 0
≤η≤
. В результате громоздких преобразований, а также ис-
2
пользования известных соотношений для функций Матье, придем к системе линейных алгебраи-
ческих уравнений относительно неизвестных векторных постоянных xm:
∞
s
s
ce
s
(α,q)
(q)
⋅
x
=
B q)
f
,
B q)
=πA q)
;
∑G
sm
m
s
s
0
π
m=0
ce
(
,q)
s
2
(22)
f
,
s
=
2k
s
f
=
,
s
=
0, 1, 2,
0,
s
=
2
k
+1
π
При получении (22) использовалась полнота на отрезке 0
≤η≤
системы функций Матье,
2
s
(
)
A
q
— нулевой коэффициент разложения функций ces(α, q) по косинусам. Матричные коэффи-
0
циенты системы (22) выражаются следующими интегралами:
π
π
2
2
16
(23)
G
(q)
=
ce
(η,q)
dη∫G η
η′)ce
′,q)
(η η′ s,
m
=
0,1,2,...);
sm
2
∫
s
s
π
0
0
G(ηη′)=G(l cosηcosα, 0|lcosη′cosα, lcosηsin
α).
При исследовании процессов излучения волн от микродефектов в частотном диапазоне
−6
0,1—5,0 МГц для реальных конструкционных материалов оказывается, что
q
≅10
Поэтому вы-
числение интегралов (23) производилось приближенно с точностью O(q2). В результате вычисле-
ний матрицы Gsm(q) приобретают вид:
µG q)
=G q)
+G
(q).
(24)
sm
0
sm
1sm
Выражение элементов матрицы Gsm(q) имеют достаточно громоздкий вид и содержат значения
π
(1)
2s
обычных
ce
(0, q)
, ce
(
,
q)
и модифицированных
Me
(0,
q)
функций Матье,
A
(q)
— коэф-
2
s
2s
2m
0
2
Дефектоскопия
№ 4
2020
48
В.Н. Беркович, С.И. Буйло
фициенты разложения функций Матье в тригонометрический ряд, а также τR — положительный
корень приведенного к безразмерному виду уравнения Релея:
2
2
R(τ) = (τ -0.5)
−τ τ-1
τ-γ
= 0.
Элементы матриц
0
sm
G q)
=
{
ij
g s,m)
}
,
1sm
G q)
=
{
ij
g s,m)
}
имеют следующее асимптоти-
ческое поведение (q→0):
2
2
g (0;0,0) = 2(1+ γ
) ln q
[
1+O(q
)
]
;
11
2
2
22
g (0;0,0) = 2(1+ γ
) ln q
[
1+O(q
)
]
;
2+2
m
2m
−
1
g s,m)
=-2ε
δ
(1+γ
) + o(q
);
(25)
11
sm sm
2+
2
m
2
m
−
1
g
22
(0;s,m)
=
2
ε
δsm sm
(1−γ
) +o(q
);
(q/4)m+s
ij
g s,m)
=
O
,
s,m
=1,2, ... ;
(2s)!(2m)!
ε
sm
=
1+( 1)s cos2
mα
Учитывая соотношения (24), (25), получим систему:
∞
s
G
0sm
(q)
x
s
=
s
B q)
f
− ∑G
1sm
(q)⋅x
m
(26)
m=0
Анализ асимптотических свойств коэффициентов (26) на основе (25) показывает, что для иссле-
дования и эффективного решения систему (26) следует преобразовать. Введем переобозначения:
D q)
=G q)
=
{
g s,
m)
}
,
R q)
=G q)
=
{
g s,m)
}
ss
0
ss
ij
sm
1sm
ij
Положим в (26) s = 0 и отделим от бесконечной суммы слагаемое Dss(q) при m=0, содержа-
щее x0, а также отделим слагаемое Rsm(q), соответствующее положительному корню τR уравнения
Релея. Это позволяет выразить через x0 остальные неизвестные и преобразовать систему к виду
(s = 1, 2, …):
−1
−1
x
=
B q)
E
−
R
(q)⋅
[
D
(q)
+
R
(q)
]
⋅
(
D fs
q
-
s
{
s
s0
00
00
}
ss
(27)
∞
-1
-1
−D
(q)
⋅∑
R
(q)
−
R
(q)
⋅
[
D
(q)
+
R
(q)
]
⋅
R
(q)
⋅
x
ss
{
sm
s0
00
00
0m
}
m
m=1
Введем пространство s(v) векторных последовательностей
X= x (
)}
j
, s = 0,1,2, …; j = 1,2, … ,
s
сходящихся к нулю с весом sβ в норме:
β
X
=
sup sup|
s
x j)
s
|
<∞,
β>
0.
s(β)
s
≥0
j ≥
1
Учитывая (25), (27), можно доказать полную непрерывность оператора левой части (27) в про-
странстве s(β), β > 0. Это позволяет сделать известные из данной теории заключения о разрешимо-
сти бесконечной системы (27) и строить ее приближенное решение методом урезания.
Ограничиваясь нулевым приближением, можно получить следующие матричные представле-
ния тензоров
G
,
G
:
0
1
∞
(1)
(1)
2µG
(kR)
=
E
J
(
γ
Kt
)
H
(γ
Kr
) +
J
(
Kt
)
H
(Kr
)cosα
p
−
0
∑γ2
p
p
p
p
p=-∞
(28)
∞
p
2
(1)
(1)
cos
α
p
(−1)
sinαp
−
γ
J
(
γKt
)H
(
γKr
)
+
J
(
Kt
)
H
(
Kr
)
;
∑
p−2
p
p
−
2
p
p=-∞
(−1)p sin
αp
−cosαp
Дефектоскопия
№ 4
2020
Реконструкция амплитуды излучения дефекта по сигналам акустической эмиссии...
49
2
−1
πσ
R R
τ
−2
µG
(x,0|
x′,
y′)
=
T
⋅
{
σ
τ
exp
[
−K(σ
y′+iτ
x′)
]
−
1
R
R R
1R
R
∆
(
τ
)
R
2
−exp
[
−k(
σ
y′+iτ
x′)
]}
exp(iK
τ
x)+
O
(q
);
2R
R
R
-1
−1
iσ
σ
τ
σ
−iσ
τ
1R
R R
1R
R R
T
R
=
=
i
;
−1
−
1
−σ
τ
iσ
iσ
τ
σ
R R
2
R
R R
2
R
2
6
2
∆(
τ
R
)
=
(1
−γ
)τ
R
+
0,5τ
R
−
0,125;
2
2
2
2
2
σ
= τ
−1,
σ
= τ
−γ
,
σ
=τ
−0,5,
q
=γ
q
2R
R
2
R
R
R
R
1
Внесем выражения (27), (28) в правую часть (13) и с учетом (25) произведем интегрирова-
ние. Тогда, в нулевом приближении, приходим к следующему асимптотическому представлению
комплексной амплитуды вектора смещений свободной поверхности Г (τR > 0 — корень уравнении
Релея):
(1)
2
(1)
τR
| |
µ
u
(x,0)
=
A
(q)H
(
K
|
x
|)
+
B
(γ
q)
H
(
γK
|
x
|) +
R(q,γ
)ei
+
1
0
0
0
0
∞
(29)
(1)
2
(1)
2
+2
(q)
H
(
K
|
x
|)
+
B
(
γ
q
)H
(γK
|
x
|)
+O
(q
),
|
x
|
>
l
∑A
m
2
m
m
2m
m=-∞
2
A q),
B
(γ
q)
Ĝ
Амплитуды
m
m
определяются компонентами тензора
0
, амплитуда R(q) —
Ĝ
компонентами тензора
1
По полученным результатам с использованием (29) проводился численный анализ. В качестве
исходного материала выбирался алюминий Al. Расчеты представлены для l=10-4м, Reu0(x,0) =
= 0,01l, Imu0 = 0,02l на расстояниях x от начала координат. Переменным параметром являлась
частота 0,1—5,0 Мгц.
Амплитудно-частотная характеристика (АЧХ) смещений Reu1(x, 0) приведена на рис. 2 для рас-
стояний x = 0,25 м (сплошная линия) и х = 5 м (штриховая линия) от точки выхода дефекта на сво-
бодную поверхность Г. Обращение амплитуд в бесконечность на резонансных частотах связано с
отсутствием затухания в идеально упругой среде, используемой в рассмотренной математической
модели. Детальное изучение данных анализа приводит к качественным результатам, которые ана-
логичны полученным при изучении установившихся колебаний упругого полупространства с из-
лучающим конечным разрезом, выходящим на границу в условиях антиплоского сдвига [15].
Предлагаемое исследование дает аналитическое описание характера волнового поля при пло-
ском напряженном состоянии среды, возбуждаемой излучающим дефектом для случая его выхода
на свободную поверхность. Используя представление (12), связывающее вектор амплитуды сме-
щений и скачок напряжений на дефекте J, а также соотношение (29) АЧХ смещений свободной
поверхности, можно восстановить амплитуды излучения дефекта.
A, 10-6 м
1,0
1
2
0,1
0,1
1
2
3
4
f, МГц
Рис. 2. Частотная характеристика амплитуды смещения свободной поверхности. Параметры излучения: Re u0 = 10-5 м;
Im u0 = 2 ⋅ 10-5 м трещины: l = 10-4 м, α = 45°.
1 — на расстоянии 0,25 м от дефекта; 2 — на расстоянии 5 м от дефекта.
Дефектоскопия
№ 4
2020
50
В.Н. Беркович, С.И. Буйло
Замечание 2. Метод наименьших квадратов в (19) приводит к конечной системе линейных урав-
нений относительно неизвестных векторов-амплитуд смещений границ дефекта J, при этом коэффи-
циенты системы зависят от ω, l, α. Тогда равенство нулю определителя этой системы порождает резо-
нансное соотношение, связывающее частоту ω с критическими значениями величин l, α и соответству-
ющее случаю подрастания дефекта. Угол α в рассматриваемом случае известен, поскольку линейные
дефекты при развитии в окрестности свободной границы тела в условиях плоского напряженного
состояния выходят на эту границу под углом, близким к 45°, как показано на рис. 1 и соответствует
надписям к рис. 2. Таким образом, из представленной выше математической модели вытекает наличие
зависимости резонансной частоты в АЧХ от критической длины дефекта на стадии его подрастания.
Однако в случае предразрушающего состояния решение обратной задачи восстановления ха-
рактеристики прочности (скачка амплитуд напряжений на дефекте J) на основе восстановленных
амплитуд излучения дефекта осуществляется для нерезонансных значений частот АЧХ [7].
Таким образом, предлагаемая модель позволяет исследовать связь параметров акустического
излучения дефекта внутри тела в условиях, близких к плоскому напряженному состоянию (напри-
мер, внутри тонких оболочечных конструкций) с параметрами акустического сигнала (смещения)
на его поверхности, что может быть использовано при решении задач повышения достоверности
результатов АЭ диагностики.
Работа поддержана Южным федеральным университетом и Минобрнауки РФ (проект
№ ВнГр/2020-04-ИМ).
СПИСОК ЛИТЕРАТУРЫ
1. Буйло С.И. Физико-механические, статистические и химические аспекты акустико-эмиссионной
диагностики. Ростов-на-Дону: Изд-во ЮФУ, 2017. 184 с.
2. Иванов В.И., Барат В.А. Акустико-эмиссионная диагностика. М.: Спектр, 2017. 368 с.
3. Буйло С.И. Физико-механические и статистические аспекты повышения достоверности результа-
тов акустико-эмиссионного контроля и диагностики. Ростов-на-Дону: Изд-во ЮФУ, 2008. 192 с.
4. Буйло С.И. Диагностика предразрушающего состояния материалов по параметрам амплитудно-
го распределения сигналов сопутствующего акустического излучения // Дефектоскопия. 2012. № 11.
С. 32—45.
5. Builo S.I. Physical, Mechanical and Statistical Aspects of Acoustic Emission Diagnostics / In: Physics
and Mechanics of New Materials and Their Applications. New York: Nova Science Publishers. Chapter 15.
2013. 444 p.
6. Berkovich V.N., Builo S.I. Reconstructing the Amplitudes of Radiation of a Defect Based on Acoustic
Emission Signals at the Free Boundary of a Massive Body // Russian Journal of Nondestructive testing. 2019.
V. 55. No. 4. P. 262—267. [Беркович В.Н., Буйло С.И. Восстановление амплитуд излучения дефекта по
сигналам акустической эмиссии на свободной границе массивного тела // Дефектоскопия. 2019. № 4.
С. 15—20.]
7. Ватульян А.О., Соловьев А.Н. Прямые и обратные задачи для однородных и неоднородных упру-
гих и электроупругих тел. Ростов-на-Дону: Изд-во ЮФУ, 2008. 175 с.
8. Амензаде Ю.А. Теория упругости. М.: Высшая школа, 1977. 272 с.
9. Рекач В.Г. Руководство к решению задач по теории упругости. М.: Высшая школа, 1977. 275 с.
10. Купрадзе В.Д. Методы потенциала в теории упругости. М.: Физматгиз, 1963. 472 с.
11. Купрадзе В.Д. Граничные задачи теории колебаний и интегральные уравнения. М.: ГИТТЛ, 1958.
280 с.
12. Лурье А.И. Теория упругости. М.: Наука, 1970. 940 с.
13. Лебедев Н.Н. Специальные функции и их приложения. М.—Л.: Наука, 1968. 358 с.
14. Бейтмен Г., Эрдейи А. Таблицы интегральных преобразований. Т. 2. Сер. Справочная математи-
ческая библиотека. М.: Наука, 1969. 343 с.
15. Бесов О.В., Ильин В.П., Никольский С.М. Интегральные представления функций и теоремы вло-
жения. М.: Наука, 1975. 478 с.
16. Беркович В.Н. О точном решении одного класса интегральных уравнений смешанных задач
упругости и математической физики // Докл. АН СССР. 1982. Т. 267. № 2. С. 327—330.
17. Беркович В.Н. Акустическое излучение в упругой среде от внутреннего дефекта с изломом //
Междун. научн.-иссл. журнал. 2018. № 3. С. 11—14.
18. Михлин С.Г. Вариационные методы в математической физике. М.: Наука. Главное изд-во физ.-
мат. лит., 1970. 512 с.
19. Мак-Лахлан Н.В. Теория и приложения функций Матье / Пер. с англ. М.: Наука. Изд. иностр.
лит., 1953. 474 с.
20. Бородачев Н.М. Динамическая контактная задача в случае деформации продольного сдвига //
Прикл. мех. 1973. Т. 9. Вып. 5. С. 231—234.
Дефектоскопия
№ 4
2020