Визуально-измерительный контроль
УДК 620.179.18
АППАРАТНО-АЛГОРИТМИЧЕСКОЕ ОБЕСПЕЧЕНИЕ ПРОЦЕССА
ДИНАМИЧЕСКОГО ИНДЕНТИРОВАНИЯ
© 2020 г. Р.А. Егоров1,*, А.В. Ильинский1,**, М.В. Кузьмичев1,***, А.В. Федоров1,2,****
1Университет ИТМО, Россия 197101 Санкт-Петербург, Кронверкский пр-т, 49
2Учреждение науки ИКЦ СЭКТ, Россия 197343 Санкт-Петербург, ул. Матроса Железняка, 57-А, пом. 141-Н
E-mail: *roman1465@yandex.ru; **allill003@mail.ru; ***kuzmichev.m92@gmail.com; ****afedor62@yandex.ru
Поступила в редакцию 05.02.2020; после доработки 23.04.2020
Принята к публикации 12.04.2020
Представлены результаты разработки и апробации алгоритма обработки измерительного сигнала, получаемого с пер-
вичного преобразователя при динамическом индентировании. Приведен сравнительный анализ использования показателей
динамической твердости. Рассмотрены поверхностный и объемный подходы к оценке динамической твердости. В рамках
экспериментальных исследований приведен их сравнительный анализ. Отмечены и обоснованы преимущества использо-
вания объемного подхода при оценке динамической твердости с использованием метода динамического индентирования.
Ключевые слова: твердость материала, алгоритмы, обработка сигнала, первичный преобразователь, датчик.
DOI: 10.31857/S0130308220060068
ВВЕДЕНИЕ
Контроль твердости — один из основных видов механических испытаний материалов, который
применяется при контроле качества как в производстве, так и при эксплуатации ответственных из-
делий в различных областях промышленности, в том числе в ракетно-космическом производстве.
Обеспечение заданного качества изделий ракетно-космической техники, выполненных по аддитив-
ным технологиям, в настоящее время является весьма актуальной задачей.
На сегодняшний день для контроля твердости материалов изделий, выполненных по аддитив-
ным технологиям, в основном применяют разрушающие методы контроля. В числе прочих следует
выделить традиционные методы: Роквелла, Виккерса, Бринелля и др. [1]. Однако, являясь образцо-
выми, они имеют свои известные недостатки. Вместе с тем в настоящее время интенсивно разви-
ваются и безобразцовые методы контроля, в том числе метод динамического индентирования (ДИ),
главным достоинством которого является возможность оперативной оценки твердости материалов
изделий без использования образцов-свидетелей [2].
С развитием вычислительных устройств и электронной элементной базы метод ДИ приобретает
новые возможности и преимущества перед другими методами неразрушающего контроля механи-
ческих свойств материалов изделий. Разработка алгоритмического, программного и технического
обеспечения является важным направлением в развитии метода динамического индентирования.
Целью настоящего исследования является повышение точности оценки твердости металлов и
сплавов с использованием метода динамического индентирования.
АЛГОРИТМ ОБРАБОТКИ ПЕРВИЧНОГО СИГНАЛА
Метод ДИ на сегодняшний день регулируется ГОСТ Р 56474—2015. Суть данного метода за-
ключается в ударном контактном взаимодействии жесткого индентора с заданной начальной кинети-
ческой энергией с испытуемым материалом и одновременной регистрацией данного процесса. Под
регистрацией процесса подразумевается непрерывное определение изменения скорости движения
индентора во времени (V(t)), а в дальнейшем и определение изменения глубины внедрения индентора
h(t) и контактного усилия индентора с материалом F(t) [3]. В основе определения изменения скоро-
сти движения индентора лежит магнитоиндукционный метод, заключающийся в измерении электро-
движущей силы (ЭДС), наводимой в катушке индуктивности датчика, в результате помещения в нее
системы индентирования ударника, а именно индентора и жестко сцепленного с ним магнита.
Основное достоинство такого типа датчиков состоит в том, что их выходной сигнал ЭДС ε(t) в
допустимом приближении можно считать линейно зависимым от скорости внедрения индентора:
ε(t) = kV(t),
(1)
где k — коэффициент пропорциональности, который зависит от конструктивных параметров пре-
образователя [4].
62
Р.А. Егоров, А.В. Ильинский, М.В. Кузьмичев, А.В. Федоров
В данном исследовании для получения первичного измерительного сигнала ЭДС применялся
датчик, входящий в состав существующего прибора ДИ [5]. При этом сигнал с датчика подавался
на вход осциллографа LeCroy Corporation WaveRunner WR 44Xi-A.
Оцифровка сигналов проводилась с частотой дискретизации в 5 МГц. Объектом контроля вы-
ступила мера твердости по Бринеллю 66HB. В общей сложности на объекте контроля было про-
ведено и оцифровано 76 измерений. Объем каждой выборки составил 104 дискретных отсчета.
Осциллограф работал в режиме увеличенного разрешения в 11 бит. Определение момента начала
записи проводилось по нарастающему фронту первичного сигнала.
Разработанный алгоритм обработки первичного сигнала выглядит следующим образом:
аналого-цифровое преобразование зависимости ε(t) на выходе датчика и запись в память ком-
пьютера в виде дискретного двумерного массива;
применение операции цифровой фильтрации к полученному массиву ЭДС для устранения вы-
сокочастотных шумов, наводимых в первичном преобразователе;
численное дифференцирование;
выделение и последующее удаление из массива областей, не несущих информации о процессе
контактного взаимодействия;
приведение полученной зависимости к V(t) путем поэлементного деления дискретной зависи-
мости на коэффициент пропорциональности согласно зависимости (1).
Реализация алгоритма обработки первичного сигнала проводилась с использованием про-
граммной среды MATLAB.
Глубина внедрения индентора h(t) и контактное усилие индентора с материалом F(t) определя-
лись по зависимостям (2) и (3) соответственно [3]:
t
h t)
=∫V t)dt
,
(2)
t0
dV t)
F t)
=-m
,
(3)
dt
где m — масса системы индентирования ударника.
Знак «-» в выражении (3) указывает на направление прикладываемого усилия.
Цифровая фильтрация исходного дискретного сигнала проводилась с использованием дискрет-
ного преобразования Фурье (ДПФ) и заключалась в переходе в область амплитуд частот, удалении
амплитуд выше заданной частоты среза и обратном переходе во временную область.
Применение фильтра на основе ДПФ обусловлено характером ЭДС. Сигнал динамического
индентирования является апериодическим, а его энергия сосредоточена в области низких частот,
поэтому основным требованием к фильтру является эффективное затухание низких частот без ис-
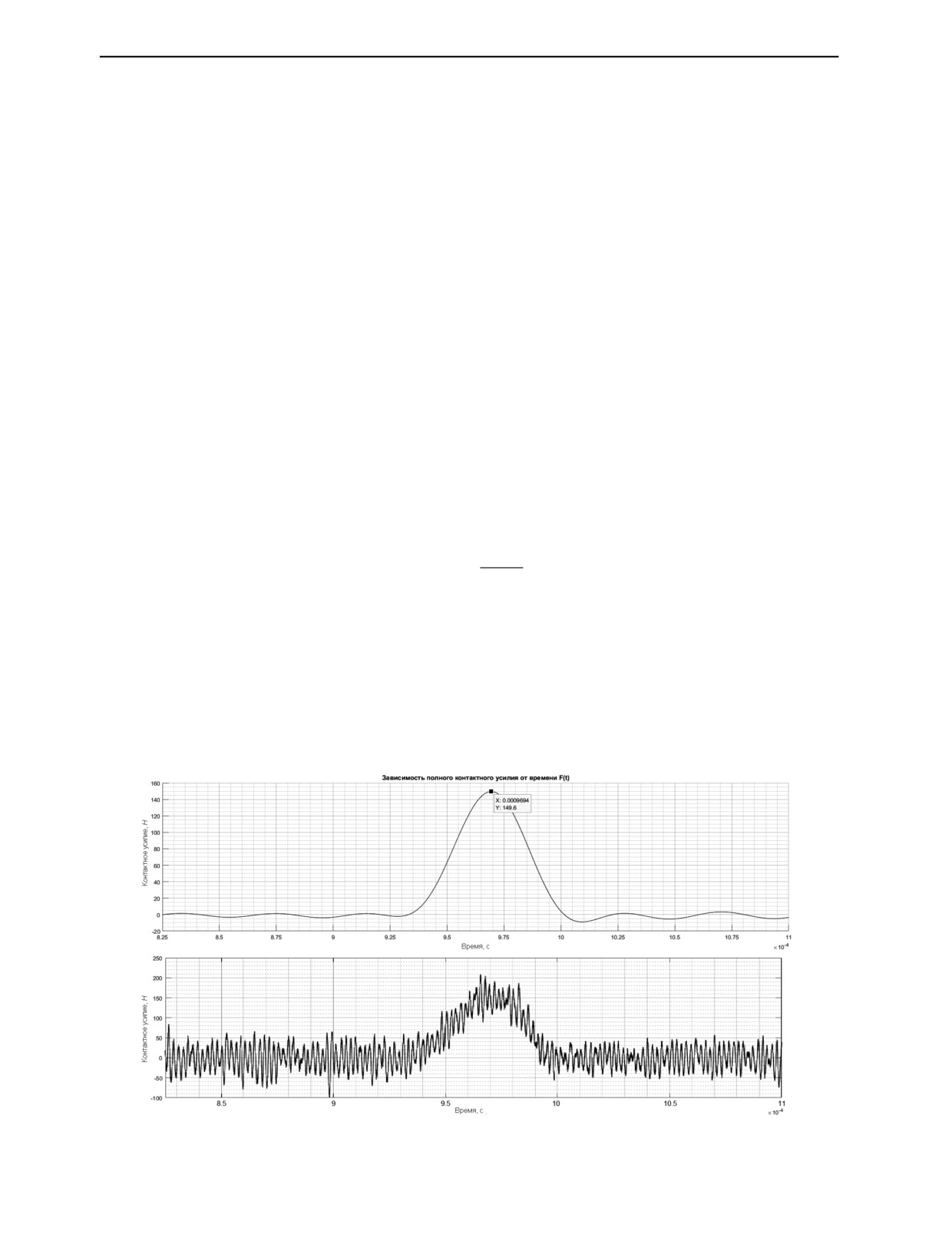
кажения формы основного сигнала (рис. 1).
Рис. 1. Результат работы фильтра на основе ДПФ при частоте среза fсрез = 25 кГц.
Дефектоскопия
№ 6
2020
Аппаратно-алгоритмическое обеспечение процесса динамического индентирования
63
40
A1
35
A2
B1
30
B2
25
20
15
10
5
Алгоритм
Прибор ИСПГ-1
0
0
10
20
30
40
50
60
70
80
90
100
Время t, мкс
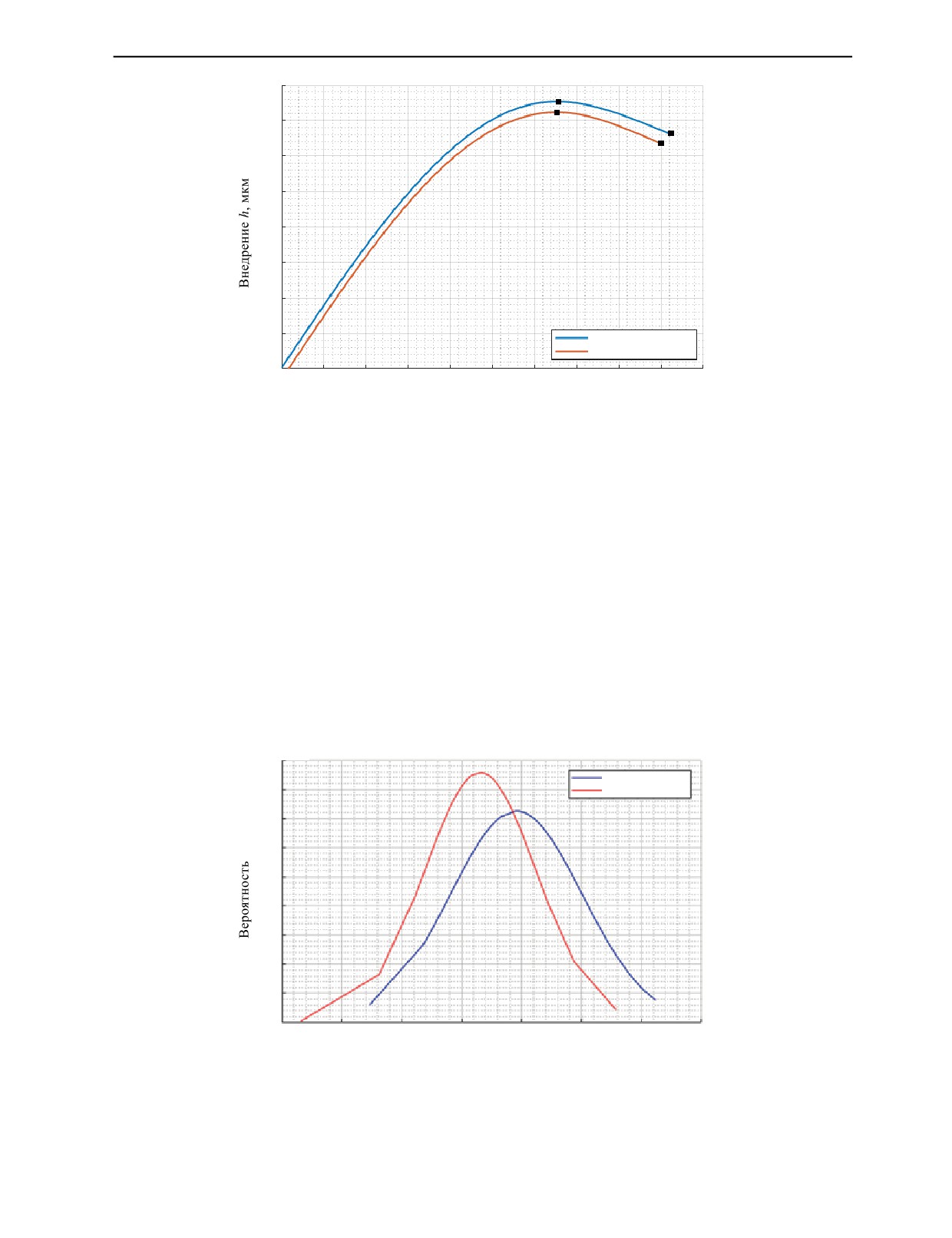
Рис. 2. Зависимость глубины внедрения индентора от времени на мере твердости 66HB.
На рис. 2 проиллюстрирован результат работы разработанного алгоритма. Точками А1, B1 и A2,
B2 обозначены максимальная и остаточная глубины внедрения системы индентирования ударника
в материал. Разница в глубине внедрения, получаемой при помощи алгоритма и прибора ДИ, об-
условлена аппаратными особенностями встроенного в прибор аналого-цифрового преобразователя
и осциллографа.
Результаты измерений имеют разброс по нормальному закону распределения. Проводится
сравнение результатов измерений, обработанных алгоритмом, и результатов, полученных с при-
бора ДИ, по величинам среднеквадратических отклонений (СКО) и математических ожиданий
(МО) для выбранной характеристики. В качестве такой характеристики была выбрана остаточ-
ная глубина внедрения индентора (точки B1 и B2 на рис. 2). Таким образом, из 76 дискретных
массивов зависимости внедрения во времени hp(t) было выбрано 76 точек, аналогичных B1 на
рис. 3. В случае прибора ДИ было проведено 40 измерений и получено соответственно 40 точек,
аналогичных B2 на рис. 2.
×105
4,5
Алгоритм
4
Прибор ИСПГ-1
3,5
3
2,5
2
1,5
1
0,5
0
29
30
31
32
33
34
35
36
Остаточные внедрения, мкм
Рис. 3. Плотности распределения для выборок значений остаточных внедрений.
Для двух выборок остаточных значений внедрения были построены кривые плотности распре-
деления (см. рис. 3).
Дефектоскопия
№ 6
2020
64
Р.А. Егоров, А.В. Ильинский, М.В. Кузьмичев, А.В. Федоров
Рис. 4. Форма отпечатка для меры твердости 66HB.
Далее с помощью оптического микроскопа трехмерного сканирования Оlympus была получена
форма отпечатка индентора на мере твердости 66HB (рис. 4).
Численные значения МО и СКО для выборок остаточных глубин внедрения и геометрические
параметры отпечатка на мере твердости 66HB приведены в табл. 1 и табл. 2.
Таблица
1
Численные значения МО и СКО
Статистические показатели
Прибор
Алгоритм
СКО, мкм
0,93
1,09
МО, мкм
32,31
32,91
Таблица
2
Геометрические параметры отпечатка на мере твердости 66HB
Геометрические параметры отпечатка
Ширина, мкм
246,21
Длина, мкм
248,50
Остаточная глубина внедрения hpr, мкм
33,70
Используя допущение о неповторяемости геометрии отпечатка, а также о наличии погреш-
ности измерения, значение остаточной глубины внедрения, полученное при помощи цифрового
микроскопа, принимается за действительное. В таком случае, можно определить относительные
погрешности средних значений остаточных глубин внедрений, полученных с помощью алгоритма
и прибора ДИ.
Относительная погрешность среднего значения остаточной глубины внедрения hpi с прибора из
табл. 1 от значения, полученного при помощи микроскопа hpr:
h
-h
pr
pi
δ
=
⋅100 %
=
4,10 %.
h
fi
h
pr
Дефектоскопия
№ 6
2020
Аппаратно-алгоритмическое обеспечение процесса динамического индентирования
65
Относительная погрешность среднего значения остаточной глубины внедрения hpa алгоритма
из табл. 2 от значения, полученного при помощи микроскопа hpr:
h
pr
-
h
pa
δ
h
=
⋅100 %
=
2,32 %.
fa
hpr
АНАЛИЗ ПОДХОДОВ К ОЦЕНКЕ ДИНАМИЧЕСКОЙ ТВЕРДОСТИ
Также в рамках данного исследования был проведен анализ подходов к оценке динамической
твердости материала.
Согласно ГОСТ Р 56474—2015 динамическая твердость материала определяется по следую-
щей зависимости:
2
(S)
F
hmax
HD
=
,
(4)
2
2
2
πRm(V
−
V
)
max
min
где Fh max — значение контактной силы при максимальной глубине вдавливания, Н; R — радиус
индентора, м; m — масса системы индентирования ударника, кг; Vmax — скорость индентора в мо-
мент времени, соответствующий началу контактного взаимодействия индентора с испытываемым
материалом, м/с; Vmin — скорость индентора в момент времени, соответствующий завершению
контактного взаимодействия с материалом, м/с.
Суть данного подхода заключается в определении отношения контактной силы, соответству-
ющей максимальной глубине внедрения, к площади поверхности остаточного пластического от-
печатка.
Вместе с тем анализ существующей литературы, а также экспериментальные исследования по-
казали, что процесс контактного ударного взаимодействия характеризуется преобразованием кине-
тической энергии системы индентирования ударника в механическую работу упругопластической
деформации испытуемого материала [6, 7]. Деформационный процесс при этом носит объемный
характер, то есть динамическая твердость при ударе характеризует сопротивление внедрению не
только на поверхности, но и в некотором объеме материала.
Исходя из вышесказанного, было предложено использовать подход, основанный на определе-
нии отношения суммарной работы к объему восстановленного отпечатка [8]:
W
(V )
p
HD
=
Vp
или
2
2
m
(V
-
V
)
(V
)
max
min
HD
=
,
(5)
2
1
πh
(R - h
)
p
p
p
3
где Wp — работа, затрачиваемая на упругопластическую деформацию материала; Vp — объем вос-
становленного отпечатка; hp — остаточная глубина отпечатка после индентирования (глубина вос-
становленного отпечатка), м; Rp — радиус кривизны поверхности восстановленного отпечатка, м.
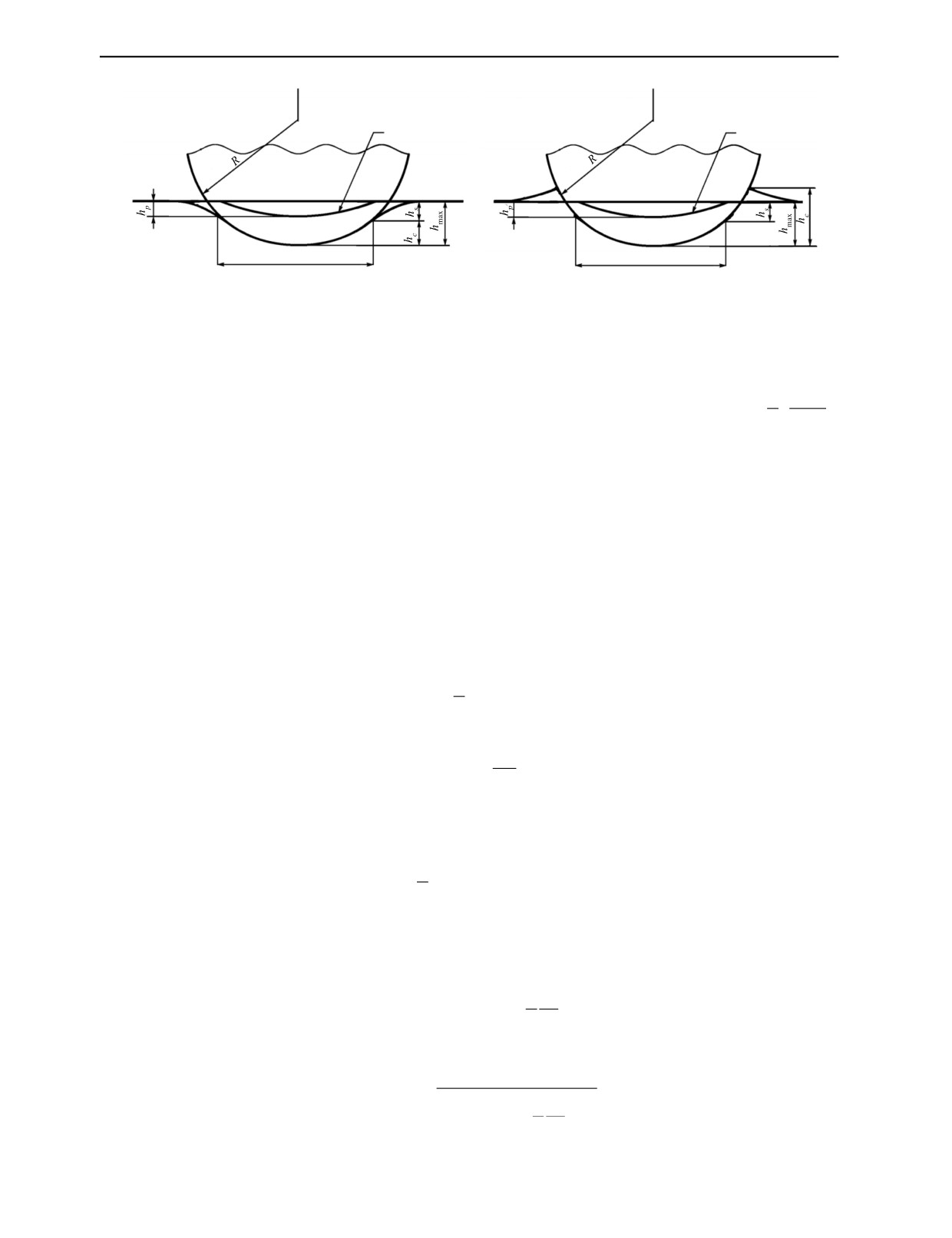
Стоит отметить, что при определении радиуса кривизны поверхности восстановленного
отпечатка Rp необходимо учитывать контактную топографию поверхности материала при ин-
дентировании. Внедрение индентора сферической формы может сопровождаться как продав-
ливанием материала ниже уровня исходной поверхности, так и выдавливанием вокруг него ма-
териала выше уровня исходной поверхности или образованием навала. Такие эффекты измене-
ния поверхности материала при индентировании в иностранной литературе получили название
«sink-in» («прогиб») и «pile-up» («навал») соответственно (рис. 5).
Такие эффекты характеризуются следующими неравенствами:
2
h
c
если
C
=
<1,
то наблюдается эффект «прогиб»;
hmax
2
h
c
если
C
=
>1,
то наблюдается эффект «навал».
hmax
Существуют различные подходы расчета характеристики C2, предложенные авторами [9—14].
Результаты анализа эффектов «прогиб» и «навал» показывают, что значение характеристики C2, в
том числе зависит от значений показателя деформационного упрочнения материала n .
Дефектоскопия
№ 6
2020
66
Р.А. Егоров, А.В. Ильинский, М.В. Кузьмичев, А.В. Федоров
а
б
Rpsink-in
pile-up
Rp
dc
dc
Рис. 5. Схема профиля поверхности материала при деформировании с эффектом «sink-in» / «прогиб» (а), с эффектом
«pile-up» / «навал» (б):
hmax — максимальная глубина внедрения индентора; hp — остаточная глубина отпечатка после индентирования (глубина восстановлен-
ного отпечатка); hc — контактная глубина внедрения индентора; hcp — контактная глубина контура восстановленного отпечатка;
sink-in, R
R — радиус индентора; Rp
pile-up — радиусы кривизны поверхности восстановленного отпечатка.
p
2
5
2-n
В данной работе было предложено расчитывать характеристику C2 по выражению
C
=
2
n
+4
[10]. Справочные данные по значениям показателя деформационного упрочнения n для различных
материалов и сплавов представлены в [15].
Анализируя выражение (5) и принимая допущение h = hmax, можно рассчитать следующие ве-
личины:
величину упругого прогиба (восстановления) контура отпечатка hs:
h
s
=
1(h
max
−h
p
) ,
2
контактную глубину внедрения индентора hc:
h
c
=
1(h
max
+h
p
) ;
2
радиус кривизны поверхности восстановленного отпечатка Rpsink-in:
1
h
sink-in
max
R
p
=
R
+1.
(6)
2
h
p
Аналогично расчитывается и радиус кривизны восстановленного отпечатка Rppile-up :
h
pile-up
pc
R
p
=
R
,
h
p
h
=
1(h
−h
),
s
max
p
2
1
h
pile-up
max
2
R
=
R
2C
−1
+1.
(7)
(
)
p
2
h
p
С учетом выражений (5)—(7), объем восстановленного отпечатка и объемная динамическая
твердость при эффектах «прогиб» и «навал» рассчитываются по следующим формулам:
1
h
2
h
sink-in
2
max
p
V
= πRh
−
+1,
(8)
p
p
2
h
p
3
R
2
2
m
(
V
−V
)
(V
)sink
-in
0
2
HD
IT
=
,
h
2
h
(9)
2
max
p
πRh
−
+1
p
h
3
R
p
Дефектоскопия
№ 6
2020
Аппаратно-алгоритмическое обеспечение процесса динамического индентирования
67
h
pile-up
2
h
max
2
2
p
V
=πRh
2C
−1
−
+1,
(10)
p
p
(
)
h
3
R
p
2
2
m
(
V
0
−V
2
)
(V
)
pile-up
HD
=
(11)
IT
h
2
h
2
max
2
p
πRh
(
2C
−1
)
−
+1
p
h
3
R
p
Полученные зависимости удобны при использовании, поскольку значения параметров hp, hmax,
Vmax, Vmin, необходимые для оценки объемной динамической твердости HD(V)sink-in и объемной дина-
мической твердости HD(V)pile-in, определяются по результатам динамического индентирования.
При проведении экспериментальной части использовался прибор ДИ со следующими характе-
ристиками ударника: R = 0,75·10-3 м, m = 4,8·10-3 кг. Исследования проводили на мерах твердости
6HB и 172HB.
При определении характеристики С2 учитывались следующие факторы:
мера твердости 66HB изготовлена из алюминиевого сплава, показатель деформационного
упрочнения которого согласно ГОСТ 25.503—97 находится с пределах 0,19—0,26;
мера твердости 172HB изготовлена из углеродистой или легированной стали, показатель де-
формационного упрочнения материала которых согласно ГОСТ 25.503—97 находится с пределах
0,18—0,25.
С учетом описанных факторов при индентировании мер твердости будет наблюдатся эффект
«навал».
На каждой мере твердости было проведено индентирование в 10 точках. С использованием
полученных массивов исходных данных (V(t), F(t), h(t)) был производен расчет поверхностной
и объемной динамических твердостей, рассмотренных в настоящем исследовании. При расчете
объемной динамической твердости для всех исследуемых мер твердости было использовано сле-
дующее допущение: n = 0,23. Стандартная неопределенность была оценена по ГОСТ Р 54500.3—
2011: среднее значение q
- и выборочное стандартное отклонение s(q
-). Результаты эксперимента
приведены в табл. 3.
Анализ полученных результатов показал, что выборочное стандартное отклонение значений
объемной динамической твердости существенно ниже выборочного стандартного отклонения
поверхностной динамической твердости. Предложенный показатель объемной динамической
твердости дополняет показатели, представленные в ГОСТ 56474—2015 и в существующем при-
боре динамического индентирования.
Таблица
3
Результаты расчета динамической твердости
Образец 66HB
HD(S), МПа
HD(V)pile-up, МПа
1
464,46
668,81
2
637,47
632,62
3
538,60
624,66
4
512,53
663,31
5
528,97
669,18
6
541,82
676,82
7
506,83
671,40
8
492,55
606,17
9
530,84
693,87
10
584,35
628,78
-
q
533,81
653,56
s(q
-)
48,43
28,26
Дефектоскопия
№ 6
2020
68
Р.А. Егоров, А.В. Ильинский, М.В. Кузьмичев, А.В. Федоров
Окончание табл. 3
Образец 172HB
HD(S), МПа
HD(V)pile-up, МПа
1
1218,32
1954,87
2
1448,98
1878,15
3
1609,08
1911,32
4
1306,85
1754,78
5
1306,85
1754,78
6
1145,31
1916,21
7
1335,07
1877,79
8
1482,89
1995,23
9
1377,53
1795,02
10
1382,40
1898,21
-
q
1361,33
1873,64
s(q
-)
132,62
81,44
ЗАКЛЮЧЕНИЕ
В работе предложен алгоритм обработки первичного сигнала динамического индентирования,
позволяющий осуществлять переход от значений ЭДС первичного преобразователя к характери-
стикам упруго-пластического внедрения индентора в испытуемый материал.
Полученные результаты показывают работоспособность разработанного алгоритма обработки
первичного измерительного сигнала. Отклонение значения остаточного внедрения с алгоритма от
значения внедрения, полученного при помощи микроскопа, не превышает 2,5 %. Для прибора ДИ
относительное отклонение составило более 4 %.
Также предложен алгоритм перехода от характеристик упруго-пластического внедрения ин-
дентора в испытуемый материал к значениям динамической твердости за счет использования объ-
емного подхода.
Таким образом, предложенные подходы, основанные на определении отношения суммарной
работы к объему восстановленного отпечатка, могут послужить основой для разработки алгоритма
оценки динамической твердости при процессе контактного ударного взаимодействия.
СПИСОК ЛИТЕРАТУРЫ
1. Мощенок В.И. Современная классификация методов определения твердости // Автомобильный
транспорт. Вып. 25. 2010. С. 129—132.
2. Рудницкий В.А., Рабцевич А.В. Метод динамического индентирования для оценки механических
характеристик металлических материалов // Дефектоскопия. 1997. № 4. С. 79—86.
3. Крень А.П., Рудницкий В.А., Зинкевич Н.В. Моделирование ударного контакта индентора с не-
жесткими стальными конструкциями при измерении твердости // Известия национальной академии
наук Беларуси. Серия Физико-технических наук. 2017. № 4. С. 38—45.
4. Крень А.П., Мацулевич О.В., Делендик М.Н. Оценка погрешности определения физико-механи-
ческих характеристик материалов при их контроля методом индентирования // Приборы и методы из-
мерений. 2018. Т. 9. № 3. С. 263—271.
5. Марусин М.П., Протасеня Т.А. Разработка первичного преобразователя прибора динамического
индентирования для измерения механических свойств материалов // Известия вузов. Приборостроение.
2014. Т. 57. № 10. С. 85—87.
6. Огар П.М., Тарасов В.А., Турченко А.В., Федоров И.Б. Применение кривых кинетического ин-
дентирования сферой для определения механических свойств материалов // Братский государственный
университет. 2013. Вып. № 1 (17). С. 41—47.
7. Мильман Ю.В., Чугунова С.И., Гончарова И.В. Характеристика пластичности, определяемая ме-
тодом индентирования // Вопросы атомной науки и техники. Физика радиационных повреждений и
радиационное материаловедение. 2011. № 4. С. 182—187.
Дефектоскопия
№ 6
2020
Аппаратно-алгоритмическое обеспечение процесса динамического индентирования
69
8. Ильинский А.В., Федоров А.В., Степанова К.А., Кинжагулов И.Ю., Краснов И.О. Исследование
динамической твердости конструкционных металлических материалов // Заводская лаборатория. Диа-
гностика материалов. 2020. Т. 86. № 1. С. 57—61.
9. Norbury A., Samuel T. The Recovery and Sinking-in or Piling-up of Material in the Brinell Test, and the
Effect of these Factors on the Correlation of the Brinell with Certain other Hardness Tests // Journal of the Iron
Steel Institute. 1928. V. 117. P. 673—687.
10. Matthews J.R. Indentation Hardness and Hot Pressing
//
Acta Materialia.
1980.
V. 28. P. 311—318.
11. Hill R., Storakers B., Zdunek A. B. A Theoretical Study of the Brinell Hardness Test // Proceedings of
the Royal Society of London. 1989. V. A. № 423. P. 301—330.
12. Taljat B., Zacharias T., Kosel T. New Analytical Procedure to Determine Stress-strain
Curve from Spherical Indentation Data // International Journal of Solids and Structures. 1998. V. 35.
P. 4411—4426.
13. Alcala J., Barone A. C., Anglada M. The Influence of Plastic Hardening on Surface
Deformation Modes Around Vickers and Spherical Indents
// Acta Materalia.
2000. V.
48.
P. 3451—3464.
14. Kucharski S., Mroz Z. Indentation of Plastic Hardening Parameters of Metals from Spherica Indentation
Tests // Materials Science and Engineering A. 2001. № 318. P. 65-76.
15. Kim S.H., Lee B.W., Choi Y. and Kwon D. Quantitative determination of contact depth during spherical
indentation of metallic materials: A FEM study // Mater. Sci. Eng. A. 2006. V. 415. P. 59. + a Frontics Inc.
Дефектоскопия
№ 6
2020