Акустические методы
УДК 620.179.16
КОЛЕБАНИЯ СЛОЯ С РАССЛОЕНИЕМ В РАМКАХ ГРАДИЕНТНОЙ ТЕОРИИ
УПРУГОСТИ
© 2021 г. А.О. Ватульян1,2,*, О.В. Явруян2,**
1Южный федеральный университет, Россия 344000 Ростов-на-Дону, ул. Мильчакова, 8а
2Южный математический институт ВНЦ РАН, Россия 362001 Владикавказ, ул. Ватутина, 53
E-mail:*vatulyan@aaanet.ru; **yavruyan@mail.ru
Поступила в редакцию 26.07.2021; после доработки 18.08.2021
Принята к публикации 18.08.2021
Рассмотрена прямая задача об антиплоских колебаниях слоя с расслоением в рамках градиентной теории упругости.
В качестве математической модели взята градиентная модель, предложенная Айфантисом. Основное внимание уделено
анализу механических полей на берегу трещины и в ее вершинах — концентраторах напряжений. Исследование про-
ведено с использованием метода граничных интегральных уравнений (ГИУ). Построено ГИУ относительно градиента
поля перемещений на трещине. Проведен анализ построенного ГИУ, выявлена явным образом кубическая сингуляр-
ность. Решение сингулярного ГИУ построено с использованием аппроксимирующих полиномов Чебышева. Проведено
исследование для трещин малой относительной длины — асимптотический подход, получены простые полуаналитиче-
ские выражения для построения функции раскрытия трещины, выявлен диапазон работоспособности асимптотического
подхода. Построены поля напряжений в окрестности вершин трещины. Представлены численные результаты вычисли-
тельных экспериментов.
Ключевые слова: слой, трещина, градиентная теория упругости, колебания, асимптотический метод, установивший-
ся режим, упругий.
DOI: 10.31857/S0130308221100018
ВВЕДЕНИЕ
Слоистые структуры варьируются от однослойных однородных до многослойных компози-
тов и функционально-градиентных структур (ФГС) и активно используются при моделировании
современных материалов с улучшенными свойствами. На сегодняшний день конструктивные
элементы, имеющие слоистую структуру, широко востребованы в современной авиационной
и аэрокосмической промышленности, в сфере изготовления ядерных реакторов и котлов, при
проектировании специальных высокопрочных строительных материалов и во многих других
приоритетных областях науки. Однако стоит отметить, что существуют проблемы, влияющие
на эффективность использования, на безопасность и прочность конструкций, элементы кото-
рых изготовлены из функционально-градиентных материалов (ФГМ) или слоистых композитов.
Одним из существенных факторов, способных значительно снизить эксплуатационную способ-
ность конструкции и привести к дальнейшему выходу ее из строя, является наличие микро-
дефектов в местах сварки или склейки слоев. Поэтому уточненные математические модели,
описывающие реальное поведение слоистых сред с дефектами и позволяющие построить и оце-
нить напряженно-деформированное состояние (НДС) в окрестности вершин трещин, особенно
актуальны.
К таким математическим моделям относятся модели неклассической теории упругости — гра-
диентной теории упругости (ГТУ), в которых определяющие соотношения включают в себя гра-
диентные параметры, соотносимые с размерными параметрами исследуемой области, например, с
длиной дефекта, толщиной покрытия или микрослоя и т.д., что позволяет учитывать масштабные
микроэффекты, уточнять поведение в окрестности интересующих подобластей. Градиентная тео-
рия упругости была впервые предложена в середине прошлого века в работах Миндлина, Айфан-
тиса, Тупина, Лурье [1—4]. В отличие от классической теории упругости, в градиентной теории
упругости плотность энергии деформации зависит не только от тензора деформаций, но и от перво-
го градиента деформации. Таким образом, полученные определяющие соотношения и уравнения
равновесия/движения имеют более высокий порядок. Однако наряду с возможностью описать бо-
лее точное поведение объекта исследования (особенно в окрестности концентраторов напряже-
ний) возникает ряд сложностей, связанных с исследованием дифференциальных операторов более
высокого порядка и выбором параметров градиентной модели. Поэтому дальнейшие исследования
были связаны с упрощением многопараметрической градиентной модели и сокращением числа
характерных градиентных параметров.
4
А.О. Ватульян, О.В. Явруян
Так, в работах Aifantis и его соавторов [5, 6] была предложена упрощенная модель градиентной
теории упругости — одна/двух/трехпараметрические модели для статических и динамических за-
дач, адекватно описывающие реальное поведение объекта исследования.
Статические задачи для тел с трещинами в рамках моделей градиентной теории упругости
представлены в работах G. Exadaktylos, I. Vardoulakis и E. Aifantis [6—8], F. Erdogan, Gupta [9,
10], L. Zhang, Y. Huang и J.Y. Chen [11,12], G.H. Paulino [13, 14]. Исследованы статические задачи
о трещинах моды I, II, III в однородных или неоднородных, функционально-градиентных средах.
Получены граничные интегральные уравнения относительно скачков полей смещений на берегах
трещины, рассчитаны коэффициенты интенсивности напряжений у вершин трещины, осуществле-
но сравнение с классическим случаем. В рамках линейной теории упругости задачи теории трещин
исследованы в работах [10,15].
В работах C.Q. Ru, E.C. Aifantis [16] предложена новая схема исследования задач механики
в рамках градиентной теории упругости, так называемый метод Ру—Айфантиса, позволяющий
перейти от сингулярных решений к регулярным в два этапа. На первом этапе строятся решения
классической теории упругости, далее рассматриваются дифференциальные уравнения более вы-
сокого порядка относительно градиентных решений, в правой части которых стоят соответствую-
щие решения классической теории упругости. В результате данного подхода удается исключить
сингулярность в полях напряжений и получить новые критерии разрушения.
Также авторами С.А. Лурье, В.В. Васильевым [17, 18] предложена эффективная обобщенная
модель для исследования задач теории упругости, в которых возникают сингулярные решения.
Уравнения градиентной теории упругости имеют более высокий порядок по сравнению с уравне-
ниями классической теории, однако, в отличие от традиционных неклассических теорий с большим
числом дополнительных параметров (например, градиентных параметров), включают независимо
от порядка уравнений всего лишь одну дополнительную постоянную, выражающуюся через ми-
кроструктурный параметр среды и не требует введения дополнительных моментных напряжений.
Обобщенная теория развита для одномерных, двумерных и трёхмерных задач, сформулированы
основные уравнения, учитывающие градиенты напряжений и записывающиеся в терминах обоб-
щенных напряжений, деформаций и перемещений. Также основным прорывным моментом пред-
лагаемой теории является возможность экспериментального определения параметра обобщенной
модели и верификация полученных теоретических результатов с результатами экспериментов.
Отметим, что статические задачи теории трещин в рамках ГТУ исследованы достаточно под-
робно, однако, динамические задачи решены в меньшем количестве, поскольку их решение ста-
новится на порядок сложнее. Как правило, основное внимание исследователей направлено на
решение динамических задач для балок, труб, пластин. Возможности развития градиентной тео-
рии упругости для динамических задач, полный обзор градиентной теории упругости для стати-
ческих и динамических задач, возможности определения градиентных параметров, обсуждение
вопросов применения конечно-элементных методов решений в рамках ГТУ обсуждены в работе
[19]. В этой же работе приведены основные уравнения ГТУ для динамических задач.
Основной целью исследования является изучение возможности применения неклассических
теорий к динамическим задачам теории трещин, в частности, к задаче о колебаниях однород-
ного слоя с расслоением. В статической постановке в рамках градиентной теории упругости
такая задача была решена многими авторами [8, 11, 13], в данной работе предложенные методы
исследования задачи были развиты и для динамической задачи градиентной теории упругости.
Проведено исследование задачи в рамках однопараметрической градиентной модели Айфанти-
са, применен асимптотический подход к решению поставленной задачи, который опирается на
предположение о малости относительного размера дефекта. Асимптотический подход позволяет
существенно упростить решение задач теории трещин и получить полуаналитические решения,
удобные для дальнейшего исследования, подобная схема исследования была апробирована авто-
рами для задач теории трещин в рамках линейной классической теории упругости и вязкоупру-
гости при исследования прямых и обратных задач о колебаниях слоя с внутренней туннельной
прямолинейной или криволинейной трещиной, а также трещиной, расположенной на стыке двух
областей и слоя с расслоением [21—25].
Определяющие соотношения классической линейной теории упругости для однородной среды
представлены следующими зависимостями между напряжениям Коши и деформациями, которые
носят линейный характер:
τ
=
λε
δ +2µε
;
(1)
ij
kk ij
ij
Дефектоскопия
№ 10
2021
Колебания слоя с расслоением в рамках градиентной теории упругости
5
1
ε
=
(u
+u
).
(2)
ij
i,
j
j,i
2
Для градиентной теории упругости [7, 8], в отличие от классической линейной теории упру-
гости, формулируется линейная зависимость между компонентами тензора напряжений Коши и
компонентами тензоров деформации и их градиентами, что позволяет в дальнейшем использовать
эти соотношения в задачах, где требуется более уточненное и детальное описание объекта исследо-
вания на микроструктурном уровне. В связи с увеличением порядка определяющих соотношений
также вводятся дополнительные моментные напряжения.
В общем случае градиентной теории упругости, которая впервые была предложена Миндлином
в 1964 г., плотность энергии деформации представлена многопараметрической моделью:
1
W
=
λε
ε
+ µε
ε
+a
ε
ε
+a
ε
ε
+a
ε
ε
+a
ε
ε
+a
ε
ε
,
(3)
ii
jj
ij
ji
1
ik,i
jj,k
2
jj,i kk,i
3
ik,i
jk,
j
4
jk,i
jk,i
5
jk,i ij,k
2
а также уточненное представление кинетической энергии:
1
1
2
T
=
+ ρl
(4)
i i
1
i,
j i,
j
2
2
Коэффициентны модели l, ai — градиентные параметры.
Компоненты тензоров напряжений Коши, моментных напряжений и полных напряжений опре-
деляются соответсвенно:
τ
ij
=
∂W
/ ∂ε
ij
;
m
ijk
=
∂W
/ ∂ε
ij
,k
;
(5)
ij
σ =τ -
ij
m
ijk
,k
Уравнения движения, принимая во внимание соотношения приведенные выше, принимают вид
[19]:
2
2
2
2
2
2
(λ+µ)
(
1
−l
∇
)
u
+µ
(
1−l
∇
)
u
=ρ
(
1−l
∇
)
;
(6)
2
j,ij
3
i,
jj
1
i
4
a
+
4
a
+3a
+
2a
+3a
2
1
2
3
4
5
l
2
=
;
2(λ+µ
)
a
+2
a
+a
2
3
4
5
l
=
3
2
µ
Отметим, что параметры l1, l2, l3 — характерные длины, определяемые градиентными эффек-
тами.
Дальнейшие упрощения градиентных соотношений были предложены Айфантисом (l1 = l2 =
= l3 = l) [19]:
1
1
2
2
W
=
λε
ii
ε
jj
+ µε
ij
ε
ji
+ λl
ε
jj
,
ε
i kk
,i
+ µl
ε
jk,i
ε
jk,i
;
2
2
2
m
ijk
=
∂W
/ ∂ε
ij,k
=l
τ
ij,k
;
(7)
2
2
σ
ij
=
τ
ij
−m
ijk,k
=
(1
−l
∇
)τ
ij
(8)
1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ О КОЛЕБАНИЯХ СЛОЯ С РАССЛОЕНИЕМ
Рассмотрим установившиеся антиплоские колебания изотропного слоя толщины h, нижняя
граница слоя жестко закреплена, за исключением участка с расслоением длины 2a. Колебания
Дефектоскопия
№ 10
2021
6
А.О. Ватульян, О.В. Явруян
слоя вызваны нагрузкой, приложенной к части верхней границы слоя. Направим оси координат
так, чтобы ось x1 совпала с нижней гранью полосы, а ось x3 направим перпендикулярно вверх,
при этом трещина расположена на нижней границе при x1 ∈[-a, a]. Рассматривается постановка,
в которой расслоение в процессе колебаний остается раскрытым, т.е. поверхность трещины сво-
бодна от напряжений. Установившиеся колебания вызываются компонентой вектора касатель-
ных напряжений σ23 = p0e-ωt, ненулевой компонентой вектора перемещений является компонента
u2(x1, x3, t) = u(x1, x3)e-iωt. Компоненты тензоров полного и моментного напряжений:
σ
=σ
=σ
= 0, σ
= 0;
11
22
33
13
2
2
σ
= 2µ(1-l
∇
)ε
,
i=1,3;
2i
2i
2
m
112
= 2µl
ε
12,1
;
2
m
= 2µl
ε
;
(9)
132
32,1
2
m
312
= 2µl
ε
12,3
;
2
m
332
= 2µl
ε
32,3
После отделения временного множителя уравнения движения и граничные условия примут
вид:
2
2
2
2
(
1-l
∇
)(
∇
u+k
u
)
= 0;
(10)
x
= h, σ
= p
δ(x
− L),m
(x
,0) = 0;
3
23
0
1
332
1
x
= 0, u = 0, x
∉[-a, a],m
(x
,0) = 0,
(11)
3
1
332
1
где L — точка приложения нагрузки (не нарушая общности рассуждений, будем рассматривать
случай приложения сосредоточенной нагрузки).
Рассматривается постановка задачи, в которой предполагется, что в процессе колебания тре-
щина остается раскрытой и к постановке задачи добавляется условие отсутствия напряжений на
трещине:
x
3
= 0, x
1
∈[-a,a], σ
23
= 0.
(12)
Замыкают постановку задачи условия излучения волн на бесконечности, при формулировке
которых используется принцип предельного поглощения [26].
2. СВЕДЕНИЕ К ГРАНИЧНОМУ ИНТЕГРАЛЬНОМУ УРАВНЕНИЮ
Рассмотрим вспомогательную задачу, в которой к краевой задаче (10)—(12) добавлены следу-
ющие граничные условия [13]:
x
3
= h, σ
23
= p
0
δ(x
1
− L), m
332
= 0,
x
= 0, u = X , m
= 0, σ
= 0, x
∈[-a,a],
(13)
3
332
23
1
здесь введена функция Х, характеризующая смещения нижней границы полосы, при этом
1
X = 0,x
∉[-a,a] и
1
X ≠ 0,x
∈[-a,a],
т.е. она определяет раскрытие трещины.
Рассмотрение вспомогательной задачи дает возможность применения преобразования Фурье
по координате x1:
+∞
i x
(x
,ξ)
u
(
x
,
x
)
e
dx
3
= ∫
1
3
1
−∞
Дефектоскопия
№ 10
2021
Колебания слоя с расслоением в рамках градиентной теории упругости
7
В результате, уравнение движения (10) преобразуется к диффрернциальному уравнению
∂
четвертого порядка (D
=
):
∂x3
2
2
2
2
2
2
(1- l
(D
−ξ
))(D
−ξ
+k
)
(14)
Характеристическое уравнение:
2
2
2
2
2
2
(1- l
(λ
−ξ
))(λ
−ξ
+k
)
(15)
Корни характеристического уравнения:
2
2
2
2
λ
=± ξ
+1/l
,
λ
=± ξ
−k
(16)
1,2
3,4
Решение (14) представимо в виде:
4
i
x
3
(ξ,x
)
=
a
(ξ)eλξ)
(17)
3
∑
i
i =1
Неизвестные функции ai определим из граничных условий относительно трансформант:
2
2
2
iξL
2
2
x
=
h,
=
,
=µD
(1−
l
(D
+ξ
)),
= p
e
,
m
=µl
D
=
0;
(18)
3
23
23
0
332
2
2
x
= 0, = ,
= µl
D
=0.
3
332
Таким образом, для определения неизвестных функций в представлении (17) имеем СЛАУ:
Ay = F;
T
y
=
(A,C,B
);
T
F
=
(X,0,
/
µ,0);
1
1
1
1
(19)
c
c
c
c
1
1
2
2
A=
,
−λ
3
h
λ
3
h
−λ
1
h
λ
1
h
-ρe
ρe
−re
re
−λ
λ
−λ
λ
3
3
1
1
c
e
c
e
c
e
c
e
1
1
2
2
2
2
2
2
2
2
2
2
2
2
где
c
1
=l
λ
3
,c
2
=l
λ
1
,ρ=λ
3
(1+ l
(ξ
−λ
3
)), r = λ
1
(1+ l
(ξ
−λ
1
)), из которой можно определить
по правилу Крамера соответствующие неизвестные функции:
1
a
a
=
(
+ a
);
i
iX
ip
∆
µ
0
3
2
(λ
1
+λ
3
)h
−2λ
1
h
−2λ
3
h
−
2(
λ
1
+λ
3
)h
2
2
2
3
2
2
2
2
∆
0
=λ
1
λ
3
l
e
(−1+ e
−e
+e
)(1
+l
k
)
=-
4
λ
1
λ
3
l
(1+l
k
)
sh(λ
1
h)ch(
λ
3
h).
Уравнение Δ0 = 0 характеризует дисперсионное множество, отметим, что точки дисперсионно-
го множеста не зависят от l и соответствуют классическому случаю.
Выражения для aiX , aip не приводятся в силу громоздкости. После определения коэффициентов,
применив обратное преобразование Фурье к (17), получим представление поля смещения в слое
4
1
λ
(ξ)x
− ξ
i
3
1
u(x
,
x
)
=
a
(ξ)e
e
d
ξ
(20)
1
3
∑∫
i
2
π
i=1
σ
Дефектоскопия
№ 10
2021
8
А.О. Ватульян, О.В. Явруян
Контур интегрирования σ выбирается в соответствии с принципом предельного поглощения.
Он всюду совпадает с вещественной осью за исключением окрестностей вещественных полюсов
и отклоняется в комплексную плоскость, огибая положительные полюса снизу, отрицательные
сверху. Как видно, каждая из функций ai представлена двумя слагаемыми, слагаемые с
p характе-
ризуют волновое поле в полосе без дефекта, вызванное приложенной нагрузкой, а слагаемые с
определяют вклад дефекта в общее волновое поле в полосе. Отсюда можно найти представление
напряжений, в частности:
µ
ξ
x
)
=
d
(x
,ξ)X (ξ) + d
(x
,ξ)(ξ);
23
3
X
3
p
3
∆
4
d (x
,ξ)
=
f
(λ
)a eλ x
;
X
3
∑
i
iX
i=1
(21)
4
λ x3
i
d
p
(x
1
,ξ)
=
∑
f
(λ
i
)a
ip
e
;
i=1
2
2
2
3
f z)
=
z
(1
+
l
ξ
) −
l
z
Неизвестную функцию раскрытия трещины X найдем из условия отсутствия напряжения на
трещине. Для этого осуществим предельный переход в выражении (21) при
x
→
0
и применим
3
обратное преобразование Фурье. В результате получим граничное интегральное уравнение (ГИУ)
относительно функции χ(x1):
a
χ
(t)
K
(
t
−
x
)
dt = F(x
);
∫
1
1
−a
iξ(
t x
)
d
X
(0,ξ)
K
(
t
−
x
)
=∫ ξ
R
e
dξ,
R(ξ)
=
;
(22)
1
∆
σ
p
d
(0,
ξ
)
0
p
iξ(
L x
)
F
(
x
)
=-
e
dξ
1
∫
µ
∆
σ
Введем функцию Φ(t) = χʹ(t), удовлетворяющую условиям:
Φ
(t)
=
0,
t ∉
(
−
a a),
a
Φ(t)
dt
=χ
(a)
−χ(
−
a)
=
0,
∫
−a
а также условиям Φ(a) = Φ(-a) = 0 [12] . Тогда получим следующее ГИУ:
a
Φ(t)
K
(
t
−
x
)
dt = F
(
x
),
x
≤
a;
∫
1
1
1
1
1
−a
-1 iξ(
t x
)
d
X
(0,ξ)
K
(t
−
x
)
=-
i∫R
(ξ)
ξ
e
dξ,
R(ξ)
=
;
(23)
1
1
∆
σ
p
d
(0,ξ
)
0
p
i
ξ(
L x
)
F
(x
)
=
e
dξ
1
1
∫
µ
∆
σ
Ядро ГИУ (23) представлено несобственным интегралом, для исследования поведения подын-
тегральной функции на бесконечности найдем главные члены разложения:
3
ÎR(ξ) =L
1
ξ
+
L
3
ξ
+
(1),
ξ
→∞,
(24)
2
2
l
k
2
L
=-
1+
,
L
= -l
1
3
2
Дефектоскопия
№ 10
2021
Колебания слоя с расслоением в рамках градиентной теории упругости
9
С учетом формул [29], запишем ГИУ (23) в виде:
a
1
L
2L
1
3
v p
−
+
N t,x
)
Φ(t)dt = F
(x
);
(25)
∫
3
1
1
1
π
t
−
x
(t
−
x
)
−a
1
1
3
−1
iξ(t-x
1
)
N t,
x
1
)
=-i
(
R(ξ)
-L
1
ξ
-
L
3
ξ
)
ξ
e
dξ
∫
σ
Полученное ГИУ (25) представлено несобственными интегралами второго рода, т.е. сингу-
лярными интегралами (кубическая сингулярность), соответсвующие интегралы не существуют в
обычном смысле, а понимаются в смысле главного значения по Коши [28]:
a
-ε
a
Φ(t)
Φ(t)
v p
dt
=
lim
+
dt;
∫
3
∫
∫
3
(
t
−
x
)
ε→0
(
t
−
x
)
−
a
1
−a
ε
1
a
a-x
1
−ε
a-x
1
dt
dy
dy
1
−2
−ε
a−x
1
v p
=
v p
=
lim
+
=-
lim
y
+
=
∫
3
∫
3
∫
∫
3
(
-a x
1
ε
)
(t
−
x
)
y
ε→0
y
2
ε→
0
−a
1
−
a x
1
−a x
1
ε
1
1
1
1
1
1
1
1
=-
−
+
-
=-
−
lim
2
2
2
2
2
2
2
ε→0
ε
(a+ x
)
(
a−x
)
ε
2
(a - x
)
(a + x
)
1
1
1
1
Регулярная часть ядра N представлена несобственным интегралом, подынтегральная функция
которой на бесконечности убывает и соответствующий контурный интеграл может быть вычислен
с использованием квадратурных формул либо по теории вычетов.
Путем замены переменных в (25) и введения безразмерных параметров
t = at
,
x
=ax
,
1
1
aˆ=
a
/
,
h k
=
kh l
,
=
l
/
h сведем его к ГИУ вида:
1
1
L
2
L
1
3
−
+aN
(at
,ax )
Φ
(t
)
dt
=
F x
), x
∈[ 1,1],
(26)
∫
2
3
1
1
1
1
π
(t
−
x )
a t
(
−
x )
−1
1
1
в дальнейших выкладках знак «шапочка» будем опускать.
Решение ГИУ (25) возможно с позиции двух подходов — первая схема численного исследова-
ния опирается на квадрутурные формулы для гиперсингулярных интегралов и разностные схемы
аппроксимации внеинтегрального слагаемого [28]; вторая схема связана с использованием аппрок-
симирующих полиномов Чебышева первого и второго родов [13]. Будем проводить дальнейшие
исследования ГИУ по второй схеме.
Учитывая поведение функции Ф(t) в вершинах трешины [12], будем искать решение ГИУ (26)
в виде разложения по полиномам Чебышева:
∞
2
Φ(t)
=
1−
t
A
U t);
(27)
∑
n n
n=0
sin
(
(
n
+
1)arccos(s)
)
U s)=
,
n
= 0,1,2,
n
(
)
sin
arccos(s)
Отметим, что в отличие от линейной теории упругости, когда интегральное уравнение пред-
2
ставлено сингулярным интегралом и функция Ф(t) разыскивается в виде
Φ(t) = g(t) /
1-t
, в
градиентной теории упругости за счет появления кубической сингулярности соответствующее
2
решение имеет иную структуру
Φ(t) =
1-t
g(t). Доказать это можно, сведя (27) к интегродиф-
ференциальному уравнению, для случая статической задачи исследование интегродифферен-
циального уравнения приведено в работе [12], в которой доказано, что его решение имеет вид
(27), этот результат может быть применен также и к динамической задаче к (26). Именно такое
представление решения ГИУ позволяет утверждать, что в градиентной теории упругости син-
гулярная в окрестности вершин трещины компонента тензора деформации линейной теории
упругости становится регулярной. Таким образом решение ГИУ сводится к нахождению коэф-
фициентов разложения An.
Дефектоскопия
№ 10
2021
10
А.О. Ватульян, О.В. Явруян
Подставим (27) в (26), воспользуемся методом коллокаций, удовлетворив уравнение в дискрет-
M
ном наборе точек {x
}
,
x
∈[−1,1], а также известными формулами для вычисления интегралов
1i
i=1
1i
от функций Чебышева [13], в результате получим СЛАУ:
B⋅A=P,
T
M
A
=
(A
,..., A
),
P
={F(x
)}
,
1
M
1i
i=1
M
L
3
2
2
B
=
B
=-
[(n
+n)U
(x
) − (2n
+3n
+2)U
(x
)]−
{
nj
}
2
n+1
1i
n−1
1i
i,
j=1
2(1−
x
)
1i
1
a
2
−L
T
(x
)
+
1−
s
U s)
N s,x
)ds
1
n+1
1i
∫
n
1i
π
-1
Функция раскрытия строится по правилу:
x
1
x
1
M
2
χ
(x
)
= ∫Φ(s)ds
=∑
A
1
−
s
U s)ds
(28)
1
n
∫
n
1
n=
-
1
−
1
Таким образом, после нахождения функции раскрытия трещины из (28) можно построить поле
смещения всюду в слое по формуле (20).
Поле напряжений вне трещины может быть рассчитано как
a
µ
L
2
L
+
1
3
σ
(x
,
x
=
0
)
=
−
+
N t,x
)
Φ
(t)dt,
x
>
a
(29)
23
1
3
∫
3
1
1
π
t
−
x
(t
−
x
)
−a
1
1
Интегралы в выражении (29) уже не являются сингулярными. Наибольший интерес представ-
ляет оценка напряженного состояния полосы в окрестности вершин трещины и возможная оценка
коэффициента интенсивносити напряжений. Если в классической теории упругости напряжения
2
2
в окрестности вершин дефекта имеют особенность порядка
1/ x
−a
, то в случае градиентной
1
2
2
3/2
теории упругости порядок сингулярности изменяется и имеет порядок
1/(x
1
−a
)
[11], коэффи-
циент интенсивности в вершинах трещин может быть рассчитан по формулам [13]:
lK
(
±
a)=
2
2π(xa)(xa
)σ
(x,0),
(
x
>
a).
(30)
III
lim
23
x → a±
∞
K a)
= πa l /a
)
(n
+
1)A
(31)
III
∑
n
n=1
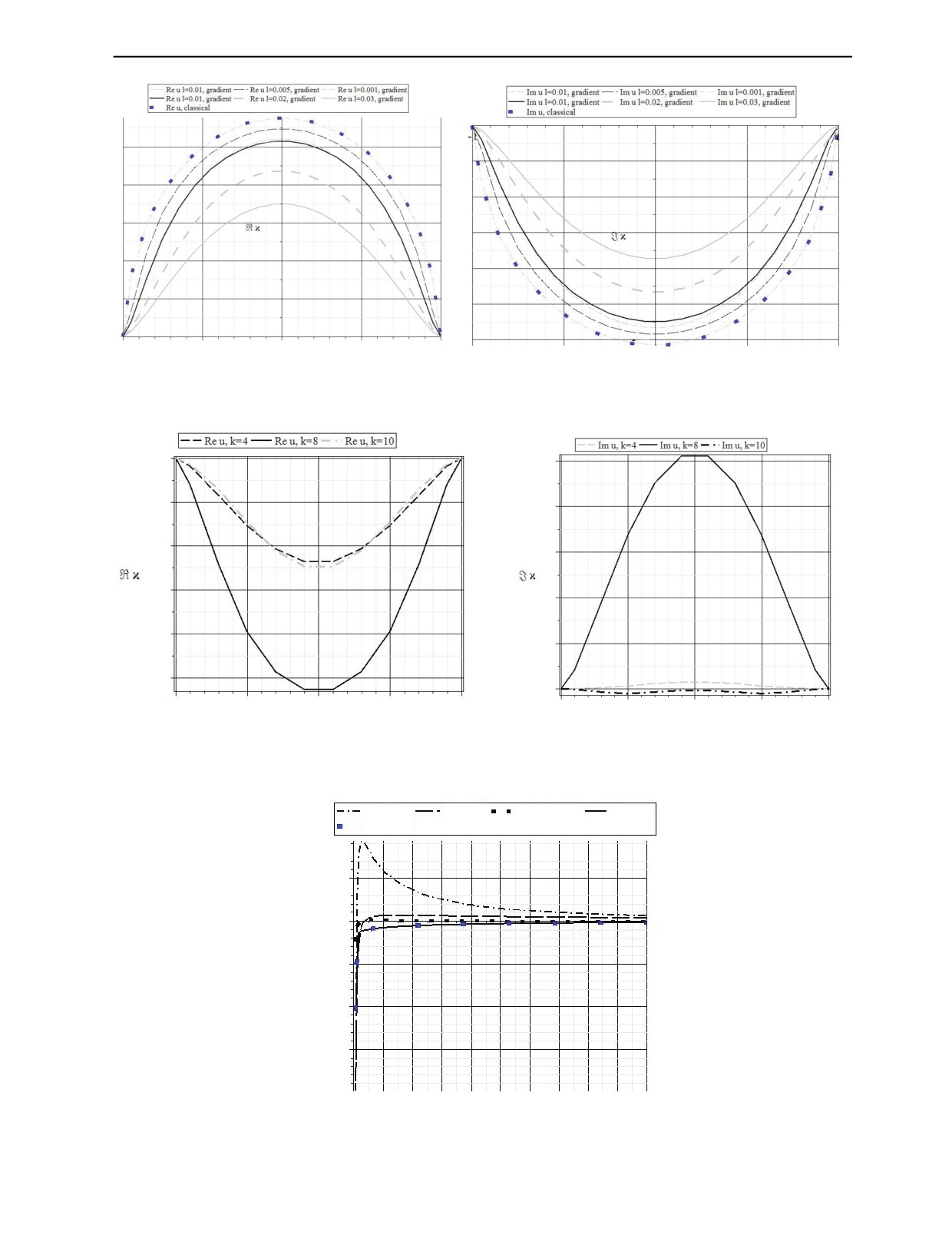
Были проведены численные расчеты для функции раскрытия трещины при различных зна-
чениях градиентных параметров и частоты колебания (рис.1, рис. 2). Сплошными линиями обо-
значены графики, соответствующие градиентной модели, точками — классическому случаю.
Можно заметить, что как и в статическом случае [13], с увеличением градиентного параметра
раскрытие трещины меньше, чем в классическом случае. Также в случае градиентной модели
при увеличении значений градиентных параметров меняется геометрия профиля раскрытия при
приближении к вершинам. На рис. 3 приведены графики вещественной части напряжений σ23(x,
0) в окрестности правой вершины трещины. Как видно из графиков, имеется комбинация гра-
диентных параметров, при которых наблюдается локальный максимум у графиков, именно зна-
чения в этих точках и может быть использовано в качестве новых критериев прочности относи-
тельно НДС и значения коэффициентна интенсивности напряжений.
3. АСИМПТОТИЧЕСКИЙ АНАЛИЗ ЗАДАЧИ
Рассмотрим предложенный для линейной теории упругости асимптотический подход [21—25]
к исследованию задачи в рамках градиентной теории упругости. В основе асимптотического под-
хода лежит предположение о малости относительного размера дефекта, что в линейной теории
упругости позволяло значительно упростить схему нахождения функций раскрытия трещины и
построения волновых полей в слое.
Дефектоскопия
№ 10
2021
Колебания слоя с расслоением в рамках градиентной теории упругости
11
а
б
-1
-0,5
0
0,5
1
0,5
x
-0,1
0,4
-0,2
0,3
-0,3
0,2
-0,4
0,1
-0,5
-0,6
-1
-0,5
0
0,5
1
x
Рис. 1. Вещественная (а) и мнимая (б) части функции раскрытия трещины при k = 5; a = 0,1; L = 0,0.
0
1
-0,1
0,8
-0,2
0,6
-0,3
0,4
-0,4
0,2
-0,5
0
-1
-0,5
0
0,5
1
-1
-0,5
0
0,5
1
x
x
Рис. 2. Вещественная (а) и мнимая (б) части функции раскрытия трещин для различных значений волнового числа k
(одна, две и три волны соответственно), a = 0,1; l = 0,05; l1 = 0,001; L = 0.
l = 0,0
l = 0,02
l = 0,015
l = 0,001
l = 0,0001
5
0
1,02 1,04 1,06 1,08 1,10 1,12 1,14 1,16 1,18 1,20
x
-5
σ
-10
-15
Рис. 3. Графики вещественного значения напряжения в окрестности правой вершины трещины при различных значени-
ях параметра l при a = 0,1; k = 0,1.
Дефектоскопия
№ 10
2021
12
А.О. Ватульян, О.В. Явруян
Проведем анализ ГИУ (26) для трещины малого относительного размера, т.е. при a→0. Пре-
дельное значение правой части ГИУ с учетом предположения представляет собой постоянную ве-
личину, определяемую выражением:
p
d
(0,ξ)
p
d
(0,ξ
)
0
p
iξL
0
p
i
iξ
i
L
F
=
F
(x
)
=-
e
dξ=-
2πi
e
,
(32)
c
lim
1
1
∫
∑
a→0
µ
∆
µ
2π
∆′
(ξ
)
σ
ξ=ξ
i
ξ
i
где ξi — полюса подынтегральной функции, сам же интеграл может быть посчитан по теории вы-
четов.
Также с учетом предположения a→0 можно исключить из ГИУ слагаемое, отвечающее за ре-
гулярную часть подынтегрального выражения. Таким образом, имеем ГИУ вида:
2 1
2
2
1
2
l
Φ(t)
1
l
k
Φ(t)
−
dt
+
1−
dt
=-
F
,
x
∈
[ 1,1].
(33)
∫
3
∫
ñ
1
π
a
(t
−
x
)
π
2
t
−
x
−1
1
−1
1
Дальнейшее исследование ГИУ (33) сводится к выделению доминирующих интегральных сла-
гаемых в левой части (33), которые определяются поведением трех параметров: a, l, k. Стоит отме-
тить, что определяющим будет поведение множителя l/a, l→0, a→0, поскольку 1 - l2k2/2 при малых
l ограничено сверху, однако рассмотрим более общий случай, учитывающий влияние волнового
числа k.
2
2
2
l
k
l
2
Введем в рассмотрение параметр
κ
=
1−
/
и три характерных случая:
2
a
−1/2
2
2
2
k
I)
κ
1
, т.е.
l
+
. Тогда в ГИУ (33) доминирующим интегральным слагаемым
2
a
2
является слагаемое, соответствующее интегралу с кубической сингулярностью, и граничное ин-
тегральное уравнение, ввиду предположения о малости относительного размера дефекта, приво-
дится к виду:
1
2
Φ(t)
π
a
dt
=
F
∫
3
c
(t
−
x
)
2
l
−1
1
Учитывая свойства функции раскрытия, получим гиперсингулярное интегральное уравнение
с постоянной правой частью
1
2
Φ′(t)
πa
dt
=-
F
,
(34)
∫
2
c
(
t
−
x
)
L
−1
1
3
которое имеет решение [29] в классе гладких функций вида:
2
a
2
Φ′
(t)
=
F
1
−
t
,
c
L3
откуда
2
t
2
2
a
2
a
t
1
−t
Φ(t)
=
F
1−
s
ds
=
F
(35)
c
∫
c
L
L
2
3
1
-
3
1/2
−
2
2
k
2
II)
κ
1, т.е.
l
+
, тогда в ГИУ (33) можно пренебречь первым интегральным
2
a
2
слагаемым и перейти к рассмотрению ГИУ вида:
2
2
1
1
l
k
Φ
(t)
1−
dt
=-F
,
x
∈[ 1,1],
(36)
∫
ñ
1
π
2
t
−
x
−1
1
с учетом Φ(t)
=χ′
(t),
имеем
Дефектоскопия
№ 10
2021
Колебания слоя с расслоением в рамках градиентной теории упругости
13
2
2
1
1
l
k
X t)
1−
dt
=-F
,
x
∈[ 1,1].
2
ñ
1
π
2
t
−
x
−1
∫(
1
)
Последнее интергальное уравнение имеет аналитическое решение вида:
F
c
2
X t)
=
1−t
(37)
2
2
1
−l
k
/2
2
2
2
k
III)
κ
≈ 1, т.е.
l
≈1/
+
2
. В ГИУ (33) остаются оба интегральных слагаемых, для его
a
2
исследования можно рассмотреть схему, описанную выше с использованием аппроксимирующих
полиномов Чебышева, либо попытаться выписать полуявное выражение для рассчета функции рас-
1
1
Φ(t)
крытия [12]. Для этого обозначим интеграл Коши через
[
H Φ x)
=
dt
и перейдем от ГИУ
∫
π
t
−
x
−1
1
(33) к рассмотрению интегродифференциального уравнения:
2
H′′ - κ
H =F,
x
1
∈[−1,1],
2
(38)
a
F
=
F
c
l
Решение неоднородного дифференциального уравнения второго рода с постоянными коэффи-
циентами (38) построим из решения однородного уравнения путем вариации произвольных по-
стоянных, в результате получим интегральное уравнение вида:
F
κ(x−1)
−κ(x+1)
κx
−κx
H
=
(−2
+e
+e
) +
A
e
+
A
e
(39)
2
1
2
2κ
С учетом ранее записанных свойств функции Φ(x), x ∈[-1,1], решение сингулярного инте-
грального уравнения можно рассчитать как:
2
1
1-
x
f t)
Φ(x)
=
dt;
∫
2
π
−1
1
−t
(t
−
x
)
F
κ(t
−1)
−κ(
t+
1)
κt
−κt
f t)
=
(−
2+
e
+
e
) +
A
e
+
A
e
;
2
1
2
2κ
1
1
f t)
tf t)
A
,
A
:
dt
=
0,
dt
=
0.
1
2
∫
∫
2
2
−1
1
−t
−
1
1
−t
Был проведен численный эксперимент при h = 1. На рис. 4 приведены графики, условно
разделяющие плоскость характерных параметров асимптотического метода a, l при разных
значениях волнового числа k (одна, две и три бегущие волны, статический случай) на зоны
случаев: I (область, расположенная ниже графиков), II (область, расположенная выше графи-
ков) и зона случая III (ε — окрестность графиков, ε определяется задаваемой точностью рас-
четов, например ε = 10-3 ). На рис. 5 приведены графики относительной погрешности расчета
функции раскрытия по асимптотическому методу (35), случай I. Как показывают результаты,
погрешность расчета составляет не более 5 % при фиксированном l = 0,05, при этом диапазон
изменения полудлины трещины составляет 0 < a ≤ 0,03h, что соответствует зоне действия
случая I. Как показывают результаты расчетов, асимптотический метод позволяет существенно
упростить и ускорить решение ГИУ, а также получить полуаналитические выражения для рас-
чета функции раскрытия.
Дефектоскопия
№ 10
2021
14
А.О. Ватульян, О.В. Явруян
Рис. 4. Графики, определяющие зоны: I (выше графиков), II (ε — окрестность графиков), III (ниже графиков) асимпто-
тического подхода для разных значений волнового числа k.
а
б
14
10
12
7
10
8
ε
5
ε
6
3
4
1
2
0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10
а
0,01
0,02 0,03
0,04 0,05
0,06
а
Рис. 5. Вещественная часть (мнимая имеет аналогичных характер) относительной погрешности вычисления функции
раскрытия трещины при асимптотическом подходе для различных значений полудлины трещины a: k = 6; l = 0,05 (а);
as
l = 0,1 (б);
ε=
max(χ
i
−χ
/ χ
i
)⋅100%.
i=1..M
i
ВЫВОДЫ
Проведено масштабное исследование актуальной задачи о колебаниях слоя с расслоением на
базе градиентной теории упругости. Получено граничное интегральное уравнение относительно
градиента функции раскрытия трещины, проведен анализ ГИУ, численное исследование ГИУ на
базе метода коллокаций, метода аппроксимации полиномами Чебышева. Осуществлен асимпто-
тический анализ задачи, определены диапазоны изменения входных параметров задачи в случае
трещин малой относительной длины, которые условно определяют три зоны. В рамках каждой из
этих зон получено полуаналитическое решение исследуемой задачи. Проведен численный анализ
задачи с позиции градиентной и классической линейной теории упругости. Определены диапазоны
эффективности асимптотического подхода.
СПИСОК ЛИТЕРАТУРЫ
1. Toupin R. Elastic materials with couple-stresses // Arch. Rat. Mech. Anal. 1962. V. 11. P. 385—414.
2. Toupin R. Theories of elasticity with couple-stress // Arch. Rat. Mech. Anal. 1964. V. 17. P. 85—112.
Дефектоскопия
№ 10
2021
Колебания слоя с расслоением в рамках градиентной теории упругости
15
3. Mindlin R.D. Micro-structure in linear elasticity // Arch. Rational Mech. Anal. 1964. V. 16. P. 51—78.
4. Лурье М.В. Задачи Ламе в градиентной теории упругости // Докл. АН СССР. 1968. Т. 181. № 5.
С. 1087—1089.
5. Altan S.B., Aifantis E.C. On the structure of the mode-III crack-tip in gradient elasticity // Scripta Met.
1992. V. 26. P. 319—324.
6. Aifantis E.C. Gradient effects at the macro, micro and nano scales // J. Mech. Behav. Mater. 1994. V. 5
(3). P. 335—353.
7. Exadaktylos G., Vardoulakis I., Aifantis E. Cracks in Gradient Elastic Bodies With Surface Energy // Int.
J. Fract. 1996. V. 79 (2). P. 107—119.
8. Vardoulakis I., Exadaktylos G., Aifantis E.С. Gradient Elasticity With Surface Energy: Mode-III Crack
Problem // Int. J. Solids Struct. 1994. P. 4531—4559.
9. Erdogan F., Gupta G. D. On the Numerical Solution of Singular Integral Equations // Q. Appl. Math.
1972. V. 30. P. 525—534.
10. Chulkov A.O., Vavilov V.P., Moskovchenko A.I. Active thermal testing of delaminations in heat-shielding
structures // Russian Journal of Nondestructive Testing. 2019. V. 55. No. 3. P. 240—247.
11. Zhang L., Huang Y., Chen J. Y., Hwang K. C. The Mode III Full-Field Solution in Elastic Materials With
Strain Gradient Effects // Int. J. Fract. 1998. V. 92 (4). P. 325—348.
12. Fannjiang A.C., Chan Y.-S., Paulino G.H. Strain Gradient Elasticity for Antiplane Shear Cracks:
A Hypersingular Integrodifferential Equation Approach // Society for Industrial and Applied Mathematics.
2006. V. 62 (3). P. 1066—1091.
13. Paulino G.H., Fannjiang A.C., Chan Y.-S. Gradient Elasticity Theory for Mode III Fracture in
functionally Graded Materials—Part I: Crack Perpendicular to the Material Gradation // Journal of Applied
Mechanics. 2003. V. 70. P. 531—542.
14. Chan Y-S., Paulino G.H., Fannjiang A.C., Chan Y.-S. Change of Constitutive Relations due to
Interaction Between Strain-Gradient Effect and Material Gradation // Journal of Applied Mechanics. 2006.
V. 73. P. 871—875.
Journal of Nondestructive Testing. 2019. V. 55. No. 4. P. 277—285.
16. Ru C.Q., Aifantis E.C. A simple approach to solve boundary-value problems in gradient elasticity //
Acta Mechanica. 1993. V. 101. P. 59—68.
17. Васильев В.В., Лурье C.А. Oбобщенная теория упругости // МТТ. 2015. № 4. С. 16—27.
18. Васильев В.В., Лурье С.А. Нелокальные решения сингулярных задач математической физики и
механики // ПММ. 2018. Т. 82. № 4. С. 459—471.
19. Askes H., Aifantis K. Gradient elasticity in static and dynamics: An overview of formulations, length
scale identification procedures, finite element implementations and new results // International Journal of Solids
and Structures. 2011. V. 48. P. 1962—1990.
20. Aifantis K., Askes H. Gradient elasticity with interfaces as surfaces of discontinuity for the strain
gradient // J. Mech. Behav. Mater. 2007. V. 18. P. 283—306.
21. Ватульян А.О., Явруян О.В. Асимптотичекий подход в задачах идентификации трещин // ПММ.
2006. № 4. С. 714—724.
22. Ватульян А.О., Явруян О.В. Исследование обратных задач теории трещин с использованием
асимптотического метода // Экологический вестник научных центров ЧЭС. 2018. Т. 15. № 2. С. 39—46.
23. Vatul’yan A.O., Yavruyan О.V. An Asymptotic Method for Solving the Problem of Identifying
a Curvilinear Crack in an Elastic Layer // Russian Journal of Nondestructive Testing. 2020. V. 56. No. 10.
P. 810—819.
24. Ватульян А.О., Беляк О.А. К реконструкции малых полостей в упругом слое // Дефектоскопия.
2006. № 10. С. 33—39.
25. Yavruyan O.V., Yavruyan Kh. S. Asymptotic approach to the problem identification of a
fringedelamination from the base // IOP Conf. Ser.: Mater. Sci. Eng. 2020.
26. Ворович И.И., Бабешко В.В. Динамические смешанные задачи теории упругости для некласси-
ческих областей. М.: Наука, 1989. C. 320.
27. Градштейн И.С., Рыжик И.М. Таблицы интегралов сумм, рядов и произведений. М.: Физматгиз,
1962. 1108 с.
28. Белоцерковский С.М., Лифанов И.К. Численные методы в сингулярных интегральных уравнени-
ях и их применение в аэродинамике, теории упругости, электродинамике. М.: Наука, 1985. 253 с.
29. Iovane G., Lifanov I.K., Sumbatyan M.A. On direct numerical treatment of hypersingular integral
equations arising in mechanics and acoustics // Acta Mechanica. 2003. № 162. Р. 99—110.
Дефектоскопия
№ 10
2021