УДК 620.179.16

ДИАГНОСТИКА УДАРНЫХ ПОВРЕЖДЕНИЙ МОНОЛИТНЫХ И СОТОВЫХ

УГЛЕПЛАСТИКОВ С ПОМОЩЬЮ УЛЬТРАЗВУКОВЫХ ВОЛН ЛЭМБА

П. С. Любутин¹, С. В. Панин^1,2,***

¹Институт физики прочности и материаловедения СО РАН, 634055 Томск, пр. Академический, 2/4

² Томский политехнический университет, 634030 Томск, пр. Ленина, 30

E-mail: ^*burkovispms@mail.ru; ^**ave@ispms.ru; ^***svp@ispms.ru

Поступила в редакцию 26.11.2020; после доработки 15.12.2020

Принята к публикации 25.12.2020

Представлены результаты использования методики на основе ультразвуковых волн Лэмба для обнаружения ударных

повреждений углепластиков и определения степени их критичности. В качестве основы выступает сеть наклеенных на

поверхность пьезопреобразователей, которая работает в переменном режиме, позволяя поочередно менять функцию

преобразователей (источник/приемник) для регистрации отклика сети в результате прохождения тестового сигнала.

Анализ результатов мониторинга осуществляется посредством сравнения трех параметров: изменение амплитуды (dA),

изменение энергии (dP) и нормированный коэффициент корреляции (NCC) сигналов в базовом неповрежденном и теку-

щем поврежденном состояниях. Испытания монолитных углепластиков показывают, что точность обнаружения повреж-

дения составляет 5—15 мм, в то время как рассчитанный индекс поврежденности линейно зависит от приложенной

энергии удара. Для сотовых углепластиков NCC не дает точных результатов, однако другие параметры позволяют иден-

тифицировать повреждения с погрешностью 5—20 мм и отражают данные о степени повреждения.

Ключевые слова: неразрушающий контроль, мониторинг состояния, ультразвуковой контроль, волны Лэмба, удар-

ные повреждения, углепластики.

DOI: 10.31857/S0130308221020044

ВВЕДЕНИЕ

Неразрушающий контроль — это область науки и техники, которая крайне важна для безопас-

ной эксплуатации во многих отраслях промышленности. Но обеспечение безопасности с помощью

неразрушающего контроля, часто требует вывода объекта контроля из эксплуатации и приносит

экономические потери из-за простоев. Поэтому, в отраслях, где требуется надежная оценка целост-

ности конструкции, большое значение приобретает концепция встроенного мониторинга состоя-

ния — SHM [1—4]. Разработка таких систем в авиакосмической отрасли — серьезная научная и

инженерная задача, которая получила дополнительный импульс после создании самолетов с широ-

ким использованием композитов (Boeing 787 и Airbus A350XWB) в основных несущих конструк-

циях: крыльях, фюзеляже, оперении и др. Самолет при эксплуатации испытывает большое коли-

чество внешних ударных воздействий: мусор при разгоне по ВПП, град, удары птиц, низкокаче-

ственное или неправильное обслуживание. Использование композитов показало, что такие удары

приводят к образованию дефектов, подавляющее большинство которых классифицируются как

малозаметные ударные повреждения (barely-visible impact damage — BVID) и не приводят к необ-

ходимости экстренной остановки эксплуатации. В углепластиках они представляет собой сложные

внутренние структурные дефекты, сочетающие расслоение, разрыв и вырыв волокон, а также рас-

трескивание матрицы. Однако далее из-за эксплуатационной нагрузки и воздействия окружающей

среды такие повреждения могут увеличиваться до больших размеров, усложняя ремонт или даже

становясь угрозой для несущей способности конструкции. Таким образом, системы мониторинга,

которые встроены в конструкцию и своевременно предоставляют данные о возникновении

повреждений, имеют большое значение в том числе и в авиакосмической сфере.

Ученые и инженеры исследуют различные физические принципы, которые можно использо-

вать в качестве основы для создания систем SHM: вибрации [5—7], ультразвуковые волны [8],

термографию [9, 10], вихревые токи [11, 12], электромагнетизм [13] и др. В случае авиакосми-

ческой отрасли задача разработки SHM усложняется из-за жестких ограничений веса самолета:

установленные датчики, провода и электроника могут свести на нет преимущества применения

SHM [14, 15]. При этом взаимопротивоположные требования по минимизации веса и высокой

безопасности способствуют использованию самых высокотехнологичных решений. Например, в

аэрокосмической сфере рассматривается акустическая эмиссия [16—20], оптоволоконные дат-

чики деформации [21—23] и другие методы, которые могут использоваться в системах монито-

М.В. Бурков, А.В. Еремин, А.В. Бяков и др.

ринга. Искусственные нейронные сети активно изучаются для обработки данных и обеспечения

эффективного принятия решения. В последнее время все большее количество работ посвящает-

ся исследованию ультразвуковых волн Лэмба [24, 25]. Из-за низкого затухания эти волны могут

преодолевать большие расстояния, что чрезвычайно важно в авиастроении, где площадь обшив-

ки из углепластика может быть очень большой. УЗ волны Лэмба широко изучаются для обнару-

жения ударных повреждений композитов [26, 27]; исследуются оптимальные сети преобразова-

телей [28—30]. Однако физический механизм распространения волн Лэмба довольно сложен

[31, 32], так как зависит от многих факторов: свойств материала, геометрии объекта контроля,

геометрии преобразователя и частоты. В тоже время при непосредственном контроле состояния

конструкции в процессе эксплуатации необходимо также учитывать стабильность адгезионного

слоя и ухудшение его свойств [33, 34], температурные отклонения [35, 36], возможный отказ

датчиков [37] и т. д., так как это будет существенно сказываться на качестве получаемых данных

и надежности контроля.

Предлагаемая в данной работе методика контроля ударных повреждений была разработана

авторами ранее и применена на образце сотового композита [38, 39]. Была проведена отработка

алгоритма с использованием имитаторов повреждений, а также при выполнении последователь-

ных многократных ударов по одной панели.

Представленная статья является результатом исследования методики на иных материалах и с

измененной процедурой проведения контроля. Целью данной работы являлось исследование алго-

ритмов обнаружения ударных повреждений различной энергии в монолитных и сотовых углепла-

стиков с использованием метода на основе волн Лэмба.

МАТЕРИАЛЫ И МЕТОДЫ

С целью тестирования УЗ методики для обнаружения малозаметных ударных повреждений

использовались образцы двух типов. Первый тип представляет собой монолитный углепластик со

следующей укладкой: [90_G/(0/-45/90/+45/0)₃]_S. Образцы были изготовлены из однонаправленных

углеродных препрегов с использованием вакуумного формования и формования в автоклаве (на

внешних поверхностях углепластика был нанесен защитный слой из стекловолокна, обозначен-

ный буквой «G»). Общая толщина 32-слойного углепластика составляет 5,2 мм. Размер образца

300×300 мм². Эти образцы будут далее обозначаться буквой «М».

Второй образец представляет собой трехслойный сэндвич с алюминиевым сотовым наполни-

телем и обшивками из углепластика со следующей укладкой: [90_G/0/-45/90/+45/0]_S. Каждая

12-слойная обшивка имеет толщину около 1,7 мм, а общая толщина образца составляет 18,2 мм.

Размер — 300×300 мм². В дальнейшем образцы будут обозначены как «С».

Пьезопреобразователи

Отступ

Шаг

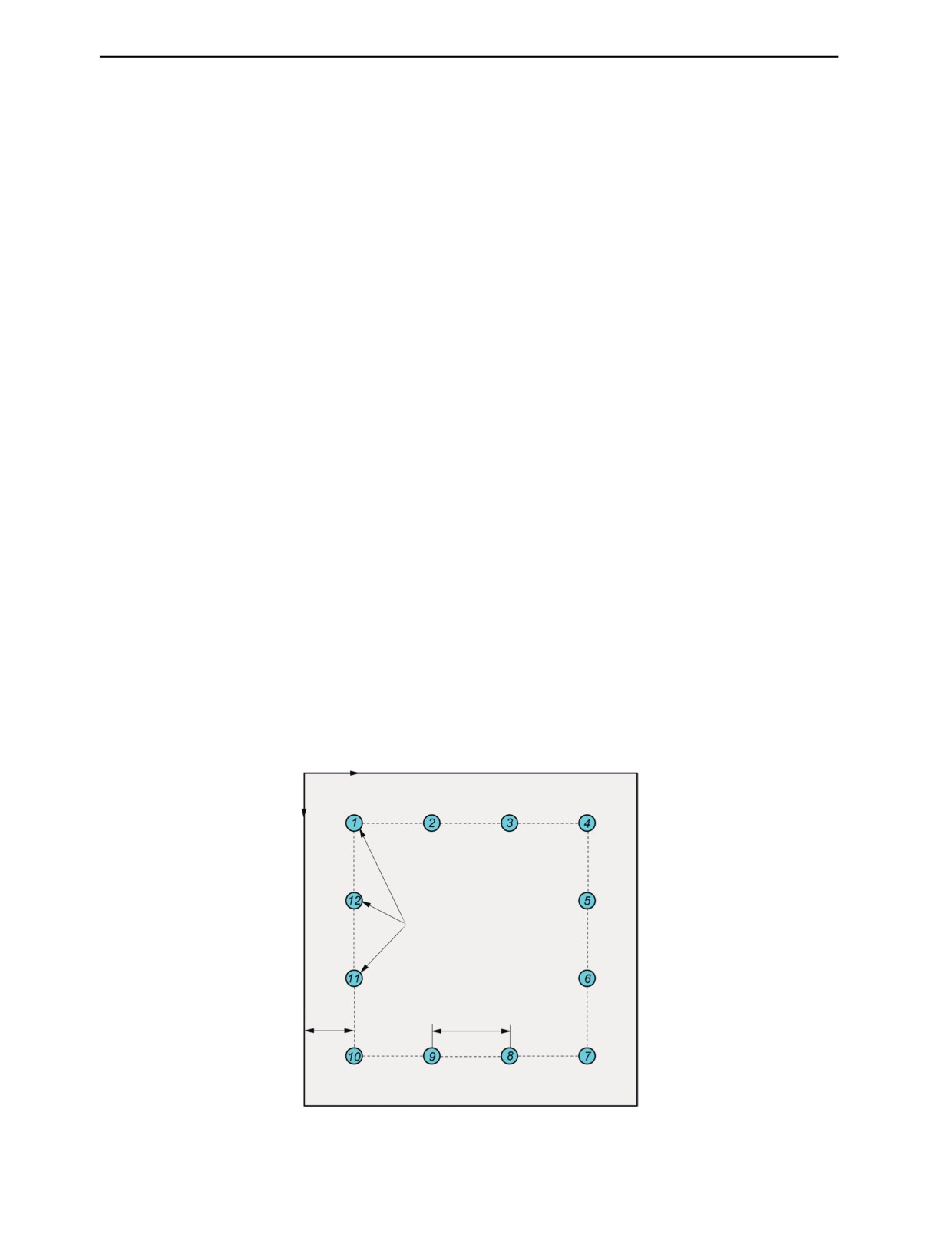
Рис. 1. Эскиз образца с сетью пьезопреобразователей (PZT).

Дефектоскопия

№ 2

2021

Диагностика ударных повреждений монолитных и сотовых углепластиков...

Каждый образец был оснащен двумя сетями пьезопреобразователей (на передней поверхности,

подвергнутой удару, и на обратной поверхности), каждый из которых мог выступать в качестве

генератора или приемника. Сеть имела размеры 4×4 со смещением 45 мм от границы образца и

шагом 70 мм. Эскиз, изображающий сеть PZT, показан на рис. 1. В качестве преобразователей

используются датчики Audiowell AW1E12G-190EFL1Z с диаметром 9 мм и толщиной 0,19 мм

керамического слоя, нанесенного на стальную подложку. Использование двух одинаковых сетей

PZT на обеих поверхностях позволяет оценить возможность обнаружения повреждений внешней

поверхности конструкции с помощью системы, установленной внутри и защищенной от воздей-

ствия окружающей среды. Это очень важно для сотового углепластика, который имеет более высо-

кое затухание ультразвуковых волн, проходящих от одной оболочки к другой через алюминиевую

сотовую сердцевину. Для приклеивания преобразователей к поверхности образцов углепластика

использовался эпоксидный клей 3M DP490.

В качестве тестового сигнала использована 5-цикловая синусоида, модулированная с помо-

щью окна Хеннинга. Частотное распределение такого сигнала позволяют получить существенно

меньшую дисперсию волны в процессе распространения по сравнению с обычным синусоидаль-

ным или ступенчатым сигналом. Это облегчает интерпретацию полученных результатов, так как

при малой дисперсии легче разделять составляющие зарегистрированных сигналов: например,

прямое прохождение волны и отражения от границ. В качестве источника сигналов и регистра-

тора используются генератор сигналов произвольной формы AWG-4105 и 4-канальный USB-

осциллограф Handyscope HS4 соответственно. AWG-4105 позволяет генерировать сигналы с

амплитудой 10 В, чего достаточно для экспериментальной проверки ультразвуковой техники на

образцах углепластика размером 300×300 мм². Однако величина принимаемого сигнала для

сотового образца была недостаточной, поэтому перед осциллографом использовался высокоча-

стотный усилитель.

В ходе предварительных испытаний пар «генератор—приемник», наклеенных на поверхность

образцов углепластика, были выбраны частоты 100 и 300 кГц. По литературным данным диспер-

сионных кривых волн Лэмба и моделирования распространении волн в программе LAMSS-

Composites [40] было установлено, что частота 100 кГц соответствует моде A0 с длиной волны

18 мм, а мода S0 пренебрежимо мала. Тогда как на частоте 300 кГц S0 генерируется намного лучше

(датчик диаметром 9 мм сопоставим с половиной длины волны). Однако A0 также генерируется,

но имеет гораздо меньшую амплитуду. Конечно, длина волны моды A0 на частоте 100 кГц доволь-

но велика по сравнению с размером сформированных BVID, но ожидается, что волны Лэмба будут

взаимодействовать с такими дефектам с повышенным затуханием. Это вызвано снижением жест-

кости материала и появлением новых границ раздела сред в области дефектов, таких как расслое-

ние, растрескивание матрицы, разрыв волокон.

Необходимо отметить, что обзор литературы [41], а также тесты, проведенные авторами ранее,

показывают, что разница в расчетных скоростях волн в направлениях 0 и 90 составляет 1—3 % и,

следовательно, нет необходимости учитывать анизотропию при контроле композитов с квази-изо-

тропной укладкой.

Для увеличения отношения S/N проводили осреднение 100 сигналов. Регистрация сигнала

осциллографом HS4 запускалась триггерным сигналом от генератора, направляемого на первый

канал осциллографа. Три оставшихся канала использовались для сбора данных. Каждое положе-

ние генератора (один из 12 датчиков) требует сбора данных с 11 датчиков, поэтому был разработан

блок реле для последовательной регистрации данных со всех датчиков. Блок реле позволяет изме-

нять положение генератора, что упрощает процедуру эксперимента. Всего в сети 4×4 может быть

зарегистрировано 132 сигнала для всех комбинаций пар «генератор—приемник». Использование

двух частот и тестирование двух сторон приводит к получению набора из 528 сигналов при кон-

троле одного образца.

Предлагаемая методика тестировалась на возможности определения местоположения и степе-

ни критичности ударных повреждений различных энергий. Образцы подвергали ударам в соот-

ветствии со стандартом ASTM D7136 с использованием методики падающего груза: ударный

элемент весом 2 кг, имеющий полусферический ударный наконечник диаметром 16 мм. Энергия

удара составляла 10, 15 и 20 Дж для монолитных образцов, в то время как сотовые углепластики

подвергались воздействию ударов с энергией 2 и 4 Дж.

Перед нанесением ударных повреждений производилась регистрация состояния образцов при

помощи ультразвуковых данных для базового состояния образцов. После удара та же процедура

проводился для поврежденного состояния. Математическое сравнение этих сигналов позволяет

обнаружить местоположение повреждения и приблизительно оценить его серьезность.

Дефектоскопия

№ 2

2021

М.В. Бурков, А.В. Еремин, А.В. Бяков и др.

Численная оценка ультразвуковых сигналов для выявления изменений, происходящих из-за

ударного повреждения углепластика, проводилась путем расчета информативных параметров

(между сигналами для двух состояний — поврежденного и базового): разности максимумов огиба-

ющих, нормированного коэффициента корреляции и разности энергий ультразвуковых сигналов.

Вычисление огибающей принятого сигнала выполняется с использованием преобразования

Гильберта в частотной области. На первом этапе вычисляется n-точечное дискретное преобразова-

ние Фурье (ДПФ) сигнала длины N, и значения спектра X(m), соответствующие отрицательной

частоте, обнуляются. Значения X(0) и X(N/2) делятся на 2. Затем выполняется обратное N-точечное

ДПФ. Сигнал имеет действительную и мнимую части. Значения огибающих определяются как

абсолютные значения полученных сигналов. Разница максимумов огибающих dA рассчитывается

следующим образом:

A -A

пов

= исх

(1)

Aисх

где А_исх — это максимум огибающей для сигнала базового состояния, а A_пов — максимум огибаю-

щей для сигнала поврежденного состояния.

Нормированный коэффициент корреляции получается по следующей формуле:

∑xисхx

пов

NCC

=1−

(2)

∑

исх

∑

пов

где x_исх и x_пов — амплитуды сигналов базового и поврежденного состояний соответственно.

Для получения спектра мощности выполняется ДПФ и значения спектра вычисляются по

выражению:

Pow(i) = 10lg X

(2i) + X

(2i +1),

(3)

где X — значения спектра Фурье. Затем для каждого сигнала рассчитывается энергия в диапазоне

0,4f :

0.4 f

Pow i),

(4)

= ∑

-0.4 f

где f — точка, соответствующая центральной частоте сигнала. Затем для двух сигналов вычисля-

ется разность dP:

P -P

пов

= исх

(5)

Pисх

где P_исх — это максимум огибающей сигнала базового состояния, а P_пов — максимум огибающей

сигнала поврежденного состояния.

После проведения всех испытаний база данных для каждой тестируемой панели содержит

следующую информацию: расположение (координаты) датчиков PZT, набор зарегистрированных

сигналов для всех пар «генератор/приемник» и информативные параметры, рассчитанные путем

сравнения исходных данных и данных, полученных для поврежденного состояния. Затем с помо-

щью разработанного программного обеспечения данные были обработаны и проанализированы с

целью определения места и степени критичности ударного повреждения. Был использован следу-

ющий алгоритм обработки:

1) траектории «генератор—приемник» сортируются по убыванию значений dA, dP или NCC в

предположении более высокого затухания из-за наличия повреждений;

2) в сортированном списке выбираются первые N траекторий (в данной статье для сравнения

выбраны 10 и 20 путей);

3) для всех траекторий попарно рассчитываются координаты их точек пересечения;

4) согласно уравнениям (6) и (7) рассчитывается координаты повреждения и его критичность.

Координаты ударных повреждений рассчитываются по формуле:

∑rwi,

(6)

⁼ ∑

где r_i — координаты i-й точки пересечения траекторий, w_i — значения выбранных информативных

параметров. Степень повреждения оценивается с помощью безразмерного индекса поврежденно-

сти (DI):

Дефектоскопия

№ 2

2021

Диагностика ударных повреждений монолитных и сотовых углепластиков...

∑

(7)

где w_i — значения выбранных информативных параметров, n — количество траекторий. Чем выше

DI, тем серьезнее повреждение. И координаты повреждения, и DI могут быть получены с исполь-

зованием каждого информативного параметра (dA или dP или NCC).

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

В разделе представлены экспериментальные результаты, полученные при проведении экспери-

ментов. В табл. 1 сведены данные по энергии и координате удара для исследованных образцов. Для

описания схемы работы экспериментальной методики ниже приведены подробные результаты

контроля образца М2/20. На рис. 2 изображена сеть PZT 4×4 с заданным в нижнем углу генерато-

ром: показаны возможные траектории волн и разности максимумов огибающих между базовым и

поврежденным состояниями. Этот пример соответствует dA, равному 0,41, то есть падению ампли-

туды на 41 % для пары «генератор—приемник» 10→5 образца М2/20.

Таблица

Образцы и параметры удара

Образец

Энергия удара, Дж

X, мм

Y, мм

М1/10

180

М2/20

180

М3/10

150

220

М4/15

150

220

М5/10

220

М6/15

220

С1/2

180

С2/4

180

С3/2

150

220

С4/4

150

220

С5/2

220

С6/4

220

dA = 0,41

dA, %

Падение амплитуды на 41 %

Место удара

Рис. 2. Пример распределения dA для образца М2/20с заданной позицией генератора.

Дефектоскопия

№ 2

2021

М.В. Бурков, А.В. Еремин, А.В. Бяков и др.

Видно, что соседние датчики 4 и 6 показывают снижение амплитуды на 12 и 23 % соответ-

ственно. Изменение сигналов при наличии повреждения для других датчиков достаточно мало.

Примеры формы тестового сигнала для исходного состояния с соответствующей огибающей для

образца М2/20 показаны на верхнем графике на рис. 3. Нижний график описывает огибающие как

для базового, так и для поврежденного состояния, а разница между максимумами огибающих

представлена графически.

6000

4000

2000

-2000

-4000

-6000

6000

ΔA

4000

2000

-2000

-4000

-6000

500

1000

1500

2000

2500

3000

3500

Время, мкс

Рис. 3. Форма принимаемого сигнала (верхний график) и графическое представление разности огибающих в базовом и

поврежденном состояниях.

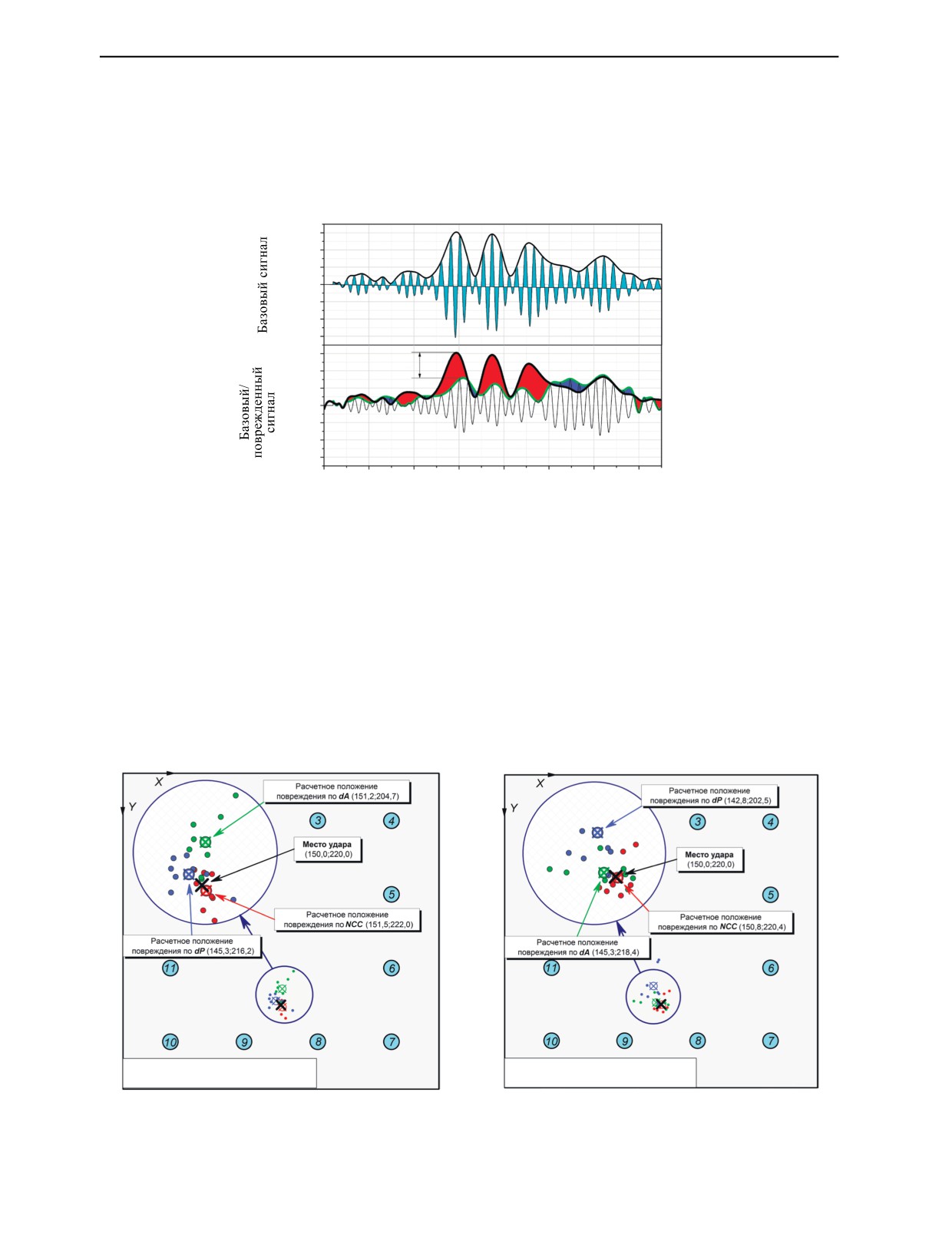
На рис. 4 и 5 показаны примеры обнаружения повреждений образцов М3/10 и М4/15, подверг-

шихся воздействию ударами 10 и 15 Дж соответственно. Каждая цветная точка соответствует про-

гнозу местоположения повреждения, определенного алгоритмом по формуле (6). Весь массив

точек рассчитан для каждой комбинации частоты испытаний, стороны образца углепластика,

количества расчетных траекторий и информативного параметра (красный для NCC; зеленый для

dA; синий для dP). Таким образом для каждого информативного параметра существует 2³=8 точек

прогнозирования местоположения повреждения. Эти точки используются для получения результи-

рующих координат X и Y, которые отображаются в виде окружностей с крестом соответствующего

цвета.

Энергия удара — 10 Дж

Энергия удара — 15 Дж

Индекс поврежденности (dA) — 0,098 Образец М3/10

Индекс поврежденности (dA) — 0,142 Образец М4/15

Рис. 4. Результаты экспериментов по обнаружению удар-

Рис. 5. Результаты экспериментов по обнаружению удар-

ных повреждений образца М3 после удара с энергией

ных повреждений образца М4 после удара с энергией

10 Дж.

15 Дж.

Дефектоскопия

№ 2

2021

Диагностика ударных повреждений монолитных и сотовых углепластиков...

Количественные результаты для всех монолитных образцов приведены в табл. 2. Видно, что

методика позволяет определять место повреждения с погрешностью 5—15 мм. Мониторинг перед-

ней стороны (поверхность удара) и задней стороны (противоположная сторона удара) дает анало-

гичные результаты в отношении прогнозируемого места повреждения. Более того, разброс ∆_avg

(расстояние от места удара до точки, рассчитываемой по методике) для всех используемых параме-

тров практически одинаков, что позволяет сделать вывод, что они могут быть использованы для

определения местоположения повреждений. В последнем столбце таблицы показаны индексы

поврежденности, рассчитанные по уравнению (7) и усредненные для каждого информативного

параметра. Эти DI имеют разные диапазоны вариации. DI_dA — самый простой для анализа индекс,

изменяющийся от 0 до 1, где 0 означает абсолютно неповрежденное состояние, полученное в

результате сравнения исходных и поврежденных ультразвуковых данных, в которых отсутствует

изменение амплитуд, в то время как 1 получается, если все поврежденные сигналы будут нулевыми.

Каждое число от 0 до 1 описывает среднее падение амплитуды сигналов, используемых для опре-

деления места повреждения. Аналогично интерпретируется индекс DI_dP, за исключением того, что

вместо амплитуды вычисляется и сравнивается энергия сигналов. Оба эти параметра предназначе-

ны для обнаружения более высокого затухания волн Лэмба при наличии повреждений. DI_NCC также

варьируется в диапазоне от 0 до 1, но демонстрирует иное поведение, поскольку корреляция может

изменяться по разным причинам, например, по фазовому сдвигу. Значение 0 данного индекса озна-

чает абсолютно неповрежденное состояние, а 1 — поврежденное, но зависимость в этом диапазоне

сильно нелинейна. Так DI_NCC для повреждений, полученных от ударов 15 и 20 Дж, достигает 0,8—

0,9, но полученные BVID довольно малы. Таким образом, можно сделать вывод, что NCC будет

иметь очень низкую классификационную способность для более крупных повреждений.

Таблица

Результаты испытаний монолитных образцов

X, мм;

Образец

Параметр

X_avg, мм

Y_avg, мм

ΔX_avg, мм

ΔY_avg, мм

Δ_avg, мм

Y, мм

NCC

176,8

185,7

3,2

-5,6

6,5

0,4

180;

М1/10

165,3

180,3

14,7

-0,3

14,6

0,092

180

171,9

177,1

8,1

2,9

8,6

0,000461

NCC

173,4

193,6

6,5

-13,7

15,1

0,82

180;

М2/20

171,3

185,5

8,7

-5,5

10,3

0,212

180

164,6

190,9

15,4

-10,1

18,9

0,001210

NCC

151,5

222,0

-1,5

-2,0

2,5

0,59

150;

М3/10

151,2

204,7

-1,2

15,3

15,4

0,098

220

145,3

216,2

4,7

3,8

6,0

0,000408

NCC

150,8

220,4

-0,8

-0,4

0,9

0,88

150;

М4/15

145,3

218,4

4,7

1,6

4,9

0,142

220

142,8

202,5

7,2

17,5

18,9

0,000613

NCC

216,1

217,0

3,9

2,9

4,9

0,51

220;

М5/10

217,7

211,5

2,3

8,5

8,8

0,080

220

209,4

210,4

10,6

9,6

14,3

0,000479

NCC

212,8

218,6

7,2

1,4

7,3

0,82

220;

М6/15

216,4

224,9

3,6

-4,9

6,1

0,129

220

214,1

221,0

5,9

-1,0

6,0

0,000830

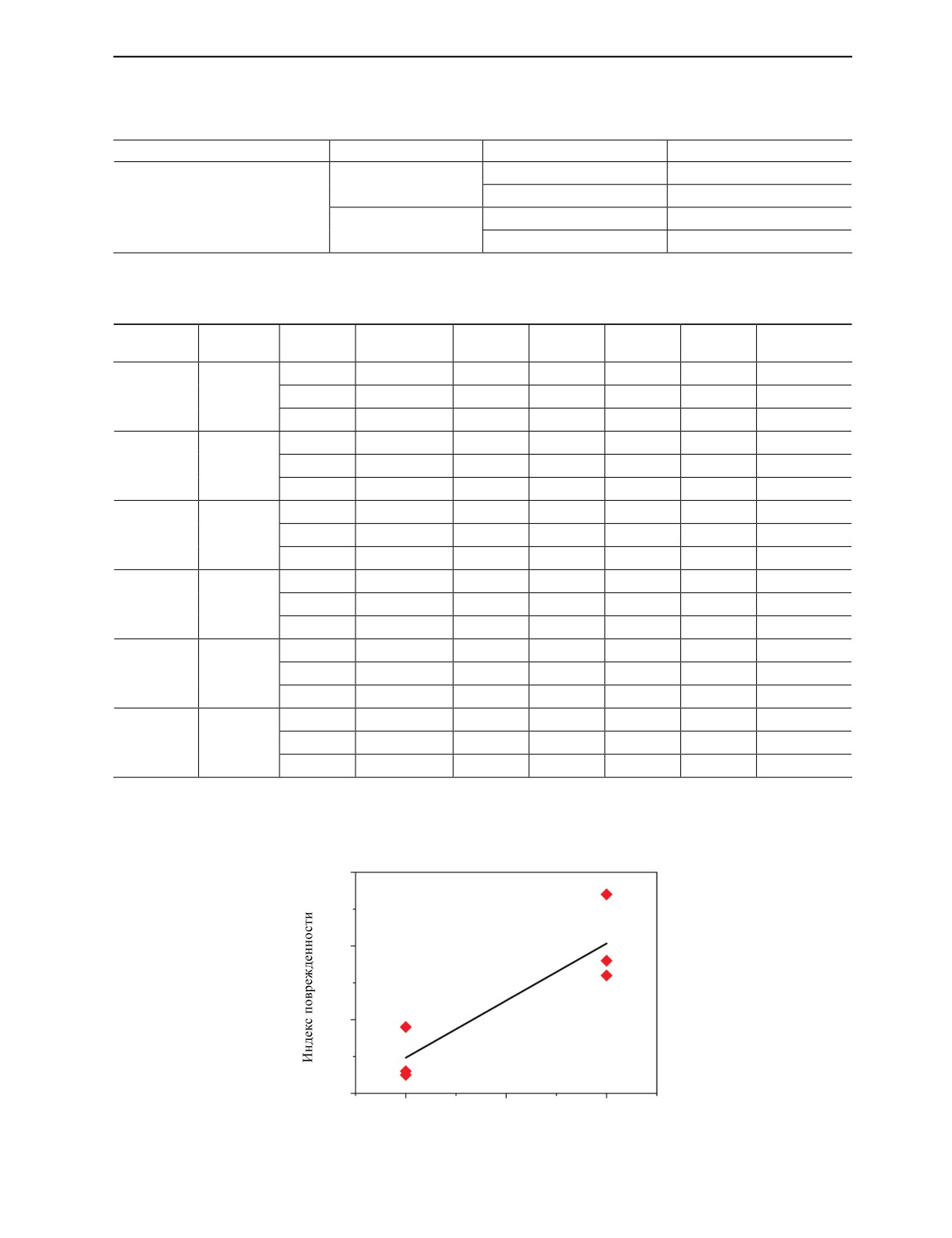
На рис. 6 представлены значения DI_dA для всех монолитных образцов. Данные аппроксимиру-

ются с использованием линейной функции, что дает хорошую линейную зависимость индекса

повреждения от энергии удара.

Далее был проведен ультразвуковой контроль всех сотовых образцов. Процедура подготовки и

испытаний сотовых образцов была абсолютно такой же, как и для монолитных, но результаты

показали некоторые различия.

Дефектоскопия

№ 2

2021

М.В. Бурков, А.В. Еремин, А.В. Бяков и др.

0,20

0,15

0,10

0,05

Энергия удара, Дж

Рис. 6. Зависимость индекса поврежденности от энергии удара для монолитных образцов.

Во-первых, было обнаружено, что процедура определения места повреждения с использова-

нием параметра NCC дает недостоверные результаты для любого образца данного типа. Расчет

координаты повреждения для каждой комбинации частоты, стороны образца и количества вол-

новых путей дает набор точек с высоким разбросом, которые после осреднения привели к тому,

что X и Y находятся очень близко к центру образца (150; 150). Вышесказанное можно увидеть на

рис. 7 и 8. Для обоих образцов С1/2 и С2/4, а также для оставшихся С3—С6 разброс красных

точек параметра NCC велик, а расчетная координата повреждения находится почти в центре.

Энергия удара — 2 Дж

Энергия удара — 4 Дж

Индекс поврежденности (dA) — 0,025 Образец С1/2

Индекс поврежденности (dA) — 0,052 Образец С2/45

Рис. 7. Результаты экспериментов по обнаружению удар-

Рис. 8. Результаты экспериментов по обнаружению удар-

ных повреждений образца С1 после удара с энергией

ных повреждений образца С2 после удара с энергией

2 Дж.

4 Дж.

Во-вторых, тестирование сотовых образцов показало, что расчетные координаты повреждений,

полученные сетью на обратной стороне, демонстрируют большой разброс информативных пара-

метров dA и dP. Это можно наблюдать практически на всех образцах типа С и следует сделать

вывод, что обнаружение повреждений на стороне, противоположной месту удара невозможно при

использовании такой методики. Подробные результаты большого разброса показаны в табл. 3, в то

время как для монолитных такие данные не представлялись из-за схожести результатов локации с

помощью сетей на лицевой и обратной сторонах.

Таким образом, для расчета усредненных координат X, Y для параметров dA и dP использова-

лись только сети PZT на лицевой стороне сотовых панелей. Все результаты сведены в табл. 4.

Дефектоскопия

№ 2

2021

Диагностика ударных повреждений монолитных и сотовых углепластиков...

Таблица

Сравнение результатов определения повреждений на сотовых образцах с помощью сетей PZT на лицевой и

обратной сторонах

Образец / Энергия удара, Дж

Параметр

Сторона

Δ_avg, мм

Лицевая

18,9

Обратная

56,3

С6/4

Лицевая

23,1

Обратная

64,9

Таблица

Результаты испытаний сотовых образцов

X, мм;

Образец

Параметр

X_avg, мм

Y_avg, мм

ΔX_avg, мм

ΔY_avg, мм

Δ_avg, мм

Y, мм

NCC

145,8

140,5

34,1

39,5

52,2

0,27

180;

С1/2

186,3

168,3

-6,3

11,7

13,3

0,025

180

177,2

183,3

2,8

-3,3

4,3

0,000178

NCC

159,1

162,0

20,9

18,0

27,6

0,31

180;

С2/4

173,6

188,0

6,4

-8,0

10,2

0,052

180

176,4

187,6

3,6

-7,6

8,4

0,000472

NCC

165,7

186,0

-15,7

34,1

37,5

0,18

150;

С3/2

151,2

200,5

-1,2

19,5

0,026

220

177,2

196,9

-27,2

23,1

35,7

0,000328

NCC

152,6

200,4

-2,6

19,6

19,8

0,29

150;

С4/4

161,2

219,6

-11,2

0,4

11,2

0,074

220

149,5

197,0

0,5

23,0

0,000432

NCC

192,3

190,8

27,7

29,2

40,3

0,2

220;

С5/2

206,7

206,3

13,3

13,7

19,0

0,038

220

209,1

210,6

10,9

9,4

14,4

0,000368

NCC

189,9

188,5

30,1

31,5

43,6

0,33

220;

С6/4

207,1

207,2

12,9

12,8

18,1

0,056

220

206,0

205,8

14,0

14,2

19,9

0,000592

Видно, что ошибка предсказания места повреждения для dA варьируется в пределах 10—20 мм,

тогда как dP имеет более высокий разброс ∆_avg: 4—35 мм.

0,08

0,06

0,04

0,02

Энергия удара, Дж

Рис. 9. Зависимость индекса поврежденности от энергии удара для сотовых образцов.

Дефектоскопия

№ 2

2021

М.В. Бурков, А.В. Еремин, А.В. Бяков и др.

Были рассчитаны индексы повреждений (рис. 9) для различных параметров, показывающие

чувствительность и классификационную способность. Разброс DI_dA выше, чем для монолитов, но

видна прямая связь между индексом поврежденности и энергией удара.

ЗАКЛЮЧЕНИЕ

В работе была исследована эффективность экспериментальной методики с использованием

подхода на основе волн Лэмба для обнаружения малозаметных ударных повреждений углепласти-

ков. Сеть пьезопреобразователей приклеивалась к поверхности и использовалась для генерации

волн Лэмба и приема прошедших через панель сигналов.

Тестирование монолитных углепластиков показывает, что все используемые параметры

(а именно dA, dP или NCC) позволяют определить место повреждения с погрешностью 5—15

мм. Расчетный индекс повреждений DI обеспечивает линейную зависимость от энергии удара.

При этом датчики могут располагаться как на лицевой, так и на задней стороне, что не суще-

ственно сказывается на точности. При этом использование параметра NCC возможно для лока-

ции повреждений, однако корректное определение степени критичности дефекта по данному

параметру затруднено.

Испытания сотовых образцов дают достаточную точность прогноза места повреждения в диа-

пазоне 5—20 мм, не смотря на то, что разброс несколько выше, чем для монолитов. Обнаружение

повреждений сетью PZT на стороне, противоположной стороне удара, является более сложным, а

точность намного ниже из-за большой толщины и наличия алюминиевых сот, поэтому волны

Лэмба не чувствительны к повреждениям на противоположной стороне. Индекс поврежденности

позволяет классифицировать степень критичности дефекта. Для сотовых образцов невозможно

использовать один из информативных параметров (NCC) для анализа из-за фазового сдвига при-

нимаемого сигнала и его влияния на вычисляемое значение NCC.

Работа выполнена в рамках государственного задания ИФПМ СО РАН, тема номер FWRW-

2021-0010.

СПИСОК ЛИТЕРАТУРЫ

1. García Márquez F.P., Peco Chacón A.M. A review of non-destructive testing on wind turbines blades //

Renew. Energy. 2020. V. 161. P. 998—1010.

2. Schubel P.J., Crossley R.J., Boateng E.K.G., Hutchinson J.R. Review of structural health and cure

monitoring techniques for large wind turbine blades // Renew. Energy. 2013. V. 51. P. 113—123.

3. Qing X., Li W., Wang Y., Sun H. Piezoelectric transducer-based structural health monitoring for aircraft

applications // Sensors (Switzerland). 2019. V. 19. I. 3. P. 1—27.

4. Annamdas V.G.M., Bhalla S., Soh C.K. Applications of structural health monitoring technology in Asia

// Struct. Heal. Monit. 2017. V. 16. I. 3. P. 324—346.

5. Jamadar N.I., Kivade S.B., Dhande K.K., Pedada S. Vibration based damage inspection in composite

structures - A critical review // Int. J. Eng. Sci. Innov. Technol. 2014. V. 3. P. 201—208.

6. Lakhdar M., Mohammed D., Boudjemaa L., Rabia A., Bachir M. Damages detection in a composite

structure by vibration analysis // Energy Procedia. 2013. V. 36. P. 888—897.

7. Kernicky T., Whelan M., Al-Shaer E. Vibration-based damage detection with uncertainty quantification

by structural identification using nonlinear constraint satisfaction with interval arithmetic // Struct. Heal.

Monit. 2019. V. 18. P. 1569—1589.

8. Beskhyroun S., Wegner L.D., Sparling B.F. Integral resonant control scheme for cancelling human-induced

vibrations in light-weight pedestrian structures // Struct. Control Heal. Monit. 2011. V. 19. I. 1. С. 55—69.

9. Talai S.M., Desai D.A., Heyns P.S. Infrared thermography applied to the prediction of structural

vibration behaviour // Alexandria Eng. J. 2019. V. 58. P. 603—610.

10. Hwang S., An Y.K., Sohn H. Continuous-wave line laser thermography for monitoring of rotating wind

turbine blades // Struct. Heal. Monit. 2019. V. 18. P. 1010—1021.

11. Chen G., Zhang W., Zhang Z., Jin X., Pang W. A new rosette-like eddy current array sensor with high

sensitivity for fatigue defect around bolt hole in SHM // NDT E Int. 2018. V. 94. P. 70—78.

12. Sodano H.A. Development of an Automated Eddy Current Structural Health Monitoring Technique

with an Extended Sensing Region for Corrosion Detection // Struct. Heal. Monit. An Int. J. 2007. V. 6.

P. 111—119.

13. Witos M., Zieja M., Fallahi N., Zurek Z., Kwasniewski J. NDE and SHM of Critical Parts using

Magnetic and Electromagnetic Methods // Acta Phys. Pol. A. 2018. V. 133. P. 697—700.

14. Structural Health Monitoring (SHM) in Aerospace Structures. Elsevier. 2016.

15. Wang Y., Qiu L., Luo Y., Ding R., Jiang F. A piezoelectric sensor network with shared signal

transmission wires for structural health monitoring of aircraft smart skin // Mech. Syst. Signal Process. 2020.

V. 141. P. 106730.

Дефектоскопия

№ 2

2021

Диагностика ударных повреждений монолитных и сотовых углепластиков...

16. Wildemann V., Spaskova E., Shilova A. Research of the Damage and Failure Processes of Composite

Materials Based on Acoustic Emission Monitoring and Method of Digital Image Correlation // Solid State

Phenom. 2015. V. 243. P. 163—170.

17. Barsuk V.E., Stepanova L.N., Kabanov S.I. Composite airplane Construction acoustic emission testing

during static loading // Kontrol’. Diagnostika. 2018. No. 4. 14—19.

18. Stepanova L.N., Bataev V.A., Chernova V.V. Studying the failure of a CFRP sample under static loading

by the acoustic-emission and fractography methods // Russ. J. Nondestruct. Test. 2017. V. 53. P. 422—429.

19. Zhou J., Mathews V.J., Adams D.O. Acoustic emissionbased impact location estimation on composite

structures // Struct. Heal. Monit. 2019. V. 18. P. 1652—1668.

20. Zhao W., Zhou W. Cluster analysis of acoustic emission signals and tensile properties of carbon/glass

fiber reinforced hybrid composites // Struct. Heal. Monit. 2019. V. 18. P. 1686—1697.

21. Guemes A., Fernandez-Lopez A., Daz-Maroto P., Lozano A., Sierra-Perez J. Structural Health

Monitoring in Composite Structures by Fiber-Optic Sensors // Sensors. 2018. V. 18. P. 1094.

22. Bashkov O.V., Romashko R.V., Zaikov V.I., Panin S.V., Bezruk M.N., Khun K., Bashkov I.O. Detecting

acoustic-emission signals with fiber-optic interference transducers // Russ. J. Nondestruct. Test. 2017. V. 53.

P. 415—421.

23. Kwon H., Park Y., Kim J. H., Kim C. G. Embedded fiber Bragg grating sensor based wing load

monitoring system for composite aircraft // Struct. Heal. Monit. 2019. V. 18. P. 1337—1351.

24. Weiland J., Hesser D.F., Xiong W., Schiebahn A., Markert B., Reisgen U. Structural health monitoring

of an adhesively bonded CFRP aircraft fuselage by ultrasonic Lamb Waves // Proc. Inst. Mech. Eng. Part G.

J. Aerosp. Eng. 2020. V. 234. I. 13. P. 2000—2010.

25. Ong W., Rajic N., Chiu W., Rosalie C. Lamb wave-based detection of a controlled disbond in a lap

joint // Struct. Heal. Monit. 2018. V. 17. I. 3. P. 668—683.

26. Sherafat M.H., Guitel R., Quaegebeur N., Hubert P., Lessard L., Masson P. Structural health monitoring

of a composite skin-stringer assembly using within-the-bond strategy of guided wave propagation // Mater.

Des. 2016. V. 90. P. 787—794.

27. Taleb S., Rittmeier L., Sinapius M., Boubenider F., Schmidt D. Experimental Study of Lamb Waves

Propagation inside an Impact Damage in the Size of the Used Wavelength // Russ. J. Nondestruct. Test. 2020.

V. 56. I. 2. P. 141—150.

28. Lee B.C., Staszewski W.J. Sensor location studies for damage detection with Lamb waves // Smart

Mater. Struct. 2007. V. 16. P. 399—408.

29. Tan Y., Zhang L. Computational methodologies for optimal sensor placement in structural health

monitoring: A review // Struct. Heal. Monit. 2020. V. 19. I. 4. P. 1287—1308.

30. Ostachowicz W., Soman R., Malinowski P. Optimization of sensor placement for structural health

monitoring: a review // Struct. Heal. Monit. 2019. V. 18. P. 963—988.

31. Nedospasov I.A., Mozhaev V.G., Kuznetsova I.E. Unusual energy properties of leaky backward Lamb

waves in a submerged plate // Ultrasonics. 2017. V. 77. P. 95—99.

32. Park I., Jun Y., Lee U. Lamb wave mode decomposition for structural health monitoring // Wave

Motion. 2014. V. 51. P. 335—347.

33. Attarian V.A., Cegla F.B., Cawley P. Long-term stability of guided wave structural health monitoring

using distributed adhesively bonded piezoelectric transducers // Struct. Heal. Monit. 2014. V. 13. P. 265—280.

34. Schubert K.J., Brauner C., Herrmann A.S. Non-damage-related inuences on Lamb wave-based

structural health monitoring of carbon fiber-reinforced plastic structures // Struct. Heal. Monit. 2013. V. 13.

P. 158—176.

35. Wandowski T., Malinowski P.H., Ostachowicz W.M. Delamination detection in CFRP panels using EMI

method with temperature compensation // Compos. Struct. 2016. V. 151. P. 99—107.

36. Dodson J.C., Inman D.J. Thermal sensitivity of Lamb waves for structural health monitoring

applications // Ultrasonics. 2013. V. 53. P. 677—685.

37. Kullaa J. Distinguishing between sensor fault, structural damage, and environmental or operational

effects in structural health monitoring // Mech. Syst. Signal Process. 2011. V. 25. P. 2976—2989.

38. Burkov Mikhail, Lyubutin Pavel, Byakov Anton. Experimental application of Lamb wave technique for

testing of CRFP // AIP Conference Proceedings 2051, 020043 (2018). https://doi.org/10.1063/1.5083286

39. Burkov M.V., Lyubutin P.S., Byakov A.V. Lamb Wave Ultrasonic Detection of Barely Visible Impact

Damages of CFRP // Russian Journal of Nondestructive Testing. 2019. V. 55. No. 2. P. 89—101.

40. Lamss-composites software. http://www.me.sc.edu/research/lamss/html/software.html (Доступ:

18 Ноября 2020).

41. Zhongqing Su, Lin Ye. Identification of Damage Using Lamb Waves From Fundamentals to

Applications. Springer-Verlag Berlin Heidelberg, 2009.

Дефектоскопия

№ 2

2021