Электромагнитные методы
УДК 620.179.14
К РАСЧЕТУ ПОЛЯ КОНЕЧНОГО МАГНИТНОГО ЦИЛИНДРА С ВНУТРЕННИМ
СООСНЫМ ЦИЛИНДРИЧЕСКИМ ДЕФЕКТОМ
© 2021 г. В. В. Дякин1,*, О. В. Кудряшова1,**, В. Я. Раевский1,***
1Институт физики металлов имени М.Н. Михеева УрО РАН,
Россия 620137 Екатеринбург, ул. С. Ковалевской, 18
E-mail:*dyakin@imp.uran.ru;**kudryashova_ov@imp.uran.ru; ***ravskii@mail.ru
Поступила в редакцию 28.04.2021; после доработки 18.05.2021
Принята к публикации 21.05.2021
С помощью сеточного метода проведено численное решение прямой задачи магнитостатики по вычислению поля
конечного цилиндра с постоянной магнитной проницаемостью, содержащего внутреннее включение в виде соосного
цилиндра с иной магнитной проницаемостью. Алгоритм создан для произвольного внешнего поля. С целью оценки
достоверности и точности метода решения проведено тестирование результатов с помощью точно решаемых задач.
Также проведено сравнение с результатами ранее решенной задачи о конечном бездефектном цилиндре. Построены
координатные зависимости компонент результирующего поля при различных исходных данных. Программа пополняет
библиотеку задач магнитного контроля и может быть использована для качественной сверки с результатами модельных
экспериментов, а также для оценки геометрических характеристик внутреннего дефекта.
Ключевые слова: дефектоскопия, теоретические задачи магнитного контроля, магнитостатика, основное уравнение
магнитостатики, сеточный метод, магнитный цилиндр с дефектом.
DOI: 10.31857/S0130308221070022
1. ВВЕДЕНИЕ
В работе [1] был реализован алгоритм приближенного численного решения прямой линейной
задачи магнитостатики для расчета компонент результирующего поля конечного цилиндра, нахо-
дящегося в произвольном стационарном внешнем поле. В основу легло интегро-дифференциаль-
ное уравнение магнитостатики [2, 3], преобразованное для случая постоянной магнитной прони-
цаемости: в результате трехмерное уравнение сводится к двумерному, содержащему интеграл по
поверхности магнетика, подынтегральная функция которого содержит нормальную составляю-
щую искомого поля. Данное уравнение обращается в выражение по расчету поля в произвольной
точке пространства (за исключением граничных точек магнетика), если нормальная составляющая
на границе оказывается известной. Уравнение для этой нормальной составляющей выводится из
основного уравнения. Для решения задачи в [1] была применена процедура дискретизации. Так,
интегральное уравнение было сведено к системе линейных алгебраических уравнений относи-
тельно значений искомой функции на фрагментах разбиений. Далее на основе решения системы
были записаны выражения для расчета напряженности результирующего поля в произвольной
точке пространства. Алгоритм был протестирован на точно решаемых задачах, путем численных
экспериментов было установлено, что в широком диапазоне изменения входных данных имеет
место стабилизация двух или трех значащих цифр окончательного результата. Кроме того, был
осуществлен подбор оптимальных параметров разбиения, позволяющих получать решение за
вполне приемлемое время.
В следующей работе над задачей в той же самой постановке [4] был использован более совер-
шенный подход: с помощью достаточно объемных аналитических преобразований с использова-
нием основных свойств гипергеометрических функций и функций Лежандра решение основного
трехмерного магнитостатического уравнения для указанной конфигурации сведено к решению
некоторого количества систем трех одномерных линейных интегральных уравнений. Преимущества
по сравнению с работой [1] несомненны: понижение размерности уравнений обеспечивает воз-
можность получения результата более высокой точности со значительно меньшими затратами
машинного времени — программа [4] выдает результат за несколько секунд, тогда как программа
[1] работает минут двадцать. В этой связи интересно ознакомиться с деталями работы над задачей
с аналогичной постановкой при ее реализации с помощью стандартных программ типа Ansys,
Elcut и других. Узнать об этом пока не удалось.
Настоящая работа выполнена в развитие примененной в [1] методики на случай, когда внутри
магнитного цилиндра находится дефектная область с иной магнитной проницаемостью. Разработка
подходов к решению задачи магнитостатики для дефектных тел конечного размера несомненно
12
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
является актуальной. Подавляющее большинство теоретических задач магнитного контроля реше-
но для неограниченных геометрических моделей тел с неограниченными либо конечными форма-
ми внутренних дефектов. Известна только одна задача о конечном теле с конечным дефектом —
задача о магнитном шаре с произвольно расположенным шаровым включением [5].
2. ПОСТАНОВКА ЗАДАЧИ
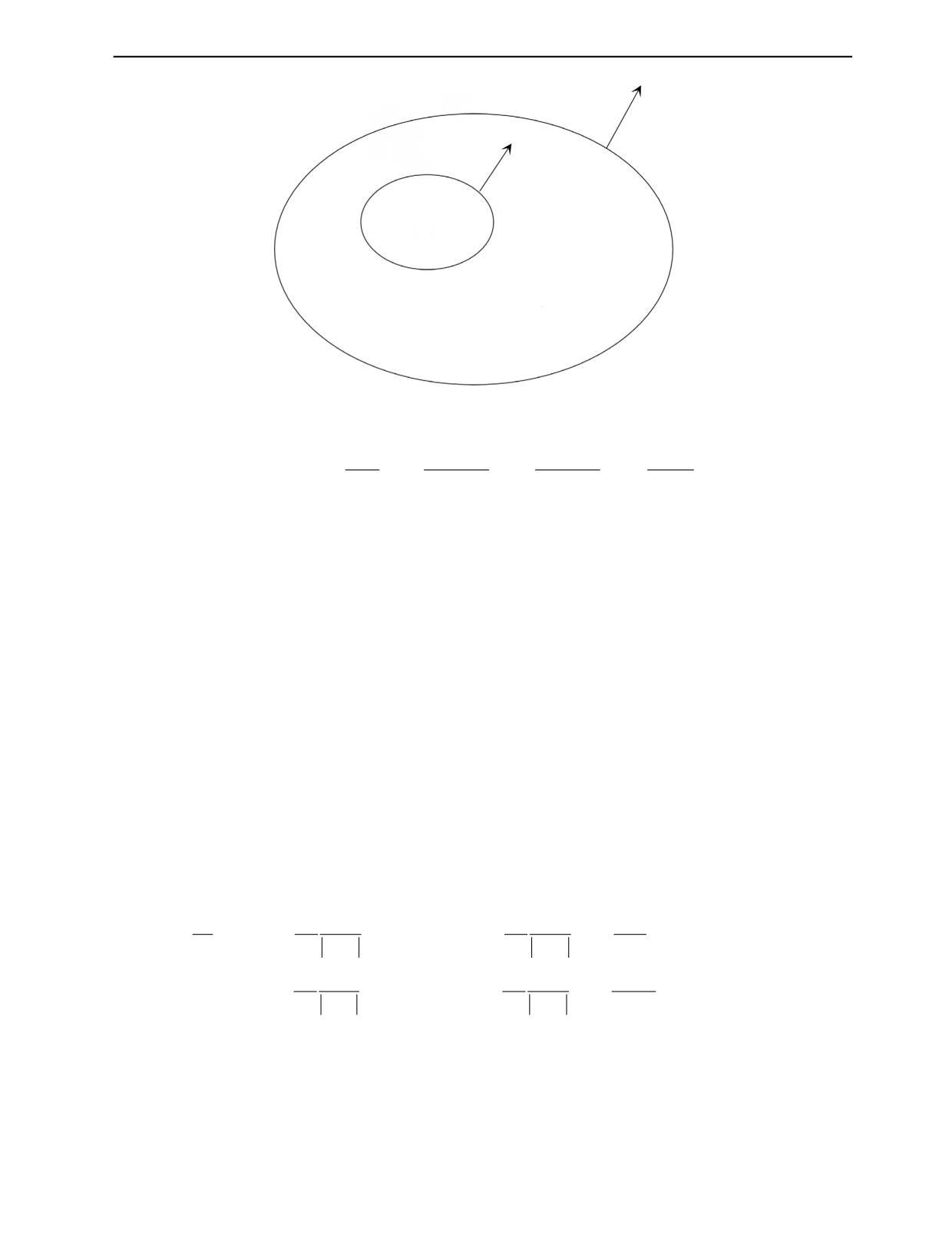
Пусть имеется магнетик, ограниченный замкнутой поверхностью S, внутри которого распо-
лагается иной магнетик (дефект), ограниченный замкнутой поверхностью Sd. Область, заклю-
ченную между поверхностями S и Sd, обозначим через Ω и положим, что внутри нее магнитная
проницаемость постоянна и равна μ. Область внутри Sd обозначим через Ωd и положим, что здесь
магнитная проницаемость также постоянна и равна μd. Немагнитную часть пространства обо-
значим через Ω0 — здесь магнитная проницаемость равна единице. Далее примем, что внешнее
3
намагничивающие поле описывается некой функцией H0(r), r∈
. Описанная общая постанов-
ка иллюстрируется рис. 1.
Вектор-функция напряженности магнитного поля H(r) подчиняется уравнению — следствию
из основного уравнения магнитостатики, полученному при условии постоянства магнитной про-
ницаемости, которое в рамках принятых условий имеет вид:
Ω
Ω
Ω
d
H
r′
H
(
r′
)
H
(r′)
µ-1
n
(
)
µ-1
n
d
d
µ -1
n
d
0
H r)+
∇
dS
′-
∇
dS
′ +
∇
dS
′ =
H
(
r
)
,
(1)
∫
∫
d
∫
d
4π
r
-r′
4π
r
−r′
4π
r
−r′
S
S
d
S
d
Ω
Ω
где r∈ Ω\{S Sd}. В (1) под интегралы входят функции
H
n
(r′)
=
(
H r′),n
)
и т.п. — так были
обозначены значения нормальной составляющей вектора напряженности поля на поверхности
интегрирования вдоль вектора, указанного в нижней подписи к основному символу, и изнутри
области, указанной в верхней подписи. Через n обозначен единичный вектор нормали, построен-
ный на поверхности S и направленный изнутри области Ω, а через nd — единичный вектор норма-
ли на поверхности Sd, направленный изнутри Ωd (рис.1). Учитывая, что на Sd выполняется гранич-
Ω
d
ное условие
µH
=µ
HΩ
,
упрощаем (1) и записываем рабочее уравнение:
n
d
d n
d
Ω
Ω
µ-1
H
(r′)
µ-µ
H
(r′)
n
d
n
d
0
H r)+
∇
dS'−
∇
dS
′
=
H r),
r
∈Ω\
{
SS
}
,
(2)
∫
∫
d
d
4π
r
-r′
4πµ
r
−r′
S
d
S
d
из которого видно, что для определения вектора напряженности магнитного поля в произвольной
точке пространства необходимо найти две функции — его нормальные составляющие изнутри Ω
на поверхностях S и Sd соответственно.
Ω
Для получения системы интегро-дифференциальных уравнений относительно
(
)
H
r
и
n
Ω
H
(
r
)
в (2) положим r ∈ Ω и скалярно умножим обе его части на векторы n и nd. Получим:
n
d
Ω
Ω
µ-1
∂
H
(r′)
µ-µ
∂
H
(r′)
n
d
n
d
0
H
+
dS′-
dS′ =
H
r
;
n
Ω (r)
∫
∫
d
n
(
)
4π ∂n
r
−r′
4πµ
∂
n
r
−
r′
S
d
S
d
(3)
Ω
Ω
µ-1
∂
H
(r′)
µ-µ
∂
H
(r′)
Ω
n
d
n
d
0
H
(r)
+
dS′-
dS
′ =
H
(
r
)
n
d
∫
∫
d
n
d
4π ∂n
r
−r′
4
πµ
∂n
r
−
r′
d S
d
d S
d
Здесь совершим предельные переходы: в первом уравнении — на поверхность S, во втором — на
Sd. Здесь следует действовать, используя свойства нормальной производной потенциала простого
слоя [6]. После преобразований приходим к системе интегральных уравнений относительно функ-
Ω
Ω
ций
H
n
(
r
)
и
H
n
(
r
)
, определенных на поверхностях S и Sd соответственно. Получим:
d
χ
∂
1
χ
∂
1
2
Ω
Ω
1
Ω
0
H
(r)
+
H
(r')
dS
'−
H
(r′)
dS
'
=
H
(
r
)
,
r
∈
S;
n
∫
n
∫
n
d
d
n
2
π
∂n
r
−r'
2π
∂n
r
−r
′
µ+1
S
S
d
(4)
χ
∂
1
χ
∂
1
2
µ
Ω
2
Ω
d
Ω
d
0
H
n
(r)
+
H
n
(r')
dS
'−
H
n
(r′)
dS
d
'
=
H
n
(
r
)
,r ∈ S
d
,
d
∫
∫
d
d
2
π
∂n
r
−r'
2π
∂n
r
−r
′
µ+µ
S
d
S
d
d
d
Дефектоскопия
№ 7
2021
К расчету поля конечного магнитного цилиндра с внутренним соосным цилиндрическим...
13
n
Ω0: μ = 1
nd
S
Sd
Ωd: μd > 1
Ω: μ > 1
Рис. 1.
µ-1
µ-µ
µ
(µ-1)
µ-µ
d
d
d
где введены обозначения:
χ:=
,χ
:=
,χ
:=
,χ
:=
1
2
d
µ+1
µ
d
(µ+1)
µ+µ
d
µ+µ
d
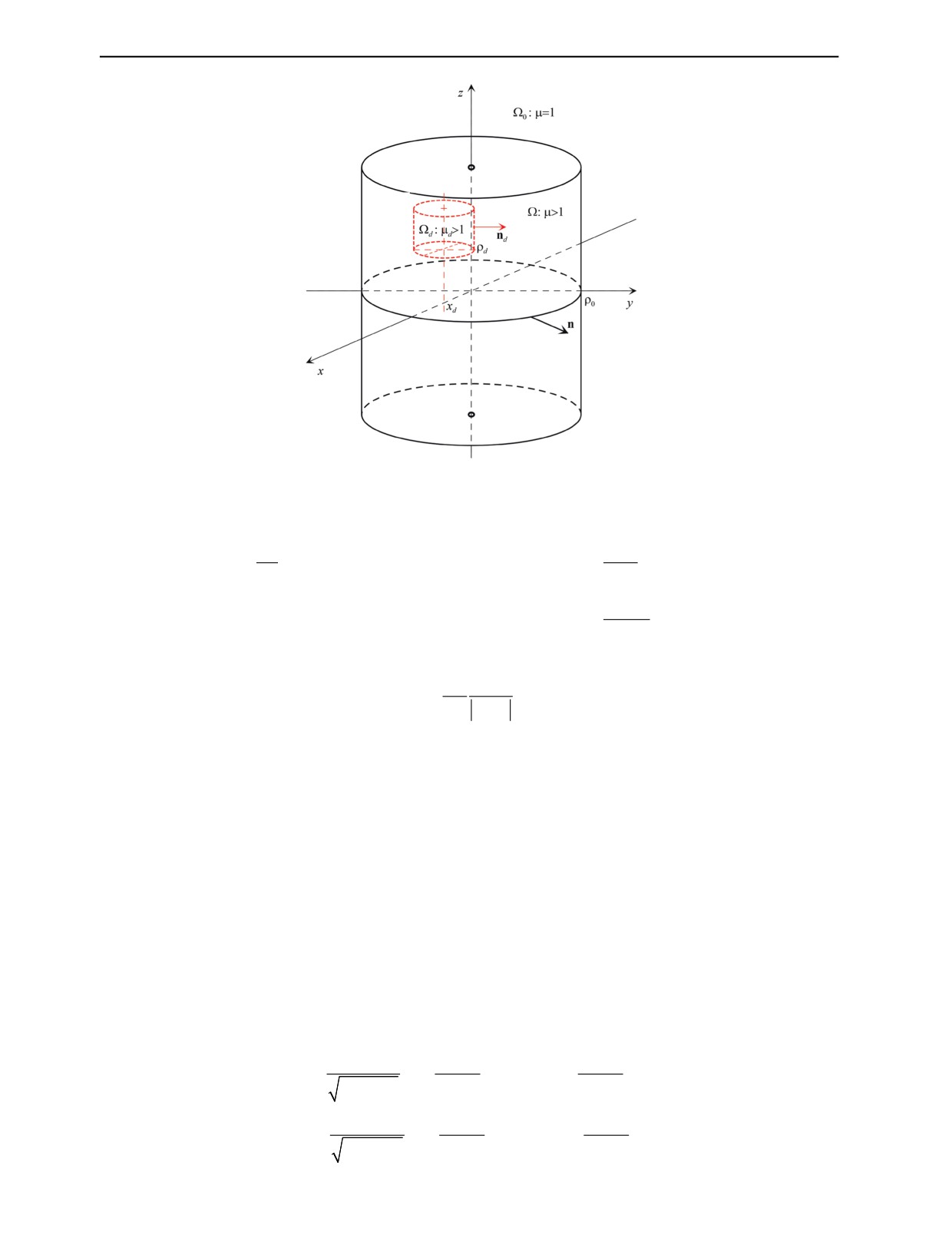
Далее примем, что геометрический образ рассматриваемого тела соответствует представленно-
му на рис. 2. Положим, что дефектное тело является конечным цилиндром, ограниченным поверх-
ностью
S=S
S
S
, где:
1
2
3
2
2
2
S
=
(
x y,z
)
:x
+
y
=ρ
;z ∈
[
−h
,h
]
;
1
{
0
1
2
}
2
2
2
S
2
=
{
(
x y,
z
)
:x
+
y
≤ρ
0
;z
=-
h
1
}
;
2
2
2
S
=
{
(
x y,z
)
:x
+
y
≤ρ
;z = h
}
3
0
2
Внутри S располагается поверхность
S
d
=S
4
S
5
S
6
,
где:
2
2
2
S
=
(
x y,z
):(
x- x
)
+
y
=ρ
;
z∈
[
h
,h
]
;
4
{
d
d
3
4
}
2
2
2
S
=
(
x y,z
):(
x- x
)
+
y
≤ρ
;z = h
;
5
{
d
d
3
}
2
2
2
S
=
(
x y,z
):(
x- x
)
+
y
≤ρ
;z = h
6
{
d
d
4
}
Нормаль к поверхности Si (i = 1, …, 6) обозначим через ni. Так, система (4) будет состоять из
шести уравнений:
3
6
χ
∂
1
χ
∂
1
2
Ω
Ω
1
Ω
0
H
(r)
+
H
(r′)
dS
′-
H
(r′)
dS′ =
H
(
r
)
,r ∈ S
,
i
=1,2,3;
n
i
∑∫
n
j
j
∑
∫
n
j
j
n
i
i
2π
∂n
r
−r′
2π
∂
n
r
−
r′
µ+1
j=1 S
j
i
j=
4
S
j
i
(5)
3
6
χ
∂
1
χ
∂
1
2
µ
Ω
2
Ω
d
Ω
d
0
H
(r)
+
H
(r')
dS
′
−
H
(r′)
dS′
=
H
(
r
)
,r ∈ S
,
i
=
4,5,6.
n
i
∑∫
n
j
j
∑
∫
n
j
j
n
i
i
2π
∂n
r
−r'
2
π
∂
n
r
−
r′
µ+µ
j=1 S
i
j=
4
S
i
d
j
j
Всякую поверхность Si = (i = 1, …, 6) разбиваем на Ni фрагментов
{S
, а через rim обозна-
im
}Nim
=
1
чим радиус-вектор центра площадки Sim. Примем, что на значение искомой нормальной составля-
ющей вектора напряженности магнитного поля на всякой площадке Sim является постоянным, эту
Ω
постоянную обозначим через
H
(
r
).
Таким образом, система (5) сводится к системе линейных
n
i
im
алгебраических уравнений относительно этих значений:
Дефектоскопия
№ 7
2021
14
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
S3: z = h2
S6: z = h4
S5: z = h3
0
S1
S2: z = -h1
Рис. 2.
3
N
j
6
N
j
χ
χ
2
Ω
Ω
(
i,
j
)
1
Ω
(
i,
j
)
0
H
(
r
)
+
H
(
r
)
A
−
H
(
r
)
A
=
H
(
r
)
,
i
=1, 2, 3;
n
i
im
∑∑
n
j
jk
mk
∑∑
n
j
jk
mk
n
i
im
2π
j=1
k=1
2π
j=4
k=1
µ+1
(6)
N
N
3
j
6
j
Ω
χ
2
Ω
(
i,
j
)
χ
d
Ω
(
i,
j
)
2µ
d
0
H
n
(
r
im
)
+
∑∑
H
n
(
r
jk
)
A
mk
−
∑∑
H
n
(
r
jk
)
A
mk
=
H
n
(
r
im
)
,
i
=
4, 5, 6,
i
j
j
i
2
π
j
=1
k
=1
2
π
j
=4
k
=1
µ+µ
d
где
(i,
j
∂
1
A
) :
=
dS
′
,
mk
∫
jk
(7)
∂
n
r
−
r
′
S
jk
i
r
=
r
im
i = 1, …, 6; j = 1, …, 6; m = 1, …, Ni; k = 1, .., Nj.
j
)
Матричные элементы
Ai,
mk
распределяются по 36-и блокам: фиксируя точку rim на i-й
поверхности, проводим интегрирование по фрагменту Sjk на j-й поверхности. Все интегралы
могут быть взяты и вычислены. Однако численные эксперименты, выполненные в ходе рабо-
ты над задачей о цилиндре без дефекта [1], показали, что брать все интегралы нет необходи-
мости: при большой плотности разбиения фрагменты интегрирования становятся сравни-
тельно малыми, и для вычисления интегралов с хорошей точностью работает формула
среднего значения. Такой подход приемлем для вычисления матричных элементов вида
(i,
j)
A
,
где i ≠ j
— в таком случае область интегрирования не содержит особую точку. Не
mk
будем подробно расписывать очевидные действия по получению расчетных формул для
j
)
Ai,
при i ≠ j . Не будем приводить и окончательные столь же очевидные формулы, чтобы
mk
не загромождать текст статьи.
Если же фрагменты содержат особую точку rim, что случается, если она находится на той же
самой площадке, по которой ведется интегрирование, то тогда необходимо корректно взять несоб-
ственный интеграл. Матричные элементы такого рода имеют вид:
2
δ
π+δ
π-δ
(
1,1
)
z
ϕ
ϕ
A
=-
F
,λ
(
ρ
)
−
F
,
λ
(
ρ
)
;
mm
2
2
0
0
4
ρ
+δ
2
2
0
z
2δ
π+δ
π-δ
(
4,4
)
z
ϕ
ϕ
A
=-
F
,
λ
(
ρ
)
−
F
,λ
(
ρ
)
,
mm
d
d
2
2
2
2
4
ρ
d
+δ
z
Дефектоскопия
№ 7
2021
К расчету поля конечного магнитного цилиндра с внутренним соосным цилиндрическим...
15
2
4t
где
λ
(t)
:=
;
δz и δφ — полушаги разбиения по полярным координатам z и φ на поверхностях
2
2
4t
+δ
z
S1 и S4 (могут отличаться для разных поверхностей в силу выбора); F(φ, λ) — неполный эллипти-
ческий интеграл первого рода:
ϕ
dτ
F
(
ϕ,λ
)
:=
∫
2
2
0
1-λ
sin
τ
(i,i)
Далее
A
=
0
для всех значений m и k при i = 2, 3, 5, 6.
mk
После того, как решение системы найдено, находим напряженность результирующего поля.
Выражение для вектора H(r) записываем исходя из (2):
3
N
i
6
N
i
µ-1
dS′
µ-µ
dS′
0
Ω
im
d
Ω
im
H r)
=
H r)−
H
(
r
)
∇
+
H
(
r
)
∇
,
(8)
∑∑
n
i
im
∫
∑∑
n
i
im
∫
4π
i=1
m=1
S
r r′
4πµ
d i=4
m=1
S
r-r′
im
im
где
r∈Ω\{SS
}
d
3. ЧИСЛЕННОЕ РЕШЕНИЕ
Вышеописанный алгоритм был запрограммирован на языке FORTRAN. Для решения системы
линейных алгебраических уравнений была использована зарекомендовавшая себя стандартная
программа из [7] с оценкой числа обусловленности матрицы системы. Матричные элементы (7)
вычислялись описанным в предыдущем пункте способом. На основе (8) были записаны интеграль-
ные выражения для вычисления полярных и декартовых компонент результирующего поля, при
этом интегралы по фрагментам разбиений вычислялись с помощью формулы о среднем значении
двойного интеграла. Величины размерности длины были нормированы к диаметру большого
цилиндра, полевые величины на рисунках — к модулю вектора напряженности постоянного внеш-
него поля. Заметим, что алгоритм можно использовать и в случае, если внешнее поле зависит от
координат, но мы не рассматривали примеры, отвечающие этой возможности.
Вообще говоря, всякий алгоритм численного решения должен быть протестирован на предмет
теоретической достоверности и на предмет точности решения. Сеточные методы, к которым относится
и используемый в настоящей работе, весьма громоздки. Поскольку аналитическая работа минимальна
и приближения принимаются на стадии записи уравнений, точность таких методов невысока и, как
правило, ее трудно оценить заранее — только в ходе численных экспериментов можно составить пони-
мание о ее количественном значении. Тестирование на достоверность и точность осуществлялось как
при решении системы, так и при вычислении компонент результирующего поля.
Конфигурация элементов разбиения и их размеры устанавливались согласно результатам,
полученным в работе [1]. Дополнительные проверки, выполненные уже с помощью новой про-
граммы, подтверждают возможность использования рекомендаций из [1]. С увеличением плотно-
сти разбиения растет количество стабильных значащих цифр решения: в нашем случае в зависи-
мости от выбранных параметров оно невелико — колеблется от двух до четырех. Однако суще-
ствует порог, при переходе через который рост числа стабильных цифр приостанавливается. При
этом матричные элементы уменьшаются в абсолютном значении, что приводит к увеличению
числа обусловленности матрицы системы, и на выходе после длительных расчетов получаем
результат сомнительной точности. Здесь необходимо соблюсти меру, которая устанавливается в
результате многих численных экспериментов.
Наиболее подходящими оказываются разбиения, в которых на единицу длины приходится от
10 до 15 точек. Дефект можно разбить плотнее. Так, чаще, если не оговорено особо, принимаем
для основного цилиндра с радиусом ρ0 = 0,5 и высотой h1 + h2 от 3,0 до 6,0 сетку на поверхности
S1, в которой от 40 до 60 точек по оси 0z, столько же точек по окружности. Разбиение граней S2 и
S3 производилось окружностями и лучами: при указанных параметрах была принята сетка с тем
же числом лучей, что и для S1 и с числом дуг от 10 до 20. При этом на компьютере со скромными
возможностями программа работает от пяти до двадцати минут.
В нашем случае для проверки результатов использованы следующие эталоны.
1) Задача о бесконечной магнитной трубе, такой, где xd = 0; если внешнее намагничивающее
поле абсолютной величины H0 направлено вдоль оси 0x, то тогда в принятых обозначениях нор-
мальные составляющие на цилиндрических поверхностях изнутри области S1 имеют вид:
Дефектоскопия
№ 7
2021
16
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
2
2
1−χ
λ
2µ
1−χ
S
1
d
S
1
d
H
(
ρ
,ϕ
)
=
⋅
cosϕ
и
H
(
ρ
,ϕ
)
=
cosϕ,
(9)
ρ
0
2
ρ
d
2
µ+1 1− χχ
λ
µ+µ
1− χχ
λ
d
d
d
а компоненты результирующего поля вне трубы выражаются формулами:
2
2
χ-χ
λ
ρ
0
d
0
H
(
ρ,ϕ
)
=
H
1+
cosϕ;
ρ
2
1− χχ
λ
ρ
d
(10)
2
2
χ-χ
λ
ρ
0
d
0
H
(
ρ,ϕ
)
=
H
-1+
sinϕ,
ϕ
2
1− χχ
λ
ρ
d
где λ := ρd /ρ0.
2) Задача о бесконечном магнитном цилиндре с несоосным, также бесконечным цилиндриче-
ским дефектом. Устойчивый алгоритм ее решения, допускающий получение результата с заведомо
большим числом верных значащих цифр, нежели в настоящей работе, представлен в [8], он ранее
был нами запрограммирован, и теперь мы обращаемся к этой программе для уяснения соответ-
ствий с новой задачей. В качестве теста можно использовать и результаты точного решения этой
же задачи, полученные в биполярной системе координат [9].
3) Задача о конечном магнитном цилиндре без дефекта [1]. Это более слабый эталон, посколь-
ку точность решения в данном случае сопоставима с таковой для настоящей задачи о конечном
цилиндре с дефектом.
Для сравнения с решением задачи 1 для бесконечной трубы были проведены расчеты при раз-
личных значениях параметров h1 и h2, при этом размеры дефекта выбирались таким образом,
чтобы имитировать фрагмент бесконечной трубы. При проведении численных экспериментов мы
интересовались значением нормальной составляющей (т.е. результатом решения системы (6)) на
поверхностях раздела вблизи плоскости z = 0. Также сверялись и значения компонент результиру-
ющего поля при z = 0. Была обнаружена устойчивая сходимость результатов численного решения
к аналитическому при увеличении длин внешнего и внутреннего цилиндров.
Были выполнены и многочисленные сверки с решением задачи 2, в ходе которых проявилась
устойчивая сходимость к аналитическому решению в широком диапазоне изменения параметров
задачи. По результатам численных экспериментов оказалось возможным сделать следующие выво-
ды. Первый — о целесообразности применения бесконечных моделей дефектных тел: такие зада-
чи при определенных постановках могут быть решены либо точно, либо полу-аналитически. Если
высота цилиндра сравнима с его утроенным диаметром, уже можно рассматривать тело как нео-
граниченное. Далее, выполненные сравнения с эталонными задачами дают возможность заклю-
чить, что относительная ошибка расчетов по программе настоящей работы не превышает 2 % —
это не окончательный вывод, его нельзя сделать, опираясь на частный результат, это лишь некото-
рое указание.
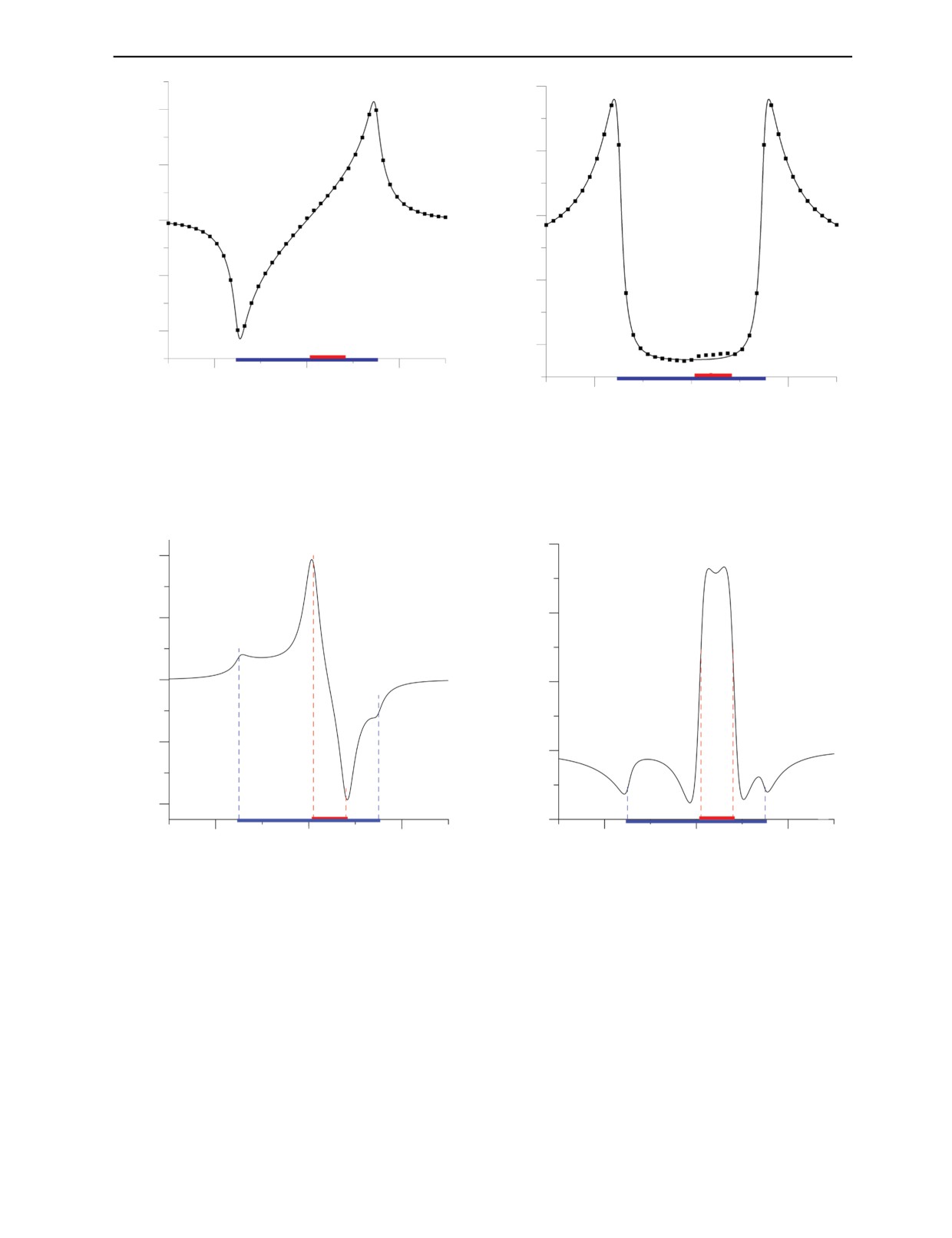
Обратимся к рис. 3 и 4, на которых соответственно изображены графики функций Hρ(φ, z)
и Hz(φ, z), построенные при φ = const и при условии намагничивания постоянным полем,
направленным вдоль оси 0z: на обоих рисунках непрерывные линии соответствуют цилиндру
без дефекта, а точки выставлены по результатам расчета по программе для цилиндра с дефек-
том. На оси абсцисс синим выделена зона протяженности большого цилиндра, а красным —
зона протяженности внутреннего дефекта. Если рис. 4 показывает, как дефект вносит видимые
изменения в кривую Hz(φ, z), то по рис. 3 обнаружить наличие дефекта непросто. Изменяя
значение параметров задачи, можно добиться более явного влияния дефекта на эти и иные
зависимости.
Для прояснения приведем аналогичные зависимости для так называемого «поля дефекта»,
вычисляемого по формуле:
цил. с деф.
цил. без деф.
Hдеф(r) = H
(r)- H
(r).
деф
На рис. 5 и рис. 6 даны зависимости H
(
ϕ,z)
и
Hдеф ϕ
z
)
, построенные при φ = const и при
ρ
z
тех же исходных данных, что и зависимости на двух предыдущих рисунках. Компоненты поля
дефекта сохраняют память о том большом цилиндре, в котором находится дефект, она выражается
в виде локальных экстремумов в зоне торцов большого цилиндра.
Дефектоскопия
№ 7
2021
К расчету поля конечного магнитного цилиндра с внутренним соосным цилиндрическим...
17
2
2
1,6
1
0
1,2
-1
0,8
-2
Дефект
0,4
z
Большой цилиндр
Дефект
z
-2
0
2
Большой цилиндр
-2
0
2
Рис. 3. Зависимость ρ-компоненты результирующего поля
Рис. 4. Зависимость z-компоненты результирующего поля
от координаты z на расстоянии ρ = 0,6 от оси большого
от координаты z на расстоянии ρ = 0,6 от оси большого
цилиндра при H0 = (0, 0, H0). Непрерывная линия — для
цилиндра при H0 = (0, 0, H0). Непрерывная линия — для
конечного цилиндра без дефекта, точки — для такого же
конечного цилиндра без дефекта, точки — для такого же
цилиндра с дефектом. Параметры расчета: μ=100; μd = 10;
цилиндра с дефектом. Параметры расчета: μ=100; μd = 10;
h1 = h2 = 1,5; h3 = 0,1; h4 = 0,8; ρ0 = 0,5; ρd = 0,15; xd = 0,3.
h1 = h2 = 1,5; h3 = 0,1; h4 = 0,8; ρ0 = 0,5; ρd = 0,15; xd = 0,3.
0,03
0,04
0,02
0,02
0
0,01
-0,02
0
-0,04
Дефект
z
Дефект
z
–0,01
Большой цилиндр
Большой цилиндр
-2
0
2
-2
0
2
Рис. 5. Зависимость ρ-компоненты поля дефекта от
Рис. 6. Зависимость z-компоненты поля дефекта от
координаты z на расстоянии ρ = 0,6 от оси большого
координаты z на расстоянии ρ = 0,6 от оси большого
цилиндра при H0 = (0, 0, H0); μ = 100; μd = 10; h1 = h2 = 1,5;
цилиндра при H0 = (0, 0, H0); μ = 100; μd = 10;
h3 = 0,1; h4 = 0,8; ρ0 = 0,5; ρd = 0,15; xd = 0,3.
h1 = h2 = 1,5; h3 = 0,1; h4 = 0,8; ρ0 = 0,5; ρd = 0,15; xd = 0,3.
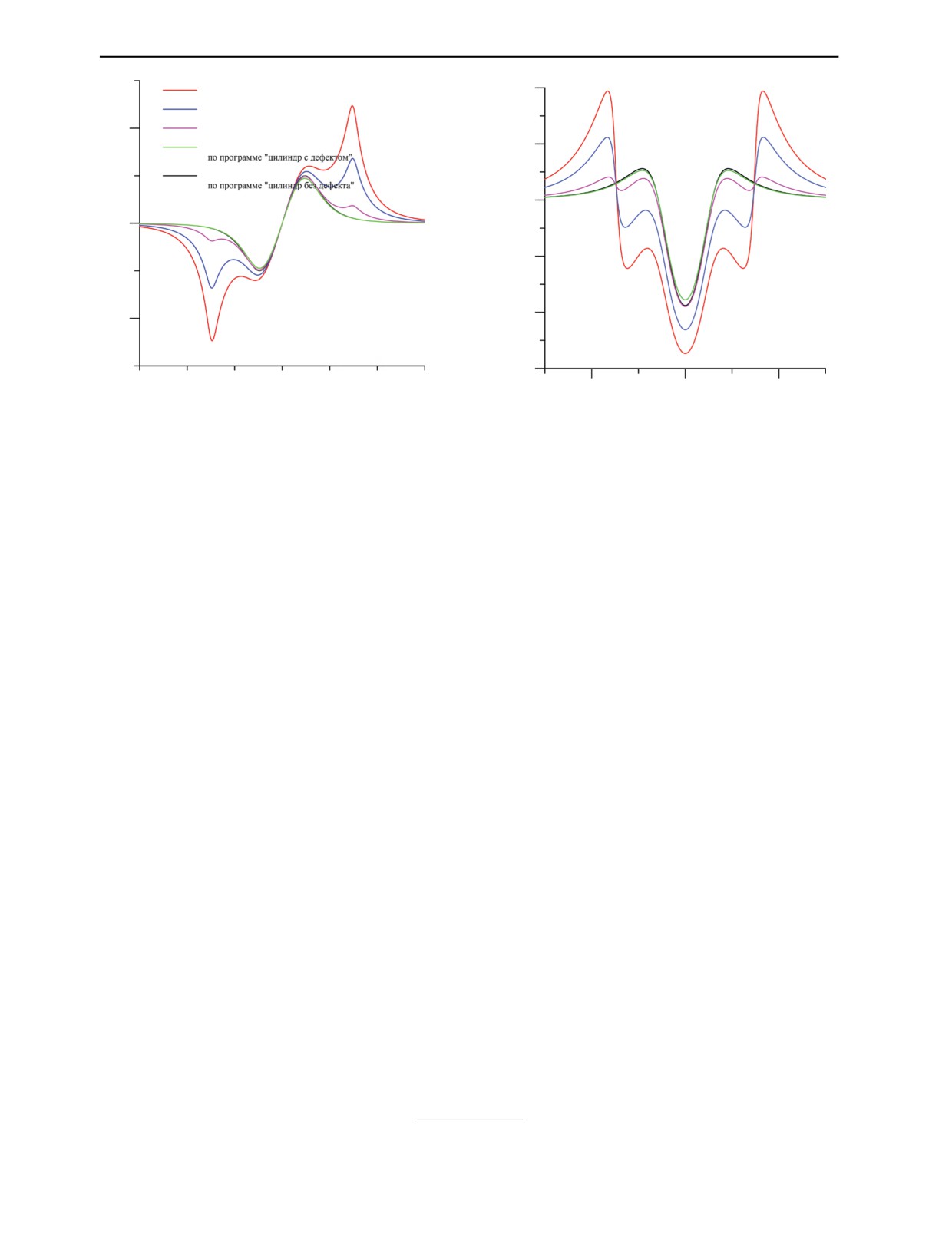
Для дополнительной проверки качества новой программы был проведен численный экспери-
мент, по результатам которого можно было наблюдать, как изменяется результирующее поле при
«исчезновении» большого цилиндра как магнетика, которое достигалось путем последовательного
сведения магнитной проницаемости μ к единице. На рис. 7 и 8 соответственно даны построенные
0
0
при
H
=
0,0, H
и при φ = const кривые зависимостей H (ϕ , z)ρ и
H ϕ
z
)
как иллюстрации к
(
)
z
данному эксперименту: цветные линии отвечают расчетам по программе «цилиндр с дефектом», а
черная линия отвечает расчету по программе «цилиндр без дефекта», выполненному для малого
цилиндра. Расхождение между черной и зеленой линиями отражает снижение точности вычисле-
ний по новой программе при μ = 1, что подтверждалось и значительным увеличением числа обу-
словленности матрицы системы линейных алгебраических уравнений. Тем не менее, результат
такого предельного перехода можно считать вполне удовлетворительным.
Дефектоскопия
№ 7
2021
18
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
μ = 2
1,1
μ = 1,5
0,2
μ = 1,1
μ = 1
1,05
μ = 1
1
0
0,95
0,9
-0,2
z
z
0,85
-2
0
2
-2
0
2
Рис. 7. Зависимость ρ-компоненты результирующего поля
Рис. 8. Зависимость z-компоненты результирующего поля
от координаты z при H0 = (0, 0, H0); μd = 20; h1 = h2 = 1,5;
от координаты z при H0
=
(0,
0, H0); μd =
20;
h
= -0,5 и h4 = 0,5; ρ0 = 0,5; ρd = 0,15; xd = 0.
h1 = h2 = 1,5; h3 = -0,5 и h4 = 0,5; ρ0 = 0,5; ρd = 0,15; xd = 0.
3
По результатам расчетов были построены многочисленные зависимости, отражающие влияние
изменений параметров задачи на окончательный результат. Мы не стали помещать в статью, чтобы
не увеличивать ее объем. Если у экспериментаторов возникнет потребность качественной сверки
модельных экспериментов и результатов расчетов, то мы будем рады такому сотрудничеству.
Очевидна необходимость продолжения работы по применению различных подходов к реше-
нию такого рода задач. Таким образом, пополняется библиотека теоретических задач магнитного
контроля. Результаты решения любой из таких задач, в частности, представленной в настоящей
работе, могут быть использованы для качественного сравнения с результатами модельных экспе-
риментов. Кроме того, на основе решения прямых задач возникает перспектива составления оце-
ночных алгоритмов по определению геометрических форм скрытых дефектов и их численных
характеристик.
Работа выполнена в рамках бюджетной темы «Электрон».
СПИСОК ЛИТЕРАТУРЫ
1. Dyakin V.V., Kudryashova O.V. To the Calculation of the Field of a Finite Magnetic Cylinder // Russian
Journal of Nondestructive Testing. 2019. V. 55. No. 10. P. 734—745. [Дякин В.В., Кудряшова О.В.,
Раевский В.Я. К расчету поля конечного магнитного цилиндра. Дефектоскопия. 2019. № 10. С. 24—34.]
2. Хижняк Н.А. Интегральные уравнения макроскопической электродинамики. Киев: Наукова
думка, 1986. 278 с.
3. Дякин В.В. Математические основы классической магнитостатики. Екатеринбург: РИО УрО РАН,
2016. 404 с.
4. Дякин В.В., Кудряшова О.В., Раевский В.Я. Один подход к численному решению основного урав-
нения магнитостатики для конечного цилиндра в произвольном внешнем поле // Дефектоскопия. 2021.
№ 4. С. 22—34.
5. Дякин В.В., Раевский В.Я., Кудряшова О.В. Дефект в шаре // Дефектоскопия. 2009. № 9. С. 16—30.
6. Михлин С.Г. Курс математической физики. М.: Наука, 1968. 575 с.
7. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений.
М.: Мир, 1980. 277с.
8. Дякин В.В., Кудряшова О.В. Дефект в цилиндре // Дефектоскопия. 2012. № 4. С. 41—55.
9. Дякин В.В., Кудряшова О.В., Раевский В.Я. Точное решение одной задачи магнитостатики в бипо-
лярных координатах (продолжение) // Дефектоскопия. 2016. № 7. С. 48—58.
Дефектоскопия
№ 7
2021