УДК 620.179.152.1

ТРЕХМЕРНАЯ РЕНТГЕНОВСКАЯ ТОМОГРАФИЯ ПРОМЫШЛЕННЫХ

ОБЪЕКТОВ ПРИ ОГРАНИЧЕННЫХ РАЗМЕРАХ РЕГИСТРИРУЮЩЕГО ЭКРАНА

А.А. Скоков^1,****

¹Федеральный научно-производственный центр «Алтай»,

Россия 659322 Бийск, ул. Социалистическая, 1

E-mail: ^*kar@frpc.secna.ru; ^**post@@frpc.secna.ru; ^***ohotnikovsan@mail.ru;

^****skeydee@yandexd.ru

Поступила в редакцию 29.04.2021; после доработки 14.07.2021

Принята к публикации 29.07.2021

Исследованы возможности применения 3D-томографа с ограниченным в размерах регистрирующим экраном для

выявления произвольно ориентированных трещиноподобных дефектов в крупногабаритных промышленных объектах.

Рассмотрены круговая и спиральная схемы сканирования, показана принципиальная возможность обнаружения дефек-

тов в случае двухзаходного спирального сканирования и регистрирующего экрана, перекрывающего половину поля зре-

ния поперечного сечения объекта контроля. Продемонстрирована работоспособность алгоритма 3D-реконструкции для

выбранного способа сканирования.

Ключевые слова: неразрушающий контроль, 3D-томография, трещиноподобные дефекты, крупногабаритный объект,

экран ограниченных размеров.

DOI: 10.31857/S0130308221090062

ВВЕДЕНИЕ

Рентгеновская компьютерная томография значительно превосходит по информативности тра-

диционные рентгеновские методы, такие как радиография и интроскопия. Современные промыш-

ленные объекты становятся все более сложными, возрастают требования к их надежности и долго-

вечности, поэтому и возникает необходимость в более тщательном неразрушающем контроле.

Основные требования, предъявляемые к средствам и методам контроля, заключаются в обе-

спечении надежного обнаружения дефектов в виде раковин, трещин, расслоений, пористости, ва-

риаций плотности. Посредством томографии можно выявлять эти дефекты с высокой чувствитель-

ностью. Кроме того, томография позволяет получить трехмерный образ контролируемого объекта,

что дает возможность обнаруживать ошибки сборки, определять практически любые размеры вну-

три изделия, находить отклонения от чертежей.

В радиационной дефектоскопии всегда считалось проблематичным обнаружение таких «тон-

ких» дефектов, как трещина или отслоение. Для их выявления требуется подходящая схема про-

свечивания, а именно, излучение должно распространяться вдоль плоскости трещины. Если ори-

ентацию искомого отслоения можно предвидеть, зная конструкцию изделия, то ориентация тре-

щины зачастую непредсказуема. Поэтому в традиционных методах применяют просвечивание в

нескольких ракурсах. Такая процедура увеличивает вероятность обнаружения трещин, но при этом

и вероятность ее пропуска остается значительной.

В трехмерной рентгеновской компьютерной томографии с конусным пучком излучения задача

выявления произвольно ориентированных трещин решается более успешно благодаря тому, что в

процессе сканирования просвечивание проводится по очень большому количеству ракурсов.

В данной работе рассматриваются задачи конусной томографии протяженных объектов, таких

как, например, балластные трубы, изделия ракетно-космической и авиационной техники, двига-

тели внутреннего сгорания и др., которые не могут поместиться целиком в поле зрения плоско-

го детектора. Работа посвящена исследованию применения известных методов сканирования и

алгоритмов, не рассматриваются другие не менее важные проблемы для конусной томографии с

экраном ограниченных размеров, такие как подавление влияния рассеянного излучения, «сшивка»

радиационных изображений и др.

СКАНИРОВАНИЕ И АЛГОРИТМЫ

В рентгеновской конусной томографии источник и детектирующий экран обычно жестко свя-

заны между собой и перемещаются относительно объекта, причем двигаться могут либо источник

Трехмерная рентгеновская томография промышленных объектов...

с детектором, либо объект, либо совместно. Для удобства рассуждений обычно полагают, что объ-

ект неподвижен, а источник и экран перемещаются по определенной траектории. Теоретически

для точной реконструкции должно выполняться условие полноты Кириллова—Туя [1, 2], согласно

которому всякая плоскость, пересекающая объект, должна пересекать траекторию источника из-

лучения.

Благодаря этому требованию к системе сканирования возможна реконструкция без артефактов.

Кроме того, для каждого плоского элемента трещины всегда найдется такой ракурс, когда излу-

чение будет распространяться вдоль него, и, следовательно, он будет зарегистрирован на экране

с максимальным значением сигнала. Под элементом трещины подразумевается достаточно малая

часть ее, которую можно считать плоской. Таким образом, корректное сканирование в конусной

томографии является максимально эффективным для регистрации произвольно ориентированных

трещин еще на этапе получения данных просвечивания, т.е. до процедуры трехмерной реконструк-

ции. Разумеется, сигнал от трещины может быть ненаблюдаем в том случае, когда ее раскрытие

ниже предела чувствительности регистрирующей аппаратуры.

Зачастую 3D-реконструкция предполагает вычисление обратных проекций путем фильтрации

исходных данных с последующим их суммированием. Если сигнал от трещины зарегистрирован

на нескольких конусных проекциях, то в результате суммирования сигнал накапливается интенсив-

нее, чем шум, и вероятность обнаружения трещины увеличивается.

В технических приложениях конусная томография реализуется с помощью прецизионного

сканера, источника рентгеновского излучения и регистрирующего экрана, например, панельного

детектора. Траекторию источника, удовлетворяющую условию полноты, выполнить достаточно

просто, например, сканированием по спирали. Трехмерная томография небольших объектов, для

которых любое рентгеновское изображение умещается на детектирующем экране, представлена в

литературе достаточно обширно [3—6].

Томография крупногабаритных объектов освещена в литературе значительно меньше. В работе [7]

представлены результаты использования компьютерного томографа на основе линейного ускорителя

электронов фирмы LINAC, имеющего энергию рентгеновского излучения 4,6—9 МэВ и позволяюще-

го контролировать объекты толщиной до 200 мм по стали. В [8] описан инспекционно-досмотровый

комплекс на основе бетатрона с энергией излучения 4—9 МэВ и мощностью дозы на расстоянии 1 м

до 13 Р/мин.

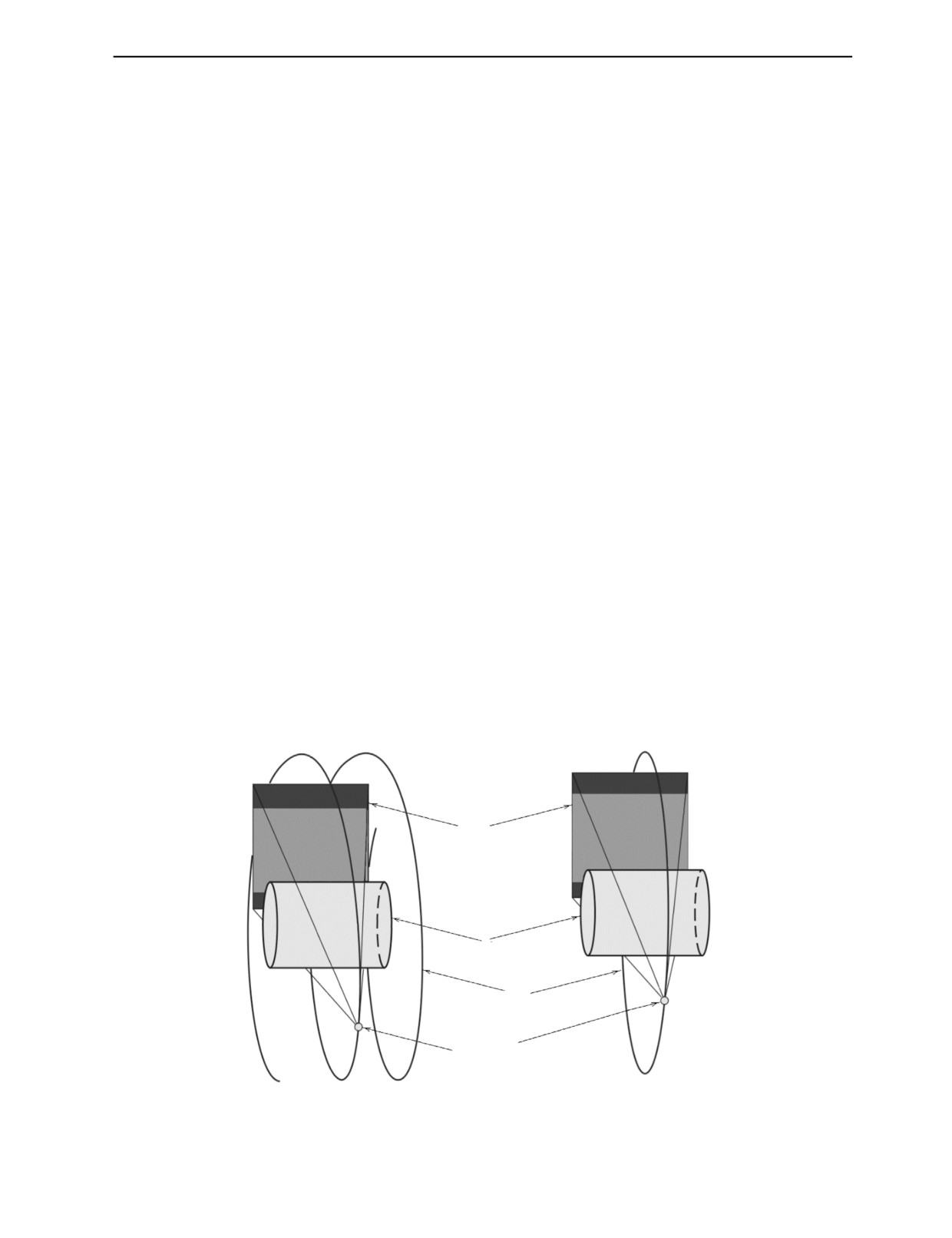
В промышленных томографах наиболее популярны схемы сканирования по круговой и спи-

ральной траекториям (рис. 1). Если экран недостаточно велик для охвата поперечного сечения объ-

екта, то этого можно добиться путем многозаходного сканирования по одной и той же траектории,

перемещая всякий раз детектор таким образом, чтобы в итоге было перекрыто все сечение (рис. 2).

Панельный

детектор

Томографируемый

объект

Траектория источника

излучения

Источник

излучения

Рис. 1. Схемы сканирования с неполным охватом объекта вдоль оси вращения:

а — спиральная траектория; б — круговая.

Дефектоскопия

№ 9

2021

В.П. Карих, Б.В. Певченко, А.В. Курбатов и др.

Панельный

детектор

Источник

излучения

Томографируемый

объект

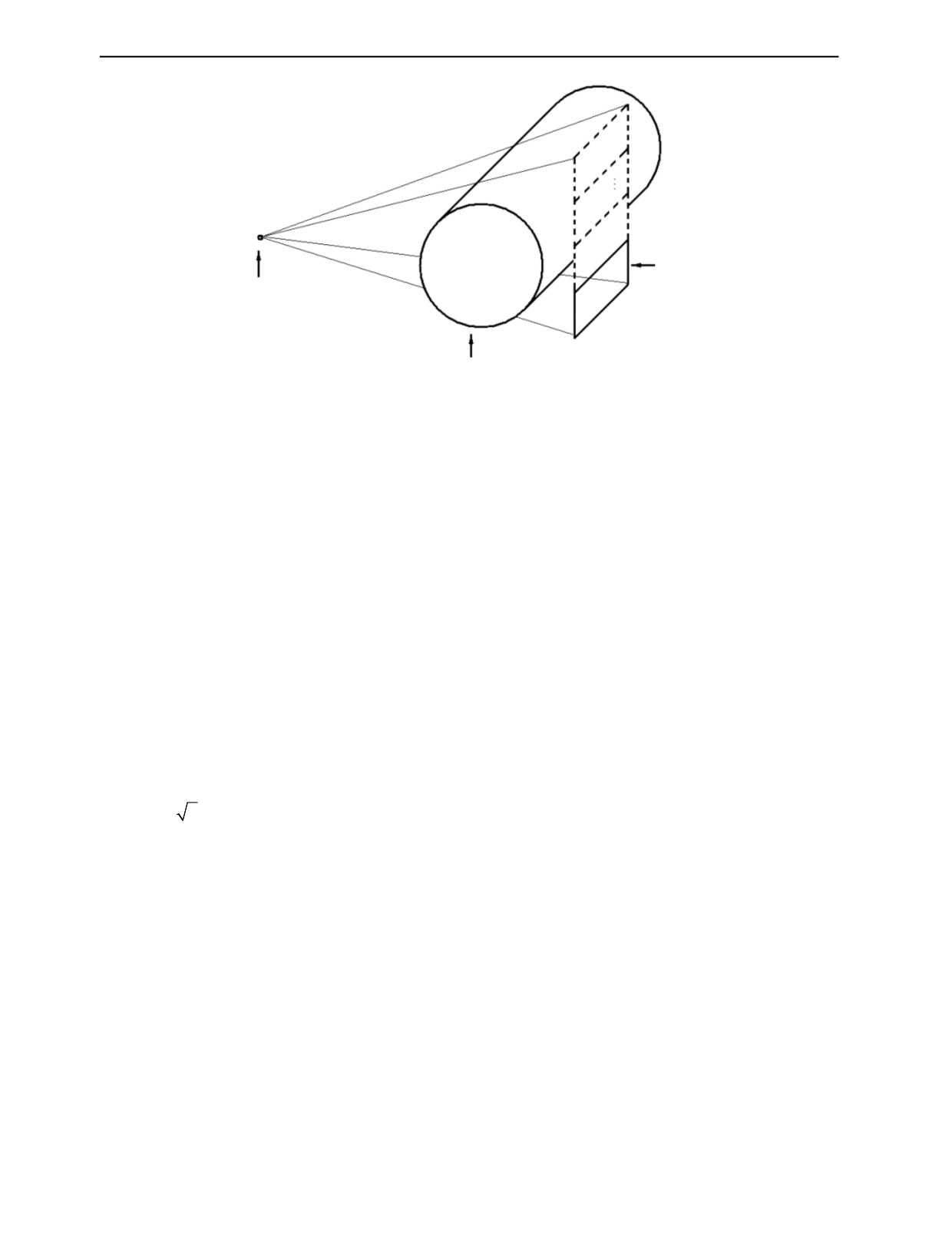
Рис. 2. Полная проекция, получаемая многозаходным сканированием с перемещением панельного детектора

(1, 2, … , n — расположения детектора в различных циклах сканирования по одной и той же траектории).

При спиральном сканировании можно проконтролировать весь объект в непрерывном ре-

жиме. В случае круговой траектории за один цикл перемещения по окружности контролируется

часть объекта. Смещая после каждого кругового цикла траекторию вдоль оси вращения, можно

проконтролировать весь объект. Рассмотрим подробнее вариант спирального сканирования с

экраном, ограниченным в направлении оси спирали, но перекрывающим поперечное сечение

объекта. Согласно строгой теории, в данном случае можно получить точную 3D-реконструкцию

объекта [9]. Следует отметить, что при этом для выявления элементов трещин произвольной

ориентации накладываются определенные условия на диаметр и шаг спирали в зависимости

от ширины экрана. При соблюдении данных условий для любого элемента трещины найдется

такое положение источника, когда излучение будет распространяться вдоль него и будет заре-

гистрировано на экране.

Известно частное решение, которое позволяет зарегистрировать произвольно ориентиро-

ванный элемент трещины при сканировании по спиральной траектории при ограниченном в

поперечном направлении конусном пучке [10]. В работе показано, что для любой точки плоско-

сти объекта, перпендикулярной оси спирали, для регистрации произвольно ориентированного

элемента трещины достаточно данных от одного витка спирали, расположенного симметрично

относительно выбранной плоскости. При этом радиус спирали должен превышать радиус ци-

линдра в

2 . Условие выявляемости выполняется и для другой плоскости, расположенной на

малом расстоянии и параллельно рассмотренной. Для ее реконструкции достаточно данных

почти от того же витка, укороченного с одной стороны и добавленного с другой. Трехмерная

реконструкция производится в последовательности плоскость за плоскостью, при этом исход-

ные данные выбираются из витка спирали, который располагается так, чтобы реконструируе-

мая плоскость делила его пополам.

Высота экрана а и ширина b определяются из следующего условия: реконструируемый круг

из каждого положения источника на витке спирали должен целиком проецироваться на экран (по-

добнее см. в [10]).

Сканирование по круговой траектории не дает такой возможности выявления произвольного

элемента трещины, как при спиральном сканировании. Можно подсчитать, какая часть элементов

трещин при круговом сканировании не выявляется. Полагаем, что объект вписывается в цилиндр с

радиусом r и длиной l. На рис. 3 иллюстрируется объем объекта, который контролируется при вы-

полнении одного цикла сканирования по окружности.

Поместим произвольный элемент трещины в какую-либо точку рассматриваемого объема и

определим, выявляется ли он в результате кругового сканирования. Полагаем, что элемент тре-

щины определяется координатами x, y, z расположения его центра и единичным вектором n, пер-

пендикулярным его плоскости. Определим функцию P(x, y, z, n) следующим образом: она равна

Дефектоскопия

№ 9

2021

Трехмерная рентгеновская томография промышленных объектов...

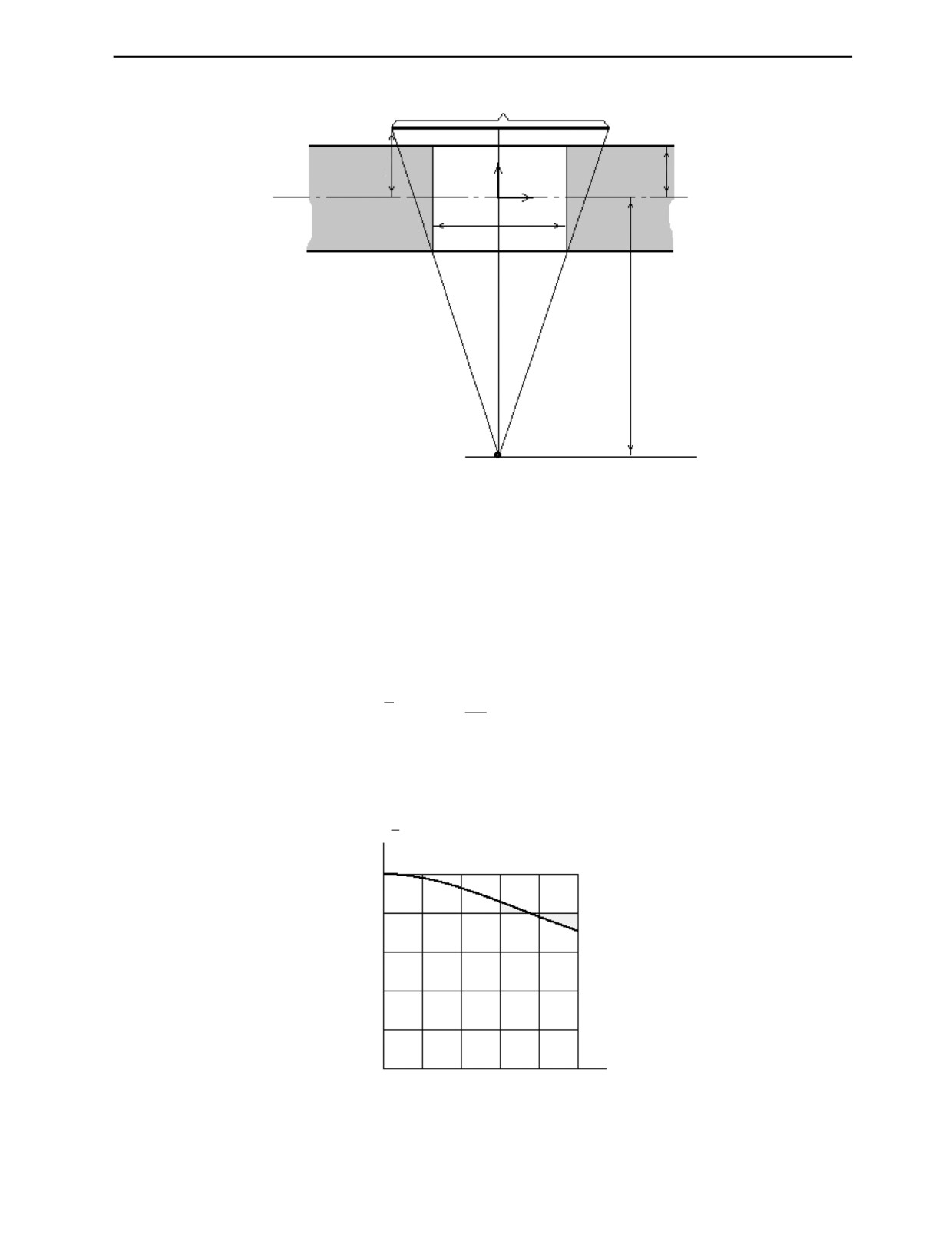
Рис. 3. Область томографирования при одном цикле кругового сканирования — цилиндр длиной l = b(R - r)/(R + d), где

b — размер панельного экрана в направлении оси вращения, R — расстояние от оси вращения до источника излучения,

r — диаметр цилиндра, в который вписывается объект, d — расстояние от оси вращения до панельного экрана.

единице, если плоскость, проходящая через точку x, y, z и перпендикулярная вектору n, пересе-

кает траекторию источника (окружность) и равна нулю в противном случае. Следовательно, если

P(x, y, z, n) = 1, то элемент трещины, перпендикулярный вектору n и расположенный в точке x, y, z,

выявляется при сканировании по траектории и не выявляется, если P(x, y, z, n) = 0. Для того чтобы

определить долю выявляемых элементов трещин в заданной точке объекта, надо выполнить усред-

нение функции P(x, y, z, n) по всем направлениям n:

P x,y,z)

P x,y,z,n)dS

∫

2π

S/2

Здесь интегрирование производится по половине единичной сферы (S/2). На рис. 4 представле-

на зависимость функции P от удаления от плоскости орбиты источника.

P (0, 0, z)

0,8

0,6

0,4

0,2

0,4

0,6

0,8

1 z/R

Рис. 4. Вероятность выявления произвольно ориентированного элемента трещины в зависимости от расстояния z от пло-

скости круговой траектории источника.

Дефектоскопия

№ 9

2021

В.П. Карих, Б.В. Певченко, А.В. Курбатов и др.

Согласно приведенным данным, при круговом сканировании возможен с достаточно большой

вероятностью (до 10 %) пропуск элемента трещины из-за того, что направление излучения не по-

падает в плоскость этого элемента, чего не происходит при спиральном сканировании.

Для 3D-реконструкции в конусной томографии наиболее популярны алгоритмы Фельдкампа и

обратного проецирования с фильтрацией двойным дифференцированием (ОПФДД). Результаты их

применения для спиральной и круговой траекторий с ограниченным экраном достаточно подробно

рассмотрены в работе [11].

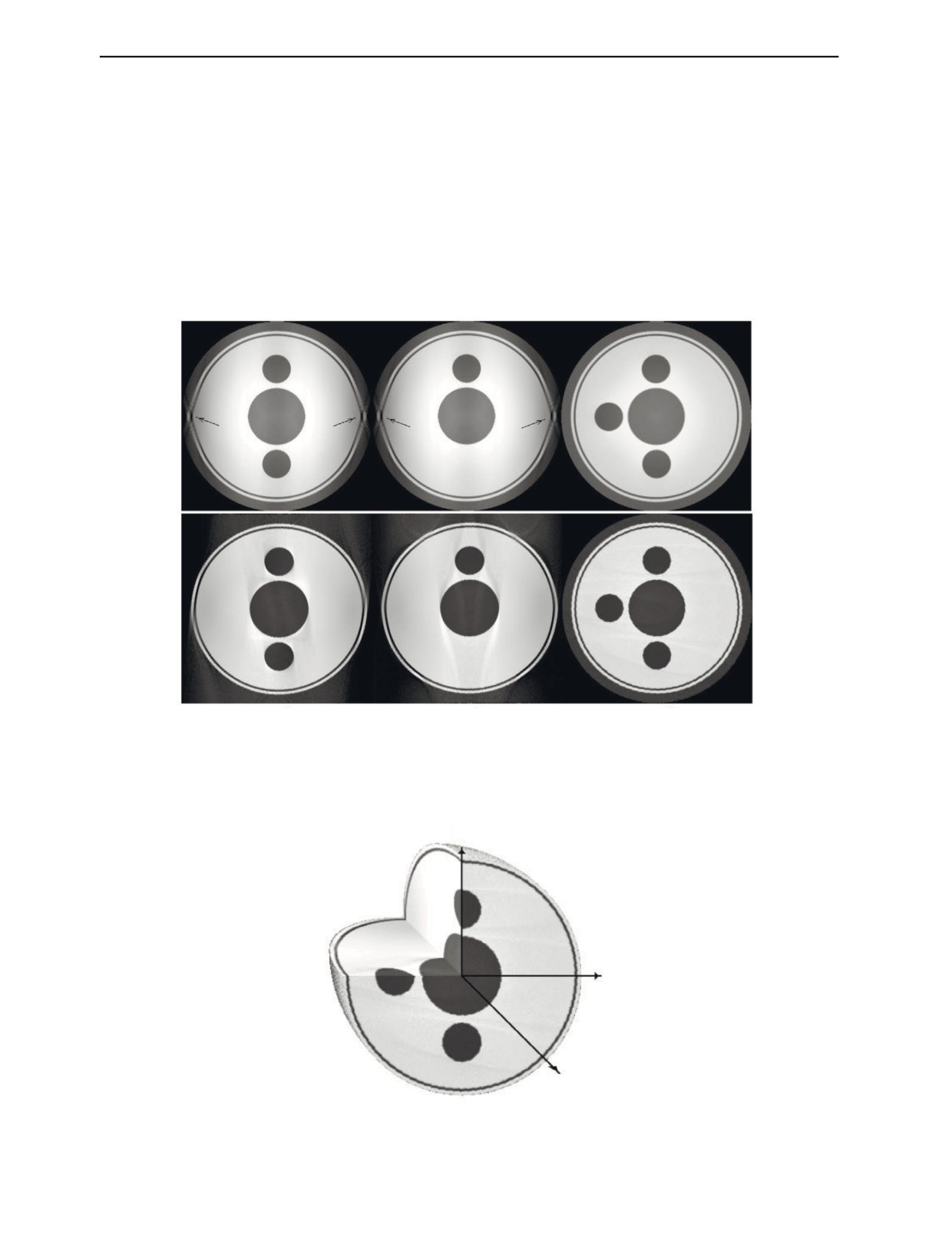
Отличие результатов реконструкции алгоритмом Фельдкампа для круговой и спиральной тра-

екторий показаны на рис. 5. Здесь приведены изображения срезов для трех плоскостей объекта,

изображенного на рис. 6. В случае круговой траектории наблюдаются значительные артефакты в

областях, отстоящих на большом расстоянии от центральной плоскости пучка (плоскость z = 0),

что согласуется с неполнотой данных (см. рис. 4).

х = 0

у = 0

z = 0

Рис. 5. Сечения в плоскостях х = 0, у = 0 и z = 0, полученные в результате реконструкции алгоритмом Фельдкампа для

круговой (вверху) и спиральной (внизу) траекторий; стрелками помечены наиболее заметные артефакты.

Рис. 6. Реконструируемый объект и координатные оси.

Дефектоскопия

№ 9

2021

Трехмерная рентгеновская томография промышленных объектов...

ВАРИАНТЫ КОНТРОЛЯ КРУПНОГАБАРИТНЫХ ОБЪЕКТОВ

Рассмотрим особенности 3D-томографического контроля различных промышленных объектов.

Если габариты объекта не велики, то его контроль может быть осуществлен посредством спираль-

ного сканирования с вертикальным расположением оси вращения. Если же объект является про-

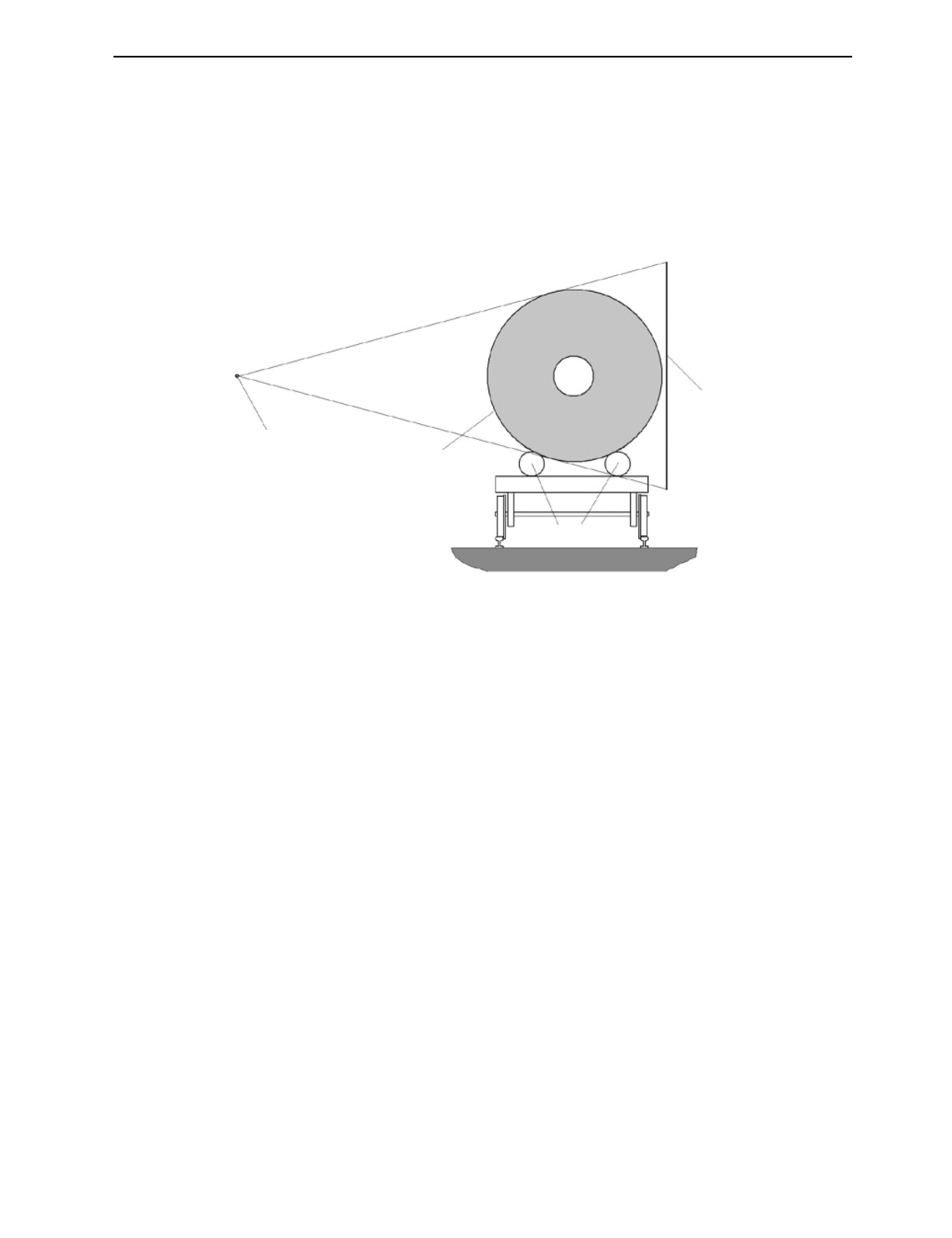
тяженным (несколько метров), то его зачастую удобнее располагать горизонтально. В этом случае

в поле регистрируемого излучения могут попадать элементы сканера, на котором вращается кон-

тролируемое изделие (рис. 7).

Экран

Источник излучения

Изделие

Валки

Рис. 7. Влияние элементов сканера на исходные данные на горизонтальном сканере.

Для устранения влияния конструктивных элементов сканера можно применить схему скани-

рования с половинным полем облучения, когда экран регистрирует излучение, проходящее лишь

выше оси вращения.

В двумерном случае схема сканирования с половинным полем облучения удовлетворяет ус-

ловию полноты. В трехмерном случае аналогичное утверждение неочевидно. Проверку полноты

данных можно выполнить путем компьютерного моделирования. Для этого потребуется рассмо-

треть всевозможные элементы трещин, которые могут находиться в объекте контроля и прове-

рить, какая часть из них будет зарегистрирована верхней половиной экрана, изображенного на

рис. 7.

Одно из преимуществ спиральной траектории, среди прочих, заключается в том, что для до-

казательства условия выявляемости произвольно ориентированного элемента трещины не нужно

анализировать весь объем объекта, а достаточно рассмотреть лишь одну плоскость, перпендику-

лярную оси спирали. Остальные плоскости, параллельные рассматриваемой, геометрически рав-

ноправны относительно спирали.

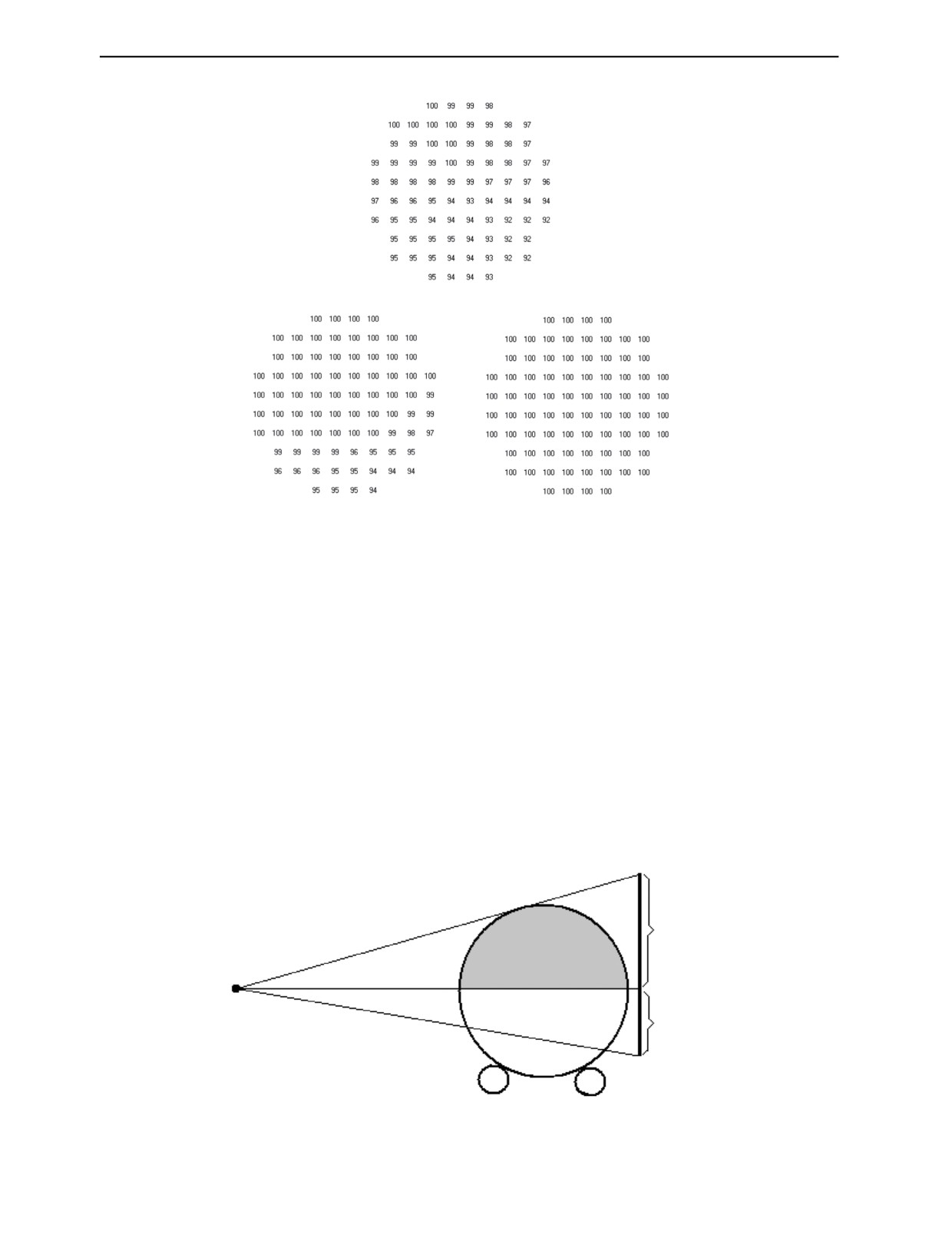
Моделирование показало, что спиральная схема сканирования с половинным экраном не удов-

летворяет условию полноты. Результат моделирования представлен на рис. 8а. Расчеты отобража-

ется в виде таблицы чисел, соответствующих долям регистрируемых элементов трещин в процен-

тах. Расчеты выполнены для ряда точек сечения цилиндра единичного радиуса. В рассматриваемом

примере радиус спиральной траектории R = 3, шаг спирали h = 1, высота экрана равна половине

требуемой величины (0,5 а).

Согласно расчетам, доля регистрируемых элементов трещин достаточно велика. Назовем эту

долю показателем условия полноты.

Повысить показатель условия полноты можно различными способами, например, увеличением

высоты экрана. Возьмем экран, который перекрывает не половину сечения изделия, а более, но на-

столько, что при этом на экран не попадают изображения элементов сканера (рис. 9).

Результаты моделирования показателя условия полноты для экрана высотой 0,75 а (более по-

ловины) представлены на рис. 8б.

Дефектоскопия

№ 9

2021

В.П. Карих, Б.В. Певченко, А.В. Курбатов и др.

Рис. 8. Результат расчета условия полноты:

а — для половинного экрана и спиральной схемы сканирования; б — для экрана высотой 0,75а и спиральной схемы

сканирования; в — для половинного экрана и двухзаходной спиральной схемы сканирования.

Здесь мы видим более высокие показатели условия полноты данных.

Еще один из вариантов повышения выявляемости элементов трещин заключается в примене-

нии сканирования многозаходной спиралью. Расчеты показывают, что для двухзаходной спирали

и половины экрана получается 100 % выявления трещин (рис. 8в), что свидетельствует о высокой

эффективности данного метода при использовании половинного экрана.

Обратимся теперь к задаче 3D-реконструкции по тем данным, в которых регистрируются эле-

менты трещин произвольной ориентации. В рассматриваемом случае с половинным охватом по-

перечного сечения объекта двумерным детектором алгоритм Фельдкампа напрямую неприменим,

поскольку часть веерной проекции отсутствует. В данном случае целесообразно использовать ло-

кальный алгоритм ОПФДД. Он достаточно эффективен для решения задач неразрушающего кон-

троля - выявления дефектов в виде раковин, трещин, а также контроля размеров деталей и их

расположения.

a/2

Рис. 9. Экран, перекрывающий более половины сечения изделия.

Дефектоскопия

№ 9

2021

Трехмерная рентгеновская томография промышленных объектов...

На рис. 10 изображены сечения объекта в трех плоскостях, реконструированные методом

ОПФДД для круговой (вверху) и спиральной (внизу) траекторий с экраном, полностью перекры-

вающим поперечное сечение объекта в плоскости, перпендикулярной оси траектории источни-

ка. Они мало отличаются от изображений, которые получены с помощью алгоритма Фельдкампа

(см. рис. 5). Основное отличие заключается в уменьшенном динамическом диапазоне плотности

и более подчеркнутом изображении границ деталей. В томограммах, полученных при спиральном

сканировании (см. нижний ряд на рис. 10), отсутствуют видимые артефакты.

х = 0

у = 0

z = 0

Рис. 10. Сечения в плоскостях х = 0, у = 0 и z = 0, полученные в результате реконструкции алгоритмом ОПФДД для кру-

говой (вверху) и спиральной (внизу) траекторий; стрелками помечены наиболее заметные артефакты.

х = 0

у = 0

z = 0

Рис. 11. Сечения в плоскостях х = 0, у = 0 и z = 0, полученные в результате реконструкции алгоритмом ОПФДД для спи-

ральной траектории при регистрации данных половиной экрана (а), для спиральной траектории при регистрации данных

экрана высотой 75 % от полного размера (б) и для двухзаходной спиральной траектории при регистрации данных поло-

виной экрана (в); стрелками помечены наиболее заметные артефакты,

Дефектоскопия

№ 9

2021

В.П. Карих, Б.В. Певченко, А.В. Курбатов и др.

В дальнейшем варианты с круговой траекторией для экрана, частично перекрывающего сече-

ние объекта, не рассматриваются.

На рис. 11а представлены томограммы, полученные при использовании экрана, перекрываю-

щего половину сечения объекта. При спиральном сканировании половиной экрана наблюдаются

артефакты, которые маскируют часть границ.

На рис. 11б демонстрируются томограммы, полученные при использовании экрана, перекрыва-

ющего 75 % поперечного сечения объекта. Здесь не наблюдается заметного отличия от использова-

ния половинного экрана при таком же спиральном сканировании.

Значительно лучший результат с половинным экраном получен при сканировании по двухза-

ходной спирали, что подтверждается еще и полнотой данных для обнаружения элементов трещин

(рис. 11в). На изображениях практически отсутствуют артефакты, характерные для предыдущих

вариантов с неполным экраном.

ЗАКЛЮЧЕНИЕ

Рентгеновская 3D-томография обладает возможностью эффективно выявлять трещиноподоб-

ные дефекты произвольной пространственной ориентации еще на этапе получения исходных ра-

диометрических данных.

Для контроля протяженных объектов предложена двухзаходная схема спирального сканирова-

ния с ограниченным экраном и алгоритм реконструкции, которые позволяют также эффективно

выявлять дефекты в виде трещин и расслоений.

СПИСОК ЛИТЕРАТУРЫ

1. Кириллов А.А. Об одной задаче И.М. Гельфанда // ДАН СССР. 1961. Т. 137. № 2. С. 276—277.

2. Tuy H.K. An inversion formula for cone-beam reconstruction // Siam J. Appl. Math. 1983. V. 43. № 3.

Р. 546—552.

3. Lichun J., Mian C. 3D imaging of fractures in carbonate rocks using X-ray computed tomography

technology // Carbonates and Evaporites. 2014. V. 29. Is. 2. P. 147—153.

4. Re F., Scavia C. Determination of contact areas in rock joints by X-ray computer tomography //

International Journal of Rock Mechanics and Mining Sciences. 1999. V. 36. Is. 7.

5. Asskar J.C., Saman S.K. Microstructure characteristics of cement-stabilized sandy soil using nanosilica

// Journal of Rock Mechanics and Geotechnical Engineering. 2017. V. 9. Is. 5.

6. Diaz M., Yeom Kim K., Yeom S., Zhuang L., Min K., Krauß F., Giese R., Alexandrakis C., Buske S. Surface

roughness characterization of open and closed rock joints in deep cores using x-ray computed tomography //

International Journal of Rock Mechanics and Mining Sciences. 2017. V. 98. P. 10—19.

7. Reims N., Schoen T., Boehnel M., Sukowski F., Firsching M. Strategies for efficient scanning and

reconstruction methods on very large objects with high-energy x-ray computed tomography // SPIE Optical

Engineering + Applications. International Society for Optics and Photonics. 2014. P. 921209.

8. Бориков В.Н., Чахлов С.В., Рычков М.М., Штейн А.М., Смолянский В.А. Промышленная томогра-

фия крупногабаритных объектов // XXI Всероссийская конференция по неразрушающему контролю и

технической диагностике: сборник трудов. Москва, 28 февраля — 2 марта 2017 г. М.: Издательский дом

«Спектр», 2017. С. 358—361.

9. Katsevich A. An improved exact filtered backprojection algorithmfor spiral computed tomography //

Advances in Applied Mathematics. October 2004. V. 32. No. 4. P. 681—697.

10. Карих В.П. Способ рентгеновской компьютерной томографии с конусным пучком для неразру-

шающего контроля // Приборы и системы. Управление. Контроль. Диагностика. 2001. № 5. С. 67—70.

11. Скоков А.А., Карих В.П. Повышение выявляемости трещин при дефектоскопии методом трех-

мерной томографии // Дефектоскопия. 2013. № 2. С. 78—89.

Дефектоскопия

№ 9

2021