Радиационные методы
УДК 620.179.15
АЛГОРИТМ ОЦЕНКИ ПОГРЕШНОСТЕЙ ПРИ РАСПОЗНАВАНИИ
МАТЕРИАЛОВ В СИСТЕМЕ РЕНТГЕНОВСКОГО КОНТРОЛЯ, СОДЕРЖАЩЕЙ
СЭНДВИЧ-ДЕТЕКТОРЫ ИЗЛУЧЕНИЯ
© 2022 г. В.А. Удод1,*, С.П. Осипов2,**, С.Ю. Назаренко2
1Томский государственный университет, Россия 634050 Томск, пр. Ленина, 36
2Томский политехнический университет, Россия 634050 Томск, пр. Ленина, 30
E-mail: *pr.udod@mail.ru; **osip1809@rambler.ru
Поступила в редакцию 03.12.2021; после доработки 21.12.2021
Принята к публикации 24.12.2021
Приводится описание предлагаемого нами алгоритма для статистического оценивания погрешности метода дуаль-
ных энергий, порождаемой квантовой природой излучения, применительно к системе рентгеновского контроля, содер-
жащей сэндвич-детекторы. Продемонстрировано его действие на конкретном примере. Даны рекомендации по дальней-
шему использованию алгоритма, в частности, для оптимизации структурных элементов сэндвич-детекторов излучения.
Ключевые слова: рентгеновское излучение, алгоритм, сэндвич-детектор, метод дуальных энергий, распознавание
материалов, атомный номер.
DOI: 10.31857/S0130308222010043
ВВЕДЕНИЕ
Угроза совершения террористических актов послужила основанием к решению проблемы по
созданию комплекса условий для обеспечения транспортной безопасности в сфере авиа и желез-
нодорожных перевозок. Как следствие этого к настоящему времени разработан целый ряд методов
обнаружения опасных грузов и недозволенных вложений. Одним из таких методов является метод
дуальных энергий (МДЭ) [1—6]. Он позволяет распознавать различные материалы по их атомному
номеру (эффективному атомному номеру), на основании чего делается заключение о принадлеж-
ности исследуемого предмета к классу опасных или безопасных предметов [4, 7, 8].
Современные рентгеновские системы, использующие МДЭ при проведении досмотрового кон-
троля, можно условно разделить на несколько основных типов. В системах первого типа объект
контроля (ОК) подвергается просвечиванию два раза — двумя сканирующими пучками излучения
с разными максимальными энергиями (иными словами — при двух разных рабочих напряжениях,
устанавливаемых для генерации рентгеновских лучей на рентгеновской трубке) [4]. При этом мак-
симальные энергии (напряжения) подбирают так, чтобы при первом просвечивании ОК основным
процессом взаимодействия излучения с радиационно-чувствительными элементами детекторов
был фотоэффект, а при втором просвечивании — комптон-эффект. Такую схемную реализацию
МДЭ можно условно назвать традиционной (классической).
В системах второго типа ОК просвечивается один раз, но при этом используется импульсный
источник рентгеновского излучения, который в определенной последовательности создает импуль-
сы с двумя разными максимальными энергиями [9]. Схемную реализацию МДЭ такого вида можно
условно назвать схемой с «дуальным» (биэнергетическим) источником излучения.
В системах третьего типа ОК просвечивается один раз, но при этом для регистрации излучения
используются сэндвич-детекторы. Структурно такие детекторы представляют собой многослойное
образование. Чаще всего это композиция из двух детекторов, которые отстоят друг от друга по ходу
падающего излучения и дополнительно разделены между собой поглотителем (фильтром), который
устанавливается с целью усиления спектральных различий излучения, падающего на первый (по
ходу распространения пучка) и второй детекторы [1, 4, 10—12]. Такую схемную реализацию МДЭ
можно условно назвать схемой с «дуальным» (биэнергетическим) детектором излучения.
Точность (эффективность) МДЭ зависит от множества факторов, в том числе — от шумов вы-
ходных сигналов детекторов, которые вызваны квантовой природой рентгеновского излучения
(квантовые шумы) [1, 4, 12, 13].
В [13] был разработан алгоритм для статистической оценки погрешности МДЭ, обусловленной
квантовыми шумами, применительно к классической схеме реализации МДЭ. В настоящей работе
предложен аналогичный алгоритм, но только применительно к схеме реализации МДЭ на основе
использования сэндвич-детекторов излучения. Насколько нам известно, такие исследования, т.е.
Алгоритм оценки погрешностей при распознавании материалов в системе...
41
разработка указанного алгоритма, в отечественной и зарубежной научно-технической литературе
ранее не проводились.
ОПИСАНИЕ АЛГОРИТМА
Алгоритм представлен последовательностью следующих шагов.
Шаг 1. Задается максимальная энергия E0 квантов, испускаемых источником рентгеновского
излучения — рентгеновским аппаратом, применяемым для просвечивания ОК (что равносильно
заданию максимального напряжения на рентгеновской трубке).
Шаг 2. Задается числовой (т. е. по числу квантов) энергетический спектр g(E, E0) излучения,
генерируемого рентгеновским аппаратом.
Шаг 3. Задаются материалы и параметры отдельных компонент сэндвич-детектора, имеющего
структуру вида: передний детектор, т.е. первый по направлению падающего излучения детектор;
промежуточный фильтр; задний детектор, т.е. второй по направлению падающего излучения де-
тектор.
Шаг 4. Задаются минимальное Zmin и максимальное Zmax значения атомного номера (эффектив-
ного атомного номера) Z материала ОК, подлежащего распознаванию.
Шаг 5. Задаются минимальное dmin и максимальное dmax значения радиационной прозрачности
ОК.
Шаг 6. Задается множество допустимых решений, т.е. задается множество контролируемых
объектов, исследование которых с помощью МДЭ может быть обеспечено физико-техническими
возможностями системы контроля:
D(Z,ρH)
=
{
(Z,ρH)
Z
min
≤Z≤Z
max
;
d
min
≤d
t1
(Z,ρH)
<d
t2
(Z,ρH)
≤d
max
}
(1)
Здесь ρ — плотность материала ОК, г/см3; H — толщина ОК, см; ρH — массовая толщина ОК,
г/см2;
d
(Z,ρH),
d
(Z,
ρH)
— теоретические значения радиационной прозрачности ОК, соответ-
t1
t2
ствующие первому (т.е. переднему) и второму (т.е. заднему) детекторам, которые вычисляются по
формулам [14]:
E0
g
(E,E
)exp(−m
(E,Z)ρ
H)E
(
E)ε
(
E
)
dE
∫
0
ab1
1
0
d
(Z,ρH)
=
;
(2)
t1
E
0
g(E,E
)E
(
E
)ε
(
E
)
dE
∫
0
ab1
1
0
E0
g
(E,
E
0
)exp(−
m(
E,Z)ρ
H-m(E
,Z
1
)ρ
1
H
1
−m(E
,Z
f
)
ρ
f
H
f
)E
ab2
(
E)
ε
2
(
E
)
dE
∫
0
d
t2
(Z,ρH)
=
,
(3)
E
0
g(E,
E
)exp(−m(
E,Z
)ρ
H
−
m
(
E
,Z
)
ρ
H
)
E
(
E)
ε
(
E
)
dE
∫
0
1
1
1
f
f
f
ab2
2
0
где m(E, Z) — массовый коэффициент ослабления (МКО) излучения для материала ОК, см2 /г;
(
)
ab
E
E
— среднее значение поглощенной детектором энергии, соответствующее одному зареги-
стрированному кванту с энергией Е, МэВ; ε(E) — эффективность регистрации излучения детекто-
ром; нижний индекс «1» в формулах (2) и (3) означает, что соответствующий параметр относится
к первому детектору (аналогично этому индекс «2» означает соответствие второму детектору, а
индекс «f» — промежуточному фильтру).
Из (1) следует, что для определенного значения параметра Z минимальное (ρH)min(Z) и макси-
мальное (ρH)max(Z) значения параметра ρH находятся из уравнений:
d
(Z
,(ρH
)
(Z))
=d
,
d
(Z
,(
ρH
)
(Z))
=d
(4)
t1
max
min
t
2
min
max
Шаг 7. Задается множество тестовых ОК:
D
t
(Z
t
,(ρH
t
))
=
{
(
Z
t
,(ρH
t
))
∈D(Z
,
ρH
)
Z
t
∈M
t
(
Z
);
d
t2
(
Z
t
,(ρH
))t
=d
s2
;d
s
2
∈P(d
t2
)
}
Дефектоскопия
№ 1
2022
42
В.А. Удод, С.П. Осипов, С.Ю. Назаренко
Здесь индекс «t» означает «тестовый»; Mt(Z) — задаваемое множество тестовых материалов;
P(dt2) — задаваемое множество значений теоретической радиационной прозрачности dt2 для
второго детектора (заметим, что в данном контексте прозрачность dt2 выступает как самосто-
ятельный физический параметр); ds2 — определенное значение (уровень) прозрачности dt2,
которое в силу (1) должно удовлетворять неравенствуdmin
<d
≤d
s2
max
Как следует из описания множества Dt(Zt, (ρH)t), массовая толщина (ρH)t тестового ОК, матери-
ал которого имеет атомным номер Zt, выбирается из условия:
d
(Z
,(ρH))
=d
t2
t
t
s2
Такой выбор массовых толщин тестовых ОК объясняется тем, что объекты с теми или иными
близкими свойствами распознать сложнее. В данном случае в роли такового свойства выступает
равенство теоретических радиационных прозрачностей объектов для второго детектора.
Шаг 8. Вычисляется для каждого тестового ОК, т.е. для каждой пары (Zt, (ρH)t), прозрачность
dt1(Zt, (ρH)t), соответствующая первому (переднему) детектору.
Шаг 9. Из множества Dt(Zt, (ρH)t) тестовых ОК выбирается один элемент и условно называется
«базовым» (основным), а соответствующие ему параметры обозначаются через Ztb и (ρH)tb .
Шаг 10. Выбирается значение σb(Φ2) среднеквадратического отклонения (СКО) шума Φ2, кото-
рый соответствует прозрачности dt2(Ztb, (ρH)tb) . Назовем его базовым СКО.
Шаг 11. Рассчитывается, используя соответствующие формулы из [14], значение СКО σ(Φ2)
шума Φ2, который соответствует прозрачности dt2(Zt, (ρH)t):
σ(Φ
)
2
σ(Φ
)
=
σ
(Φ
)
=
2
b
2
σ
(Φ
)
b
2
E0
2
g(E,E
)exp(−m(E,Z
)(ρH)
−m(E,Z
)ρ
H
−m(E,Z
)ρ
H
)E
(E)ε
(
E
)
dE
∫
0
t
t
1
1
1
f
f
f
ab2
2
0
=
⋅σ
(Φ
).
b
2
E
0
2
g(E,E
)exp(−m(E,Z
)(ρH)
−
m(E,
Z
)ρ
H
−
m(E,
Z
)ρ
H
)E
(E)ε
(
E
)
dE
∫
0
tb
tb
1
1
1
f
f
f
ab2
2
0
2
Здесь
E
(
E)
— средний квадрат поглощенной вторым детектором энергии для одного зареги-
ab2
стрированного кванта с энергией Е, МэВ2.
Шаг 12. Рассчитывается, используя соответствующие формулы из [14], значение СКО σ(Φ1)
шума Φ1, соответствующего прозрачности dt1(Zt, (ρH)t):
σ(Φ
)
1
σ
(
Φ
)
=
σ
(Φ
)
=
1
b
2
σ
(Φ
)
b
2
E0
2
g
(E,E
)exp(−m(E,Z
)(ρ
H
))E
(E)ε
(
E
)
dE
∫
0
t
t
ab1
1
0
=
×
E0
2
g
(E
, E
)exp(
−
m(E
,Z
)(ρH)
−m
(
E,Z
)ρ
H
−m
(E,Z
)ρ
H
)E
(E
)
ε
(
E
)
dE
∫
0
tb
tb
1
1
1
f
f
f
ab2
2
0
E0
g(
E,E
)exp(−m
(E,Z
)ρ
H
−m(E,Z
)ρ
H
)E
(E)ε
(
E
)
dE
∫
0
1
1
1
f
f
f
ab2
2
0
×
×σ
(Φ
).
E0
b
2
g
(
E
,
E
0
)E
ab1
(E)ε
1
(
E
)
dE
∫
0
2
Здесь
E
ab1
(
E)
— средний квадрат поглощенной первым детектором энергии для одного зареги-
стрированного кванта с энергией Е, МэВ2 .
Дефектоскопия
№ 1
2022
Алгоритм оценки погрешностей при распознавании материалов в системе...
43
Шаг 13. Разыгрываются значения шумов Φ1 и Φ2. Как и в [13], для этого полагаем:
Φ
∈N(0,σ(Φ
)); Φ
∈N(0,σ(Φ
)).
1
1
2
2
Наряду с этим считаем, что Φ1 и Φ2 являются независимыми случайными величинами. Такое до-
пущение следует из результатов корреляционного анализа выходных сигналов сэндвич-детектора [14].
Заметим также, что СКО σ(F1) и СКО σ(F2) могут быть соответственно интерпретированы как уровни
квантового шума для первого и второго детекторов.
Шаг 14. Рассчитываются фактические (реальные) радиационные прозрачности для каждого
тестового ОК:
d
(Z
,(ρH))
=d
(Z
,(ρH)) +Φ
;
1
t
t
t1
t
t
1
d
(Z
,(ρH))
=d
(Z
,(ρH)) +Φ
2
t
t
t2
t
t
2
Шаг 15. Получаем для каждого тестового ОК оценки его параметров Zt и (ρH)t как решение от-
носительно (Z, ρH)∈D(Z, ρH) системы уравнений:
d
(Z,ρH)
=
d
(Z
,(ρH))
t1
1
t
t
d
t2
(Z,ρ
H)
=
d
2
(
Z
t
,(ρH
t
))
Шаг 16. Действия, описанные на шагах 13—15, воспроизводятся n раз подряд, т.е. осущест-
вляется n однотипных моделирований. В итоге формируется и сохраняется в памяти набор данных
(Zi, (ρH)i ) (i = 1, 2,…, n), где Zi и (ρH)i — оценки параметров Zt и (ρH)t, тестового ОК, полученные
в результате i-го моделирования (i = 1, 2, …, n).
Шаг 17. Для каждого тестового ОК рассчитываются среднее значение Zm, среднеквадратическая
mz и относительная среднеквадратическая δz погрешности оценки Zt:
n
n
1
1
m
2
Z
Z
m
=
∑
Z
i
,
m
Z
=
∑
(
Z
i
−
Z
t
)
,
δ
Z
=
⋅100 %.
n
i=1
n
i=1
Z
t
Принципиальное отличие вышеописанного алгоритма от его прообраза — алгоритма из [13]
заключается в содержании шагов (этапов) 1—3. Кроме того, между ними имеется существенная
разница и для шагов 6, 8, 11, 12, 15. Она обусловлена тем, что теоретические радиационные про-
зрачности ОК здесь и в [13] вычисляются по значительно отличающимся формулам, что вполне за-
кономерно, т.к. классическая схемная реализация МДЭ сильно отличается от схемной реализации
МДЭ с применением сэндвич-детекторов.
ПРИМЕР ИСПОЛЬЗОВАНИЯ АЛГОРИТМА
Шаг 1. Положим максимальную энергию E0 = 160 кэВ, что достаточно типично для ряда до-
смотровых систем [13].
Шаг 2. Числовой энергетический спектр излучения зададим по аналогии с [13] следующим
образом:
E
−
E
0
g(E,
E
)
=
C
exp(
−
m
(E,Z
)(ρH
)
).
0
g
g
E
Здесь С — постоянный множитель (согласно формулам, представленным на шагах 6, 11 и 12, мож-
но считать, что С = 1); m(E, Zg) — МКО излучения для поглотителя в виде выходного окна рент-
геновской трубки толщиной 1,5 мм, изготовленного из силикатного стекла (SiO2 [15]) с массовой
толщиной (ρH)g .
Шаг 3. В работе [1] представлен сэндвич-детектор вида: первый детектор из иодида цезия (CsI)
толщиной 0,3 мм; промежуточный фильтр в форме пластины из меди (Cu) толщиной 0,7 мм; второй
детектор из иодида цезия (CsI) толщиной 5 мм.
Нами были проведены предварительные расчеты, в ходе которых было установлено, что эф-
фективность регистрации квантов излучения в диапазоне энергий от 0 до 125 кэВ для второго
Дефектоскопия
№ 1
2022
44
В.А. Удод, С.П. Осипов, С.Ю. Назаренко
детектора — 5 мм CsI составляет не менее 95 % и это значение плавно уменьшается до 81 % в
диапазоне энергий от 130 до 160 кэВ. Поэтому для моделирования будем предполагать, что второй
(задний) детектор характеризуется полным поглощением падающего излучения (детектор полного
поглощения), т.е.
2
2
ε
2
(E)
=E
ab2
(E)
E=E
ab2
(E)
E
=1.
Добавим к этому, что такое предположение вполне естественно, т.к. в этом случае происходит
максимальное использование прошедшего через ОК излучения. Предположим также, по аналогии
с [8], что преобладающим процессом взаимодействия излучения с первым (передним) детектором
является фотоэффект, а значит
E
(E)
E=1.
1
ab
Таким образом, для проведения моделирования относительно сэндвич-детектора будем пола-
гать, что он представляет собой композицию вида: первый детектор 0,3 мм CsI (с преобладающим
процессом взаимодействия с излучением в виде фотоэффекта); промежуточный фильтр 0,7 мм Cu;
второй детектор есть детектор полного поглощения.
Шаг 4. Значения Zmin и Zmax зададим по аналогии с [13]:
Zmin = 3(Li), Zmax = 30(Zn).
Шаг 5. Значения dmin и dmax зададим по аналогии с [13]:
16
−5
d
=1/2
≈1,526⋅10
;
d
=
d
(Z
,(ρH
)
)
=
d
(26;0,063)
=
0,96894.
min
max
t2
Fe
min
Fe
t2
Здесь 216 — число уровней квантования аналого-цифровых преобразователей (АЦП) с разрядно-
стью m = 16, которые используются в структуре измерительных каналов системы контроля (за-
метим, что применение АЦП с разрядностью m = 16 является достаточно типичным для многих
досмотровых систем); ZFe = 26 — атомный номер железа; (ρHmin)Fe= 0,063 г/см2 — массовая тол-
щина ОК в виде стальной проволоки диаметром (Hmin)Fe=0,08 мм (такая проволока характеризует
разрешение досмотрового интроскопа конвейерного типа ТС-СКАН 6040, описанного в [16]).
Шаг 6. Формируем в соответствии с (1) множество допустимых решений:
−5
D(Z,ρH)
=
(Z,ρH)
3≤
Z
≤
30; 1,526⋅10
≤
d
(Z,
ρH)
<
d
(Z,ρH)
≤
0,96894
(5)
{
t1
t2
}
Для проведения численного моделирования использовали дискретизацию множества (5). Для
параметра Z, изменяющегося в диапазоне от 3 до 30, был выбран шаг дискретизации равный 0,1.
Для параметра ρH, изменяющегося в диапазоне от (ρH)min(Z), до (ρH)max(Z), шаг дискретизации
составил 0,1 г/см2. При этом (ρH)min(Z) и (ρH)max(Z) находились, в соответствии с (4), а также с за-
данными на шаге 5 минимальным и максимальным значениями радиационной прозрачности ОК,
из следующих уравнений:
5
−
d
t2
(Z,(ρH)
min
(Z
))
=
0,96894;
d
t1
(Z,(ρH
)
max
(
Z
))
=1,526⋅10
Для полноты описания множества допустимых решений (5) на рис. 1 приведены графики функ-
ций (ρH)min(Z) и (ρH)max(Z), рассчитанные в системе MathCad по таблице целочисленных и некото-
рых нецелочисленных значений Z.
Проверим теперь взаимную однозначность отображения пар (Z, ρH) в пары (dt1, dt2), т.е. про-
верим взаимную однозначность отображения R множества допустимых решений D(Z, ρH) во мно-
жество теоретических прозрачностей:
5
−
Q(d
t1
,d
t2
)
=
{
(d
t1
,d
t2
)
1,526⋅10
≤
d
t1
<
d
t2
≤
0,96894
}
Такая проверка необходима для того, чтобы быть уверенным (в последующем), что именно
квантовые шумы приводят к погрешности в оценке атомного номера, а не систематические по-
грешности, вызванные неоднозначностью данного отображения.
Дефектоскопия
№ 1
2022
Алгоритм оценки погрешностей при распознавании материалов в системе...
45
ρH
80
ρHmax
70
ρHmin ×100
60
50
40
30
20
10
0
0
5
10
15
20
25
30
Z
Рис. 1. Зависимости минимального ρHmin и максимального ρHmax значений массовой толщины ОК от эффективного атом-
ного номера Z.
С этой целью следует вычислить и исследовать якобиан J преобразования переменных (Z, ρH)
в переменные (dt1, dt2):
∂d
t1
(Z,ρH)
∂d
t1
(Z,ρH)
∂Z
∂
(ρH)
J
=
∂d
(Z,ρH)
∂d
(Z,ρH)
t2
t2
∂Z
∂(
ρH
)
Однако вычисление данного якобиана крайне затруднительно ввиду сложности аналитических
зависимостей (2), (3), описывающих величины dt1(Z, ρH) и dt2(Z, ρH) как функции от переменных
Z и ρH, и учитывая тот факт, что МКО излучения задаются не аналитически, а в дискретной форме
— таблично. Вследствие этого оценим взаимную однозначность отображения R с помощью линий
уровня.
Формирование линий уровня можно осуществлять в равной степени на основе функций dt1(Z,
ρH) или dt2(Z, ρH). Для определенности будем использовать функцию dt1(Z, ρH), т.е. теоретическую
прозрачность ОК для первого детектора.
В аналитической форме линия уровня функции dt1(Z, ρH) имеет вид:
L(d
)
=
{
(Z,
ρH)∈D(Z,ρH)
d
(Z,ρH)
=d
}
,
10
t1
10
где d10 — некоторый уровень теоретической прозрачности ОК для первого детектора. Задавая раз-
ные значения параметра d10 будем получать разные линии уровня функции dt1(Z, ρH). Далее, для
всех элементов линии уровня L(d10) вычисляются значения функции
d
(Z,ρH)
(теоретической
t2
прозрачности ОК для второго детектора). Эти значения символически обозначим так: dt2(Z |L(d10)).
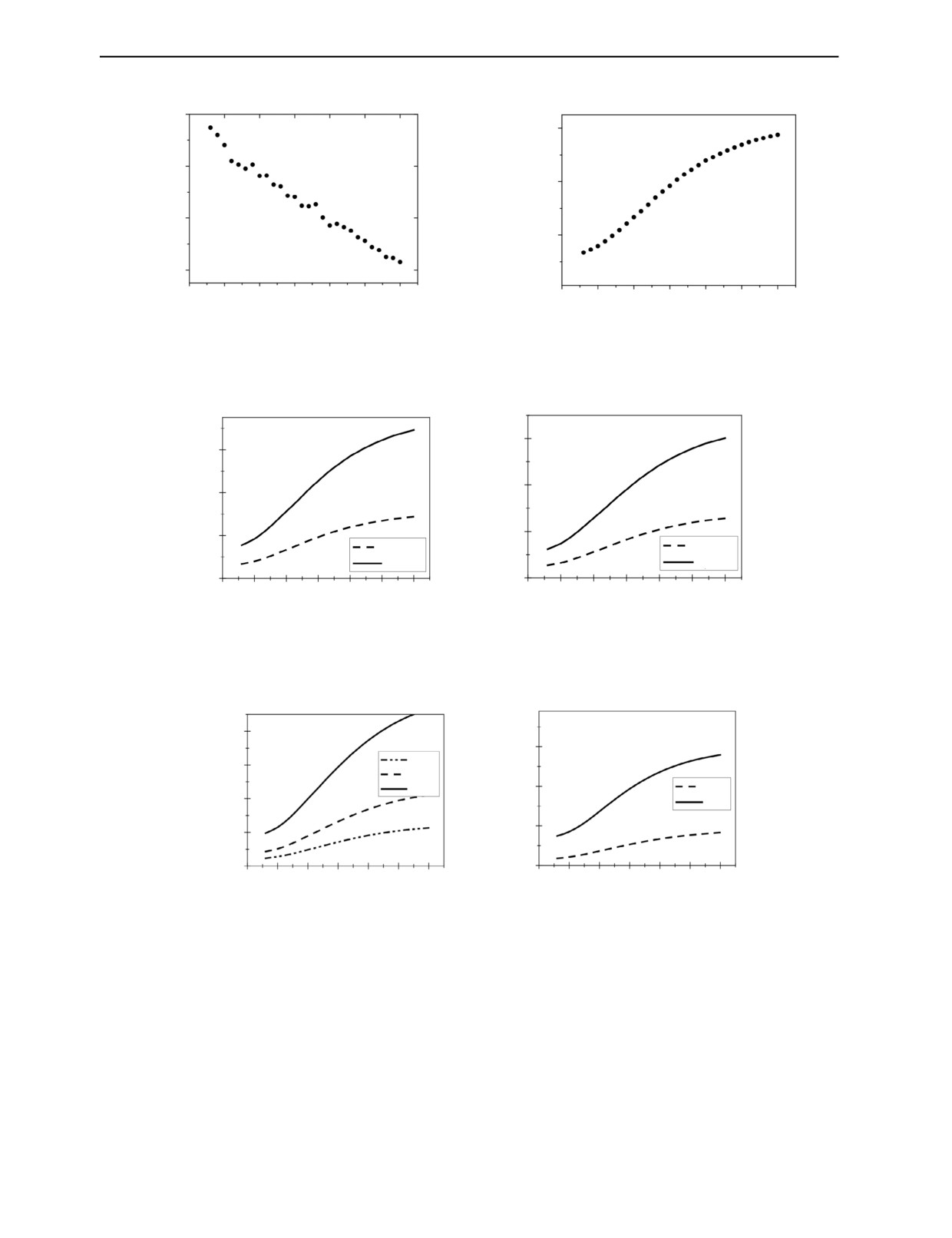
На рис. 2 в качестве примера приведена линия уровня L(d10) при d10 = 0,00002 (рис. 2a), рас-
считанная в системе MathCad, и соответствующие ей значения прозрачности dt2(Z |L(d10)) (рис. 2б).
На рис. 3—5 приведены графики функции dt2(Z |L(d10)) (от переменной Z) для различных ли-
ний уровня L(d10). При этом уровень d10 изменялся дискретно от значения 0,00002 (что близко к
16
5
минимальному значению прозрачности
d
=
1/2
≈
1,526⋅10-
) до значения 0,75 (что близко к
min
значению прозрачности
d
(26;0,063)
=
0,779
для первого детектора для ОК из железа с массовой
t1
толщиной
(ρH
)
= 0,063 г/см2).
min Fe
Как видно, графики на рис. 3—5 носят монотонный характер, что свидетельствует о взаимной
однозначности отображения R множества допустимых решений D(Z, ρH) во множество теоретиче-
ских прозрачностей
Q(d
,d
)
t1
t2
Шаги 7, 8. Зададим следующее множество тестовых материалов
M
(Z)
={6;13;26
}
, т.е. в каче-
t
стве таковых, по аналогии с [13], выберем углерод (C), алюминий (Al) и железо (Fe). Соответству-
ющие этим материалам массовые толщины (ρH)t и прозрачности dt1(Zt,(ρH)t) для первого детектора
приведены на рис. 6.
Дефектоскопия
№ 1
2022
46
В.А. Удод, С.П. Осипов, С.Ю. Назаренко
ρH
dt2(Z|L(d10))
80
0,0003
60
0,0002
40
0,0001
20
0
5
10
15
20
25
30
0
5
10
15
20
25
30
Z
Z
Рис. 2. Линия уровня L(d10) при d10 = 0,00002 (a); значения прозрачности dt2(Z|L(d10 ) для данной линии уровня (б).
dt2(Z|L(d10 )
dt2(Z|L(d10 )
0,006
0,0006
0,004
0,0004
0,0002
0,002
2е-005
0,0002
5е-005
0,0005
0,0000
0,000
0
5
10
15
20
25
30
0
5
10
15
20
25
30
Z
Z
Рис. 3. Графики функции dt2(Z|L(d10 ) при d10
= 0,00002; 0,00005; 0,0002; 0,0005.
dt2(Z|L(d10 )
dt2(Z|L(d10 )
0,04
0,3
0,03
0,001
0,002
0,003
0,2
0,01
0,02
0,05
0,1
0,01
0,00
0,0
0
5
10
15
20
25
30
0
5
10
15
20
25
30
Z
Z
Рис. 4. Графики функции dt2(Z|L(d10 ) при d10
= 0,001; 0,002; 0,005; 0,01; 0,05.
Заметим, что все тестовые ОК включаются как отдельное подмножество во множество допу-
стимых решений D(Z,ρH ). Заметим также, что тестовый ОК может быть описан не только как
пара (Zt, (ρH)t), но и как пара (Zt, ds2). При этом монотонное уменьшение массовой толщины (ρH)t
эквивалентно монотонному увеличению радиационной прозрачности ds2.
Шаг 9. В качестве базового тестового ОК выберем углерод (Ztb = 6) с массовой толщиной
(ρH)tb=15,042 г/см2, которая соответствует базовому значению теоретической радиационной про-
зрачности для второго (заднего) детектора равному db2 = 0,1.
Шаг 10. Положим σb(Φ2) = 0,0025; 0,005; 0,01; 0,03.
Дефектоскопия
№ 1
2022
Алгоритм оценки погрешностей при распознавании материалов в системе...
47
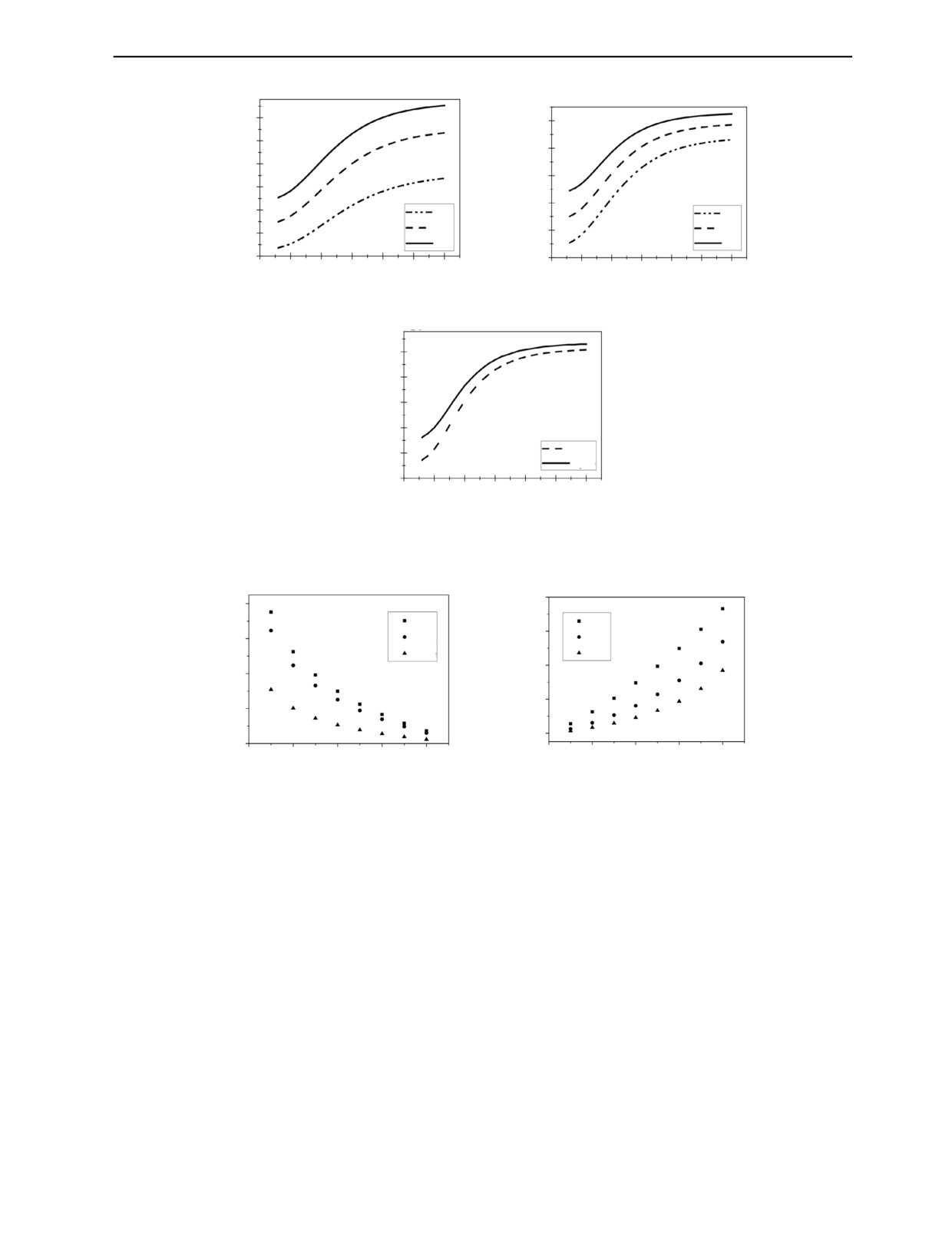
dt2(Z|L(d10 )
dt2(Z|L(d10 )
0,7
0,9
0,6
0,8
0,5
0,7
0,4
0,6
0,3
0,1
0,4
0,2
0,5
0,5
0,2
0,3
0,6
0,1
0,4
0
5
10
15
20
25
30
0
5
10
15
20
25
30
Z
Z
dt2(Z|L(d10 )
0,95
0,90
0,85
0,80
0,7
0,75
0,75
0,70
0
5
10
15
20
25
30
Z
Рис. 5. Графики функции dt2(Z|L(d10 ) при d10 = 0,1; 0,2; 0,3; 0,4; 0,5; 0,6; 0,7; 0,75.
a
dt1(Zt, (ρH)t)
б
(ρH)t
0,8
16
C
C
0,6
12
Al
Al
Fe
Fe
0,4
8
0,2
4
0,0
0
0,0
0,2
0,4
0,6
0,8
0,0
0,2
0,4
0,6
0,8
ds2
ds2
Рис. 6. Зависимость массовой толщины (ρH)t тестового ОК от радиационной прозрачности ds2 для разных тестовых
ОК (a); зависимость прозрачности dt1(Zt,(ρH)t) тестового ОК от радиационной прозрачности ds2 для разных тестовых
ОК (б).
Шаги 11, 12. В табл. 1 представлены результаты вычисления значений СКО шумов Φ1 и Φ2 для
тестовых ОК для всех выбранных (на шаге 10) базовых значений σb(Φ2) СКО шума Φ2.
Шаги 13—17. Выполнение шагов 13—17 проводились с помощью математического программ-
ного обеспечения «MathCad» для n = 10000 моделирований. Соответствующие результаты отобра-
жены в табл. 2, а также на рис. 7.
Из этих результатов следует, что погрешность оценки атомного номера для разных материалов
имеет сильную зависимость от квантовых шумов. Вместе с тем указанная погрешность:
строго возрастает при возрастании уровней шумов (что естественно и вполне закономерно);
для ОК из материала с низким атомным номером (углерод) имеет максимальное значение при
минимальной массовой толщине ОК (что равносильно максимальному значению радиационной
прозрачности ОК);
для ОК из материала со средним (алюминий) или высоким (железо) атомным номером имеет
максимальное значение при максимальной массовой толщине ОК (что равносильно минимальному
значению радиационной прозрачности ОК);
увеличивается при увеличении атомного номера материала ОК.
Дефектоскопия
№ 1
2022
48
В.А. Удод, С.П. Осипов, С.Ю. Назаренко
Таблица
1
СКО шумов Φ
и Φ2 для тестовых ОК при разных базовых значениях СКО шума Φ2
1
ds2
Zt
σb(Φ2)
СКО
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,0025
0,0025
0,0035
0,0043
0,0049
0,0055
0,006
0,0065
0,007
0,005
0,005
0,007
0,0086
0,0099
0,011
0,0121
0,013
0,0139
σ(Φ2)
0,01
0,01
0,0141
0,0172
0,0198
0,0221
0,0242
0,0261
0,0278
0,03
0,03
0,0422
0,0515
0,0594
0,0663
0,0725
0,0782
0,0835
6
0,0025
0,0009
0,0014
0,0017
0,002
0,0023
0,0026
0,0029
0,0031
0,005
0,0018
0,0027
0,0035
0,0041
0,0047
0,0052
0,0057
0,0062
σ(Φ1)
0,01
0,0037
0,0055
0,0069
0,0082
0,0093
0,0104
0,0114
0,0124
0,03
0,0111
0,0164
0,0207
0,0245
0,028
0,0312
0,0343
0,0372
0,0025
0,0026
0,0036
0,0044
0,005
0,0056
0,0061
0,0066
0,007
0,005
0,0051
0,0072
0,0087
0,01
0,0111
0,0122
0,0131
0,014
σ(Φ2)
0,01
0,0102
0,0143
0,0174
0,02
0,0223
0,0243
0,0262
0,0279
0,03
0,0307
0,043
0,0523
0,0601
0,0669
0,073
0,0786
0,0838
13
0,0025
0,0007
0,0011
0,0014
0,0017
0,002
0,0022
0,0025
0,0028
0,005
0,0014
0,0022
0,0028
0,0034
0,0039
0,0045
0,005
0,0056
σ(Φ1)
0,01
0,0029
0,0043
0,0056
0,0067
0,0078
0,009
0,0101
0,0113
0,03
0,0086
0,013
0,0167
0,0202
0,0235
0,0269
0,0303
0,0339
0,0025
0,0027
0,0037
0,0045
0,0051
0,0057
0,0062
0,0066
0,007
0,005
0,0054
0,0074
0,009
0,0103
0,0114
0,0124
0,0133
0,0141
σ(Φ2)
0,01
0,0107
0,0149
0,018
0,0205
0,0228
0,0247
0,0265
0,0282
0,03
0,0321
0,0446
0,0539
0,0616
0,0683
0,0742
0,0796
0,0845
26
0,0025
0,0006
0,0009
0,0011
0,0014
0,0016
0,0019
0,0022
0,0025
0,005
0,0012
0,0018
0,0023
0,0028
0,0033
0,0038
0,0043
0,005
σ(Φ1)
0,01
0,0023
0,0035
0,0046
0,0056
0,0065
0,0076
0,0087
0,01
0,03
0,007
0,0106
0,0137
0,0167
0,0196
0,0227
0,0261
0,0299
Из табл. 2 и рис. 7 вместе с тем вытекает, что погрешность mz (как и δz) является немонотонной
зависимостью от массовой толщины (радиационной прозрачности) ОК.
Аналогичная немонотонность оказалось присущей и для традиционной (классической) схе-
мы реализации МДЭ, что объясняется, главным образом, поведением обратной зависимости
Z = Z(dt1, dt2), т.е. зависимости атомного номера от радиационных прозрачностей ОК [13].
Дефектоскопия
№ 1
2022
Алгоритм оценки погрешностей при распознавании материалов в системе...
49
Таблица
2
Среднее значение Zm, погрешности mz и δz оценки атомного номера
для разных тестовых ОК в зависимости от базового значения σb(Φ2) СКО шума Φ2
ds2
Zt
σb(Φ2)
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
Zm
5,99
5,99
5,99
5,96
5,85
5,98
6
5,99
0,0025
mz
0,3
0,24
0,23
0,41
0,77
0,31
0,3
0,42
δz,%
4,95
3,94
3,78
6,93
13,21
5,15
5,05
6,94
Zm
5,97
5,99
5,97
5,96
5,87
5,98
5,97
5,95
mz
0,62
0,5
0,51
0,55
0,8
0,54
0,62
0,88
0,005
δ
, %
10,45
8,3
8,54
9,29
13,57
9
10,41
14,75
z
6
Zm
5,89
5,91
5,93
5,94
5,85
5,91
5,87
5,8
0,01
mz
1,32
1,05
1
0,98
1,11
1,13
1,35
1,82
δ
, %
22,34
17,83
16,83
16,58
19
19,11
23
31,45
z
Zm
6,16
6
5,95
5,91
5,91
6,01
6,1
6,6
0,03
mz
3,17
2,64
2,49
2,49
2,6
2,88
3,44
4,7
δ
, %
51,5
44
41,8
42,07
44,02
47,87
56,32
71,1
z
Zm
13,01
13,01
13,01
13,01
13
13
13,01
13,03
0,0025
mz
0,54
0,38
0,32
0,29
0,29
0,3
0,33
0,43
δ
, %
4,12
2,95
2,48
2,25
2,19
2,28
2,55
3,31
z
Zm
13,06
13,02
13,02
13,01
13,01
13,02
13,02
13,05
mz
1
0,71
0,6
0,56
0,55
0,59
0,65
0,84
0,005
δ
, %
7,69
5,48
4,59
4,27
4,2
4,53
5,01
6,44
z
13
Zm
13,24
13,09
13,05
13,07
13,06
13,04
13,09
13,17
0,01
mz
2,2
1,47
1,2
1,1
1,09
1,15
1,35
1,79
δ
, %
16,62
11,25
9,17
8,4
8,34
8,8
10,32
13,56
z
Zm
15,12
14,09
13,72
13,59
13,67
13,77
13,75
14,03
0,03
mz
7,98
5,73
4,49
3,88
4
4,13
4,45
5,19
δ
, %
52,75
40,68
32,73
28,57
29,25
29,97
32,33
36,96
z
Zm
26,3
26,17
26,17
26,05
25,66
26,58
24,53
24
0,0025
mz
2,53
1,86
1,65
1,23
1,14
0,85
0,92
1,12
δz,%
9,64
7,09
6,32
4,71
4,43
3,21
3,74
4,66
Zm
26,39
26,41
26,48
25,98
25,45
26,12
24,61
23,53
mz
4
3,27
3
2,17
1,81
1,82
1,57
1,62
0,005
δ
, %
15,15
12,4
11,34
8,37
7,09
6,96
6,38
6,87
z
26
Zm
25,91
26,28
26,36
25,66
25,05
25,65
24,38
22,84
0,01
mz
5,63
4,76
4,42
3,36
2,95
3,18
2,55
2,34
δ
, %
21,74
18,11
16,78
13,08
11,78
12,39
10,46
10,26
z
Zm
23,66
24,69
24,89
23,96
24,08
24,41
22,82
20,93
0,03
mz
9,01
7,72
7,09
5,75
5,84
5,99
4,92
4,26
δz, %
38,09
31,26
28,48
24,01
24,24
24,54
21,56
20,35
Дефектоскопия
№ 1
2022
50
В.А. Удод, С.П. Осипов, С.Ю. Назаренко
mz
а
mz
б
5
8
4
6
3
4
2
2
1
0
0
0,0025
0,01
0,0175
0,025
σb(Φ2)
0,0025
0,01
0,0175
0,025
σb(Φ2)
mz
в
8
6
4
2
0
0,0025
0,01
0,0175
0,025
σb(Φ2)
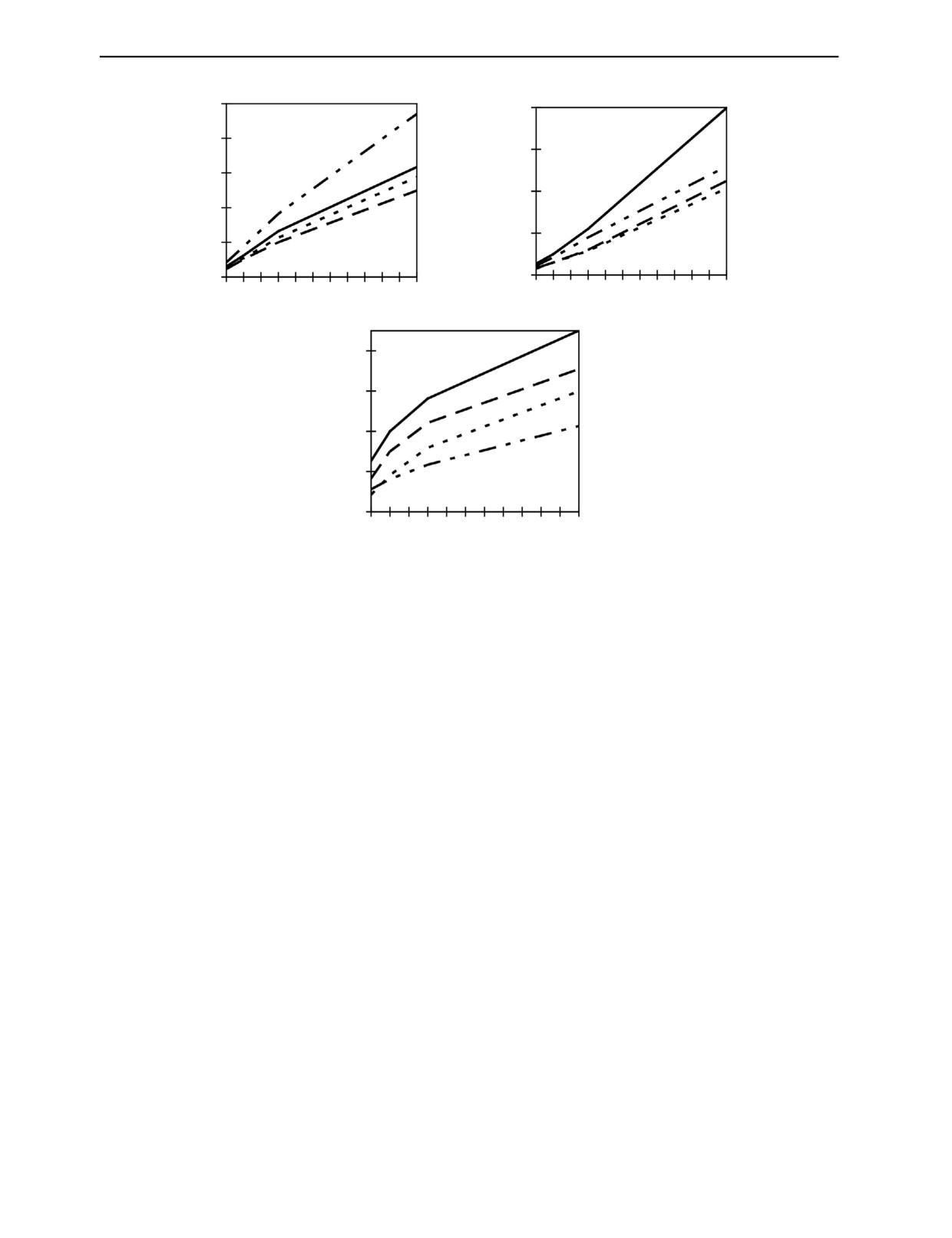
Рис. 7. Среднеквадратические погрешности mz оценок атомных номеров материалов для разных тестовых ОК
(a — Zt = 6, б — Zt = 13, в — Zt = 26):
▬▬ — ds2 = 0,1; ▬ ▬ — ds2 = 0,3; ▪ ▪ ▪ — ds2= 0,6; ▬ ▪ ▪ ▬ — ds2 = 0,8.
ЗАКЛЮЧЕНИЕ
В ходе выполненных исследований представлены аналитические описания множества допу-
стимых решений и множества тестовых объектов контроля для метода дуальных энергий примени-
тельно к рентгеновским системам досмотрового контроля с сэндвич-детекторами излучения. Для
данных систем создан алгоритм оценки погрешностей определения атомного номера, порожден-
ных квантовым шумом, при распознавании материалов на основе метода дуальных энергий и про-
иллюстрировано его действие на конкретном примере.
Созданный алгоритм может быть использован в дальнейшем, в частности, для оптимизации
сэндвич-детекторов излучения из условия минимума погрешности распознавания материалов, по-
рожденной квантовым шумом.
СПИСОК ЛИТЕРАТУРЫ
1. Rebuffel V., Dinten J.M. Dual-energy X-ray imaging: benefits and limits // Insight-non-
insi.2007.49.10.589
2. Chang C.H., Ni Y.C., Tseng S.P. Calculation of effective atomic numbers using a rational polynomial
approximation method with a dual-energy X-ray // Journal of X-Ray Science and Technology. 2021. V. 29.
3. Duvillier J., Dierick M., Dhaene J., Van Loo D., Masschaele B., Geurts R., Hoorebeke L.V., Boone M.N.
Inline multi-material identification via dual energy radiographic measurements // NDT & E International. 2018.
4. Огородников С.А. Распознавание материалов при радиационном таможенном контроле на базе
линейного ускорителя электронов / Дис
канд. техн. наук. Санкт-Петербург, 2002. 121 с.
5. Гавриш Ю.Н., Бердников Я.А., Спирин Д.О., Передерий А.Н., Сафонов М.В., Романов И.В. Про-
граммный комплекс для восстановления интроскопических изображений с использованием мето-
да дуальной энергии // Рroblems of atomic science and technology. 2010. № 3. Series: Nuclear Physics
Дефектоскопия
№ 1
2022
Алгоритм оценки погрешностей при распознавании материалов в системе...
51
6. Gil Y., Oh Y., Cho M., Namkung W. Radiography simulation on single-shot dual-spectrum X-ray for cargo
apradiso.2010.11.011
7. Osipov S.P., Udod V.A., Wang Y. Identification of materials in X-Ray inspections of objects by the
dual-energy method // Russian Journal of Nondestructive Testing. 2017. V. 53. No. 8. P. 568—587.
лов методом дуальных энергий при радиационном контроле объектов // Дефектоскопия. 2017. № 8.
С. 33—56.]
8. Osipov S.P., Usachev E.Y., Chakhlov S.V., Shchetinkin S.A., Kamysheva E.N. Selecting parameters
of detectors when recognizing materials based on the separation of soft and hard X-ray components //
S1061830918110074 [Осипов С.П., Усачев Е.Ю., Чахлов С.В., Щетинкин С.А., Камышева Е.Н. Выбор
параметров детекторов в методе распознавания материалов на основе разделения мягкой и жесткой со-
ставляющих рентгеновского излучения // Дефектоскопия. 2018. № 11. С. 60—71.]
9. Свистунов Ю.А., Ворогушин М.Ф., Петрунин В.И., Сидоров А.В., Гавришин Ю.Н.,
Фиалковский А.М. Развитие работ по созданию рентгеновских и ядерно-физических инспекционных
комплексов в НИИЭФА им. Д.В. Ефремова // Рroblems of atomic science and technology. 2006. No. 3.
10. Fredenberg E. Spectral and dual-energy X-ray imaging for medical applications // Nuclear Instruments
and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment.
11. Iovea M., Neagu M., Duliu O.G., Oaie G., Szobotka S., Mateiasi G. A Dedicated on-board dual-energy
0104-x
12. Khan S.U., Khan I.U., Ullah I., Saif N., Ullah I. A review of airport dual energy X-ray baggage inspection
techniques: Image enhancement and noise reduction // Journal of X-Ray Science and Technology. 2020.
13. Udod V.A., Osipov S.P., Wang Y. Estimating the influence of quantum noises on the quality of material
identification by the dual-energy method // Russian Journal of Nondestructive Testing. 2018. V. 54. No. 8.
квантовых шумов на качество распознавания материалов методом дуальных энергий // Дефектоскопия.
2018. № 8. С. 50—65.]
objects when using sandwich X-ray radiation detectors // Russian Journal of Nondestructive Testing. 2020.
Назаренко С.Ю. Математические модели радиационных прозрачностей объекта контроля при исполь-
зовании сэндвич-детекторов рентгеновского излучения // Дефектоскопия. 2020. № 2. С. 31—41.]
15. Евстропьев К.С. Химия кремния и физическая химия силикатов. М.: Промстройиздат, 1956.
124 с.
16. Открытый обзор продукции российских производителей специальных средств и техники для
обеспечения общественной безопасности / Научно-технический информационный сборник. Вып. 1.
М.: ФКУ НПО «СТиС» МВД России, 2018. 103 c.
Дефектоскопия
№ 1
2022