Акустические методы
УДК 620.179.16
РАСПРОСТРАНЕНИЕ ВОЛН ЛЯВА В ПЛОСКОМ СЛОИСТОМ ПОЛУПРО-
СТРАНСТВЕ ПРИ НЕЖЕСТКОМ КОНТАКТЕ НА ГРАНИЦАХ
© 2022 г. А.В. Вагин1,*
1Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
им. В.И. Ульянова (Ленина), Россия 197376 Санкт-Петербург, ул. Профессора Попова, 5
E-mail: *av.vagin@bk.ru
Поступила в редакцию 29.06.2022; после доработки 23.09.2022
Принята к публикации 04.10.2022
Исследовано распространение волны Лява в слоистом твердом полупространстве с однородными и неоднородными
граничными условиями на границах. Решена задача нахождения дисперсионного уравнения для волны Лява, распростра-
няющейся в однородной и неоднородной среде. Найденные дисперсионные уравнения решены относительно волнового
числа, а также построены графические зависимости найденной скорости от частоты ультразвука и шероховатости для
неоднородной среды.
Ключевые слова: волна Лява, дисперсионное уравнение, слоистая среда, неоднородные граничные условия.
DOI: 10.31857/S013030822211001X, EDN: BTUANT
ВВЕДЕНИЕ
Безальтернативное применение ультразвука в прикладных задачах (неразрушающий контроль,
структуроскопия, сейсмическая акустика, геофизика, техника, микроэлектроника и др.) обуслов-
лено, во-первых, широким спектром информативных возможностей при исследовании строения
и вещественного состава материалов, во-вторых, требованием к созданию более новых видов ма-
териалов и устройств для решения задач достижения высоких качеств при изготовлении акусти-
ческих элементов, в-третьих, существующей возможностью инженерных изысканий в доработке
созданных новых материалов и технологий.
Решение задачи нахождения физико-механических характеристик упругой среды основано на
анализе волн, распространяющихся в исследуемой среде.
Анализ распространения волн Лява в различных средах в научной литературе вызывает большой
интерес. Так как волны Лява являются частным случаем поверхностных волн, которые обладают
важным свойством, они часто используются для контроля поверхностных дефектов материалов [1].
Обоснованность использования данного типа волн подтверждается тем, что поверхностные волны
распространяются в приповерхностном слое образца контроля толщиной порядка двух длин волн,
что дает определяющую зависимость параметров волны от свойств исследуемого слоя. Волна Лява с
увеличением толщины слоя все меньше проникает в полупространство и почти локализуется в слое.
Так, например, в [2] исследуются волны Лява с позиций сейсмической активности. Новше-
ством этой работы является моделирование сейсмических волн Релея и Лява в трехмерном случае.
Исследование структуры волн Лява принципиально трехмерной, приведенное в [2], было выпол-
нено впервые. Однако, несмотря на обширный спектр полученных результатов для конкретной
математической модели, они не дают целостного представления о численных величинах, характе-
ризующих распространение волны в среде.
Результаты анализа распространения волны Лява в твердом слое с твердым полупростран-
ством приведены в [3]. Неоднородность между слоями имитируется наличием непрерывных уси-
лий «сцепления», но отсутствием непрерывности поля перемещений. В упомянутой статье принят
формальный учет особенностей зацеплений в виде задания численных значений коэффициентов
жесткости. Такой учет «зацепления» между слоями говорит лишь о степени жесткости и не дает
представления о форме и величине неоднородности, описываемой величиной шероховатости.
Исследование распространения волны Лява в слоистой структуре «твердое тело—упругое по-
лупространство» приведено в [4]. Для случая «жесткого контакта» [5,6], т.е. для однородных гра-
ничных условий, приведено дисперсионное уравнение для волны Лява.
В данной статье рассматриваются волновые процессы в виде распространения волны Лява
вдоль границы твердого слоя с твердым полупространством при неоднородных граничных услови-
ях между ними. Под твердой средой понимается изотропная, идеально упругая среда. Для решения
задачи нахождения скорости распространения волны Лява в неоднородной среде, что и определяет
4
А.В. Вагин
цель работы, целесообразно рассмотреть случай распространения волн в однородной среде. Реше-
ние такой задачи начинается с нахождения дисперсионного уравнения и последующего его реше-
ния относительно волнового числа (скорости звука).
Однородная среда описывается граничными условиями, учитывающими полную передачу со-
ставляющих упругих смещений и упругих напряжений [7]. В качестве неоднородной среды рас-
сматриваем микронеоднородную структуру, описываемую граничными условиями, учитывающи-
ми неполную передачу составляющих упругих смещений при сохранении передачи упругих на-
пряжений. Разрывы в передаче упругих смещений возникают из-за наличия выступов и/или впадин
микрорельефа на границе твердого слоя и полупространства, а также взаимодействия между ними.
Это соответствует определению граничных условий, описываемых в приближении «линейного
скольжения» [8]. Такая неоднородность возникает во многих практических случаях, например при
механической обработке поверхности (в частности, при упрочнении поверхностного слоя стекла
методом ионной имплантации), при освещении поверхности фоточувствительного полупроводни-
кового пьезокристалла (CdS, CdSe, ZnO, ZnS и т.д.) поглощаемым светом и т.д. [9].
Количественная модель выступов и/или впадин микрорельефа строится на основе введения
величины шероховатости в коэффициенты жесткости. Тогда величина шероховатости будет опре-
деляться средним расстоянием между соседними неоднородностями на контактирующих поверх-
ностях. Учет шероховатости при решении задачи поиска скорости распространения волны Лява
дает представление о форме и величине неоднородности, что дает основу для поиска физически
корректной функциональной зависимости упругих свойств жесткости от параметров контактирую-
щих поверхностей, которые образуются за счет большого количества микроконтактов [10].
Из [11] известно, что поверхностная волна в изотропном твердом полупространстве являет-
ся комбинацией плоских неоднородных волн — продольной и поперечной, векторы смещения
которых лежат в плоскости, перпендикулярной границе. Другим типом поверхностной волны
является волна Лява. Существование такой волны основано на взаимно дополнительном типе по-
ляризации — горизонтальной поляризации. Волна Лява представляет собой плоские поперечные
волны со смещениями, параллельными границе раздела слоя и полупространства и перпендику-
лярными направлению волны [4].
Исследование с помощью волны Лява слоистых сред, имеющих широкое разнообразие физи-
ко-механических характеристик, наряду с отсутствием трудностей в технологиях изготовления,
находит на данный момент большое применение и практический интерес в акустике, акустооптике,
авиации, космической технике и пр.
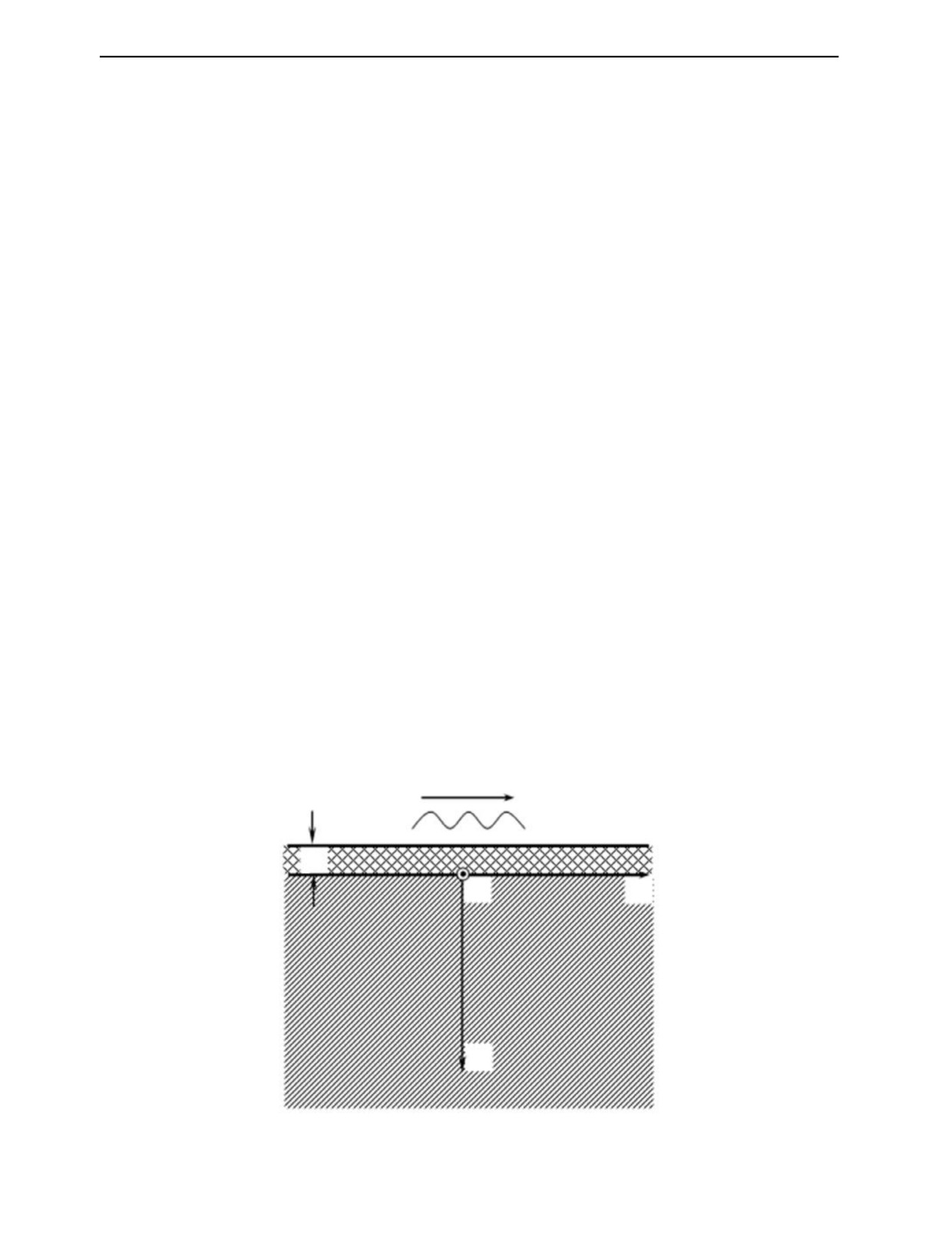
Описание распространения волн Лява. Рассмотрим слоистую структуру «твердое тело—
упругое полупространство» (рис. 1).
В качестве материалов сред примем те, для которых наиболее полно известен набор физико-
механических характеристик, например «сталь—графит» [12].
Волна Лява
h
y
x
z
Рис. 1. Модель структуры «твердая среда—упругое полупространство».
Дефектоскопия
№ 11
2022
Распространение волн Лява в плоском слоистом полупространстве ...
5
Так как волна Лява является чисто поперечной волной, то она имеет только одну компоненту
упругого смещения. Для рассмотрения волнового движения целесообразно выбрать плоскости для
волнового вектора — xz, а также определить, что смещения параллельны оси y (см. рис. 1).
Волны Лява с горизонтальной поляризацией удовлетворяют уравнению движения (1) [13]:
2
∂
ξ
ρ
=
(
λ+2µ
)
grad
(
divξ
)
−µ⋅rot
(
rotξ
)
,
(1)
2
∂t
где ρ — плотность среды; ξ — вектор упругого смещения; λ, µ — параметры Лямэ; µ — модуль
сдвига.
Для уравнения движения (1) волна Лява является вторым линейно-независимым решением в
виде уравнения (2) [14]:
2
∂
ξ
t
ρ
− µ∆ξ
=
0,
(2)
2
t
∂
t
где ξt — вектор поперечного смещения; Δ ξt = grad (div(ξt)).
В случае плоских волн упругие смещения в направлении оси y отличны от 0, а смещения в
направлении оси x и z равны между собой и равны 0, откуда получается волновое уравнение для
поперечной волны. Но для полного рассмотрения распространения волны Лява необходимо при-
нимать во внимание распространение не только в слое, но и в полупространстве.
Тогда помимо волнового уравнения для волны Лява, распространяющейся в слое, запишем об-
щую систему, включающую волновое уравнение для полупространства (3) [15]:
2
1
∂
ξ
2
y
,c
∇
ξ
=
,
−h≤ z
≤
0;
y,c
2
2
c
∂t
t,c
(3)
2
1
∂
ξ
2
y
∇
ξ
=
,
z
≥
0,
y
2
2
c
t
∂t
2
2
где
ξ
y,c
,
c
t,c
,
ξ
y
,
c
t
— компоненты смещения и скорости поперечной волны в слое и в полупростран-
стве соответственно; h — толщина слоя.
Из физических соображений следует, что при распространении волны из плотной среды в
менее плотную скорость распространения волны должна возрастать. Условием распространения
волны Лява будет соотношение скорости в слое и полупространстве, которое выглядит следующим
образом:
c
t,c
<c
t
Простейшим типом волны с горизонтальной поляризацией является объемная поперечная вол-
на, распространяющаяся вдоль границы полупространства. Данная волна описывается уравнения-
ми (4) для упругих смещений на границе твердой среды и в полупространстве:
j
(
ωt kx
)
ξ
y,c
=
B
c
Φ
(
z
)
e
,
−h≤ z
≤
0;
(4)
−sz j
(
ωt kx
ξ
y
=
Be
e
),
z
≥
0,
где Bc — неизвестная постоянная; Φ(z) — функция распределения амплитуды волны в слое;
2
ω
B — неизвестная постоянная;
s
=
k
−k
t
2,
k
t
=
— волновое число поперечной волны.
c
t
Выполняя подстановку выражений для упругих смещений поперечной волны (4) в выражения
(3), получим выражение для функции распределения амплитуды в слое (5):
2
∂
Φ
(z)
2
+
s
Φ
(
z
)
=
0,
(5)
2
c
∂z
Дефектоскопия
№ 11
2022
6
А.В. Вагин
2
2
2
ω
ω
где
s
c
=
k
t,c
−k
,
k
=
— волновое число;
k
t
,c
=
— волновое число поперечной волны в слое;
c
c
t
,c
c — фазовая скорость волны Лява.
Решая уравнение (5) относительно функции распределения амплитуды, получаем для нее вы-
ражение:
Φ z)= Csin
(
s
z
)
+ Dcos
(
s
z
)
,
c
c
где C, D — пока неизвестные постоянные.
Выполняя подстановку полученного уравнения для функции распределения амплитуды Φ(z) в
уравнения (4), получим итоговую систему уравнений (6) для рассмотрения распространения волны
Лява в слоистой среде:
j
(
ωt kx
)
ξ
=
(
C
sins
z+D
coss
z
)
e
,
−h≤ z
≤
0;
y,c
c
c
c
c
(6)
−
sz j
(
ωt kx
ξ
=
Be
e
),
z
≥
0,
y
где Cc = BcC, Dc = BcD.
Таким образом, получены уравнения для упругих смещений волны Лява в слое и полупростран-
стве, подставляя которые в граничные условия для конкретной модели среды, можно получить дис-
персионное уравнение для нахождения скорости волны и последующего определения физико-ме-
ханических характеристик сред. Слоистая среда определяется пятью упругими постоянными [16,
17], которые в свою очередь определяются по найденным скоростям поперечных и продольных
волн при различных направлениях распространения.
Распространение волн Лява в однородных средах. Для нахождения дисперсионного урав-
нения для волны Лява необходимо рассмотреть граничные условия для структуры «твердая сре-
да—упругое полупространство». Граничные условия для однородной среды будут определяться
непрерывностью касательных компонент смещения и напряжения при z = 0 и z = - h [18].
Уравнение (7) определяет первое граничное условие, которое характеризует равенство компо-
нент механических напряжений на границе твердой среды и полупространства при z = 0:
σ
yz,c
z=
0
=σ
yz
z=
0
,
(7)
где σyz,c, σyz — компоненты механических напряжений в слое и полупространстве соответственно.
Уравнение (8) определяет второе граничное условие, которое характеризует равенство нулю
компонент механического напряжения на границе твердого слоя и полупространства при z = -h:
σ
yz
,c
z=-h
=
0.
(8)
Уравнение (9) определяет третье граничное условие — условие «жесткого контакта» для ком-
понент упругого смещения ξz:
ξz,c = ξz.
(9)
Граничные условия (7)—(9) полным образом определяют волновые процессы в системе «твер-
дая среда — упругое полупространство».
При решении задачи определения фазовой скорости волны необходимо принять во внимание
изменение взаимного положения частиц твердого тела, связанное с их перемещением относитель-
но друг друга. Это определяет результат изменения межатомных расстояний и перегруппировки
блоков атомов. Это сопровождается изменением величин межатомных сил, мерой которого являет-
ся упругое механическое напряжение.
Используя обобщенный закон Гука [13]:
σik = Ciklmulm,
где σik — тензор напряжения; Ciklm — тензор модулей упругости; ulm — тензор деформации, т.е.
линейную зависимость между тензором деформаций и тензором напряжений, компоненту тензора
упругого напряжения можно представить в виде выражения (10):
Дефектоскопия
№ 11
2022
Распространение волн Лява в плоском слоистом полупространстве ...
7
∂ξ
∂ξ
1
y
∂ξ
z
y
σ
=
2µu
=
2µ
+
=µ
(10)
yz
yz
2
∂z
∂y
∂z
После определения полного состава уравнений для решения задачи необходимо выполнить
только подстановку известных компонент упругих смещений (6) и механических напряжений (10)
в граничные условия (7)—(9).
Таким образом, выполняя такую подстановку, получаем три уравнения:
µ
Cs
= -µsB;
c c c
C
c
coss
c
(
−h
)
−
D
c
sins
c
(
−h
)
=
0;
D
=
B,
c
из которых составляем систему уравнений для нахождения дисперсионного уравнения:
C
c
coss
c
h+B
sins
c
h
=
0.
(11)
+µ
sB
=
0
µcCs
Найдем определитель системы (11) и приравняем его к нулю для нахождения нетривиального
решения:
cos
s
h
sin
s
h
c
c
=
0.
µ
s
µ
s
c c
Решая определитель, получим дисперсионное уравнение (12), необходимое для нахождения
скорости волны Лява:
µ
s ⋅tg
(
s
h
)
= µs,
(12)
c c
c
2
2
где
µ =ρc
,
µ
=ρ
c
— модули сдвига в полупространстве и слое соответственно.
t
c
c
t,c
Как видно из уравнения (12), в правой части этого дисперсионного уравнения стоит действи-
тельное положительное число, поэтому левая часть также является действительной.
2
2
2
2
Учитывая ранее введенные обозначения, а именно
s
= k
−k
,
s= k
−k
, то соотношение
c
t,c
t
2
2
2
для волновых чисел будет следующим:
k
>k
>k
, тогда скорости в слое и полупространстве
t,c
t
будут соотноситься неравенством:ct
>c>c
(замедляющий слой) [5].
t,c
Таким образом, фазовая скорость волны Лява для случая жесткого контакта во всем частотном
диапазоне изменяется от скорости поперечной волны в слое до скорости поперечной волны в полу-
пространстве.
Так как дисперсионное уравнение для волны Лява в однородной среде (12) содержит в себе
тригонометрическую функцию тангенса, то в этом случае оно является трансцендентным и име-
ет бесконечное множество корней. Различные корни соответствуют волнам Лява разных поряд-
ков (распространяющихся мод). Количество этих мод определяется соотношением kt,ch.
Для построения зависимости фазовой скорости волны Лява от частоты ультразвука проведем
анализ возможных предельных случаев существования такой волны.
Пусть фазовая скорость распространения волны Лява стремится к значению скорости сдви-
говых волн в полупространстве ct. Тогда, принимая во внимание неравенство по соотношению
скоростей, можно сказать, что эффективная скорость стремится к скорости поперечной волны,
а переходя к рассмотрению волновых чисел, можно сказать, что эффективное волновое число
стремится к волновому числу поперечной волны, что в свою очередь влечет стремление к нулю
коэффициента s, т.е. c→ct ⇒ k→kt⇒ s→0. Тогда, переходя к рассмотрению дисперсионного урав-
нения (12), можно записать следующее:
tg
(
s
c
h
)
→0⇒s
c
h → nπ,
Дефектоскопия
№ 11
2022
8
А.В. Вагин
тогда
2
2
2
k
c
c
2
2
t,c
t,c
s
h=h k
−k
=
k
h
1−
=
k
h
1−
=
k
h
1−
,
c
t,c
t,c
2
t,c
c→c
t
t,c
k
c
c
t
,c
t
т.е. при стремлении фазовой скорости к скорости поперечной волны в полупространстве возможно
появление новой волны на критических частотах, которые определяются как
nπ
k
h
=
,
t,c
2
ct,c
1
−
c
t
где n = 1, 2, 3 … — номер моды.
Аналогично рассмотренному предельному случаю следующим вариантом может быть случай
стремления фазовой скорости к скорости поперечной волны в слое, при котором получаем, что
c→ct,c ⇒ k→kt,c⇒ sc→0, тогда дисперсионное уравнение принимает вид:
π
tg
(
s
h
)
→∞⇒
s
h
→
(
n
+1
)
⇒
h
→∞⇒
k
h
→∞,
c
c
t,c
2
т.е. данный случай существования волны возможен в области высоких частот.
Решая дисперсионное уравнение (12) относительно скорости волны Лява, построим графиче-
скую зависимость полученной скорости волны Лява от частоты ультразвука f (рис. 2).
CЛява, м/с
3250
2650
2050
1450
850
0
1
2
3
4
f, МГц
Рис. 2. Графическая зависимость скорости волны Лява от частоты ультразвука.
При малых толщинах слоя фазовые и групповые скорости волн определяются параметрами по-
лупространства и очень близки к значению скорости в первой среде (упругая среда), при больших
толщинах — параметрами слоя и соответственно близки к значению скорости во второй среде, т.е.
в упругом полупространстве [10].
Фазовые скорости монотонно уменьшаются с ростом толщины слоя, а групповые имеют ми-
нимум и области очень сильной дисперсии перед этим слоем. Имея известную фазовую скорость,
можно вычислить смещения и напряжения в волнах Лява согласно [19].
Интересным обобщением волн Лява являются поперечные поверхностные волны в полупро-
странстве с небольшой поверхностной неоднородностью, рассмотренные в работе [20].
Достигнутые результаты исследования распространения волн Лява в неоднородных средах рас-
сматриваются в следующем разделе.
Распространение волн Лява в неоднородных средах. Рассмотрим распространение волны Лява
в неоднородной структуре «твердая среда—упругое полупространство». Неоднородность возникает
во многих практических случаях, например при механической обработке поверхности, при освеще-
нии поверхности фоточувствительного полупроводникового пьезоэлемента поглощаемым светом.
Пусть плотность и модуль сдвига для рассматриваемой модели среды изменяются по следую-
щим законам [21]:
Дефектоскопия
№ 11
2022
Распространение волн Лява в плоском слоистом полупространстве ...
9
z
-
∆ρ
z0
ρ=ρ
1+
e
;
0
ρ
0
(13)
z
-
∆µ
z
0
µ=µ
1−
e
,
0
µ
0
где z — координата, направленная вглубь полупространства; z0 — характерная глубина неоднород-
ного слоя; ρ0, µ0 — соответствующие значения ρ, µ на большой глубине.
Динамическое уравнение движения для неоднородного полупространства имеет вид:
2
∂
ξ
i
∂σ
ik
ρ
=
,
(14)
2
∂t
∂xk
где σik — тензор механических напряжений с модулями упругости, являющимися функциями ко-
ординат (x, y, z). Как уже было сказано ранее, ξx = ξz = 0, ξ ≠ 0, а также учитывая в (13) зависимость
только от координаты z, то уравнение (14) выглядит как
2
∂
ξ
dµ
∂ξ
y
y
ρ
−µ
(
z
)
∆ξ
−
=
0.
(15)
2
y
∂t
dz ∂z
Решение этого уравнения будем искать в виде гармонической волны:
ξ
= AF z)exp
(
kx - ωt
)
− sz,
(16)
y
i
где A — произвольная постоянная; F(z) — неизвестная функция.
Выполняя подстановку выражения (16) в уравнение (15) без последнего члена, так как он много
меньше остальных в виду слабых неоднородностей, получим выражение для неизвестной функции
F(z):
2
d
F
dF
2
ξ
(
1−ξ
)
+
(
1+2sz
)
−ξ
(
1+
2
sz
)
+
(
k
z
)
F
=
0,
2
0
0
t
0
dξ
d
ξ
∆µ
∆ρ
z
z
2
где введена новая переменная:
ξ=
-
exp−
=
d
exp
−
.
µ
ρ
z
z
0
0
0
0
Это гипергеометрическое уравнение, и его решением является гипергеометрическая функция
F = F(α, β, γ, ξ), где α = (s - k)z0, β = (s + k)z0, γ = 1 + 2sz0.
Приближенное решение для F:
αβ
2
F
=1
+ ξ+
O
(
ξ
)
γ
Выражение (16) должно удовлетворять граничному условию отсутствия сдвиговых напряже-
ний на плоскости z = 0:
∂ξ
y
µ
(z)
=
0.
∂
z
z=0
Подставляя выражение (16) в граничное условие, получим дисперсионное уравнение, которое
приводит к выражению для искомого волнового числа поверхностной волны:
2
(
k
z
)
t
0
4
6
k = k
1
+
d
+
O
(
d
)
(17)
t
2
Дефектоскопия
№ 11
2022
10
А.В. Вагин
Таким образом, анализируя выражения (16), (17), можно сказать, что в случае поверхностной
неоднородности слоя в твердом полупространстве может существовать и распространяться наряду
с рэлеевской дополнительная поверхностная волна, являющаяся обобщением волны Лява.
1
Эта волна локализована в поверхностном слое толщиной
z
=
, которая тем больше, чем
л
s
слабее неоднородность:
−1
∆µ
∆ρ
1
1
z
л
=
+
µ
ρ
k
z
k
0
0
t
0
t
Характеристикой неоднородности слоев является коэффициент жесткости, который определяет
передачу нормальных и касательных составляющих упругих смещений.
Не изменяя по существу общности постановки задачи нахождения скорости распространения
волны Лява в однородной среде, за исключением постановки выражений для граничных условий,
рассмотрим распространение волны Лява в неоднородной среде.
Уравнения (7), (8) для случая распространения волны Лява в неоднородной среде остаются не-
изменными.
Третье граничное условие — неоднородное условие, рассматриваемое в приближении «линей-
ного скольжения» для компонент ξz, которые учитывают непрерывность передачи компонент из
одного слоя в другой:
σ
yz
ξ
−ξ =
,
z,c
z
K
T
где KT - тангенциальный коэффициент жесткости.
Тангенциальный коэффициент жесткости определяется выражением:
µ
µc
c
2π
(
1−ζ
)
c
t,c
t
K
=
,
T
2
µ
c
+µc
ω
d
ζ
c
t
,c
t
где µc, µ — коэффициенты Лямэ в слое и полупространстве соответственно; ct,c, ct — скорости по-
перечных волн в граничных средах; ζ = b2/d2 — коэффициент перфорации; d — среднее расстояние
между контактными участками; b — размер участка с отсутствием контакта.
Если выступы микрошероховатости поверхности моделировать участками сферических по-
верхностей радиусом R, то среднее расстояние между контактными участками будет:
2
d =
2
2RR
z
−R
z
,
где Rz — шероховатости поверхности границы.
Выполняя аналогичную подстановку упругих компонент смещений в неоднородные граничные
условия, получаем три уравнения, два из которых — аналогичны уравнениям, полученным для
однородной среды, а третье уравнение имеет следующий вид:
µ
Cs
µ
s
c c c
D
c
=
B
−
=
B
1
+
K
K
T
T
Из полученных выражений составляем определитель и приравниваем его к нулю для нахожде-
ния дисперсионного уравнения:
µs
coss
h
1+
sin
s
h
c
c
K
=
0.
T
µ
s
µs
c c
Решая данный определитель, получим дисперсионное уравнение для волны Лява, распростра-
няющейся в неоднородной среде (13):
µs
µ
s
⋅
1
+
tg
(
s
h
)
=µ
s
(18)
c c
c
K
T
Дефектоскопия
№ 11
2022
Распространение волн Лява в плоском слоистом полупространстве ...
11
Оценка возможного наличия другого типа волн на критических частотах совпадает с оценкой
дисперсионного уравнения для случая распространения волны Лява в однородной среде.
Для проведения расчетов необходимо определить характеристики неоднородности, присут-
ствующей в твердом слое и полупространстве.
Как уже было сказано, характеристикой неоднородности служит величина шероховатости. При
принятом значении коэффициента перфорации, определяющего степень сплошности границы,
равном ζ =0,5, примем значение величины шероховатости Rz = 1; 10 мкм [22].
Для такой модели построим графическую зависимость фазовой скорости волны Лява от
частоты ультразвука по полученным аналитическим зависимостям — дисперсионному урав-
нению (18).
CЛява, м/с
3010
2470
1930
1390
850
0
1
2
3
4
f, МГц
Рис. 3. Графическая зависимость скорости волны Лява от частоты ультразвука при шероховатости Rz = 1 мкм.
CЛява, м/с
2850
2350
1850
1350
850
0
1
2
3
4
f, МГц
Рис. 4. Графическая зависимость скорости волны Лява от частоты ультразвука при шероховатости Rz = 10 мкм.
Анализ графической зависимости, приведенной на рис. 3, 4, показывает, что нарушение сплош-
ности акустического контакта, вызванное микрошероховатостью в виде выпуклостей и вогнуто-
стей прилегающих поверхностей сред при всех значениях коэффициента перфорации, существенно
влияет на фазовую скорость волны Лява по сравнению с условиями жесткого «сварного» контакта.
Наличие неоднородности приводит к снижению амплитудного значения скорости распростра-
нения волны Лява в среде при прочих одинаковых частотах ультразвука [23].
Анализ предельных случаев граничных условий показывает, что полученные графические за-
висимости фазовой скорости волны от частоты при нулевом значении коэффициента перфорации
соответствуют рассмотренному случаю «жесткого контакта» — однородная среда.
Дефектоскопия
№ 11
2022
12
А.В. Вагин
Для неоднородной среды в случае нарушения акустического контакта за счет наличия на по-
верхности сред выпуклостей и вогнутостей, образующих шероховатость границы, фазовая ско-
рость волны Лява уменьшается, причем скорость волны тем меньше, чем больше коэффициент
перфорации — т.е. чем менее плотно соприкосновение сред.
Также стоит отметить, что высокое значение шероховатости, в свою очередь определяющее
неоднородность среды, приводит к уменьшению контактной жесткости, что, как уже известно, вы-
зывает уменьшение фазовой скорости.
ВЫВОДЫ
1. Показано влияние на абсолютные значения фазовых скоростей волн Лява таких параметров
микротрещин, как величина шероховатости, взаимодействующих в приближении «линейного
скольжения» краев трещин и других неоднородностей среды.
2. Решена задача о нахождении скорости волны Лява для однородной и неоднородной струк-
туры «твердая среда—упругое полупространство» с объемной трещиноватостью путем решения
относительно волнового числа дисперсионного уравнения.
3. Полученные зависимости используются применительно к задачам нахождения основ-
ных физико-механических характеристик среды на основе акустических измерений, а также в
качестве основного материала для проведения предызмерительных изысканий с целью полу-
чения максимального объема информации без применения средств ультразвукового контроля.
СПИСОК ЛИТЕРАТУРЫ
1. Капцов А.В., Кузнецов С.В. Волны Лява в трехслойном упругом полупространстве // Прикладная
математика и механика. 2015. Т. 79. № 4. С. 550—557.
2. Хохлов Н.И., Петров Б.И. Моделирование сейсмических явлений сеточно-характеристическим
методом // Труды МФТИ. 2011. Т. 3. № 3. С. 159—167.
3. Аббакумов К.Е., Попокова Е.С. Волновые процессы в области границы твердых сред с нарушен-
ным акустическим контактом // Изв. СПбГЭТУ «ЛЭТИ». 2007. № 1. C. 26—30.
4. Викторов И.А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 287 с.
5. Бреховских Л.М. Волны в слоистых средах. М.: Наука, 1973. 340 с.
6. Рытов С.М. Акустические свойства мелкослоистой среды // Акустический журн. 1956. Т. 2. № 1.
С. 71—83.
7. Аббакумов К.Е., Кириков А.В., Львов Р.Н. Преломление упругих волн на плоской границе раздела
с нарушенной адгезией твердых сред // Изв. СПбГЭТУ «ЛЭТИ». 2003. № 1. С. 10—17.
8. Abbakumov K.E., Vagin A.V. Dispersion Equation for Longitudinal Waves in a Layered Medium
with Inhomogeneous Boundary Conditions in Different Propagation Directions // Russian Journal of
Nondestructive Testing. 2020. V. 56. No. 1. P. 20—27. [Аббакумов К.Е., Вагин А.В. Дисперсионное урав-
нение для продольной волны в слоистой среде с неоднородными граничными условиями при различ-
ных направлениях распространения // Дефектоскопия. 2020. № 1. С. 22-30.]
9. Викторов И.А. Физические основы применения ультразвуковых волн Рэлея и Лэмба в технике.
М.: Наука, 1996. 196 с.
10. Хлыбов А.А. Исследование влияния микронеоднородности среды на распространение поверх-
ностных волн // Дефектоскопия. 2018. № 6. С. 3—10.
11. Evel’son R.L A fine-layered medium of finite-thickness in an electromagnetic field // Journal of
communications technology and electronics. 2015. V. 60. I. 6. P. 552—559.
12. Brun M., Guenneau S., Movchan A.B., Bigoni D. Dynamics of structural interfaces: Filtering and
focussing effects for elastic waves // J. Mech. Physics Solids. 2010. V. 58. P. 1212—1224.
13. Егоров Н.Н., Яковлев Л.А. Колебания и волны: учеб. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ»,
1997. 111 с.
14. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука, 1989. 412 с.
15. Luk’yashko O.A., Saraikin V.A. Transient one-dimensional wave processes in a layered medium //
Journal of Mining Science. 2007. V. 43. P. 145—158.
16. Вавакин А.С., Салганик Р.Л. Эффективные упругие характеристики тел с изолированными тре-
щинами, полостями и жесткими неоднородностями // Механика твердого тела. 1978. № 2. С. 95—107.
17. Jose M. Carcione anisotropic Q and velocity dispersion of finely layered media // Geophysical
Prospecting. 1992. V. 40. P. 761—783.
18. Панасюк О.Н. Анализ влияния граничных условий на распространение волн в слоистых компо-
зитных материалах // Прикладная механика. 2014. № 4. С. 52—58.
19. Akbarov S.D., Guliev M.S, Kepceler T. Propagation of axisymmetric waves in an initially twisted
circular compound bimaterial cylinder with a soft inner and a stiff outer constituents // Mech. Comp. Mater.
2011. V. 46. P. 627—638.
Дефектоскопия
№ 11
2022
Распространение волн Лява в плоском слоистом полупространстве ...
13
20. Петрашень Г.И. Распространение волн в анизотропных упругих средах. Л.: Наука, 1980. 280 с.
21. Аббакумов К.Е., Вагин А.В. Волновые процессы в слоистой микронеоднородной среде с неодно-
родными граничными условиями // Изв. СПбГЭТУ «ЛЭТИ». 2019. № 5. С. 12—18.
22. Аббакумов К.Е., Голубев А.С. Оценка акустических свойств тонких расслоений и однострочных
неметаллических включений в стальных листах // Дефектоскопия. 1982. № 9. С. 22—31.
23. Сибиряков Б.П., Максимов Л.А., Татарников М.А. Анизотропия и дисперсия упругих волн в сло-
истых периодических структурах. Новосибирск: Наука, 1980. 73 с.
Дефектоскопия
№ 11
2022