Электромагнитные методы
УДК 620.179.14
ИМПУЛЬСНОЕ МАГНИТНОЕ ПОЛЕ ВБЛИЗИ ПОВЕРХНОСТИ МЕТАЛЛА
© 2022 г. В.В. Павлюченко1, Е.С. Дорошевич1,*
1Белорусский Национальный Технический Университет, Беларусь
220013 Минск, пр-т Независимости, 65
E-mail: *ess.doroshevich@gmail.com
Поступила в редакцию 06.09.2022; после доработки 30.09.2022
Принята к публикации 30.09.2022
Представлены экспериментальные зависимости максимальной напряженности вторичного импульсного магнитного
поля вблизи поверхности металлических пластин от их толщины H(d), полученные с помощью дискретного датчика
магнитного поля (ДДМП) и отнесенные к напряженности поля первичного источника. Толщина пластин изменялась от
0,015 до 2 мм. На ДДМП с пластинами из алюминия и свинца воздействовали импульсами магнитного поля линейного
индуктора со временем нарастания от 5 до 60 мкс. Найдены арктангенсные аналитические функции H(d), которые
использованы для расчетов гистерезисной интерференции импульсного магнитного поля в отраженной волне с целью
повышения чувствительности и точности контроля толщины металлических объектов, удельной электропроводности их
материала и дефектов сплошности в них.
Ключевые слова: импульсное магнитное поле, алюминиевая пластина, магнитный носитель.
DOI: 10.31857/S0130308222110021, EDN: BUBJHX
ВВЕДЕНИЕ
Для осуществления контроля толщины металлических объектов, удельной электропроводно-
сти их материала и наличия в них дефектов сплошности и структурных неоднородностей необхо-
димо иметь информацию о магнитных полях на поверхности объекта при воздействии на него
импульсными магнитными полями. Экспериментальные зависимости максимальной напряжен-
ности вторичного импульсного магнитного поля вблизи поверхности металлических пластин от их
толщины получены нами ранее в [1]. Там показано, что начальные участки этих зависимостей
являются квазилинейными. В дальнейшем эти результаты были использованы в последующих
работах авторов. Так, проведены расчеты с использованием экспериментальной зависимости вели-
чины электрического напряжения U, снимаемого с преобразователя магнитного поля, от величины
напряженности приложенного магнитного поля H [2]. Там указанная зависимость аппроксимиро-
вана шестью линейными участками и применен метод гистерезисной интерференции.
Более точно можно определить толщину объекта из алюминия с помощью магнитного носи-
теля, описанного авторами арктангенсной характеристикой [3], воздействуя на него сериями
разнополярных импульсов магнитного поля линейного индуктора из одного, двух, трех, четы-
рех, пяти и пятнадцати импульсов. При этом обеспечивали одинаковую амплитуду гистерезис-
ных колебаний электрического напряжения и получали линейную разностную зависимость
напряжения U(x), снимаемого с магнитной головки, от координаты x для клинообразного и пло-
ского алюминиевых объектов.
Отметим значительные успехи контроля различных свойств объектов, их толщины и дефектов
сплошности вихретоковым методом [4—7]. Там, в частности, представлены результаты определе-
ния параметров трещин, внутреннего диаметра труб, параметров поверхностных дефектов конеч-
ной и бесконечной глубины и качества теплообменных труб парогенераторов АЭС. Известны
многочисленные работы [8, 9] по описанию вихревых токов проводящих и намагничивающихся
включений и влиянию кривизны поверхности трубопровода на результаты контроля.
Огромным преимуществом разрабатываемого метода является тот факт, что метод позволяет
записывать мгновенные распределения магнитных полей на большой площади объекта и в про-
странстве, чего нельзя сделать вихретоковым и другими методами. Развитие метода гистерезисной
интерференции может быть осуществлено, например, при использовании перекрывающихся
импульсных магнитных полей [10]. При этом следует учитывать дифференциальный фон электри-
ческого сигнала преобразователя магнитного поля [11], содержащий фоны электромагнитных
помех, резонансные фоны и другие сигналы, не связанные с полезным сигналом.
Методом вихревых токов достаточно полно осуществляется отстройка от электропроводности
основания при измерении толщины токопроводящих покрытий [12], а магнитодинамическим
методом можно выявлять ферромагнитную составляющую в нержавеющих сталях [13] и вести
Импульсное магнитное поле вблизи поверхности металла
15
контроль толстослойных никелевых покрытий на двухслойных основаниях [14]. Разрабатываемый
нами метод имеет существенное преимущество и перед магнитодинамическим методом, так как
является не точечным методом, а поверхностным (объемным) с высоким пространственным раз-
решением и быстродействующим и может быть осуществлен как в отраженной, так и в прошед-
шей волне [15]. При разработке метода гистерезисной интерференции авторам значительную
помощь оказали работы по магнитоиндукционной томографии [16] и работа по контролю токопро-
водящих покрытий топливных баков летательных аппаратов [17].
Исходя из вышеизложенного, следует, что полученные нами результаты использования гисте-
резисной интерференции должны быть уточнены, а также проведены дополнительные исследова-
ния в широком диапазоне толщин объектов с поиском таких аналитических функций, каждая из
которых описывает пространственные распределения магнитных полей во всем измеряемом диа-
пазоне толщин.
Целью работы является повышение чувствительности и точности контроля свойств электро-
проводящих объектов в импульсном магнитном поле. Поставленная цель достигается путем про-
ведения исследований импульсных магнитных полей вблизи поверхности металлических объек-
тов, получением соответствующих экспериментальных зависимостей, нахождением аналитиче-
ских функций, описывающих эти зависимости, и использованием этих функций для расчетов
магнитных полей при гистерезисной интерференции для контроля свойств объектов.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ
Исследуем импульсные магнитные поля вблизи поверхности металлических пластин и найдем
аналитические функции, описывающие полученные экспериментальные зависимости.
Обозначим через tmax время нарастания импульса. Пусть Н0m — максимальная величина танген-
циальной составляющей напряженности магнитного поля первичного источника в результате
действия этого импульса в точке измерения, а Нsm — максимальная величина тангенциальной
составляющей напряженности вторичного магнитного поля в точке измерения. Тогда отношение
максимальной напряженности вторичного магнитного поля к максимальной напряженности пер-
вичного поля, т.е. величина относительной напряженности вторичного магнитного поля, будет
равно: Нrm = Нsm/ Н0m.
На основании проведенных нами исследований найдено, что зависимость величины Нrm от тол-
щины d объекта из алюминия для источника поля в виде линейного индуктора может быть представ-
лена двумя видами формул, первый из которых выглядит так:
Нrm = 0,6366 arctg(ad + bd2),
(1)
где Нrm — величина безразмерная, d измеряется в мм, а коэффициенты a и b — соответственно
в мм-1 и мм-2.
Измерения проведены на проекции оси линейного индуктора на плоскость магнитного носи-
теля.
Указанному времени нарастания импульсов соответствуют следующие величины коэффициен-
тов а и b: для tmax = 5 мкс (a = 19 мм-1, b = 250 мм-2); для tmax = 10 мкс (a = 8,5 мм-1, b = 62 мм-2);
для tmax = 18 мкс (a = 6,6 мм-1, b = 19 мм-2); для tmax = 60 мкс (a = 1,8 мм-1, b = 2,1 мм-2).
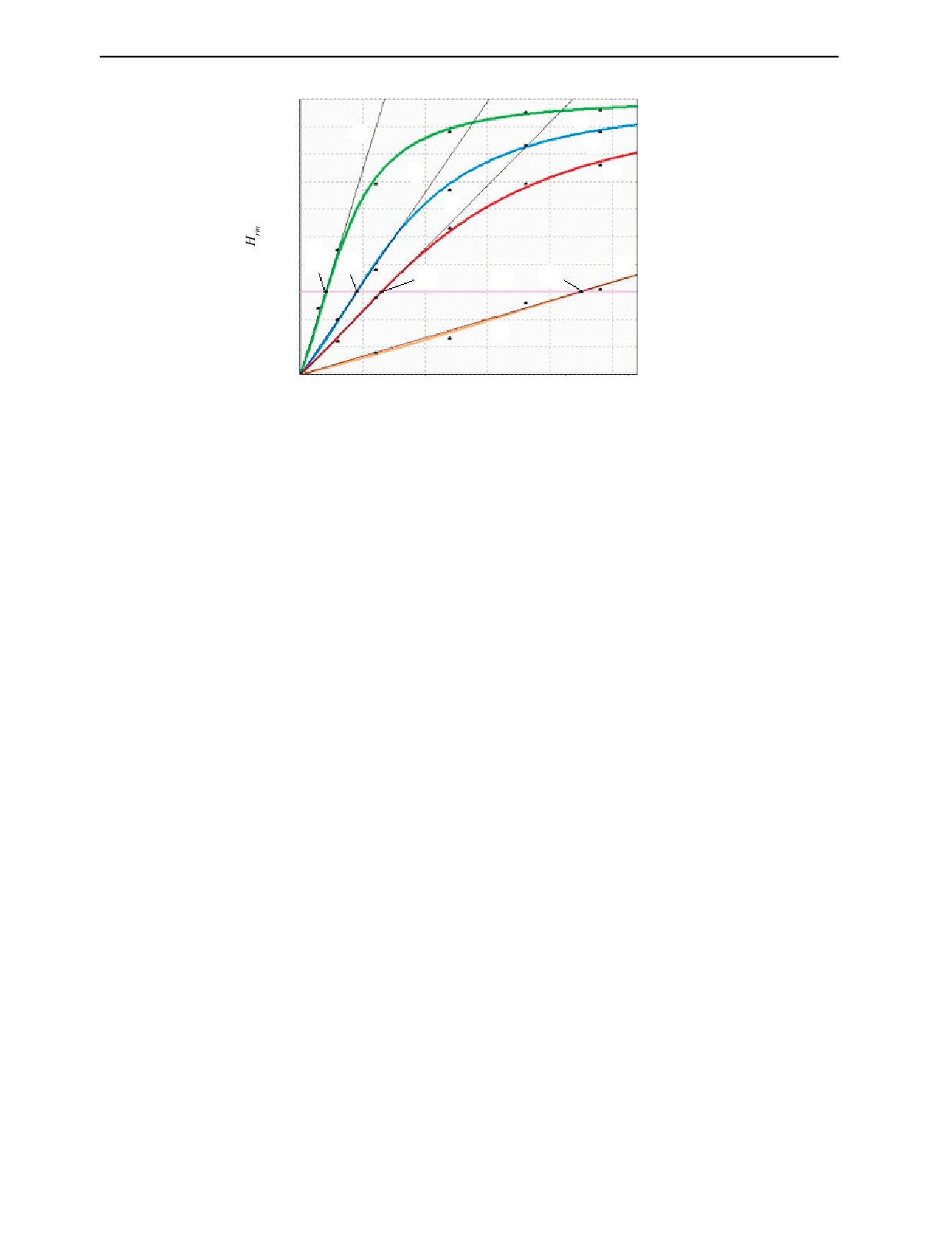
Графики зависимостей величины Нrm от толщины d объекта из алюминия для разного времени
нарастания импульсов показаны на рис. 1.
Здесь отмечены точки 10 — 13, в которых Нrm= 0,3Н0m, через которые проведены отрезки
прямых 5—9. На рис. 1 отрезок прямой 8 сливается с зависимостью 4. Экспериментальные зави-
симости Нsm вблизи поверхности металлических пластин от их толщины получены нами ранее
[1]. Начальные участки этих зависимостей являются линейными. Полученные нами в данной
работе зависимости описываются функцией арктангенс. Начальные участки этих зависимостей
с большой точностью можно считать линейными. Зададим точность измерений 1 %. Тогда с
указанной точностью можно считать участки зависимостей 1—4 линейными вплоть до величи-
ны Нsm = 0,3Н0m. Параметры каждой экспериментальной точки на рис. 1 (и рис. 2) получены
путем нахождения средних значений по 30 измерениям.
Как показано в [1], способность электропроводящего материала отражать электромагнитное поле
может быть охарактеризована приведенной толщиной материала d0. Это толщина материала, при
которой величина максимальной напряженности магнитного поля на его поверхности удваивается
при условии выполнения линейной зависимости максимальной напряженности магнитного поля от
Дефектоскопия
№ 11
2022
16
В.В. Павлюченко, Е.С. Дорошевич
d01
d02
d03
1
1
0,9
5
2
0,8
6
3
0,7
0,6
7
0,5
0,4
10
4
11
13
12
9
0,3
0,2
8
0,1
0
0
0,05
0,1
0,15
0,2
0,25
d, мм
Рис. 1. Зависимости Нrm(d) 1, 2, 3 и 4 для tmax, равные 5, 10, 18 и 60 мкс, построенные по (1); 5, 6, 7, 8, 9 — отрезки
прямых, проходящих через точки 10—13.
толщины материала. Величину d0 находили путем экстраполяции указанных линейных участков
зависимостей 1—4 отрезками 5—8 прямых до удвоенной величины Н0m. Времени нарастания
импульсов 5, 10, 18 и 60 мкс соответствуют приведенные толщины d01 = 0,068 мм, d02 = 0,152 мм,
d03 = 0,22 мм и d04 = 0,75 мм.
На основании полученных результатов нами найдена зависимость Нrm от толщины d объекта
из алюминия и времени нарастания импульса tmax:
Нrm = 0,6366 arctg(100c·d/tmax + 6250 c2 ·d2/t2max),
(2)
где d измеряется в мм, tmax — в мкс, а с — единичный коэффициент размерности, равный
1 мкс/мм.
Соответствующие указанным экспериментальным точкам зависимости относительной напря-
женности магнитного поля от толщины пластин из алюминия могут быть достаточно точно опи-
саны также формулой, учитывающей смещение нулевого уровня сигнала:
Нrm = 0,11564 + 0,563 arctg(ad + bd2 - 0,21),
(3)
где d измеряется в мм, а коэффициенты a и b — соответственно в мм-1 и мм-2.
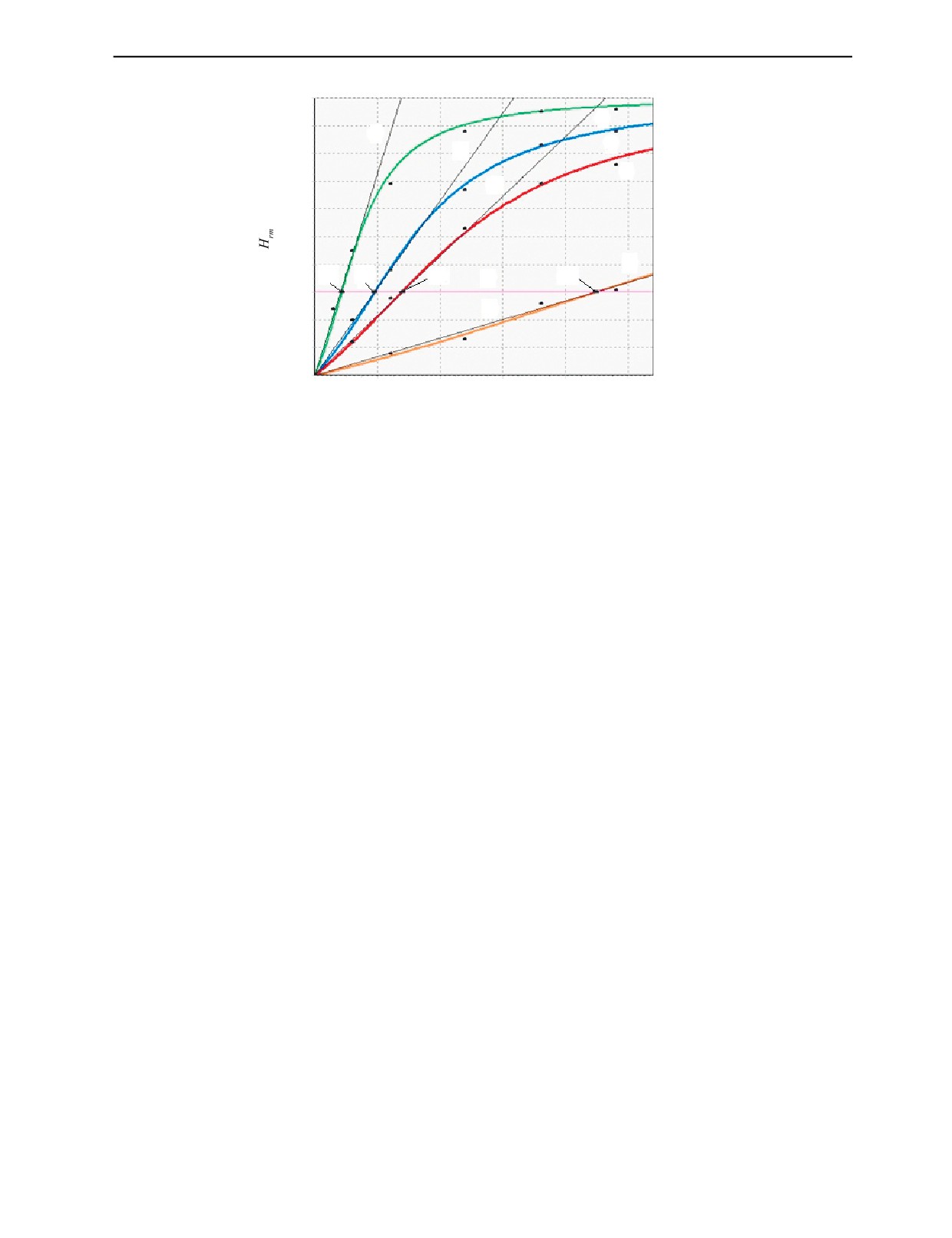
Графики зависимостей Нrm(d) объекта из алюминия, рассчитанные по (3), для разного времени
нарастания импульсов показаны на рис. 2. Здесь также отмечены точки 10—13, в которых
Нrm = 0,3Н0m, через которые проведены отрезки прямых 5—9. На рис. 2 отрезок прямой 8 (тонкая
линия) расположен выше зависимости 4 и практически сливается с ней.
Указанному времени нарастания импульсов соответствуют следующие величины коэффициен-
тов а и b: для tmax = 5 мкс (a = 20 мм-1, b = 250 мм-2); для tmax = 10 мкс (a = 9 мм-1, b = 52 мм-2); для
tmax = 18 мкс (a = 6,6 мм-1, b = 19 мм-2); для tmax = 60 мкс (a = 2 мм-1, b = 2 мм-2).
Времени нарастания импульсов 5, 10, 18 и 60 мкс соответствуют приведенные толщины
d01 = 0,071 мм, d02 = 0,159 мм, d03 = 0,233 мм и d04 = 0,746 мм. Таким образом, указанные значения
d0 близки найденным из графиков на рис. 1.
В этом случае зависимость относительной напряженности вторичного магнитного поля от
толщины объекта из алюминия и времени нарастания импульса может быть представлена в виде:
Нrm = 0,11564 + 0,563 arctg(100c · d/tmax + 6250 c2 ·d2/t2max - 0,21),
(4)
где, как и ранее, d измеряется в мм, tmax — в мкс, а с = 1 мкс/мм.
Зависимости (1)—(4) получены для источника поля в виде линейного индуктора и могут отли-
чаться от аналогичных зависимостей, полученных при воздействии на объект полями других
Дефектоскопия
№ 11
2022
Импульсное магнитное поле вблизи поверхности металла
17
d01
d02
d03
1
1
0,9
5
2
6
0,8
3
0,7
7
0,6
0,5
4
0,4
10
11
12
9
13
0,3
8
0,2
0,1
0
0
0,05
0,1
0,15
0,2
0,25
d, мм
Рис. 2. Зависимости Нrm (d) 1, 2, 3 и 4 для tmax, равные 5, 10, 18 и 60 мкс, построенные по (3); 5, 6, 7, 8, 9 — отрезки
прямых, проходящих через точки 10—13.
источников, например, полем соленоида. Одной из причин такого отличия является зависимость
распределения напряженности отраженного импульсного магнитного поля от соотношения тол-
щины объекта и расстояния от него до оси индуктора.
Воздействуем на дискретный датчик [1] магнитного поля (ДДМП) серией из двух импульсов
линейного индуктора. Применим разработанный нами метод нулевого максимума. Положение
нулевого максимума соответствует проекции оси индуктора на ДДМП. При осуществлении ука-
занного метода в результате воздействия вторым импульсом противоположного направления
величина нулевого максимума должна быть равной нулю для получения максимальной чувстви-
тельности и оптимального диапазона измерения с этой чувствительностью. Расчет начальной
кривой остаточного намагничивания применяемого ДДМП, представленной в виде зависимости
величины электрического напряжения U1(H), снимаемого с преобразователя магнитного поля,
сканирующего магнитный носитель с записанной на нем информацией, от напряженности H
приложенного к нему магнитного поля, осуществляли с использованием найденной авторами
функции [10]:
U1 = 23,5 + 24,3 arctg (0,011H - 1,45).
(5)
Расчет произведен в интервале напряженности магнитного поля
0
≤ H ≤ 1000 А/см.
Электрическое напряжение выражено в милливольтах, а напряженность магнитного поля измеря-
ли в А/см.
При намагничивании магнитного носителя вторым импульсом поля в обратном направлении
зависимость сигнала от величины напряженности магнитного поля и от результатов предшеству-
ющего воздействия находили по [10]:
U2i = -23,5 + 0,61U1 + (24,5 + 0,4U1) arctg((0,011 + 0,000087U1) H + 1,45 - 0,0016U1).
(6)
Расчет произведен в интервале напряженности магнитного поля -1000 А/см ≤ H ≤ 0.
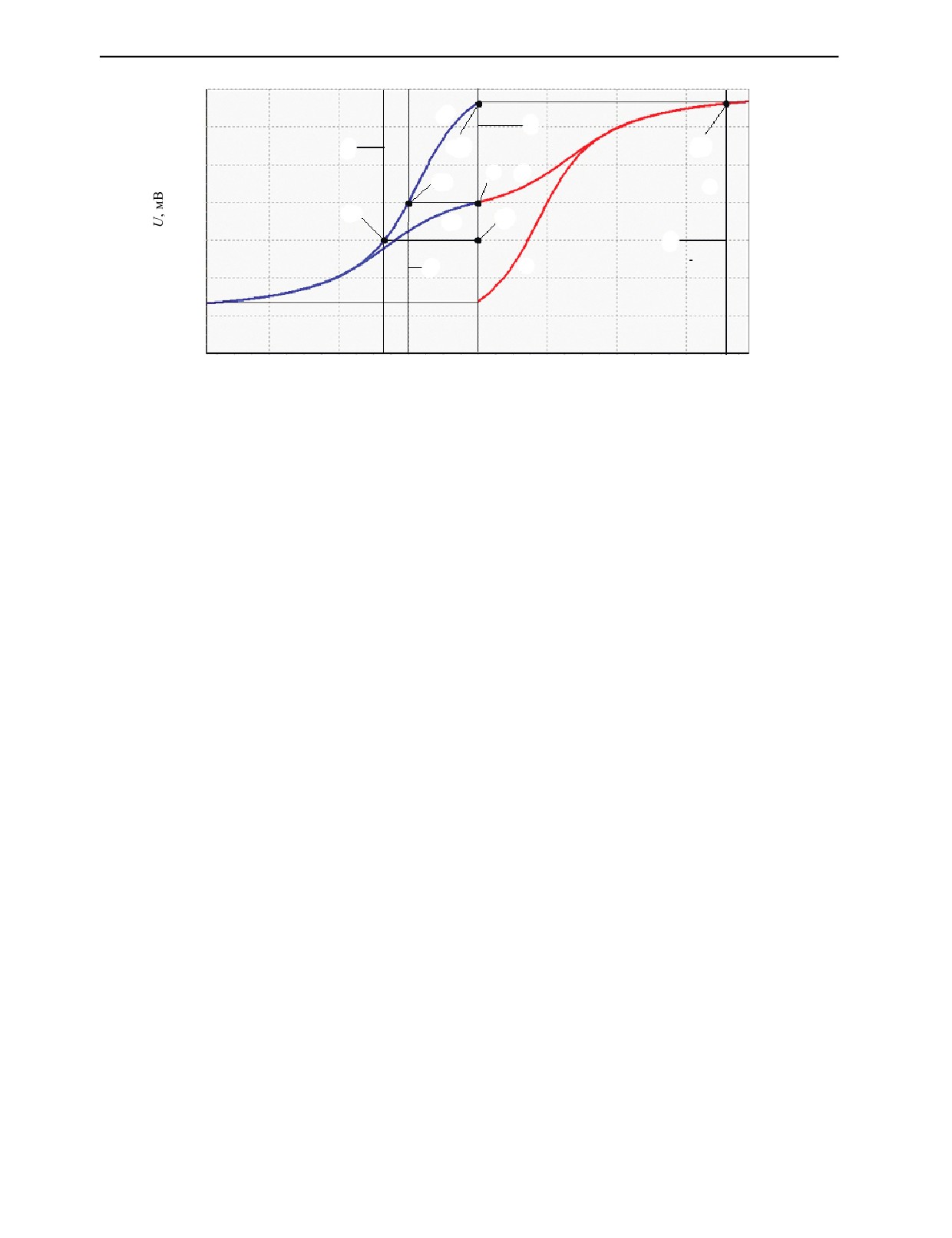
Гистерезисные ветви магнитного носителя, рассчитанные по (5) и (6), представлены на рис. 3
для разных начальных значений электрического напряжения, соответствующих разным величинам
остаточного намагничивания магнитного носителя (МН). Зависимости 1, 2 (восходящие ветви
гистерезиса) получены при намагничивании МН в прямом направлении, а зависимости 3, 4 (нис-
ходящие ветви гистерезиса) — при намагничивании в обратном направлении.
Зададим максимальную напряженность магнитного поля первого импульса, равную
Н0m1 = 360 А/см (ось 6). Воздействуем этим импульсом на МН без объекта и переходим из началь-
ной точки 9 (0 мВ) в точку 10 и далее в точку 11 (54 мВ) на оси 5.
Дефектоскопия
№ 11
2022
18
В.В. Павлюченко, Е.С. Дорошевич
60
4
5
40
8
11
10
20
9
1
12
0
13
3
14
6
-20
7
2
-40
-60
-300
-200
-100
0
100
200
300
H, А/см
Рис. 3. Зависимость величины электрического напряжения, снимаемого с магнитного гистерезиса (МГ), от напряженности
воздействующего магнитного поля U(H).
Зададим максимальную напряженность магнитного поля второго импульса, равную
Н0m2 = -100 А/см (ось 7). Воздействуем этим импульсом на намагниченный первым импульсом
магнитный носитель без объекта и переходим из точки 11 в точку 12 (0 мВ) и далее в начальную
точку 9.
Выведем первым импульсом магнитный носитель в состояние, соответствующее точке 11.
Воздействуем на МН с алюминиевой пластиной толщиной 0,05 мм вторым импульсом магнит-
ного поля с Н0m2 = -100 А/см и tmax = 10 мкс. Тогда согласно рис. 1 величина Нrm2 = 0,34Н0m2 и
суммарная максимальная напряженность магнитного поля вблизи поверхности пластины будет
равна -134 А/см (ось 8). В результате по гистерезисной ветви 4 мы попадаем в точку 13 и далее
в точку 14 (-20 мВ).
Рассчитанные по (1) и (3) на основании экспериментальных данных зависимости и графики на
рис. 1 и рис. 2 позволяют более точно определить толщину пластин по сравнению с найденными
ранее зависимостями [1].
В (6) используется абсолютная величина напряженности магнитного поля H. Поскольку мы
используем метод нулевого максимума, то максимальная величина U2i должна быть равна нулю в
отсутствие объекта. На основании зависимости 4 на рис. 3 находим величину напряженности соот-
ветствующего магнитного поля Н0m = -100 А/см. Объект создает вторичное магнитное поле, напря-
женность которого определяется по (1). С учетом сказанного в (6) подставляем следующее выра-
жение для напряженности магнитного поля:
H= Н0m (1+ 0,6366 arctg(ad + bd2)),
(7)
где Н0m = -100 А/см.
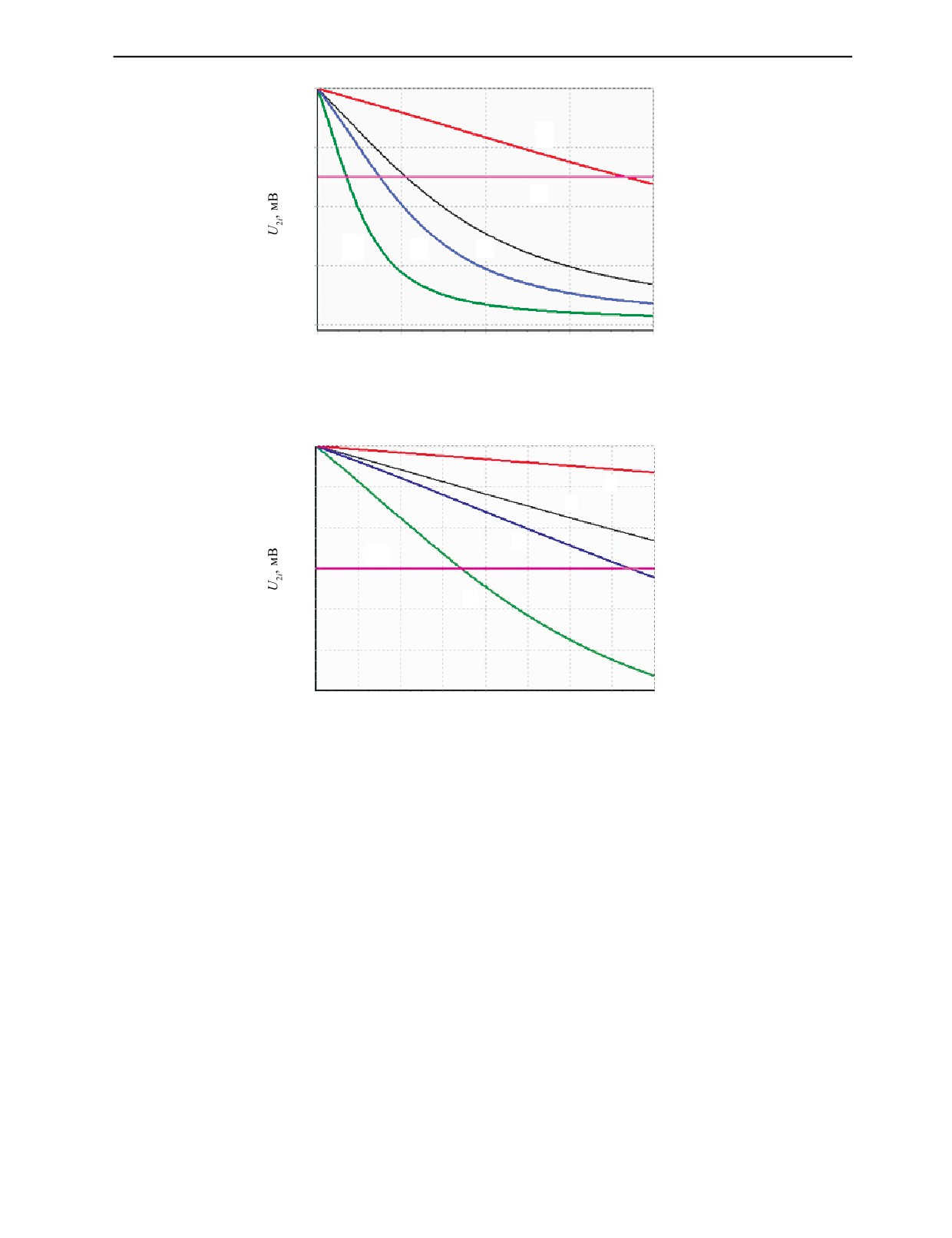
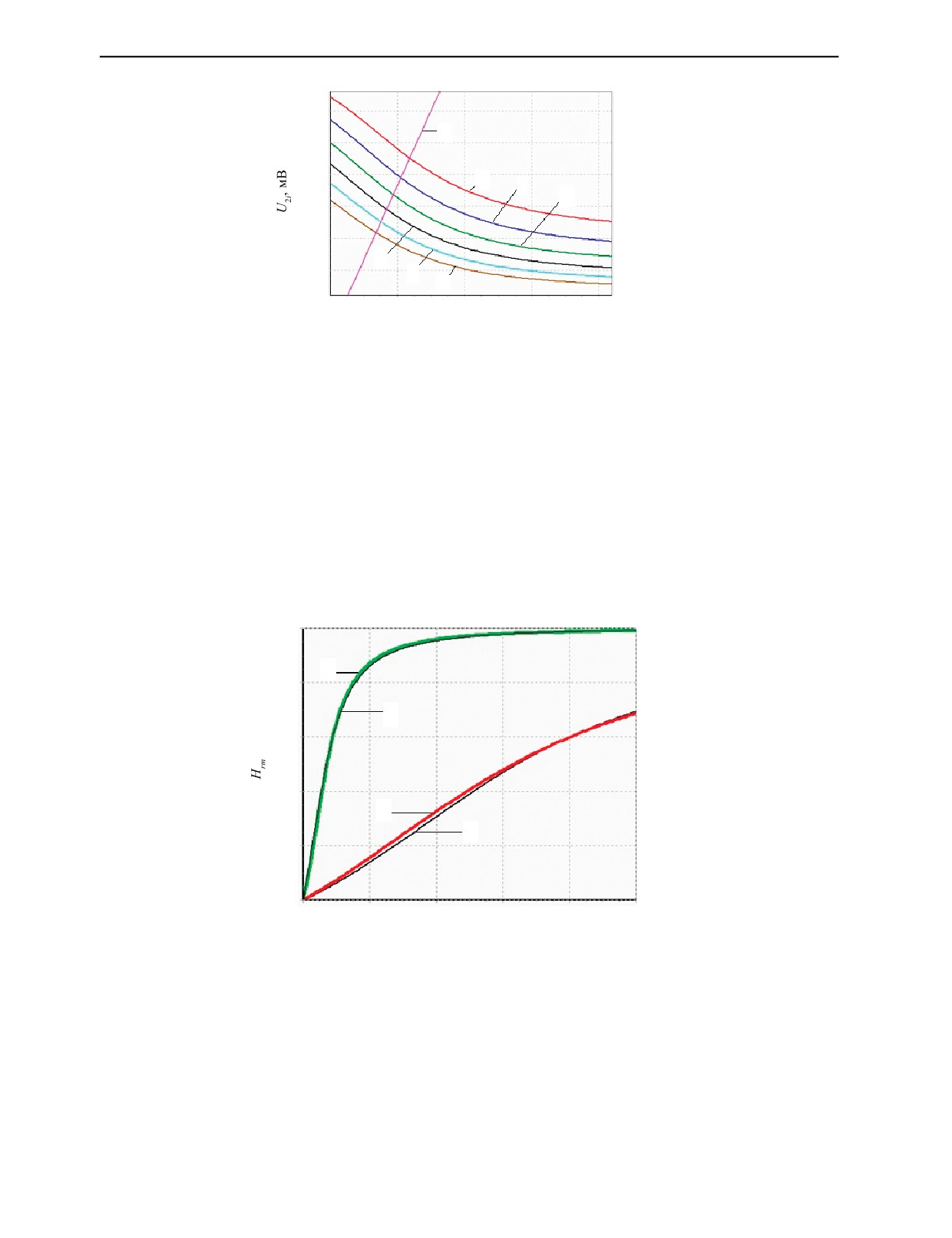
Графики зависимостей U2i(d), найденных по (6) с использованием (7) и с соответствующими
коэффициентами для разного времени нарастания импульсов магнитного поля, изображены
на рис. 4.
Из графиков на рис. 4 следует, что начальные участки всех указанных зависимостей с точно-
стью до 1 % можно считать линейными вплоть до напряжения 15 мВ.
Полученные формулы для построения зависимостей величины сигнала U2i (x) от координаты x
могут быть применены для контроля объектов разной формы. Так, на рис. 5 представлены зави-
симости U2i(x) для клина при разном времени нарастания импульса поля.
Толщина клина изменяется с координатой по его длине по формуле d = 0,1x, которую подставили
в (7), т.е. толщина клина в точке x = 0 равна нулю. Естественно, что графики на рис. 5 имеют такой
же вид, что и графики на рис. 4. При этом чувствительность и точность определения толщины объ-
екта в интересующих диапазонах измерения могут быть определены из кривых 1 — 4 и устанавлива-
емого порогового уровня сигнала 5, обеспечивающего, как и ранее, точность контроля около 1 %.
Дефектоскопия
№ 11
2022
Импульсное магнитное поле вблизи поверхности металла
19
0
4
-10
5
-20
1
2
3
-30
-40
0
0,05
0,1
0,15
0,2
d, мм
Рис. 4. Зависимости U2i(d) для tmax: 1 — 5 мкс; 2 — 10 мкс; 3 — 18 мкс; 4 — 60 мкс; 5 — уровень чувствительности.
0
4
-5
3
-10
2
5
-15
1
-20
-25
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
x, мм
Рис. 5. Зависимости U2i(x) для клина при tmax: 1 — 5 мкс; 2 — 10 мкс; 3 — 18 мкс; 4 — 60 мкс; 5 — уровень
чувствительности.
Для определения оптимальных параметров импульсов магнитного поля при использовании
метода нулевого максимума провели исследование влияния величины напряженности магнитного
поля Н0m в (6) на результаты измерений, которые представлены на рис. 6. Графики 1 — 6 зависи-
мостей U21 — U26 на этом рисунке построены для времени нарастания импульса поля 5 мкс по
формуле:
H= Н0m (1+ 0,6366 arctg(19d + 250d2)).
(8)
Из рис. 6 видно, что максимальная чувствительность (и точность) измерений достигается в
интервале зависимостей от d = 0 до точек пересечения указанных зависимостей с прямой 7:
U27 = U0 + γd,
(9)
где U0 = -60 мВ; γ = 2330 мВ/мм. Из графиков на рис. 6 можно найти диапазоны чувствительности
при разных величинах Н0m.
Как показали исследования, зависимости Нrm(d) для пластин из свинца совпадают с аналогич-
ными зависимостями для пластин из алюминия при условии, что их толщина в 9 раз больше.
Удельная электропроводность свинца во столько же раз меньше удельной электропроводности
Дефектоскопия
№ 11
2022
20
В.В. Павлюченко, Е.С. Дорошевич
10
7
0
-10
1
2
3
-20
-30
4
-40
5
6
0
0,02
0,04
0,06
0,08
d, мм
Рис. 6. Зависимости U2i(d) для величины Н0m: 1 (- 80 А/см); 2 (- 90 А/см); 3 (- 100 А/см); 4 (- 110 А/см); 5 (- 120 А/см);
6 (- 130 А/см); 7 — уровень чувствительности U27.
алюминия. Тогда для объектов из свинца формулы для относительной напряженности будут
выглядеть следующим образом:
Нrm = 0,6366 arctg(11c + d /tmax + 77c2·d2 /t2max),
(10)
Нrm = 0,11564 + 0,563 arctg(11c · d /tmax + 77c2·d2 /t2max - 0,21),
(11)
Зависимости Нrm (d) для алюминия и свинца, рассчитанные по формулам (10) и (11), изображе-
ны на рис. 7.
1
1
0,8
2
0,6
0,4
3
4
0,2
0
0
0,02
0,04
0,06
0,08
0,1
d/ tmax, мм/мкс
Рис. 7. Зависимости Нrm (d): 1 и 2 для алюминия, построенные по (2) и (4), и зависимости 3 и 4 для свинца, построенные
по (10) и (11); tmax = 18 мкс.
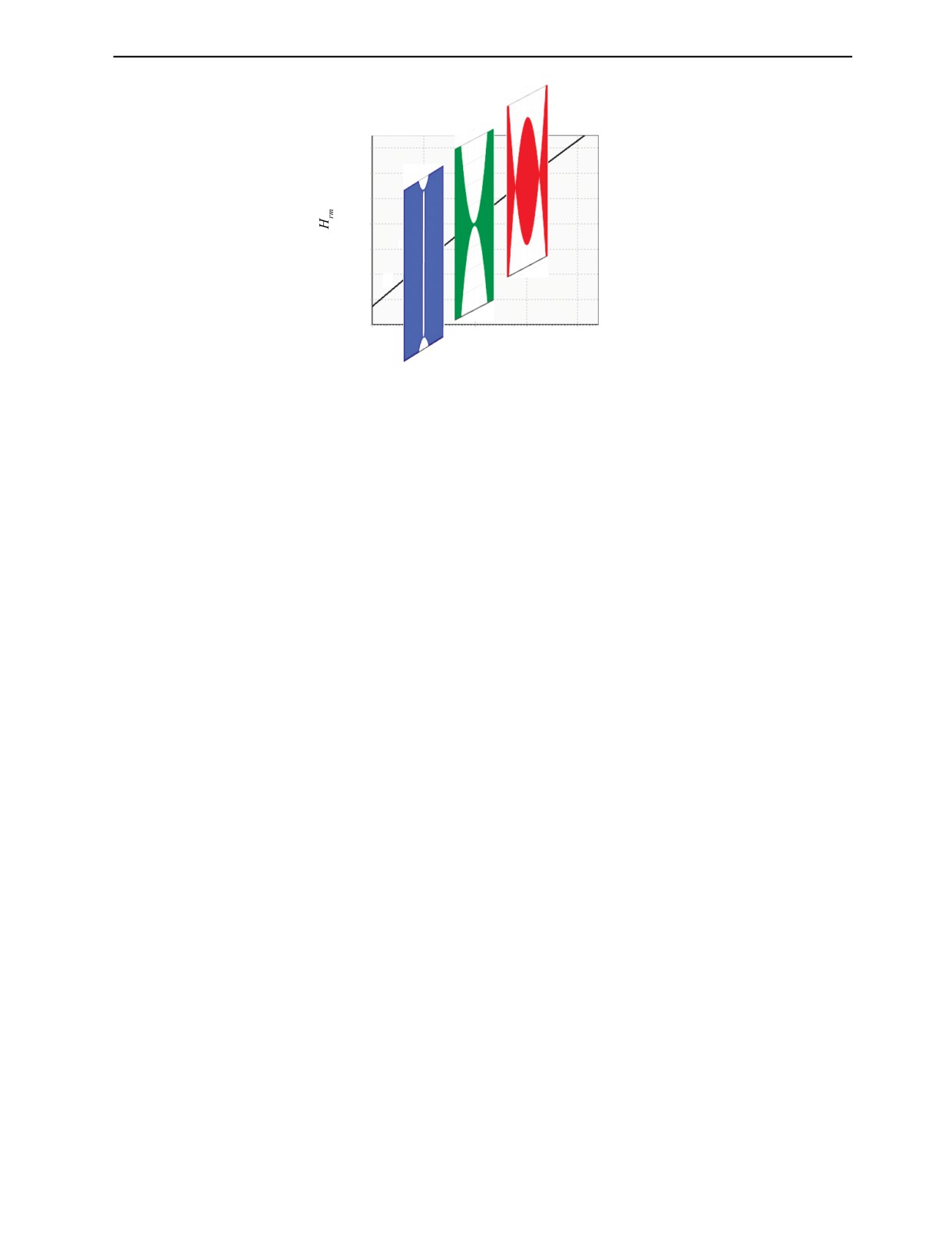
Пример использования полученных зависимостей Нrm (d) для пластин из алюминия разной
толщины при воздействии на них полем линейного индуктора с tmax = 10 мкс показан на рис. 8.
Здесь представлена зависимость 1 (часть зависимости 2, рис. 1) и оптические изображения маг-
нитных полей для этих пластин, совмещенные с соответствующими точками зависимости 1.
Размах сигнала составляет 1,7 мВ для толщины пластины 0,055 мм (отрезок белой вертикальной
прямой). Для пластины 0,06 мм он равен 0, а для пластины 0,065 мм размах сигнала составляет
-1,6 мВ. Отрицательный знак означает, что соответствующий участок МН перемагничен вторым
Дефектоскопия
№ 11
2022
Импульсное магнитное поле вблизи поверхности металла
21
4
3
0,46
0,44
2
0,42
0,4
0,38
0,36
0,34
1
0,32
0,05
0,06
0,065
0,07
d, мм
Рис. 8. Зависимость Нrm (d) 1 и оптические изображения магнитных полей 2, 3 и 4 для d соответственно 0,055 мм,
0,06 мм и 0,065 мм; tmax = 10 мкс.
импульсом поля противоположного направления. Здесь использован разработанный метод нулево-
го максимума, значительно повышающий чувствительность и точность контроля толщины объек-
тов. При этом найдены такие параметры двух импульсов магнитного поля, в результате воздей-
ствия которыми сигнал, снимаемый с МГ, равен 0 для пластины из алюминия толщиной 0,06 мм.
Диапазон измерения 1,7 мВ + 1,6 мВ = 3,3 мВ при интервале толщин 0,065 мм - 0,055 мм =
= 0,01 мм. Отсюда находим чувствительность 330 мВ/мм.
Чувствительность и точность контроля могут быть значительно повышены, если настройку на
нулевой уровень считываемого сигнала производить не в отсутствие объекта, а для объекта задан-
ной толщины, например для пластины толщиной 0,06 мм.
Из зависимостей (10) и (11) с учетом удельной электропроводности материалов могут быть
найдены также обобщенные зависимости H(d) для пластин из алюминия и свинца.
Получаемые гистерезисные картины не являются просто результатом алгебраических опера-
ций с изображениями магнитных полей. Они соответствуют реальным распределениям остаточ-
ных магнитных полей МН (остаточной намагниченности МН) в результате воздействия на них
последовательностями импульсов. Точность контроля в случае использования HI увеличивается, в
частности, благодаря тому, что увеличивается отношение величины измеряемого сигнала к диа-
пазону измерения. Поскольку количество вариантов составления серий из нескольких импульсов
по амплитуде, знаку, времени нарастания и их последовательности практически неисчерпаемо, то
можно получать разные соотношения максимумов интерференции в разных интервалах измере-
ния и составлять алгоритмы их оптимального использования.
Так как повышение точности определения толщины объектов связано с повышением точности
нахождения распределений импульсных магнитных полей на их поверхности, то полученные
гистерезисные картины позволяют повысить точность контроля удельной электропроводности их
материала и дефектов сплошности в них, как это показано в предшествующих работах авторов.
ВЫВОДЫ
На основании полученных экспериментальных зависимостей максимальной напряженности
вторичного импульсного магнитного поля вблизи поверхности металлических пластин от их тол-
щины H(d) найдены арктангенсные аналитические функции H(d), позволяющие повысить чув-
ствительность и точность контроля толщины металлических объектов, электропроводности их
материала и дефектов сплошности в них.
Зависимости H(d) представлены двумя практически равнозначными функциями арктангенс и
использованы для расчетов гистерезисной интерференции импульсного магнитного поля в отра-
женной волне. Зависимости H(d) получены с помощью дискретного датчика магнитного поля и
отнесены к напряженности поля первичного источника, в качестве которого использовали линей-
ный индуктор. Из полученных зависимостей с учетом удельной электропроводности материалов
могут быть найдены также обобщенные зависимости H(d) для пластин из алюминия и свинца.
Дефектоскопия
№ 11
2022
22
В.В. Павлюченко, Е.С. Дорошевич
СПИСОК ЛИТЕРАТУРЫ
1. Pavlyuchenko V.V., Doroshevich E.S. Nondestructive control of objects made of electroconductive
materials in pulsed magnetic fields // Russian Journal of Nondestructive Testing. 2010. V. 46. No. 1.
P. 810—818.
2. Pavlyuchenko V.V., Doroshevich E.S., Pivovarov V.L. Calculation of residual magnetic-field distributions
upon hysteretic interference of a pulsed magnetic field // Russian Journal of Nondestructive Testing.
2015.
V. 51. No. 1. P. 8—16.
3. Pavlyuchenko V.V., Doroshevich E.S. Imaging Electric Signals of a Magnetic Field Transducer with
Hysteretic Interference for Testing Metals in Pulsed Magnetic Fields // Russian Journal of Nondestructive
Testing. 2020. V. 56. No. 11. P. 907—914.
4. Астахов В.И., Данилина Э.М., Ершов Ю.К. К вопросу о диагностике пластины с трещиной вих-
ретоковым методом // Дефектоскопия. 2018. № 3. С. 39—49.
5. Киселев Е.К., Гольдштейн А.Е. Вихретоковая система контроля внутреннего диаметра труб //
Дефектоскопия. 2019. № 3. С. 25—30.
6. Ферстер Ф. Неразрушающий контроль методом магнитных полей рассеяния. Теоретические и
экспериментальные основы выявления поверхностных дефектов конечной и бесконечной глубины //
Дефектоскопия. 1984. № 12. С. 13—18.
7. Жданов А.Г., Щукис Е.Г., Лунин В.П., Столяров А.А. Алгоритмы предварительной обработки
вихретоковых сигналов при контроле теплообменных труб парогенераторов АЭС // Дефектоскопия.
2018. № 4. С. 54—64.
8. Печенков А.Н., Щербинин В.Е. Вихревые токи и поля проводящих и намагничивающихся шаро-
вых включений в немагнитную среду // Дефектоскопия. 2016. № 4. С. 48—55.
9. Санников М.А. Влияние кривизны поверхности трубопровода при диагностике вихретоковыми
приборами // Контроль. Диагностика. № 9. 2006. С. 24—27.
10. Pavlyuchenko V.V., Doroshevich E.S. Hysteretic Interference of Time-Overlapping Magnetic Field
Pulses // Russian Journal of Nondestructive Testing. 2019. V. 55. No. 12. P. 949—956.
11. Pavlyuchenko V.V., Doroshevich E.S. Differential Background of Electric Signal Readfrom an
Induction Magnetic Head // Russian Journal of Nondestructive Testing. 2021. V. 57. No. 8. P. 706—716.
12. Атавин В.Г., Узких А.А., Исхужин Р.Р. Отстройка от электропроводности основания при изме-
рении толщины токопроводящих покрытий методом вихревых токов // Дефектоскопия. 2018. № 1.
С. 58—64.
13. Лухвич А.А., Шарандо В.И., Шукевич А.К., Янушкевич К.И. Выявление ферромагнитной состав-
ляющей в нержавеющих сталях магнитодинамическим методом // Дефектоскопия. 2015.
№ 3.
С. 3—10.
14. Лухвич А.А., Булатов О.В., Лукьянов А.Л. Контроль толстослойных никелевых покрытий на
двухслойных (неферромагнетик—ферромагнетик) основаниях магнитодинамическим методом толщи-
нометрии // Дефектоскопия. 2014. № 4. С. 3—12.
15. Pavlyuchenko V.V., Doroshevich E.S. Testing for Defects in Pulsed Magnetic Field Transmitted
Through Metal // Russian Journal of Nondestructive Testing. 2021. V. 57. No. 10. P. 856—864. [Павлючен-
ко В.В., Дорошевич Е.С. Контроль дефектов в прошедшем через металл импульсном магнитном поле //
Дефектоскопия. 2021. № 10. С. 25—33.]
16. Суханов Д.Я., Совпель Е.С. Магнитоиндукционная томография электрических схем и приборов
// Известия высших учебных заведений. 2015. Т. 58. № 10/3. С. 73—75.
17. Скворцов Б.Г., Самсонов А.С., Борминский С.А., Живоносновская Д.М. Теоретические основы
контроля токопроводящих покрытий топливных баков летательных аппаратов // Дефектоскопия. 2017.
№ 5. С. 46—54.
Дефектоскопия
№ 11
2022