Общие вопросы дефектоскопии
УДК 620.179.1
МЕТОД ВЫДЕЛЕНИЯ ПРИЗНАКОВ ДЕФЕКТОВ ПОДШИПНИКОВ,
ОСНОВАННЫЙ НА РАЗЛОЖЕНИИ НА ВАРИАЦИОННЫЕ МОДЫ С ДРОБНЫМ
ФУРЬЕ-ПРЕОБРАЗОВАНИЕМ
© 2022 г. Мин Хуэй Вэй1,2,*, Лися Цзян1,2,**, Ди Чжан3,***,
Бин Ван4, Фэн Мяо Ту1,2, Пэн Бо Цзян1,2
1 Юго-западный нефтяной университет, Чэнду 610500, Китай
2Сычуаньский университет, Чэнду 610500, Китай
3Синьцзиньский филиал летной академии гражданской авиации Китая,
Чэнду 611430, Китай
43-607, Ченхуили, улица Дагана, Новый район Биньхай, Тяньцзинь, 300280,Китай
E-mail: *wmh881988@163.com; **jlx19982016@163.com; ***403750039@qq.com
Поступила в редакцию 23.10.2021; после доработки 23.12.2021
Принята к публикации 14.01.2022
Предложен новый метод выделения признаков дефектов, основанный на методе разложения на вариационные моды
с дробным фурье-преобразованием (ДФП-РВМ). Во-первых, основная идея этого метода заключается в выполнении
оптимального дробного фурье-преобразования (ДФП) исходного сигнала. Затем преобразованный сигнал подвергается
разложению на вариационные моды (РВМ). Для решения проблемы, заключающейся в сложности определения порядка
ДФП, предлагается метод центрального момента четвертого порядка (ЦМЧП) для определения оптимального порядка.
А использование критерия асимметрии и эксцесса (КАЭ) оптимизирует параметры РВМ. Вследствие этого может быть
оптимизирован и ДФП—РВМ. Наконец, вычисление эксцесса и фильтрации с помощью скользящего среднего (ФСС)
разложенного сигнала, чтобы реализовать извлечение признаков дефектов. Экспериментальные результаты исследова-
ния показывают, что сигналы, извлеченные этим методом, содержат все больше и больше явных характеристических
частот дефектов, что значительно повышает точность контроля дефектов в различных состояниях: нормального состоя-
ния подшипника, с дефектом внутреннего кольца, с дефектом тела качения, с дефектов наружного кольца и т.д.
Ключевые слова: дробное фурье-преобразование, разложение по вариационным модам, выделение признаков, диа-
гностика дефектов.
DOI: 10.31857/S0130308222030058
1. ВВЕДЕНИЕ
Подшипник качения является одной из важных частей вращающихся механизмов, входящих в
устройство таких транспортных средств, как локомотивы [1], подшипник имеет характеристики
сложной конструкции, высокоскоростного движения и большой нагрузки. Подшипники качения
являются одной из наиболее уязвимых частей вращающихся механизмов. Условия их эксплуата-
ции оказывают огромное влияние на оборудование, в состав которых входят вращающиеся меха-
низмы. Любая мелкая неисправность может повлиять на нормальную работу оборудования и
нанести огромный ущерб стране и людям [2]. Если дефекты в подшипнике можно диагностиро-
вать до того, как он выйдет из строя, то можно не только свести к минимуму потери, но и снизить
затраты на техническое обслуживание оборудования [3]. Поэтому необходимо диагностировать
неисправности подшипников качения. Однако при измерениях сигналы, свидетельствующие о
неисправностях подшипников качения, часто смешиваются с большим количеством сигналов
помех, что делает собранные сигналы нестационарными и нелинейными. Способ извлечения необ-
ходимой информации о характеристиках неисправностей из этих сигналов стал ключом к диагно-
стике неисправностей подшипников качения [4].
Huang и др. [5] предложил метод разложения на эмпирические моды (РЭМ), который адаптив-
но извлекает эмпирических моды, отражающие основные характеристики сигнала (в соответствии
с локальной структурой признаков сигнала на временной шкале), но алгоритму не хватает теоре-
тической поддержки, появятся конечные эффекты и модальное наложение, которые будут влиять
на результаты обработки сигнала. Wu Zhenhua и др. [6] представили шумовой метод анализа сиг-
налов при РЭМ и предложили множественное разложение на эмпирические моды (МРЭМ). Хотя
этот метод в определенной степени подавляет явление модового алиасинга, эффект не является
полным и будет создавать ложные компоненты, а добавление шума увеличивает ошибку восста-
новления. В 2014 г. Dragomiretskiy и др. [7] предложил разложение на вариационные моды, новый
нерекурсивный адаптивный метод обработки сигналов. В последние годы этот метод стал центром
Метод выделения признаков дефектов подшипников, основанный на разложении...
51
исследований, но они все лишь привели к улучшению в целочисленной области. Из-за ограниче-
ний самого алгоритма проблемы чрезмерного и недостаточного разложения неизбежны.
На основе вышеуказанных исследований в данной статье предлагается ДФП—РЭМ-метод
выделения признаков, основанный на оптимизации ЦМЧП и КАЭ. Во-первых, ЦМЧП использует-
ся для определения оптимального порядка ДФП. Сигнал подвергается ДФП оптимального поряд-
ка. Во-вторых, оптимальные параметры РВМ определяются по КАЭ, а преобразованный сигнал
подвергается РВМ. После этого коэффициенты эксцесса и ФСС разложенного сигнала рассчиты-
ваются как собственные векторы. Наконец, вектор признаков вводится в классификатор случайно-
го леса для контроля дефектов. По сравнению с методами разложения на вариационные моды,
эмпирические моды и множественное разложение на эмпирические моды, метод, предложенный
автором статьи, имеет более высокую точность распознавания.
Структура этой статьи следующая. Во втором разделе выводится модель ДФП и предлагается
метод определения ее оптимального порядка. В разделе 3 дается введение в РВМ и предлагается
лучший метод получения параметров. В разделе 4 описан процесс реализации алгоритма ДФП—
РВМ. В разделе 5 приведены эксперименты, иллюстрирующие эффективность предлагаемого
метода, а окончательные выводы приведены в разделе 5.
2. ДРОБНОЕ ФУРЬЕ-ПРЕОБРАЗОВАНИЕ
2.1. Определение дробного фурье-преобразования
ДФП, как более обобщенное фурье-преобразования в пространстве области преобразования,
позволяет представить сигнал на оси координат, повернутой на любой угол по оси времени, и в
определенной степени информация во временной области и информация в частотной области объ-
единяются. Затем выделяются некоторые его параметры [8]. Из-за нестационарного характера
сигнала неисправности в последние годы для диагностики неисправностей применялся метод
комбинирования ДФП и разложения сигнала [9—12]. Первым, кто дал его определение с матема-
тической точки зрения, был Namias [13], который проводил исследования и анализ с точки зрения
собственных значений и собственных функций:
Традиционное преобразование Фурье определяется как непрерывный линейный оператор,
существующий в пространстве сигналов. Характеристическое уравнение, соответствующее этому
оператору, имеет вид:
jnπ
−
2
(1)
ξψ
(t)
=λ
ψ
(t)
=
e
ψ
(t),
n
=
0,1,2,3,
n
n n
n
Уравнение (1) — это определение преобразования Фурье, данное с точки зрения собственных
значений и собственных функций, где λn — собственное значение; ψn(t) — собственная функция,
которая может быть выражена как ψn = Hn(t)e-t2/2, где Hn(t) — полином Эрмита порядка n и выра-
жается как
n
-t
2
2
n t
2 2
d
e
H t)
=
(−1)
e
(2)
n
n
dt
Как можно видеть из формулы (1), преобразование Фурье сигнала ψn эквивалентно произведе-
нию самого себя на комплексное число λn. Далее будет введено определение, которое может быть
непосредственно выведено из основного определения ДФП.
Определение 1: пусть ψn — собственная функция с собственным значением λn при обычном
преобразовании Фурье, выражаемая как функция Эрмита—Гаусса, и может быть использована как
собственная функция конечного пространства сигналов. Затем дробное фурье-преобразование
может быть определено как линейное и удовлетворять:
p
jnπ
jnpπ
-
-
p
p
2
2
ξ
ψ
(t)
=λ
ψ
(u)
=
e
ψ
(u)=e
ψ
(u),
n
=
0,1,2,3,
(3)
n
n n
n
n
Уравнение (3) определяет дробное фурье-преобразование через собственную функцию и соб-
ственное значение. Согласно выражению выше, функция с конечной энергией x(t) может быть
сначала разложена в линейную суперпозицию собственных функций фурье-преобразования, а
затем записана как
Дефектоскопия
№ 3
2022
52
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
∞
x t)
=
∑
n n
X ψ t),
(4)
n=0
где коэффициент разложения
X
=∫ψ t)x(t)dt
Тогда пусть ДФП по обеим концам формулы:
n
n
∞
jpnπ
∞
jpnπ
−
-
p
2
2
ξ
x t)
=
e
X ψ u)
=
e
ψ
(u)ψ
(t)x(t)dt
(5)
∑
n n
∫∑
n
n
n
=0
n
=0
Уравнение (5) называется спектральным разложением ядра ДФП, и функция Эрмита—Гаусса
ψn должна удовлетворять:
∞
jnπ
-
-
j2πut
2
e
=
∑
e
ψ
n
(u)ψ
n
(t),
(6)
n=0
∞
jnπ
2
2
-
jπ(
u
cotα-2utcscα+t
cotα)
2
1−
j
cot
α⋅e
=
e
ψ
(u)ψ
(t),
(7)
∑
n
n
n=0
где α = pπ/2. Из указанной выше формулы может быть видно, что когда p = 1, ДФП становится
традиционным фурье-преобразованием. В то же время основное определение ДФП [14]:
+∞
X u)
=
K u,t)x(t)
dt,
0<|
p
|<
2,
0<|α|<π,
(8)
P
∫
α
-∞
где Kα(u, t) — функция ядра ДФП:
2
2
jπ
(
t
cotα+u
cotα-2tucscα
)
B e
,α≠
nπ
α
K
α
(
u,t
)
=
x(u-t
),a
=
2
n
π
(9)
x
(u+t
),
a
=
(2n
±
1)π
-
jpnπ
2
Сравнивая формулу
(8) с формулой
(5), функции ядра
K
(
u,t
)
=
e
ψ
(u)
ψ
(t)
и
α
n
n
Pπ
B
1
jcot
/2
,
=(
−
α)
π
где α — это угол вращения, а связь с порядком p следующая:
α=
α
2
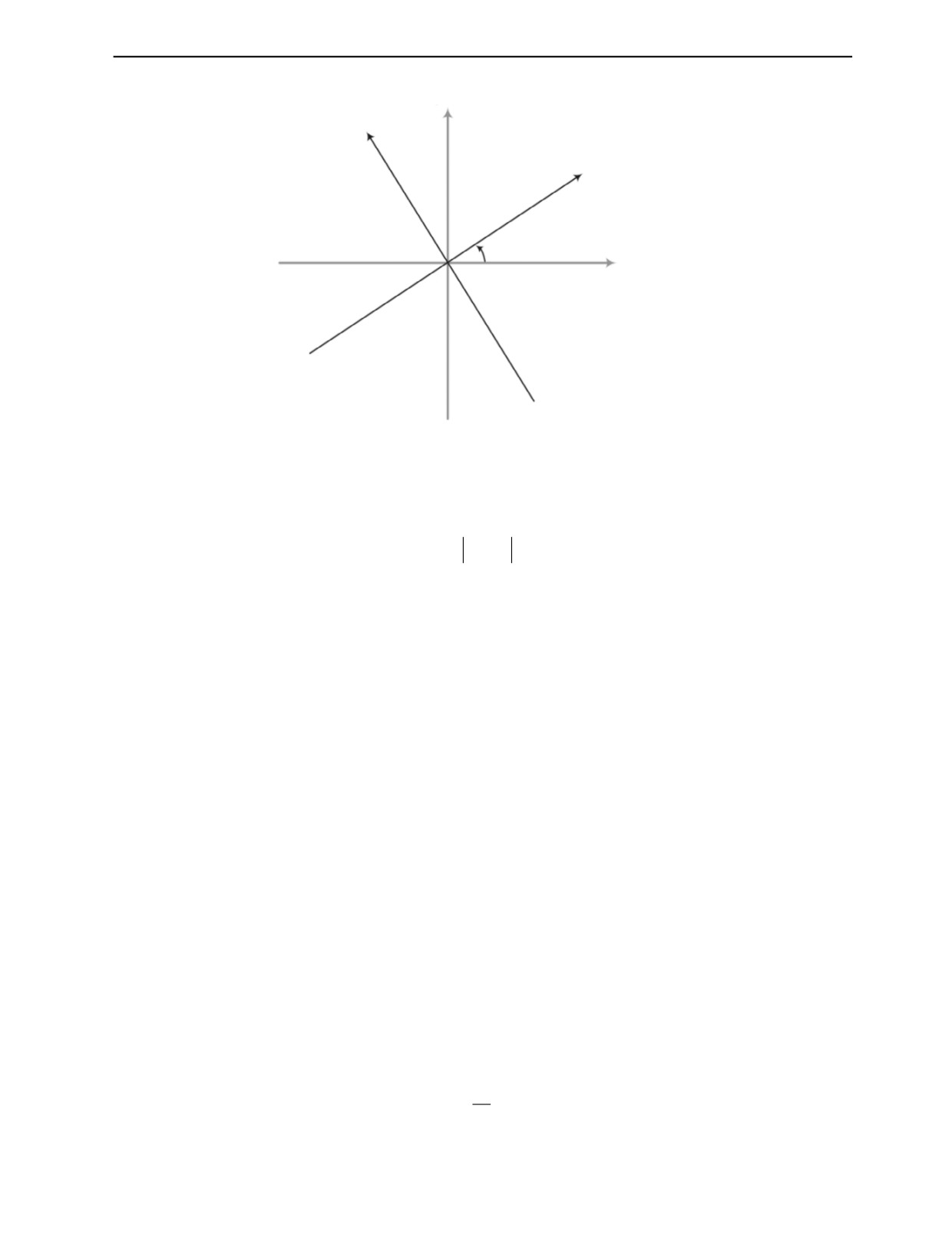
В 1993 г. Almeida указал на физический смысл ДФП. Он интерпретировал ДФП как вращение
в частотно-временной плоскости. Как показано на рис. 1, на частотно-временной плоскости осу-
ществляется вращение (t, ω) на угол α против часовой стрелки и его преобразование в домен (u, v),
чтобы получить новое представление сигнала. Следовательно, используя ДФП, можно проследить
преобразование всех характеристик сигнала из временной области в частотную, изменяя угол α
или порядок p.
2.2. Порядок выбора дробного фурье-преобразования
Сигнал может получить свою полосу пропускания во временной или частотной области
посредством оценки центрального момента второго порядка [15]. Из оценки центрального момен-
та второго порядка дробного фурье-преобразования сигнала можно получить ширину полосы
сигнала в области дробного фурье-преобразования [16, 17]. Но он очень чувствителен к помехам
и его оценочный эффект очень слаб, когда отношение сигнал/шум низкое, поэтому в этой статье
используется центральный момент четвертого порядка дробного фурье-преобразования:
∞
4
4
P
=
R u) (
u-m
)
du
,
(10)
α
∫
x
α
-∞
α
где
(
)
R
u
−α — порядок ДФП сигнала и mα — центральный момент первого порядка дробного
x
фурье-преобразования:
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
53
ω, F(ω)
υ
u, Fα(u)
α
-t, f(-t)
t, f(t)
0
-ω, F(-ω)
Рис. 1. Схематичная диаграмма вращения в частотно-временной плоскости при дробном фурье-преобразовании.
∞
2
m
R u)
udu
(11)
α
= ∫
x
−∞
Рассчитывая центральный момент четвертого порядка дробного фурье-преобразования, может
быть получен спектр центрального момента четвертого порядка дробного фурье-преобразования.
Когда сигнал имеет наименьшую полосу пропускания при дробном фурье-преобразовании, цен-
тральный момент четвертого порядка при ДФП сигнала будет иметь максимальное значение в
соответствующей области. Поскольку ДФП имеет период 2π и существует формула (12), в интер-
вале α∈[0, π) будет наблюдаться максимум. Значение величины α, соответствующее каждой ком-
поненте сигнала, может быть найдено при нахождении локального максимума. Такое значение
позволяет сигналам иметь наименьшую полосу пропускания в домене ДФП:
α
Rα+π u)=
R
(
−u).
(12)
x
x
3. РАЗЛОЖЕНИЕ НА ВАРИАЦИОННЫЕ МОДЫ
3.1. Определение разложения на вариационные моды
Основная идея алгоритма РВМ заключается в том, что большая часть каждой моды исходного
сигнала тесно связана с конкретной центральной частотой [18, 19]. С помощью фильтрации
Винера, смешения частот и преобразования Гильберта проблема полосы пропускания каждой под-
моды разбивается на несколько задач ограничения, а затем используется ряд итерационных мето-
дов решения для получения оптимального решения центральной частоты [20]. По сравнению с
традиционным методом РЭМ, математическая основа РВМ является более прочной, с лучшими
характеристиками сходимости и большей надежностью [21].
Таким образом, РВМ окончательно раскладывает заданный сигнал f(t) на k ЭМ и обеспечивает,
чтобы сумма общей ширины полосы разложенных ЭМ была наименьшей. Опишем дальнейшие
шаги реализации алгоритма. Во-первых, получить аналитический сигнал каждой ЭМ посредством
преобразования Гильберта и рассчитать соответствующий односторонний частотный спектр [22]:
j
δ
(t)
+
⋅
k
u t).
(13)
πt
Дефектоскопия
№ 3
2022
54
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
После этого оценивается центральная частота каждой ЭМ, и частотный спектр каждой ЭМ
модулируется в соответствующую полосу частот посредством смешения частот:
j
-
jw
k
δ
(t)
+
⋅u t)
⋅e
t
(14)
k
πt
Наконец, для расчета нормы квадрата градиента сигнала модуляции L2 используется гауссова
фильтрация. И, исходя из этого, оценивается полоса пропускания каждой ЭМ, а сумма ЭМ полос
пропускания минимизируется посредством уравнения ограничения. Выражение уравнения:
j
t
2
min
|| d
[(δ(t) +
)⋅
e jωk
] ||
∑
t
2
{u
k
},{ω
k
}
πt
k
,
(15)
st
u
=
f
∑
k
k
где dt представляет собой частную производную по времени t; функции {uk}={u1, u2, u3, …, uk}
представляют собой k-е ЭМ-компоненты, полученные при разложении сигнала {ωk}={ω1, ω2, ω3,
…, ωk}, F — центральная частота каждой ЭМ. Вводится расширенное уравнение Лагранжа с
квадратичной поправкой на потери α и оператором множителя Лагранжа λ, так что вышеуказан-
ное вариационное уравнение ограничения преобразуется в вариационное уравнение без ограни-
чений и получается оптимальное решение модели:
j
−
jω
k
t
2
2
L({u
k
},{ω λ)k
=α
∑
||[(δ(t) +
)⋅
k
u t)]⋅e
||
2
+
||
f t) −
∑
k
u t)||
2
+ λ(t),
f t) −
∑
k
u t)
(16)
k
π
t
k
k
Из-за увеличения поправки на потери и оператора множителя Лагранжа модель имеет боль-
шую точность распознавания и более строгие ограничения при наличии белого гауссова шума.
n+1
Метод переменного направления множителей используется для поочередного обновления
u
,
k
n+1
n+1
ω
k
и
λ
в уравнении (16), чтобы получить седловую точку уравнения в вариациях без ограни-
чений:
n+1
j
−
jω
t
2
2
k
u
=
argmin
α δ(t)
+
)
⋅u t)]⋅
e
||
)+
||
f t) −
u t)||
,
(17)
k
k
2
∑
i
2
πt
i
n+1
n
где ωk эквивалентно
ω
, а
u t)
также эквивалентно
u + t)
. Затем используется эквиди-
k
∑
i
∑
i
i≠k
i≠k
стантное преобразование Фурье для преобразования вышеуказанного уравнения в частотно-вре-
менной области и ω - ωk, чтобы провести замену переменной на ω для получения следующего
уравнения:
^
^
n+1
2
u
=
argmin
α
(|| j(ω-ω
)[(1
+ ω))u
(ω)]||
) +κ
k
{
k
k
2
}
^
(18)
^
^
2
λ ω
2
||
κ= ω
f
−
u
(ω)
+
||
∑
i
2
i
2
Используя преимущество симметрии эрмитового реального сигнала, уравнение (18) преобра-
зуется в интегральное уравнение в полупространстве с неотрицательной частотой. Вместе с этим
n+1
обновленное уравнение
u
может быть получено при квадратичной оптимизации:
k
^
^
^
2
λ ω
f
(ω)
-
u
(ω)
+
^
∑
i
(19)
n+1
i≠k
2
u
(ω)
=
k
2
1
+2α
(
ω-ω
)
k
Схожим образом, в соответствии с условием ограничения минимальной суммы пропускных
полос, задача минимума преобразуется в частотную область с использованием эквидистантного
n+1
n+1
преобразования Фурье и получается переменное обновленное уравнение
ω
k
и
λ
:
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
55
^
∞
2
| u
ω ω)|
dω
∫
k
n+1
0
ω
=
,
(20)
k
∞
^
2
| u
(ω)|
dω
∫
k
0
n+1
n
n+1
λ
=λ
+τ(
f t)
u
).
k
−∑
k
(21)
k
РВМ использует метод рекурсивного цикла для разделения исходного сигнала слой за слоем
[23], эффективно избегая недостатков модального алиасинга РЭМ, и имеет возможность адапта-
ции [24]. В то же время РВМ использует принцип фильтра Винера для построения задачи с вари-
ационными ограничениями, так что сигнал может быть эффективно и точно разложен в условиях
интерференции гауссовского шума [30]. Полученная мода частотной модуляции и амплитудной
модуляции (ЧМ—АМ) преобразуется во временной области по эквидистантной теореме Фурье, а
затем получаются полоса пропускания и центральная частота каждого компонента, так что каждая
мода отражает характеристики различных частотных диапазонов разложенного сигнала [25].
3.2. Выбор параметров алгоритма разложения на вариационные моды
Хотя алгоритм РВМ преодолевает недостатки традиционного РЭМ и его усовершенствованных
методов, необходимо установить уровень разложения K и поправку на потери α перед разложением.
Выбор параметров оказывает большое влияние на результаты разложения [26]. В этой статье для
оптимизации параметров используется КАЭ [27]. Эксцесс — это числовая статистическая величи-
на, отражающая распределение случайных величин. Это безразмерный параметр, очень чувстви-
тельный к импульсным сигналам [28]. Эксцесс демонстрирует высокую повторяемость в подшип-
никах. В момент, когда подшипник только вводится в эксплуатацию, будучи исправным, распреде-
ление амплитуды его вибрационного сигнала близко к нормальному распределению, а значение
эксцесса составляет около 3. Когда подшипник начинает выходить из строя, амплитуда сигнала
будет значительно отклоняться от нормального распределения, а значение эксцесса будет соответ-
ственно увеличиваться. В таком случае можно считать, что произошла поломка. И значение экс-
цесса при разных неисправностях подшипника также будет разным [29, 30]. Стандартное отклоне-
ние может отражать степень дисперсии между отдельными элементами в группе набора данных и
результат измерения величины дисперсии. КАЭ может отражать разницу между различными ЭМ
после РВМ. Чем больше КАЭ, тем больше разница между различными ЭМ.
4. АЛГОРИТМ РАЗЛОЖЕНИЯ, ОСНОВАННЫЙ НА ДФП—РВМ
В данной статье предлагается новый метод выделения признаков при ДФП—РВМ, основан-
ный на ЦМЧП—СКОЭ-оптимизации. Основная идея этого метода состоит в том, чтобы отобра-
зить плохо разделяемые данные в исходных данных в соответствующее пространство дробного
порядка, а затем провести РВМ. Экспериментальные данные предоставлены подшипниковым
дата-центром электротехнической лаборатории Западного резервного университета Кейза. Модель
подшипника качения SKF6205. Скорость вращения двигателя составляет 1797 об/мин, а частота
дискретизации — 12 кГц. Диаметр дефекта подшипника со стороны привода составляет 0,1778
мм. Характеристическая частота данных неисправности составляет 107,365 Гц. Конкретные шаги
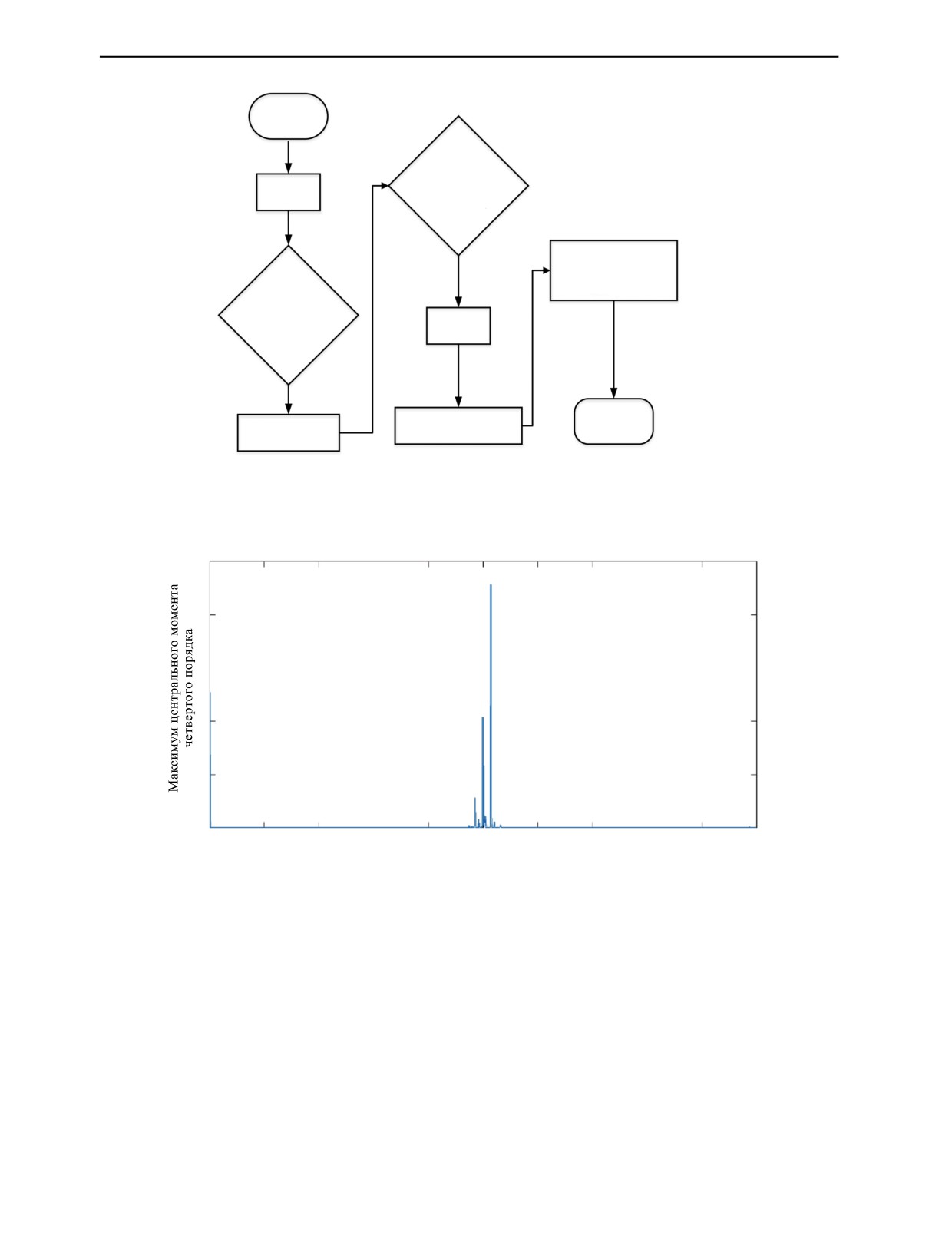
и блок-схема следующие (рис. 2).
Шаг 1: после вычисления центрального момента четвертого порядка каждого дробного поряд-
ка находится максимальное значение центрального момента четвертого порядка; соответствую-
щий угол преобразования является оптимальным углом ДФП, по данным выполняется оптималь-
ное ДФП.
Шаг 2: рассчитывается КАЭ, при котором α увеличивается с 1000 до 10000 с шагом 100. K
увеличивается с 2 до 11 с шагом 1. Выполняется оптимизация поправки на потери α и уровня раз-
ложения K, затем производится РВМ по данным после ДФП.
Шаг 3: выполняется обратное ДФП на каждой ЭМ после РВМ.
Шаг 4: выполняется анализ спектра огибающей по каждой ЭМ.
Из рис. 3 видно, что когда X равно 1,028, значение центрального момента четвертого порядка
является наибольшим, поэтому оптимальный порядок ДФП равен 1,028. Затем рассчитывается
КАЭ, где поправка на потери α увеличивается от 1000 до 10000 с шагом 100. K увеличивается с 2
Дефектоскопия
№ 3
2022
56
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
Старт
Максимум
коэффициента
Cигнал
эксцесса
Анализ спектра
огибающей
Максимум
центрального
момента
РВМ
четвертого
порядка
Конец
Оптимальное
Обратное ДФП
ДФП
Рис. 2. Блок-схема ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ.
×1013
5
4
3
2
1
00
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
Дробный порядок
Рис. 3. Порядок ДФП.
до 11 с шагом 1. Из рис. 4 видно, что поправка на потери α увеличивается в 15 раз, что равно 2500,
а число уровней разложения K увеличивается в три раза, что равно 4. Видно, что оптимальные
параметры α и K РВМ равны 2500 и 4 соответственно.
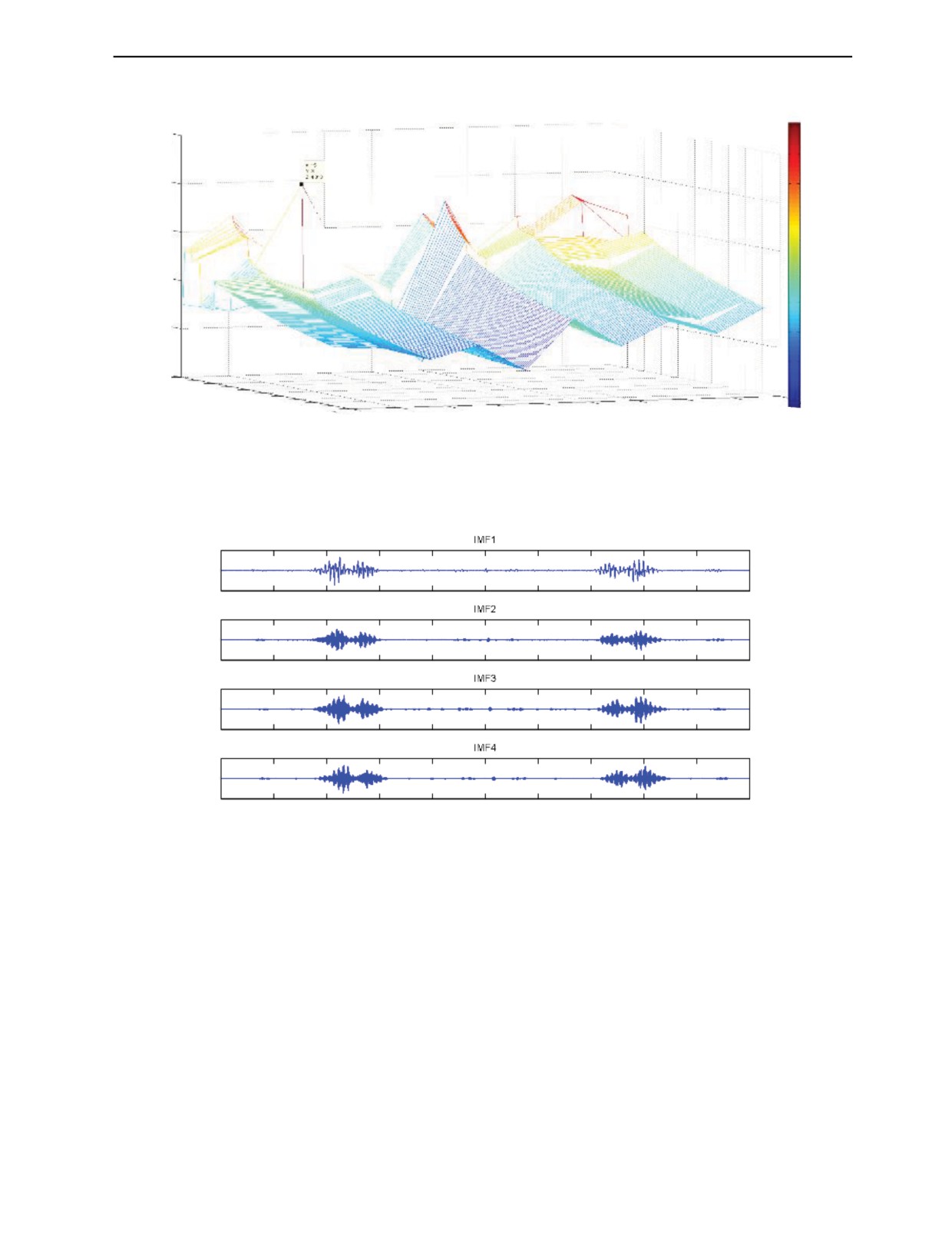
Из рис. 6 видно, что как разложение РВМ, так и ДФП—РВМ, оптимизированное по ЦМЧП—
КАЭ могут эффективно извлекать характеристическую частоту дефекта 107 Гц в сигнале от дефек-
та. Однако ЭМ1 из РВМ, очевидно, не может выделить характеристическую частоту дефекта, а
четыре ЭМ, основанные на ДФП—РВМ, оптимизированные по ЦМЧП—КАЭ, предлагаемые в
этой статье, вполне могут выделить среднюю характеристическую частоту дефекта и ее частотное
умножение.
В то же время, сравнивая амплитуду характеристической частоты, извлеченную двумя метода-
ми, амплитуда характеристической частоты и соответствующий ей умножитель частоты на основе
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
57
Поправка на потери и уровень разложения
4
4,5
3,8
4
3,6
3,4
3,5
3,2
3
3
2,8
2,5
2,6
2,4
2
010
20
30
2,2
40
50
60
10
11
70
80
7
8
9
90
4
5
6
100
2
3
α
K
Рис. 4. Оптимизация поправок на потери и уровни разложения.
2
0
-2
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
2
0
-2
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
2
0
-2
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
2
0
-20
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
Рис. 5. Компоненты ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ.
метода ДФП—РВМ, оптимизированного по ЦМЧП—СКОЭ, очевидно больше амплитуды харак-
теристической частоты, полученной из РВМ. Выше показано, что метод, предложенный в данной
статье, может предоставить более эффективную информацию о характеристиках дефекта для диа-
гностики подшипников.
5. ЭКСПЕРИМЕНТАЛЬНОЕ ПОДТВЕРЖДЕНИЕ
5.1. Процедура эксперимента
В этом разделе для дальнейшей проверки роли этого метода в диагностике дефектов подшип-
ников для экспериментальной проверки будут использованы данные из базы данных Западного
резервного университета и данных, полученных на построенной в этом университете эксперимен-
тальной платформе. Конкретный экспериментальный процесс показан на рис. 7.
Дефектоскопия
№ 3
2022
58
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
a
б
Рис. 6. Спектр огибающей каждой компоненты:
a — спектр огибающей компоненты ДФП—РВМ, основанный на ЦМЧП—КАЭ; б — спектр огибающей каждой компоненты РВМ.
Старт
Максимум
Случайный лес
Cигнал
коэффициента
эксцесса
Максимум
центрального
Точность
момента
расчета
РВМ
четвертого
порядка
Расчет собственного
Конец
Оптимальное
вектора
ДФП
Рис. 7. Блок-схема эксперимента.
5.2. Диагностика дефектов
Используемые экспериментальные данные взяты из базы данных подшипников Западного
резервного университета. Экспериментальная платформа состоит из двигателя мощностью
1,5 Вт, датчика крутящего момента, тестера мощности и электронного контроллера. Дефект под-
шипника — это одноточечное повреждение от электроискровой обработки (ЭИО). Модель под-
шипника SKF6205, частота дискретизации 12 кГц. Используемые данные являются нормальны-
ми базовыми данными для скорости 1797 об/мин. Дефектные подшипники так же вращались со
скоростью 1797 об/мин, а диаметр неисправности составляет 0,1778 мм. Временная диаграмма
данных показана на рис. 8.
Чтобы проиллюстрировать эффективность ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ
при извлечении признаков дефектов сигналов подшипника, в этой статье в качестве векторов при-
знаков дефектов используются коэффициент эксцесса и ФСС. Коэффициент эксцесса и ФСС очень
чувствительны к импульсному сигналу дефекта подшипника. Когда подшипник выходит из строя,
значения этих двух характеристик значительно изменяются [31]. Векторы признаков, извлеченные
с помощью ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ, и векторы признаков, извлеченные
с помощью РВМ, РЭМ и МРЭМ, соответственно кластеризуются. Из графика результатов класте-
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
59
Норма
0,5
0
-0,5
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
×104
Дефект внутреннего кольца
2
0
-2
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
×104
Дефект тела качения
1
0
-1
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
×104
Дефект внешнего кольца
5
0
-5
0
0,2
0,4
0,6
0,8
1
1,2
1,4
1,6
1,8
2
×104
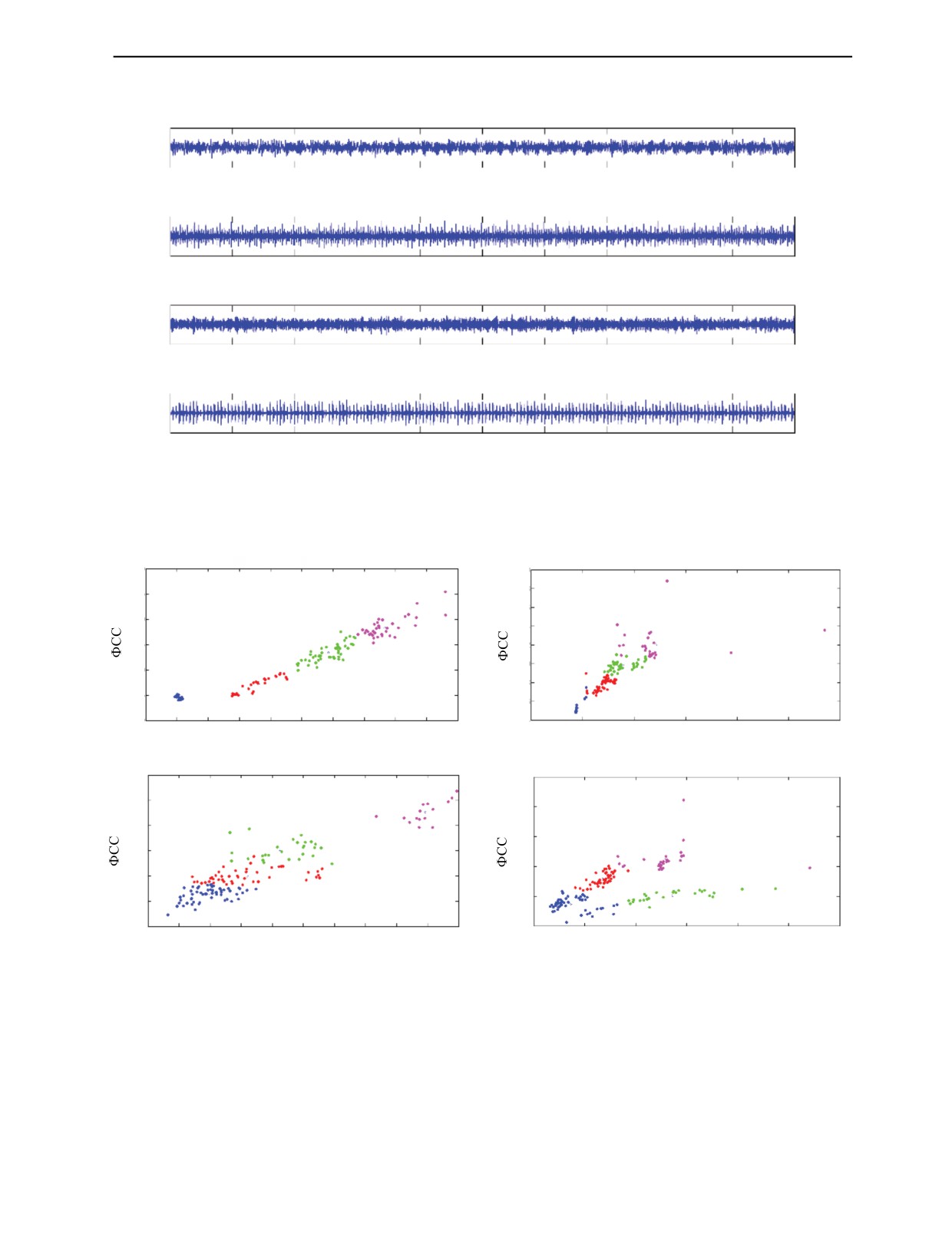
Рис. 8. Исходная временная диаграмма подшипника в каждом состоянии.
a
б
ДФП—РВМ
РВМ
30
20
18
25
16
20
14
15
12
10
10
8
5
6
0
4
0
5
10
15
20
25
30
35
40
45
50
0
2
4
6
8
10
12
Коэффициент эксцесса
Коэффициент эксцесса
в
г
РЭМ
МРЭМ
18
30
16
25
14
20
12
15
10
8
10
5
62
2,5
3
3,5
4
4,5
5
5,5
6
6,5
7
2
4
6
8
10
12
14
Коэффициент эксцесса
Коэффициент эксцесса
Рис. 9. График результатов кластеризации:
a —график кластеризации дробного РМВ; б — график результата кластеризации РВМ; в — график кластеризации РЭМ; г — график
кластеризации МРЭМ.
ризации на рис. 9 видно, что векторы признаков, извлеченные с помощью ДФП—РВМ, оптимизи-
рованного по ЦМЧП—КАЭ, обладают сильными свойствами кластеризации. Однако эффект кла-
стеризации векторов признаков, извлеченных с помощью РВМ, РЭМ и МРЭМ, слабый, а типы
дефекты нечеткие и разрозненные.
Дефектоскопия
№ 3
2022
60
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
Чтобы в дальнейшем проверить эффективность предложенного метода, в этой статье в каче-
стве векторов признаков дефекта используются коэффициенты эксцесса и ФСС, а для диагностики
неисправности используется классификатор случайного леса [32]. Во-первых, различные типы
неисправностей разделены на 10 групп по 10 000 данных, которые в общей сложности разделены
на 40 групп данных. Выполняется ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ для этих 40
наборов данных. Во-вторых, коэффициент эксцесса и ФСС извлекаются из полученных ЭМ в виде
векторов признаков дефектов. Для каждого типа неисправности будет получено 40 наборов векто-
ров признаков коэффициента эксцесса и ФСС. Наконец, 32 группы различных типов дефектов
используются в качестве обучающего набора классификатора случайного леса, а 8 групп исполь-
зуются в качестве данных тестового набора для проверки точности классификации всей модели.
Количество каждого состояния подшипника — как показано в табл. 1. Устанавливается количество
деревьев решений в классификаторе случайного леса равным 800, а затем выполняется диагности-
ка дефектов. Используется РВМ, РЭМ и МРЭМ для извлечения соответствующих векторов при-
знаков дефектов из одних и тех же данных и отправки их в классификатор случайного леса для
диагностики дефектов.
Таблица
1
Число подшипников в различных состояниях
Состояние подшипника
Обучающий набор
Тестовый набор
Номер
Норма
32
8
1
Дефект внутреннего кольца
32
8
2
Дефект тела качения
32
8
3
Дефект внешнего кольца
32
8
4
a
б
5
5
Тестовый набор
Тестовый набор
Результаты расчета
Результаты расчета
4
4
3
3
2
2
1
1
0
0
0
Норма Внутреннее кольцо Тело качения Внешнее кольцо
Норма Внутреннее кольцо Тело качения Внешнее кольцо
Типы дефектов
Типы дефектов
в
г
5
5
Тестовый набор
Тестовый набор
Результаты расчета
Результаты расчета
4
4
3
3
2
2
1
1
0
0
Норма Внутреннее кольцо Тело качения Внешнее кольцо
0
0
Норма Внутреннее кольцо Тело качения Внешнее кольцо
Типы дефектов
Типы дефектов
Рис. 10. График результатов классификации:
a — диаграмма результатов ДФП—РВМ-классификации; б — диаграмма результатов РВМ-классификации; в — диаграмма результатов
РЭМ-классификации; г — диаграмма результатов МРЭМ-классификации.
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
61
В ходе контроля тестового набора результаты классификации четырех методов показаны на
рис. 10. Из рисунка видно, что векторы признаков между различными типами дефектов, извлечен-
ные методом выделения признаков ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ, могут быть
лучше идентифицированы и классифицированы. График результатов классификации показывает,
что прогнозируемый результат в основном соответствует ожидаемому значению. В результатах
классификации трех других методов наблюдается большое расхождение между прогнозируемым
результатом и ожидаемым значением.
Результаты классификации при использовании четырех различных методов обобщены
в табл. 2—5 соответственно. Общая точность процедуры классификации, полученная с исполь-
зованием метода выделения признаков ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ,
составляет 93,75 %. Общая точность классификации на основе РВМ-метода выделения призна-
ков составляет 78,1 %. Общая точность классификации на основе РЭМ-метода выделения при-
знаков составляет 68,75 %. Общая точность классификации, основанной на методе выделения
признаков МРЭМ, составляет 75 %. Экспериментальные результаты показывают, что векторы
признаков, полученные на основе дробного РЭМ, имеют лучшее разрешение.
Таблица
2
Результаты ДФП—РВМ-классификации
Количество правильно
Состояние
Размер дефекта,
Обучающая
Номер
классифицированных
Точность, %
подшипника
мм
выборка
образцов
Норма
-
1
8
8
100
Дефект
внутреннего
0,1778
2
8
8
100
кольца
Дефект тела
0,1778
3
8
8
100
качения
Дефект
внешнего
0,1778
4
8
7
87,5
кольца
Итог
-
-
32
31
96,875
Таблица
3
Результаты РВМ-классификации
Количество правильно
Состояние
Размер дефекта,
Обучающая
Номер
классифицированных
Точность, %
подшипника
мм
выборка
образцов
Норма
-
1
8
4
50
Дефект
внутреннего
0,1778
2
8
8
100
кольца
Дефект тела
0,1778
3
8
8
100
качения
Дефект
внешнего
0,1778
4
8
5
62,5
кольца
Итог
-
-
32
25
78,1
Дефектоскопия
№ 3
2022
62
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
Таблица
4
Результаты РЭМ-классификации
Количество правильно
Состояние
Размер дефекта,
Обучающая
Номер
классифицированных
Точность, %
подшипника
мм
выборка
образцов
Норма
-
1
8
6
75
Дефект
внутреннего
0,1778
2
8
5
62,5
кольца
Дефект тела
0,1778
3
8
5
62,5
качения
Дефект
0,1778
4
8
6
75
внешнего кольца
Итог
-
-
32
22
68,75
Таблица
5
Результаты МРЭМ-классификации
Количество правильно
Состояние
Размер дефекта,
Обучающая
Номер
классифицированных
Точность, %
подшипника
мм
выборка
образцов
Норма
-
1
8
5
62,5
Дефект
внутреннего
0,1778
2
8
6
75
кольца
Дефект тела
0,1778
3
8
6
75
качения
Дефект
внешнего
0,1778
4
8
7
87,5
кольца
Итог
-
-
32
24
75
5.3. Диагностика на наличие дефектов по данным измерений
В этом разделе проводятся эксперименты по диагностике неисправностей по данным, измерен-
ным на самодельной экспериментальной установке для подшипников качения. Экспериментальная
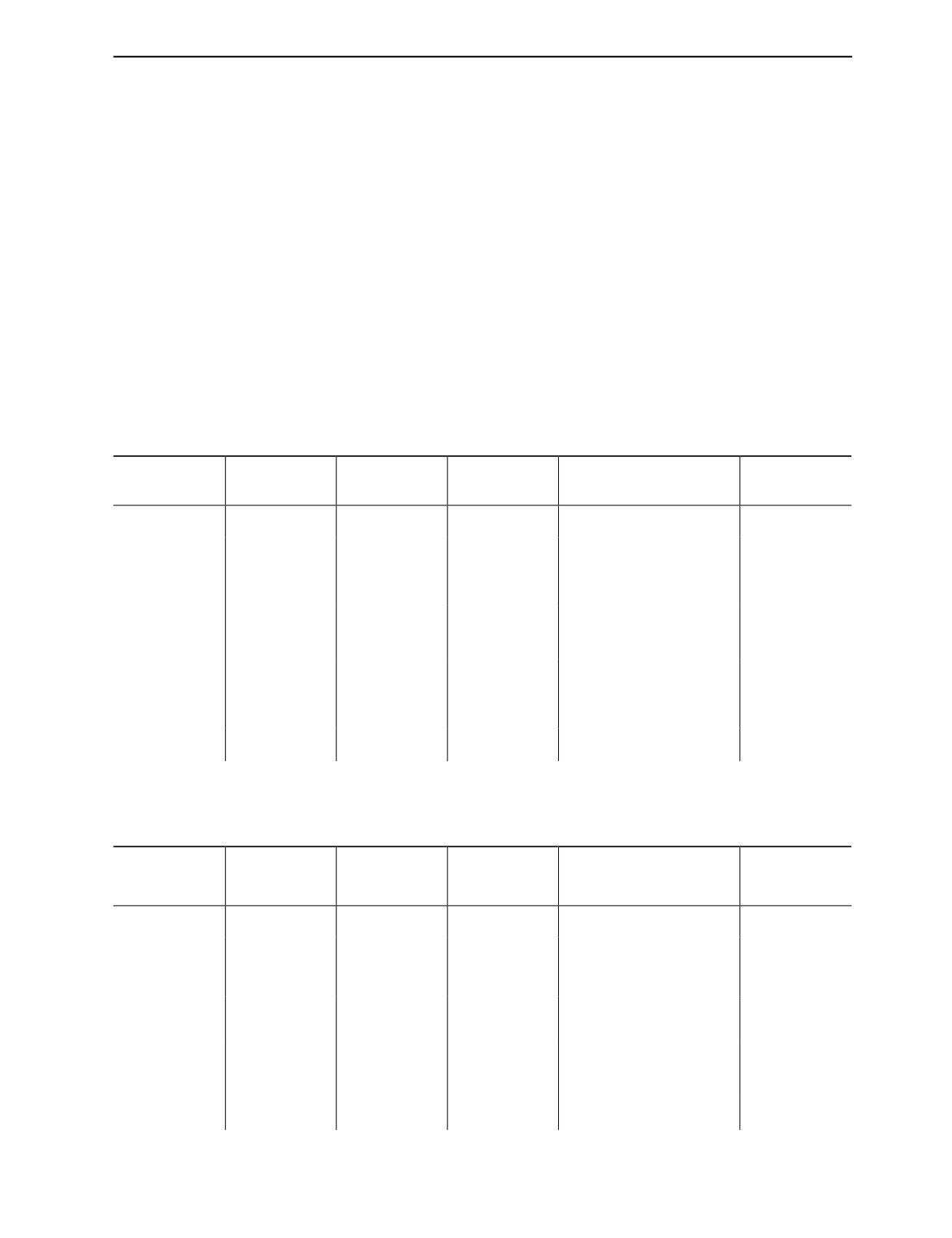
установка для работы с подшипниками качения состоит из двух частей: вращающегося механизма
и системы сбора данных (как показано на рис. 11). Часть вращающегося механизма состоит из
нормальных/дефектных подшипников и трехфазного двигателя с короткозамкнутым ротором.
Подшипник устанавливается на конце вращающегося вала трехфазного двигателя с короткозам-
кнутым ротором, а скорость вращения измеряется фотоэлектрическим датчиком. Система сбора
данных состоит из датчика ускорения ICP, установленного на валу двигателя, и 24-битного сете-
вого устройства для распределенного сбора данных INV 3060A (включает встроенное служебное
программное обеспечение Coinv DASP V10 для сбора данных). Дефект подшипника получают при
помощи ЭИО. Прямую линию глубиной и шириной 0,2 мм получают на внутреннем кольце, на
внешнем кольце и на шаре для имитации их дефектов. Частота дискретизации составляет 12 кГц,
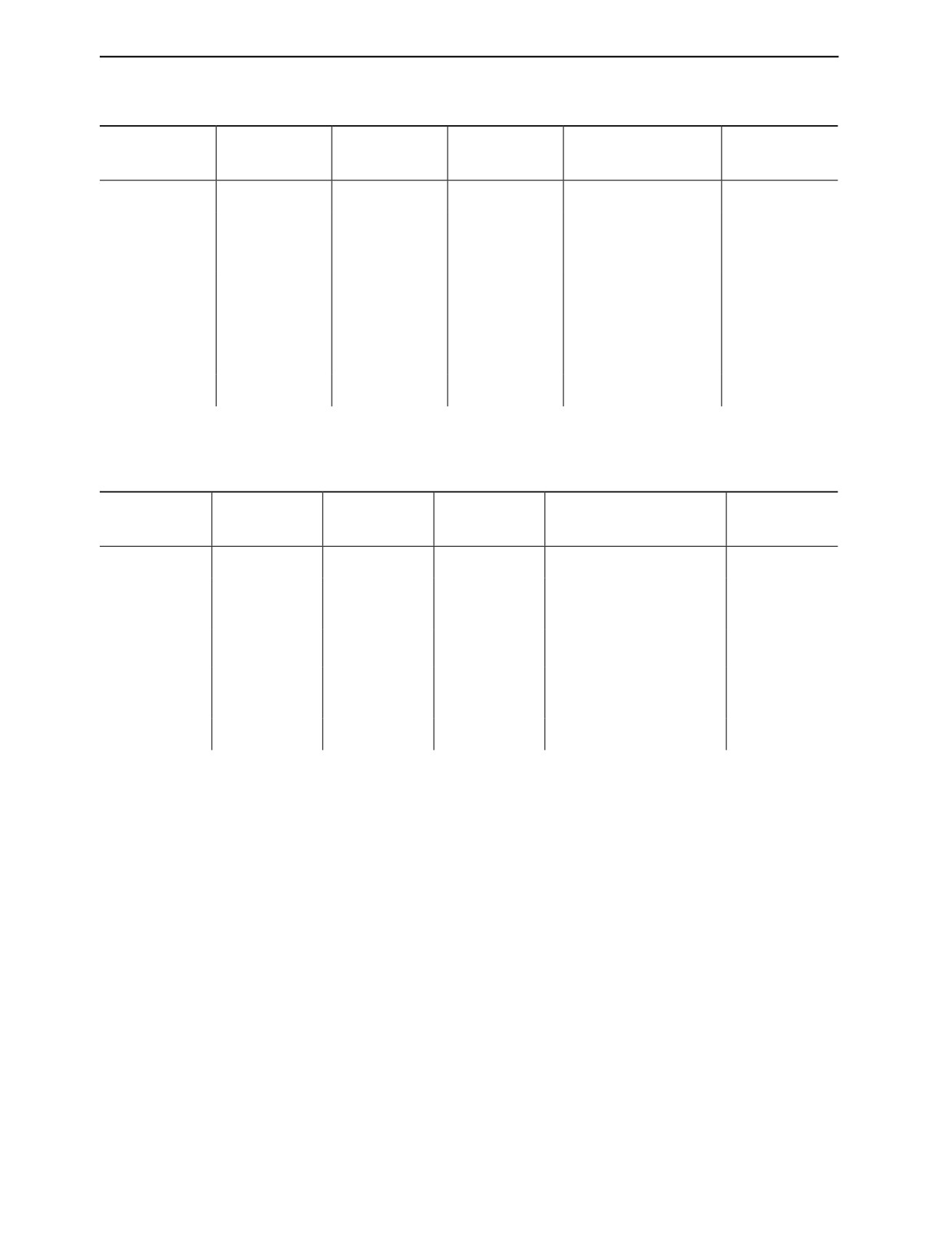
а экспериментальная установка показана на рис. 12.
С помощью экспериментальную установки получены данные по вибрации для четырех
состояний, количество данных составило около 119 000 точек. В первую очередь, данные по
вибрации для каждого состояния подшипника разделяются и группируются так, что каждая
группа имеет 10 000 точек из выборки и итого имеется 20 групп для каждого состояния подшип-
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
63
Фотоэлектрический
Вращающийся
Система сбора
датчик скорости
механизм
данных
вращения
Дефектные/
Вал трехфазного
24-битное сетевое
бездефектные
двигателя с
Датчик ускорения
устройство для
Данные
подшипники
короткозамкнутым
ICP типа INV9822A
распределенного сбора
о вибрации
качения
ротором
данных
Рис. 11. Блок-схема экспериментальной установки.
Рис. 12. Внешний вид экспериментальной установки.
ника. В общей сложности имелось 80 наборов данных. Во-вторых, над 80 наборами данных
были было проведено ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ. Затем из полученных
ЭМ извлекаются коэффициенты эксцесса и ФСС в виде векторов признаков дефекта. Каждому
типу дефекта соответствует 80 наборов собственных векторов коэффициента эксцесса и ФСС.
Наконец, 50 групп для различных типов дефектов используются в качестве обучающего набора
для классификатора случайного леса, а 30 групп используются в качестве контрольных данных
для проверки точности классификации всей модели. Количество решающих деревьев в класси-
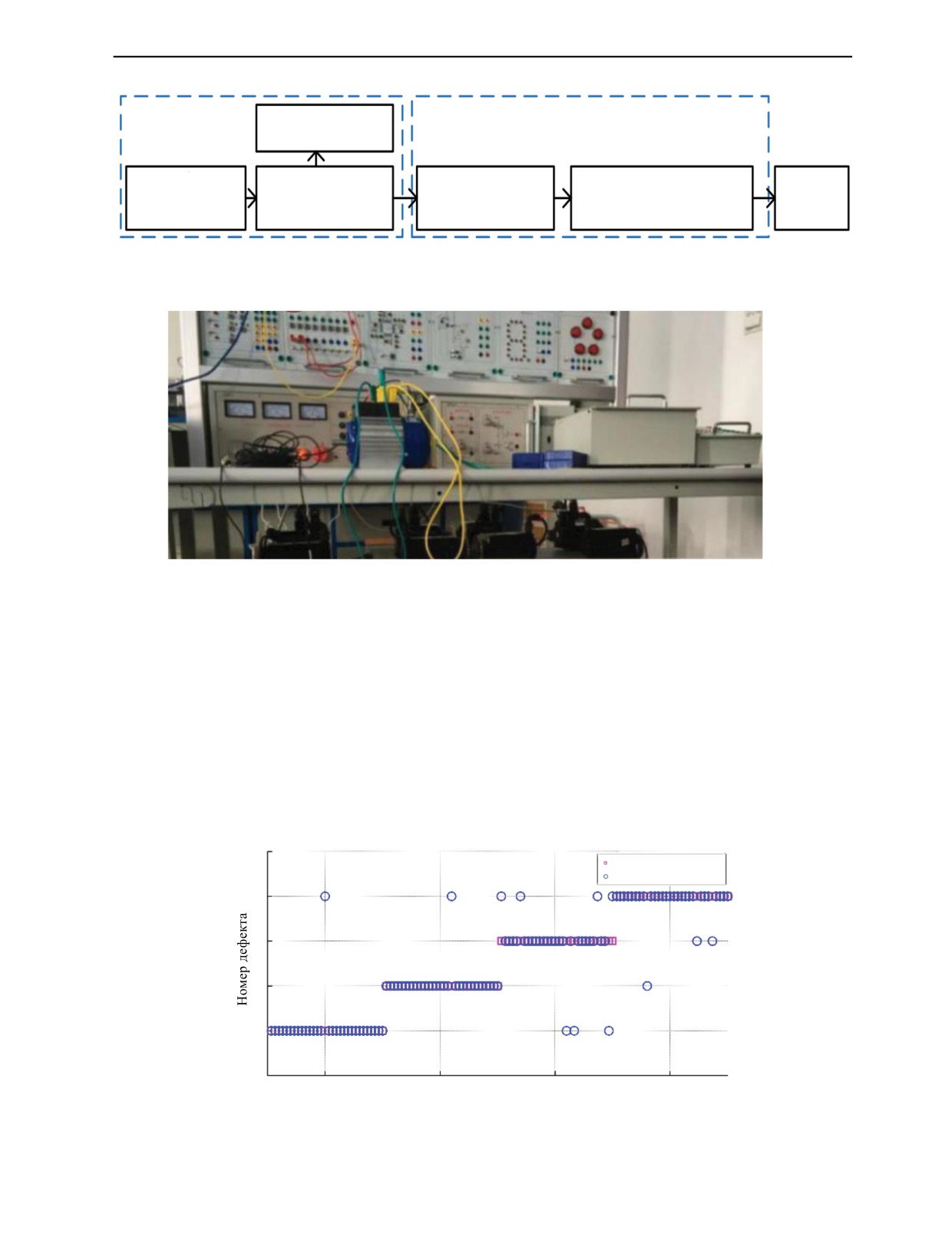
фикаторе устанавливается равным 800. Результат проверки работоспособности модели с помо-
щью контрольного набора показывает, что уровень точности классификации составляет 90 %, а
результат классификации показан на рис. 13.
5
Тестовый набор
Результаты расчета
4
3
2
1
0
0
Норма
Внутреннее кольцо
Тело качения
Внешнее кольцо
Типы дефектов
Рис. 13. Результаты классификации данных по ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ.
Дефектоскопия
№ 3
2022
64
Мин Хуэй Вэй, Лися Цзян, Ди Чжан и др.
По результатам работы метод ДФП—РВМ, оптимизированного по ЦМЧП—КАЭ, не только
имеет более высокий показатель точности контроля дефектов по данным вибродиагностики, но и
применение этого метода также позволяет определить тип дефекта с более высокой точностью.
Это показывает, что метод имеет конкретное практическое применение.
6. ЗАКЛЮЧЕНИЕ
В данной работе объединяются методы дробного фурье-преобразования и разложение на
вариационные моды, предложен метод выделения дефектов подшипника дробного фурье-преоб-
разования—разложение на вариационные моды, оптимизированного по центральному моменту
четвертого порядка—критерию асимметрии и эксцесса. Во-первых, метод определяет дробный
оптимальный порядок через центральный момент четвертого порядка. Во-вторых, параметры
метода РВМ оптимизируются по критерию асиметрии и эксцесса. Для сигнала, обработанного
этим методом, выполняется спектральный анализ огибающей. Результаты показывают, что по
сравнению с прямым РВМ сигнала, сигнал, обработанный этим методом, может получить более
очевидные и более характерные сигналы дефекты. Кроме того, коэффициент эксцесса и филь-
трации с помощью скользящего среднего извлекается из сигнала, разложенного на основе дроб-
ного фурье-преобразования—разложение на вариационные моды, оптимизированного по цен-
тральному моменту четвертого порядка—критерию асимметрии и эксцесса, в виде векторов
признаков, и отправляются в классификатор случайного леса для диагностики дефектов. По
сравнению с РВМ, РЭМ и множественным разложением на эмпирические моды точность диа-
гностики неисправности предлагаемого в данной работе метода значительно выше и достигает
93,75 %. А показатель точности диагностики неисправностей по измеренным данным также
высок, что доказывает, что метод имеет конкретное практическое применение и инженерную
значимость.
Работа поддержана Государственной Ведущей Лабораторией Нефтяных Ресурсов и Разведки
Китайского Университета Нефти (Пекин)
(№ PRP/open-1610) и Национальным Фондом
Естественных Наук Китая (№ 51804267)
СПИСОК ЛИТЕРАТУРЫ
1. Guan Yang et al. 2MNet: Multi-sensor and multi-scale model toward accurate fault diagnosis of rolling
bearing // Reliability Engineering and System Safety. 2021. V. 216.
2. He Deqiang et al. A rolling bearing fault diagnosis method using novel lightweight neural network //
Measurement Science and Technology. 2021. V. 32 (12).
3. Zhan Jun, Cheng Longsheng, Peng Zhaoming. Rolling Bearing Fault Intelligent Diagnosis Based on
VMD and Improved Multi-classification Matte System // Vibration and shock. 2020. V. 39 (02). P. 32—39.
4. Lu Ou, Dejie Yu, Hanjian Yang. A new rolling bearing fault diagnosis method based on GFT impulse
component extraction // Mechanical Systems and Signal Processing. 2016. V. 81. P. 162—182.
5. Huang Norden E. et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and
non-stationary time series analysis // Proceedings of the Royal Society A: Mathematical, Physical and
Engineering Sciences. 1998. V. 454 (1971). P. 903—995.
6. Wu Z.H., Huang N.E. Ensemble empirical mode decomposition: a noise-assisted data analysis method
// Advances in Adaptive Data Analysis. 2009. V. 01 (01). P. 1—41.
7. Zosso D., Dragomiretskiy K. Variational Mode Decomposition // IEEE Transactions on Signal
Processing. 2014. V. 62 (3). P. 531—544.
8. Zhang Lei, Xu Shuwen. Nonlinear Frequency Modulation Signal Detection Based on FRFT // Electronic
Science and Technology. 2010. V. 23 (02). P. 68—71.
9. Zhang Y., Du X., Wen G. et al. An adaptive method based on fractional empirical wavelet transform and
its application in rotating machinery fault diagnosis // Measurement Science and Technology.
2019.
V. 30 (3).
10. Shao Y., Lu D., Yang G.X. Application of fractional Fourier transform in fault diagnostics of rolling
bearing // Journal of Harbin University of Science and Technology. 2017. V. 22 (03). P. 68—72+79.
11. Mei J.M., Jia J.D., Zeng R.L. et al. A multi-order FRFT self-adaptive filter based on segmental
frequency fitting and early fault diagnosis in gears // Measurement. 2016. V. 91. P. 532—540.
12. Wang H.Q. Fractional S transform and its application to gearbox fault diagnosis // Journal of Electronic
Measurement and Instrument. 2019. V. 33 (08). P. 133—139.
13. Namias V. The fractional order Fourier transform and its application to quantum mechanics // IMA
Journal of Applied Mathematics. 1980. V. 25 (3). P. 241—265.
14. Haldun M. Ozaktas et al. Digital Computation of the Fractional Fourier Transform // IEEE, Transactions
on Signal Processing. 1996. V. 44. No. 9. P. 2141—2150.
Дефектоскопия
№ 3
2022
Метод выделения признаков дефектов подшипников, основанный на разложении...
65
15. Alieva T., Bastiaans M.J. On fractional Fourier transform moments // IEEE Signal Processing Letters.
2000. V. 7 (11). P. 320—323.
16. Guo Xuewei, Shen Yongjun, Yang Shaopu. Rolling Bearing Fault Feature Extraction Based on Sample
Entropy and Fractional Fourier Transform // Vibration and Shock. 2017. V. 36 (18). P. 65—69.
17. Xinyu Liu et al. Automatic extracellular spike denoising using wavelet neighbor coefficients and level
dependency // Neurocomputing. 2015. V. 149. P. 1407—1414.
18. Wang Y., Markert R. Filter bank property of variational mode decomposition and its applications //
Signal Process. 2016. V. 120. P. 509—521.
19. Wang Fei, Cao Fan. Separation and Enhancement of multi-component LINEAR FM Signals based on
Time-frequency Space Singular Value Decomposition // Data acquisition and processing. 2009. V. 24 (06).
P. 767—771.
20. Zhang Shu, Liu Deping. Bearing Fault Diagnosis based on BFA Optimization of VMD Parameters //
Modular Machine Tool and Automatic Processing Technology. 2020. V. 05. P. 45—47.
21. Liu Xingdou et al. Ultra-short-term Wind Power Prediction Model Based on VMD Decomposition and
LSTM // IOP Conference Series: Earth and Environmental Science. 2021. V. 838 (1).
22. Huang Darong, Ke Lanyan, Lin Mengting, Sun Guoxi. A New Method for Bearing Fault Diagnosis
based on Parameter Optimization VMD Multi-Scale Entropy // Control and Decision. 2020. V. 35 (07).
P. 1631—163.
23. Benammar Abdessalem, Chibane Farid. Resolution Improvement of Ultrasonic Signals Using Sparse
Deconvolution and Variational Mode Decomposition Algorithms // Russian Journal of Nondestructive Testing.
2020. V. 56 (6). P. 479—489.
24. Fengtao Wang, Chenxi Liu, Tao Zhang, Bosen Dun, Qingkai Han, Hongkun Li. Rolling Bearing Fault
Diagnosis Method Based on K-Value Optimization VMD // Vibration. Testing and Diagnosis. 2018. V. 38 (03).
P. 540—547.
25. Zhang Chenchen. Research on defect recognition method of ultrasonic nondestructive testing based on
VMD. Dalian Ocean University, 2020.
26. Yang Wei, Wang Hongjun. Rolling Bearing Fault Diagnosis Based on VMD Resonance Sparse
Decomposition // Journal of Electronic Measurement and Instrumentation. 2018. V. 9. P. 20—27.
27. Zhang Chen, Zhao Rongzhen, Deng Linfeng, Wu Yaochun. Rolling Bearing Weak Fault Feature
Extraction Based on SVD-EEMD and TEO* // Vibration. Testing and diagnosis. 2019. V. 39 (04). P. 720—
726+900.
28. Liu Zerui, Xing Jishui, Wang Hongjun, Han Fengxia, Gu Fengfeng. Rolling Bearing Fault Diagnosis
Based on VMD and Fast Spectrum Kurtosis // Journal of Electronic Measurement and Instrument. 2021.
V. 35 (2). P. 73—79.
29. Benammar Abdessalem, Chibane Farid. Resolution Improvement of Ultrasonic Signals Using Sparse
Deconvolution and Variational Mode Decomposition Algorithms// Russian Journal of Nondestructive Testing.
2020. V. 56 (6). P. 479—489.
30. Hua Li, Tao Liu, Xing Wu, Qing Chen. Application of optimized variational mode decomposition based
on kurtosis and resonance frequency in bearing fault feature extraction // Transactions of the Institute of
Measurement and Control. V. 42. Is. 3. P. 518—527.
31. Tian Jing, Wang Zhi, Zhang Fengling et al. Dynamic Modeling and Simulation Analysis of
Intermediate Bearing Outer Ring Failure // J. Propulsion Technology. 2019. V. 40. No. 03. P. 660—666.
DOI:10.13675/j.cnki.tjjs.180081
32. Roy S.S., Dey S., Chatterjee S. Autocorrelation Aided Random Forest Classifier-Based Bearing Fault
Detection Framework // IEEE Sensors Journal. 15 Sept. 2020. V. 20. No.18. P. 10792—10800.
Дефектоскопия
№ 3
2022