Электромагнитные методы
УДК 620.179.118.7
КОМПЛЕКСНЫЙ ЭЛЕКТРОИСКРОВОЙ КОНТРОЛЬ СПЛОШНОСТИ И
НЕДОПУСТИМЫХ УТОНЕНИЙ ДИЭЛЕКТРИЧЕСКИХ ПОКРЫТИЙ
© 2022 г. В.А. Сясько1,*, Б.Я. Литвинов2,**, А.С. Мусихин2,***
1ООО «КОНСТАНТА», Россия 198095 С.-Петербург, Огородный переулок, 21
2ФГУП ВНИИМ им. Д.И. Менделеева, Россия 190005 С.-Петербург, Московский пр-т, 19
E-mail: *9334343@gmail.com; **sztul@mail.ru; ***musikhinaleksei@gmail.com
Поступила в редакцию 29.06.2022; после 15.07.2022
Принята к публикации 15.07.2022
В настоящее время основным методом выявления дефектов сплошности диэлектрических покрытий является
электроискровой метод неразрушающего контроля (НК). Однако к большинству современных покрытий так же приме-
няются требования по минимальной толщине покрытия. Представляется перспективным проведение допускового кон-
троля толщины диэлектрических покрытий в одном технологическом процессе с контролем их сплошности за счет
изменения существующих методик контроля и способа формирования испытательного напряжения.
Проведен теоретический и экспериментальный анализ процессов искрообразования, происходящих при обнару-
жении сквозных и несквозных дефектов диэлектрических покрытий на электропроводящих основаниях. Измерены и
рассчитаны минимальные контрольные напряжения для исследуемых диэлектрических покрытий с учетом выявления
как сквозных дефектов, так и недопустимых утонений. Предложено применение вероятностного подхода к обнаруже-
нию вышеописанных дефектов. Показано, что при известном значении электрической прочности покрытия можно с
расчетной вероятностью обнаружить как сквозные, так и несквозные дефекты покрытий при заданном испытательном
напряжении.
Ключевые слова: электрическая прочность, электроискровой контроль, пробивное напряжение, сплошность, покры-
тие, толщина.
DOI: 10.31857/S0130308222090056, EDN: BSFFSC
Проблема оценки технического состояния и продления срока службы диэлектрических анти-
коррозионных и гидроизоляционных покрытий имеет большое практическое значение, что под-
тверждается опытом эксплуатации различных типов промышленных металлических изделий, в
том числе на объектах трубопроводной транспортной инфраструктуры.
Одним из основных требований к таким покрытиям является обеспечение стопроцентной
сплошности покрытий [1—3]. Но при нарушении технологии нанесения покрытий и правил экс-
плуатации изделий в покрытиях могут возникать дефекты сплошности: непрокрасы, сквозные и
несквозные поры, трещины, отрывы, проколы и т.д.
В большинстве случаев предполагается послойное нанесение диэлектрических покрытий. В случае
нарушения технологии нанесения количество слоев покрытия может не соответствовать заявленному.
Таким образом, существует актуальная задача контроля количества слоев конечной системы.
Большинство современных технологий контроля предполагают измерение конечной толщины
покрытия приборами, которые проводят дискретные измерения в различных точках конструкций,
например, электромагнитными толщиномерами. Однако осуществление непрерывного контроля
толщины покрытия является нетривиальной технической задачей.
Одним из наиболее распространенных методов неразрушающего контроля (НК) сплошности
диэлектрических покрытий является электроискровой, при котором для выявления дефектов
между поверхностью покрытия и электропроводящим основанием формируется электрическое
поле высокой напряженности E. За счет того, что дефектные участки покрытия имеют электриче-
скую прочность меньшую, чем бездефектное покрытие, при соответствующей напряженности
электрического поля в них формируется искровой разряд (рис. 1).
Современные [1—5] методики выбора испытательного напряжения Uи, прикладываемого с
использованием электрода к поверхности покрытия, позволяют выявлять только сквозные дефек-
ты покрытий. При этом не уделяется должного внимания связи толщины dп контролируемых
покрытий и их пробивного напряжения Uпп для задачи выявления недопустимо малой толщины и
несквозных дефектов покрытий. В связи с этим актуальна разработка единой методики обнаруже-
ния не только нарушений сплошности покрытий, но и недопустимых утонений.
Так, в работах [6, 7] предлагается оценивать геометрические параметры сквозных дефектов
покрытий по изменению электрического импеданса при возникновении в них коронного или
искрового разрядов. Подобный подход мог бы быть применен и для оценки тока утечки через
недопустимое утонение покрытия, однако метод, основанный на расчете и определении электри-
50
В.А. Сясько, Б.Я. Литвинов, А.С. Мусихин
Измеритель тока
Источник
напряжения
Электрод
Электропроводящее соединение
Покрытие
Рис. 1. Схематичное изображение принципа электроискрового контроля диэлектрических покрытий.
ческого сопротивления материала, не может быть применен к участкам покрытия, где происходят
разрядные процессы [8].
Для рассматриваемой задачи сквозные дефекты диэлектрических покрытий представляют
собой воздушные межэлектродные промежутки, для которых расчет пробивного напряжения
воздушного промежутка Uпв для dп от 5 мкм до 50 мм в однородном электрическом поле может
быть осуществлен с использованием основных положений теории электрического пробоя
Таунсенда [9, 10]. Согласно указанной теории, искровой разряд в газовой среде формируется за
счет лавинного размножения свободных носителей заряда в межэлектродном промежутке и
образования электропроводящего канала (стримера), формирование которого условно можно
разделить на стадии формирования первичной и вторичных лавин. Для формирования первич-
ной лавины носителей заряда (электронов) необходимо, чтобы свободные электроны, имеющи-
еся в газе, которым заполнен сквозной дефект покрытия, получали энергию от внешнего элек-
трического поля, создаваемого в межэлектродном промежутке (между электродом и электропро-
водящим основанием), большую или равную энергии ионизации атомов газа на длине свободно-
го пробега электрона. С учетом коэффициентов первичной ионизации α и прилипания η можно
определить общее число электронов в лавине, прошедшей расстояние Δd [11]:
(
α-η
)
⋅∆d
n=n
⋅e
0
После прохождения первой лавины в межэлектродном промежутке лавинный процесс может
возобновиться или затухнуть. Для возобновления лавинного процесса (организации самостоятель-
ного разряда) необходим хотя бы один вторичный эффективный электрон, который может возник-
нуть, в том числе в результате прохождения первичной лавины, при увеличении Uи.
Основным положением теории является условие самостоятельности разряда в местах несплош-
ности:
(
α-η
)
⋅d
п
γ⋅
e
−1
≥1,
(1)
(
)
где γ — коэффициент вторичной ионизации электронов; α —коэффициент ударной ионизации;
η — количество свободных электронов; dп — толщина покрытия.
Ключевым элементом достоверного электроискрового НК является обеспечение условий само-
стоятельности искрового разряда в местах дефектов покрытия (в том числе нарушений их сплош-
ности).
Зависимость (1) показывает, что в результате прохождения первичной лавины необходимо обра-
зование, как минимум, одного эффективного электрона, способного зажечь вторичную лавину.
При рассмотрении условия самостоятельности разряда в однородном поле (пробой всего
межэлектродного промежутка) допустимо принять η = 0 и привести выражение (1) к виду:
Дефектоскопия
№ 9
2022
Комплексный электроискровой контроль сплошности...
51
α⋅d
п
γ⋅
(
e
−1
)
=1.
(2)
Экспериментально установлено [10], что
B
0
⋅P
−
E
(3)
α=
A
⋅
P⋅e
,
0
где E — напряженность однородного электрического поля в межэлектродном промежутке;
A0 — коэффициент, зависящий от состава газа; B0 — коэффициент, зависящий от энергии иони-
зации газа; P — давление газа.
Из (2) и (3) следует:
1
ln
1+
B
0
⋅P
γ
−
(4)
E
=
A
⋅ P
⋅e
0
dп
Как известно [12], для однородного поля E = Uпв/dп, поэтому подставим это выражение в (4):
B
0
⋅P⋅d
п
−
1
U
пв
ln
1+
=
A
⋅ P⋅d
⋅e
(5)
0
п
γ
Прологарифмировав (5), получим:
B
0
⋅ P⋅d
п
A
0
⋅ P⋅d
п
=
ln
U
1
(6)
пв
ln
1+
γ
Поскольку нас интересует Uпв, то для его определения (6) преобразуем к виду:
B
⋅ P⋅d
0
п
U
=
пв
A ⋅
P⋅d
0
п
ln
(7)
1
ln
1
+
γ
Из (7) следует, что при неизменной внешней температуре воздуха в однородном поле
Uпв = f(P∙dп), а при квазипостоянном атмосферном давлении — Uпв = f(dп) (рис. 2).
Uпв, В
1
105
2
3
104
103
102
0,01
0,1
1
10
dп, мм
Рис. 2. Расчетные значения Uпв:
1 — Uпв(dп) по формуле (7) для атмосферного воздуха при нормальных условиях; 2 — Uпв(dп) по формуле (8) для dп > 1 мм; 3 — Uпв(dп)
по формуле (8) для dп < 1 мм.
Дефектоскопия
№ 9
2022
52
В.А. Сясько, Б.Я. Литвинов, А.С. Мусихин
В то же время стандартизованные методики определения испытательного напряжения, учиты-
вающие неоднородности электрического поля в процессе контроля, предлагают расчет Uи на осно-
ве эмпирической зависимости [2, 3] (см. рис. 2):
U =M⋅ dип
,
(8)
где M — постоянный эмпирический коэффициент, зависящий от dп (М = 3294 для покрытий тол-
щиной dп < 1 мм и М = 7843 для dп > 1 мм).
Как видно из рис. 2, стандартизованные методики расчета испытательного напряжения пред-
назначены исключительно для выявления сквозных дефектов покрытия. Для выявления недопу-
стимых утонений покрытий электроискровым методом необходимо рассмотреть процессы пробоя
твердых диэлектриков.
Электрическую прочность диэлектриков можно рассчитать в зависимости от их структуры и
энергетических характеристик материала [15].
В [13] предлагается эмпирическая зависимость пробивного напряжения покрытия Uпп для
широкого ряда диэлектрических покрытий:
K
1.1
a
m
0
U
пп
=
⋅ K
B
⋅
(
A
c
)
⋅exp
+
,
(9)
d
b+lg
(b)
n
+lg
(
τ
)
п
где K — коэффициент пропорциональности, зависящий от dп; τ — длительность воздействия при-
ложенного напряжения; KB — вероятность пробоя; Ac0 — энергия каналообразования; а, b,
n, m — некоторые постоянные, зависящие от состава диэлектрика.
Полученная формула может применяться при расчетах электрической прочности диэлектриков
толщиной от 0,01 до 40 мм при длительности импульса приложенного напряжения τ = 0,1—10 мкс.
В табл. 1 приведены значения Uпп для ряда твердых диэлектриков, полученные эксперимен-
тально и вычисленные по вышеприведенным формулам для образцов толщиной dп = 0,1 мм [14].
Таблица
1
Расчетные и экспериментальные значения электрической прочности Uпп для диэлектрических материалов
толщиной d = 0,1 мм
, кВ
Uпп
Материал покрытия
Экспериментальные значения
Расчетные значения
Полиэтилен
6,75—7
6,2
Полистирол
5,5—7,3
4,3
Фторопласт-4
3,5
4
Оценка Uпп по (9) возможна для однокомпонентных одно- или многослойных покрытий, пара-
метры которых можно найти в справочной литературе, например, антикоррозионных покрытий
трубопроводов. Вместе с тем следует учесть, что требуемые для расчета параметры многокомпо-
нентных покрытий (например, лакокрасочных), как правило, не нормируются. Поэтому Uпп много-
компонентных покрытий или покрытий, для которых Uпп не удается определить расчетным путем,
можно определить экспериментально. Для экспериментального определения Uпп предлагается
использовать покрытие, идентичное или близкое контролируемому по составу и толщине, нане-
сенное на металлическое основание.
В качестве примера приведены результаты эксперимента по определению Uпп, в котором в
качестве оснований использовались листы фольгированного текстолита и алюминия, на которые
было нанесено лакокрасочное покрытие (ЛКП) — эмаль MLS 306.
После изготовления образцов (нанесения трех, шести и девяти слоев покрытия на поверх-
ность основания) была замерена толщина в контрольных точках, в которых определялось про-
бивное напряжение. Прикладываемое напряжение увеличивалось до пробоя покрытия, фиксиро-
валось значение Uпп с использованием осциллографа DSO-X 2002A. В результате была получена
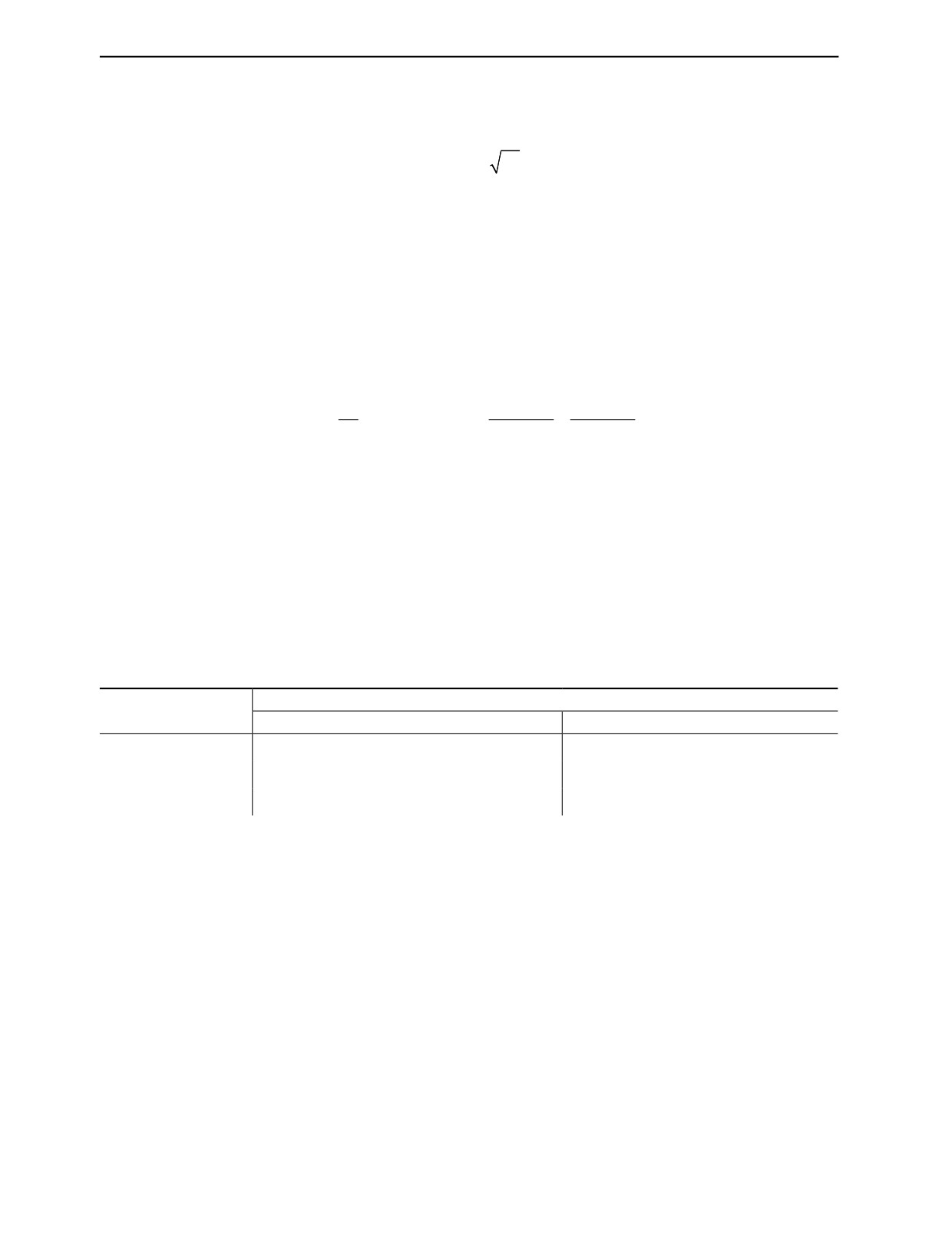
зависимость Uпп(dп), представленная на рис. 3.
Дефектоскопия
№ 9
2022
Комплексный электроискровой контроль сплошности...
53
Uпп, В
6·104
4·104
2·104
1·104
8·103
6·103
4·103
2·103
00
20
60
100
140
180
220
260
dп, мкм
Рис. 3. Зависимость пробивного напряжения покрытий Uпп от толщины покрытия dп.
Как видно из рис. 3, полученные значения Uпп имеют достаточно большой разброс.
Предположительно это связано с формированием разряда в точке с наименьшей толщиной покры-
тия и некоторым разбросом параметров покрытия [16, 17]. По этой причине требуется проведение
оценки вероятности выявления недопустимых утонений покрытия в зависимости от Uи и dп.
Для этого был применен алгоритм, основанный на построении линии регрессии зависимости
Uпп(dп) и построении на ее основе нормальных функций распределения с заданными параметра-
ми [18, 19].
На исследуемом участке зависимость Uпп(dп) имеет квазилинейный вид. Следовательно, по
полученным экспериментальным данным была построена линейная регрессия вида U = k · d + b,
для которой была построена функция нормального (гауссовского) распределения вероятности
формирования искрового разряда от величины Uи (см. рис. 3):
U
и
(
t−µ
)2
1
−
2
2σ
P
(
U
)
=
e
dt
,
и
∫
2σ
-∞
где dп — толщина покрытия; Uи — испытательное напряжение; k, b — параметры линии регрес-
сии; μ — математическое ожидание; σ — СКО.
Границы доверительного интервала P(Uи) для регрессионной модели (см. рис. 3) в соответ-
ствии с [20]:
2
(
lnU -U
)
1
и
и
P
(
U
)
=
P
(
U
)
±t
D
+
,
±
и
и
P
n
2
n
∑
(
l U i
и
-U
и
)
i=1
где n — количество измерений; tP — коэффициент Стьюдента для доверительной вероятности
95 % и (n-2)-степеней свободы; D — дисперсия значений пробивного напряжения.
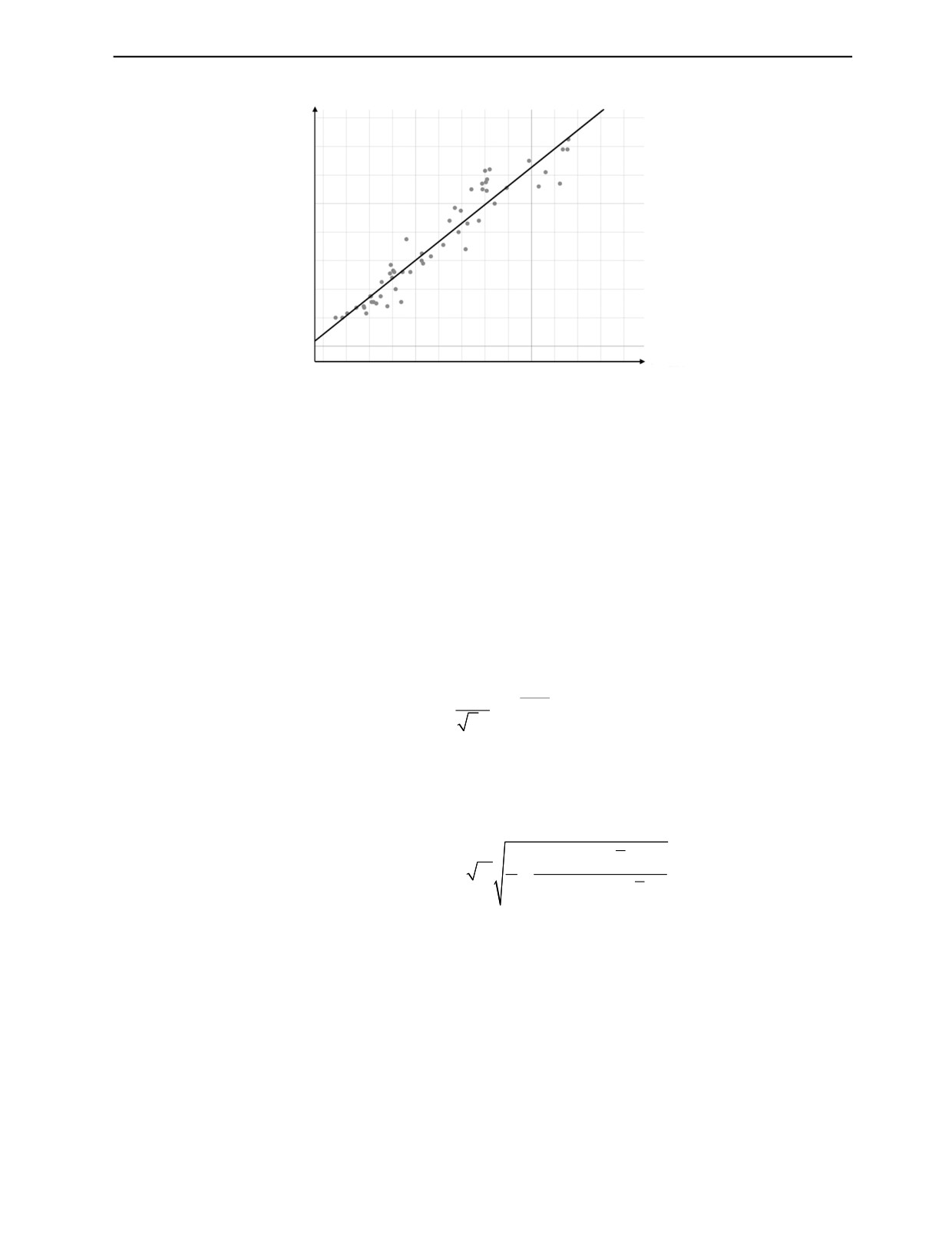
График зависимости вероятности обнаружения дефекта Р(Uпп) характеризует достоверность
НК. На графике, являющемся сигмовидной функцией, представлены границы интервала с задан-
ной доверительной вероятностью (показаны пунктиром). Очевидно, что с увеличением dп характе-
ристика P(Uпп) сдвигается вправо. Так же при проведении допускового контроля покрытия (выяв-
ления мест недопустимого утонения) рекомендуется строить зависимость Р(Uпп) для доверитель-
ной вероятности выявления дефекта 0,9 (90 %). Следовательно, можно определить электрическую
прочность покрытия Eп для вероятности обнаружения дефекта, равной 90 % для каждой исследо-
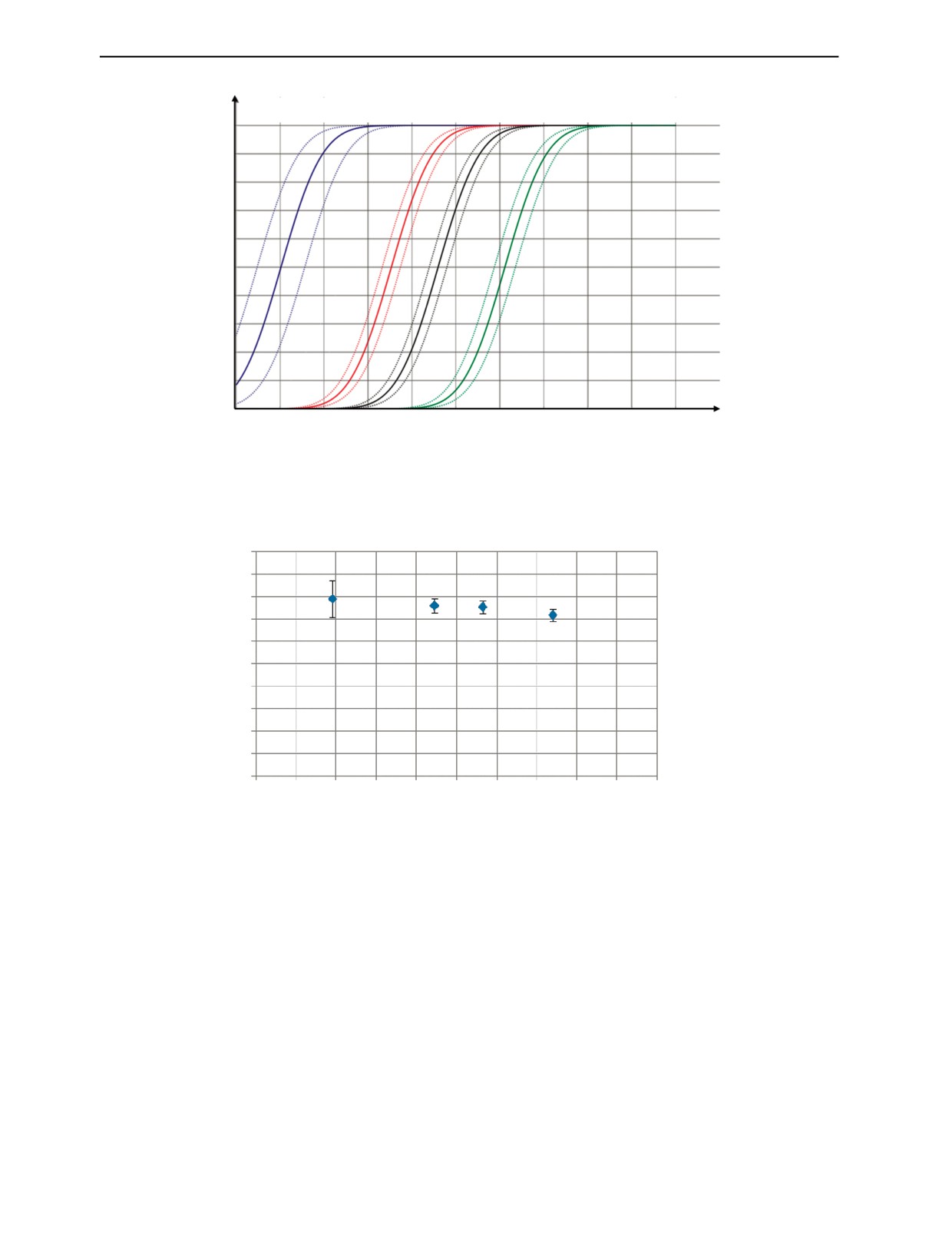
ванной толщины покрытия (рис. 5).
Данные эксперимента показывают, что расчетное значение Eп в указанном диапазоне толщин
составляет 75,4 ± 8,2 кВ. С учетом того, что электрическая прочность практически постоянна в
Дефектоскопия
№ 9
2022
54
В.А. Сясько, Б.Я. Литвинов, А.С. Мусихин
P(U)
Pd1(Uи)
Pd2(Uи)
Pd3(Uи) Pd4(Uи
)
1
0,9
0,8
0,7
0,6
0,5
0,4
0,3
0,2
0,1
0
1,5
3
4,5
6
7,5
9
10,5
12
13,5
15 U
, кВ
и
Рис. 4. Распределение вероятности пробоя покрытия в зависимости от приложенного напряжения для d1 = 38 мкм,
d2 = 89 мкм, d3 = 113, d4 = 148 мкм.
E, кВ/мм
100
90
80
70
60
50
40
30
20
10
0
0
0,02
0,04
0,06
0,08
0,1
0,12
0,14
0,16
0,18
0,2 d, мкм
Рис. 5. Зависимость электрической прочности покрытия Eп от его толщины для исследуемых образцов.
указанном диапазоне толщин, вероятность выявления дефекта заданной толщины (исходя из элек-
трической прочности покрытия) составит 0,8 (80 %).
Таким образом, при известном значении электрической прочности покрытия (рассчитанном
или определенном экспериментально) можно с заданной вероятностью выявлять недопустимые
утонения, производя контроль испытательным напряжением, величина которого равна Uи = Eп /dп.
ЗАКЛЮЧЕНИЕ
В работе проведен теоретический и экспериментальный анализ процессов искрообразования
применительно к задачам выявления сквозных и несквозных дефектов диэлектрических покрытий
на электропроводящих основаниях. Рассчитаны минимальные испытательные напряжения для
сквозных дефектов покрытий и показана невозможность использования существующих методик
НК для выявления несквозных дефектов покрытий. Измерены и рассчитаны минимальные кон-
трольные напряжения исследуемых диэлектрических покрытий с учетом необходимости выявле-
Дефектоскопия
№ 9
2022
Комплексный электроискровой контроль сплошности...
55
ния как сквозных дефектов, так и недопустимых утонений. Предложено применение вероятност-
ного подхода при обнаружении описанных дефектов. Показано, что при известном значении
электрической прочности покрытия можно с расчетной вероятностью обнаружить как сквозные,
так и несквозные дефекты покрытий при заданном испытательном напряжении.
Полученные результаты позволяют разработать методику проведения испытаний, которая рас-
ширяет диапазон применимости метода и повышает достоверность результатов контроля.
СПИСОК ЛИТЕРАТУРЫ
1. ГОСТ Р51164—98 Трубопроводы стальные магистральные. Общие требования к защите от
коррозии. М.: Изд-во стандартов, 1998. 46 с.
2. ГОСТ 34395—2018 Материалы лакокрасочные. Электроискровой метод контроля сплошности
диэлектрических покрытий на токопроводящих основаниях. М.: ФГУП «СТАНДАРТИНФОРМ», 2018.
11 с.
3. ASTM G62 — 14/Standard Test Methods for Holiday Detection in Pipeline Coatings.
4. Ерехинский Б.А., Пахомов А.В. Современные технологии диагностики объектов добычи газа и
газового конденсата. Применяемая техника и оборудование. Воронеж: АО «Воронежская областная
типография», 2017. 374с.
Materials. 1983. No. 12. P. 4—12. ISSN: 0003-5599.
6. Гаджиев Я.М., Ибрагимова Э.Н. Экспериментальное исследование измерения размеров трещин
силикатно-эмалевого покрытия трубы // Дефектоскопия. 2020. № 1. С. 61—65.
7. Ибрагимов Н.Ю., Ибрагимова Э.Н. Дефектоскопическая установка трещиномер силикатных
покрытий труб // Дефектоскопия. 2017. № 11. С. 55—57.
8. Неразрушающий контроль. Электрический контроль / Справочник в 7 т. Под общ. ред.
В.В. Клюева. М.: Машиностроение, 2004. 679 с.
9. Райзер Ю.П. Физика газового разряда / Учебное руководство. 2-е изд. М.: Наука, 1992. 536 с.
10. Тренькин А.А., Алмазова К.И., Белоногов А.Н., Боровков В.В., Горелов Е.В., Морозов И.В.,
Харитонов С.Ю. Исследования начальной фазы искрового разряда в воздухе в промежутке острие
(катод)—плоскость методом лазерного зондирования // Журнал технической физики. 2020. Т. 90.
№ 12.
11. Смирнов А.С. Прикладная физика. Физика газового разряда / Учеб. пособие. СПб.: Изд-во
СПбГТУ, 1997. 68 с.
12. Мик Дж., Крэгс Дж. Электрический пробой в газах / Перевод с англ. М.: Изд-во иностранной
лит-ры, 1960. 605 с.
13. Важов В.Ф., Лавринович В.А., Лопаткин С.А. Техника высоких напряжений / Курс лекций.
Томск: Изд-во ТПУ, 2006. 119 с.
14. Воробьев Г.А., Похолков Ю.П., Королев Ю.Д. Физика диэлектриков (область сильных полей) /
Учебное пособие и др. Томск: Изд-во ТПУ, 2003. 244 с.
15. Григорьев А.Н., Павленко А.В., Ильин А.П., Карнаухов Е.И. Электрический разряд по поверхности
твердого диэлектрика. Ч. 1. Особенности развития и существования поверхностного разряда // Известия
ТПУ. 2006. № 1. С. 66—69.
16. Старикова Н.С., Редько В.В. Исследование методов контроля целостности изоляции в области
слабых и сильных электрических полей [Электронный ресурс] // Вестник науки Сибири. 2013. № 3 (9).
С. 55—59.
17. Галеева Н.С. Повышение информативности контроля кабельных изделий на основе комплексного
использования электроискрового и электроемкостного методов. 05.11.13 / Дисс
на соискание ученой
степени канд. наук. ФГАОУ ВО «Национальный исследовательский Томский политехнический
университет», 2017. 143 с.
18. Чертищев В.Ю. Оценка вероятности обнаружения дефектов акустическими методами в
зависимости от их размера в конструкциях из ПКМ для выходных данных контроля в виде
бинарных величин // Авиационные материалы и технологии. 2018. № 3 (52). DOI: 10.18577/2307-
6046-2018-0-3-65-79
19. Бойчук А.С., Генералов А.С., Далин М.А., Степанов А.В. Вероятностная оценка достоверности
результатов ультразвукового неразрушающего контроля конструкций из ПКМ, применяемых в
авиационной промышленности // Ремонт. Восстановление. Модернизация. 2013. № 9. С. 36—39.
20. Лебедев А.М. Исследование достоверности допускового контроля // Научный вестник МГТУ ГА.
2005. Т. 86. № 4. С. 65—70.
Дефектоскопия
№ 9
2022