Электромагнитные методы
УДК 620.179.14
К РЕШЕНИЮ ОДНОЙ ЗАДАЧИ МАГНИТОСТАТИКИ ДЛЯ ТРУБЫ
С ДЕФЕКТОМ НА ВНУТРЕННЕЙ ПОВЕРХНОСТИ
© 2023 г. В.В. Дякин1, О.В. Кудряшова1,*, В.Я. Раевский1
1Институт физики металлов имени М.Н. Михеева УрО РАН,
Россия 620108 Екатеринбург, ул. С. Ковалевской, 18
Е-mail: *kudryashova.olga.valeryevna@gmail.com
Поступила в редакцию 13.12.2022; после доработки 09.02.2023
Принята к публикации 10.02.2023
Разработан и реализован алгоритм численного решения прямой линейной задачи магнитостатики по расчету резуль-
тирующего поля трубы с поверхностным дефектом на внутренней ее стенке в предположениях, что перпендикулярное
сечение трубы и вектор напряженности внешнего намагничивающего поля остаются неизменными вдоль оси протяжен-
ности трубы — это позволило взять за основу двумерное интегро-дифференциальное уравнение магнитостатики.
Алгоритм реализован на языке программирования FORTRAN. Результаты протестированы на достоверность с помощью
точно решаемых задач. Построены иллюстративные кривые. Указаны возможности применения полученной методики
расчета для класса задач, в чем-то отличающихся по постановке.
Ключевые слова: интегро-дифференциальное уравнение магнитостатики, магнитный неразрушающий контроль,
двумерная задача магнитостатики, поверхностный дефект на внутренней стенке трубы.
DOI: 10.31857/S0130308223020045, EDN: BWRUNZ
ВВЕДЕНИЕ
Для практики магнитного неразрушающего контроля является важным рассмотрение теоре-
тической задачи магнитостатики для широкого класса геометрических моделей, которые учиты-
вают наличие дефектов на поверхностях, ограничивающих магнетик. Первые работы по данной
проблематике вышли в 60-х годах прошлого века. Существующие тогда ограничения в возмож-
ностях использования вычислительной техники понуждали прибегать к рассмотрению эквива-
лентных аналитически решаемых задач. Так, был разработан подход, в рамках которого поверх-
ностный дефект в виде бесконечно протяженной вдоль поверхности пластины трещины прямо-
угольного сечения моделировался так называемым ленточным диполем — комбинацией двух
пластин, по поверхностям которых «магнитный заряд» предполагался распределенным с посто-
янными одинаковыми по абсолютному значению и отличающимися по знаку плотностями.
Размеры пластин выбирались в соответствии с размерами моделируемого дефекта [1]. При
последующем подборе значения плотности магнитного заряда было достигнуто согласие с
результатами экспериментов [2].
В настоящее время применение процедур численного решения подобных задач становится все
более распространенным. В работе [3] рассмотрение прямой линейной задачи магнитостатики для
пластины с синусоидальной границей проводили с помощью конечно-элементных процедур,
доступных в пакете Matlab. На основе анализа результатов был осуществлен подход к решению
одной обратной задачи [4].
В недавней работе [5] мы обратились к прямой линейной задаче магнитостатики для беско-
нечной магнитной пластины с бесконечно протяженным поверхностным дефектом с неизмен-
ным вдоль линии протяженности профилем. Хотя внешнее намагничивающее поле предполага-
лось однородным, направленным тангенциально либо нормально к поверхности пластины,
однако оказалось, что уравнения легко модифицируются и на случай, когда внешнее поле зави-
сит от координат. Для решения был использован сеточный метод, который был реализован в
компьютерной программе. Путем численных экспериментов установлена точность решения: как
и в прочих аналогичных по постановке двумерных задачах, решение которых осуществлялось
путем дискретизации предварительно преобразованного интегро-дифференциального уравне-
ния магнитостатики, в [5] при широком диапазоне изменения входных данных имела место
стабилизация как минимум трех значащих цифр окончательного результата. Настоящей работой
мы продолжаем применение использованного в [5] подхода на случай бесконечно протяженной
трубы с дефектом на внутренней стенке.
36
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
ПОСТАНОВКА ЗАДАЧИ И АЛГОРИТМ ЕЕ РЕШЕНИЯ
Пусть имеется бесконечно протяженное вдоль некой оси Oz магнитное тело, такое, что его
перпендикулярное к этой оси сечение S остается неизменным вдоль нее. Также примем, что это
тело располагается во внешнем намагничивающем поле, пространственная конфигурация которо-
го не изменяется вдоль этой оси протяженности. На рис. 1 изображено упомянутое сечение, через
L обозначен ограничивающий его контур. Примем, что μ, магнитная проницаемость тела, является
величиной постоянной. В таком случае для решения задачи о нахождении вектора напряженности
магнитного поля H следует воспользоваться двумерным интегро-дифференциальным уравнением
магнитостатики:
µ-1
S
0
2
H ρ)-
∇
H
(
ρ′
)
ln
ρ ρ
dL′=
H
(
ρ
)
,
ρ∈
\
L,
(1)
∫
n
2π
L
которое выводится из трехмерного [6, 7] с учетом вышеописанных условий постановки. В уравне-
нии (1) через ρ обозначен радиус-вектор текущей точки плоскости, по штрихованным координатам
ведется интегрирование; под H0 понимаем вектор напряженности внешнего намагничивающего
S
поля; под
(
)
H
ρ′
— составляющую вектора H(ρ′), взятую изнутри области S вдоль единичного
n
вектора n, направленного по нормали к контуру L в точке с радиус-вектором ρ′ наружу из области
2
S (см. рис. 1). Уравнение (1) имеет силу всюду на плоскости
за исключением точек, лежащих
на контуре L.
n
μ = 1
S : μ
L
Рис. 1.
Далее конкретизируем геометрическую модель, полагая, что при оговоренных условиях
область S имеет вид, представленный на рис. 2, имитирующий срез трубы с дефектной внутренней
поверхностью. Ограничивающие ее контуры обозначены символами L1 и L2. Контур L2 определим
как окружность радиуса ρ2, а форму контура L1 пока задавать не будем, принимая только, что он
целиком расположен внутри L2. Начало координат поместим в центре окружности L2. Единичные
векторы нормали к контурам L1 и L2 обозначим через n1 и n2 соответственно и направим их наружу
из области S. В таком случае уравнение (1) принимает вид:
µ-1
S
µ-1
S
0
2
H ρ)−
∇
H
(
ρ′
)
ln
ρ ρ
dL′-
∇
H
(
ρ′
)
ln
ρ ρ
dL′ =
H ρ)
, ρ∈
\
L
L
∫
n
1
1
∫
n
2
2
{
1
∪
2
}
(2)
2π
2
π
L
1
L
2
Из уравнения видно: для того, чтобы найти вектор напряженности магнитного поля в произ-
вольной точке плоскости, прежде необходимо найти две функции — его нормальные составляю-
S
S
щие
H
(
ρ
)
и
H
(
ρ
)
на контурах L1 и L2 соответственно. Приступим к выводу уравнений, позво-
n
1
n
2
Дефектоскопия
№ 2
2023
К решению одной задачи магнитостатики для трубы с дефектом на внутренней поверхности
37
y
n2
μ = 1
S : μ
n1
μ = 1
0
x
L1: ρ = σ(φ)
L2: ρ = ρ2
Рис. 2.
ляющих решить эту задачу. Для этого воспользуемся уравнением (2), положим, что ρ∈S, и умно-
жим обе части на вектор ni (i = 1, 2). Получим уравнение:
S
µ-1
∂
S
µ-1
∂
S
0
H
(ρ)
−
H
(
ρ′
)
ln
ρ ρ
dL′-
H
(
ρ′
)
ln
ρ ρ
dL′ =
H
(
ρ
)
(3)
n
i
∫
n
1
1
∫
n
2
2
n
i
2π ∂n
2π ∂n
i L
1
i L
2
Для того, чтобы, исходя из (3), записать уравнение относительно нормальной составляющей
HS (ρ
)
при ρ∈Li, нужно применить теорему о предельном значении нормальной производной
n
i
простого слоя [8], согласно которой:
∂
S
S
S
∂
H
(
ρ′)ln
ρ ρ
dL′=-πH
(ρ)
+
H
(
ρ′
)
ln
ρ ρ
dL′,
i
=1,2
и
ρ
∈L
(4)
∫
n
i
i
n
i
∫
n
i
i
i
∂
n
∂n
i L
i
L
i
i
В случае, когда производная от интеграла по контуру Li берется по вектору nj (i ≠ j), то она
проносится под знак интеграла свободно в силу отсутствия особой точки в подынтегральной
функции.
Таким образом, преобразовывая (3) с помощью (4), выводим систему интегральных уравнений
относительно искомых нормальных составляющих вектора H на граничных контурах:
S
χ
S
∂ln
ρ ρ
χ
S
∂ln
ρ ρ
2
0
H
(ρ)
−
H
(
ρ′
)
dL′-
H
(
ρ′
)
dL′ =
H
(
ρ
)
,
i
=1,2
и
ρ∈L
,
(5)
n
i
∫
n
1
1
∫
n
2
2
n
i
i
π
∂n
π
∂n
µ+1
L
1
i
L
2
i
µ-
1
где принято обозначение
χ:
=
µ+1
Рассмотрим уравнение системы (5) при i = 2 и запишем его полярных координатах,
2
2
∂
∂
где ρ = (ρ, φ),
ρ ρ′ = ρ
+ ρ′
−
2
ρρ′cos
(
ϕ-ϕ′
)
,
=
Тогда осуществляем выкладку:
∂n
∂ρ
2
∂ln
ρ
−
ρ′
1
1
S
S
H
(
ρ′
)
dL′
=
H
(
ρ′
)
dL
′
=
=
0,
∫
n
2
2
∫
n
2
2
∫ HdS
∂
n
2
ρ
2ρ
L
2
2
2
L
2
2
S
Дефектоскопия
№ 2
2023
38
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
при проведении которой был использован двумерный вариант теоремы Остроградского—Гаусса и
учтено, что при условии μ = const: divB = μdivH = 0. Факт равенства нулю интеграла по замкнуто-
му контуру от нормальной составляющей к этому контуру вектора напряженности магнитного
поля будет использован и при дальнейших преобразованиях. Полагаем это очевидным, в нужном
S
месте используем без дополнительных оговорок. Таким образом, для функции
H
n
(
ρ
)
верно выра-
2
жение:
2
χ
ρ
− ρ′cos
(
ϕ-ϕ′
)
S
0
S
2
H
(ρ)
=
H
(ρ)
+
H
(
ρ′
)
dL′,
ρ∈L
(6)
n
2
n
2
∫
n
1
2
2
1
2
µ+1
π
ρ
+ ρ′
−2ρ
ρ′
cos
(
ϕ-ϕ′
)
L
1
2
2
Если здесь к ядру интегрального оператора применить формулу разложения [9, стр. 54, 1.447]:
∞
1-
pcost
m
=
p
cosmt
,
p
<1,
(7)
2
∑
1+
p
−2
p tsm
=0
полагая p = ρ′/ρ2, то можно записать (6) в более удобном для дальнейших промежуточных преоб-
разований виде:
∞
S
2
0
χ
1
S
m
H
(ρ)
=
H
(ρ)
+
H
(
ρ′
)
ρ′
cos
m
(
ϕ-ϕ′
)
dL′
(8)
n
2
n
2
∑
m+1
∫
n
1
1
µ+1
π
ρ
m=
1
2
L
1
Теперь рассмотрим (5) при i = 1 и ρ∈L1, подставляя под знак второго интеграла в левой части
S
H
(
ρ′
)
на основе (8). Рассмотрим этот интеграл отдельно:
n
2
∂ln
ρ ρ
2
∂
ln
ρ ρ
S
0
I
(ρ)
:=
H
(
ρ
′
)
dL′ =
H
(
ρ
′
)
dL′
+
∫
n
2
2
∫
n
2
2
∂
n
µ+1
∂n
L
2
1
L
2
1
(9)
∞
χ
1
∂ln
ρ
−ρ
′
+
dL
′′ρ′′
mHS (
ρ′′
)
dL′
cos
m
(
ϕ′ - ϕ′′
)
∑
m+1
∫
1
n
1
∫
2
π
ρ
∂n
m
=1
2
L
1
L
2
1
Применяя известное разложение [9, стр. 55, 1.448]:
k
∞
1ρ
ln
ρ ρ′ =
ln
ρ′ -
cosk
(
ϕ-ϕ′
)
,
ρ <ρ′
(10)
∑
k
=
1
k
ρ′
и последовательно выполняя очевидные действия, получаем выражение для интеграла:
∂
ln
ρ−
ρ
′
π
∂
m
dL′
cosm
(
ϕ′ - ϕ′′
)
=-
ρ
cos
m
(
ϕ-ϕ
′
)
,
ρ∈L
,
∫
2
m−1
1
∂n
mρ
∂
n
L
2
1
2
1
подставляем его в (9), а полученное — в (5), и, уже без ущерба смыслу заменяя дважды штрихо-
ванные координаты на единожды штрихованные, имеем следующее уравнение относительно
H
n
S (
ρ
)
:
1
2
∞
χ
∂
ln
ρ
−ρ
χ
1
∂
S
S
S
m
m
H
(ρ)
−
H
(
ρ
′
)
dL
′+
H
(ρ)
ρ′
ρ
cosm
(
ϕ-ϕ
′
)
dL′=
n
1
∫
n
1
1
∑
2m
∫
n
1
1
π
∂
n
π
mρ
∂n
L
1
1
m=1
2
L
1
1
(11)
2
1
=
H
n
(
ρ
)
,
ρ
∈
L
1
,
1
µ
+
1
где введено обозначение новой функции:
Дефектоскопия
№ 2
2023
К решению одной задачи магнитостатики для трубы с дефектом на внутренней поверхности
39
χ
∂ln
ρ−ρ′
1
0
0
H
(ρ)
:=
H
(ρ)
+
H
(
ρ′
)
dL′,
n
1
n
1
∫
n
2
2
(12)
π
∂n
L
2
1
целиком зависящей от исходных данных задачи.
С помощью ранее использованной формулы [9, стр. 55, 1.448] сворачиваем бесконечную сумму
и сводим (11) к виду:
2
2
S
χ
S
∂
χ
S
∂
ρρ′
ρρ′
H
(ρ)
−
H
(
ρ′
)
ln
ρ ρ
dL
′-
H
(
ρ′
)
ln
1+
-2
cos
(
ϕ-ϕ′
)
dL′
=
n
1
∫
n
1
1
∫
n
1
2
2
1
π
∂n
π
∂n
ρ
ρ
L
1
L
1
2
2
1
1
(13)
2
1
=
H
n
(
ρ
)
,
ρ∈
L
1
1
µ+1
S
Итак, уравнение (13) позволяет найти функцию
H
n
(
ρ
)
— нормальную составляющую векто-
1
ра напряженности искомого магнитного поля, взятую изнутри области S на контуре L1 вдоль век-
S
S
тора n1, при произвольной форме контура L1. После нахождения функции
H
(
ρ
)
функция
H
(
ρ
)
n
1
n
2
определяется согласно (6) простой подстановкой. Таким образом, численное решение предстоит
осуществить, реализуя разбиение только контура L1. В частных задачах есть возможность добить-
ся снижения размерности уравнения и тем самым сделать алгоритм вычислений более устойчи-
вым к ошибкам и менее требовательным к затратам компьютерных ресурсов.
Далее следует определиться с контуром L1. Примем, что в полярных координатах он задается
функцией ρ = σ(ϕ),
[
ϕ∈
−π π].
Тогда можем записать следующее разложение вектора n1 по ортам
полярной системы координат eρ и eφ:
−σ ϕ)e
+ ϕ)
e
ρ
ϕ
n
1
=
,
(14)
2
2
ϕ)
+σ
(
ϕ
)
оператор производной вдоль вектора n1:
∂ ϕ)
∂
−σ ϕ)
+
∂
∂ρ ρ
∂ϕ
(15)
=
,
2
2
∂
n
1
ϕ)
+σ
(
ϕ
)
dσ ϕ)
где принято обозначение для производной:
ϕ)
:
=
d
ϕ
Криволинейные интегралы в (13) сводим к определенным по отрезку [-π, π], учитывая, что
2
2
dL
(
ϕ′
)
+σ
(
ϕ′
)
dϕ′
В дальнейших преобразованиях оказалось удобным представить функ-
1
цию σ(φ) в виде σ(φ):=ρ1τ(φ), соответствующим образом подставляя эту форму в (14), (15) и в
выражение для dL′1.
С учетом сказанного преобразовываем (13) и получаем интегральное уравнение:
π
χ
2
1
H
(ϕ)
-
H
(
ϕ′
(
ϕ
,
ϕ
′
)
+χ
(
ϕ
,
ϕ
′
d
ϕ′=
H
(ϕ)
,
ϕ∈
[
−π
,
π
]
,
(16)
∫
)(
1
2
))
π
µ+1
−π
при записи которого введены новые функции:
ϕ)
S
2
2
1
1
2
2
:=H σ(ϕ),ϕ
)
ϕ)
+τ ϕ)
и ϕ):
=H σ(ϕ),ϕ
)
ϕ)
+τ
(
ϕ
)
,
(17)
n
1
n
1
приняты обозначения для ядер:
Дефектоскопия
№ 2
2023
40
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
-τ ϕ)
+τ ϕ)τ(ϕ′
)
cos
(
ϕ-ϕ′
)
+ ϕ)τ(ϕ′
)
sin
(
ϕ-ϕ′
)
,
ϕ≠ϕ′;
2
2
τ ϕ)+τ
(
ϕ′
)
−2τ ϕ)τ(ϕ′
)
cos
(
ϕ-ϕ′
)
(
ϕ,ϕ′
)
(18)
1
=
2
2
0,5τ ϕ)(ϕ)-0,5τ ϕ)
−
(
ϕ
)
,
ϕ=ϕ
′
;
2
2
ϕ)+
τ
(
ϕ
)
4
2
2
2
−λ
τ ϕ)τ
(
ϕ′
)
+λ
τ
(
ϕ
′
)
τ ϕ)cos
(
ϕ-ϕ′
)
+ ϕ)sin
(
ϕ-ϕ′
)
(
ϕ,ϕ′
)
=
,
(19)
2
4
2
2
2
1+λ
τ ϕ)
τ
(
ϕ
′
)
−2
λ
τ ϕ)τ(
ϕ
′
)
cos
(
ϕ− ϕ′
)
1
ρ
где принято обозначение
:
λ
=
ρ2
В данном случае увиделось удобным приступить к решению (16) с помощью численных мето-
дов. Для этого строим дискретный аналог уравнения, выполняя следующие действия: фиксируем
N
разбиение отрезка [-π, π] на N частей; составляем массив {
}
ϕ
из центров фрагментов разбиения
i i=1
N
и массив их длин {
}
δ
; полагаем, что на каждом i-м фрагменте в силу его малости значение иско-
i i=1
мой функции
постоянно и условно равно
H
(
ϕ
)
. Таким образом, на основе (16) записыва-
i
ем систему линейных алгебраических уравнений относительно величин
(
)
{
}N
H
ϕ
:
i
i=1
N
χ
2
1
H
ϕ
−
H
ϕ
ϕ
,
ϕ
+χ
ϕ
,
ϕ
δ
=
H
ϕ
,
i
=1,2,…,N
(20)
(
i
)
∑
(
j
)(
1
(
i
j
)
2
(
i
j
))
j
(
i
)
π
µ+
1
1
j=
Так, на основе решения системы (20) имеем возможность получить массив значений функции
в точках разбиения. Далее эти значения используем для расчета компонент результирующе-
го поля, выражения для которых получаем на основе (2), где под знак интеграла по контуру L2
S
2
подставляем
H
(
ρ′
)
согласно выражению (8). Так, при
ρ
∈
\
{
L
L
} имеем:
n
2
1
∪
2
0
µ-
1
S
H
(ρ)
=
F
(ρ)
+
dL
′H
(
ρ′
)
∇ln
ρ ρ
+
∫
1
n
1
2
π
L1
(21)
∞
m 2
π
µ-
1χ
ρ′′
+
∇
dL′
S (
ρ
′′
)
d
ϕ
′
cosm
(
ϕ′-ϕ′′
)
ln
ρ ρ
,
∫
1
n
1
∑
∫
ρ
′∈L
2
2
π
π
ρ
L
1
m=1
2
0
где принято обозначение для вектор-функции, целиком зависящей от исходных данных задачи:
0
0
χ
0
F ρ)
:=
H ρ)
+
∇
dL
′
H
(
ρ
′
)
ln
ρ ρ
(22)
∫
2
n
2
π
L
2
Отправляемся от формы (21), выполняем необходимые преобразования, подробности которых
опускаем, чтобы не увеличивать объем текста, и получаем выражения для результирующего поля
2
в точке наблюдения ρ для трех областей пространства
: внутри трубы (при ρ: ρ < σ(φ),
φ∈[-π, π]); в теле трубы (при ρ: σ(φ) < ρ < ρ2, φ∈[-π, π]); вне трубы (при ρ: ρ > ρ2). Различный вид
итоговых выражений диктуется спецификой разложения (10) в каждой из упомянутых областей.
Итак, внутри трубы:
π
2
ξ
r
,
τ
ϕ′
,
ϕ-ϕ
'
ξ
r
λ
τ
ϕ
′
,1,
ϕ-ϕ'
0
µ-1
(
(
)
)
2
(
(
)
)
H
(ρ)
=
F
(ρ)
+
e
H
(
ϕ′ τ(
ϕ
′
)
+ χλ
dϕ′+
ρ
∫
2
2
π
ζ
r
,
τ
(
ϕ′
)
,
ϕ-ϕ
'
ζ
r
λ
τ
ϕ
′
,1,
ϕ-ϕ'
−π
(
)
(
(
)
)
(23)
π
2
1
χλ
+e
H(ϕ′)τ(ϕ
′
)
sin
(
ϕ-ϕ′
)
+
d
ϕ
′
;
ϕ
∫
2
ζ
r
,
τ
(
ϕ
′
)
,
ϕ-ϕ
'
ζ
r
λ
τ
ϕ
′
,1,
ϕ-
ϕ
'
-π
(
)
(
(
)
)
в теле трубы:
Дефектоскопия
№ 2
2023
К решению одной задачи магнитостатики для трубы с дефектом на внутренней поверхности
41
0
H
(ρ)
=
F
(
ρ
)
+
π
2
′
ξ
rλ
τ
ϕ′
,1,ϕ-ϕ'
µ-1
−ξ τ(ϕ
)
,r,
ϕ-ϕ
'
)
(
(
)
)
2
+
e
H
(
ϕ′ τ(ϕ′
)
+ χλ
dϕ′+
ρ
∫
2
2π
ζ
(
r,τ
(
ϕ
′
)
,ϕ-ϕ'
)
ζ
rλ
τ
(
ϕ′
)
,1,ϕ-ϕ'
-π
(
)
(24)
π
2
1
χλ
+e
H
(
ϕ′ τ(ϕ′
)
sin
(
ϕ-ϕ
′
)
+
dϕ′;
ϕ
∫
2
ζ
(
r,
τ
(
ϕ′
)
,ϕ-ϕ'
)
ζ
(
rλ
τ
(
ϕ′
)
,1,ϕ-ϕ'
)
-π
вне трубы:
0
H
(ρ)
=
F
(
ρ
)
+
π
π
−ξ τ(ϕ′
,r,
ϕ-ϕ
′
′
(25)
µχ
)
)
sin
(
ϕ-ϕ
)
+
e
H
(
ϕ′ τ(
ϕ
′
)
d
ϕ′+
e
H
(
ϕ′ τ(ϕ
′
)
dϕ′
ρ
∫
ϕ
∫
π
ζ
(
r
,τ
(
ϕ
′
)
,ϕ-ϕ
′
)
ζ
(
r,τ
(
ϕ′
)
,
ϕ-ϕ′
)
-π
-π
При записи формул (23)—(25) использованы обозначения:
ρ
α
2
2
r:
=
;
ξ
(
αβ
γ
)
=
- γ,
ζ
(
αβ
γ
)
:
=α
+β
−
2αβ γ.
ρ
β
1
В процессе выкладок были использованы формулы [4, стр. 54]:
∞
2
∞
m
p
cos
t
−
p
m
p
sint
p
cosmt
=
и
p
sin
mt
=
p
<1.
∑
2
∑
2
1
+
p
−
2
p
cos
t
1
+
p
−
2p
cos
t
m=1
m=1
С точки зрения практиков может оказаться избыточным получение выражений результирую-
щего поля в областях, которые им, как они говорят, «не интересны». Но пренебрегать этим не
стоит в связи с необходимостью выстраивания процедур тестирования решения на достоверность,
например, на предмет совпадения с результатами точно решаемых задач, на выполнение условий
сопряжения вектора поля на границе раздела сред.
В настоящем пункте полностью изложен алгоритм решения сформулированной задачи, при
этом остается произвол для выбора формы дефектного контура L1 и напряженности внешнего
намагничивающего поля. Конкретизируем эти данные.
В качестве контура L1 возьмем такой, что для всякой лежащей на нем точки имеет место сле-
дующая функциональная связь полярных координат ρ и φ:
2
η
ϕ
ρ=σ ϕ)
≡ρ =ρτ ϕ)
1
+
exp
−
,
ϕ∈
[
−π,π
]
,
(26)
1
1
2
ρ
2
ε
1
тогда производные имеют вид:
2
2
2
ηϕ
ϕ
η ϕ
ϕ
ϕ) =-
exp
−
и
(
ϕ
)
=-
1
−
exp
−
2
2
2
2
2
ρ
ε
2
ε
ρ
ε
ε
2ε
1
1
На рис. 3 приводится изображение сечения трубы, внутренний контур которого отвечает зависи-
мости (26) при η > 0. Естественные ограничения на значения параметров η и ε, входящих в опреде-
ление функции σ(φ): -ρ1 < η < ρ2 - ρ1; ε > 0. На лучах φ = ±ε лежат точки перегиба функции σ(φ).
Принимаем, что внешнее намагничивающее поле является однородным, при этом рассмотрим
1
два варианта, одновременно записывая на основе (12) и (17) функцию
H
(
ϕ
)
,
необходимую для
подстановки в правую часть системы (16), а на основе (22) — функцию F0(ρ), необходимую для
расчета компонент вектора напряженности результирующего поля:
Дефектоскопия
№ 2
2023
42
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
y
n2
μ = 1
S : μ
n1
μ = 1
0
x
L1: ρ = σ(φ)
L2: ρ = ρ2
Рис. 3.
1) H0 = H0ex = H0 (eρ cosφ - eφ sin φ),
0
1
2H
ϕ)
=-
(τ(ϕ)
cosϕ+ ϕ)sinϕ
)
,
µ+1
0
2H
F
0(
ρ
)
=
(
e
ρ
cosϕ-e
ϕ
sinϕ
)
при
ρ<ρ
2
,
µ+1
2
2
ρ
ρ
0
0
2
0
2
F
(
ρ
)
=
H
1
+χ
e
cosϕ-
H
1−χ
e
sinϕ
приρ>ρ
;
2
ρ
2
ϕ
2
ρ
ρ
2) H0 = -H0ey = -H0 (eρ sinφ + eφ cos φ),
0
1
2H
ϕ)
=
sinϕ- ϕ)
cosϕ
,
(τ(ϕ)
)
µ+
1
0
2H
F
0(
ρ
)
=-
(
e
ρ
sinϕ+e
ϕ
cosϕ
)
при
ρ<ρ
2
,
µ+1
2
2
ρ
ρ
0
0
2
0
2
F
(
ρ
)
=-H
1+χ
e
sinϕ-
H
1−χ
e
cos
ϕ
приρ>ρ
2
ρ
2
ϕ
2
ρ
ρ
Численный алгоритм какой бы то ни было задачи следует, по возможности, подвергать про-
веркам путем сравнения с результатом схожей по постановке задачи, желательно решаемой точно.
В качестве такого инструмента тестирования естественно взять задачу о бесконечной трубе с вну-
Дефектоскопия
№ 2
2023
К решению одной задачи магнитостатики для трубы с дефектом на внутренней поверхности
43
тренним радиусом, равным ρ1, наружным, равным ρ2, и магнитной проницаемостью μ, в рамках
которой компоненты результирующего поля определяются по известным формулам:
2
1-χ
0
H
(
ρ
)
=
H
внутри трубы;
2
2
1−χ
λ
2
1
-χ
ρ
0
0
1
H
(
ρ
)
=
H H
+χ
в теле трубы;
2
2
2
1
−χ
λ
ρ
2
2
1-λ
ρ
0
0
2
H
(
ρ
)
=
H
−χ
H
вне трубы,
2
2
2
1−χ
λ
ρ
при использовании которых в случае H0 = H0ex = H0 (eρ cosφ - eφ sin φ) надо полагать
0
0
H
=-H
(
e
ρ
cosϕ+e
ϕ
sinϕ
)
,
а в случае H0 = -H0ey = -H0 (eρ sinφ + eφ cos φ) надо полагать
0
0
H
=
H
(
e
ρ
sinϕ-e
ϕ
cosϕ
)
Эти выражения были использованы в качестве эталона для многочисленных проверок.
ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ
Представленный в предыдущем пункте алгоритм численного решения задачи был реализо-
N
ван на языке программирования Fortran. При построении разбиения {
}
ϕ
отрезка [-π, π] обе-
i i=1
спечена возможность свободного выбора различной плотности разбиения в области выражен-
ности дефекта и вне ее. «Область выраженности дефекта» может быть выбрана с определенным
произволом — так был взят отрезок [-4ε, 4ε]. Далее под nπ понимаем число точек на отрезках
[-π, -4ε] и [4ε, π], а под nε — число точек на отрезках [-4ε, 0] и [0, 4ε]. Таким образом, общее
число точек разбиения N = 2(nπ + nε).
Для получения решения системы линейных алгебраических уравнений (20) была использована
хорошо зарекомендовавшая себя стандартная программа из известной книги [10, §3], позволяю-
щая получить оценку числа обусловленности матрицы системы. На данном этапе были выполнены
различные проверки на соответствие численного решения точному, имеющему место для безде-
а
б
Hρ(ρ = 0,9, φ)
0,1
Hφ(ρ = 0,9, φ)
Для трубы без дефекта по точным
формулам: ≅ - 0,091727sinφ
0,08
0,05
0
0,04
Для трубы без дефекта по точным
формулам: ≅ 0,091727cosφ
Для трубы с дефектом при ε = 0,05
-0,05
Для трубы с дефектом
и η = 0,05
при ε = 0,05 и η = 0,05
Для трубы с дефектом при ε = 0,1
и η = 0,1
Для трубы с дефектом
при ε = 0,1 и η = 0,1
φ
-0,1
0
φ
-1
0,5
0
0,5
1
-1
0,5
0
0,5
1
Рис. 4. Зависимости Hρ(ρ = 0,9, φ) (а) и Hφ(ρ = 0,9, φ) (б) при ρ1 = 1,0; ρ2 = 1,3; μ = 99; H0 = (H0, 0), H0 = 1.
Дефектоскопия
№ 2
2023
44
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
а
б
0,004
Hρdef(ρ = 0,9, φ)
0,01
Hφdef(ρ = 0,9, φ)
0
0,005
-0,004
ε = 0,01 и η = 0,01
0
ε = 0,05 и η = 0,05
ε = 0,01 и η = 0,01
-0,008
ε = 0,1 и η = 0,1
-0,005
ε = 0,05 и η = 0,05
ε = 0,1 и η = 0,1
-0,012
φ
-0,01
φ
-3
-2
-1
0
1
2
3
-3
-2
-1
0
1
2
3
Рис. 5. Угловая зависимость ρ-компоненты (а) и φ-компоненты (б) поля дефекта для ρ1 = 1,0; ρ2 = 1,3; μ = 99;
H0 = (H0, 0), H0 = 1.
а
б
0
Hφ(ρ = 0,9, φ)
0,1
Hρ(ρ = 0,9, φ)
Для трубы без дефекта по точным
Для трубы без дефекта по точным
формулам: ≅ - 0,091727cosφ
формулам: ≅ - 0,091727sinφ
Для трубы с дефектом при ε = 0,05
и η = 0,05
0,05
-0,04
Для трубы с дефектом при ε = 0,1
и η = 0,1
0
-0,08
-0,05
Для трубы с дефектом
при ε = 0,05 и η = 0,05
Для трубы с дефектом
при ε = 0,1 и η = 0,1
-0,12
-0,1
φ
φ
-1
-0,5
0
0,5
1
-1
-0,5
0
0,5
1
Рис. 6. Hρ(ρ = 0,9, φ)(а) и Hφ(ρ = 0,9, φ)(б) при ρ1 = 1,0; ρ2 = 1,3; μ = 99; H0 = (0, -H0), H0 = 1.
фектной трубы в рамках выбранной модели — группа проверочных формул приводится в конце
предыдущего пункта. Численный эксперимент показал, что уже при nπ = nε = 2 точки приближен-
ного решения укладываются на кривую, соответствующую точному. Для дальнейших расчетов
выбрано nπ = nε = 80. Если же возникнет необходимость вычисления компонент результирующего
поля вблизи ограничивающих магнетик контуров, тогда число точек лучше увеличить. Так или
иначе, затраты времени на работу программы при таких условиях крайне невелики.
Сравнения с эталонными результатами проводились и на этапе вычисления компонент резуль-
тирующего поля. В частности, благодаря этим проверкам была дана апостериорная оценка устой-
чивости и точности численного алгоритма: в зависимости от сочетания данных задачи в оконча-
тельных значениях обнаруживается стабилизация от трех до шести значащих цифр.
Дефектоскопия
№ 2
2023
К решению одной задачи магнитостатики для трубы с дефектом на внутренней поверхности
45
а
б
Hρdef(ρ = 0,9, φ)
0,01
Hφdef(ρ = 0,9, φ)
0,02
ε = 0,01 и η = 0,01
ε = 0,05 и η = 0,05
0
0,01
ε = 0,1 и η = 0,1
-0,01
ε = 0,01 и η = 0,01
0
ε = 0,05 и η = 0,05
-0,02
ε = 0,1 и η = 0,1
-0,01
-0,03
-0,02
φ
φ
-2
-1
0
1
2
-3
-2
-1
0
1
2
3
Рис. 7. Угловая зависимость ρ-компоненты (а) и φ-компоненты (б) поля дефекта для ρ1 = 1,0; ρ2 = 1,3; μ = 99;
H0 = (0, -H0), H0 = 1.
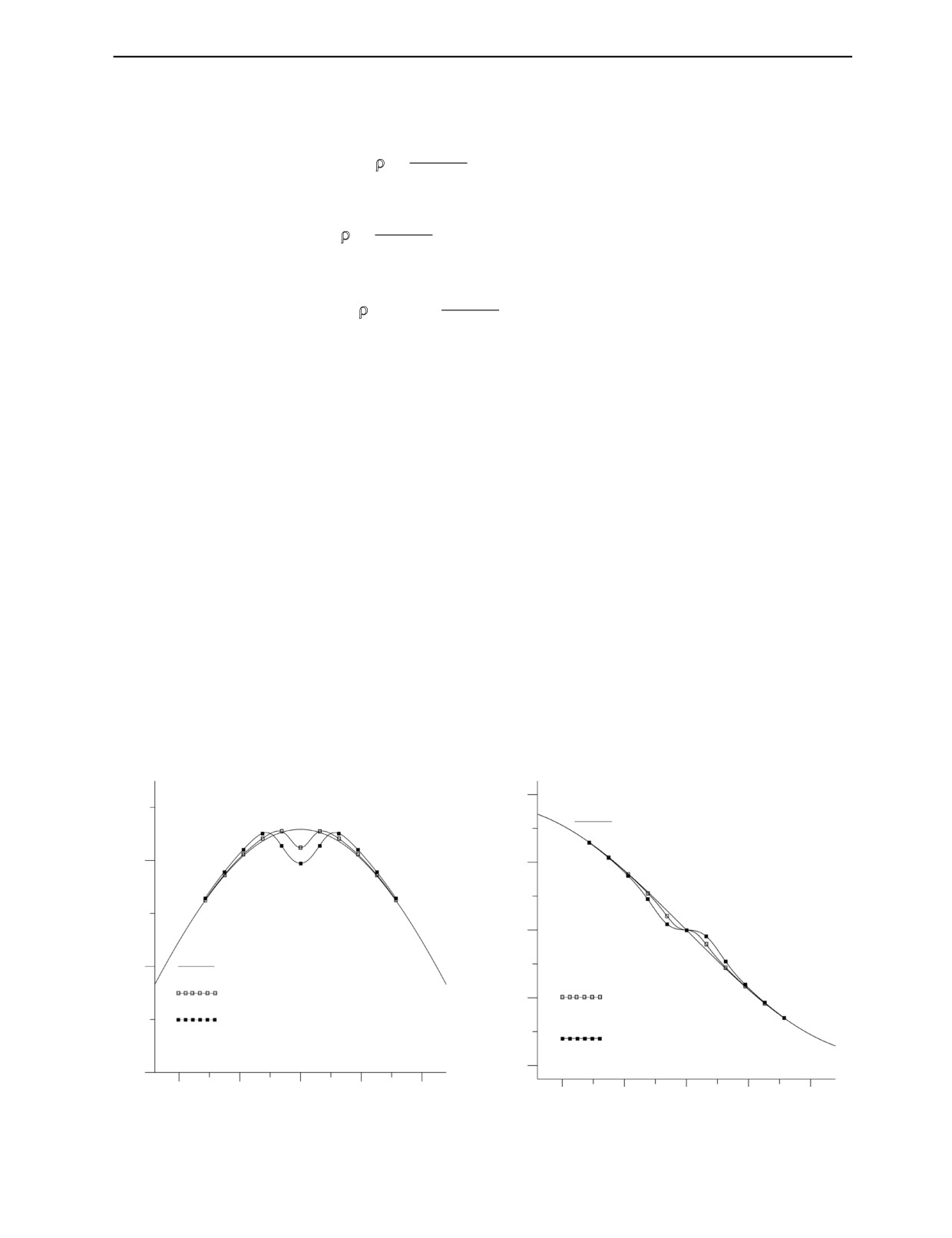
На рис. 4а и б соответственно приводятся графики зависимости Hρ (ρ, φ) и Hφ (ρ, φ), построен-
ные при ρ = 0,9 (точки наблюдения лежат внутри трубы) и H0 = H0ex. Сплошная линия отвечает
случаю бездефектной трубы, а маркированные — случаям дефектной трубы с различными значе-
ниями параметров дефекта ε и η. На практике контроля зачастую рассматривается так называемое
«поле дефекта», определяемое по формуле:
Hdef(ρ) = Hдля тела с дефектом(ρ) - Hдля тела без дефекта(ρ).
def
На рис. 5а изображена зависимость
(
0,9,
),
Hρ
ρ=
ϕ
а на рис. 5б — зависимость
def
(
0,9,
).
Hϕ
ρ=
ϕ
Расчеты показали, что аналогичные кривые, построенные для случая, когда
точки наблюдения располагаются вовне трубы, имеют в десятки раз меньшие абсолютные зна-
чения экстремумов. Тем самым, результаты численных расчетов согласуются с эксперименталь-
ными данными — известно, сигнал от поверхностного дефекта существенно выше, если изме-
рения проводятся со стороны дефектной поверхности.
Аналогичные построения были выполнены для случая внешнего поля H0 = -H0ey: результиру-
ющие кривые изображены на рис. 6 и 7.
ЗАКЛЮЧЕНИЕ
Разработанный алгоритм решения задачи легко может быть адаптирован под различные формы
внутреннего дефектного контура путем выбора желаемого вида функции σ(φ). В рамках рассмо-
тренного в настоящей работе вида функции σ(φ) вариацией параметра η можно задавать глубину
дефекта, а, меняя ε, задавать узкие или размытые дефекты. Кроме того, меняя знак η, легко полу-
чаем возможность решить задачу для трубы с дефектом в виде нароста на ее внутренней поверх-
ности. Алгоритм допускает рассмотрение и различных конфигураций внешнего намагничивающе-
го поля.
На основе анализа результатов численного решения вполне имеет смысл рассмотреть и вопрос
об условиях решения обратной задачи по раздельному определению глубины и раскрытия поверх-
ностного дефекта.
Авторы открыты для взаимодействия с практиками магнитного контроля в плане возможной
работы по сопоставлению результатов расчетов и соответствующих экспериментов.
Авторы благодарят А.В. Гапонцева за помощь в постановке задачи и интерес к результатам ее
решения.
Работа выполнена в рамках государственного задания по теме «Квант» (“Quantum”)
№ АААА-А18-118020190095-4.
Дефектоскопия
№ 2
2023
46
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
СПИСОК ЛИТЕРАТУРЫ
1. Зацепин Н.Н., Щербинин В.Е. К расчету магнитостатического поля поверхностных дефектов. I.
Топография полей моделей дефектов // Дефектоскопия. 1966. № 5. С. 50—59.
2. Щербинин В.Е., Зацепин Н.Н. К расчету магнитостатического поля поверхностных дефектов. II.
Экспериментальная проверка основных расчетных закономерностей // Дефектоскопия. 1966. № 5.
С. 59—65.
3. Кротов Л.Н. Реконструкция границы раздела сред по пространственному распределению маг-
нитного поля рассеяния. 1. Постановка и метод решения обратной геометрической задачи магнито-
статики // Дефектоскопия. 2004. № 6. С. 76—82.
4. Кротов Л.Н. Реконструкция границы раздела сред по пространственному распределению маг-
нитного поля рассеяния. 1. Исследование свойств решения вспомогательной прямой задачи //
Дефектоскопия. 2004. № 2. С. 76—82.
5. Дякин В.В., Кудряшова О.В., Раевский В.Я. Поле рассеяния пластины с поверхностным дефек-
том в однородном внешнем поле // Дефектоскопия. 2018. № 12. С. 23—31.
6. Хижняк Н.А. Интегральные уравнения макроскопической электродинамики. Киев: Наукова
думка, 1986. 278 с.
7. Дякин В.В. Математические основы классической магнитостатики. Екатеринбург: РИО УрО
РАН, 2016. 404 с.
8. Михлин С.Г. Курс математической физики. М.: Наука, 1968, 575 с.
9. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: ГИФМЛ,
1962. 1100 с.
10. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. М.:
Мир, 1980. 277 с.
Дефектоскопия
№ 2
2023