Акустические методы
УДК 620.179.16:534.2
АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТВЕРДЫХ УПРУГИХ СРЕД
С ОРИЕНТИРОВАННОЙ МИКРОТРЕЩИНОВАТОСТЬЮ
© 2023 г. К.Е. Аббакумов1,*, А.В. Вагин1,**, И.Г. Сидоренко1,***
1Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
им. В.И. Ульянова (Ленина), Россия 197022 Санкт-Петербург, ул. Проф. Попова, 5
Поступила в редакцию 20.12.2022; после доработки 18.03.2023
Принята к публикации 20.03.2023
Разработана в условиях распространения плоских упругих продольных волн модель их взаимодействия с упругой
средой, содержащей ориентированные микротрещины, обладающие особенностью граничных условий в приближении
«линейного скольжения». В приближении теории волн Блоха и Флокé определен вид дисперсионного уравнения. Полу-
чены и проанализированы результаты его решения, определяющие характер зависимостей фазовой скорости распро-
странения и коэффициента затухания эффективной продольной волны от параметров микрошероховатости берегов
трещин и других параметров модели.
Ключевые слова: микрошероховатые поверхности, фазовая скорость и коэффициент затухания продольных волн,
коэффициенты отражения, коэффициенты прохождения, контактная жесткость в нормальном и тангенциальном направ-
лениях.
DOI: 10.31857/S0130308223040012, EDN: XSOSKF
ВВЕДЕНИЕ
Постоянное совершенствование традиционных конструкционных материалов и разработка
новых сталкиваются с проблемой разработки и применения новых видов контрольной аппаратуры.
Причина этого заключается в формировании в изделиях из таких материалов новых видов
несплошностей, не описываемых известными ранее моделями. Очевидно, что появление новых
видов несплошностей (дефектов) требует соответствующих изменений в структуре средств нераз-
рушающего контроля, проектирование которых должно базироваться на использовании замещаю-
щих моделей при теоретическом анализе измерительных трактов аппаратных средств [1]. Интерес
представляет и решение обратной задачи, позволяющей оценивать количественно структурные
параметры материалов по результатам ультразвуковых измерений [2—5].
Наиболее широкое распространение для этих целей получили модели плоскослоистых сред,
очевидно, в силу сходства структур несплошностей и соответствующих моделей [6—8]. Научный
раздел, связанный с изучением волновых процессов в сложноструктурированных средах, имеет
обширную библиографию, отдельные фрагменты которой представлены в списке литературных
источников [9—19].
Приближение слоистых сред имеет широкую практику использования по отношению к раз-
нообразным прикладным задачам, применительно и к геоакустике [20, 21], и к условиям нераз-
рушающего контроля [22] и т.д.
Так, например, в [22] такое приближение использовалось применительно к решению задач
обнаружения и определения характеристик флокеносодержащего металла. В [22] подобные задачи
решались применительно и к изделиям, изготовленным по технологиям порошковой металлургии.
Образование новых видов несплошностей возможно как для традиционных металлургических
технологий, так и новых видов, как, например, аддитивные технологии изготовления композици-
онных материалов, например, на основе углепластиковых волокон и т.п.
Применительно к аддитивным технологиям слоистая структура получающихся материалов
определяется послойным нанесением исходных компонентов с последующим лазерным воздей-
ствием [23].
Применительно к изготовлению композитов образование несплошностей связано, в частности,
с «неплотным» прилеганием слоев материала при формовке и склейке (автоклавное формирова-
ние, вакуумная диффузия) [24, 25].
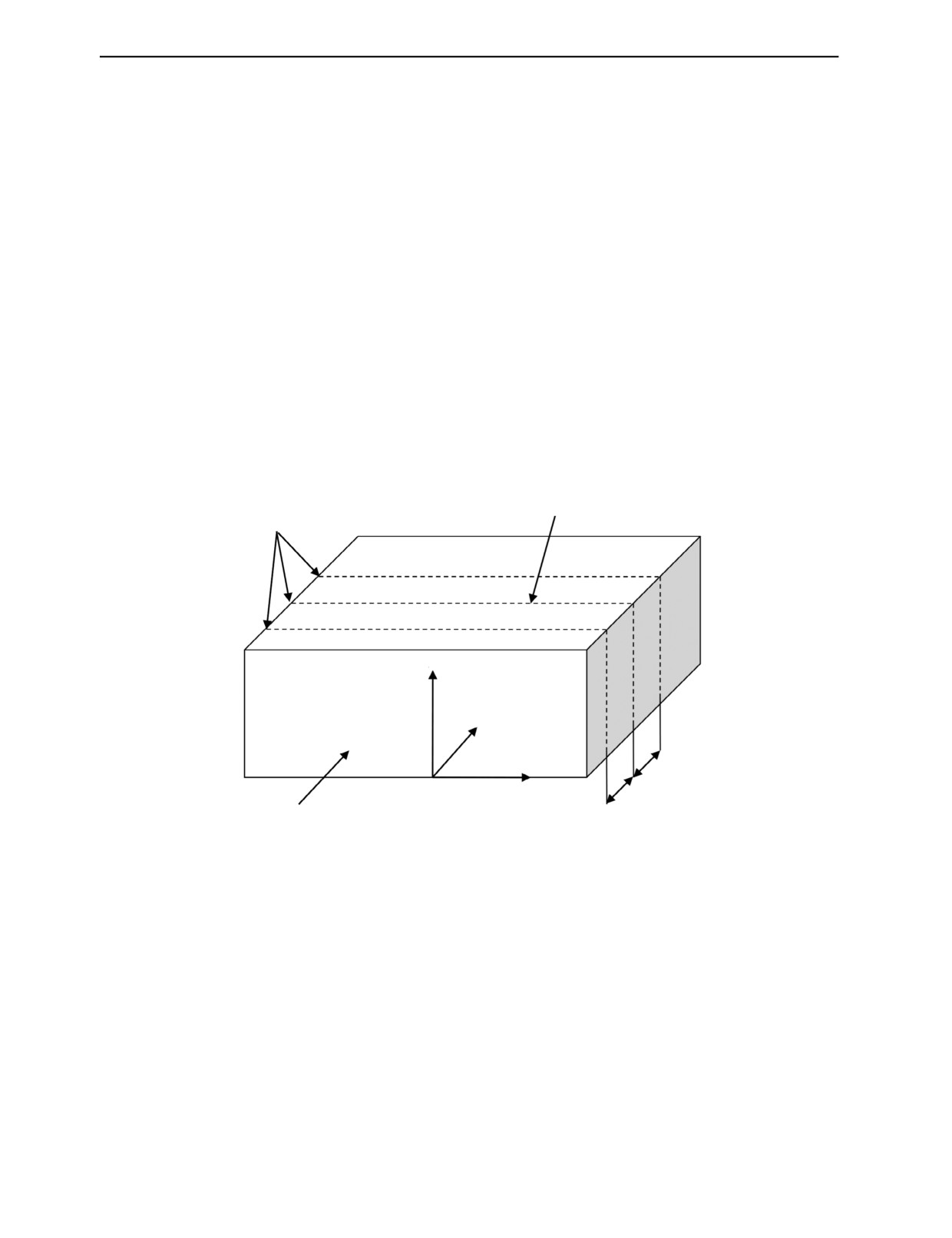
Если плоскостные неоднородности, изображенные на рис. 1, имеют выход на поверхность
изделия, то для их изучения, кроме объемных, целесообразно привлекать и поверхностные
волны, характеристики которых определяются на основании характеристик объемных волн
[26—28].
4
К.Е. Аббакумов, А.В. Вагин, И.Г. Сидоренко
В отдельных случаях, при невозможности обеспечения требуемых параметров за счет извест-
ных материалов, становится необходимым решение задачи создания специальных метаматериалов
путем внедрения в известную структуру системы несплошностей, способствующих образованию
новых физико-механических характеристик. Известно также, что отдельные виды технологиче-
ской обработки, например термообработки металлов, способны вызывать характерные только для
них виды дефектов, связанных с поверхностным растрескиванием и т.д. [7].
Учитывая изложенное, можно утверждать, что задача разработки модели микротрещиноватой
среды, охватывающей влияние ранее не учитываемых параметров взаимодействующих «берегов»
микротрещин, является актуальной задачей, решение которой представлено в данной работе. В
плосковолновом приближении для гармонических сигналов низкочастотного диапазона для моде-
ли, учитывающей взаимодействие «берегов» микротрещин, предлагается вывод дисперсионного
уравнения. Его решения определяют значения фазовой скорости и коэффициента затухания (рас-
сеяния) эффективной продольной волны. Анализ полученного решения предполагается осуще-
ствить на основе численных оценок для набора значений параметров сплошности и шероховато-
сти актуальных для задач ультразвуковых измерений в технических приложениях.
ИСХОДНЫЕ ПОЛОЖЕНИЯ И МЕТОДИКА ПРОВЕДЕНИЯ ИССЛЕДОВАНИЙ
По аналогии с известными моделями «слоистых» сред [9] одной из возможных моделей такого
класса является модель слоистой среды, представленная на рис. 1.
R; D
Микротрещины
Образец: ρ, λ, μ
Y
Z
0
X
h
Направление распространения
продольной волны
Рис. 1. Схема образования эффективной волны при прохождении ультразвука через области металла с ориентированной
трещиноватостью.
Граничные условия в областях металла с ориентированной трещиноватостью в приближении
«линейного скольжения» определяются следующим образом: σik(1) = σik(2), Ui(1) = Ui(2) - σik(1,2)/
KG, где Ui — упругое смещение; σik — упругое напряжение; KG — коэффициент жесткости.
Рассмотрим процесс распространения плоской продольной волны в направлении оси Z декар-
товой системы координат, показанной на рис. 1. Во всем объеме среды образца с параметрами: ρ
— плотность, λ и μ — коэффициенты Ламэ [9, 26] расположены плоскостные протяженные неод-
нородности, параллельные друг другу и плоскости XOY. Каждая из этих неоднородностей облада-
ет комплексными коэффициентами отражения: R = R1 + iR2 и прохождения: D = D1 + iD2, где R1,
D1 и R2, D2 — их вещественные и мнимые части соответственно. Расстояние между несплошно-
стями равно h. Для гармонических волновых процессов с частотой ω предполагается, что длина
продольной волны существенно превосходит расстояние между несплошностями: λ >> h (низкоча-
Дефектоскопия
№ 4
2023
Акустические характеристики твердых упругих сред с ориентированной...
5
стотное приближение). Кроме того, если несплошность имеет перфорированную структуру, то
следует выбирать степень перфорации, определяемую специальным коэффициентом ξ, как отно-
сительную периодическую площадь участка с отсутствием акустического контакта, низкой, с тем,
чтобы на расстоянии h после прохождения несплошности могла образовываться «квазиплоская»
эффективная волна.
На основании теории волн Блоха и Флоке [29, 30] при распространении упругих волн в пери-
одических средах для волны, бегущей и имеющей вектор упругих смещений в направлении оси Z,
можно считать:
z
U z)
=U z)exp(iqz),
(1)
где q — искомое волновое число эффективной волны. По определению Uz(z) (1) обладает свой-
ством периодичности:
U z)
=U
(z+h).
(2)
z
z
Функция (1) непрерывна и выражение (2) справедливо для любой точки на оси Z. Это позволя-
ет ограничиться рассмотрением волнового процесса внутри слоя |ζ| ≤ h/2, где координата ζ (на
рис. 1 не показана) имеет начало в точках z = l · h, где l = 0, 1, 2, …, ∞. Поэтому выражение (2)
можно переписать:
U
z
(h
/ 2)
=U
z
(−h
/ 2)⋅exp(-iqh
/ 2).
(3)
Кроме того, выполняя граничное условие для непрерывности упругих напряжений, можно
получить:
∂
U
(
h
/ 2)
∂U
(−h
/ 2)
z
z
=
⋅exp(−
iqh).
(4)
∂
z
∂z
Представим, что выделяемый на рис. 1 слой состоит из двух областей: -h/2 ≤ ζ < 0 и
0 ≤ ζ < h/2. В этих двух областях могут распространяться волны в двух направлениях:
U ζ)
=A⋅exp(ik
ζ)
и
U ζ)
=B⋅exp(
−ik
ζ)
. Каждая из этих волн отражается и ослабляется при
z
l
z
l
переходе через границу ζ = 0. Учитывая это, вводя коэффициенты отражения R и прохождения
D, можно записать:
U ζ)
=D⋅Aexp(ik
ζ
) +Bexp(−ik
ζ)+R⋅Bexp(−ik
ζ)
при 0 < ξ ≤ h/2,
(5)
z
l
l
l
U ξ
=Aexp(ik
ξ)+R⋅A
exp(−ik
ξ)+D⋅Bexp(−ik
ξ)
при -h/2 ≤ ξ ≤ 0,
(6)
z
l
l
l
где kl - волновое число продольной волны.
Подстановка выражений (5), (6) в выражения (3), (4) приводит к системе линейных однород-
ных уравнений (7), (8) для амплитуд A, B:
[
D-[exp(−ik
h)+R]exp(
−iqh
)]A+
[exp(−ik
h)+R-Dexp(−iqh)]B=
0,
(7)
l
l
[
D-[exp(−ik
h)
−R
]exp(iqh
)]A-
[exp(−ik
h)−R-D⋅exp(iqh)]B=
0.
(8)
l
l
Решение системы уравнений (7), (8) может существовать, только если ее определитель равен
нулю. Это приводит к уравнению:
2
2
Dexp(−iqh)
−
(D
−R
)exp(ik
l
h
) exp(-ik
l
h)+Dexp(iqh)
=
0.
(9)
Собственно уравнение (9) и является дисперсионным, связывая qh c klh. Для целей вычислений
его можно привести к более удобному виду:
2
2
(
D
−
R
−
1)exp(ik
h)
l
2cos(
qh)
=
D
+cos(k
h)
(10)
l
2
Дефектоскопия
№ 4
2023
6
К.Е. Аббакумов, А.В. Вагин, И.Г. Сидоренко
Легко видеть, что для заданной частоты, т.е. для заданной величины klh из уравнения (10),
вычисляется эффективное волновое число q. Правая часть дисперсионного уравнения (10) в
общем случае является комплексной величиной. Тогда для выполнения равенства необходимо
также представить q в виде комплексной величины: q = q1 + iq2. Подстановка этого выражения в
(10) и выделение реальной и мнимой частей приводит к выражениям:
cos(q1h)⋅ch(q2h)
=
P,
(11)
sin(q1h)⋅sh(q2h)
=
Q,
{
D F1cos(k
h)−
F3sin(k
h)]+
D2[
F
2 sin(k
h)+
F3cos(k
h)]
}
l
l
l
l
где
P
=
,
2
2⋅D
{
D F1cos(k
h)−
F3sin(k
h)]+
D1[
F
2 sin(k
h)+
F3cos(k
h)]
}
l
l
l
l
Q
=
,
2
2⋅D
2
2
2
2
F1= D1
− D2
− R1
+ R2
+ 1,
2
2
2
2
F2 = D1
− D2
− R1
+ R2
−1,
F
3
=
2⋅(
D1
⋅
D
2
−
R1
⋅
R
2)
Решая систему уравнений (11), можно получить следующие выражения:
для вещественной части волнового числа:
1
1
2
2
2
2
2
2
1−
P
−Q
1−
P
−Q
2
2
arcsin
+
(
)
+Q
(12)
2
2
q1=
,
h
для мнимой части волнового числа:
Q
arsh
sin(k
h)
(13)
l
q2
=
h
Используя выражение для вещественной части волнового числа эффективной продольной
волны (12), легко получить значение фазовой скорости эффективной продольной волны: cэфф =
= ω/q1. Вычисления по (13) сразу дают значения коэффициента затухания (рассеяния) в Нп/м.
Вычисления по формулам (12), (13) для учитываемых моделей несплошностей можно осу-
ществлять после подстановки функциональных зависимостей комплексных в общем случае выра-
жений коэффициентов отражения и прохождения для конкретных типов несплошностей. Это
повышает значимость решения задач определения соответствующих коэффициентов отражения и
прохождения для плоскостных неоднородностей, подтверждая перспективность концепции моде-
лирования плоскостных протяженных неоднородностей применительно к задачам в области уль-
тразвукового контроля.
РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ И ИХ ОБСУЖДЕНИЕ
Выберем в качестве модели несплошности трещиноподобный объект, шероховатые поверхно-
сти которого имитируются микровыступами сферической формы, их взаимодействие сопровожда-
ется эффектом «проскальзывания» [31]. При этом, исходя из рис. 1, упругие напряжения σik пере-
даются без изменений, а упругие смещения Ui могут испытывать «разрыв» В качестве количе-
ственной меры, определяющей степень проскальзывания (разрыва), выступают модули контакт-
ных жесткостей, действующих в нормальном и тангенциальном по отношению к плоскости тре-
щины направлениях, в общем случае представляемые в виде тензора второго ранга [31]:
Дефектоскопия
№ 4
2023
Акустические характеристики твердых упругих сред с ориентированной...
7
KGN
0
0
KG
0
KGT1
0
(14)
=
0
0
KGT
2
В случае плоской задачи в (14) неизвестными можно считать только две величины: нормаль-
ную и тангенциальную жесткости, для которых в [31, 32] получены выражения KGN, KGT. Там
показано, в частности, что в случае малости высоты микровыступов по сравнению с длиной пада-
ющей упругой волны для разнородных материалов модуль нормальной контактной жесткости
определяется зависимостью:
(λ
+2µ
)(λ
+2µ
)c
c
2πξ
1
1
2
2
l1
l2
KGN
=
,
(15)
2
(λ
+2µ
)
c
+(λ
+
2µ
)c
ωd
(1−ξ)
1
1
l1
2
2
l2
по аналогии модуль тангенциальной контактной жесткости имеет вид:
µ
µ
c
c
2πξ
1
2
t1
t2
KGT
=
,
(16)
2
µ
1
c
t1
+µ
2
c
t2
ω
d
(1−ξ)
где ρ1, λ1, μ1 и ρ2, λ2, μ2 — плотность и коэффициенты Ламэ для сред, лежащих выше и ниже гра-
ницы раздела соответственно; ω = 2πf — круговая частота, а f — линейная частоты; d — среднее
расстояние между соседними микровыступами на контактирующих поверхностях; ξ — коэффи-
циент перфорации: ξ = 1 - b2/d2, где b — средний размер участка с отсутствием контакта [33].
Величины d и ξ являются параметрами модели.
В предположении малости высоты микровыступов сферической формы по сравнению с дли-
ной волны, также в соответствие с другими рекомендациями в [31, 32], показано, что величина
среднего расстояния между микровыступами может быть представлена в виде (17):
2
d =2 2aRz - (Rz)
,
(17)
где a — радиус замещающего сферического микровыступа; Rz — величина шероховатости [31,
32]. Кроме того, было показано, что средний радиус площади контактного пятна r ≈ (2 / 3) 2aRz ,
откуда d2 - b2 ≈ 2πr2.
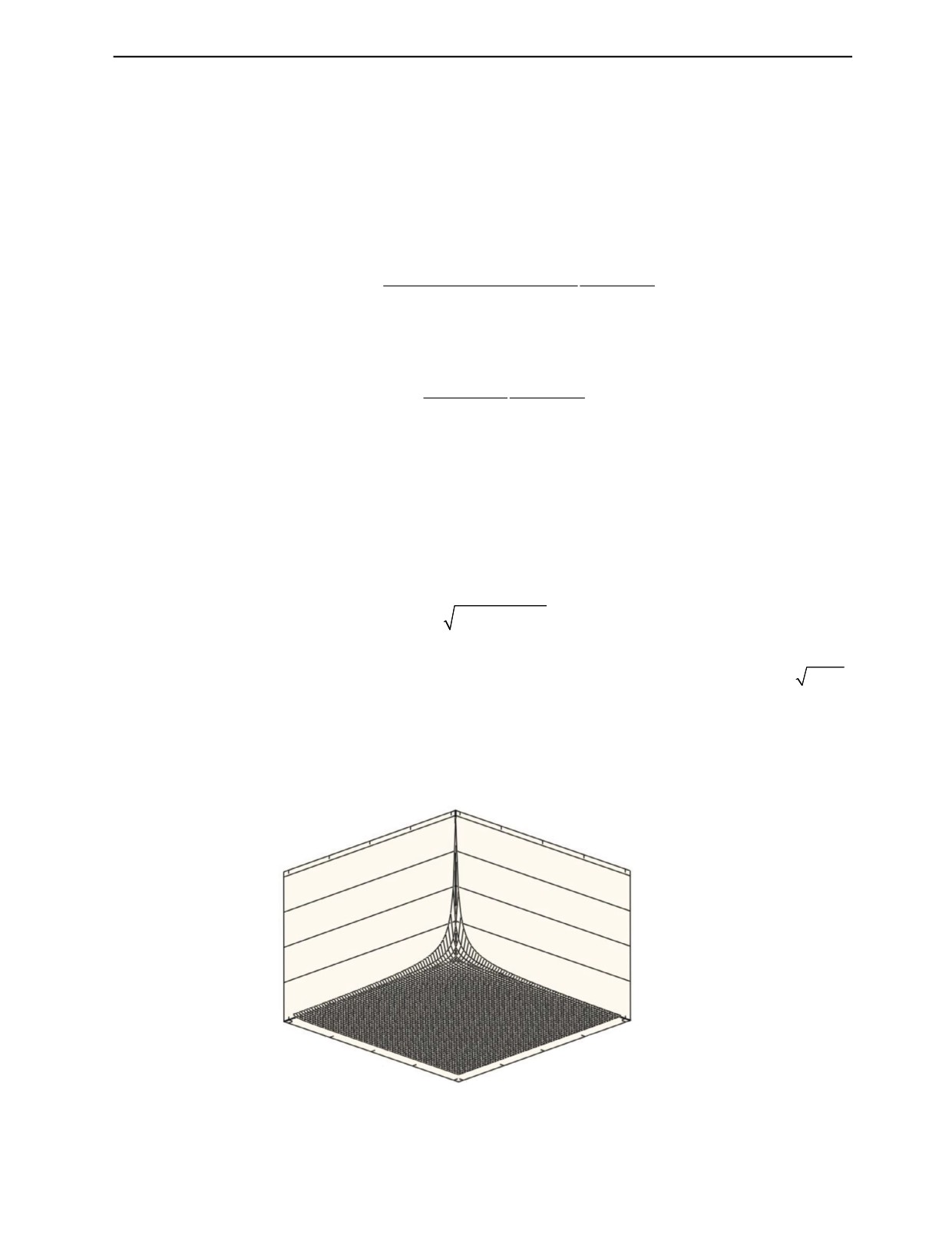
Общий вид зависимостей нормальной и тангенциальной контактных жесткостей для микро-
трещины в стали от коэффициента перфорации ξ и от параметра шероховатости Rz при заданных
значениях радиусов микросфер и частоты представлен на рис. 2, 3.
KGN, Н/м3
3 · 1018
2 · 1018
1 · 1018
0
0,01
5
0,16
85
0,32
165
0,48
245
ξ Rz, мкм
Рис. 2. Зависимость KGN-нормальной контактной жесткости от коэффициента перфорации ξ (0,01 < ξ < 0,64) и значений
параметра шероховатости: 5·10-6 м < Rz < 320·10-6 м; f = 1,25 МГц, a = 0,5 мм, материал — сталь.
Дефектоскопия
№ 4
2023
8
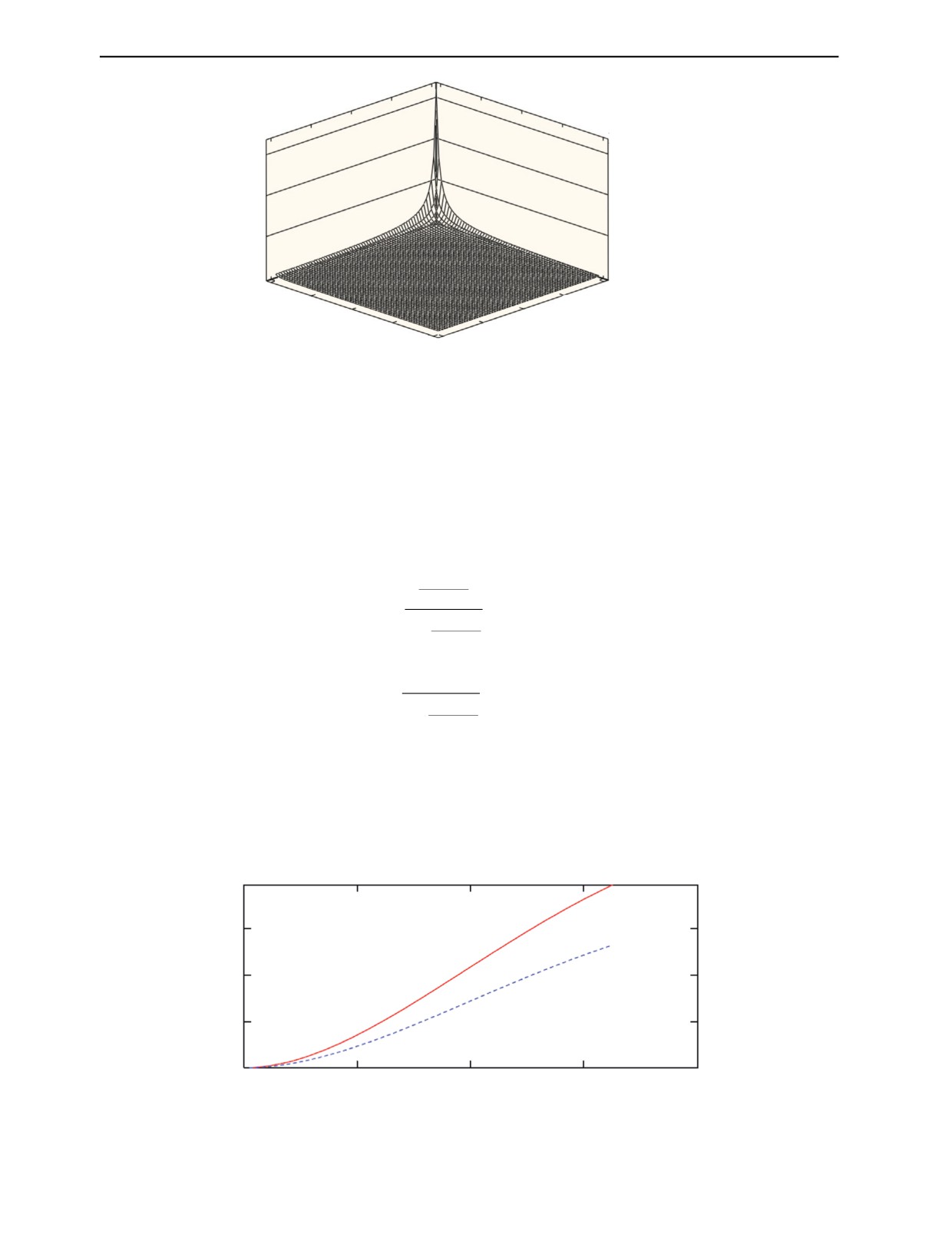
К.Е. Аббакумов, А.В. Вагин, И.Г. Сидоренко
KGT, Н/м3
6 · 1017
4 · 1017
2 · 1017
0
0,01
5
0,16
85
0,32
165
0,48
245
ξ Rz, мкм
Рис. 3. Зависимость KGT-тангенциальной контактной жесткости от коэффициента перфорации ξ (0,01 < ξ < 0,64)
и значений параметра шероховатости: 5·10-6 м < Rz < 320·10-6 м; f = 1,25 МГц, a = 0,5 мм, материал — сталь.
Как следует из рис. 3, 4, указанные зависимости представляют собой гладкие функции, обе-
спечивая при вычислениях плавный переход от условий «сварного» контакта до условий «свобод-
ной» границы. При этом величина нормальной контактной жесткости превосходит величину тан-
генциальной при всех сочетаниях, учитываемых в модели параметров.
Выражения для коэффициентов отражения и прохождения продольной волны при ее нормаль-
ном падении для однородных материалов с выделением в них вещественных и мнимых частей
примут вид [31]:
ωρ c1
i
l
KGN
R
=
=
R1+iR2,
(18)
iωρ
c
1
l1
2-
KGN
2
D
=
=
D1+iD2.
iωρ
c
(19)
1
l1
2−
KGN
Подстановка выражений (18) и (19) в уравнения (12) и (13) с учетом (17) приводит к оконча-
тельным выражениям, на основании которых осуществлялись численные оценки фазовой скоро-
сти и коэффициента затухания эффективной продольной волны. Из-за громоздкости эти выраже-
ния в окончательном виде не приводятся.
R1
0,06
0,04
0,02
0
0
1 · 10-4
2 · 10-4
3 · 10-4
Rz, м
Рис. 4. Зависимость вещественной части коэффициента отражения ультразвука от параметра шероховатости при задан-
ных значениях коэффициента перфорации: (--) — ξ = 0,65; (----) — ξ = 0,6; частота ультразвука f = 1,25 МГц, a = 0,5 мм,
материал — сталь.
Дефектоскопия
№ 4
2023
Акустические характеристики твердых упругих сред с ориентированной...
9
0
-0,1
-0,2
R2
0
1 · 10-4
2 · 10-4
3 · 10-4
Rz, м
Рис. 5. Зависимости мнимой части коэффициента отражения ультразвука от параметра шероховатости при заданных
значениях коэффициента перфорации: (--) — ξ = 0,65; (----) — ξ = 0,6; частота ультразвука f = 1, 25 МГц, a = 0, 5 мм,
материал — сталь.
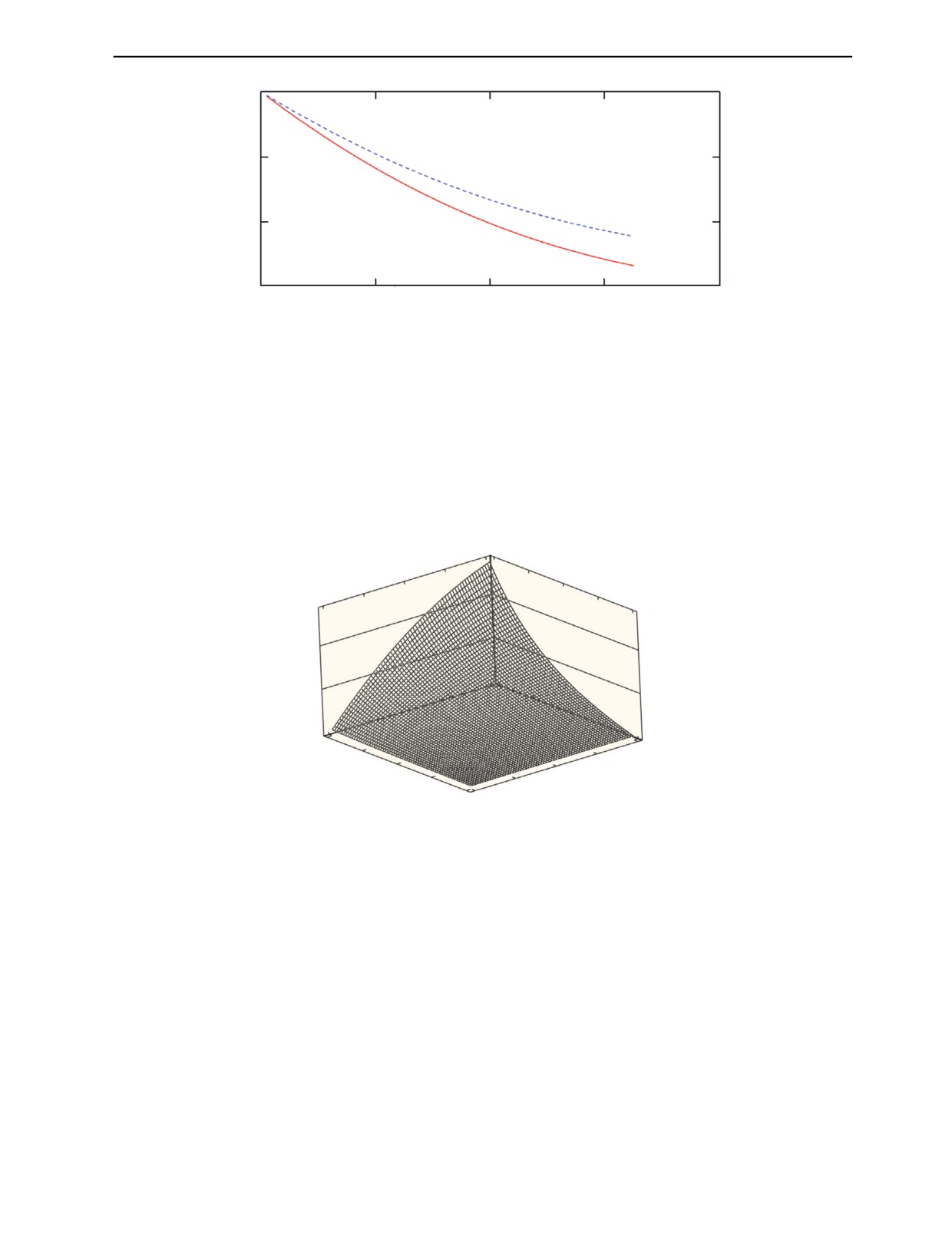
Предварительно для наглядности вычислялись зависимости вещественных и мнимых частей
для актуальных сочетаний значений коэффициента перфорации и параметра шероховатости и дру-
гих параметров модели. На рис. 4, 5 представлены зависимости вещественной и мнимой частей
коэффициента отражения ультразвука от параметра шероховатости при заданных значениях коэф-
фициента перфорации, а рис. 6 — модуля коэффициента отражения при заданной частоте и ради-
усе сферического микроконтакта.
|Rотн|
0,2
0,1
0
0,01
5
0,16
85
0,32
165
0,48
245
ξ Rz, мкм
Рис. 6. Зависимость модуля коэффициента отражения ультразвука |Rотн| от параметра шероховатости и коэффициента
перфорации; частота ультразвука f = 1,25 МГц, a = 0,5 мм, материал — сталь.
На рис. 7, 8 представлены зависимости вещественной и мнимой частей коэффициента прохож-
дения от параметра шероховатости при заданных значениях коэффициента перфорации, а на
рис. 9 — модуля коэффициента прохождения при заданной частоте и радиусе сферического микро-
выступа.
Отметим, что представленные на рис. 6 и 9 значения коэффициентов отражения и прохождения
могут носить приближенный характер, особенно для предельно малых значений коэффициента
перфорации и параметра шероховатости, из-за накапливающейся погрешности вычислений.
Кроме того, указные коэффициенты (18) и (19) и для однородных, и для разнородных сред [31]
являются амплитудными коэффициентами по колебательной скорости (смещению), а для проверки
энергетических соотношений они должны заменяться соответствующими коэффициентами по
энергии [12]. Отметим также, что при стремлении значений контактных жесткостей KGN→∞ и
KGT→∞ указанные выражения переходят в известные формулы для «сварного» контакта [12], для
которых нарушения закона сохранения энергии не отмечается.
Дефектоскопия
№ 4
2023
10
К.Е. Аббакумов, А.В. Вагин, И.Г. Сидоренко
D1
0,98
0,96
0,94
0.92
0
1 · 10-4
2 · 10-4
3 · 10-4
Rz, м
Рис. 7. Зависимости вещественной части коэффициента прохождения ультразвука от параметра шероховатости при
заданных значениях коэффициента перфорации: (--) — ξ = 0,65; (----) — ξ = 0,6; частота ультразвука f = 1, 25 МГц,
a = 0, 5 мм, материал — сталь.
D2
0,2
0,1
0
0
1 · 10-4
2 · 10-4
3 · 10-4
Rz, м
Рис. 8. Зависимость мнимой части коэффициента прохождения ультразвука от параметра шероховатости при заданных
значениях коэффициента перфорации: (--) — ξ = 0,65; (----) — ξ = 0,6; частота ультразвука f = 1,25 МГц, a = 0,5 мм,
материал — сталь.
|Dотн|
0,99
0,98
0,97
0,96
0,01
5
0,16
85
165
0,32
245
0,48
ξ
Rz, мкм
Рис. 9. Зависимость модуля коэффициента прохождения ультразвука |Dотн| от параметра шероховатости и коэффициента
перфорации; частота ультразвука f = 1, 25 МГц, a = 0,5 мм, материал — сталь.
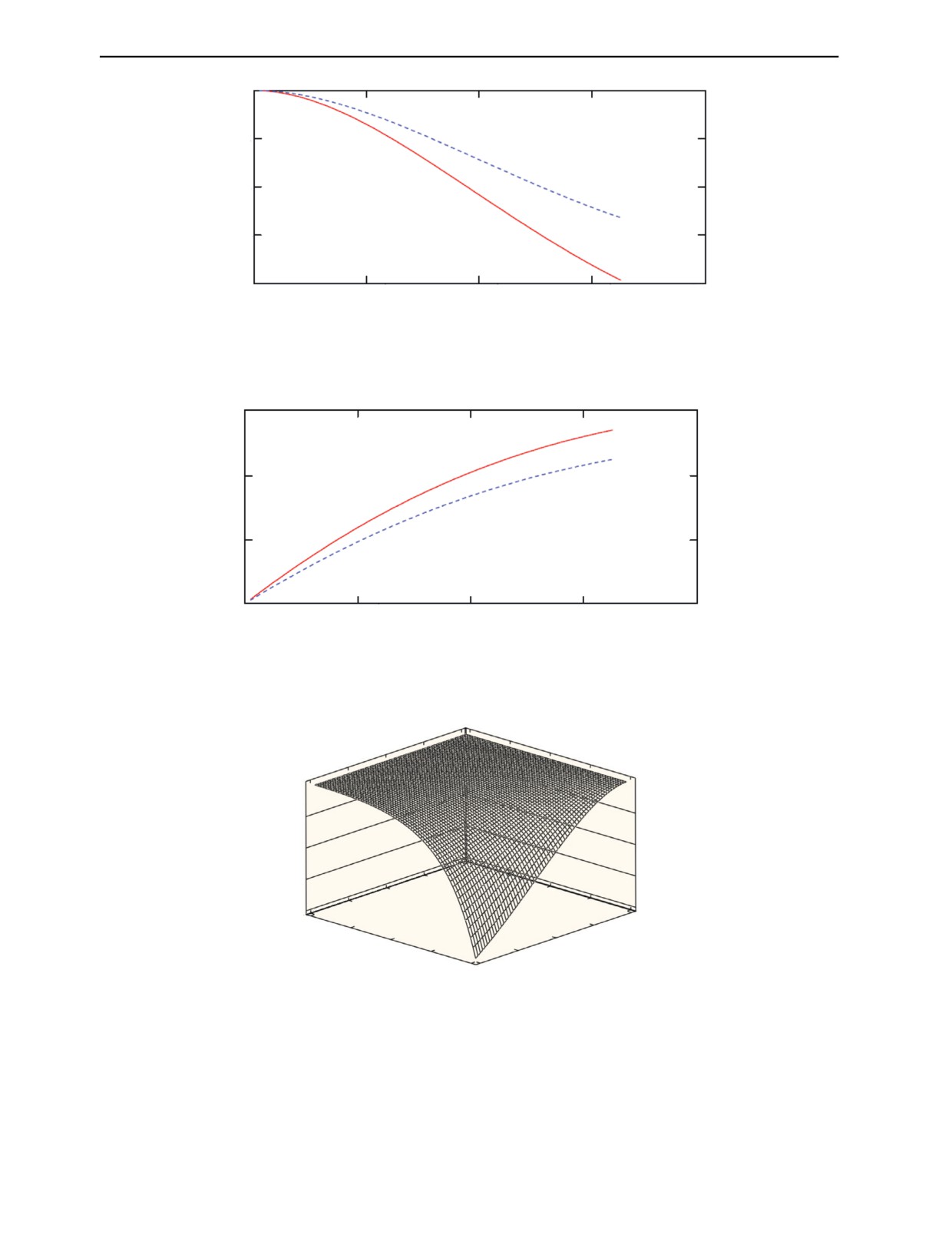
Результаты вычислений значений эффективной скорости продольной волны Cl,эфф представле-
ны на рис. 10.
Как следует из данных графика поверхности на рис. 10, скорость эффективной плоской продоль-
ной волны с ростом концентрации микротрещин и частоты монотонно убывает от максимального
значения, характерного для невозмущенной среды (стали), до существенно меньших значений.
Дефектоскопия
№ 4
2023
Акустические характеристики твердых упругих сред с ориентированной...
11
Cl,эфф, м/с
5500
5000
4500
0,01
5
0,16
85
0,32
165
0,48
245
ξ Rz, мкм
Рис. 10. Зависимость значений эффективной скорости продольной волны Cl,эфф ультразвука от параметра шероховатости
и коэффициента перфорации; частота ультразвука f = 1,25 МГц, a = 0,5 мм, материал — сталь.
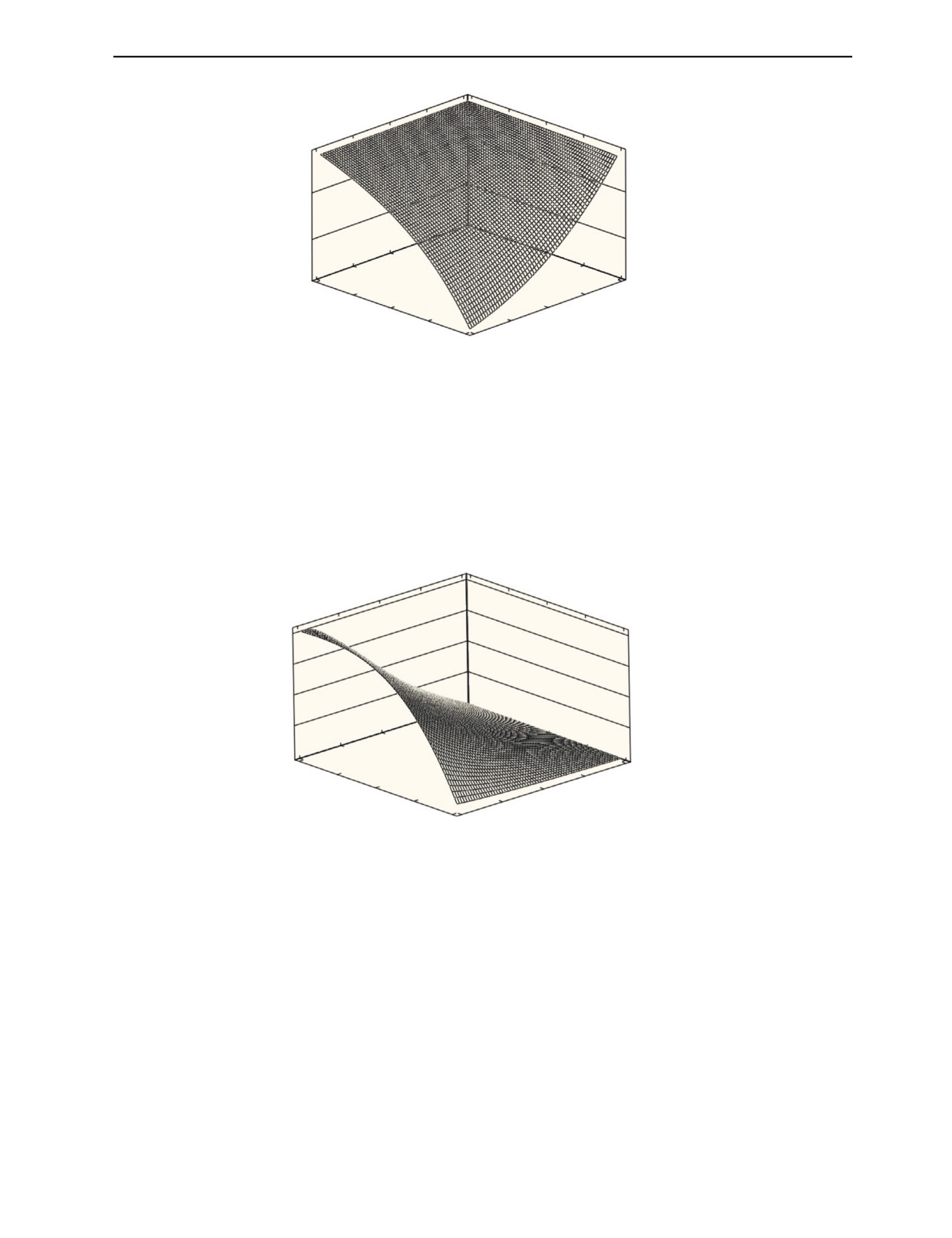
На рис. 11 представлены зависимости коэффициента затухания эффективной плоской продоль-
ной волны от параметров плоскостной протяженной несплошности: коэффициента перфорации ξ
и параметра шероховатости Rz при заданных значениях частоты ультразвука и радиуса микросфер,
моделирующих выступы шероховатостей в стали.
αl,эфф, Нп/м
80
60
40
20
0
0,01
5
0,16
85
0,32
165
0,48
245
ξ Rz, мкм
Рис. 11. Зависимость коэффициента затухания эффективной плоской продольной волны αl,эфф от параметра шероховато-
сти и коэффициента перфорации; частота ультразвука f = 1,25 МГц, a = 0,5 мм, материал — сталь.
Как показал результат анализа графика поверхности на рис. 11, зависимость коэффициента
затухания эффективной продольной волны имеет сходный характер по сравнению с фазовой
скоростью, сопровождается возрастанием с ростом частоты. Видно также, что динамический
диапазон изменения коэффициента затухания в исследованном диапазоне изменения параметра
шероховатости и коэффициента перфорации может составлять примерно 20 и более дБ и увели-
чивается с ростом частоты. Наличие изменений фазовых скоростей и дополнительного затуха-
ния должно учитываться при исследованиях распространения и поверхностных, и близких к ним
типов волн, образующихся в приповерхностных областях в материалах с упорядоченной струк-
турой. Обратим внимание, что в исходной среде (без трещин) малым поглощением из-за влияния
процессов вязкости и теплопроводности пренебрегалось, и для вычислений параметры Ламэ
выбирались как вещественные величины.
Дефектоскопия
№ 4
2023
12
К.Е. Аббакумов, А.В. Вагин, И.Г. Сидоренко
Отметим, что в исследованных случаях при стремлении параметров микротрещин (параме-
тра шероховатости и коэффициента перфорации) к нулю значение фазовой скорости эффектив-
ной продольной волны стремится к значению скорости объемной продольной волны в исходной
изотропной бездефектной среде, а дополнительный коэффициент затухания (рассеяния) — к
нулю.
При изучении распространения поперечных волн в микротрещиноватой среде достаточно в
формулы (18), (19) подставить значения импеданса для поперечных волн, а жесткость KGN заме-
нить на KGT. Если полученные выражения подставить в (12) и (13), то проведенные после этого
вычисления дают сходные результаты с вычислениями для продольных волн, поэтому из объемной
записи не приводятся.
Влияние на свойства материалов, содержащих несплошности, выходящие на поверхность,
можно оценивать с помощью поверхностных волн [27]. При этом значения эффективных скоро-
стей поверхностных волн необходимо оценивать при решении дисперсионных уравнений, содер-
жащих значения эффективных скоростей объемных упругих волн [27].
Одной из последних работ, в которой проведено сравнение теории с экспериментом, являет-
ся [34]. В ней удалось обосновать значения акустических характеристик графитовых включений
в медных сплавах, полученных по технологии двойного вакуумного переплава [34] путем обо-
снования гипотезы о выполнении граничных условий в приближении «линейного скольжения»
на поверхностях графитовой прослойки в меди и возможной структуре графита, близкой по
свойствам к гранулированной (консолидированной) среде [22]. К сожалению, прямые экспери-
менты, связанные с построением натурной модели выполнения условий «линейного скольже-
ния» в настоящее время пока не обеспечивают необходимой стабильности и повторяемости
результатов. Косвенным подтверждением корректности разработанной модели является своди-
мость ее результатов к частным случаям, известным по более ранним работам [9].
ВЫВОДЫ
Предложена модель, учитывающая влияние шероховатости контактирующих поверхностей
микротрещин на параметры информационных сигналов, образуемых при преломлении упругих
волн на множестве ориентированных плоских границ раздела твердых слоев, имитирующих также
отдельные виды объемных несплошностей с ориентированной микротрещиноватостью.
Полученные выражения для дисперсионных уравнений (10)—(13) образуют полные системы
уравнений, необходимых для определения фазовой скорости и коэффициента затухания (рассе-
яния) эффективных плоских продольных волн применительно к неоднородностям с усложнен-
ной структурой, которые могут быть распространены на свойства других объемных и поверх-
ностных волн.
Указанные уравнения и результаты их решений имеют как самостоятельный интерес, так и
обладают потенциальной полезностью прикладного характера при интерпретации результатов
ультразвуковых измерений с применением неучитываемых ранее параметров прилегающих
поверхностей микротрещин для оценки физико-механических характеристик как традиционных,
так и новых материалов, обладающих слоистыми особенностями внутренней структуры.
СПИСОК ЛИТЕРАТУРЫ
1. Ермолов И.Н. Теория и практика ультразвукового контроля. М.: Машиностроение, 1981. 240 с.
с илл.
2. Ермолов И.Н., Алешин Н.П., Потапов А.И. Неразрушающий контроль. В 5 кн. Кн. 2. Акустические
методы контроля: Практ. пособие / Под. ред. В.В. Сухорукова. М.: Высш. шк., 1991. 283 с.
3. Алешин Н.П., Бобров В.Т., Ланге Ю.В., Щербинский В.Г. Ультразвуковой контроль. Учеб. пособие
/ Под общ. ред. В.В. Клюева. М.: Изд. Дом Спектр, 2011. 224 с.
4. Муравьев В.В., Зуев Л.Б., Комаров К.Л. Скорость звука и структура сталей и сплавов. Новосибирск:
Наука, Сибирская издательская фирма РАН, 1996. 184 с.
5. Муравьев В.В., Муравьева О.В., Байтеряков А.В. Структурно-чувствительные акустические пара-
метры конструкционных сталей. Ижевск: Изд-во ИжГТУ имени М.Т. Калашникова, 2022. 152 с.
6. Гегузин Я.Е. Макроскопические дефекты в металлах. М.: Металлургиздат, 1962. С. 252.
7. Атлас дефектов стали / Под ред. М.Л. Бернштейна. М.: Металлургия, 1979. 178 с.
8. Фрактография и атлас фрактограмм. Справочник / Под ред. М.Л. Бернштейна. М.: Металлургия,
1982. 489 с.
9. Бреховских Л.М. Волны в слоистых средах. М.: Изд-во Академии Наук СССР, 1956.
Дефектоскопия
№ 4
2023
Акустические характеристики твердых упругих сред с ориентированной...
13
10. Бриллюэн Л., Пароди М. Распространение волн в периодических структурах. М.: Изд-во иностр.
лит-ры, 1959. 447 с.
11. Кунин И.А. Теория упругих сред с микроструктурой. Нелокальная теория упругости. М.: Изд-во
Наука, 1975. 416 с.
12. Лепендин Л.Ф. Акустика / Учеб. пособие для втузов. М.: Высшая школа, 1978.
13. Вавакин А.С., Салганик Р.Л. Эффективные упругие характеристики тел с изолированными тре-
щинами, полостями и жесткими неоднородностями // Механика твердого тела. 1978. № 2. С. 95—107.
14. Петрашень Г.И. Распространение волн в анизотропных упругих средах. Л.: Наука, 1980. 280 с.
15. Гузь А.Н. Упругие волны в телах с начальными напряжениями. Киев: Наукова думка, 1986. 536 с.
16. Jose M. Carcione anisotropic Q and velocity dispersion of finely layered media // Geophysical
Prospecting. 1992. V. 40. P. 761—783.
17. Luk’yashko O.A., Saraikin V.A. Transient one-dimensional wave processes in a layered medium //
Journal of Mining Science. 2007. V. 43. P. 145—158.
18. Brun M., Guenneau S., Movchan A.B., Bigoni D. Dynamics of structural interfaces: Filtering and
focussing effects for elastic waves // J. Mech. Physics Solids. 2010. V. 58. P. 1212—1224.
19. Panasyuk O.N. Propagation of Quasishear Waves in Prestressed Materials with Unbonded Layers //
Int. Appl. Mech. 2011. V. 47. P. 276—282.
20. Ямщиков В.С., Бауков Ю.И. Геоакустика. Раздел: Упругие волны в неоднородном массиве.
Изд-во МГИ, 1973. С. 256.
21. Горбацевич Ф.Ф. Отражение и преломление упругих волн на границе раздела сред. Апатиты:
Кольский филиал РАН. 1985.
22. Аббакумов К.Е., Цаплев В.М. Волновые задачи акустических методов неразрушающего
контроля. СПб.: Изд-во СПбГЭТУ “ЛЭТИ”, 2015. 336 с.
23. Алешин Н.П., Мурашов В.В., Щипаков Н.А., Краснов И.С., Ложкова Д.С. Экспериментальное
исследование возможностей и особенностей ультразвукового контроля деталей, изготовленных по
аддитивным технологиям // Дефектоскопия. 2016. № 12. С. 17—24.
24. Потапов А.И., Махов В.Е. Физические основы контроля упругих характеристик анизотропных
композиционных материалов ультразвуковым методом // Дефектоскопия. 2017. № 11. С. 33—49.
25. Панасюк О.Н. Анализ влияния граничных условий на распространение волн в слоистых компо-
зитных материалах // Прикладная механика. 2014. № 4. С. 52—58.
26. Ультразвук. Маленькая энциклопедия / Глав. Ред. И.П. Голямина. М.: Советская энциклопедия,
1979.
27. Викторов И. А. Звуковые поверхностные волны в твердых телах. М.: Наука, 1981. 287 с.
28. Хлыбов А.А. Исследование влияния микронеоднородности среды на распространение поверх-
ностных волн // Дефектоскопия. 2018. № 6. С. 3—10.
29. Reusseau M. Floquet wave properties in a periodically lagered medium // J. Acoust. Soc. Amer. 1989.
V. 86. No. 6. P. 2369—2378.
30. Achenbach J., Kitachara M. Reflection and transmission of an obliquely incident wave by an array of
spherical cavities // J. Acoust. Soc. Amer. 1986. V. 80. No. 4. P. 1209—1214.
31. Аббакумов К.Е. Рассеяние плоских упругих волн на микрошероховатой границе раздела твер-
дых сред // Дефектоскопия. 2017. № 7. C. 3—13.
32. Abbakumov K.E., Vagin A.V. Dispersion Equation for Longitudinal Waves in a Layered Medium with
Inhomogeneous Boundary Conditions in Different Propagation Directions // Russian Journal of Nondestructive
Testing. 2020. V. 56. No. 1. P. 20—27.
33. Справочник по триботехнике. В 3 т. Т.1. Теоретические основы / Под общей ред. М. Хебды. М.:
Машиностроение, 1989. С. 56—58.
34. Аббакумов К.Е., Вагин А.В., Сидоренко И.Г. Акустические характеристики графитовых включе-
ний в листах из медного сплава, полученного по технологии двойного вакуумного переплава / Сб.
статей 8-й Международной научно-технической конференции «Современные методы и приборы кон-
троля качества и диагностики состояиия объектов». С. 11—16. Могилев, 29—30 сентября 2022 г.
Изд-во Белорус. Рос. ун-та, 2022. 306 с.
Дефектоскопия
№ 4
2023