Радиационные методы

УДК 620.179.15

ИТЕРАЦИОННАЯ РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЙ АЛЮМИНИЕВОГО

ЛИТЬЯ С УЧЕТОМ АПРИОРНОЙ ИНФОРМАЦИИ

¹ГНУ «Институт прикладной физики НАН Беларуси»,

Республика Беларусь 220072 Минск, ул. Академическая, 16

²Белорусский национальный технический университет, Республика Беларусь 220013 Минск,

пр-т Независимости, 65

³ГНУ «Физико-Технический Институт НАН Беларуси»,

Республика Беларусь 220141 Минск, ул. Купревича, 10

E-mail: ^*zolotarev@iaph.bas-net.by; ^**vjgi994@gmail.com; ^***bilenko@phti.by

Поступила в редакцию 15.02.2023; после доработки 10.03.2023

Принята к публикации 10.03.2023

Задача малоракурсной рентгеновской томографии является типичным представителем класса некорректно постав-

ленных задач. Практическое решение этой задачи позволит расширить область применения метода рентгеновской томо-

графии. Задача малоракурсной рентгеновской томографии часто является задачей с дефицитом исходных данных и

может быть решена только с привлечением априорной информации. Для введения в численный алгоритм необходимой

дополнительной информации наиболее пригодными являются методы итерационной реконструкции томографических

изображений. Один из подходов для введения такого рода информации изложен в данной статье.

Ключевые слова: итерационные методы, реконструкция изображений, априорная информация, томография, недо-

статок входных данных.

DOI: 10.31857/S0130308223040048, EDN: YNVEJC

ВВЕДЕНИЕ

В настоящее время среди методов неразрушающего контроля особое место занимает метод

рентгеновской томографии. Преимущество этого метода заключается в том, что его информатив-

ность о каждом элементарном объеме исследуемого объекта во много раз выше, чем в других

известных методах. Высокая эффективность метода рентгеновской томографии впервые была

продемонстрирована на примерах его использования в медицине и биологии. Создание первых

рентгеновских компьютерных томографов и их применение в медицине было отмечено

Нобелевской премией за 1979 г. Современное изложение принципов томографии можно найти в

монографии [1].

Техническая реализация и область применения метода рентгеновской томографии жестко свя-

заны с математическим аппаратом, который используется для реконструкции пространственного

распределения коэффициента линейного ослабления рентгеновского излучения по рентгеновским

проекциям, и возможностями вычислительной техники. В основу первых рентгеновских томогра-

фов было положено предложенное еще в 1917 г. двухмерное обратное преобразование Радона [2],

который показал, что распределение коэффициента линейного ослабления μ(x, y) в бесконечно

тонком слое объекта однозначно определяется множеством всех линейных интегралов:

∞

2π

∂

µ(x,

lim

p xcosθ+

ysin

θ+ θ

dθdq,

(1)

∫

2π

ε→0

q ∂l

где p(l, θ) — интеграл функции μ(x, y) вдоль линии, которая удалена на расстояние l от начала

координат, а ее перпендикуляр составляет угол θ с осью x; ε — бесконечно малая величина, стре-

мящаяся к 0.

Основанный на преобразовании (1) принцип современной компьютерной томографии заклю-

чается в следующем. Исследуемый объект облучают во множестве ракурсов, регистрируют резуль-

таты измерений характеристик излучения, прошедшего через тонкий слой объекта, преобразуют

эти результаты в числовые коды, вводят в ЭВМ, с помощью которой посредством численного

обратного преобразования Радона находят пространственное распределение коэффициента линей-

ного ослабления, которое затем визуализируют с помощью соответствующих устройств (см. рабо-

ту [3], стр. 12). При этом, с одной стороны, применение обратного преобразования Радона наибо-

Итерационная реконструкция изображений алюминиевого литья...

лее эффективно при использовании узко коллимированных источников излучения (в этом случае

мал нелинейный вклад рассеянных фотонов) и электронных детекторов излучения (из-за большо-

го объема измеряемых данных), с другой стороны, оно требует строго заданную схему просмотра

объекта, требующую для удовлетворительной аппроксимации функции p(l, θ) значительное число

ракурсов (как правило, несколько сотен) при перемещении системы детектор-источник относи-

тельно объекта на угол 180 или 360°.

Дальнейшее совершенствование рентгеновских томографов было достигнуто за счет разра-

ботки и использования математического аппарата трехмерных обобщений преобразования

Радона [4, 5]. Это позволило использовать конический источник излучения и двухмерный

матричный детектор, что существенно увеличило скорость сбора информации для трехмерной

реконструкции. Но практическое применение нашли томографы, которые используют некоторые

приближенные трехмерные преобразования. Основные принципы, изложенные в данной работе,

применены были также в публикациях [9—12].

1. ИТЕРАЦИОННЫЕ АЛГЕБРАИЧЕСКИЕ МЕТОДЫ РЕКОНСТРУКЦИИ ИЗОБРАЖЕНИЙ

ОБЪЕКТОВ

Предельно малый объем проекционных данных, характерный для промышленных малоракурс-

ных систем томографии, заставляет разрабатывать такие алгоритмы реконструкции, которые

позволяют использовать дополнительную априорную информацию о восстанавливаемом объекте

и являются легко адаптируемыми для различных нетрадиционных схем сканирования. Выбор кон-

кретного алгоритма реконструкции определяется, прежде всего, особенностями системы томогра-

фии, точнее, особенностями регистрируемых в системе проекционных данных.

Возможны такие ситуации, когда из-за особенностей системы регистрации либо число проек-

ций очень малое, либо они известны не полностью, либо получены в ограниченном диапазоне

углов. Задачи восстановления при таком задании проекционных данных становятся сильно некор-

ректными и для них нарушаются теоремы единственности и устойчивости. Поэтому прямое при-

менение аналитических алгоритмов для их решения не дает приемлемых результатов и приходит-

ся разрабатывать другие, более подходящие алгоритмы. В этих случаях наиболее предпочтитель-

ными оказываются методы разложения в конечные ряды ортогональных функций.

Восстановление изображений по их проекциям при помощи методов разложения в конечные

ряды принципиально отличается от методов интегральных преобразований. Дело в том, что в

методах интегральных преобразований используются операторы, действующие на множестве

функций, которые заданы на всем континууме вещественных чисел. И лишь для реализации реше-

ния на компьютерах и рабочих станциях непрерывные операторы заменяются на дискретные опе-

раторы, которые действуют на функциях, заданных на конечных множествах, но это выполняется

в самом конце процедуры выполнения алгоритма восстановления.

Методы разложения в конечные ряды предполагают дискретизацию изображения до начала

алгоритма восстановления, что сводит основную задачу восстановления к решению систем линей-

ных (или нелинейных) алгебраических уравнений, т.е. к задачам вычислительной линейной алге-

бры. Известно, что систему линейных алгебраических уравнений (СЛАУ) можно решать с помо-

щью как прямых, так и итерационных методов. Итерационные методы применяются главным

образом для задач очень большой размерности, которыми, как правило, являются задачи компью-

терной томографии.

Для применения алгоритмов разложения в конечные ряды к решению задач реконструктив-

ной вычислительной томографии первоначально необходимо построить полную дискретную

модель задачи восстановления. Для этого выберем систему базисных функций b_j(x), j = 1, 2, ..., J

 функции f по отношению к этой системе:

и рассмотрим дискретизированную форму f

 x)

×b

(x),

(2)

∑

где f_j = const. Пусть R_i, i = 1, 2, ..., I — множество линейных непрерывных функционалов, каждый

из которых ставит в соответствие функции f(х) вещественное число R_if, которое обозначим р_i.

Тогда, применяя операторы R_i к равенству (2), учитывая их непрерывность и линейность и обо-

значив

Дефектоскопия

№ 4

2023

C.А. Золотарев, А.Т. Таруат, Э.Г. Биленко

a_ij = R_i b_j(x),

(3)

получаем искомую СЛАУ

Af = p,

(4)

где А = (a_ij) — проекционная матрица; f = (f₁, f₂, …, f_J) — вектор изображения; р = (p₁, ..., p_I) —

вектор проекций. Таким образом, решение основной задачи восстановления изображения по

заданному набору проекций р_i сводится к решению СЛАУ вида (4), при этом вектор р заведомо

задан с некоторой погрешностью.

Существует несколько различных источников зашумления вектора р: 1) вместо функции f(х)



мы рассматриваем ее приближенное выражение в виде дискретизированной функции

;

2) вектор проекций р получаем на практике из экспериментальных или практических физических

измерений, которые неизбежно зашумлены; 3) при вычислении элементов a_ij матрицы А мы пред-

полагаем идеализацию естественных лучей, как это будет рассмотрено ниже.

Предположим, что функция f(х) задана в пространственной области V. Разобьем область V на

некоторое конечное число подобластей, которые будем называть вокселями. Перенумеруем все

воксели некоторым удобным образом от 1 до J. Будем считать, что восстанавливаемая функция f(х)

принимает постоянное значение f_j внутри j-го вокселя, т.е. функцию f(х) заменяем ее дискретизи-

рованным выражением:

 x)

= f

если (x) ∈ вокселю j - у;

0 в противном случае.

(5)

Пусть

{

(

)}

— система базисных функций, которые задаются следующим образом:

b_j(x) = 1, если (x) ∈ вокселю j - у ;

0 в противном случае.

(6)

Предположим, что в качестве линейных функционалов Rвыбираем прямое преобразование

Радона вдоль набора некоторых прямых L_s:

∫ x)

Тогда

(x)

= ∫b

(x)ds = a

(7)

геометрически представляет собой длину пересечения i-го луча с j-м вокселем. Мы в своей статье

используем именно такую систему базисных функций, другие виды базисных функций не рассма-

триваются в данной работе. Дискретизация является равномерной.

Из вышерассмотренного очевидна гибкость предлагаемого алгебраического подхода к реше-

нию задач восстановления. Во-первых, следует отметить свободу выбора базисных функций, что

связано с выбором сетки разбиения области D (кроме декартовой квадратной сетки можно выби-

рать полярную сетку в двухмерном случае и вообще сетку произвольной геометрической конфи-

гурации).

Кроме того, постановка задачи не зависит от геометрии лучей. Изменяются при этом только

элементы a_ij, которые, как правило, вычисляются заранее. Следует также заметить, что все

вышесказанное можно перенести на трехмерный случай. Таким образом, алгебраический метод

при фиксированном выборе линейных непрерывных операторов R_i и базисных функций b_j сво-

дит задачу восстановления к решению СЛАУ (4), т.е., казалось бы, к стандартной задаче вычис-

лительной линейной алгебры. Однако применительно к проблеме реконструкции изображения

данная задача имеет ряд характерных особенностей: размерность системы чрезвычайно велика:

Дефектоскопия

№ 4

2023

Итерационная реконструкция изображений алюминиевого литья...

как правило, число уравнений и неизвестных порядка 10⁷ — 10¹⁰. При этом отличные от нуля

элементы матрицы А, в основном, не образуют никакой определенной упорядоченной структуры

для того, чтобы можно было применить какой-нибудь из известных методов решения систем

линейных алгебраических уравнений с разреженными матрицами; матрица А является прямоу-

гольной размера т × п, причем т ≠ п, как правило, т < п (здесь т — число уравнений,

a n — число неизвестных). В последнем случае система является недоопределенной; система

уравнений (4) является неустойчивой относительно задания начальных данных, т.е. малым изме-

нениям вектора р = (p₁, ..., p_m) могут отвечать сколь угодно большие изменения вектора неиз-

вестных f = (f₁, f₂, …, f_n). Эти характерные особенности превращают простую, на первый взгляд,

задачу вычислительной линейной алгебры в весьма трудно реализуемую вычислительную про-

цедуру. При этом для каждой конкретной задачи приходится подбирать наиболее оптимальный

алгоритм реконструкции.

2. КЛАССИЧЕСКИЙ АЛГОРИТМ АЛГЕБРАИЧЕСКОЙ РЕКОНСТРУКЦИИ

Здесь мы рассмотрим решение задачи реконструктивной вычислительной томографии с помо-

щью классических итерационных алгебраических методов восстановления, основанных на раз-

ложении в конечные ортогональные ряды [5]. Для случая задания систем базисных функций в виде

формул (6) это приводит к необходимости решения СЛАУ вида:

Ах = р,

(8)

где А = (a_ij) — проекционная матрица; х = (x₁, x₂, ..., x_n) — вектор неизвестных; р = (p₁, ..., p_m) —

вектор проекций. Впервые применение итерационного алгебраического алгоритма для вычисли-

тельной томографии было описано в 1970 г. в работе [8]. В этом алгоритме в качестве начального

приближения вектора изображений выбирается произвольное значение х⁽⁰⁾∈ Rⁿ, если система

является совместной, (k+1)-я итерация получается из k-й итерации некоторым аддитивным спо-

собом. При этом последовательно в порядке перебора рассматривается только один луч, напри-

мер i-й, а изменению подвергаются только те компоненты вектора х(k), которые соответствуют

вокселям, пересекаемым данным лучом. Величина невязки между измеренным значением р_i и

приближенной величиной проекции

⁾,

полученной при подстановке k-й итерации х(k),

∑

перераспределяется между вокселями, расположенными вдоль i-го луча, пропорционально их

весам a_ij в луче. Таким образом, в одном цикле k-й итерации изменяются значения только тех

вокселей, которые находятся вдоль данного i-го луча, а остальные значения функции остаются

без изменения. Этот алгоритм известен в литературе как ART и его можно определить следую-

щим образом:

1) начальное приближение х⁽⁰⁾∈ Rⁿ выбирается произвольно;

2) k +1-я итерация вычисляется по формуле:

х(k+1) = х(k)+ λ(k) ((p_i - (ai , х(k))) / ||aⁱ||²) ai ,

(9)

где

)

j=1

— i-я строка матрицы А, параметры релаксации λ(k) представляют собой после-

довательность вещественных чисел, а i = i_k = k(mod_m) + 1, т.е. лучи перебираются циклически.

Этот алгоритм характеризуется эффективным использованием памяти, поскольку п-мерный

вектор х(k+1) можно запоминать в том же блоке оперативной памяти, что и вектор х(k), необходи-

мость хранения которого отпадает после k-й итерации. Исследователями доказано, что он при-

надлежит к классу итерационных алгоритмов, основанными на методе проектирования на выпу-

клые множества. Однако качество реконструкции алгоритма ART уступает качеству алгоритмов

SIRT, ILST и алгоритму байесовой реконструкции в силу наличия полосовых артефактов.

Поэтому мы предпочтительно используем последние вышеназванные алгоритмы.

3. АЛГОРИТМЫ РЕКОНСТРУКЦИИ ИЗОБРАЖЕНИЙ С ИСПОЛЬЗОВАНИЕМ

АПРИОРНОЙ ИНФОРМАЦИИ

Как отмечалось выше, на практике часто приходится решать так называемые задачи восстанов-

ления с неполным набором данных. Этого набора данных, как правило, недостаточно для решения

задачи восстановления. Однако для многих таких задач, в частности для задач исследования физи-

ческих процессов, бывает, что известна некоторая дополнительная информация об исходном вос-

Дефектоскопия

№ 4

2023

C.А. Золотарев, А.Т. Таруат, Э.Г. Биленко

станавливаемом объекте. Эта различная априорная информация может быть эффективно учтена в

алгебраических итерационных алгоритмах. Использование этой априорной дополнительной

информации часто дает существенное улучшение для скорости сходимости итерационных про-

цессов. В этом подразделе рассматриваются различные комбинации итерационных алгебраиче-

ских реконструктивных алгоритмов, рассмотренных в предыдущих разделах, с использованием

наиболее важной и доступной априорной информации о восстанавливаемом объекте и устанавли-

ваются свойства сходимости таких алгоритмов.

Предположим, что итерационный алгебраический алгоритм для решения СЛАУ (4) задан в

виде следующей рекуррентной формулы:

x(k + 1) = Q x(k),

(10)

где Q : Rⁿ→ Rⁿ — некоторый оператор. Дополнительную информацию об объекте в общем случае

можно также задать с помощью некоторого оператора S : Rⁿ→ Rⁿ в виде:

x(k + 1) = S x(k),

(11)

тогда общий итерационный процесс будет представляться в виде суперпозиции этих двух опера-

торов:

x(k + 1)= S Q x(k).

(12)

Следует при этом заметить, что не всегда из сходимости последовательности (10) к решению

системы (4) следует сходимость последовательности (12) и наоборот. Операторы Q и S должны

удовлетворять определенным свойствам, чтобы гарантировать эту сходимость. Заранее эти свой-

ства неизвестны, поэтому мы практически устанавливаем их на основании численных экспери-

ментов. Предположим, априорно известно, что искомое решение х принадлежит подпростран-

ству L⊂Rⁿ. Тогда в качестве оператора S можно взять оператор ортогонального проектирования

Р = Р_L на подпространство L. Например, если априорно известны границы значений искомого

вектора решений х, т.е. известно, что i-я компонента x_i находится в интервале [α_i, β_i], то в каче-

стве множества L может быть взято прямое произведение этих интервалов:

L = [α₁, β₁] × [α₂, β₂]× ... × [α_n, β_n].

В этом случае оператор ортогонального проецирования Р_L задается в виде:

α

если

<α





)

если

≤

≤β

(13)

L i







если

>β





несмотря на кажущуюся тривиальность этих ограничений, они являются весьма полезными при

итерационной реконструкции искомого изображения.

В качестве априорного знания об объекте могут быть заранее известны также границы его про-

тяженности, т.е. известно множество S⊂Rⁿ, вне которого восстанавливаемая функция равна 0. В

этом случае оператор проектирования на подмножество S определяется как



если

x∈S







(14)



в противномслучае

Мы применим описанный выше принцип (14) введения априорной информации в итерацион-

ный процесс для реконструкции изображений алюминиевых корпусов.

Первый набор 32 рентгеновских проекций был предоставлен господином Dr. Martin Simon,

сотрудником германской фирмы Зауэрвайн (Sauerwein). Все эти проекции были получены в

Дефектоскопия

№ 4

2023

Итерационная реконструкция изображений алюминиевого литья...

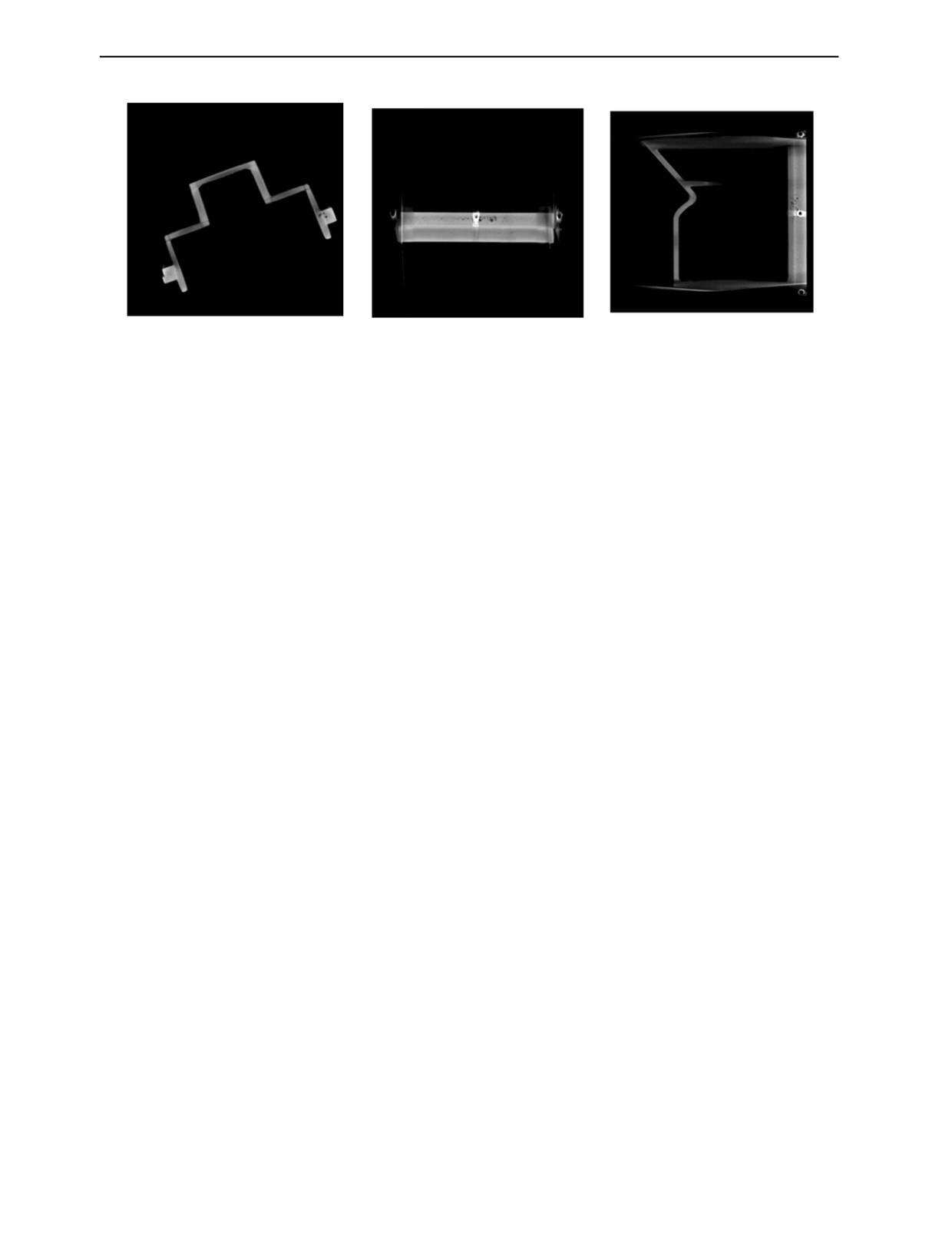
Рис. 1. Проекции алюминиевого корпуса для углов 0, 45 и 90 град.

угловом диапазоне 180 град, т.е. при одностороннем доступе к объекту реконструкции. Мы

имеем характерную задачу именно для малоракурсной томографии. Число проекционных видов

несколько десятков, причем все они расположены в неполном угловом диапазоне, который мень-

ше 360 град. На рис. 1 показаны три проекции алюминиевого корпуса для углов 0, 45

и 90 град.

4. ПОСТРОЕНИЕ НАЧАЛЬНОГО ПРИБЛИЖЕНИЯ ДЛЯ РАСЧЕТА ИЗОБРАЖЕНИЯ

АЛЮМИНИЕВОГО КОРПУСА

Для уменьшения числа вокселей, для которых необходимо оценить приближенное значение

коэффициента линейного ослабления, целесообразно уменьшить их количество, исходя из прин-

ципа наблюдаемости реконструируемого объекта на всех проекциях.

Определим трехмерную область предполагаемого положения объекта:



Pixel





Volume=j:

η



(15)

∑















где η(x) — пороговая функция:

1,x

η(x)

=

0,x

≤

Это означает, что воксель j принадлежит Volume, если значения соответствующих ему пик-

селей Pixel_jn, в которые он проецируется, больше некоторого минимального значения на всех

проекциях. В соответствии с (15) воксель j принадлежит Volume, если значения соответствую-

щих ему пикселей превышают погрешность измерения ε_jn на всех N-проекциях.

Все воксели пронумерованы последовательно. Это всегда используется при пребразовании

трехмерного массива в одномерный с целью упрощения программного кода. Заметим, что по

индексам конкретного вокселя (i, j, k) этот одномерный индекс вычисляется однозначно:

position=dims[0]*(dims[1]*k + j) + i, где dims[0] и dims[1] — размерности зоны реконструкции

по осям абсцисс и ординат. Верно и обратное утверждение: по индексу position можно однознач-

но восстановить индексы конкретного вокселя (i, j, k).

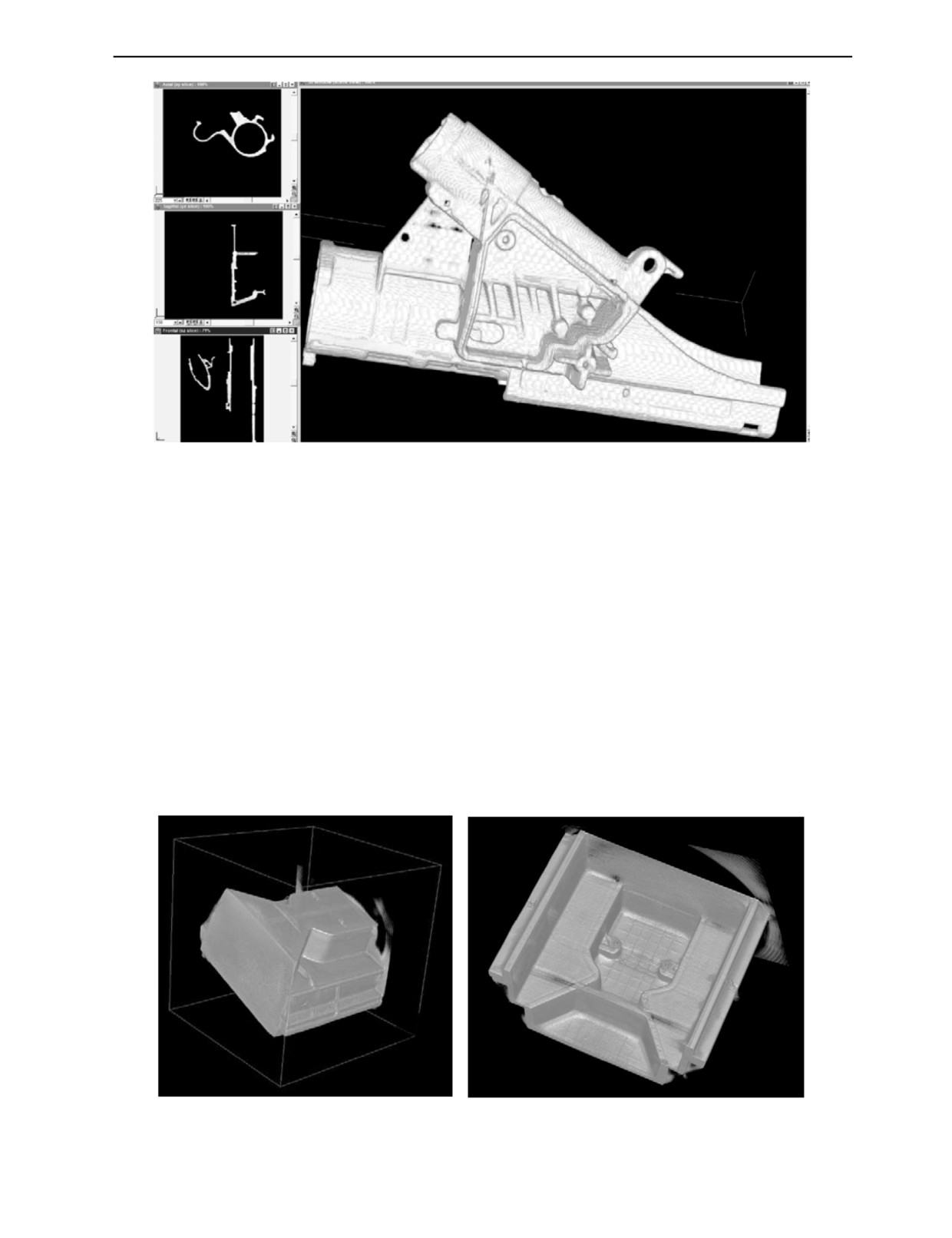
Сначала на рис. 2 покажем перспективные изображения реконструируемого объекта для разно-

го числа итераций, когда в качестве начального приближения взята вся область реконструкции.

Далее на рис. 3 покажем перспективные изображения реконструируемого объекта для разно-

го числа итераций, когда в качестве начального приближения взята область Volume. Понятно, что

при этом мы учитываем априорную информацию о пространственном положении объекта рекон-

струкции. Роль подмножества S в соотношениях (14) играет подмножество зоны реконструкции

Volume.

Видно, что при использовании второго способа выбора начального приближения мы более

точно и качественно восстанавливаем форму и внутреннюю структуру объекта.

Дефектоскопия

№ 4

2023

C.А. Золотарев, А.Т. Таруат, Э.Г. Биленко

Рис. 2. Перспективные изображения алюминиевого корпуса для 1, 5 и 10 итераций. Начальное приближение: вся зона

реконструкции.

Рис. 3. Перспективные изображения алюминиевого корпуса для 5, 10 и 30 итераций. Начальное приближение: область

Volume.

5. РЕКОНСТРУКЦИЯ ИЗОБРАЖЕНИЯ С ИСПОЛЬЗОВАНИЕМ АПРИОРНОЙ

ИНФОРМАЦИИ О ГРАНИЦАХ ЗНАЧЕНИЙ РЕШЕНИЯ

Поскольку коэффициент ослабления алюминиевого корпуса является однородным, мы можем

использовать условие (13) для улучшения качества реконструкции изображения. Путем умноже-

ния всех проекций на некоторый постоянный коэффициент можно так откалибровать их, что плот-

ность реконструируемого объекта станет равной единице. Денкевич Ю.Б. в кандидатской диссер-

тации [6] для улучшения выполнения условий (13) для вокселей, границы значений которых при-

надлежат отрезку 0 = < x_j< = 1, j = 1 ... N, предложил одновременно минимизировать функционал

B(x) = (4,0 × x × x] - 6,0 × x + 2,0)). Численный алгоритм решения нашей задачи можно построить

с помощью вариационной задачи минимизации функционала:



arg min {||

Ax- p

+αB(x)},

(16)

x∈Volume

где

 — приближенное решение уравнения

x= p;

||Ах - р||² — невязка; B(x) — стабилизирую-

щий функционал; α — параметр регуляризации.

Дефектоскопия

№ 4

2023

Итерационная реконструкция изображений алюминиевого литья...

Рис. 4. Изображение алюминиевого блока, которое получается при учете априорной информации с помощью решения

вариационной задачи (16). Слева показаны центральные ортогональные сечения объекта.

На рис. 4 показано изображение алюминиевого блока, которое получается при решении вари-

ационной задачи (16).

Второй набор из 2300 рентгеновских проекций был предоставлен Иваном Георгиевым, науч-

ным сотрудником Института информационных и коммуникационных технологий (ИИКТ)

Болгарской академии наук. Они были получены на промышленном томографе XT H 225 фирмы

Nikon Metrology. Проекции имели размерности 1840×1446 пикселей. Размер пикселя был равен

0,127 × 0,127 мм. Расстояние от рентгеновского источника до матрицы детекторов было равно

1009 мм, а расстояние от источника до объекта — 775 мм. Угловой шаг был равен 0,156°. Была

произведена реконструкция алюминиевого бокса итерационным методом SART по 575 проекциям,

снятым через угловой интервал 0,626°. На рис. 5 показаны различные перспективные виды рекон-

струированного изображения алюминиевого бокса.

Рис. 5. Два различных перспективных вида алюминиевого бокса.

Дефектоскопия

№ 4

2023

C.А. Золотарев, А.Т. Таруат, Э.Г. Биленко

Рис. 6. Сечения изображения алюминиевого бокса плоскостями XOZ, YOZ и XOY:

a — слой XOZ 360 вдоль оси ОY; б — слой YOZ 646 вдоль оси ОХ; в — слой XOY 328 вдоль оси ОZ.

На рис. 6 показаны сечения трехмерного реконструированного изображения алюминиевого

бокса плоскостями XOZ, YOZ и XOY в месте расположения поры максимального размера, обнару-

женной в слое XOZ № 360 при анализе изображения объекта вдоль оси ОY. ПО VGStudioMAX

позволяет одновременно выводить сразу все три этих изображения на дисплей и проводить вирту-

альные измерения размеров поры на каждом из этих изображений. Оцененный размер этой поры

равен 1,5 мм.

РЕЗУЛЬТАТЫ И ВЫВОДЫ

Результатом проведенных экспериментальных исследований является подтверждение воз-

можности решения задачи малоракурсной рентгеновской томографии для конкретного класса

объектов алюминиевого литья. Разработка прикладных численных алгоритмов решения дан-

ной задачи для этого класса объектов позволит расширить область применения метода рентге-

новской томографии для неразрушающего контроля изделий, содержащих такие распростра-

ненные дефекты, как поры, включения, расслоения, трещины, раковины и т.п.

Вклад авторов является одинаковым по 33 %.

СПИСОК ЛИТЕРАТУРЫ

1. Herman Gabor T. Fundamentals of Computerized Tomography. Image Reconstruction from Projections.

Second Edition. Springer-Verlag London Limited. 2009. 297 p.

2. Radon J. Über die Bestimmung von Funktionen durch ihre Integralwerte langs gewisser

Mannigfaltigkeiten. Ber. Verb. Saechs. Akad. Wiss., Leipzig, Math. Phys. Kl. 1917. № 69. P. 262—277.

3. Тихонов А.Н., Арсенин В.Я., Тимонов А.А. Математические задачи компьютерной томографии. М.:

Наука. Гл. ред. физ-мат. лит., 1987. 160 с.

4. Smith Bruce D. Cone-beam tomography: recent advances and a tutorial review // Optical Engineering.

1990. V. 29. No. 5. P. 524—534.

5. Reimers P., Goebbels J. History of computerized tomography at BAM / Int. Simp. on Computerized

Tomography for Industrial Applications. Berlin. Juni 1994. P. 13—22.

6. Венгринович В.Л., Золотарев С.А. Итерационные методы томографии. Минск: Белорусская

наука, 2009. 227 с.

7. Денкевич Ю.Б. Восстановление изображений и свойств объектов путем решения обратных задач

малоракурсной рентгеновской томографии и магнитошумовой структуроскопии / Дисс. Минск: ИПФ

НАН Беларуси, 2000. 138 с.

8. Gordon R., Bender R., Herman G.T. Algebraic reconstruction techniques (ART) for three-dimensional

electron microscopy and X-ray photography // J. Theor. Biol. 1970. No. 29. P. 471—481.

9. Krammer J., Zolotarev S.A., Hillman I. Evaluation of a new image reconstruction method for digital

breast tomosynthesis: Effects on the visibility of breast lesions and breast density // The British journal of

radiology. 2019. V. 92. No. 1103. DOI: 10.1259/bjr.20190345

10. Zolotarev S.A., Vengrinovich V.L., Smagin S.I. Iterative tomography of pipes during operation //

Proceedings of the National Academy of Sciences of Belarus Physical. Technical Series. 2021. V. 66. No.4.

P. 505—512.

Дефектоскопия

№ 4

2023