УДК 620.179.14
РАСЧЕТ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ОТ ПОЛУБЕСКОНЕЧНОГО
ЦИЛИНДРА, ПОМЕЩЕННОГО В ПРОИЗВОЛЬНОЕ ВНЕШНЕЕ ПОЛЕ
© 2023 г. В.В. Дякин1, О.В. Кудряшова1,*, В.Я. Раевский1,**
1Институт физики металлов имени М.Н. Михеева УрО РАН,
Россия 620108 Екатеринбург, ул. С. Ковалевской, 18
E-mail: *kudryashova_ov@imp.uran.ru; **ravskii@mail.ru
Поступила в редакцию 06.03.2023; после доработки 07.04.2023
Принята к публикации 07.04.2023
В модели полубесконечного цилиндра выведены формулы и представлен соответствующий алгоритм нахождения
напряженности магнитного поля внутри и вне однородного цилиндра, помещенного во внешнее магнитное поле произ-
вольной конфигурации. Проведено тестирование результатов расчетов по этим формулам на их соответствие известным
физическим законам, а также на их совпадение с известными аналитическими ответами в предельных частных случаях
формы магнетика.
Ключевые слова: интегро-дифференциальное уравнение магнитостатики, цилиндрический магнетик, расчет магни-
тостатических полей.
DOI: 10.31857/S0130308223050044, EDN: ZDVVPM
1. ВВЕДЕНИЕ
Для решения многих практических задач из области магнетизма, например, задач неразруша-
ющего магнитного контроля, актуальной является проблема создания обоснованных алгоритмов
аналитического или численно-аналитического решения задач магнитостатики по вычислению на-
пряженности результирующего поля применительно к магнитным телам различной формы, поме-
щенным во внешнее магнитное поле. Такие алгоритмы, позволяющие вычислять напряженность
поля внутри и вне магнитного тела с гарантированной и контролируемой точностью, представляют
собой как реальный практический интерес, так и пополняют базу алгоритмов точно решаемых за-
дач (в указанном выше смысле), которая необходима для тестирования известных пакетов универ-
сальных программ (типа ELCUT, ANSYS, ELMER), формальное использование которых приводит
ко многим проблемам. Подробному описанию недостатков этих программ и подводных камней при
их использовании посвящена работа [1].
В статье авторов [2] предложен и обоснован подход, сводящий вычисление напряженности маг-
нитного поля от однородного цилиндра конечных размеров, помещенного в произвольное внешнее
поле, к решению некоторого количества систем трех одномерных линейных интегральных урав-
нений. В следующей работе [3] предложен численный алгоритм, основанный на дискретизации
указанных интегральных уравнений методом квадратур [4, с. 157], а в качестве квадратурной фор-
мулы, приближенно заменяющей интегралы, выбрана формула средних прямоугольников, которая
при разбиении используемого в интегральных уравнениях отрезка интегрирования [0, 1] на m рав-
ных частей имеет вид:
1
m
1
f x)dx
≈
f
(x
),
(1)
∫
∑
i
m
i=1
0
где узлы квадратурной формулы выбираются в середине отрезков разбиения:
2i
−
x
=
1,
i = 1, …, m .
(2)
i
2
m
Указанный алгоритм успешно прошел различные тестовые проверки, описанные в [3], од-
нако обнаружил и ряд недостатков, проявляющихся при расчетах в случае достаточно длинных
цилиндров. Для дискретизации интегральных уравнений оказалось неудачным применение ква-
дратурной формулы (1) с равномерным распределением узлов интегрирования (2) при больших
значениях длины l цилиндра из-за «нетривиального» поведения в этом случае соответствующих
подынтегральных функций (ниже об этом подробнее). В связи с этим для поддержания достаточ-
ной точности расчетов при использовании этой формулы с ростом длины цилиндра приходилось
значительно увеличивать число разбиений m (до нескольких тысяч) в (1). Это приводило к резкому
Расчет напряженности магнитного поля от полубесконечного цилиндра, помещенного...
33
увеличению порядка (равному 3m) систем линейных уравнений, получаемых при дискретизации
интегральных уравнений, что, в свою очередь, влекло ужесточение требований к объему памяти
используемого компьютера и, что наиболее важно, к увеличению числа обусловленности этих си-
стем и, тем самым, неконтролируемо увеличивало ошибки в их решениях.
Для преодоления этих недостатков при необходимости расчета напряженности результирую-
щего поля внутри и вне достаточно длинного цилиндра предлагается не использовать описанный в
[3] общий алгоритм, а использовать значительно более простые и более точные (в этой ситуации)
формулы, полученные в модели бесконечного или полубесконечного цилиндра. Выводу таких фор-
мул и проверке их адекватности и посвящена настоящая работа. Формулы для полубесконечного
цилиндра предполагается использовать в том случае, когда требуется вычисление напряженности
поля в точке, достаточно близкой к плоскости одного из торцов длинного цилиндра. А форму-
лы для бесконечного цилиндра — в случае, когда такая точка удалена от обеих торцевых плоско-
стей длинного цилиндра. Существующие ограничения на объем материала статьи не позволяют
в рамках одной работы рассмотреть случаи полубесконечного и бесконечного цилиндра. Поэтому
в настоящей работе будет рассмотрен случай только полубесконечного цилиндра. Выводу формул
для бесконечного цилиндра в дальнейшем тоже будет посвящена отдельная работа. Но даже такое
сокращение материала не позволяет сколько-нибудь подробно изложить достаточно объемные вы-
кладки, приводящие к расчетным формулам. Поэтому при их выводе будет, в основном, даваться
направление выкладок и указываться способы преодоления возникающих на этом пути подводных
камней.
2. СХЕМА РАСЧЕТА НАПРЯЖЕННОСТИ ПОЛЯ РЕАКЦИИ КОНЕЧНОГО ЦИЛИНДРА
Для решения задач магнитостатики мы исходим из так называемого основного уравнения маг-
нитостатики, которое в случае однородного магнетика с постоянной магнитной проницаемостью
μ имеет вид:
µ-1
H(r′)
0
3
H r)−
∇div
dr′
=
H r),
r∈R
\
S
(3)
∫
4π
| r
−r′|
Ω
Это трехмерное интегро-дифференциальное уравнение эквивалентно системе уравнений Мак-
свелла для случая магнитостатики (см. [5, с. 17; 6, с. 149; 7—9]) и связывает искомую напряженность
результирующего магнитного поля H(r) = {Hx(r), Hy(r), Hz(r)} в произвольной точке пространства
0
0
0
0
r = (x, y, z) (не лежащей на границе магнетика) с напряженностью
H r)
=
x
{H r),
y
H r),H
z
(r)}
заданного поля внешнего источника. В уравнении (3) Ω есть область в пространстве R3, огра-
ниченная поверхностью S и занятая исследуемым магнетиком с заданной постоянной магнитной
проницаемостью μ.
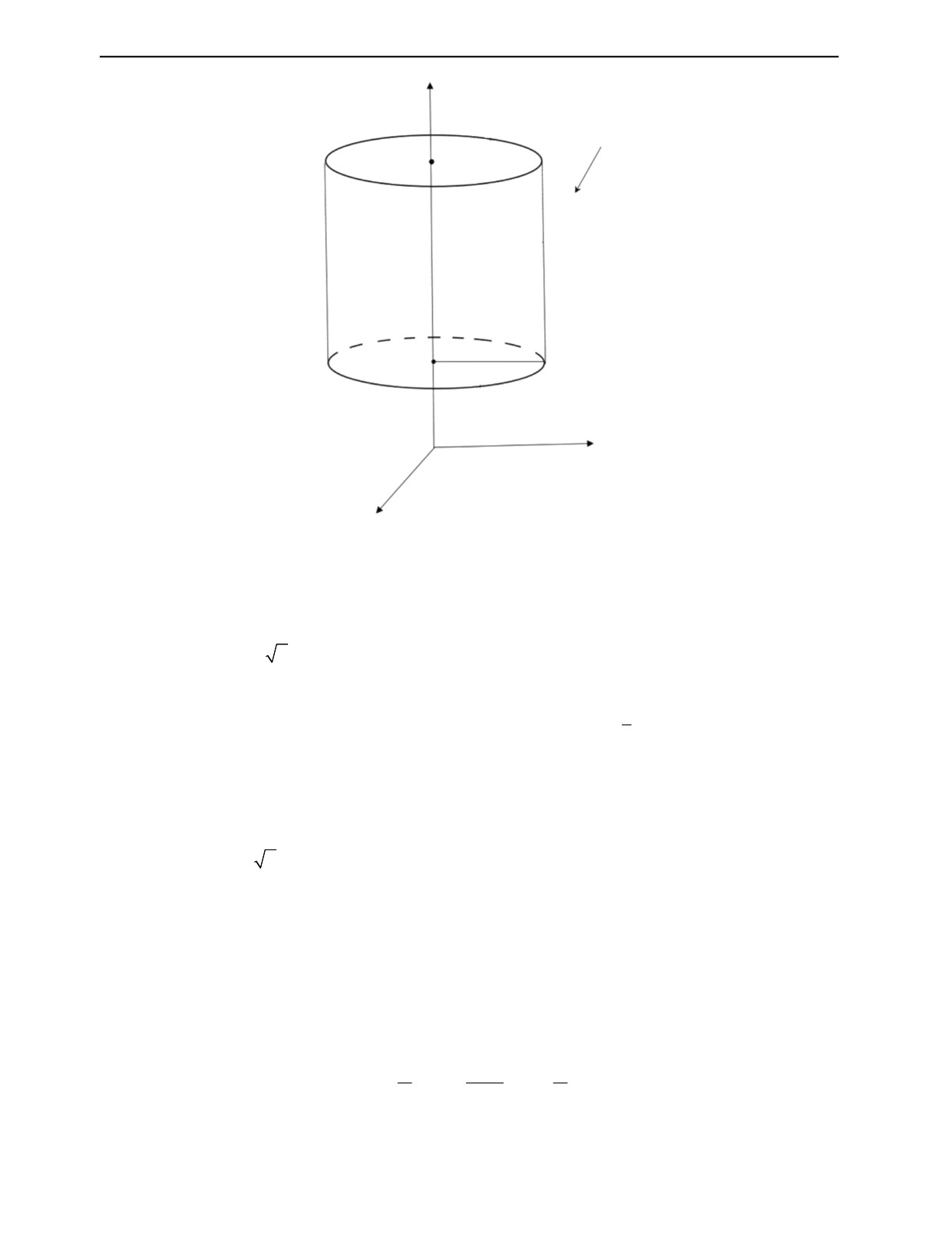
Рассмотрим магнетик в форме прямого кругового цилиндра (см. рис. 1). Область Ω, занятая
магнетиком, представляет собой прямой круговой цилиндр длины l с боковой поверхностью S1, ось
которого совмещена с осью z, а нижнее и верхнее основания S2 и S3 суть круги радиуса R, располо-
женные в плоскостях z = d и z = d + l соответственно.
В нашей работе [2] разработана и обоснована методика вычисления так называемого поля реак-
ции (магнетика) HR(r) := H(r) - H0(r), которая сводится к схеме, представленной ниже.
R
R
R
R
Цилиндрические координаты поля реакции
H ϕ,z)
=
H r,ϕ,z),
H r,ϕ,z),
H r,ϕ,z)
{
r
ϕ
z
}
в произвольной точке пространства с цилиндрическими координатами (r, φ, z), не лежащей на по-
верхности магнетика
S=S
1
S
2
S
3
или на его оси, вычисляются по формулам:
∞
1
1
R
(1)
(2)
H r,ϕ,z)
= π(µ-1)
cosnϕ t∫a
(z′)α
(r, 1,
z -tz′)dz′+
a r′)α
(r,
r′,
z
)
dr′+
z
r
∑
n
n
∫
n
n
n=0
0
0
1
1
(3)
(1)
+
a r′)
α
(r,
r′,
z -t)
dr′ +sinnϕ t∫b
(
z′)
(r, 1,
α ′
z -t⋅z
)
dz
′+
∫
n
n
n
n
0
0
1
1
(2)
(3)
+ ∫b r′
α r,
r′,
z
)
dr′ + ∫b
(r′)α
(r,
r′,
z -t)
dr′
;
(4)
n
n
n
n
0
0
Дефектоскопия
№ 5
2023
34
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
z
H0
S3
d + l
μ
S1
R
S2
d
y
x
Рис. 1. Однородный цилиндр в магнитном поле.
∞
1
1
R
(1)
(2)
H r,ϕ,z)
=- π(µ-1)
cosnϕt∫b
(z′)β
(r, 1,
z -tz′)dz′+
b r′)β
(r,
r′,
z)
dr′+
ϕ
∑
n
n
∫
n
n
n=1
0
0
1
1
(3)
(1)
+
b r′)β
(r,
r′,
z -t)
dr′ -sinnϕt∫a
(z′)
(r, 1,
β ′
z -t⋅z
)dz′+
∫
n
n
n
n
0
0
1
1
(2)
(3)
+∫a r′
β r,
r′,
z)dr′ + ∫a
(
r′ β (r, r′, z −t) dr′
;
(5)
n
n
n
n
0
0
∞
1
1
R
(1)
(2)
H r,ϕ,z)
= π(µ-
1)
cosnϕt∫a
(z′)γ
(r, 1,
z -tz′)dz′+
a r′)γ
(r,
r′,
z)dr′+
z
∑
n
n
∫
n
n
n=0
0
0
1
1
(3)
(1)
+
a r′)γ
(r,
r
′
,
z -t
)dr′ +sinnϕt∫b
(z′)γ
(r, 1,
z -tz
′)
dz′+
∫
n
n
n
n
0
0
1
1
(2)
(3)
+∫b r′
γ r,
r′
,
z)
dr′ + ∫b r′
γ
(r,
r′, z −t) dr′
,
(6)
n
n
n
n
0
0
где приняты обозначения:
r
z-d
l
r
:=
,
z
:=
,
t
:
=
;
(7)
R
R
R
Дефектоскопия
№ 5
2023
Расчет напряженности магнитного поля от полубесконечного цилиндра, помещенного...
35
n+1
2
2
2
(−1)
bδ a,b,
q)
n
(a
+b
+
q
)
2ab
2
n
n+1
α
(a,b,
q):=
a
−
P ε a,b,
q))+
P
(ε(a,b,
q))
;
(8)
n
1/2
2
1/2
aΓ(n
−1/2)
2n
+1
4n
−1
n+1
2
2
2
(−1)
nbδ a,b,
q)
a
+b
+
q
n
4ab
n+1
β
(a,b,
q):=
[
(
P ε a,b,
q)
)
+
P
(ε(a,b,
q))];
(9)
n
1/2
2
1/2
aΓ(
n
−1/2)
2n
+1
4n
−1
n+1
(−1)
bqδ a,b,
q)
n
γ
(a,b,
q):=
P ε a,b,
q)).
(10)
n
1/2
Γ(n
−1/2)
В формулах (8)—(10):
-1/2
−
3/4
2ab
2
2
2
2
2
2
2
δ(a,b,q)
=(a
+b
+
q
)
−4a
b
,
ε
(a,b,q)
=
1
−
(
)
,
(11)
2
2
2
a
+b
+q
n
P
1
(⋅)
— присоединенная функция Лежандра [10];
Γ ⋅
— гамма-функция.
2
∞
(1)
(2)
(3)
a z),
a r),
a
(r)
в (4)—(6) для каждого n = 0, 1, 2, … являются решением
Функции {
n
n
n
}
n
=0
системы следующих одномерных линейных интегральных уравнений:
1
1
(1)
(1)
(2)
a z)-2λ π
(
z′)α
(1, 1,
t
(
z- z′))
dz′ +
a r′)α
(1,
r′,
tz)
dr′ +
n
∫a
n
n
∫
n
n
0
0
1
2
(3)
(01)
+
a r′)α
(1,
r
′,
t(1
−
z
))
dr′ =
a z);
(12)
∫
n
n
n
µ+1
0
1
1
2
(2)
(1)
(3)
(02)
a r)−2λ π
t∫a
(
z
′
)γ
(r, 1,
tz
′)
dz
′ +
a r′)γ
(r,
r′
,
t
)
dr′ =
a r);
(13)
n
n
n
∫
n
n
n
µ+1
0
0
1
1
2
(3)
(1)
(2)
(03)
a r)−2λ π
t∫a
(z
′
)
γ
(r, 1,
t(1
−
z′
))
dz
′+
a r′)
γ
(r,
r
′,
t)
dr′ =
a r).
(14)
n
n
n
∫
n
n
n
µ+1
0
0
∞
(1)
(2)
(3)
b z),
b r),
b
(
r)
в (4)—(6) для каждого n = 1, 2, … есть решение системы
Функции {
n
n
n
}
n
=1
одномерных линейных интегральных уравнений:
1
1
(1)
(1)
(2)
b z)-2λ π
(
z′)α
(1, 1,
t
(
z- z′))
dz′ +
b r′)α
(1,
r′,
tz)
dr′+
n
∫b
n
n
∫
n
n
0
0
1
2
(3)
(01)
+
b r′)α
(1,
r′
,
t
(1
−
z))
dr′ =
b z);
(15)
∫
n
n
n
µ+1
0
1
1
(2)
(1)
(3)
2
(02)
b r)−2
λ π[
t∫b
(
z′)
γ r, 1,
tz′
)
dz′ + ∫b r′
γ r,
r′
,
t)
dr′]
=
b r);
(16)
n
n
n
n
n
n
µ+1
0
0
1
1
2
(3)
(1)
(2)
(03)
b r)−2λ π
t∫b
(z
′
)
γ
(r, 1,
t(1
−
z
′
))
dz
′+
b r′)
γ
(r,
r
′,
t
)
dr′ =
b r).
(17)
n
n
n
∫
n
n
n
µ+1
0
0
Дефектоскопия
№ 5
2023
36
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
В системах (12)—(14) и (15)—(17) параметр λ: = (μ - 1)/(μ + 1), а сами системы отличают-
ся только правыми частями и обозначениями искомых функций. Функции в правых частях этих
∞
∞
(01)
(02)
(03)
(01)
(02)
(03)
систем
a z),
a r),
a
(r)
и
b z),
b r),
b
(r)
выражаются следующим
{
n
n
n
}
{
n
n
n
}
n=0
n=1
образом
через декартовы компоненты напряженности заданного поля внешних источников
0
0
0
0
H x,y,z)
=
H x,y,z),
H x,y,z),
H x,y,z)
:
{
x
y
z
}
π
(01)
0
0
a z)
=
h
H Rcosϕ,
Rsinϕ,lz + d)cosϕ+
H Rcosϕ,
Rsinϕ,lz + d) sinϕcosnϕ d
ϕ;
(18)
n
n
∫
x
y
−π
π
(02)
0
a r)
=-h
H
(Rrcosϕ,
Rrsinϕ,d)cosnϕ d
ϕ;
(19)
n
n
∫
z
−π
π
(03)
0
a r)
=
h
H
(Rrcosϕ,
Rrsinϕ,d +l)cosnϕ d
ϕ;
(20)
n
n
∫
z
−π
π
(01)
0
0
b z)
=
h
H Rcosϕ,
Rsin
ϕ,
lz + d)cosϕ+
H Rcosϕ,
Rsinϕ,lz + d) sinϕsinnϕd
ϕ;
(21)
n
n
∫
x
y
−π
π
(02)
0
b r)
=-h
H
(Rrcosϕ,
Rrsinϕ,
d) sinnϕ d
ϕ;
(22)
n
n
∫
z
−π
π
(03)
0
b r)
=
h
H
(Rrcosϕ,
Rr
sinϕ,d +l) sinnϕ d
ϕ
(23)
n
n
∫
z
−π
В формулах (18)—(23):
z, r ∈ (0, 1), n = 0, 1, 2, …, h0 := 1/2π, hn := 1/π, n = 1, 2, …;
(24)
В часто встречаемом случае постоянного в окрестности цилиндра внешнего поля
0
0
0
0
H
={H
x
, H
y
, H
z
}= const
формулы (18)—(23) очевидным образом упрощаются:
(01)
(01)
0
(01)
0
(01)
(01)
a
=
0,
a
=H
,
b
=H
,
a
=b
=
0,
n=
2,3,;
(25)
0
1
x
1
y
n
n
(02)
0
(03)
0
(02)
(02)
(03)
(03)
a
=-H
,
a
=H
,
a
=b
=a
=b
=
0,
n=
1, 2, 3,;
0
z
0
z
n
n
n
n
(03)
0
(02)
(02)
(03)
(03)
a
=H
,
a
=b
=a
=b
=
0,
n=1,2,3,
(26)
0
z
n
n
n
n
Следовательно, для n = 2, 3, … системы (12)—(14) и (15)—(17) являются однородными с нуле-
выми решениями соответственно, а потому в формулах напряженности поля реакции (4)—(6) не-
(1)
(2)
(3)
нулевыми могут быть только функции
{a
(z), a
(r), a
(r)} — решение системы (14)—(16) для
0
0
0
(1)
(2)
(3)
(1)
(2)
(3)
n = 0,
{a
1
(z), a
1
(r), a
1
(r)} — решение этой системы для n = 1;
{b
1
(z), b
1
(r), b
1
(r)} — реше-
ние системы (17)—(19) для n = 1 с правыми частями в соответствии с (25), (26). Таким образом,
в случае H0 = const ряды в формулах напряженности (4)—(6) обрываются на первом или втором
слагаемом.
Для расчета декартовых координат поля реакции HR(r) в точках r = (0, 0, z) на оси цилиндра
(внутри или вне его, т.е. z либо внутри интервала (d, d + l), либо вне отрезка [d, d + l]) , помещенного
в произвольное внешнее поле H0(r), в работе [2] получены следующие расчетные формулы:
Дефектоскопия
№ 5
2023
Расчет напряженности магнитного поля от полубесконечного цилиндра, помещенного...
37
1
1
µ-1
R
(1)
2
−32
(2)
2
2
2
−32
H
(0, 0,z)
=-
(z′)[1+ (z -tz′)
]
dz′+
a r′)
r′
(
r′
+
z
)
dr′+
x
∫a
1
∫
1
4
0
0
1
(3)
2
2
2
−32
+
a
(r′)r′
[r′
+
(z -t
)
]
dr′
;
(27)
∫
1
0
1
1
µ-1
R
(1)
2
−32
(2)
2
2
2
−32
H
(0, 0,z)
=-
(z′)[1+ (z -tz′)
]
dz′+
b r′)
r′
(
r′
+
z
)
dr′+
y
∫b
1
∫
1
4
0
0
1
(3)
2
2
2
−32
+
b
(r′)r′
[r′
+
(z -t
)
]
dr′
;
(28)
∫
1
0
1
1
µ-1
R
(1)
2
−32
(2)
2
2
−32
H
(0, 0,z)
=
(z
)(
′ ′
z -t⋅z
)[1+(z -tz′)
]
dz′+ z∫a r′)r′(r′
+
z
)
dr′ +
z
∫a
0
0
2
0
0
1
(3)
2
2
−32
+
(z -t)∫a
(r′)r′[r′
+
(z -t
)
]
dr′,
(29)
0
0
(1)
(2)
(3)
(1)
(2)
(3)
(1)
(2)
(3)
где функции{a
(z), a
(r), a
(r)},
{a
(z), a
(r), a
(r)},
{b
(z), b
(r), b
(r)}суть решения
0
0
0
1
1
1
1
1
1
систем (14)—(16) и (17)—(19) с правыми частями (18)—(23) с соответствующим значением n.
3. НАПРЯЖЕННОСТЬ ПОЛЯ РЕАКЦИИ ПОЛУБЕСКОНЕЧНОГО ЦИЛИНДРА
Полубесконечным цилиндром мы считаем предельную форму конечного цилиндра, нижнее ос-
нование которого S2 остается в плоскости z = d, а длина l→+∞. Для получения формул напряженно-
сти поля реакции полубесконечного цилиндра необходимо перейти к пределу l→+∞ (эквивалентно
t = l/R→+∞) в формулах конечного цилиндра (4)—(6), (12)—(23), (27)—(29). Однако некоторые
определенные интегралы по отрезку [0, 1] в этих формулах являются несобственными (второго
рода — от неограниченных функций), что делает невозможным непосредственный переход к та-
кому пределу под знаком интеграла. Опишем неоднократно используемый в дальнейшем прием
(назовем его «прием (*)»), позволяющий для вычисления такого предела выразить несобственный
интеграл через собственный. Этот прием также неоднократно применялся в программной реализа-
ции предлагаемого алгоритма, поскольку стандартные квадратурные формулы могут применяться
только к собственным интегралам.
1
Прием (*). Пусть имеется несобственный интеграл второго рода
g(x) f (x)dx
, причем функ-
∫0
ция g(x) достаточно гладкая на [0, 1], а f(x)→∞ при x → b∈[0, 1] (но эта особенность интегрируе-
мая). Тогда, вычитая и добавляя g(b), получаем:
1
1
1
g(x) f (x)dx =
[g(x)- g(b)]f (x)dx + g(b)∫ f (x)dx.
(30)
∫
∫
0
0
0
Первый интеграл в правой части (30) является собственным, поскольку подынтегральное вы-
ражение можно представить в виде [(g(x) - g(b)) (x -b)](x -b) f (x), и при x→b дробь имеет
пределом конечную производную g′(b), а (x - b)f(x)→ 0, так как особенность в f(x) интегриру-
1
ема. Что касается несобственного интеграла
f (x)dx
в правой части (30), то либо он может
∫
0
быть вычислен аналитически, либо, в противном случае, выделением порядка особенности в
f(x) подбирается простая (в смысле аналитической интегрируемости) функция p(x), такая, что
f(x) = p(x) + O(1) при x→b. Тогда
Дефектоскопия
№ 5
2023
38
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
1
1
1
f (x)dx =
(
f(x)-p(x)
)
dx +∫ p(x)dx,
(31)
∫
∫
0
0
0
причем первый интеграл в правой части особенности не имеет, а второй вычисляется аналитиче-
ски.
Для получения формул напряженности поля реакции для полубесконечного цилиндра не-
обходимо в аналогичных формулах
(4)—(6) для конечного цилиндра перейти к пределу
∞
(1)
(2)
(3)
l → +∞ . Прежде всего получим «предельный» вид функций
{
a z),
a r),
a
(r)
}
и
n
n
n
n=0
∞
(1)
(2)
(3)
{
b z),
b r),
b
(r)
}
в этих формулах как решение «предельных» систем, полученных
n
n
n
n=1
переходом к пределу l → +∞ в правых и левых частях систем (12)—(14) и (15)—(17). Непо-
средственный переход к такому пределу под знаком первого интеграла в левой части (12) не-
возможен, так как его ядро имеет логарифмическую (интегрируемую) особенность при z′ = z ,
а именно, используя асимптотические формулы для присоединенных функций Лежандра [10],
можно показать, что для всех n = 0, 1, 2, … при q → 0:
n+1
1
1
1
α
(1, 1,
q)
=-
(
ln | q | −D
)
+O qln |q|),
D
:= ln8-2
−
-1.
n
32
n
n
∑
4π
k=1
2k
−1
2n
+1
Применяя к этому интегралу прием (*), в котором переменная интегрирования x = z′, b = z,
(1)
g x)
=a
n
(x) , f(x) = tαn(1, 1, t(z - x)), можно получить с учетом асимптотики:
α0(a, b, q) = O(1/q3), αn(a, b, q) = O(1/q2n + 1), q → ∞, n = 0, 1, 2, …,
(32)
что при t→+∞ в выражении (30) первое слагаемое в правой части имеет пределом ноль, а второе
слагаемое имеет пределом
(1) (
)
n n
A
a
z
, где числа:
+∞
A
:=
2
α
(1,1,x)dx,
A
= 0,282095299 ,
A
=A
== 0.
(33)
n
n
∫
0
1
2
0
Второй и третий интеграл в (12) особенностей не имеют, поэтому с учетом асимптотики (32)
можно показать, что эти интегралы имеют пределом ноль при t → +∞. При переходе к пределу
t → +∞ в левых частях уравнений (13) и (14) оба слагаемых в квадратных скобках этих уравнений,
содержащих интегралы без особенностей, имеют пределом ноль, что легко получить, учитывая
2n+2
асимптотику
γ
n
(a,b,
q)
=O(1
q
),
q→∞, n = 0, 1, 2, … . Переходя в формулах (18)—(20) к
пределу t → +∞, имеем следующие предельные значения параметров, входящих в правые части
системы (12)—(14):
π
(01)
0
0
a z)
=
h
H Rcosϕ,Rsinϕ,+∞)cosϕ+
H Rcosϕ,Rsinϕ,
+∞ ϕcosnϕ d
ϕ;
(34)
n
n
∫
x
y
−π
π
(02)
0
a r)
=-h
H
(Rrcosϕ,Rrsinϕ,d)cosnϕ d
ϕ
;
(35)
n
n
∫
z
−π
π
(03)
0
a r)
=
h
H
(Rrcosϕ,Rrsinϕ,+∞)cosnϕ d
ϕ
,
(36)
n
n
∫
z
−π
где введено обозначение
f x,y,+∞
):= lim
f x,y,z)
. Учитывая изложенное выше, получаем
z→+∞
следующий предельный (l → +∞) вид системы (12)—(14) для случая полубесконечного цилиндра:
(1)
(1)
2
(01)
a z)−
2
λ πA
a z)
=
a z);
(37)
n
n n
n
µ+1
(2)
2
(02)
(3)
2
(03)
n
a r)
=
n
a r),
n
a r)
=
n
a r).
(38)
µ+1
µ+1
Дефектоскопия
№ 5
2023
Расчет напряженности магнитного поля от полубесконечного цилиндра, помещенного...
39
Из (37) получаем:
(1)
2
(01)
a z)
=
a z).
(39)
n
n
(µ+1)(1− 2λ πA
)
n
Таким образом, (39) и (38) суть решение предельных систем (полученных из (12)—(14) при
l → +∞), где в правых частях стоят функции (34)—(36), n = 0, 1, 2, … . Аналогично, решение пре-
дельных систем, полученных из (15)—(17) при l → +∞, с учетом (33) имеет вид:
(1)
2
(01)
b z)
=
b z);
(40)
n
n
(µ+1)(1− 2λ π
A
)
n
(2)
2
(02)
(3)
2
(03)
b r)
=
b r),
b r)
=
b r),
(41)
n
n
n
n
µ+
1
µ+1
где в правых частях стоят функции (n = 1, 2, …):
π
(01)
0
0
b z)
=
h
H Rcosϕ,Rsinϕ,+∞)cosϕ+
H Rcosϕ,Rsinϕ,
+∞ ϕsinnϕ d
ϕ;
(42)
n
n
∫
x
y
−π
π
(02)
0
b r)
=-h
H
(Rrcosϕ,Rrsinϕ
,d ) sin nϕ d
ϕ;
(43)
n
n
∫
z
−π
π
(03)
0
n
b r)
=
h
n
H
z
(Rrcosϕ,Rrsinϕ,+∞) sinnϕ d
ϕ
(44)
∫
−π
0
0
0
0
В случае постоянного в окрестности цилиндра внешнего поля
H
={H
, H
, H
}= const
фор-
x
y
z
мулы (34)—(36) и (42)—(44) снова переходят в простые формулы (25), (26), подстановка которых в
(38), (39) и (40), (41) дает следующие решения предельных систем для полубесконечного цилиндра:
(1)
(2)
2
0
(3)
2
0
(1)
2
0
a z)
=
0,
a r)
=-
H
,
a r)
=
H
,
a z)
=
H
;
(45)
0
0
z
0
z
1
x
µ+1
µ+1
(µ+1)
(2)
(3)
(1)
(2)
(3)
1
a r)
1
=a r)
=
0,
n
a z)
n
=a r)
n
=a r)
=
0,
n=
2, 3, ... ;
(46)
(1)
2
0
(2)
(3)
b z)
=
H
,
b r)
=b r)
=
0;
(47)
1
1
1
(µ+
1)y
(1)
(2)
(3)
b z)
=b r)
=b r)
=
0,
n=
2,3,
(48)
n
n
n
Получим формулы для поля реакции на оси полубесконечного цилиндра, переходя к пределу
t
→ +∞ в формулах
(27)—(29). При переходе к пределу в первом слагаемом
1
(1)
2
−32
2
32
a
(z′)t[1+(z -tz′)
]
dz′
в фигурной скобке (27) ядро
t[1
+
(z -tz′)
]-
на левом конце от-
∫
1
0
резка интегрирования z′ = 0 имеет пределом бесконечность при t→+∞, а потому формальный
переход к пределу под знаком интеграла некорректен. Поэтому к этому интегралу применяем
(1)
2
−32
формулу (30) приема (*) , где x = z′, b = 0,
g x)
=a
(x)
,
f (x)= t[1+ (z −tx)
]
Тогда первый
n
интеграл в (30) является собственным, подынтегральное выражение в котором при t → +∞
равномерно идет к нулю, а второй интеграл легко вычисляется аналитически с последующим
переходом к пределу t → +∞. Второй интеграл правой части (27) от t не зависит, а третий ин-
теграл является собственным, подынтегральное выражение в котором при t → +∞ равномерно
идет к нулю. Учитывая вышеизложенное и (38), (39), получаем из (27) формулу для вычисле-
ния х-компоненты поля реакции на оси полубесконечного цилиндра:
Дефектоскопия
№ 5
2023
40
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
1
(02)
2
λ
z
a r′)r′
dr′
R
(01)
1
H
(0, 0,z)
=-
a
(0)
1+
+
(49)
x
1
2
∫
2
2
32
2
[r′
+
z
]
1+
z
0
Аналогично получаем из (28) формулу для вычисления у-компоненты поля реакции на оси по-
лубесконечного цилиндра:
1
(02)
2
λ
z
b r′)r′
dr′
R
(01)
1
H
(0, 0,z)
=-
b
(0)
1+
+
(50)
y
1
∫
2
2
32
2
2
[r′
+
z
]
1+
z
0
R
Переход к пределу t→+∞ в формуле (29) для
(0,0,
)
z
H
z
проводится по той же схеме, что и
R
переход к этому пределу в (27) для
(0,0,
)
H
z
: предел первого слагаемого в фигурных скобках (29)
x
считается с использованием приема (*), второе слагаемое от t не зависит, а третье имеет пределом
ноль. Получаем:
(01)
2
1
(02)
a
(0)
1+
z
a r′)r′dr′
R
0
0
H
(0, 0,z)
= -λ
−
z
(51)
z
∫
2
2
32
1−2λ πA
[r′
+
z
]
0
0
Таким образом, компоненты поля реакции на оси полубесконечного цилиндра внутри и вне его
(но не на его поверхности: z ≠ d , т.е. z ≠ 0 ), помещенного в произвольное внешнее поле, вычис-
ляются по формулам (49)—(51), где входящие в них функции определяются формулами (34), (35),
0
0
0
0
(42), (43). В случае постоянного в области цилиндра поля
H
={H
,
H
,
H
}= const
подстановка в
x
y
z
(49)—(51) соответствующих этому случаю значений (25), (26) дает следующие простые формулы
для поля реакции на оси цилиндра:
λ
z
λ
z
R
0
R
0
H
x
(0, 0,z)
=-
H
x
1+
;
H
y
(0, 0,z)
=-
H
y
1
+
;
(52)
2
2
2
z
+1
2
z
+1
z
x
R
0
H
(0, 0,z)
= -λH
sgn(z)−
,
sgn(x):
=
(53)
z
z
2
z
+1
|
x
|
В ходе тестовых расчетов поля реакции от однородного цилиндра конечной длины по общим
формулам (4)—(6), (12)—(17) и (27)—(29) выявили существенные недостатки численной реали-
зации расчетов по этим формулам в подходе [3], основанном на дискретизации входящих в эти
формулы интегралов квадратурной формулой средних прямоугольников (1), (2) с равномерным
распределением узлов интегрирования. Оказалось, что этот подход дает большую погрешность
результата в случае достаточно длинных цилиндров, что привело к необходимости получения для
этого случая более простых и более точных асимптотических формул расчета поля реакции, что
и реализовано в настоящей работе. Поясним на примере использования формулы (27) для рас-
R
чета х-компоненты
(0, 0,
)
H
z
поля реакции на оси конечного цилиндра в случае постоянного
x
внешнего поля. По логике вещей при увеличении длины цилиндра результаты расчета по этой
формуле должны приближаться к результатам расчета по соответствующей асимптотической фор-
муле
(52). Однако этого не происходило, более того, при увеличении длины цилиндра резуль-
таты расчетов по (27) все более расходились с результатом по (52). Численные эксперименты и
более глубокий анализ формулы (27) выявил следующую причину такого явления. При увеличе-
нии длины цилиндра l→∞ (т.е. t→∞) последние два интеграла в (27) стремятся к нулю, а потому
1
R
(1)
2
32
основной вклад в
H
(0, 0,
z)
вносит первый интеграл:
a
(x)t
[
1+(tx - z)
]
dz′
В нем при
x
∫
1
0
(1)
0
l→∞ по (45) будет
a
(z′)
→
2H
(µ+1) = const,
поэтому особенности при приближенном вычис-
1
x
лении этого интеграла квадратурными формулами определяются особенностями поведения его
2
32
ядра
t
f x):=t
[1+
(tx - z)
]
на отрезке интегрирования [0, 1]. А особенности эти таковы, что при
больших t = l/R (t→∞) данная функция почти на всем отрезке интегрирования принимает практи-
чески нулевые значения, однако имеет очень большой всплеск на очень узком отрезке с началом в
нуле (чем больше t, тем уже этот отрезок и тем выше всплеск). А потому при использовании для
Дефектоскопия
№ 5
2023
Расчет напряженности магнитного поля от полубесконечного цилиндра, помещенного...
41
приближенного вычисления этого интеграла квадратурных формул (1), (2) с равноотстоящими
узлами при больших t основная масса узлов попадает на «нулевой» участок, а на «несущий» узкий
участок попадает один-два (иногда ни одного) узла, а потому интеграл получается практически
нулевым, что не соответствует его истинному значению. Чтобы при описанной методике в узкий
«несущий» интервал попало достаточно много узлов, надо брать большое число разбиений отрезка
интегрирования m. Но тогда возникающая в методике работы [3] система линейных уравнений при
дискретизации системы интегральных уравнений (12)—(17) оказывается очень большого порядка
3m. Это приводит к проблеме с объемом компьютерной памяти и увеличению времени расчетов, а,
главное, к неприемлемому увеличению числа обусловленности системы, что ведет к низкой точ-
ности ее решения.
Получим формулы напряженности поля реакции полубесконечного цилиндра (вне и внутри, но
не на его поверхности и не на оси), для чего перейдем к пределу l → +∞ (т.е. t = l/R → +∞) в формулах
∞
(1)
(2)
(3)
(4)—(6) для напряженности поля реакции конечного цилиндра. Функции {
n
a z),
n
a r),
a
n
(r)
}
n=0
∞
(1)
(2)
(3)
и {
n
b z),
n
b r),
b
n
(r)
}
в этих формулах заменяются полученными их предельными значения-
n=1
ми (38), (39), (34)—(36), (40)—(44). Рассмотрим предельные переходы в самих интегралах, входящих
1
(1)
в эти формулы. В первом интеграле
(
)tα r, 1,
)
n
n
a
z′
z -tz′
dz′
формулы (4) нельзя непосредствен-
0
∫
но переходить к пределу t→+∞, так как его ядро
tα r, 1,
)
n
z -tz′
имеет особенность на левом конце
отрезка интегрирования z′ = 0 (неограниченно возрастает при t→+∞), которая выделяется приемом
(*). По (30) получаем:
1
1
(1)
(1)
(1)
a
(z′) −a
(0)
tα r, 1,
z -tz′)
dz′ + a
(0)
tα r, 1,
z -tz′)
dz′
(54)
∫
n
n
n
n
∫
n
0
0
Учитывая асимптотическое поведение присоединенных функций Лежандра [10], можно дока-
зать следующую асимптотическую формулу при q → +∞:
n
2
2
2
2
b(4ab)
p
n
(2n
+5n
+
2)a
+(2n
+n)b
1
n
α
(a,b,q)
=
−
+
+O
;
(55)
n
2n+1
2n+3
2n+5
a
q
2q
q
2n
−1
n
1
n
1
p
:=
Γ
(
− Γ(
+
2,
n = 0, 1, 2 … .
n
2
1
2
4
2
4
32π
Γ(n
−
)
2
Из представления (55) следует, что ядро
tα r, 1,
z -tz′)
первого интеграла в (54) при t → +∞
n
стремится к нулю не медленнее, чем 1/t2, чем обеспечивает его сходимость к нулю, делая нулевым
предел первого слагаемого в (54). Интеграл во втором слагаемом заменой переменной интегриро-
t-z
+∞
вания сводится к
α
(r, 1,
x)
dx
, а потому при t→+∞ имеет пределом
α
(r, 1,
x
)
dx
. Ядро
∫
n
∫
n
−z
-z
второго интеграла в (4) вообще от t не зависит, а ядро третьего интеграла в силу (55) идет к нулю
не медленнее, чем 1/t3, зануляя в пределе весь интеграл. Следующие три интеграла в (4) совершен-
но аналогичны первым трем, разобранным выше. Таким образом, переходя к пределу t → +∞ в
формуле (4) с учетом вышесказанного и формул (38), (39), (34)—(36), (40)—(44), получаем форму-
лу для цилиндрической r-компоненты поля реакции полубесконечного цилиндра в произвольной
точке, не лежащей на поверхности цилиндра или на его оси, при произвольном внешнем поле
0
0
0
0
H x,y,z)
=
x
{H x,y,z),
y
H x,y,z),
z
H x,y,z)}:
∞
(01)
+∞
1
a
(0)
R
n
(02)
H r,ϕ,z)
=
2
πλ
cosnϕ
α
(r, 1,
x)dx+∫a r′)α
(r,
r′,
z)dr′ +
r
∑
∫
n
n
n
1−2
πλA
n=0
n -z
0
(01)
+∞
1
b
(0)
n
(02)
+sinnϕ
α
(r, 1,
x)dx+∫b r′)α
(r,
r′,
z)dr′
(56)
∫
n
n
n
1−2
πλ
A -z
0
Аналогичные рассуждения о вычислении предела t → +∞ в (5), (6) дают формулы для осталь-
ных двух компонент поля реакции полубесконечного цилиндра:
Дефектоскопия
№ 5
2023
42
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
∞
(01)
+∞
1
b
(0)
R
n
(02)
H r,ϕ,z)
=-2
πλ
cosnϕ
β
(r, 1,
x)dx+∫b r′)β
(r,
r′,
z)
dr′ -
ϕ
∑
∫
n
n
n
1−2
πλA
n=1
n -z
0
(01)
+∞
1
a
(0)
n
(02)
−sinn
ϕ
β
(r, 1,
x)
dx+∫a r′)β
(r,
r′,
z)
dr
′
;
(57)
∫
n
n
n
1−2
πλ
A -z
0
∞
(01)
+∞
1
R
a
n
(0)
(02)
H r,ϕ,z)
=
2
πλ
cosnϕ-
γ
(r, 1,
x)dx+
a r′)γ
(r,
r′,
z)
dr′
+
z
∑
∫
n
∫
n
n
n=0
1−2
πλA
n z
0
(01)
+∞
1
b
(0)
n
(02)
+ sinnϕ-
γ
(r, 1,
x)
dx
+
b r′)γ
(r,
r′,
z)
dr′
(58)
∫
n
∫
n
n
1−2
πλA
n z
0
В формулах (56)—(58) r = r R , z = (z - d ) R , λ = (µ -1) (µ +1), числа An считаются по (33),
(01)
(02)
(01)
(02)
a
,
a
,
b
,
b
— по формулам (34), (35), (42), (43).
n
n
n
n
0
0
0
0
Для постоянного внешнего поля
H
={H
, H
, H
}= const
формулы напряженности поля ре-
x
y
z
акции полубесконечного цилиндра (56) - (58) с учетом (25), (26) упрощаются следующим об-
разом:
1
+∞
R
0
0
r
H r,ϕ,z)
=
2
πλ-H
z
α
0
(r,
x,
z)
dx+H
r
α
1
(r, 1,
x
)
dx
;
(59)
∫
∫
0
-
z
+∞
R
0
ϕ
H r,ϕ,z)
=-2
πλH
ϕ
β
1
(r, 1,
x)
dx;
(60)
∫
-
z
1
+∞
R
0
0
z
H r,ϕ,z)
=-2
πλ
z
H z)
γ
0
(r,
x z |)
dx+H
r
γ
1
(r, 1,
x)
dx
,
(61)
∫
∫
0
|
z
|
0
0
0
где цилиндрические компоненты напряженности внешнего поля
H
=H
cosϕ+H
sinϕ,
r
x
y
0
0
0
H
ϕ
=-H
x
sinϕ+
H
y
cosϕ
4. ПРОВЕРКА ПОЛУЧЕННЫХ ФОРМУЛ НА ИЗВЕСТНЫХ ПРЕДЕЛЬНЫХ СЛУЧАЯХ
В виду сложности и объемности аналитических преобразований, приведших к получению при-
веденных выше формул для напряженности поля реакции однородного полубесконечного цилин-
дра, помещенного в произвольное внешнее магнитное поле, важное значение приобретает про-
верка этих формул на их соответствие известным физическим законам, а также известным анали-
тическим формулам для предельных случаев рассматриваемой формы полубесконечного цилиндра
(бесконечно длинный цилиндр, магнитное полупространство). Для указанной проверки была
составлена на языке фортран соответствующая программа, реализующая расчеты по полученным
формулам. Сразу отметим, что все описанные ниже виды тестирования пройдены успешно.
В точках границы S магнетика для нормальной составляющей Hn напряженности результиру-
0
R
ющего поля
H r)
=H r)+H
(
r)
должно выполняться:
( )
e
H
n
=µ
,
(62)
(i
)
Hn
(i)
гдеH(e)n и
H
n
суть предельные значения Hn на поверхности S извне и изнутри магнетика соот-
ветственно [11]. На основании полубесконечного цилиндра нормальная составляющая Hn совпа-
дает с обратной z-компонентой напряженности, поэтому (62) имеет вид:
Дефектоскопия
№ 5
2023
Расчет напряженности магнитного поля от полубесконечного цилиндра, помещенного...
43
( )e
H
z
=µ
(63)
(i)
Hz
Выполнение равенства (63) было проверено аналитически в точке центра основания полубес-
конечного цилиндра с декартовыми координатами (0, 0, d) как для формулы (53), выражающей
R
R
H
z
(0,0,z)
на оси цилиндра в постоянном внешнем поле, так и для формулы (51) для
H
z
(0, 0,
z)
в случае произвольного внешнего поля. Выполнение (63) в остальных точках основания полубес-
конечного цилиндра проверялось расчетами по упомянутой компьютерной программе для форму-
лы (61), выражающей компонентуHRz в произвольной точке пространства (не на поверхности
цилиндра и не на его оси) в случае постоянного внешнего поля.
На боковой поверхности полубесконечного цилиндра нормальная составляющая Hn совпадает
с r-компонентой напряженности, поэтому (62) имеет вид:
( )
e
H
r
=µ
(64)
(i
)
Hr
Выполнение (64) в различных точках боковой поверхности полубесконечного цилиндра про-
верялось компьютерными расчетами для формулы (59), выражающей компонентуHRr в произ-
вольной точке пространства (не на поверхности цилиндра и не на его оси) в случае постоянного
внешнего поля.
Следующая проверка основывалась на том, что при безграничном увеличении радиуса основа-
ния полубесконечного цилиндра (R→∞) получается однородное магнитное полупространство, для
0
0
0
0
которого, в случае его погружения в постоянное внешнее поле
H
={H
, H
, H
},
известны анали-
x
y
z
тические формулы для напряженности результирующего поля [12]: внутри и вне полупространства
0
0
0
H
x
=H
x
0,
H
y
=H
y
; внутри полупространства
H
z
=
2H
z
(µ+1) , а вне его
H
z
=
2µH
z
(µ+1). При-
ближенное выполнение этих соотношений для больших значений радиуса R основания полубеско-
нечного цилиндра проверялось компьютерными расчетами по формулам (59)—(61) для вычисления
напряженности поля реакции такого цилиндра, погруженного в постоянное внешнее поле.
Заключительная проверка полученных формул основана на том, что при значительном удале-
нии точки расчета напряженности от плоскости основания полубесконечного цилиндра (ее коор-
дината z → +∞) значение напряженности поля реакции в ней (вне или внутри цилиндра) должно
приближаться к значению в этой точке напряженности поля реакции для бесконечного в обе сто-
0
0
0
0
роны цилиндра, формулы для которой в случае постоянного внешнего поля
H
={H
,
H
, H
}
x
y
z
известны [13, с. 209; 11, с. 339; 14, с. 245], а именно, в точке с цилиндрическими координатами (r,
R
0
R
0
2
φ, z) внутри или вне такого цилиндра выполнено:
H r,ϕ,z)
= -λH
,
r < R;
H r,ϕ,z)
=λH
r
,
r
r
r
r
R
0
R
0
2
R
r > R;
H r,ϕ,z)
= -λH
,
r < R;
H r,ϕ,z)
= -λH
r
,
r > R;
H r,ϕ,z)
=
0
, r < R или r > R.
ϕ
ϕ
ϕ
ϕ
z
Справедливость этого для формул напряженности поля реакции на оси цилиндра (52), (53) легко
проверяется непосредственно аналитически, а для формул напряженности поля реакции в произ-
вольной (не на оси или поверхности цилиндра) точке пространства
(59)—(61) проверялась с
помощью упомянутой компьютерной программы.
5. ЗАКЛЮЧЕНИЕ
Кратко сформулируем основные результаты, полученные в настоящей работе.
1. Выяснены причины потери точности вычисления по алгоритму, предложенному в [3], напря-
женности магнитного поля реакции однородного цилиндра в случае большой его длины.
2. Для указанного случая получены эффективные асимптотические формулы расчета напря-
женности поля реакции полубесконечного цилиндра, погруженного в произвольное внешнее маг-
нитное поле.
3. Составлена реализующая предложенный подход компьютерная программа (на языке фор-
тран), работающая на бытовом компьютере быстро (несколько секунд расчета в одной точке) и не
требующая больших ресурсов памяти.
4. Проведено тестирование полученных формул и компьютерной реализации соответствую-
щего алгоритма, состоящее в проверке результатов расчета на соответствие физическим законам
явления, а также сравнение этих результатов в предельных частных случаях формы магнетика с
известными аналитическими ответами.
Дефектоскопия
№ 5
2023
44
В.В. Дякин, О.В. Кудряшова, В.Я. Раевский
Работа выполнена в рамках государственного задания по теме
«Квант»
(“Quantum”)
№ АААА-А18-118020190095-4.
СПИСОК ЛИТЕРАТУРЫ
1. Дякин В.В., Кудряшова О.В., Раевский В.Я. О проблемах использования пакетов универсальных
программ для решения задач магнитостатики // Дефектоскопия. 2018. № 11. С. 23—34.
2. Dyakin V.V., Kudryashova O.V. , Raevskii V.Ya. One Approach to the Numerical Solution of the
Basic Equation of Magnetostatics for a Finite Cylinder in an Arbitrary External Field // Russian Journal of
Nondestructive Testing. 2021. V. 57. No. 4. P. 291—302. [Дякин В.В., Кудряшова О.В., Раевский В.Я. Один
подход к численному решению основного уравнения магнитостатики для конечного цилиндра в произ-
вольном внешнем поле // Дефектоскопия. 2021. № 4. С. 22—34.]
3. Dyakin V.V., Kudryashova O.V., Raevskii V.Ya. Calculating the Strength of Magnetic Field from a
Homogeneous Cylinder of Finite Dimensions Placed in an Arbitrary External Field // Russian Journal of
Nondestructive Testing. 2022. V. 58. No. 4. P. 308—319. [Дякин В.В., Кудряшова О.В., Раевский В.Я. Рас-
чет напряженности магнитного поля от однородного цилиндра конечных размеров, помещенного в про-
извольное внешнее поле // Дефектоскопия. 2022. № 4. С. 63—74.]
4. Верлань А.Ф., Сизиков В.С. Интегральные уравнения: Методы, алгоритмы, программы / Справоч-
ное пособие. Киев: Наукова думка, 1986. 544 с.
5. Хижняк Н.А. Интегральные уравнения макроскопической электродинамики. Киев: Наукова дум-
ка, 1986. 280 с.
6. Дякин В.В. Математические основы классической магнитостатики. Екатеринбург: РИО УрО РАН,
2016. 404 с.
7. Friedman M.J. Mathematical study of the nonlinear singular integral magnetic field equation. 1 // SIAM
Journal Appl. Math. 1980. V. 39. № 1. P. 14—20.
8. Friedman M.J. Mathematical Study of the Nonlinear Singular Integral Magnetic Field Equation. 2 //
SIAM J. Numer. Anal. 1981. V. 18. N 4. P. 644—653.
9. Friedman M.J. Mathematical Study of the Nonlinear Singular Integral Magnetic Field Equation. 3 //
SIAM J. Math. Analys. 1981. V. 12. N 4. P. 536—540.
10. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Т. 1. М.: Наука, 1973. 294 с.
11. Ахиезер А.И. Общая физика. Электрические и магнитные явления. Киев: Наукова думка, 1981.
471 с.
12. Дякин В.В., Умергалина О.В., Раевский В.Я. Поле конечного дефекта в трехмерном полупро-
странстве // Дефектоскопия. 2005. № 8. С. 28—42.
13. Татур Т.А. Основы теории электромагнитного поля. М.: Высшая школа, 1989. 271 с.
14. Неразрушающий контроль и диагностика / Под ред. В.В. Клюева. М.: Машиностроение, 1995.
487 с.
Дефектоскопия
№ 5
2023