ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 10, с. 1367-1383

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.925.52

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

У НЕЛИНЕЙНОЙ СИСТЕМЫ ТРЕТЬЕГО ПОРЯДКА

Р. Р. Бегишев, Р. П. Митрев, Т. С. Тодоров

Рассматривается нелинейная автономная система ОДУ третьего порядка, зависящая от

числовых параметров, которая описывает движения энергетического комбайна, преобра-

зующего остаточную тепловую энергию в электрическую. Для правильной работы комбай-

на необходимо, чтобы указанная система имела периодическое решение, поэтому ставится

задача отыскания параметров системы, при которых оно существует. Сформулированная

задача решается с использованием метода малого параметра.

DOI: 10.31857/S0374064121100095

Введение. Рассматривается нелинейная система ОДУ 3-го порядка

Ż₁ = z₂,

Ż₂ = -γ₁z₁ - γ₂z₂ + E(Δ - z₁)th(z₃ - T),

Ż₃ = -βz₃ + α(cos(ζ arctg z₁) + 1).

(1)

Здесь положительные постоянные α, β, γ₁, γ₂, E, Δ, ζ и действительная постоянная T -

параметры системы. Система уравнений (1) (упрощённая для уменьшения числа её парамет-

ров) предложена в работе [1] и описывает движения энергетического комбайна, перерабатыва-

ющего остаточную тепловую энергию в электрическую. Ключевым фактором для правильной

работы комбайна является периодическое движение пьезоэлектрической консоли [1]. Таким

движениям соответствуют периодические решения системы (1).

В статье [2] указаны некоторые значения параметров системы (1), при которых у неё су-

ществуют периодические решения. Однако этот результат подтверждается лишь численным

интегрированием уравнений системы, без строгого доказательства периодичности решений.

В данной работе даётся строгое доказательство того, что у системы (1) существуют такие

значения её параметров, при которых она имеет периодические решения.

Исследование системы ОДУ на наличие периодических решений является классической

задачей теории дифференциальных уравнений, которая рассматривалась многими исследова-

телями. Для некоторых классов систем эта задача хорошо изучена (например, доказано су-

ществование периодических решений у консервативных систем [3, с. 41], систем Ляпунова [4,

с. 148]; в некоторых случаях исследование на наличие периодических решений у двумерных ав-

тономных систем может быть проведено с использованием теоремы Пуанкаре-Бендиксона [5,

с. 426] и её обобщений [6]; исследовано большое число частных систем ОДУ [7-9]; разрабаты-

ваются численные методы нахождения периодических решений [10] и т.п.). Важным частным

случаем этой задачи является рассмотрение её для систем ОДУ с малым параметром [11,

с. 75]. В этом случае при условии наличия у невозмущённой системы периодического решения

ставится вопрос о существовании таких решений при достаточно малых возмущениях правой

части. Метод малого параметра успешно применяется как для неавтономных систем ОДУ, у

которых правая часть является периодической функцией времени (см., например, [12, с. 478]),

так и для автономных систем (см., например, [5, с. 396; 4, с. 25]).

В данной работе доказывается, что значения параметров, при которых у системы (1) име-

ются периодические решения, существуют. Для доказательства мы используем незначитель-

ную модификацию метода малого параметра, изложенного в монографии [5, с. 396].

1. Достаточные условия существования периодических решений. Введём малый

параметр μ, положив E = μ, γ₂ = γμ, γ ∈ R. Для удобства дальнейших выкладок положим

также γ₁ = 1, T = 0. Тогда уравнения системы (1) примут вид

Ż₁ = z₂,

Ż₂ = -z₁ + μ(-γz₂ + (Δ - z₁)th z₃),

Ż₃ = -βz₃ + α(cos(ζ arctg z₁) + 1).

(2)

1367

1368

ФОМИЧЕВ и др.

Так как решение z(t) = (z₁(t), z₂(t), z₃(t))^т этой системы зависит от начальных условий z(0) =

= z₀ ∈ R³ и от параметра μ, далее обозначаем его как z(t,z₀,μ) (остальные параметры сис-

темы - α, β, γ, Δ, ζ - считаем фиксированными, поэтому зависимость от них не отмечаем).

В силу автономности системы (2) её решение z(t, z₀, μ) будет периодическим, если и только

если z(ξ, z₀, μ) - z₀ = 0 для некоторого ξ > 0. Согласно формуле Коши решение z(t, z₀, μ)

удовлетворяет интегральному уравнению

∫t

z(t) = e^Atz₀ + eA(t-s)f(z(s)) ds.

Здесь e^At - матрица Коши линейной части невозмущённой системы, f(z(s)) - нелинейная

вектор-функция в правой части системы (2) (мы также относим к ней линейное слагаемое

-μγz₂ из второго уравнения, чтобы при μ = 0 решение было периодическим), т.е.

⎛

⎞

⎛

⎞

⎛

⎞

cos t sin t

A = ^⎝-1 0

⎠_,eAt₌ ⎝-sintcost

⎠,f(z)= ⎝μ(-γz2 + (Δ - z₁)th z₃)⎠,

-β

e^-βt

α(cos(ζ arctg z₁) + 1)

⎛

⎞

μ sin (t - s)(-γz₂ + (Δ - z₁) th z₃)

⎠_.

eA(t-s)f(z) = ⎝μ cos (t - s)(-γz2 + (Δ - z1)th z3)

e-β(t-s)α(cos(ζ arctg z₁) + 1)

Решение z(t) будет периодическим с периодом 2π + τ, если и только если z(2π + τ) -

- z(0) = 0 при некотором τ > -2π, т.е.

⎛

⎞

cos τ - 1

sin τ

∫

⎝ -sinτ cosτ - 1

⎠z0 +

eA(2π+τ-s)f(z(s))ds = 0.

(3)

e-β(2π+τ)

−1

Мы приходим к следующему утверждению:

Утверждение 1. Пусть на некотором отрезке [0, μ] определены такие непрерывные

функции z₀₁(μ), z₀₂(μ), z₀₃(μ) и τ(μ), что решение z(t, (z₀₁(μ), z₀₂(μ), z₀₃(μ))^т, μ) систе-

мы (2) удовлетворяет уравнению (3) при τ = τ(μ) для каждого фиксированного μ из отрез-

ка [0, μ], причём решение z(t, (z₀₁(0), z₀₂(0), z₀₃(0))^т, 0) отлично от константы и τ(μ) > -2π

при μ ∈ [0, μ]. Тогда найдётся такое число μ ≤ μ, что при всех μ ∈ [0, μ] система (3) име-

ет периодическое решение с периодом (не обязательно наименьшим) 2π+τ(μ), отличное от

константы.

Доказательство. Так как по условию решение z(t, (z₀₁(μ), z₀₂(μ), z₀₃(μ))^т, μ) удовлетво-

ряет уравнению (3) при всех μ ∈ [0, μ], то в силу автономности системы (2) это решение

периодично. Покажем, что при достаточно малых μ оно не является положением равновесия.

Все положения равновесия системы (2) (и только они) удовлетворяют системе уравнений

z₂ = 0,

-z₁ + μ(Δ - z₁)th z₃ = 0,

-βz₃ + α(cos(ζ arctg z₁)) + α = 0.

Из второго уравнения выразим z₁ = μΔ th z₃/(1+μ th z₃). Правая часть этого выражения при

μ < 1 очевидно непрерывна. Подставляя её вместо z₁ в третье уравнение, получаем

(

)

μΔ th z₃

Φ(z₃, μ) ≡ -βz₃ + α cos ζ arctg

+ α = 0.

(4)

1 + μthz₃

При μ = 0 из этого уравнения найдём z₃ =2α/β. Несложно проверить, что ∂Φ(z₃, 0)/∂z₃ =

= -β = 0. Тогда, согласно теореме о неявной функции, на некотором отрезке [0, μ],

μ < 1,

существует функция z₃ = z₃(μ), удовлетворяющая уравнению (4), причём эта функция непре-

рывна и единственна (так как функция в левой части (4) монотонна по переменной z₃ при

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1369

малых μ). Таким образом, положение равновесия z^c(μ) системы (2) при μ ∈ [0, μ] единствен-

но и непрерывно зависит от μ. Рассмотрим функцию

ϕ(μ) = ∥z^c(μ) - (z₀₁(μ), z₀₂(μ), z₀₃(μ))^т∥²²

на отрезке [0, min(μ, μ)]. Эта функция непрерывна: непрерывность первого под знаком нормы

слагаемого установлена выше, а непрерывность второго - одно из предположений утвержде-

ния 1. Согласно условию решение z(t, (z₀₁(0), z₀₂(0), z₀₃(0))^т, 0) не является положением рав-

новесия системы (2), поэтому ϕ(0) > 0. Тогда, поскольку функция ϕ(μ) непрерывна, найдётся

такое число μ > 0, что на отрезке [0, μ] справедливо неравенство ϕ(μ) > 0. При таких μ в

силу единственности положения равновесия решение z(t, (z₀₁(μ), z₀₂(μ), z₀₃(μ))^т, μ) является

периодическим (см. выше) и отличным от константы. Утверждение доказано.

Утверждение 2. Пусть на некотором отрезке [0, μ] определены такие непрерывные

функции z₀₁(μ), z₀₃(μ) и ν(μ), что решение z(t, (z₀₁(μ), 0, z₀₃(μ))^т, μ) системы (2) удовле-

творяет уравнению

⎛

⎞

cos(μν(μ)) - 1

z₀₁(μ)

⎛

⎞

⎜

⎟

∫

⎜

⎟²

sin (μν(μ) - s)(-γz₂ + (Δ - z₁) th z₃)

⎜

⎟

- sin(μν(μ))

⎝cos (μν(μ) - s)(-γz2 + (Δ - z1) th z3)⎠ds=0,

⎜

⎟+

(5)

⎜

z₀₁(μ)

⎟

⎝

⎠

αe-β(2π+μν(μ)-s)(cos(ζ arctg z₁) + 1)

(e-β(2π+μν(μ)) - 1)z₀₃(μ)

причём (z₀₁(0),0,z₀₃(0))^т не является положением равновесия системы (2). Тогда найдётся

такое число

μ ≤ μ, что при всех μ ∈ [0, μ] система (3) имеет отличное от константы

периодическое решение с периодом 2π + μν(μ) (не обязательно наименьшим).

Доказательство. Покажем, что решение z(t, (z₀₁(μ), 0, z₀₃(μ))^т, μ) удовлетворяет систе-

ме (3) при τ = μν(μ). В самом деле, домножив уравнение (5) на матрицу diag(μ, μ, 1), будем

иметь

⎞⎛

⎞

^⎛cos(μν(μ)) - 1

sin(μν(μ))

z₀₁(μ)

⎝ -sin(μν(μ)) cos(μν(μ)) - 1

⎠⎝

⎠₊

e-β(2π+μν(μ)) - 1

z₀₃(μ)

⎛

⎞

∫

μ sin (μν(μ) - s)(-γz₂ + (Δ - z₁) th z₃)

⎝μ cos (μν(μ) - s)(-γz2 + (Δ - z1) th z3)⎠ ds = 0.

αe-β(2π+μν(μ)-s)(cos(ζ arctg z₁) + 1)

Полученная система совпадает с системой (3) при τ(μ) = μν(μ). При этом τ(0) = 0, поэто-

му при достаточно малых μ верно неравенство τ(μ) > -2π. Таким образом, выполняются

все условия утверждения 1, следовательно, система (2) имеет нетривиальное периодическое

решение при малых μ. Утверждение доказано.

Итак, достаточно показать, что выполняются условия утверждения 2. Для этого восполь-

зуемся теоремой о неявной функции.

Теорема 1. Пусть функция H(p), p ∈ R, задана равенством

∫2π

H(p) = γπp + (Δ - p cos s) th(ω(s, p)) sin s ds,

где

(

∫

2π

∫

)

ω(s, p) = e^-βs

e^βq cos(ζ arctg(p cos q))dq + α e^βq cos(ζ arctg(p cos q))dq

(6)

e2πβ - 1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1370

ФОМИЧЕВ и др.

Пусть также параметры α, β, γ, Δ, ζ таковы, что существует число

p > 0, при

котором H(p) = 0, dH(p)/dp = 0. Тогда найдётся такое число

μ > 0, что система (2)

имеет отличное от константы периодическое решение при всех μ ∈ [0, μ].

Доказательство. Рассмотрим вектор-функцию

⎛

⎞

∫

⎜

⎟

sin (μν - s)(-γz₂ + (Δ - z₁) th ω(s, p₁, p₂, ν, μ)) ds

⎜

⎟

⎛

⎞

⎜

⎟

cos(μν)-1

⎜

⎟

p₁

⎜

⎟

⎜

⎟

∫

⎜

⎟

⎜

⎟

⎜

⎟

F (p₁, p₂, ν, μ)=^⎜

sin(μν)

⎟+⎜

cos (μν - s)(-γz₂ + (Δ - z₁) th ω(s, p₁, p₂, ν, μ)) ds⎟,

⎜

⎟

p₁

⎜

⎟

⎝^-

⎠

⎜

⎟

⎜

⎟

-p₂

⎜

∫

⎟

⎜

⎟

⎝

e^βs cos(ζ arctg z₁)ds +

⎠

e2πβ+βμν - 1

где

z = z(s,(p₁,0,p₂)^т,μ),

ω(s, p₁, p₂, ν, μ) = e^-βs ×

(

∫

)

e^βq cos(ζ arctg z₁)dq + α e^βq cos(ζ arctg z₁)dq

e2πβ+βμν - 1

Заметим, что для функции ω(s, p₁, p₂, ν, μ) справедливо равенство

ω(2π + μν, p₁, p₂, ν, μ) - ω(0, p₁, p₂, ν, μ) = 0.

Действительно,

ω(2π + μν, p₁, p₂, ν, μ) =

(

∫

)

=e-2πβ-βμν

e^βq cos(ζ arctg z₁)dq + α

e^βq cos(ζ arctg z₁)dq

e2πβ+βμν - 1

∫

e^βq cos(ζ arctg z₁)dq +

= ω(0,p₁,p₂,ν,μ).

(7)

e2πβ+βμν - 1

Несложно проверить, что функция F (p₁, p₂, ν, μ) является непрерывно дифференцируемой

в R⁴ (если функции (cos(μν)-1)/μ, sin(μν)/μ доопределить при μ = 0 по непрерывности).

Покажем, что найдутся такие числа p∗1, p∗2, ν^∗, при которых F (p∗1, p∗2, ν^∗, 0) = 0. Найдём

решение z(s, (p₁, 0, p₂)^т, 0). При μ = 0 система (2) принимает вид

Ż₁ = z₂,

Ż₂ = -z₁,

Ż₃ = -βz₃ + α(cos(ζ arctg z₁) + 1).

Решение этой системы, соответствующее начальным условиям (p₁, 0, p₂)^т, таково:

z₁(t) = p₁ cos t, z₂(t) = -p₁ sin t,

∫t

z₃(t) = e^-βtp₂ + αe^-βt e^βs(cos(ζ arctg(p₁ cos s)) + 1)ds.

(8)

Заметим, что при p₁ = 0 первые две компоненты решения являются 2π-периодическими,

отличными от константы.

Учитывая вид решения (8), нетрудно заметить, что при μ = 0 справедливо равенство

ω(s, p₁, p₂, ν, 0) = ω(s, p₁),

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1371

поэтому вектор-функция F (p₁, p₂, ν, 0) имеет следующий вид:

⎛

⎞

∫

2π

⎜

sin (-s)(-γz₂ + (Δ - z₁) th ω(s, p₁)) ds⎟

⎜

⎟

⎜

⎟

⎛

⎞

⎛

⎞

⎜

⎟

⎜

∫

2π

⎟

F₁(p₁,p₂,ν,0)

⎜

⎟

⎠₌ ⎝-νp1⎠+

⎜

⎟

F (p₁, p₂, ν, 0) =^⎝F₂(p₁, p₂, ν, 0)

cos (-s)(-γz₂ + (Δ - z₁) th ω(s, p₁)) ds

⎜

⎟

F₃(p₁,p₂,ν,0)

-p₂

⎜

⎟

⎜

⎟

⎜

2π

⎟

∫

⎜

⎟

⎝

⎠

e^βs cos(ζ arctg z₁)ds +

e2πβ - 1

где, как и выше, z(s) = z(s, (p₁, 0, p₂)^т, 0). При этом

∫2π

F₁(p₁,p₂,ν,0) = sin (-s)(-γz₂ + (Δ - z₁)th ω(s,p₁))ds =

∫2π

∫

2π

= sin (-s)(-γ(-p₁ sin s)) ds + (Δ - p₁ cos s) th ω(s, p₁) sin(-s) ds =

∫2π

= -πγp₁ - (Δ - p₁ cos s)th ω(s,p₁)sin s ds = -H(p₁).

Таким образом, если p∗1 = p > 0, то, согласно условию, F₁(p∗1, p₂, ν, 0) = 0 для всех p₂, ν ∈ R.

Далее найдём такое ν^∗, при котором F₂(p∗1, p₂, ν^∗, 0) = 0. Имеем

∫2π

F₂(p∗1,p₂,ν) = -νp∗1 + cos s(-γz₂ + (Δ - z₁)th ω(s,p∗1))ds.

Тогда, если

2π

∫

ν^∗ =

cos s(γp∗1 sin s + (Δ - p∗1 cos s) th ω(s, p∗1)) ds,

p^∗

то F₂(p∗1, p₂, ν^∗, 0) = 0 для любого p₂ ∈ R. Наконец, найдём p∗2 такое, что F₃(p∗1, p∗2, ν^∗, 0) = 0.

Справедливо равенство

2π

∫

F₃(p∗1,p₂,ν^∗,0) = -p₂ +

e^βs cos(ζ arctg(p∗1 cos s))ds +

e2πβ - 1

Отсюда следует, что если

2π

∫

p∗2 =

e^βs cos(ζ arctg(p∗1 cos s))ds +

e2πβ - 1

то F₃(p∗1, p∗2, ν^∗, 0) = 0.

Таким образом, найдены такие значения p∗1 = p, p∗2, ν^∗, при которых F (p∗1, p∗2, ν^∗, 0) = 0.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1372

ФОМИЧЕВ и др.

Найдём якобиан вектор-функции F по переменным p₁, p₂, ν в точке (p∗1, p∗2, ν^∗, 0). Учтём

при этом, что F₁(p∗1, p∗2, ν^∗, 0) = H(p∗1) (см. выше) и F₃(p₁, p₂, ν, 0) не зависит от ν. Тогда



∂F1(p∗1,p∗2,ν∗,0)



dH(p∗1)



D(F₁, F₂, F₃)



∂p₁



dH(p∗1)



p∗1.

D(p₁, p₂, ν)



∗

-p∗1



∗

-p∗1



∗

-1

∗

-1

По условию dH(p∗1)/dp = 0, p∗1 = 0, поэтому якобиан отличен от нуля. Тогда, согласно теореме

о неявной функции, на отрезке [0, μ] определены такие непрерывные функции p₁(μ), p₂(μ),

ν(μ), что F (p₁(μ), p₂(μ), ν(μ), μ) = 0 для всех μ ∈ [0, μ], причём p₁(0) = p∗1, p₂(0) = p∗2,

ν(0) = ν^∗.

Так как F₃(p₁(μ), p₂(μ), ν(μ), μ) = 0 для всех μ ∈ [0, μ], то третья компонента решения z(t)

системы (2), соответствующего начальным условиям (p₁(μ), 0, p₂(μ))^т, имеет следующий вид:

∫

z₃(t) = e^-βtp₂(μ) + αe^-βt e^βs(cos(ζ arctg z₁(s)) + 1)ds =

(

∫

)

∫

=e^-βt

e^βs cos(ζ arctg z₁(s))ds+

+αe^-βt e^βs(cos(ζ arctg z₁(s))+1) ds =

e2πβ+βμν(μ) -1

(

∫

)

∫

=e^-βt

e^βs cos(ζ arctg z₁(s))ds+

+ αe^-βt e^βs cos(ζ arctg z₁(s)) ds +

e2πβ+βμν(μ) - 1

(1 - e^-βt) = ω(t, p₁(μ), p₂(μ), ν(μ), μ).

(9)

Причём в силу (7) для функции z₃(t) при всех μ из отрезка [0, μ] справедливо равенство

z₃(2π + μν(μ)) - z(0) =

∫

= (e-β(2π+μν(μ)) - 1)p₂(μ) + α

e-β(2π+μν(μ)-s)(cos(ζ arctg z₁(s)) + 1)ds = 0.

(10)

Учитывая равенство (9) и равенства F_i(p₁(μ), p₂(μ), ν(μ), μ) = 0, i = 1, 2, получаем

⎛

⎞

∫

⎛

⎞

⎜

⎟

cos μν(μ) - 1

⎜

sin (μν - s)(-γz₂(s) + (Δ - z₁(s)) th z₃(s)) ds⎟

p₁(μ)

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

= 0.

(11)

⎝

⎠⁺

sin μν(μ)

⎜

∫

⎟

p₁(μ)

⎜

⎟

⎝

cos (μν - s)(-γz₂(s) + (Δ - z₁(s)) th z₃(s)) ds⎠

Таким образом, при всех μ ∈ [0, μ] справедливы равенства (10), (11). Это означает, что при

указанных μ и τ(μ) = μν(μ) решение z(t, (p₁(μ), 0, p₂(μ)), μ) удовлетворяет уравнению (5).

Тогда, согласно утверждению 2, система (2) имеет нетривиальное периодическое решение при

малых μ. Теорема доказана.

Замечание 1. Применённый при доказательстве теоремы 1 метод почти полностью по-

вторяет метод из [5, с. 396]. Отличие лишь в том, что в данном случае порождающая система

является нелинейной, хотя и легко интегрируемой (а в работе [5, с. 396] рассматривались воз-

мущённые линейные системы). Заметим, что применить для системы (2) указанный метод без

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1373

изменений нельзя. В самом деле, если рассматривать возмущённую линейную систему (т.е. по-

ложить α = μ), то при μ = 0 для периодичности решения необходимо выполнение равенства

z₃ ≡ 0, поэтому F₁(p₁,p₂,ν,0) = -γπp₁, т.е. указанная функция обращается в нуль только

при p₁ = 0.

Следствие 1. Пусть параметры α, β, Δ, ζ таковы, что существуют числа p > p > 0,

для которых справедливы неравенства

I(p) < 0, I(p) > 0.

Тогда найдётся такое число γ > 0, что система (2) имеет периодическое решение при

каждом μ ∈ [0, μ]. Здесь

∫2π

I(p) = (Δ - p cos s) th(ω(s, p)) sin s ds,

(12)

а функция ω(s, p) определяется равенством (6).

Доказательство. Заметим, что H(p) = πγp + I(p). Нетрудно видеть, что функция I(p)

непрерывно дифференцируема. Так как I(p) < 0 и I(p) > 0, то найдётся такая точка p^∗ ∈

∈ (p, p), в которой I(p^∗) = 0. Заметим также, что I(0) = 0. В самом деле,

(

∫

2π

∫

)

(

)

ω(s, 0) = e^-βs

e^βq dq + α e^βq dq

=e^-βs

(e^βs - 1)

e2πβ - 1

Тогда

2π

∫

2α

I(0) = th

(Δ - p cos s) sin s ds = 0.

Рассмотрим функцию I(p) на отрезке [0, p^∗]. Так как функция непрерывна на этом отрез-

ке, она достигает на нём своего минимума m_I . Поскольку p ∈ [0, p^∗], справедливо неравенство

m_I < 0. Это означает, что найдётся число p^∗∗ ∈ (0,p^∗) такое, что I(p^∗∗) < 0, I^′(p^∗∗) = 0.

Положим γ = -I(p^∗∗)/(πp^∗∗) > 0, тогда H(p^∗∗) = -I(p^∗∗) + I(p^∗∗) = 0. При этом

dH(p^∗∗)

= πγ + I^′(p^∗∗) = πγ > 0.

Таким образом, при указанном γ > 0 выполняются все условия теоремы 1. Следствие до-

казано.

Итак, для доказательства существования периодических решений у системы (2) достаточ-

но найти такие значения 0 < p < p, что интеграл I(p) принимает при этих значениях p

отрицательное и положительное значения соответственно. Для вычисления I(p) можно непо-

средственно применять квадратурные формулы. Однако выражение под интегралом является

довольно громоздким (содержит интеграл с переменным верхним пределом), поэтому такой

подход затруднительно реализовать с вычислительной точки зрения. Покажем, как можно

преобразовать функцию I(p) и получить для неё более простые оценки. Для этого нам по-

требуются некоторые вспомогательные утверждения.

2. Вспомогательные утверждения. Для удобства дальнейшего изложения введём сле-

дующие обозначения:

∫s

∫

C(s, p) = e^βq cos (ζ arctg(p cos q)) dq, S(s, p) = e^βq cos (ζ arctg(p sin q)) dq.

(13)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1374

ФОМИЧЕВ и др.

Утверждение 3. Имеют место равенства

C(s + π, p) = C(π, p) + e^βπC(s, p), C(s + π/2, p) = C(π/2, p) + eβπ/2S(s, p),

S(s + π, p) = S(π, p) + e^βπS(s, p), S(s + π/2, p) = S(π/2, p) + eβπ/2C(s, p).

Доказательство. Воспользовавшись определением (13) и очевидными преобразованиями,

получаем

s+π

C(s + π, p) = e^βq cos (ζ arctg(p cos q)) dq =

∫π

∫

= e^βq cos(ζ arctg(pcosq))dq +

e^βq cos (ζ arctg(p cos q))dq =

∫π

∫s

= eβq cos(ζ arctg(pcosq))dq + eβ(q+π) cos(ζ arctg(pcos(q + π)))dq = C(π,p) + e^βπC(s,p);

∫

C(s + π/2, p) =

e^βq cos(ζ arctg(p cos q)) dq =

∫

= e^βq cos(ζ arctg(pcosq))dq +

e^βq cos (ζ arctg(p cos q)) dq =

π/2

∫

= eβq cos(ζ arctg(pcosq))dq + eβ(q+π/2) cos(ζ arctg(pcos(q + π/2)))dq =

= C(π/2,p) + eβπ/2S(s,p).

Для функции S(s, p) выкладки аналогичны. Утверждение доказано.

Следствие 2. Для функции ω(s, p), определяемой равенством (6), справедливо представ-

ление

(

)

ω(s, p) = e^-βs

C(π, p) + αC(s, p)

e^βπ - 1

Доказательство. С учётом утверждения 3 имеем

(

)

ω(s, p) = e^-βs

C(2π, p) + αC(s, p)

e2πβ - 1

(

)

(

)

=e^-βs

(1 + e^βπ)C(π, p) + αC(s, p)

=e^-βs

C(π, p) + αC(s, p)

e2πβ - 1

e^βπ - 1

Следствие доказано.

Следствие 3. Функция ω(s, p), определяемая равенством (6), является π-периодической

по переменной s.

Доказательство. Согласно следствию 2 и утверждению 3 получаем

(

)

ω(s + π, p) = e-β(s+π)

C(π, p) + αC(s + π, p)

e^βπ - 1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1375

(

)

=e-β(s+π)

C(π, p) + αC(π, p) + αe^βπC(s, p)

e^βπ - 1

(

)

=e^-βs

C(π, p) + αC(s, p)

= ω(s,p).

e^βπ - 1

Следствие доказано.

Следствие 4. Для функции I(p), определяемой равенством (12), справедливо представ-

ление

∫

I(p) = -p sin(2s) th ω(s, p) ds.

Доказательство. Преобразовывая интеграл в определении (12), получаем

∫2π

I(p) = (Δ - p cos s) th(ω(s, p)) sin s ds =

∫π

∫

2π

= (Δ - p cos s) th(ω(s, p)) sin s ds + (Δ - p cos s) th (ω(s, p)) sin s ds =

∫π

= (Δ - p cos s) th(ω(s, p)) sin s ds + (Δ - p cos (s + π)) th(ω(s + π, p)) sin(s + π) ds =

∫π

∫

= Δ th(ω(s,p))sinsds - p cossth(ω(s,p))sinsds -

∫π

∫

− Δ th(ω(s,p))sinsds - p cossth(ω(s,p))sinsds =

∫π

= -2p cos s th(ω(s,p))sin s ds = -p th(ω(s,p))sin(2s)ds.

Следствие доказано.

Следствие 5. При s ∈ [0, π/2] справедливо равенство

(

)

ω(s + π/2, p) - ω(s, p) = e^-βs

(C(π/2, p) - S(π/2, p)) - α(C(s, p) - S(s, p))

eβπ/2 + 1

Доказательство. Рассмотрим выражение из условия и воспользуемся утверждением

3, а

также следствием 2:

(

)

(

)

e^βs(ω(s+π/2,p)-ω(s,p))=e-βπ/2

C(π, p)+αC(s+π/2, p) -

C(π, p)+αC(s, p) =

e^βπ -1

(

)

=e-βπ/2

(C(π/2, p) + eβπ/2S(π/2, p)) + αC(π/2, p) + αeβπ/2S(s, p)

e^βπ - 1

(

)

−

(C(π/2, p) + eβπ/2S(π/2, p)) + αC(s, p)

e^βπ - 1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1376

ФОМИЧЕВ и др.

)

(

)

⁽e-βπ/2α

αeβπ/2

= C(π/2,p)

+αe-βπ/2-

+S(π/2,p)

-α(C(s, p)-S(s, p)) =

e^βπ - 1

(C(π/2, p) - S(π/2, p)) - α(C(s, p) - S(s, p)).

eβπ/2 + 1

Следствие доказано.

Утверждение 4. Пусть функции g(s), h(s) определены и непрерывны на отрезке [a, b]

и m ≤ h(s) ≤ M, s ∈ [a,b]. Тогда справедливы неравенства

∫

m-M

M+m

|g(s)| ds +

g(s) ds ≤ g(s)h(s) ds ≤

∫

M-m

M +m

≤

|g(s)| ds +

g(s) ds.

Доказательство. Согласно условию, если s таково, что g(s) > 0, то

g(s)m ≤ g(s)h(s) ≤ g(s)M.

Если же s таково, что g(s) < 0, то

g(s)M ≤ g(s)h(s) ≤ g(s)m.

Таким образом, при всех s ∈ [a, b] справедливы неравенства

)

⁽m-M

M+m

⁽M-m

M+m

sgn g(s) +

g(s) ≤ g(s)h(s) ≤

sgn g(s) +

g(s),

т.е.

m-M

M+m

M-m

M+m

|g(s)| +

g(s) ≤ g(s)h(s) ≤

|g(s)| +

g(s).

Интегрируя это двойное неравенство, получаем требуемое. Утверждение доказано.

3. Основной результат. Установленные утверждения позволяют сформулировать и дока-

зать основной результат работы. Сначала для упрощения записи введём обозначения величин

(

)

2α

α(1 + ch-2(2α/β))

a₁ = a₁(α,β) =

a₂ = a₂(α,β) =

(14)

ch²(2α/β)

β² + 4

и интеграла

∫

Ω(p) = cos(2s)(cos(ζarctg(p sin s)) - cos(ζarctg(p cos s)))ds,

(15)

а также обозначим

I(p) = a₁(α, β) + a₂(α, β)Ω(p) и I(p) = -a₁(α, β) + a₂(α, β)Ω(p).

(16)

Теорема 2. Пусть числа α, β, ζ,

p таковы, что

I(p) < 0, I(p) > 0

(17)

для некоторых 0 < p < p. Тогда найдётся такое число γ > 0, что система (2) (при данных

значениях α, β, γ, ζ) имеет периодическое решение при всех μ из некоторого отрез-

ка [0, μ].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1377

Доказательство. Представим функцию I(p) в удобном для дальнейшего виде:

∫π

∫

I(p) = -p th ω(s, p) sin(2s) ds = -p th ω(s, p) sin(2s) ds - p th ω(s, p) sin(2s) ds =

π/2

∫

= -p th ω(s,p) sin(2s)ds - p th ω(s + π/2,p) sin2(s + π/2)ds =

∫

[th ω(s + π/2, p) - th ω(s, p)] sin(2s) ds = p Ψ(s)(ω(s + π/2, p) - ω(s, p)) sin(2s) ds.

Здесь

⎧

⎨th ω(s + π/2, p) - th ω(s, p)

если ω(s + π/2) - ω(s) = 0,

Ψ(s) =

ω(s + π/2, p) - ω(s, p)

^⎩ch-2 ω(s, p),

если ω(s + π/2) - ω(s) = 0.

Заметим, что функция Ψ(s) непрерывна, при этом, согласно теореме Лагранжа,

Ψ(s) = ch-2 ξ(s),

где ξ(s) ∈ [min(ω(s + π/2, p), ω(s, p)), max(ω(s + π/2, p), ω(s, p))]. Таким образом, справедливы

неравенства

ch-2 max |ω(s, p)| ≤ Ψ(s) ≤ 1.

s∈[0,π]

Оценим функцию ω(s, p):



(

∫

)



α



|ω(s, p)| ≤e^-βs

e^βq cos(ζ arctg(p cos q))dq + α e^βq cos(ζ arctg(p cos q))dq

≤

e^βπ - 1

(

∫

)

2α

≤e^-βs

e^βq dq +α e^βq dq

=e^-βs

(e^βπ - 1) + e^-βs

(e^βs - 1) +

e^βπ - 1

e^βπ - 1 β

Таким образом,

ch-2(2α/β) ≤ Ψ(s) ≤ 1.

Тогда, согласно утверждению 4, для I(p) при p > 0 имеют место следующие оценки:

(

)

(

)

I(p)

I₁(p) +

I₂(p) ≤

≤

ch²(2α/β)

(

)

(

)

≤

I₁(p) +

I₂(p),

(18)

ch²(2α/β)

где

∫

I₁(p) =

|(ω(s + π/2, p) - ω(s, p)) sin(2s)| ds, I₂(p) = (ω(s + π/2, p) - ω(s, p)) sin(2s) ds.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1378

ФОМИЧЕВ и др.

Заметим, что

∫

I₁(p) =

|(ω(s + π/2, p) - ω(s, p)) sin(2s)| ds ≤

(|ω(s + π/2, p)| + |ω(s, p)|) sin(2s) ds ≤

∫

4α

≤

sin(2s) ds =

(19)

Покажем, как можно упростить I₂(p):

∫

I₂(p) = (ω(s + π/2,p) - ω(s,p))sin(2s)ds = [Следствие 5] =

∫

(

))

e^-βs

(C(π/2, p) - S(π/2, p)) - α(C(s, p) - S(s, p)) sin(2s) ds =

eβπ/2 + 1

∫

(

)

(C(π/2, p)-S(π/2, p))-α(C(s, p)-S(s, p)) de^-βs(2 cos(2s)+β sin(2s)) =

β²+4

eβπ/2+1

{(

)

}

π/2

-1



(C(π/2, p)-S(π/2, p))-α(C(s, p)-S(s, p)) e^-βs(2 cos(2s)+β sin(2s))



β²+4

eβπ/2+1

∫

-α(C(s, p) - S(s, p))^′e^-βs(2 cos(2s) + β sin(2s)) ds =

β² + 4

(

)

-1

2α

-2e-βπ/2

-α (C(π/2,p)-S(π/2,p))-

(C(π/2, p)-S(π/2, p))

β² + 4

eβπ/2 + 1

∫

α(S(s, p) - C(s, p))^′e^-βs(2 cos(2s) + β sin(2s)) ds =

β² + 4

∫

(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s)))(2 cos(2s) + β sin(2s)) ds.

(20)

β² + 4

Из неравенства (18) с учётом (19), (20) получаем

(

)

2α

α(1 + ch-2(2α/β))

I(p)

I₃(p) ≤

≤

ch²(2α/β)

2(β² + 4)

(

)

2α

α(1 + ch-2(2α/β))

≤

I₃(p).

(21)

ch²(2α/β)

2(β² + 4)

Здесь

∫

I₃(p) = (cos(ζ arctg(p sin s)) - cos(ζ arctg(pcos s)))(2cos(2s) + β sin(2s))ds.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1379

Покажем, что

∫

(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s))) sin(2s) ds = 0.

В самом деле,

∫

(

)

cos(ζ arctg(p cos s)) sin(2s) ds = - cos(ζ arctg(p cos(π/2 - s))) sin 2

- s ds =

π/2

∫

= cos(ζ arctg(p sin s)) sin(2s) ds.

Таким образом, I₃(p) = Ω(p) (см. (15)), а значит, оценки (21) вследствие обозначений (14)-

(16) примут вид I(p) ≤ I(p)/p

I (p). Отсюда вследствие условия (17) вытекают неравенства

I(p) < 0, I(p) > 0, которые, согласно следствию 1, означают, что система (2) имеет периоди-

ческие решения при малых неотрицательных μ. Теорема доказана.

Итак, согласно теореме 2, для того, чтобы утверждать существование периодического ре-

шения у системы (2), достаточно найти значения параметров, при которых существуют такие

0 < p < p, что

I(p) < 0 и I(p) > 0. Для вычисления интеграла (15), входящего в функ-

ции (16), можно использовать квадратурные формулы.

Поиск подходящих параметров. Для проверки условий (17) достаточно приближённо

вычислить интегралы, указанные в этих условиях, и показать, что они имеют требуемые знаки

с учётом погрешности.

Для вычисления интегралов воспользуемся методом трапеций. При этом, поскольку вы-

числения будут проводиться на ЭВМ, необходимо также учесть погрешность при вычислении

значений подынтегральной функции.

Утверждение 5. Пусть g(s) - дважды непрерывно дифференцируемая на отрезке [a, b]

функция. Пусть далее числа g₀,

g₁, ...,

gn таковы, что |g(a + ih) - gi| ≤ ε, i = 0, n, где

h = (b - a)/n. Тогда

 ∫

(

)



∑



g₀ + g_n

(b - a)h²



g(s) ds - h



M₂

+ ε(b - a),



≤

i=1

где M₂ = max |g^′′(s)|.

s∈[a,b]

Доказательство. Известно [13, с. 164], что формула трапеций имеет погрешность h².

Более точно, если g_i = g(a + i(b - a)/n), i = 0, n, то

 ∫

(

)



∑



g₀ + g_n

h²(b - a)



g(s) ds - h

+ g_i



M₂.



≤

i=1

Оценим указанную в условии разность:

∫

(

)

 ∫

(

)



∑



∑



g₀ + g_n



g(s) ds - h

+ g_i



≤



⁺

i=1



∑



g₀ - g₀ + g_n - g_n

b-a

+^

+ h (g_i - g_i)

h²

M₂ + εnh,

≤

i=1

Остаётся заметить, что nh = b - a. Утверждение доказано.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

6^∗

1380

ФОМИЧЕВ и др.

Для вычисления интегралов

I(p), I(p) воспользуемся формулой трапеций, при этом для

получения значений подынтегральной функции будем использовать библиотеку npmath [14],

позволяющую проводить вычисления с любой заданной точностью.

Оценим погрешность при вычислени

I(p). Далее пользуемся обозначениями (14)-(16).

Пусть ã₁ и ã₂ - приближённые значения коэффициентов a₁ и a₂ соответственно, вычис-

ленные с точностью ε, т.е.

|a₁ - ã₁| ≤ ε,

|a₂ - ã₂| ≤ ε.

Пусть, далее,

Ω(p) - приближённое значение интеграла, вычисленное по приближённым зна-

чениям подынтегральной функции:

(

)

∑

g₀ + g_n

Ω(p) = h

gi ,

|g_i - cos(2s_i)(cos(ζ arctg(p sin s_i)) + cos(ζ arctg(p cos s_i)))| ≤ ε,

i=1

s_i = ih, i = 0,n, h =

|π - π| ≤ ε.

Здесь

π - рациональное приближение числа π. Таким образом,

Ω(p) - это приближённое

значение интеграла

∫

cos(2s)(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s))) ds.

Тогда, с учётом утверждения 5, получим



∫



∫



∫



|Ω(p) -Ω(p)| =  g(q) dq -Ω(p)



g(q) dq - g(q) dq



g(q) dq -Ω(p)

≤



⁺



≤



_π

π

πh²



≤

|g(s)| + M₂

+ε

≤ 2ε + M₂

+ε

 m

s∈[0,π/2]

(

) (

)

h²

4ε

h²

≤2 M₂

+ 3ε ,

M₂ 12+ε+

где

g(s) = cos(2s)(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s))),

|g(s)| ≤ 2, M₂ = max

|g^′′(s)|.

s∈[0,π/2]

Таким образом, есл

I(p) = ã₁ + ã₂ Ω(p), то справедливо неравенство

I (p)

I(p)| = |a₁ + a₂Ω(p) - ã₁ - ã₂ Ω(p)| ≤ |a₁ - ã₁| + |a₂ - ã₂||Ω(p)| + |Ω(p) -Ω(p)||ã₂| ≤

(

)

(

)(

)

h²

2α

≤ ε + επ + 2 M₂

+ 3ε |ã₂| ≤ 5ε + 2 M₂

+ 3ε

+ε .

β² + 4

Здесь мы воспользовались тем, что

|ã₂| ≤ 2α/(β² + 4) + ε,

|Ω(p)| ≤ π.

Точно такая же оценка получается для разности |I(p) -Ĩ(p)|.

Найдём, наконец, коэффициент M₂:

g^′′(s) = -4cos(2s)(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s))) -

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1381

(

)

pζ cos s sin(ζ arctg(p sin s))

pζ sin s sin(ζ arctg(p cos s))

- 4sin(2s)

p² sin²(s) + 1

p² cos²(s) + 1

+ cos(2s)(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s)))^′′,

где

(cos(ζ arctg(p sin s)) - cos(ζ arctg(p cos s)))^′′ =

p²ζ² sin² s cos(ζ arctg(p cos s)) + 2p³ζ sin² s cos s sin(ζ arctg(p cos s))

(p² cos² s + 1)²

2p³ζ sin s cos² s sin(ζ arctg(p sin s)) - p²ζ² cos² s cos(ζ arctg(p sin s))

(p² sin² s + 1)²

pζ sins sin(ζ arctg(p sin s))

pζ cos s sin(ζ arctg(p cos s))

p² sin² s + 1

p² cos² s + 1

Таким образом,

|g^′′(s)| ≤ 8 + 10pζ + 2p²ζ² + 4p³ζ = M₂.

Рассмотрим систему (2) при следующих значениях параметров:

α = 0.3, β = 2, ζ = 5.6,

p= 2.1,

p=9,Δ=0.1.

Здесь параметр Δ можно взять произвольным, поскольку, как показано выше, он не влияет

на величину I(p). Вычисляя для этих значений параметров приближённые значения

I(p) и

^Ĩ(p), найдём, что

( p) ≈ -0.0598,

^Ĩ(p) ≈ 0.0213.

При этом погрешность вычисления функции была выбрана равной ε = 10-50, а шаг - равным

h = π/(2 · 10⁵), общая погрешность вычислений составила менее 10-7. Таким образом, при

указанных значениях параметров система удовлетворяет условиям теоремы 2.

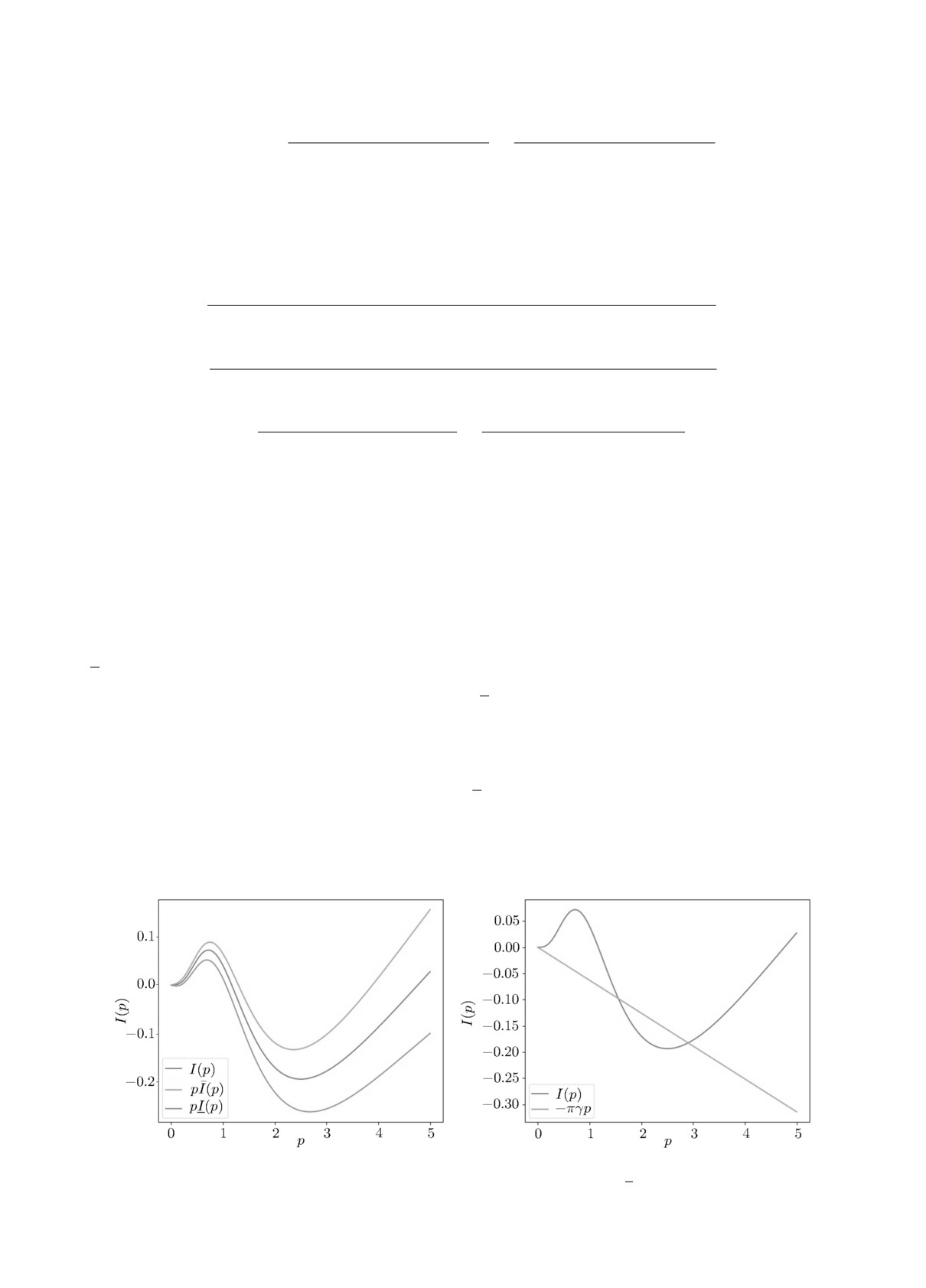
График функции I(p) и её оценок

I(p), pI(p), вычисленных при указанных значениях

параметров, приведён на рис. 1, а. При γ = 0.02 прямая y(p) = -πγp пересекает график

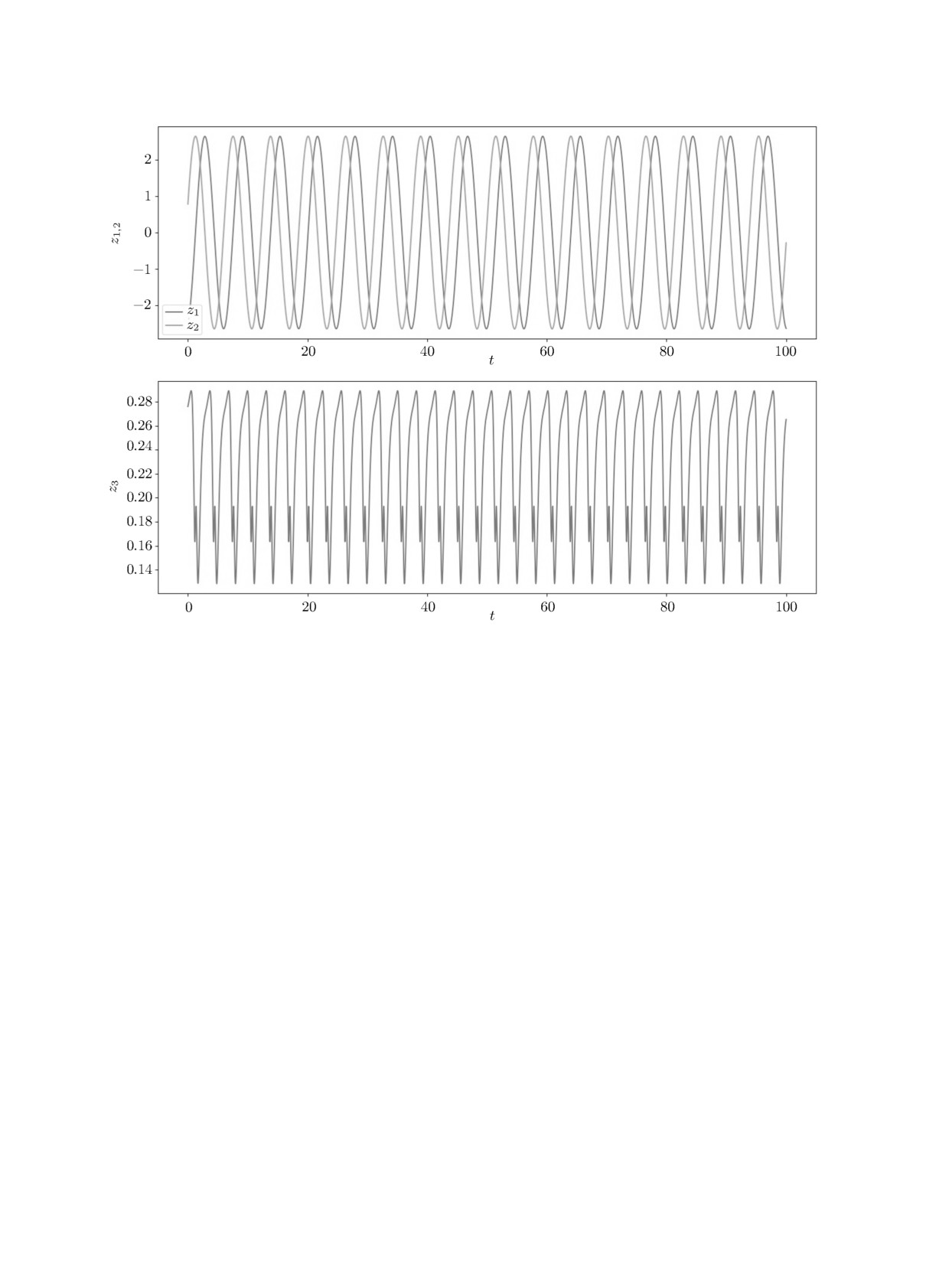
функции I(p) (см. рис. 1, б), поэтому система имеет периодическое решение при малых μ.

График этого решения при μ = 0.01 приведён на рис. 2.

(а)

(б)

Рис. 1. График функции I(p) и её оценок

I(p), pI(p).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1382

ФОМИЧЕВ и др.

Рис. 2. График решения, приведённого на рис. 1, б.

Заключение. В работе получены достаточные условия существования периодических ре-

шений у дифференциальной системы (2). Эти условия формулируются в виде требований к

знаку некоторых определённых интегралов. Данные интегралы вычислены с достаточно высо-

кой точностью, позволяющей однозначно говорить об их знаке и, следовательно, о выполнении

установленных достаточных условий. Численное интегрирование системы (2) подтверждает

наличие у неё периодических решений при указанных значениях параметров.

Работа выполнена при финансовой поддержке Министерства образования и науки Рос-

сийской Федерации в рамках реализации программы Московского центра фундаментальной

и прикладной математики по соглашению № 075-15-2019-1621 и при финансовой поддержке

Российского фонда фундаментальных исследований (проекты 19-57-18006 Болг_а, 20-07-00827

и 20-57-00001 Бел_а).

СПИСОК ЛИТЕРАТУРЫ

1. Todorov T., Nikolov N., Todorov G., Ralev Ya. Modelling and investigation of a hybrid thermal energy

harvester // MATEC Web Conf. 2018. V. 148. P. 12002.

2. Fomichev V.V., Iline A.V., Rogovskii A.I., Todorov G.D., Sofronov Ya. P. Search for periodic regimes

in an energy-harvester model by simulation // Comput. Math. and Model. 2020. V. 31. № 1. P. 293-307.

3. Моисеев Н.Н. Асимптотические методы нелинейной механики. М., 1969.

4. Малкин И.Г. Методы Ляпунова и Пуанкаре в теории нелинейных колебаний. М., 2014.

5. Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений. М., 1958.

6. Grasman W. Periodic solutions of autonomous differential equations in higher dimensional spaces // The

Rocky Mountain J. of Math. 1977. V. 7. № 3. P. 457-466.

7. Lefschetz S. Existence of periodic solutions for certain differential equations // Proc. of the Nat. Acad.

of Sci. of the USA. 1943. V. 29. № 1. P. 29-32.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О СУЩЕСТВОВАНИИ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ

1383

8. Browder F.E. Existence of periodic solutions for nonlinear equations of evolution // Proc. of the Nat.

Acad. of Sci. of the USA. 1965. V. 53. № 5. P. 1100-1103.

9. Красносельский А.М., Рачинский Д.И. О существовании циклов в автономных системах // Докл.

РАН. 2002. T. 384. С. 161-166.

10. Голицын Д.Л., Рябков О.И., Буров Д.А. Алгоритм численного доказательства существования пе-

риодических траекторий в двумерных неавтономных системах обыкновенных дифференциальных

уравнений // Дифференц. уравнения. 2013. Т. 49. № 2. С. 216-222.

11. Пуанкаре А. Избранные труды в трех томах. Т. 1. Новые методы небесной механики. М., 1972.

12. Хартман Ф. Обыкновенные дифференциальные уравнения. М., 1970.

13. Самарский А.А., Гулин А.В. Численные методы. М., 1989.

14. Johansson F. et al. mpmath: a Python library for arbitrary-precision floating-point arithmetic (versi-

on 1.2). 2021-02.

Электротехнический университет,

Поступила в редакцию 27.05.2021 г.

г. Ханчжоу, Китай,

После доработки 27.05.2021 г.

Московский государственный университет

Принята к публикации 08.09.2021 г.

им. М.В. Ломоносова,

Технический университет,

г. София, Болгария

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021