ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 10, с. 1407-1420

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956.226+517.956.227

О ПОВЕДЕНИИ СПЕКТРА

ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

СО СЛАБОЙ СИНГУЛЯРНОСТЬЮ

Для уравнения Лапласа в ограниченной области пространства Rⁿ, n ≥ 3, граница кото-

рой содержит кусок Γ гиперплоскости L, рассматривается краевая задача типа Стеклова

с однородным условием Дирихле на одной части границы и условием Стеклова на другой.

Вне Γ задано условие Дирихле. На Γ граничные условия задаются следующим образом.

Пусть R_δ - (n - 1)-мерная решётка с ребром δ в L, а A_εδ и A2εδ - совокупности шаров

с центрами в вершинах решётки R_δ радиусов εδ и 2εδ соответственно, B_εδ = A2εδ \ A_εδ,

A_εδ = Γ

^⋂A_εδ и

B_εδ = Γ

^⋂B_εδ, где ε - малый параметр и δ = δ(ε) → 0 при ε → 0.

На куске Γ условие Дирихле задано только на множестве

A_εδ. Вне этого множества за-

дано спектральное условие Стеклова, коэффициент в котором вне множества

B_εδ равен

единице, а на множестве

B_εδ он равен (εδ)^-m, где m < 2. Для предельных (усреднённых)

задач и исходной задачи получены отклонения их решений в норме соболевского прост-

ранства W¹², а также оценки отклонения собственных значений.

DOI: 10.31857/S0374064121100125

Введение. Исследования краевых задач в областях с сингулярно возмущённой плотностью

были начаты более века назад (см., например, [1]).

В [2] авторы изучали случай одной сингулярности для обыкновенного дифференциально-

го оператора. В работе [3] рассматривалось колебание тела, имеющего большой набор суще-

ственных сингулярностей, расположенных периодически вдоль границы (более общий случай

см. [4]). Дальнейшее развитие эти задачи получили в работах [5-7]. Работы [8] и [9] посвя-

щены изучению аналогичных задач для стационарой системы линейной теории упругости с

непериодическими быстро меняющимися граничными условиями и большим количеством кон-

центрированных масс около границы. В работах [10] и [11] детально изучено поведение соб-

ственных значений и собственных функций оператора Лапласа в областях с непериодическими

слабыми сингулярностями (стохастический случай см. в [12] и [13]). В работе [14] применён

“unfolding”-метод для изучения задач с сингулярностями. Отметим также работу [15], в ко-

торой обнаружены новые эффекты влияния одной массы на другую. В работах [16] и [17]

построены асимптотики собственных значений задач с концентрированными массами, пери-

одически расположенными вдоль части границы, причём расстояния между массами имеют

тот же порядок, что и диаметр масс. Изучены “лёгкие”, “средние” и “тяжёлые” массы.

Задачи с краевым условием Стеклова исследовались во многих работах. В работе [18] про-

анализирована вся совокупность случаев, возникающих при быстрой смене условия Стеклова

и условия Дирихле. Особенности асимптотики спектра задач Стеклова в областях с сингуляр-

ностями обнаружены в работах [19-24]. В работах [19-21] найдены асимптотики собственных

значений и собственных функций задачи в области, разделённой перфорированным интер-

фейсом (так называемым “ситом”), на котором поставлено условие Стеклова. Работы [22-24]

посвящены построению асимптотик собственных значений и собственных функций в областях

с малой полостью при стремлении малого параметра, характеризующего размер полости, к

нулю. В статье [25] рассматривается плоская задача с условием Стеклова, чередующимся с

условием Дирихле, при этом предполагается, что размеры участков Дирихле и Стеклова име-

ют один и тот же порядок малости. Получены асимптотики собственных значений. Задачи с

быстро меняющимся типом граничных условий изучались также в работах [26-31], в которых

рассматривались в том числе и спектральные задачи.

1407

1408

ЧЕЧКИНА

Более подробно остановимся на недавних работах [32-34]. В работе [32] исследуется за-

дача для системы теории упругости в анизотропной трёхмерной среде с условием Дирихле,

которое чередуется со спектральным условием Винклера-Стеклова. В ней с помощью техники

декомпозиции Флоке-Блоха строится семейство спектральных задач типа Винклера-Стеклова

в полубесконечной призме, которое потом используется в доказательстве теорем о сходимости

собственных значений и собственных функций исходной задачи. Масштабированные преде-

лы собственных значений исходной задачи оказываются нижними гранями соответствующих

семейств собственных значений задач в призме. Кроме низкочастотных колебаний рассмот-

рены также высокочастотные колебания и доказаны теоремы о сходимости соответствующих

семейств собственных значений исходной задачи. В работах [33] и [34] рассматриваются спек-

тральные задачи для системы теории упругости в ограниченной области с чередующимися

условиями Винклера-Робэна (упругое закрепление) и однородного условия Неймана (нулевое

напряжение). В зависимости от значений параметров (диаметра пятен, на которых задано

условие Винклера-Робэна, и расстояния между ближайшими пятнами) и коэффициентов в

условии Винклера-Робэна исходной задачи получены различные предельные краевые условия

(однородные условия Винклера-Робэна, Неймана и Дирихле). При этом применена техника

асимптотического анализа для построения усреднённого спектра и доказательства сходимости

собственных значений и собственных функций.

В настоящей работе рассматривается многомерная задача (размерность больше или равна

трём) с быстрой сменой однородного условия Дирихле и условия Стеклова со слабой син-

гулярностью. Предполагается, что размеры сингулярностей и расстояния между ними имеют

различный порядок, что приводит к нетривиальному смещению спектра в критическом случае.

В работе даются в соответствующих нормах оценки отклонения (оценки скорости сходимости)

решений соответствующих краевых задач от решений предельных краевых задач при стрем-

лении малого параметра к нулю, кроме этого аналогичные оценки получены для собственных

значений соответствующей спектральной задачи.

В п. 1 работы ставится задача и даются определения нужных в дальнейшем понятий, а

также формулируются основные её теоремы. В п. 2 доказываются вспомогательные утвержде-

ния. В п. 3 приводятся те результаты из монографии [35], которые используются в п. 4 при

доказательстве основных утверждений работы.

1. Постановка задачи. Обозначим через x = (x₁, . . . , x_n) декартовы координаты в Rⁿ,

n ≥ 3. Пусть Ω - область в Rⁿ с гладкой границей ∂Ω. Предполагается, что ∂Ω = Γ₁

^⋃Γ₂,

где Γ₂ - область в гиперплоскости x_n = 0, состоящая из трёх частей α_ε, β_ε и γ_ε. Здесь γ_ε =

⋃Nδ

⋃N_δ

γ^iε - дизъюнктное объединение (n - 1)-мерных шаров, а β_ε =

β^iε - дизъюнктное

i=1

объединение (n - 1)-мерных шаровых слоёв, α_ε = Γ₂ \ (β_ε

^⋃γ_ε). Обозначим Γε = αε

^⋃β_ε.

Поясним строение области Γ₂. Через ξ = x/δ

обозначим “растянутые” координаты, ξ =(ξ₁, . . . , ξ_n),

а через γ₀ и β₀ - (n - 1)-мерные шар

{ξ : ∥ξ∥²¹ +

+ ξ2n-1 < ε², ξ_n = 0}

и шаровой слой

{ξ : ε² < ξ²¹ + . . . + ξ2n-1 < 2ε², ξ_n = 0}

соответственно. Пусть γ и β - множества, получен-

ные всевозможными сдвигами множеств γ₀ и β₀ на

целочисленные векторы (k₁, . . . , kn-1, 0), k_i ∈ Z, i =

Рис. 1. Область с микронеоднородной струк-

= 1, n - 1, а γ_ε и

β_ε - гомотетичные сжатия δγ и

турой границы.

δβ множеств γ и β соответственно. Тогда (рис. 1)

γ_ε = γ_ε

^⋂∂Ω, β_ε =

β_ε

^⋂∂Ω, α_ε = Γ₂ \ (βε ⋃ γ_ε).

Подчеркнём, что рассматривается случай, когда параметр δ(ε), определяющий характерное

расстояние между шарами γ^iε, стремится к нулю при ε → 0. Отметим также, что N_δ =

= O(1/δn-1). В дальнейшем буквой C с нижними индексами или без них обозначаются по-

стоянные.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О ПОВЕДЕНИИ СПЕКТРА ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

1409

Рассмотрим следующую спектральную задачу:

⎧

⎪Δukε = 0

в Ω,

⎪

⎨

u^kε = 0

на Γ₁

^⋃γ_ε,

(1)

⎪

u^k

⎩^∂

^ε = λ^kερ^ε(x)u^kε на Γ_ε,

∂x_n

где

{

(εδ)^-m, если x ∈ β_ε,

ρ^ε(x) =

если x ∈ α_ε.

Изучается случай m < 2 (слабая сингулярность).

Собственные значения λ^kε, k ∈ N, занумерованы в порядке неубывания, т.е. λ1ε ≤ λ2ε ≤

... ≤ λ^kε ≤ ..., и повторяются с учётом кратности. При этом

∫

ρ^ε(x,0)u^kε(x,0)u^lε(x,0)dx = δ_kl,

Γ₂

здесь x = (x₁, . . . , xn-1).

Для формулировки теорем нам понадобится следующая вели-

чина:

εn-2

P := lim

ε→0

δ(ε)

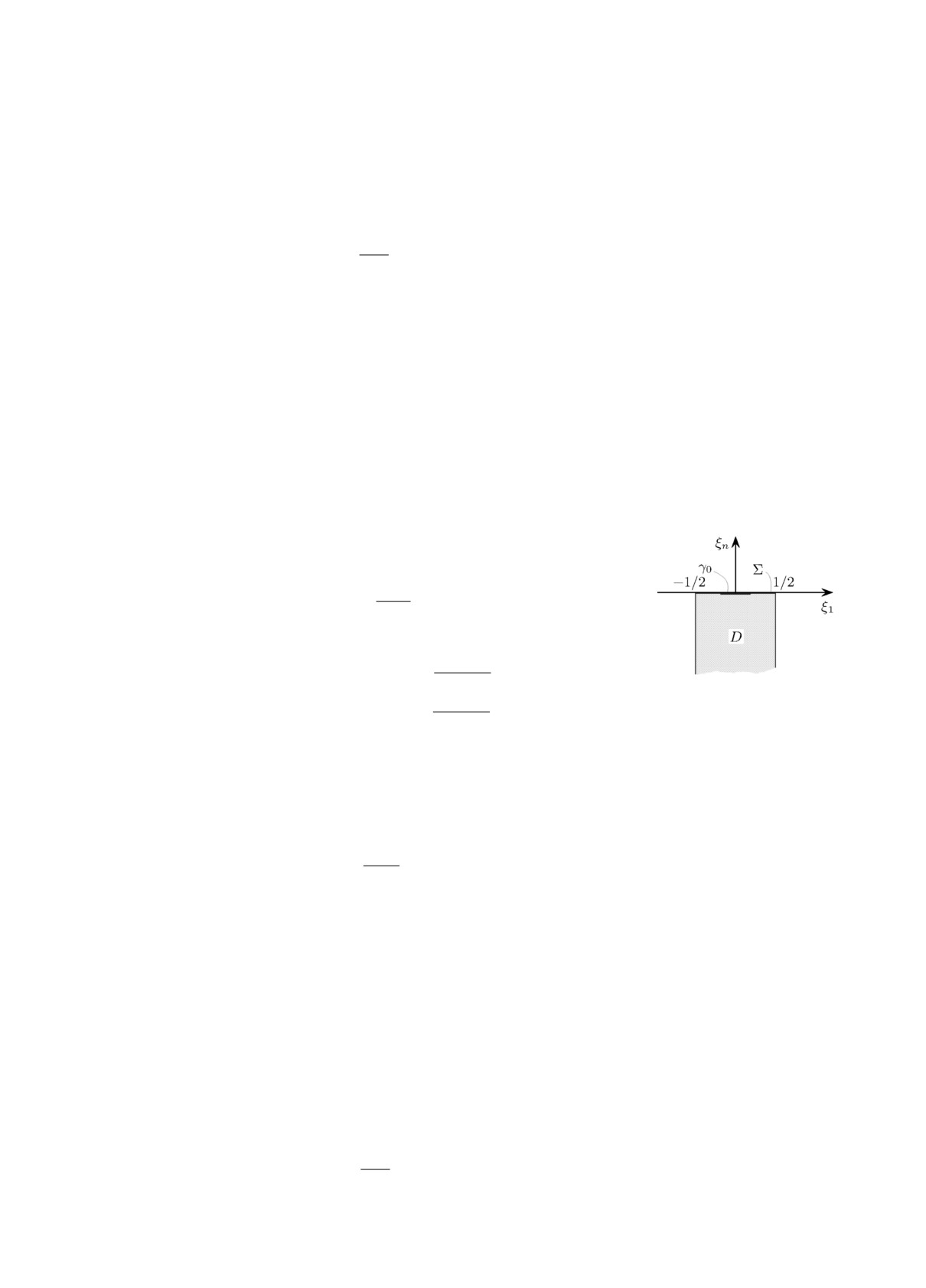
Обозначим (рис. 2)

D = {ξ ∈ Rⁿ : -1/2 < ξ_i < 1/2, i = 1,n - 1, ξ_n < 0},

Рис. 2. Ячейка периодич-

ности.

Σ = {ξ ∈ Rⁿ : -1/2 < ξ_i < 1/2, i = 1,n - 1, ξ_n = 0}.

Пусть функция W^ε, периодическая по переменным ξ₁, . . . , ξn-1, является первой соб-

ственной функцией задачи с условием Стеклова

⎧

⎪ΔWε = 0

в D,

⎨

W^ε = 0

на γ₀,

⎪∂Wε

⎩

= θ_εW^ε на Σ\γ₀.

∂ξ_n

Зададим функцию w^δε формулой

w^δε(x) = 1 + ψ(x_n)(W^ε(x/δ) - 1)

(2)

и продолжим её по периодичности относительно x. Здесь ψ(t) - гладкая срезающая функция

одной переменной, 0 ≤ ψ ≤ 1, причём ψ ≡ 1 в некоторой достаточно малой окрестности об-

ласти Γ₂. Свойства функции w^δε приведены в лемме в начале следующего пункта и подробно

изучены в работе [18].

Сформулируем далее основные результаты, которые будут доказаны в п. 4. Рассмотрим

краевые задачи

⎧

⎪Δuε = 0

в Ω,

⎨

u^ε = 0

на Γ₁

^⋃γ_ε,

(3)

⎪∂uε

⎩

= ρ^ε(x)f(x) на Γ_ε;

∂x_n

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1410

ЧЕЧКИНА

⎧

⎪Δu0 = 0

в Ω,

⎪

⎨u0 = 0

на

∂Ω (P = +∞),

⎤

^⎡∂u

σ_ncγ0

(P < +∞),

(4)

⎪

u⁰ = f(x) на Γ₂,

⎪

⎦

^⎣∂x_n +^P

⎩

u⁰ = 0

на Γ₁

где σ_n - площадь единичной n-мерной сферы, а cγ0 := cap γ₀ - гармоническая ёмкость (n - 1)-

мерного шара γ₀.

Оценки решений этих задач даёт

Теорема 1. Пусть u^ε и u⁰ - обобщённые решения задач (3) и (4) соответственно. Если

P < +∞, то существует такая постоянная C₁(f,γ₀,n), не зависящая от ε и δ, что для

достаточно малых ε выполняется неравенство

∥u⁰w^δε - u^ε∥_H1_(Ω) ≤ C₁(ε(n-2)/2 + |εn-2/δ - P | + ε2-mδ2-m).

Если P = +∞, то существует постоянная C₂(f, γ₀, n) такая, что

∥u^ε∥_L

2(Ω) ≤^C2(δ1/2/ε(n-2)/2 +ε2-mδ2-m)^.

Теперь рассмотрим спектральную задачу

⎧

⎪Δuk0 = 0

в Ω,

⎪

⎪uk0 = 0

на

∂Ω (P = +∞),

⎪

⎡

⎤

⎨

∂uk0

σ_ncγ0

uk0 = λk0uk0

на Γ₂,

⎢

⎥

(5)

∂x_n

⎪⎢

⎥

⎪⎢

uk0 = 0

на Γ₁,

⎥

⎪⎢∫

⎥ (P < +∞).

⎪⎢

⎥

⎪⎣

ul0 dx = δ_kl,

0<λ¹⁰ ≤λ²⁰ ≤...,⎦

⎩ u

Γ₂

Связь между собственными значениями и собственными функциями задач (5) и (1) уста-

навливает

Теорема 2. Пусть λk0 и λ^kε - k-е собственные значения задач (5) и (1) соответственно.

Тогда

|λk0 - λ^kε| ≤ C₃(ε(n-2)/2 + |εn-2/δ - P | + ε2-mδ2-m), если P < +∞,

λ^kε → +∞ при ε → 0, если P = +∞,

где постоянная C₃ не зависит от ε.

Если кратность собственного значения λl0 задачи (5) равна r, т.е.

λl0 = λl+10 = ... = λl+r-10,

то для любой собственной функции ul0 задачи (5), соответствующей собственному значе-

нию λl0,

∥ul0∥L2(Ω) = 1, существует линейная комбинация u^ε собственных функций задачи

(1), соответствующих собственным значениям λ^lε, ..., λl+r-1ε, такая, что

∥u^ε - ul0∥_L

2(Ω) ≤^C4(ε(n-2)/2 +|εn-2/δ-P|+ε2-mδ2-m),еслиP<+∞,

∥u^ε∥L2(Ω) ≤ C5(δ1/2/ε(n-2)/2 + ε2-mδ2-m), если P = +∞,

где постоянные C₄, C₅ не зависят от ε и ul0.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О ПОВЕДЕНИИ СПЕКТРА ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

1411

2. Вспомогательные утверждения. Будем изучать предельное поведение решений спек-

тральной задачи (1) при ε, стремящемся к нулю. Существование и единственность решения

u^kε задачи (1) в пространстве H¹(Ω,γ_ε) могут быть доказаны на основании леммы Лакса-

Мильграма. Пространство H¹(Ω, γ_ε) определяем как пополнение по норме

(∫

)1/2

∥u∥_H1_(Ω) ≡

(u² + |∇u|²) dx

множества функций из пространства C^∞(Ω), обращающихся в нуль в окрестности множества

Γ₁

^⋃γ_ε. Пространство H¹(D,γ₀) - замыкание по норме

(∫

∫

)1/2

∥u∥₁ ≡

|∇_ξu|² dξ + u² dξ

множества 1-периодических поξ ≡ (ξ₁, . . . , ξn-1) функций из C^∞(D), обращающихся в нуль

в окрестности шара γ₀ и обладающих конечным интегралом Дирихле по области D.

Пусть

(∫

∕∫

)

θ_ε =

inf

|∇_ξv|² dξ

v² dξ .

(6)

v∈H¹(D,γ₀)\{0}

В работе [27] исследовался вопрос поведения собственного значения θ_ε и установлена сле-

дующая его асимптотика (см. [27, формула (25)]).

Лемма 1. Пусть σ_n - площадь единичной n-мерной сферы, а cγ0 - гармоническая ём-

кость шара γ₀. Тогда

σ_n

θ_ε = εn-2

cγ0 + o(εn-2) при ε → 0.

В работе [18] доказана

Лемма 2. Существует гармоническая в D функция W^ε(ξ) ∈ H¹(D, γ₀), на которой

достигается нижняя грань в (6), т.е.

∫

|∇_ξW^ε|² dξ = θ_ε,

∥W^ε∥_L

2(Σ) =1,

причём граничное условие

∂W^ε

= θ_εW^ε на Σ\γ₀

(7)

∂ξ_n

выполняется в следующем смысле:

∫

∂W^ε

vdξ→θ_ε

W^εv dξ при ρ → 0 для любой v ∈ H¹(D,γ₀).

∂ξ_n

Здесь

Σ_ρ := {ξ ∈ Rⁿ : 0 < ξ_i < 1, i = 1,n - 1, ξ_n = -ρ}.

В работе [18] подробно обсуждается вопрос о существовании таких функций и их свойствах.

Рассмотрим функцию w^δε(x), определённую равенством (2). Заметим, что в силу условия

(7) выполняется соотношение

∂w^δε

θ_ε

w^δε на Γ_ε.

∂x_n

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

8^∗

1412

ЧЕЧКИНА

Аналогично тому, как это сделано в [18], несложно получить следующую оценку:

∫∫



Δw^δεv dx

C₆θ1/2ε∥v∥_H1(Ω,γ

(8)



≤

ε)

для любой функции v ∈ H¹(Ω, γ_ε).

Через C^ε обозначим цилиндр с основанием γ^ε

^⋃β^jε и высотой εδ, т.е. C^jε = {x ∈ Ω : (x,0) ∈

∈γ^ε

^⋃β^jε, -εδ < xn < 0}.

Лемма 3. Для функций v ∈ H¹(Ω, γ_ε) справедливо неравенство

∫

v² dx ≤ C(εδ)²

|∇v|² dx, j = 1, N_δ.

(9)

C^ε

Доказательство. Доказательство этого неравенства типа Фридрихса проводится в два

этапа. На первом этапе получаем классическое неравенство в растянутой области в коорди-

натах η = x/(εδ), поскольку функции имеют нулевой след на фиксированной части границы

растянутой области. Далее, делая обратную замену координат, замечаем, что в градиенте по-

является множитель εδ и, таким образом, получаем неравенство (9) (см. похожий приём в

[35], а также неравенство Фридрихса в [36] и [37]).

Лемма 4. Для функций v ∈ H¹(Ω, γ_ε) справедливо неравенство

∫

v² dx ≤ C₈(εδ)2

|∇v|² dx, j = 1, N_δ.

(10)

β^ε

C^ε

Доказательство. В растянутых координатах η = x/(εδ) имеем неравенство для следов

∥v∥L2(∂C) ≤ C∥v∥H1(C),

где C = {η ∈ Rⁿ : εδη ∈ C^ε}. Далее, используя лемму 3 и проводя обратную замену перемен-

ных, приходим к доказываемому неравенству.

Лемма 5. Для последовательности функций {v_ε} ∈ H¹(Ω, γ_ε) выполняется равенство

∫

lim(εδ)-2

|v_ε|² dx = 0,

ε→0

β^iε

если ∥v_ε∥_H1_(Ω) ≤ C₉, где постоянная C₉ не зависит от ε.

Доказательство. Пусть v ∈ H¹(Ω, γ_ε). Для любого числа κ > 0 существует функция

v_κ ∈ C^∞(Ω,γ_ε) такая, что

√

C₇∥v - v_κ∥_H1_(Ω) < κ,

где C₇ - постоянная из неравенства (9). Тогда, применяя оценки (9) и (10) к функции v -v_κ, а

также учитывая неравенство для следов и ограниченность градиента функции v_κ, получаем

(∫

)1/2

(∫

)1/2

(∫

)1/2

(εδ)-2|v|² dx

≤ (εδ)-2|v - v_κ|² dx

+ (εδ)-2|v_κ|² dx

≤

β^iε

(∫

)1/2

√

≤

C₇

|∇(v - v_κ)|² dx

+ C_κ(εδ)-1+n/2 ≤ κ + C_κ(εδ)-1+n/2.

Так как n ≥ 3, по определению предела завершаем доказательство леммы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О ПОВЕДЕНИИ СПЕКТРА ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

1413

Лемма 6. Для решения u^ε ∈ H¹(Ω, γ_ε) задачи (3) справедливо неравенство

∫

(∫

∫

)

|∇u^ε|²

dx ≤ C₁₀

f² dx + (εδ)2-m ρ^εf² dx

αε

βε

Доказательство. Вследствие интегрального тождества, учитывая леммы 3, 4 и неравен-

ство типа Фридрихса (см., например, [28, 30, 36]), получаем

∫

∥∇u^ε∥2L

|∇u^ε|² dx = ρ^εfu^ε dx = fu^ε dx + (εδ)^-m fu^ε dx ≤

(Ω)

Γε

αε

βε

(∫

)1/2(∫

)1/2

(∫

)1/2(∫

)1/2

≤ f²dx

(u^ε)² dx

+ (εδ)^-m

f² dx

(u^ε)² dx

≤

αε

βε

(∫

)1/2

(∫

)1/2

≤C f²dx

∥∇u^ε∥_L

+ C(εδ)-m+1

f² dx

∥∇u^ε∥_L

2(Ω)

αε

βε

для разных постоянных C. Отсюда непосредственно вытекает доказываемое неравенство.

Лемма доказана.

Пусть f ∈ C(Γ₂). Если u⁰ ∈ H¹(Ω) - обобщённое решение задачи (4), то, согласно теории

регулярности решений эллиптических уравнений [38], u⁰ ∈ W2r(Ω) для любого r > 1. Тогда

в силу теорем вложения Соболева u⁰, ∇_xu⁰ ∈ C(Ω); из первого уравнения задачи (4) следует,

что u⁰ ∈ C(Ω), причём

∥u⁰∥C(Ω) + ∥∇_xu⁰∥C(Ω) + ∥Δu⁰∥C(Ω) ≤ C₁₁∥f∥C(Γ

(11)

2).

Слабая сходимость u^ε к u⁰ в H¹(Ω) при ε → 0 доказана в [18].

Обозначим

εn-2σ_ncγ0

σ_ncγ0

p := lim

т.е. p =

ε→0

2δ(ε)

Имеет место

Лемма 7. Пусть f ∈ C(Γ₂), а u^ε и u⁰ - обобщённые решения задач (3) и (4) соот-

ветственно. Если p < +∞, то существует постоянная C₁₂, не зависящая от ε, δ и f,

такая, что для достаточно малых ε выполняется неравенство

∥u⁰w^δε - u^ε∥_H1_(Ω) ≤ C₁₂∥f∥C(Γ

2)((θε)1/2 +^|θε/δ-p|+(εδ)2-m)^.

Доказательство. Рассмотрим область

Ω_μ = {x ∈ Ω : x_n ≤ -μ},

обозначим Γ2μ - часть границы ∂Ω_μ \ ∂Ω. С учётом гладкости функций u⁰, w^δε и u^ε (см.,

например, [38]), следующее интегральное выражение

∫

(∇_x(u⁰w^δε - u^ε), ∇_xv) dx

Ωμ

корректно для любой функции v ∈ H¹(Ω, γ_ε). Вычисляя этот интеграл по частям и учитывая,

что Δu⁰ = 0, получаем

∫

∂u^ε

(∇_x(u⁰w^δε - u^ε), ∇_xv) dx =

(∇_x(u⁰w^δε), ∇_xv) dx -

v dx =

∂x_n

Ωμ

Γ2μ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1414

ЧЕЧКИНА

∫

∂(u⁰w^δ

∂u^ε

= - Δ(u⁰w^δε)v dx +

⁾vdx-

v dx =

∂x_n

Ωμ

Γ2μ

∫

∂u⁰

∂w^δ

∂u^ε

(2(∇_xu⁰, ∇_x(w^δε - 1)) + u⁰Δw^δε)v dx +

w^δεv dx +

u⁰

^εvdx-

v dx =

∂x_n

Ωμ

Γ2μ

∫

∂u⁰

∂w^δε

(w^δε - 1)(∇_xv, ∇_xu⁰) dx +

w^δεv dx +

u⁰

v dx -

∂x_n

Ωμ

Γ2μ

∫

∂u^ε

∂u⁰

v dx - 2

(w^δε - 1)

v dx -

u⁰Δw^δεv dx.

(12)

∂x_n

Γ2μ

Ωμ

Нетрудно видеть, что при μ → 0 имеют место сходимости

∫

(w^δε - 1)(∇_xv, ∇_xu⁰) dx → (w^δε - 1)(∇_xv, ∇_xu⁰) dx,

Ωμ

∫

∂u⁰

w^δεv dx →

w^δεv dx,

∂x

∂x_n

Γ2μ

Γ₂

∫

∂u^ε

v dx →

v dx =

ρ_εfv dx,

∂x

∂x_n

Γ2μ

Γ₂

Γε

∫

u⁰Δw^δεv dx → u⁰Δw^δεv dx,

Ωμ

∫

∂u⁰

(w^δε - 1)

v dx →

(w^δε - 1)

v dx.

∂x

∂x_n

Γ2μ

Γ₂

В силу свойств функции w^δε, заданной равенством (2), заключаем, что

∫

∂w

θ_ε

u⁰

v dx →

u⁰w^δεv dx при μ → 0.

∂x_n

Γ2μ

Γ₂

Перейдём в (12) к пределу при μ → 0. Вследствие граничного условия задачи (4), т.е.

условия ∂u⁰/∂x_n = -pu⁰ + f на Γ₂, получаем

∫

(

)∫

θ_ε

(∇_x(u⁰w^δε - u^ε), ∇_xv) dx = 2 (w^δε - 1)(∇_xv, ∇_xu⁰) dx + d

-p u⁰w^δεvdx-

Γ₂

∫

− (w^δε - 1)fv dx -

((εδ)^-m - 1)fv dx + 2 (w^δε - 1)pu⁰v dx - u⁰Δw^δεv dx.

(13)

Γ₂

βε

Γ₂

Оценим интегралы, стоящие в правой части равенства (13). Для первого интеграла имеем

 ∫



(∫

)1/2



(w^δε - 1)(∇_xv, ∇_xu⁰) dx

∥w^δ

(∇_xu⁰, ∇_xv)² dx

≤



⁼

- 1∥L2(Ω)

≤ C(θ_εδ)1/2∥f∥C(Γ

2)∥v∥H¹(Ω,γε)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О ПОВЕДЕНИИ СПЕКТРА ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

1415

в силу свойств функций u⁰ и w^δε (см. (11) и лемму 2). Используя неравенства (11) и (8), для

последнего интеграла в (13) получаем оценку

∫



u⁰Δw^δεv dx



≤

C₆θ1/2ε∥u⁰v∥_H1_(Ω) ≤ C′6θ1/2ε∥u⁰∥C1(Ω)^∥v∥H¹(Ω)≤C6′θε/2∥f∥C(Γ2)^∥v∥H¹(Ω)^.

Далее, воспользовавшись неравенством (11) и свойствами функции w^δε (см. [18]), второй ин-

теграл в (13) оценим следующим образом:



∫



θ_ε/δ - p) u⁰(w^δε - 1)v dx + (θ_ε/δ - p) u⁰v dx

⁽

≤

Γ₂

≤ |θ_ε/δ - p|C′11θ1/2ε∥v∥_H1(Ω,γ

ε)∥f∥C(Γ2)+C1′1^|θε^{/δ-p|∥v∥}H¹(Ω,γε)^∥f∥C(Γ2)^≤

≤ C′′′11|θ_ε/δ - p|∥v∥_H1(Ω,γ

ε)∥f∥C(Γ2)^.

Оставшиеся интегралы допускают следующие оценки:

 ∫



(w^δε - 1)pu⁰v ds

Cθ1/2ε∥v∥_H1(Ω,γ



≤

ε)∥f∥C(Γ2)^,

∂Ω

 ∫



(w^δε - 1)fvds

Cθ1/2ε∥v∥_H1(Ω,γ



≤

ε)∥f∥C(Γ2)^,

∂Ω

 ∫



((εδ)^-m - 1)fv dx

C(εδ)m-2∥v∥_H1(Ω,γ



≤

ε)∥f∥C(Γ2)

βε

для разных постоянных C ввиду неравенства (11), леммы 4 и свойств функции w^δε (см. [18]).

Окончательно имеем

 ∫



(

)



(∇_x(u⁰w^δε - u^ε), ∇_xv) dx

/δ - p| + (εδ)m-2

(14)



≤

C∥f∥C(Γ2) θε/2 + |θε

∥v∥_H1(Ω,γε)

для произвольной функции v ∈ H¹(Ω, γ_ε).

Положим v = u⁰w^δε -u^ε. На основании оценки (14), применяя неравенство типа Фридрихса,

получаем нужную оценку. Лемма доказана.

Лемма 8. Пусть f ∈ C(Γ₂). Если p = +∞, то существует постоянная C₁₃ такая,

что

∥u^ε∥_L

2(Ω) ≤^C13^∥f∥C(Γ2)((δ/θε)1/2 +(εδ)2-m)^.

Доказательство проводится аналогично доказательству леммы 7 с использованием ре-

зультатов работы [18].

3. Предварительные замечания. Поведение собственных значений и собственных функ-

ций задачи (1) будем изучать основываясь на общей схеме, предложенной в монографии [35].

Пусть H_ε, H₀ - сепарабельные гильбертовы пространства со скалярными произведениями

(u, v)_ε, (u, v)₀ и нормами ∥u∥ε,

∥u∥₀ соответственно, ε - малый положительный параметр.

Пусть также A_ε ∈ L(H_ε), A₀ ∈ L(H₀) - линейные непрерывные операторы, причём Im A₀ ⊂

⊂ V ⊂ H₀; где V - линейное подпространство в H₀.

Будем предполагать, что выполнены следующие условия С1-С4.

С1. Существуют линейные непрерывные операторы R_ε : H₀ → H_ε такие, что для любого

элемента f ∈ V имеет место сходимость (R_εf, R_εf)_ε → κ(f, f)₀ при ε → 0, где κ = const > 0

не зависит от f.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1416

ЧЕЧКИНА

C2. Операторы A_ε и A₀ являются положительными, компактными и самосопряжёнными

в пространствах H_ε и H₀ соответственно, причём

sup

∥A_ε∥L(Hε) < ∞.

C3. Для любого элемента f ∈ V имеет место сходимость ∥A_εR_εf - R_εA₀f∥_ε → 0 при

ε → 0.

C4. Семейство операторов A_ε равномерно компактно в следующем смысле. Из любой по-

следовательности {f^ε}, f^ε ∈ H_ε, такой, что sup ∥f^ε∥_ε < ∞, можно выбрать подпоследова-

тельность {fε′ } и найти функцию w ∈ V такие, что

∥A_ε′ fε′ - R_ε′ w∥_ε′ → 0 при ε^′ → 0.

Для операторов A_ε и A₀ рассмотрим следующие спектральные задачи:

A_εu^kε = μ^kεu^kε, k ∈ N, (u^iε,u^jε) = δ_ij,

(15)

A₀uk0 = μk0uk0, k ∈ N, (ui0,uj0) = δ_ij,

(16)

где δ_ij - символ Кронекера, а собственные значения μ^kε и μk0 занумерованы в порядке невоз-

растания, причём каждое собственное значение повторяется столько раз, какова его кратность.

Теорема (Олейник-Иосифьян-Шамаев). Пусть выполнены условия C1-C4. Тогда спра-

ведлива оценка

|μ^kε - μk0| ≤ M_ε sup ∥A_εR_εf - R_εA₀f∥_ε, k ∈ N,

в которой μ^kε и μk0 - k-е собственные значения задач (15) и (16) соответственно, верхняя

грань берётся по всем функциям f ∈ N(μk0, A₀) = {v ∈ H₀ : A₀v = μk0v} таким, что ∥f∥₀ = 1,

а постоянные M_ε удовлетворяют условиям

sup{M_ε : 0 < ε ≤ 1} < +∞

и M_ε → const > 0 при ε → 0.

Пусть k ∈ Z₊, l ∈ N и кратность собственного значения μk+10 задачи (16) равна l, т.е.

μk+10 = ... = μk+l0.

Тогда для любой функции u₀ ∈ N(μk+10, A₀) существует линейная комбинация u_ε собствен-

ных функций uk+1ε, ..., uk+lε задачи (15) такая, что

∥u_ε - R_εu₀∥_ε ≤ M_k∥A_εR_εu₀ - R_εA₀u₀∥_ε,

где постоянная M_k не зависит от ε.

Для того чтобы воспользоваться схемой исследования, дающей возможность применять

сформулированную теорему, нужно подходящим образом ввести пространства H₀, H_ε, V,

операторы A₀, A_ε, R_ε и проверить для них выполнимость условий С1-С4.

Отождествим пространства H_ε и H₀ с пространством L₂(Γ₂), в котором заданы скаляр-

ные произведения

∫

(h^ε, g^ε)Hε ≡ ρ^εh^εg^ε dx и (h⁰, g⁰)H0 ≡ h⁰g⁰ dx

Γ₂

соответственно. В качестве V возьмём пространство L₂(Γ₂). Положим R_εf = f для любого

f ∈H₀.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О ПОВЕДЕНИИ СПЕКТРА ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

1417

Если f ∈ V, то при ε → 0 имеем

∫

(R_εf, R_εf)Hε

= f2 dx + (εδ)^-m f2 dx → f2 dx = (f,f)H0

αε

βε

Γ₂

в силу леммы 5. Действительно, имеем

∫

lim(εδ)^-m

f² dx = lim(εδ)2-m

f²(εδ)-2 dx,

ε→0

βε

но

∫

lim(εδ)-2

f² dx = 0,

ε→0

βε

а m < 2. Это означает, что справедливо условие С1 при κ = 1.

Обозначим через A_ε : H_ε → H_ε оператор, ставящий в соответствие функции f ∈ H_ε

след u^ε|Γ2 решения u^ε ∈ H¹(Ω, γ_ε) задачи (3). Через A₀ : H₀ → H₀ обозначим оператор,

переводящий f ∈ H₀ в след u⁰|Γ2 решения u⁰ ∈ H¹(Ω, Γ₁) задачи (4).

Нетрудно проверить, что операторы A_ε и A₀ являются положительными, компактны-

ми и самосопряжёнными в пространствах H_ε и H₀ соответственно (см. [18]). Равномерная

ограниченность семейства операторов в соответствующей операторной норме

sup

∥A_ε∥L(Hε) < M

вытекает из леммы 6, поскольку при m < 2 в силу лемм 4 и 6 и неравенства типа Фридрихса

получаем

∫

(∫

∫

)

∫

∥A_εf∥2H

= ρ^ε(u^ε)2 dx ≤ (u^ε)2 dx + (εδ)-2 (u^ε)2 dx

≤C

|∇u^ε|² dx ≤

Γ₂

αε

βε

(

∫

)

(∫

∫

)

≤ C (εδ)2-m ρ^εf2 dx + ρ^εf2 dx + f2 dx

≤C ρ^εf²dx+ ρ^εf²dx

= C₆∥f∥2H

βε

αε

βε

αε

βε

Таким образом, условие С2 имеет место.

Докажем выполнимость условия С3. Пусть f ∈ H₀. Тогда

A_εR_εf = u^ε|Γ2 , R_εA₀f = u⁰|Γ2 ,

где u^ε - решение задачи (3), а u⁰ - решение задачи (4). Пользуясь леммой 3 и неравенством

Фридрихса, устанавливаем, что

∫

∥A_εR_εf - R_εA₀f∥2H

= ρ^ε|u^ε - u⁰|² dx ≤

|u^ε - u⁰|² dx + (εδ)^-m|u^ε - u⁰|² dx ≤

Γε

αε

βε

∫

≤C

|∇(u^ε - u⁰)|² dx + C(εδ)2-m

|∇(u^ε - u⁰)|² dx ≤ C

|∇(u^ε - u⁰)|² dx ≤

Cε

∫

(

)

≤

|∇(u^ε - u⁰w^δε)|² dx +

|∇u⁰|²(1 - w^δε)² + (u⁰)²|∇(1 - w^δε)|2

dx → 0

при ε → 0. Здесь мы воспользовались свойствами функций u⁰ и w^δε, а также леммами 5, 7

и 8. Таким образом, условие C3 проверено.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1418

ЧЕЧКИНА

Докажем справедливость условия С4. Если sup∥f∥Hε < ∞, то из леммы 6 и неравенства

Фридрихса вытекает, что

sup

∥u^ε∥_H1(Ω,γ

ε) <∞,

где u^ε - решение задачи (3). Следовательно, по теореме Реллиха найдутся U^∗ ∈ V и подпо-

следовательность ε^′ → 0, для которых

uε′ → U^∗ слабо в H¹(Ω) и сильно в L₂(Ω).

При этом из единственности решения предельной задачи с помощью интегрального тождества

несложно показать (аналогично [31]), что

uε′ → U^∗ сильно в H¹(Ω).

(17)

Поэтому, пользуясь леммой 3, получаем оценки

∫

∥A_εf - R_εU^∗∥2H

= ρ^ε(x)|u^ε - U^∗|2 dx ≤

|u^ε - U^∗|² dx + (εδ)^-m

|u^ε - U^∗|² dx ≤

αε

βε

(∫

∫

)

≤C

|∇(u^ε - U^∗)|² dx + (εδ)2-m

|∇(u^ε - U^∗)|² dx

где u^ε = A_εf и постоянная C не зависит от ε. Отсюда следует соотношение из условия С4,

так как m < 2 и имеет место сходимость (17).

Таким образом, выполнены условия С1-С4 и мы можем применить теорему Олейник-

Иосифьяна-Шамаева о сходимости спектров последовательности операторов, заданных в раз-

ных гильбертовых пространствах.

Задача на собственные значения для оператора A₀ имеет вид (16), где μk0 = 1/λk0, а λk0 -

собственные значения задачи (5).

Итак, имеет место

Теорема 3. Пусть λk0 и λ^kε - k-е собственные значения задач (5) и (1) соответственно.

Тогда

|λk0 - λ^kε| ≤ C₁₄((θ_ε)1/2 + (εδ)2-m + |θ_ε/δ - p|), если p < +∞,

λ^kε → +∞ при ε → 0, если p = +∞,

где постоянная C₁₄ не зависит от ε.

Если кратность собственного значения λl0 задачи (5) равна r, т.е.

λl0 = λl+10 =

=λl+r-10,

то для любой собственной функции ul0 задачи (5), соответствующей собственному значе-

нию λl0,

∥ul0∥L2(Ω) = 1, существует линейная комбинация u^ε собственных функций задачи

(1), соответствующих собственным значениям λl+1ε, ..., λl+r-1ε, такая, что

∥u^ε - ul0∥_L

2(Ω) ≤^C15((θε)1/2 +(εδ)2-m +^|θε/δ-p|),еслиp<+∞,

∥u^ε∥L2(Ω) ≤ C16((δ/θε)1/2 + (εδ)2-m), если p = +∞,

где постоянные C₁₅, C₁₆ не зависят от ε и ul0.

4. Доказательство основных утверждений. Воспользовавшись леммами 1, 7, 8 и тео-

ремой 3 с учётом асимптотики (6), получаем утверждения теорем 1 и 2.

Автор выражает благодарность рецензенту, замечания которого позволили существенно

улучшить представление результатов работы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

О ПОВЕДЕНИИ СПЕКТРА ВОЗМУЩЁННОЙ КРАЕВОЙ ЗАДАЧИ СТЕКЛОВА

1419

СПИСОК ЛИТЕРАТУРЫ

1. Крылов А.Н. О некоторых дифференциальных уравнениях математической физики, имеющих при-

ложения в технических вопросах // Изв. Николаевской морской академии. 1913. Вып. 2. С. 325-348.

2. Головатый Ю.Д., Назаров С.А., Олейник О.А., Соболева Т.С. О собственных колебаниях струны

с присоединенной массой // Сиб. мат. журн. 1988. Т. 29. № 5. С. 71-91.

3. Lobo M., Pérez E. Asymptotic behavior of the vibrations of a body having many concentrated masses

near the boundary // Comp. Rend. Acad. Sci. Paris. Série II. 1992. V. 314. P. 13-18.

4. Sanchez-Palenсia

É., Tchatat H. Vibration de systemes elastiques avec masses concentrees // Rend. del

Semi. mat. della Univer. e politecnico di Torino. 1984. V. 42. № 3. P. 43-63.

5. Gómez D., Lobo M., Pérez E. On the eigenfunctions associated with the high frequencies in systems with

a concentrated mass // J. Math. Pures Appl. 1999. V. 78. P. 841-865.

6. Chechkin G.A. On vibration of partially fastened membrane with many “light” concentrated masses on

the boundary // Comp. Rend. Mécanique. 2004. V. 332. № 12. P. 949-954.

7. Чечкин Г.А. Расщепление кратного собственного значения в задаче о концентрированных массах

// Успехи мат. наук. 2004. Т. 59. Вып. 4. С. 205-206.

8. Доронина Е.И., Чечкин Г.А. О собственных колебаниях тела с большим количеством непериоди-

чески расположенных концентрированных масс // Тр. Мат. ин-та им. В.А. Стеклова РАН. 2002.

Т. 236. С. 158-166.

9. Rybalko V. Vibration of elastic systems with a large number of tiny heavy inclusions // Asymptot. Anal.

2002. V. 32. № 1. P. 27-62.

10. Перес М.Е., Чечкин Г.А., Яблокова (Доронина) Е.И. О собственных колебаниях тела с “лёгкими”

концентрированными массами на поверхности // Успехи мат. наук. 2002. Т. 57. Вып. 6. С. 195-196.

11. Chechkin G.A., Pérez M.E., Yablokova E.I. Non-periodic boundary homogenization and “light” concen-

trated masses // Indiana Univ. Math. J. 2005. V. 54. № 2. P. 321-348.

12. Chechkin G.A., Chechkina T.P. Asymptotic behavior of spectrum of an elliptic problem in a domain

with aperiodically distributed concentrated masses // Comp. Rend. Mécanique. 2017. V. 345. № 10.

P. 671-677.

13. Chechkin G.A., Chechkina T.P. Random homogenization in a domain with light concentrated masses

// Mathematics. 2020. V. 8. № 5. Art. 788.

14. Chechkin G.A., Cioranescu D., Damlamian A., Piatnitski A.L. On boundary value problem with singular

inhomogeneity concentrated on the boundary // J. de Math. Pures et Appl. 2012. V. 98. № 2. P. 115-138.

15. Cainzos J., Pérez M.E., Vilasanchez M. Asymptotics for the eigenelements of the Neumann spectral

problem with concentrated masses // Indiana Univ. Math. J. 2007. V. 56. № 4. P. 1939-1987.

16. Nazarov S.A., Pérez M.E. New asymptotic effects for the spectrum of problems on concentrated masses

near the boundary // Comp. Rend. Mécanique. 2009. V. 337. № 8. P. 585-590.

17. Nazarov S.A., Pérez M.E. On multi-scale asymptotic structure of eigenfunctions in a boundary value

problem with concentrated masses near the boundary // Rev. Mat. Commpl. 2018. V. 31. № 1. P. 1-62.

18. Чечкина А.Г. Усреднение спектральных задач с сингулярным возмущением условия Стеклова

// Изв. РАН. Сер. Мат. 2017. Т. 81. № 1. С. 203-240.

19. Amirat Y., Bodart O., Chechkin G.A., Piatnitski A.L. Asymptotics of a spectral-sieve problem // J. of

Math. Anal. and Appl. 2016. V. 435. № 2. P. 1652-1671.

20. Гадыльшин Р.Р., Пятницкий А.Л., Чечкин Г.А. О спектральной задаче с условием Стеклова на

тонком перфорированном интерфейсе // Докл. РАН. 2016. Т. 466. № 4. С. 389-394.

21. Гадыльшин Р.Р., Пятницкий А.Л., Чечкин Г.А. Об асимптотическом поведении собственных пар

краевой задачи в плоской области типа сита Стеклова // Изв. РАН. 2018. Т. 82. № 6. С. 37-64.

22. Gryshchuk S., Lanza de Cristoforis M. Simple eigenvalues for the Steklov problem in a domain with a

small hole. A functional analytic approach // Math. Meth. Appl. Sci. 2014. V. 37. № 12. P. 1755-1771.

23. Назаров С.А. Моделирование сингулярно возмущенной спектральной задачи при помощи самосо-

пряженных расширений операторов предельных задач // Функц. анализ и его прил. 2015. Т. 49.

№ 1. С. 31-48.

24. Chiado Piat V., Nazarov S.A. Steklov spectral problems in a set with a thin toroidal hole // Partial

Differ. Equat. in Appl. Math. 2020. V. 1. P. 100007.

25. Pérez M.E. On periodic Steklov type eigenvalue problems on half-band and the spectral homogenization

problem // Discrete Contin. Dyn. Systems. Ser. B. 2007. V. 7. № 4. P. 859-883.

26. Chechkin G.A. On vibration of partially fastened membrane with many “light” concentrated masses on

the boundary // Comp. Rend. Mécanique. 2004. V. 332. № 12. P. 949-954.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021

1420

ЧЕЧКИНА

27. Гадыльшин Р.Р., Чечкин Г.А. Краевая задача для Лапласиана с быстро меняющимся типом гра-

ничных условий в многомерной области // Сиб. мат. журн. 1999. Т. 40. № 2. С. 271-287.

28. Олейник О.А., Чечкин Г.А. О краевых задачах для эллиптических уравнений с быстро меняющимся

типом граничных условий // Успехи мат. наук. 1993. Т. 48. Вып. 6. С. 163-164.

29. Беляв А.Ю., Чечкин Г.А. Усреднение операторов с мелкомасштабной структурой граничных усло-

вий // Мат. заметки. 1999. Т. 65. Вып. 4. С. 496-510.

30. Oleinik O.A., Chechkin G.A. Solutions and eigenvalues of the boundary value problems with rapidly

alternating boundary conditions for the system of elasticity // Rend. Lincei: Math. Appl. Ser. 9. 1996.

V. 7. № 1. P. 5-15.

31. Gadyl’shin R.R., Chechkin G.A. On boundary-value problems for the laplacian in bounded domains with

micro inhomogeneous structure of the boundaries // Acta Math. Sinica. 2007. V. 23. № 2. P. 237-248.

32. Gómes D., Nazarov S.A., Pérez M.E. Homogenization of Winkler-Steklov spectral conditions in three-

dimensional linear elasticity // Zeitschr. für Angew. Math. und Physik. 2018. Bd. 69. № 2. S. 35.

33. Gómes D., Nazarov S.A., Pérez-Martinez M.E. Spectral homogenization problems in linear elasticity

with large reaction terms concentrated in small regions of the boundary // Computational and Analytic

Methods in Science and Engineering. Cham, 2020. P. 121-143.

34. Gómes D., Nazarov S.A., Pérez-Martinez M.E. Asymptotics for spectral problems with rapidly

alternating boundary conditions on a strainer Winkler foundation // J. of Elasticity. 2020. V. 142.

P. 89-120.

35. Oлейник О.А., Иосифьян Г.А., Шамаев А.С. Математические задачи теории сильно неоднородных

упругих сред. М., 1990.

36. Chechkin G.A., Koroleva Yu.O., Persson L.-E. On the precise asymptotics of the constant in the

Friedrich‘s inequality for functions, vanishing on the part of the boundary with microinhomogeneous

structure // J. of Inequalities and Appl. 2007. V. 2007. Art. ID 34138.

37. Chechkin G.A., Koroleva Yu.O., Meidell A., Persson L.-E. On the Friedrichs inequality in a domain

perforated along the boundary. Homogenization procedure. Asymptotics in parabolic problems // Rus.

J. of Math. Phys. 2009. V. 16. № 1. P. 1-16.

38. Агмон С., Дуглис А., Ниренберг Л. Оценки решений эллиптических уравнений вблизи границы.

М., 1962.

Московский государственный университет

Поступила в редакцию 30.08.2020 г.

им. М.В. Ломоносова

После доработки 23.05.2021 г.

Принята к публикации 08.09.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 10

2021