ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 11, с. 1503-1515

ТЕОРИЯ УПРАВЛЕНИЯ

УДК 517.977.58

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ

СИСТЕМОЙ С НЕОПРЕДЕЛЁННОСТЯМИ

ПО РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ

Рассматривается задача управления кусочно-линейной системой на конечном отрезке

времени в условиях неопределённости на основании неполной и неточной информации.

Разработана схема приближённого решения, включающая построение вспомогательных

кусочно-квадратичных функций цены. Приведены формулы для расчёта такой функции,

позволяющей оценить извне информационное множество кусочно-линейной системы. Пред-

ложен алгоритм построения позиционного управления, минимизирующего (в соответству-

ющей метрике) отклонение внешней оценки информационного множества от внутренней

оценки множества разрешимости и решающего задачу о переводе траектории системы в

малую окрестность целевого множества за заданное время.

DOI: 10.31857/S037406412111008X

Введение. В работе рассматривается задача целевого управления для кусочно-линейной

системы с переключениями (частного случая гибридной системы) [1, 2]. Необходимо перевести

траекторию системы из начального множества в малую окрестность целевого множества на

заданном отрезке времени. Начальное положение системы считается неизвестным, а в уравне-

ниях динамики имеются погрешности (неопределённости). Единственная доступная информа-

ция о текущем состоянии системы поступает из уравнений наблюдения. При этом наблюдения

являются неполными и неточными.

Как известно [3], при решении задач управления на основании неполной и неточной инфор-

мации о текущем состоянии наиболее важным является правильный выбор позиции системы.

В [3] предложены несколько вариантов конструкций позиций, включающих либо информаци-

онные множества системы, либо соответствующие функции цены. В частном случае линейной

динамики могут быть реализованы эффективные приближённые методы для решения задачи

управления [4]. В настоящей работе указанные выше общие идеи реализованы для специаль-

ного случая кусочно-линейной динамики, а в позицию системы включена внешняя оценка

информационного множества.

Из задачи позиционного управления по результатам наблюдений можно выделить несколь-

ко ключевых подзадач: 1) построение множеств разрешимости (попятных множеств достижи-

мости) [5] или их внутренних оценок; 2) построение информационных множеств; 3) синтез

управлений за счёт применения модификации метода экстремального прицеливания [6]. Осо-

бенностью данной работы является то, что для решения указанных подзадач используется

специальный класс непрерывных кусочно-квадратичных функций цены, ранее применявших-

ся авторами при решении задач достижимости [7], разрешимости и синтеза управлений [8, 9]

на основании полной информации о состоянии системы.

В работе, используя кусочно-квадратичные функции цены, а также идею принципа срав-

нения [5, 10], получены формулы для построения внешних оценок информационных множеств

кусочно-линейной системы и разработана общая схема вычисления синтеза управлений за счёт

прицеливания оценками информационных множеств на внутренние аппроксимации множеств

разрешимости.

1. Математическая модель системы. Рассмотрим математическую модель системы с

переключениями, которую также будем называть кусочно-линейной системой. Она состоит из

совокупности N подсистем, каждая из которых задаётся системой обыкновенных дифферен-

циальных уравнений

x = A(i)(t)x + B(i)(t)u + C(i)(t)v + d(i)(t), t ∈ [t₀,t₁], i = 1,N.

(1)

1503

1504

МАЯНЦЕВ, ТОЧИЛИН

В любой момент времени активной является ровно одна из этих систем. Вектор x(t) ∈ Rnx -

фазовая траектория системы; u ∈ Rnu является управляющим параметром, v ∈ Rnv - неопре-

делённостью (помехой) динамики. Матричнозначные функции A(i)(t) ∈ Rnx×nx , B(i)(t) ∈

∈ Rnx×nu, C(i)(t) ∈ Rnx×nv и вектор-функции d(i)(t) ∈ Rnx заданы и непрерывны на [t₀,t₁].

Модель рассматриваемой кусочно-линейной системы включает в себя также набор пра-

вил мгновенных переключений активной подсистемы. В фазовом пространстве Rnx задана

ограниченная замкнутая область Ω. Область Ω поделена на подобласти Ω(i), i = 1, N , с

помощью гиперплоскостей переключений:

H(k) = {x ∈ Rnx : 〈x,c(k)〉 = γ(k)},

∥c(k)∥ = 1, k = 1, N_H.

Траектория системы x(t) удовлетворяет i-му уравнению из (1), если x(t) ∈ Ω(i). В момент

перехода x(t) из Ω(i) в Ω(j) (через границу между i-й и j-й областями) происходит обя-

зательная смена активной подсистемы (“режима функционирования”) с i-й на j-ю, которую

также будем называть переключением. В случае возможного движения вдоль границы между

областями Ω(i) и Ω(j) время переключения определяется как первый момент схода траек-

тории с границы внутрь области Ω(j). Далее будем рассматривать только такие траектории

системы (1), которые не покидают Ω. Предполагаем, что область Ω подобрана таким образом,

что множество траекторий с указанным свойством не пусто.

Кусочно-линейная система указанного вида может быть получена, например, в результате

кусочной линеаризации нелинейных дифференциальных уравнений [9].

Будем считать, что точное текущее положение системы x(t) неизвестно (в том числе в на-

чальный момент времени t₀). Однако его можно оценить на основании поступающих в режиме

реального времени результатов измерений. Рассматриваем следующее правило измерений:

y(t) = G(t)x(t) + w(t), t ∈ [t₀, t₁],

(2)

в котором вектор y(t) ∈ Rny - доступное измерение траектории, а w ∈ Rny - погрешность

измерений, матричнозначная функция G(t) ∈ Rny×nx задана и непрерывна. Кроме того, пред-

положим, что существует априорная оценка начального состояния:

x(t₀) ∈ X₀,

где множество X₀ ⊂ Ω является выпуклым и компактным.

Управление u и помехи (неопределённости) v, w удовлетворяют следующим жёстким

поточечным ограничениям: u = u(π) ∈ P(t), v = v(t) ∈ Q(t), w = w(t) ∈ R(t), где P(t) ⊂

⊂ Rnu, Q(t) ⊂ Rnv, R(t) ⊂ Rny - многозначные отображения, непрерывные в смысле метрики

Хаусдорфа и принимающие выпуклые компактные значения. Позиция π системы определя-

ется ниже.

Пусть ζ_t( · , t₀) - совокупность неопределённостей, присутствующих в системе:

ζ_t(·,t₀) = {x₀,v(τ),w(τ): x₀ ∈ X₀, v(τ) ∈ Q(τ), w(τ) ∈ R(τ), τ ∈ [t₀,t]}.

Произвольная допустимая реализация ζt1 ( · , t₀) вместе с заданным допустимым управлением

u(·) определяют траекторию x(t) = x(t, t₀, x₀)|u(·),v(·) системы (1), а также вектор-функцию

измерений y(t), определённую согласно (2). Здесь t ∈ [t₀, t₁].

Предположим, что для любых двух соседних областей Ω(i) и Ω(j), общей границей кото-

рых является гиперплоскость H, выполняется

либо условие односторонней проницаемости: при любых t ∈ [t₀, t₁], x ∈ H

^⋂Ω и для всех

u(i) ∈ P(t), v(i) ∈ Q(t), u(j) ∈ P(t), v(j) ∈ Q(t) имеет место равенство

sgn (〈c, A(i)(t)x + B(i)(t)u(i) + C(i)(t)v(i) + d(i)(t)〉) =

= sgn (〈c,A(j)(t)x + B(j)(t)u(j) + C(j)(t)v(j) + d(j)(t)〉) = ±1

(здесь c ∈ Rnx - нормаль к H, ∥c∥ = 1);

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ СИСТЕМОЙ

1505

либо условие непрерывного сопряжения: при любых t ∈ [t₀, t₁], x ∈ H

^⋂Ω и для всех

u ∈ P(t), v ∈ Q(t) выполняются равенства B(i)(t) = B(j)(t) и

A(i)(t)x + B(i)(t)u + C(i)(t)v + d(i)(t) = A(j)(t)x + B(j)(t)u + C(j)(t)v + d(j)(t).

Рассмотрим класс U_f допустимых позиционных управлений, содержащий многозначные

отображения u = u(π). Такое управление u(π) будем называть допустимым, если при под-

становке его в (1) полученные дифференциальные включения имеют решения при любом на-

чальном векторе фазовых переменных x₀ ∈ Ω.

Для неопределённостей v, w будем использовать классы допустимых помех, представ-

ляющие собой множества измеримых функций v(t) и w(t) соответственно, заданных при

t ∈ [t₀,t₁] и удовлетворяющих почти всюду ограничениям v(t) ∈ Q(t), w(t) ∈ R(t).

Заметим, что при выполнении условий односторонней проницаемости или непрерывно-

го сопряжения для любой траектории x(t) системы, соответствующей допустимым помехам

ζt1 (·,t₀) и допустимому управлению u(·), на гиперплоскостях переключений H(k) невозмож-

но возникновение скользящих режимов [1], при которых x(t) не удовлетворяет какому-либо

из уравнений (1).

Уравнения наблюдений (2) можно интерпретировать как фазовые ограничения на состоя-

ние системы, которые становятся известными в режиме реального времени:

x(t) ∈ Y(t) := {x: y(t) - G(t)x = r(t) ∈ R(t)}, t ∈ [t₀, t₁].

(3)

Информационным множеством [11, с. 12] системы (1) при доступных измерениях y(t) и

фиксированном управлении u(τ), τ ∈ [t₀, t], назовём множество

X (t, t₀, X₀) = {x : существует v(·) такое, что

x(t₀, t, x)|u(·),v(·) ∈ X₀, x(τ) ∈ Y(τ) для всех τ ∈ [t₀, t]},

(4)

где x(t₀, t, x)|u(·),v(·) - значение траектории, выпущенной из позиции (t, x) в обратном времени,

в момент времени t₀. Информационная трубка X [t] - это соответствующее многозначное

отображение X ( · , t₀, X₀).

Позицией системы назовём пару π = {t,X(t)}, где t ∈ [t₀,t₁] определяет текущее время, а

информационное множество X (t) = X (t, t₀, X₀) содержит неизвестное состояние системы x(t),

т.е. является его гарантированной оценкой, учитывающей полученные к моменту t результаты

наблюдений y(τ), τ ∈ [t₀, t].

2. Расширенные переменные. Будем далее считать, что множества P(t), Q(t), R(t)

являются эллипсоидами:

P(t) = E(p(t), P (t)), p(t) ∈ Rnu , P (t) ∈ Rnu×nu , P (t) = P^т(t) > 0,

Q(t) = E(q(t), Q(t)), q(t) ∈ Rnv , Q(t) ∈ Rnv×nv , Q(t) = Q^т(t) > 0,

R(t) = E(0, R(t)), R(t) ∈ Rny×ny , R(t) = R^т(t) > 0,

центры эллипсоидов p(t), q(t) и матрицы конфигураций P (t), Q(t), R(t) непрерывны по

t ∈ [t₀,t₁]. Матрицы P(t), Q(t), R(t) являются положительно определёнными при любом

фиксированном t.

Рассмотрим также “расширенное” пространство переменных x = (x^т, 1)^т ∈ Rnx+1.

Эллипсоид E(q, Q) в пространстве R^k задаётся следующим соотношением:

E (q, Q) = {x ∈ R^k : 〈x - q, Q-1(x - q)〉 ≤ 1} = {x ∈ R^k : 〈x,Qx〉 ≤ 1},

где

(

)

Q-1

-Q-1q

x = (x^т,1)^т,

^Q=

-q^тQ-1

q^тQ-1q

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

1506

МАЯНЦЕВ, ТОЧИЛИН

Рассмотрим дифференциальные уравнения (1) в “расширенном” пространстве:

A(i)(t)x

C(i)(t)v, t ∈ [t₀,t₁].

Фазовые ограничения, представленные уравнением наблюдений (2), принимают вид

^G(t)x ∈ R(t),

а “расширенные” матрицы задаются следующим образом:

(

)

A(i)(t) d(i)(t) + B(i)(t)u(t) + C(i)(t)q(t)

A(i)(t) =

O1×nx

(

)

C(i)(t)

C(i)(t) =

^G(t) =

⁽-G(t) y(t)⁾,

O1×nv

на неопределённость v наложены поточечные ограничения: v ∈ E(0, Q(t)).

3. Задача синтеза управлений по результатам наблюдений. Зафиксируем целевое

компактное множество X₁ ⊂ Ω ⊂ Rnx .

Задача синтеза управлений по результатам наблюдений состоит в построении допусти-

мого управления u^∗(π(t)), переводящего траектории системы (1) из произвольной начальной

позиции π₀ = {t₀, X₀} в целевое множество X₁ для произвольной допустимой реализации

неопределённостей ζt1 ( · , t₀).

Для некоторых π₀, X₁ сформулированная задача может не иметь решения. В таком случае

будем решать следующую задачу оптимизации: для заданной начальной позиции π₀ = {t₀, X₀}

требуется найти минимальное μ > 0 такое, что существует управление u^∗(π(t)), переводящее

позицию π₀ в μ-окрестность (в некоторой метрике) множества X₁ для любой допустимой

реализации ζt1 ( · , t₀).

Согласно общей схеме решения задачи синтеза управлений по результатам наблюдений,

изложенной в [3], эта задача может быть представлена в виде совокупности двух подзадач:

задачи гарантированного оценивания, состоящей в построении информационного множе-

ства X(t,π₀) по результатам наблюдений y(τ), τ ∈ [t₀,t];

задачи синтеза управлений u^∗(π(τ)), решаемой на полуинтервале (t, t₁].

Здесь t ∈ [t₀, t₁] - произвольный промежуточный момент времени.

Далее последовательно рассмотрим указанные подзадачи для рассматриваемой математи-

ческой модели кусочно-линейной системы с переключениями.

4. Задача гарантированного оценивания. Пусть ϕ_A(x) - какая-либо неотрицательная

гладкая функция, для которой A - следующее её лебегово множество:

A = {ξ: ϕ_A(ξ) ≤ 0}.

Замечание. В силу неотрицательности функции ϕ_A(x) неравенство в определении мно-

жества A можно заменить на равенство. При x ∈ A очевидно неравенство ϕ_A(x) > 0.

Пусть известны начальная позиция π₀ = {t₀, X₀}, наблюдения y(τ) и реализация управ-

ления u(τ), τ ∈ [t₀, t]. Рассмотрим следующую функцию цены:

{

∫

}

V_X (t,x) = max

ϕX₀ (x(t0)) + ϕR(τ)(r(τ)) dτ : x(t) = x

(5)

v∈Q(t)

t₀

Здесь r(τ) = y(τ) - G(τ)x(τ) - полученное в момент времени τ наблюдение. Функции ϕX0 (·)

и ϕR(·)(·) могут быть различными по форме.

Связь между информационным множеством (4) и функцией цены (5) задаётся следующим

соотношением: X (t, t₀, X₀) = {x: V_X (t, x) ≤ 0}.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ СИСТЕМОЙ

1507

Функция цены V_X (t, x) в любой точке (t, x), x ∈ int Ω(i), в которой она является диффе-

ренцируемой, удовлетворяет уравнению Гамильтона-Якоби-Беллмана-Айзекса (ГЯБА) [12]

∂V_X(t,x)

^%∂V_X(t,x)

+ max

,A(i)(t)x + B(i)(t)u(t) + C(i)(t)v + d(i)(t)

- ϕR(t)(r(t)) = 0

(6)

∂t

v∈Q(t)

∂x

и начальному условию

V_X (t₀,x) = ϕX0 (x).

Преобразуем уравнение (6):

V ′t + 〈V ^′x,A(i)(t)x + B(i)(t)u(t) + d(i)(t)〉 + ρ(V ^′x|C(i)(t)Q(t)) - ϕR(t)(r(t)) = 0,

(7)

где V^′t и V^′x - частные производные V_X (t, x) по переменным t и x соответственно, ρ(l|X ) -

значение опорной функции ко множеству X в направлении l.

5. Кусочно-квадратичные функции цены. Построим аппроксимацию функции це-

ны V_X (t, x) в классе функций W(i)X(t, x) = 〈x, K(i)X(t)x〉, K(i)X(t) = (K(i)X(t))^т ∈ R(nx+1)×(nx+1).

Здесь функция W(i)X(t, x) определена только при x ∈ Ω(i). Матричнозначные функции K(i)X(t)

считаем непрерывно дифференцируемыми всюду на [t₀, t₁] за исключением, быть может, ко-

нечного числа точек.

Для совокупности функций W(i)X(t, x) при различных i потребуем выполнения условия

“непрерывной склейки”:

W(i)X(t, x) = W(j)X(t, x) для всех t ∈ [t₀,t₁] и x ∈ H(k),

(8)

здесь H(k) - гиперплоскость переключений, разделяющая области Ω(i) и Ω(j).

Согласно [8] условие (8) будет выполнено, если имеют место равенства

K(i)X(t)Γ_k = K(j)X(t)Γ_k для всех t ∈ [t₀,t₁],

(9)

K(i)(t)Γk =

K(j)(t)Γk для всех t ∈ [t0, t1],

(10)

где Γ_k - матрицы параметризации гиперплоскости H(k), т.е.

x ∈ H(k) ⇔ x = Γ_ky,

y = (y^т,1)^т ∈ Rnx.

При выполнении условий “непрерывной склейки” (9), (10) получается непрерывная кусоч-

но-квадратичная функция W_X (t, x):

W_X (t, x) = W(i)X(t, x) = 〈x,K(i)X(t)x〉, t ∈ [t₀,t₁], x ∈ Ω(i), i = 1,N,

(11)

дифференцируемая по любому ненулевому направлению ℓ = (ℓ_t, ℓ_x):

W^′X (t, x;ℓ) = ℓ_t〈x,K(i)X(t)x〉 + 2〈ℓ_x,K(i)X(t)x〉, ℓ_t ∈ R, ℓ_x ∈ Rnx+1.

6. Внешняя аппроксимация информационного множества. Рассмотрим задачу га-

рантированного оценивания в новых, “расширенных”, переменных x из начального множества

X₀×{1}. Положи

V_X (t, x) = V_X (t,x) - функция цены в “расширенном” пространстве. В таком

случае уравнение (7) принимает вид

V′t +

V′˜x

A(i)(t)x〉 +

V′˜x,Q(i)(t

V ′˜x〉1/2 - ϕR(t)( ^G(t)x) = 0,

(12)

где

V′t,

V ′˜x - частные производные функции

V_X (t, x), а Q(i)(t)

C(i)(t)Q(t)

C(i)(t))^т.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

5^∗

1508

МАЯНЦЕВ, ТОЧИЛИН

Выберем функцию ϕR(t)(r) следующим образом:

ϕR(t)(r) = (〈r, R-1(t)r〉 - 1)+ ≥ 0.

Тогда

ϕR(t)(^G(t)x) = 〈x, R(t)x〉+, R(t) =Gт(t)R-1(t)^G(t) - diag(0, . . . , 0, 1).

Заметим, что 〈x, R(t)x〉 ≥ -1 для любого x, причём равенство достигается при

^G(t)x = 0.

Используем далее принцип сравнения [5, 10] для построения внешней аппроксимации ин-

формационного множества X (t, t₀, X₀). Этой аппроксимации соответствует нижняя оценка

функци

V_X (t, x). Приведём способ построения такой оценки W_X (t, x), заданной в виде непре-

рывной кусочно-квадратичной функции (11), удовлетворяющей условиям “непрерывной склей-

ки” (9), (10).

Пусть в начальный момент времени t₀ верно неравенство

W_X (t₀, x) ≤ ϕX0 (x)

V_X (t₀, x) для всех x ∈ Ω.

(13)

В частном случае, когда множество X₀ является эллипсоидом E(x₀, X₀), можно взять

(

)

X-10

-X-10x₀

K(i)X(t₀) =

i = 1,N.

−x^т0X-10

x^т0X-10x₀ - 1

Запишем левую часть уравнения ГЯБА (12) в области Ω(i) для функции W_X (t, x) - иско-

мой оценки снизу функци

V_X (t, x):

K(i)

〈x,

(t)x〉 + 〈x, (K(i)X(t

A(i)(t) +

A(i)(t))^тK(i)X(t))x〉 +

+ 2〈x, K(i)X (t)Q(i)(t)K(i)X (t)x〉1/2 - 〈x, R(t)x〉₊,

(14)

здесь ∂W_X (t, x)/∂t = 〈x,K(i)X(t)x〉,

∂W_X(t, x)/∂x = 2K(i)X(t)x.

Воспользуемся следующими неравенствами:

〈x, K(i)X(t)Q(i)(t)K(i)X(t)x〉1/2 ≤ γ(i)(t) +

〈x, K(i)X(t)Q(i)(t)K(i)X(t)x〉,

(15)

4γ(i)(t)

〈x, R(t)x〉₊ ≥ β(t)〈x, R(t)x〉 = 〈x, β(t)R(t)x〉,

(16)

справедливыми для любых скалярных функций γ(i)(t) > 0 и β(t) ∈ [0, 1].

В неравенстве (15) равенство достигается при

γ(i)(t) =

〈x, K(i)X(t)Q(i)(t)K(i)X(t)x〉1/2.

Неравенство (16) обращается в равенство на границе и вне “эллипсоида наблюдений” R(t)

при β(t) = 1, во внутренних точках R(t) при β(t) = 0.

Используя (15), (16), получаем оценку сверху для (14):

〈x,

K(i)X(t) + F(i)X(t) - β(t)R(t))x〉 + 2γ(i)(t), x ∈ Ω(i),

F(i)X(t) = K(i)X(t

A(i)(t) +

A(i)(t))^тK(i)X(t) +

K(i)X(t)Q(i)(t)K(i)X(t).

(17)

2γ(i)(t)

Введём следующие обозначения:

R(i)X(t) =

K(i)(t) + F(i)X(t) - β(t)R(t),

(18)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ СИСТЕМОЙ

1509

α(i)X(t) = max{〈x,R(j)X(t)x〉 + 2γ(j)(t): j ∈ I_i(t), x ∈ Ω(j)}, t ∈ [t₀,t₁], α(i)X(t₀) = 0.

(19)

Здесь множество I_i(t) ⊂ {1, . . . , N} зависит от взаимного расположения гиперплоскостей

переключений H(k) и содержит все значения индекса j такие, что

существуют τ₀ ∈ [t₀, t), x₀ ∈ Ω(j) и v(·), для которых x(t, τ₀, x₀)|u(·),v(·) ∈ Ω(i).

Теорема 1. Пусть при t ∈ [t₀, t₁] заданы некоторые управление u(π) ∈ U_f , непрерывные

положительные функции γ(i)(t), i = 1, N, и функция β(t) ∈ [0, 1]. Пусть матричнозначные

функции K(i)X(t), i = 1, N , дифференцируемы всюду на [t₀, t₁] за исключением, быть может,

конечного числа точек и почти всюду удовлетворяют условиям “непрерывной склейки” (9),

(10), а матрицы K(i)X(t₀) таковы, что выполняется неравенство (13). Функции α(i)X(t) яв-

ляются решениями задач Коши (19). Тогда при любом t ∈ [t₀, t₁] множество

⋃

X^ext

(t) :=

{x ∈ Ω(j) : W_X (t, x) ≤ α(j)X(t)}

β,γ(i)

является надмножеством информационного множества X (t, t₀, X₀), т.е.

X (t, t₀, X₀) ⊆ X^ext

(t) при любом t ∈ [t₀, t₁].

(20)

β,γ(i)

Доказательство включения (20) проведём для t = t₁. Для всех остальных значений t

доказательство аналогично.

Для произвольных вектора x₁ ∈ X (t₁, t₀, X₀)

^⋂Ω(i1⁾ и допустимой помехи v(·) рассмотрим

решение x(t) = x(t, t₁, x₁)|u(·),v(·) замкнутой системы. Очевидно, что

x(t₀) ∈ X₀, а значит, из

неравенства (13) вытекает оценка W_X (t₀, x(t₀)) ≤ 0.

Используя свойство дифференцируемости кусочно-квадратичной функции W_X (t, x) по

направлениям, оценим её изменение вдоль траектории {t, x(t)}. Пусть ℓ(t) = (ℓt(t), ℓx(t)),

ℓ_t(t) = 1, ℓ_x(t)

A(i(t))(t)x(t)

C(i(t))(t)v(t). Тогда

∫t1

∫t1(

K(i(t))

W_X (t₁, x(t₁)) - W_X (t₀, x(t₀)) = W^′X (t, x(t);ℓ(t))dt =

ℓ_t(t)〈x(t),

(t)x(t)〉 +

t₀

)

∫t1

+ 2〈ℓ_x(t), K(i(t))X(t)x(t)〉 dt ≤

(〈x, R(i(t))X(t)x〉 + 2γ(i(t))(t)) dt ≤

t₀

∫t1

≤ max{〈x,R(j)X(t)x〉 + 2γ(j)(t): j ∈ Ii1 (t), x ∈ Ω(j)}dt = α(i1)_X(t₁).

t₀

Отсюда следует, что

W_X (t₁, x(t₁)) ≤ α(i1)_X(t₁) + W_X (t₀, x(t₀)) ≤ α(i1)_X(t₁).

Таким образом, x₁ ∈ X^ext

(t₁). Теорема доказана.

β,γ(i)

7. Задача синтеза управлений. Сформулируем задачу синтеза управлений по резуль-

татам наблюдений в пространстве информационных множеств: для заданной начальной по-

зиции π(t) = {t, X }, целевого множества X₁ и величины μ ≥ 0 требуется построить позицион-

ное управление u^∗(π(τ)), τ ∈ [t, t₁], переводящее позицию π(t) в μ-окрестность (в некоторой

метрике) множества X₁ для любой допустимой реализации неопределённостей ζt1 ( · , t).

Среди всех значений μ ≥ 0, для которых задача синтеза разрешима, требуется указать

наименьшее.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

1510

МАЯНЦЕВ, ТОЧИЛИН

Слабо инвариантным множеством W_μ(t) = W_μ(t, t₁, X₁) системы (1) относительно мно-

жества X₁ назовём совокупность множеств X ⊂ Ω, для которых при заданном μ ≥ 0 разре-

шима задача синтеза управлений из начальной позиции {t, X }.

Для решения задачи синтеза управлений по результатам наблюдений будет использован

метод экстремального прицеливания [6, 3] информационного множества X (t) (его внешней

оценки) на множество W_μ(t) (его внутреннюю оценку): необходимо построить многозначное

управление U(π(t)), которое в каждый момент времени t не увеличивает расстояние между

множествами X (t) и W_μ(t).

Отметим, что определение управления U(π(t)) - задача в бесконечномерном пространст-

ве (в силу бесконечномерности W_μ(t)), что существенно усложняет вычисления. В случае

линейных систем, согласно [3], можно перейти к конечномерной задаче, рассматривая вместо

W_μ(t) множество разрешимости W_μ(t) = W_μ(t,t₁,X₁) системы (1) без учёта наблюдений,

т.е. множество, выпущенное (в обратном времени) из позиции {t₁, X₁}. Для этого множества

верно соотношение

}

⋃{⋃

W_μ(t) =

{x: x ∈ X }: X ∈ W_μ(t)

Построению внутренних аппроксимаций W^int

(t) множества W_μ(t) кусочно-линейной

μ,γ(i)W,S(i)

системы (1) посвящена работа [8]. В ней, в частности, показано, что оценка W^int

(t) может

μ,γ(i)W,S(i)

быть найдена в виде множества уровня кусочно-квадратичной функции цены:

⋃

W^int

(t) =

{x ∈ Ω(j) : W_W (t, x) ≤ α(j)(t) + μ},

μ,γ(i)W,S(i)

W_W(t, x) = 〈x,K(i)W(t)x〉,

∀t ∈ [t₀,t₁], x ∈ Ω(i), i = 1,N,

ϕX₁ (x) ≤ WW (t1, x) для всех x ∈ Ω,

F(i)W(t) = K(i)W(t)D(i)(t) + (D(i)(t))^тK(i)W(t) +

K(i)W(t)Q(i)(t)K(i)W(t),

2γ(i)W(t)

D(i)(t)

A(i)0(t) -

√

(P(i)(t))1/2(S(i)(t))^т, P(i)(t)

B(i)(t)P(t)

B(i)(t))^т,

C2x + 1

K(i)

R(i)W(t) =

(t) + F(i)W(t),

α(i)W(t) = max{〈x,R(j)W(t)x〉 + 2γ(j)W(t): j ∈ I(i), x ∈ Ω(j)}, t ∈ [t₀,t₁], α(i)W(t₁) = 0.

Здесь C_x > 0 - такая константа, для которой ∥x∥² ≤ C2x + 1 при всех x ∈ Ω. Конкретная

внутренняя оценка множества разрешимости определяется параметрами: функциями γ(i)W(t) >

> 0 и S(i)(t), i = 1,N, t ∈ [t₀,t₁], причём (S(i)(t))^т = (S(i)(t))-1.

8. Метод экстремального прицеливания. Зафиксируем параметры - функции β(t),

γ(i)(t), γ(i)W(t), S(i)(t), t ∈ [t0, t1], i = 1, N , задающие внешнюю оценку информационно-

го множества и внутреннюю оценку множества разрешимости. Для краткости через X (t) и

W_μ(t) будем обозначать множества X^ext

(t) и W^int

(t) соответственно. Введём также

β,γ(i)

μ,γ(i)W,S(i)

следующие обозначения:

W(i)X(t, x) = W(i)X(t, x) - α(i)X(t) = 〈x,K(i)X(t)x〉 - α(i)X(t),

(21)

W(i)W(t, x) = W(i)W(t, x) - α(i)W(t) = 〈x,K(i)W(t)x〉 - α(i)W(t).

(22)

В таком случае множества X (t) и W_μ(t) задаются следующими соотношениями:

⋃

X (t) = X(i)(t) =

{x ∈ Ω(i) : W(i)X(t, x) ≤ 0},

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ СИСТЕМОЙ

1511

⋃

W_μ(t) = W(i)μ(t) =

{x ∈ Ω(i) : W(i)W(t, x) ≤ μ}.

Отметим, что каждое из множеств X(i)(t), Wμi)(t) является выпуклым и компактным.

Рассмотрим полурасстояние между рассматриваемыми множествами, порождаемое кусоч-

но-квадратичными функциями (21), (22):

h(t) = min{μ: X (t) ⊆ Wμ(t)}.

μ≥0

Из определения множеств X (t) и W_μ(t) следует, что

h(t) = max{0,ĥ(t)},

^ĥ(t) = maxh(i)(t) = max max

{W(i)W(t, x) : W(i)X(t, x) ≤ 0}.

(23)

x∈Ω(i)

Случай^ĥ(t) ≤ 0 соответствует ситуации, когда X (t) ⊂ W₀(t).

Нас интересуют такие допустимые управления u^∗(π(t)), при которых значение производ-

ной

h(t) минимально при любой возможной неопределённости системы, т.е.

u^∗(π(t)) = {u ∈ P(t): u ∈ Arg min

max

h(t)}.

(24)

ζt( · ,t0)

В силу сложной структуры функций h(i)(t) перейдём к рассмотрению функции H(t), яв-

ляющейся верхней оценкой функции^ĥ(t):

H(t) = maxH(i)(t) = max max

H(i)(t, x) = max max

{W(i)W(t, x) - W(i)X(t, x)}.

(25)

x∈Ω(i)

Заметим, что для любых i и x, для которых W(i)X(t, x) ≤ 0, выполнено неравенство

W(i)W(t, x) - W(i)X(t, x) ≥ W(i)W(t, x),

а значит,^ĥ(t) ≤ H(t).

Исследуем поведение производной функции H(t). Согласно [13, с. 86] при вычислении

производной операции дифференцирования и максимизации по конечному числу функций

можно поменять местами:

^H(t) = max{H(i)(t), i: H(i)(t) = H(t)}.

Согласно теореме о дифференцировании максимума функции [14, с. 61] производная H(t)

представляется в виде

(i)

^H(t) = max{W˙

(t, x) -

W_X (t, x), x ∈ Ω⁽

i),

(i, x) ∈ Argmax H(t)}.

(26)

(i,x)

Вследствие определения функций W(i)W(t, x) и W(i)X(t, x) для производных в (26) имеем

(i)

W_X (t, x) = 〈x,K

(t)x〉 - α(i)X(t),

W_W(t, x) = 〈x,K

(t)x〉 - α(i)W(t).

Переходя от h(t) к H(t) в (24), будем искать управление u^∗(π(t)) в виде

u^∗(π(t)) = Arg min

max

^H(t).

u∈P(t)

ζt( · ,t0)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

1512

МАЯНЦЕВ, ТОЧИЛИН

K(i)

При этом значения

(t),

α(i)W(t) могут быть вычислены заранее согласно приведён-

ным выше формулам (подробнее см. в [8]) и доступны при любых i, t. Значения производ-

ных α(i)X(t) в момент времени t при реализовавшихся ранее неопределённостях не зависят от

управляющего параметра.

Максимизация производной

^H(t) по всем допустимым помехам равносильна минимизации

выражения 〈x,K(i)X(t)x〉. Используя обозначение (18), заключаем, что минимум достигается

при минимальном значении выражения 〈x, β(t)R(t)x〉, которое, согласно определению R(t),

не менее -1.

Замечание. Указанный минимум соответствует случаю, когда наблюдение y(t) не даёт

никакой новой информации. Более того, значение r(t) в (3) является центром эллипсоида

R(t).

Таким образом,

u^∗(π(t)) =

{

}

(i)

= Arg min

max

W_W(t, x) - 〈x,(R⁽

(t) - F(i)X(t))x〉 + 1 + α(i)X(t) : (i, x) ∈ Argmax H(t)

(27)

u∈P(t)

Формула (27) позволяет в общем случае определить управление в позиционной форме, ми-

нимизирующее отклонение информационного множества от множества разрешимости в смыс-

ле полурасстояния (25). Выражение в (27) допускает дальнейшие преобразования. Для упро-

щения промежуточных выкладок сделаем следующее

Предположение. Для текущей позиции π(t) множество Argmax H(t) состоит из конеч-

ного числа пар (i₁, x(i1)), . . . , (i_M , x(iM )).

Тогда

{

}

(i)

max

W_W(t, x) - 〈x,(R⁽

(t) - F(i)X(t))x〉 + 1 + α(i)X(t)|(i, x) ∈ Argmax H(t)

{_M∑

(i_k )

= max λ_k

(t, x(ik )) - 〈x(ik), (R(ik )_X(t) - F(ik )_X(t))x(ik )〉 + α(ik )_X(t)) + 1 :

k=1

}

(λ₁, . . . , λ_M ) ∈ Λ_M

(28)

где

{

}

∑

Λ_M = ξ = (ξ₁,... ,ξ_M )^т ∈ R^M : ξ_i ≥ 0, i = 1,M,

ξ_i = 1

- симплекс.

i=1

Заменим в (27) выражение в фигурных скобках согласно (28). В полученном представлении,

в силу теоремы о минимаксе [14, с. 81-82], можно поменять местами min

и max . После этого

подсчитаем внутренний минимум по u. Зависимость от управления имеется лишь в F(ik )_X(t),

а именно, в значении матриц

A(ik)(t). Представим

A(ik)(t) в виде суммы:

(

)

A(ik)(t) d(ik)(t) + C(ik)(t)q(t)

A(ik)(t)

A(ik)0(t)

A(ik)_u(t),

A(ik)0(t) =

O1×nx

(

)

(

)

Onx×nx B(ik)(t)u

A(ik)_u(t) =

B(ik)(t)u

= O(nx+1)×nx

O1×nx

Учитывая определение (17) матриц F(ik)_X(t), получаем, что требуется минимизировать по u

выражение

∑

λ_k〈x(ik),K(ik)_X(t

A(ik)_u(t)x(ik)〉 =

λ_k〈x(ik),K(ik)_X(t

B(ik)(t)u〉.

k=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ СИСТЕМОЙ

1513

В результате приходим к следующему управлению:

⎧

⎨

P (t)ℓ^∗

p(t) -

ℓ^∗ = 0,

u^∗(π(t)) =

〈ℓ^∗, P (t)ℓ^∗〉1/2

(29)

⎩

E (p(t), P (t)),

ℓ^∗ = 0,

∑_M

где ℓ^∗ =

λ_k

B(ik)(t))^тK(ik)_X(t)x(ik⁾. При найденном управлении верно равенство

k=1

∑

λ_k〈x(ik),K(ik)_X(t

A(ik)_u(t)x(ik)〉 = 〈ℓ^∗,p(t)〉 - 〈ℓ^∗,P(t)ℓ^∗〉1/2.

k=1

Итоговое выражение для производной полурасстояния имеет вид

{_M∑

K(ik⁾

min^H = max

λ_k(〈x(ik),

(t)x(ik )〉 - α(ik )_W(t) - 〈x(ik ), (R(ik )_X(t) - F(ik )X,0(t))x(ik )〉 +

k=1

}

+ ˙α(ik )_X(t)) + 1 + 2〈ℓ^∗, p(t)〉 - 2〈ℓ^∗, P (t)ℓ^∗〉1/2 : (λ₁, . . . , λ_M ) ∈ Λ_M

(30)

Далее необходимо решить задачу максимизации вогнутой функции на ограниченном компакт-

ном множестве Λ_M и найти соответствующий максимизатор (λ∗1, . . . , λ^∗M ). После его подста-

новки в выражение для ℓ^∗ из (29) получим итоговое позиционное управление.

Заметим, что максимизатор (λ∗1, . . . , λ^∗M ) в (30) может быть выбран таким образом, чтобы

он непрерывно зависел от текущей позиции π(t), а значит, и от неизвестной величины x(t) -

решения системы (1). После подстановки такого максимизатора в управление (29) получаем

многозначное отображение с выпуклыми компактными значениями, полунепрерывное сверху

по x. Следовательно, после подстановки такого управления в систему (1) для полученных

дифференциальных включений будет выполнена теорема о существовании решений [15, с. 60-

61], т.е. найденное управление является допустимым.

Общий случай, когда сделанное предположение не выполняется, может быть разобран ана-

логичным образом, при помощи замены суммы по различным максимизаторам (i_k, x(ik )) на

сумму интегралов по множеству максимизаторов.

9. Априорная оценка качества управления. Полученное выше позиционное управ-

ление (29) минимизирует производную

^H(t). Однако нельзя утверждать, что эта производ-

ная будет неотрицательна. Таким образом, при t ∈ [t₀, t₁] может накапливаться погрешность,

увеличивающая размеры окрестности целевого множества, попадание в которую можно гаран-

тировать. Для априорной оценки размеров такой окрестности поступим следующим образом.

Пусть π(t₀) - известная начальная позиция. Воспользуемся формулам из п. 6 для постро-

ения оценок информационных множеств

X (t), t ∈ [t₀, t₁]. При построении этих множеств

используем управление (29), а также наиболее неблагоприятные наблюдения:

^G(t)x(t) ≡ 0.

Для информационной трубки

X (t) подсчитаем соответствующую величину

∫t1

^Ĥ(t₁) =^Ĥ(t₀) +

H(τ) dτ.

t₀

Теорема 2. Для любых допустимых погрешностей ζt1 ( · , t₀) управление (29) переведёт

любую соответствующую траекторию кусочно-линейной системы (1) в μ-окрестность це-

левого множества, где μ ≤^Ĥ(t₁).

Доказательство этого утверждения следует из того, что информационные множества

X (t), t ∈ [t₀, t₁], использующие реально поступающую информацию об измерениях (2), удо-

влетворяют при всех t ∈ [t₀, t₁] включению X (t) ⊆

X (t). Тогда в силу равенств (25) заклю-

чаем, что H(t) ≤^Ĥ(t₁) для всех t ∈ [t₀, t₁]. Наконец, из (23) вытекает двойное неравенство

μ ≤ h(t₁) ≤ H(t₁) ≤^Ĥ(t₁).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

1514

МАЯНЦЕВ, ТОЧИЛИН

10. Пример. Рассмотрим кусочно-линейную систему (1), состоящую из трёх подсистем:

x = A(i)x + Bu + Cv, t ∈ [0,3], i = 1,2,3.

Уравнение измерений (2) имеет вид

y(t) = Gx(t) + w = x₁(t) + x₂(t) + w.

Матрицы A(i), B, C, G следующие:

(

)

(

)

(

)

(

)

(

)

0.1

A⁽¹⁾ =

A⁽²⁾ =

A⁽³⁾ =

C =

⁽1

-1

0.2

Начальное X₀ = E(x₀, X₀) и целевое X₁ = E(x₁, X₁) множества заданы равенствами

(

)

(

)

(

)

(

)

-2.0

1.5

x₀ =

X₀ = 0.3

x₁ =

X₁ = 0.5

На управление u, неопределённость v и погрешность w наложены ограничения:

|u| ≤ 1,

|v| ≤ 1,

|w| ≤ 0.2.

Области Ω(i) заданы следующим образом:

Ω⁽¹⁾ = {x ∈ R² : - 6 ≤ x₁ ≤ -1,

|x₂| ≤ 6},

Ω⁽²⁾ = {x ∈ R² : |x₁| ≤ 1,

|x₂| ≤ 6},

Ω⁽³⁾ = {x ∈ R² : 6 ≥ x₁ ≥ 1,

|x₂| ≤ 6}.

В качестве начальной (но неизвестной системе) точки выберем значение x(0) = x₀. Случай-

ные реализации неопределённости v и помехи w получены с использованием равномерного

распределения.

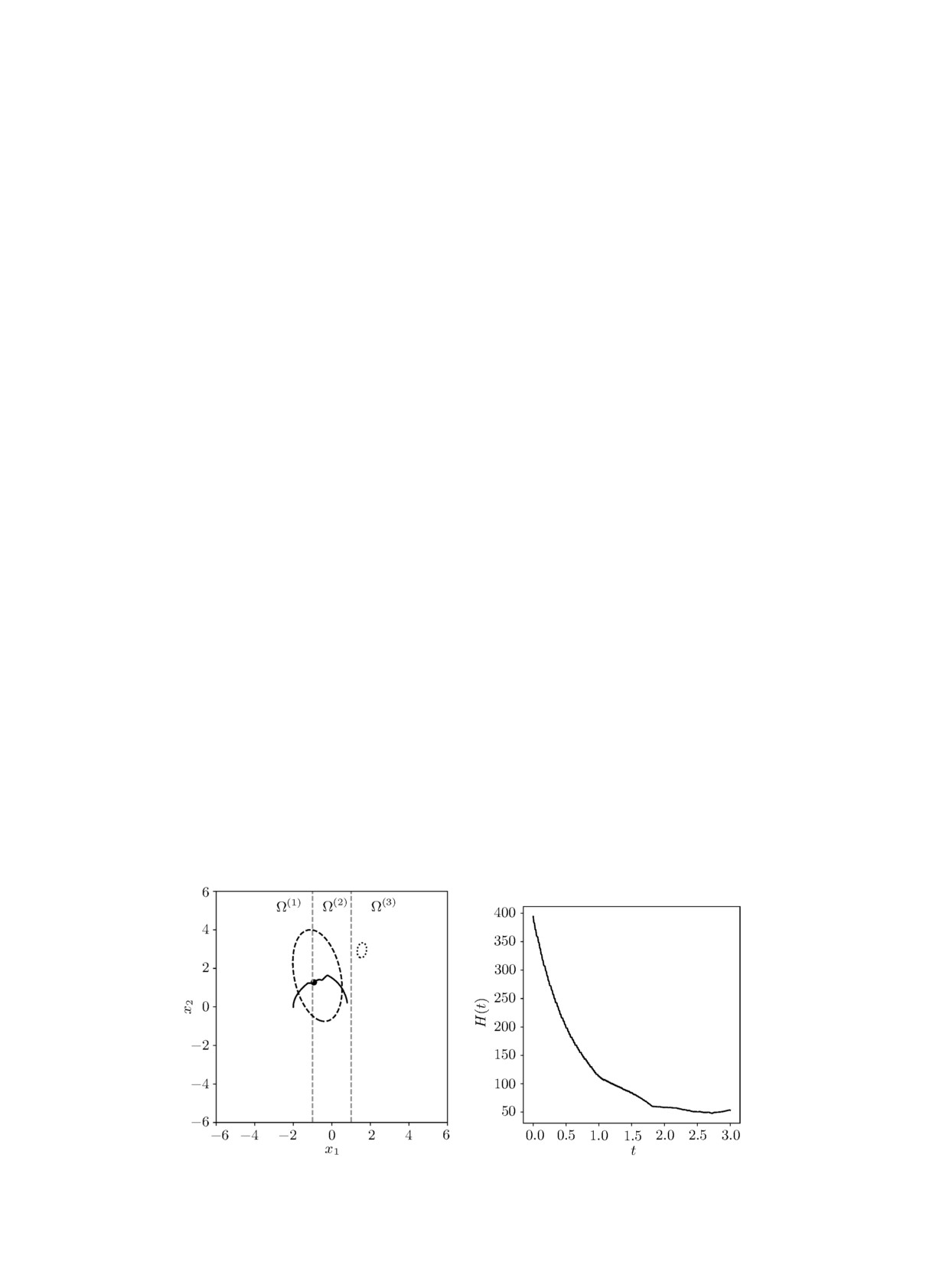
На рис. 1 изображены: траектория системы x(t) с выделенной точкой x(1.5), внешняя

оценка информационного множества X (1.5, t₀, X₀), внутренняя оценка множества разреши-

мости W(1.5, t₁, X₁) (лежит в области Ω⁽³⁾).

На рис. 2 приведён график функции H(t) - реальное изменение полурасстояния между

множествами по мере обработки поступающих результатов измерений с использованием пред-

ложенного позиционного управления.

Рис. 1. Траектория x(t) системы.

Рис. 2. График функции H(t).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021

ЗАДАЧА УПРАВЛЕНИЯ КУСОЧНО-ЛИНЕЙНОЙ СИСТЕМОЙ

1515

Заключение. В работе получены формулы для построения внешних оценок информаци-

онного множества кусочно-линейной системы с неопределённостями (помехами) в уравнениях

динамики и измерений. Предложен метод для вычисления позиционного управления, решаю-

щего задачу о переводе системы из заданного начального множества в заданное целевое мно-

жество. Рассмотренные в статье вопросы, безусловно, должны быть впоследствии дополнены

эффективными вычислительными схемами и алгоритмами. Их разработка является одной из

ближайших целей авторов.

Работа выполнена при финансовой поддержке Министерства образования и науки Россий-

ской Федерации в рамках реализации программы Математического центра фундаментальной

и прикладной математики по соглашению № 075-15-2019-1621, а также Российского фонда

фундаментальных исследований (проект 19-01-00613а).

СПИСОК ЛИТЕРАТУРЫ

1. Liberzon D. Switching in Systems and Control. Boston, 2003.

2. Куржанский А.Б., Точилин П.А. Слабо инвариантные множества гибридных систем // Диффе-

ренц. уравнения. 2008. Т. 44. № 11. С. 1523-1533.

3. Kurzhanski A.B., Varaiya P. Optimization of output feedback control under set-membership uncertainty

// J. Optim. Theory Appl. 2011. V. 151. № 1. P. 11-32.

4. Куржанский А.Б., Точилин П.А. К задаче синтеза управлений при неопределённости по данным

финитных наблюдателей // Дифференц. уравнения. 2011. Т. 47. № 11. С. 1599-1607.

5. Kurzhanski A.B., Varaiya P. Dynamics and Control of Trajectory Tubes. Theory and Computation.

Basel, 2014.

6. Красовский Н.Н. Управление динамической системой. М., 1985.

7. Точилин П.А. О построении невыпуклых аппроксимаций множеств достижимости кусочно-линей-

ных систем // Дифференц. уравнения. 2015. Т. 51. № 11. С. 1503-1515.

8. Маянцев К.С., Точилин П.А. Об одном методе построения кусочно-квадратичных функций цены

для задачи управления системой с переключениями // Дифференц. уравнения. 2018. Т. 54. № 11.

С. 1497-1507.

9. Чистяков И.А., Точилин П.А. Приближённое решение задачи целевого управления в случае нели-

нейности по одной переменной // Дифференц. уравнения. 2019. Т. 55. № 11. С. 1560-1571.

10. Куржанский А.Б. Принцип сравнения для уравнения типа Гамильтона-Якоби в теории управления

// Тр. Ин-та математики и механики УрО РАН. 2006. Т. 12. № 1. С. 173-183.

11. Куржанский А.Б. Управление и наблюдение в условиях неопределенности. М., 1977.

12. Fleming W.H., Soner H.M. Controlled Markov Processes and Viscosity Solutions. New York, 1993.

13. Демьянов В.Ф. Условия экстремума и вариационное исчисление. М., 2005.

14. Пшеничный Б.Н. Необходимые условия экстремума. М., 1982.

15. Филиппов А.Ф. Дифференциальные уравнения с разрывной правой частью. М., 1985.

Московский государственный университет

Поступила в редакцию 10.05.2021 г.

им. М.В. Ломоносова

После доработки 13.06.2021 г.

Принята к публикации 05.10.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 11

2021