ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 12, с. 1589-1598

ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.926.4+517.927.25

ИНТЕГРАЛЬНАЯ ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ

НЕЛИНЕЙНОЙ ЗАДАЧИ ШТУРМА-ЛИУВИЛЛЯ

Предложен новый подход к изучению нелинейных по спектральному параметру задач

Штурма-Лиувилля. Он основывается на введении связанной с изучаемой задачей транс-

цендентной функции, названной интегральной характеристической функцией и определя-

ющей собственные значения рассматриваемой задачи Штурма-Лиувилля. Исследование

этой функции позволяет доказать разрешимость задачи, найти асимптотику собственных

значений, получить теоремы сравнения, ввести естественную нумерацию собственных зна-

чений и нулей собственных функций. С помощью предложенного подхода изучена нели-

нейная задача Штурма-Лиувилля на отрезке с краевыми условиями первого рода.

DOI: 10.31857/S0374064121120013

1. Постановка задачи и вводные замечания. Рассмотрим уравнение

(P (x, λ)y^′(x))^′ + Q(x, λ)y(x) = 0,

(1.1)

где λ - спектральный параметр λ ∈ Λ := [b, +∞), b - вещественная постоянная, x = [0, a],

1 < a < ∞. Функции P и Q предполагаются непрерывными по совокупности переменных

(x, λ) ∈ x × Λ, а P ещё и однократно непрерывно дифференцируемой по x при x ∈ x; кроме

того P (x, λ) > 0 и Q(x, λ) > 0 при (x, λ) ∈ x × Λ.

Задачей P назовём задачу определения тех (собственных) значений параметра λ, при

которых существует нетривиальное классическое решение y ≡ y(x; λ) уравнения (1.1), удо-

влетворяющее краевым условиям

y(0; λ) = 0, y(1; λ) = 0.

(1.2)

При изучении разрешимости задачи P будут введены дополнительные ограничения (по

второму аргументу), которым должны удовлетворять функции P и Q (см. п. 2.2). Отме-

тим, что в рамках излагаемого ниже подхода можно изучать задачу P и в том случае, когда

аргумент λ коэффициентов P и Q принадлежит ограниченному множеству, а сами коэф-

фициенты не обязательно всюду непрерывны по λ. Также можно рассмотреть случай, когда

функции P и/или Q обращаются в нуль в некоторых точках своей области определения.

Задача Штурма-Лиувилля для уравнения (1.1) изучалась многими авторами, укажем здесь

работы [1-6]. Отметим, что в нашем рассмотрении условия на коэффициенты P и Q уравне-

ния являются менее ограничительными, чем используемые в [1].

Задачи Штурма-Лиувилля, коэффициенты или краевые условия в которых зависят от

спектрального параметра, в том числе нелинейно, возникают в различных вопросах как чи-

стой, так и прикладной математики и поэтому активно исследуются (см., например, рабо-

ты [2, 7-17] и приведённую в них библиографию). Интерес для исследователей представляют

свойства собственных значений и собственных функций, в частности, вопросы, связанные с

базисностью собственных функций [6, 18-20] таких задач.

Один из способов исследования задачи Штурма-Лиувилля основывается на изучении от-

вечающей ей характеристической функции, которая определяется следующим образом. Рас-

смотрим семейство тех решений уравнения (1.1), для которых выполняется только условие

задачи Штурма-Лиувилля при x = 0. Обозначим это семейство снова через y(x; λ), не от-

мечая его зависимости ещё от одного вещественного параметра - значения производной ре-

шения при x = 0. Тогда, требуя, чтобы для решений этого семейства выполнялось ещё и

1589

1590

ВАЛОВИК, ЧАЛЫШОВ

условие задачи Штурма-Лиувилля при x = 1, получаем уравнение y(1; λ) = 0 относитель-

но спектрального параметра λ; очевидно, что множество нулей этого уравнения совпадает

с множеством собственных значений задачи Штурма-Лиувилля. Такое уравнение в теории

задач Штурма-Лиувилля называется характеристическим уравнением, а его левая часть -

характеристической функцией (параметра λ) [21, с. 31].

В настоящей работе мы также используем для уравнения (1.1) решение y(x; λ) вспомо-

гательной задачи Коши (см. задачу (2.2) ниже) для построения функции относительно спек-

трального параметра λ, нули которой и только они являются собственными значениями ис-

следуемой задачи Штурма-Лиувилля. Другими словами, построенная таким образом функция

имеет смысл характеристической функции. В связи с тем, что она задаётся в виде интеграла от

некоторого выражения, её естественно называть интегральной характеристической функцией

(ИХФ). Приравняв к нулю ИХФ, получаем уравнение относительно λ, которое будем назы-

вать интегральным характеристическим уравнением (ИХУ). Оказывается, что с помощью

элементарных оценок можно получить результаты о разрешимости ИХУ, а следовательно, и

результаты о разрешимости исследуемой задачи и свойствах собственных значений и собствен-

ных функций. Подчеркнём, что предлагаемый здесь подход, по-видимому, является новым, в

частности, в нём не используется ни анализ функции Грина [16], ни теория целых функций,

которая обычно применяется для исследования характеристической функции y(1; λ) [21, 22].

2. Основные результаты. Собственные значения задачи P будем обозначать какλn, так

и λ, где n ∈ Z₊ - индекс, равный числу нулей соответствующей собственной функции y ≡

≡ y(x;λn) при x ∈ (0,1). Собственные значения

λ_n предполагаются упорядоченными по

возрастанию.

Из свойств функций P (x, λ) и Q(x, λ) следует, что

0 < p_-(λ) ≤ P(x,λ) ≤ p₊(λ),

0 < q_-(λ) ≤ Q(x,λ) ≤ q₊(λ),

(2.1)

где

p_-(λ) = minP (x, λ), q-(λ) = minQ(x, λ) и p+(λ) = maxP (x, λ), q+(λ) = max Q(x, λ).

x∈x

Обозначим через y ≡ y(x; λ), где x ∈ x, решение задачи Коши для уравнения (1.1) с

начальными данными

y(0; λ) = 0, y^′(0; λ) = 1.

(2.2)

Известно, что задача Коши (1.1), (2.2) глобально однозначно разрешима [22, c. 12; 23, c. 62].

2.1. Интегральное характеристическое уравнение задачи P. Пусть при некотором

λ ∈ Λ решение y ≡ y(x;λ) задачи Коши (1.1), (2.2) имеет ровно n + 1 нуль x₁,...,xn+1 ∈ x,

где x = (0, a], и 0 < x₁ < . . . < xn+1 ≤ a. Число n и точки x_i, вообще говоря, зависят от λ.

Так как y(x; λ) ≡ 0, то y^′(x_i; λ) = 0 при i = 0, n + 1, где x₀ = 0.

⋃_n

Пусть x_i := (x_i, xi+1), где i = 0, n, а x₀ = 0. При x ∈

x_i существует и непрерывна

i=0

функция

P (x, λ)y^′(x; λ)

η(x; λ) =

y(x; λ)

Принимая во внимание уравнение (1.1), несложно убедиться, что для функции η имеет

место равенство

η^′ = -w(η,x;λ),

(2.3)

⋃_n

в котором w(η, x; λ) = Q(x, λ) + η²/P (x, λ) при x ∈

x_i.

i=0

Замечание. Равенство (2.3) представляет собой относительно η уравнение Риккати, кото-

рое часто используется в теории задач Штурма-Лиувилля [23, c. 392; 24, c. 243] (см. также [1,

с. 193]).

Из условий P (x, λ) > 0, Q(x, λ) > 0 при (x, λ) ∈ x × Λ вытекает неравенство

w(x, η; λ) > 0

(2.4)

при (x, η, λ) ∈ x × R × Λ.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

ИНТЕГРАЛЬНАЯ ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ

1591

Из соотношений (2.3) и (2.4) следует, что η^′ < 0, а значит, функция η ≡ η(x; λ), опреде-

⋃_n

лённая при x ∈

x_i, монотонно убывает на каждом интервале x_i. Тогда очевидно, что

i=0

lim

η(x; λ) = +∞;

lim

η(x; λ) = ±∞, i = 1, n;

lim η(x; λ) = -∞.

(2.5)

x→x₀+0

x→x_i±0

x→xn+1-0

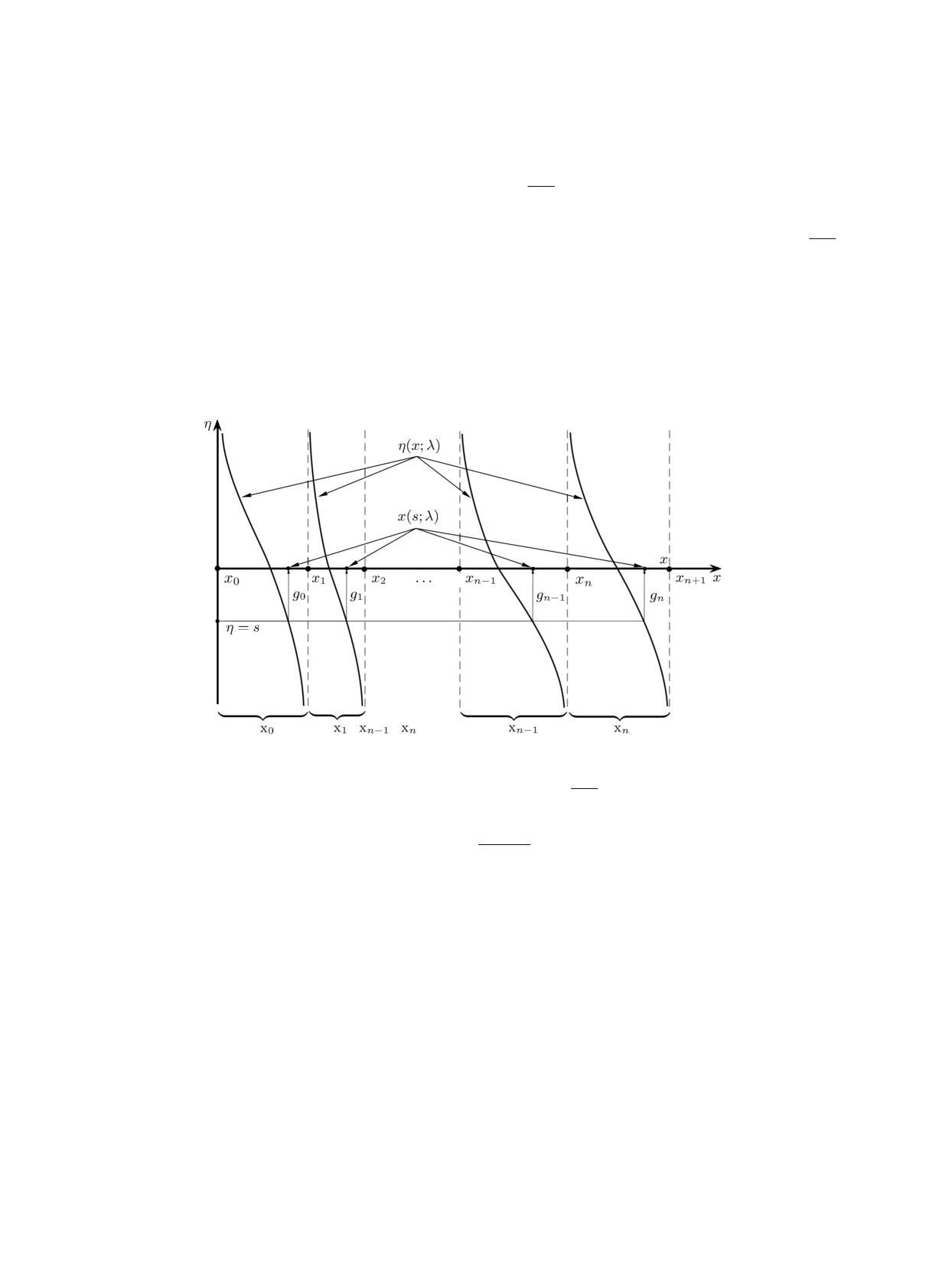
Отсюда вытекает, что существуют непрерывные биекции g_i : R → x_i (η → x) при i = 0, n

(рисунок). Другими словами, определены положительные монотонно убывающие непрерывные

функции x = g_i(η; λ), где η ∈ R, а x ∈ x_i. Отметим, что последнее соотношение в (2.5) имеет

место только при условии, что рассматриваемое решение y(x; λ) задачи Коши (1.1), (2.2)

обращается в нуль при x = xn+1. Если это не так, то, во-первых, указанный предел является

некоторой функцией от λ (которая обращается в -∞, когда y(x; λ)|x=xn+1 = 0), а во-вторых,

область определения отображения g_n, вообще говоря, отлична от R (и совпадает с R, когда

y(x; λ)|x=xn+1 = 0).

Рисунок. Функция η(x; λ) и отображения gi.

Проведённые рассуждения позволяют для каждого i = 0, n корректно определить выра-

жение

∫

T_i(λ) :=

(2.6)

ς_i(v;λ)

где ς_i(v; λ) = Q(g_i(v; λ); λ) + v²/P (g_i(v; λ); λ) при v ∈ R. Сразу отметим, что функция T_i(λ)

определена только для тех λ, при которых решение y(x; λ) задачи Коши (1.1), (2.2) имеет

не менее i + 2 нулей в x (множество таких λ обозначим через Λ_i ). Если указанное выше

решение y(x; λ) обращается в нуль в x меньше, чем i+2 раз, то функция T_i(λ) не определена.

Зададим функцию

∑

Φ(λ; n) :=

T_i(λ).

(2.7)

i=0

⋃

Как отмечено выше, областью определения функции Φ является множествоj∈Z+ (Λ_j ×{j}).

Важнейшим результатом является

Теорема 1 (об эквивалентности). Числоλ ∈ Λ является собственным значением зада-

чи P, если и только если найдётся n ∈ Z₊ такое, что λ =λ при n = n удовлетворяет

уравнению

Φ(λ; n) - 1 = 0.

(2.8)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1592

ВАЛОВИК, ЧАЛЫШОВ

Формула (2.8) представляет собой семейство уравнений относительно λ при различных

n = 0,1,...; также (2.8) можно трактовать как одно уравнение (относительно λ), зависящее

от параметра n. Уравнение (2.8) назовём ИХУ задачи P, а функцию Φ(λ; n) - 1 - ИХФ этой

задачи.

Из теоремы 1 вытекает

Следствие 1. Пусть λ =λ - решение уравнения (2.8) при n = n. Тогда при λ =λ реше-

ние y ≡ y(x;^λ) задачи Коши (1.1), (2.2) удовлетворяет краевым условиям (1.2) и имеет n+2

простых (кратности 1) нуля x_j ∈ [0,1], j = 0, n + 1.

Если n ≥ 1, то x_j = Φ(^λ; j - 1), где 1 ≤ j ≤ n.

Отсюда получаем, что расстояние между двумя последовательными нулями x_i и xi+1

собственной функции y(x;^λ) определяется формулой

∫

xi+1 - x_i =

ς_i(v;^̃)

Вопрос о нахождении верхней и нижней оценок расстояния между последовательными ну-

лями решения уравнения второго порядка является

∫

и нижняя оценки для приведённого выше интеграла_R являются соответственно верхней и

нижней оценками для указанного расстояния, которые согласуются с известным результатом

из монографии [25, c. 138].

Введённое выше обозначение

λ_n для собственных значений задачи P связывает номер

n собственного значения

λ_n с числом нулей соответствующей собственной функции y_n ≡

≡ y(x;λn), лежащих внутри интервала x = (0,1). Другими словами, индекс n в обозначении

собственного значенияλn означает, что пара (λn, n) является решением уравнения (2.8). За-

метим, что поскольку уравнение (2.8) содержит n + 1 слагаемое, то очевидно, что оценки для

λ_n будут выражаться через функции от (n+1)-го аргумента; приведение таких оценок к стан-

дартному виду, когда оценка дляλn выражается через функцию от аргумента n, достижимо

при изменении нумерации.

Если уравнение (2.8) при одном и том же значении n = n имеет k > 1 различных решений

λ =λ, то во избежание путаницы достаточно эти решения снабдить ещё одним индексом,

например,λ̃n,1, . . . ,

n,k, где для определённости перечисленные решения упорядочены по

возрастанию. В дальнейшем мы не будем акцентировать на этом внимание.

Так как линейное уравнение (1.1) при данном λ имеет не более двух линейно независимых

решений, то отсюда следует, что совокупность всех собственных функций, соответствующих

одному и тому же собственному значению, является конечномерным векторным пространством

размерности, не большей двух. Размерность этого пространства совпадает с наибольшим чис-

лом линейно независимых решений краевой задачи (1.1), (1.2) при данном собственном зна-

чении λ =^λ; это число называется кратностью собственного значения [22], а собственное

значение кратности 1 - простым собственным значениемы.

Справедливо

Утверждение 1. Всякое собственное значениеλ задачи P является простым.

Полезным будет

Утверждение 2. Если функция T_i(λ) определена, то она является положительной и

непрерывно зависит от λ ∈ Λ_i.

Разрешимость уравнения (2.8) позволяет сформулировать

Утверждение 3. Для любого i ∈ Z₊ при λ ∈ Λ_i = ∅ справедливы оценки

√

p_-(λ)

p₊(λ)

π√

≤ T_i(λ) ≤ π√

(2.9)

q₊(λ)

q_-(λ)

Из утверждения 3 и определения (2.7) элементарно вытекает

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

ИНТЕГРАЛЬНАЯ ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ

1593

Следствие 2. Для λ ∈ Λ_n = ∅ имеет место двусторонняя оценка

√

p_-(λ)

p₊(λ)

π(n + 1)√

≤ Φ(λ;n) ≤ π(n + 1)√

(2.10)

q₊(λ)

q_-(λ)

Оценки (2.9) и (2.10) являются основным инструментом при исследовании разрешимости

уравнения (2.8) и доказательстве существования собственных значений задачи P.

2.2. Существование собственных значений задачи P. Чтобы получить содержатель-

ные результаты о разрешимости уравнения (2.8), а следовательно, и задачи P, необходимо

наложить дополнительные ограничения на функции P и Q. Естественно получить условия,

из которых будет следовать существование бесконечного числа собственных значений зада-

чи P. Некоторые из возможных условий такого рода указаны в теоремах 2 и 3.

Теорема 2. Если

p₊(λ)

lim

= 0,

(2.11)

λ→+∞ q_-(λ)

то найдётся такое n₀ ∈ Z₊, что уравнение (2.8) имеет не меньше одного решения λ =

= λ_n ∈ Λ для каждого n = n₀,n₀ + 1,...; при этом lim

λ_n = +∞ и Λ_i являются неогра-

n→∞

ниченными множествами для всех i ∈ Z₊.

Из теоремы 2 очевидно вытекает

Следствие 3 (теорема I о разрешимости). Если выполняется условие (2.11), то задача P

имеет бесконечное число собственных значенийλn с точкой накопления на бесконечности.

Теорема 3. Пусть для достаточно больших λ справедливы оценки

p_-(λ)

p₊(λ)

= O(λ-2c1 ) и

= O(λ-2c2 ),

(2.12)

q₊(λ)

q_-(λ)

где c₁, c₂ - положительные вещественные постоянные, c₁ ≥ c₂, и без потери общности

предполагается, что коэффициенты первых членов асимптотик в (2.12) равны единице. Тог-

да найдётся такое n₀ ∈ Z₊, что уравнение (2.8) имеет не меньше одного решения λ =λ ∈ Λ

для каждого n = n₀, n₀ + 1, . . . и для достаточно больших λ справедливы неравенства

(πn)1/c1 - Δ ≤λn-1 ≤ (πn)1/c2 + Δ,

(2.13)

где Δ > 0 - постоянная. Если же c₁ = c₂ = c > 0, то

λn-1 = O(n1/c),

(2.14)

где коэффициент при главном члене асимптотики (2.14) равен π1/c.

В силу теорем 2 и 3 получаем

Следствие 4 (теорема II о разрешимости). Если выполняются условия (2.11) и (2.12),

то задача P имеет бесконечное число собственных значенийλn с точкой накопления на

бесконечности; при этом для достаточно больших номеров n справедливы оценка (2.13) и,

если c₁ = c₂ = c > 0, оценка (2.14).

Исследование асимптотического поведения собственных значений задачи Штурма-Лиу-

вилля является классической задачей спектральной теории (см., например, [1, с. 204; 21, с. 35;

22, с. 52; 26 с. 12]). Следствие 4 содержит результат об асимптотическом поведении собствен-

ных значений задачи P. Техника получения оценок (2.13) и (2.14) позволяет устанавливать

аналогичные оценки и в случае других свойств функций P и Q.

2.3. Сравнение собственных значений задач типа P. Рассмотрим две задачи типа P,

которые обозначим P¹ и P². Все величины, входящие в постановку этих задач, имеют те

же свойства, что и аналогичные величины в задаче P (см. п. 1); буквенные обозначения

используемых величин те же, что и в задаче P, но дополнены верхним индексом 1 или 2

соответственно.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1594

ВАЛОВИК, ЧАЛЫШОВ

Итак, пусть Φ¹(λ; n) - 1 = 0 и Φ²(λ; m) - 1 = 0 - ИХУ задач P¹ и P² соответственно.

Как и в п. 2, обозначим

pi+(λ) = maxPi(x,λ), qi-(λ) = min Qi(x,λ), i = 1,2,

x∈x

p^i-(λ) = minPi(x,λ), qi+(λ) = maxQi(x,λ), i = 1,2,

x∈x

где P¹, Q¹ и P², Q² - коэффициенты задач P¹ и P² соответственно.

Имеет место

Теорема 4. Пусть выполняются условия

p¹⁺(λ)

p²⁺(λ)

lim

и lim

(2.15)

λ→+∞ q1-(λ)

λ→+∞ q2-(λ)

и, кроме того, при больших λ справедливо неравенство

p¹⁺(λ)

p2-(λ)

≤

(2.16)

q1-(λ)

q²⁺(λ)

Тогда каждое из уравнений Φ¹(λ; n) - 1 = 0 и Φ²(λ; m) - 1 = 0 имеет бесконечное чис-

λ1

λ2

ло решенийλ1

, ... и

, ... соответственно, где n¹⁰ и n²⁰ - некоторые

n¹⁰

n¹⁰+1

n²⁰

n²⁰+1

целые неотрицательные числа; при этом для достаточно больших номеров n справедливо

неравенство

λ1

≤λ2n,

(2.17)

которое переходит в строгое неравенство, если неравенство (2.16) строгое.

Из теоремы 4 вытекает

Следствие 5 (теорема сравнения). Если выполнены условия теоремы 4, то каждая из

задач P¹ и P² имеет бесконечное число собственных значений {λ1n}+∞

и {λ2n}+∞

; при

n=n¹⁰

n=n²

этом для всех достаточно больших номеров n собственные значенияλ1n задачи P¹ иλ2n

задачи P² удовлетворяют неравенству (2.17), которое переходит в строгое неравенство,

если неравенство (2.16) является строгим.

3. Доказательства.

3.1. Доказательство теоремы 1. Необходимость. Пусть число λ является собствен-

ным значением задачи P, т.е. решение y(x; λ) задачи Коши (1.1), (2.2) является собственной

функцией задачи P. Пусть это решение имеет n нулей x₁, . . . , x_n на интервале (0, 1). По

⋃n

решению y(x; λ) построим, как в п. 2.1, функцию η = η(x; λ), определённую на

x_i.

i=0

Используя отображения g_i и заданные с их помощью непрерывные при η ∈ R функ-

ции P (g_i(η; λ); λ) и Q(g_i(η; λ); λ), заключаем, что функция η = η(x; λ) удовлетворяет урав-

нению

η^′ = -ς_i(η;λ),

(3.1)

правая часть которого определена после равенства (2.6).

Очевидно, что справедливы соотношения

η(x_j ± 0; λ) = ±∞, j = 0, n + 1.

(3.2)

Интегрируя автономное уравнение (3.1) на интервале x_i, где i = 0, n, и учитывая, что

функция η = η(x; λ) является решением этого уравнения, получаем равенство

∫

dη(x; λ)

(

) = dx,

(3.3)

ς_i

η(x; λ); λ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

ИНТЕГРАЛЬНАЯ ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ

1595

справедливое для любых α, β ∈ x_i. Сделав в определённом интеграле в левой части равен-

ства (3.3) замену переменной v = η(x; λ), будем иметь

∫

= β - α.

ς_i(v;λ)

η(α;λ)

Устремляя в этом равенстве α к x_i + 0 и β к xi+1 - 0, получаем, учитывая соотноше-

ния (3.2), равенство

−∞

=xi+1 -x_i,

(3.4)

ς_i(v;λ)

+∞

где i = 0, n. Так как правые части равенств (3.4) конечны, то конечны и их левые части. От-

сюда следует сходимость всех несобственных интегралов. Почленно суммируя равенства (3.4)

по i = 0, n, приходим к соотношению

∫

∑

Φ(λ; n) ≡

=xn+1.

(3.5)

ς_i(v;λ)

i=0_-∞

Так как y(x; λ) - собственная функция задачи P, то в рассматриваемом случае xn+1 =

= 1, а следовательно, Φ(λ; n)-1 = 0. Заметим, что в общем случае, т.е. когда решение y(x; λ)

задачи Коши (1.1), (2.2) не обязательно является собственной функцией задачи P, xn+1 ≤ a.

Из проведённых рассуждений следует, что всякое решение (собственное значение) задачи P

удовлетворяет уравнению (2.8) при некотором n = n.

Достаточность. Пусть^λ - решение уравнения (2.8) при n = n. Так как имеет место ра-

венство Φ(^λ; n) - 1 = 0, то это означает, что в силу (3.5) решение y(x;^λ) задачи Коши (1.1),

(2.2) удовлетворяет равенству y(1;^λ) = 0 и что число нулей функции y(x;^λ) на интерва-

ле (0, 1) равно в точности

n. Равенство y(1;^λ) = 0 для решения задачи Коши (1.1), (2.2)

равносильно тому, что^λ - собственное значение задачи P. Теорема 1 доказана.

3.2. Доказательство следствия 1. То, что функция y(x;^λ) удовлетворяет краевым

условиям (1.2), следует из доказательства теоремы 1.

Если y(x_i; λ) = y^′(x_i; λ) = 0, то y(x; λ) ≡ 0, а это противоречит условию y^′(0; λ) = 1 = 0.

Отсюда следует результат об однократности нулей x_i.

Формулы (3.4) дают расстояния между соседними нулями решения y(x;^λ). Складывая

первые j членов в (3.4), приходим к формуле для j-го нуля. Следствие 1 доказано.

3.3. Доказательство утверждения 1. Предположим, что найдётся такое собственное

значение

λ ∈ Λ, что ему отвечают два линейно независимых решения y ≡ y₁(x;^λ) и y ≡

≡ y₂(x;^λ) задачи (1.1), (1.2). Пусть W(x) - определитель Вронского, составленный для этих

двух решений. Так как y₁ и y₂ - линейно независимые решения уравнения (1.1), то W (x) = 0

для всех x ∈ [0, 1]. Но, как легко видеть,



^y₁(0;^λ) y₂(0;^λ)



W (0) =^

⁼

y′1(0;^λ) y′2(0;^λ)

^y′1(0;^λ) y′2(0;^λ)

Это означает, что решения y₁ и y₂, вопреки первоначальному предположению, линейно зави-

симы. Отсюда следует, что всякое собственное значениеλ ∈ Λ задачи P является простым.

Утверждение 1 доказано.

3.4. Доказательство утверждения 2. Так как w(x, η; λ) > 0, а значит, и ς_i(v; λ) > 0,

то T_i(λ) > 0 для всех λ ∈ Λ_i и всякого i ∈ Z₊.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1596

ВАЛОВИК, ЧАЛЫШОВ

Решение y ≡ y(x; λ) задачи Коши (1.1), (2.2) непрерывно зависит от λ при λ ∈ Λ в силу

классических результатов теории обыкновенных дифференциальных уравнений [23, c. 117].

Учитывая это и принимая во внимание способ построения отображений g_i, получаем, что

функции x ≡ g_i(η; λ) непрерывны по аргументам η и λ при (η, λ) ∈ R × Λ_i. Но тогда

подынтегральные выражения в T_i(λ) непрерывны при (η, λ) ∈ R × Λ_i как суперпозиции

непрерывных функций. Отсюда следует, что при каждом значении индекса i функция T_i(λ)

непрерывно зависит от λ при λ ∈ Λ_i. Утверждение 2 доказано.

3.5. Доказательство утверждения 3. Рассмотрим функцию T_i(λ), заданную равен-

ством (2.6). Введём обозначение

ξ_i(v,t;λ) := Q(g_i(t;λ);λ) +

P (g_i(t; λ); λ)

и пусть ξ+i(v; λ) := maxξi(v,t;λ) и ξ-i(v;λ) := minξi(v,t;λ).

t∈R

Тогда, как легко видеть, выполняются неравенства

∫

≤

(3.6)

ξ⁺(v; λ)

ς_i(v; λ)

ξ^-i(v;λ)

где величина ς_i(v; λ) определена равенством (2.6).

Величины ξ+i(v; λ) и ξ^-i(v; λ) оцениваются следующим образом:

ξ+i(v;λ) ≤ max supξi(v,t;λ) ≤ ξ+(v;λ) и ξ-i(v;λ) ≥ min

inf

ξ_i(v,t;λ) ≥ ξ^-(v;λ),

i=0,n t∈R

i=0,n

t∈R

где ξ⁺(v; λ) = q₊+v²/p_- и ξ^-(v; λ) = q_-+v²/p₊, а p_± и q_± определены после неравенств (2.1)

и зависят от λ. Согласно предыдущему, если t пробегает вещественную ось, то значения x =

= g_i(t,λ) пробегают интервал x_i.

Тогда неравенство (3.6) принимает вид

∫

≤

ξ⁺(v;λ)

ξ+i(v; λ)

ς_i(v; λ)

ξ^-i(v;λ)

ξ^-(v;λ)

Вследствие предыдущего получаем оценки

∫

≤ T_i(λ) ≤

(3.7)

ξ⁺(v;λ)

ξ^-(v;λ)

−∞

-∞

Интегралы в левой и правой частях двойного неравенства (3.7) вычисляются точно:

∫

π√p

π√p+

√

(3.8)

ξ⁺(v;λ)

q₊

ξ^-(v;λ)

q_-

-∞

−∞

С учётом (3.8) неравенство (3.7) принимает вид (2.9). Утверждение 3 доказано.

3.6. Доказательство теоремы 2. Из оценок (2.9) и условия (2.11) следует, что, во-первых,

Λ_i являются неограниченными множествами для всех i ∈ Z₊, а во-вторых, для каждого i ∈

∈ Z₊ найдётся неограниченное связное множествоΛi ⊂ Λ_i.

Далее, из оценок (2.9), (2.10) и условия (2.11) вытекает, что min Φ(λ; n) < 1. В силу того,

λ∈^Λn

что Φ - это сумма расстояний между нулями x_i решения y(x; λ) задачи Коши (1.1), (2.2),

то, начиная с некоторого n = n₀ ≥ 0, получаем

max Φ(λ; n) = a > 1.

λ∈^Λn

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

ИНТЕГРАЛЬНАЯ ХАРАКТЕРИСТИЧЕСКАЯ ФУНКЦИЯ

1597

Так как min Φ(λ; n) < 1, а max Φ(λ; n) > 1, то в силу непрерывности T_i(λ) по λ при

λ∈^Λn

λ ∈ Λi найдётся такое значениеλ ∈ Λn, что Φ(^λ;n) = 1.

Проведённое рассуждение справедливо для каждого n = n₀, n₀ + 1, . . . , и, значит, для

каждого n = n₀, n₀ + 1, . . . существует по крайней мере одно решение λ =λn ∈ Λ уравне-

ния (2.8). Другими словами, при условии (2.11) существует бесконечное число решенийλn ∈ Λ

уравнения (2.8).

Очевидно, что lim

λ_n = +∞. Теорема 2 доказана.

n→∞

3.7. Доказательство теоремы 3. Так как из условий (2.12) вытекает условие (2.11), то

результат о существовании бесконечного числа решений

λ_n ∈ Λ уравнения (2.8), где n =

= n₀,n₀ + 1,... , следует из теоремы 2.

Докажем оценку (2.13). В силу оценки (2.10) и соотношений (2.12) заключаем, что найдутся

такие положительные числа δ₁, δ₂, для которых при всех достаточно больших λ имеет место

соотношение

C₁ - δ₁ ≤ Φ(λ;n) ≤ C₂ + δ₂,

(3.9)

в котором C_i = π(n + 1)λ-ci + O(λ-ci-δi ), i = 1, 2. Заменяя в (3.9) Φ единицей и обращая

полученные неравенства, приходим к оценке (2.13).

Если положить c₁ = c₂ = c > 0, то оценка (2.13) переходит в оценку (2.14). При этом

коэффициент при главном члене асимптотической формулы (2.14) равен π1/c. Теорема 3 до-

казана.

3.8. Доказательство теоремы 4. Если выполняются соотношения (2.15), то, согласно

теореме 2, найдутся такие целые неотрицательные числа n¹⁰ и n²⁰, что каждое из уравнений

Φ¹(λ;n) - 1 = 0 и Φ²(λ;n) - 1 = 0 имеет не меньше одного решения λ =λ1 ∈ Λ и λ =λ2 ∈ Λ

при n = n¹⁰, n¹⁰+1, . . . и n = n²⁰, n²⁰+1, . . . соответственно. Таким образом, если выполняются

условия (2.15), то каждое из уравнений Φ¹(λ; n) - 1 = 0 и Φ²(λ; n) - 1 = 0 имеет бесконечное

λ1

λ2

число решенийλ1

, ... и

, ... соответственно.

n¹⁰

n¹⁰+1

n²⁰

n²⁰+1

Используя следствие 3, получаем оценки

√

p^i-(λ)

pi+(λ)

π(n + 1)√

≤ Φⁱ(λ;n) ≤ π(n + 1)√

i = 1,2,

(3.10)

qi+(λ)

q^i-(λ)

где функции pi+(λ), p^i-(λ) и qi+(λ), q^i-(λ) определены в п. 2.3.

Если справедливо неравенство (2.16), то, как нетрудно видеть, из оценок (3.10) следует, что

√

p¹⁺(λ)

p2-(λ)

Φ¹(λ;n) ≤ π(n + 1)√

≤ π(n + 1)√

≤ Φ²(λ;n),

q1-(λ)

q²⁺(λ)

т.е. Φ¹(λ; n) ≤ Φ²(λ; n). Полученное неравенство влечёт за собой неравенство (2.17). Теорема 4

доказана.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 18-71-

10015).

СПИСОК ЛИТЕРАТУРЫ

1. Сансоне Дж. Обыкновенные дифференциальные уравнения. Т. I. М., 1953.

2. Mennicken R., Schmid H., Shkalikov A. A. On the eigenvalue accumulation of Sturm-Liouville problems

depending nonlinearly on the spectral parameter // Math. Nachr. 1998. Bd. 189. Hf. 1. S. 157-170.

3. Bohner M., Kratz W., Hilscher R.

Š. Oscillation and spectral theory for linear hamiltonian systems with

nonlinear dependence on the spectral parameter // Math. Nachr. 2012. Bd. 285. Hf. 11-12. S. 1343-1356.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1598

ВАЛОВИК, ЧАЛЫШОВ

4. Hilscher R.Š. Eigenvalue theory for time scale symplectic systems depending nonlinearly on spectral

parameter // Appl. Math. and Comput. 2012. V. 219. № 6. P. 2839-2860.

5. Hartman P. Boundary value problems for second order, ordinary differential equations involving a

parameter // J. of Differ. Equat. 1972. V. 12. № 1. P. 194-212.

6. Atkinson F.V., Langer H., Mennicken R. Sturm-Liouville problems with coefficients which depend

analytically on the eigenvalue parameter // Acta Sci. Math. (Szeged). 1993. V. 57. № 1-4. P. 25-44.

7. Валовик Д.В. Об интегральной характеристической функции задачи Штурма-Лиувилля // Мат.

сб. 2020. Т. 211. № 11. С. 41-53.

8. Hochstadt H. Asymptotic estimates for the Sturm-Liouville spectrum // Comm. on Pure and Appl. Math.

1961. V. 14. № 4. P. 749-764.

9. Binding P.A., Browne P.J., Seddighi K. Sturm-Liouville problems with eigenparameter dependent

boundary conditions // Proc. of the Edinburgh Math. Soc. 1994. V. 37. № 1. P. 57-72.

10. Бен Амара Ж., Шкаликов А.А. Задача Штурма-Лиувилля с физическим и спектральным пара-

метрами в граничном условии // Мат. заметки. 1999. Т. 66. № 2. C. 163-172.

11. Cocskun H., Bayram N. Asymptotics of eigenvalues for regular Sturm-Liouville problems with eigenvalue

parameter in the boundary condition // J. of Math. Anal. and Appl. 2005. V. 306. № 2. P. 548-566.

12. Капустин Н.Ю. Осцилляционные свойства решений одной несамосопряженной спектральной зада-

чи со спектральным параметром в граничном условии // Дифференц. уравнения. 1999. Т. 35. № 8.

P. 1024-1027.

13. Керимов Н.Б., Мамедов Х.Р. Об одной краевой задаче со спектральным параметром в граничных

условиях // Сиб. мат. журн. 1999. Т. 40. № 2. C. 325-335.

14. Binding P.A., Browne P.J., Watson B.A. Sturm-Liouville problems with boundary conditions rationally

dependent on the eigenparameter, ii // J. of Comput. and Appl. Math. 2002. V. 148. № 1. P. 147-168.

15. Binding P.A., Browne P.J., Watson B.A. Transformations between Sturm-Liouville problems with

eigenvalue dependent and independent boundary conditions // Bull. of the London Math. Soc. 2001.

V. 33. № 6. P. 749-757.

16. Смирнов Ю.Г. Задачи сопряжения на собственные значения, описывающие распространение ТЕ-

и ТМ-волн в двухслойных неоднородных анизотропных цилиндрических и плоских волноводах

// Журн. вычислит. математики и мат. физики. 2015. Т. 55. № 3. C. 460-468.

17. Zhang Maozhu, Li Kun. Dependence of eigenvalues of Sturm-Liouville problems with eigenparameter

dependent boundary conditions // Appl. Math. and Comput. 2020. V. 378. Art. 125214.

18. Алиев З.С., Дуньямалиева А.А. Базисные свойства корневых функций задачи Штурма-Лиувилля

со спектральным параметром в граничных условиях // Докл. РАН. 2013. Т. 451. № 5. С. 487-491.

19. Керимов Н.Б., Поладов Р.Г. Базисные свойства системы собственных функций задачи Штурма-

Лиувилля со спектральным параметром в граничных условиях // Докл. РАН. 2012. Т. 442. № 1.

С. 14-19.

20. Марченков Д.Б. Базисность в пространстве l_p(0, 1) системы собственных функций, отвечающей

задаче со спектральным параметром в граничном условии // Дифференц. уравнения. 2006. Т. 42.

№ 6. C. 847-849.

21. Марченко В.А. Спектральная теория операторов Штурма-Лиувилля. Киев, 1972.

22. Наймарк М.А. Линейные дифференциальные операторы. М., 1969.

23. Хартман Ф. Обыкновенные дифференциальные уравнения. М., 1970.

24. Аткинсон Ф. Дискретные и непрерывные граничные задачи. М., 1968.

25. Трикоми Ф. Дифференциальные уравнения. М., 1962.

26. Левитан Б.М., Саргсян И.С. Операторы Штурма-Лиувилля и Дирака. М., 1988.

Пензенский государственный университет

Поступила в редакцию 16.09.2020 г.

После доработки 07.07.2021 г.

Принята к публикации 08.09.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021