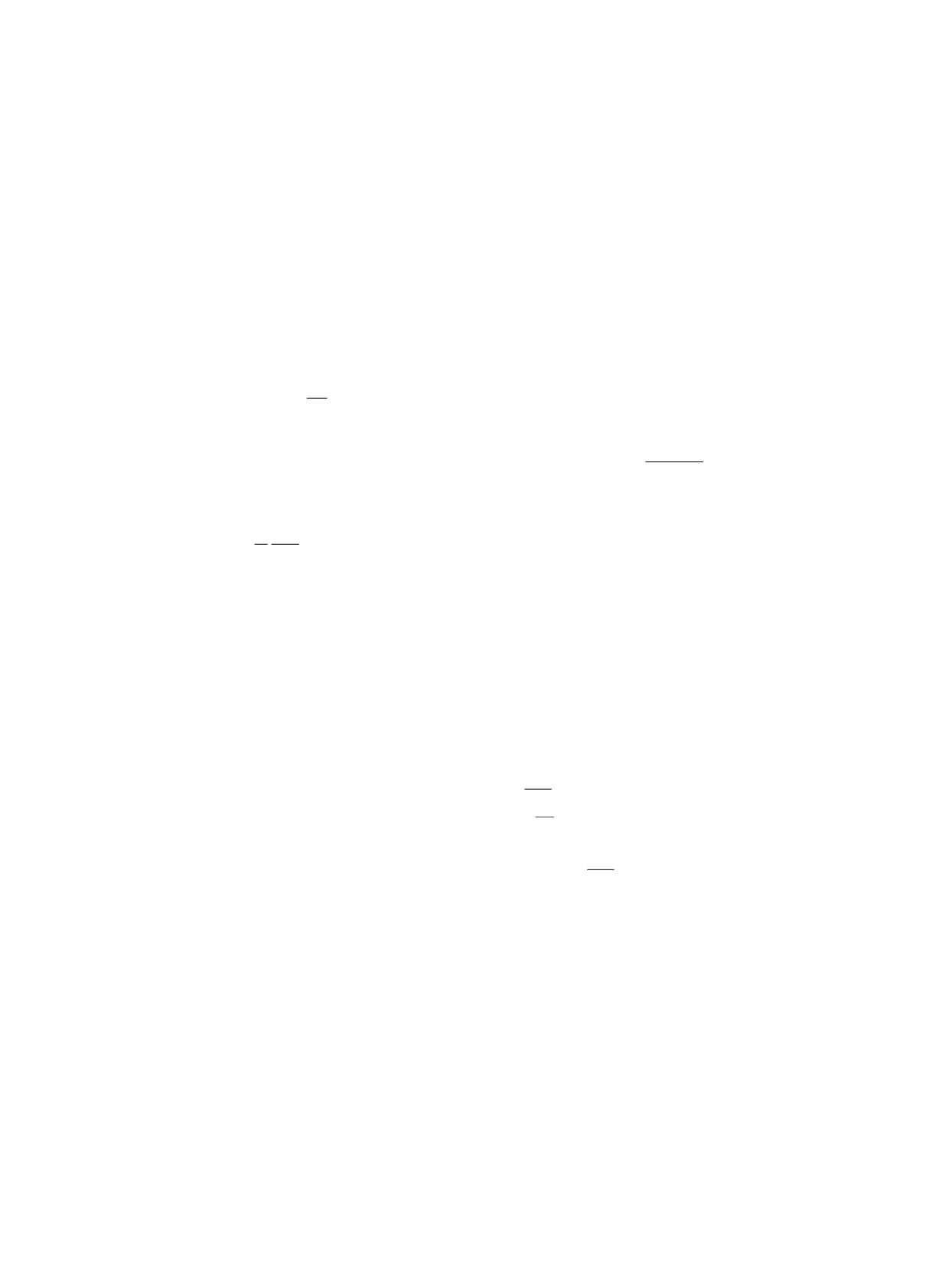ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 12, с. 1654-1664

ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ

УДК 517.968.4

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВОЛЬТЕРРЫ

С НАГРУЗКАМИ И БИФУРКАЦИОННЫМИ

ПАРАМЕТРАМИ: ТЕОРЕМЫ СУЩЕСТВОВАНИЯ

И ПОСТРОЕНИЕ РЕШЕНИЙ

Рассматривается нелинейное интегральное уравнение Вольтерры c локальными и/или ин-

тегральными нагрузками на искомое решение, заданными с помощью интеграла Стилтьеса.

Уравнение содержит бифуркационный параметр и при любом его значении имеет триви-

альное решение. Получены необходимые и достаточные условия на те значения параметра

(точки бифуркации), в окрестности которых уравнение имеет нетривиальные непрерыв-

ные вещественные решения. Построены главные члены асимптотики ветвей решений и

указан способ их уточнения. Приведены иллюстрирующие примеры. Установлен принцип

линеаризации, позволяющий находить точки бифуркации, используя только информацию

о линейной части нелинейного уравнения с векторной нагрузкой и векторным бифуркаци-

онным параметром.

DOI: 10.31857/S0374064121120086

Введение. Рассмотрим уравнение

x(t) = L(x(t), x_α, t, λ),

(1)

где t ∈ [0, T ], λ ∈ R - бифуркационный параметр, x(t) ∈ C[0, T ] - искомая функция, функ-

ционал x_α, называемый в приложениях нагрузкой, задаётся с помощью интеграла Стилтьеса:

∫t₂

x_α =

x(t) dα(t), где α(t) - заданная функция ограниченной вариации, [t₁, t₂] ∈ (0, T ). По-

t₁

этому нагрузка x_α может быть как локальной вида x_α = x(α), α ∈ (0, T ), так и нелокальной.

Нелинейное интегральное отображение L(x(t), x_α, t, λ) определяется формулой (2) (см. ниже).

Уравнения с нагрузками по свойствам и по области приложений близки нестандартным

дифференциально-интегральным уравнениям [1] и уравнениям нейтрального типа [2]. Отме-

тим, что метод выпуклых мажорант позволяет исследовать области существования нелиней-

ных интегральных уравнений (см., например, [3]). Функционал x_α и функция x(t) зависят

от параметра λ. В дальнейшем для упрощения записи эта зависимость не всегда указывается

явно.

В последние годы части этих разделов теорий дифференциальных и интегральных урав-

нений оформились в самостоятельные направления. Однако несмотря на наличие большого

числа работ (см. работы [4-10] и библиографию в них) даже простейшие классы уравнений

Вольтерры с нагрузками и бифуркационными параметрами оставались неизученными. Цель

настоящей работы - указать подход к исследованию таких уравнений достаточно общего вида.

1. Постановка задачи. Пусть выполняется условие

I. Нелинейное отображение L : C[0,T] → C([0,T] × R) имеет вид

∑

L(x(t), x_α, t, λ) = a(t, λ)x_α +

f_ik(t,λ)xⁱ(t)x^kα +

i+k=l

∫^t

∑

K_ik(t,s,λ)xⁱ(s)x^kα ds + R(x(t),x_α,t,λ),

(2)

i+k=l

1654

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВОЛЬТЕРРЫ

1655

здесь l и N

- заданные натуральные числа, l ≥ 2, t ∈ [0, T ], функции x(t), f_ik(t, λ),

K_ik(t,s,λ), R(x(t),x_α,t,λ) являются непрерывными по совокупности переменных и доста-

точно гладкими по переменной λ ∈ R, которая в приложениях играет роль параметра. Кроме

того, в окрестности точки λ₀ предполагается выполненной следующая оценка, указывающая

порядок малости при ∥x∥ → 0, |xα| → 0 нелинейного члена R :

∥R(x(t), x_α, t, λ)∥ = O((∥x∥ + |x_α|)N+1),

где ∥x∥ = max |x(t)|.

0≤t≤T

Очевидно, что при любом λ уравнению (1), (2) удовлетворяет пара x(t) = 0, x_α = 0. Об-

ластью значений отображения L является пространство функций непрерывных по аргументу

t и достаточно гладких по параметру λ.

Определение 1. Точка λ₀ называется точкой бифуркации уравнения (1), если для лю-

бых ε > 0, δ > 0 найдутся непрерывная функция x(t) и число λ ∈ R, удовлетворяющие

неравенствам 0 < ∥x(t)∥ < ε, |λ - λ0| < δ и уравнению (1).

В данной работе находятся условия, при выполнении которых точка λ₀ ∈ R является

точкой бифуркации уравнения (1), (2) и можно построить асимптотику нетривиальных вет-

вей малых решений уравнения (1), (2). Под ветвью понимается непрерывное вещественное

решение x(t) такое, что x(t) → 0 при λ → λ₀ + 0 (или λ → λ₀ - 0). Очевидно, что каждому

решению x(t) ставится в соответствие единственная нагрузка с помощью заданного линейного

функционала.

Известно (см., например, [4-7]), что нагруженные уравнения моделируют процессы, состо-

яние которых в какие-либо моменты (или локальные промежутки времени) оказывает влияние

на их протекание в целом. Нагруженным дифференциальным уравнениям (обыкновенным и в

частных производных) посвящено достаточно много работ (см. библиографию в [5]). Но клас-

сы интегральных уравнений Вольтерры с нагрузками и бифуркационный анализ в моделях с

нагрузками в известной нам литературе ранее не изучались.

Мы получим решение поставленной задачи, построив уравнение относительно нагрузки с

бифуркационным параметром λ и исследовав его с помощью метода последовательных при-

ближений, методов степенной геометрии и при помощи вращения конечномерных векторных

полей. Сочетание таких методов восходит к классическим подходам, изложенным в [11-17],

и нашло приложение при решении ряда сложных задач механики, математической физики и

энергетики [1, 17-20].

2. Построение уравнения относительно нагрузки и необходимые условия бифур-

кации. Для большей наглядности предлагаемого подхода сначала проведём его изложение при

наличии только одной нагрузки (т.е. в приведённой выше постановке; случай же, когда λ и

x₂ - векторы, рассматривается в п. 5 работы). Используя метод последовательных приближе-

ний и теорему о неявном отображении в аналитическом случае, решение x(t) интегрального

уравнения Вольтерры (1) построим при t ∈ [0, T ] и |λ - λ₀| ≤ ρ₁,

|x_α| ≤ ρ₂ в виде ряда

∑

x(t) =

a_n(t,λ)x^nα.

(3)

n=1

Функции a_n(t, λ) вычислим последовательно, использовав рекуррентные формулы

a₁(t,λ) = a(t,λ),

)

(n-1∑



∂



a_n(t,λ) =

a_k(t,λ)x^kα,x_α,t,λ

n = 2,3,...



n! ∂x^nα

k=1

xα=0

При этом в силу структуры оператора (2) очевидно, что для первых 2l - 2 коэффициентов

ряда (3) получим простые формулы

a₂(t,λ) = ... = al-1(t,λ) ≡ 0,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1656

СИДОРОВ Н.А., СИДОРОВ Д.Н.

[

∫

]

∑

a_n(t,λ) =

f_ik(t,λ)aⁱ(t,λ) + K_ik(t,s,λ)aⁱ(s,λ)ds ,

n = l,2l - 2.

i+k=n

На основании теоремы о неявном отображении ряд (3) сходится в достаточно малой окрест-

ности |x_α| ≤ ρ₂. Величину ρ₂ можно оценить снизу, используя метод выпуклых мажорант

[3, 18]. Эту возможность продемонстрируем ниже в п. 4 при рассмотрении примера 2. Из из-

ложенного вытекает

Лемма 1. Пусть выполнены условия I. Тогда нагрузка x_α удовлетворяет уравнению

∑

A₁(λ)x_α + A_i(λ)x^iα = 0,

(4)

i=l

где

t₂

∫t2

∫

A₁(λ) = a₁(t,λ)dα(t) - 1, A_i(λ) = a_i(t,λ)dα(t), i = l,l + 1,...

t₁

Доказательство вытекает из возможности представления решения x(t) в виде ряда (3)

и задания нагрузки с помощью линейного функционала (интеграла Стилтьеса).

Следствие 1 (необходимое условие бифуркации). Для того чтобы число λ₀ могло быть

точкой бифуркации интегрального уравнения (1), (2), необходимо выполнение равенства

A₁(λ₀) = 0.

Доказательство. Уравнение (4) при каждом λ имеет тривиальное решение x_α ≡ 0. Если

A₁(λ₀) = 0, то при |λ - λ₀| ≤ ρ₁ в окрестности |x_α| < ρ₂ на основании теоремы о неявной

функции малое решение уравнения (4) единственно. Следовательно, в этом случае x_α ≡ 0

и λ₀, согласно определению 1, не является точкой бифуркации уравнения (1). Следствие

доказано.

Следствие 2. Пусть в уравнении (4) все коэффициенты A_i(λ) в точке λ₀ равны нулю.

Тогда λ₀ будет точкой бифуркации. Более того, уравнение (1), (2) при λ = λ₀ имеет c-пара-

метрическое нетривиальное решение x(t,c), зависящее от достаточно малого параметра c.

При 0 < |λ - λ₀| < ρ₁ других малых решений уравнение (1), (2) не имеет.

Доказательство очевидно, так как в силу условий следствия 2 нагрузка x_α при λ =

= λ₀ в разложении (3) решения уравнения (1), (2) остаётся произвольным параметром c из

интервала |c| ≤ ρ₂, в котором сходится ряд (3). Следствие доказано.

3. Достаточные условия существования точки бифуркации и асимптотика ре-

шений. Конструктивные достаточные условия существования точек бифуркации получим,

определив вещественные решения x_α → 0 при λ → λ₀ + 0 (λ → λ₀ - 0) уравнения (4) и

подставив их в правую часть представления (3). Напомним, что в уравнении (4)

(

∫

)

∑

A_l(λ) =

f_ik(α,λ)aⁱ(α,λ) + K_ik(α,s,λ)aⁱ(s,λ)ds

i+k=l

в случае локальной нагрузки и

t₂

∫

)

∑(

A_l(λ) =

f_ik(t,λ)aⁱ(t,λ) + K_ik(t,s,λ)aⁱ(s,λ)ds dα(t)

i+k=l

t₁

в случае интегральной (нелокальной) нагрузки.

В силу леммы 1 для построения асимптотики величины x_α следует в уравнении (4) поло-

жить λ = λ₀ + μ, где μ - малый вещественный параметр.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВОЛЬТЕРРЫ

1657

Потребуем выполнения условий.

II. Число λ₀ - корень уравнения A₁(λ) = 0 кратности p.

III. Имеет место соотношение A_l(λ₀) = 0.

Тогда уравнение (4) при λ = λ₀ + μ преобразуется к виду

(

)

A(p)1(λ₀)μ^p + O(|μ|p+1) x_α + (A_l(λ₀) + O(|μ|))x^lα + O(|x_α|l+1) = 0

(5)

в окрестности точек x_α = 0, μ = 0. Решение уравнения (5) будем искать, используя разло-

жение Ньютона-Пьюизё (диаграмма Ньютона определяет показатель p/(l - 1)):

x_α = (c₀ + O(|μ|))μp/(l-1), c₀ = 0.

Очевидно, что значение c₀ удовлетворяет уравнению



1 d^pA₁(λ)



sign μ^p

c + A_l(λ₀)c^l = 0.

(6)



p! dλ^p

λ=λ₀

Поэтому при нечётном p получаем два уравнения, а именно

A(p)1(λ₀)c + A_l(λ₀)c^l = 0 при μ > 0,

(7)

−

A(p)1(λ₀)c + A_l(λ₀)c^l = 0 при μ < 0.

(8)

При нечётном p и любом l уравнение (6) хотя бы в одной из полуокрестностей точки

μ = 0 имеет простой вещественный корень c₀ = 0.

Случай 1. При чётном l вещественным корнем уравнения (7) является

√

(p)

1 A

(λ₀)

c₀ =l-1 -

p! A_l(λ₀)

а уравнение (5) имеет вещественное решение x_α ∼ c₀|μ|p/(l-1) при μ → +0 и соответственно

x_α ∼ -c₀|μ|p/(l-1) при μ → -0.

Случай 2. При нечётном l и A(p)1(λ₀)A_l(λ₀) < 0 у уравнения (7) будет два вещественных

корня

√



A(p)1(λ0)

c0±

=±l-1



^,

A_l(λ₀)

а у уравнения (5) при 0 ≤ μ ≤ ρ₁ - два вещественных решения xα± ∼ c0±μp/(l-1) при μ → +0.

Если l нечётно и A(p)1(λ₀)A_l(λ₀) > 0, верен аналогичный результат при -ρ₁ ≤ μ ≤ 0.

Из изложенного вытекает

Теорема 1. Пусть выполнены условия I, II, III. Тогда λ₀ - точка бифуркации уравне-

ния (1), (2). Более того, при чётном l уравнение (1), (2) имеет в окрестности точки λ₀

единственное малое вещественное решение x(t,λ), при этом

√

(p)

1 A

(λ₀)

x(t, λ) ∼ a₁(t, λ₀)l-1 -

(λ - λ₀)p/(l-1) при λ → λ₀.

p! A_l(λ₀)

При нечётном l уравнение (1), (2) имеет в одной из полуокрестностей точки λ₀ два

вещественных решения с аналогичной асимптотикой.

Из доказательства теоремы 1 с учётом следствия 2 вытекает

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1658

СИДОРОВ Н.А., СИДОРОВ Д.Н.

Теорема 2. Пусть выполнены условия I, II и λ₀ - корень уравнения A₁(λ) = 0 нечётной

кратности. Тогда λ₀ - точка бифуркации уравнения (1), (2).

Теорема 1 с учётом возможности представления других многообразий решений уравнения

(4) в виде разложений Ньютона-Пюизё допускает обобщения.

Действительно, рассмотрим коэффициенты A₁(λ), A_l(λ), Al+1(λ), . . . , An-1(λ) уравне-

ния (4) и введём условие

IV. Число λ₀ является нулём функции A_i(λ) кратности p_i, i=1, l, . . . , n-1, а A_n(λ₀) = 0.

Нанесём на координатную плоскость точки

(1, p₁),

(l, p_l), . . . , (n - 1, pn-1), (n, 0) и построим диаграмму

Ньютона для этих точек (рисунок).

Возьмём на рисунке грань (a, b). На этой грани лежат

точки (i, p_i), удовлетворяющие равенству ir/s + k = θ,

где r/s = tg ϕ, а θ - ордината точки пересечения про-

должения грани (a, b) с осью ординат. Очевидно, что θ

также будет рациональным числом.

Будем искать решение уравнения (4) в виде xα =

= c(μ)|μ|^r/s, c(0) = 0. Тогда c(0) должно удовлетворять

по крайней мере одному из двух уравнений

∑

Рисунок. Диаграмма Ньютона.

P_±(c) :=

sign μ^k

a(pi)_i(λ₀)cⁱ = 0.

p_i!

ir/s+k=θ

Построив простые вещественные корни c^∗ = 0 этих уравнений, запишем, как и в дока-

зательстве теоремы 1, асимптотики малых решений x(t, λ) уравнения (1), (2) в двух полу-

окрестностях точки бифуркации λ₀.

4. Построение решений уравнения (1), (2) методом неопределённых коэффи-

циентов. Изложенный выше подход позволяет строить решения уравнения (1), (2) непосред-

ственно в виде ряда по целым или дробным степеням параметра λ - λ₀, где λ₀ - точка

бифуркации. Коэффициенты ряда, как и в известном методе Некрасова-Назарова [13, 15]

продолжения решения, определяются из рекуррентной последовательности линейных уравне-

ний. Особенность этого аналитического метода состоит в том, что произвольные постоянные

на каждом шаге находятся из условий разрешимости последующих уравнений этой последо-

вательности.

Пример 1 демонстрирует такой способ решения уравнений с нагрузками в условиях теоре-

мы 1, а пример 2 - построение параметрического семейства решений при выполнении условий

следствия 2.

Пример 1. Рассмотрим уравнение

∫t

x(t) = t(λ - 2)x(1) - tsx³(s) ds, t ∈ [0, T ].

(9)

Для него находим, что уравнение (4) для нагрузки имеет следующие коэффициенты: A₁(λ) =

= λ-3, A₃(λ) = -(λ-2)³/5. Поэтому, согласно следствию 1, точкой бифуркации уравнения

(9) может быть только точка λ₀ = 3. Для этой точки выполнены условия I, II при p = 1,

l = 3. Следовательно, согласно теореме 1, решение будем искать в виде ряда

∑

x(t) =

a_n(t)μn/2, где μ = λ - 3.

n=1

Используя метод неопределённых коэффициентов, для вычисления коэффициентов a_n(t)

получаем последовательность линейных уравнений

∫^t

a₁(t) = ta₁(1), a₂(t) = ta₂(1), a₃(t) = ta₃(1) + ta₁(1) - tsa³¹(s)ds,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВОЛЬТЕРРЫ

1659

∫^t

∫

a₄(t) = ta₄(1) + ta₂(1) - 3 tsa²¹(s)a₂(s)ds, a₅(t) = ta₅(1) + ta₃(1) - 3 tsa²¹(s)a₃(s)ds, ...

Следовательно, a₁(t) = tc₁, a₂(t) = tc₂, . . . Постоянные c₁, c₂ определятся из условий

разрешимости последующих урав√ений цепочки. Именно, c1 - из алгебраического уравнения

c₁ - c³¹/5 = 0. Поэтому c₁ = ±

5, а интегральное уравнение (9) имеет в положительной

полуокрестности точки бифуркации λ₀ = 3 два малых нетривиальных вещественных решения

√

x1,2 ∼ ±t(λ - 3)1/2

при λ → 3.

Пример 2. Рассмотрим интегральное уравнение

∫t

x(t) = tb(λ)x(1) - (t - 1)x³(s) ds, t ∈ [0, T ], T > 1.

(10)

Пусть b(1) = 1. Тогда, согласно следствию 2, точка λ₀ = 1 будет точкой бифуркации уравне-

ния (10). Более того, при λ₀ = 1 малое решение этого уравнения можно построить в виде ряда

∑

x(t) = tc +

a_n(t)cⁿ,

n=3

равномерно сходящегося при t ∈ [0, T ] и |c| ≤ ρ, где ρ > 0 достаточно мало. Коэффициенты

a_n(t) также легко вычислить методом неопределённых коэффициентов.

Для оценки радиуса ρ сходимости этого ряда построим, следуя [3], мажорирующую си-

стему

r=Tρ+T²r³,

1 = 3T²r².

√

Пара r^∗ = 1/(

3T), ρ∗ = 2r∗/(3T ) удовлетворяет этой системе. Поэтому при |c| ≤ ρ <

√

< 2/(3

3T²) ряд равномерно сходится, а интегральное уравнение (10) в пространстве C[0, T ]

имеет c-параметрическое решение.

5. Интегральные уравнения Вольтерры с векторной нагрузкой и векторным би-

фуркационным параметром. Пусть в уравнении (1) x_α = (xα1,... ,xαn ), λ = (λ₁,... ,λ_m).

Значения нагрузки и бифуркационный параметр лежат в окрестностях нулей векторных про-

странств Rⁿ и R^m. Рассмотрим уравнение (1) с правой частью L, которая теперь задаётся

равенством

∑

L(x(t), x_α, t, λ) =

b_k(t,λ₁,... ,λ_m)xαk +

k=1

[

∑

fjk1...kn(t,λ1^,...,λm)xj(t)xα11...xαn +

s=l j+k₁+...+kn=s

∫t

]

(11)

+ Kjk1,...,kn(t,s,λ1^,...,λm)xj(s)xα11...xαnn^ds,

где b_k, fjk1,...,kn^,Kjk1,...,kn-непрерывныефункции,достаточногладкиеповсемλi^{вокрест-}

ности ∥λ - λ₀∥ ≤ δ. Далее, для краткости, (1), (11) обозначает интегральную систему (1) с

правой частью вида (11).

Найдём достаточные условия, когда вектор λ₀ ∈ R^m будет точкой бифуркации и можно

построить асимптотику вещественных решений при λ_i = λ0i + μ, i = 1, . . . , m, где μ ∈ [0, δ]

(или μ ∈ [-δ, 0]).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1660

СИДОРОВ Н.А., СИДОРОВ Д.Н.

Начнём с построения системы для определения векторной нагрузки. Для этого построим

решение x(t) с помощью ряда

∑

a_j(t,λ,x_α)

(12)

j=1

по однородным формам компонент векторной нагрузки x_α. Здесь a_j(t, λ, μxα1 , . . . , μxαn ) =

= μ^ja_j(t,λ,xα1,...,xαn). Отметим, что j-однородные формы вычисляются однозначно ре-

куррентным образом:

∑

a₁(t,λ,x_α) =

b_k(t,λ)xαk ; a₁ = ... = al-1 = 0;

k=1

[

∑

a_m(t,λ,x_α) =

fjk1,...,kn(t,λ)a1(t,λ,xα)jxα11...xαn +

j+k₁+...+kn=m

∫t

]

m = l,2l - 1;

+ Kjk1,...,kn(t,s,λ)a1(s,λ,xα)jxα11

...xknαn^ds

)

(j-1∑



∂



a_j(t,λ,x_α) =

a_n(t,μxα1 ,... ,μxαn ),μx_α,t,λ

j = 2l,2l + 1,...



j! ∂μ^j

n=1

μ=0

Замечание. Последовательность {x_m}, где x_m(t) = L(xm-1(t), x_α, t, λ) при начальном

∑_n

приближении x₀(t) =

b_k(t,λ)xαk и при ∥xα∥ ≤ ρ, равномерно сходится к сумме ря-

k=1

да (12). Поэтому в неаналитическом случае для построения решения и коэффициентов a_j

можно использовать метод последовательных приближений.

Лемма 2. Искомая нагрузка x_α в решении (12) должна удовлетворять n нелинейным

с параметрами λ_i уравнениям

∑

A₁(λ)x_α + F_j(λ,x_α) = 0.

(13)

j=l

Здесь F_j = (Fj1, . . . , F_jn)^т, λ = (λ₁, . . . , λ_m), F_ji, i = 1, n, - j-однородные формы компонент

вектора x_α = (xα1 , . . . , xαn ), A₁(λ) = [(b_k(t, λ), α_i)]i,k=1,n - n × n-матрица, α_i - линейные

функционалы в пространстве C[0, T ] (интегралы Стилтьеса).

Доказательство леммы проводится применением функционалов α₁, . . . , α_n к обеим час-

тям равенства (12) с учётом обозначения xαi = (x(t), α_i), i = 1, n, для функционалов.

Рассмотрение системы (13) приводит к следующему результату.

Теорема 3 (необходимое условие бифуркации). Для того чтобы вектор λ₀ ∈ R^m мог

быть точкой бифуркации интегрального уравнения (1), (11), необходимо выполнение равен-

ства detA₁(λ₀) = 0.

Доказательство. Вектор λ₀ может быть точкой бифуркации уравнения (1), (11) тогда и

только тогда, когда он является точкой бифуркации и системы (13). Но если det A₁(λ₀) = 0,

то у системы (13) кроме тривиального нет других малых решений, как это следует из теоремы

о неявных функциях. Следовательно, так как ряд (12) устанавливает взаимнооднозначное

соответствие между малым решением интегрального уравнения и малым решением системы

(13), то интегральное уравнение также имеет только тривиальное малое решение x(t) ≡ 0.

Теорема доказана.

6. Достаточное условие бифуркации в векторном случае: принцип линеариза-

ции. Пусть выполнено необходимое условие бифуркации (т.е. теорема 3) и rankA₁(λ₀) = r.

Пусть {φ₁, . . . , φ_n-r} и {ψ₁, . . . , ψ_n-r} - ортонормированные базисы в подпространствах нулей

N (A₁(λ₀)) и N (A∗1(λ₀)) соответственно.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВОЛЬТЕРРЫ

1661

∑_n-r

Введём квадратную матрицу

A₁(λ) = A₁(λ) +

(·,φ_i)ψ_i порядка n. Отметим, что

i=1

эта матрица обратима, поскольку несложно показать, что однородная система

A₁(λ₀)l = 0

имеет только тривиальное решение l = 0. Поэтому в силу непрерывности A₁(λ) относительно

λ матрица

A₁(λ) также обратима по крайней мере в малой окрестности ∥λ - λ₀∥ ≤ ρ на

основании теоремы об обратном операторе.

Введём обозначение λ₀ + μ := (λ₀₁ + μ, λ₀₂ + μ, . . . , λ0m + μ), вспомогательные параметры

ξ₁, ..., ξ_n-r и запишем систему (13) в виде

∑

A₁(λ₀ + μ)x_α = ξ_kψ_k - F_j(λ₀ + μ,x_α),

(14)

k=1

j=l

где ξ_i = (x_α, φ_i), i = 1, n - r.

Так как x_α → 0 при μ → 0, то параметры ξ_i являются бесконечно малыми величинами.

Матрица

A₁(λ₀ + μ) имеет обратную при |μ| < ρ. Поэтому можно построить сходящуюся

последовательность {x^nα}, используя рекурсию

∑

x^nα =

A₁(λ₀ + μ)]-1

ξ_kψ_k -

A₁(λ₀

+ μ)]-1

Fk(λ0 + μ, xα-1)

k=1

k=l

при начальном приближении x0α = 0. Тогда lim

x^nα = x_α. Следовательно,

n→∞

∑

x_α =

A₁(λ₀ + μ)]-1ψ_kξ_k + R(ξ₁,... ,ξ_n-r,μ),

(15)

k=1

где ∥R(ξ₁, . . . , ξ_n-r, μ)∥ = O(∥ξ∥^l). Подставляя построенный вектор x_α в равенство (14), по-

лучаем n - r уравнений для определения компонент вектора ξ(μ):

∑

[

A₁(λ₀ + μ)-1ψ_k,φ_i) - δ_ki]ξ_k + r_i(ξ,μ) = 0,

(16)

k=1

i = 1,n - r, |ri(ξ, μ) = O(∥ξ∥l)|. Найдём достаточные условия, не зависящие от вида нелиней-

ных функций r_i(ξ, μ), при выполнении которых μ = 0 будет точкой бифуркации системы (16).

Введём непрерывную функцию

Δ(μ) = det [

A₁(λ₀ + μ)-1ψ_k,φ_i) - δ_ki]n-ri,k=1.

(17)

Ввиду равенства

A₁(λ₀)φ_k = ψ_k верно тождество

A-11(λ₀)ψ_k = φ_k, k = 1,n - r. Поэтому

lim Δ(μ) = 0 и точка μ = 0 является нулём функции Δ(μ).

μ→0

Пусть выполняется условие

V. Значение μ = 0 является k-кратным нулём функции Δ(μ).

Тогда Δ(μ) ∼ cμ^k при μ → 0 и dⁱΔ(μ)/dμ|μ=0 = 0, i = 0, k - 1, d^kΔ(μ)/dμ^k|μ=0 = 0. Если

матрица A₁(λ + μ) в изолированной особой точке λ₀ имеет полный обобщённый жорданов

набор (см. [17, § 30]) из n - r цепочек длины p_i, i = 1, n - r, то k = p₁ + . . . + p_n-r.

Определение 2. Назовём число k корневым числом матрицы A₁(λ) в точке λ₀.

В монографии [17, гл. 9] показано, что корневое число не зависит в фредгольмовой особой

точке λ₀ от выбора базисов в подпространствах N (A(λ₀)) и N (A^∗(λ₀)).

Теорема 4 (принцип линеаризации). Пусть корневое число k матрицы A₁(λ) в точке

λ₀ нечётное. Тогда λ₀ будет точкой бифуркации интегрального уравнения (1), (11).

Доказательство. Вследствие (12), (15) λ₀ будет точкой бифуркации уравнения (1), (11)

тогда и только тогда, когда μ = 0 является точкой бифуркации системы (16). Запишем сис-

тему (16) в векторном виде

S(μ)ξ + r(ξ, μ) = 0,

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1662

СИДОРОВ Н.А., СИДОРОВ Д.Н.

где S(μ) = [

A₁(λ₀ + μ)-1ψ_k,φ_i) - δ_ki]k,i=1,n-r - квадратная матрица, ξ ∈ R^n-r, ∥r(ξ, μ)∥ =

= O(∥ξ∥^l). Зададим сколь угодно малые δ > 0 и ε > 0 и введём векторное поле

H(ξ, t) := S((2t - 1)δ)ξ + r(ξ, (2t - 1)δ) : R^n-r × R¹ → R^n-r,

определённое при ξ, t ∈ M, где M = {ξ, t : ∥ξ∥ < ε, 0 ≤ t ≤ 1}.

Случай 1. Если существует пара (ξ^∗, t^∗) ∈ M, для которой H(ξ^∗, t^∗) = 0, то, согласно

определению 1, точка μ = 0 будет точкой бифуркации системы (16), и теорема 4 справедлива.

Случай 2. Предположим, что H(ξ, t) = 0 при любых (ξ, t) ∈ M и, следовательно, теорема 4

неверна. Ввиду непрерывности поля H(ξ, t) при ξ, t ∈ M поля H(ξ, 0) и H(ξ, 1) гомотопны

на сфере ∥ξ∥ = ε, поэтому их вращения на этой сфере равны между собой, т.е.

J (H(ξ, 0), ∥ξ∥ = ε) = J(H(ξ, 1), ∥ξ∥ = ε).

(18)

В силу малости ε поля H(ξ, 0) и H(ξ, 1) гомотопны своим невырожденным линейным

частям S(-δ)ξ и S(+δ)ξ соответственно, т.е.

J (H(ξ, 0), ∥ξ∥ = ε) = J(S(-δ)ξ, ∥ξ∥ = ε) и J(H(ξ, 1), ∥ξ∥ = ε) = J(S(+δ)ξ, ∥ξ∥ = ε).

В силу условия V имеем det S(-δ) ∼ c(-δ)^k и det S(+δ) ∼ c(+δ)^k. Поэтому по теореме

Кронекера об индексе получаем

J (S(-δ)ξ, ∥ξ∥ = ε) = sign (-δ)^k, J(S(+δ)ξ, ∥ξ∥ = ε) = sign (+δ)^k.

В силу нечётности k приходим к равенствам

J (S(-δ)ξ, ∥ξ∥ = ε) = -1, J(S(+δ)ξ, ∥ξ∥ = ε) = +1,

а значит, равенство (18) невозможно. Следовательно, при нечётном k найдётся пара (ξ^∗, t^∗) ∈

∈ M, для которой H(ξ^∗,t^∗) = 0 и, согласно определению 1, точка μ = 0 является точкой

бифуркации системы (16), а точка λ₀ - точкой бифуркации интегрального уравнения (1), (11).

Теорема доказана.

Замечание. Из теоремы 4 в случае одной нагрузки как следствие вытекает справедливость

теоремы 2.

Следствие 3. Пусть для уравнения (1), (11) det A₁(λ₀) = 0, rank A₁(λ₀) = r, а {φ_i}n-r1

и {ψ_i}n-r1 - базисы в подпространствах N (A₁(λ₀)) и N (A∗1(λ₀)) соответственно. Если при

этом n - r - нечётное число и det [(A⁽¹⁾¹(λ₀)φ₁,ψ_k)]n-ri,k=1 = 0, то λ₀ - точка бифуркации

этого уравнения.

Доказательство. В условиях следствия 3 в изолированной фредгольмовой точке λ₀ мат-

рица A₁(λ₀ + μ) при |μ| < r не имеет присоединённых элементов. Поэтому векторы φ₁,

..., φ_n-r составляют её полный обобщённый жорданов набор и корневое число k равно n-r.

Таким образом, условия теоремы 4 выполнены. Следствие доказано.

Следствие 4. Пусть для уравнения (1), (11) det A₁(λ₀) = 0, rank A₁(λ₀) = r, а {φ_i}n-r1

и {ψ_i}n-r1 - базисы в подпространствах N (A₁(λ₀)) и N (A∗1(λ₀)) соответственно.

Пусть, кроме того,

[

]_n-r



d^j

d^p



A₁(λ)φ_i|λ=λ0 = 0, j = 0,p - 1, i = 1,n - r, и det

〈A₁(λ)φ_i, ψ_j 〉

= 0,



dλ^j

dλ^p

i,j=1

λ=λ₀

а число p(n - r) - нечётное. Тогда λ₀ - точка бифуркации уравнения (1), (11).

Доказательство. В условиях следствия 4 у функции Δ(μ), определённой выше формулой

(17), точка μ = 0 является p(n - r)-кратным нулём. Так как число p(n - r) нечётно, то

справедливость следствия 4 вытекает из доказательства принципа линеаризации. Следствие

доказано.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

НЕЛИНЕЙНЫЕ УРАВНЕНИЯ ВОЛЬТЕРРЫ

1663

Принцип линеаризации является достаточным условием существования точки бифурка-

ции, при проверке которого используется только информация о линейной части уравнения

(1), (11). При выполнении условий теоремы 4 уравнение (1), (11) с n нагрузками может иметь

многообразие малых вещественных решений x(t, λ₀), зависящих от n - r малых параметров,

где r - ранг матрицы A₁(λ₀), а λ₀ - точка бифуркации.

Далее, как и в п. 3, получим в векторном случае достаточные условия, когда нетривиальные

вещественные решения x(t, λ) → 0 при λ → λ₀ можно построить по крайней мере в одной из

полуокрестностей точки бифуркации, используя дополнительную информацию о нелинейной

части уравнения (1), (11).

Так как ряд (12) устанавливает взаимнооднозначное соответствие между решениями урав-

нения (1), (11) и системы (13), то для построения указанных решений уравнения (1), (11)

достаточно уметь строить вещественное решение x_α → 0 при λ → λ₀ + 0 (λ → λ₀ - 0)

системы (13).

Пусть для системы (13) выполняется условие

VI. При μ → 0 справедливы асимптотические оценки

A₁(λ₀ + μ)x_α ∼F1p1 (λ₀)-1x_αμp1 , F_i(λ₀ + μ,x_α) ∼ Fipi (λ₀,x_α)μpi, i = l,l + 1,...

При этом p_i > 0, i = 1, l, l + 1, . . . , n - 1, p_n = 0, F1p1 - n × n-матрица, Fipi (λ₀, x_α) -

i-однородные формы относительно компонент вектора нагрузки x_α.

Как и в случае одной нагрузки, нанеся на координатную плоскость точки (1, p₁), (l, p_l),

(l + 1, pl+1), . . . , (n - 1, pn-1), (n, 0) (см. рисунок), построим диаграмму Ньютона и будем

искать вектор нагрузки в виде x_α = c(μ)|μ|^r/s, c(0) = 0.

Для определения вектора c(0) получим две разные системы - одну для μ > 0, а другую

для μ < 0:

∑

P_±(c) :=

sign μ^kF_ik(λ₀, c) = 0.

k+ir/s=θ

Компоненты векторов F_ik(λ₀, c) - i-однородные формы относительно вектора c. Построив

простое ненулевое вещественное решение c одной из этих систем, запишем в соответствующей

полуокрестности точки бифуркации λ₀ асимптотику

∑

x(t, λ) ∼

b_k(t,λ₀)c^∗k|λ - λ₀|^rs

k=1

при λ → λ₀ + 0 (λ → λ₀ - 0) решения интегрального уравнения (1), (11).

Заключение. Предложенный метод позволяет при λ ∈ R^m получить достаточные условия

существования более общих многообразий, а именно кривых и поверхностей бифуркации для

интегро-дифференциального уравнения

dx(t)

+ a(t, λ)x(t) = L(x(t), x_α, t, λ), x(0) = 0,

с нагрузками. С его помощью можно провести бифуркационный анализ и более общих классов

дифференциально-операторных уравнений в банаховых пространствах с нагрузками в окрест-

ностях точек ветвления решений, а также решения задачи Коши для дифференциального

уравнения с нагрузками. Результаты работы могут быть применены при анализе нестандарт-

ных нелинейных интегральных моделей с нагрузками, возникающих при исследовании эреди-

тарных процессов в приложениях.

Работа выполнена при финансовой поддержке Министерства науки и высшего образования

Российской Федерации, программы фундаментальных исследований Российской Федерации

на 2021-2030 гг.; проект государственного задания (№ FWEU-2021-0006) с использованием ре-

сурсов ЦКП ”Высокотемпературный контур” (Министерство образования и науки Российской

Федерации, проект 13.ЦКП.21.0038).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021

1664

СИДОРОВ Н.А., СИДОРОВ Д.Н.

СПИСОК ЛИТЕРАТУРЫ

1. Sidorov N., Sidorov D., Sinitsyn A. Toward General Theory of Differential-Operator and Kinetic Models.

V. 97. Book Series: World Scientific Series on Nonlinear Science. Ser. A / Ed. Prof. L. Chua. Singapore;

London, 2020.

2. Ахмеров Р.Р., Каменский М.И., Потапов А.С., Родкина А.Е., Садовский Б.Н. Теория уравнений

нейтрального типа // Итоги науки и техники. Сер. Мат. анал. 1982. Т. 19. С. 55-126.

3. Sidorov D.N., Sidorov N.A. Convex majorants method in the theory of nonlinear Volterra equations

// Banach J. Math. Anal. 2021. V. 6. № 1. P. 1-10.

4. Айда-заде К.Р., Абдуллаев В.М. О численном решении систем обыкновенных дифференциальных

уравнений с неразделенными многоточечными и интегральными условиями // Сиб. журн. вычис-

лит. математики. 2014. Т. 17. № 1. С. 1-16.

5. Нахушев А.М. Нагруженые уравнения и их применения. М., 2012.

6. Дикинов Х.Ж., Керефов А.А., Нахушев А.М. Об одной краевой задаче для нагруженного уравнения

теплопроводности // Дифференц. уравнения. 1977. Т. 12. № 1. С. 177-179.

7. Agarwal P., Baltaeva U., Alikulov Y. Solvability of the boundary-value problem for a linear loaded

integro-differential equation in an infinite three-dimensional domain // Chaos, Solitons & Fractals. 2020.

V. 140. P. 110108.

8. Сидоров Н.А., Сидоров Д.Н. О разрешимости одного класса операторных уравнений Вольтерра

первого рода с кусочно-непрерывными ядрами // Мат. заметки. 2014. Т. 96. Вып. 5. С. 773-789.

9. Сидоров Н.А., Сидоров Д.Н. Существование и построение обобщенных решений нелинейных инте-

гральных уравнений Вольтерры первого рода // Дифференц. уравнения. 2006. Т. 42. № 9. С. 124-129.

10. Sidorov N.A. Special Issue "Solvability of Nonlinear Equations with Parameters: Branching, Regulariza-

tion, Group Symmetry and Solutions Blow-Up". Symmetry, MDPI, 2021.

11. Красносельский М.А. Топологические методы в теории нелинейных уравнений. М., 1956.

12. Dancer E.N. Bifurcation theory // Indiana Univ. Math. 1974. V. 23. № 11. P. 1069-1076.

13. Ахмедов К.Т. Аналитический метод Некрасова-Назарова в нелинейном анализе // Успехи мат.

наук. 1957. Т. 12. Вып. 4 (76). С. 135-153.

13. Брюно А.Д. Степенная геометрия в алгебраических и дифференциальных уравнениях. М., 1998.

15. Люстерник Л.А. Некоторые вопросы нелинейного функционального анализа // Успехи мат. наук.

1956. Т. 11. Вып. 6. С. 145-168.

16. Сидоров Н.А., Треногин В.А. Точки бифуркации нелинейных уравнений // Нелинейный анализ и

нелинейные дифференциальные уравнения / Под ред. В.А. Треногина, А.Ф. Филиппова. М., 2003.

17. Вайнберг М.М., Треногин В.А. Теория ветвления решений нелинейных уравнений. М., 1969.

18. Сидоров Д.Н. Методы анализа интегральных динамических систем / Под ред. А. Лоренци. Иркутск,

2013.

19. Sidorov N., Loginov B., Sinitsyn A., Falaleev V. Lyapunov-Schmidt Methods in Nonlinear Analysis and

Applications. Dordrecht, 2013.

20. Sidorov D., Muftahov I. et al. A dynamic analysis of energy storage with renewable and diesel generation

using Volterra equations // IEEE Trans. on Industr. Inf. 2020. V. 16. № 5. P. 3451-3459.

Иркутский государственный университет,

Поступила в редакцию 07.05.2021 г.

Институт систем энергетики

После доработки 07.05.2021 г.

им. Л.А. Мелентьева СО РАН, г. Иркутск

Принята к публикации 23.11.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№ 12

2021