ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 12, с. 1682-1697
ЧИСЛЕННЫЕ МЕТОДЫ.
УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ
УДК 517.958:537.8
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ
ЗАДАЧ ЭКРАНИРОВАНИЯ
ИМПУЛЬСНЫХ ЭЛЕКТРОМАГНИТНЫХ ПОЛЕЙ
ЭКРАНАМИ ИЗ ПЕРМАЛЛОЯ
© 2021 г. В. Т. Ерофеенко, Г. Ф. Громыко, Г. М. Заяц
Предложена начально-краевая задача для моделирования проникновения импульсных
электромагнитных полей через плоский экран, заполненный пермаллоем. Материал пер-
маллоя характеризуется нелинейным дифференциальным уравнением второго порядка для
поля намагниченности, распространяющегося в слое экрана. Рассмотрен случай, когда
поток энергии импульсного поля направлен перпендикулярно экрану. Начально-краевая
задача представлена в виде системы шести скалярных параболических нелинейных диф-
ференциальных уравнений с граничными условиями третьего и первого рода на лицевых
плоскостях экрана. Разработан численный метод решения задачи. Численно исследованы
характеристики электромагнитного поля в экране в зависимости от начального импульса.
На основе вычислительных экспериментов получены зависимости коэффициента экрани-
рования от проводимости и от толщины экрана.
DOI: 10.31857/S0374064121120104
Введение. Разработка математических методов моделирования проникновения импульс-
ных электромагнитных полей через экраны является актуальным направлением прикладной
электродинамики. Одним из веществ, используемых для создания экранов, является пер-
маллой∗) [1-4]. Математическая модель задачи экранирования основывается на использовании
системы уравнений Максвелла и дополнительного нелинейного уравнения для поля намагни-
ченности, характеризующего пермаллой. Для моделирования поля M намагниченности ма-
териала экрана используется уравнение Ландау-Лифшица [3], которое нелинейным образом
связывает магнитное поле H и поле M. В работе [4] предложена математическая модель нели-
нейной краевой задачи экранирования импульсных полей плоским экраном из пермаллоя, в
которой для упрощения решения задачи исключены величины второго порядка малости, вхо-
дящие в нелинейное уравнение. Это позволило нелинейную задачу преобразовать в линейную
и аналитически вычислить амплитуды отражённого и прошедшего через экран электромагнит-
ных полей. Численные методы моделирования экранирующих свойств экранов из нелинейных
материалов других типов без учёта намагниченности материала рассматривались в [5-7].
В данной работе использована модификация уравнения Ландау-Лифшица, содержащая
вторые производные поля M, что значительно усложняет модель. Рассмотрено воздействие
импульсного первичного электромагнитного поля E0, H0 и магнитного поля Hsm, ортого-
нально падающих на экран. Магнитное поле Hsm используется для возбуждения поля намаг-
ниченности M в материале экрана. При этом зависимость поля Hsm от времени выбрана
специальным образом, сглаживающим поля в угловых точках прямоугольной расчётной об-
ласти. Построена начально-краевая задача для моделирования проникновения импульсных
электромагнитных полей через плоский экран и разработан численный метод её решения.
Численно исследованы компоненты магнитного поля H и поля M намагниченности в экране
в зависимости от начального импульса. Для численной оценки экранирующих свойств экрана
получены зависимости коэффициента экранирования от проводимости и от толщины экрана.
1. Система нелинейных дифференциальных уравнений, описывающих распро-
странение электромагнитных полей в материале из пермаллоя. Рассмотрим плоский
∗) Пермаллой - магнитно-мягкий сплав никеля и железа, иногда легированный другими металлами; обла-
дает высокой магнитной проницаемостью и практически не изменяется в размерах при намагничивании.
1682
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1683
слой D(0 < z < Δ) толщины Δ, заполненный пермаллоем. Для моделирования электромаг-
нитного поля E(r, t), H(r, t) и поля намагниченности M(r, t), распространяющихся в слое
D, воспользуемся системой дифференциальных уравнений [1]
∂
rot E = -μ0
(H + M),
(1)
∂t
rot H = σE,
(2)
∂M
= γP,
(3)
∂t
P = M × (H + ˙aΔM - ġM × H).
(4)
Преобразуем уравнения (1)-(3) в систему нелинейных уравнений параболического типа.
Из уравнения (1) исключим вектор E с помощью уравнения (2) и временную производную от
вектора намагниченности M с помощью уравнения (3). Получим систему уравнений
∂H
1
=
(ΔH - grad div H) - γP,
0 < z < Δ,
(5)
∂t
σμ0
∂M
= γP,
0 < z < Δ,
(6)
∂t
где μ0 - магнитная постоянная,
σ - удельная проводимость пермаллоя, величины
γ,
a,
ġ
определяют связь намагниченности M(z, t) и напряжённости магнитного поля H(z, t) [1, с. 97];
постоянные имеют физические размерности [ γ] = м/(А · с), [ a] = м2, [ġ] = м/А, [σ] = См/м,
μ0 = 4π · 10-7 Гн/м.
Решения системы уравнений (5), (6) будем искать в виде плоских электромагнитных полей,
равномерно распределённых вдоль слоя D и не зависящих от координат x, y, т.е.
H = Hx(z,t)ex + Hy(z,t)ey + Hz(z,t)ez,
M = Mx(z,t)ex + My(z,t)ey + Mz(z,t)ez,
(7)
E = Ex(z,t)ex + Ey(z,t)ey + Ez(z,t)ez.
(8)
Найдём выражение для поля (4), вычисляя векторные произведения
M × H = ex(MyHz - MzHy) + ey(MzHx - MxHz) + ez(MxHy - MyHx),
M × ΔM = ex(MyΔMz - MzΔMy) + ey(MzΔMx - MxΔMz) + ez(MxΔMy - MyΔMx),
M × (M × H) = ex(My(MxHy - MyHx) - Mz(MzHx - MxHz)) +
+ ey(Mz(MyHz - MzHy) - Mx(MxHy - MyHx)) +
+ ez(Mx(MzHx - MxHz) - My(MyHz - MzHy)).
Для вектора P с учётом соотношений ΔMα = ∂2Mα/∂z2 (α = x, y, z) получаем пред-
ставление
P = Px(z,t)ex + Py(z,t)ey + Pz(z,t)ez,
в котором
(
)
∂2Mz
∂2My
Px = ˙a My
-Mz
+MyHz -MzHy - ġ(My(MxHy - MyHx) -Mz(MzHx - MxHz)),
∂z2
∂z2
(
)
∂2Mx
∂2Mz
Py = ˙a Mz
-Mx
+MzHx -MxHz - ġ(Mz(MyHz -MzHy)-Mx(MxHy -MyHx)),
∂z2
∂z2
(
)
∂2My
∂2Mx
Pz = ˙a Mx
-My
+MxHy-MyHx-ġ(Mx(MzHx-MxHz)-My(MyHz-MzHy)). (9)
∂z2
∂z2
7
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
1684
ЕРОФЕЕНКО и др.
Аналогичным образом вычислим слагаемые, входящие в уравнение (5):
∂2Hx
∂2Hy
∂2Hz
∂2Hz
ΔH =
ex +
ey +
ez, grad div H =
ez.
(10)
∂z2
∂z2
∂z2
∂z2
Выражая с помощью уравнения (2) компоненты поля E, получаем
(
)
1
∂Hy(z,t)
∂Hx(z,t)
E(z, t) = Ex(z, t)ex + Ey(z, t)ey =
-
ex +
ey
,
Ez(z,t) = 0.
(11)
σ
∂z
∂z
Сформулируем краевую задачу для системы уравнений (5), (6).
2. Постановка краевой задачи экранирования импульсных электромагнитных
полей экраном из пермаллоя. В трёхмерном пространстве с электрической и магнитной
постоянными ε0 и μ0 расположен плоский экран D(0 < z < Δ) из пермаллоя, ограниченный
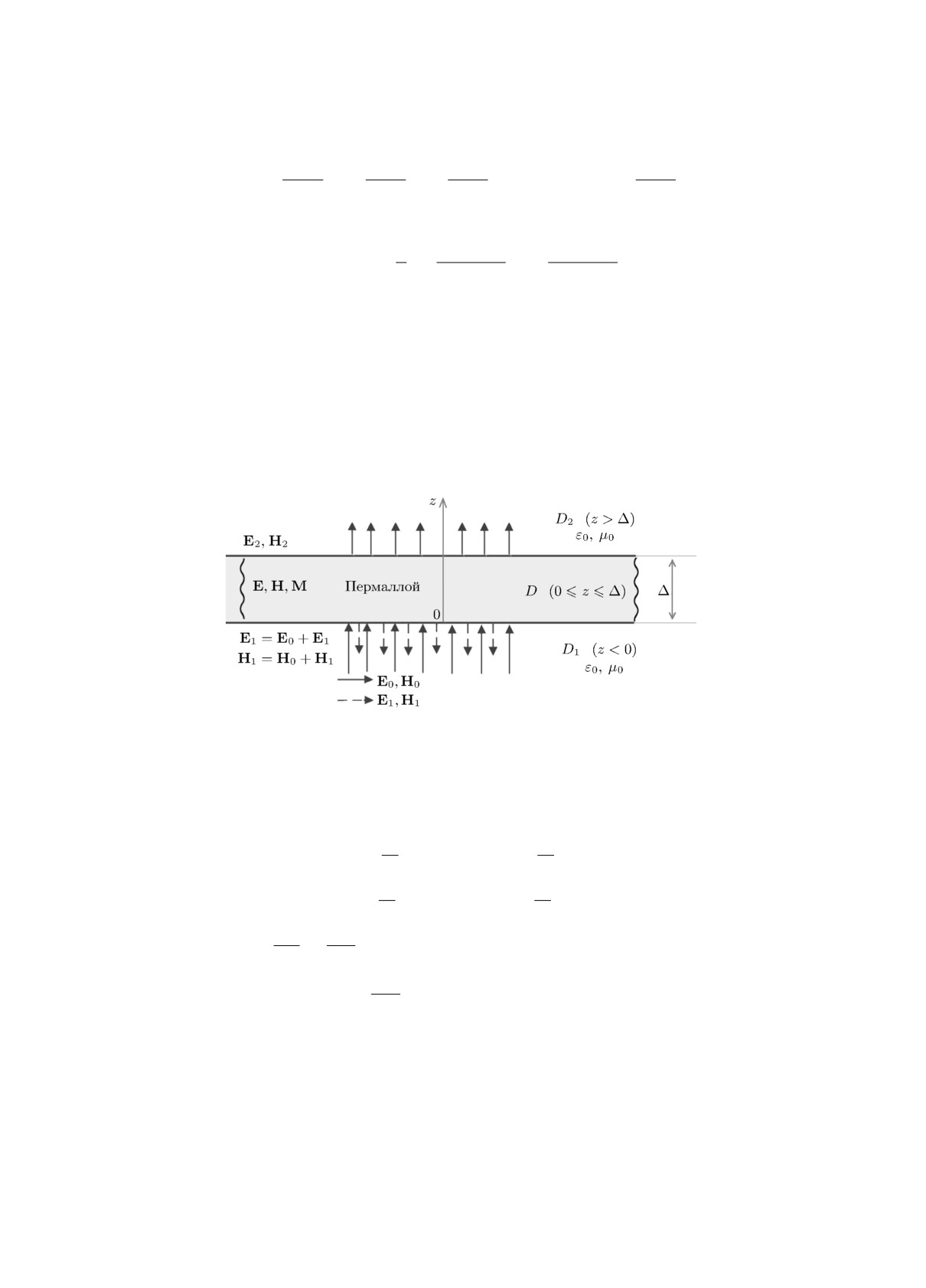
плоскостями Γ1(z = 0), Γ2(z = Δ) (рис. 1). Из полупространства D1(z < 0) на слой D
воздействует первичное электромагнитное поле E0(z, t), H0(z, t). В результате в области D1
(z, t) и суммарное электромагнитное поле E1(z, t) =
1
1
(z, t). В полупространство D2(z > Δ) через экран
D проникает поле E2(z, t), H2(z, t).
Рис. 1. Экранирование электромагнитного импульса E0, H0 экра-
ном D.
Краевая задача. Для заданного первичного поля E0(z, t), H0(z, t) требуется опреде-
1
(z, t) и E2(z, t), H2(z, t) в областях D1 и D2 соот-
ветственно и поля E(z, t), H(z, t), M(z, t) в области D, которые удовлетворяют уравнениям
Максвелла
∂
∂
rot E′
= -μ0
H′1, rotH′
=ε0
E′1, z < 0,
1
1
∂t
∂t
∂
∂
rot E2 = -μ0
H2, rotH2 = ε0
E2, z > Δ,
(12)
∂t
∂t
∂H
1
=
(ΔH - grad div H) - γP,
0 < z < Δ,
(13)
∂t
σμ0
∂M
= γP,
0 < z < Δ,
(14)
∂t
и следующим условиям:
1) граничным условиям непрерывности тангенциальных составляющих электрического по-
ля, магнитного поля и поля намагниченности на плоскости Γ1 :
(Eτ - E1τ )|z=0 = 0,
((H + M)τ - H1τ )|z=0 = 0;
(15)
2) граничным условиям непрерывности тангенциальных составляющих электрического по-
ля, магнитного поля и поля намагниченности на плоскости Γ2 :
(Eτ - E2τ )|z=Δ = 0,
((H + M)τ - H2τ )|z=Δ = 0;
(16)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1685
3) граничным условиям для поля намагниченности на плоскостях Γ1, Γ2 :
Mx|z=0 = 0, My|z=0 = 0, (H + M,n)|z=0 = Hsmc(t′), n = ez,
Mx|z=Δ = 0, My|z=Δ = 0, (H + M,n)|z=Δ = 0,
(17)
где Hsmc(t′) - импульс внешнего магнитного поля, воздействующего на экран, t′ = t/τ, τ -
время фронта импульса;
4) условиям излучения на бесконечность в областях D1 и D2.
Краевая задача (12)-(17) является трёхобластной краевой задачей для полупространств:
перед экраном D1, за экраном D2 и для слоя D с граничными условиями сопряжения на
поверхностях Γ1 и Γ2 раздела сред. В последующем трёхобластная краевая задача будет
преобразована в однообластную краевую задачу с односторонними граничными условиями на
лицевых плоскостях Γ1 и Γ2 экрана. При этом области D1 и D2 исключаются из рассмотре-
ния. Такая процедура необходима для упрощения численной реализации решения нелинейной
краевой задачи (12)-(17).
3. Импульсные электромагнитные поля, воздействующие на экран D. Полагаем,
что в областях D1 и D2 находится вакуум; тогда электромагнитные поля в этих областях
подчиняются уравнениям
∂
∂
rot E = -μ0
H, rotH = ε0
E.
(18)
∂t
∂t
Структура полей в областях D1, D2 предполагается аналогичной структуре полей (7), (8):
E = Ex(z,t)ex + Ey(z,t)ey + Ez(z,t)ez, H = Hx(z,t)ex + Hy(z,t)ey + Hz(z,t)ez.
(19)
Подставляя выражения (19) в уравнения (18), получаем
∂Ey(z,t)
∂Ex(z,t)
∂
-
ex +
ey = -μ0
(Hx(z, t)ex + Hy(z, t)ey + Hz(z, t)ez ),
∂z
∂z
∂t
∂Hy(z,t)
∂Hx(z,t)
∂
−
ex +
ey = ε0
(Ex(z, t)ex + Ey(z, t)ey + Ez(z, t)ez ),
∂z
∂z
∂t
откуда следует, что
∂
∂
Ez(z,t) = 0, Ez(z,t) = C1(z),
Hz(z,t) = 0, Hz(z,t) = C2(z).
(20)
∂t
∂t
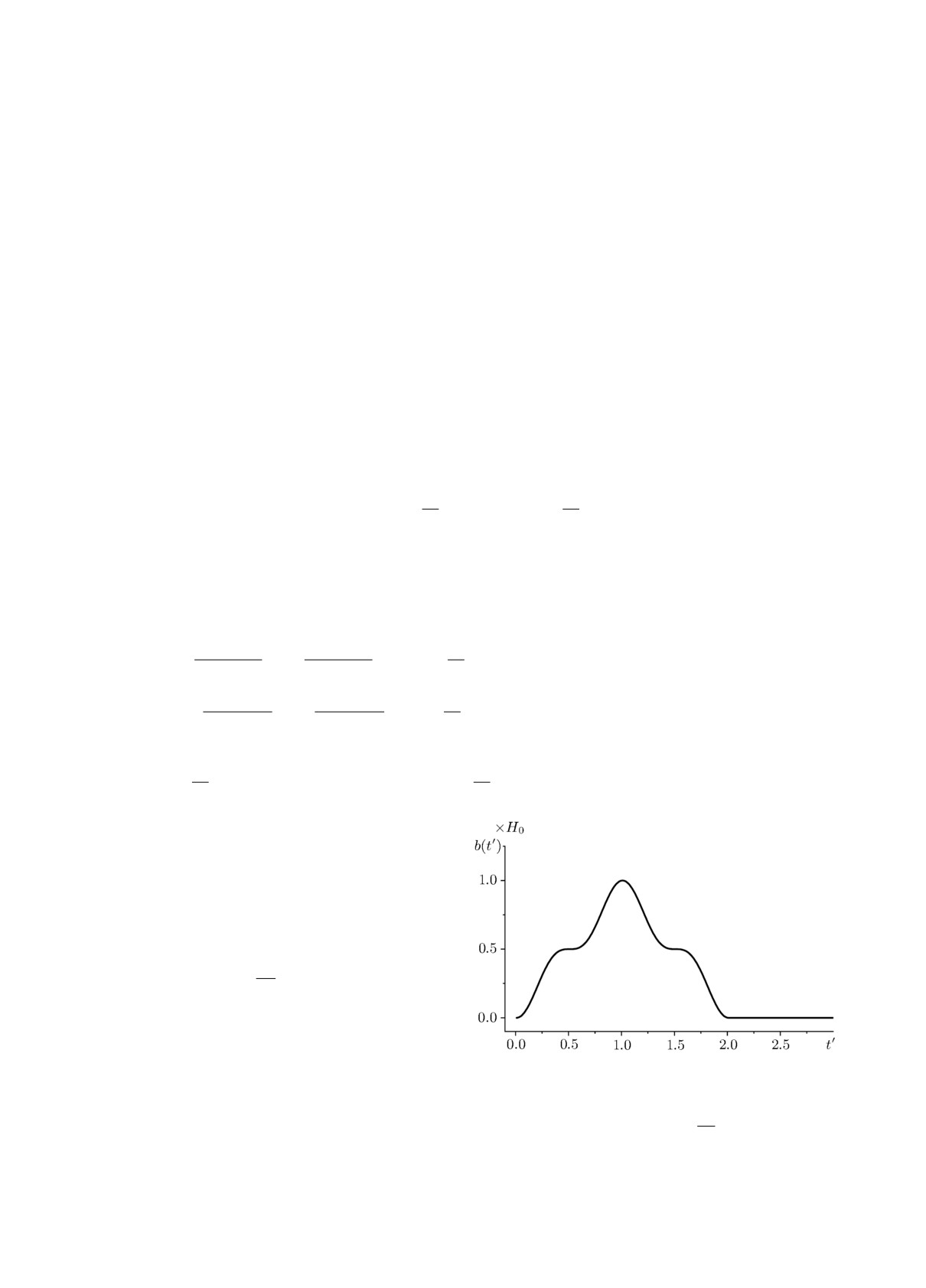
Для постановки краевой задачи проник-
новения первичного электромагнитного поля
E0, H0 через плоский экран из пермаллоя
в качестве первичного поля рассмотрим им-
пульсное электромагнитное поле (рис. 2)
E0(z,t) = -B0(T(-))ey,
1
H0(z,t) =
B0(T(-))ex,
(21)
Z
0
где T(∓) = (ct ∓ z)/(cτfr), τfr - время фронта
импульса, c - скорость света, Z0 = 377 Ом.
Дополнительно на экран из области D1
Рис. 2. Вид импульса b(t′).
воздействует магнитное поле
{
sin(πt′),
0 ≤ t′ ≤ 1/2,
Hsm = Hsmc(t′)ez, c(t′) =
t′ = t=t ,
(22)
1,
t′ ≥ 1/2,
τfr
которое возбуждает поле намагниченности M и направлено ортогонально экрану.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
7∗
1686
ЕРОФЕЕНКО и др.
В качестве импульсной функции первичного поля выберем функцию
{
0.5 sin3(π(t′ - 0.5)) + 0.5,
0 ≤ t′ ≤ 2,
B0(t′)=Z0H0b(t′), max
b(t′)=1, b(t′)=
(23)
0≤t′<2
0,
t′ ≤ 0 и t′ ≥ 2,
где H0 - максимальное значение напряжённости магнитного поля H0.
Импульсная функция (23) при t = 0 равна нулю. В связи с этим в начальный момент
времени t = 0 импульсные поля перед экраном и за экраном отсутствуют. Из равенств (20)
следует, что Ez(z, 0) = C1(z) = 0, Hz(z, 0) = C2(z) = 0.
В результате воздействия первичного поля (21) на экран в области D1(z < 0) образуется
отражённое импульсное поле
1
(z, t) =
(B1(T(+))ex + A1(T(+))ey).
(24)
1
Z0
Суммируя поля (21), (22), (24), получаем поле в области D1 :
E1(z,t) = E0(z,t) + E′1(z,t) = -A1(T(+))ex + (-B0(T(-)) + B1(T(+)))ey,
1
[(B0(T(-)) + B1(T(+)))ex + A1(T(+))ey] + Hsm.
(25)
H1(z,t) = H0(z,t) + H′1(z,t) =
Z0
Соответственно поле в области D2(z > Δ) имеет вид
1
E2(z,t) = A2(T(-))ex - B2(T(-))ey, H2(z,t) =
(B2(T(-))ex + A2(T(-))ey).
(26)
Z0
Импульсные функции Aj(t′), Bj(t′) полей (24), (26) определяются в результате решения
краевой задачи экранирования (12)-(17).
4. Граничные условия для нормальных составляющих полей на границах экра-
на. Рассмотрим плоскость Γ(z = const), разделяющую среды D1 и D2, в которых распро-
страняются поля Ej , Hj (j = 1, 2), описываемые уравнениями Максвелла
∂
∂
rot Ej = -
Bj, rot Hj =
Dj + Jj.
∂t
∂t
Граничные условия, связывающие нормальные составляющие полей на поверхности Γ,
определяются формулами [8, с. 195]
(
∫
t
∫
t
)
(D2, n) - (D1, n) + (J2, n)dt -
(J1, n)dt
= 0,
((B2, n) - (B1, n))|Γ = 0,
(27)
Γ
0
0
где n - нормаль к плоскости Γ, направленная в область D2.
В соответствии с формулами (27) построим граничные условия на плоскости Γ1(z = 0)
плоского экрана D, где D1 = D1, D2 = D. Из уравнений (1), (2) вытекают следующие
равенства: B2 = μ0(H + M), D2 = 0, J2 = σE.
В области D1 - вакуум, поэтому B1 = μ0H1, D1 = ε0E1, J1 = 0, где поля H1, E1
определены равенствами (25).
В результате граничные условия (27) на плоскости Γ1 принимают вид
(
∫
t
)
-ε0(E1,n) + σ
(E, n)dt
= 0,
z=0
0
((H + M, n) - (H1, n))|z=0 = (H + M, n)|z=0 - Hпостc(t′) = 0, n = ez,
(28)
где Hпост - максимальное значение магнитного поля, воздействующего на экран.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1687
Выведем граничные условия на плоскости Γ2(z = Δ) экрана D, где D1 = D, D2 = D2.
Из уравнений (1), (2) следует, что B1 = μ0(H+M), D1 = 0, J1 = σE. В области D2 - вакуум,
следовательно, B2 = μ0H2, D2 = ε0E2, J2 = 0, где поля H2, E2 определены уравнениями
(26).
В результате граничные условия (27) на плоскости Γ2 принимают вид
(
∫
t
)
ε0(E2,n) - σ
(E, n)dt
= 0,
((H + M, n) - (H2, n))|z=Δ = (H + M, n)|z=Δ = 0. (29)
z=Δ
0
Из равенств (25), (26) следует, что (Ej, n) = 0, а из представления (11) электрического
поля - что (E, n) = 0. Таким образом, интегральные условия в уравнениях (28), (29) на
плоскостях Γ1, Γ2 выполнены.
Заметим, что на поверхностях экрана касательные составляющие поля намагниченности в
областях D1 и D2 отсутствуют, т.е. M1x|z=0 = 0, M1y|z=0 = 0, M2x|z=Δ = 0, M2y|z=Δ =
= 0. В силу непрерывности касательных составляющих полей граничные условия для поля
намагниченности на плоскостях Γ1, Γ2 принимают вид, соответствующий условиям (17), т.е.
Mx|z=0 = 0, My|z=0 = 0, (H + M,n)|z=0 = Hsmc(t′),
Mx|z=Δ = 0, My|z=Δ = 0, (H + M,n)|z=Δ = 0.
5. Односторонние граничные условия для касательных составляющих полей
на плоскостях экрана. Преобразуем двухсторонние граничные условия сопряжения (15),
(16) в односторонние граничные условия. Для магнитных полей и поля намагниченности в
областях D и D1 на плоскости Γ1(z = 0) выполнены граничные условия (15) непрерывности
тангенциальных составляющих полей. С учётом того, что Mx|z=0 = 0, My|z=0 = 0, из условий
(17) получаем равенство
[n, [H, n]]|z=0 = [n, [H1, n]]|z=0.
(30)
Учитывая представления (7), (25) при z = 0 для магнитных полей в областях D, D1,
преобразуем условия (30) в граничные условия для декартовых составляющих
(
1
(t)
(t))
1
(t)
Hx(0,t) =
B0
+B1
,
Hy(0,t) =
A1
(31)
Z0
τ
τ
Z0
τ
Для электрических полей в областях D и D1 на плоскости Γ1(z = 0) выполнены гранич-
ные условия сопряжения (15):
[n, [E, n]]|z=0 = [n, [E1, n]]|z=0.
(32)
Аналогично, учитывая представления (8), (25) при z = 0 для электрических полей, пре-
образуем условия (32) в скалярные граничные условия для декартовых составляющих полей
Ex(0,t) = -A1(t/τ), Ey(0,t) = -B0(t/τ) + B1(t/τ).
(33)
Из условий (31), используя равенства (33), исключим неизвестные функции A1, B1. В ре-
зультате получаем
1
1
Hx(0,t) =
(2B0(t/τ) + Ey(0, t)), Hy(0, t) = -
Ex(0,t).
(34)
Z0
Z0
С помощью соотношений (11) при z = 0 исключим компоненты
1 ∂Hy(z,t)
1 ∂Hx(z,t)
Ex(0,t) = -
,
Ey(0,t) =
σ
∂z
σ
∂z
z=0
z=0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
1688
ЕРОФЕЕНКО и др.
из равенств (34). В результате граничные условия для касательных составляющих магнитного
поля примут вид
)
)
(∂Hx(z,t)
(t)
(∂Hy(z,t)
- Z0 σHx(z,t)
= -2˙σB0
,
- Z0 σHy(z,t)
= 0.
(35)
∂z
τ
∂z
z=0
z=0
Аналогично, для магнитных и электрических полей в областях D, D2 на плоскости Γ2(z =
= Δ) выполнены граничные условия (16). С учётом первых двух в условиях (17) равенств
Mx|z=Δ = 0, My|z=Δ = 0 находим, что
[n, [H, n]]|z=Δ = [n, [H2, n]]|z=Δ,
[n, [E, n]]|z=Δ = [n, [E2, n]]|z=Δ.
(36)
Учитывая представления (7), (8), (26) при z = Δ для магнитных и электрических полей
в областях D и D2, преобразуем условия (36) к виду
)
1
( ct - Δ
1
( ct - Δ)
Hx(Δ,t) =
B2
,
Hy(Δ,t) =
A2
,
(37)
Z0
cτ
Z0
cτ
( ct - Δ)
( ct - Δ)
Ex(Δ,t) = A2
,
Ey(Δ,t) = -B2
(38)
cτ
cτ
Исключая из равенств (37) и (38) функции A2 и B2, получаем
1
1
Hx(Δ,t) = -
Ey(Δ,t), Hy(Δ,t) =
Ex(Δ,t).
(39)
Z0
Z0
В силу соотношения (11) имеем
1 ∂Hy(z,t)
1 ∂Hx(z,t)
Ex(Δ,t) = -
,
Ey(Δ,t) =
σ
∂z
σ
∂z
z=Δ
z=Δ
и, подставляя эти выражения для Ex и Ey в равенства (39), находим граничные условия на
плоскости Γ2 :
)
)
(∂Hx(z,t)
(∂Hy(z,t)
+ Z0 σHx(z,t)
= 0,
+ Z0 σHy(z,t)
= 0.
(40)
∂z
∂z
z=Δ
z=Δ
Заметим, что односторонние граничные условия (35), (40) содержат компоненты магнит-
ного поля и поля намагниченности слоя D.
6. Безразмерные параболические дифференциальные уравнения в слое из перм-
аллоя. Введём безразмерное время t = t/τ и безразмерную координату z = z/Δ. Обезраз-
мерим поля H(z, t), M(z, t), определённые равенствами (7), полагая
Hx(z,t) = Hx(Δz,τt) = H0u1(z, t), Hy(z,t) = Hy(Δz,τt) = H0u2(z, t),
Hz(z,t) = Hz(Δz,τt) = H0u3(z, t);
Mx(z,t) = Mx(Δz,τt) = H0v1(z, t), My(z,t) = My(Δz,τt) = H0v2(z, t),
Mz(z,t) = Mz(Δz,τt) = H0v3(z, t).
(41)
Для безразмерных функций u1, u2, u3 и v1, v2, v3 построим систему безразмерных
дифференциальных уравнений.
Векторное дифференциальное уравнение (14) запишем для компонент поля (7):
∂Mx(z,t)
∂My(z,t)
∂Mz(z,t)
= γPx(z,t),
= γPy(z,t),
= γPz(z,t).
(42)
∂t
∂t
∂t
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1689
Обезразмерим уравнения (42), учитывая представления (9), (41). Получим безразмерные
уравнения в слое D :
∂v1(z, t)
∂v2(z, t)
∂v3(z, t)
= p1(z, t),
= p2(z, t),
= p3(z, t),
0 < z < 1,
0 < t< ∞,
(43)
∂t
∂t
∂t
где
(
(
)
(
))
∂
∂v3
∂
∂v2
p1(z,t)=F1
v2
-
v3
+ F2(v2u3 - v3u2) +
∂z
∂z
∂z
∂z
+ F3[v2(v2u1 - v1u2) + v3(v3u1 - v1u3)],
(
(
)
(
))
∂
∂v1
∂
∂v3
p2(z,t)=F1
v3
-
v1
+ F2(v3u1 - v1u3) +
∂z
∂z
∂z
∂z
+ F3[v3(v3u2 - v2u3) + v1(v1u2 - v2u1)],
(
(
)
(
))
∂
∂v2
∂
∂v1
p3(z,t)=F1
v1
-
v2
+ F2(v1u2 - v2u1) +
∂z
∂z
∂z
∂z
+ F3[v1(v1u3 - v3u1) + v2(v2u3 - v3u2)];
(44)
F1 = γτ aH0/Δ2, F2 = γτH0, F3 = γτ ġH20 - безразмерные постоянные.
Аналогичным образом векторное дифференциальное уравнение (13) запишем для компо-
нент поля с учётом равенств (7) и (10). В результате получим скалярные уравнения
∂Hx(z,t)
1
∂2Hx(z,t)
∂Hy(z,t)
1
∂2Hy(z,t)
=
- γPx(z,t),
=
- γPy(z,t),
∂t
σμ0
∂z2
∂t
σμ0
∂z2
∂Hz(z,t)
= -γPz(z,t).
(45)
∂t
Обезразмерим дифференциальные уравнения (45), учитывая равенства (41), (44). Получим
безразмерные скалярные уравнения
∂u1(z, t)
∂2u1(z, t)
∂u2(z, t)
∂2u2(z, t)
∂u3(z, t)
=G
-p1(z, t),
=G
-p2(z, t),
=-p3(z, t), (46)
∂t
∂z2
∂t
∂z2
∂t
где
τ
G=
,
0 < z < 1,
0 < t< ∞.
σμ0Δ2
7. Безразмерные односторонние граничные условия на плоскостях экрана. Обез-
размерим импульсную функцию B0(t′) первичного поля (21):
B0(t/τ) = E0b(t) = Z0H0b(t),
где E0 - максимальное значение напряжённости электрического поля E0, b(t) - импульсная
функция (23).
Приведём граничные условия (17), (35) на плоскости Γ1(z = 0) к безразмерному виду,
учитывая вид функций (22), (23), (41). Получим двухсторонние граничные условия
)
)
(∂u1(z, t)
(∂u2(z, t)
- K0u1(z, t)
= -2˙σΔZ0b(t),
- K0u2(z, t)
= 0;
∂z
∂z
z=0
z=0
v1|z=0 = 0, v2|z=0 = 0, (v3 + u3)|z=0 = Hsc(t′),
(47)
где K0 = σZ0Δ, Hs = Hsm/H0.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
1690
ЕРОФЕЕНКО и др.
Аналогично, преобразовывая граничные условия (17), (40) на плоскости Γ2(z = 1), прихо-
дим к безразмерным граничным условиям
)
)
(∂u1(z, t)
(∂u2(z, t)
+ K0u1(z, t)
= 0,
+ K0u2(z, t)
= 0;
∂z
∂z
z=1
z=1
v1|z=1 = 0, v2|z=1 = 0, (v3 + u3)|z=1 = 0.
(48)
Для системы скалярных дифференциальных уравнений (43), (46) сформулируем начально-
краевую задачу с односторонними граничными условиями (47), (48), добавив начальные усло-
вия при t= 0.
8. Начально-краевая задача экранирования. Для нахождения безразмерных компо-
нент магнитного поля ui(z, t), i = 1, 2, 3, и компонент поля намагниченности vi(z, t), i =
= 1, 2, 3, рассмотрим следующие взаимосвязанные начальные и краевые задачи:
a) для функций u1(z, t), u2(z, t), удовлетворяющих уравнениям
∂ui(z, t)
∂2ui(z, t)
=G
- pi(z, t),
0 < z < 1,
0 ≤ t≤ 3, i = 1,2,
(49)
∂t
∂z2
краевая задача с граничными
)
)
(∂u1(z, t)
(∂u2(z, t)
- K0u1(z, t)
= -2K0b(t),
- K0u2(z, t)
= 0,
0 ≤ t≤ 3, (50)
∂z
∂z
z=0
z=0
)
)
(∂u1(z, t)
(∂u2(z, t)
+ K0u1(z, t)
= 0,
+ K0u2(z, t)
= 0,
0 ≤ t≤ 3,
(51)
∂z
∂z
z=1
z=1
и начальными
0 ≤ z ≤ 1,
u1(z, t)|t=0 = 0, u2(z,t)|t=0 = 0,
условиями;
b) для функции u3(z, t), удовлетворяющей уравению
∂u3(z, t)
= -p3(z, t),
0 < z < 1,
0 ≤ t≤ 3,
(52)
∂t
задача Коши с начальным условием
u3(z, t)|t=0 = 0,
0 ≤ z ≤ 1,
и условиями на границах u3(0, t) = 0, u3(1, t) = 0,
0 ≤ t≤ 3, которые следуют из условий
v1(0, t) = 0, v2(0, t) = 0, v1(1, t) = 0, v2(1, t) = 0, p3(0, t) = 0, p3(1, t) = 0;
c) для функций v1(z, t), v2(z, t), v3(z, t), удовлетворяющих уравнениям
∂vj(z, t)
= pj(z,t),
0 < z < 1,
0 ≤ t≤ 3, j = 1,2,3,
(53)
∂t
краевая задача с граничными
v1(z, t)|z=0 = 0, v2(z, t)|z=0 = 0, v3(z, t)|z=0 = Hsc(t′),
0 ≤ t≤ 3,
(54)
v1(z, t)|z=1 = 0, v2(z, t)|z=1 = 0, v3(z, t)|z=1 = 0,
0 ≤ t≤ 3,
(55)
и с начальными
v1(z, t)|t=0 = 0, v2(z,t)|t=0 = 0, v3(z,t)|t=0 = 0,
0 ≤ z ≤ 1,
(56)
условиями.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1691
Здесь b(t)- безразмерная импульсная функция (23), функции p1(z, t), p2(z, t), p3(z, t)
определены равенствами (44), а функция c(t′) задана в (22).
Исходными параметрами задачи являются физически размерные величины:
γ,
σ,
a,
ġ,
Δ, τ, H0, Hsm, μ0.
Физически безразмерные постоянные, входящие в постановку задачи (49)-(56), определя-
ются равенствами
τ
γτ aH0
Hsm
G=
,
K0 = ˙σZ0Δ, F1 =
,
F2 = γτH0, F3 = γτ ġH20, Hs =
σμ0Δ2
Δ2
H0
9. Численный метод. Для построения разностной схемы численного решения начально-
краевой задачи (49)-(56) предварительно преобразуем функции pk(z, t), k = 1, 2, 3, опреде-
лённые равенствами (44), представив их в виде линейной комбинации
pk(z, t) = akuk(z, t) + bkvk(z, t) + dk,
(57)
функций uk(z, t), vk(z, t), где
∑
∑
ak = F3
v2l
(z, t), bk = -F3
vl(z, t)ul(z, t), dk = Pk + Rk,
l=1
l=1
l=k
l=k
)
(
))
( ∂(
∂
P1 = F1
v2(z, t)∂v3(z,t)
-
v3(z, t)∂v2(z,t)
,
∂z
∂z
∂z
∂z
R1 = F2(v2(z, t)u3(z, t) - v3(z, t)u2(z, t)),
)
(
))
( ∂(
∂
P2 = F1
v3(z, t)∂v1(z,t)
-
v1(z, t)∂v3(z,t)
,
∂z
∂z
∂z
∂z
R2 = F2(v3(z, t)u1(z, t) - v1(z, t)u3(z, t)),
)
(
))
( ∂(
∂
P3 = F1
v1(z, t)∂v2(z,t)
-
v2(z, t)∂v1(z,t)
,
∂z
∂z
∂z
∂z
R3 = F2(v1(z, t)u2(z, t) - v2(z, t)u1(z, t)).
С учётом представления (57) запишем уравнения (49), (52) в виде следующей системы
нелинейных эволюционных уравнений:
∂uk(z, t)
= -akuk(z, t) - bkvk(z, t) + Φk,
0 < z < 1,
0 ≤ t≤ 3, k = 1,2,3,
(58)
∂t
∂vk(z, t)
= akuk(z, t) + bkvk(z, t) + dk,
0 < z < 1,
0 ≤ t≤ 3, k = 1,2,3,
(59)
∂t
где
∂2uk(z, t)
Φk = -dk + G
(1 - δk,3), δk,3 - символ Кронекера, k = 1, 2, 3.
∂z2
Для решения системы уравнений (58), (59) используем сеточный метод [9, с. 73]. Область
непрерывного изменения временного аргумента [0, 3] заменим областью его дискретного из-
менения: введём временную сетку ωt = {tj =tj-1 + Δt: j = 1, M, Δt = (tM -t0)/M,
t0 = 0,
tM = 3}. Обозначимt =tj - текущий временной слой, на котором находим решение,t =tj-1 -
предыдущий временной слой, на котором решение уже найдено. Тогда шаг по времени Δt =
= t-t. Функции на текущем временном слое обозначим через uk(z) = uk(z, t), vk(z) = vk(z, t),
на предыдущем временном слое - через ǔk(z) = uk(z,t),
vk(z) = vk(z,t), k = 1, 2, 3.
Построение решения будем проводить рекуррентно по временным слоям.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
1692
ЕРОФЕЕНКО и др.
Для решения системы (58), (59) относительно пары функций uk(z, t), vk(z, t) для каждого
k = 1,2,3 рассмотрим неявную схему
uk(z) - ǔk(z)
= -akuk(z) - bkvk(z) + Φk,
0 < z < 1,
0 ≤ t≤ 3,
(60)
Δt
vk(z) - vk(z)
= akuk(z) + bkvk(z) + dk,
0 < z < 1,
0 ≤ t≤ 3.
(61)
Δt
Разностная схема (60), (61) аппроксимирует систему уравнений (58), (59) с погрешностью
O(Δt).
Преобразуем систему (60), (61) к виду
(1 + Δt ak)uk(z) + Δt bkvk(z) = ǔk(z) + Δt Φk,
-Δtakuk(z) + (1 - Δtbk)vk(z) = vk(z) + Δtdk.
(62)
Система (62) - линейная алгебраическая система уравнений относительно неизвестных
uk(z), vk(z). Её определитель имеет вид
1 + Δtak)
Δtbk
Δ=(
1 + Δt(ak - bk).
-Δtak
(1 - Δt bk)=
При достаточно малом Δt значение Δ отлично от нуля. Решение системы (62) запишем
по правилу Крамера
(ǔk(z) + ΔtΦk)(1 - Δtbk) - (vk(z) + Δtdk)Δtbk
uk(z) =
,
(63)
det A
(1 + Δt ak)(vk(z) + Δt dk) + Δt ak(ǔk(z) + Δt Φk)
vk(z) =
(64)
det A
Преобразовывая выражения в (63), (64), получаем для uk(z) и vk(z) на временном слое
t нелинейные уравнения
1
(ǔk(z) + vk(z))bk
dk
uk(z) = ǔk(z)
- Δt
- Δt
+
1 + Δt(ak - bk)
1 + Δt(ak - bk)
1 + Δt(ak - bk)
(1 - Δt bk)
∂2uk(z)
+ Δt
G
(1 - δk,3),
(65)
1 + Δt(ak - bk)
∂z2
1
(vk(z) + ǔk(z))ak
dk
vk(z) = vk(z)
+ Δt
+ Δt
+
1 + Δt(ak - bk)
1 + Δt(ak - bk)
1 + Δt(ak - bk)
ak
∂2uk(z)
+ (Δt)2
G
(1 - δk,3).
(66)
1 + Δt(ak - bk)
∂z2
Нелинейные уравнения (65), (66) будем решать разностным методом. Для этого введём по
переменной z неравномерную сетку ωz = {zi ∈ [0, 1] : i = 0, N , z0 = 0, zN = 1}, Δzi = zi -
- zi-1 - сеточные шаги, Δzi = 0.5(Δzi + Δzi+1). Значения функций uk(z) и vk(z) в узлах
сетки zi обозначим через uk(zi) = uk;i и vk(zi) = vk;i соответственно.
Аппроксимируя дифференциальные операторы, входящие в уравнения (65), (66), получаем
следующую разностную схему:
uk;i = ǔk;iDk;i - ΔtDk;i(ǔk;i + vk;i)bk;i - ΔtDk;idk;i +
)
G
(uk;i+1 -uk;i
uk;i - uk;i-1
+ ΔtDk;i(1 - Δtbk;i)
-
(1 - δk,3),
(67)
Δzi
Δzi+1
Δzi
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1693
vk;i = vk;iDk;i - ΔtDk;i(ǔk;i + vk;i)ak;i + ΔtDk;idk;i +
)
G
(uk;i+1 -uk;i
uk;i - uk;i-1
+ (Δt)2
Dk;iak;i
-
(1 - δk,3),
(68)
Δzi
Δzi+1
Δzi
где
∑
∑
1
Dk;i =
,
ak;i = F3
v2
,
bk;i = -F3
vl;iul;i,
dk;i = Pk;i + Rk;i,
l;i
1 + Δt(ak;i - bk;i)
l=1
l=1
l=k
l=k
R1;i = F2(v2;iu3;i - v3;iu2;i), R2;i = F2(v3;iu1;i - v1;iu3;i), R3;i = F2(v1;iu2;i - v2;iu1;i),
P1;i = F1(Ki2,3 - Ki3,2), P2;i = F1(Ki3,1 - Ki1,3), P3;i = F1(Ki1,2 - Ki2,1),
здесь
(
)
1
vm;i+1 - vm;i
vm;i - vm;i-1
Kik,m =
vk;i+0.5
-vk;i-0.5
,
k,m = 1,2,3,
Δzi
Δzi+1
Δzi
и vk;i±0.5 = 0.5(vk;i±1 + vk;i), k = 1,2,3.
Неявная разностная схема (67), (68) аппроксимирует систему уравнений (65), (66) с поряд-
ком аппроксимации O(Δzmax), где Δzmax = max
Δzi.
0≤i≤N
Граничные условия (50), (51) аппроксимируем, используя уравнения (49). В результате
получим следующие разностные соотношения:
)
G
( GK0
1
G
1
2GK0b(t)
uk;1 -
+
+
uk;0 = -
ǔk;0 -
(1 - δk,2), k = 1, 2,
(69)
(Δz1)2
Δz1
2Δt
(Δz1)2
2Δt
Δz1
на границе Γ1 и
(
)
G
GK0
1
G
1
uk;N-1 -
+
+
uk;N = -
ǔk;N, k = 1,2,
(70)
(ΔzN-1)2
ΔzN-1
2Δt
(ΔzN-1)2
2Δt
на границе Γ2.
Разностные схемы (69) аппроксимируют граничные условия (50) с порядком аппроксима-
ции O(Δt+Δz1). Разностные схемы (70) аппроксимируют граничные условия (51) с порядком
аппроксимации O(Δt + ΔzN ).
Аппроксимация граничных условий (54), (55) имеет вид
vk;0 = 0, k = 1,2, v3;0 = Hsc(t); vk;N = 0, k = 1,2,3.
(71)
Начальные условия на сетке ωz аппроксимируем следующими соотношениями:
uk
zi,0) = 0, vk
zi,0) = 0, k = 1,2,3, i = 0,N.
(72)
Для реализации нелинейной разностной схемы (67)-(72) построим итерационный процесс:
s+1
s
s
s
s
s
uk;i = ǔk;iDk;i - Δt
Dk;i
bk;i(ǔk;i + vk;i) - Δt
Dk;idk;i +
( s+1
s+1
+1
)
s
s
G
uk;i
uk;i-1
+ ΔtDk;i(1 - Δt
bk;i)
-
(1 - δk,3), k = 1, 2,
(73)
Δzi
Δzi+1
Δzi
во внутренних точках zi, i = 1, N - 1,
)
G
s+1
( GK0
1
G
s+1
1
2GK0b(t)
uk;1 -
+
+
uk;0 = -
ǔk;0 -
(1 - δk,2), k = 1, 2,
(74)
(Δz1)2
Δz1
2Δt
(Δz1)2
2Δt
Δz1
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
1694
ЕРОФЕЕНКО и др.
в граничной точке
z0 = 0,
(
)
G
s+1
GK0
1
G
s+1
1
uk;N-1 -
+
+
uk;N = -
ǔk;N k = 1,2,
(75)
(ΔzN-1)2
ΔzN-1
2Δt
(ΔzN-1)2
2Δt
в граничной точке zN = 1,
s+1
s
s
s
s
s
u3;i = ǔ3;iD3;i - Δt
D3;i
b3;i(ǔ3;i + v3;i) - Δt
D3;i
d3;i, i = 1, N - 1,
(76)
s+1
s+1
u3;0 = 0,
u3;N = 0,
в граничных точках z0 = 0,
zN = 1;
для значений vk;i, k = 1, 2, 3, итерационный процесс имеет вид
s+1
s
s
s
s
s
vk;i = vk;iDk;i - Δt
Dk;i
ak;i(ǔk;i + vk;i) + Δt
Dk;idk;i +
( s+1
s+1
s+1
s+1
)
s
s
G
uk;i+1 -uk;i
uk;i -uk;i-1
+ (Δt)2
Dk;i
ak;i
-
(1 - δk,3), k = 1, 2, 3,
(77)
Δzi
Δzi+1
Δzi
s+1
s+1
s+1
vk;0 = 0, k = 1,2,
v3;0 = Hsc(t
);
vk;N = 0, k = 1,2,3,
где
s
∑
2
s
∑
s
s
s
1
s
s
s
Dk;i =
s
,
ak;i = F
3
v
l;i
,
bk;i = -F3
ul;i,
dk;i =
P k;i +
Rk;i,
s
1 + Δt(ak;i -
bk;i)
l=1
l=1,
l=k
l=k
s
s
s
s
s
s
R1;i = F2(
u2;i),
R2;i = F2(
u3;i),
R3;i = F2(
u1;i),
s
s
s
s
s
s
s
s
s
P 1;i = F1(
K2,3 -
K3,2),
P 2;i = F1(
K3,1 -
K1,3),
P 3;i = F1(
K1,2 -
K2,1),
здесь
(
s
s
)
s
1
s
vm;i+1 -svm;i
s
vm;i -svm;i-1
Kk,m =
vk;i+0.5
-
vk;i-0.5
,
k,m = 1,2,3, s = 0,1,2,...
Δzi
Δzi+1
Δzi
На каждом временном слое реализация итерационного процесса осуществляется следую-
щим образом.
0
0
В качестве нулевой итерации берём значения с нижнего временного слоя:
uk;i = ǔk;i,
vk;i =
= vk;i. Затем
s+1
1) решаем систему уравнений (73)-(75) при k = 1 методом прогонки и находим
u1;i,
s+1
i = 0,N; вычисляем сеточные значения
v1;i по формуле (77), учитывая найденные значения
s+1
u1;i, i = 0,N;
s+1
2) решаем систему уравнений (73)-(75) при k = 2 методом прогонки и находим
u2;i,
s+1
i = 0,N; вычисляем сеточные значения
v2;i по формуле (77), учитывая найденные значения
s+1
u2;i, i = 0,N;
s+1
s+1
3) вычисляем сеточные значения
u3;i,
v3;i по формулам (76), (77) соответственно.
Итерационный процесс продолжается рекуррентно для s = 1, 2, . . . и прекращается при
vk;i принимаются за
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1695
uk;i, vk;i = vk(zi, tj) =
vk;i . Далее переходим к следующему слою по времени.
В результате получим множество значений {uk;i, vk;i} для каждого tj , j = 0, M, харак-
теризующее компоненты магнитного поля и намагниченности в узлах сетки.
10. Коэффициент эффективности экранирования. На плоскости Γ2 имеют место
граничные соотношения (37). Приведём их, учитывая равенства (41), к безразмерному виду
1
1
H0u1(1, t) =
B2(t- t0), H0u2(1, t) =
A2(t- t0),
t0 =Δ,
Z0
Z0
cτ
где t0 - временной сдвиг.
Вычислим амплитуды поля (26), прошедшего через экран:
A2(t) = H0Z0u2(1, t+ t0), B2(t) = H0Z0u1(1, t+ t0).
(78)
Коэффициент эффективности экранирования определим соотношением
max
|E0(0, t)|
0≤t<∞
Э=
(79)
max
|E2(Δ, t)|
0≤t<∞
Вычислим модули электрических полей (21), (26). Учитывая (21), (23), получаем, что
|E0(0, t)| = |B0(t)| = H0Z0|b(t)|,
а значит,
max
|E0(0, t)| = H0Z0.
0≤t<∞
Используя равенства (26), (78), находим
√
√
|E2(Δ, t)| = A22(t- t0) + B22(t- t0) = H0Z0 u21(1, t) + u22(1, t).
Подставляя найденные значения E0(0, t) и E2(Δ, t) в (79), получаем расчётную формулу для
коэффициента эффективности экранирования
(
√
)-1
Э = max
u21(1, t) + u22(1, t)
0≤t<∞
11. Вычислительный эксперимент. Для численного эксперимента выберем следующие
материальные параметры экрана из пермаллоя и параметры импульсного поля E0, H0, воз-
действующего на экран:
γ = 5.51 · 102 м/(А · с),
σ = 1.71 · 106 См/м,
a = 1.75 · 10-6 м2,
ġ = 3.27 · 10-6 м/А,
Δ = 10-4 м, τ = τfr = 10-3 с, H0 = 103 А/м, Hsm = 102 А/м,
μ0 = 1.26 · 10-6 Гн/м, Z0 = 377 Ом.
(80)
В этом случае безразмерные постоянные, входящие в постановку задачи, определяются вели-
чинами G = τ/( ˙σμ0Δ2) = 4.65·104, K0 = σZ0Δ = 6.45·104, F1 = γτ ˙aH0/Δ2 = 9.64·104, F2 =
= γτH0 = 5.51 · 102, F3 = γτ ġH20 = 1.8, Hs = Hsm/H0 = 10-1.
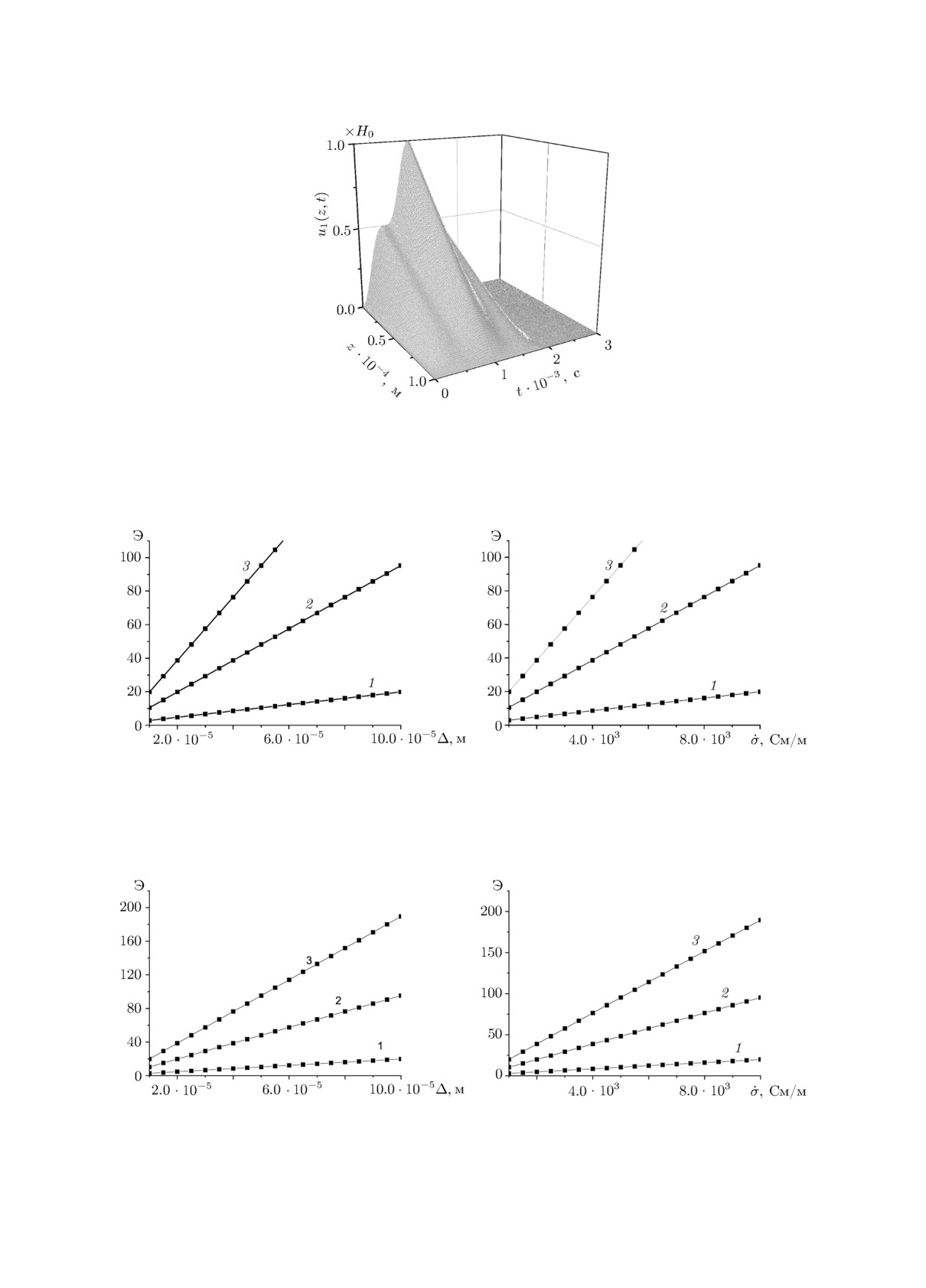
На рис. 3-5 представлены результаты моделирования. Рис. 3 отражает результаты моде-
лирования компонент магнитного поля в экране из пермаллоя. На рис. 4 и 5 представлены
графики коэффициента эффективности экранирования Э в зависимости от изменения па-
раметров экрана Δ и
σ при значениях Hsm = 102 А/м и Hsm = 104 А/м соответственно.
Остальные параметры экрана определены в (80).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
1696
ЕРОФЕЕНКО и др.
Рис. 3. Структура импульсного магнитного
поля в материале экрана из пермаллоя: пара-
метры экрана определены в (80).
(а)
(б)
Рис. 4. Зависимость коэффициента эффективности экранирования от изменения параметра Δ при
Hsm = 102 А/м - a (1 - σ = 103, 2 - σ = 5·103, 3 - σ = 104) и параметра σ - б (1 - Δ = 10-5, 2 -
Δ = 5 · 10-5, 3 - Δ = 10-4).
(а)
(б)
Рис. 5. Зависимость коэффициента эффективности экранирования от изменения параметра Δ при
Hsm = 104 А/м - a (1 - σ = 103, 2 - σ = 5·103, 3 - σ = 104) и параметра σ - б (1 - Δ = 10-5, 2 -
Δ = 5 · 10-5, 3 - Δ = 10-4).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ЗАДАЧ ЭКРАНИРОВАНИЯ
1697
Заключение. В статье разработан численный метод решения начально-краевой задачи,
описывающей проникновение импульсных электромагнитных полей через плоский экран из
пермаллоя. Рассмотрен случай, когда на слой из пермаллоя воздействует заданное импульс-
ное электромагнитное поле с потоком энергии, перпендикулярным слою. Дополнительно на
экран воздействует постоянное магнитное поле, возбуждающее поле намагниченности. Исход-
ная трёхобластная нелинейная краевая задача преобразована в однообластную краевую задачу
для слоя. Построены односторонние граничные условия третьего и первого рода на лицевых
поверхностях слоя, эквивалентные граничным условиям сопряжения для трёхобластной зада-
чи. Однообластная краевая задача для нелинейных уравнений Максвелла сформулирована в
виде нелинейной начально-краевой задачи с нулевыми начальными условиями для системы
параболических дифференциальных уравнений (49)-(53) с шестью неизвестными функция-
ми, зависящими от безразмерных пространственных переменных и безразмерного времени.
Разработан численный метод для нахождения компонент магнитного поля и намагниченности
внутри экрана из пермаллоя. Для численной оценки экранирующих свойств такого экрана най-
ден коэффициент эффективности экранирования, показывающий во сколько раз ослабевает
электромагнитный импульс при прохождении через экран при различных значениях исходных
параметров.
СПИСОК ЛИТЕРАТУРЫ
1. Ринкевич А.Б., Перов Д.В., Васьковский В.О., Лепаловский В.Н. Закономерности проникновения
электромагнитных волн через металлические магнитные пленки // Журн. техн. физики. 2009. Т. 79.
Вып. 9. С. 96-106.
2. Ерофеенко В.Т. Математическая модель экранирования монохроматических электромагнитных по-
лей плоскими экранами из пермаллоя // Информатика. 2019. Т. 16. № 2. С. 40-51.
3. Никольский В.В., Никольская Т.И. Электродинамика и распространение радиоволн. М., 1989.
4. Ерофеенко В.Т., Урбанович А.И. Нелинейная модель краевой задачи экранирования импульсных
полей плоским экраном из пермаллоя // Тр. XXX междунар. конф. “Радиационная физика твердого
тела” / Под ред. Г.Г. Бондаренко. Севастополь, 24-29 августа 2020 г. М., 2020. С. 416-430.
5. Ерофеенко В.Т., Громыко Г.Ф., Заяц Г.М. Краевые задачи экранирования магнитных полей мно-
гослойными пленочными цилиндрическими экранами с нелинейными свойствами слоёв // Диффе-
ренц. уравнения. 2019. Т. 55. № 7. С. 996-1008.
6. Громыко Г.Ф., Грабчиков С.С., Ерофеенко В.Т., Заяц Г.М. Эффективность экранирования постоян-
ных магнитных полей цилиндрическим экраном с учётом нелинейных эффектов // Физич. основы
приборостроения. 2015. Т. 4. № 4. С. 30-39.
7. Громыко Г.Ф., Ерофеенко В.Т., Заяц Г.М. Численное исследование структуры магнитного поля в
цилиндрическом пленочном экране // Информатика. 2016. № 2 (50). С. 5-18.
8. Ерофеенко В.Т., Козловская И.С. Аналитическое моделирование в электродинамике. М., 2014.
9. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М., 1978.
Белорусский государственный университет, г. Минск,
Поступила в редакцию 22.01.2021 г.
Институт математики НАН Беларуси, г. Минск
После доработки 29.07.2021 г.
Принята к публикации 08.09.2021 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№ 12
2021