ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 2, с.210-223
ОБЫКНОВЕННЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
УДК 517.911+517.925.51
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ
НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНО-АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ,
ОГРАНИЧЕННОСТЬ И УСТОЙЧИВОСТЬ ИХ РЕШЕНИЙ. II
© 2021 г. М. С. Филипковская
Доказаны теоремы об устойчивости, асимптотической устойчивости и неустойчивости по
Ляпунову положения равновесия нестационарных полулинейных дифференциально-алгеб-
раических уравнений (ДАУ), а также теоремы об асимптотической (полной) устойчивости
этих уравнений. В качестве примера применения доказанных в первой части работы теорем
о глобальной разрешимости нестационарных полулинейных ДАУ исследована математи-
ческая модель некоторой электрической цепи.
DOI: 10.31857/S0374064121020096
Настоящая работа является второй частью работы [1], поэтому в ней продолжается начатая
в [1] нумерация пунктов, формул, лемм и теорем.
В данной работе, как и в [1], рассматриваются неявные дифференциальные уравнения
d
[A(t)x(t)] + B(t)x(t) = f(t, x(t)), t ∈ [t+, ∞),
(1.1)
dt
d
A(t)
x(t) + B(t)x(t) = f(t, x(t)), t ∈ [t+, ∞),
(1.2)
dt
и начальное условие
x(t0) = x0,
(1.3)
где t0 ≥ t+ ≥ 0, A, B : [t+, ∞) → L(Rn) (через L(X, Y ) обозначается векторное пространство
непрерывных линейных операторов, действующих из векторного пространства X в векторное
пространство Y ; L(X, X) = L(X)) и f : [t+, ∞) × Rn → Rn. Операторы A(t) и B(t) могут
быть вырожденными (необратимыми). Уравнения вида (1.1), (1.2) с вырожденным (при неко-
тором t) оператором A(t) называют вырожденными дифференциальными уравнениями или
дифференциально-алгебраическими уравнениями. В терминологии ДАУ уравнения вида (1.1),
(1.2) принято называть полулинейными. Поскольку операторы A(t) и B(t) нестационарны,
то уравнения (1.1), (1.2) называются нестационарными полулинейными ДАУ или нестацио-
нарными вырожденными дифференциальными уравнениями. В дальнейшем, для общности,
уравнения (1.1) и (1.2), где A(t) (A: [t+, ∞) → L(Rn)) - произвольный (не обязательно вы-
рожденный) оператор, будем называть нестационарными полулинейными ДАУ.
Левой (линейной) части уравнений (1.1) и (1.2) отвечает пучок операторов λA(t) + B(t)
(λ ∈ C - параметр). Пусть для каждого t ≥ t+ пучок регулярен, т.е. для каждого t ≥ t+
множество его регулярных точек не пусто (множеством регулярных точек пучка λA(t) + B(t)
является множество регулярных точек его комплексного расширения). Для регулярных точек
λ существует резольвента R(λ, t) = (λA(t) + B(t))-1.
Ниже даны некоторые сведения из [1, п. 1] относительно нестационарных спектральных
проекторов Pj (t), Qj (t), j = 1, 2, и оператора G(t), использующиеся в работе. Эти проекто-
ры и оператор G(t) и их свойства подробно описаны в монографии [2].
В дальнейшем предполагается, что для каждого t ≥ t+ пучок регулярен и выполнено
следующее условие: существуют функции C1 : [t+, ∞) → (0, ∞) и C2 : [t+, ∞) → (0, ∞) такие,
что для любого t ∈ [t+, ∞) выполнена оценка
∥R(λ, t)∥ ≤ C1(t),
|λ| ≥ C2(t).
(1.4)
210
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
211
Тогда для каждого t ∈ [t+, ∞) существуют две пары взаимно дополнительных проекторов
P1(t), P2(t) и Q1(t), Q2(t) (Pi(t)Pj(t) = δijPi(t), P1(t)+P2(t) = IRn , и Qi(t)Qj(t) = δijQi(t),
Q1(t)+Q2(t) = IRn, где IRn - тождественный оператор в Rn, δij - символ Кронекера), которые
могут быть определены по формулам [1, (1.15)] (см. [2, с. 82-83]), являются вещественными
(поскольку A(t) и B(t) вещественные) и порождают прямые разложения пространств
Rn = X1(t) +X2(t), Xj(t) = Pj(t)Rn, Rn = Y1(t) +Y2(t), Yj(t) = Qj(t)Rn, j = 1,2,
такие, что пары подпространств X1(t), Y1(t) и X2(t), Y2(t) инвариантны относительно A(t),
B(t) (т.е. A(t), B(t): Xj (t) → Yj(t)), а суженные операторы Aj (t) = A(t)|Xj (t) : Xj (t) → Yj(t),
Bj(t) = B(t)|Xj(t) : Xj(t) → Yj(t), j
= 1, 2, таковы, что A2(t) = 0 и существуют A-11(t)
(если X1(t) = {0}) и B-12(t) (если X2(t) = {0}). Проекторы Pj (t), Qj (t) удовлетворяют
следующим свойствам:
A(t)P1(t) = Q1(t)A(t) = A(t), A(t)P2(t) = Q2(t)A(t) = 0, B(t)Pj (t) = Qj(t)B(t), j = 1, 2.
Они также используются при построении вспомогательного оператора
G(t) = A(t) + B(t)P2(t) = A(t) + Q2(t)B(t) ∈ L(Rn),
G(t): Xj(t) → Yj (t) (G(t)Xj (t) = Yj(t)), который имеет обратный G-1(t) = A-11(t)Q1(t) +
+ B-12(t)Q2(t) ∈ L(Rn) (G-1(t): Yj(t) → Xj(t)).
Пусть A, B ∈ C1([t+, ∞), L(Rn)) и C2 ∈ C1([t+, ∞), (0, ∞)), тогда проекторы Pi(t), Qi(t),
i = 1, 2, и операторы G(t), G-1(t) также непрерывно дифференцируемы как оператор-
функции на [t+, ∞), т.е. Pi, Qi, G, G-1 ∈ C1([t+, ∞), L(Rn)).
Для каждого t любой вектор x ∈ Rn единственным образом представим в виде
x = P1(t)x + P2(t)x = xp1(t) + xp2(t), xpi(t) = Pi(t)x ∈ Xi(t).
Функцию x ∈ C([t0, t1), Rn), [t0, t1) ⊆ [t+, ∞), называют решением уравнения (1.1) на про-
межутке [t0,t1), если A(t)x(t) непрерывно дифференцируема на [t0,t1) и x(t) удовлетво-
ряет уравнению (1.1) на [t0, t1). Функцию x ∈ C1([t0, t1), Rn) называют решением уравнения
(1.2) на промежутке [t0,t1), если x(t) удовлетворяет уравнению (1.2) на [t0,t1). Если ре-
шение x(t) уравнения (1.1) (уравнения (1.2)) удовлетворяет начальному условию (1.3), то его
называют решением задачи Коши или начальной задачи (1.1), (1.3) (решением задачи Коши
или начальной задачи (1.2), (1.3)).
В первой части настоящей работы, т.е. в [1], для ДАУ (1.1) и (1.2) получены теоремы, да-
ющие достаточные условия существования и единственности глобальных решений, теоремы
об устойчивости по Лагранжу, диссипативности (предельной ограниченности) и неустойчиво-
сти по Лагранжу. Устойчивость по Лагранжу (диссипативность ДАУ) означает существование
глобальных решений для всех согласованных начальных значений, т.е. для всех возможных
начальных значений, и ограниченность (предельную ограниченность) всех решений.
Одной из особенностей теорем о существовании и единственности глобальных решений,
представленных в [1], является то, что в них не используется глобальное условие Липшица
или подобные ему ограничения. Подробнее это обсуждается в [1, пп. 2.1]. В настоящей работе
в п. 5 продемонстрировано применение теорем 2.1, 2.2 [1] о глобальной разрешимости (которые
не содержат глобальных условий Липшица) для решения одной задачи по электротехнике, а
также показано, что условия теорем могут выполняться для функций, не удовлетворяющих
условию утверждения 2.1 [1] о глобальной разрешимости, в котором требуется, чтобы ”алгебра-
ическая часть” ДАУ удовлетворяла глобальному условию Липшица по компоненте P2(t)x пе-
ременной x (некоторые условия теорем 2.1, 2.2 и утверждения 2.1 совпадают), а для функций,
удовлетворяющих условиям утверждения, условия теорем также будут выполнены. Вообще,
из доказательства утверждения 2.1 [1] следует, что если его условия выполнены, то выполнены
и условия теорем 2.1, 2.2 [1].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№2
2021
5∗
212
ФИЛИПКОВСКАЯ
В настоящей работе получены теоремы об устойчивости, асимптотической устойчивости и
неустойчивости по Ляпунову положения равновесия ДАУ (1.1) и (1.2), а также теоремы об
асимптотической (полной) устойчивости ДАУ (1.1) и (1.2).
3. Устойчивость и асимптотическая устойчивость по Ляпунову. Рассмотрим ДАУ
(1.1) и (1.2), где f(t, 0) ≡ 0. Их иногда называют ДАУ возмущённого движения (по анало-
гии с соответствующим термином для явных ОДУ). Эти ДАУ имеют положение равновесия
(стационарное решение) x∗(t) ≡ 0. Напомним, что согласованной начальной точкой для за-
дачи Коши (1.1), (1.3) (задачи Коши (1.2), (1.3)) называется точка (t0, x0), принадлежащая
Lt
Lt
многообразию Lt+ (многообразию
+
), где Lt+ и
+
имеют вид (см. [1, формулы (1.21),
(1.22)])
Lt+ = {(t,x) ∈ [t+,∞) × Rn | Q2(t)[A′(t)P1(t)x + B(t)x - f(t,x)] = 0},
Lt
= {(t, x) ∈ [t+, ∞) × Rn | Q2(t)[B(t)x - f(t, x)] = 0}.
+
Очевидно, точка (t, 0) принадлежит Lt+ иLt+ для каждого t ∈ [t+, ∞) (если f(t, 0) ≡ 0).
,r2
(0) обозначаются множества
UxR(0) = {x ∈ Rn | ∥x∥ < R}, Br1 (0) = {z ∈ Rn | ∥z∥ ≤ r1}
и
,r2
(0) = {x ∈ Rn | ∥xpi (t)∥ ≤ ri, xpi (t) = Pi(t)x, i = 1, 2}.
Пусть f : [t+, ∞) × UxR(0) → Rn.
Определение 3.1. Положение равновесия x∗(t) ≡ 0 ДАУ (1.1), где f(t,0) ≡ 0, называ-
ется устойчивым по Ляпунову, или просто устойчивым, если для любых ε > 0 (ε < R),
t0 ∈ [t+,∞) существует число δ = δ(ε,t0) > 0 (δ ≤ ε) такое, что для любой согласованной
начальной точки (t0, x0), удовлетворяющей условию ∥x0∥ < δ, существует глобальное реше-
ние x(t) задачи Коши (1.1), (1.3) и это решение удовлетворяет неравенству ∥x(t)∥ < ε для
всех t ∈ [t0, ∞). Если, кроме того, существуетδ =δ(t0) > 0
(δ ≤ δ) такое, что для каждого
решения x(t) с начальной точкой (t0, x0), удовлетворяющей условию ∥x0∥ <δ, выполнено
требование lim
x(t) = 0, то положение равновесия x∗(t) ≡ 0 называется асимптотически
t→∞
устойчивым по Ляпунову (или просто асимптотически устойчивым).
Если в определении 3.1 число δ не зависит от t0, т.е. δ = δ(ε), то положение равновесия
называется равномерно устойчивым по Ляпунову, или просто равномерно устойчивым, (на
[t+, ∞)).
Определение 3.2. Положение равновесия x∗(t) ≡ 0 ДАУ (1.1), где f(t,0) ≡ 0, называется
неустойчивым по Ляпунову, или просто неустойчивым, если для некоторых ε > 0 (ε < R),
t0 ∈ [t+,∞) и любого δ > 0 существуют решение xδ(t) задачи Коши (1.1), (1.3) и момент
времени t1 > t0 такие, что ∥x0∥ < δ и ∥xδ(t1)∥ ≥ ε.
Пусть теперь f : [t+, ∞) × Rn → Rn.
Определение 3.3. Если положение равновесия x∗(t) ≡ 0 ДАУ (1.1), где f(t,0) ≡ 0,
асимптотически устойчиво и, более того, для каждой точки (t0, x0) ∈ Lt+ (т.е. для каждой
согласованной начальной точки) существует глобальное решение x(t) задачи Коши (1.1), (1.3)
и lim
x(t) = 0, то положение равновесия x∗(t) ≡ 0 называется асимптотически устойчивым
t→∞
в целом, а ДАУ - полностью устойчивым, или асимптотически устойчивым.
Аналогичные определения имеют место для ДАУ (1.2), где f(t, 0) ≡ 0.
Приведённые определения устойчивости и асимптотической устойчивости положения рав-
новесия ДАУ подобны тем, что даны в [3-5], и представляют собой обобщения соответству-
ющих классических определений для (явных) ОДУ, а определение асимптотической устойчи-
вости в целом положения равновесия (полной устойчивости) ДАУ обобщает соответствующее
определение для (явных) ОДУ из [6, с. 35-36] ([7, с. 85]).
Заметим, что для полулинейного ДАУ (невозмущённого движения), так же, как и в случае
явного нелинейного ОДУ, из устойчивости по Ляпунову нестационарного решения, в общем,
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№2
2021
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
213
не следует его устойчивость по Лагранжу. Также из устойчивости по Лагранжу решения по-
лулинейного ДАУ, вообще говоря, не следует его устойчивость по Ляпунову.
Замечание 3.1. Поскольку из неустойчивости решения по Лагранжу следует его неустой-
чивость по Ляпунову, то теоремы о неустойчивости по Лагранжу ДАУ можно рассматривать
и как теоремы о неустойчивости по Ляпунову.
Теорема 3.1 (устойчивость и асимптотическая устойчивость по Ляпунову положения рав-
новесия ДАУ (1.1)). Пусть f ∈ C([t+, ∞) × UxR(0), Rn), f(t, 0) ≡ 0,
∂f/∂x ∈ C([t+,∞) ×
× UxR(0),L(Rn)), A,B ∈ C1([t+,∞),L(Rn)) и пучок λA(t) + B(t) удовлетворяет условию
(1.4), где C2 ∈ C1([t+, ∞), (0, ∞)). Пусть для каждого t∗ ∈ [t+, ∞) и x∗p1 (t∗) = 0, x∗p2 (t∗) = 0
оператор∗)
[
]
∂
[Q2(t∗)f(t∗, x∗p
(t∗) + x∗p
(t∗))] - B(t∗) P2(t∗): X2(t∗) → Y2(t∗)
Φt∗,x∗p
(t∗),xp2 (t∗) =
1
2
1
∂x
имеет обратный. Тогда верны следующие утверждения.
1. Пусть существуют числа r1, r2 > 0, r1 + r2 < R, и положительно определённая
функция V
,r2
(0)
выполнено неравенство
V ′(1.14)(t,xp1(t)) ≤ 0,
(3.1)
где V′(1.14)(t, xp1 (t)) имеет вид∗∗)
∂V
(∂V
V ′(1.14)(t,xp1(t)) =
(t, xp1 (t)) +
(t, xp1 (t)), [P′1(t) - G-1(t)Q1(t)[A′(t) + B(t)]]xp1 (t) +
∂t
∂z
)
+ G-1(t)Q1(t)f(t,xp1(t) + xp2(t))
Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.1) устойчиво по Ляпунову.
2. Пусть существуют числа r1, r2 > 0, r1 + r2 < R, и положительно определённые
функции V
∈ C1([t+,∞) × Br1(0),R), W ∈ C(Br1(0),R), U ∈ C(Br1(0),R) такие, что
V (t, z) ≤ W (z) для всех t ∈ [t+, ∞), z ∈ Br1 (0) и
V ′(1.14)(t,xp1(t)) ≤ -U(xp1(t))
(3.2)
,r2
(0), xp1 (t) = 0; пусть также выполнено условие:
G-1(t)Q2(t)[f(t, P1(t)x + P2(t)x) - A′(t)P1(t)x] → 0
при x → 0 равномерно по t на [T,∞) для некоторого T > t+.
(3.3)
Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.1) асимптотически устойчиво по Ляпунову.
Доказательство. Доказательство утверждения 1. Введём отображения Π, F ∈
∈ C([t+,∞) × Rn × Rn,Rn) вида (2.5), (2.6) и рассмотрим систему (2.9), (2.10). Очевидно,
f (t, 0) ≡ 0 тогда и только тогда, когда Π(t, 0, 0) ≡ 0 и F (t, 0, 0) ≡ 0. Напомним, что ДАУ
(1.1) эквивалентно системе (1.14), (1.15) (или (1.12), (1.13)).
Без потери общности можем считать, что оператор A(t) не является нулевым или обрати-
мым при всех t, так как в случае, если A(t) обратим (при всех t), ДАУ можно свести к явному
ОДУ, а в случае, если A(t) тождественно равен нулю, ДАУ становится чисто алгебраическим
уравнением, т.е. не содержит производной. Для этих особых случаев теорема остаётся верной,
но её доказательство представляет интерес именно для ДАУ. Поэтому в дальнейшем будем
∗) См. [1, формула (2.2)]. Здесь и ниже в формулировках теорем мы для удобства воспроизводим некоторые
формулы работы [1].
∗∗) См. [1, формула (2.4)].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
214
ФИЛИПКОВСКАЯ
предполагать, что X1(t) = {0} и X2(t) = {0}. Напомним, что размерности подпространств
X1(t), X2(t) постоянны при всех t ∈ [t+,∞) (см. замечание 1.1).
Очевидно, что существуют некоторые области Dz, Du ⊂ Rn, содержащие начало коорди-
нат, для которых определены отображения Π, F, т.е. P1(t)Dz + P2(t)Du ⊂ UxR(0) и Π(t, z, u):
[t+, ∞) × Dz × Du → Rn, F (t, z, u): [t+, ∞) × Dz × Du → Rn. Отображения Π, F ∈ C([t+, ∞) ×
× Dz × Du,Rn) непрерывно дифференцируемы по z, u и частные производные отображе-
ния F (t, z, u) имеют вид (2.7), (2.8), где Φt,P1(t)z,P2(t)u - оператор (2.2). Обозначим
Φt,z,u =
= Φt,P1(t)z,P2(t)u как в теореме 2.1. Очевидно, что лемма 2.1 остаётся в силе. Заметим, что если
u(t) ∈ Rn удовлетворяет равенству F (t, z(t), u(t)) = 0 (т.е. равенству (2.10)), то u(t) ∈ X2(t).
По условию теоремы для каждого t∗ ∈ [t+, ∞) обратим оператор
Φt
∗,0,0
= Φt∗,0,0. Сле-
довательно, для каждой точки (t, z, u) = (t∗, 0, 0) обратим оператор Ψt,z,u = ∂F (t, z, u)/∂u
(см. (2.12)). Пусть t∗ ∈ [t+, ∞) - произвольный фиксированный элемент. Так как F (t∗, 0, 0) =
= 0 и выполнены условия теорем о неявной функции, то существуют окрестности Uσ1(t∗) ×
× Uzδ1(0) ⊂ [t+,∞) × Dz (Uσ1(t∗) = [t∗,t∗ + σ1) при t∗ = t+), Uu (0) ⊂ Du и единственнаяγ
1
функция u = μ(t, z) ∈ C(Uσ1 (t∗) × Uzδ1 (0), Uuγ1 (0)), которая является непрерывно дифферен-
цируемой по z на Uσ1 (t∗) × Uz (0) и удовлетворяет уравнению (2.11), т.е. F (t, z, μ(t, z)) =δ
1
= 0 для (t,z) ∈ Uσ1(t∗) × Uzδ1(0), и μ(t∗,0) = 0. Так как u = μ(t,z) удовлетворяет (2.11)
для (t, z) ∈ Uσ1 (t∗) × Uzδ1 (0), то μ(t, z) ∈ X2(t) и (t, P1(t)z + μ(t, z)) ∈ Lt+ для каждого
(t, z) ∈ Uσ1 (t∗) × Uzδ1 (0). Таким образом, доказано, что для каждого t ∈ [t+, ∞) и каждого
z из достаточно малой окрестности Uz (0) существует единственное u из достаточно малойδ
1
окрестности Uu (0), удовлетворяющее (2.11). Поскольку полученная неявная функция u =γ
1
= μ(t,z) непрерывна в точке (t∗,0), то для всякого ε1 > 0 найдутся σ1 = σ1(ε1,t∗) > 0,
δ1 =δ1(ε1,t∗) > 0 (σ1 ≤ σ1,
δ1 ≤ δ1) такие, что для (t,z) ∈ Uσ1 (t∗) × Uz (0) выполнено нера-˜
δ1
венство ∥μ(t, z)∥ < ε1 и, следовательно, ∥u∥ < ε1 при u = μ(t, z). Таким образом, доказана
следующая
Лемма 3.1. Для любых εu > 0, t ∈ [t+, ∞) и любого z ∈ Uzδ∗ (0), где δ∗ > 0 достаточно
мало, существует единственное u ∈ Uuεu (0), удовлетворяющее уравнению (2.11), и это u
принадлежит X2(t) (т.е. ∥u∥ < εu, F(t,z,u) = 0 и u = P2(t)u).
Пусть ε > 0 - произвольное число (ε < R). Представим его в виде суммы ε = εz + εu
чисел εz > 0, εu > 0, которые будут указаны ниже.
Подобно тому, как это сделано выше, используя теоремы о неявной функции и лемму 3.1,
получаем следующее утверждение. Для любого фиксированного t∗ ∈ [t0, ∞) существуют про-
межуток Uσ2 (t∗) ⊂ [t+, ∞) (σ2 = σ2(εu, t∗), Uσ2 (t+) = [t+, t+ +σ2)), окрестность Uzδ2 (0) (δ2 =
= δ2(εu,t∗) ≤ εz) и единственная функция νt∗(t,z) ∈ C(Uσ2(t∗) × Uzδ2(0),Uuεu(0)), являющаяся
решением уравнения (2.11) относительно u (т.е. F (t, z, νt∗ (t, z)) = 0 для (t, z) ∈ Uσ2 (t∗) ×
×Uzδ2(0)), непрерывно дифференцируемая по z и принадлежащая X2(t) для каждого (t,z) ∈
∈ Uσ2(t∗) × Uzδ2(0), а также удовлетворяющая равенству νt∗(t∗,0) = 0. Введём функцию u =
= η(t,z): [t+,∞) × Uzδ2 (0) → Uuεu(0) и определим η(t,z) = νt∗(t,z) в точке (t,z) = (t∗,z∗) для
каждой точки (t∗, z∗) ∈ [t+, ∞) × Uz (0). Тогда функция u = η(t, z), непрерывная по (t, z) иδ
2
непрерывно дифференцируемая по z, является единственным решением уравнения (2.11) и
принадлежит X2(t) для каждого (t, z) ∈ [t+, ∞) × Uz (0). Очевидно, η(t, 0) ≡ 0.δ
2
Подставим полученную функцию u = η(t, z) в (2.5) и обозначим
Π(t, z) = Π(t, z, η(t, z)).
Тогда уравнение (2.9) примет вид (2.13), т.е. z′(t) =Π(t, z(t)). В силу свойств функций η и Π
функцияΠ непрерывна по (t, z) и непрерывно дифференцируема по z на [t+, ∞) × Uz (0),δ
2
а также
Π(t, 0) ≡ 0. Очевидно, что для каждой начальной точки (t0, z0) ∈ [t+, ∞) × Uz (0)δ
2
существует единственное локальное решение уравнения (2.13).
Возьмём любое начальное значение t0 ∈ [t+, ∞) и выберем любое согласованное началь-
ное значение x0, т.е. (t0, x0) ∈ Lt+ , или F (t0, P1(t0)x0, P2(t0)x0) = 0, удовлетворяющее усло-
вию ∥x0∥ < δ ≤ ε, где δ = δ(ε, t0) > 0 выбрано так, что ∥P1(t0)x0∥ < δz ≤ min{εz, δ2}
и δz - достаточно малое число, которое будет определено ниже, и ∥P2(t0)x0∥ < εu. Обо-
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
215
значим z0 = P1(t0)x0 и u0 = P2(t0)x0, тогда η(t0, z0) = u0 (поскольку F (t0, z0, u0) = 0).
Для выбранной начальной точки (t0, z0) существует единственное локальное решение z =
= ζ(t) уравнения (2.13), удовлетворяющее начальному условию ζ(t0) = z0. Тогда функции
z = ζ(t), u = η(t,ζ(t)) являются единственным локальным решением системы (2.9), (2.10),
удовлетворяющим начальным условиям ζ(t0) = z0, η(t0, ζ(t0)) = u0, и по лемме 2.1 функция
x(t) = ζ(t) + η(t, ζ(t)) (ζ(t) = P1(t)x(t) = xp1 (t) ∈ X1(t), η(t, ζ(t)) = P2(t)x(t) = xp2 (t) ∈ X2(t))
является единственным локальным решением ДАУ (1.1), удовлетворяющим начальному усло-
вию (1.3), где x0 = z0 + u0. Без потери общности можем считать, что δ2 ≤ r1 и εu ≤ r2, где
числа r1, r2 определены в утверждении 1. В силу условия (3.1) для любых t ∈ [t0, ∞) и z ∈
∈ X1(t) таких, что ∥z∥ < δ2, производная функции V в силу уравнения (2.13) удовлетворяет
неравенству
V ′(2.13)(t,z) ≤ 0.
(3.4)
Напомним, что ∥z0∥ < δz ≤ min{εz , δ2}, где z0 = P1(t0)x0 = ζ(t0). Далее, как и в доказатель-
стве классической теоремы Ляпунова об устойчивости, получаем, что число δz = δz(εz, t0) > 0
можно выбрать таким, что решение z = ζ(t) имеет продолжение на [t0, ∞) (т.е. является
глобальным) и ∥ζ(t)∥ < εz для всех t ∈ [t0, ∞). Это выполнено для любого εz > 0. Выберем
такие δz, εz и εu, что εz + εu = ε,
∥ζ(t)∥ < εz для t ∈ [t0, ∞) и ∥η(t, ζ(t))∥ < εu при
∥ζ(t)∥ < εz, t ∈ [t0, ∞). Тогда ∥x(t)∥ = ∥ζ(t) + η(t, ζ(t))∥ < εz + εu = ε для всех t ∈ [t0, ∞).
Поскольку ε > 0 и t0 ∈ [t+, ∞) выбирались произвольно, то утверждение 1 доказано.
Доказательство утверждения 2. Устойчивость по Ляпунову положения равновесия
x∗(t) ≡ 0 доказывается так же, как и выше. Покажем, что решение x(t) = ζ(t) + η(t,ζ(t))
с начальной точкой (t0, x0) (x0 = z0 + u0), построенное в доказательстве утверждения 1,
удовлетворяет требованию lim
x(t) = 0 при ∥x0∥ < δ и достаточно малом δ = δ(t0) > 0.
t→∞
Как и выше, δ выбрано так, что ∥z0∥ = ∥P1(t0)x0∥ < δz , где δz - достаточно малое число,
которое будет определено ниже. Очевидно, что числа δ и δz отличаются от тех, которые были
выбраны в доказательстве утверждения 1, но для удобства мы сохраняем за ними прежние
обозначения.
Так как по условию утверждения 2 существует функция W ∈ C(Br1 (0), R) такая, что
W (0) = 0 и 0 ≤ V (t, z) ≤ W (z) для всех t ∈ [t+, ∞), z ∈ Br1 (0), то V (t, z) допускает беско-
нечно малый высший предел в Br1 (0) (см. определение [6, c. 11, определение 1.7]). Поскольку
в силу условия (3.2) вместо неравенства (3.4) выполнено неравенство V ′(2.13)(t, z) ≤ -U(z), где
скалярная функция U(z) непрерывна и положительно определена, то, как и в доказатель-
стве классической теоремы Ляпунова об асимптотической устойчивости, получаем, что число
δz = δz(t0) > 0 можно выбрать таким, чтобы lim ζ(t) = 0. Тогда, учитывая условие (3.3) и
t→∞
равенства (2.31) и η(t, 0) ≡ 0, получаем, что lim
η(t, ζ(t)) = 0. Следовательно, lim x(t) = 0
t→∞
t→∞
и утверждение 2 доказано. Теорема 3.1 доказана.
Теорема 3.2 (асимптотическая устойчивость в целом (полная устойчивость ДАУ (1.1))).
Пусть f ∈ C([t+, ∞)×Rn, Rn), f(t, 0) ≡ 0, ∂f/∂x ∈ C([t+, ∞)×Rn, L(Rn)), A, B ∈C1([t+, ∞),
L(Rn)) и пучок λA(t) + B(t) удовлетворяет условию (1.4), где C2 ∈ C1([t+, ∞), (0, ∞)).
Пусть выполнены условия 1), 2) теоремы 2.1 или 1), 2) теоремы 2.2, а также условие (3.3).
Пусть, кроме того, существуют положительно определённые функции V ∈ C1([t+,∞) ×
× Rn,R), W ∈ C(Rn,R), U ∈ C(Rn,R) такие, что:
1) V (t, z) ≤ W (z) для всех t ∈ [t+, ∞), z ∈ Rn;
2) V (t, z) → ∞ равномерно по t на [t+, ∞) при ∥z∥ → ∞;
3) для всех (t, xp1 (t) + xp2 (t)) ∈ Lt+ , xp1 (t) = 0 (xpi (t) = Pi(t)x, i = 1, 2), выполнено
неравенство (3.2).
Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.1) асимптотически устойчиво в целом
(ДАУ (1.1) полностью устойчиво).
Доказательство. Поскольку условия теоремы включают условия утверждения 2 теоре-
мы 3.1, то положение равновесия асимптотически устойчиво. Как и в доказательстве тео-
рем 2.1 или 2.2, где вместо неравенства (2.15) выполнено неравенство v′ ≤ 0, получаем,
что для каждой согласованной начальной точки (t0, x0) существует единственное глобаль-
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
216
ФИЛИПКОВСКАЯ
ное решение x(t) = ζ(t) + η(t, ζ(t)) задачи Коши (1.1), (1.3), где ζ(t) = P1(t)x(t) = xp1 (t),
η(t, ζ(t)) = P2(t)x(t) = xp2 (t). Докажем, что lim x(t) = 0. Поскольку f(t, 0) ≡ 0, то, как
t→∞
и в доказательстве теоремы 3.1, η(t,0) ≡ 0. Заметим, что для t ≥ t0, ζ(t) = 0 выполнено
неравенство V′(2.13)(t, ζ(t)) ≤ -U(ζ(t)) (так как выполнено неравенство (3.2)), где функция
U (z) непрерывна и положительно определена, и V′(2.13)(t, 0) ≡ 0. Из свойств функций V (t, z)
и W(z) следует, что V (t,z) допускает бесконечно малый высший предел в Rn (см. опреде-
ление в [6, c. 11, определение 1.7]). Учитывая свойства функций V (t, z), W (z) и U(z), как
и в доказательстве теоремы Барбашина-Красовского об асимптотической устойчивости в це-
лом [6, с. 36, теорема 5.2], получаем, что lim ζ(t) = 0. Тогда так же, как и в доказательстве
t→∞
утверждения 2 теоремы 3.1, получаем, что lim
η(t, ζ(t)) = 0, и, значит, lim x(t) = 0. Теорема
t→∞
t→∞
доказана.
Теорема 3.3 (неустойчивость по Ляпунову положения равновесия ДАУ (1.1)). Пусть f ∈
∈ C([t+,∞) × UxR(0),Rn), f(t,0) ≡ 0, ∂f/∂x ∈ C([t+,∞) × UxR(0),L(Rn)), A,B ∈ C1([t+,∞),
L(Rn)) и пучок λA(t) + B(t) удовлетворяет условию (1.4), где C2 ∈ C1([t+, ∞), (0, ∞)).
Пусть для каждого t∗ ∈ [t+, ∞) оператор (2.2), где x∗p1 (t∗) = 0 и x∗p2 (t∗) = 0, имеет обрат-
ный. Пусть, кроме того, существуют числа T ≥ t+ и r1, r2 > 0, r1 + r2 < R, и функция
V ∈ C1([T,∞) × Br1(0),R) такие, что:
1) V (t, z) → 0 равномерно по t на [T, ∞) при ∥z∥ → 0;
2) существует положительная функция U ∈ C(Br1(0),[0,∞)) такая, что
V ′(1.14)(t,xp1(t)) ≥ U(xp1(t)) > 0 или V ′(1.14)(t,xp1(t)) ≤ -U(xp1(t)) < 0
,r2
(0), xp1 (t) = 0 (V′(1.14)(t, xp1 (t)) имеет вид (2.4));
3) для любых Δ1 > 0, Δ2 > 0, Δi ≤ ri найдутся xp1 (T ) = 0, xp2 (T ) такие, что
∥xpi (T )∥ < Δi, i = 1, 2, и V (T, xp1 (T ))V′(1.14)(T, xp1 (T )) > 0 (т.е. знак функции V совпадает
со знаком производной V′(1.14) в точке (T,xp1(T))).
Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.1) неустойчиво по Ляпунову.
Доказательство. Пусть εu > 0 - произвольное число, удовлетворяющее неравенству
εu ≤ r2, где r2 определено в условиях настоящей теоремы. Как и в доказательстве утвержде-
ния 1 теоремы 3.1 (где εz = r1), строим такую функцию η(t, z) ∈ C([t+, ∞) × Uzδ2 (0), Uuεu (0)),
где 0 < δ2 ≤ r1 (r1 определено в условиях настоящей теоремы), что u = η(t, z) непрерывно
дифференцируема по z, принадлежит X2(t) для каждого (t, z) ∈ [t+, ∞)× Uz (0), удовлетво-δ
2
ряет тождеству η(t, 0) ≡ 0 и является единственным решением уравнения (2.11). Подставляя
полученную функцию u = η(t, z) в (2.5) и обозначаяΠ(t, z) = Π(t, z, η(t, z)), получаем урав-
нение (2.13) (т.е. z′(t) =Π(t, z(t))). В силу свойств функции
Π для каждой начальной точки
(t0, z0) ∈ [t+, ∞) × Uz (0) существует единственное локальное решение этого уравнения.δ
2
Как и в доказательстве утверждения 1 теоремы 3.1, получаем, что для любой согласованной
начальной точки (t0, x0), для которой выполняется неравенство ∥x0∥ < Δ, где Δ = δ2 +
+ εu > 0 выбрано так, что ∥P1(t0)x0∥ < δ2 и ∥P2(t0)x0∥ < εu, существует единственное
локальное решение z = ζ(t), u = η(t, ζ(t)) системы (2.9), (2.10), удовлетворяющее начальным
условиям ζ(t0) = z0 = P1(t0)x0, η(t0, ζ(t0)) = u0 = P2(t0)x0. Тогда по лемме 2.1 функция
x(t) = ζ(t) + η(t, ζ(t)) (ζ(t) = P1(t)x(t) = xp1 (t), η(t, ζ(t)) = P2(t)x(t) = xp2 (t)) является
единственным локальным решением ДАУ (1.1), удовлетворяющим начальному условию (1.3),
где x0 = z0 + u0.
Из условия 1) следует, что для некоторых чисел M > 0 и δ′2 > 0 выполнено неравенство
|V (t, z)| < M при всех t ∈ [T, ∞),
∥z∥ ≤ δ′2 < δ2. Пусть δz > 0, δu > 0 (δz < δ′2, δu <
< εu) - произвольные сколь угодно малые числа. Возьмём начальное значение t0 = T, где
T удовлетворяет условиям теоремы. Предположим, что в условии 2) имеет место неравенство
V ′(1.14)(t,xp1(t)) ≥ U(xp1(t)) > 0. Тогда в силу условия 3) найдётся такое согласованное на-
чальное значение x0 (т.е. (t0, x0) ∈ Lt+ ), удовлетворяющее неравенствам ∥x0∥ < δ = δz + δu,
0 < ∥P1(t0)x0∥ < δz и ∥P2(t0)x0∥ < δu, что V (t0, P1(t0)x0) = m > 0, где m - некоторое
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
217
число. Следовательно, как и в доказательстве классической теоремы Ляпунова о неустойчи-
вости, получаем, что для решения z = ζ(t) уравнения (2.13), удовлетворяющего начальному
условию ζ(t0) = z0 = P1(t0)x0, где t0 = T,
0 < ∥z0∥ < δz, существует t1 > t0 такое, что
∥ζ(t1)∥ > δ′2. Значит, для соответствующего решения x(t) = ζ(t) + η(t, ζ(t)) с начальной точ-
кой (t0, x0) выполнены неравенства ∥x0∥ < δ и ∥x(t1)∥ > ε = δ′2/∥P1(t1)∥ > 0 (так как
∥ζ(t1)∥ = ∥P1(t1)x(t1)∥). Это доказывает теорему.
Аналогичным образом доказываются следующие теоремы для ДАУ (1.2).
Теорема 3.4 (устойчивость и асимптотическая устойчивость по Ляпунову положения рав-
новесия ДАУ (1.2)). Пусть f ∈ C1([t+, ∞)× UxR(0), Rn), f(t, 0) ≡ 0, A, B ∈ C1([t+, ∞), L(Rn))
и пучок λA(t) + B(t) удовлетворяет условию (1.4), где C2 ∈ C1([t+,∞),(0,∞)). Пусть для
каждого t∗ ∈ [t+, ∞) и x∗p1 (t∗) = 0, x∗p2 (t∗) = 0 оператор (2.2) имеет обратный. Тогда верны
следующие утверждения.
1. Пусть выполнены условия утверждения 1 теоремы 3.1, где производная V′(1.14)(t,xp1 (t))
заменена на∗)
∂V
(∂V
V ′(1.19)(t,xp1(t)) =
(t, xp1 (t)) +
(t, xp1 (t)), G-1(t)[-B(t)xp1 (t) +
∂t
∂z
)
+ Q1(t)f(t,xp1(t) + xp2(t))] + P′1(t)[xp1(t) + xp2(t)]
Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.2) устойчиво по Ляпунову.
2. Пусть выполнены условия утверждения 2 теоремы 3.1, где производная V′(1.14)(t,xp1 (t))
заменена на V′(1.19)(t, xp1 (t)) (см. (2.21)) и условие (3.3) имеет вид
G-1(t)Q2(t)f(t, P1(t)x + P2(t)x) → 0 при x → 0
равномерно по t на [T, ∞) для некоторого T > t+.
(3.5)
Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.2) асимптотически устойчиво по Ляпунову.
Теорема 3.5 (асимптотическая устойчивость в целом (полная устойчивость ДАУ (1.2))).
Пусть f ∈ C1([t+, ∞) × Rn, Rn), f(t, 0) ≡ 0, A, B ∈ C1([t+, ∞), L(Rn)) и пучок λA(t) + B(t)
удовлетворяет условию (1.4), где C2 ∈ C1([t+,∞),(0,∞)). Пусть выполнены условия 1), 2)
теоремы 2.3 или 1), 2) теоремы 2.4, а также условие (3.5), и, кроме того, существуют
положительно определённые функции V ∈ C1([t+, ∞) × Rn, R), W ∈ C(Rn, R), U ∈ C(Rn, R)
такие, что выполнены условия 1), 2) теоремы 3.2 и условие 3) теоремы 3.2, где Lt+ за-
менено наLt+ и производная V′(1.14)(t,xp1 (t)) в левой части неравенства (3.2) заменена на
V ′(1.19)(t,xp1(t)) (см. (2.21)). Тогда положение равновесия x∗(t) ≡ 0 ДАУ (1.2) асимптотиче-
ски устойчиво в целом (ДАУ (1.2) полностью устойчиво).
Теорема 3.6 (неустойчивость по Ляпунову положения равновесия ДАУ (1.2)). Пусть вы-
полнены условия теоремы 3.3, в которые внесены следующие изменения: f ∈ C1([t+, ∞) ×
× UxR(0),Rn), производная V ′(1.14)(t,xp1(t)) заменена на V ′(1.19)(t,xp1(t)) (см. (2.21)). Тогда
положение равновесия x∗(t) ≡ 0 ДАУ (1.2) неустойчиво по Ляпунову.
4. Замечание относительно выбора функцииV. Положительно определённую ска-
лярную функцию V (t, z) будем называть функцией Ляпунова, если она удовлетворяет теоре-
мам (полученным в п. 3) об устойчивости, асимптотической устойчивости и неустойчивости по
Ляпунову, а также асимптотической устойчивости в целом, и функцией типа Ляпунова, если
она удовлетворяет теоремам, полученным в [1, п. 2]. Эту функцию часто удобно выбирать в
виде
V (t, z) = (H(t)z, z),
(4.1)
где H ∈ C1([t+, ∞), L(Rn)) - положительно определённая самосопряжённая оператор-функ-
ция (см. [1, определение 1.1]). Тогда функция (4.1) удовлетворяет условиям теорем 2.1-2.6, 2.9,
∗) См. [1, формула (2.21)].
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
218
ФИЛИПКОВСКАЯ
2.10 о глобальной разрешимости, устойчивости и неустойчивости по Лагранжу, а также усло-
виям утверждения 1 об устойчивости по Ляпунову из теоремы 3.1 и утверждения 1 об устой-
чивости по Ляпунову из теоремы 3.4, но выполнение условий на производные V′(1.14)(t, xp1 (t))
и V ′(1.19)(t,xp1(t)) в этих теоремах, естественно, требует проверки. Если дополнительно
sup
∥H(t)∥ < ∞,
t∈[t+,∞)
то функция (4.1) удовлетворяет также условиям теорем 2.7, 2.8, 3.2, 3.5, 3.3, 3.6 о предельной
ограниченности (диссипативности), асимптотической устойчивости в целом и неустойчивости
по Ляпунову, а также условиям утверждения 2 об асимптотической устойчивости из теоре-
мы 3.1 и утверждения 2 об асимптотической устойчивости из теоремы 3.4, но условия на про-
изводные V′(1.14)(t, xp1 (t)) и V′(1.19)(t, xp1 (t)), естественно, остаются в теоремах и нуждаются в
проверке.
Функция V (t, z) вида
V (t, z) ≡ (Hz, z),
где H ∈ L(Rn) - положительный самосопряжённый оператор, удовлетворяет условиям всех
теорем, но выполнение условий на производные V′(1.14)(t, xp1 (t)) и V′(1.19)(t, xp1 (t)) в теоремах,
естественно, требует проверки.
Производная V′(1.14)(t, xp1 (t)) (2.4) функции V (см. (4.1)) в силу уравнения (1.14) имеет
вид
V ′(1.14)(t,xp1(t)) = (H′(t)xp1(t),xp1(t)) + 2(H(t)xp1(t),[P′1(t) - G-1(t)Q1(t)[A′(t) + B(t)]]xp1(t) +
+ G-1(t)Q1(t)f(t,xp1(t) + xp2(t))).
(4.2)
Производная V′(1.19)(t, xp1 (t)) (2.21) функции V (см. (4.1)) в силу уравнения (1.19) имеет вид
V ′(1.19)(t,xp1(t)) = (H′(t)xp1(t),xp1(t)) +
+ 2(H(t)xp1 (t), G-1(t)[-B(t)xp1 (t) + Q1(t)f(t, xp1 (t) + xp2 (t))] + P′1(t)[xp1 (t) + xp2 (t)]).
5. Применение к исследованию математических моделей. В качестве примера при-
менения доказанных в [1] теорем (а также утверждения) о глобальной разрешимости ДАУ
рассмотрим математическую модель электрической цепи с нестационарными и нелинейными
параметрами: индуктивностью L(t), проводимостью G3(t) и сопротивлениями R1(t), R2(t),
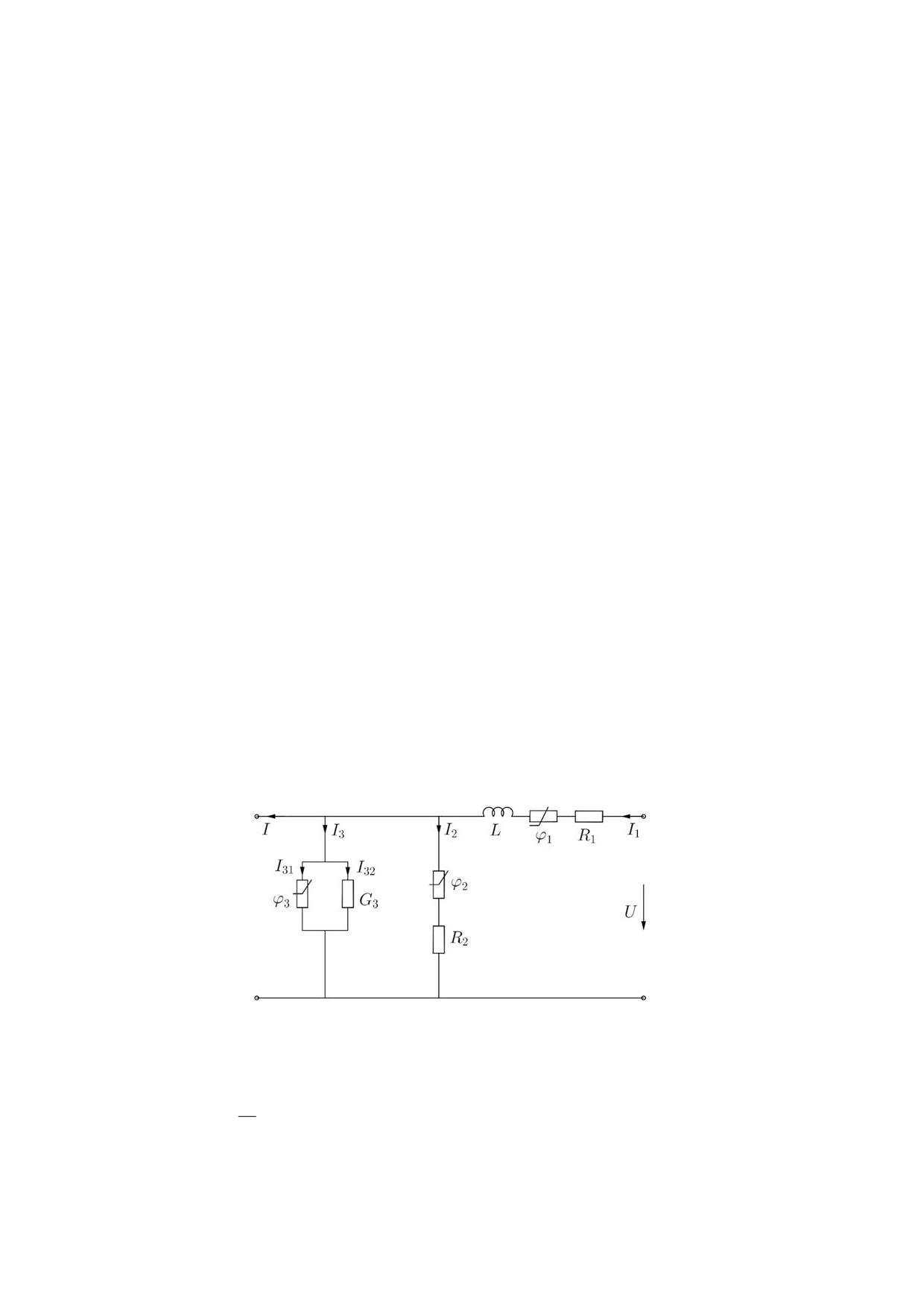
ϕ1(I1), ϕ2(I2) и ϕ3(I31). Схема электрической цепи представлена на рисунке (направления
отсчёта токов и напряжений на элементах цепи совпадают).
Рисунок. Схема электрической цепи.
Учитывая законы Кирхгофа и связи между токами и напряжениями на элементах цепи,
получаем систему уравнений
d
[L(t)I1(t)] + R1(t)I1(t) = U(t) - ϕ1(I1(t)) - ϕ3(I31(t)),
(5.1)
dt
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
219
I1(t) - I31(t) - I2(t) = I(t) + G3(t)ϕ3(I31(t)),
(5.2)
R2(t)I2(t) = ϕ3(I31(t)) - ϕ2(I2(t)),
(5.3)
которая описывает переходный процесс в электрической цепи. Ток I(t) и напряжение U(t)
заданы. Решив полученную систему, найдём токи I1(t), I31(t) и I2(t). Остальные токи и
напряжения в цепи однозначно выражаются через искомые и заданные.
Обозначим неизвестные токи через x1(t) = I1(t), x2(t) = I31(t) и x3(t) = I2(t) и в даль-
нейшем, для краткости, будем опускать зависимость от t в обозначениях xj (t) (j = 1, 2, 3).
Векторная форма системы (5.1)-(5.3) имеет вид нестационарного полулинейного ДАУ (1.1), где
⎛
⎞
⎛
⎞
⎛
⎞
x1
L(t)
0
0
R1(t)
0
0
x = ⎝x2⎠,A(t)= ⎝0
0
0⎠,B(t)= ⎝
1
-1
-1
⎠,
x3
0
0
0
0
0
R2(t)
⎛
⎞
U (t) - ϕ1(x1) - ϕ3(x2)
⎠.
f (t, x) =⎝ I(t)+G3(t)ϕ3(x2)
(5.4)
ϕ3(x3) - ϕ2(x2)
Предполагается, что L, R1, R2 ∈ C1([t+, ∞), R), I, U, G3 ∈ C([t+, ∞), R) и ϕj ∈ C1(R),
j = 1,2,3. Тогда A,B ∈ C1([t+,∞),L(R3)), f ∈ C([t+,∞) × R3,R3) и ∂f/∂x ∈ C([t+,∞) ×
×R3,L(R3)). Также предполагается, что функции L(t), R1(t), R2(t) и G3(t) положительны
при всех t ∈ [t+, ∞). Тогда при каждом t пучок λA(t) + B(t) регулярен и, следовательно,
существует резольвента (для регулярных точек λ)
⎞
⎛(λL(t) + R1(t))-1
0
0
R(λ, t) = (λA(t) + B(t))-1 = ⎝(λL(t) + R1(t))-1
-1
-R-12(t)⎠,
0
0
R-12(t)
√
а также для всех t ∈ [t+, ∞) выполнена оценка (1.4), где C1(t) =
2(1 + R-12(t)) + 1 и C2(t) =
= L-1(t)(1 + R1(t)) + 1.
Проекционные матрицы Pj(t), Qj(t), j = 1, 2, и матрица G-1(t) (см. (1.5), (1.8)) пред-
ставляются в виде
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
1
0
0
0
0
0
1
0
0
0
0
0
P1(t) =⎝1
0
0⎠,P2(t) = ⎝-1
1
0⎠, Q1(t) = ⎝0
0
0⎠, Q2(t) = ⎝0
1
0⎠,
0
0
0
0
0
1
0
0
0
0
0
1
⎞
⎛L-1(t)
0
0
G-1(t) = ⎝L-1(t)
-1
-R-12(t)⎠.
0
0
R-12(t)
Компоненты (проекции) xpj (t) = Pj (t)x ∈ Xj (t) вектора x имеют вид
⎛
⎞
⎛
⎞
x1
0
xp1(t) = xp1 =⎝x1⎠,xp
(t) = xp2
=⎝x2 - x1⎠.
2
0
x3
Обозначим z = x1, u = x2 - x1, w = x3, тогда xp1 = (z, z, 0)т, xp2 = (0, u, w)т.
Условие согласования (t, x) ∈ Lt+ выполняется, если (t, x) удовлетворяет алгебраическим
уравнениям (5.2), (5.3), т.е.
x1 - x2 - x3 = I(t) + G3(t)ϕ3(x2),
(5.5)
R2(t)x3 = ϕ3(x2) - ϕ2(x3),
(5.6)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
220
ФИЛИПКОВСКАЯ
которые в векторной форме представимы в виде уравнения Q2(t)[A′(t)P1(t)x + B(t)P2(t)x -
- f(t,x)] = 0, определяющего многообразие Lt+. Используя введённые выше обозначения,
запишем систему (5.2), (5.3) в виде
u = -I(t) - G3(t)ϕ3(u + z) - w,
(5.7)
w = R-12(t)[ϕ3(u + z) - ϕ2(w)].
(5.8)
Преобразуем систему (5.7), (5.8) к виду
w = -I(t) - u - G3(t)ϕ3(u + z),
(5.9)
u = ψ(t,z,u),
(5.10)
где ψ(t, z, u) = -I(t) - (G3(t) + R-12(t))ϕ3(u + z) + R-12(t)ϕ2(-I(t) - u - G3(t)ϕ3(u + z)).
Условие 1) теоремы 2.1 (теоремы 2.2) принимает следующий вид: для каждых t ∈ [t+, ∞),
z ∈ R существуют единственные u,w ∈ R (существуют u,w ∈ R) такие, что выполнены
равенства (5.9), (5.10). Поскольку для каждых t ∈ [t+, ∞), z ∈ R и любого u ∈ R существу-
ет единственный w ∈ R такой, что справедливо равенство (5.9), то условие 1) теоремы 2.1
выполнено, если
для каждых t ∈ [t+, ∞), z ∈ R существует
единственный u ∈ R такой, что u = ψ(t, z, u) (т.е. выполняется (5.10)).
(5.11)
Условие 1) теоремы 2.2 выполнено, если имеет место (5.11) без требования единственности u.
Легко убедиться, что условие (5.11) выполнено, если функции ϕ2 и ϕ3 являются возрас-
тающими (неубывающими) на R, например,
ϕ2(y) = ay2k-1, ϕ3(y) = by2m-1 или
ϕ2(y) = ay1/(2k-1), ϕ3(y) = by1/(2m-1), a,b > 0, k,m ∈ N.
(5.12)
Заметим, что в случае (5.12) отображение ψ(t, z, u) не является глобально сжимающим по
u (см. (5.13) ниже) и не выполнено условие (2.22). Очевидно, что если ψ(t, z, u) является
глобально сжимающим по u для любых t, z, т.е. существует константа α < 1 такая, что для
любых t ∈ [t+, ∞), z ∈ R справедливо неравенство
|ψ(t, z, u1) - ψ(t, z, u2)| = |(G3(t) + R-12(t))[ϕ3(u1 + z) - ϕ3(u2 + z)] -
- R-12(t)[ϕ2(-I(t) - u1 - G3(t)ϕ3(u1 + z)) - ϕ2(-I(t) - u2 - G3(t)ϕ3(u2 + z))]| ≤
≤ α|u1 - u2|, u1, u2 ∈ R,
(5.13)
то условие (5.11) выполнено. Условие Липшица (5.13) можно заменить на
∂ψ(t,z,u)
|(G3(t) + R-12(t))ϕ′3(u + z) +
=
∂u
+ R-12(t)ϕ′2(-I(t) - u - G3(t)ϕ3(u + z))[1 + G3(t)ϕ′3(u + z)]| ≤ α, u ∈ R.
(5.14)
В частном случае при
ϕ2(y) = asin y, ϕ3(y) = bsin y, a,b ∈ R,
(5.15)
условие (5.11) и, соответственно, условие 1) теоремы 2.1 выполнены, если
G3(t)|b| + R-12(t)(|a| + |b| + G3(t)|a||b|) < 1, t ∈ [t+,∞),
(5.16)
а условие 1) теоремы 2.2 выполнено всегда.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
221
Возьмём любые фиксированные t∗, x∗p1 = (x∗1, x∗1, 0)т = (z∗, z∗, 0)т, x∗p2 = (0, x∗2 - x∗1, x∗3)т =
= (0, u∗, w∗)т такие, что (t∗, x∗p1 + x∗p2 ) ∈ Lt+ , т.е. выполнены равенства (5.9), (5.10) (или (5.7),
(5.8)). Рассмотрим оператор
[
]
∂
Φ
[Q2(t∗)f(t∗, x∗p
(t∗) + x∗p
(t∗))] - B(t∗) P2(t∗): R3 → Y2(t∗)
t∗,xp1 (t∗),xp2 (t∗) =
1
2
∂x
Φ
(x∗pi (t∗) = x∗pi ∈ Xi(t∗), i = 1, 2,
∈ L(R3)), которому относительно стандарт-
t∗,xp1 (t∗),xp2 (t∗)
ного базиса в R3 соответствует матрица
⎛
⎞
0
0
0
Φ
⎠.(5.17)
1 + G3(t∗)ϕ′3(u∗ + z∗)
1
t∗,xp1 (t∗),xp2 (t∗) =⎝-(1+G3(t∗)ϕ3(u∗+z∗))
−ϕ′3(u∗ + z∗)
ϕ′3(u∗ + z∗)
-ϕ′2(w∗)-R2(t∗)
Очевидно, чтоΦt
∗,xp1(t∗),xp2 (t∗) обратимкакоператор,действующийизX2(t∗)вY2(t∗)(т.е.
оператор Φt∗,x∗p
∈
1
,x∗p
(t∗),xp2 (t∗)
1
∈ L(Y2(t∗),X2(t∗))), если
ϕ′3(u∗ + z∗) + [ϕ′2(w∗) + R2(t∗)][1 + G3(t∗)ϕ′3(u∗ + z∗)] = 0.
(5.18)
Таким образом, если
для каждых t∗ ∈ [t+, ∞), z∗ ∈ R и u∗, w∗ ∈ R,
удовлетворяющих равенствам (5.9), (5.10), выполнено соотношение (5.18),
(5.19)
то выполнено условие 2) теоремы 2.1. Заметим, что если записать (5.18) в виде
(G3(t∗) + R-12(t∗))ϕ′3(u∗ + z∗) + R-12(t∗)ϕ′2(w∗)[1 + G3(t∗)ϕ′3(u∗ + z∗)] = -1
и учесть, что t∗, z∗, u∗, w∗ удовлетворяют (5.9), т.е. w∗ = -I(t∗) - u∗ - G3(t∗)ϕ3(u∗ + z∗),
а равенство (5.10) не учитывать, т.е. рассматривать любые t∗ ∈ [t+, ∞), z∗ ∈ R, u∗ ∈ R, то
условие (5.19) примет вид: для каждых t∗ ∈ [t+, ∞), z∗ ∈ R и u∗ ∈ R выполнено соотношение
∂ψ(t∗,z∗,u∗)
= -1.
∂u
Снова возьмём любые фиксированные число t∗ и векторы x∗p1 = (x∗1, x∗1, 0)т = (z∗, z∗, 0)т,
xp2 = (0,x∗2,j - x∗1,j,x∗3,j)т = (0,u∗,w∗)т такие, что (t∗,x∗p
+ xp2) ∈ Lt+, j = 1,2, т.е. t∗, z∗,
1
u∗, w∗ удовлетворяют равенствам (5.9) и (5.10), j = 1,2. Выберем проекторы Θk(t∗): R3 →
→ Y2(t∗), k = 1,2, Θi(t∗)Θj(t∗) = δijΘi(t∗), Θ1(t∗) + Θ2(t∗) = Q2(t∗) (Θk(t∗) ∈ L(R3)),
которым относительно стандартного базиса в R3 соответствуют матрицы
⎛
⎞
⎛
⎞
0
0
0
0
0
0
⎠.
Θ1(t∗) =⎝0
1
0⎠, Θ2(t∗) = ⎝0
0
0
0
0
0
0
0
1
Тогда система проекторов {Θk(t∗) = Θk(t∗)|Y
2(t∗)}k=1будетаддитивнымразложениемедини-
Φ
цы Q2(t∗)|Y2(t∗)вY2(t∗).Рассмотримоператор-функцию
t∗,xp1 (t∗) :X2(t∗)→L(R3,Y2(t∗)),
[
]
∂
Φ
[Q2(t∗)f(t∗, x∗p
(t∗) + xp2 (t∗))] - B(t∗) P2(t∗)
t∗,xp1 (t∗)(xp2(t∗))=
1
∂x
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
222
ФИЛИПКОВСКАЯ
(x∗pi (t∗) = x∗pi , i = 1, 2), и оператор-функцию Φt∗,x∗p
(t∗) :X2(t∗)→L(X2(t∗),Y2(t∗))(см.(2.16)),
1
= Φt
= x∗p2(t∗)
т.е. Φt∗,x∗p
(t∗)(xp2(t∗))
∗,xp1(t∗)(xp2(t∗))|X2(t∗).Очевидно,прикаждомxp2(t∗)
1
Φ
Φ
справедливо равенство
t∗,xp1 (t∗)(xp2(t∗))=
t∗,xp1 (t∗),xp2 (t∗) иэтомуоператору(относитель-
но стандартного базиса в R3) соответствует матрица (5.17). Следовательно, оператору
Λ = Θ1(t∗)Φt
∗,xp1(t∗)(xp2,1(t∗))+Θ2(t∗)Φt∗,x∗p1(t∗)(xp2,2(t∗))∈L(R3,Y2(t∗)),
где xp2,k(t∗) = xp2,k = (0, uk, wk)т (k = 1, 2) - произвольные элементы из [xp2 , xp2 ], относи-
тельно стандартного базиса в R3 соответствует матрица
⎛
⎞
0
0
0
Λ= ⎝-(1+G3(t∗)ϕ′3(u1 + z∗))
1 + G3(t∗)ϕ′3(u1 + z∗)
1
⎠.
−ϕ′3(u2 + z∗)
ϕ′3(u2 + z∗)
-ϕ′2(w2) - R2(t∗)
Очевидно, что оператор
Λ обратим как оператор из X2(t∗) в Y2(t∗) (т.е. оператор Λ =
= Λ|X
2(t∗) :X2(t∗)→Y2(t∗)обратим),если
ϕ′3(u2 + z∗) + [ϕ′2(w2) + R2(t∗)][1 + G3(t∗)ϕ′3(u1 + z∗)] = 0.
(5.20)
Таким образом, если
для каждых t∗ ∈ [t+, ∞), z∗ ∈ R и uj∗, wj∗ ∈ R, j = 1, 2, удовлетворяющих
равенствам (5.9), (5.10), выполнено соотношение (5.20)
при любых uk ∈[u1∗, u2∗], wk ∈[w1∗, w2∗], k =1, 2,
(5.21)
то выполнено условие 2) теоремы 2.2. Очевидно, что условие 2) также выполнено, если (5.20)
справедливо для каждых t∗ ∈ [t+, ∞), z∗ ∈ R и любых uk, wk ∈ R.
В частности, условия (5.19), (5.21) выполнены для возрастающих (неубывающих) на R
функций ϕ2, ϕ3, например, для ϕ2, ϕ3 вида (5.12), и выполнены для функций (5.15), если
справедливо требование (5.16).
Заметим, что вместо условий 1), 2) теоремы 2.1 (или теоремы 2.2) можно использовать
условие (2.22) утверждения 2.1, которое будет выполнено, если существует константа α < 1
такая, что
G3(t)|ϕ3(u1 + z) - ϕ3(u2 + z)| + R-12(t)|ϕ3(u1 + z) - ϕ3(u2 + z) - ϕ2(w1) + ϕ2(w2)| ≤
√
≤α
|u1 - u2|2 + |w1 - w2|2
(5.22)
для любых t ∈ [t+, ∞), z ∈ R и ui, wi ∈ R, i = 1, 2, или использовать (эквивалентное)
условие (2.23), которое будет выполнено, если
√ √
2
([G3(t) + R-12(t)]2 + R-22(t))|ϕ′3(u + z)|2 + R-22(t)|ϕ′2(w)|2 ≤ α < 1
(5.23)
для любых t ∈ [t+, ∞), z ∈ R и u, w ∈ R, однако эти условия являются более ограничи-
тельными. Если учесть, что график решения x(t) должен лежать в многообразии Lt+ и,
соответственно, t, z, u, w связаны соотношениями (5.9), (5.10), то, используя эти соотноше-
ния, можно преобразовать неравенства (5.22), (5.23) так, что они будут схожи с (5.13), (5.14).
Возьмём оператор H = 0.5IR3 (IR3 - единичный оператор в R3). Тогда условие 3) тео-
ремы 2.1 (теорема 2.2 содержит такое же условие), где V′(1.14)(t, xp1 (t)) имеет вид (4.2) и
H(t) ≡ H∫ будет выполнено, если найдутся функции U ∈ C(0, ∞) и k ∈ C([t+, ∞), R) та-
∞
кие, что
(U(v))-1 dv = ∞ (v0 > 0) и при некотором R > 0 неравенство
v0
2L-1(t)[-(L′(t) + R1(t))z2 + U(t)z - (ϕ1(z) + ϕ3(u + z))z] ≤ k(t)U(z2)
(5.24)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021
ГЛОБАЛЬНАЯ РАЗРЕШИМОСТЬ НЕСТАЦИОНАРНЫХ ПОЛУЛИНЕЙНЫХ ДАУ
223
выполнено для любых t ∈ [t+, ∞), z, u, w ∈ R, удовлетворяющих равенствам (5.9), (5.10) и
неравенству |z| ≥ R. Легко проверить, что условие (5.24), где k(t) = 2L-1(t)(|L′(t)| + |U(t)|),
U (v) = v (напомним, что L(t) > 0, R1(t) > 0), выполнено, если существует R > 0 такое, что
-(ϕ1(z) + ϕ3(u + z))z ≤ R1(t)z2
(5.25)
для любых t ∈ [t+, ∞), z, u, w ∈ R, удовлетворяющих равенствам (5.9), (5.10) и неравенству
|z| ≥ R.
В общем случае, согласно теореме 2.1, для каждой начальной точки (t0, x0) ∈ [t+, ∞) × R3,
где x0 = (x0,1, x0,2, x0,3)т, для которой справедливы равенства (5.5), (5.6) (т.е. (t0, x0) ∈ Lt+ ),
существует единственное глобальное решение x(t) ДАУ (1.1) с (5.4), удовлетворяющее на-
чальному условию x(t0) = x0, если L, R1, R2 ∈ C1([t+, ∞), R), I, U, G3 ∈ C([t+, ∞), R), ϕj ∈
∈ C1(R), j = 1,2,3; L(t) > 0, R1(t) > 0, R2(t) > 0 и G3(t) > 0 при всех t ∈ [t+,∞);
выполнены условия (5.11) и (5.19) и существует R > 0 такое, что неравенство (5.25) име-
ет место для любых t ∈ [t+, ∞), z, u, w ∈ R, удовлетворяющих равенствам (5.9), (5.10) и
неравенству |z| ≥ R.
Аналогичное утверждение имеет место согласно теореме 2.2, если выполнены приведённые
выше условия со следующими изменениями: в условии (5.11) нет требования, чтобы u был
единственным; условие (5.19) заменено на (5.21).
Возможные изменения или уточнения приведённых условий, а также частные случаи функ-
ций (классов функций), для которых эти условия выполняются, указаны выше.
Исследование выполнено при финансовой поддержке Национальной академии наук Укра-
ины (проект “Качественный, асимптотический и численный анализ различных классов диф-
ференциальных уравнений и динамических систем, их классификация и практическое приме-
нение”, государственный регистрационный номер 0119U102376).
СПИСОК ЛИТЕРАТУРЫ
1. Филипковская М.С. Глобальная разрешимость нестационарных полулинейных дифференциально-
алгебраических уравнений, ограниченность и устойчивость их решений. I // Дифференц. уравне-
ния. 2021. Т. 57. № 1. С. 22-42.
2. Власенко Л.А. Эволюционные модели с неявными и вырожденными дифференциальными уравне-
ниями. Днепропетровск, 2006.
3. Чистяков В.Ф., Щеглова А.А. Избранные главы теории алгебро-дифференциальных систем. Но-
восибирск, 2003.
4. Lamour R., März R., Tischendorf C. Differential-Algebraic Equations: A Projector Based Analysis.
Heidelberg, 2013.
5. Riaza R. Differential-Algebraic Systems: Analytical Aspects and Circuit Applications. New Jersey, 2008.
6. Красовский Н.Н. Некоторые задачи теории устойчивости движения. М., 1959.
7. Ла-Салль Ж., Лефшец С. Исследование устойчивости прямым методом Ляпунова. М., 1964.
Физико-технический институт низких температур
Поступила в редакцию 02.01.2020 г.
им. Б.И. Веркина НАН Украины, г. Харьков
После доработки 28.08.2020 г.
Принята к публикации 13.10.2020 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57 № 2 2021