ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 2, с.235-254

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956.226+517.956.227

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ

ТИПА ПРЫГАЮЩЕГО МЯЧИКА

ОПЕРАТОРА ∇D(x)∇ В ОБЛАСТИ,

ОГРАНИЧЕННОЙ ПОЛУЖЁСТКИМИ СТЕНКАМИ

Рассматривается задача о квазиклассическом спектре оператора ∇D(x)∇ с вырождением

бесселева типа на границе двумерной области (полужёсткие стенки). Известно, что можно

построить асимптотические собственные функции, связанные с лагранжевыми многооб-

разиями, используя модификацию метода канонического оператора Маслова. Получены

асимптотические собственные функции, связанные с простейшими периодическими траек-

ториями соответствующей гамильтоновой системы с отражениями на границе области.

DOI: 10.31857/S0374064121020114

1. Введение.

1.1. Асимптотики типа прыгающего мячика оператора Лапласа с условиями

Дирихле в эллипсе. Хорошо известна задача об асимптотическом при k → ∞ спектре опе-

ратора Лапласа в области M, ограниченной эллипсом ∂M, с нулевыми условиями Дирихле

на границе:

-Δu = k²u, u|_∂M = 0.

(1)

Согласно [1] (см. также [2]) существуют асимптотические собственные функции, сконцентри-

рованные в окрестности малой оси эллипса и быстро убывающие при отдалении от неё.

Рассмотрим биллиардную систему внутри эллипса с обычными отражениями от границы.

Такая система имеет периодическую траекторию, лежащую на малой оси эллипса. Существуют

асимптотические собственные функции, соответствующие этой траектории (моды прыгающего

мячика). Динамическим свойством периодической траектории, лежащей на малой оси эллипса,

которое обуславливает их существование, является орбитальная устойчивость периодического

движения в линейном приближении. Этим свойством не обладает, например, периодическое

движение на большой оси эллипса.

Приведём асимптотические собственные значения, соответствующие модам прыгающего

мячика, представленные в [2, с. 100]. Пусть g - длина малой оси эллипса, ρ - радиус кривизны

эллипса в точке пересечения с малой осью. Собственные значения имеют вид

[

2ν + 1

^√ g

⁽⁽ν)2)]

k_n,ν =

n+1+

arcsin

2ρ

и нумеруются квантовыми номерами N ∋ n ≫ 1, Z₊ ∋ ν ≪ n. Видно, что если менять один

из квантовых номеров, то все соседние точки будут располагаться “почти” на одинаковом

расстоянии друг от друга.

1.2. Системы с жёсткими, мягкими и полужёсткими стенками. Асимптотические

при h → +0 собственные функции, соответствующие периодическим траекториям, можно

рассматривать и для оператора Шрёдингера с гладкой функцией V (x), задающей потенци-

альную яму (система с мягкими стенками):

-h²Δψ + V (x)ψ = Eψ.

235

236

КЛЕВИН

В одном из частных случаев такая система рассматривалась в [3]. Типичной ситуацией здесь

является наличие семейства периодических траекторий гамильтоновой системы с гамильтони-

аном p² + V (x), параметризованных значениями полной энергии, т.е. постоянными на траек-

ториях значениями функции Гамильтона. Проквантованному множеству орбитально устойчи-

вых в линейном приближении периодических траекторий мы можем поставить в соответствие

серию асимптотических мод.

Задачу (1) с условиями Дирихле можно (по крайней мере на уровне нестрогих рассужде-

ний) представить в виде спектральной задачи для уравнения Шрёдингера, если сделать замену

E = k²h² и положить V (x) = 0, если x ∈ M, и V (x) = +∞, если x ∈ M. Такую систему

называют системой с жёсткими стенками.

Перейдём к спектральной задаче, которая рассматривается в настоящей работе. Пусть

(x₁, x₂) ∈ [b₁, b₂] × R = M ⊂ R² - полоса. Будем рассматривать частный случай спектральной

задачи (конкретная её постановка будет приведена ниже)

[

]

∂

-h²

D₁(x₁,x₂)

-h²

D₂(x₁,x₂)

Ψ = EΨ, Ψ = Ψ(x₁,x₂,h),

(2)

∂x₁

∂x₂

где оператор в левой части является оператором с бесселевым вырождением (термин введён

в [4]), т.е. D_i(x₁, x₂) > 0 при b₁ < x₁ < b₂, D_i(b_s, x₂) = 0,

(∂D_i/∂x₁)(b_s, x₂) = 0, i = 1, 2,

s = 1,2. Оператору в левой части (2) соответствует движение в области M по геодезическим

траекториям метрики ds² = (D₁(x₁, x₂))-1 dx²¹ + (D₂(x₁, x₂))-1 dx²² с обычным отражением от

границы ∂M, на которой метрика обращается в бесконечность. В терминах гамильтоновой

системы это движение задаётся гамильтонианом H(x₁, x₂, p₁, p₂) = D₁(x₁, x₂)p²¹ +D₂(x₁, x₂)p²².

Из свойств функций D₁, D₂ следует обращение в бесконечность импульсной переменной за

конечное время при достижении границы. Подобные системы названы в [5] биллиардами с

полужёсткими стенками.

Мы рассматриваем асимптотические при h → +0 собственные функции спектральной

задачи (2), которые соответствуют периодическим движениям такой системы с траекториями,

лежащими на отрезке (в общем случае можно рассматривать и криволинейные траектории),

ограниченном двумя точками на границе ∂M. Такие асимптотические собственные функции

мы также будем называть функциями типа прыгающего мячика.

Отметим, что задачи, рассмотренные во введении, можно соотнести с резонаторами раз-

личных типов.

2. Постановка задачи и результат.

2.1. Постановка задачи. Пусть заданы числа b₁ < b₂ и вещественные гладкие в окрест-

ности полосы b₁ ≤ x₁ ≤ b₂ функции D₁(x₁, x₂), D₂(x₁, x₂) такие, что

D_i(x₁,x₂) > 0 при b₁ < x₁ < b₂, D_i(b_s,x₂) = 0,

∂D_i

∂D₁

(b_s, x₂) = 0,

(x₁, 0) = 0, i = 1, 2, s = 1, 2.

(3)

∂x₁

∂x₂

Введём дифференциальный оператор

∂

L ≡ -h² ∂

D₁(x₁,x₂)

-h²

D₂(x₁,x₂)

∂x₁

∂x₂

В данной работе мы построим серию асимптотических при h → +0 собственных E(h)

значений и соответствующих им собственных функций Ψ(x₁, x₂), локализованных в окрест-

ности множества {x₂ = 0}, которая удовлетворяет условиям квазиклассической спектральной

задачи в полосе b₁ ≤ x₁ ≤ b₂ :

∥LΨ - EΨ∥_L2([b

1,b2]×R) =O(h3/2)^,

∥Ψ∥_L2([b1,b₂]×R) = Θ(1).

Напомним, что отношение f = Θ(g) между функциями f и g по определению означает, что

одновременно выполняются отношения f = O(g) и g = O(f). В нашем случае это означает

равномерную ограниченность нормы сверху и снизу положительными константами.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

237

От функции Ψ будем требовать выполнения условия конечности энергетического ин-

теграла

(Ψ, (L - E)Ψ)_L2([b

(4)

1,b2]×R) <∞.

Рассматривая замыкание в L²([b₁, b₂]×R) симметрического оператораL, заданного на функ-

циях из C∞0([b₁, b₂] × R), удовлетворяющих условию (4), получаем самосопряжённое расшире-

ние оператора

L методом Фридрихса. Условие (4) для оператора с вырождающимися коэф-

фициентами является аналогом граничных условий, которые обычно возникают при рассмот-

рении операторов, действующих на функции, заданные в какой-нибудь области. Обсуждение

этого вопроса и дальнейшие ссылки можно найти в [6].

2.2. Результат. Введём функции t(x₁),

t(x₁), заданные на множестве x₁ ∈ [b₁, b₂], и

число T :

x₁

∫

t(x₁) =

√

= t(b₂),

t(x₁) =^T

- t(x₁).

(5)

D₁(q,0)

b₁

Обратную к t(x₁) функцию, заданную на множестве [0, T/2], продолжим чётным образом

на множество [-T/2, T/2], после чего периодически распространим её на всё множество R.

Полученная функция X₁(t) является T -периодическим решением задачи Коши

x²¹ = 4D₁(x₁,0), x₁(0) = b₁.

Рассмотрим фундаментальную систему решений (z₂(t),

w₂(t)),

(z₂(t),w2(t)) линейной сис-

темы с периодическими коэффициентами

(∂²D₁/∂x²²)(X₁(t), 0)

Ż₂ = 2D₂(X₁(t),0)w₂,

w₂ = -

z₂

(6)

D₁(X₁(t),0)

относительно неизвестных функций z₂(t), w₂(t) с начальными условиями

z₂(0) = 1,

w₂(0) = 0,

2(0) = 0,

2(0) = 1.

Составим из них матрицу монодромии

(

)

z₂(T)

2(T )

(7)

w₂(T)

2(T )

Предположим, что выполнено условие

|tr R| < 2.

(8)

У периодической системы (6) при правильном выборе знака числа β существует решение

Флоке (Z₂(t),W₂(t)) с показателем β и комплексно-сопряжённое решение Флоке (Z₂(t),W₂(t))

с показателем -β, и при таком выборе выполнено условие положительности:

(Z₂(t + T ), W₂(t + T )) = (exp(iβ)Z₂(t), exp(iβ)W₂(t)), Im (W₂Z-12) > 0,

(9)

где левая часть неравенства в зависимости от выбора знака β будет всегда либо положитель-

ной, либо отрицательной. Известно, что такое решение единственно с точностью до умножения

на ненулевую постоянную. Пусть Arg Z₂(t) - непрерывная ветвь аргумента комплекснозначной

функции Z₂(t), не обращающейся в нуль. Произвол по модулю 2π в выборе β мы устраняем,

полагая β = Arg Z₂(T ) - Arg Z₂(0).

Пусть на отрезке [b₁, b₂] заданы некоторые гладкие функции f₁(x₁), f₂(x₁) со связными

носителями supp f_s ⊂[b₁, b₂], s=1, 2, такие, что b₁ ∈supp f₂, b₂ ∈supp f₁, f₁(x₁) + f₂(x₁)=1.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

238

КЛЕВИН

Введём числовые серии ω_n, E_n,ν (h) равенствами

(

)

(

)

βν

ω_n =

E_n,ν(h) = h2 ω2

+ω_n

4π

n ∈ N, n = O(1/h), ν ∈ Z₊, ν = O(1),

(10)

и серию функций

(

)1/2

2ω_nπ

Ψ_n,ν(x₁,x₂) =

√

|Z₂(t(x₁))|ν-1/2(Im W₂Z-12(t(x₁)))ν/2 ×

D₁(x₁,0)

(

√

)[

√

×H_ν x₂

ω_n Im W₂Z-12(t(x₁)) f₁(x₁)

t(x₁) ×

(

)

× J₀(2ω_nt(x₁))Re (G_n,ν(x₁,x₂)) - J₁(2ω_nt(x₁))Im (G_n,ν(x₁,x₂))

√

(

+ (-1)ⁿf₂(x₁)

t(x₁) J₀(2ω_nt(x₁)) Re (exp(iβ/4)G_n,ν (x₁, x₂)) +

)]

+ J₁(2ω_nt(x₁))Im (exp(iβ/4)G_n,ν(x₁,x₂))

(11)

где J_k - функция Бесселя первого рода порядка k, функция H_ν - ν-й полином Эрмита в

физическом определении (H₀(x) = 1, H₁(x) = 2x) и

( (

)

βνt(x₁)

x²²

Gn,ν (x1, x2) = exp -i ν +

Arg Z₂(t(x₁)) + i

+ iω_nW₂Z-12(t(x₁))

Утверждение. Пусть выполнено неравенство (8). Тогда

∥(L - E_n,ν (h))Ψ_n,ν (x₁, x₂)∥_L2([b

1,b2]×R) =O(h3/2)^,

∥Ψ_n,ν(x₁, x₂)∥_L2([b1,b₂]×R) = Θ(1).

(Символ Θ определён в п. 2.1.)

2.3. Замечание о доказательстве утверждения. В работе [4] квазиклассическая тео-

рия, связанная с дифференциальными операторами, коэффициенты которых имеют вырожде-

ние бесселева типа, сведена к стандартной ситуации без вырождения с помощью рассмотрения

задачи в более сложном пространстве. К такой регуляризованной задаче можно затем приме-

нить метод канонического оператора Маслова, соответствующего или лагранжевому многооб-

разию, или, в нашей ситуации, изотропному многообразию с комплексным ростком (опреде-

ление дано в [7, с. 56]). Последний случай является предметом теории комплексного ростка

Маслова.

В лагранжевом случае, используя результаты работы [8], можно получить выражение для

канонического оператора в виде интеграла по естественно возникающей координате лагранже-

ва многообразия. Асимптотику полученного интеграла можно затем представить в виде функ-

ции Бесселя при помощи формул из работы [9]. Подробное изложение описанной процедуры

анонсировано в [4]. В настоящей работе сформулированное выше утверждение доказывается

при помощи адаптации данного подхода к изотропному случаю.

2.4. Пример. Введём функцию

D(x₁, x₂) = (1 - x²¹)(1 - ax²²),

где a = 0 - вещественный параметр. Рассмотрим пример, когда

D₁(x₁,x₂) = D₂(x₁,x₂) = D(x₁,x₂).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

239

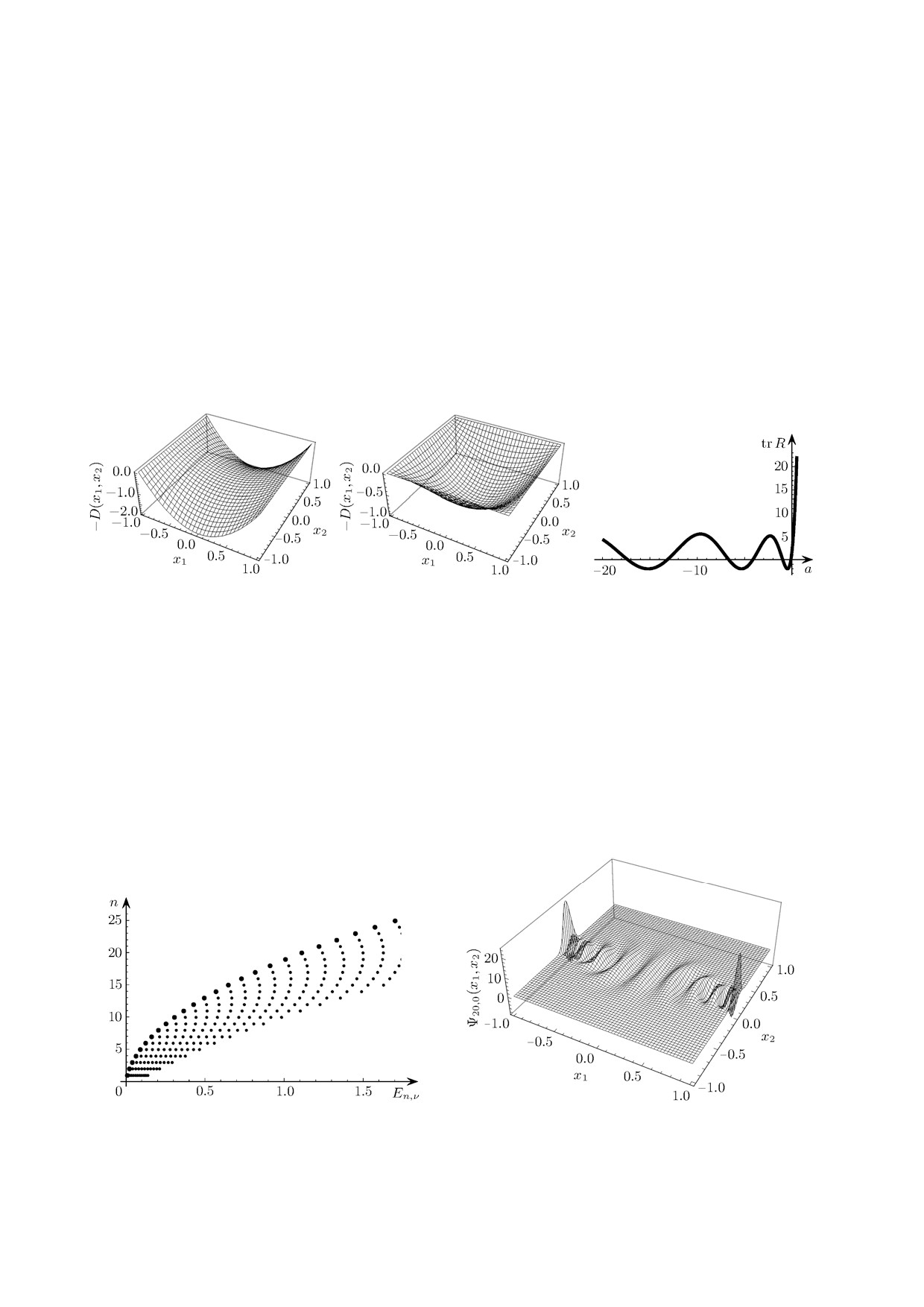
Для параметров a = ±1 графики функции -D(x₁, x₂) представлены на рис. 1, a, рис. 1, б. При

a > 0 функции D₁, D₂ удовлетворяют условиям (3) лишь вблизи множества {x₂ = 0}. До-

бавлением к D₁, D₂ гладкой функции, равной нулю в окрестности {x₂ = 0}, можно добиться

выполнения условий (3). При такой модификации оператора его асимптотическая собственная

функция, локализованная в окрестности {x₂ = 0}, не изменится. В нашем примере b₁ = -1,

b₂ = 1, t(x₁) = (π + 2arcsin x₁)/4, T = π,

t(x₁) = (arccos x₁)/2, X₁(t) = - cos 2t.

Уравнение (6), которое принимает вид

Ż₂ = 2sin²(2t)w₂,

w₂ = 2az₂,

(12)

исключая переменную z₂, представим в виде уравнения Матьё

w₂ = 4asin²(2t)w₂. Известно

(см., например, [10, с. 206]), что для выполнения условия |tr R| < 2 необходимо, чтобы a < 0.

На рис. 2 изображён график зависимости tr R от параметра a.

(a)

(б)

Рис. 1. Графики функции -D(x1, x2) при a = -1 (а) и при a = 1 (б). Рис. 2. График зависимости ве-

личины tr R от параметра a.

Положим далее a = -4. Тогда tr R ≈ 0.416935. Функции Z₂(t), W₂(t) определены

как решения системы (12) с начальными условиями Z₂(0) ≈ -0.112821, W₂(0) = 1. Тог-

да Im (W₂Z-12(0)) ≈ 8.86362 и условие положительности (9) выполнено. Вычисления дают

β = ArgZ₂(T) - ArgZ₂(0) ≈ 7.64397.

В качестве примера положим далее h = 0.05. Точки асимптотического спектра E_n,ν изоб-

ражены на рис. 3, а. По вертикальной оси отложен номер n. Большие точки соответствуют

значению ν = 0, по горизонтали точки следуют друг за другом в порядке увеличения пара-

метра ν. Для n = 20, ν = 0 (в этом случае E20,0 ≈ 1.1139) на рис. 3, б представлен график

асимптотической собственной функции Ψ_n,ν .

(a)

(б)

Рис. 3. Точки En,ν асимптотического спектра (а) и одна из асимптотических собственных функций (б).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

240

КЛЕВИН

3. Формулировка в виде спектральной задачи для квазиклассического ПДО.

3.1. Символ оператора и гамильтониан. Оператор^L можно рассматривать как квази-

классический псевдодифференциальный оператор с вейлевским символом L(x, p, h), который

с точностью до O(h²) представляется функцией H(x, p) = H(x₁, x₂, p₁, p₂):

(

)

-ih∇ - ih∇

L(x, p, h) = H(x, p) + O(h²),

H(x, p) = D₁(x₁, x₂)p²¹ + D₂(x₁, x₂)p²².

(13)

Разложим функции D₁, D₂ по формуле Тейлора по координате x₂, учитывая при этом

условия (3) на эти функции. Введём коэффициенты разложения D₁₀(x₁), D₂₀(x₁), D₁₂(x₁):

x²²

D₁(x₁,x₂) = D₁₀(x₁) +

D₁₂(x₁) + O(x³²), D₂(x₁,x₂) = D₂₀(x₁) + O(x₂),

Di0(x₁) > 0 при b₁ < x₁ < b₂, Di0(b_s) = 0, D₁₂(b_s) = 0,

D′i0(b_s) = 0, s = 1,2, i = 1,2.

3.2. Быстроубывающие асимптотики. Мы рассматриваем асимптотики, локализован-

ные в окрестности множества {x₂ = 0}. Согласно [7] такого вида асимптотики можно рассмат-

ривать, когда асимптотическая собственная функция в обычной ситуации без учёта фокальных

точек является комбинацией функций вида

√

Ψ(x₁, x₂, h) = A(x₁, x₂/

h) exp((i/h)(S(x₁) + P₂(x₁)x₂ + G(x₁)x²²)),

где S, P₂ - вещественнозначные, а A, G - комплекснозначные функции, причём Im G > 0.

Последнее неравенство делает функцию Ψ убывающей как гауссова экспонента при x²²/h →

→ ∞.

Геометрический объект, соответствующий такого вида функциям, - периодическая тра-

ектория (одномерное изотропное многообразие) гамильтоновой системы с гамильтонианом

H(x, p) в фазовом пространстве (x, p). Проекция траектории на конфигурационное прост-

ранство (пространство с координатами x) определяет множество, вне которого функция Ψ

является быстроубывающей. В нашем случае таким множеством является отрезок [b₁, b₂] ×

× {0}. При этом функции S и P₂ являются соответственно действием и второй импульсной

координатой на этой траектории, выраженными через координату x₁.

Для того чтобы периодической траектории соответствовали асимптотические собственные

функции необходимо, чтобы она была орбитально устойчива в линейном приближении. Обыч-

но мы имеем семейство периодических траекторий, параметризованных полной энергией (зна-

чением функции Гамильтона). Из этого семейства выбираются траектории, устойчивые в ли-

нейном приближении. Проквантовав их, мы получаем дискретный набор орбитально устой-

чивых в линейном приближении траекторий, которым соответствует серия асимптотических

собственных функций.

В нашей задаче гамильтониан по импульсной переменной p однороден со степенью 2. По-

этому все траектории указанного семейства получаются из одной траектории заменой времени

и растяжением по переменной p. В результате все траектории одновременно либо устойчивы,

либо неустойчивы.

3.3. Каустики, соответствующие границе. Известно, что в фазовом пространстве тра-

ектория гамильтоновой системы над точками (b_s, 0), s = 1, 2, уходит на бесконечность по

импульсным координатам за конечное время. При этом говорят, что возникает сильная кау-

стика. От неё можно избавиться с помощью рассмотрения задачи на большем фазовом прост-

ранстве (см. [4]). С точки зрения траектории гамильтоновой системы результат выражается в

добавлении точки p = ∞. При этом траектория становится периодической.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

241

4. Квантование устойчивых траекторий гамильтоновой системы.

4.1. Система Гамильтона. Система Гамильтона с гамильтонианом H(p,x) имеет вид

∂D₁

∂D₂

x₁ = 2p₁D₁(x₁,x₂),

p₁ = -p²

(x₁, x₂) - p²

(x₁, x₂),

¹ ∂x₁

∂x₁

∂D₁

∂D₂

x₂ = 2p₂D₂(x₁,x₂),

p₂ = -p²

(x₁, x₂) - p²

(x₁, x₂).

(14)

¹ ∂x₂

∂x₂

Подпространство с координатами x₂ = p₂ = 0 является инвариантным по отношению к данной

системе. На это подпространство система ограничивается как система Гамильтона с приведён-

ным гамильтонианом H(x₁, p₁) = H(x₁, 0, p₁, 0):

H(x₁, p₁) = D₁₀(x₁)p²¹,

x₁ = 2D₁₀(x₁)p₁,

p₁ = -D′10(x₁)p²¹.

(15)

Траектории системы (15) над точками (b_s, 0), s = 1, 2, уходят на бесконечность по пе-

ременной p₁ за конечное время. Эта система инвариантна относительно замены (x₁, p₁, t) →

→ (x₁, -p₁, -t), где t - независимая переменная (время). Мы будем склеивать над точками

(b_s, 0), s = 1, 2, две траектории, симметричные относительно отражения (x₁, p₁) → (x₁, -p₁).

При этом будем считать, что точка склейки имеет координаты (x₁, p₁) = (b_s, ∞), s = 1, 2. Да-

лее там, где точки склейки могут быть естественным образом учтены, мы будем обращаться

с такими склеенными траекториями как с обычными.

Пара (X₁(t), P₁(t)), где функция X₁(t) определена в п. 2.2, а функция P₁(t) определяет-

ся равенством P₁(t) =

X₁(t)/(2D₁₀(X₁(t))), является периодическим решением системы (15) с

периодом T, определённым в (5). Вектор-функция (X₁(t), 0, P₁(t), 0) представляет собой ре-

шение системы (14). Гамильтониан H однороден по p₁ со степенью 2. Это позволяет вложить

решение (X₁(t), 0, P₁(t), 0) в зависящее от параметра E > 0 семейство T (E)-периодических

решений (X(t, E), P (t, E)) такое, что

H(X(t, E), P (t, E)) = H(X₁(t, E), P₁(t, E)) = E, X₂(t, E) = P₂(t, E) = 0,

√

X(t, E) = X(

Et,1), P(t,E) =

EP(

Et,1), T(1) =

ET(E).

Решение (X₁(t), 0, P₁(t), 0) соответствует значению E = 1. При каждом E имеем

⋃

{X(t, E)} = [b₁, b₂] × {0}.

t∈R

Введём обозначение для замкнутой кривой R4xp ⊃ Λ(E) = {(X(t, E), P (t, E))}⁼ S¹ и для

её накрывающей Λ_C (E)= R. Параметр t ∈ R является координатой на Λ_C (E) с коорди-

натными функциями X(t, E), P (t, E). На Λ(E) лежат две точки, для которых p₁ = ∞. На

Λ_C(E) такие точки образуют счётное множество.

4.2. Система в вариациях. Рассмотрим систему в вариациях для пары неизвестных

вектор-функций w(t) и z(t), каждая из которых принимает значения из C² :

Ż=H_pxz+H_ppw,

w = -H_xxz - H_xpw.

(16)

Здесь матричные функции H_px(x, p), H_pp(x, p), H_xx(x, p), H_xp(x, p) состоят из вторых про-

изводных:

(

)

(

)

Hx1x₁

Hx1x₂

Hp1p₁

Hp1p₂

H_xx =

H_pp =

Hx2x₁

Hx2x₂

Hp2p₁

Hp2p₂

(

)

(

)

Hx1p₁

Hx1p₂

Hp1x₁

Hp1x₂

H_xp =

H_px = Hтxp =

Hx2p₁

Hx2p₂

Hp2x₁

Hp2x₂

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

242

КЛЕВИН

и в их аргументы производится подстановка X(t,E), P(t,E). Таким образом, система (16)

задаёт семейство систем, зависящее от параметра E. Запишем эту систему в явном виде:

(

)

(

)

2D′10(X₁(t, E))P₁(t, E)

2D₁₀(X₁(t, E))

Ż=

2D₂₀(X₁(t, E))

)

(

)

⁽D′′10(X₁(t,E))

2D′10(X₁(t, E))P₁(t, E)

w=-

D₁₂(X₁(t,E))P²¹(t,E)^z-

Пусть векторная функция (z(t), w(t)) - некоторое её решение при E = 1. Тогда вектор

√

(z(

Et),

Ew(

Et)) является решением этой системы при произвольном E > 0.

4.3. Редуцированная система в вариациях. Система в вариациях распадается на две

системы для (z₁, w₁) и для (z₂, w₂). Для координат (z₂, w₂) система имеет вид

Ż₂ = 2D₂₀(X₁(t,E))w₂,

w₂ = -D₁₂(X₁(t,E))P²¹(t,E)z₂

(17)

и при E = 1 совпадает с системой (6).

Рассмотрим решения (z₂(t, E),

w₂(t,E)),

(z₂(t, E),w2(t, E)) системы (17) такие, что

z₂(0,E) = 1,

w₂(0,E) = 0,

z₂(0,E) = 0,

w₂(0,E) = 1.

Эти семейства решений, зависящие от параметра E, выражаются через решения, соответству-

ющие значению E = 1, следующим образом:

√

z₂(t,E) = z₂(

Et,1),

w₂(t,E) =

w₂(

Et,1),

√

2(t, E) =

√

Et,1),

2(t, E) =^w2(

Et,1).

При E = 1 эти решения введены выше: z₂(t) = z₂(t, 1),

w₂(t) =

w₂(t,1),

2(t) =^z2(t, 1),

w₂(t) =w2(t,1).

4.4. Устойчивость траектории. Согласно [7] для существования асимптотических соб-

ственных функций, соответствующих периодической траектории, необходима орбитальная ус-

тойчивость периодической траектории в линейном приближении, т.е. линеаризация соответ-

ствующего ей отображения Пуанкаре, ограниченного на поверхность уровня {H = E}, долж-

на иметь норму, не превышающую единицу. Как сказано выше, все замкнутые кривые Λ(E)

устойчивы или неустойчивы одновременно. Таким образом, существование асимптотических

функций обусловлено конкретным видом функций D₁₀, D₂₀, D₁₂, входящих в условие задачи.

Поставим более сильное условие устойчивости. Будем требовать сильную устойчивость

траекторий. По определению это означает, что линеаризованные отображения Пуанкаре, огра-

ниченные на поверхность уровня {H = E}, которые всегда являются симплектическими отоб-

ражениями, не имеют близких симплектических отображений с нормой, большей единицы.

Невыполнение этого условия приводит к таким усложнениям, как вырожденность асимптоти-

ческого спектра в главном приближении, что требует рассмотрения поправок к нему. Случай

сильной устойчивости является более простым и с точки зрения топологии в пространстве

линейных симплектических отображений: для него отображения, соответствующие по описан-

ному выше правилу сильно устойчивым замкнутым кривым, образуют в этом пространстве

открытое множество. В общем случае структура этого множества исследована в работе [11].

Введём симплектическую матрицу монодромии, зависящую от параметра E :

(

)

z₂(T(E),E)

2(T (E), E)

R(E) =

w₂(T(E),E)

Её собственные значения λ₁, λ₂ не зависят от E, поскольку её характеристический многочлен

от E не зависит. Из симплектичности матрицы R(E) следует равенство λ₁λ₂ = 1. Матрица

R = R(1) определена равенством (7).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

243

Условие сильной устойчивости равносильно следующему свойству: собственные значения

λ₁, λ2 лежат на единичной окружности в комплексной плоскости и отличны от ±1. Экви-

валентно, |tr R(E)| < 2. Очевидно, что это свойство также не зависит от E. Поэтому можно

положить E = 1 и получить неравенство (8).

Если последнее неравенство выполнено, то возможно представление λ1,2 = exp(±iβ), β ∈

∈ R, β = πk, k ∈ N. При E = 1 выше были определены решения Флоке Z₂(t), W₂(t) с

показателем β. При остальных E введём следующие решения Флоке с показателем β :

√

Z₂(t,E) = Z₂(

Et), W₂(t,E) =

EW₂(

Et).

(18)

Известно, что (при фиксированном E) величина -2i(W₂Z₂ -Z₂W₂) принимает вещественное

ненулевое значение, не зависящее от t. Очевидно, что знак этой величины не зависит от

E. В теории комплексного ростка требуется выполнение условия -2i(W2Z2 - Z2W2) > 0,

которое вследствие равенства 4|Z₂|² Im W₂Z-12 = -2i(W₂Z₂ - Z₂W₂) эквивалентно условию

положительности из (9). Таким образом, имеем

(Z₂(t + T (E), E), W₂(t + T (E), E)) = (exp(iβ)Z₂(t, E) exp(iβ)W₂(t, E)),

4|Z₂|² Im W₂Z-12 ≡ -2i(W₂Z₂ - Z₂W₂) > 0.

√

Функция Arg Z₂(t, E) = Arg Z₂(

Et) - непрерывная ветвь аргумента не обращающейся в нуль

комплекснозначной функции Z₂(t, E). Число β в п. 2.2 было выбрано так, что

β = ArgZ₂(T(E),E) - ArgZ₂(0,E) = ArgZ₂(T) - ArgZ₂(0).

4.5. Условие квантования. Согласно общей теории при каждом значении параметра h

из семейства устойчивых периодических траекторий выделяется дискретное множество тех

траекторий, которые удовлетворяют условию квантования. В общем виде это условие записы-

вается следующим образом (см. [7, с. 215]):

∮

⁽1⁾

p₁ dx₁ + p₂ dx₂ =

+ n, n ∈ N, n = O

2πh

4π

Λ(E)

В приведённой формуле слагаемое 1/2 равно разделённому на 4 индексу Маслова кривой

Λ(E), рассматриваемой в плоскости (x₁, p₁) (согласно [12] этот индекс равен 2). Интеграл по

Λ(E) от формы p₁ dx₁ + p₂ dx₂ равен

∮

∫

√

p₁ dx₁ + p₂ dx₂ =

P₁(t,E

X₁(t,E)dt = 2ET(E) = 2

ET(1).

Λ(E)

Поэтому условие квантования принимает вид

ET(E)

⁽1⁾

+ n, n ∈ N, n = O

(19)

πh

4π

Из семейства траекторий выбираются те, которые удовлетворяют этому условию, а именно те,

которые соответствуют следующим значениям параметра E :

(

))₂

)

πh

⁽1

E(n, h) =

n ∈ N, n = O

T (1)

4π

Серия асимптотических собственных значений, соответствующая проквантованному семей-

ству периодических сильно устойчивых траекторий, принимает вид (см. [7, с. 218])

)

hβν

⁽1

E_n,ν(h) = E(n,h) +

n ∈ N, n = O

ν ∈ Z₊, ν = O(1).

T (E(n, h))

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

7^∗

244

КЛЕВИН

Последнее выражение эквивалентно выражению (10) для серии асимптотических собственных

значений.

Далее мы будем заниматься построением асимптотических собственных функций.

5. Вспомогательные конструкции.

5.1. Карты и разбиение единицы, симметричные относительно отражения. Пусть

выбраны значения h и n. Положим E = E(n, h). Кривая Λ(E) симметрична относительно

отображения плоскости Ref (x₁, p₁) = (x₁, -p₁). Введём функцию g = Ref |Λ(E).

Пусть t∗1, t∗2 ∈ Λ(E) - две точки такие, что X(t^∗s) = (b_s, 0), s = 1, 2. Покроем кривую

Λ(E) двумя областями U₁, U₂ такими, что t^∗s ∈ U_s, g(U_s) = U_s, s = 1, 2. Введём разбиение

единицы, подчинённое данному покрытию, которое реализуется функциями e₁(t), e₂(t) с

носителями в U₁ и U₂ такими, что e_s = e_s ◦ g, s = 1, 2.

5.2. Индексы, обращение координатной функции. На кривой Λ(E) определена ори-

ентация, совпадающая с направлением гамильтоновой системы. Поэтому локально можно го-

ворить об одной точке из Λ(E), стоящей перед (или после) другой точкой из Λ(E).

Выберем начальную точку t⁰ ∈ Λ(E) такую, что t⁰ = t∗1, t⁰ = t∗2. Пусть γ_s, s = 1, 2, -

произвольный путь, соединяющий точки t⁰ и t^∗s. Введём полуцелые числа m₁, m₂ равен-

ством 2m_s = Ind (γ_s

^⋃ {t^∗s → t^∗s - 0}) + Ind (γ_s ⋃ {t^∗s → t^∗s + 0}), где Ind (γ_s ⋃ {t^∗s → t^∗s - 0})

(соответственно Ind (γ_s

^⋃ {t^∗s → t^∗s + 0})) - индекс Маслова пути, получающегося объедине-

нием пути γ_s и кратчайшего пути, соединяющего точку t^∗s и близкую к ней точку перед

(соответственно после) t^∗s. Таким образом, m_s - среднее значение индексов Маслова двух

областей, разделённых особой точкой t^∗s. Известно (см. [13]), что

Ind(γ_s

^⋃ {t^∗s → t^∗s - 0}) + 1/2 = m_s = Ind (γ_s ⋃ {t^∗s → t^∗s + 0}) - 1/2.

Для каждого s = 1, 2 выберем произвольным образом ветвь обратной к X₁(t) функции

t_s(x₁), принимающую значения в U_s. Введём также число σ_s, равное -1, если t_s(x₁) при-

нимает значения, лежащие перед t^∗s, и равное 1, если t_s(x₁) принимает значения, лежащие

после t^∗s. Таким образом, σ_s = sign (t_s(x₁) - t^∗s) при b₁ < x₁ < b₂.

Рассмотрим пример. Пусть

T (E)

X₁(0) = b₁, t∗1 = 0, t∗2 =

t⁰ = +0,

(20)

γ₁ - путь нулевой длины, γ₂ - кратчайший путь по направлению гамильтоновой системы.

Пусть функции t₁(x₁), t₂(x₁) принимают значения в точках t∗1 ≤ t ≤ t∗2. Тогда

t(x₁)

t₁(x₁) = t₂(x₁) =

√

m₁ = -

m₂ =

σ₁ = 1, σ₂ = -1.

(21)

5.3. Вспомогательные функции. Далее для удобства будем пользоваться накрытием

Λ_C(E). Поднимем на него точку t⁰ произвольным образом. Кривые γ₁, γ₂ и точки t∗1, t∗2

будем рассматривать как кривые и точки на Λ_C (E), которые по поднятию точки t⁰ опре-

деляются однозначным образом. Также однозначно определены поднятия областей U₁, U₂ и

функций e₁, e₂.

Пусть ν ∈ Z₊. Введём вспомогательные числа и функции

(

)

(

)

x₂

exp(-i2 Arg Z₂(t, E))

tβν

x²²

A t,

√

exp i

W₂Z-12(t,E)

(Z₂(t, E))^ν ×

|Z₂(t, E)|

T (E)

(

)

x₂

× (Im W₂Z-12(t, E))ν/2H_ν (Im W₂Z-12(t, E))1/2√

(

)

(

)

∫

x₂

A_s t,

√

= e_s(t)A t,

√

τ (t) =

P (t, E

X (t, E) dt = 2E(t - t⁰),

t⁰

τ^∗s = τ(t^∗s),

τs(x1) = |τ(ts(x1)) - τ(t^s)|, s = 1, 2.

(22)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

245

Функция A зависит от вещественного параметра E и от целого неотрицательного парамет-

ра ν.

Лемма 1. Выполняются равенства

(

)

(

)

X₁(t^∗s + t,E)

X₁(t^∗s

- t,E)

e_s(t^∗s + t) = e_s(t^∗s - t).

P₁(t^∗s + t,E)

-P₁(t^∗s - t,E)

Доказательство. Подстановкой в уравнение (15) непосредственно проверяется, что век-

торные функции, стоящие в обеих частях первого равенства, являются решениями уравне-

ния (15). Первое равенство следует из определения введённой склейки траекторий в точках

(x₁, p₁) = (b_s, ∞), соответствующих значению параметра t = 0.

Последнее равенство следует из определения функций e₁, e₂. Лемма доказана.

Лемма 2. Выполняются равенства

|Z₂(t^∗s - t, E)| = |Z₂(t^∗s + t, E)|,

Arg Z₂(t^∗s + t, E) - Arg Z₂(t^∗s, E) = Arg Z₂(t^∗s, E) - Arg Z₂(t^∗s - t, E),

iW₂Z-12(t^∗s - t, E) = iW₂Z-12(t^∗s + t, E), Im W₂Z-12(t^∗s - t, E) = Im W₂Z-12(t^∗s + t, E).

Доказательство. Прямой подстановкой проверяется, что пара функций

(Z₂(2t^∗s - t, E), -W₂(2t^∗s - t, E))

является решением системы (17). Это решение является решением Флоке с показателем -β.

Пара комплексно-сопряжённых функций (Z₂(t, E), W₂(t, E)) также является решением Флоке

системы (17) с вещественными коэффициентами, соответствующим показателю -β. Из един-

ственности решения Флоке с показателем -β = πk, k ∈ Z, с точностью до умножения на

постоянную и неравенства нулю Z₂(t, E) следует (в определённых выше векторных функциях

сделаем замену t → t + t^∗s), что

(

)

(

)

Z₂(t^∗s - t,E)

Z₂(t^∗s + t,E)

Z₂(t^∗s,E)

= Z₂(t^∗s,E)

-W₂(t^∗s - t,E)

W₂(t^∗s + t,E)

Отсюда вытекает утверждение леммы.

Лемма 3. Выполняются равенства

(

)

(

)

(

)

(

)

x₂

A_s t^∗s + |t - t^∗s|,

√

+ A_s t^∗s - |t - t^∗s|,

√

= A_s t,

√

+ A_s 2t^∗s - t,

√

(

)

x₂

= e_s(t)|Z₂(t,E)|ν-1/2(Im W₂Z-12(t,E))ν/2H_ν (Im W₂Z-12(t,E))1/2

√

(

)

it^∗sβν

× exp

-i ν +

Arg Z₂(t^∗s, E) +

T (E)

[

(

)

)]

i(t - t^∗s)βν

× 2Re exp

-i ν +

(Arg Z₂(t, E) - Arg Z₂(t^∗s, E)) +

W₂Z-12(t,E)

T (E)

(

)

(

)

(

)

(

))

x₂

A_s t^∗s + |t - t^∗s|,

√

- A_s t^∗s - |t - t^∗s|,

√

= σ_s A_s t,

√

- A_s 2t^∗s - t,

√

(

)

x₂

= e_s(t)|Z₂(t,E)|ν-1/2(Im W₂Z-12(t,E))ν/2Hν (Im W2Z-12(t,E))1/2

√

(

)

it^∗sβν

× exp

-i ν +

Arg Z₂(t^∗s, E) +

T (E)

[

(

)

)]

i(t - t^∗s)βν

x²²

× 2iσ_s Im exp

-i ν +

(Arg Z₂(t, E) - Arg Z₂(t^∗s, E)) +

W₂Z-12(t,E)

T (E)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

246

КЛЕВИН

Доказательство. Сначала следует записать действие операторов Re, Im на их аргумен-

ты в виде комбинации аргументов с их комплексными сопряжениями, затем воспользоваться

леммой 1 и леммой 2, в которых нужно сделать замену t → t - t^∗s. Лемма доказана.

Для рассмотренного выше примера, т.е. при выполнении соотношений (20), (21), можно

взять

Arg Z₂(t∗1, E) = 0, Arg Z₂(t∗2, E) = β/2, e_s(t_s(x₁)) = f_s(x₁), s = 1, 2,

√

τ∗1 = 0, τ∗2 = ET(E),

τ₁ = 2

Et(x₁),

τ₂ = 2

E t(x₁).

(23)

6. Асимптотика спектральной задачи.

6.1. Канонический оператор в случае лагранжевой кривой. Рассмотрим кривую

Λ(E) как лагранжеву кривую, вложенную в двумерное пространство (x₁, p₁). Для каждой

функции a(t) на этой кривой введём локализованные функции a_s(t) = a(t)e_s(t), s = 1, 2.

√

Пусть y_s(t, E) = 2

|X₁(t, E) - b_s|, s = 1, 2. Канонический оператор, соответствующий кри-

вой Λ(E), на которой функция действия представлена линейной функцией τ(t), определяется

следующим выражением (см. [13]):

(

)(

)1/2

∑

iπm_s

iτ^∗s

πτ_s(x₁)

[KΛ(E)a](x₁) =

exp

hy_s(t_s(x₁), E)

s=1,2

[

∑

⁽τ_s(x₁)⁾

⁽τ_s(x₁)^)] a_s(t^∗s + q|t_s(x₁) - t^∗s|)

J₀

+ (-1)(q-1)/2iJ1

(24)

|y_s(t^∗s + q|t_s(x₁) - t^∗s|,E)|1/2

q=±1

6.2. Асимптотические собственные функции. Имеем



√



y_s(t,E)| y_s(t,E)| =

(t, E)

X₁(t,E)| = 4

ED₁₀(X₁(t,E)).

⁼

2 dty

Воспользовавшись симметрией X(t^∗ + t, E) = X(t^∗ - t, E), получим

√

y_s(t_s(x₁),E)| y_s(t^∗s + q|t_s(x₁) - t^∗s|,E)| = 4

ED₁₀(x₁).

Подставив в выражение для канонического оператора (24) в качестве функции a(t) функ-

√

цию A_s(t, x₂/

h), зависящую также от x₂/

h, будем иметь

[

(

)]

(

)(

)1/2

∑

x₂

iπm_s

iτ^∗s

πτ_s(x₁)

KΛ(E)A_s t,

√

(x₁) =

exp

√

ED₁₀(x₁)

s=1,2

[(

(

)

⁽τ_s(x₁)⁾

⁽τ_s(x₁)⁾⁾

x₂

× J₀

+ iJ₁

A_s t^∗s + |t_s(x₁) - t^∗s|,

√

(

)]

⁽τ_s(x₁)⁾

⁽τ_s(x₁)⁾⁾

x₂

+ J₀

- iJ₁

A_s t^∗s - |t_s(x₁) - t^∗s|,

√

(25)

Данное выражение определяет асимптотическую собственную функцию. Такое её определе-

√

ние путём подстановки функции A_s(t, x₂/

h) в аргумент канонического оператора (24) не

является строго обоснованным. Обоснование приводится ниже.

Раскроем в представлении (25) скобки, содержащие линейные комбинации функций Бес-

селя J₀, J₁, и приведём затем подобные члены относительно этих функций:

[

(

)]

(

)(

)1/2

∑

x₂

iπm_s

iτ^∗s

πτ_s(x₁)

KΛ(E)A_s t,

√

(x₁) =

exp

√

ED₁₀(x₁)

s=1,2

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

247

[

(

)

(

))

⁽τ_s(x₁)⁾⁽

x₂

× J₀

A_s t^∗s + |t_s(x₁) - t^∗s|,

√

+ A_s t^∗s - |t_s(x₁) - t^∗s|,

√

(

)

(

))]

⁽τ_s(x₁)⁾⁽

x₂

+ iJ₁

A_s t^∗s + |t_s(x₁) - t^∗s|,

√

- A_s t^∗s - |t_s(x₁) - t^∗s|,

√

Воспользовавшись леммой 3, придём к представлению

[

(

)]

(

)(

)1/2

∑

x₂

iπm_s

iτ^∗s

πτ_s(x₁)

KΛ(E)A_s t,

√

(x₁) =

exp

√

ED₁₀(x₁)

s=1,2

× |Z₂(t_s(x₁), E)|ν-1/2(Im W₂Z-12(t_s(x₁), E))ν/2e_s(t_s(x₁)) ×

(

)

( (

)

x₂

it^∗sβν

× H_ν (ImW₂Z-12(t_s(x₁),E))1/2√

exp

-i ν +

Arg Z₂(t^∗s, E) +

T (E)

[

(

)

⁽τ_s(x₁)⁾

i(t_s(x₁) - t^∗s)βν

× 2J₀

Re exp

-i ν +

(Arg Z₂(t_s(x₁), E) - Arg Z₂(t^∗s, E)) +

T (E)

))

(

( (

)

x²²

⁽τ_s(x₁)⁾

W₂Z-12(t_s(x₁),E)

- 2σ_sJ₁

Im exp

-i ν +

(Arg Z₂(t_s(x₁), E) -

))]

i(t_s(x₁) - t^∗s)βν

x²²

- Arg Z₂(t^∗s, E)) +

W₂Z-12(t_s(x₁),E)

T (E)

Выражение

(11) получается после подстановок

(18)-(21),

(23) и умножения на число

exp(-iπ/4)E(1-ν)/4.

6.3. Асимптотические собственные функции в форме ВКБ вдали от границы.

Рассмотрим собственные функции на подмножествах, в которых значения координаты x₂ от-

делены от граничных значений b₁, b₂. Такие подмножества не содержат каустики, соответ-

ствующие границе, и на них асимптотические собственные функции допускают представление

в форме ВКБ (см. [7, с. 223])

[ (

) (

)

∑

exp(-iπm_s/2 + iτ^∗s/h)

τs(x1)

x₂

√

exp

-i

A_s t^∗s + |t_s(x₁) - t^∗s|,

√

2(ED₁₀(x₁))1/4

s=1,2

(

) (

)]

τs(x1)

x₂

+ exp i

-i

A_s t^∗s - |t_s(x₁) - t^∗s|,

√

(26)

Множители m_s ± 1/2, s = 1, 2, в показателях экспонент соответствуют индексам Маслова

четырёх областей на Λ_C (E), каждая из которых расположена по одну из сторон точек t^∗s,

s = 1,2.

Если в представлении (25) воспользоваться для функций Бесселя асимптотическими фор-

мулами

(

)1/2(

(

)

(

)1/2( (

)

J₀(z) =

cos z -

+ O(z-1) ,

J₁(z) =

sin z -

+ O(z-1)

πz

при z → +∞, то получим с точностью до O(h) выражение (26). Обратно, начав с представ-

ления (26), получим выражение (25), справедливое вдали от граничных точек b₁, b₂. Это

выражение распространим затем на весь отрезок [b₁, b₂]. Тем самым, если не стремиться к

строгости рассуждений, можно получить справедливое на всём отрезке [b1, b2] выражение

для асимптотической собственной функции.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

248

КЛЕВИН

7. Технические подробности доказательства.

7.1. Устранение каустики, связанной с вырождением на границе. Пусть M =

= [b₁, b₂] × R. Следуя [4], рассмотрим многообразие

^M= S² × R вместе с проекцией λ: M →

→ M.

Для некоторых положительных чисел ε_s < |b₂ - b₁|, s = 1, 2, ε₁ + ε₂ > |b₂ - b₁|, введём

множества V₁ = [b₁, b₁ + ε₁) × R, V₂ = (b₂ - ε₂, b₂] × R, покрывающие множество [b₁, b₂] ×

× R. Определим линейные функции z₁(x₁) = x₁ - b₁, z₂(x₁) = b₂ - x₁ и обратные к ним

z-11(ζ) = b₁ + ζ, z-12(ζ) = b₂ - ζ.

Рассмотрим три карты, покрывающие^M = λ-1(M). Карта λ-1((b₁, b₂) × R) имеет коор-

динаты (φ, x₁, x₂), φ ∈ S¹. При каждом s = 1, 2 карта λ-1(V_s) имеет координаты (y₁, y₂, x₂),

|y|² < 4ε_s. Проекция в этих картах записывается в виде

(

)

⁽y²¹ +y²²)

λ(φ, x₁, x₂) = (x₁, x₂), λ(y₁, y₂, x₂) = z-1

,x₂

На пересечении λ-1((b₁, b₂) × R)

^⋂λ-1(V_s) отображения склейки принимают вид

√

g(φ, x₁, x₂) = (2

z_s(x₁) cos φ,2

z_s(x₁) sin φ,x₂),

y²¹ + y²²

g-1(y₁,y₂,x₂) = (Arg (y₁ + iy₂),z-1s(

,x₂)).

Рассматриваются функции на многообразии

M, постоянные на множествах вида

λ-1(x₁,x₂), (x₁,x₂) ∈ M, которые можно интерпретировать как функции на M, и диффе-

ренциальные операторы, для которых множество таких функций является инвариантным. Со-

гласно [4] для оператораL, заданного формулой (13), существует дифференциальный опера-

тор

L, который сохраняет множество функций, постоянных на множествах вида λ-1(x₁,x₂),

(x₁, x₂) ∈ M, и действует на такие функции как оператор

L, если их рассматривать как

функции на M.

Введём фазовое пространство в виде кокасательного расслоения T^∗ M с двумя типами

координат: (φ, x₁, x₂; p_φ, p₁, p₂) и (y₁, y₂, x₂; ξ₁, ξ₂, p₂), где p_φ, p₁, p₂, ξ₁, ξ₂ - импульсные

координаты. Теперь при рассмотрении оператора

L не возникает каустик, связанных с обра-

щением в бесконечность импульсных переменных, и можно обычным методом построить его

асимптотические собственные функции, требуя при этом, чтобы они были постоянными на

множествах вида λ-1(x₁, x₂), (x₁, x₂) ∈ M.

На многообразии

^M можно ввести действие группы U(1) сдвигами по углу φ (в других

координатах - вращениями в плоскости (y₁, y₂) на соответствующий угол). Тогда множества

вида λ-1(x₁, x₂), (x₁, x₂) ∈ M, являются орбитами этого действия. Это действие переносится

и на многообразие T^∗ M.

Для построения асимптотических собственных функций, быстроубывающих при отдале-

нии от одномерной кривой в M, мы используем изложенный в [7] метод комплексного ростка

Маслова. Основным объектом здесь является изотропное многообразие с комплексным рост-

ком, инвариантное относительно гамильтонова потока. Инвариантное относительно гамильто-

нова потока изотропное многообразие в T^∗ M с комплексным ростком должно принадлежать

множеству {p_φ = 0} ⊂ T^∗ M (в координатах (y₁, y₂, x₂; ξ₁, ξ₂, p₂) это множество задаётся урав-

нением y₁ξ₂ - y₂ξ₁ = 0) и быть инвариантным (вместе с комплексным ростком) относительно

введённого выше U(1)-действия.

В нашем случае изотропное многообразие лежит в подпространстве {x₂ = p₂ = 0} и имеет

размерность 2, а комплексный росток представляет собой прямую сумму комплексифициро-

ванной касательной плоскости к изотропному многообразию и прямой в комплексифициро-

ванной плоскости (x₂, p₂).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

249

7.2. Изотропное многообразие с комплексным ростком. Далее мы рассмотрим ка-

нонический оператор на изотропном многообразии с комплексным ростком следующего вида.

Пусть изотропное многообразие с координатами ψ ∈ S¹, t в шестимерном пространстве с

координатами (y₁, y₂, x₂, ξ₁, ξ₂, p₂) задано функциями Y (t, ψ) = (Y₁(t, ψ), Y₂(t, ψ)), X₂(t, ψ),

Ξ(t, ψ) = (Ξ₁(t, ψ), Ξ₂(t, ψ)), P₂(t, ψ) вида

Y (t, ψ) = η(t)n(ψ), Ξ(t, ψ) = ρ(t)n(ψ), X₂(t, ψ) = 0, P₂(t, ψ) = 0,

где n(ψ) = (cos ψ, sin ψ), а η, ρ - некоторые функции со свойствами η(-t) = -η(t), ρ(t) >

> 0,

η(t) > 0. Пусть на изотропном многообразии задан комплексный росток, натянутый на

векторы

∂

(Y₁(t, ψ), Y₂(t, ψ), 0, Ξ₁(t, ψ), Ξ₂(t, ψ), 0),

∂t

∂

(Y₁(t, ψ), Y₂(t, ψ), 0, Ξ₁(t, ψ), Ξ₂(t, ψ), 0),

(0, 0, Z₂(t), 0, 0, W₂(t)),

∂ψ

где Z₂(t), W₂(t) - некоторые комплекснозначные функции.

Если выбрать подходящим образом функции η, ρ (а именно так, чтобы при всех t выпол-

нялось тождество D₁₀((η(t))²/4)(2ρ(t)/η(t))² = E), а в качестве Z₂(t), W₂(t) взять функции,

определённые равенством (18), то под действием проекции λ на множестве λ-1(M) данное

изотропное многообразие с комплексным ростком перейдёт в кривую, определённую траек-

торией системы (14), с инвариантным относительно этой системы комплексным ростком над

ней.

Якобиан det[∂(Y₁, Y₂)/∂(t, ψ)] = η(t) η(t) равен нулю в точке t = 0, поэтому канонический

оператор, согласно общей теории, должен быть записан в виде интеграла по крайней мере по

одной из импульсных переменных ξ₁ или ξ₂.

7.3. Канонический оператор в виде интеграла по импульсным переменным. Рас-

смотрим функции вида

(

)

(

)

x₂

⁽i

x²²

A t,

√

= a t,

√

exp

W₂(t)Z-12(t)

Im W₂(t)Z-12(t) > 0, Z₂(t) = 0,

(27)

где a - некоторая гладкая комплекснозначная функция. Функция A, определённая в (22),

является функцией такого вида. Введём также функцию действия τ(t) такую, что

dτ(t) = Ξ₁(t, ψ) dY₁(t, ψ) + Ξ₂(t, ψ) dY₂(t, ψ) = ρ(t) dη(t).

Для построения канонического оператора в виде интеграла по импульсным переменным

обобщим формулы, полученные в работе [14]. На изотропном многообразии введём карты Ω₁ =

= {ψ ∈ (-3π/8, 3π/8)}, Ω₃ = {ψ ∈ (5π/8, 11π/8)} с координатами (y₁, ξ₂) и карты Ω₂ = {ψ ∈

∈ (π/8, 7π/8)}, Ω₄ = {ψ ∈ (9π/8, 15π/8)} с координатами (ξ₁, y₂). Введём также подчинённое

покрытию многообразия этими картами разбиение единицы

e₁(ψ) + e₂(ψ) + e₃(ψ) + e₄(ψ) = 1.

Асимптотическая собственная функция u(y, x₂, h) оператора

L в окрестности точки y₁ =

= y₂ = x₂ = 0 строится методом комплексного ростка Маслова и имеет следующий вид

(см. [7, с. 223]):

√

∫



(

)

∑



-1/2

2πh

∂(y₁, ξ₂)

x₂

u(y, x₂, h) =



A t,

√

^d



exp(iπ/4)

∂(t, ψ)

j=1,3_-∞

)

∫



(

)



∑



-1/2

⁽i

∂(ξ₁, y₂)

x₂



×e_j(ψ)exp

(τ(t)-Y₂(t, ψ)Ξ₂(t, ψ)+y₂ξ₂)

dξ₂+

A t,

√

 t=t(y₁,ξ₂)

^d



∂(t, ψ)

ψ=ψ(y₁,ξ₂)

j=2,4_-∞

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

250

КЛЕВИН

)

⁽i



× e_j(ψ)exp

(τ(t) - Y₁(t, ψ)Ξ₁(t, ψ) + y₁ξ₁)

ξ₁,

(28)

 t=t(ξ₁,y₂) ^d

ψ=ψ(ξ₁,y₂)

где пары функций t(y₁, ξ₂), ψ(y₁, ξ₂) и t(ξ₁, y₂), ψ(ξ₁, y₂) являются обращениями функций

Y (t, ψ), Ξ(t, ψ) в областях Ω_j, j = 1, 2, 3, 4.

7.4. Канонический оператор в виде интеграла по окружности. Сделаем замену

переменной ξ₂ → ψ в первом интеграле в (28), которая задаётся функцией ξ₂ = Ξ₂(t(y₁, ξ₂), ψ),

и замену переменной ξ₁ → ψ во втором интеграле, которая задаётся функцией

ξ₁ = Ξ₁(t(ξ₁,y₂),ψ).

Вычислим матрицы Якоби обратных отображений и нужные нам частные производные:

⎛

⎞

∂t

(

)

)-1⁽

⎜∂y1

∂ξ₂⎟

⁽∂(y₁,ξ₂))-1

∂(y₁, ξ₂)

ρ cos ψ η sin ψ

⎜

⎟

= det

⎝_∂ψ

⎠⁼

- ρsinψ

η cos ψ

∂ψ

∂(t, ψ)

∂y₁

∂ξ₂

⎛

⎞

∂t

(

)

)-1⁽

⎜∂ξ1

∂y₂⎟

⁽∂(ξ₁,y₂))-1

∂(ξ₁, y₂)

η cos ψ ρ sin ψ

⎜

⎟

= det

⎝_∂ψ

⎠⁼

-η sinψ

ρ cos ψ

∂ψ

∂(t, ψ)

∂ξ₁

∂y₂

(

)-1

∂ψ

∂(y₁, ξ₂)

η cos ψ

= ηcosψ det

∂ξ₂

∂(t, ψ)

ηρcos² ψ + ηρ˙ sin² ψ

(

)-1

∂ψ

∂(ξ₁, y₂)

η sin ψ

= -η sinψ det

∂ξ₁

∂(t, ψ)

η ρcos2 ψ + ηρsin2 ψ

Пусть η-1 - обратная к η функция. После замены переменных получаем

√

∫

2π

(

)

∑

2πh

x₂

| η(t)ρ(t)cos2 ψ + η(t)ρ˙(t)sin2 ψ|1/2

u(y, x₂, h) =

A t,

√

e_j(ψ)

exp(iπ/4)

|η(t)cos ψ|

j=1,3 0

(

)

∫

2π

(

)



∑

x₂

× exp

(τ(t) + ρ(t)(〈y, n(ψ)〉 - η(t)))



dψ +

A t,

√

e_j(ψ) ×



t=η-1(y1/cos ψ)

j=2,4 0

)

|η(t)ρ˙(t) cos² ψ + η(t)ρ(t) sin² ψ|

1/2

⁽i



exp

(τ(t)+ρ(t)(〈y, n(ψ)〉-η(t)))

dψ. (29)



|η(t)sin ψ|

t=η-1(y₂/sin ψ)

Рассмотрим первый интеграл в (29). Запишем фазовую функцию, стоящую в аргументе

экспоненты в следующем виде:

(

)) (

(

))(

)

y₁

Φ(y₁, y₂, ψ) = τ η-1

+ρ η-1

〈y, n(ψ)〉 -

cos ψ

Введём функцию

Φ(y₁, y₂, ψ) = τ(η-1(〈y, n(ψ)〉)).

Множества нулей у функций ∂^Φ/∂ψ и ∂Φ/∂ψ в пространстве (y₁, y₂, ψ) одинаковы и совпа-

дают с множеством

C_Φ = {(y₁,y₂,ψ) : y = αn(ψ), α ∈ R} ⊂ R² × S¹.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

251

Более того, разность функцийΦ и Φ на множестве C_Φ имеет нуль второго порядка. Чтобы

это увидеть, достаточно воспользоваться формулой Тейлора:

(

))

(

))(

)

y₁

τ (η-1(〈y, n(ψ)〉)) = τ η-1

+ρ η-1

〈y, n(ψ)〉 -

cos ψ

(

)₂

((

)₃)

1 ρ(η-1(y₁/cos ψ))

y₁

〈y, n(ψ)〉 -

2 η(η-1(y₁/cos ψ))

cos ψ

Из теории осциллирующих интегралов следует, что существует замена переменной в инте-

грале, приводящая его к осциллирующему интегралу с фазовой функцией Φ. Пусть отноше-

= f₂ означает их равенство на множестве C_Φ, т.е. f₁|CΦ = f₂|CΦ

√

(если функции зависят также от параметра x₂/

h, то равенство понимается в смысле ра-

венства при всех фиксированных его значениях). Введём для амплитудной функции в первом

интеграле в (29) обозначение

(

)

(

)



x₂

| η(t)ρ(t)cos² ψ + η(t)ρ˙(t)sin² ψ|1/2

a y₁,y₂,ψ,

√

= A t,

√

e_j(ψ)



|η(t)cos ψ|

t=η-1(y₁/cos ψ)

√

Для некоторой функции a(y₁, y₂, ψ, x₂/

h) такой, что

(

)



(

)

1/2

x₂



∂(t, ψ, Φ^′ψ)



∂(t, ψ,Φ′ψ)-1/2

x₂

a y₁,y₂,ψ,

√

C_Φ=



a y₁,y₂,ψ,

√

(30)

^d



^d



∂(y₁, y₂, ψ)

где t(y₁, y₂, ψ) = η-1(〈y, n(ψ)〉), ψ(y₁, y₂, ψ) = ψ, верно равенство (см. [15, раздел 3.2])

∫

2π

(

)

(

)

∫

2π

(

)

(

)

a y₁,y₂,ψ,

√

exp

Φ(y₁, y₂, ψ) dψ = a y₁, y₂, ψ

√

exp

Φ(y₁, y₂, ψ) dψ.

Вычислим в равенстве (30) отношение определителей, ограниченное на множество C_Φ. Пре-

образуем это отношение следующим образом:

(

∂(t, ψ,Φ′ψ))-1

∂(t, ψ, Φ^′ψ)

det

∂(y₁, y₂, ψ)

(

∂(t, ψ, Φ^′ψ)

∂(t, ψ, (Φ -Φ)^′ψ))-1

∂(t, ψ, Φ^′ψ )

= det

- det

det

∂(y₁, y₂, ψ)

(

∂(t, ψ, Φ^′ψ))-1

∂(t, ψ, (Φ -Φ)^′ψ))-1

1 - det

det

(31)

∂(y₁, y₂, ψ)

Для частной производной Φ^′ψ верно равенство Φ^′ψ = ρ(η-1(〈y, n(ψ)〉))〈y, n^′(ψ)〉. Один из опре-

делителей равен

⎛

⎞

∂t

⎛

⎞

∗

∂t

⎜

⎟

∂y₁

∂y₂

⎜

⎟

∂(t, ψ, Φ^′ψ)

⎜

∂y₁

∂y₂

⎟

⎜

⎟

⎜

⎟

det

= det⎜

⎟

= -det

⎝∂Φ′

⎠⁼

∂(y₁, y₂, ψ)

⎜

⎟

∂Φ^′ψ

⎝∂Φ^′ψ

∂Φ^′ψ

⎠

∗

∂y₁

∂y₂

∂y₁

∂y₂

⎛

⎞

cos ψ

sin ψ

= -det^⎝

η(η-1(〈y, n(ψ)〉))

⎠=-ρ(η-1(〈y,n(ψ)〉))

η(η-1(〈y, n(ψ)〉))

ρ(η-1(〈y, n(ψ)〉))(- sin ψ) ρ(η-1(〈y, n(ψ)〉)) cos ψ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

252

КЛЕВИН

Для разности функций

(

)₂

((

)₃)

y₁

Φ-Φ=1ρ(η-1(y1/cosψ))

〈y, n(ψ)〉 -

2 η(η-1(y₁/cos ψ))

cos ψ

рассмотрим частную производную второго порядка на множестве C_Φ :

(

)_′

(

)_′

ρ(η-1(y₁/cos ψ))

y₁

〈y, n(ψ)〉 -

C_Φ=

η(η-1(y₁/cos ψ))

cos ψ_ψ

cos ψ_y

(

)(

)т

y₁ sinψ

-1/cos ψ

C_Φ=ρ(η-1(〈y,n(ψ)〉))

η(η-1(〈y, n(ψ)〉))

cos² ψ

(

)т

sin ψ

C_Φ=ρ(η-1(〈y,n(ψ)〉))〈y, n(ψ)〉

+ n(ψ)(...).

η(η-1(〈y, n(ψ)〉))

cos² ψ

На множестве C_Φ вычислим определитель

⎛

⎞

∂t

⎜

⎟

∂(t, ψ, (Φ -Φ)^′ψ)

∂y₁

∂y₂

⎜

⎟

ρ(η-1(〈y, n(ψ)〉))

sin² ψ

det

C_Φ= - det⎜

⎟

C_Φ=

〈y, n(ψ)〉

∂(y₁, y₂, ψ)

⎝∂(Φ -Φ)′ψ

∂(Φ -Φ)^′ψ⎠

η²(η-1(〈y,n(ψ)〉))

cos² ψ

∂y₁

∂y₂

Подставив результаты вычислений в равенство (31), получим отношение определителей в (30)

на множестве C_Φ :

(

)-1

∂(t, ψ,Φ′ψ))-1

∂(t, ψ, Φ^′ψ)

ρ(η-1(〈y, n(ψ)〉))〈y, n(ψ)〉

sin² ψ

det

C_Φ=

∂(y₁, y₂, ψ)

∂(y₁, y₂,ψ)

η(η-1(〈y, n(ψ)〉))ρ(η-1(〈y, n(ψ)〉)) cos² ψ

Запишем соотношение (30) следующим образом:

√

(

) (

)

x₂

ρ(η-1(〈y, n(ψ)〉))

a y₁,y₂,ψ,

√

C_Φ= A η-1(〈y,n(ψ)〉)

√

e_j(ψ)

|η(η-1(〈y,n(ψ)〉))|

Получаем

∫

2π

(

)

(

)

x₂

a y,ψ,

√

exp

Φ(y, ψ) dψ =

∫2π

( (

)

(

))

(

)

x₂

a₀

y,ψ,

√

e_j(ψ) + a₁ y,ψ,

√

exp

Φ(y, ψ) dψ,

= 0, и

(

)

(

)√

x₂

ρ(η-1(〈y, n(ψ)〉))

a₀

y,ψ,

√

= A η-1(〈y,n(ψ)〉),

√

|η(η-1(〈y,n(ψ)〉))|

При этом имеем стандартную оценку для интеграла

∫

2π

(

)

(

)

x₂

a₁

y,ψ,

√

exp

Φ(y, ψ) dψ = O(h),

(32)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

АСИМПТОТИКА СОБСТВЕННЫХ ФУНКЦИЙ ТИПА ПРЫГАЮЩЕГО МЯЧИКА

253

которая может быть доказана интегрированием по частям (см., например, рассуждения в [16,

раздел 4.2]). Из вида функции A следует, что функции a₀ и a₀ + a₁, а следовательно, и

√

a₁, являются ограниченными по y и x₂/

h вместе со всеми производными по переменным

√

x₂/

h, y, ψ. Поскольку оценка (32) может быть доказана интегрированием по частям, из

ограниченности функции a₁ вместе с производными следует, что оценка (32) является равно-

√

мерной по переменным y, x₂/

Такие же, как и проведённые выше, рассуждения справедливы и для второго интеграла

в (29). В результате получаем

√

∫

2π

(

)

(

)

2πh

x₂

u(y, x₂, h) = a₀ y, ψ,

√

exp

Φ(y, ψ) dψ + O(h).

(33)

exp(iπ/4)

7.5. Асимптотика интеграла в виде функций Бесселя. Для интеграла из равен-

ства (33) воспользуемся асимптотикой, предложенной в работе [9] (чтобы привести интеграл

из (33) к рассматриваемому в [9] типу нужно сделать замену ψ = Arg (y₁ + iy₂) + φ, перево-

дящую функцию 〈y, n(ψ)〉 в |y| cos φ). Тогда будем иметь

√

∫

2π

(

)

(

)

exp(iπ/4)

x₂

πF_odd(|y|)

u(y, x₂, h) =

√

a₀

y,ψ,

√

exp

Φ(y, ψ) dψ =

2πh

2h|y|

(

){[

)

)](

√

)

iπ

⁽F_odd(|y|)

A(η-1(|y|), x₂/

× exp

Fev(|y|)

J₀

+ iJ₁

√

+ O(h)

|η(η-1(|y|))|

[ (

)

)](

√

)}

Fodd(|y|)

⁽F_odd(|y|)

A(η-1(-|y|), x₂/

+ J₀

- iJ₁

√

+ O(h)

(34)

|η(η-1(-|y|))|

где 2F_ev(r) = τ(η-1(r)) + τ(η-1(-r)), 2Fodd(r) = τ(η-1(r)) - τ(η-1(-r)). Полученная асимп-

тотика инвариантна относительно вращения в плоскости (y₁, y₂). Если теперь положить

√

|y| = 2

z_s(x₁), η(t) = sign (t) · 2

z_s(X₁(t,E)), τ(t) = 2Et,

то функция (34) в окрестности точки x₁ = b_s с точностью до умножения на не зависящую от h

постоянную совпадёт с формулой (24) для канонического оператора, соответствующего одно-

мерной кривой в двумерном пространстве. Таким образом, асимптотика спектральной задачи

может быть выражена через канонический оператор (24) на одномерной кривой в двумерном

√

пространстве с аргументом, включающим зависимость от x₂/

h вида (27).

Автор благодарен С. Ю. Доброхотову за постановку задачи и помощь в работе. Исследова-

ние выполнено при финансовой поддержке Российского научного фонда (проект 16-11-10282).

СПИСОК ЛИТЕРАТУРЫ

1. Keller J.B., Rubinow S.I. Asymptotic solution of eigenvalue problems // Annals of Physics. 1960. V. 9.

P. 24-75.

2. Бабич В.М., Булдырев В.С. Асимптотические методы в задачах дифракции коротких волн. М.,

1972.

3. Клевин А.И. Асимптотические собственные функции типа “прыгающего мячика” двумерного опе-

ратора Шрёдингера с симметричным потенциалом // ТМФ. 2019. Т. 199. № 3. С. 429-444.

4. Доброхотов С.Ю., Назайкинский В.Е. Униформизация уравнений с граничным вырождением бес-

селева типа и квазиклассические асимптотики // Мат. заметки. 2020. Т. 107. № 5. С. 780-786.

5. Аникин А.Ю., Доброхотов С.Ю., Назайкинский В.Е., Цветкова А.В. Асимптотики собственных

функций двумерного оператора ∇D(x)∇, связанные с бильярдами с полужёсткими стенками, и за-

хваченные береговые волны // Мат. заметки. 2019. Т. 105. № 5. С. 792-797.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021

254

КЛЕВИН

6. Назайкинский В.Е. Канонический оператор Маслова на лагранжевых многообразиях в фазовом

пространстве, соответствующем вырождающемуся на границе волновому уравнению // Мат. за-

метки. 2014. Т. 96. № 2. С. 261-276.

7. Maslov V.P. The Complex WKB Method for Nonlinear Equations I. Birkhäuser, Basel, 1994.

8. Доброхотов С.Ю., Назайкинский В.Е., Шафаревич А.И. Новые интегральные представления кано-

нического оператора Маслова в особых картах // Изв. РАН. Сер. матем. 2017. Т. 81. № 2. С. 53-96.

9. Доброхотов С.Ю., Назайкинский В.Е. Об асимптотике интеграла типа Бесселя, имеющего прило-

жения в теории набега волн на берег // Мат. заметки. 2017. Т. 102. № 6. С. 828-835.

10. Демидович Б.П. Лекции по математической теории устойчивости. СПб, 2008.

11. Гельфанд И.М., Лидский В.Б. О структуре областей устойчивости линейных канонических систем

дифференциальных уравнений с периодическими коэффициентами // Успехи мат. наук. 1955. Т. 10.

№ 1(63). С. 3-40.

12. Доброхотов С.Ю., Назайкинский В.Е. Нестандартные лагранжевы особенности и асимптотические

собственные функции вырождающегося оператора -^ddxD(x)^ddx // Тр. Мат. ин-та им. В.А. Стеклова

РАН. 2019. Т. 306. С. 83-99.

13. Аникин А.Ю., Доброхотов С.Ю., Назайкинский В.Е. Простые асимптотики обобщённого волнового

уравнения с вырождающейся скоростью и их приложения в линейной задаче о набеге длинных волн

на берег // Мат. заметки. 2018. Т. 104. № 4. С. 483-504.

14. Доброхотов С.Ю., Макракис Г.Н., Назайкинский В.Е., Тудоровский Т.Я. Новые формулы для ка-

нонического оператора Маслова в окрестности фокальных точек и каустик в двумерных квазиклас-

сических асимптотиках // ТМФ. 2013. Т. 177. № 3. С. 355-386.

15. Hörmander L. Fourier integral operators. I // Acta Mathematica. 1971. V. 127. P. 79-183.

16. Dobrokhotov S.Y., Makrakis G., Nazaikinskii V.E. Fourier integrals and a new representation of Maslov’s

canonical operator near caustics // Amer. Math. Soc. Transl. 2014. V. 233. P. 95-115.

Институт проблем механики

Поступила в редакцию 26.06.2020 г.

им. А.Ю. Ишлинского РАН, г. Москва

После доработки 24.09.2020 г.

Принята к публикации 11.12.2020 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№2

2021