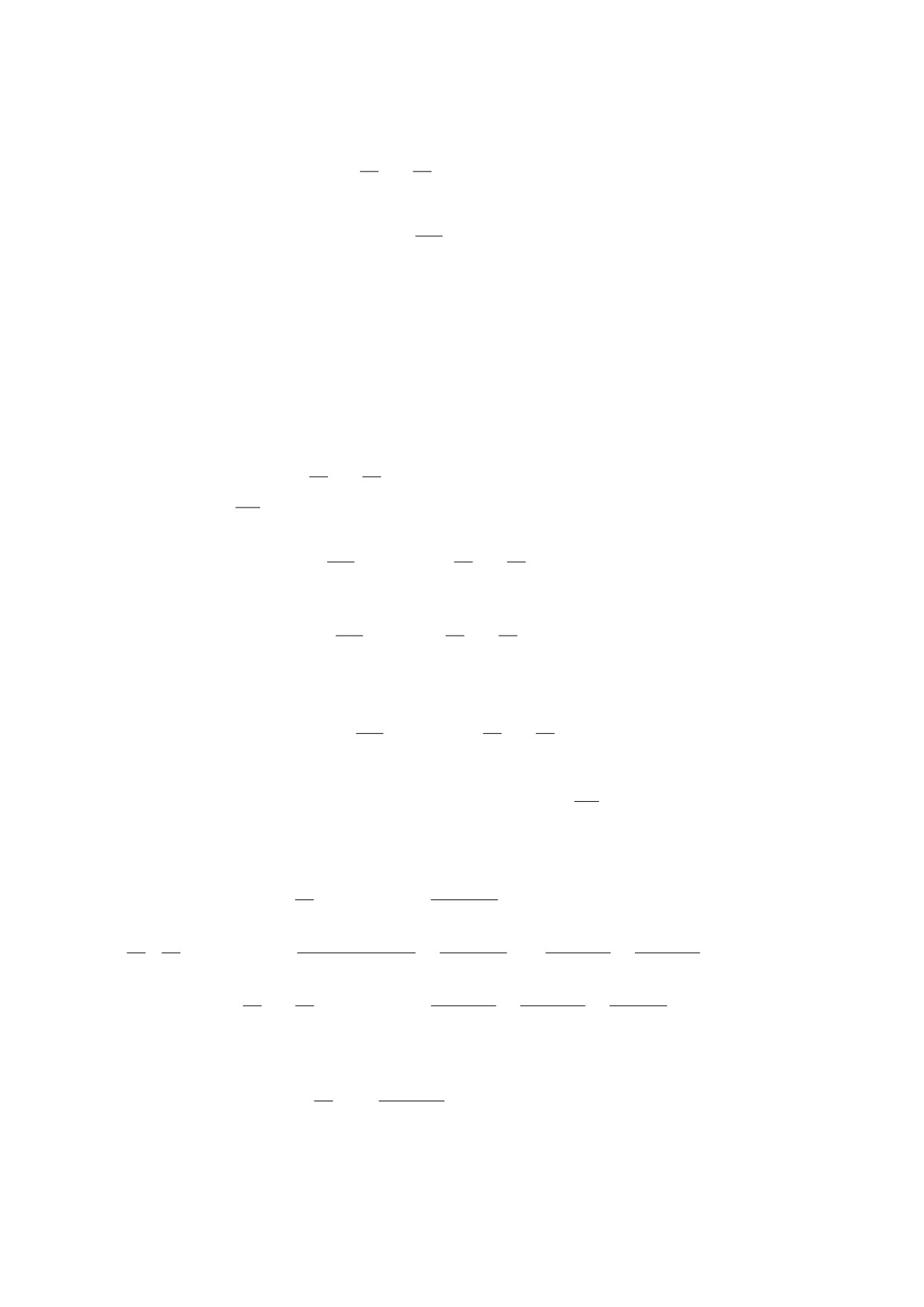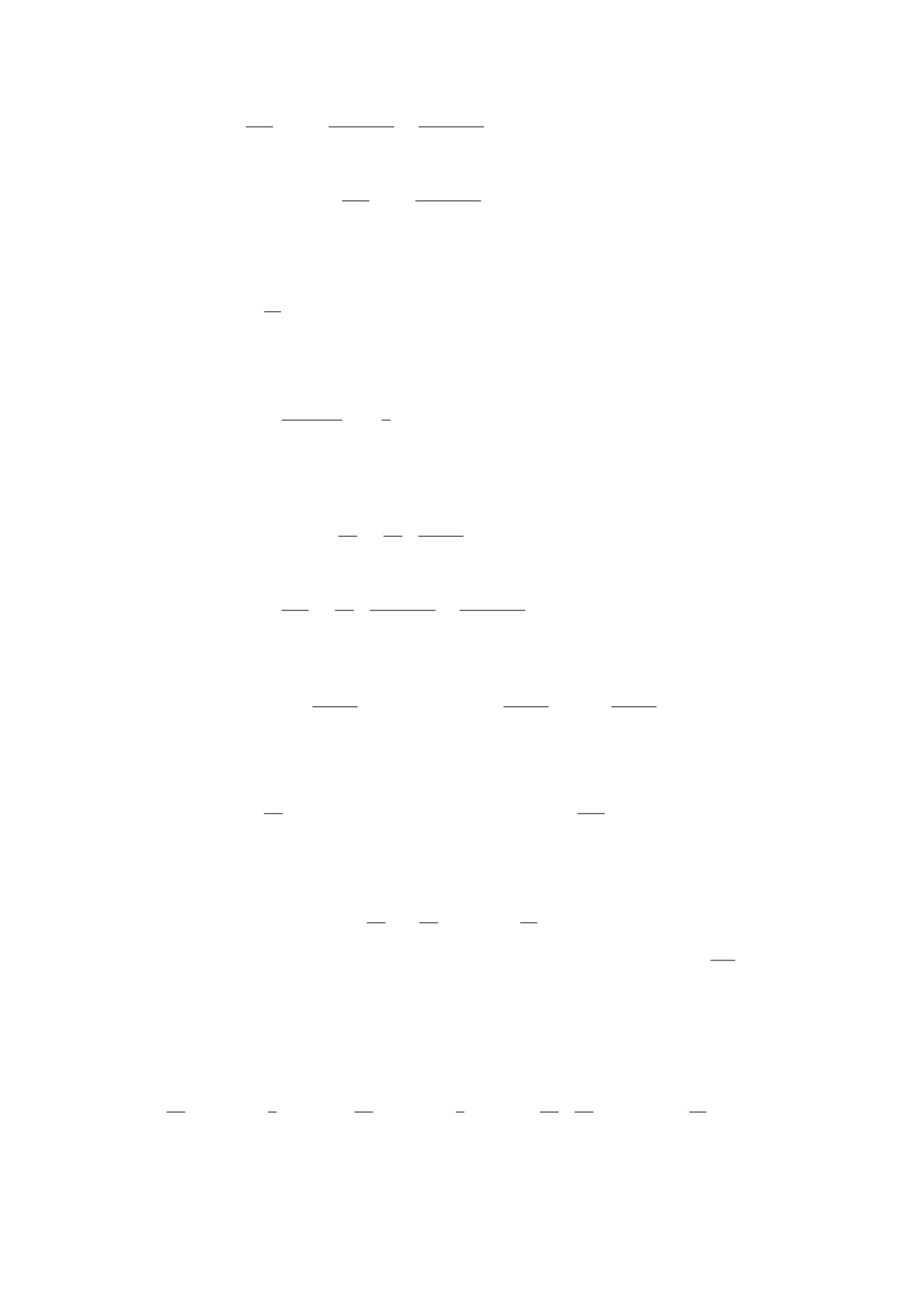ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 3, с.326-337
УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
УДК 517.956
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
СУЩЕСТВОВАНИЯ КЛАССИЧЕСКОГО РЕШЕНИЯ
НЕОДНОРОДНОГО БИГАРМОНИЧЕСКОГО УРАВНЕНИЯ
© 2021 г. Г. Э. Гришанина, Э. М. Мухамадиев
Доказано, что необходимым и достаточным условием существования в ограниченной плос-
кой области классического решения у неоднородного бигармонического уравнения являет-
ся требование усиленной непрерывности функции, стоящей в правой части уравнения.
DOI: 10.31857/S0374064121030043
1. Постановка задачи. Рассмотрим задачу о существовании классического решения неод-
нородного бигармонического уравнения
Δ2u(x,y) = f(x,y), (x,y) ∈ G,
(1)
где Δ - оператор Лапласа, G - ограниченная область в R2, а f(x, y) - непрерывная в G
функция. Напомним [1-5], что функция u(x, y) называется классическим решением уравне-
ния (1), если она в области G имеет все непрерывные частные производные до 4-го порядка
включительно и удовлетворяет уравнению (1). Очевидно, что если уравнение (1) имеет клас-
сическое решение, то функция f(x, y) является непрерывной функцией. Однако существуют
непрерывные функции f(x, y), при которых уравнение (1) не имеет классических решений.
Возникает вопрос, каким дополнительным условиям, кроме непрерывности, должна удовле-
творять функция f(x, y), чтобы уравнение (1) имело классическое решение. Ответ на этот
вопрос для уравнения Пуассона получен в работе [6], а для неоднородной системы Коши-
Римана - в работе [7].
Отметим, что наличие свойства гладкости решения важно не только для качественной
теории дифференциальных уравнений, но имеет практические приложения, например, при
приближённом построении решения дифференциального уравнения и оценке точности при-
ближённого решения.
2. Необходимое условие существования классического решения. Определим мно-
жество
G= {(x,y,s) ∈ R3 : M = (x,y) ∈ G, |s| < ρ(M, ∂G)},
где ρ(M, ∂G) - расстояние от точки M до границы ∂G области G, и функцию
g(x, y, s, ϕ) = f(x + s cos ϕ, y + s sin ϕ)
на
G × [0,2π]. Очевидно, эта функция непрерывна по совокупности переменных. Комплекс-
нозначная функция
∫2π
Fk(x,y,s) = g(x,y,s,ϕ)exp(ikϕ)dϕ, k ∈ Z \ {0},
0
определена и непрерывна на множестве
G, и для неё справедливо равенство
Fk(x, y, 0) = 0, (x, y) ∈ G.
326
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
327
Определим функции
∫r1
ds
1
fk(x,y,r) = Fk(x,y,s)
,
0 < r ≤ r1(x,y) ≡
ρ(M, ∂G).
s
2
r
Определение. Непрерывную функцию f(x,y) назовём k-усиленно непрерывной, если
функция fk(x, y, r) имеет непрерывное продолжение на множество {(x, y, 0) : (x, y) ∈ G} ⊂G.
Непрерывная по Гёльдеру функция является k-усиленно непрерывной для любого k. Бо-
лее общее, чем непрерывность по Гёльдеру, достаточное условие k-усиленной непрерывности
функции f(x, y) даёт следующая оценка для функции Fk(x, y, r):
|Fk(x, y, r)| ≤ C(1 + | ln r|)ν , ν < -1, C = const > 0,
0 < r ≤ r1(x,y).
Теорема 1. Если уравнение (1) имеет в области G классическое решение, то функция
f (x, y) является k-усиленно непрерывной при k = 2 и k = 4 в этой области.
Прежде чем перейти к доказательству теоремы, сформулируем и докажем несколько вспо-
могательных утверждений. Пусть функция u(x, y), (x, y) ∈ G, имеет в области G непрерыв-
ные частные производные до m-го порядка включительно. Определим функцию
v(x, y, r, ϕ) = u(x + r cos ϕ, y + r sin ϕ)
G×[0,2π]икомплекснозначныефункции
на множестве
∫2π
Uk(x,y,r) = v(x,y,r,ϕ)exp(ikϕ)dϕ, (x,y,r) ∈G.
0
Так как подынтегральная функция на множестве
G× [0,2π] имеет непрерывные по сово-
купности переменных частные производные по r до порядка m включительно, то функции
Uk(x,y,r) имеют в области
G непрерывные частные производные по r до m-го порядка
включительно.
Лемма 1. Пусть функция u(x, y) непрерывна в области G вместе со всеми частными
производными до m-го порядка включительно. Тогда при любом 0 < k ≤ m для функции
Uk(x,y,r) справедливы равенства
∂Uk
∂k-1Uk
Uk(x,y,0) =
(x, y, 0) = . . . =
(x, y, 0) = 0,
(2)
∂r
∂rk-1
и равномерно на каждом компактном подмножестве области G имеют место предельные
соотношения
k!
(k - 1)! ∂Uk(x, y, r)
1 ∂k-1Uk(x,y,r)
∂kUk
lim
Uk(x,y,r) = lim
= ... = lim
=
(x, y, 0).
(3)
r→0 rk
r→0
rk-1
∂r
r→0 r
∂rk-1
∂rk
Доказательство. В силу непрерывной дифференцируемости функции u(x, y) в области
G справедливы представления
2
∂v
∂2v
r
v(x, y, r, ϕ) = u(x, y) +
(x, y, 0, ϕ)r +
(x, y, 0, ϕ)
+...
∂r
∂r2
2!
∫
1
k-1
∂k-1v
r
rk
∂kv
...+
(x, y, 0, ϕ)
+
(1 - s)k-1
(x, y, rs, ϕ) ds,
(4)
∂rk-1
(k - 1)!
(k - 1)!
∂rk
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
3∗
328
ГРИШАНИНА, МУХАМАДИЕВ
∂qv
∂qv
∂q+1v
∂q+2v
r2
(x, y, r, ϕ) =
(x, y, 0, ϕ) +
(x, y, 0, ϕ)r +
(x, y, 0, ϕ)
+...
∂rq
∂rq
∂rq+1
∂rq+2
2!
∫
1
k-q-1
∂k-1v
r
rk-q
∂kv
...+
(x, y, 0, ϕ)
+
(1 - s)k-q-1
(x, y, rs, ϕ) ds,
(5)
∂rk-1
(k - q - 1)!
(k - q - 1)!
∂rk
0
где 0 < q < k и
∑
∂lv
∂lu
l!
(x, y, r, ϕ) =
Cj
cosl-j ϕ sinj ϕ, Cjl =
,
∂rl
l ∂xl-j∂yj
j!(l - j)!
j=0
∂lu
∂lu
=
(x + r cos ϕ, y + r sin ϕ).
∂xl-j∂yj
∂xl-j∂yj
Так как
1
1
cos ϕ =
(exp(iϕ) + exp(-iϕ)), sin ϕ =
(exp(iϕ) - exp(-iϕ))
2
2i
и
2π
{
∫
0,
если p = 0,
exp(ipϕ) dϕ =
2π,
если p = 0,
0
то при 0 ≤ j ≤ l < k имеем
2π
∫
cosl-j ϕ sinj ϕ exp(ikϕ) dϕ = 0.
(6)
0
Из представлений (4) и (5) и равенства (6) следует, что
∫2π
∫
2π
Uk(x,y,0) = u(x,y)exp(ikϕ)dϕ = u(x,y) exp(ikϕ)dϕ = 0,
0
0
∫
2π
∂Uk
∂v
(x, y, 0) =
(x, y, 0, ϕ) exp(ikϕ) dϕ = 0, . . . ,
∂r
∂r
0
2π
∫
∂k-1Uk
∂k-1v
(x, y, 0) =
(x, y, 0, ϕ) exp(ikϕ) dϕ = 0.
∂rk-1
∂rk-1
0
Равенства (2) доказаны.
В силу (2) и представлений (4) и (5) получаем
2π
∫
1
∫
k
r
∂kv
Uk(x,y,r) =
(1 - s)k-1
(x, y, rs, ϕ) exp(ikϕ) ds dϕ,
(k - 1)!
∂rk
0
0
∫
2π
∫1
∂qUk
rk-q
∂kv
(x, y, r) =
(1 - s)k-q-1
(x, y, rs, ϕ) exp(ikϕ) ds dϕ, q = 1, k - 1.
(7)
∂rq
(k - q - 1)!
∂rk
0
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
329
Из равенств (7), согласно правилу Лопиталя, имеем
∫
2π
∫
1
Uk(x,y,r)
∂kv
lim
k! = k lim
(1 - s)k-1
(x, y, rs, ϕ) exp(ikϕ) ds dϕ =
r→0
rk
r→0
∂rk
0
0
∫2π
∂kv
=
(x, y, 0, ϕ) exp(ikϕ) dϕ,
∂rk
0
2π
1
∫
∫
(k - 1)! ∂Uk
∂kv
lim
(x, y, r) = (k - 1) lim
(1 - s)k-2
(x, y, rs, ϕ) exp(ikϕ) ds dϕ =
r→0
rk-1
∂r
r→0
∂rk
0
0
∫2π
∂kv
=
(x, y, 0, ϕ) exp(ikϕ) dϕ, . . . ,
∂rk
0
∫
2π
∫
1
1 ∂k-1Uk(x,y,r)
∂kv
lim
= lim
(x, y, rs, ϕ) exp(ikϕ) ds dϕ =
r→0 r
∂rk-1
r→0
∂rk
0
0
∫2π
∂kv
=
(x, y, 0, ϕ) exp(ikϕ) dϕ.
∂rk
0
Равенства (3) доказаны. Лемма доказана.
Пусть функция u(x, y), (x, y) ∈ G, имеет в области G непрерывные частные производные
до 4-го порядка включительно. Положим
f (x, y) = Δ2u(x, y), (x, y) ∈ G.
(8)
По функциям
g(x, y, r, ϕ) = f(x + r cos ϕ, y + r sin ϕ), v(x, y, r, ϕ) = u(x + r cos ϕ, y + r sin ϕ),
w(x, y, r, ϕ) = (Δu)(x + r cos ϕ, y + r sin ϕ)
на множестве
G × [0,2π] определим комплекснозначные функции
∫2π
Fk(x,y,r) = g(x,y,r,ϕ)exp(ikϕ)dϕ,
0
∫2π
Uk(x,y,r) = v(x,y,r,ϕ)exp(ikϕ)dϕ, (x,y,r) ∈G, k = 1,4,
0
∫2π
Vk(x,y,r) = w(x,y,r,ϕ)exp(ikϕ)dϕ, (x,y,r) ∈G, k = 1,2.
0
Отметим, что функции Fk(x, y, r) непрерывны по совокупности переменных, а функции
Vk(x,y,r) и Uk(x,y,r) имеют непрерывные частные производные по всем переменным до 2-го
и 4-го порядка включительно соответственно.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
330
ГРИШАНИНА, МУХАМАДИЕВ
Лемма 2. Справедливы тождества
)
2
∂
(1∂3Uk
3 ∂2Uk
5 - 2k
∂Uk
4(4 - k2)
(4 - k2)(16 - k2)
Fk(x, y, r) = r
+
+
+
Uk
+
Uk,
(9)
∂r r ∂r3
r2 ∂r2
r3
∂r
r4
r4
)
∂
(1∂Vk
2Vk
(4 - k2)
Fk(x, y, r) = r
+
+
Vk,
(10)
∂r r ∂r
r2
r2
где Uk = Uk(x, y, r), k = 1, 4, Vk = Vk(x, y, r), k = 1, 2, и (x, y, r) ∈G, r = 0.
Доказательство. Используя определение (8) функции f(x, y), несложно проверить, что
функция g(x, y, r, ϕ) удовлетворяет тождеству
)
2
∂4v
2∂3v
1 ∂2v
1 ∂v
∂
(2 ∂2v
2 ∂v
v
1 ∂4v
g(x, y, r, ϕ) =
+
-
+
+
-
+4
+
,
(11)
∂r4
r ∂r3
r2 ∂r2
r3 ∂r
∂ϕ2
r2 ∂r2
r3 ∂r
r4
r4 ∂ϕ4
где (x, y, r, ϕ) ∈G×[0, 2π], r = 0. Умножим тождество (11) на exp(ikϕ) и получившееся тож-
дество проинтегрируем от 0 до 2π, воспользовавшись следующим свойством гладких 2π-пе-
риодических по ϕ функций v(x, y, r, ϕ):
∫
2π
∫
2π
∂lv
exp(ikϕ) dϕ = (-ik)l v exp(ikϕ) dϕ, l ∈ N,
∂ϕl
0
0
которое следует из легко проверяемого тождества
)
)
∂lv
∂
(∂l-1
v
(∂l-1
v
exp(ikϕ) =
exp(ikϕ)
- ik
exp(ikϕ)
∂ϕl
∂ϕ
∂ϕl-1
∂ϕl-1
Поменяв местами порядок интегрирования по ϕ и дифференцирования по r, получим
4
∂4Uk
2∂3Uk
2k2 + 1 ∂2Uk
2k2 + 1 ∂Uk
4k2 - k
Fk(x, y, r) =
+
-
+
-
Uk.
(12)
∂r4
r ∂r3
r2
∂r2
r3
∂r
r4
Нетрудно видеть, что правые части равенств (9) и (12) совпадают между собой при r = 0:
)
2
∂
(1∂3Uk
3 ∂2Uk
5 - 2k
∂Uk
4(4 - k2)
(4 - k2)(16 - k2)
r
+
+
+
Uk
+
Uk =
∂r r ∂r3
r2 ∂r2
r3
∂r
r4
r4
2
∂4Uk
1∂3Uk
3∂3Uk
6 ∂2Uk
5 - 2k
∂2Uk
=
-
+
-
+
-
∂r4
r ∂r3
r ∂r3
r2 ∂r2
r2
∂r2
3(5 - 2k2) ∂Uk
4(4 - k2) ∂Uk
16(4 - k2)
(4 - k2)(16 - k2)
−
+
-
Uk +
Uk =
r3
∂r
r3
∂r
r4
r4
4
∂4Uk
2∂3Uk
2k2 + 1 ∂2Uk
2k2 + 1 ∂Uk
4k2 - k
=
+
-
+
-
Uk.
∂r4
r ∂r3
r2
∂r2
r3
∂r
r4
Тождество (9) доказано.
Аналогично устанавливается тождество (10). Лемма доказана.
Доказательство теоремы 1. 1) Рассмотрим случай k = 2. Из тождества (10) при k = 2
имеем
)
∂
(1∂V2
2V2
F2(x,y,r) = r
+
(13)
∂r r ∂r
r2
Разделив равенство (13) на r и проинтегрировав его по отрезку [r, r1],
0 < r < r1(x,y) =
= 2-1ρ(M,∂G), получим
∫r1
ds
1 ∂V2
2
1 ∂V2
2
f2(x,y,r) ≡
F2(x,y,s)
=
(x, y, r1)+
V2(x,y,r1)-
(x, y, r)-
V2(x,y,r). (14)
s
r1 ∂r
r21
r ∂r
r2
r
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
331
Согласно лемме 1 имеем
)
(1 ∂
2
∂2V1
lim
V1(x,y,r) +
V1(x,y,r)
=2
(x, y, 0).
(15)
r→0
r ∂r
r2
∂r2
Следовательно, в силу (15) из тождества (14) следует, что функция f2(x, y, r) продолжается
по непрерывности в точку r = 0, причём сходимость lim
f2(x,y,r) = f2(x,y,0) равномерна
r→0
на каждом компакте из области G.
2) Пусть k = 4. В силу леммы 2 имеем
)
∂
(1∂3U4
3 ∂2U4
27 ∂U4
48
F4(x,y,r) = r
+
-
-
U4
,
∂r r ∂r3
r2 ∂r2
r2 ∂r
r4
где U4 = U4(x, y, r), (x, y) ∈ G,
0 < r ≤ r1(x,y) ≡ ρ(M,∂G)/2. Разделив это равенство на r
и проинтегрировав его по отрезку [r, r1], получим
∫r1
ds
1 ∂3U4(x,y,r1)
3
∂2U4(x,y,r1)
27
∂U4(x,y,r1)
f4(x,y,r) =
F4(x,y,s)
=
+
-
-
s
r1
∂r3
r2
∂r2
r3
∂r
1
1
r
48
1 ∂3U4(x,y,r)
3 ∂2U4(x,y,r)
27 ∂U4(x, y, r)
48
−
U4(x,y,r1) -
-
+
+
U4(x,y,r).
r41
r
∂r3
r2
∂r2
r3
∂r
r4
Из леммы 1 следует, что существуют пределы
U4(x,y,r)
1 ∂4U4(x,y,0)
1
∂lU4(x,y,r)
1
∂4U4(x,y,0)
lim
=
,
lim
=
,
l = 1,3,
r→0
r4
4!
∂r4
r→0 r4-l
∂rl
(4 - l)!
∂r4
причём сходимость равномерна относительно (x, y) из компактного подмножества области
G. Следовательно, функция f4(x, y, r) продолжается по непрерывности в точку r = 0 и
сходимость lim
f4(x,y,r) = f4(x,y,0) равномерна на каждом компакте из области G. Теорема
r→0
доказана.
3. Достаточное условие существования классического решения. Предположим,
что функция f(x, y) непрерывна и интегрируема (например, ограничена: |f(x, y)| ≤ const) в
области G. Тогда функция
∫∫
1
u0(x,y) =
f (ξ, η)r2 ln r dξ dη, r2 = (x - ξ)2 + (y - η)2,
8π
G
имеет непрерывные частные производные до третьего порядка включительно и является обоб-
щённым решением уравнения (1).
При этих предположениях о функции f(x, y) необходимые условия существования класси-
ческого решения уравнения (1) являются и достаточными, а именно, справедлива следующая
Теорема 2. Пусть функция f(x, y) интегрируема и k-усиленно непрерывна при k = 2 и
k = 4 в области G. Тогда функция u0(x,y) является классическим решением уравнения (1).
Для доказательства теоремы удобно выразить операции дифференцирования по x и y
через дифференциальный оператор Коши-Римана и сопряжённый к нему оператор. Пусть
z = x + iy, z = x - iy. Тогда
(
)
(
)
(
)
∂
1
∂
∂
∂
1
∂
∂
∂
∂
∂
∂
∂
∂
=
+i
,
=
-i
и
=
+
,
=i
-
∂z
2
∂x
∂y
∂z
2
∂x
∂y
∂x
∂z
∂z
∂y
∂z
∂z
Из этих формул следует, что
)4
(
)3
(
)2(
)2
∂4
( ∂
∂
( ∂)4
∂
∂
∂
∂
( ∂)( ∂)3
( ∂)4
=
+
=
+4
+6
+4
+
,
∂x4
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
332
ГРИШАНИНА, МУХАМАДИЕВ
)3
(
)3
∂4
( ∂
∂
)( ∂
∂
(( ∂)4
∂
∂
( ∂)( ∂)3
( ∂)4)
=i
-
+
=i
+2
-2
-
,
∂y∂x3
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
)2(
)2
(
)2(
)2
∂4
( ∂
∂
∂
∂
(( ∂)4
∂
∂
( ∂)4)
=i2
-
+
=-
-2
+
,
∂y2∂x2
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
)3(
)
(
)3
∂4
( ∂
∂
∂
∂
(( ∂)4
∂
∂
( ∂)( ∂)3
( ∂)4)
=i3
-
+
= -i
-2
+2
-
,
∂y3∂x
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
)4
(
)3
(
)2(
)2
∂4
( ∂
∂
( ∂)4
∂
∂
∂
∂
( ∂)( ∂)3
( ∂)4
=
-
=
-4
+6
-4
+
∂y4
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
∂z
Таким образом, все частные производные 4-го порядка представляют собой линейные комби-
нации произведений степеней (∂/∂z)k(∂/∂z)l оператора Коши-Римана и сопряжённого к нему
оператора, где k + l = 4, l = 0, 4.
Ниже нам понадобятся действия этих дифференциальных операторов на функции вида
K(zz), где K(u) - гладкая функция скалярного аргумента u > 0. Нетрудно проверить, что
справедливы следующие формулы:
( ∂)4
( ∂)3 ∂
K(zz) = KIV (zz)z4,
K(zz) = KIV (zz)z3 z + 3K′′′(zz)z2,
∂z
∂z
∂z
( ∂)2( ∂)2
K(zz) = KIV (zz)z2 z2 + 4K′′′(zz)zz + 2K′′(zz),
∂z
∂z
∂
( ∂)3
( ∂)4
K(zz) = KIV (zz)zz3 + 3K′′′(zz)z2,
K(zz) = KIV (zz)z4,
∂z
∂z
∂z
где через K′, K′′, K′′′, KIV обозначены производные первого, второго, третьего и четвёртого
порядка от функции K(u) по переменной u > 0 соответственно.
Например, для функции K(u) = u ln u имеем
1
1
2
K′(u) = ln u + 1, K′′(u) =
,
K′′′(u) = -
,
KIV (u) =
u
u2
u3
и, следовательно,
( ∂)4
z
( ∂)3 ∂
1
( ∂)2( ∂)2
K(zz) = 2
,
K(zz) = -
,
K(zz) = 0,
∂z
z3
∂z
∂z
z2
∂z
∂z
∂
( ∂)3
1
( ∂)4
z
K(zz) = -
,
K(zz) = 2
∂z
∂z
z2
∂z
z3
Рассмотрим несобственный интеграл в смысле главного значения Коши с сингулярным
ядром (ζ - z)k|ζ - z|-k-2 :
∫∫
∫∫
1
f (ζ)(ζ - z)k
1
f (ζ)(ζ - z)k
fk(z) ≡
dξ dη =
lim
dξ dη,
(16)
π
|ζ - z|k+2
π
ε→0
|ζ - z|k+2
G
G\U(z,ε)
где U(z, ε) - круг с центром в точке z радиуса ε. Заметим, что для вещественной функции
f (z) несобственный интеграл (16) существует или не существует одновременно для значения
±k, k = 0.
Следующее утверждение устанавливает связь между свойством k-усиленной непрерывно-
сти и существованием и непрерывностью функции fk(z).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
333
Лемма 3. Пусть непрерывная функция f(z) = f(x, y) является k-усиленно непрерывной
в области G и принадлежит пространству Лебега L1(G). Тогда несобственный интеграл
fk(z) существует во всех точках области z ∈ G, предельное соотношение (16) выполняется
равномерно на каждом компакте K ⊂ G и функция fk(z) непрерывна в G.
Доказательство. Нетрудно проверить, что для функций f(z) = f(x, y), принадлежащих
пространству Лебега L1(G), при r0 > 0 интеграл
∫∫
f (ζ)(ζ - z)k
dξ dη
|ζ - z|k+2
G\U(z,r0)
определяет непрерывную функцию в G. Пусть K ⊂ G - компакт, r0 = 2-1 min ρ(z, ∂G) и
z∈K
z ∈ K - фиксированная точка. При 0 < ε ≤ r0 имеем
∫∫
∫∫
∫∫
f (ζ)(ζ - z)k
f (ζ)(ζ - z)k
f (ζ)(ζ - z)k
dξ dη =
dξ dη +
dξ dη.
(17)
|ζ - z|k+2
|ζ - z|k+2
|ζ - z|k+2
G\U(z,ε)
G\U(z,r0)
U (z,r0)\U(z,ε)
Переходя к полярным координатам ζ - z = reiθ в последнем слагаемом в правой части (17),
получаем
∫∫
∫∫
∫
r0
∫
2π
f (ζ)(ζ - z)k
f (ζ)(ζ - z)k
dr
dξ dη =
dξ dη +
f (z + reiθ)eikθ dθ
(18)
|ζ - z|k+2
|ζ - z|k+2
r
G\U(z,ε)
G\U(z,r0)
ε
0
Поскольку
r0
2π
r0
∫
∫
∫
dr
dr
f (z + reiϕ)eikϕ dϕ
= Fk(z,r)
= fk(z,ε) - fk(z,r0),
r
r
ε
0
ε
то из (18) следует равенство
∫∫
∫∫
f (ζ)(ζ - z)k
f (ζ)(ζ - z)k
dξ dη =
dξ dη + fk(z, ε) - fk(z, r0), z ∈ K.
(19)
|ζ - z|k+2
|ζ - z|k+2
G\U(z,ε)
G\U(z,r0)
Так как функция f является k-усиленно непрерывной, то равномерно по z ∈ K суще-
ствует предел
lim
fk(z,ε) = fk(z,0).
ε→0
Таким образом, из равенства (19) следует, что предельное соотношение (16) выполняется
равномерно на каждом компакте K ⊂ G и имеет место представление
∫∫
1
f (ζ)(ζ - z)k
1
fk(z) =
dξ dη +
(fk(z, 0) - fk(z, r0)), z ∈ K.
π
|ζ - z|k+2
π
G\U(z,r0)
Отсюда следует утверждение леммы. Лемма доказана.
Рассмотрим общее представление вида
∫R
∂
w(z, δ) =
L(ρ, δ) · h(z, ρ) dρ,
(20)
∂ρ
0
где функция h(z, ρ) непрерывна на множестве G × (0, 1], а вещественнозначная функция
L(ρ, δ) непрерывна на множестве [0, R] × (0, 1] и удовлетворяет условиям:
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
334
ГРИШАНИНА, МУХАМАДИЕВ
1) L(0, δ) ≡ 0, lim L(ρ, δ) = 1 при ρ ∈ (0, R];
δ→0
2) (∂/∂ρ)L(ρ, δ) непрерывна и неотрицательна при ρ > 0, δ ∈ (0, 1].
Справедлива
Лемма 4. Пусть сходимость
lim h(z, ρ) = h(z, 0)
ρ→0
имеет место равномерно по z на каждом компактном подмножестве области G. Тогда
справедливо равенство
lim w(z, δ) = h(z, 0),
δ→0
сходимость в котором равномерна по z на каждом компактном подмножестве области G.
Доказательство. Пусть G1 ⊂ G1 ⊂ G. По ε > 0 выберем σ ∈ (0, R) такое, что
ε
|h(z, ρ) - h(z, 0)| <
при
0 < ρ < σ, z ∈ G1.
3
Из представления (20) вытекают равенства
∫R
∂
w(z, δ) - h(z, 0) =
L(ρ, δ)(h(z, ρ) - h(z, 0)) dρ + h(z, 0)(L(R, δ) - L(0, δ)) - h(z, 0) =
∂ρ
0
∫σ
∫
R
∂
∂
= h(z, 0)(L(R, δ) - 1) +
L(ρ, δ)(h(z, ρ) - h(z, 0)) dρ +
L(ρ, δ)(h(z, ρ) - h(z, 0)) dρ.
∂ρ
∂ρ
0
σ
Здесь использовано условие L(0, δ) ≡ 0. Положим M = max{|h(z, ρ)| : z ∈ G1,
0 ≤ ρ ≤ R}.
В силу условия 1) существует δ0 > 0 такое, что
0 < L(R,δ) - L(σ,δ) ≤ |L(R,δ) - 1| + |1 - L(σ,δ)| < ε/(6M), δ < δ0.
Используя условие 2) для функции L(ρ, δ), имеем оценку
ε
|w(z, δ) - h(z, 0)| ≤ M|L(R, δ) - 1| + K(σ, δ)
+ 2M(L(R, δ) - L(σ, δ)) <
3
(
)
2
ε
ε
ε
ε
ε
1
1
<
+
+
+ 2M
<
+1+
+1
= ε,
6
3
6M
6M
3
2
2
если ε < M, 0 < δ < δ0 и z ∈ G1. Лемма доказана.
Доказательство теоремы 2. Рассмотрим семейство функций
∫∫
1
uδ(x,y) =
f (ξ, η)(r2 + δ) ln(r2 + δ) dξ dη, δ > 0, r2 = (x - ξ)2 + (y - η)2.
16π
G
Функции uδ(x, y) при каждом δ > 0 бесконечно дифференцируемы на всей плоскости.
Несложно видеть, что все частные производные ∂k+luδ(x, y)/∂xk∂yl при δ → 0 равномер-
но сходятся к соответствующим частным производным ∂k+lu0(x, y)/∂xk ∂yl, если k + l ≤ 3.
Поэтому для доказательства существования непрерывных частных производных четвёртого
порядка у функции u0(x, y) достаточно показать, что функции ∂4uδ(x, y)/∂xk ∂yl, где k + l =
= 4, при δ → 0 равномерно на каждом компакте области G сходятся к некоторым функциям
4
∂
wkl(x,y) = lim
uδ(x,y), k + l = 4.
(21)
δ→0 ∂xk∂yl
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
335
В силу приведённых выше замечаний существование равномерных пределов (21) равносильно
существованию равномерных пределов
)l
( ∂)k( ∂
lim
uδ(z), k + l = 4,
(22)
δ→0
∂z
∂z
где
∫∫
1
uδ(z) ≡ uδ(x,y) =
f (ζ)K(r2 + δ) dξ dη,
16π
G
δ > 0, z = x + iy, ζ = ξ + iη, r2 = |z - ζ|2, K(u) = ulnu.
Согласно лемме Гейне-Бореля при δ → 0 пределы (22) существуют равномерно по z на
любом компактном подмножестве области G тогда и только тогда, когда они равномерно
сходятся по z в некоторой окрестности любой точки области G. Поэтому теорема 2 будет
доказана, если мы покажем существование равномерного предела (22) в некоторой окрестности
любой точки области G.
Пусть z0 ∈ G и число d удовлетворяет условию 0 < 3d ≤ ρ(z0, ∂G), обозначим U(z, d) =
= {ζ : |ζ - z| < d}. Для |z - z0| ≤ d имеем
( ∂)k( ∂)l
uδ(z) = Jk1(z,δ) + Jk2(z,δ),
(23)
∂z
∂z
где l = 4 - k, k = 0, 4, и
∫∫
1
( ∂)k( ∂)l
Jk1(z,δ) =
f (ζ)
K(r2 + δ) dξ dη,
16π
∂z
∂z
G\U(z,d)
∫∫
1
( ∂)k( ∂)l
Jk2(z,δ) =
f (ζ)
K(r2 + δ) dξ dη.
16π
∂z
∂z
U (z,d)
Нетрудно показать, что имеет место равенство
∫∫
1
( ∂)k( ∂)l
lim
Jk1(z,δ) =
f (ζ)
K(r2) dξ dη,
(24)
δ→0
16π
∂z
∂z
G\U(z,d)
сходимость в котором равномерна по z ∈ U(z0, d). Поэтому для доказательства теоремы доста-
точно показать, что при δ → 0 предел функции Jk2(z, δ), k = 0, 4, существует равномерно по
¯
¯
z ∈ U(z0,d). Так как имеют место тождества J02 ≡
J
42, J12 ≡
J
32, то достаточно рассмотреть
случаи k = 2, 3, 4.
В силу равенств
( ∂)4
2(z - ζ)4
K(r2 + δ) =
,
r2 = |z - ζ|2,
∂z
(r2 + δ)3
(
)
∂
( ∂)3
2(z - ζ)3(z
ζ)
3(z - ζ)2
2r2
3
K(r2 + δ) =
-
=
-
(z - ζ)2,
∂z
∂z
(r2 + δ)3
(r2 + δ)2
(r2 + δ)3
(r2 + δ)2
( ∂)2( ∂)2
2r4
4r2
2
K(r2 + δ) =
-
+
,
∂z
∂z
(r2 + δ)3
(r2 + δ)2
(r2 + δ)
переходя к полярным координатам ζ - z = ρ exp(iθ), для функции Jk2(z, δ) при k = 4, 3, 2
имеем
∫
d
∫
2π
1
ρ5
J42(z,δ) =
f (z + ρ exp(iθ)) exp(4iθ) dθ dρ,
(25)
8π
(ρ2 + δ)3
0
0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
336
ГРИШАНИНА, МУХАМАДИЕВ
∫
d
∫
2π
(
)
1
2ρ2
3
J32(z,δ) =
-
ρ3f(z + ρexp(iθ))exp(2iθ)dθ dρ,
(26)
16π
(ρ2 + δ)3
(ρ2 + δ)2
0
0
∫
d
∫
2π
1
2δ2ρ
J22(z,δ) =
f (z + ρ exp(iθ)) dθ dρ.
(27)
16π
(ρ2 + δ)3
0
0
Вследствие условия k-усиленной непрерывности функции f(z) = f(x, y) при k = 2, 4,
функции
∫
d
∫
2π
ds
f (z + s exp(iθ)) exp(ikθ) dθ = fk(z, ρ) - fk(z, d)
(28)
s
ρ
0
непрерывны по ρ на отрезке [0, d], дифференцируемы при ρ > 0 и
∫
2π
dfk(z, ρ)
1
=-
f (z + ρ exp(iθ)) exp(ikθ) dθ.
(29)
dρ
ρ
0
Воспользовавшись интегрированием по частям, равенства (25), (26) в силу (28) и (29) за-
пишем в виде
∫
d
(
)3
1
∂
ρ2
J42(z,δ) =
(f4(z, ρ) - f4(z, d)) dρ,
(30)
8π
∂ρ ρ2 + δ
0
∫
d
(
)
1
∂
2ρ6
3ρ4
J32(z,δ) =
-
(f2(z, ρ) - f2(z, d)) dρ.
(31)
16π
∂ρ (ρ2 + δ)3
(ρ2 + δ)2
0
Каждая из функций
(
)3
(
)3
(
)2
2
ρ
ρ2
ρ2
L(ρ, δ) =
и L(ρ,δ) = 3
-2
ρ2 + δ
ρ2 + δ
ρ2 + δ
на множестве [0, R] × (0, 1], где R = d, удовлетворяет условиям 1) и 2). Поэтому из представ-
лений (30), (31) и леммы 4 следует, что имеют место следующие равенства:
1
1
lim
J42(z,δ) =
(f4(z, 0) - f4(z, d)), lim
J32(z,δ) = -
(f2(z, 0) - f2(z, d)),
δ→0
8π
δ→0
16π
причём сходимость в них равномерна на круге |z - z0| ≤ d.
Из равенства (27) вытекает, что равномерно по z ∈ U(z0, d) имеет место сходимость
)2
( ∂)2( ∂
1
lim
uδ(z) =
f (z).
δ→0
∂z
∂z
16
Таким образом, установлено существование предела функции Jk2(z, δ), k = 0, 4, при δ →
→ 0 равномерного по z ∈ U(z0,d). Поэтому из представления (23) и равенства (24) следует
существование равномерного по z ∈ U(z0, d) предела (22), что и требовалось доказать. Теоре-
ма 2 доказана.
Замечание. Из приведённого доказательства вытекает, что для частных производных
(∂/∂z)k (∂/∂z)lu0(z) функции u0(z) справедливы представления
( ∂)4
1
( ∂)4
1
∂
( ∂)3
1
u0(z) =
f4(z),
u0(z) =
f-4(z),
u0(z) = -
f2(z),
∂z
8
∂z
8
∂z
∂z
16
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
НЕОБХОДИМОЕ И ДОСТАТОЧНОЕ УСЛОВИЕ
337
( ∂)2( ∂)2
1
( ∂)3 ∂
1
u0(z) =
f (z),
u0(z) = -
f-2(z),
∂z
∂z
16
∂z
∂z
16
или для частных производных (∂/∂x)k(∂/∂y)lu0(x, y) функции u0(x, y) - представления
(
)4
∂
1
u0(x,y) =
[f4(z) + f-4(z) - 2f2(z) - 2f-2(z) + 3f(z)],
∂x
8
(
)4
∂
1
u0(x,y) =
[f4(z) + f-4(z) + 2f2(z) + 2f-2(z) + 3f(z)],
∂y
8
(
)3(
)
∂
∂
i
u0(x,y) =
[f-4(z) - f4(z) + f2(z) - f-2(z)],
∂x
∂y
8
(
)2(
)2
∂
∂
1
u0(x,y) =
[f(z) - f4(z) - f-4(z)],
∂x
∂y
8
(
)(
)3
∂
∂
i
u0(x,y) =
[f4(z) - f-4(z) + f2(z) - f-2(z)].
∂x
∂y
8
Пример. Функция, определённая формулой
⎧
⎨0,
если (x, y) = (0, 0),
f (x, y) =
x2y2
⎩
,
если 0 < x2 + y2 ≤ 3/4,
(x2 + y2)2| ln(x2 + y2)|β
при β > 0 непрерывна в замкнутой области G = {(x, y) : x2 + y2 ≤ 3/4}. В этой области
уравнение Пуассона Δy = f(x, y) имеет классическое решение при любом β > 0, а уравнение
Δ2y = f(x,y) не имеет классического решения при β ≤ 1 и имеет классическое решение при
β > 1.
Так как всякое обобщённое решение однородного уравнения Δ2(u) = 0 в области G явля-
ется бесконечно дифференцируемой функцией (см., например, [5]), то из теоремы 2 следует
Теорема 3. В условиях теоремы 2 каждое обобщённое решение уравнения (1) в области
G является классическим решением этого уравнения в этой области.
Доказательство этой теоремы аналогично доказательству теоремы 5 из работы [6].
СПИСОК ЛИТЕРАТУРЫ
1. Тихонов А.Н., Самарский А.А. Уравнения математической физики. М., 1977.
2. Берс Л., Джон Ф., Шехтер М. Уравнения с частными производными. М., 1966.
3. Михайлов В.П. Дифференциальные уравнения в частных производных. М., 1983.
4. Владимиров В.С. Уравнения математической физики. М., 1976.
5. Олейник О.А. Лекции об уравнениях с частными производными. М., 2005.
6. Мухамадиев Э.М., Гришанина Г.Э., Гришанин А.А. О применении метода регуляризации к постро-
ению классического решения уравнения Пуассона // Тр. Ин-та математики и механики УрО РАН.
2015. Т. 21. № 4. С. 196-211.
7. Байзаев С., Гришанина Г.Э., Мухамадиев Э. О необходимых и достаточных условиях существова-
ния классического решения неоднородной системы Коши-Римана // Дифференц. уравнения. 2018.
Т. 54. № 2. С. 215-227.
Государственный университет “Дубна”, г. Дубна,
Поступила в редакцию 22.07.2020 г.
Вологодский государственный университет
После доработки 22.07.2020 г.
Принята к публикации 11.12.2020 г.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021