ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 3, с.338-348

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956.6

ЗАДАЧА ТРИКОМИ

ДЛЯ ОПЕРЕЖАЮЩЕ-ЗАПАЗДЫВАЮЩЕГО

УРАВНЕНИЯ ЛАВРЕНТЬЕВА-БИЦАДЗЕ

Исследуется задача Трикоми для опережающе-запаздывающего уравнения смешанного

типа. Доказаны теоремы единственности и существования дважды непрерывно дифферен-

цируемого решения.

DOI: 10.31857/S0374064121030055

Введение. Учёт последствия и преддействия в классических задачах математической фи-

зики приводит к уравнениям с сосредоточенным или функциональным карлемановским или

некарлемановским запаздыванием и опережением по временной и (или) пространственной пе-

ременным. Такие уравнения позволяют провести глубокий и достаточно полный качественный

анализ реальных гидродинамических [1] систем (вихреобразование, перемежаемость, форми-

рование сложных когерентных пятен); построить теорию многослойных оболочек и пластин [2],

теорию плазмы [3]; изучить колебания кристаллической решётки [4].

В предлагаемой работе исследуется аналог задачи Трикоми для обобщённого уравнения

Лаврентьева-Бицадзе с сосредоточенным некарлемановским запаздыванием и опережением

по пространственной координате вида

∑

(sgn y)U_xx(x, y) +

an+n1 U_yy(x - nτ,y) = 0

(1)

n=-n₁

в области D = D⁺

^⋃D^-, где D⁺ = {(x,y) : 0 < x < (n₂ + 1)τ, y > 0} = ⋃n2k=0 D^k и D^- =

⋃n2

k=0

Dγn2k - эллиптическая и гиперболическая части области D, причём D^k = {(x,y) : kτ <

< x < (k + 1)τ, y > 0} (k = -n₁,n₂); n₁,n₂ ∈ N; τ = const > 0, an+n1 ≡ const; Dγn2k =

= {(x, y) : -y + kτγn2 < xγn2 < y + (k + 1)τγn2 ,

-γn2 τ/2 < y < 0} (k = -n₁,n₂ + 1);

0 < γ₀ < γ₁ < ... < γn2; γ2j (j = 0,n₂) - действительные собственные значения матрицы

коэффициентов системы уравнений, к которой приводится уравнение (1).

Пусть D_k = D+k

^⋃D-k ⋃I_k (k = -n₁,n₂ + 1); I = ⋃n2+1n=-n

I_n, I_n = {(x,y) : nτ < x <

⋃n2-1

< (n + 1)τ, y = 0}; J =

Jk =

{(x, y) : x = (k + 1)τ, y > 0}. Тогда D =

k=0

⋃n2

D_k)

^⋃(⋃n2-1j=0 J_j).

k=0

1. Постановка задачи. Однозначная разрешимость. Не ограничивая общности, для

наглядности и упрощения записи рассмотрим уравнение (1) при n₁ = n₂ = 1, т.е. рассмотрим

уравнение

(sgn y)U_xx(x, y) + a₀U_yy(x + τ, y) + a₁U_yy(x, y) + a₂U_yy(x - τ, y) = 0,

(2)

где (x, y) ∈ D = D₀

^⋃D₁⋃J₀.

Задача T. Найти в области D = D₀

^⋃D1 ⋃J₀ решение U(x,y) ∈ C(D)^⋂C²(D \ J₀)

уравнения (2), удовлетворяющее условиям

U (x, y) = r(x, y), (x, y) ∈ D-1;

(3)

U (x, y) = ρ(x, y), (x, y) ∈ D₂;

(4)

338

ЗАДАЧА ТРИКОМИ

339

lim U(x, y) = 0,

0 ≤ x ≤ 2τ;

(5)

y→+∞

U (x, γ_j (kτ - x)) = ψ_k(x), kτ ≤ x ≤ (2k + 1)τ/2 (j, k = 0, 1);

(6)

условиям сопряжения

U (x, 0-) = U(x, 0+) = ω(x),

0 ≤ x ≤ 2τ,

(7)

U_y(x,0-) = U_y(x,0+) = ν(x),

0 < x < 2τ, x = τ,

(8)

причём

√

ψ₀(0) = r(0,0); r(x,+∞) = ρ(x,+∞) = 0, γ_j = a₁ + (-1)^ja₀ (j = 0,1),

(9)

где r(x, y), ρ(x, y), ψ_k(x) - заданные непрерывные достаточно гладкие функции; ω(x), ν(x)

и γ_j - искомые функции и собственные значения, которые находятся в процессе решения

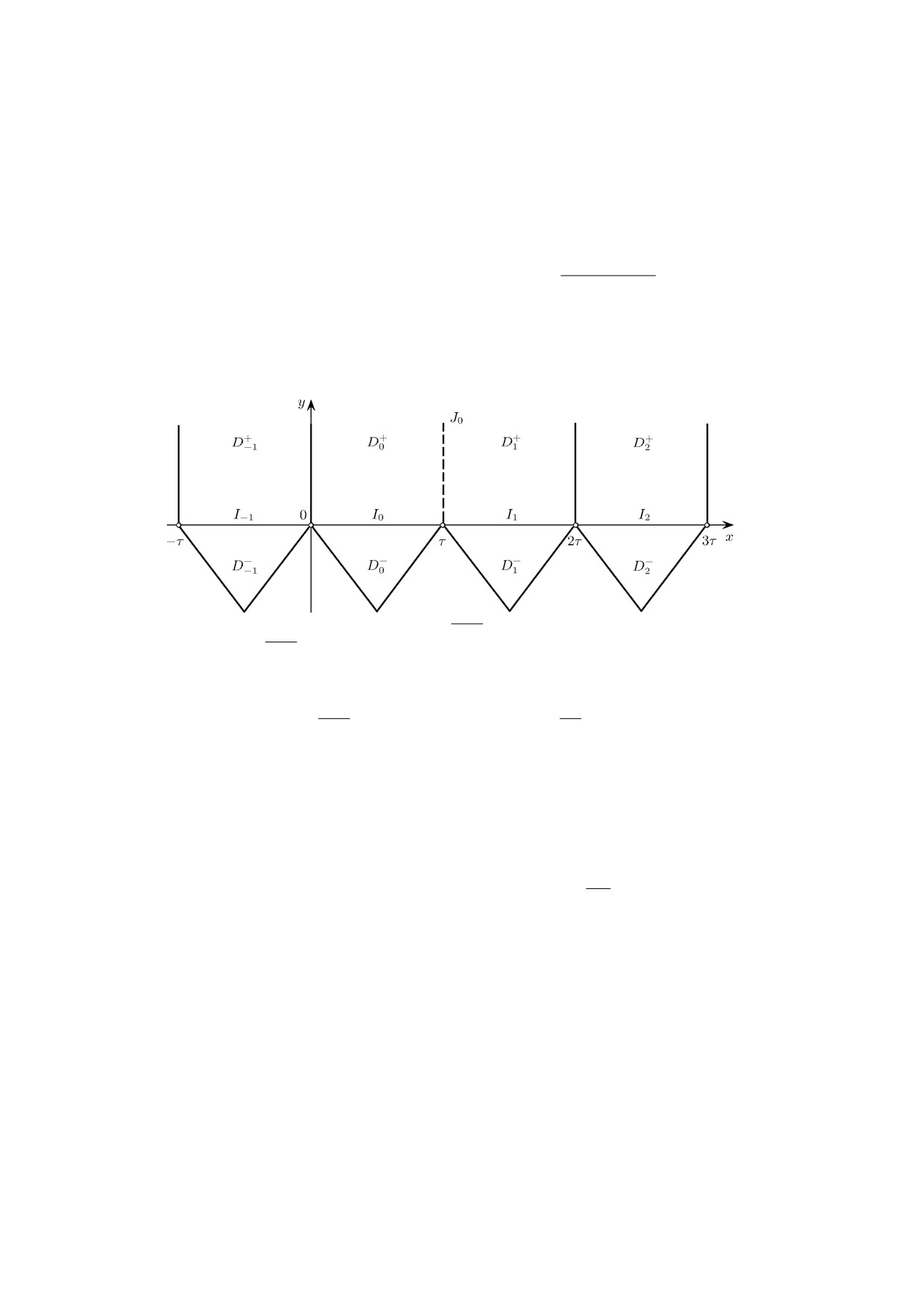
задачи. Области D и D-1, D₂ показаны на рисунке.

Рисунок. Области D_k = D+k

^⋃ D-k , k = -1,2; область D = D0 ^⋃ D1 ^⋃ J0; интер-

⋃₂

валы I_k, k = -1, 2; I =

I_k; луч J0.

k=-1

Теорема. Если имеют место включения

⋂

r(x, y) ∈ C(D-1)

C⁴(D-1), ρ(x,y) ∈ C(D₂)

C⁴(D₂),

⋂

ψ_k(x) ∈ C[kτ,(2k + 1)τ/2]

C²(kτ,(2k + 1)τ/2) (k = 0,1),

справедливо равенство a₀ = a₂ и выполняются соотношения a₁ > a₀ > 0; r(0,y) = ρ(2τ,y),

y ≥ 0; ψ₀(0) = r(0,0); r(x,+∞) = ρ(x,+∞) = 0,

0 ≤ x ≤ 2τ, то существует единственное

решение U(x,y) задачи T.

Доказательство. В терминах функций

U_j(x,y) = U(x,y), (x,y) ∈ D_j (j = -1,2),

(10)

уравнение (2) представим с учётом условий (3), (4) в виде системы уравнений смешанного

типа, определённых соответственно в областях D₀ и D₁ :

(sgn y)U0xx(x, y) + a₀U1yy(x + τ, y) + a₁U0yy(x, y) = -a₂r_yy(x - τ, y), (x, y) ∈ D₀,

(sgn y)U1xx(x, y) + a₁U1yy(x, y) + a₂U0yy(x - τ, y) = -a₀ρ_yy(x + τ, y), (x, y) ∈ D₁.

Заменяя во втором уравнении системы x на x + τ, получаем

(sgn y)U0xx(x, y) + a₀U1yy(x + τ, y) + a₁U0yy(x, y) = -a₂r_yy(x - τ, y), (x, y) ∈ D₀,

(11)

(sgn y)U1xx(x + τ, y) + a₁U1yy(x + τ, y) + a₂U0yy(x, y) = -a₀ρ_yy(x + 2τ, y), (x, y) ∈ D₀.

(12)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

340

ЗАРУБИН

Пусть a₀ = a₂ и

q_j(x,y) = (U₀(x,y) + (-1)^jU₁(x + τ,y))/2 (j = 0,1).

(13)

Тогда, складывая и вычитая уравнения (11), (12), на основании (13) и (9) приходим к системе

уравнений смешанного типа

(sgn y)q_jxx(x, y) + γ2jq_jyy(x, y) = -a₀f_j(x, y), (x, y) ∈ D₀,

(14)

где

f_j(x,y) = (r_yy(x - τ,y) + (-1)^jρ_yy(x + 2τ,y))/2 (j = 0,1).

(15)

Множество решений неоднородных уравнений Лаврентьева-Бицадзе (14) содержит все ре-

шения уравнения (2), которые можно выделить в силу (13), (10), используя соотношение

U (x, y) = U₀(x, y) = q₀(x, y) + q₁(x, y), (x, y) ∈ D₀,

(16)

или

U (x, y) = U₁(x, y) = q₀(x - τ, y) - q₁(x - τ, y), (x, y) ∈ D₁.

(17)

Таким образом, поставленная задача редуцируется к двум задачам Трикоми для уравнения

(14) относительно функции q_j(x, y) ∈ C(D₀)

^⋂C²(D₀), причём q_j(x,y), согласно (13), (3)-(8)

и равенствам

U₀(0,y) = U₀(τ,y) = U₁(τ,y) = U₁(2τ,y) = r(0,y) = ρ(2τ,y),

должны удовлетворять граничным условиям

q_j(0,y) = q_j(τ,y) = r_j(y) ≡ r(0,y) + (-1)^jρ(2τ,y), y ≥ 0;

(18)

lim

q_j(x,y) = 0,

0≤x≤τ;

(19)

y→+∞

q_j(x,γ_j(-x)) = ψ_j(x) ≡ ψ₀(x) + (-1)^jψ₁(x + τ),

0 ≤ x ≤ τ/2;

(20)

q_j(x,0-) = q_j(x,0+) = ω_j(x) ≡ ω(x) + (-1)^jω(x + τ),

0≤x≤τ;

(21)

q_jy(x,0-) = q_jy(x,0+) = ν_j(x) ≡ ν(x) + (-1)^jν(x + τ),

0<x<τ.

(22)

Здесь и далее j = 0, 1.

Единственность решения задачи T для уравнения (2) в области D следует из того,

что однородная задача T имеет только тривиальное решение U(x, y) ≡ 0 в D, поскольку

эквивалентна однородной задаче T для уравнения

(sgn y)q_jxx(x, y) + γ2jq_jyy(x, y) = 0, (x, y) ∈ D₀,

(23)

при однородных условиях (18)-(20), имеющей только тривиальное решение q_j (x, y) ≡ 0 в D₀.

Доказательство этого факта основано на установлении знакоопределённости интеграла

∫τ

β_j = ω_j(x)ν_j(x)dx.

Лемма 1. Если q_j(x, y) - решение уравнения (23) в области D⁺⁰, принадлежащее классу

C(D⁺⁰)

^⋂C²(D⁺⁰) и обращающееся в нуль при x = 0, x = τ (y ≥ 0) и y → +∞ (0 ≤ x ≤ τ),

то

β_j ≤ 0

(24)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ТРИКОМИ

341

∫∫

γ2jβ_j +

[q2jx(x, y) + γ2jq2jy(x, y)] dx dy = 0.

(25)

D⁺

Доказательство проводится известным методом Трикоми [5, с. 491-493; 6, с. 128-130].

Лемма 2. Если q_j (x, y) ∈ C(D-0)

^⋂C²(D-0) - решение уравнения (23) в области D-0,

обращающееся в нуль на характеристике y = -γ_jx

(0 ≤ x ≤ τ/2), то

β_j ≥ 0.

(26)

Доказательство проводится аналогично [5, с. 491-493; 6, с. 128-130].

Из неравенств (24), (26) следует, что β_j = 0, а потому в силу (25) имеем равенство

∫∫

[q2jx(x, y) + γ2jq2jy(x, y)] dx dy = 0,

D⁺⁰

из которого следует, что q_jx(x, y) = q_jy(x, y) ≡ 0, т.е. q_j(x, y) ≡ const в D⁺⁰. Однородность

граничных условий в D⁺⁰ и включение q_j(x, y) ∈ C(D⁺⁰) позволяют утверждать, что q_j(x, y) ≡

≡ 0 в D+0 . Значит, q_j(x,0) ≡ 0, 0 ≤ x ≤ τ. Последнее тождество в совокупности с однородным

условием (20) обеспечивают тривиальность решения q_j(x, y) ≡ 0 первой задачи Дарбу в D-0.

Из доказанной тривиальности решений q_j(x, y) в D⁺⁰ и D-0 вытекает тривиальность решения

q_j(x,y) ≡ 0 в D₀. Таким образом, единственность решения задачи Трикоми для уравнения

(14) и граничных условий (18)-(20) в области D₀ доказана.

Тривиальность решения однородной задачи T для уравнения (2) и граничных условий

(3)-(6) в области D следует из того, что q_j(x, y) ≡ 0 в D₀, и равенств (16), (17): U(x, y) =

= U_j(x,y) ≡ 0, (x,y) ∈ D_j. Это означает единственность решения задачи T для уравнения

(2) и граничных условий (3)-(6) в области D.

Доказательство существования решения U(x, y) задачи T в области D для урав-

нения (2) основано на решениях q_j(x, y) задач в области эллиптичности D⁺⁰ и в области

гиперболичности D-0 для уравнения (14).

Задача Неймана-Дирихле. Найти в области D⁺⁰ решение q_j(x, y) ∈ C(D⁺⁰)

^⋂C²(D⁺⁰)

уравнения (14)

q_jxx(x,y) + γ2jq_jyy(x,y) = -a₀f_j(x,y), (x,y) ∈ D⁺⁰,

(27)

удовлетворяющее условиям (18), (19), (22).

Задача Дарбу. Найти в области D-0 решение q_j(x, y) ∈ C(D-0)

^⋂C²(D-0) уравнения (14)

q_jxx(x,y) - γ2jq_jyy(x,y) = a₀f_j(x,y), (x,y) ∈ D-0,

(28)

удовлетворяющее условиям (20), (22).

Вопрос о существовании решения q_j(x,y) задачи Трикоми для уравнения (14) в области

D₀ связан с разрешимостью сингулярного интегрального уравнения относительно функции

ν_j(x), 0 < x < τ, которое будет получено из функциональных соотношений между функциями

ω_j(x) и ν_j(x), привнесённых на линию изменения типа y = 0,

0 < x < τ решениями задачи

Неймана-Дирихле из D⁺⁰ и задачи Дарбу из D-0.

Лемма 3. Если имеют место включения r_j(y) ∈ C[0, +∞)

^⋂C²(0,+∞), ν_j(x) ∈ C¹(0,τ)

и соотношение lim

r_j(y) = 0, то существует единственное решение задачи Неймана-

y→+∞

Дирихле q_j(x, y) ∈ C(D⁺⁰)

^⋂C²(D⁺⁰). Это решение представимо в виде

∫τ

∫

a₀

q_j(x,y) = -γ_j

ν_j(ζ)M_j(x,y;ζ,0)dζ -

dz f_j(ζ, 0)M_j (x, y; ζ, z) dζ +

2γ_j

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

342

ЗАРУБИН

∫

a₀

f_j(ζ,z)M_j(x,y;ζ,z)dζ +

dz f_j(ζ, z + y)M_j (x, 0; ζ, z) dζ +

2γ_j

∫

[

πx

ch (π(y - t)/γ_j τ)

sin

r_j(t)

γ_jτ

ch (2π(y - t)/γ_j τ) - cos(2πx/τ)

]

ch (π(y + t)/γ_j τ)

dt, (x, y) ∈ D⁺⁰,

(29)

ch (2π(y + t)/γ_j τ) - cos(2πx/τ)

где

ch (π(z + y)/γ_j τ) - cos(π(ζ + x)/τ)

M_j(x,y;ζ,z) =

2π

ch (π(z + y)/γ_j τ) - cos(π(ζ - x)/τ)

Доказательство. Решение задачи Неймана-Дирихле для уравнения (27) будем искать в

виде суммы решений

q_j(x,y) = qj1(x,y) + qj2(x,y)

(30)

двух вспомогательных задач, где функция qj1(x, y) удовлетворяет уравнению

qj1xx(x,y) + γ2jqj1yy(x,y) = -a₀f_j(x,y), (x,y) ∈ D⁺⁰,

(31)

и условиям

qj1(0,y) = qj1(τ,y) = 0, y ≥ 0,

(32)

lim

qj1(x,y) = 0,

0≤x≤τ,

(33)

y→+∞



∂qj1(x,y)



= ν_j(x),

0<x<τ;

(34)



∂y

y=0

а функция qj2(x, y) - уравнению

qj2xx(x,y) + γ2jqj2yy(x,y) = 0, (x,y) ∈ D⁺⁰,

(35)

и условиям

qj2(0,y) = qj2(τ,y) = r_j(y), y ≥ 0,

(36)

lim

qj2(x,y) = 0,

0≤x≤τ,

(37)

y→+∞



∂qj2(x,y)



= 0,

0<x<τ.

(38)



∂y

y=0

Решение первой вспомогательной задачи (31)-(34) будем искать в виде ряда

∑

nπ

qj1(x,y) =

C_nj(y)sin(μ_nx), (x,y) ∈ D⁺⁰, μ_n =

(39)

n=1

удовлетворяющего условиям (32), предполагая его равномерную сходимость в D⁺⁰ и равно-

мерную сходимость в D⁺⁰ рядов, полученных из него почленным дифференцированием по x

и y дважды.

Подстановка ряда (39) в уравнение (31) приводит к разложению в ряд Фурье по синусам

правой части уравнения (31), а его обращение - к уравнению

∫

μ2n

a₀

2a₀

C^′′nj(y) -

C_nj(y) = -

f_jn(y) ≡ -

f_j(ζ,y)sin(μ_nζ)dζ, y > 0,

(40)

γ2j

τγ²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ТРИКОМИ

343

в котором в силу (33), (34), (39) функции C_nj (y) удовлетворяют соотношениям

lim

C_nj(y) = 0,

(41)

y→+∞

∫

C^′nj(0) =

ν_j(ζ)sin(μ_nζ)dζ;

(42)

причём, согласно (40), (15) и условиям теоремы, справедливо равенство

lim

f_jn(y) = 0.

(43)

y→+∞

Общее решение уравнения (40), удовлетворяющее условию (41), запишем в виде

∫

a₀

C_nj(y) = k_ne-μny/γj +

f_jn(ζ)e-μn(ζ-y)/γj dζ, y > 0, k_n ≡ const,

(44)

2γ_j μ_n

так как абсолютная сходимость интеграла в (44) вместе с соотношением (43) и правилом Ло-

питаля позволяют утверждать, что

∫

a₀

lim

C_nj(y) =

lim eμny/γj

f_jn(ζ)e-μnζ/γj dζ =

y→+∞

2γ_j μ_n

y→+∞

a₀

-f_jn

(y)e-μny/γj

a₀

lim

f_jn(y) = 0.

2γ_j μ_n

y→+∞ -μ_nγ-1je^-μn^y/γ

2μ2n

y→+∞

Подстановка в (44) значения k_n, которое найдено с помощью условия (42), приводит к

решению C_nj(y) уравнения (40), удовлетворяющему условиям (41), (42) и имеющему вид

∫

γ_j

a₀

C_nj(y) = -

C^′nj(0)e-μny/γj +

f^′jn(z)e-μn(z+y)/γj dz +

μ_n

2μ2n

∫

a₀

f_jn(z + y)e-μnz/γj dz, y > 0.

(45)

2γ_j μ_n

Равенство (39) вместе с (45), (40), (42) и формулой 5.4.12.6 из [7] для суммирования рядов

приводит к искомому решению задачи (31)-(34):

∫

∑

qj1(x,y) =

C_nj(y)sin(μ_nx) = -γ_j ν_j(ζ)M_j(x,y;ζ,0)dζ -

n=1

∫

a₀

f_j(ζ,0)M_j(x,y;ζ,z)dζ +

dz f_j(ζ, z)M_j (x, y; ζ, z) dζ +

2γ_j

∫

a₀

dz f_j(ζ, z + y)M_j (x, 0; ζ, z) dζ,

(46)

2γ_j

где M_j (x, y; ζ, z) определено в формулировке леммы 3.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

4^∗

344

ЗАРУБИН

Решение второй вспомогательной задачи (35)-(38) будем искать, используя косинус-

преобразование Фурье, удовлетворяющее условиям (37), (38):

+∞

qj2(x,y) =

(A_j (λ)eλγj x + B_j(λ)e-λγj x) cos(λy) dλ, (x, y) ∈ D⁺⁰.

(47)

Для нахождения функций A_j (λ) и B_j(λ) воспользуемся краевыми условиями (36), т.е.

+∞

qj2(0,y) = r_j(y) =

(A_j (λ) + B_j (λ)) cos(λy) dλ,

+∞

qj2(τ,y) = r_j(y) =

(A_j (λ)eλγj τ + B_j(λ)e-λγj τ ) cos(λy) dλ.

Так как r_j(y) - функция ограниченной вариации на [0,+ ∞), r_j(+∞) = 0, то, обратив

косинус-преобразование Фурье, получим

∫

A_j(λ) + B_j(λ) =

r_j(t)cos(λt)dt,

∫

A_j(λ)eλγj τ + B_j(λ)e-λγj τ =

r_j(t)cos(λt)dt.

Поэтому

∫

-λγ_j τ

11-e

1eλγjτ -1

A_j(λ) =

r_j(t)cos(λt)dt, B_j(λ) =

r_j(t)cos(λt)dt.

π sh(λγ_jτ)

π sh (λγ_jτ)

Значит,

∫

2 ch (λγ_j (2x - τ)/2)

A_j(λ)eλγj x + B_j(λ)e-λγj x =

r_j(t)cos(λt)dt.

π ch (λγ_j τ/2)

Заменяя подынтегральную функцию в (47) согласно последнему равенству и применяя

формулу 1.9.(12) из [8], получаем искомое решение qj2(x, y) задачи (35)-(38):

∫

[

πx

ch (π(y - t)/γ_j τ)

qj2(x,y) =

sin

r_j(t)

γ_jτ

ch (2π(y - t)/γ_j τ) - cos(2πx/τ)

]

ch (π(y + t)/γ_j τ)

dt, (x, y) ∈ D⁺⁰.

(48)

ch (2π(y + t)/γ_j τ) - cos(2πx/τ)

Таким образом, решение задачи Неймана-Дирихле (27), (18), (19), (22) в силу (30), (46),

(48) имеет вид (29).

Функциональное соотношение между функциями ω_j(x) и ν_j(x), привнесённое из D⁺⁰

на линию изменения типа y = 0,

0 ≤ x ≤ τ, найдём из решения задачи Неймана-Дирихле

(29), полагая в нём y = 0 и дифференцируя:

∫

γ_j

ω^′j(x) =

ν_j(ζ)[ctg (π(ζ - x)/2τ) - ctg (π(ζ + x)/2τ)]dζ + δ_j(x),

0<x<τ,

(49)

2τ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ТРИКОМИ

345

где

∫

[

a₀

sin(π(ζ + x)/τ)

δ_j(x) =

[2f_j (ζ, z) - f_j(ζ, 0)]

4τγ_j

ch (πz/γ_j τ) - cos(π(ζ + x)/τ)

]

sin(π(ζ - x)/τ)

dζ +

ch (πz/γ_j τ) - cos(π(ζ - x)/τ)

∫

2π

πx

ch (πt/γ_j τ)[sh²(πt/γ_j τ) - sin²(πx/τ)]

cos

r_j(t)

dt,

γ_jτ²

[ch²(πt/γ_j τ) - cos²(πx/τ)]²

причём δ_j (x) ∈ C¹[0, τ].

Лемма 4. Если выполняются включения ν_j(x) ∈ C¹(0, τ), ψ_j(x) ∈ C[0, τ/2]

^⋂C²(0,τ/2)

и равенство ψ_j (0) = r_j(0), то существует единственное решение q_j (x, y) ∈ C(D-0 )

^⋂C²(D-0)

задачи Дарбу. Это решение имеет вид

∫

q_j(x,y) = γ_j

ν_j(ζ)dζ - ψ_j(0) + ψ_j((x - y/γ_j)/2) + ψ_j((x + y/γ_j)/2) - B_j(x,y) +

+ B_j((x - y/γ_j)/2,-γ_j(x - y/γ_j)/2) + B_j((x + y/γ_j)/2,-γ_j(x + y/γ_j)/2), (x,y) ∈ D-0 ,

(50)

где

∫

a₀

B_j(x,y) =

f_j(ζ,t)dζ.

2γ_j

x-(y-t)/γ_j

Доказательство представления (50) вытекает из общего решения неоднородного уравне-

ния (28) колебаний струны

q_j(x,y) = Pj1(x - y/γ_j) + Pj2(x + y/γ_j) -

∫

a₀

f_j(ζ,t)dζ, (x,y) ∈ D-0, Pj1,Pj2 ∈ C²[0,τ],

2γ_j

x-(y-t)/γ_j

и краевых условий (20), (22).

Функциональное соотношение между функциями ω_j(x) и ν_j(x), привнесённое из D-0

на линию изменения типа y = 0, 0 ≤ x ≤ τ, найдём из решения (50) задачи Дарбу, полагая в

нём y = 0 и дифференцируя:

ω^′j(x) = γ_jν_j(x) - m_j(x),

0<x<τ,

(51)

где

∫

a₀

m_j(x) =

f_j(x + t/γ_j,t)dt - ψ^′j(x/2),

γ_j

причём m_j (x) ∈ C¹[0, τ].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

346

ЗАРУБИН

Вопрос о существовании решения задачи Трикоми (14), (18)-(20) в силу условий со-

пряжения (21), (22) и функциональных соотношений (49), (51) сведён к разрешимости сингу-

лярного интегрального уравнения

∫

ν_j(x) -

ν_j(ζ)[ctg (π(ζ - x)/2τ) - ctg (π(ζ + x)/2τ)]dζ = Θ_j(x),

0<x<τ,

(52)

2τ

которое после очевидного преобразований ядра запишем в виде

∫

sin(πζ/τ)dζ

ν_j(x) -

ν_j(ζ)

= Θ_j(x),

0<x<τ,

(53)

cos(πζ/τ) - cos(πx/τ)

где Θ_j(x) = (δ_j (x) + m_j (x))/γ_j .

Проведя в уравнении (53) замену переменных и функций по формулам

ν_j(x) = ν_j(y), Θ_j(x) = Θ_j(y), y = cos(πx/τ), t = cos(πζ/τ),

(54)

получим уравнение

∫

ν_j(y) -

ν_j(t)

= Θ_j(y),

-1 < y < 1.

(55)

t-y

−1

Переход от уравнения (53) к уравнению (55) законен ввиду монотонности функции cos(πx/τ),

0<x<τ.

Уравнение (55) является уравнением нормального типа [9, с. 177]. Его индекс [9, с. 101,

176] равен нулю. В силу единственности решения задачи Трикоми (14), (18)-(20) уравнение

(55) однозначно обратимо.

Регуляризацию сингулярного интегрального уравнения (55) проведём в классе

функций ν_j(y), удовлетворяющих условию Гёльдера при y ∈ (-1, 1), методом сингуляриза-

ции [10, 11].

Действуя на обе части уравнения (55) оператором

∫

Kϕ ≡ ϕ(s) +

ϕ(p)

p-s

−1

получаем

∫

[

∫

]

∫

ν_j(y) +

ν_j(p)

ν_j(t) +

ν_j(p)

dt = Θ_j(y) +

Θ_j(p)

p-y

t-y

p-t

p-y

−1

-1

где -1 < y < 1, т.е.

∫

ν_j(y) -

ν_j(p)

= Θ_j(y) +

Θj (p)

-1 < y < 1.

(56)

π²

t-y

p-t

p-y

−1

-1

Формула Пуанкаре-Бертрана [9, с. 63] позволяет поменять порядок интегрирования в син-

гулярном повторном интеграле с ядром Коши, а необходимые при этом преобразования при-

водят к решению уравнения (56) вида

∫

ν_j(y) =

Θ_j(y) +

Θj (p)

-1 < y < 1.

(57)

2π

p-y

−1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ТРИКОМИ

347

Возвращаясь к старым переменным и функциям по формулам (54), из уравнения (57)

получаем решение сингулярного интегрального уравнения (53):

∫

sin(πζ/τ)

ν_j(x) =

Θ_j(x) +

Θ_j(ζ)dζ,

0<x<τ,

2τ

cos(πζ/τ) - cos(πx/τ)

а следовательно, уравнения (52):

∫

ν_j(x) =

Θ_j(x) +

Θ_j(ζ)[ctg (π(ζ - x)/2τ) - ctg (π(ζ + x)/2τ)]dζ,

0<x<τ,

(58)

4τ

единственность которого устанавливается теоремой Нётера [9, с. 208].

Найденное в (58) представление функции ν_j (x) позволяет получить с помощью (49) или

(51) выражение для ω_j(x).

Подставляя ν_j (x) в (29) и (50), находим искомые решения q_j(x, y) задачи Неймана-

Дирихле (27), (18), (19), (22) в области D⁺⁰ и задачи Дарбу (28), (20), (22) в области D-0.

Таким образом, задача Трикоми (14), (18)-(20) решена в области D₀ = D⁺⁰

^⋃D-0⋃I₀.

Вернёмся к задаче Трикоми для опережающе-запаздывающего уравнения Лаврентьева-

Бицадзе (2) в области D₀.

Её решение в силу (16) и (29) имеет в области D⁺⁰ вид

∑

U (x, y) = U₀(x, y) = q₀(x, y) + q₁(x, y) =

q_j(x,y) =

j=0

{

∫

∑

a₀

-γ_j

ν_j(ζ)M_j(x,y;ζ,0)dζ -

dz f_j(ζ, 0)M_j (x, y; ζ, z) dζ +

2γ_j

j=0

∫

a₀

f_j(ζ,z)M_j(x,y;ζ,z)dζ +

dz f_j(ζ, z + y)M_j (x, 0; ζ, z) dζ +

2γ_j

∫

[

πx

ch (π(y - t)/γ_j τ)

sin

r_j(t)

γ_jτ

ch (2π(y - t)/γ_j τ) - cos(2πx/τ)

]

}

ch (π(y + t)/γ_j τ)

(x, y) ∈ D⁺⁰;

(59)

ch (2π(y + t)/γ_jτ) - cos(2πx/τ)

а в области D-0 согласно (16), (50) - вид

∑

U (x, y) = U₀(x, y) = q₀(x, y) + q₁(x, y) =

q_j(x,y) =

j=0

∫

∑

γ_j

ν_j(ζ)dζ - ψ_j(0) + ψ_j((x - y/γ_j)/2) + ψ_j((x + y/γ_j)/2) - B_j(x,y) +

j=0

}

+ B_j((x - y/γ_j)/2,-γ_j(x - y/γ_j)/2) + B_j((x + y/γ_j)/2,-γ_j(x + y/γ_j)/2)

(x, y) ∈ D-0; (60)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

348

ЗАРУБИН

где функции f_j(x, y), r_j (y), ψ_j (x), ν_j(x) (j = 0, 1) определяются равенствами (15), (18),

(20), (22) соответственно, причём ν_j(x) - решение сингулярного интегрального уравнения

(52), найденное в явной форме (58).

Решение задачи Трикоми для опережающе-запаздывающего уравнения Лаврентьева-Бица-

дзе (2) в области D₁ можно получить из представлений (59) и (60) для D⁺¹ и D-1 соот-

ветственно, если в них заменить x на x - τ. Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Шарковский А.Н., Майстренко Ю.А., Романенко Е.Ю. Разностные уравнения и их приложения.

Киев, 1986.

2. Онанов Г.Г., Скубачевский А.Л. Дифференциальные уравнения с отклоняющимися аргументами

в стационарных задачах механики деформируемого тела // Прикл. механика. 1979. Т. 15. № 5.

С. 39-47.

3. Самарский А.А. О некоторых проблемах теории дифференциальных уравнений // Дифференц.

уравнения. 1980. Т. 16. № 11. С. 1925-1935.

4. Маслов В.П. Операторные методы. М., 1973.

5. Франкль Ф.И. Избранные труды по газовой динамике. М., 1973.

6. Зарубин А.Н. Уравнения смешанного типа с запаздывающим аргументом. Орёл, 1997.

7. Прудников А.П., Брычков Ю.А., Маричев О.И. Интегралы и ряды. М., 1981.

8. Бейтман Г., Эрдейи А. Таблицы интегральных преобразований. М., 1969.

9. Гахов Ф.Д. Краевые задачи. М., 1977.

10. Флайшер Н.М. Новый метод решения в замкнутой форме для некоторых классов сингулярных

интегральных уравнений с регулярной частью // Rev. Roum. Math. Pures Appl. 1965. V. 10. № 5.

P. 615-620.

11. Бабурин Ю.С. О сингуляризации сингулярных интегральных уравнений // Дифференц. уравнения.

Рязань, 1977. Вып. 10. с. 3-11.

Орловский государственный университет

Поступила в редакцию 08.05.2020 г.

им. И.С. Тургенева

После доработки 08.05.2020 г.

Принята к публикации 11.12.2020 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021