ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 3, с.349-363

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

ЧЕТВЁРТОГО ПОРЯДКА

Для уравнения Бианки четвёртого порядка доказаны существование и единственность ре-

шения задачи Дарбу. Для задачи Дарбу определена функция Римана-Адамара, в терминах

которой и построено решение этой задачи.

DOI: 10.31857/S0374064121030067

Задача Дарбу для гиперболического уравнения второго порядка с двумя независимыми

переменными рассматривалась многими авторами. Можно указать, например, работы [1, гл. 3,

§ 1; 2-7].

В статье [8] для уравнения Бианки третьего порядка доказаны существование и единствен-

ность решения задачи Дарбу, а также определена функция Римана-Адамара, с помощью ко-

торой построено решение этой задачи.

В данной работе для уравнения Бианки четвёртого порядка доказаны существование и

единственность решения задачи Дарбу и определена функция Римана-Адамара. Уравнения

Бианки четвёртого и произвольного порядков рассматривались в работах [9-17].

1. Через C(k1,...,kn)(D), где k_i - фиксированные неотрицательные целые числа, i = 1, n,

обозначим класс функций u(x) = u(x₁, . . . , x_n), определённых в области D ⊂ Rⁿ и имеющих

в ней непрерывные производные ∂r1+...+rn u/∂xr11 . . . ∂xnn при всех 0 ≤ ri ≤ ki, i = 1, n.

Далее считаем, что в R⁴ задана декартова система координат Oxyzt.

Уравнением Бианки четвёртого порядка называют уравнение

L(u) ≡ u_xyzt + a₁₁₁₀u_xyz + a₁₁₀₁u_xyt + a₁₀₁₁u_xzt + a₀₁₁₁u_yzt + a₁₁₀₀u_xy + a₁₀₁₀u_xz + a₁₀₀₁u_xt +

+a₀₁₁₀uyz +a₀₁₀₁uyt +a₀₀₁₁uzt +a₁₀₀₀ux +a₀₁₀₀uy +a₀₀₁₀uz +a₀₀₀₁ut +a₀₀₀₀u = f(x,y,z,t). (1)

Коэффициенты уравнения (1) зависят от (x, y, z, t). Решение класса C(1,1,1,1)(D) уравнения

(1) назовём регулярным в области D.

Пусть D - область в R⁴, ограниченная плоскостями x = 0, y = 0, y = y₁ > 0, z = 0,

z = z₁ > 0, t = x, t = t₁ > 0. Считаем, что коэффициенты уравнения (1) удовлетворяют

условиям a_ijkl ∈ C(i,j,k,l)(D). Обозначим через X, Y, Z, S грани многогранника D при

x = 0, y = 0, z = 0, t = x соответственно.

Задача Дарбу. В области D найти регулярное решение уравнения (1), удовлетворяющее

граничным условиям

u|_X = ϕ₁(y, z, t), u|_Y = ϕ₂(x, z, t), u|_Z = ϕ₃(x, y, t), u|_S = ψ(x, y, z),

(2)

где ϕ_j , j = 1, 3, и ψ - заданные функции, для которых выполнены включения

ϕ₁ ∈ C(1,1,1)(X), ϕ₂ ∈ C(1,1,1)(Y ), ϕ₃ ∈ C(1,1,1)(Z), ψ ∈ C(1,1,1)(S)

и условия согласования

ϕ₁(y,0,t) = ϕ₃(0,y,t), ϕ₁(0,z,t) = ϕ₂(0,z,t), ϕ₂(x,0,t) = ϕ₃(x,0,t),

ϕ₁(y,z,0) = ψ(0,y,z), ϕ₂(x,z,x) = ψ(x,0,z), ϕ₃(x,y,x) = ψ(x,y,0).

349

350

МИРОНОВ

Следуя подходу из [1, гл. 3, § 1, п. 2^◦], докажем существование и единственность решения

задачи Дарбу. Формулу решения задачи Гурса [11; 9, § 3, п. 1, с. 49-51] будем рассматривать

как представление произвольного регулярного решения уравнения (1). Из указанной форму-

лы выведем интегральное уравнение Вольтерры второго рода для определения условия Гурса

u(x, y, z, t₁) на плоскости t = t₁; из существования и единственности решения этого инте-

грального уравнения будет следовать существование и единственность решения задачи Дарбу

(1), (2).

Задача Гурса. В области G = {x₀ < x < x₂, y₀ < y < y₂, z₀ < z < z₂, t₀ < t < t₂}

найти регулярное решение уравнения (1), удовлетворяющее условиям

u|X0 = θ₁(y, z, t), u|Y0 = θ₂(x, z, t), u|Z0 = θ₃(x, y, t), u|T0 = θ₄(x, y, z),

(3)

где θ_k, k = 1, 4, - заданные функции, для которых выполнены включения

θ₁ ∈ C(1,1,1)(X₀), θ₂ ∈ C(1,1,1)(Y₀), θ₃ ∈ C(1,1,1)(Z₀), θ₄ ∈ C(1,1,1)(T₀)

и условия согласования

θ₁(y₀,z,t) = θ₂(x₀,z,t), θ₁(y,z₀,t) = θ₃(x₀,y,t), θ₁(y,z,t₀) = θ₄(x₀,y,z),

θ₂(x,z₀,t) = θ₃(x,y₀,t), θ₂(x,z,t₀) = θ₄(x,y₀,z), θ₃(x,y,t₀) = θ₄(x,y,z₀).

Здесь X₀, Y₀, Z₀, T₀ - грани параллелотопа G при x = x₀, y = y₀, z = z₀, t = t₀.

Решение задачи Гурса существует и единственно, что можно доказать, переходя к эквива-

лентному интегральному уравнению Вольтерры. Именно, непосредственно интегрируя уравне-

ние (1) с учётом условий (3), приходим к интегральному уравнению Вольтерры - аналогично

тому, как это сделано в [11, § 2, п. 1, с. 25-26] в случае задачи Гурса для уравнения Бианки

третьего порядка. Следовательно, решение задачи Гурса (1), (3) существует, единственно и

записывается с помощью резольвент интегральных уравнений.

Кратко опишем построение формулы решения задачи Гурса в терминах функции Римана

[9; 11, § 3, п. 1]. Рассмотрим интегральное уравнение

∫t

∫

v(x, y, z, t) - a₁₁₁₀(x, y, z, δ)v(x, y, z, δ) dδ - a₁₁₀₁(x, y, γ, t)v(x, y, γ, t) dγ -

∫

− a₁₀₁₁(x,β,z,t)v(x,β,z,t)dβ - a₀₁₁₁(α,y,z,t)v(α,y,z,t)dα +

∫z

∫

a₁₁₀₀(x,y,γ,δ)v(x,y,γ,δ)dδ dγ +

a₁₀₁₀(x,β,z,δ)v(x,β,z,δ) dδ dβ +

ζ τ

η τ

∫x

∫

a₀₁₁₀(α,y,z,δ)v(α,y,z,δ) dδ dα +

a₁₀₀₁(x,β,γ,t)v(x,β,γ,t)dγ dβ +

ξ τ

η ζ

∫x

∫

a₀₁₀₁(α,y,γ,t)v(α,y,γ,t)dγ dα +

a₀₀₁₁(α,β,z,t)v(α,β,z,t)dβ dα -

ξ ζ

ξ η

∫

a₁₀₀₀(x,β,γ,δ)v(x,β,γ,δ)dδ dγ dβ -

a₀₁₀₀(ξ,y,γ,δ)v(ξ,y,γ,δ)dδ dγdξ -

η ζ τ

ξ ζ τ

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

351

∫x

∫

a₀₀₁₀(ξ,β,z,δ)v(ξ,β,z,δ) dδ dβdξ -

a₀₀₀₁(ξ,β,ζ,t)v(ξ,β,ζ,t)dζ dβdξ +

ξ η τ

ξ η ζ

∫x

∫

a₀₀₀₀(α,β,γ,δ)v(α,β,γ,δ) dδ dγ dβ dα = 1.

(4)

ξ η ζ τ

Решение v уравнения (4) существует и единственно и представляет собой функцию Римана [9]

для уравнения (1). Понятно, что v зависит также от входящих в уравнение (4) переменных

ξ, η, ζ, τ. Если нужно подчеркнуть эту зависимость, то пишут v = R(x,y,z,t,ξ,η,ζ,τ).

Введём следующие обозначения:

A₀₀₀₁ = R_t - a₁₁₁₀R, A₀₀₁₀ = R_z - a₁₁₀₁R, A₀₁₀₀ = R_y - a₁₀₁₁R, A₁₀₀₀ = R_x - a₀₁₁₁R,

A₀₀₁₁ = R_zt - (a₁₁₁₀R)_z - (a₁₁₀₁R)_t + a₁₁₀₀R, A₀₁₀₁ = R_yt - (a₁₁₁₀R)_y - (a₁₀₁₁R)_t + a₁₀₁₀R,

A₀₁₁₀ = R_yz - (a₁₁₀₁R)_y - (a₁₀₁₁R)_z + a₁₀₀₁R, A₁₀₀₁ = R_xt - (a₁₁₁₀R)_x - (a₀₁₁₁R)_t + a₀₁₁₀R,

A₁₀₁₀ = R_xz - (a₁₁₀₁R)_x - (a₀₁₁₁R)_z + a₀₁₀₁R, A₁₁₀₀ = R_xy - (a₁₀₁₁R)_x - (a₀₁₁₁R)_y + a₀₀₁₁R,

A₀₁₁₁ = R_yzt - (a₁₁₁₀R)_yz - (a₁₁₀₁R)_yt - (a₁₀₁₁R)_zt + (a₁₁₀₀R)_y + (a₁₀₁₀R)_z + (a₁₀₀₁R)_t - a₁₀₀₀R,

A₁₀₁₁ = R_xzt - (a₁₁₁₀R)_xz - (a₁₁₀₁R)_xt - (a₀₁₁₁R)_zt + (a₁₁₀₀R)_x + (a₀₁₁₀R)_z + (a₀₁₀₁R)_t - a₀₁₀₀R,

A₁₁₀₁ = R_xyt - (a₁₁₁₀R)_xy - (a₁₁₀₁R)_xt - (a₀₁₁₁R)_yt + (a₁₀₁₀R)_x + (a₀₁₁₀R)_y + (a₀₀₁₁R)_t - a₀₀₁₀R,

A₁₁₁₀ = R_xyz-(a₁₁₀₁R)_xy-(a₁₀₁₁R)_xz-(a₀₁₁₁R)_yz+(a₁₀₀₁R)_x+(a₀₁₀₁R)_y+(a₀₀₁₁R)_z-a₀₀₀₁R, (5)

где функция R зависит от переменных x, y, z, t, ξ, η, ζ, τ, а коэффициенты уравне-

ния (1), как сказано выше, - от переменных x, y, z, t.

Непосредственным вычислением несложно убедиться в справедливости тождества

(Ru)_xyzt ≡ RL(u) + (A₀₀₀₁)_xyz + (A₀₀₁₀)_xyt + (A₀₁₀₀)_xzt + (A₁₀₀₀)_yzt - (A₀₀₁₁)_xy - (A₀₁₀₁)_xz -

- (A₀₁₁₀)_xt - (A₁₀₀₁)_yz - (A₁₀₁₀)_yt - (A₁₁₀₀)_zt + (A₀₁₁₁)_x + (A₁₀₁₁)_y + (A₁₁₀₁)_z + (A₁₁₁₀)_t,

(6)

где u(x, y, z, t) - любая функция класса C(1,1,1,1).

Дифференцируя уравнение (4), получаем тождества

A₀₀₀₁ ≡ 0 при x = ξ, y = η, z = ζ; A₀₀₁₀ ≡ 0 при x = ξ, y = η, t = τ;

A₀₁₀₀ ≡ 0 при x = ξ, z = ζ, t = τ; A₁₀₀₀ ≡ 0 при y = η, z = ζ, t = τ;

A₀₀₁₁ ≡ 0 при x = ξ, y = η; A₀₁₀₁ ≡ 0 при x = ξ, z = ζ;

A₀₁₁₀ ≡ 0 при x = ξ, t = τ; A₁₀₀₁ ≡ 0 при y = η, z = ζ;

A₁₀₁₀ ≡ 0 при y = η, t = τ; A₁₁₀₀ ≡ 0 при z = ζ, t = τ;

A₀₁₁₁ ≡ 0 при x = ξ, t = τ; A₁₀₁₁ ≡ 0 при y = η;

A₁₁₀₁ ≡ 0 при z = ζ; A₁₁₁₀ ≡ 0 при t = τ.

(7)

Считая в тождестве (6) функцию u(x, y, z, t) решением уравнения (1), меняя ролями пе-

ременные (x, ξ), (y, η), (z, ζ), (t, τ) и вычисляя четырёхкратный интеграл по ξ, η, ζ, τ в

пределах x₀ < ξ < x, y₀ < η < y, z₀ < ζ < z, t₀ < τ < t с учётом тождеств (7), получаем

формулу (4) из [9], которая даёт решение задачи Гурса.

Докажем теперь существование и единственность решения задачи Дарбу при помощи её

редукции к задаче Гурса в области D : найти регулярное решение уравнения (1) в D по

условиям на плоскостях x = 0, y = 0, z = 0, t = t₁. Для этого по данным задачи Дарбу

надо однозначно определить недостающее условие задачи Гурса, т.е. функцию u(x, y, z, t₁).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

352

МИРОНОВ

В [9, формула (4)] получена формула для функции v(x, y, z, t). Положим в этой формуле

x₀ = 0, y₀ = 0, z₀ = 0, t₀ = t₁, t = x. Тогда левая часть указанной формулы для u(x,y,z,t)

обращается в функцию ψ(x, y, z), а сама эта формула примет вид

∫z

∫

R(x, y, z, t₁, x, y, z, x)u(x, y, z, t₁) - (A₀₀₁₀u)(x, y, γ, t₁) dγ - (A₀₁₀₀u)(x, β, z, t₁) dβ -

∫x

∫

− (A₁₀₀₀u)(α, y, z, t₁) dα +

(A₀₁₁₀u)(x, β, γ, t₁) dγ dβ +

(A₁₀₁₀u)(α, y, γ, t₁) dγ dα +

∫x

∫

(A₁₀₁₀u)(α, β, z, t₁) dβ dα -

(A₁₁₁₀u)(α, β, γ, t₁) dγ dβ dα = F,

(8)

где правая часть F - известная функция, выражающаяся через функции ϕ₁(y, z, t), ϕ₂(x, z, t),

ϕ₃(x,y,t). Уравнение (8) - интегральное уравнение Вольтерры второго рода, решение которого

u(x, y, z, t₁) существует и единственно. Действительно, из интегрального уравнения (4) для

функции Римана следует, что

(∫t

)

R(x, y, z, t, x, y, z, τ) = exp

a₁₁₁₀(x,y,z,δ)dδ

> 0.

Таким образом, задача Дарбу однозначно редуцируется к задаче Гурса, т.е. решение задачи

Дарбу существует и единственно.

2. Очевидно, что решение задачи Дарбу может быть построено в резольвентах интеграль-

ных уравнений (т.е. методом последовательных приближений). Перейдём вопросу о возможно-

сти построения формулы для решения задачи Дарбу в явном виде в терминах функции типа

функции Римана-Адамара, аналогичной по своим свойствам функции Римана-Адамара для

уравнения с двумя независимыми переменными [7]. Далее изложение ведётся, следуя схеме

рассуждений статьи [8].

Возьмём внутри области D произвольную точку P (ξ, η, ζ, τ). Она определяет область

D_P , ограниченную плоскостями x = 0, x = ξ, y = 0, y = η, z = 0, z = ζ, t = τ, t =

= x. Очевидно, область D_P можно разбить на две части: область D¹, которая ограничена

плоскостями x = 0, x = ξ, y = 0, y = η, z = 0, z = ζ, t = τ, t = ξ; и область D²,

которая ограничена плоскостями x = 0, x = ξ, y = 0, y = η, z = 0, z = ζ, t = ξ, t = x.

В трёхмерном случае (см. [8, рис. 1]) области D¹ и D² представляют собой параллелепипед и

призму соответственно. Аналогичные многогранники получаются и в четырёхмерном случае.

Функцию Римана-Адамара задачи Дарбу H(x, y, z, t, ξ, η, ζ, τ) определим равенством

{

R(x, y, z, t, ξ, η, ζ, τ), (x, y, z, t) ∈ D¹,

H(x, y, z, t, ξ, η, ζ, τ) =

(9)

V (x, y, z, t, ξ, η, ζ, τ), (x, y, z, t) ∈ D².

Требуется определить функцию V. Этому посвящён нижеследующий текст п. 2.

Нам потребуются следующие обозначения: будем обозначать через A_ijkl конструкции (5),

в которых R заменена на H, через A^-ijkl конструкции (5), в которых R заменена на V, а те

же конструкции с функцией R обозначим A+ijkl.

Будем обозначать пересечение границы области D_P с плоскостью x = ξ через DP[x=ξ], с

плоскостями x = ξ, y = η через DP[x=ξ,y=η] и т.д. Обозначим пересечение границы области

D_P с плоскостью x = t через T. Пусть

V |_T ≡ 0.

(10)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

353

Далее, потребуем выполнения соотношения

[A₁₀₀₀](x, η, ζ, ξ, ξ, η, ζ, τ) := A⁺¹⁰⁰⁰(x, η, ζ, ξ + 0, ξ, η, ζ, τ) - A-1000(x, η, ζ, ξ - 0, ξ, η, ζ, τ) ≡ 0, (11)

где, как уже сказано выше, A⁺¹⁰⁰⁰ = R_x -a₀₁₁₁R, A-1000 = V_x -a₀₁₁₁V. Данное равенство вместе

с очевидным условием (вытекающим из тождества (10))

V (ξ, η, ζ, ξ, ξ, η, ζ, τ) = 0

приводит для определения функции V на отрезке DP[y=η,z=ζ,t=ξ], где очевидно 0 ≤ x ≤ ξ, к

задаче Коши для обыкновенного дифференциального уравнения первого порядка

V_x - a₀₁₁₁V = g(x), V (ξ,η,ζ,ξ,ξ,η,ζ,τ) = 0,

g(x) = (R_x - a₀₁₁₁R)|DP[y=η,z=ζ,t=ξ] .

(12)

Решение задачи (12) имеет вид

∫x

(∫x

)

V (x, η, ζ, ξ) = g(α) exp

a₀₁₁₁(α₁,η,ζ,ξ)dα₁ dα.

(13)

Потребуем, чтобы в плоской области DP[y=η,z=ζ] функция V удовлетворяла уравнению

A-1001 = V_xt - (a₁₁₁₀V )_x - (a₀₁₁₁V )_t + a₀₁₁₀V = 0.

(14)

Тогда функция V в плоской области DP[y=η,z=ζ] определена как решение задачи Дарбу для

уравнения (14) с граничными условиями V |DP[y=η,z=ζ,t=x] = 0 (следствие (10)) и (13). Решение

указанной двумерной задачи Дарбу существует и единственно [7].

Далее, потребуем, чтобы скачок функции A₁₁₀₀ на многообразии DP[z=ζ,t=ξ] равнялся

нулю, т.е. должно выполняться соотношение

[A₁₁₀₀](x, y, ζ, ξ, ξ, η, ζ, τ) := A⁺¹¹⁰⁰(x, y, ζ, ξ + 0, ξ, η, ζ, τ) - A-1100(x, y, ζ, ξ - 0, ξ, η, ζ, τ) ≡ 0, (15)

где A⁺¹¹⁰⁰ = R_xy - (a₁₀₁₁R)_x - (a₀₁₁₁R)_y + a₀₀₁₁R, A-1100 = V_xy - (a₁₀₁₁V )_x - (a₀₁₁₁V )_y + a₀₀₁₁V.

В результате для определения граничного значения функции V на плоскости DP[z=ζ,t=ξ] по-

лучаем задачу Гурса для гиперболического уравнения второго порядка [1, гл. 1, § 4, п. 4^◦] с

заданными условиями на характеристиках и известной правой частью (которая вычисляется

по функции Римана R, которую считаем известной)

V_xy - (a₁₀₁₁V )_x - (a₀₁₁₁V )_y + a₀₀₁₁V = R_xy - (a₁₀₁₁R)_x - (a₀₁₁₁R)_y + a₀₀₁₁R,

∫x

(∫x

)

V|DP[y=η,z=ζ,t=ξ] =

g(α) exp

a₀₁₁₁(α₁,η,ζ,ξ)dα₁ dα,

V |DP[z=ζ,x=ξ,t=ξ] = 0.

(16)

Здесь граничные значения являются следствиями соотношений (10), (13). Решение задачи (16)

существует и единственно.

Аналогично потребуем, чтобы скачок функции A₁₀₁₀ на многообразии DP[y=η,t=ξ] равнял-

ся нулю, т.е. должно выполняться соотношение

[A₁₀₁₀](x, η, z, ξ, ξ, η, ζ, τ) := A⁺¹⁰¹⁰(x, η, z, ξ + 0, ξ, η, ζ, τ) - A-1010(x, η, z, ξ - 0, ξ, η, ζ, τ) ≡ 0. (17)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

354

МИРОНОВ

Снова получаем для определения граничного значения функции V на плоскости DP[y=η,t=ξ]

задачу Гурса для гиперболического уравнения второго порядка

V_xz - (a₁₁₀₁V )_x - (a₀₁₁₁V )_z + a₀₁₀₁V = R_xz - (a₁₁₀₁R)_x - (a₀₁₁₁R)_z + a₀₁₀₁R,

∫x

(∫x

)

V|DP[y=η,z=ζ,t=ξ] =

g(α) exp

a₀₁₁₁(α₁,η,ζ,ξ)dα₁ dα,

V |DP[y=η,x=ξ,t=ξ] = 0.

(18)

Решение задачи (18) существует и единственно [1, гл. 1, § 4, п. 4^◦].

Потребуем выполнения на многообразии DP[y=η] условия

A-1011 = V_xzt - (a₁₁₁₀V )_xz - (a₁₁₀₁V )_xt - (a₀₁₁₁V )_zt + (a₁₁₀₀V )_x +

+ (a₀₁₁₀V )_z + (a₀₁₀₁V )_t - a₀₁₀₀V = 0.

(19)

Для определения функции V получаем задачу Дарбу в трёхмерном пространстве с гранич-

ными условиями

V |DP[y=η,t=ξ] = ϕ₂₄(x,z), V |DP[y=η,z=ζ] = ϕ₂₃(x,t), V |DP[y=η,t=x] = 0;

(20)

первые два условия из (20) определяются из соотношений (18), (14) соответственно, а по-

следнее является следствием тождества (10). Решение задачи Дарбу (19), (20) существует и

единственно [8].

Аналогично потребуем, чтобы на многообразии DP[z=ζ] выполнялось условие

A-1101 = V_xyt - (a₁₁₁₀V )_xy - (a₁₁₀₁V )_xt - (a₀₁₁₁V )_yt + (a₁₀₁₀V )_x +

+ (a₀₁₁₀V )_y + (a₀₀₁₁V )_t - a₀₀₁₀V.

(21)

Снова получаем задачу Дарбу в трёхмерном пространстве с граничными условиями

V |DP[z=ζ,t=ξ] = ϕ₃₄(x,y), V |DP[y=η,z=ζ] = ϕ₂₃(x,t), V |DP[z=ζ,t=x] = 0;

(22)

первые два условия в (22) определяются из соотношений (16), (14) соответственно, а последнее

является следствием тождества (10).

Наконец, потребуем, чтобы скачок функции A₁₁₁₀ на многообразии DP[t=ξ] равнялся

нулю:

[A₁₁₁₀](x, y, z, ξ, ξ, η, ζ, τ) := A⁺¹¹¹⁰(x, y, z, ξ + 0, ξ, η, ζ, τ) - A-1110(x, y, z, ξ - 0, ξ, η, ζ, τ) ≡ 0. (23)

В результате для определения значения функции V на трёхмерном многообразии DP[t=ξ]

(которое является параллелепипедом) получаем задачу Гурса для гиперболического уравнения

третьего порядка с заданными условиями на характеристиках и известной правой частью

(выраженной через функцию Римана R)

V_xyz - (a₁₁₀₁V )_xy - (a₁₀₁₁V )_xz - (a₀₁₁₁V )_yz + (a₁₀₀₁V )_x + (a₀₁₀₁V )_y + (a₀₀₁₁V )_z - a₀₀₀₁V =

= R_xyz - (a₁₁₀₁R)_xy - (a₁₀₁₁R)_xz - (a₀₁₁₁R)_yz + (a₁₀₀₁R)_x + (a₀₁₀₁R)_y + (a₀₀₁₁R)_z - a₀₀₀₁R,

V |DP[x=ξ,t=ξ] = ϕ₁₄(y,z), V |DP[y=η,t=ξ] = ϕ₂₄(x,z), V |DP[z=ζ,t=ξ] = ϕ₃₄(x,y).

(24)

Граничные условия в (24), очевидно, представляют собой значения функции V, получаемые

из соотношений (14), (18), (16) соответственно. Решение задачи (24) существует и единственно

[11, § 2, п. 1, с. 25-26].

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

355

Функцию Римана-Адамара в области D² определим как решение задачи Дарбу для со-

пряжённого к (1) уравнения

L^∗(V ) ≡ V_xyzt - (a₁₁₁₀V )_xyz - (a₁₁₀₁V )_xyt - (a₁₀₁₁V )_xzt - (a₀₁₁₁V )_yzt +

+ (a₁₁₀₀V )_xy + (a₁₀₁₀V )_xz + (a₁₀₀₁V )_xt + (a₀₁₁₀V )_yz + (a₀₁₀₁V )_yt + (a₀₀₁₁V )_zt -

- (a₁₀₀₀V )_x - (a₀₁₀₀V )_y - (a₀₀₁₀V )_z - (a₀₀₀₁V )_t + a₀₀₀₀V = 0

с условиями на многообразиях D2P[y=η], D2P[z=ζ], D2P[t=ξ], T = D2P[x=t], которые вследствие

изложенного выше считаем вполне определёнными.

Итак, функция Римана-Адамара определена, существует и единственна в D_P .

3. Перейдём к построению формулы для решения задачи Дарбу в терминах функции

Римана-Адамара (9).

Запишем тождество (6) в дивергентной форме (здесь и всюду далее функция Римана за-

меняется на функцию Римана-Адамара H = H(x, y, z, ξ, η, ζ)):

∂W₁

∂W₂

∂W₃

∂W₄

HL(u) =

(25)

∂x

∂y

∂z

∂t

W₁ =

(Hu)_yzt -

(A₀₀₀₁u)_yz -

(A₀₀₁₀u)_yt -

(A₀₁₀₀u)_zt +

(A₀₀₁₁u)_y +

(A₀₁₀₁u)_z +

(A₀₁₁₀u)_t - A₀₁₁₁u,

W₂ =

(Hu)_xzt -

(A₀₀₀₁u)_xz -

(A₀₀₁₀u)_xt -

(A₁₀₀₀u)_zt +

(A₀₀₁₁u)_x +

(A₁₀₀₁u)_z +

(A₁₀₁₀u)_t - A₁₀₁₁u,

W₃ =

(Hu)_xyt -

(A₀₀₀₁u)_xy -

(A₀₁₀₀u)_xt -

(A₁₀₀₀u)_yz +

(A₀₁₀₁u)_x +

(A₁₀₀₁u)_y +

(A₁₁₀₀u)_t - A₁₁₀₁u,

W₄ =

(Hu)_xyz -

(A₀₀₁₀u)_xy -

(A₀₁₀₀u)_xz -

(A₁₀₀₀u)_yz +

(A₀₁₁₀u)_x +

(A₁₀₁₀u)_y +

(A₁₁₀₀u)_z - A₁₁₁₀u.

Введём следующие обозначения. Обозначим пересечение границы области D² с плоско-

стью t = ξ через E, с плоскостью x = 0 через D2[x=0], с плоскостью y = 0 через D2[y=0], с

плоскостями t = x, y = η через D2[y=η,t=ξ] и т.д.

Проинтегрируем тождество (25) по области D². Применяя общую формулу Стокса [18,

гл. 13, § 3, п. 4], получаем

∫∫∫∫

∫∫∫

HL(u)dxdy dz dt =

W₁ dy ∧ dz ∧ dt -

W₂ dx ∧ dz ∧ dt +

D²

+D²

[x=0]

[y=0]

[y=η]

∫∫∫

W₃ dx ∧ dy ∧ dz +

W₄ dx ∧ dy ∧ dz +

W₁ dy ∧ dz ∧ dt -

D²

+D²

E²

[z=0]

[z=ζ]

− W2 dx ∧ dz ∧ dt + W3 dx ∧ dy ∧ dt - W4 dx ∧ dz ∧ dz.

(26)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

356

МИРОНОВ

Очевидно, что вектором нормали к поверхности S является вектор n = (1, 0, 0, 1); следова-

тельно, гиперплоскости (x, z, t), (y, z, t) ортогональны к поверхности S. Поэтому

∫∫∫

W₂ dx ∧ dz ∧ dt = 0,

W₃ dx ∧ dy ∧ dt = 0.

Интегралы по многообразиям D2[x=0], D2[y=0], D2[z=0] представляют собой известные величины,

полностью определяемые граничными значениями.

Рассмотрим интеграл

∫∫∫

⁽1

W₁ dy ∧ dz ∧ dt =

(V u)_yzt -

(A-0001u)_yz -

(A-0010u)_yt -

(A-0100u)_zt +

)

(A-0011u)_y +

(A-0101u)_z +

(A-0110u)_t - A-0111u dy ∧ dz ∧ dt.

(27)

На поверхности T имеем

V ≡ 0, A-0010 = V_z - A-1101V ≡ 0, A-0100 = V_y - A-1011V ≡ 0,

A-0110 = V_yz - (A-1101V )_y - (A-1011V )_z + A-1001V ≡ 0,

а величины u, u_y, u_z известны (дифференцирование по y и по z производится вдоль поверх-

ности S). Следовательно, интеграл (27) вычисляется по известным граничным значениям.

Совершенно аналогично вычисляется интеграл

∫∫∫

W₄ dx ∧ dy ∧ dz.

Вычислим интеграл

∫∫∫

⁽1

W₂ dx ∧ dz ∧ dt =

(V u)_xzt -

(A-0001u)_xz -

(A-0010u)_xt -

(A-1000u)_zt +

D²

[y=η]

)

(A-0011u)_x +

(A-1001u)_z +

(A-1010u)_t - A-1011u dx ∧ dz ∧ dt =

∫∫

(

)

(V u)_zt -

(A-0001u)_z -

(A-0010u)_t +

A-0011u dz ∧ dt -

D²

[y=η,t=x]

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt +

(

)

(V u)_xz -

(A-0010u)_x -

(A-1000u)_z +

A-1010u dx ∧ dz +

∫∫

(

)

(V u)_zt -

(A-0001u)_z -

(A-0010u)_t +

A-0011u dz ∧ dt -

D²

[y=η,x=0]

∫∫

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt +

D²

[y=η,z=0]

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

357

∫∫

(

)

(V u)_xz -

(A-0010u)_x -

(A-1000u)_z +

A-1010u dx ∧ dz -

D²

[y=η,t=ξ]

∫∫

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt.

(28)

D²

[y=η,z=ζ]

Здесь A-1011 ≡ 0 при y = η в силу условия (19) (по определению функции Римана-Адамара),

интегралы по многообразиям D2[y=η,t=x], D2[y=η,x=0], D2[y=η,z=0] вычисляются по данным за-

дачи Дарбу.

Рассмотрим оставшиеся два последних слагаемых в (28). Первое из них представляет собой

интеграл по прямоугольнику

∫∫

(

)

(V u)_xz -

(A-0010u)_x -

(A-1000u)_z +

A-1010u dx ∧ dz =

D²

[y=η,t=ξ]

(V u)(ξ, η, ζ, ξ) -

(Ru)(ξ, η, 0, ξ) -

(V u)(0, η, ζ, ξ) +

(Ru)(0, η, 0, ξ) -

∫

(A-0010u(ξ, η, z, ξ) - A-0010u(0, η, z, ξ)) dz -

∫

∫∫

(A-1000u(x, η, ζ, ξ) - A-1000u(x, η, 0, ξ)) dx +

A-1010udx ∧ dz.

D²

[y=η,t=ξ]

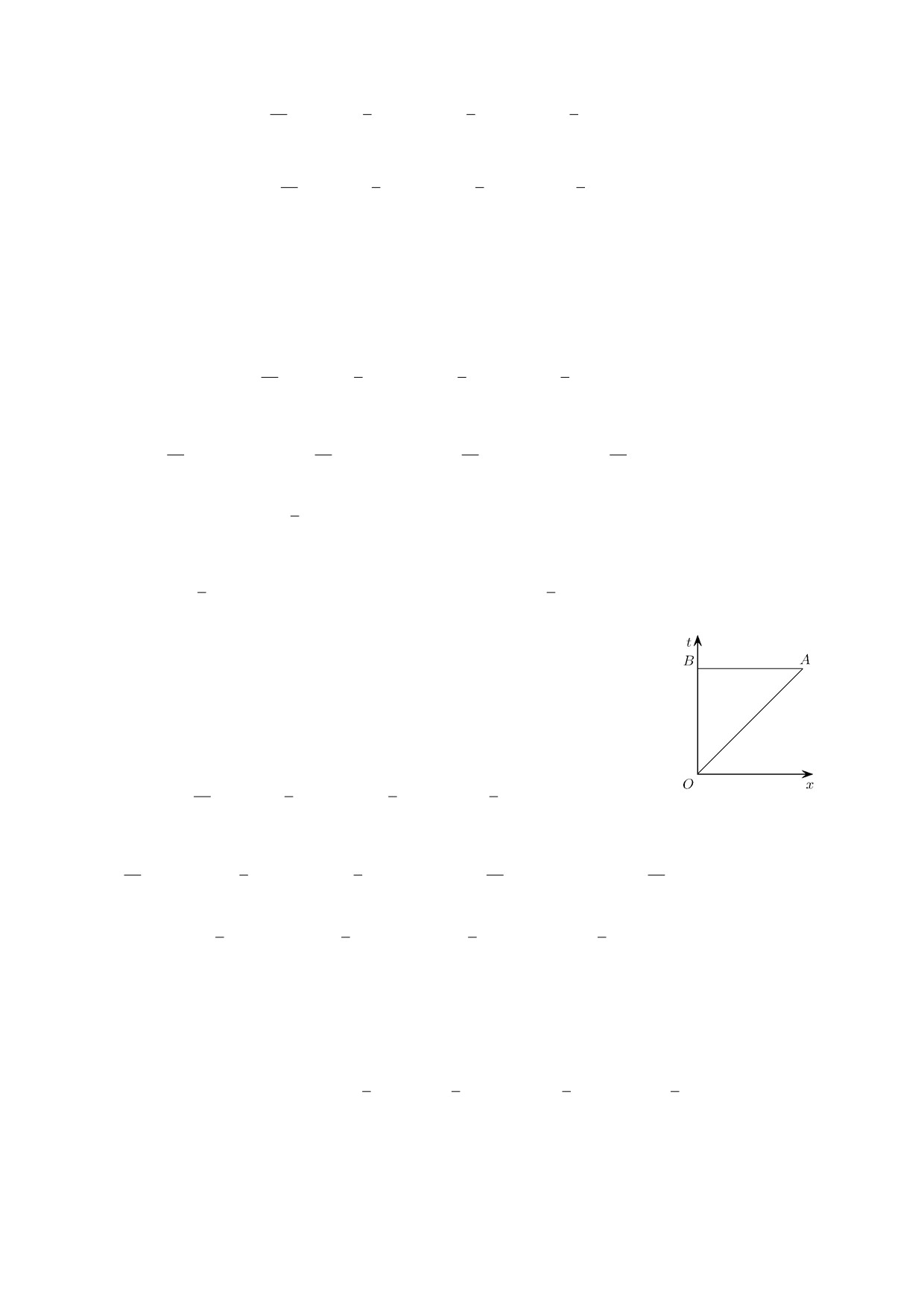
В последнем слагаемом из (28) верно тождество A-1001 ≡ 0 при y =

= η и z = ζ в силу (14) (по определению функции Римана-Адамара),

а интеграл в плоскости (x, t) вычисляется по треугольнику OAB (см.

рисунок, AB - отрезок прямой t = ξ, OA - отрезок прямой t = x).

Обозначим положительно ориентированный контур треугольника OAB

через L. Применяя формулу Грина, получаем

∫∫

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt =

Рисунок. Область

вычисления инте-

D²

[y=η,z=ζ]

грала.

∫

(V u)_t dt -

A-0001udt +

A-1000udx = -

(V_tu + V u_t) dt -

∫

A-0001udt -

A-0001udt +

A-1000udx +

A-1000udx.

(29)

Здесь в первом криволинейном интеграле в правой части равенства верно тождество V ≡

≡ 0 на OA; следовательно, все интегралы, кроме последнего, вычисляются по данным задачи

Дарбу.

Совершенно аналогично преобразуется интеграл

∫∫∫

⁽1

W₃ dx ∧ dy ∧ dt =

(V u)_xyt -

(A-0001u)_xy -

(A-0100u)_xt -

(A-1000u)_yt +

D²

[z=ζ]

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

358

МИРОНОВ

)

(A-0101u)_x +

(A-1001u)_y +

(A-1100u)_t - A-1101u dx ∧ dy ∧ dt =

∫∫

(

)

(V u)_yt -

(A-0001u)_y -

(A-0100u)_t +

A-0101u dy ∧ dt -

D²

[z=ζ,t=x]

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt +

(

)

(V u)_xy -

(A-0100u)_x -

(A-1000u)_y +

A-1100u dx ∧ dy +

∫∫

(

)

(V u)_yt -

(A-0001u)_y -

(A-0100u)_t +

A-0101u dy ∧ dt -

D²

[z=ζ,x=0]

∫∫

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt +

D²

[z=ζ,y=0]

∫∫

(

)

(V u)_xy -

(A-0100u)_x -

(A-1000u)_y +

A-1100u dx ∧ dy -

D²

[z=ζ,t=ξ]

∫∫

(

)

(V u)_xt -

(A-0001u)_x -

(A-1000u)_t +

A-1001u dx ∧ dt.

(30)

D²

[y=η,z=ζ]

Здесь снова A-1101 ≡ 0 при z = ζ в силу условия (21) (по определению функции Римана-

Адамара), интегралы по многообразиям D2[z=ζ,t=x], D2[z=ζ,x=0], D2[z=ζ,y=0] вычисляются по

данным задачи Дарбу.

Рассмотрим оставшиеся два последних слагаемых в (30). Первое из них представляет собой

интеграл по прямоугольнику

∫∫

(

)

(V u)_xy -

(A-0100u)_x -

(A-1000u)_y +

A-1100u dx ∧ dy =

D²

[z=ζ,t=ξ]

(V u)(ξ, η, ζ, ξ) -

(V u)(0, η, ζ, ξ) -

(V u)(ξ, 0, ζ, ξ) +

(V u)(0, 0, ζ, ξ) -

∫

(A-0100u(ξ, y, ζ, ξ) - A-0100u(0, y, ζ, ξ)) dy -

(A-1000u(x, η, ζ, ξ) -

∫∫

- A-1000u(x,0,ζ,ξ))dx +

A-1100udx ∧ dz.

D²

[z=ζ,t=ξ]

Второе оставшееся слагаемое из (30) совпадает с последним слагаемым из (28) и вычисляется

так же, в результате получаем (29).

Далее вычисляем интеграл

∫∫∫

⁽1

W₄ dx ∧ dy ∧ dz =

(V u)_xyz -

(A-0010u)_xy -

(A-0100u)_xz -

(A-1000u)_yz +

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

359

)

(A-0110u)_x +

(A-1010u)_y +

(A-1100u)_z - A-1110u dx ∧ dy ∧ dz =

∫∫

(

)

(V u)_yz -

(A-0010u)_y -

(A-0100u)_z +

A-0110u dy ∧ dz -

E[x=ξ]

∫∫

(

)

(V u)_xz -

(A-0010u)_x -

(A-1000u)_z +

A-1010u dx ∧ dz +

E[y=η]

∫∫

(

)

(V u)_xy -

(A-0100u)_x -

(A-1000u)_y +

A-1100u dx ∧ dy +

E[z=ζ]

∫∫

(

)

(V u)_yz -

(A-0010u)_y -

(A-0100u)_z +

A-0110u dy ∧ dz -

E[x=0]

∫∫

(

)

(V u)_xz -

(A-0010u)_x -

(A-1000u)_z +

A-1010u dx ∧ dz +

E[y=0]

∫∫

(

)

(V u)_xy -

(A-0100u)_x -

(A-1000u)_y +

A-1100u dx ∧ dy.

E[z=0]

Первое, четвёртое, пятое и шестое слагаемые в правой части этого равенства вычисляются по

известным данным Дарбу. Второе и третье слагаемые дают

∫∫ (

)

(V u)_xz -

(A-0010u)_x -

(A-1000u)_z +

A-1010u dz ∧ dx +

E[y=η]

∫∫

(

)

(V u)_xy -

(A-0100u)_x -

(A-1000u)_y +

A-1100u dx ∧ dy =

E[z=ζ]

V u(ξ, η, ζ, ξ) -

Ru(ξ, η, 0, ξ) -

V u(0, η, ζ, ξ) +

Ru(0, η, 0, ξ) -

∫

((A-0010u)(ξ, η, z, ξ) - (A-0010u)(0, η, z, ξ)) dz -

(A-1000u)(x, η, 0, ξ) dx -

−

V u(ξ, η, ζ, ξ) -

V u(0, η, ζ, ξ) -

V u(ξ, 0, ζ, ξ) +

V u(0, 0, ζ, ξ) -

∫

((A-0100u)(ξ, y, ζ, ξ) - (A-0100u)(0, y, ζ, ξ)) dy +

(A-1000u)(x, 0, ζ, ξ) dx -

∫

∫∫

(A-1000u)(x, η, ζ, ξ) dx +

A-1010udz ∧ dx -

E¹

[y=η]

∫

∫∫

(A-1000u)(x, η, ζ, ξ) dx +

A-1100udx ∧ dy.

E[z=ζ]

Здесь известны все слагаемые, кроме четырёх последних интегралов.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

5^∗

360

МИРОНОВ

Теперь интегрируем тождество (25) по области D¹, где H = R - функция Римана (решение

интегрального уравнения (4) в этой области):

∫∫∫∫

∫∫∫

HL(u)dxdy dz dt =

W₁ dy ∧ dz ∧ dt -

W₂ dx ∧ dz ∧ dt +

D₁

D¹

+D¹

D¹

+D¹

[x=0]

[x=ξ]

[y=0]

[y=η]

∫∫∫

W₃ dx ∧ dy ∧ dz +

W₄ dx ∧ dy ∧ dz +

W₄ dx ∧ dy ∧ dz.

(31)

D¹

+D¹

D¹

[z=0]

[z=ζ]

[t=τ]

Здесь интегралы по многообразиям D1[x=0], D1[y=0], D1[z=0] представляют собой известные

величины, полностью определяемые граничными значениями.

Преобразуем интеграл

∫∫∫

⁽1

W₁ dy ∧ dz ∧ dt =

(Ru)_yzt -

(A⁺⁰⁰⁰¹u)_yz -

(A⁺⁰⁰¹⁰u)_yt -

(A⁺⁰¹⁰⁰u)_zt +

D¹

D_[

[x=ξ]

x=ξ]

)

(A⁺⁰⁰¹¹u)_y +

(A⁺⁰¹⁰¹u)_z +

(A⁺⁰¹¹⁰u)_t - A⁺⁰¹¹¹u dy ∧ dz ∧ dt =

∫∫

(

)

(Ru)_zt -

(A⁺⁰⁰⁰¹u)_z -

(A⁺⁰⁰¹⁰u)_t +

A⁺⁰⁰¹¹u dz ∧ dt -

D¹

[x=ξ,y=η]

∫∫

(

)

(Ru)_yt -

(A⁺⁰⁰⁰¹u)_y -

(A⁺⁰¹⁰⁰u)_t +

A⁺⁰¹⁰¹u dy ∧ dt +

D¹

[x=ξ,z=ζ]

∫∫

(

)

(Ru)_yz -

(A⁺⁰⁰¹⁰u)_y -

(A⁺⁰¹⁰⁰u)_z +

A⁺⁰¹¹⁰u dy ∧ dz +

D¹

[x=ξ,t=τ]

∫∫

(

)

(Ru)_zt -

(A⁺⁰⁰⁰¹u)_z -

(A⁺⁰⁰¹⁰u)_t +

A⁺⁰⁰¹¹u dz ∧ dt -

D¹

[x=ξ,y=0]

∫∫

(

)

(Ru)_yt -

(A⁺⁰⁰⁰¹u)_y -

(A⁺⁰¹⁰⁰u)_t +

A⁺⁰¹⁰¹u dy ∧ dt -

D¹

[x=ξ,z=0]

∫∫

(

)

(Ru)_yz -

(A⁺⁰⁰¹⁰u)_y -

(A⁺⁰¹⁰⁰u)_z +

A⁺⁰¹¹⁰u dy ∧ dz.

(32)

D¹

[x=ξ,t=ξ]

Последние три слагаемых вычисляются по известным данным Дарбу. Первые три слагаемых

дают

∫∫

(

)

(Ru)_zt -

(A⁺⁰⁰⁰¹u)_z -

(A⁺⁰⁰¹⁰u)_t +

A⁺⁰⁰¹¹u dz ∧ dt -

D¹

[x=ξ,y=η]

∫∫

(

)

(Ru)_yt -

(A⁺⁰⁰⁰¹u)_y -

(A⁺⁰¹⁰⁰u)_t +

A⁺⁰¹⁰¹u dy ∧ dt +

D¹

[x=ξ,z=ζ]

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

361

∫∫

(

)

(Ru)_yz -

(A⁺⁰⁰¹⁰u)_y -

(A⁺⁰¹⁰⁰u)_z +

A⁺⁰¹¹⁰u dy ∧ dz =

D¹

[x=ξ,t=τ]

Ru(ξ, η, ζ, τ) -

Ru(ξ, η, 0, τ) -

Ru(ξ, η, ζ, 0) +

Ru(ξ, η, 0, 0) -

∫

((A⁺⁰⁰⁰¹u)(ξ, η, ζ, t)-(A⁺⁰⁰⁰¹u)(ξ, η, 0, t)) dt-

((A⁺⁰⁰¹⁰u)(ξ, η, z, τ)-(A⁺⁰⁰¹⁰u)(ξ, η, z, 0)) dz+

Ru(ξ, η, ζ, τ) -

Ru(ξ, η, ζ, 0) -

Ru(ξ, 0, ζ, τ) +

Ru(ξ, 0, ζ, 0) -

∫

((A⁺⁰⁰⁰¹u)(ξ, η, ζ, t)-(A⁺⁰⁰⁰¹u)(ξ, 0, ζ, t)) dt-

((A⁺⁰¹⁰⁰u)(ξ, y, ζ, τ)-(A⁺⁰¹⁰⁰u)(ξ, y, ζ, 0)) dy+

Ru(ξ, η, ζ, τ) -

Ru(ξ, η, 0, τ) -

Ru(ξ, 0, ζ, τ) +

Ru(ξ, 0, 0, τ) -

∫

((A⁺⁰⁰¹⁰u)(ξ, η, z, τ) - (A⁺⁰⁰¹⁰u)(ξ, 0, z, τ)) dz -

∫

((A⁺⁰¹⁰⁰u)(ξ, y, ζ, τ) - (A⁺⁰¹⁰⁰u)(ξ, y, 0, τ)) dy.

Здесь первые слагаемые под знаками определённых интегралов обращаются в нуль согласно

(7), оставшиеся слагаемые представляют собой сумму известных в силу условий задачи Дарбу

величин и слагаемого Ru(ξ, η, ζ, τ)/4.

Интегралы

∫∫∫

W₂ dx ∧ dz ∧ dt,

W₃ dx ∧ dy ∧ dt,

W₄ dx ∧ dy ∧ dz

D¹

[y=η]

[z=ζ]

[t=τ]

вычисляются по той же схеме, что и интеграл (32). Результат вычислений может быть записан

с помощью очевидной перестановки переменных в соответствующих формулах. Поэтому на

вычислении этих трёх интегралов мы не останавливаемся.

Наконец, преобразуем интеграл

∫∫∫

⁽1

W₄ dx ∧ dy ∧ dz =

(Ru)_xyz -

(A⁺⁰⁰¹⁰u)_xy -

(A⁺⁰¹⁰⁰u)_xz -

(A⁺¹⁰⁰⁰u)_yz +

)

(A⁺⁰¹¹⁰u)_x +

(A⁺¹⁰¹⁰u)_y +

(A⁺¹¹⁰⁰u)_z - A⁺¹¹¹⁰u dx ∧ dy ∧ dz =

∫∫

(

)

(Ru)_yz -

(A⁺⁰⁰¹⁰u)_y -

(A⁺⁰¹⁰⁰u)_z +

A⁺⁰¹¹⁰u dy ∧ dz -

E[x=ξ]

∫∫

(

)

(Ru)_xz -

(A⁺⁰⁰¹⁰u)_x -

(A⁺¹⁰⁰⁰u)_z +

A⁺¹⁰¹⁰u dx ∧ dz +

E[y=η]

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

362

МИРОНОВ

∫∫

(

)

(Ru)_xy -

(A⁺⁰¹⁰⁰u)_x -

(A⁺¹⁰⁰⁰u)_y +

A⁺¹¹⁰⁰u dx ∧ dy +

E[z=ζ]

∫∫

(

)

(Ru)_yz -

(A⁺⁰⁰¹⁰u)_y -

(A⁺⁰¹⁰⁰u)_z +

A⁺⁰¹¹⁰u dy ∧ dz -

E[x=0]

∫∫

(

)

(Ru)_xz -

(A⁺⁰⁰¹⁰u)_x -

(A⁺¹⁰⁰⁰u)_z +

A⁺¹⁰¹⁰u dx ∧ dz +

E[y=0]

∫∫

(

)

(Ru)_xy -

(A⁺⁰¹⁰⁰u)_x -

(A⁺¹⁰⁰⁰u)_y +

A⁺¹¹⁰⁰u dx ∧ dy.

E[z=0]

Первое, четвёртое, пятое и шестое слагаемые в правой части вычисляются по известным дан-

ным Дарбу. Второе и третье слагаемые дают

∫∫ (

)

(Ru)_xz -

(A⁺⁰⁰¹⁰u)_x -

(A⁺¹⁰⁰⁰u)_z +

A⁺¹⁰¹⁰u dz ∧ dx +

E[y=η]

∫∫

(

)

(Ru)_xy -

(A⁺⁰¹⁰⁰u)_x -

(A⁺¹⁰⁰⁰u)_y +

A⁺¹¹⁰⁰u dx ∧ dy =

E[z=ζ]

Ru(ξ, η, ζ, ξ) -

Ru(ξ, η, 0, ξ) -

Ru(0, η, ζ, ξ) +

Ru(0, η, 0, ξ) -

∫

((A⁺⁰⁰¹⁰u)(ξ, η, z, ξ) - (A⁺⁰⁰¹⁰u)(0, η, z, ξ)) dz -

(A⁺¹⁰⁰⁰u)(x, η, 0, ξ) dx -

−

Ru(ξ, η, ζ, ξ) -

Ru(0, η, ζ, ξ) -

Ru(ξ, 0, ζ, ξ) +

Ru(0, 0, ζ, ξ) -

∫

((A⁺⁰¹⁰⁰u)(ξ, y, ζ, ξ) - (A⁺⁰¹⁰⁰u)(0, y, ζ, ξ)) dy -

(A⁺¹⁰⁰⁰u)(x, 0, ζ, ξ) dx -

∫

∫∫

(A⁺¹⁰⁰⁰u)(x, η, ζ, ξ) dx +

A⁺¹⁰¹⁰udz ∧ dx -

E[y=η]

∫

∫∫

(A⁺¹⁰⁰⁰u)(x, η, ζ, ξ) dx +

A⁺¹¹⁰⁰udx ∧ dy.

E[z=ζ]

Здесь известны все слагаемые, кроме четырёх последних интегралов.

Почленно сложим равенства (26) и (31) с учётом всех сделанных преобразований. Учитывая

соотношения (11), (15), (17), (23), а также тождество R(ξ, η, ζ, ξ, η, ζ) ≡ 1, получаем

∫∫∫

u(P ) = F (P ) +

Hf dxdy dz dt,

(33)

D¹+D²

где функция F (P ) полностью определена граничными данными задачи Дарбу. Другими сло-

вами, все не определяемые через данные задачи Дарбу слагаемые взаимно уничтожаются в

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021

ЗАДАЧА ДАРБУ ДЛЯ УРАВНЕНИЯ БИАНКИ

363

силу равенства нулю скачков, определяемых соотношениями (11), (15), (17), (23). Таким об-

разом, равенство (33) даёт искомое представление решения задачи Дарбу u(P ) в терминах

функции Римана-Адамара.

СПИСОК ЛИТЕРАТУРЫ

1. Бицадзе А.В. Некоторые классы уравнений в частных производных. М., 1981.

2. Моисеев Е.И. Об одном интегральном представлении решения задачи Дарбу // Мат. заметки. 1982.

Т. 32. Вып. 2. С. 175-186.

3. Моисеев Е.И. О приближении классического решения задачи Дарбу гладкими решениями // Диф-

ференц. уравнения. 1984. Т. 20. № 1. С. 73-87.

4. Моисеев Е.И. Уравнения смешанного типа со спектральным параметром. М., 1988.

5. Сабитов К.Б. Построение в явном виде решений задач Дарбу для телеграфного уравнения и их

применение при обращении интегральных уравнений. I // Дифференц. уравнения. 1990. Т. 26. № 6.

С. 1023-1032.

6. Сабитов К.Б., Шарафутдинова Г.Г. Задачи Коши-Гурса для вырождающегося гиперболического

уравнения // Изв. вузов. Математика. 2003. № 5. С. 21-29.

7. Джохадзе О.М., Харибегашвили С.С. Некоторые свойства функций Римана и Римана-Адамара для

линейных гиперболических уравнений второго порядка и их приложения // Дифференц. уравнения.

2011. Т. 47. № 4. С. 477-492.

8. Миронов А.Н. Задача Дарбу для уравнения Бианки третьего порядка // Мат. заметки. 2017. Т. 102.

Вып. 1. С. 64-71.

9. Жегалов В.И., Севастьянов В.А. Задача Гурса в четырехмерном пространстве // Дифференц.

уравнения. 1996. Т. 32. № 10. С. 1429-1430.

10. Севастьянов В.А. Об одном случае задачи Коши // Дифференц. уравнения. 1998. Т. 34. № 12.

С. 1706-1707.

11. Жегалов В.И., Миронов А.Н. Дифференциальные уравнения со старшими частными производны-

ми. Казань, 2001.

12. Жегалов В.И., Миронов А.Н., Уткина Е.А. Уравнения с доминирующей частной производной.

Казань, 2014.

13. Миронов А.Н. О построении функции Римана для одного уравнения четвёртого порядка // Диф-

ференц. уравнения. 2001. Т. 37. № 12. С. 1698-1701.

14. Миронов А.Н. Метод Римана для уравнений со старшей частной производной в Rⁿ // Сиб. мат.

журн. 2006. Т. 47. Вып. 3. С. 584-594.

15. Кощеева О.А. О построении функции Римана для уравнения Бианки в n-мерном пространстве

// Изв. вузов. Математика. 2008. № 9. С. 40-46.

16. Миронов А.Н. Об инвариантах Лапласа одного уравнения четвертого порядка // Дифференц. урав-

нения. 2009. Т. 45. № 8. С. 1144-1149.

17. Миронов А.Н. О некоторых классах уравнений Бианки четвертого порядка с постоянными отноше-

ниями инвариантов Лапласа // Дифференц. уравнения. 2013. Т. 49. № 12. С. 1572-1581.

18. Зорич В.А. Математический анализ. Ч. 2. М., 1984.

Елабужский институт (филиал)

Поступила в редакцию 28.10.2020 г.

Казанского (Приволжского) федерального университета

После доработки 28.10.2020 г.

Принята к публикации 22.01.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№3

2021