ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 3, с.411-427
ЧИСЛЕННЫЕ МЕТОДЫ
УДК 519.622.2
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
ИНТЕРВАЛЬНЫХ МОДЕЛЕЙ ТЕЙЛОРА В АЛГОРИТМАХ
ВЫЧИСЛИТЕЛЬНОГО ДОКАЗАТЕЛЬСТВА
СУЩЕСТВОВАНИЯ ПЕРИОДИЧЕСКИХ
ТРАЕКТОРИЙ В СИСТЕМАХ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
© 2021 г. Н. М. Евстигнеев, О. И. Рябков, Д. А. Шульмин
С помощью интервальных моделей Тейлора (ТМ) строятся алгоритмы вычислительного
доказательства существования периодических траекторий в системах обыкновенных диф-
ференциальных уравнений (ОДУ). Хотя ТМ позволяют проводить построение гарантиро-
ванных оценок семейств решений систем ОДУ, но при интегрировании ОДУ на больших
временных промежутках входящий в ТМ интервальный остаток начинает расти экспонен-
циально и становится доминирующей частью оценки пучка решений, делая её практически
непригодной. Для устранения этого недостатка создатели ТМ К. Макино и М. Берц предло-
жили идею т.н. “стягивающего обрамления”. Мы формализуем исходный алгоритм в рамках
принятых нами определений ТМ и предлагаем свою версию “стягивающего обрамления”,
более точно приспособленную к задаче вычислительного доказательства существования
периодических траекторий.
DOI: 10.31857/S0374064121030110
Введение. Интервальная арифметика (см. монографии [1-5]) представляет собой основ-
ной инструмент для проведения доказательных вычислений (ДВ) в математическом и функ-
циональном анализе и теории дифференциальных уравнений. ДВ можно рассматривать как
состоявшийся метод современной математики, с помощью которого уже разрешён ряд проблем,
решение которых более традиционными методами либо до сих пор не было найдено, либо яв-
ляется крайне трудоёмким (см., например, обзорную статью [6] или статью [7], посвящённую
решению 14-й проблемы Смейла методами ДВ). Развитие данной области ускоряется за счёт
появления всё более мощных вычислительных систем, с одной стороны, и за счёт создания всё
более эффективных алгоритмов ДВ - с другой.
В наших предыдущих работах [8, 9] ДВ рассматривались в качестве инструмента для до-
казательства существования периодических траекторий в автономных системах ОДУ. Как в
наших, так и в работах других авторов, использующих данный подход к системам ОДУ (на-
пример, [10]), проводится построение доказательных оценок для решений и семейств решений
систем. Для этого могут применяться методы интервального анализа (например, алгоритм
Мура [1] или [11]). Однако в [8] мы использовали методы интегрирования ОДУ, основанные на
интервальных моделях Тейлора. Модели Тейлора в некотором смысле обобщают интерваль-
ную арифметику и изначально применялись именно в задачах построения гарантированных
оценок для задачи Коши в [12-15], хотя их применение не ограничено только этим [16]. В [8]
мы воспользовались собственной версией формализации ТМ, в большей степени, чем ранее,
сводящей алгоритмы ТМ к использованию интервальной арифметики, в том числе для учёта
влияния округлений при работе с коэффициентами полиномов. Указанный подход несколь-
ко упрощает реализацию ТМ на различных платформах, в т.ч. на архитектуре CUDA [17].
Однако идея метода при этом остаётся прежней.
Использованный в [8] подход к доказательству существования циклов у автономных систем
ОДУ, основывающийся на сечениях Пуанкаре, требует построения оценок решения на доста-
точно большом временном промежутке, а именно - на промежутке, равном периоду цикла.
Поэтому даже в примере двумерной системы осциллятора Ван дер Поля, рассмотренном в [8],
411
412
ЕВСТИГНЕЕВ и др.
потребовалось использовать ТМ четвёртого порядка для того, чтобы такое доказательство
стало возможным. К сожалению, при переходе к системам высокой размерности, которые в
конечном итоге и являются предметом нашего рассмотрения, подобные алгоритмы непригод-
ны из-за слишком высокой сложности. В [9] мы попытались обойти эту трудность, воспользо-
вавшись идеями, применяемыми в топологическом подходе к доказательству существования
циклов (см., например, работу [10] и ссылки в ней). При использовании этого подхода не
требуется исследовать поведение решения на длительном промежутке времени, вместо этого
достаточно показать попадание под действием фазового потока всей окрестности цикла в себя
за сколь угодно малое время. На практике численные погрешности не позволяют использо-
вать любые сколь угодно малые промежутки времени и практически пригодными оказываются
промежутки, имеющие порядок одной десятой периода цикла. Тем не менее, оказывается, что
даже такое уменьшение длин рассматриваемых временных промежутков позволяет для дока-
зательства существования периодического решения в осцилляторе Ван дер Поля использовать
ТМ всего лишь второго порядка, как это было показано в примере [9].
Более того, данный подход сделал практически возможным доказательство существования
цикла в маломодовом приближении Галёркина для задачи о течении Колмогорова [17] при ис-
пользовании ТМ третьего порядка. В указанной работе была рассмотрена аппроксимация с
79-ю гармониками, что требовало решения соответствующей системы ОДУ. Очевидно, что для
системы такой размерности снижение степени сложности алгоритма даже на единицу может
быть критическим. Однако у топологического подхода есть и свой недостаток - необходимость
рассмотрения всей окрестности цикла, а не только её части, пересекающей сечение Пуанкаре.
Это приводит к появлению в выражении для сложности алгоритма дополнительного посто-
янного (не зависящего от размерности системы) множителя. Данный множитель на практике
может быть достаточно большим. В [17] мы показываем, что, согласно нашим оценкам, рас-
чётное время, требуемое для проведения доказательства существования цикла в указанной
79-мерной аппроксимации уравнений Навье-Стокса на кластере из 5 GPU GTX Titan Black,
составляет порядка одного месяца. При увеличении размерности системы время расчёта вновь
выходит за практически разумные границы.
В настоящей работе мы рассматриваем один из алгоритмических способов ускорения ДВ
существования периодических решений. Можно заметить, что оценки решений, получаемые с
помощью ТМ низкого порядка (например, второго, из примера в [9]), на начальном отрезке
времени интегрирования могут быть достаточно близкими к реальным границам пучка реше-
ний, что позволяет показать попадание окрестности цикла в себя в топологическом подходе.
Однако при дальнейшем интегрировании эти оценки начинают экспоненциально расходить-
ся. Такое, на первый взгляд, странное поведение отмечалось ещё основоположниками идеи
ТМ К. Макино и М. Берцем [18]. Его причина заключается в том, что по мере разрастания
интервального остатка ТМ начинает вести себя подобно интервальному числу, а алгоритм ин-
тегрирования на основе итераций Пикара вырождается в алгоритм Мура. В этой же работе [18]
была предложена и идея устранения подобного недостатка, названная авторами стягивающим
обрамлением. Суть её состоит в том, чтобы после каждого шага интегрирования модифициро-
вать полученную ТМ при помощи специальной процедуры. Эта процедура должна обладать
двумя основными свойствами. Во-первых, получающаяся в её результате ТМ должна содер-
жать в себе все точки исходной ТМ. Во-вторых, новая ТМ должна обладать нулевым остатком
или остатком с шириной [1, с. 10] порядка машинной точности. На следующем шаге интегри-
рования используется уже модифицированная ТМ. Данный подход в ряде случаев позволяет
избежать экспоненциального роста остатков - см., например, табл. 7.2 в [19].
Структура статьи следующая. В п. 1 напоминаются основные используемые понятия и обо-
значения из наших предыдущих работ, а также вводится ряд вспомогательных обозначений
и алгоритмов. В п. 2 мы формализуем метод [18] в рамках используемых определений и обо-
значений и предлагаем свою версию алгоритма стягивающего обрамления. В п. 3 приводим
полный алгоритм интегрирования ОДУ с помощью ТМ, включающий в себя шаг применения
стягивающего обрамления. В п. 4 сравниваются эффективности двух вариантов стягивающе-
го обрамления как между собой, так и с наивным алгоритмом (без обрамления) на примере
попытки доказательства существования периодического решения в системе Ван дер Поля с
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
413
помощью ТМ второго порядка. Наконец, в заключении содержится обсуждение проделанной
работы и возможных вариантов её развития.
1. Определения и вспомогательные утверждения. Необходимые для работы с ин-
тервальными моделями Тейлора обозначения, определения, утверждения и алгоритмы пред-
ставлены в [8, 9]. В этом пункте мы напоминаем некоторые наиболее важные из них, а также
вводим несколько дополнительных операций над ТМ и соответствующие алгоритмы, которые
понадобятся нам далее. Как и в предыдущих наших работах, нотация, относящаяся к интер-
вальной арифметике, в основном следует монографии [4].
Напомним, что множество интервальных чисел обозначается через R. Интервал (интер-
вальное число) a ∈ R имеет нижнюю L(a) и верхнюю H(a) границы, таким образом a =
= [L(a), H(a)]. Интервал от числа a, заданного в приближённой арифметике, обозначает-
ся через [a, ]. Любую операцию, выполняемую с машинной точностью (т.е. в приближённой
арифметике), обозначаем через /·/, а также считаем, что /0/ = 0. Для доказательства утвер-
ждений 7 и 8 нам понадобится дополнительное предположение о приближённой арифметике:
/0x/ = 0. Последнее требование выполнено в любой реализации чисел с плавающей точкой.
Для упрощения в дальнейшем записи обозначим через Rm(n) множество m-к (i1, . . . , im)
целых неотрицательных чисел, удовлетворяющих неравенству i1+. . .+im ≤ n, а через Sm(n) -
→
равенству i1 + . . . + im = n. Через
idX обозначается тождественное отображение множества
X в себя. Если из контекста понятно, о каком множестве X идёт речь, то индекс в этом
обозначении будем опускать.
Напомним также, что интервальной моделью Тейлора, или тейлоровской моделью
(ТМ), степени n от m переменных (x1, . . . , xm) и размерности q называется дуплет
Pn(x1,... ,xm),⃗I〉, гдеPn = (Pn1,... ,Pnq)т - векторный полином размерности q, степень ко-
торого не выше n,⃗I ∈ Rq - векторный интервал, называемый остатком. Различные модели
Тейлора обозначаются как TM, TM1 и т.д. Если вектор-функци
f : M → Rq (M = [-1,1]m)
удовлетворяет TM (т.е. для любых x ∈ M и j = 1, q имеет место включение fj(x) ∈ [Pnj(x) +
+ L(Ij),Pnj(x) + H(Ij)]), то это обозначается как TM
f ). Внешняя оценка тейлоровской мо-
дели обозначается EB(TM) , она обладает следующим свойством: если выполнено TM
f ), то
f (x) ∈ EB(TM) для каждого x ∈ M. Подробнее см. работу [8], в которой также введены
основные арифметические операции над ТМ (сложение, вычитание, умножение). В работе [9]
дополнительно вводятся операции умножения ТМ на интервал, сложение ТМ с интервальным
вектором и умножение на интервальную матрицу.
При изложении материала этого и следующего пунктов будем использовать интервальные
модели Тейлора TM1 =
P1,n(x),⃗I1〉, TM2
=
P2,n(x),⃗I2〉, TM3
=
P3,n(x),⃗I3〉, TM4=
=
P4,n(x),I4〉 и TM =
Pn(x),I〉 и коэффициенты их полиномов обозначать через an1,...,nm,
bn1,...,nm,
cn1,...,nm ,
dn1,...,nm и
en1,...,nm соответственно. Некоторые алгоритмы будут прини-
мать на вход q натуральных чисел (i1, . . . , iq) ∈ Nq, будем считать, что эти числа находятся
в диапазоне 2 ≤ ij ≤ m и различны, точнее, справедливы неравенства i1 < i2 < . . . < iq.
Данное соглашение считаем выполненным также и для входа алгоритма 6 в п. 3.
Начнём с расширения списка введённых в предыдущих статьях базовых операций над ТМ,
а именно, введём операции разности ТМ и векторного интервала, суммы и разности ТМ и
(неинтервального) вектора, умножения ТМ на (неинтервальный) скаляр и (неинтервальную)
матрицу.
Алгоритм 1. Вход (TM1, y). Выход (TM).
Полагаем
e0,...,0 := /a0,...,0 - y/,
I :=
⃗I1 + ([a0,...,0,] - y - [e0,...,0,]).
Для (n1, . . . , nm) = (0, . . . , 0) полагаем
en1,...,nm := an1,...,nm.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
414
ЕВСТИГНЕЕВ и др.
Определение 1. Под разностью между TM1 размерности q и интервалом y размерно-
сти q будем понимать результат работы алгоритма 1 и обозначать её как TM1 - y.
Утверждение 1. Пусть TM1
f ),
y∈y и TM=TM1-y. Тогдасправедливо TM
f -y).
Утверждение непосредственно следует из того, что вектор-функци
f удовлетворяет TM1.
Следующие операции между ТМ и объектами в приближённой арифметике (скаляр, век-
тор, матрица) являются по существу чуть более краткой записью операций между ТМ и со-
ответствующими точеными интервалами и не требуют отдельных алгоритмов.
Определение 2. Произведением TM1 и числа u, заданного в приближённой арифметике,
будем называть произведение TM1[u, ] и обозначать его как TM1u или uTM1.
Утверждение 2. Пусть TM1
f ), TM = uTM1. Тогда выполняется TM(
f ).
Определение 3. Суммой TM1 размерности q и вектора y размерности q, заданного в
приближённой арифметике, будем называть сумму TM1 + [y, ] и обозначать её как TM1 + y
или y + TM1.
Утверждение 3. Пусть TM1
f ), TM = y + TM1. Тогда имеет место TM(y
f ).
Определение 4. Разностью между TM1 размерности q и вектором y размерности q,
заданным в приближённой арифметике, будем называть разность TM1 - [y, ] и обозначать её
как TM1 - y.
Утверждение 4. Пусть TM1
f ), TM = TM1 - y. Тогда справедливо TM
f - y).
Определение 5. Произведением TM1 размерности q и матрицы W ∈ Rq×q, заданной
в приближённой арифметике, будем называть произведение [W, ]TM1 и обозначать его как
WTM1.
Утверждение 5. Пусть TM1
f ), TM = W TM1. Тогда выполняется TM(
f ).
Доказательство утверждений 2-5 следует непосредственно из аналогичных свойств опера-
ций ТМ с интервалами (утверждение 1 данной статьи и утверждения 2-4 из [9]) и элементар-
ного свойства точечного интервала u ∈ [u, ].
Дополнительно введём новый специальный скалярный интервал Bmonn
. Основное его
1,...,nm
∈ Bmonn
при x ∈ M. Это свойство выполнено, ес-
свойство следующее: xn11 x2s . . . xmm
1,...,nm
ли, например, положить Bmonn
равным [-1, 1] для любых n1, . . . , nm. Однако оценку
1,...,nm
можно несколько улучшить, положив Bmon0,...,0 = [1, 1] и оставив Bmonn
равным [-1, 1] при
1,...,nm
(n1, . . . , nm) = (0, . . . , 0). Конкретный выбор при соблюдении указанного включения не влияет
на доказательства свойств TM, но изменяет оценки, получаемые при практическом примене-
нии алгоритмов.
В п. 2 при формализации алгоритма из [18] нам понадобится ранее не определённая опера-
ция дифференцирования полиномиальной части интервальной модели Тейлора, в результате
которой получается новая ТМ.
Алгоритм 2. Вход
P1,n(x),k). Выход (TM =
Pn(x),I〉).
Положим
{
0,
(n1, . . . , nm) ∈ Sm(n),
en1,...,nk,...,nm :=
/(nk + 1)an1,...,nk+1,...,nm /, (n1, . . . , nm) ∈ Rm(n - 1),
∑
I :=
Bmonn
1,...,nm
([(nk + 1), ][an1,...,nk+1,...,nm , ] - [en1,...,nk,...,nm,]).
(n1,...,nm)∈Rm(n-1)
Определение 6. Под операцией ТМ-дифференцирования полином
P1,n(x) по переменной
xk будем понимать результат работы алгоритма 2 и обозначать её как (∂TM
P1,n(x)/∂xk).
Утверждение 6. Пусть TM является TM-производной полином
P1,n(x) по перемен-
ной xk. Тогда имеет место TM(
P1,n(x)/∂xk).
Доказательство. Пусть
P1,n(x)/∂xk : M → Rq, где M ≜ [-1,1]m ⊂ Rm.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
415
Утверждение, что имеет место TM(
P1,n(x)/∂xk), равносильно тому, что для любых век-
тора x ∈ M и числа j ∈ {1, . . . , q} справедливо неравенство
1,n
∂Pj
Pnj(x) + L(Ij) ≤
(x) ≤ Pnj(x) + H(Ij).
(1)
∂xk
Покажем справедливость этого неравенства.
Для любых вектора x ∈ M и числа j ∈ {1, . . . , q} имеем
∑
P1,nj(x) =
{an1,...,nm }j x11 x22 . . . xmm ,
(n1,...,nm)∈Rm(n)
∑
Pnj(x) =
{en1,...,nm }j x11 x22 . . . xmm ,
(n1,...,nm)∈Rm(n)
∂P1,nj(x)
∑
=
(nk + 1){an1,...,nk+1,...,nm }j x11 x22 . . . xmm .
∂x
k
(n1,...,nm)∈Rm(n-1)
Учитывая, что согласно алгоритму при (n1, . . . , nm) ∈ Sm(n) коэффициенты
en1,...,nk,...,nm
равны нулю, представим производную полинома
P1,n(x) по переменной xk в следующем
виде:
∂P1,nj(x)
∂P1,nj(x)
∑
= Pnj (x) - Pnj (x) +
= Pnj (x) -
{en1,...,nm }j x11 x22 . . . xmm +
∂xk
∂xk
(n1,...,nm)∈Rm(n-1)
∑
+
(nk + 1){an1,...,nk+1,...,nm }j x11 x22 . . . xmm =
(n1,...,nm)∈Rm(n-1)
∑
= Pnj (x) +
(2)
((nk + 1){an1,...,nk+1,...,nm }j - {en1,...,nm}j)x11 x22 . . . xmm .
(n1,...,nm)∈Rm(n-1)
Так как
,
(nk + 1) ∈ [(nk + 1), ],
,...,nm
{an1,...,nk+1,...,nm }j ∈ [{an1,...,nk+1,...,nm}j,],
{en1,...,nm }j ∈ [{en1,...,nm}j,],
то, согласно основной теореме интервального анализа, справедливо следующее включение:
∑
((nk + 1){an1,...,nk+1,...,nm }j - {en1,...,nm}j)x11 x22 . . . xmm ∈
(n1,...,nm)∈Rm(n-1)
∑
∈
Bmonn
([(nk + 1), ][{an1,...,nk+1,...,nm }j , ] - [{en1,...,nm}j,]).
1,...,nm
(n1,...,nm)∈Rm(n-1)
Из определения ТМ-дифференцирования полинома вытекает, что
∑
Ij =
Bmonn
1,...,nm
([(nk + 1), ][{an1 ,...,nk+1,...,nm }j , ] - [{en1,...,nm}j,]),
(n1,...,nm)∈Rm(n-1)
поэтому для любых вектора x ∈ M и числа j ∈ {1, . . . , q} получаем оценки
∑
(3)
((nk + 1){an1,...,nk+1,...,nm }j - {en1,...,nm}j)x11 x22 . . . xmm ≥ L(Ij),
(n1,...,nm)∈Rm(n-1)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
416
ЕВСТИГНЕЕВ и др.
∑
((nk + 1){an1,...,nk+1,...,nm }j - {en1,...,nm}j)x11 x22 . . . xmm ≤ H(Ij ).
(4)
(n1,...,nm)∈Rm(n-1)
Из соотношений (2)-(4) следуют неравенства
∂P1,nj
∂P1,nj
(x) ≥ Pnj(x) + L(Ij),
(x) ≤ Pnj(x) + H(Ij ),
∂xk
∂xk
которые равносильны неравенству (1). Утверждение доказано.
Приведём теперь теорему из [18], сформулировав её в терминах и обозначениях, использу-
емых в настоящей статье. Эта теорема является основой соответствующего метода стягиваю-
щего обрамления.
Теорема 1. Пусть вектор-функци
f (z),
g(z) и числа β, γ ∈ R удовлетворяют следу-
ющим условиям:
1)
f,g : [-1,1]q → Rq;
2)
f,g ∈ C1([-1,1]q);
3)
f (z)
id(z) + g(z) (напомним, чт
id(z) = z);
4) |gi(z)| < β,
|∂gi(z)/∂zj | < γ для всех i, j ∈ {1, . . . , q} и z ∈ [-1, 1]q, причём
{
(1 - qγ) > 0,
(1 - β) > 0.
Тогда для любых векторов z0 ∈ [-1, 1]q и v ∈ [-α, α]q (α ∈ R, α > 0) существует
вектор z′0 ∈ [-1, 1]q такой, что выполнено равенство
f (z0) + v =
f(z′0),
где
1 + (q - 1)γ
μ=1+α
(1 - (q - 1)γ)(1 - β)
2. Алгоритмы стягивающего обрамления интервальных моделей Тейлора.
Определение 7. Будем говорить, что интервальная модель Тейлора TM является обрам-
лением интервальной модели Тейлора TM1 (или что TM обрамляет TM1), если имеет место
включение Im (TM1) ⊂ Im (TM).
Определение 8. Будем говорить, что алгоритм Algo является алгоритмом обрамления
(обрамляющим алгоритмом), если для него выполняются следующие условия:
1) Algo на вход принимает одну модель Тейлора TM1 и набор индексов (i1, . . . , iq), причём
полино
P1,n(x) модели TM1 не зависит от xi при i ∈ {i1,... ,iq};
2) на выходе Algo имеет флаг завершения операции (целое число res, равное 1 в случае
успешного завершения работы и 0 в противном случае) и ровно одну модель Тейлора TM;
3) при успешном завершения Algo (res = 1) TM является обрамлением TM1, а полином
Pn(x) модели TM не зависит от xi при i ∈ {i1,... ,iq}.
Будем говорить, что TM является стягивающим обрамлением TM1, если TM обрамляет
TM1 и, кроме того, имеет нулевой или близкий к нулевому (на уровне точности приближённой
арифметики) остаток. Аналогично можно ввести и понятие алгоритма стягивающего обрам-
ления. Поскольку мы не формализуем здесь понятие “близкий к нулевому” и данные опреде-
ления не используются в доказываемых нами свойствах алгоритмов, мы не будем вводить эти
понятия строго. С другой стороны, при практическом использовании ТМ для интегрирования
ОДУ именно устранение остатка ТМ на каждом шаге предотвращает их экспоненциальное
разрастание.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
417
Оба рассматриваемых в статье алгоритма стягивающего обрамления используют общий
принцип (рис. 1): исходная ТМ с помощью линейных преобразований изменяется таким обра-
зом, чтобы её линейная часть переводилась в эталонный гиперкуб; осуществляется определён-
ная модификация линейно преобразованной ТМ (основной шаг, свой для каждого алгоритма);
к модифицированной ТМ применяются обратные линейные преобразования.
Как сказано во введении, мы рассмотрим два алгоритма стягивающего обрамления. Ос-
новной шаг первого (алгоритм 3) основан на результатах, приведённых в работе [18], и предпо-
лагает использование теоремы 1. Основной шаг второго алгоритма (алгоритм 4) основывается
на использовании интервальной внешней оценки ТМ.
Начнём с формального описания алгоритма, суть которого была изложена в [18]. В этом
алгоритме используется операция ТМ-дифференцирования, введённая выше определением 6.
(а)
(б)
(в)
(г)
Рис. 1. Общий принцип модификации ТМ (на примере ТМ размерности q = 2, пунк-
тирной линией отмечена линейная часть исходной ТМ): а) образ исходной ТМ, б) образ
линейно преобразованной ТМ, в) образы линейно преобразованной ТМ и её модифи-
кации, г) образы исходной ТМ и её модификации.
Алгоритм 3. Вход (TM1, (i1, . . . , iq)). Выход (TM, res).
Шаг 1. Сформируем матрицу W = (Wlk)l,k=1 ∈ Rq×q, элементы которой возьмём следую-
щими:
{W }lk := {a0,...,1,0,...,0}l, k ∈ {1, . . . , q}, l ∈ {1, . . . , q}.
ik
Шаг 2. Численно обратим матрицу W, полученную в результате матрицу обозначим
W -1.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
418
ЕВСТИГНЕЕВ и др.
Шаг 3. Применим алгоритм 4 из [9] к матрице
W -1, на выходе получим res1 и интерваль-
ную матрицу W. Если res1 = 0, положим res := 0 и завершим выполнение алгоритма.
Шаг 4. Положим TM2 := [W-1, ](TM1 - a0,...,0).
Шаг 5. Построим TM3 =
P3,n(x),⃗I3〉, все коэффициенты полинома которой возьмём рав-
ными нулю, кроме следующих:
{c0,...,1,0,...,0}l := δkl,
k ∈ {1,...,q}, l ∈ {1,...,q},
ik
и положимI3 :=
[0,].
Шаг 6. Положим TM4 :=
P2,n(x),
[0,]〉 - TM3.
Шаг 7. Найдём такое число α, что⃗I2 ⊂ [-α,α]q.
Шаг 8. Найдём такое число β, что EB(TM4) ⊂ [-β, β]q.
Шаг 9. Найдём такое число γ, что
)
(∂T
P2,n(x)
∂TM
P3,n(x)
EB
-
⊂ [-γ, γ]q, k ∈ {i1, . . . , iq}.
∂xk
∂xk
Шаг 10. Проверим выполнение условия
{
([1, ] - [q, ][γ, ]) > [0, ],
([1, ] - [β, ]) > [0, ].
Если это условие выполнено, то положим res := 1. В противном случае положим res := 0 и
завершим выполнение алгоритма.
[1, ] + ([q, ] - [1, ])[γ, ]
Шаг 11. Положим μ := [1, ] + [α, ]
([1, ] - ([q, ] - [1, ])[γ, ])([1, ] - [β, ])
Шаг 12. Положим TM := Wμ
P2,n(x),
[0,]〉 + a0,...,0.
Покажем, что в случае успешного завершения (res = 1) полученная в результате работы
алгоритма 3 TM является обрамлением исходной TM1 и её полином зависит только от нужных
аргументов, т.е. алгоритм 3 является алгоритмом обрамления.
Утверждение 7. Пусть алгоритм 3 с входом (TM1, (i1, . . . , iq)) возвращает res = 1
и TM , причём полином
P1,n(x) не зависит от xi при i ∈ {i1,... ,iq}. Тогда справедливо
включение Im (TM1) ⊂ Im (TM) и полино
Pn(x) не зависит от xi при i ∈ {i1,... ,iq}.
Доказательство. Пусть y ∈ Im (TM1), тогда существует x0 ∈ M = [-1, 1]m такой, что
для всех j ∈ {1, . . . , q} выполнено двойное неравенство
P1,nj(x0) + L(I1j) ≤ {y}j ≤ P1,nj(x0) + H(I1j).
Прибавив полином P1,nj(x) - P1,nj(x0) ко всем частям этого неравенства, будем иметь
P1,nj(x) + L(I1j) ≤ {y}j + P1,nj(x) - P1,nj(x0) ≤ P1,nj(x) + H(I1j),
это означает, что имеет место TM1(y
P1,n(x)
P1,n(x0)).
Так как TM1(y
P1,n(x)-P1,n(x0)),
W -1 ∈ [W-1,] и в соответствии с алгоритмом TM2 =
= [ W -1,](TM1 - a0,...,0), то, согласно утверждениям 3 и 4 из [9], справедливо TM2( W -1(y -
-a0,...,0
P1,n(x)
P1,n(x0))). Поэтому для всех x ∈ M и j ∈ {1,... ,q} выполнено неравенство
P2,nj(x) + L(I2j) ≤ {W-1(y - a0,...,0
P1,n(x)
P1,n(x0))}j ≤ P2,nj(x) + H(I2j),
причём [L(I2j), H(I2j)] ⊂ [-α, α]. В частности, для x = x0 имеем
P2,nj(x0) + L(I2j) ≤ {W-1(y - a0,...,0)}j ≤ P2,nj(x0) + H(I2j).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
419
Представим полученное неравенство в следующем виде:
P2,nj(x0) + L(I2j) ≤ P2,nj(x0) + {W-1(y - a0,...,0)
P2,n(x0)}j ≤ P2,nj(x0) + H(I2j),
откуда следует, что для всех j ∈ {1, . . . , q} справедливо включение
{W-1(y - a0,...,0)
P2,n(x0)}j ∈ [L(I2j),H(I2j)] ⊂ [-α,α].
Согласно предположению утверждения полином
P1,n(x) не зависит от xi при i
∈
∈ {i1, . . . , iq}, поэтому полиномы
P2,n(x),
P3,n(x) и
P4,n(x) также можно рассматривать
как не зависящие от xi при i ∈ {i1, . . . , iq} (см. замечание 1). Сформируем вектор
z =
= (z1, . . . , zq)т ∈ [-1, 1]q c элементами zk = xik , k ∈ {1, . . . , q}, и рассмотрим вектор-функцию
f (z)
P2,n(z). Тогда для вектора z0, соответствующего вектору x0, при всех j ∈ {1,... ,q}
справедливо включение
{W-1(y - a0,...,0)
f (z0)}j ⊂ [-α, α].
Функци
f (z) может быть представлена в вид
f (z)
id(z) +g(z), тогда согласно алгоритму
для всех z∗ ∈ [-1, 1]q и j ∈ {1, . . . , q} выполнены включения
gj(z∗) ∈ {EB(TM4)}j ⊂ [-β,β],
{
)}
∂gj(z∗)
(∂T
P2,n(z)
∂TM
P3,n(z)
∈ EB
-
⊂ [-γ, γ], k ∈ {1, . . . , q},
∂zk
∂zk
∂zk
j
которые позволяют применить к
f (z) теорему 1, вследствие которой при всех j ∈ {1, . . . , q}
имеет место равенство
{ W -1(y - a0,...,0)}j = μfj(z′0),
z′0 ∈ [-1,1]q.
(5)
При переходе от вектора z′0 ∈ [-1, 1]q к вектору x′0 ∈ M по правилу
∑
x′0 =
{z′0}kei
, где eik = (0, . . . , 0, 1, 0, . . . , 0)т ∈ Rm,
k
k=1
ik
равенство (5) при любом j ∈ {1, . . . , q} может быть преобразовано к виду
{ W -1(y - a0,...,0)}j = μP2,nj(x ′0),
x′0 ∈M,
причём, согласно основной теореме интервального анализа, μ ∈ μ.
Прибавив полином μP2,nj(x) - μP2,nj(x′0) к обеим частям этого равенства, получим
{ W -1(y - a0,...,0)}j + μP2,nj(x) - μP2,nj(x ′0) = μP2,nj(x),
это означает, что справедливо
TM(W-1(y - a0,...,0) +
P2,n(x) -
P2,n(x′0)),
где TM = μ
P2,n(x),
[0,]〉.
Так как TM(W-1(y - a0,...,0) +
P2,n(x) -
P2,n(x′0)),
[ W -1]-1 ∈ W и в соответствие с
алгоритмом TM = Wμ
P2,n(x),
[0,]〉 + a0,...,0, то, согласно утверждениям 3 и 4 из [9], имеет
место TM([W-1]-1[W-1(y -a0,...,0) +
P2,n(x) -
P2,n(x′0)] +a0,...,0). Поэтому для всех x ∈ M
и j ∈ {1,...,q} выполнено двойное неравенство
Pnj(x) + L(Ij) ≤ {[W-1]-1[W-1(y - a0,...,0) +
P2,n(x) -
P2,n(x′0)] + a0,...,0}j ≤ Pnj(x) + H(Ij).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
420
ЕВСТИГНЕЕВ и др.
В частности, для x = x′0 имеем Pnj (x′0) + L(Ij) ≤ {y}j ≤ Pnj (x′0) + H(Ij), из чего следует, что
y ∈ Im(TM).
Из сказанного выше вытекает, что если y ∈ Im (TM1), то y ∈ Im (TM). Это равносильно
включению Im (TM1) ⊂ Im (TM). О независимости полином
Pn(x) от xi при i ∈ {i1,... ,iq}
см. замечание 1. Утверждение доказано.
Замечание 1. Тот факт, что полино
P3,n(x) в доказательстве утверждения 7 не зависит
от xi при i ∈ {i1, . . . , iq}, вытекает из самого алгоритма 3. Для полиномов
P2,n(x) и
P4,n(x)
это свойство следует из алгоритма 3, алгоритмов, используемых при построении TM2 и TM4
(разность ТМ, разность ТМ и вектора, умножение ТМ на матрицу и число), а также из свой-
ства приближённой арифметики /0x/ = 0, указанного в п. 1. Аналогично показывается, что
это же свойство выполнено и для результирующего полинома
Pn(x), который получается из
полинома
P2,n(x) при помощи того же набора операций (см. алгоритм 3).
Реализуем второй подход и построим алгоритм стягивающего обрамления ТМ, основанный
на использовании интервальной внешней оценки ТМ.
Алгоритм 4. Вход (TM1, (i1, . . . , iq)). Выход (TM, res).
Шаг 1. Сформируем матрицу W = (Wlk)ql,k=1 ∈ Rq×q, элементы которой возьмём следую-
щими:
{W }lk := {a0,...,1,0,...,0}l, k ∈ {1, . . . , q}, l ∈ {1, . . . , q}.
ik
Шаг 2. Численно обратим матрицу W, полученную в результате матрицу обозначим
W -1.
Шаг 3. Применим алгоритм 4 из [9] к матрице
W -1, на выходе получим res1 и интерваль-
ную матрицу W. Если res1 = 0, положим res := 0 и завершим выполнение алгоритма. Если
res1 = 1, положим res := 1 и продолжим выполнение алгоритма.
Шаг 4. Положим TM2 := [W-1, ](TM1 - a0,...,0).
Шаг 5. Положим z := EB(TM2).
Шаг 6. Построим TM3, все коэффициенты полинома которой возьмём равными нулю,
кроме следующих:
{c0,...,1,0,...,0}j := max{|L(zj )|, |H(zj )|}, j ∈ {1, . . . , q},
ij
и положимI3 :=
[0,].
Шаг 7. Положим TM := WTM3 + a0,...,0.
Покажем, что алгоритм 4 также является алгоритмом обрамления. Заметим, что в отличие
от алгоритма 3 алгоритм 4 может завершиться неуспешно (res = 0) только в случае числен-
ного вырождения матрицы линейной части исходной TM, в то время как алгоритм 3 может
прийти к негативному результату также и на основном шаге.
Утверждение 8. Пусть алгоритм 4 с входом (TM1, (i1, . . . , iq)) возвращает res = 1 и
TM. Тогда имеет место включение Im (TM1) ⊂ Im (TM) и полино
Pn(x) не зависит от
xi при i ∈ {i1,... ,iq}.
Доказательство. Пусть y ∈ Im (TM1), тогда существует x0 ∈ M = [-1, 1]m такой, что
для всех j ∈ {1, . . . , q} выполнено двойное неравенство
P1,nj(x0) + L(I1j) ≤ {y}j ≤ P1,nj(x0) + H(I1j).
Прибавив полином P1,nj(x) - P1,nj(x0) ко всем частям этого неравенства, получим
P1,nj(x) + L(I1j) ≤ {y}j + P1,nj(x) - P1,nj(x0) ≤ P1,nj(x) + H(I1j),
это означает, что имеет место TM1(y
P1,n(x)
P1,n(x0)).
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
421
Так как TM1(y
P1,n(x)-P1,n(x0)),
W -1 ∈ [W-1,] и в соответствии с алгоритмом TM2 =
= [ W -1,](TM1 - a0,...,0), то, согласно утверждениям 3 и 4 из [9], выполняется TM2( W -1(y -
-a0,...,0
P1,n(x)
P1,n(x0))). Тогда, согласно утверждению 7 из [8], (W-1(y-a0,...,0
P1,n(x)-
−
P1,n(x0))) ∈ EB(TM2) для всех x ∈ M, в частности, для x = x0 справедливо включение
( W -1(y - a0,...,0)) ∈ EB(TM2) = z, т.е. для всех j ∈ {1,... ,q} верны неравенства
-max{|L(zj)|,|H(zj)|} ≤ L(zj) ≤ {W-1(y - a0,...,0)}j ≤ H(zj) ≤ max{|L(zj)|,|H(zj)|}.
Для каждого j ∈ {1, . . . , q} такого, что max{|L(zj )|, |H(zj )|} = 0, разделив все части полу-
ченного неравенства на max{|L(zj )|, |H(zj )|}, будем иметь
{ W -1(y - a0,...,0)}j
-1 ≤
≤ 1.
max{|L(zj )|, |H(zj )|}
Согласно алгоритму P3,nj(x) = max{|L(zj )|, |H(zj )|}xij при всех j ∈ {1, . . . , q}, поэтому
существует такой вектор x′0 ∈ M, что при всех j ∈ {1, . . . , q} справедливо равенство
{ W -1(y - a0,...,0)}j = P3,nj(x ′0),
(6)
вектор x′0 в котором определяется следующим образом:
∑
{ W -1(y - a0,...,0)}j
x′0 =
eij , где eij = (0,... ,1,0,... ,0)т ∈ Rm.
max{|L(zj )|, |H(zj )|}
j=1
ij
max{|L(zj )|,|H(zj )|}=0
Прибавив полином P3,nj(x) к обеим частям равенства (6), получим
{ W -1(y - a0,...,0)}j + P3,nj(x) - P3,nj(x ′0) = P3,nj(x),
это означает, что имеет место TM3(W-1(y - a0,...,0)
P3,n(x)
P3,n(x′0)).
Так как TM3(W-1(y - a0,...,0)
P3,n(x)
P3,n(x′0)),
[ W -1]-1 ∈ W и в соответствии с
алгоритмом TM = WTM3 + a0,...,0, то, согласно утверждениям 3 и 4 из [9], справедливо
TM([W-1]-1[W-1(y - a0,...,0)
P3,n(x)
P3,n(x′0)] + a0,...,0). Поэтому для всех
x ∈ M и j ∈
∈ {1, . . . , q} выполнено двойное неравенство
Pnj(x) + L(Ij) ≤ {[W-1]-1[ W-1(y - a0,...,0) +
P3,n(x)
P3,n(x′0)] + a0,...,0}j ≤ Pnj(x) + H(Ij).
В частности, для x = x′0 имеем Pnj(x′0) + L(Ij) ≤ {y}j ≤ Pnj(x′0) + H(Ij ), откуда следует, что
y ∈ Im(TM).
Из сказанного выше вытекает, что если y ∈ Im (TM1), то y ∈ Im (TM). Это равносильно
включению Im (TM1) ⊂ Im (TM). О независимости полином
Pn(x) от xi при i ∈ {i1,... ,iq}
см. замечание 2. Утверждение доказано.
Замечание 2. Для утверждения 8 рассуждения относительно полином
Pn(x) полностью
аналогичны тем, которые проведены в замечании 1: полином
P3,n(x) не зависит от xi при
i ∈ {i1, . . . , iq} согласно построению, а сам
Pn(x) получается из
P3,n(x) умножением на
матрицу и прибавлением вектора (см. алгоритм 4).
Замечание 3. Интервал Bmonn
не вводился нами в статьях [8, 9], вместо него в алгорит-
1,...,nm
мах мы явно использовали интервал [-1, 1] для всех мономов. При практическом использова-
нии последняя оценка для свободного члена оказывается достаточно грубой. Для улучшения
результата работы алгоритмы 1-6 из статьи [8] и алгоритмы 1 и 5 из [9] могут быть модифи-
цированы следующим образом. Во всех формулах для вычисления остаткаI результирую-
щей TM необходимо в сумме по индексам n1, . . . , nm заменить интервал [-1, 1] на интервал
9
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
422
ЕВСТИГНЕЕВ и др.
Bmonn
. Например, в [8] в алгоритме 1 изменится присваивание (1), в алгоритме 4 - присва-
1,...,nm
ивание дляA, в алгоритме 5 - присваивание (6) и т.д. Все доказательства остаются верными,
”.
,...,nm
Наиболее существенное улучшение результата получается при изменении алгоритма 3 из [8]
(вычисление оценки полинома) и использующего этот алгоритм алгоритма 7 из [8] (внешняя
оценка ТМ). Во всех остальных алгоритмах происходит улучшение результата на уровне точ-
ности приближённой арифметики.
3. Алгоритм интегрирования ОДУ и систем ОДУ с использованием модифици-
рованных интервальных моделей Тейлора. Рассмотрим задачу Коши
dy
=
f (y),
dt
y(0) = y0,
(7)
где правая часть
f уравнения задана в некоторой области и является в ней липшицевой
функцией с константой L, т.е. удовлетворяет неравенству
f (y2)
f (y1)∥2 ≤ L∥y2 - y1∥2.
Через
F обозначим TM-расширение функции
f, а интервальное расширение [Δt, ] числа
Δt - через Δt.
На основе алгоритма 10 из [8] построим алгоритм интегрирования ОДУ и систем ОДУ с ис-
пользованием модифицированных интервальных моделей Тейлора. В данной статье в отличие
от [8] мы выделим из общего алгоритма интегрирования один логический блок - выполне-
ние одного шага интегрирования по времени методом итераций Пикара без использования
стягивающего обрамления. Одним из входных параметров приводимого ниже алгоритма 5 яв-
ляется величина ϵ. Этот параметр нужен для задания критерия сходимости итераций Пикара
и может быть разным в различных реализациях алгоритма. Величина ϵ может быть как ве-
щественным числом, задающим границу изменения остатка ТМ от итерации к итерации, так и
целым числом, определяющим количество итераций или комбинацией этих параметров. Кон-
кретный критерий не имеет значения с т.з. доказательных свойств алгоритма, но существенно
влияет на качество получаемых оценок и скорость работы.
Алгоритм 5. Вход (TM0, Δt, S, ϵ
F ). Выход (res, TM).
Шаг 1. Положим s := 1, TM1 := TM0.
Шаг 2. Положим TMs+1 равной выходу алгоритма 9 из [8] с входом (TM0,TMs,Δt,
F ).
Шаг 3. Если s = n, перейдём на шаг 4, в противном случае положим s := s+1 и перейдём
на шаг 2
Шаг 4. Положим s := 1. Построим TM1 следующим образом: её полиномиальную часть
положим равной полиномиальной части TMn+1, а остаток выберем, основываясь на свойствах
TM0 и полиномиальной части TMn+1 (например, расширив остаток TM0 или используя
оценку полиномиальной части TMn+1).
Шаг 5. Положим TMs+1 равной выходу алгоритма 9 из [8] с входом (TM0, TMs, Δt,
F ).
Шаг 6. Если алгоритм 8 из [8] с входом (TMs+1, TMs) вернул 1, перейдём на шаг 7, иначе
положим TMs+1 равной некоторой модификации TMs (например, умножив её остаток на
какое-либо число) и перейдём на шаг 8.
Шаг 7. Проверим TMs+1 на соответствующее условие сходимости остатка, определяемое
параметром ϵ (например, сравнив остаток TMs+1 по некоторому критерию близости с остат-
ком TMs или проверив минимальное количество итераций, для которых проверка из п. 6
завершилась успешно). Если это условие сходимости выполнено, положим TM := TMs+1,
res := 1 и завершим алгоритм.
Шаг 8. Если s = S, завершим алгоритм, положив res := 0, в противном случае положим
s := s + 1 и перейдём на шаг 5.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
423
Замечание 4. На шагах 1, 2 и 3 выполняется вычисление полиномиальной части ТМ,
которая при дальнейших итерациях меняться не будет. Заметим, что во всех используемых на
этих шагах алгоритмах работы с ТМ остаток никак не влияет на полиномиальную часть (что,
по сути, верно для почти всех базовых ТМ алгоритмов). Поскольку в алгоритме 5 используется
только полиномиальная часть TMn+1, на указанных шагах остатки ТМ могут не вычисляться,
что даёт возможность для некоторой оптимизации.
Алгоритм 6. Вход (TM10, Δt, N, S, ϵ, Algo, NAlgo
F,(i1,...,iq)). Выход (N,{TMl}Nl=1).
Шаг 1. Положим l := 1.
Шаг 2. Положим TMl и res равными выходу алгоритма 5 с входом (TMl0, Δt, S, ϵ
F ).
Если res = 1, перейдём на шаг 3, в противном случае положим N := l - 1 и закончим
выполнение.
l+1
Шаг 3. Если l = N, закончим выполнение, в противном случае положим TM
:=
0
:= TMl|x1=1 и перейдём на шаг 4.
Шаг 4. Если l mod NAlgo = 0, положим TMl+10 равным TMl+10 и перейдём на шаг 2, в
противном случае перейдём на шаг 5.
Шаг 5. Положим TMl+10 и res равными выходу алгоритма Algo с входом (TMl+10, (i1, . . . , iq)).
Если res = 0, положим N := l - 1 и закончим выполнение, в противном случае положим l :=
:= l + 1 и перейдём на шаг 2.
Покажем, что алгоритм 6 может быть использован для построения решений ОДУ и сис-
тем ОДУ.
Утверждение 9. Пусть TMl0 =
Pl,n0,Il0〉 и TMl =
Pl,n,Il〉 для l = 1,N. Пусть для
задачи (7) заданы:
1) TM-расширение
F функции f - правой части уравнения задачи (7);
2) число Δt и его интервальное расширение Δt;
3) TM10, полином которо
P1,n0 не зависит от x1 и для которой существуют x02,... ,x0m
из отрезка [-1,1] такие, что y0 ∈
P1,n0(x02,... ,x0m) + L(I10)
P1,n0(x02,... ,x0m) + H(⃗I10)] (иначе
говоря, y0 ∈ Im (TM10)).
Пусть алгоритм Algo является алгоритмом обрамления. Пусть, далее, алгоритм 6 с вхо-
дом (TM10, Δt, N, S, ϵ, Algo, NAlgo
F,(2,...,m)) вернул (N,{TMl}Nl=1). Тогда классическое ре-
шение y(t) задачи (7) с начальными условиями y0 существует хотя бы на отрезке [0,NΔt]
и для всех l = 1,N найдутся такие xl2,... ,xlm ∈ [-1,1], для которых при всех j ∈ {1,... ,q}
выполнено двойное неравенство
(
)
(
)
t
t
Pl,n
- l + 1,xl2,...,xlm
+ L({⃗Il}j) ≤ yj(t) ≤ Pl,n
- l + 1,xl2,...,xl
+H({⃗Il}j),
j
j
m
Δt
Δt
где t ∈ [(l - 1)Δt, lΔt].
Доказательство. Утверждение 9 полностью совпадает с доказательством утверждения 19
из [9] с тем лишь отличием, что при доказательстве неравенства (18) из [9] на каждом шаге
индукции необходимо учитывать определение 8 и то, что Algo - алгоритм обрамления, а также
способ построения TMl+10 на шаге 4 алгоритма 6. Кроме того, в силу этого значения x02, . . . , x0m,
использовавшиеся в оценках на каждом шаге в утверждении 19 из [9], должны быть заменены
значениями xl2, . . . , xlm, которые в общем случае различны для разных шагов l. Утверждение
доказано.
Напомним, что, согласно утверждениям 7 и 8, алгоритмы 3 и 4 являются алгоритмами
обрамления, т.е. могут быть использованы в качестве Algo.
4. Пример применения. Рассмотрим задачу Коши для классической системы, описыва-
ющей осциллятор Ван дер Поля:
dx
1
dy
=x-
x3 - y,
= x, t > 0,
dt
3
dt
x(0) = x0, y(0) = y0.
(8)
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
9∗
424
ЕВСТИГНЕЕВ и др.
Решение данной задачи получено аналитически и представляет собой при x0 ≈ -2.0085,
y0 ≈ 0 в фазовом пространстве замкнутую траекторию, что позволяет её наглядно визу-
ализировать. Это обуславливает выбор задачи (8) в качестве модельной для демонстрации
построенных в настоящей работе алгоритмов, а полученные результаты можно использовать
для доказательства существования периодического решения с использованием методов ДВ.
Для численного описания множества решений задачи (8) используем интервальную мо-
дель Тейлора с параметрами n = 2, m = 3, q = 2. При этом полиномиальная часть ТМ
P2(x1,x2,x3) определена на множестве [-1,1]3, остаток⃗I принадлежит R2, переменная x1
соответствует переменной t исходной задачи, переменная x2 - значению функции x, пере-
менная x3 - значению функции y.
Из численного моделирования известно, что решение задачи (8) имеет замкнутую траекто-
рию в окрестности начальных условий x0 ≈ -2.0085, y0 ≈ 0, поэтому в качестве начального
приближения выберем следующую ТМ:
(
)
(
)
-2.0086 + 0.004x2 + 0.00002x3
[0, ]
TM10 =
,
-0.0011x2 + 0.0125x3
[0, ]
ТМ-расширениеF (TM) правой части (8) строится естественным образом.
Применим следующие алгоритмы: алгоритм 10 из [8], не использующий обрамление (“на-
ивный” алгоритм Пикара); алгоритм 6 с алгоритмом обрамления 3 (стягивающее обрамление
Макино-Берца); алгоритм 6 с алгоритмом обрамления 4 (предложенный в настоящей статье
вариант стягивающего обрамления). Используем следующие входные данные:
TM10, Δt = 0.0005, N = 14000 (на один период),
S = 5, NAlgo = 1,
F (TM), (i1, i2) = (2, 3).
В качестве критерия завершения итераций Пикара используется условие малости изменения
всех остатков от итерации к итерации относительно ширины самих остатков (ϵ = 10-2). На
выходе получим последовательность {TMl}Nl=1, описывающую множество решений задачи (8).
На рис. 2 и 3 представлены графики, демонстрирующие полученный результат для различных
алгоритмов.
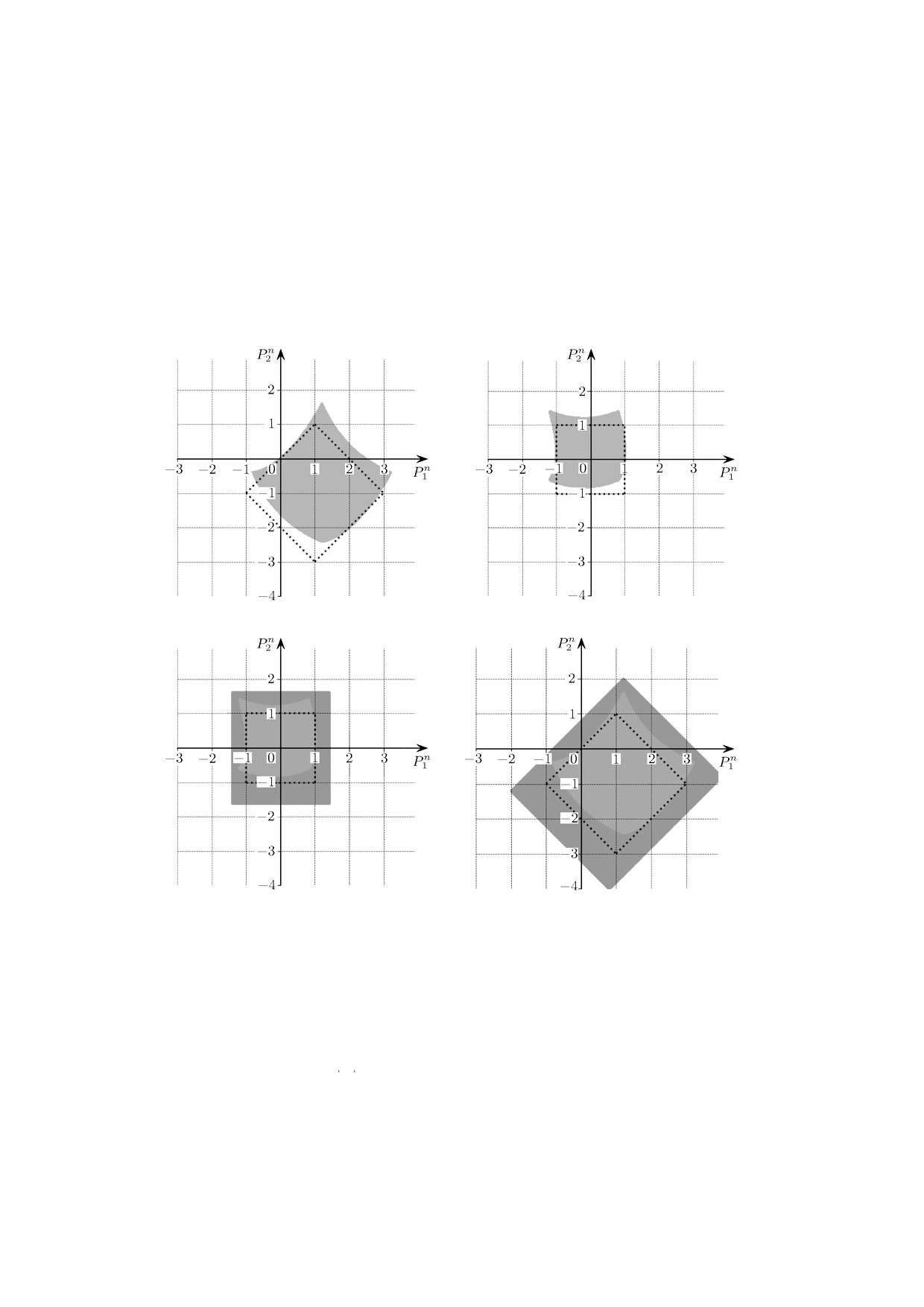
Из рис. 2 видно, что множество решений, построенных “наивным” алгоритмом Пикара,
претерпевает экспоненциальное расширение в двух направлениях, отвечающих переменным
фазового пространства (пунктирная линия). Для алгоритма интегрирования, использующего
стягивающее обрамления Макино-Берца, характерно быстрое разрастание оценок множества
решений в направлении, касательном циклу (штриховая линия на рис. 2, подробнее - рис. 3, а).
Это можно связать с особенностями построения модифицированных ТМ алгоритмом 3, а так-
же структуры ТМ, выбранной в качестве начального приближения.
При прочих равных условиях (ТМ второго порядка) из рассматриваемых алгоритмов тра-
екторию решения задачи (8) за один период позволяет описать только алгоритм интегрирова-
ния, использующий предложенный нами вариант стягивающего обрамления. Кроме того, при
движении по траектории множество решений, описываемых ТМ, сужается (рис. 3, б), что мо-
жет быть использовано при доказательстве существования периодического решения в системе
(8) (для завершения доказательства необходимо аккуратно описать сечение и использовать
результаты интегрирования для оценки отображения Пуанкаре).
Отметим, что попадание начальной окрестности цикла в себя удаётся доказать только в
случае использования специально выбранной начальной ТМ, расположенной вдоль собствен-
ных векторов матрицы монодромии цикла, как это делалось в [9]. В противном случае проис-
ходит численное вырождение линейной части ТМ, ухудшающее результат применения предло-
женного алгоритма стягивающего обрамления, так как в последнем соответствующая матрица
обращается. Однако остальные рассмотренные алгоритмы в этом случае также приводят к от-
рицательному результату.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
425
Рис. 2. Множества решений задачи (8), полученные с помощью
различных алгоритмов: пунктирная линия - “наивный” алго-
ритм Пикара; штриховая - стягивающее обрамление Макино-
Берца; сплошная - стягивающее обрамление, предложенный ва-
риант.
(а)
(б)
Рис. 3. Множества решений задачи (8), полученные с помощью различных алгоритмов (увеличение, обозна-
чения совпадают с обозначениями на рис. 2): область разрастания оценок для алгоритма Макино-Берца (a);
попадание начальной ТМ в себя за период цикла при использовании предложенного в настоящей статье ва-
рианта стягивающего обрамления (б): первый период - пунктирная линия, второй - сплошная, начальный
параллелограмм залит серым цветом.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
426
ЕВСТИГНЕЕВ и др.
Заключение. В работе представлен новый вариант алгоритма стягивающего обрамления
и проведено его сравнение с исходным алгоритмом Макино-Берца в применении к задаче
о доказательстве существования периодического решения в системе ОДУ. Оба алгоритма и
доказательства их свойств изложены в терминологии ТМ, введённой в наших предыдущих
работах [8, 9]. Рассмотренный пример позволяет сделать вывод о том, что исходный алго-
ритм в задаче о циклах не даёт существенных преимуществ относительно “наивного” алго-
ритма ТМ-интегрирования. Это, однако, не означает, что исходный алгоритм будет проиг-
рывать предложенному в любых задачах построения оценок решений в системах ОДУ, но
подобное сравнение выходит за рамки нашего исследования. К недостаткам предложенного
метода можно отнести использование только линейной части при переходе к “эталонной” сис-
теме координат. В качестве одного из возможных вариантов продолжения настоящей работы
можно предложить использование нелинейных членов ТМ. Однако сложность алгоритма стя-
гивающего обрамления в этом случае будет выше. Другое направление, развивающее данную
работу, связано с формализацией в рамках используемых нами определений т.н. алгоритмов
предобуславливания и с их применением к задаче о доказательстве периодических решений.
Как указано в [20], данные алгоритмы также решают проблему разрастания остатков ТМ при
интегрировании ОДУ.
Вернёмся к результатам другой нашей работы [17], упомянутой во введении. Как было
сказано, доказательство существования периодического решения для системы ОДУ с 79-ю
переменными, являющейся галёркинским приближением задачи о двумерном течении Кол-
могорова, с помощью “наивного” алгоритма в сочетании с топологическим подходом требует
примерно одного месяца непрерывных расчётов на пяти видеокартах. При использовании алго-
ритма стягивающего обрамления в сочетании с техникой сечения Пуанкаре соответствующий
результат может быть получен в течении 6 ч на одной видеокарте. Из этого можно сделать
общий вывод, что развитие области доказательных вычислений в равной степени зависит как
от использования новейших параллельных вычислительных архитектур, так и от развития и
оптимизации самих алгоритмов ДВ.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных ис-
следований (проект 18-29-10008мк).
СПИСОК ЛИТЕРАТУРЫ
1. Moore R.E. Methods and Applications of Interval Analysis. SIAM, 1979.
2. Moore R.E., Kearfott R.B., Cloud M.J. Introduction to Interval Analysis. SIAM, 2009.
3. Шокин Ю.И. Интервальный анализ. Новосибирск, 1981.
4. Добронец Б.С. Интервальная математика. Красноярск, 2004.
5. Шарый С.П. Конечномерный интервальный анализ. Новосибирск, 2010.
6. Бабенко К.И. О доказательных вычислениях и математическом эксперименте на ЭВМ // Успехи
мат. наук. 1985. Т. 40. Вып. 4 (244). С. 137-138.
7. Tucker W. A Rigorous ODE solver and Smale’s 14th problem // Found. Comput. Math. 2002. № 2.
P. 53-117.
8. Евстигнеев Н.М., Рябков О.И. К вопросу о применении интервальных моделей Тейлора к вычис-
лительному доказательству существования периодических траекторий в системах обыкновенных
дифференциальных уравнений // Дифференц. уравнения. 2018. Т. 54. № 4. С. 530-543.
9. Евстигнеев Н.М., Рябков О.И. Об алгоритмах построения изолирующих множеств фазовых пото-
ков и вычислительных доказательствах с применением интервальных моделей Тейлора // Диффе-
ренц. уравнения. 2019. Т. 55. № 9. С. 1242-1260.
10. Pilarczyk P. Topological-numerical approach to the existence of periodic trajectories in ODE’s. // Proc.
of the Fourth Int. Conf. on Dynam. Syst. and Differential Equat. May 24-27, 2002. Wilmington, 2002.
P. 701-708.
11. Rihm R. Interval methods for initial value problems in ODEs // Topics in Validated Computations
/ J. Herzberger, ed. Amsterdam, 1994. P. 173-207.
12. Berz M., Makino K. Verified integration of ODEs and flows using differential algebraic methods on
high-order Taylor models // Reliable Computing. 1998. V. 4. P. 361-369.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021
ОБ ИСПОЛЬЗОВАНИИ СТЯГИВАЮЩЕГО ОБРАМЛЕНИЯ
427
13. Berz M., Makino K. Suppression of the wrapping effect by Taylor model-based verified integrators: long-
term stabilization by shrink wrapping // Int. J. of Differential Equat. and Appl. 2005. V. 10. № 4.
P. 385-403.
14. Berz M., Makino K. Performance of Taylor model methods for validated integration of ODEs // Lect.
Notes in Comp. Scie. 2006. V. 3732. P. 65-74.
15. Lin Y., Stadtherr M.A. Validated solutions of initial value problems for parametric ODEs // Appl.
Numer. Math. 2007. V. 57. P. 1145-1162.
16. Berz M., Hoefkens J. Verified high-order inversion of functional dependencies and interval Newton
methods // Reliable Computing. 2001. V. 7. № 5. P. 379-398.
17. Evstigneev N.M., Ryabkov O.I. On the implementation of Taylor models on multiple graphics processing
units for Rigorous computations // Parallel Computational Technologies. PCT 2020 / Sokolinsky L.,
Zymbler M. (eds). Commun. in Comp. and Inform. Scie. V. 1263. Cham, 2020. Р. 85-99.
18. Makino K., Berz M. The method of shrink wrapping for the validated solution of ODEs // Michigan
State University Report MSU HEP 020510, 2002.
19. Neher M., Jackson K.R., Nedialkov N.S. On Taylor model based integration of ODEs // SIAM J. Numer.
Anal. 2007. V. 45. № 1. P. 236-262.
20. Berz M., Makino K. Suppression of the wrapping effect by Taylor model-based verified integrators:
long-term stabilization by preconditioning // Int. J. of Differential Equat. and Appl. 2005. V. 10. № 4.
P. 353-384.
Федеральный исследовательский центр
Поступила в редакцию 30.09.2020 г.
“Информатика и управление” РАН, г. Москва,
После доработки 30.09.2020 г.
Институт системного анализа РАН, г. Москва,
Принята к публикации 11.12.2020 г.
Московский государственный университет
им. М.В. Ломоносова
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57
№3
2021