ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ, 2021, том 57, № 5, с.700-716

УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ

УДК 517.956.2+517.958:539.3(5)

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ ПЛАСТИНЫ

СО СТЕРЖНЯМИ, ОСНОВАННЫЕ НА ТОЧЕЧНЫХ

УСЛОВИЯХ СОБОЛЕВА И САМОСОПРЯЖЁННЫХ

РАСШИРЕНИЯХ ДИФФЕРЕНЦИАЛЬНЫХ ОПЕРАТОРОВ

Двумерная и одномерные модели Кирхгофа тонких изотропных пластины и стержней со-

единены в единую задачу, описывающую деформацию сочленения этих упругих объектов.

Условия сопряжения в точках присоединения стержней к пластине назначаются при по-

мощи техники самосопряжённых расширений дифференциальных операторов, имеющих

четвёртый порядок в двумерной области и второй порядок на одномерных отрезках. При-

ведены постановки задач, содержащих нелинейные условия сопряжения, в частности, од-

носторонние связи.

DOI: 10.31857/S0374064121050113

1. Постановка задачи. Пусть Ω - область на плоскости R² с гладкой (класса C^∞ для

упрощения) границей Γ = ∂Ω и компактным замыканием Ω = Ω

^⋃Γ. Внутри Ω зафикси-

руем J различных точек P¹, . . . , P^J . Пусть ещё Υ^j - отрезок длиной l_j > 0, лежащий в

пространстве R³, имеющий с областью Ω общей только точку P^j (рис. 1, а) и параметри-

зованный переменной z_j ∈ (0, l_j ) так, что этой точке отвечает координата z_j = 0, j = 1, J.

Интерпретируя область Ω и отрезки Υ¹, . . . , Υ^J как двумерную пластину и одномерные

стержни соответственно, рассмотрим задачу Неймана (свободный край пластины) для бигар-

монического уравнения

D₀Δ2xu₀(x) = f₀(x), x = (x₁,x₂) ∈ Ω \ {P¹,... ,P^J},

(1)

N^q(x,∇_x)u₀(x) = 0, x ∈ Γ, q = 2,3,

(2)

и обыкновенные дифференциальные уравнения с условиями Дирихле (зафиксированы внеш-

ние концы стержней)

-D_j∂2z

u_j(z_j) = f_j(z_j), z_j ∈ (0,l_j),

(3)

u_j(l_j) = 0 (j = 1,J),

(4)

где D₀, D₁, . . . , D_j - положительные множители.

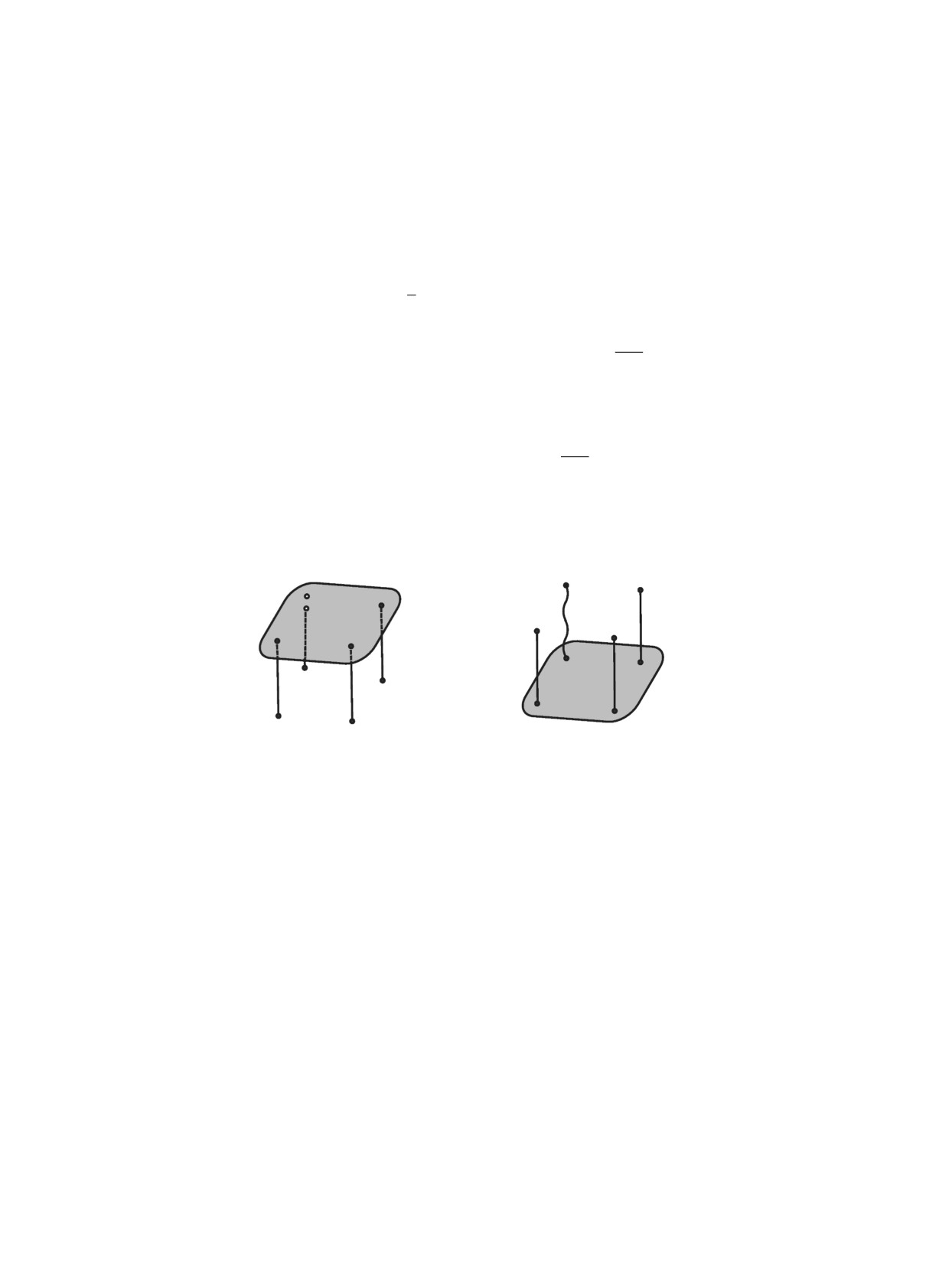
(а)

(б)

Рис. 1. Сочленение пластины со стержнями: простое (а) и с

жёсткими стрингерами (б).

700

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

701

Поясним принятые обозначения: u₀ - прогиб пластины и u_j - продольные смещения в

стержнях, а f₀ и f_j - поперечные и продольные силы соответственно. Дифференциальные

операторы в краевых условиях (2) имеют вид (см. [1; 2, § 30] и др.)

N²(x,∇_x) = Δ_x - (1 - ν)(∂2s + κ(s)∂_n),

N³(x,∇_x) = ∂_nΔ_x - (1 - ν)(∂_sκ(s)∂_s - ∂_n∂2s),

(5)

где ∇_x = grad, Δ_x = ∇_x ·∇_x - оператор Лапласа и (n, s) - локальная система криволинейных

координат в окрестности V контура Γ, n - ориентированное расстояние до Γ, n < 0 в Ω

^⋂V,

s - длина дуги на Γ, а κ(s) - кривизна контура в точке s ∈ Γ, положительная на выпуклых

участках. Множители D₀ > 0 в (1) и D_j > 0 в (3) - цилиндрическая жёсткость пластины

и приведённый модуль Юнга стержня, а ν ∈ [0, 1/2) - коэффициент Пуассона материала

пластины, отсутствующий в уравнении Софи Жермон (1), но присутствующий в операторах

(5) и функционале удвоенной упругой энергии D₀E₀(u⁰, u⁰; Ω) пластины Ω:

∫

(

))

∂²u

∂²x

∂²u

∂²υ

E₀(u,υ;Ω) = D₀

Δ_xuΔ_xυ + (1 - ν) 2

dx.

(6)

∂x₁∂x₂ ∂x₁∂x₂

∂x²

∂x²²

∂x²

Масштабированием сведём характерный размер упругого сочленения Ξ = Ω⋃Υ1⋃ . . .⋃ΥJ

к единице и тем самым сделаем координаторы и все геометрические параметры безразмерны-

ми. Множители D₀ и D₁, . . . , D_J зависят от поперечных размеров исходных трёхмерных

пластины и стержней (прототипов их моделей Ω и Υ¹, . . . , Υ^J ; см., например, [3, гл. 4, § 2;

гл. 5, § 2]), однако в данной работе считаем их величинами одного порядка, т.е., в частности,

предполагаем, что исходные жёсткостные характеристики изотропного материала пластины

превосходят такие же характеристики у стержней. Сделаем обсуждаемые множители безраз-

мерными, положив D₀ = 1.

Уравнение (1) поставлено в проколотой области Ω \ {P¹, . . . , P^J } - вне точек множества

P = {P¹,...,P^J} - и ещё не назначены краевые условия для уравнений (3) в точках z_j = 0.

Основная цель работы - при помощи техники самосопряжённых расширений дифференци-

альных операторов (см. публикации [4-13] и многие др.) осуществить корректную постановку

задачи о деформации упругого сочленения областей с различными предельными размерно-

стями, учитывающую разнообразные способы взаимодействия его элементов - пластины и

стержней.

В п. 2 рассматривается простейший вариант: абсолютно жёсткие стержни фиксируют про-

гиб пластины Ω в точках P¹, . . . , P^J , т.е. задача (1), (2) снабжается точечными условиями

Соболева

u₀(P^j) = 0, j = 1,J,

(7)

корректность постановки которых обеспечена теоремой Соболева о вложении H² ⊂ C на

плоскости (см. монографии [14, 15] и др.). Подобные задачи широко используются, например,

при моделировании вантовых и подвесных мостов (см. справочник [16] и, например, моногра-

фию [17]) при интерпретации поддерживающих тросов, стальных и обычно предварительно

напряжённых, именно как абсолютно жёстких стержней. Вместе с тем в определённых си-

туациях, особенно для пенькового или синтетического такелажа, приходится принимать во

внимание деформацию тросов. С этой целью в п. 3 вводится положительный неограниченный

симметрический замкнутый оператор A в гильбертовом пространстве

H = L²(Ω) × L²(Υ¹) × ... × L²(Υ^J),

(8)

где L²(Σ) - пространство Лебега с натуральным скалярным произведением ( · , · )_Σ, и находит-

ся область определения самосопряжённого оператора A^∗. В п. 4 описываются все возможные

самосопряжённые расширения оператора A, при помощи которых можно смоделировать лю-

бые (жёсткие, упругие, шарнирные и прочие) способы прикрепления стержней к пластине,

но в п. 5 выделяется то из расширений, которое отвечает рассматриваемой первичной модели

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

702

НАЗАРОВ

упругого сочленения Ξ при игнорировании продольной деформации пластины и изгиба вместе

с закручиванием стержней. Наконец, в п. 6 обсуждаются задачи с односторонними связями:

в определённых условиях пластина перестаёт контактировать с тем или иным стержнем (ср.

статью [18] о мембране, натянутой на несколько стоек). При этом помимо корректных постано-

вок дифференциальных и вариационных задач основная цель - сведение их к алгебраическим

задачам на основе схемы, разработанной в п. 2 с использованием обобщённых функций Гри-

на с особенностями в точках P¹, . . . , P^J . Полное изучение нелинейных задач планируется

провести в более общей ситуации систем дифференциальных уравнений, учитывающих все

возможные способы деформации элементов упругой конструкции.

2. Задача Соболева. В силу формулы Грина (см., например, монографию [2, § 30])

(Δ2xu, v)_Ω = E(u, v; Ω) - (N²u, ∂_nv)_Γ + (N³u, v)_Γ

(9)

вариационная постановка задачи (1), (2), (7) реализуется как интегральное тождество

E(u₀, v₀; Ω) = (f₀, v₀)_Ω для любой v₀ ∈ H²(Ω; P)

(10)

на подпространстве

H²⁰(Ω;P) = {u₀ ∈ H²(Ω) : u₀(P^j) = 0, j = 1,J}.

(11)

Поскольку пространство Соболева H²(Ω) вкладывается в пространство непрерывных функ-

ций C(Ω), подпространство (11) замкнуто.

В силу простого алгебраического неравенства

E(u₀, u₀; Ω) ≥ (1 - ν)∥∇2xu₀; L²(Ω)∥²,

(12)

в котором ∇^xu₀ - вектор, составленный из производных функции u₀ порядка p, в частности,

∇2xu₀ = (∂²u₀/∂x²¹,2∂²u₀/∂x₁∂x₂,∂²u₀/∂x²²), билинейная форма (6) вырождается только на

линейных функциях ℓ(x) = ℓ₀ + ℓ₁x₁ + ℓ₂x₂ и, следовательно, обладает полиномиальным

свойством [18], обеспечивающим полезные свойства операторам задачи (1), (2) (см. ниже).

Далее придётся различать три геометрические ситуации:

1◦. J = 1, т.е. отмечена только одна точка, для определённости, начало координат P¹ =

= (0, 0), и

L := {ℓ(x) = ℓ₁x₁ + ℓ₂x₂ : ℓ₁, ℓ₂ ∈ R};

(13)

2◦. J ≥ 2 и точки P1, ..., PJ лежат на одной прямой, для определённости, на оси

ординат, и

L := {ℓ(x) = ℓ₁x₁ : ℓ₁ ∈ R};

(14)

3◦. J ≥ 3 и в множестве P есть три точки, являющиеся вершинами невырожденного

треугольника, и поэтому L = {0}.

В силу теоремы Рисса о представлении непрерывного функционала в гильбертовом прост-

ранстве справедливо следующее

Предложение 1. Задача (10) с правой частью f₀ ∈ L²(Ω) имеет решение u₀ ∈ H²⁰(Ω; P)

в том и только в том случае, если

(f₀, ℓ)_Ω = 0 для всех ℓ ∈ L.

(15)

Само решение определено с точностью до слагаемого из подпространства L, но, будучи

подчинено условиям ортогональности

(u₀, ℓ)_Ω = 0 для всех ℓ ∈ L,

(16)

становится единственным и удовлетворяет оценке ∥u₀;H²(Ω)∥ ≤ c∥f₀;L²(Ω)∥, в которой

постоянный множитель c не зависит от функции f₀.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

703

Замечание 1. Пусть P = ∅, т.е. задача (1), (2) ставится в цельной, а не проколотой

области Ω. Предложение 1 сохраняет силу, если в формулах (15) и (16) взять

L = {ℓ(x) = ℓ₀ + ℓ₁x₁ + ℓ₂x₂ : ℓ_q ∈ R, q = 0,1,2}.

(17)

В ситуации 3^◦ задача (10) однозначно разрешима - в этом пункте работы для краткости

имеем дело только с таким расположением точек. Включение u₀ ∈ H²(Ω; P) не даёт пол-

ной информации о дифференциальных свойствах решения и её можно уточнить, а именно,

справедливо представление

∑

u₀(x) = u₀(x) +

χ_j(x)a_jΦ(x - P^j),

(18)

j=1

где

u₀ ∈ H⁴(Ω),

u₀(P^j) = 0, χ_j ∈ C^∞c(Ω) - срезающая функция, равная единице в окрест-

ности точки P^j , причём supp χ_j

^⋂ suppχ_k = ∅ при j = k, а Φ - фундаментальное решение

бигармонического оператора на плоскости,

Φ(x) =

|x|² ln

(19)

8π

|x|

для которого, согласно его назначению, верна формула

∫

N³(x,∇_x)Φ(x)ds_x = 1.

(20)

{x:|x|=ρ}

Наконец, a₁, . . . , a_j - коэффициенты, определяемые при решении всей задачи (10) (или (1),

(2), (7) в дифференциальной постановке), и верна оценка

∑

∥u₀; H⁴(Ω)∥ +

|a_j | ≤ C∥f₀; L²(Ω)∥.

j=1

В рамках теории распределений (см., например, книги [19, 20]) уравнение (1) распростра-

няем на всю область Ω следующим образом:

∑

Δ2xu₀(x) = f₀(x) +

a_jδ(x - P^j), x ∈ Ω.

j=1

Здесь δ - дельта-функция Дирака. Найдём представление этого решения, используя обобщён-

ную функцию Грина задачи (1), (2), отыскиваемую как решение краевой задачи

Δ2xG(x;y) = δ(x - y) - L(x;y), x ∈ Ω,

N^q(x,∇_x)G(x;y) = 0, x ∈ Γ, q = 2,3,

(21)

и подчинённую трём условиям ортогональности (ср. предложение 1)

∫

xG(x; y) dx = 0 ∈ R³.

(22)

При этом x = (1, x₂, x₃)^т (здесь и всюду в статье^т - знак транспонирования), а линейная

функция x → L(x; y) с вектором коэффициентов L(y) ∈ R³ выбрана так, что

∫

L(x; y) dx = y := (1, y₁, y₂)^т ∈ R³.

(23)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

704

НАЗАРОВ

Согласно замечанию 1 существование решений задачи (21), (22) обеспечено непрерывностью

функционала

∫

H²(Ω) ∋ ϕ → δ(x - y)ϕ(x)dx = ϕ(y)

и выполнением условий разрешимости (23). Положим G_j (x) = G(x; P^j ), L^j = L(P^j) и заме-

тим, что

∫

G_jk := G_j(P^k) = G_j(x)Δ2xG_k(x)dx = E(G_j,G_k;Ω),

(24)

т.е. J × J-матрица G с элементами (24) является матрицей Грама, симметричной и положи-

тельно определённой. Ещё одна 3 × 3-матрица Грама

∫

M = xxт dx

(25)

содержится в вытекающем из (23) равенстве ML = P, связывающем между собой 3 × J-

матрицы

⎛

⎞

⎛

⎞

L¹⁰

... LJ0

L=^⎝L11

... LJ1⎠,P= ⎝P1

... PJ1⎠.

(26)

L¹²

... LJ2

P¹²

... P^J

Решение u₀ ∈ H²⁰(Ω; P) задачи (10) ищем в виде

∑

u₀(x) = u_•(x) + ℓ(x) +

a_jG_j(x).

(27)

j=1

Здесь ℓ - линейная функция с коэффициентами ℓ_q, столбцы a = (a₁, . . . , a_j )^т и l = (ℓ₀, ℓ₁, ℓ₂)^т

подлежат определению, а u_• ∈ H⁴(Ω) - решение задачи (1), (2) с правой частью f_•(x) = f₀(x)+

+ℓ_•(x) в цельной области Ω, причём в соответствии с замечанием 1 линейная функция ℓ_• со

столбцом коэффициентов

∫

l_•

= -M-1

xf₀(x) dx ∈ R³

(28)

обеспечивает существование решения u_•, подчинённого условиям ортогональности (16), (17).

Функция (27) удовлетворяет уравнению (1) с правой частью f₀ при условии

La = l_• ∈ R³

(29)

(уничтожили линейные функции в правых частях бигармонических уравнений для G_j и u_•).

Условия Соболева (7) принимают вид системы алгебраических уравнений

u_• + P^тl + Ga = 0 ∈ R^J,

где u_• = (u_•(P¹), . . . , u_•(P^J ))^т, а значит,

a = -G-1P^тl - G-1u_• ∈ R^J.

(30)

Поскольку L = M-1P, выводим из формул (29) и (30) ещё одну систему

PG-1P^тl = MPG-1u_• - Ml_• ∈ R³.

(31)

Матрица из левой части последней системы симметрична и положительно определена. В самом

деле, эти же свойства матрицы Грама G гарантируют, что в случае b^тP^тG-1Pb = 0 для

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

705

некоторого столбца b ∈ R³ выполнены равенства P^тb = 0 ∈ R^J и тогда b = 0, так как ранг

второй матрицы (26) равен трём в силу принятого ограничения 3^◦.

Итак, находим столбец l ∈ R³ из уравнений (31), а затем и столбец a ∈ R^J из уравнений

(30). Следовательно, справедливо представление (27), а вместе с ним и разложение (18).

Замечание 2. Ограничение 3^◦ назначено лишь для упрощения проверки нужных фактов.

В ситуациях 1^◦ или 2^◦ коэффициенты ℓ₁, ℓ₂ или ℓ₁ линейной функции ℓ из (27) остаются

произвольными, а компоненты ℓ•1, ℓ•2 или ℓ•1 столбца (28) обращаются в нуль благода-

ря соотношению (15) из предложения 1. Иными словами, системы (29) и (30) сужаются на

соответствующее подпространство в R³, на котором матрица PG-1P^т обратима.

3. Исходный симметрический оператор модели упругого сочленения и его со-

пряжённый. Пусть A_c - неограниченный оператор в гильбертовом пространстве (8) с диф-

ференциальным выражением

(Δ2x, -D₁∂2z

,...,-D_J∂² )

(32)

z_J

и областью определения

D_c = {U = (u₀,u₁,... ,u_J) : u₀ ∈ C^∞c(Ω \ P), N^q(x,∇_x)u₀(x), x ∈ Γ, q = 2,3;

u_j ∈ C^∞c(0,l_j], u_j(l_j) = 0, j = 1,J}.

(33)

Здесь C^∞c(Ω \ P) - пространство бесконечно дифференцируемых в проколотом замыкании

Ω \ P функций, обращающихся в нуль в какой-то окрестности множества P, и столь же

гладкие функции u_j ∈ C^∞c(0, l_j ] аннулируются около точки z_j = 0.

Оператор A_c симметрический и положительный, однако незамкнутый. Для описания его

замыкания A и сопряжённого оператора A^∗ понадобятся пространства Кондратьева V^lβ(Ω; P)

(см. первоисточник [21] и, например, монографию [22]), полученные пополнением линейного

пространства C^∞c(Ω \ P) по весовой соболевской норме

(∑s

)1/2

∥u; V^sβ(Ω; P)∥ =

∥rβ-s+p∇^pxu; L2(Ω)∥2

(34)

p=0

где s ∈ N₀ := {0, 1, 2, . . .} и β ∈ R - показатели гладкости и веса, а r(x) - расстояние от

точки x до множества P. Пространство V^sβ(Ω; P) состоит из тех функций u ∈ Hsloc(Ω \ P),

для которых конечна норма (34). Поскольку r(x) > c_Γ > 0 при x ∈ Γ, то в случае s ≥ 1

пространство следов на Γ функций из V^sβ(Ω; P) есть не что иное как пространство Соболева-

Слободецкого Hs-1/2(Γ).

Понятно, что отображение

N_β = {Δ2x,N²,N³} : V4β(Ω;P) → V0β(Ω;P) × H3/2(Γ) × H1/2(Γ)

(35)

непрерывно при любом весовом показателе. Более того, верна оценка (см. [21] и, например,

[22, гл. 4, § 1])

∥u₀; V4β(Ω; P)∥ ≤ c_β(∥Δ2xu₀; V0β(Ω; P)∥ +

+ ∥N²u₀; H3/2(Γ)∥ + ∥N³u₀; H1/2(Γ)∥ + ∥u₀; V 0β-4(Ω; P)∥).

(36)

Принципиально присутствие в правой части неравенства (36) нормы функции u₀ в прост-

ранстве V0β-4(Ω; P), содержащем пространство V4β(Ω; P) из левой части: такая оценка окажет-

ся полезной, но она все-таки не даёт сколь-нибудь важной информации о самом отображении

(35), так как вложение V4β(Ω; P) ⊂ V0β-4(Ω : P) является непрерывным, но не компактным. Со-

гласно теории Кондратьева [21] (см. также [23; 22, гл. 6, § 6] и др.) для придания фредгольмова

свойства оператору N_β требуется, чтобы весовой показатель β не был “запретным” - такие

запретные показатели образуют счётное множество B на вещественной оси с двумя точками

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

706

НАЗАРОВ

сгущения ±∞. Благодаря полиномиальному свойству формы (6) (см. комментарий к форму-

ле (12)) известно (см. [24, пример 1.14 и предложение 2.21]), что B = Z := {0, ±1, ±2, . . .} -

множество целых чисел. К сожалению, L²(Ω) = V⁰⁰(Ω; P), а индекс β = 0 как раз запретный.

Поэтому далее придётся также оперировать со ступенчатым весовым пространством V^4#(Ω; P)

с нормой∗)

∥u; V-4#(Ω; P)∥ = (∥∇2xu; H¹(Ω)∥² + ∥u; V2-1-ε(Ω; P)∥²)1/2,

(37)

где ε - любое число из интервала (0, 1). Пространство V^4#(Ω; P) не зависит от выбора ε ни

алгебраически, ни топологически (см. замечание 3). Отображение

N_# = {D₀Δ2x,N²,N³} : V^4#(Ω : P) → V⁰⁰(Ω;P) × H3/2(Γ) × H1/2(Γ)

остаётся непрерывным, но дополнительно приобретает фредгольмово свойство, выражаемое

оценкой

∥u₀; V^4#(Ω; P)∥ ≤ c_Σ(∥Δ2xu₀; V⁰⁰(Ω; P)∥ + ∥N²u₀; H3/2(Γ)∥ + ∥N³u₀; H1/2(Γ)∥ + ∥u₀; L²(Σ)∥, (38)

где Σ - компакт в Ω \ P, а множитель c_Σ зависит от выбора подмножества Σ, но не от

функции u₀.

Предложение 2. Замыкание A оператора A_c сохраняет дифференциальное выражение

(32), но приобретает область определения

D = {U ∈ V ^4#(Ω;P) × H²(0,l₁) × ... × H²(0,l_J) :

N^q(x,∇_x)u₀(x), x ∈ Γ, q = 2,3, u_j(l_j) = 0, u_j(0) = ∂zj u_j(0) = 0, j = 1,J}.

Доказательство. Согласно определению оператор A будет замыканием оператора A_c,

если из того, что U^k ∈ D_c, U^k → U^∞, F^k = A_cU^k → F^∞ сильно в H вытекают соотношения

U^∞ ∈ D и AU^∞ = F^∞. Для первых компонент вектор-функций U^k, U^m из линейного

множества (33) оценка (38) гарантирует, что

∥uk0 - um0; V^4#(Ω; P)∥ ≤ c_Σ(∥Δ2x(uk0 - um0); L²(Ω)∥ + ∥uk0 - um0; L²(Σ)∥) ≤

≤ c₀(∥fk0 - fm0 ;L²(Ω)∥ + ∥uk0 - um0 ;L²(Ω)∥).

Следовательно, фундаментальность последовательностей {uk0} и {fk0 = Δ2xuk0} в L²(Ω) вле-

чёт за собой фундаментальность первой из них в V^4#(Ω; P). Аналогичное свойство последова-

тельностей {u^kj} и {f^kj = -D_j ∂2zj u^kj} в L²(0, l_j ), обеспеченное простым следствием интерпо-

ляционного неравенства

∥u_j ; H²(0, l_j )∥ ≤ c_j (∥∂2z

u_j;L²(0,l_j)∥ + ∥u_j;L²(0,l_j)∥),

вместе с элементарным следовым неравенством [27, гл. 1]

|u_j(0)| + |∂zj u_j(0)| + |u_j (l_j )| ≤ c_j∥u_j ; H²(0, l_j )∥

заканчивает доказательство предложения.

∗) Следует упомянуть, что в последнем параграфе работы [21] приведены наметки возможной модификации

кондратьевских весовых классов V^sβ при наличии у модельной задачи в конусе или проколотом пространстве

полиномиальных решений, однако законченная теория краевых задач для эллиптических систем в ступенча-

тых весовых пространствах, инициированная вопросами механики трещин [25], представлена в статье [26] и

книге [22, гл. 8, § 4]. Сам термин “ступенчатый” связан с тем, что график зависимости от порядка дифферен-

цирования p в норме (34) - наклонная прямая, а в норме (37) график имеет уступ на уровне p = 3.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

707

Замечание 3. Поскольку V^4#(Ω; P) ⊂ H⁴(Ω) ввиду определений весовых норм (37), (34)

и любой квадратичный полином x → p(x) не попадает в пространство V 2-1-ε(Ω; P) из-за рас-

ходимости интегралов в точках P¹, . . . , P^J , возможна подмена V^4#(Ω; P) подпространством

пространства Соболева H⁴(Ω), выделенном равенствами

u₀(P^j) = 0,

∇_xu₀(P^j) = 0 ∈ R²,

∇2xu₀(P^j) = 0 ∈ R³, j = 1,J.

(39)

Обратная подмена обеспечена трёхкратным применением одномерного неравенства Харди

∫



_dU

²

r-2γ-1|U(r)|² dr ≤

r-2γ+1

r)

(40)

 d

γ²

dr⁽

для любых U ∈ C¹[0, d], U(0) = 0, d > 0, γ > 0. При этом функцию u₀ следует записать в

полярной системе координат (r_j, ϕ_j ) с центром в точке P^j и дополнительно проинтегрировать

по угловой переменной ϕ_j ∈ [0, 2π) неравенство (40), в котором

U (r_j , ϕ_j ) = χ_j(x)∇^qxu₀(x),

(41)

γ = ε-q+5/2, q = 2,1,0, а χ_j - срезки, введённые в представлении (18). Требование U(0) = 0

в (40) для вектор-функций (41) обеспечено соотношениями (39).

В статье [6], относящейся к задаче Дирихле для бигармонического уравнения в случае J =

= 1, содержится именно описание области определения оператора задачи как пространства

H⁴(Ω) с условиями (39). В данной работе удобно применить теорию Кондратьева, обслужи-

вающую эллиптические краевые задачи с асимптотическими условиями на подмногообразиях

границы (см. [22, гл. 6, § 7 и гл. 12, §§ 1-3; 19, § 2, п. 7] и др. публикации), поскольку эта теория

позволяет также исследовать полную модель тонкой упругой анизотропной и неоднородной

пластины (ср. [3] и [11]) без особых изменений в схеме рассуждений, но с несоизмеримо более

длинными выкладками.

Оператор A симметрический и замкнутый, но не самосопряжённый. Для описания сопря-

жённого для него оператора A^∗ понадобится следующий базис в шестимерном пространстве

квадратичных полиномов:

p₀(x) = 1, p₁(x) = x₁, p₂(x) = x₂,

p₃(x) = 2-1/2x²¹, p₄(x) = x₁,x₂, p₅(x) = 2-1/2x²².

(42)

Обозначив δ_p,m символ Кронекера, получаем равенства

p_k(∇_x)p_m(x)|x=0 = δ_m,p, m,p = 0,5.

(43)

Предложение 3. Сопряжённый для оператора A оператор A^∗ сохраняет дифференци-

альное выражение (32), но приобретает область определения

{

∑

D^∗ = U : u₀(x) = χ_j(x) (b+jkp_k(x - P^j) + b^-jkp_k(-∇_x)Φ(x - P^j)) + u₀(x),

j=1

k=0

}

b^±j = (b±j0,... ,b±j5)^т ∈ R⁶,

u₀ ∈ V^4#(Ω;P), u_j ∈ H²(0,l_j), u_j(l_j) = 0, j = 1,J

(44)

Доказательство. Сопряжённый оператор находится по правилу: если U, F

∈ H и

〈U, AV 〉 = 〈F, V 〉 для всех V

∈ D, то U ∈ D^∗ и F = A^∗U. Здесь 〈·,·〉_H - скалярное

произведение в пространстве (8), т.е.

〈U, V 〉_H = (u₀, v₀)_Ω + (u₁, v₁)Υ1 + . . . + (u_J , v_J )ΥJ .

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

708

НАЗАРОВ

Взяв в качестве компонент пробной вектор-функции V = (v₀, v₁, . . . , v_J ) ∈ D в определении

сопряжённого оператора функции v₀ ∈ C^∞c(Ω \ P), v_j ∈ C^∞c(0, l_j ], получим интегральное

тождество

∑

(f₀, v₀)_Ω - (u₀, Δ2xv₀)_Ω +

((f_j, v_j )Υj + (u_j , D_j ∂2z

v_j)Υj ) = 0.

(45)

j=1

Пусть сначала v₁ = 0, . . . , v_J = 0. Тогда оставшееся в (45) интегральное тождество в

области Ω позволяет заключить, что в силу общих результатов [28, гл. 2, §§ 5, 6] об улучшении

дифференциальных свойств решений эллиптических краевых задач и дважды применённой

формулы Грина (9) справедливо тождество

(f₀ - Δ2xu₀, v₀)_Ω - (N²u₀, ∂_nv₀)_Γ + (N³u₀, v₀)Γ = 0

(46)

для всех таких функций v₀ ∈ C^∞c(Ω \ P), что N^qv₀ = 0 на Γ, q = 2, 3. Благодаря произволь-

ности функции v₀ в проколотой области Ω \ P и следов v₀,

∂_nv0 на Γ = ∂Ω выводим из

тождества (46) соотношения (1) и (2). Кроме того, безусловная оценка (36) с β = 4, правая

часть которой конечна, так как V⁰⁴(Ω; P) ⊂ V⁰⁰(Ω; P) = L²(Ω), гарантирует, что u₀ ∈ V⁴⁴(Ω; P).

Теперь воспользуемся теоремой Кондратьева об асимптотике (см. [21, 23], а также [22, гл. 3,

§ 5 и гл. 4, § 2] и др.) и получим указанное формулой (44) представление функции u₀. Пояс-

ним, что отделённые асимптотические члены представляют собой степенно-логарифмические

решения

ψ(x) = r^ΛΨ(ϕ; ln r)

(47)

модельного уравнения на проколотой плоскости

Δ2xψ(x) = 0, x ∈ R² \ {(0,0)}.

(48)

При этом Λ ∈ C и Ψ - полином переменной ln r, коэффициенты которого - гладкие 2π-

периодические функции угловой переменной ϕ, а в асимптотику включены те функции (47),

которые принадлежат классу V⁴⁴ в окрестности начала координат, но не содержатся в классе

V^4# ⊂ V2-1-ε. Как показано в цитированной литературе (см., в частности, [19, пример 1.14 и

предложение 2.21]) степенными решениями (47) уравнения (48) служат только полиномы и

производные фундаментального решения (19). Упомянутые факты объясняют формулу для

компоненты u₀ в определении (44).

Аналогичные рассуждения в значительно более простом исполнении показывают, что инте-

гральное тождество (45) с пробной функцией V, имеющей только одну ненулевую компоненту

v_j, приводит к формуле

(f_j + D_j∂2z

u_j,v_j)_Υ - u_j(l_j)D_j∂zj v_j(l_j) = 0 для любой v_j ∈ C∞0(0,l_j], v_j(l_j) = 0,

из которой следует, что

u_j ∈ H²(0,l_j), u_j(l_j) = 0,

-D_j∂2z

u_j(z_j) = f_j(z_j), z_j ∈ (0,l_j).

Это заканчивает проверку предложения 3.

4. Обобщённая формула Грина. Для вектор-функции U ∈ D^∗ введём проекции

π±0U := (b±1,... ,b^±j)^т ∈ R6×J, π+jU := u_j(0), π^-jU =: -D_j∂zj u_j(0),

(49)

где b^±j - векторы коэффициентов из представления функции u₀ в формуле (44), а также

π^± = π±0 = (b±1,... ,b^±J)^т, π = (π⁺,π^-)^т.

(50)

Подчеркнём, что все векторы (49) и (50) реализованы как столбцы.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

709

Отображения π^± : H ⇀ R6J+6 непрерывны; здесь H - гильбертово пространство вектор-

функций U ∈ D^∗ с нормой

(

)1/2

∑

∥U; H∥ =

∥u₀;V^4#(Ω;P)∥² + |π⁺u₀|² + |π^-u₀|² +

∥u_j ; H²(Υ_j)∥2

j=1

Лемма 1. Для вектор-функций U, V ∈ H справедлива формула

Q(U, V ) := (Δ2xu₀, v₀)_Ω - (u₀, Δ2xv₀)_Ω -

∑

((D_j ∂2z

u_j,v_j)Υj - (u_j,D_j∂2z

v_j)Υj ) = (π^-V )^тπ⁺U - (π⁺V )^тπ^-U.

(51)

j=1

Доказательство. Все скалярные произведения в пространствах Лебега определены кор-

ректно. Сразу же запишем простые формулы

-(D_j ∂2z

u_j,v_j)Υj + (u_j,D_j∂2z

v_j)Υj = D_j(v_j(0)∂zj u_j(0) - u_j(0)∂zj v_j(0)).

(52)

Для вычисления интегралов по области Ω воспользуемся методом [29] (см. также [22, гл. 4,

§ 3]). Обозначив через B_ρ(P^j) круг с центром P^j и радиусом ρ, применим формулу Грина

на множестве Ω_ρ = Ω \ (B_ρ(P¹)

^⋃ ...⋃B_ρ(P^J)) и выполним предельный переход ρ → +0.

Имеем

(Δ2xu₀, v₀)_Ω - (u₀, Δ2xv₀)_Ω = lim

((Δ2xu₀, v₀)Ωρ - (u₀, Δ2xv₀)Ωρ ) =

ρ→+0

∫

∑

= lim

(v₀N³u₀ - ∂_nv₀N²u₀ + ∂_nu₀N²v₀ - u₀N³v₀) ds_x

I^ρj(u₀,v₀).

ρ→+0

j=1

∂Bρ(Pj )

Учтём указанные в (44) разложения функций u₀ и v₀ с коэффициентами b^±ujk и b^±vjk. Удалим

из подынтегральных выражений в I^ρj(u₀, v₀) величины o(ρ-1) при ρ → +0, исчезающие в

пределе после интегрирования вдоль дуг длиной 2πρ. Обозначим S^uj(x - P^j ), S^vj(x - P^j ) и

T^uj(x - P^j), T^vj(x - P^j) соответственно полиномы и линейные комбинации производных фун-

даментального решения, входящие в разложения рассматриваемых функций. В итоге получим

равенство

I^ρj(u₀,v₀) = I^ρj(S^uj + T^uj,S^vj + T^uj) = (b^-vj)^тb+uj - (b^-uj)^тb+vj,

(53)

которое вместе с (52) и (49), (50) приводит к формуле (51). Само равенство (53) вытекает

из базового соотношения (20) для фундаментального решения Φ или выводится при помощи

следующих вычислений в рамках теории распределений (см. учебник [19]):

∫

lim

(S^vjN³T^uj - ∂_nS^vjN²T^uj + ∂_nT^ujN²S^vj - T^ujN³S^vj) ds_x =

ρ→+0

∂Bρ(P^j )

∫

= - lim

S^vj(x - P^j)Δ2xT^uj(x - P^j)dx =

ρ→+0

Bρ(P^j )

∫

= lim

b+vjkp_k(x - P^j)Δ2x(b^-ujmp_m(-∇_x)Φ(x - P^j))dx =

ρ→+0

Bρ(P^j )

∫

∑

b+vjkb^-u

p_k(x)p_m(-∇_x)δ(x)dx = -

b+vjkb^-ujkδ_k,m = -(b^-uj)^тb+vj.

k,m=0

R²

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

710

НАЗАРОВ

Здесь приняты во внимание соотношения (43) и определение производной дельта-функции

Дирака. Наконец, похожие выкладки показывают, что интегралы I^ρj(S^uj, S^vj) и I^ρj(T^uj, T^vj) об-

ращаются в нуль. Лемма доказана.

Следуя [22, гл. 6, § 2 и гл. 12, § 2], называем соотношение (51) обобщённой формулой Грина.

Приступим к описанию самосопряжённых расширений оператора A. Если A_• - такое рас-

ширение, полученное сужением сопряжённого оператора A^∗ на подпространство D_• ⊂ D^∗

коразмерностью 6J + J = 7J (согласно проведённым в п. 3 вычислениям индекс дефекта

оператора A равен (7J : 7J); ср. замечание 4), то

Q(U, V ) = 〈A_•U, V 〉_H - 〈U, A_•, V 〉_H = 0 для любых U, V ∈ D_•.

Таким образом, требуется выяснить условия вырождения симплектической (билинейной и

антисимметричной) формы из правой части формулы (51). Этот вопрос решён в работе [30]

(см. также публикации [9-11, 13] и иные подходы в статьях [4-7] и [8, 12]).

Теорема 1. 1) Пусть R^-

^⊕R0 ⊕R+ - ортогональное разложение евклидова простран-

ства R6J+J, а A : R⁰ → R⁰ - симметричный изоморфизм. Сужение оператора A^∗ на

подпространство

D_• = {U ∈ D^∗ : π⁺U = a⁺ + a⁰, π^-U = a^- + Aa⁰, a^α ∈ R^τ , τ = 0,±}

(54)

оказывается самосопряжённым расширением оператора A.

2) Всякое самосопряжённое расширение допускает указанное описание.

Доказательство. Проверка первого утверждения проста:

(π⁺U, π^-V ) - (π^-U, π⁺V ) = (a+U + a0U , a^-V + Aa0V ) -

- (a^-U + Aa0U , a+V + a0V ) = (a0U , Aa0V ) - (Aa0U , a0V ) = 0.

(55)

Здесь (· , · ) - скалярное произведение в R7J , aαU и aαV - столбцы, предписанные вектор-

функциям U, V ∈ D_• формулой (54), а в выкладке (55) использованы назначенные ортого-

нальности столбцов и симметричность оператора A.

Второе утверждение требует чуть более долгих рассуждений - см. первоисточник [30], а

также, например, статью [10, § 6] и монографию [23, гл. 6, § 3].

Замечание 4. Коразмерность подпространства D_• ⊂ D^∗ в самом деле равна 7J, так как

в определении (54) наложены именно 7J линейных связей. Отсюда вытекает и упомянутая

формула для индекса дефекта оператора A.

Замечание 5. Если точка P^j попала на границу Γ, то предложение 3 в целом сохраня-

ет силу, однако размерность подпространства полиномов, входящих в формулу (44) и далее,

уменьшается на единицу, так как линейные комбинации полиномов (42) должны удовлетворять

в точке P^j ∈ Γ краевым условиям (2) с главными частями Nq0(P^j, ∇) дифференциальных опе-

раторов (5), причём заведомо N³⁰(P^j , ∇)p_k(x) = 0, k = 0, 5, т.е. приходится наложить только

одно дополнительное ограничение. Разумеется, сингулярные составляющие p_k(-∇)Φ(x - P^j )

также подлежат изменению.

5. Выбор параметров самосопряжённого расширения. Механическая интерпрета-

ция рассматриваемой задачи требует специфического подбора параметров самосопряжённого

расширения A_•. В согласии со списком полиномов (42) коэффициенты b+j0 и b+j1, b+j2 суть

прогиб и углы поворотов вокруг осей x₂ - Pj2, x₁ - Pj1 пластины в точке P^j ∈ Ω. Соот-

ветственно b-j0 и b-j1, b-j2 - сосредоточенные поперечная сила и изгибающие моменты вокруг

названных осей. Остальные элементы столбцов b^±j не имеют очевидного физического смыс-

ла, а сингулярности b^-jkp_k(-∇_x)Φ(x - P^j) с индексами k ≥ 3 выводят функцию u₀ даже из

класса H¹(Ω). Поэтому положим

b^-jk = 0, k = 3,4,5, j = 1,J,

(56)

но оставим произвольными коэффициенты b+jk с такими же индексами.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

711

В выстраиваемой простейшей модели упругого сочленения Ξ следует пренебречь и сосре-

доточенными моментами: для их привлечения требуются полные модели пластины и стержней,

а именно, 3 × 3- и 4 × 4-системы дифференциальных уравнений в Ω и на Υ¹, . . . , Υ^J (см.,

например, монографию [22] и ср. конец замечания 3). Таким образом, введём ограничения

b-j1 = 0, b-j2 = 0, j = 1,J.

(57)

Равенства (56), (57) и формула (19) для Φ, в частности, означают, что b+j0 = u₀(P^j ).

Поскольку стержни прикреплены к пластине, логично наложить условия

u₀(P^j) = b+j0 = u_j(0), j = 1,J.

(58)

При учёте требований (56)-(58) выберем следующие подпространства в ортогональном раз-

ложении из теоремы 1:

R⁰ = {0}, R⁺ = {c = (c₁,... ,c7J )^т ∈ R6J+J : c6(j-1)+1 = c6J+p+1, j = 1,J},

R^- = R6J+j ⊖ R⁺ = {c ∈ R6J+J : c6(j-1)+1 + c6J+j+1 = 0,

c6(j-1)+p = 0, p = 2,6, j = 1,J}.

(59)

Согласно определениям (49) и (50) включение π⁺U ∈ R⁺ гарантирует выполнение равенств

(58), а включение π^-U ∈ R^- - равенств (56), (57), а также соотношения

b-j0 = -π^-jU = D_j∂zj u_j(0), j = 1,J,

означающего обращение в нуль суммы сил, приложенных к точкам P^j присоединения одно-

мерных стержней Υ^j к двумерной пластине Ω.

Лемма 2. Для вектор-функций U, V из пространства (54), построенного по ортого-

нальному разложению (59) пространства R6J+J , справедлива формула

∑

〈A_•U, V 〉_H = E(u₀, v₀; Ω) +

D_j(∂zj u_j,∂zj v_j)Υj .

(60)

j=1

Доказательство. Поскольку условия (56) и (57) оставляют отделёнными в представле-

нии компонент u₀ и v₀ только полиномы и само фундаментальное решение, справедливы

включения u₀, v₀ ∈ H²(Ω). Таким образом, верны формулы (вторые очевидны)

∑

(Δ2xu₀, v₀)_Ω = E(u₀, v₀; Ω) +

b-uj0v₀(P^j),

(61)

j=1

(-D_j ∂2z

u_j,v_j)Υj = D_j(∂zj u_j,∂zj v_j)Υj + D_j∂zj u_j(0), j = 1,J.

Почленно сложим указанные равенства и при учёте условий сопряжения, назначенных соглас-

но определениям (54) и (59), получим соотношение (60). Лемма доказана.

Теорема 2. Самосопряжённое расширение A_• оператора A с областью определения (54),

найденной по ортогональному разложению (59) пространства R6J+J , является положи-

тельно определённым оператором лишь в случае 3^◦ из п. 2.

Доказательство. Применим формулу (60) с V = U. В силу условий Дирихле (4) имеем

|u_j(0)|² + ∥u_j ; L²(0, l_j )∥² ≤ c_j ∥∂zj u_j ; L²(0, l_j )∥².

(62)

Для функции u₀ напишем представление

u₀(x) = u_⊥(x) + ℓ₀ + ℓ₁x₁ + ℓ₂x₂,

(63)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

9^∗

712

НАЗАРОВ

а коэффициенты ℓ_q линейной функции ℓ из (63) выберем так, чтобы выполнялись равенства

∫

∂u_⊥

u_⊥(x)dx = 0,

(x) dx = 0, j = 1, 2.

(64)

∂x_j

Вследствие формул (6) и (12) неравенства Пуанкаре, опирающиеся на условия ортогонально-

сти (64), показывают, что справедливы оценки

E(u₀, u₀; Ω) = E(u_⊥, u_⊥; Ω) ≥ c₁∥∇_xu_⊥; L²(Ω)∥² ≥ c₀∥u_⊥; L²(Ω)∥², c₀ > 0.

Следовательно,

|u_⊥(P^j )|² ≤ C∥u_⊥; H²(Ω)∥² ≤ CE(u₀, u₀; Ω).

(65)

Кроме того, в силу соотношений (63) и (58) получаем, что

|ℓ(P^j )| = |u₀(P^j ) - u_⊥(P^j )| ≤ |u_j (0)| + |u_⊥(P^j )| ≤

≤ C(∥∂zju_j;L²(Υ^j)∥ + ∥u_⊥;H²(Ω)∥), j = 1,J.

(66)

Как указано в комментариях к формуле (31), в случае 3^◦ оценки (66) гарантируют такое

неравенство для линейной функции:

(

)

∑

∥ℓ; L²(Ω)∥² ≤ c(|ℓ₀|² + |ℓ₁|² + |ℓ₂|²) ≤ c E(u₀, u₀; Ω) +

∥∂zj u_j;L2(Υj)∥2

j=1

Оно вместе с формулами (62) и (65) приводит к нужному неравенству

∥U; H²∥² ≤ c〈A_•U, U〉_H

(см. определение (8)).

В ситуациях 1^◦ или 2^◦ подстановка в соотношение (60) пробной вектор-функции U =

= (ℓ, 0, . . . , 0), где ℓ - какой-то элемент линейного множества (13) или (14), показывает, что

форма 〈A^•U, U〉_H вырождается. Теорема доказана.

Введённые точечные условия (58), (59) и (56), (57) локальные: стержни взаимодействуют

только через упругую пластину. Между тем можно соорудить механизм из стрингеров (абсо-

лютно жёстких тонких стержней), выравнивающий прогибы пластины в точках P¹, . . . , P^K

(перенумеровали при необходимости). В такой конструкции (см. рис. 1, б) связи (58) дополня-

ются равенствами

b⁺¹⁰ = ... = b+K0,

(67)

и соответственно подпространства в разложении из теоремы 1 выглядят следующим образом:

P⁺ = {c ∈ R6J+J : c₁ = c6k+1, k = 1,K - 1, c6(j-1)+1 = c6J+j, j = 1,J},

P⁰ = {0}, P^- = R6J+J ⊖ P⁺.

(68)

Включение π^-U ∈ P^- обеспечивает выполнение равенств

∑

(b-k0 - D_k∂_z

u_k(0)) = 0, b-j0 = D_j∂zj u_j(0), j = K + 1,J.

k=1

В случае K = J соотношения (58), (67) и (68) представляют собой не что иное, как клас-

сические условия сопряжения Кирхгофа. При любом K ∈ [1, J] ортогональное разложение

(68) пространства R6J+J порождает самосопряжённое расширение оператора A с областью

определения (54) и энергетической билинейной формой (60).

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

713

6. Нелинейные задачи. В этом пункте полное исследование сформулированных задач

проводить не будем, а ограничимся только рассмотрением деформации пластины под дей-

ствием силы тяжести (f₀(x) = -f_grav с положительной постоянной f_grav), причём стержни

считаем невесомыми (f_j = 0).

Пусть пластина Ω опирается на абсолютно жёсткие стержни (рис. 2, а). Отрицательные

величины прогиба пластины в точках P¹, . . . , P^J невозможны, и поэтому задача о минимуме

функционала полной (упругой плюс потенциальной) энергии пластины

J_△(u₀) =

E(u₀, u₀; Ω) - (f₀, u₀)_Ω

(69)

ставится на выпуклом замкнутом конусе

H2△(Ω;P) = {u₀ ∈ H²(Ω) : u₀(P^j) ≥ 0, j = 1,J}

(70)

и оказывается эквивалентной вариационному неравенству [31]

E(u₀, v₀ - u₀; Ω) - (f₀, v₀ - u₀)_Ω ≥ 0 для любой v₀ ∈ H2△(Ω; P).

(71)

Обобщённая формула Грина (61) показывает, что при j = 1, J верны импликации

u₀(P^j) > 0

⇒ b-j0 = 0 и u₀(P^j) = 0

⇒ b-j0 > 0,

(72)

представляющие собой математически строгое истолкование механических ограничений.

(а)

(б)

Рис. 2. Пластины: опёртая (а) и подвешенная (б). Присоеди-

нённые концы стержней помечены значком •, а отсоединён-

ные - значком ◦. Ослабленный канат - волнистая линия.

Сформулируем ещё одну задачу, сводящуюся к бигармоническому уравнению с нелиней-

ным возмущением, а именно, задачу о деформации плиты Ω, подвешенной на невесомых

эластичных канатах, которые воздействуют на плиту только в случае растяжения, т.е. при

u₀(P^j) < 0, но в случае u₀(P^j) ≥ 0 канат “провисает” (ср. рис. 2, б), и поэтому сосредоточен-

ная в точке P^j сила равна нулю (b^-j = 0). Однородная (f_j = 0) задача (3), (4) с краевым

условием u_j (0) = [u₀(P^j )]_- решается явно: из того, что u_j(z_j ) = [u₀(P^j )]_-l-1j(l_j - z_j ) следует

равенство b^-j = -π^j-u_j = D_j l-1j[u₀(P^j )]_-. Здесь [t]_- = (t - |t|)/2 - отрицательная часть числа

t ∈ R. Итак, заменив воздействия стержней сосредоточенными силами с интенсивностью b-j ,

приходим к уравнению

∑

Δ2xu₀(x) - D_jl-1j[u₀(P^j)]_-δ(x - P^j) = f₀(x), x ∈ Ω,

(73)

j=1

снабжённому краевыми условиями (3). В силу обобщённой формулы Грина (ср. леммы 1 и 2)

вариационная формулировка задачи (73), (3) принимает вид

∑

E(u₀, v₀; Ω) -

D_jl-1j[u₀(P^j)]_-[v₀(P^j)] = (f₀,v₀)_Ω для любой v₀ ∈ H²(Ω).

(74)

j=1

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

714

НАЗАРОВ

Замечание 6. Если часть Σ = ∅ кромки Γ пластины Ω жёстко защемлена, т.е. условия

Неймана (2) заменены смешанными краевыми условиями

N^q(x,∇_x)u₀(x) = 0, x ∈ Γ \ Σ, q = 2,3, и u₀(x) = ∂_nu₀(x), x ∈ Σ,

(75)

то ввиду неравенства

∥u₀; H²(Ω)∥² ≤ cE(u₀, u₀; Ω),

(76)

обеспеченного условиями Дирихле на Σ, однозначная разрешимость обеих задач (71) и (74),

(75) вытекает из базовых результатов выпуклого анализа (см., например, теоремы 2.1 и 2.2

из [32, гл. 1]). Упомянем работу [18], в которой проводился аналогичный анализ задачи о

мембране с препятствиями на исчезающе малых множествах.

В случае полностью свободной кромки Γ и условий Неймана на ней неравенство (76) на-

рушено для линейных функций, и для проверки разрешимости задач требуются несколько до-

полнительных требований. Пусть, во-первых, выполнено ограничение 3^◦ из п. 2 и, во-вторых,

центр тяжести плиты находится во внутренности int P_span выпуклой оболочки P_span множе-

ства P = {P¹, . . . , P^J } точек крепления. Совместим начало координат O с этим центром,

обеспечив тем самым равенства

∫

x_j dx = 0, j = 1,2.

(77)

Воспользуемся обозначениями из п. 2 и будем искать решение задачи (71) в виде

∑

u₀(x) =

a_jG_j(x) + ℓ(x).

(78)

j=1

Столбец l коэффициентов линейной функции ℓ и столбец a множителей при функциях

Грина (см. формулы (21)-(24)) являются неизвестными. При этом согласно определениям (49)

столбцы π-0u₀ = a и π⁺⁰u₀ = u₀ = (u₀(P¹), . . . , u₀(P^J ))^т имеют вид

π-0u₀ = a ≥ 0 и u₀ = Ga + P^тl ≥ 0.

(79)

При этом формула a ≥ 0 означает, что a_j ≥ 0, j = 1, J. Таким образом, импликации (72)

превращаются в следующие:

(Ga + P^тl)_j > 0

⇒ a_j =0

и (Ga + P^тl)_j = 0

⇒ a_j ≥ 0.

(80)

В силу равенств (77) матрица Грама (25) является блочно-диагональной, т.е. M₀₀ = |Ω| и

M₀₁ = M₀₂ = 0. Поэтому для соблюдения уравнения (1) в проколотой области Ω\P требуется,

чтобы выполнялось равенство La = f₀e₍₀₎ ∈ R³, которое, очевидно, равносильно равенству

Pa = f := |Ω|f₀e₍₀₎,

(81)

здесь и выше P и L - 3 × J-матрицы (26) и e₍₀₎ = (1, 0, 0)^т. Зафиксируем какой-то столбец

a^f , удовлетворяющий соотношениям (81), и назначим a⁰ = a - a^f новой неизвестной.

По стандартной схеме (см., например, монографии [31, 32]) соотношения (80) и (81) порож-

дают вариационное неравенство

(Ga⁰ + F)(b⁰ - a⁰) ≥ 0 для любого b⁰ ∈ K,

(82)

включающее слагаемое F = Ga^f и поставленное на выпуклом замкнутом конусе

K = {b⁰ ∈ R^J : b0j ≥ -afj, j = 1,J, Pb⁰ = 0 ∈ R^J}.

(83)

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

МОДЕЛИ УПРУГОГО СОЧЛЕНЕНИЯ

715

Благодаря последнему условию в (83) слагаемое P^тl, входящее в (80), исчезло из (83). Тре-

бование O ∈ int P_span означает, что множество (83) не пусто. Наконец, задача (80) сводится к

задаче о минимизации функционала

K ∋ a⁰ → J(a⁰) =

(a⁰)^тGa⁰ + (a⁰)^тF.

(84)

Поскольку G - симметричная положительно определённая J × J-матрица, задача о миними-

зации функционала (84) и задача (82) могут быть решены при помощи базовых результатов

выпуклого анализа (см., например, теоремы 2.1 и 2.2 из монографии [32, гл. 1]).

Теорема 3. При указанных ограничениях задача (71) имеет единственное решение u₀ ∈

∈ H2△(Ω). Оно представимо в виде линейной комбинации (78), в которой столбец коэффициен-

тов a⁰ находится как решение вариационного неравенства (82), а коэффициенты l линейной

функции ℓ восстанавливаются при помощи формулы (80), так как ранг матрицы P равен

трём.

Обратимся к задаче (74), решение которой по-прежнему ищем в виде (78). Формулы (79)

и (81) сохраняют силу, а множители при функциях Грина в линейной комбинации (78) и

множители при дельта-функциях в уравнении (74) связаны соотношением

D-1a = -[Ga + P^тl]_-,

(85)

где D - диагональная матрица diag {l-11D₁, . . . , l-1JD_J }. Очевидно, что компоненты a_j реше-

ния a системы (85), (81) неотрицательные. Следовательно, накладывая ограничение a ≥ 0,

приходим к равенству D-1a + P^тl = -Ga, из которого следует, что Ga + P^тl ≤ 0. В итоге,

используя частное решение a^f уравнения (81) и переходя к новой неизвестной a⁰ = a - a^f ,

получаем уравнение

(D-1 + G)a⁰ + Pl = F := -Ga^f - D-1a^f на K,

которое эквивалентно задаче о минимизации на конусе (83) функционала (84) с симметрич-

ной положительно определённой матрицей D-1 + G на месте матрицы G. Итак, по тем же

причинам, что и выше, справедлива

Теорема 4. При перечисленных геометрических ограничениях задача (74), (2) имеет

единственное решение u₀ ∈ H²(Ω), которое находится в виде (78) как решение алгебраи-

ческих задач по указанной схеме.

Приведём пояснения к введённым ограничениям. Допустим, что включение O ∈ P_span не

выполнено и точки P¹, . . . , P^J лежат в полуплоскости R²⁺ = {x : x₁ > 0}. Тогда конус (70)

содержит линейную функцию ℓ_K (x) = K(x₁ - L) при 2L = min{P¹¹, . . . , PJ1 } > 0 и любом

K > 0. При этом в силу формул (78) и (6) функционал (69) удовлетворяет соотношению

J_△(ℓ) = 0 - (f₀,ℓ)_Ω = -f_grav|Ω|KL → -∞ при K → +∞,

т.е. задача (71) неразрешима. На практике этот факт очевиден: пластина сваливается с опор,

если центр тяжести лежит вне множества P_span. Если O ∈ ∂P_span или нарушено требо-

вание 3◦, а значит, int Pspan = ∅, то положение пластины Ω на опорах неустойчивое, а

применение приближённой двумерной модели неправомерно - необходим учёт малых сечений

стержней и, весьма возможно, сил трения.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных ис-

следований (проект 18-01-00325).

СПИСОК ЛИТЕРАТУРЫ

1. Бирман М.Ш. O вариационном методе Треффца для уравнения Δ²u = f // Докл. АН СССР. 1955.

Т. 101. № 2. С. 201-204.

2. Михлин С.Г. Вариационные методы в математической физике. М., 1970.

3. Назаров С.А. Асимптотическая теория тонких пластин и стержней. Понижение размерности и ин-

тегральные оценки. Новосибирск, 2002.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021

716

НАЗАРОВ

4. Березин Ф.А., Фаддеев Л.Д. Замечание об уравнении Шредингера с сингулярным потенциалом

// Докл. АН СССР. 1961. Т. 137. № 5. С. 1011-1014.

5. Демков Ю.Н., Островский В.Н. Метод потенциалов нулевого радиуса в атомной физике. Л., 1975.

6. Капешина Ю.Е., Павлов Б.С. Взаимодействия нулевого радиуса для бигармонического и полигар-

монического уравнений // Мат. заметки. 1986. Т. 40. № 1. С. 49-59.

7. Павлов Б.С. Теория расширений и явно решаемые модели // Успехи мат. наук. 1987. Т. 42. № 6.

С. 99-131.

8. Exner P.,

Šeba P. Applications of self-adjoint extensions in quantum physics // Lect. Not. in Phys.

V. 324. Heidelberg, 1989.

9. Назаров С.А. Самосопряженные расширения оператора задачи Дирихле в весовых функциональ-

ных пространствах // Мат. сб. 1988. Т. 137. № 2. С. 224-241.

10. Назаров С.А. Асимптотические условия в точках, самосопряженные расширения операторов и ме-

тод сращиваемых асимптотических разложений // Тр. Санкт-Петербургского мат. о-ва. 1996. Т. 5.

С. 112-183.

11. Назаров С.А. Эллиптические задачи на гибридных областях // Функц. анализ и его приложения.

2004. Т. 38. № 4. С. 55-72.

12. Brüning J., Geyler V., Pankrashkin K. Spectra of self-adjoint extensions and applications to solvable

Schrödinger operators // Rev. in Math. Phys. 2008. V. 20. P. 1-70.

13. Назаров С.А. Моделирование сингулярно возмущённой спектральной задачи при помощи самосо-

пряженных расширений операторов предельных задач // Функц. анализ и его приложения. 2015.

Т. 49. № 1. С. 31-48.

14. Соболев С.Л. Некоторые применения функционального анализа в математической физике. М., 1988.

15. Adams R. Sobolev Spaces. New York, 1976.

16. Петропавловский А.А. Вантовые мосты. М., 1985.

17. Gazzola A. Mathematical Models for Suspension Bridges. Nonlinear Structural Instability. Modeling,

Simulation and Applications. V. 15. Berlin, 2015.

18. Назаров С.А. Асимптотическое решение задачи с малыми препятствиями // Дифференц. уравне-

ния. 1995. Т. 31. № 6. С. 1031-1041.

19. Владимиров В.С. Обобщенные функции в математической физике. М., 1979.

20. Хёрмандер Л. Линейные дифференциальные операторы с частными производными. М., 1965.

21. Кондратьев В.А. Краевые задачи для эллиптических уравнений в областях с коническими или

угловыми точками // Тр. Московского мат. об-ва. 1963. Т. 16. С. 219-292.

22. Nazarov S.A., Plamenevsky B.A. Elliptic Problems in Domains with Piecewise Smooth Boundaries.

Berlin, New York, 1994.

23. Pazy A. Asymptotic expansions of solutions of ordinary differential equations in Hilbert space // Arch.

Rational Mech. Anal. 1967. V. 24. P. 193-218.

24. Назаров С.А. Полиномиальное свойство самосопряжённых эллиптических краевых задач и алгеб-

раическое описание их атрибутов // Успехи мат. наук. 1999. Т. 54. № 5. С. 77-142.

25. Арутюнян Н.Х., Назаров С.А., Шойхет Б.А. Оценки и асимптотика напряженно-деформирован-

ного состояния трехмерного тела с трещиной в теории упругости и теории ползучести // Докл. АН

СССР. 1982. Т. 266. № 6. С. 1365-1369.

26. Назаров С.А., Пламеневский Б.А. Задача Неймана для самосопряженных эллиптических систем в

области с кусочно гладкой границей // Тр. Ленинградского мат. об-ва. 1990. Т. 1. С. 174-211.

27. Ладыженская О.А. Краевые задачи математической физики. М., 1973.

28. Лионс Ж.-Л., Мадженес Э. Неоднородные граничные задачи и их приложения. М., 1971.

29. Мазья В.Г., Пламеневский Б.А. О коэффициентах в асимптотике решений эллиптических краевых

задач в области с коническими точками // Math. Nachr. 1977. Bd. 76. S. 29-60.

30. Рофе-Бекетов Ф.С. Самосопряженные расширения дифференциальных операторов в пространстве

вектор-функций // Докл. АН СССР. 1969. Т. 184. С. 1034-1037.

31. Дюво Г., Лионс Ж.-Л. Неравенства в механике и физике. М., 1980.

32. Гловински Р., Лионс Ж.-Л., Тремольер Р. Численное исследование вариационных неравенств М.,

1979.

Институт проблем машиноведения РАН,

Поступила в редакцию 09.12.2020 г.

г. Санкт-Петербург

После доработки 09.12.2020 г.

Принята к публикации 15.04.2021 г.

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ том 57

№5

2021